-
The level structures of nuclei near the Z = 38 semimagic and N = 50 magic shells have been the focus of experimental and theoretical research in recent years [1-9]. A number of interesting phenomena, such as single-particle excitation [3-8], isomeric states [8-12], collective rotation [13, 14], and core breaking [15-18], have been reported in this mass region. The level structures of Zr, Nb, and Tc isotones around
$ N = 50 $ have been extended to higher spins and are well described by the shell model [16-19]. The research has shown that the low-lying states are dominated by the particle-hole excitations from the$ \pi $ $ p_{1/2} $ orbital into the$ \pi $ $ g_{9/2} $ orbital. In contrast, the higher level structures can be interpreted via the multi-particle excitations in a larger configuration space, where even the excitation of the core has to be considered. However, there are relatively few studies on the neighboring Mo isotopes around the N = 50 magic shell closure, especially on the N = 51 nucleus$ ^{93} $ Mo.The previous theoretical studies on the
$ ^{93} $ Mo nucleus have largely focused on several low-lying levels using a small truncation space, i.e., they have ignored certain orbitals, such as the proton 1$ f_{5/2} $ [8] and neutron 1$ g_{9/2} $ [8, 20] and 1$ h_{11/2} $ [20] orbitals. Nevertheless, these orbitals play an important role in the neighboring N = 51 isotones, where the excited states are principally generated via three different mechanisms: (a) (1$ f_{5/2} $ , 2$ p_{3/2} $ , 2$ p_{1/2} $ )$ \rightarrow $ 1$ g_{9/2} $ proton excitations, (b) 1$ g_{9/2} $ $ \rightarrow $ 2$ d_{5/2} $ neutron-core excitation, and (c) 2$ d_{5/2} $ $ \rightarrow $ 1$ h_{11/2} $ neutron excitation [15-23]. Thus, to adequately describe the level structures of$ ^{93} $ Mo, the proton 1$ f_{5/2} $ and neutron (1$ g_{9/2} $ , 1$ h_{11/2} $ ) orbitals must be considered in the calculations. Large scale shell model calculations that account for these orbitals were therefore performed to investigate the origin and components of the excited states in$ ^{93} $ Mo. Moreover, although$ ^{93} $ Mo has been observed up to higher excitation energies of approximately 10 MeV [9], due to the limitations of the experimental conditions, the spin-parity assignments of the higher-lying states remain indefinite. It was thus necessary to predict the multipolarities of the higher-spin states in$ ^{93} $ Mo theoretically. -
The level structures of
$ ^{93} $ Mo were investigated using large scale shell model calculations with the NUSHELLX code [24]. The SNE model space and SNET interactions were adopted in the code; the model space included eight proton orbitals (1$ f_{5/2} $ , 2$ p_{3/2} $ , 2$ p_{1/2} $ , 1$ g_{9/2} $ , 1$ g_{7/2} $ , 2$ d_{5/2} $ , 2$ d_{3/2} $ , 3$ s_{1/2} $ ) and nine neutron orbitals (1$ f_{5/2} $ , 2$ p_{3/2} $ , 2$ p_{1/2} $ , 1$ g_{9/2} $ , 1$ g_{7/2} $ , 2$ d_{5/2} $ , 2$ d_{3/2} $ , 3$ s_{1/2} $ , 1$ h_{11/2} $ ) relative to an inert$ ^{56} $ Ni (Z = 28, N = 28) core. The single-particle energies relative to the$ ^{56} $ Ni core were set as$ \varepsilon^{\pi}_{1f_{5/2}} $ = 0.525 MeV,$ \varepsilon^{\pi}_{2p_{3/2}} $ = 1.228 MeV,$ \varepsilon^{\pi}_{2p_{1/2}} $ = 5.106 MeV,$ \varepsilon^{\pi}_{1g_{9/2}} $ = 5.518 MeV,$ \varepsilon^{\pi}_{1g_{7/2}} $ = 20.656 MeV,$ \varepsilon^{\pi}_{2d_{5/2}} $ = 18.893 MeV,$ \varepsilon^{\pi}_{2d_{3/2}} $ = 20.016 MeV,$ \varepsilon^{\pi}_{3s_{1/2}} $ = 16.895 MeV,$ \varepsilon^{\nu}_{1f_{5/2}} $ = 0 MeV,$ \varepsilon^{\nu}_{2p_{3/2}} $ = 0 MeV,$ \varepsilon^{\nu}_{2p_{1/2}} $ = 0 MeV,$ \varepsilon^{\nu}_{1g_{9/2}} $ = 0 MeV,$ \varepsilon^{\nu}_{1g_{7/2}} $ = 4.352 MeV,$ \varepsilon^{\nu}_{2d_{5/2}} $ = 2.313 MeV,$ \varepsilon^{\nu}_{2d_{3/2}} $ = 3.440 MeV,$ \varepsilon^{\nu}_{3s_{1/2}} $ = 1.532 MeV, and$ \varepsilon^{\nu}_{1h_{11/2}} $ = -0.589 MeV. These single-particle energies and the corresponding strengths of the residual interactions were used to calculate the level energies [17, 24]. -
The
$ ^{93} $ Mo nucleus has 14 valence protons and 23 valence neutrons in the configuration space. Due to the large dimensionality of the matrices involved, truncations were employed to make the calculations feasible. To employ an appropriate truncation, we examined the contribution of proton excitation across the Z = 50 shell closure with two sets of shell model calculations, SM1 and SM1*. For SM1, the valence proton space was restricted to$ \pi $ ($ 1f_{5/2}^{4-6} $ ,$ 2p_{3/2}^{3-4} $ ,$ 2p_{1/2}^{0-2} $ ,$ 1g_{9/2}^{2-5} $ ,$ 1g_{7/2}^{0-0} $ ,$ 2d_{5/2}^{0-0} $ ,$ 2d_{3/2}^{0-0} $ ,$ 3s_{1/2}^{0-0} $ ). Simultaneously, only a single$ 1g_{9/2} $ neutron was allowed to be excited across the N = 50 closed shell. Considering the distance of the$ 2d_{3/2} $ and$ 3s_{1/2} $ orbitals from the Fermi surface, no neutrons were allowed to be excited to these orbitals. On the basis of the SM1 truncation, in SM1* an additional proton was considered across the Z = 50 core into the 2$ d_{5/2} $ orbital. The excitation energies for the positive and negative parity states of$ ^{93} $ Mo obtained from the SM1 and SM1* calculations are shown in Fig. 1 and Fig. 2, respectively, in comparison with the experimental values taken from Refs. [9, 25, 26] . As evident in Figs. 1 and 2, the predicted energies in SM1 and SM1* are very similar. Moreover, the calculated occupation number of protons in the 2$ d_{5/2} $ orbital above the Z = 50 core is small with a value of 0.0$ \sim $ 0.1, indicating a small contribution from proton excitation beyond Z = 50 to the states presented in Figs. 1 and 2. Meanwhile, the calculated energies in SM1, excluding proton excitation beyond the Z = 50 core, are closer to the experimental values than the calculated energies in SM1*. Hence, proton excitation across the Z = 50 shell closure is not accounted for in the subsequent SM2 calculations.
Figure 1. Comparison of the experimental and calculated energy levels of the positive-parity states in
$^{93}$ Mo within SM1 and SM2 configuration spaces.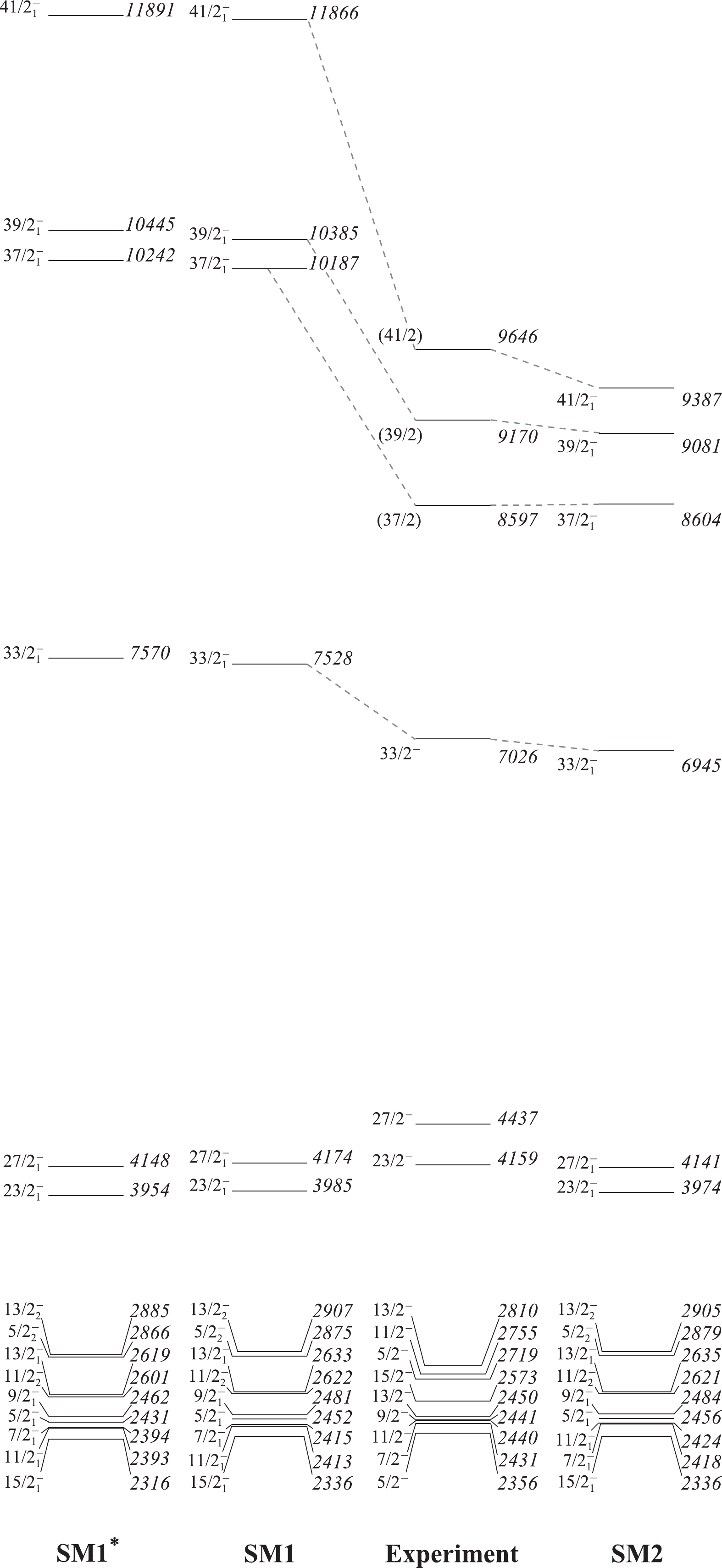
Figure 2. Comparison of the experimental and calculated energy levels of the negative-parity states in
$^{93}$ Mo within the SM1 and SM2 configuration spaces.SM2 used the same proton configuration space as SM1, and on the basis of the neutron configuration space of SM1, in SM2, excitation of the valence neutron across the N = 56 subshell closure into the higher-lying
$ 1h_{11/2} $ orbital was allowed. The excitation energies for the positive and negative parity states of$ ^{93} $ Mo obtained from the SM2 calculations are also presented in Fig. 1 and Fig. 2, respectively. The main partitions of the wave function for each state within SM1 and SM2 are presented in Table 1; they are characterized by two main configurations with larger contributions.$I^{\pi}\;(\hbar)$ 

$E_{(\rm exp)}$ /keV

SM1 SM2 $E_{(\rm cal)}$ /keV

wave function $\pi\otimes\nu$ 

partitions (%) $E_{(\rm cal)}$ /keV

wave function $\pi \otimes\nu $ 

partitions (%) $1/2_{1}^{+}$ 

943 1342 6 4 2 2 $\otimes$ 2 10 1 0

64.51 1334 6 4 2 2 $\otimes$ 2 10 1 0

64.21 6 4 0 4 $\otimes$ 2 10 1 0

25.30 6 4 0 4 $\otimes$ 2 10 1 0

25.44 $1/2_{2}^{+}$ 

2437 2753 6 4 0 4 $\otimes$ 2 10 1 0

41.80 2752 6 4 0 4 $\otimes$ 2 10 1 0

41.73 6 4 2 2 $\otimes$ 2 10 1 0

27.70 6 4 2 2 $\otimes$ 2 10 1 0

27.90 $3/2_{1}^{+}$ 

1492 1721 6 4 2 2 $\otimes$ 2 10 1 0

59.79 1718 6 4 2 2 $\otimes$ 2 10 1 0

59.55 6 4 0 4 $\otimes$ 2 10 1 0

26.50 6 4 0 4 $\otimes$ 2 10 1 0

26.53 $3/2_{2}^{+}$ 

2181 2523 6 4 2 2 $\otimes$ 2 10 1 0

67.84 2523 6 4 2 2 $\otimes$ 2 10 1 0

67.63 6 4 0 4 $\otimes$ 2 10 1 0

23.35 6 4 0 4 $\otimes$ 2 10 1 0

23.38 $5/2_{1}^{+}$ 

0 0 6 4 2 2 $\otimes$ 2 10 1 0

59.01 0 6 4 2 2 $\otimes$ 2 10 1 0

58.92 6 4 0 4 $\otimes$ 2 10 1 0

30.26 6 4 0 4 $\otimes$ 2 10 1 0

30.25 $5/2_{2}^{+}$ 

1695 1443 6 4 2 2 $\otimes$ 2 10 1 0

55.40 1443 6 4 2 2 $\otimes$ 2 10 1 0

55.33 6 4 0 4 $\otimes$ 2 10 1 0

24.87 6 4 0 4 $\otimes$ 2 10 1 0

24.95 $5/2_{3}^{+}$ 

2142 1643 6 4 2 2 $\otimes$ 2 10 1 0

43.21 1647 6 4 2 2 $\otimes$ 2 10 1 0

42.84 6 4 0 4 $\otimes$ 2 10 1 0

24.43 6 4 0 4 $\otimes$ 2 10 1 0

25.23 $5/2_{4}^{+}$ 

2398 2439 6 4 2 2 $\otimes$ 2 10 1 0

66.75 2437 6 4 2 2 $\otimes$ 2 10 1 0

66.23 6 4 0 4 $\otimes$ 2 10 1 0

22.22 6 4 0 4 $\otimes$ 2 10 1 0

22.46 $7/2_{1}^{+}$ 

1363 1230 6 4 2 2 $\otimes$ 2 10 1 0

58.13 1229 6 4 2 2 $\otimes$ 2 10 1 0

58.14 6 4 0 4 $\otimes$ 2 10 1 0

25.41 6 4 0 4 $\otimes$ 2 10 1 0

24.48 $7/2_{2}^{+}$ 

1520 2066 6 4 2 2 $\otimes$ 2 10 1 0

34.76 2070 6 4 2 2 $\otimes$ 2 10 1 0

34.45 6 4 0 4 $\otimes$ 2 10 1 0

23.88 6 4 0 4 $\otimes$ 2 10 1 0

24.00 $7/2_{3}^{+}$ 

2479 2536 6 4 2 2 $\otimes$ 2 10 1 0

68.22 2536 6 4 2 2 $\otimes$ 2 10 1 0

67.93 6 4 0 4 $\otimes$ 2 10 1 0

20.72 6 4 0 4 $\otimes$ 2 10 1 0

20.82 $9/2_{1}^{+}$ 

1477 1410 6 4 2 2 $\otimes$ 2 10 1 0

61.43 1410 6 4 2 2 $\otimes$ 2 10 1 0

61.37 6 4 0 4 $\otimes$ 2 10 1 0

25.11 6 4 0 4 $\otimes$ 2 10 1 0

25.09 $9/2_{2}^{+}$ 

2409 2478 6 4 2 2 $\otimes$ 2 10 1 0

61.41 2479 6 4 2 2 $\otimes$ 2 10 1 0

60.86 6 4 0 4 $\otimes$ 2 10 1 0

22.19 6 4 0 4 $\otimes$ 2 10 1 0

22.32 $11/2_{1}^{+}$ 

2247 2137 6 4 2 2 $\otimes$ 2 10 1 0

73.06 2135 6 4 2 2 $\otimes$ 2 10 1 0

72.95 6 4 0 4 $\otimes$ 2 10 1 0

17.41 6 4 0 4 $\otimes$ 2 10 1 0

17.40 $13/2_{1}^{+}$ 

2162 2164 6 4 2 2 $\otimes$ 2 10 1 0

72.85 2161 6 4 2 2 $\otimes$ 2 10 1 0

72.54 6 4 0 4 $\otimes$ 2 10 1 0

18.62 6 4 0 4 $\otimes$ 2 10 1 0

18.70 $13/2_{2}^{+}$ 

2668 2902 6 4 2 2 $\otimes$ 2 10 1 0

60.38 2901 6 4 2 2 $\otimes$ 2 10 1 0

59.55 6 4 0 4 $\otimes$ 2 10 1 0

27.87 6 4 0 4 $\otimes$ 2 10 1 0

28.23 $15/2_{1}^{+}$ 

2642 2861 6 4 2 2 $\otimes$ 2 10 1 0

59.21 2859 6 4 2 2 $\otimes$ 2 10 1 0

59.06 6 4 0 4 $\otimes$ 2 10 1 0

29.04 6 4 0 4 $\otimes$ 2 10 1 0

29.08 $17/2_{1}^{+}$ 

2430 2830 6 4 2 2 $\otimes$ 2 10 1 0

30.95 2830 6 4 2 2 $\otimes$ 2 10 1 0

30.95 6 4 0 4 $\otimes$ 2 10 1 0

25.51 6 4 0 4 $\otimes$ 2 10 1 0

25.28 $21/2_{1}^{+}$ 

2425 2312 6 4 2 2 $\otimes$ 2 10 1 0

73.32 2309 6 4 2 2 $\otimes$ 2 10 1 0

73.09 6 4 0 4 $\otimes$ 2 10 1 0

19.51 6 4 0 4 $\otimes$ 2 10 1 0

19.52 Continued on next page Table 1. Main partitions of the wave functions for
$^{93}$ Mo in the SM1 and SM2 configuration spaces. The wave function for a particular angular momentum state is composed of several partitions. Each partition is of the form$P = \pi[p(1), p(2), p(3), p(4)]$ $\otimes$ $\nu[n(1), n(2), n(3), n(4)]$ , where$p(i)$ represents the number of valence protons occupying the$1f_{5/2}$ ,$2p_{3/2}$ ,$2p_{1/2}$ , and$1g_{9/2}$ orbitals, and$n(j)$ represents the number of valence neutrons in the$2p_{1/2}$ ,$1g_{9/2}$ ,$2d_{5/2}$ , and$1h_{11/2}$ orbitals.The
$ I^{\pi} $ = 5/2$ ^{+} $ ground state is predominantly generated by the coupling of a 1$ g_{9/2} $ proton pair and an unpaired neutron in the 2$ d_{5/2} $ orbital. The state with an energy of 1363 keV may correspond to the predicted 7/2$ _{1}^{+} $ state, which is consistent with the observed result in Ref. [25]. As presented in Table 1, the dominating contributions to the 1/2$ ^{+} $ , 3/2$ ^{+} $ , 7/2$ ^{+} $ , 9/2$ ^{+} $ , 11/2$ ^{+} $ , 13/2$ ^{+} $ , 15/2$ ^{+} $ , 17/2$ ^{+} $ , and 21/2$ ^{+} $ states obtained in the shell model arise from the$ \pi(1g_{9/2})^{2} $ $ \otimes $ $ \nu(2d_{5/2}) $ configurations, mixed with the$ \pi(1g_{9/2})^{4} $ $ \otimes $ $ \nu(2d_{5/2}) $ , i.e., a proton pair is excited from the completely filled 2$ p_{1/2} $ orbital across the Z = 40 subshell closure into the 1$ g_{9/2} $ orbital. The calculations predict that the 25/2$ ^{+} $ and 29/2$ ^{+} $ yrast states involve the same neutron configurations as the ground state 5/2$ _{1}^{+} $ and have the$ \pi(1g_{9/2})^{4} $ proton configuration. For the observed I = (35/2) state at 7268 keV, the parity was not assigned, due to the weak experimental statistics in previous work [9]. The present large scale shell model calculations show that the predicted energy is much closer to the experimental value with positive parity rather than negative parity. Thus, the I = (35/2) state is tentatively suggested to be a positive parity state, i.e., 35/2$ _{1}^{+} $ . The 35/2$ _{1}^{+} $ state could be interpreted as$ \pi[(1f_{5/2})^{-1}(2p_{1/2})^{1}(1g_{9/2})^{4}] $ $ \otimes $ $ \nu(2d_{5/2}) $ , involving excitations of a 2$ p_{1/2} $ proton pair across the Z = 40 closed subshell into the 1$ g_{9/2} $ orbital and an unpaired 1$ f_{5/2} $ proton across the Z = 38 subshell into the 2$ p_{1/2} $ orbital. Furthermore, the 35/2$ _{1}^{+} $ state also includes proton excitation from the completely filled 2$ p_{3/2} $ orbital to the 2$ p_{1/2} $ orbital, leading to the configuration$ \pi[(1f_{5/2})^{-1} (2p_{3/2})^{-1}(1g_{9/2})^{4}] $ $ \otimes $ $ \nu(2d_{5/2}) $ . As shown in Fig. 1, the predicted excitation energies from the ground state 5/2$ ^{+} $ to the 35/2$ _{1}^{+} $ state within SM1 and SM2 are similar and are in reasonable agreement with the experimental values. However, there are significant discrepancies (of approximately 2 MeV) between SM1 and SM2 for the higher-spin states at energies of 8335 and 8820 keV (see Fig. 1). Considering the electromagnetic transition multipolarities and the discrepancies between the calculated and experimental values, we assign the states with energies of 8335 and 8820 keV as the yrast and yrare 37/2$ ^{+} $ states, respectively. One can see from Fig. 1 that the predicted energies of the 37/2$ _{1}^{+} $ and 37/2$ _{2}^{+} $ states within SM2 are more reasonable than those in SM1. However, the large discrepancies between the SM1 calculations and experimental values may be owing to the truncation space. As listed in Table 1, the 37/2$ _{1}^{+} $ and 37/2$ _{2}^{+} $ states in SM2 are mainly generated by the excitation of one neutron across the N = 56 subshell closure into the 1$ h_{11/2} $ orbital. This indicates that the high-j intruder 1$ h_{11/2} $ orbital may play an important role in the higher-spin states.Table 2-continued from previous page $I^{\pi}\;(\hbar)$ 

$E_{(\rm exp)}$ /keV

SM1 SM2 $E_{(\rm cal)}$ /keV

wave function $\pi\otimes\nu$ 

partitions (%) $E_{(\rm cal)}$ /keV

wave function $\pi \otimes\nu $ 

partitions (%) $25/2_{1}^{+}$ 

4899 4363 6 4 0 4 $\otimes$ 2 10 1 0

62.57 4360 6 4 0 4 $\otimes$ 2 10 1 0

62.48 4 4 2 4 $\otimes$ 2 10 1 0

10.68 4 4 2 4 $\otimes$ 2 10 1 0

10.57 $29/2_{1}^{+}$ 

5585 5214 6 4 0 4 $\otimes$ 2 10 1 0

71.07 5206 6 4 0 4 $\otimes$ 2 10 1 0

70.42 6 3 1 4 $\otimes$ 2 10 1 0

11.26 6 3 1 4 $\otimes$ 2 10 1 0

11.14 $35/2_{1}^{+}$ 

7268 7397 5 4 1 4 $\otimes$ 2 10 1 0

85.75 7383 5 4 1 4 $\otimes$ 2 10 1 0

83.91 5 3 2 4 $\otimes$ 2 10 1 0

10.96 5 3 2 4 $\otimes$ 2 10 1 0

10.87 $37/2_{1}^{+}$ 

8335 10310 4 4 2 4 $\otimes$ 2 10 1 0

78.55 7996 5 4 0 5 $\otimes$ 2 10 0 1

65.81 5 3 2 4 $\otimes$ 2 10 1 0

8.47 5 4 2 3 $\otimes$ 2 10 0 1

14.37 $37/2_{2}^{+}$ 

8820 10791 5 4 1 4 $\otimes$ 2 9 2 0

76.21 9182 5 4 0 5 $\otimes$ 2 10 0 1

69.97 5 3 2 4 $\otimes$ 2 9 2 0

9.16 5 3 1 5 $\otimes$ 2 10 0 1

11.49 $5/2_{1}^{-}$ 

2356 2452 6 4 1 3 $\otimes$ 2 10 1 0

72.02 2456 6 4 1 3 $\otimes$ 2 10 1 0

71.95 5 4 2 3 $\otimes$ 2 10 1 0

12.87 5 4 2 3 $\otimes$ 2 10 1 0

12.87 $5/2_{2}^{-}$ 

2719 2875 6 4 1 3 $\otimes$ 2 10 1 0

50.68 2879 6 4 1 3 $\otimes$ 2 10 1 0

50.93 5 4 2 3 $\otimes$ 2 10 1 0

10.28 6 3 2 3 $\otimes$ 2 10 1 0

25.89 $7/2_{1}^{-}$ 

2431 2415 6 4 1 3 $\otimes$ 2 10 1 0

71.48 2418 6 4 1 3 $\otimes$ 2 10 1 0

71.49 5 4 2 3 $\otimes$ 2 10 1 0

10.02 5 4 2 3 $\otimes$ 2 10 1 0

10.00 $9/2_{1}^{-}$ 

2441 2481 6 4 1 3 $\otimes$ 2 10 1 0

69.97 2484 6 4 1 3 $\otimes$ 2 10 1 0

69.73 6 3 2 3 $\otimes$ 2 10 1 0

12.49 6 3 2 3 $\otimes$ 2 10 1 0

12.57 $11/2_{1}^{-}$ 

2440 2413 6 4 1 3 $\otimes$ 2 10 1 0

71.09 2424 6 4 1 3 $\otimes$ 2 10 1 0

66.13 6 3 2 3 $\otimes$ 2 10 1 0

14.41 6 3 2 3 $\otimes$ 2 10 1 0

15.77 $11/2_{2}^{-}$ 

2755 2622 6 4 1 3 $\otimes$ 2 10 1 0

65.96 2621 6 4 1 3 $\otimes$ 2 10 1 0

63.21 5 4 2 3 $\otimes$ 2 10 1 0

14.22 5 4 2 3 $\otimes$ 2 10 1 0

10.78 $13/2_{1}^{-}$ 

2450 2633 6 4 1 3 $\otimes$ 2 10 1 0

67.04 2635 6 4 1 3 $\otimes$ 2 10 1 0

66.92 5 4 2 3 $\otimes$ 2 10 1 0

11.98 5 4 2 3 $\otimes$ 2 10 1 0

12.02 $13/2_{2}^{-}$ 

2810 2907 6 4 1 3 $\otimes$ 2 10 1 0

69.76 2905 6 4 1 3 $\otimes$ 2 10 1 0

69.83 5 4 2 3 $\otimes$ 2 10 1 0

12.76 5 4 2 3 $\otimes$ 2 10 1 0

11.92 $15/2_{1}^{-}$ 

2573 2336 6 4 1 3 $\otimes$ 2 10 1 0

79.49 2336 6 4 1 3 $\otimes$ 2 10 1 0

75.01 5 4 2 3 $\otimes$ 2 10 1 0

10.42 5 4 2 3 $\otimes$ 2 10 1 0

10.36 $23/2_{1}^{-}$ 

4159 3985 6 4 1 3 $\otimes$ 2 10 1 0

83.76 3974 6 4 1 3 $\otimes$ 2 10 1 0

82.46 5 4 2 3 $\otimes$ 2 10 1 0

5.26 5 4 2 3 $\otimes$ 2 10 1 0

4.95 $27/2_{1}^{-}$ 

4437 4174 6 4 1 3 $\otimes$ 2 10 1 0

87.89 4141 6 4 1 3 $\otimes$ 2 10 1 0

68.96 6 3 2 3 $\otimes$ 2 10 1 0

4.56 6 4 2 2 $\otimes$ 2 10 0 1

13.41 $33/2_{1}^{-}$ 

7026 7528 5 4 0 5 $\otimes$ 2 10 1 0

74.01 6945 6 4 0 4 $\otimes$ 2 10 0 1

72.95 5 3 1 5 $\otimes$ 2 10 1 0

13.57 6 3 1 4 $\otimes$ 2 10 0 1

8.96 $37/2_{1}^{-}$ 

8597 10187 4 4 1 5 $\otimes$ 2 10 1 0

77.63 8604 5 4 1 4 $\otimes$ 2 10 0 1

78.94 4 3 2 5 $\otimes$ 2 10 1 0

14.28 5 3 2 4 $\otimes$ 2 10 0 1

10.54 $39/2_{1}^{-}$ 

9170 10385 4 4 1 5 $\otimes$ 2 10 1 0

80.41 9081 5 4 1 4 $\otimes$ 2 10 0 1

83.79 4 3 2 5 $\otimes$ 2 10 1 0

10.70 5 3 2 4 $\otimes$ 2 10 0 1

12.24 $41/2_{1}^{-}$ 

9646 11866 5 4 2 3 $\otimes$ 2 9 2 0

48.24 9387 5 4 1 4 $\otimes$ 2 10 0 1

84.79 5 4 0 5 $\otimes$ 2 9 2 0

39.44 5 3 2 4 $\otimes$ 2 10 0 1

11.11 A similar situation appears in the negative parity states of
$ ^{93} $ Mo. As evident in Fig. 2, the SM2 calculations that include the 1$ h_{11/2} $ orbital more adequately describe the higher-spin states than SM1. In SM2, the energy difference between the predicted 37/2$ _{1}^{-} $ and 39/2$ _{1}^{-} $ states is 477 keV, which is close to the energy of the observed 573 keV$ \gamma $ ray [9], and the calculated 41/2$ _{1}^{-} $ state is in reasonable agreement with the experimental one. Thus, the states at energies of 8597, 9170, and 9646 keV may respectively correspond to the predicted states with energies of 8604, 9081, and 9387 keV, namely the 37/2$ _{1}^{-} $ , 39/2$ _{1}^{-} $ , and 41/2$ _{1}^{-} $ states. However, for the levels mentioned above, the predicted energies in SM1 greatly exceed the experimental values, with relatively large differences of 1.2$ \sim $ 2.2 MeV, which indicates that the contribution of excitations from the neutron 2$ d_{5/2} $ orbital to the high-j intruder 1$ h_{11/2} $ orbital across the N = 56 subshell cannot be ignored. The yrast 33/2$ ^{-} $ state is also reproduced well in SM2, with an energy difference of only 81 keV, whereas the calculated energy in SM1 is 502 keV higher than experimental value. Therefore, using the extended truncation space of SM2 yields better agreement between experiment and theory for higher-spin states.Based on the two sets of shell model calculations, the 41/2
$ _{1}^{-} $ state involves the neutron-core excitation$ \nu[(1g_{9/2})^{-1}(2d_{5/2})^{2}] $ in SM1. However, when obtained in SM2, this state mainly arises from (2$ d_{5/2} \rightarrow 1h_{11/2} $ ) neutron excitation without neutron-core excitation. This result indicates that the neutron-core excitation may not be involved below the 41/2$ _{1}^{-} $ state in$ ^{93} $ Mo. For the 37/2$ _{1}^{-} $ , 39/2$ _{1}^{-} $ , and 41/2$ _{1}^{-} $ states, the SM2 calculations predict the involvement of mainly one neutron excitation from the 2$ d_{5/2} $ orbital to the 1$ h_{11/2} $ orbital, i.e., a configuration of$ \pi[(1f_{5/2})^{-1}(2p_{1/2})^{1}(1g_{9/2})^{4}] $ $ \otimes $ $ \nu(1h_{11/2}) $ . Furthermore, the aforementioned states include the excitation of one proton from the completely filled 2$ p_{3/2} $ orbital to the 2$ p_{1/2} $ orbital. The 33/2$ ^{-} $ state also has$ \nu(1h_{11/2}) $ as its main component, involving a proton pair excitation from the 2$ p_{1/2} $ orbital into the 1$ g_{9/2} $ orbital. For these reasons, the contribution of the 1$ h_{11/2} $ orbital to the higher-spin states cannot be ignored, whether for the positive parity or negative parity states in$ ^{93} $ Mo.The lower negative parity states with spin
$ I^{\pi} $ = 5/2$ ^{-} $ , 7/2$ ^{-} $ , 9/2$ ^{-} $ , 11/2$ ^{-} $ , 13/2$ ^{-} $ , 15/2$ ^{-} $ , 23/2$ ^{-} $ , and 27/2$ ^{-} $ are reasonably reproduced by SM1 and SM2, as shown in Table 1. Meanwhile, these states obtained in the shell model show the characteristics of multiplets, with$ \pi[(2p_{1/2})^{1}$ $ (1g_{9/2})^{3}] $ $ \otimes $ $ \nu(2d_{5/2}) $ configurations contributing maximally.In order to more intuitively understand the contribution of different orbitals to each state, we also calculated the occupation numbers for protons and neutrons based on the configuration space of SM2. The calculated occupation numbers for protons and neutrons are shown in Figs. 3 and 4, respectively. It can be seen from Fig. 3 that a large contribution to both kinds of parity states (I
$ \geqslant $ 25/2) is coming from the proton$ 1g_{9/2} $ orbital. The results listed in Table 1 also suggest that the wave functions of these states involve proton excitations from the$ 1f_{5/2} $ , 2$ p_{3/2} $ , or 2$ p_{1/2} $ orbitals into the 1$ g_{9/2} $ orbital. As can be seen from Fig. 4, in the higher-spin states, a major contribution from the intruder 1$ h_{11/2} $ orbital to both kinds of parity states is clearly evident, especially for the negative parity states. Thus, the level structures of$ ^{93} $ Mo in higher-spin states should include the component of the neutron 1$ h_{11/2} $ orbital. -
Large Scale Shell Model calculations were performed for
$ ^{93} $ Mo based on two different configuration spaces. The SM1 calculations reproduced the low-lying states well but did not reasonably describe the higher-spin states. An improved description of the higher-spin states was obtained with an extended space including the$ \nu(1h_{11/2}) $ orbital in SM2. SM2 predicts that the higher-spin states of$ ^{93} $ Mo can be principally interpreted via the configurations dominated by (i) proton excitations from the completely filled 1$ f_{5/2} $ , 2$ p_{3/2} $ , and 2$ p_{1/2} $ subshells into the higher orbitals and (ii) neutron excitation from the interior of the N = 56 subshell closure into the high-j intruder 1$ h_{11/2} $ orbital. This indicates that the neutron 1$ h_{11/2} $ orbital is essential for obtaining a more appropriate description of the higher-spin levels.
Multi-quasiparticle excitations and the impact of the high-j intruder orbital in the N = 51 93Mo nucleus
- Received Date: 2020-07-23
- Available Online: 2021-01-15
Abstract: The level structures of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: