Electromagnetic properties of neutron-rich Ge isotopes

In recent years, considerable experimental and theoretical effort has been directed to the studies of the shell structure of neutron-rich nuclei near the proton number $ Z = 28 $. In this region, the germanium isotopes ($ Z = 32 $) have attracted much attention due to their complex low-lying structure [1-20]. It shows an irregular behavior when the neutron number varies from $ N<40 $ to $ N>40 $, and is accompanied with the competition between the $ N = 40 $ single-particle energy gap and the collective effects.

The low-lying states of even-even Ge nuclei were described in terms of shape transition from nearly spherical in ⁷⁰Ge to weakly deformed in ^72,74Ge, and even soft triaxial in ^76,78Ge, with shape coexistence possibly occurring in these nuclei [1-3]. To understand the structure of these nuclei, the electric quadrupole moment $ Q $ and the magnetic moment $ \mu $ (or the $ g $ factor) have been of experimental interest [4-12]. Among these experiments, $ Q(2_1^+) $ in stable nuclei ^70-76Ge was studied using multiple Coulomb excitation [4-7]. The overall trend of $ Q(2_1^+) $ is from a small positive value in ⁷⁰Ge (indicating a weakly prolate shape) to negative values in ^72,74,76Ge (indicating an oblate shape). $ g(2_1^{+}) $ in ^70-76Ge was measured by the integral perturbed angular correlation method [8] and the transient field techniques [9-12], and the values obtained in different experiments are in agreement.

The above experimental measurements of Ge isotopes provide a challenging testing ground for theoretical calculations. Recently, shell model calculations [13, 14] of the low-lying structure of even-even nuclei ^70-76Ge were carried out using two effective interactions (JUN45 and JJ4B) in the $ f_{5/2} $, $ p_{3/2} $, $ p_{1/2} $, and $ g_{9/2} $ model space. It was shown that $ E(2_1^+) $ and $ B(E2;2_1^+\rightarrow 0_1^+) $ are generally well described by these studies, but $ Q(2_1^+) $ is not. With the JUN45 interaction, the sign of the calculated and experimental $ Q(2_1^+) $ is opposite for ^72,74,76Ge [13]. In the case of the JJ4B interaction, the sign of $ Q(2_1^+) $ is reproduced for ^74,76Ge, but is still opposite for ⁷²Ge [14]. It was suggested that such a discrepancy between theoretical and experimental $ Q(2_1^+) $ values is possibly due to the excitations from the $ f_{7/2} $ orbit [14]. However, further shell model studies with larger valence space, including the proton subshell $ f_{7/2} $, can not reduce this discrepancy [15]. In the case of the $ g $ factor, the shell model results (JUN45 and JJ4B) in general agree with the experimental $ g(2_2^{+}) $ values, but tend to underestimate the $ g(2_1^{+}) $ and $ g(4_1^{+}) $ values [12].

The purpose of this paper is to apply the nucleon pair approximation (NPA) [21] of the shell model to investigate the low-lying structure of even-even nuclei ^72-80Ge and the neighboring odd-mass nuclei ^75-79Ge, with the focus on their electromagnetic properties. NPA has proven to be a reliable and economic approximation of the shell model [22] for studying the low-lying states of transitional nuclei with medium and heavy masses. It has been successfully applied in recent years to even-even, odd-mass and odd-odd nuclei in the regions of $ A\sim 80 $ [23], 100 [24], 130 [25] and 210 [26]. In addition to the studies of realistic nuclei, this model has also been applied to study the phase transitions of collective motions [27], and regularities of low-lying states in nuclei with random interactions [28]. In the NPA calculations, a phenomenological and separable form of the shell model Hamiltonian is widely used. It would be very interesting to study whether the discrepancy between the theoretical and experimental values of $ Q(2_1^+) $ and $ g(2_1^{+}) $ for Ge isotopes are reduced if an appropriate phenomenological Hamiltonian is used in NPA.

The paper is organized as follows. In Sec. 2, a brief introduction to NPA is given, including the Hamiltonian, the transition operators, and the model space. In Sec. 3, we discuss the validity of the optimized parameters obtained in our calculations. In Sec. 4, we present our results for the electromagnetic properties of the low-lying states in even-even nuclei ^72-80Ge and odd-mass nuclei ^75-79Ge. A summary and conclusions are given in Sec. 5.

In this paper, the Hamiltonian is assumed to have the following form,

where $ \sigma = \pi, \nu $ corresponds to the proton and neutron degrees of freedom, respectively. The pairing and quadrupole operators are defined as follows.

Here, $ q(jj') \,=\, \frac{\Delta_{jj'}(-)^{l+l'+1}(-)^{j-\frac{1}{2}}\hat{ j} \hat{j'}}{\sqrt{20\pi} } C_{j\frac{1}{2}, j' -\frac{1}{2}}^{2 0}\langle n l|r^2 |n l' \rangle $ with$ \Delta_{jj'} $ $= \frac{1}{2}[1+(-)^{l+l'+2}] $ , and $ C_{j\frac{1}{2}, j' -\frac{1}{2}}^{2 0} $ is the Clebsch-Gordan coefficient.

$ \epsilon_{j_{\sigma}} $ refers to the single-particle energy. Here we adopt the same values of $ \epsilon_{j_{\sigma}} $ as in our previous work for Zn ($ Z = 30 $) and Ga ($ Z = 31 $) isotopes [23], shown in Table 1. $ G_{0\sigma} $, $ G_{2\sigma} $, $ \kappa_{\sigma} $ and $ \kappa_{\pi\nu} $ are the two-body interaction strengths corresponding to the monopole, quadrupole pairing and quadrupole-quadrupole interactions between all valence nucleons. Here we use the empirical formulas [29] for the parametrization of $ G_{0\sigma} $, $ G_{2\sigma} $, $ \kappa_{\sigma} $ and $ \kappa_{\pi\nu} $ as follows. $ G^{0}_{\sigma} = -\alpha_{\sigma}\frac{27}{A}, \; G^{2}_{\sigma} = \beta_{\sigma}\frac{G^{0}_{\sigma}}{r_0^4},\; \kappa_{\sigma} = \frac{1}{2}\chi\eta_{\sigma}^{2}, \; \kappa_{\pi\nu} = \chi\eta_{\pi}\eta_{\nu},\; $ with $ \eta_{\nu} = -\gamma_{\nu}\left[\frac{2(A-Z)}{A}\right]^{\frac{2}{3}}, \eta_{\pi} = \gamma_{\pi}\left(\frac{2Z}{A}\right)^{\frac{2}{3}}, $ $ \chi = -\{242 \left[1+(\frac{2}{3A})^{\frac{1}{3}} \right] $ $-\frac{10.9}{A^{\frac{1}{3}}} [1+2(\frac{2}{3A})^{\frac{1}{3}}] (19-0.36\frac{Z^2}{A})] \}A^{-\frac{5}{3}}. $ Therefore, there are in total six parameters for the two-body interactions, i.e. $ \alpha_{\sigma} $, $ \beta_{\sigma} $ and $ \gamma_{\sigma} $ ($ \sigma = \pi, \nu $). The two sets of parameters are listed in Table 2. The parameters in NPA-1 are the same as in Ref. [23]. The optimized parameters are denoted as NPA-2. $ \alpha_{\pi} $, $ \beta_{\pi} $ and $ \gamma_{\pi} $ are the same for all nuclei in NPA-1 and NPA-2.

	$j_{\nu}$	$p_{1/2}$	$p_{3/2}$	$f_{5/2}$	$g_{9/2}$
	$\epsilon_{j_{\nu}}$	0.5	1.0	3.0	0.0
$N_\nu$	$j_{\pi}$	$p_{1/2}$	$p_{3/2}$	$f_{5/2}$	$g_{9/2}$
0	$\epsilon_{j_{\pi}}$	1.3	0.5	0.0	3.3
1	$\epsilon_{j_{\pi}}$	1.3	0.4	0.0	3.3
2	$\epsilon_{j_{\pi}}$	1.3	0.0	0.5	3.3
3	$\epsilon_{j_{\pi}}$	1.3	0.0	0.6	3.3
4	$\epsilon_{j_{\pi}}$	1.3	0.0	0.7	3.3
5	$\epsilon_{j_{\pi}}$	1.3	0.0	0.7	3.3

Table 1.  Adopted single-particle energies (in MeV) for protons and neutron holes.

		NPA-1			NPA-2
		$\alpha_{\pi}$	$\beta_{\pi}$	$\gamma_{\pi}$	$\alpha_{\pi}$	$\beta_{\pi}$	$\gamma_{\pi}$
		0.70	3.74	0.90	0.70	4.98	1.00
$A$	$N_\nu$	$\alpha_{\nu}$	$\beta_{\nu}$	$\gamma_{\nu}$	$\alpha_{\nu}$	$\beta_{\nu}$	$\gamma_{\nu}$
80	1	0.60	4.67	0.90	0.60	5.32	0.98
78	2	0.60	4.59	0.70	0.60	5.03	0.76
76	3	0.60	4.51	0.80	0.60	4.81	0.74
74	4	0.60	4.43	0.80	0.60	4.63	1.00
72	5	0.60	4.43	0.80	0.60	4.43	1.00

Table 2.  Parameters $\alpha_{\sigma}$, $\beta_{\sigma}$, $\gamma_{\sigma}$ ($\sigma = \pi, \nu$) of our two-body interactions. The parameters in NPA-1 are the same as in Ref. [23]. The optimized parameters are denoted as NPA-2. The values of $\alpha_{\pi}$, $\beta_{\pi}$, $\gamma_{\pi}$ for protons are taken to be the same for all nuclei in each set of parameters. The values of $\beta_{\nu}$ and $\gamma_{\nu}$ for neutron holes are assumed to change with the valence neutron pair $N_{\nu}.$

The model space in NPA is constructed with the collective nucleon-pairs. The pairs with spin $ r = 0,2,4,6,8\cdots $ are defined as S, D, G, I and K pairs, respectively. Because our focus is on the electromagnetic properties of the $ 2_1^+ $ state in even-even nuclei, our model space is constructed by the $ S $ and $ D $ pairs of valence protons (and neutron holes) with respect to the doubly closed shell nucleus ⁷⁸Ni$ _{50} $. The $ G $, $ I $ and $ K $ pairs are found not to contribute significantly to the very low states (in particular the $ 2_1^+ $ states) of the nuclei studied in this paper.

The $ E2 $ transition operator is defined by $T(E2) = $ $ e_{\pi} Q_{\pi} + e_{\nu}Q_{\nu}, $ where $ e_{\pi} $ and $ e_{\nu} $ are the effective charges of valence proton and neutron holes, respectively. Here we adopt $ e_{\pi} = 1.81e $ and $ e_{\nu} = -1.02e $, the same as in Ref. [23]. $ B(E2) $ in units of $ \rm W.u. $ is given by

with reduced matrix element $ X_{\sigma} = \langle \zeta_{f},J_{f}||Q_{\sigma}||\zeta_{i},J_{i}\rangle $ ($ \sigma = \pi, \nu $) and $ r_0^2 = 1.012A^{1/3} $ fm². $ |\zeta_{i},J_{i}\rangle $ is the eigenfunction of the $ J_{i} $ state, and the symbol $ \zeta_{i} $ represents all quantum numbers other than the angular momentum $ J_{i} $. The electric quadrupole moment is related to the $ E2 $ transition operator. Its value in units of $ e{\rm{b}} $ is

The magnetic moment operator is given by $\mu = g_{l\pi} L_{\pi} + $$ g_{l\nu} L_{\nu} + g_{s\pi} S_{\pi} + g_{s\nu} S_{\nu} $. Here, $ L_{\sigma} $ and $ S_{\sigma} $ are the orbital and spin angular momenta, and $ g_{l\sigma} $ and $ g_{s\sigma} $ are the orbital and spin gyromagnetic ratios. The orbital gyromagnetic ratios are taken to be $ g_{l\pi} = 1 $ and $ g_{l\nu} = 0 $. Both the free and effective spin gyromagnetic ratios are used in this paper. The free ratios are $ g_{s\pi} = 5.586 $ and $ g_{s\nu} = -3.826 $, and the effective ratios are $ g_{s\pi} = 5.586\times 0.7 $ and $ g_{s\nu} = -3.826\times $ 0.7. The $ g $ factor is defined by $ \displaystyle\frac{\mu(J_i)/\mu_N}{J_i} $, with $ \mu_N $ the nuclear magneton.

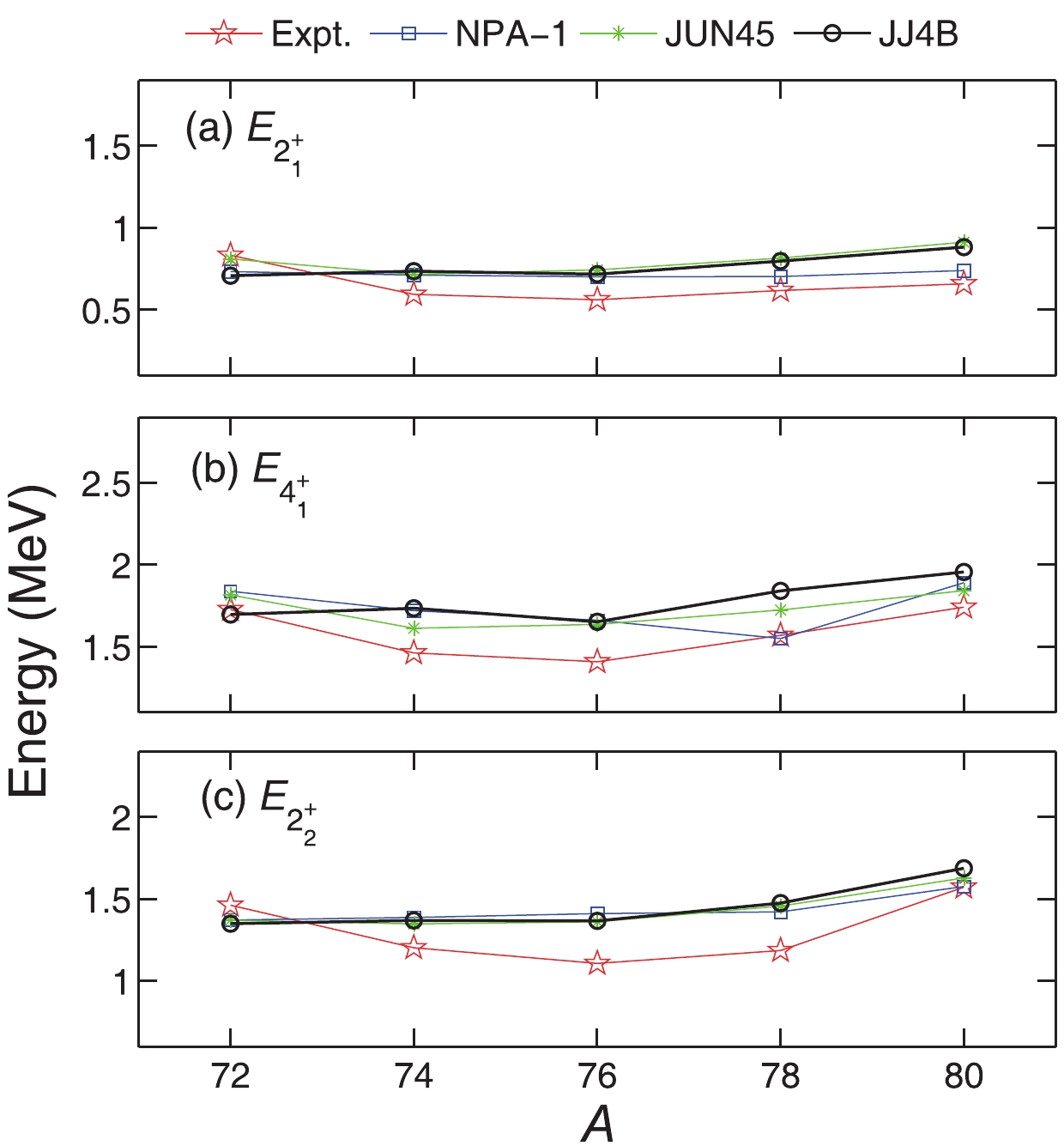
Recently, the low-lying structures of even-even Zn and odd-mass Ga isotopes with neutron numbers between 42 and 50 were calculated using NPA [23]. As these nuclei are neighbors of Ge isotopes investigated in this paper, their two-body interaction parameters (i.e. NPA-1 in Table 2) provide a starting point (and additional restriction) for adjusting the parameters of Ge isotopes. We first make use of NPA-1 to calculate the energy levels and electromagnetic properties of the low-lying states in even-even ^72-80Ge to see whether this parameter set can describe the experimental data. One can see in Fig. 1 and Table 3 that our results with NPA-1 are similar to the SM calculations, i.e. $E(2_1^+)$ and $B(E2;2_1^+\rightarrow 0_1^+)$ are in general well reproduced, but the signs of the calculated and experimental $Q(2_1^+)$ for ^72,74Ge are opposite.

Figure 1.  (color online) Partial low-lying excitation energy (in MeV) for even-even nuclei ^72-80Ge using the NPA-1 parameters. The experimental data are taken from Ref. [30]. The shell model results (JUN45 and JJ4B) [15] are shown for comparison.

nuclei	state			$ B(E2:J_i^{\pi}\rightarrow J_f^{\pi}) $						$ Q(J_i^{\pi}) $
	$ J_i^{\pi} $	$ J_f^{\pi} $		expt.	JJ4B	JUN45	NPA−1	NPA−2		expt.	JJ4B	JUN45	NPA−1	NPA−2
72Ge	$ 2^+_1 $	$ 0^+_1 $		$ 23.5(4) $	$ 19.88/40.01 $	$ 14.55/28.27 $	27.35	$ 33.84 $		$ {-0.12(8)^{\rm a}}\\{-0.13(6)^{\rm b}} $	$ +0.11/+0.19 $	$ +0.13/+0.22 $	$ +0.11 $	$ -0.13 $
	$ 4^+_1 $	$ 2^+_1 $		$ 37(5) $	$ 27.62/56.44 $	$ 25.08/49.57 $	35.27	$ 42.89 $			$+0.03/+0.10$	$+0.08/+0.08$	$+0.02$	−0.24
	$6^+_1$	$4^+_1$		$37(^{+21}_{-37})$			34.04	41.93					−0.03	−0.32
	$ 8^+_1 $	$ 6^+_1 $		$ 42(^{+11}_{-27}) $			19.18	$ 33.97 $					−0.58	−0.58
	$2^+_2$	$2^+_1$		$62(^{+9}_{-11})$	29.34/54.78	24.70/42.73	36.74	43.28		$+0.23(8)^{\rm a}$	−0.11/−0.19	−0.13/−0.22	−0.14	+0.08
	$2^+_2$	$0^+_1$		$0.130(^{+18}_{-24})$	1.37/1.48	1.21/1.11	1.98	0.04
74Ge	$2^+_1$	$0^+_1$		33.0(4)	19.90/38.24	16.59/32.01	27.10	32.25		${-0.19(2)^{\rm c}}\\{-0.25(6)^{\rm b}}$	−0.06/−0.06	+0.12/+0.20	+0.01	−0.16
	$4^+_1$	$2^+_1$		41(3)	27.04/53.09	23.46/46.48	34.18	40.72			−0.08/−0.09	+0.11/+0.19	−0.09	−0.29
	$6^+_1$	$4^+_1$					32.25	38.88					−0.21	−0.39
	$2^+_2$	$2^+_1$		43(6)	29.17/55.63	24.88/43.29	36.60	39.60		$+0.26(6)^{\rm c}$	+0.05/+0.06	−0.12/−0.19	−0.07	+0.10
	$2^+_2$	$0^+_1$		0.71(11)	0.12/0.09	1.35/1.35	0.99	0.004
76Ge	$ 2^+_1 $	$ 0^+_1 $		$ 29(1) $	$ 18.24/33.47 $	$ 16.36/29.77 $	25.30	$ 26.17 $		$ {-0.14(4)^{\rm c}}\\{-0.19(6)^{\rm b}} $	$ -0.15/-0.19 $	$ +0.02/+0.05 $	$ -0.12 $	$ -0.15 $
	$ 4^+_1 $	$ 2^+_1 $		$ 38(9) $	$ 24.15/45.15 $	$ 22.04/40.93 $	31.25	$ 31.37 $		$ -0.01(5)^{\rm c} $	$ -0.14/-0.17 $	$ -0.01/+0.01 $	$ -0.26 $	$ -0.27 $
	$ 6^+_1 $	$ 4^+_1 $		$ 91(^{+55}_{-48}) $			27.35	$ 27.97 $					−0.37	−0.40
	$2^+_2$	$2^+_1$		42(9)	22.94/41.80	25.38/44.21	30.78	31.76		+0.28(6)c	+0.15/+0.20	−0.001/−0.02	+0.03	+0.08
	$2^+_2$	$0^+_1$		0.90(22)	0.01/0.004	0.42/0.41	0.27	0.01
78Ge	$2^+_1$	$0^+_1$		23(4)	15.91/27.18	14.40/24.25	20.23	23.11			$ -0.16/-0.19 $	$ -0.11/-0.13 $	$ -0.19 $	$ -0.27 $
	$ 4^+_1 $	$ 2^+_1 $		$ >11 $			$ 21.20 $	$ 26.77 $					−0.36	−0.41
	$6^+_1$	$4^+_1$					$ 23.34 $	$ 24.90 $					−0.48	−0.50
	$2^+_2$	$2^+_1$		19(11)			17.40	19.80					$ -0.01 $	$ +0.19 $
	$ 2^+_2 $	$ 0^+_1 $		$ 0.53(24) $			$ 0.44 $	$ 0.17 $
80Ge	$ 2^+_1 $	$ 0^+_1 $		$ 13.6(27) $	$ 11.18/16.99 $	$ 9.38/14.70 $	$ 16.81 $	$ 18.70 $			−0.23/-0.29	−0.23/-0.29	−0.29	−0.34
	$4^+_1$	$2^+_1$					$ 20.90 $	$ 21.91 $					−0.40	−0.44
	$6^+_1$	$4^+_1$					$ 15.07 $	$ 15.56 $					−0.41	−0.45
	$2^+_2$	$2^+_1$					$ 2.35 $	$ 5.51 $					−0.15	+0.29
	$2^+_2$	$0^+_1$		1.1(3)			0.36	0.99

Table 3.  $ B(E2) $ (in units of W.u.) and the electric quadrupole moment $ Q $ (in units of $ e{\rm{b}}$) for even-even ^72-80Ge. A comparison is given between the experimental data, SM results (JJ4B and JUN45) [14, 15], and the results of this work (NPA-1 and NPA-2). Most experimental values for$ B(E2) $ are taken from Ref. [30], except for $ B(E2;6_1^+\rightarrow 4_1^+) $ for ⁷⁶Ge which is from Ref. [19], and $ B(E2;2_2^+\rightarrow 0_1^+) $for ⁸⁰Ge from Ref. [20]. The measured $ Q $ values are from $ {\rm a:} $ Ref. [6], $ {\rm b:} $ Ref. [5], and $ {\rm c:} $ Ref. [7]. Two sets of effective charges are adopted in the SM calculations (shown separated by "/"), $ e_{\pi} = 1.5 e $ and $ e_{\nu} = 0.5 e $, and $ e_{\pi} = 1.5 e $ and $ e_{\nu} = 1.1 e $. The SM results for ^{72, 74, 76}Ge are from Ref. [14], and for ^{78, 80}Ge from Ref. [15].

We refine the two-body interaction parameters, starting from the parameters obtained in the NPA-1 calculations. In order to reduce the number of free parameters, we fix $\alpha_{\pi}$ and $\alpha_{\nu}$ , which correspond to the monopole pairing interaction parameters $G_{0\pi}$ and $G_{0\nu}$, respectively. We adjust the parameters $\beta_{\pi}$, $\gamma_{\pi}$, $\beta_{\nu}$, and $\gamma_{\nu}$ within reasonable ranges to get the best fit of the experimental low-lying excitation energies, $B(E2)$, electric quadrupole moments $Q$, and magnetic moments $\mu$ (or $g$ factors) for both even-even and odd-mass Ge isotopes. For nuclei with an odd number of valence neutrons, we assume the same set of parameters as the nearest even-even neighboring core. The obtained optimized parameters are denoted as NPA-2, and are listed in Table 2.

In Fig. 2, we plot the behavior of $Q(2_1^+)$ for ^72,74Ge as a function of $\beta_{\pi}$, $\gamma_{\pi}$, $\beta_{\nu}$, and $\gamma_{\nu}$. In these plots, when one of the parameters is adjusted, the others are the same as in NPA-1 of Table 2. It can be seen in Fig. 2 that larger $\gamma_{\pi}$ and $\gamma_{\nu}$, i.e. larger values of the quadrupole-quadrupole interaction parameters $\kappa_{\sigma}$ and $\kappa_{\pi\nu}$, improve the agreement between the experimental and theoretical values of $Q(2_1^+)$. The calculated $Q(2_1^+)$ values are not sensitive to $\beta_{\pi}$. However, it is found that larger $\beta_{\pi}$ improves the predicted $g(2_1^+)$ . Smaller $\beta_{\nu}$ can also improve the prediction of $Q(2_1^+)$ values, but then the $B(E2;2_1^+\rightarrow 0_1^+)$ values deviate from the experimental data. One sees in Table 2 that the optimized parameters consistent with the above analysis, i.e. the NPA-2 parameters for ^72,74Ge, have larger $\gamma_{\pi}$, $\gamma_{\nu}$, and $\beta_{\pi}$ than in NPA-1, while $\beta_{\nu}$ remains almost unchanged.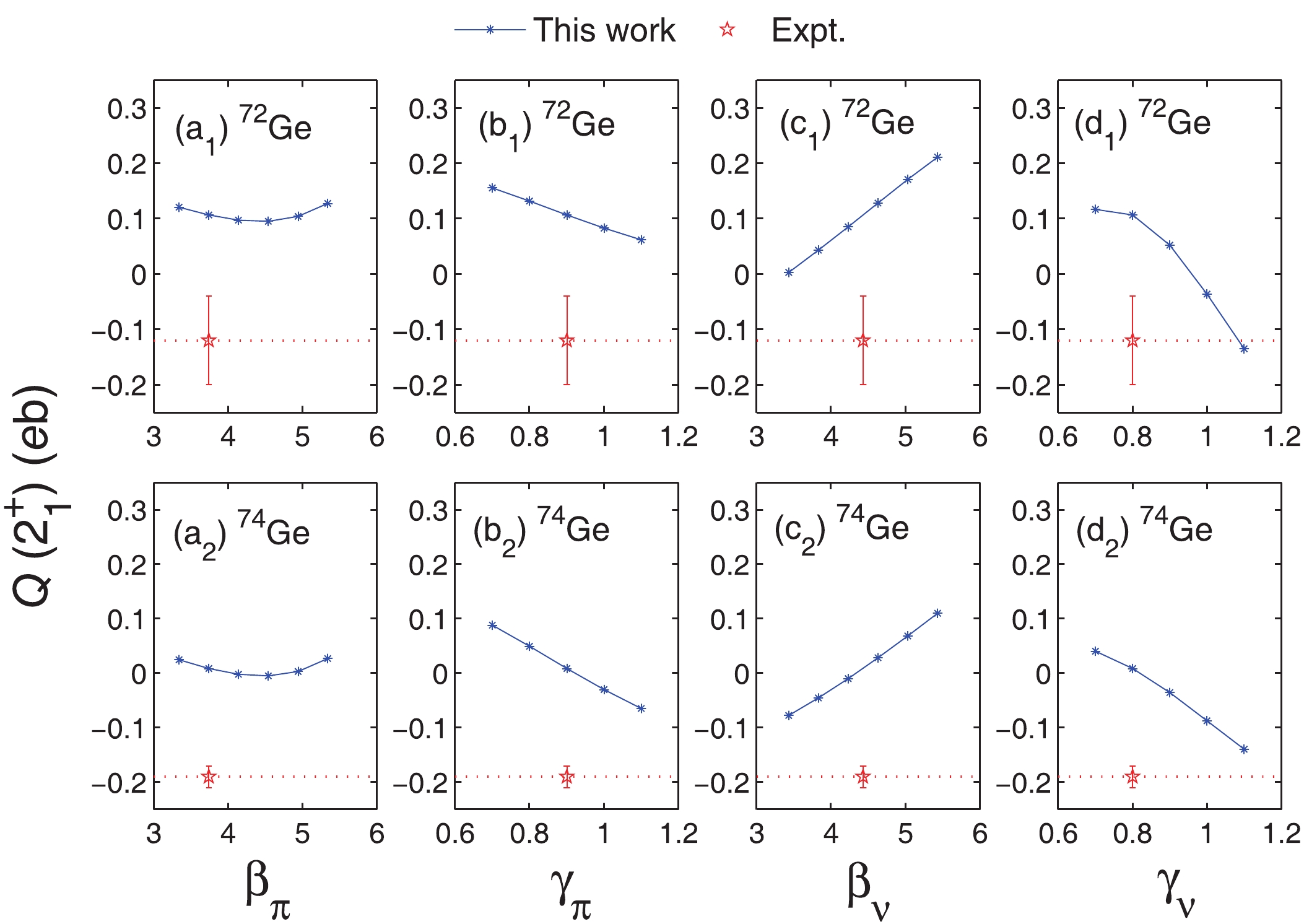

Figure 2.  (color online) The electric quadrupole moment $Q(2_1^+)$ (in ${\rm{eb}}$) for ⁷²Ge and ⁷⁴Ge as a function of the two-body interaction parameters $\beta_{\pi}$, $\gamma_{\pi}$, $\beta_{\nu}$, and $\gamma_{\nu}$. The experimental data, including Kotlinski 1990 [6] for ⁷²Ge and Toh 2001 [7] for ⁷⁴Ge, are shown for comparison.

In Fig. 3 and Tables 3-6, we present the calculated low-lying excitation energies, $B(E2)$, $Q$, and $\mu$ (or $g$ factors) for even-even and odd-mass Ge isotopes using the NPA-2 parameters. The experimental data and the shell model predictions (JUN45 and JJ4B) [12-16] are presented for comparison. One can see that our results with NPA-2 are reasonably consistent with the experimental data for both even-even and odd-mass Ge isotopes. For even-even isotopes, our calculated energy levels reproduce well the energies of the $0_1^+$, $2_1^+$, and $4_1^+$ states. The root-mean-square (RMS) deviations of the $2_1^+$, $4_1^+$, $6_1^+$ and $8_1^+$ levels of these nuclei with respect to the experimental data are 0.09 MeV, 0.17 MeV, 0.39 MeV, and 0.83 MeV, respectively. The large RMS deviations of the $6_1^+$ and $8_1^+$ levels come mainly from the results for ^72,74Ge (e.g. $6_1^+$ and $8_1^+$ levels in ⁷⁴Ge are about 0.65 MeV and 1.13 MeV higher than the experimental data). Such deviations are mainly due to the limitation of our model space ($SD$ nucleon-pair subspace) rather than the NPA-2 parameter set. It can be improved by the inclusion of one $K$ nucleon pair with spin eight, which is an alignment of two neutrons in the $g_{9/2}$ orbit. For example, with the same NPA-2 parameter set, our calculated $6_1^+$ and $8_1^+$ levels of ⁷⁴Ge would be depressed by 0.57 MeV and 1.82 MeV if the $SDK$-pair subspace is adopted, which match better with the experimental data. For the low-lying states, in particular the $2_1^+$ states, the contribution of the $K$ nucleon-pair is negligible, and it is excluded in our calculations. The structure of the odd-mass systems in Fig. 3 is more complicated than of their even-even neighbors, and our calculations reproduce well most of the experimental levels of these odd-mass nuclei.

Figure 3.  The low-lying states in even-even nuclei ^72-80Ge and odd-mass nuclei ^75-81Ge in the NPA-2 calculations. The experimental data are taken from Refs. [19] and [30]. The experimental levels with "()" mean that the spin and/or parity of the corresponding states are not well established.

nuclei	$J_i^{\pi}$	expt.	JJ4Beff	JUN45eff	NPA−1free	NPA−1eff	NPA−2free	NPA−2eff
75Ge	$9/2^+_1$		$-0.823$	$-0.940$	$-1.73$	$-1.17$	$-1.66$	$-1.11$
	$7/2^+_1$		$-0.850$	$-0.885$	$-1.42$	$-0.98$	$-1.40$	$-0.96$
	$5/2^+_1$		$-0.626$	$-0.667$	$-1.09$	$-0.77$	$-1.20$	$-0.86$
	$1/2^-_1$	$+0.510(5)$		$+0.425$	$+0.68$	$+0.49$	+0.69	$+0.50$
77Ge	$9/2^+_1$		$ -0.781 $	$ -0.954 $	$ -1.77 $	$ -1.21 $	$ -1.58 $	$ -1.04 $
	$ 7/2^+_1 $		$-0.865$	$-0.939$	$-1.44$	$-0.99$	$-1.39$	$-0.95$
	$5/2^+_1$		$ -0.947 $	$ -0.912 $	$ -1.11 $	$ -0.79 $	−1.14	$ -0.81 $
	$ 1/2^-_1 $				$+0.67$	$+0.48$	$+0.69$	$+0.50$
79Ge	$9/2^+_1$		$ -0.938 $	$ -0.978 $	$ -1.71 $	$ -1.14 $	$ -1.42 $	$ -0.88 $
	$ 7/2^+_1 $		$-0.831$	$-0.854$	$-1.39$	$-0.94$	$-1.29$	$-0.85$
	$5/2^+_1$		$ -1.483 $	$ -1.511 $	$ -2.01 $	$ -1.62 $	$ -2.18 $	$ -1.76 $
	$ 1/2^-_1 $				$ +0.67 $	$ +0.48 $	$ +0.69 $	$ +0.50 $

Table 6.  The magnetic moment $\mu$ (in units of $\mu_N$) for odd-mass ^{75, 77, 79}Ge. A comparison is given between the experimental data [30], SM results [13,16], and the NPA results obtained in this work. Here, $g_{s(\rm eff)} = 0.7 g_{s(\rm free)}$. For the orbital gyromagnetic ratios, we adopt in our calculations the values $g_{l\pi} = 1$ and $g_{l\nu} = 0$ . The SM result for the $1/2^-_1$ state in ⁷⁵Ge is from Ref. [13], and the other SM results are from Ref. [16].

In order to investigate whether our NPA-2 parameters provide proper interactions for the low-lying states of Ge nuclei, we have performed NPA calculations of their neighboring isotope chains Zn, Ga, As and Se. We note without details that the calculated results reproduce well the experimental ​​​​​​yrast levels of even-even nuclei (^78,76,74Zn and ^82,80,78Se), although for the open-shell nuclei ⁷²Zn and ⁷⁶Se (whose valence neutron-hole number is eight) our calculated $4_1^+$ and $6_1^+$ levels are higher than the corresponding experimental data. This disagreement can be easily remedied by considering the $G$ and $I$ pairs of valence neutrons, similarly to the case of ^{72, 74}Ge. For odd-mass nuclei, the experimental ground state spins of even-$Z$-odd-$N$ nuclei (i.e. Zn and Se isotopes) are different from their odd-$Z$-even-$N$ neighbors (i.e. Ga and As isotopes), and the agreement of our calculated low-lying states for these nuclei is also reasonable. Therefore, the calculations of the electromagnetic quantities of Ge isotopes are very useful to constrain and refine the interaction parameters of the phenomenological shell model Hamiltonian in this region.

In this section, we discuss the electromagnetic properties of the low-lying states in even-even ^72-80Ge and odd-mass ^75-79Ge, presented in Tables 3-6.

We first look at $ Q(2_1^+) $ for even-even nuclei. The behavior of the measured $ Q(2_1^+) $ values in ^70-76Ge is from a positive value in ⁷⁰Ge to negative values in ^{72, 74, 76}Ge. One sees in Table 3 that our calculations with NPA-2 reproduce well the experimental $ Q(2_1^+) $ values in ^72,74,76Ge. In order to study their structure in more detail, we calculate the major components of the $ 2^+_1 $ states with corresponding percentages, which can be calculated as $ \langle {\rm NPA \; basis}|2^+_1\rangle^2 $. The percentages less than 0.2 are omitted. We use the abbreviation $|(D_{\pi}^{\dagger})^{n_{\pi}} (S_{\pi}^{\dagger})^{N_{\pi}-n_{\pi}} (D_{\nu}^{\dagger})^{n_{\nu}} $ $ (S_{\nu}^{\dagger})^{N_{\nu}-n_{\nu}} \rangle\rightarrow|(D_{\pi})^{n_{\pi}}(D_{\nu})^{n_{\nu}} \rangle $ to label the NPA basis. For example, $ |D_{\nu}\rangle $ means the NPA basis $ |(S_{\pi}^{\dagger})^{N_{\pi}}D_{\nu}^{\dagger}(S_{\nu}^{\dagger})^{N_{\nu}-1} \rangle $. It is found that the $ 2^+_1 $ states in all Ge isotopes are dominated by one-$ D $-pair excitation (i.e. $ |D_{\nu}\rangle $ and $ |D_{\pi}\rangle $). In Fig. 4, we present the percentage of dominant components $ |D_{\nu}\rangle $ and $ |D_{\pi}\rangle $ in the $ 2^+_1 $ wave-function of ^{72, 74}Ge with the NPA-1 and NPA-2 parameters. We note that for ^72,74Ge, the $ |D_{\nu}\rangle $ contribution in the $ 2^+_1 $ states with NPA-2 decreases by 17% compared with NPA-1, while the contribution of the other major component $ |D_{\pi}\rangle $ is unchanged. This indicates that with NPA-2, the above reduced percentage (17%) might come from some minor components mixed in the $ 2^+_1 $ states, such as $ |D_{\pi}^2D_{\nu}\rangle $, $ |D_{\pi}D^2_{\nu}\rangle $ etc. The strong quadrupole-quadrupole interactions ($ \gamma_{\pi} $ and $ \gamma_{\nu} $) and the quadrupole pairing strength for protons $ \beta_{\pi} $ in NPA-2 may explain such enhancement of configuration mixing in ^72,74Ge.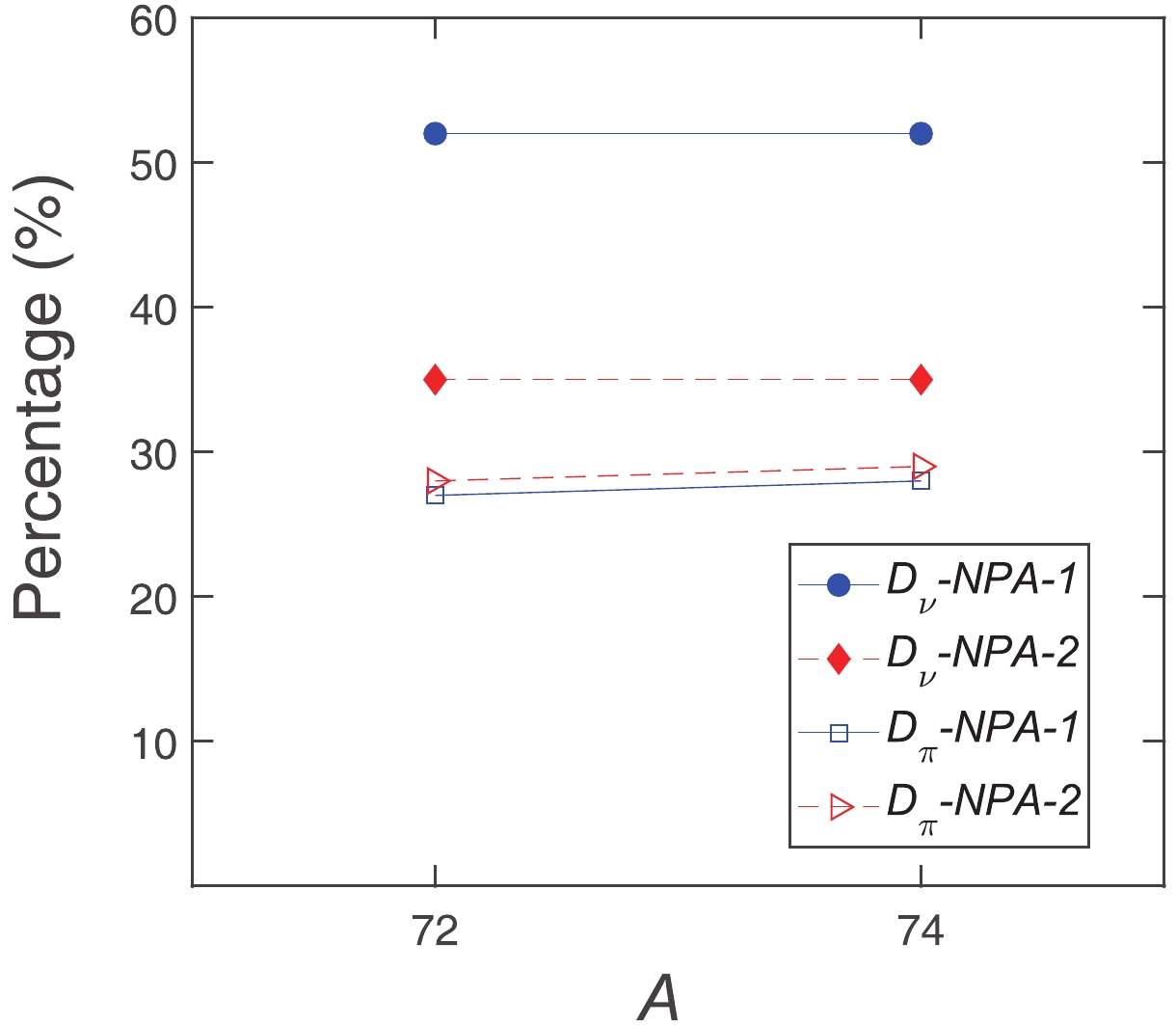

Figure 4.  (color online) Percentage of the dominant components $|D_{\nu}\rangle$ and $|D_{\pi}\rangle$ in the $2^+_1$ wave-function for ^72,74Ge with the NPA-1 and NPA-2 parameters.

In Fig. 5, we present the proton and neutron contributions to the total $ Q(2_1^{+}) $ with NPA-1 and NPA-2. The structure of the $ 2^+_1 $ states is consistent with our analysis of the $ Q(2^+_1) $ results. With NPA-1, $ Q(2^+_1) $ for ^72,74Ge are positive, because of the strong positive contribution of the neutron excitation (mainly the $ |D_{\nu}\rangle $ component), as shown in Fig. 4. The NPA-2 parameter set quenches the $ |D_{\nu}\rangle $ component for ^72,74Ge, which leads to an almost zero contribution of the neutron excitation, and thus negative $ Q(2^+_1) $ values. We recall that the experiments [5-7] also suggested a negative $ Q(2^+_1) $ , contrary to the shell-model calculations [13,14]. The major difference between the NPA-2 and NPA-1 calculations is that NPA-1 introduces less configuration mixing in ^72,74Ge when the $ N = 40 $ subshell is near, while NPA-2 quenches the $ |D_{\nu}\rangle $ component and introduces stronger configuration mixing, as described above. Therefore, the success of NPA-2 ​​​​​in reproducing the sign of $ Q(2^+_1) $ in ^72,74Ge may suggest that Ge isotopes actually do not loss configuration mixing or collectivity near the $ N = 40 $ subshell, and that a shell-weakening effect or deformation can be expected.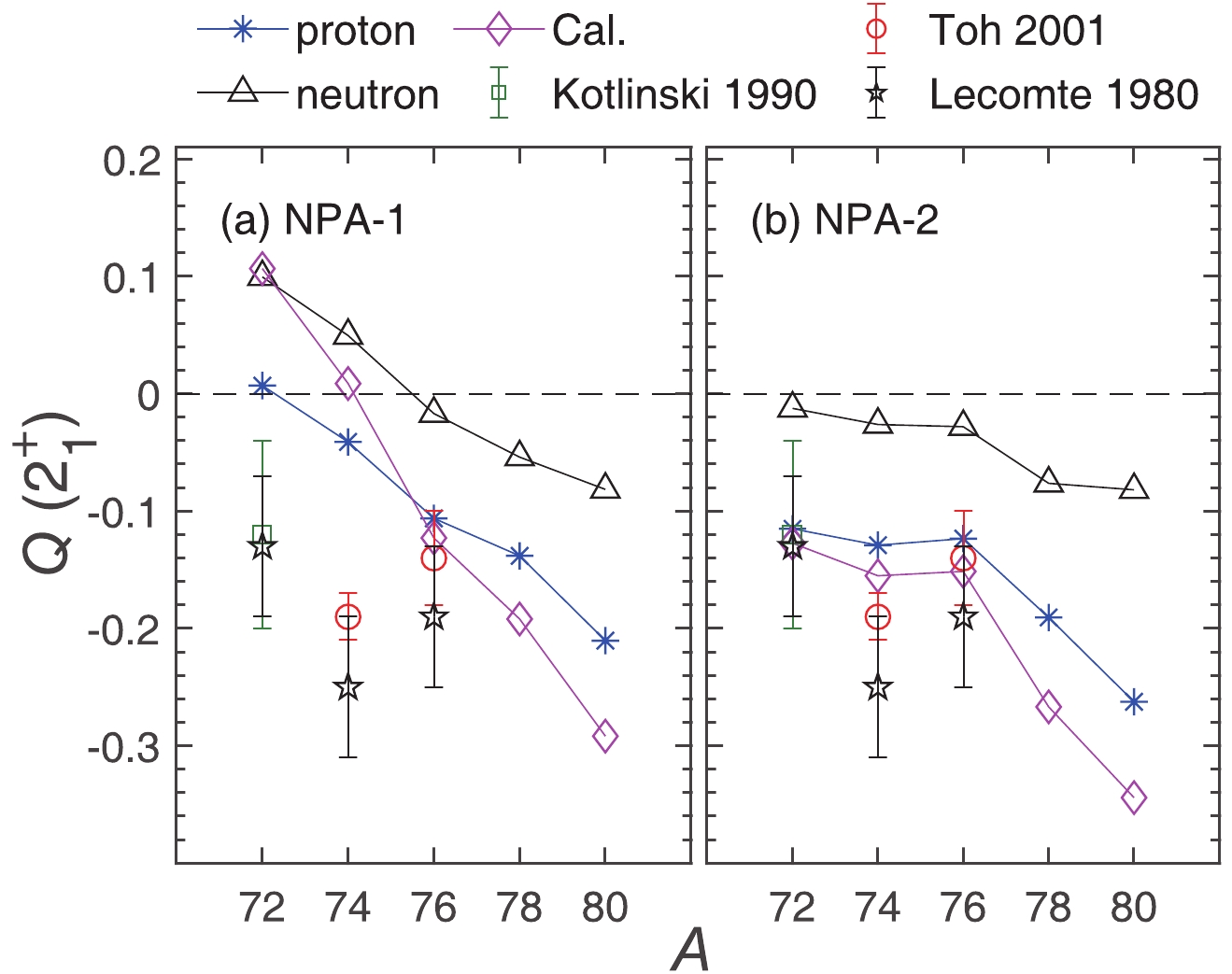

Figure 5.  (color online) The proton/neutron contribution to $Q(2_1^{+})$ (in units of ${\rm{eb}}$) for even-even Ge isotopes in (a) NPA-1 and (b) NPA-2. The total calculated $Q(2_1^{+})$ values are denoted by "Cal.". The experimental data include Kotlinski 1990 [6], Lecomte 1980 [5], and Toh 2001 [7].

We now turn to the $ g $ factors of even-even Ge isotopes. Our results for the $ 2_1^{+} $, $ 4_1^{+} $, $ 6_1^{+} $, and $ 2_2^{+} $ states with NPA-1 and NPA-2 are presented in Table 4. The subscripts "free" and "eff" refer to the results using the free and effective spin gyromagnetic ratio, with $ g_{s(\rm eff)} = 0.7 g_{s(\rm free)} $. One can see in this table that our results with NPA-1 generally reproduce the measured $ g(2_2^{+}) $ factors, but underestimate the $ g(2_1^{+}) $ and $ g(4_1^{+}) $ factors, similarly to the shell-model calculations [12]. Our results with NPA-2$ _{\rm eff} $ give a better description of the experimental data, especially for the $ g(2_1^{+}) $ factors.

nuclei	$J_i^{\pi}$	expt.	JJ4Bfree	JUN45free	JUN45eff	NPA-1free	NPA-1eff	NPA-2free	NPA-2eff
72Ge	$2^+_1$	$+0.421(16)$	+0.228	+0.271	+0.304	$+0.12$	$+0.18$	$+0.27$	$+0.31$
	$4^+_1$	$+0.39(13)$	+0.134	+0.236	+0.276	$+0.05$	$+0.11$	$+0.18$	$+0.24$
	$6^+_1$					$ -0.09 $	$ -0.01 $	$ +0.06 $	$ +0.12 $
	$ 2^+_2 $	$ +0.42(21) $	+0.472	+0.636	+0.627	$ +0.49 $	$ +0.52 $	$ +0.35 $	$ +0.39 $
74Ge	$ 2^+_1 $	$ +0.365(8) $	+0.260	+0.247	+0.289	$ +0.11 $	$ +0.17 $	$ +0.29 $	$ +0.33 $
	$ 4^+_1 $	$ +0.40(12) $	+0.180	+0.152	+0.206	$ +0.03 $	$ +0.10 $	$ +0.23 $	$ +0.28 $
	$ 6^+_1 $					-0.08	≈0	+0.13	+0.18
	$2^+_2$	$+0.47(10)$	+0.437	+0.570	+0.576	$+0.45$	$+0.48$	$+0.38$	$+0.42$
76Ge	$2^+_1$	$+0.330(7)$	+0.235	+0.304	+0.347	$+0.15$	$+0.21$	$+0.28$	$+0.33$
	$4^+_1$	$+0.24(17)$	+0.160	+0.229	+0.286	$+0.06$	$+0.13$	$+0.11$	$+0.17$
	$6^+_1$					$ -0.04 $	$ +0.04 $	$ -0.02 $	$ +0.06 $
	$ 2^+_2 $	$ +0.39(5) $	+0.480	+0.513	+0.497	$ +0.40 $	$ +0.44 $	$ +0.50 $	$ +0.54 $
78Ge	$ 2^+_1 $					$ +0.14 $	$ +0.21 $	$ +0.33 $	$ +0.37 $
	$ 4^+_1 $					$ -0.04 $	$ +0.04 $	$ +0.17 $	$ +0.23 $
	$ 6^+_1 $					$ +0.20 $	$ +0.26 $	$ +0.22 $	$ +0.28 $
	$ 2^+_2 $					$ +0.46 $	$ +0.49 $	$ +0.59 $	$ +0.62 $
80Ge	$ 2^+_1 $					+0.24	+0.33	+0.44	+0.52
	$4^+_1$					$ +0.39 $	$ +0.48 $	$ +0.43 $	$ +0.51 $
	$ 6^+_1 $					$+0.41$	$+0.50$	$+0.45$	$+0.52$
	$2^+_2$					$ +0.23 $	$ +0.33 $	$ +0.78 $	$ +0.81 $

Table 4.  $g$ factors for even-even ^72-80Ge. A comparison is given between the experimental data [12], SM results [12], and the NPA results in this work. The subscripts "free" and "eff" refer to the calculations using the free and effective spin gyromagnetic ratios, with $g_{s(\rm eff)} = 0.7 g_{s(\rm free)}$. For the orbital gyromagnetic ratios, we adopt in our calculations the values $g_{l\pi} = 1$ and $g_{l\nu} = 0 $.

The $ g(2_1^+) $ factor in NPA is expressed as $ g(2^+_1) = \frac{C_{22,10}^{2 \; 2}}{2} \langle 2_1^+||g_{l\pi} L_{\pi} + g_{l\nu} L_{\nu} + g_{s\pi} S_{\pi} + g_{s\nu} S_{\nu}||2_1^+\rangle $. It can be rewritten as $ g(2^+_1) = g_{\pi}(2^+_1)+g_{\nu}(2^+_1) = g_{s}(2^+_1)+g_{l}(2^+_1) $, with

Here, $ g_{\pi}(2^+_1) $, $ g_{\nu}(2^+_1) $, $ g_{s}(2^+_1) $, and $ g_{l}(2^+_1) $ refer to the proton, neutron, spin, and orbital contributions to the total $ g(2_1^{+}) $ factor, respectively. We calculate these four contributions and present our results with the effective spin gyromagnetic ratios in Fig. 6.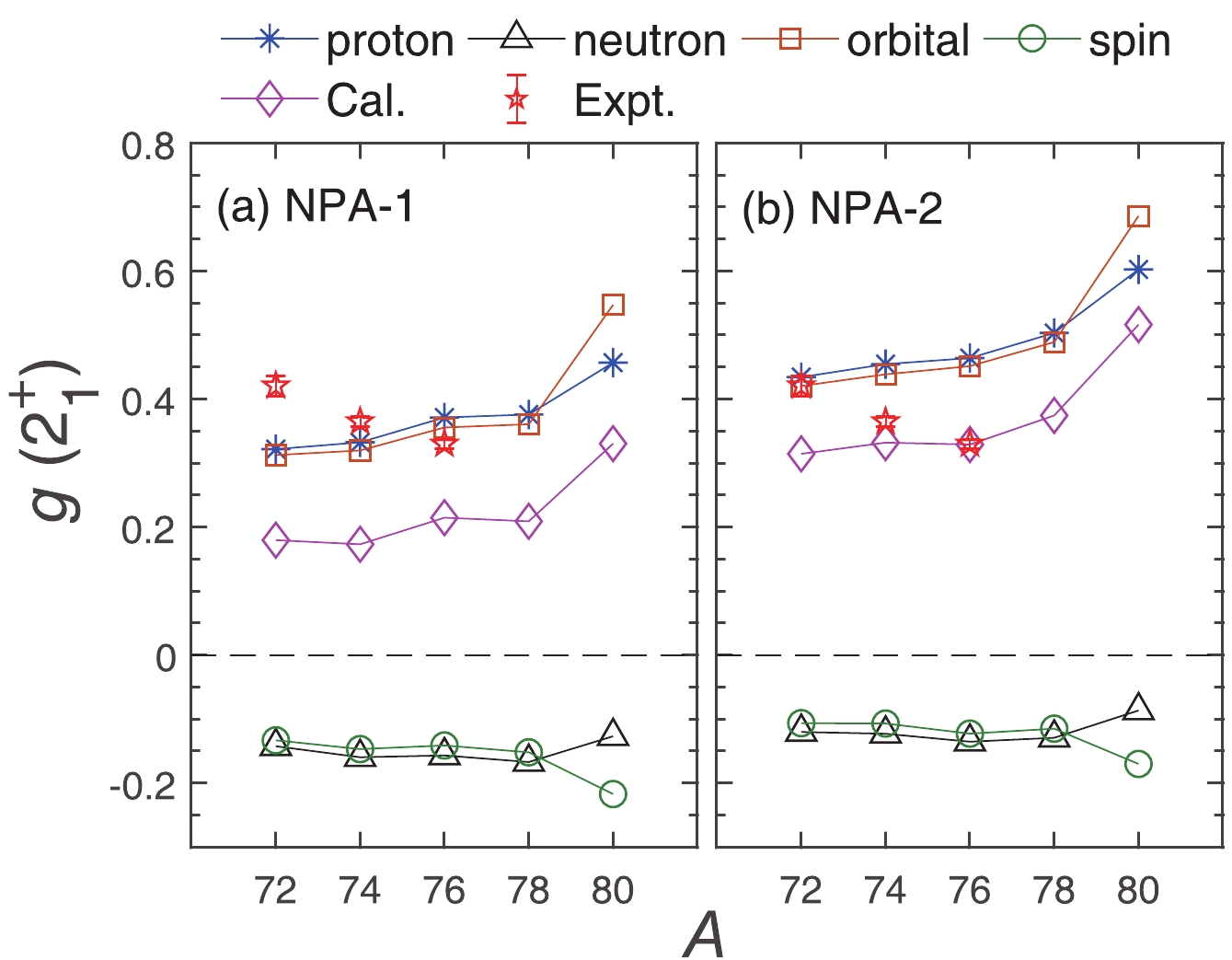

Figure 6.  (color online) The proton, neutron, orbital and spin contributions to the total $g(2_1^{+})$ for even-even Ge isotopes with (a) NPA-1 and (b) NPA-2. Our results are obtained using the effective spin gyromagnetic ratios ($g_{s\pi} = 5.586\times 0.7 $ and $g_{s\nu} = -3.826\times 0.7 $). The total $g(2_1^{+})$ is represented by purple rhombus. The experimental data are from Ref. [12].

In Fig. 6, the positive sign of the total $ g(2_1^{+}) $ originates from the proton contribution. The neutron contribution is negative and relatively small. It is found that the proton contribution has larger positive values with NPA-2 than with NPA-1, so that the calculated total $ g(2_1^{+}) $ with NPA-2 is closer to the experimental data. As we have discussed before, the configuration mixing of $ |D_{\nu}\rangle $, $ |D_{\pi}\rangle $ and other components are stronger with NPA-2. The dominant effect of the proton contribution in Fig. 6(b), as well as the dominant proton character of $ Q(2_1^{+}) $ in Fig. 5(b), indicate the importance of collective effects in these nuclei. This is consistent with the result that the simple collective estimate of $ Z/A $ is in better agreement with the observed $ g $ factors [12].

In Table 4, we present our calculated $ g $ factors with the two kinds of spin gyromagnetic ratio, with $ g_{s(\rm eff)} = $$0.7 g_{s(\rm free)} $. Our results with the free spin gyromagnetic ratio are always smaller than with the effective spin gyromagnetic ratio. To understand better this result, we present the spin and orbital contributions to $ g(2_1^{+}) $ in Fig. 6. It is interesting that the orbital (or spin) contributions almost coincide with the proton (or neutron) contributions, except for ⁸⁰Ge. This is because the spin contribution of the proton is very small (about 0.01 for ^{72, 74, 76, 78}Ge and $ -0.08 $ for ⁸⁰Ge), and in our calculations the orbital gyromagnetic ratio of the neutron is taken as $ g_{l\nu} = 0 $. Therefore, the resultant orbital contributions are due to protons, with relatively large and positive values. The spin contributions are mainly from neutrons, with relatively small and negative value. As a result, our $ g $ factors with the free spin gyromagnetic ratio are smaller than with the effective spin gyromagnetic ratio.

We finally come to our results for $ B(E2) $, the electric quadrupole moment $ Q $ and the magnetic moment $ \mu $ , corresponding to the partial yrast states for odd-mass ^{75, 77, 79}Ge isotopes, presented in Tables 5-6. Odd-mass nuclei are more complicated than their even-even neighbors, and the experimental data for these nuclei are relatively scarce. One can see in Tables 5-6 that our results agree well with the available measurements for ⁷⁵Ge.

Nuclei	$ B(E2) $							$ Q $
	state	expt.	JJ4B	JUN45	NPA−1	NPA−2		state	expt.	JJ4B	JUN45	NPA−1	NPA−2
75Ge	$ 5/2^+_1\rightarrow 7/2^+_1 $	$ 30(24) $	25.70	21.45	$ 39.27 $	$ 32.07 $		$ 9/2^+_1 $		+0.008	−0.031	$-0.09$	$-0.13$
	$9/2^+_1\rightarrow 5/2^+_1$		2.66	1.42	$ 0.69 $	$ 2.96 $		$ 7/2^+_1 $		$+0.087$	$-0.089$	$-0.10$	$-0.22$
	$9/2^+_1\rightarrow 7/2^+_1$		22.47	19.46	$ 27.63 $	$ 27.48 $		$ 5/2^+_1 $		$+0.271$	$-0.295$	$+0.09$	$+0.23$
77Ge	$9/2^+_1\rightarrow 7/2^+_1$		21.43	17.71	$ 20.82 $	$ 27.59 $		$ 9/2^+_1 $		$+0.176$	$+0.096$	$+0.02$	$+0.03$
	$5/2^+_1\rightarrow 9/2^+_1$		6.86	3.96	$ 1.41 $	$ 2.24 $		$ 7/2^+_1 $		$+0.470$	$+0.237$	$+0.07$	$+0.15$
	$5/2^+_1\rightarrow 7/2^+_1$		5.85	12.90	$ 30.56 $	$ 33.35 $		$ 5/2^+_1 $		$-0.137$	$-0.179$	$+0.17$	$+0.22$
79Ge	$9/2^+_1\rightarrow 7/2^+_1$		11.94	11.37	$ 18.02 $	$ 24.10 $		$ 9/2^+_1 $		$+0.285$	$+0.219$	$+0.26$	$+0.29$
	$9/2^+_1\rightarrow 5/2^+_1$		3.76	3.79	$ 8.06 $	$ 5.62 $		$ 7/2^+_1 $		$+0.446$	$+0.415$	$+0.53$	$+0.60$
								$5/2^+_1$		+0.012	$-0.048$	$+0.01$	$-0.01$

Table 5.  $ B(E2) $ (in units of W.u.) and the electric quadrupole moment $ Q $ (in units of $ {\rm{eb}} $) for odd-mass ^75,77,79Ge. A comparison is given between the experimental data [30], SM results (JJ4B and JUN45) [16] and the results of this work (NPA-1 and NPA-2). The effective charges in the SM results [16] are $ e_{\pi} = 1.5 e $ and $ e_{\nu} = 0.5 e $. For $ e_{\pi} = 1.5 e $ and $ e_{\nu} = 1.1 e $, $ B(E2;5/2_1^+\rightarrow 7/2_1^+) = 40.8 $ W.u. in JUN45 for ⁷⁵Ge [13].

In NPA, the signs of $ \mu(5/2_1^+,7/2_1^+,9/2_1^+) $ and $ \mu(1/2_1^-) $ for ^{75, 77, 79}Ge are negative and positive, respectively. In the dominant NPA configurations, the unpaired neutron in the $ 5/2_1^+ $, $ 7/2_1^+ $, $ 9/2_1^+ $ states is in the $ \nu g_{9/2} $ orbit, and that in the $ 1/2_1^- $ state is in the $ \nu p_{1/2} $ orbit. Therefore, the signs of $ \mu(5/2_1^+,7/2_1^+,9/2_1^+) $ and $ \mu(1/2_1^-) $ are related to the neutron single-particle motion, whose Schmidt single-particle $ \mu $ values are $ \mu(g_{9/2})\approx -1.91 $ and $ \mu(p_{1/2})\approx +0.64 $, respectively.

In this paper, we presented the calculations of the low-lying structure of even-even ^72-80Ge and odd-mass ^75-79Ge isotopes in the framework of the nucleon-pair approximation (NPA) of the shell model, with the focus on the electric quadrupole moment $ Q $ and the magnetic moment $ \mu $ (or the $ g $ factor). We employed the monopole and quadrupole pairing plus quadrupole-quadrupole interaction in the $ p_{1/2} $, $ p_{3/2} $, $ f_{5/2} $, and $ g_{9/2} $ model space with respect to the doubly closed shell nucleus ⁷⁸Ni for both the valence protons and neutron holes.

We performed our calculations using two sets of two-body interaction parameters. The first one, denoted as NPA-1, is the same as for Zn and Ga isotopes [23]. The other is the optimized parameter set, denoted as NPA-2. The present calculations provide constraints for the parameters of the phenomenological shell model Hamiltonian. The optimized parameter set for ^72,74Ge has a larger quadrupole-quadrupole interaction for both neutrons and protons, and a larger quadrupole pairing strength for protons, than NPA-1. Our results with NPA-2 reproduce well the experimental data, especially for $ Q(2_1^+) $ for ^72,74,76Ge and $ g(2_1^+) $ for ^74,76Ge.

We studied the main components of the $ 2_1^{+} $ states in ^72-80Ge in terms of the NPA pair basis. It was found that configuration mixing is stronger in ^{72, 74}Ge with NPA-2. We investigated the proton and neutron contributions to the total $ Q(2_1^{+}) $ moments and $ g(2_1^+) $ . The negative $ Q(2^+_1) $ in ^{72, 74}Ge, as well as the systematic evolution of $ g(2_1^+) $ with the mass number $ A $, essentially originate from the proton component. The good agreement of $ Q(2^+_1) $ and $ g(2_1^+) $ with NPA-2 demonstrates that strong configuration mixing in ^{72, 74}Ge plays an important role in these low-lying states.

We presented tabulated values of $ B(E2) $ , the electric quadrupole moment $ Q $ and the magnetic moment $ \mu $ (or the $ g $ factor) for some low-lying states in both even-even and odd-mass Ge isotopes. The experimental data for these nuclei are relatively scarce. Our results could be very useful for future studies of nuclei in this region.