-
With more and more experimental data available for rare isotope heavy ion collisions at intermediate energies, there is an opportunity to explore the properties of nuclear matter at high density and large isospin asymmetry using the tools of transport models. Both the mean field and the in-medium two-body scattering cross-sections, coming from the same nucleon-nucleon (NN) interaction [1-4], should be treated self-consistently in a transport model. However, it is very difficult to solve the dynamical equation and the G-matrix simultaneously, so that most transport models deal with the mean field and collisions separately, for which accurate in-medium nucleon-nucleon cross-sections (NNCS) are required. On the other hand, the in-medium NNCS can provide information which is very important to study the structure of nuclei, especially of the rare isotopes. Also, the in-medium NNCS are of interest in their own right, as they are related to viscosity, mean free path of nucleons in nuclear matter, and other nuclear transport coefficients [5-7].
Unlike the NNCS in free space, which can be directly measured in experiments, the in-medium NNCS can only be calculated using theoretical models, such as the Brueckner-Hartree-Fock and the Dirac-Brueckner-Hartree-Fock theory, the Green function approach, and the relativistic mean field model. The in-medium NNCS depend on several quantities, such as the density and isospin asymmetry of nuclear matter, the total momentum of a nucleon pair in the nuclear matter rest frame, the relative momentum of a nucleon pair, and even on the temperature. There have been many studies which demonstrate that the NNCS in medium should be suppressed compared to free NNCS [2, 8-19]. However, the modification factors given in these works differ significantly, due to the different treatment of their dependence on different levels of approximation.
Another way to get information on the in-medium NNCS is to compare the simulation results from transport theory with experimental data for nuclear reactions [20, 21]. As basic ingredients of transport models, simple parametrization of the in-medium NNCS are widely used, such as the parametrization given by G. Li [14, 15] and Q. Li [22-24]. The phenomenological in-medium NNCS can be scaled by the effective mass [25-28]
$ \sigma^*_{\rm NN} = \left[\frac{\mu^*(\rho, p)}{\mu(p)} \right]^2\sigma^{\rm free}_{\rm NN}, $

(1) where
$ \mu $ and$ \mu^* $ are the reduced masses of colliding nucleon pairs in vacuum and the medium, respectively, or by the empirical relation$ \sigma^*_{\rm NN} = ( 1+\eta \rho/\rho_0 )\sigma^{\rm free}_{\rm NN}, $

(2) where
$ \eta $ is an adjustable parameter. In agreement with the theoretical results, most of the experimental evidence, such as the energy balance [29-31], stopping power [32], collective flow [24, 27, 32, 33], etc, support a reduced in-medium nucleon-nucleon elastic cross-section (NNECS). However, the reduction factor has not been determined definitely. Since the mean field and two body collisions are convoluted, the model dependent treatment of the nuclear potential and of the collisions may lead to considerable discrepancies in the model output even for the simplest box calculations. In comparison to heavy ion collisions, some kind of direct reactions involving a smaller number of degrees of freedom in the reaction process may reduce model dependence. Hence, nucleon induced reactions are more suitable for studying the in-medium NNCS not only because of their simple mechanism but also because they reflect the in-medium NNCS around the incident beam energy and below the saturation density [34-38].In this work, within the improved quantum molecular dynamics (ImQMD) model, we try to extract the in-medium NNECS from the experimental data for the nucleon induced reaction cross-sections (RCSs). The paper is organized as follows. In Section 2, we briefly introduce the model we adopted. In Section 3, we introduce the form of medium modification of NNCS and the method to determine the modification factor. Finally, a brief summary is given in Section 4.
-
In the frame of the ImQMD05 model [32, 39], each nucleon is described as a Gaussian wave-packet. The motion of the center of the wave-packets in the mean field follows the evolution of the Hamilton canonical equation. The potential energy
$ U $ , including the local nuclear potential energy and Coulomb energy, reads$ U = U_{\rm{loc}}+U_{\rm{Coul}}. $

(3) The local part is obtained from the Skyrme interaction,
$ U_{\rm{loc}} = \int V_{\rm{loc}}[\rho(\mathit{\boldsymbol{r}})] {\rm d} \mathit{\boldsymbol{r}} $ .$ V_{\rm{loc}} $ is the Skyrme potential energy density functional with the spin-orbit term omitted, which reads$ \begin{split}V_{\rm{loc}} =& \frac{\alpha}{2}\frac{\rho ^{2}}{\rho _{0}}+\frac{\beta }{\eta +1} \frac{\rho ^{\eta +1}}{\rho _{0}^{\eta }}+\frac{g_{\rm{sur}}}{2\rho _{0}}\left(\nabla \rho \right)^{2} \\&+\frac{g_{\rm{sur, iso}}}{\rho_{0}}[\nabla(\rho_{\rm{n}}-\rho_{\rm{p}})]^{2} +(A\rho^{2}+B\rho^{\eta+1}+C\rho^{8/3})\delta^{2}\\&+g_{\rho\tau}\frac{\rho^{8/3}}{\rho_{0}^{5/3}}. \end{split}$

(4) The subscript symbols "n" and "p" indicate neutron and proton, respectively, and "
$ \delta $ " is the isospin asymmetry$ \delta = (\rho_{{\rm n}}-\rho_{{\rm p}})/(\rho_{{\rm {\rm n}}}+\rho_{{\rm p}}) $ . The coefficients in Eq. (4) can be obtained from the parameters of the standard Skyrme interactions, one can refer to [32, 39] for details.In this work, the isospin dependent NNCS given by Cugnon et al. [40] is adopted as free NNCS in the collision term. The reaction cross-sections depend directly on the collision term, and the isospin dependent Pauli blocking effect should be carefully considered. The final states of each pair of nucleons undergoing collision must satisfy the uncertainty principle
$ \frac{4\pi}{3} r_{ij}^{3} \cdot \frac{4\pi}{3} p_{ij}^{3} \geqslant \frac{h^{3}}{8}. $

(5) The
$ r_{ij} $ and$ p_{ij} $ are the distances between two nucleons in the coordinate and momentum spaces. The probability for a state to be occupied can be calculated as$ P_{i} = \sum_{k, k\neq i}^{A} \frac{1}{(\pi \hbar)^{3}} \exp\left[-\frac{(\mathit{\boldsymbol{r}}_{i}-\mathit{\boldsymbol{r}}_{k})^{2}}{2\sigma_{r}^{2}}\right] \exp\left[-\frac{(\mathit{\boldsymbol{p}}_{i}-\mathit{\boldsymbol{p}}_{k})^{2}}{2\sigma_{p}^{2}}\right]. $

(6) For two nucleons scattered to the final states
$ i $ and$ j $ , the Pauli blocking is$ P_{\rm{block}} = 1-(1-P_{i})(1-P_{j}). $

(7) The RCS for the nucleon induced reactions can be calculated as
$ \sigma_R = \int_0^{b_{\rm{max}}} 2\pi P_{\rm{inel}}(b) b {\rm d} b, $

(8) where
$ P_{\rm{inel}}(b) $ is the probability of the inelastic scattering event with impact parameter$ b $ .$ b_{\rm{max}} $ is the maximum impact parameter, i.e., there are no inelastic collisions when$ b > b_{\rm{max}} $ .$ P_{\rm{inel}}(b) $ is indirectly determined from the experimentally measured probability of elastic scattering events, i.e,$ P_{\rm{inel}}(b) $ is defined as$ P_{\rm{inel}} = 1-P_{\rm{un}}-P_{\rm{el}} $ . Any scattering event in which the emitted nucleon has an energy close to the incident energy, whether it had collided or not, is defined as the elastic scattering event.$ P_{\rm{un}} $ is the probability of the unaffected event, i.e., for an incident nucleon to pass through the target while keeping its momentum direction and magnitude.$ P_{\rm{el}} $ is the probability of the elastic event, i.e., for the incident nucleon to change its momentum direction while keeping its momentum magnitude. The calculation of RCS in this work follows the analyzing method used in the experiments. -
As mentioned above, the mean field and NN collisions affect the nuclear reaction process simultaneously. To obtain the correct modification factor for NNCS, the effect of the mean field on RCS should be checked first. As a test, four Skyrme parameter sets MSL0 [41], BSk1 [42], SkP [43], SkI2 [44] are adopted to simulate the reaction
$ {\rm p}+^{56} $ Fe. The comparison between the calculated excitation functions of RCS and the experimental data is illustrated in Fig. 1.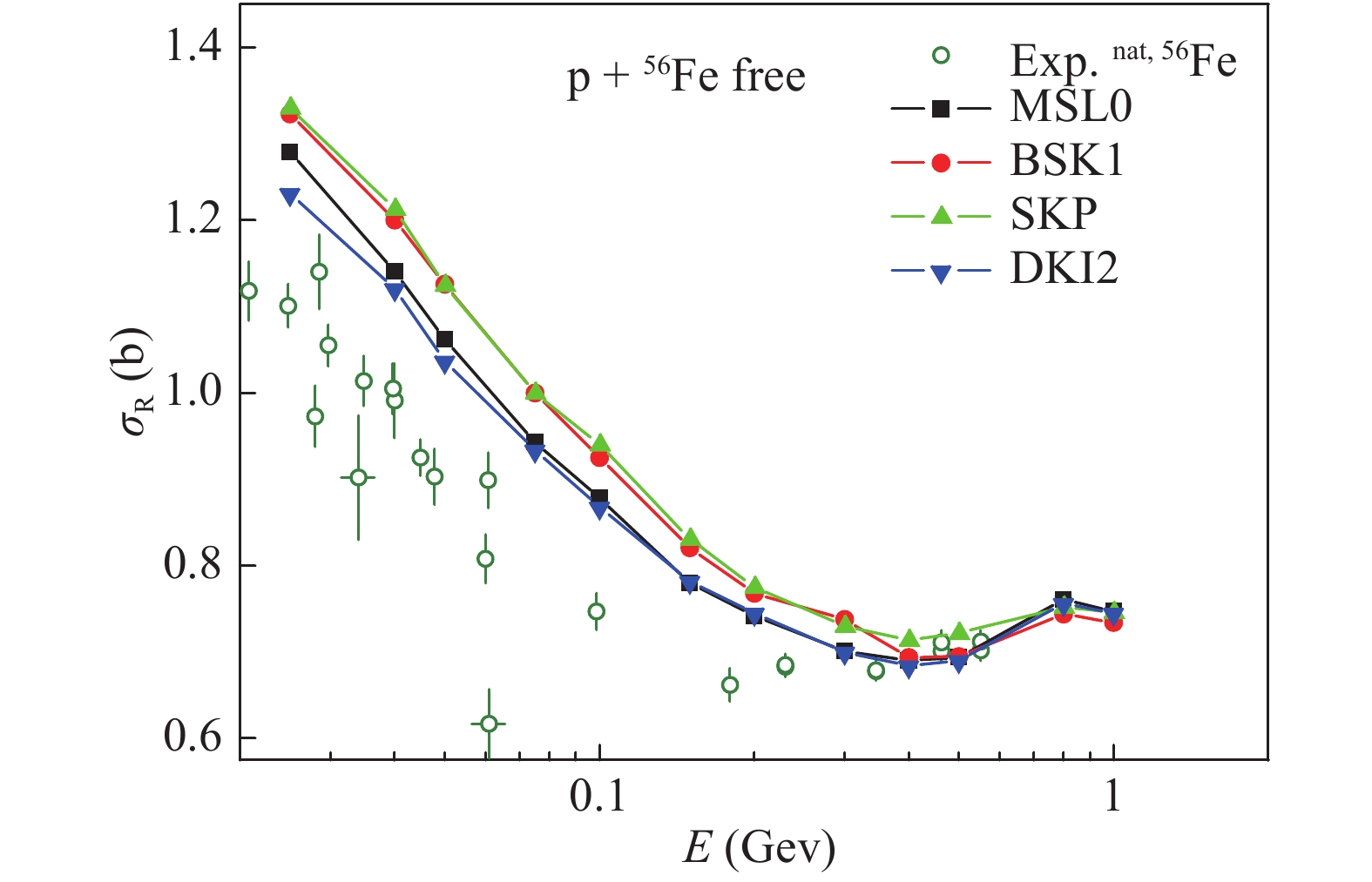
Figure 1. (color online) Excitation functions of RCS for
${\rm p}+^{56}$ Fe calculated with free NNECS and four Skyrme parameter sets compared with the experimental data. The data are taken from Ref. [45].One can see that with various EOS adopted, the calculated RCS are different. The difference becomes smaller with increasing energy, since the NN collisions dominate the reaction. In the case of energies higher than 500 MeV, the results using free NNECS reproduce the experimental data well. However, all calculation results overestimate the experimental data below 500 MeV. This means that the in-medium NNECS below 500 MeV are smaller than free NNECS, and that the in-medium NNECS above 500 MeV are very close to free NNECS. To obtain the correct medium correction factors for NNECS, a reasonable EOS tested by other methods should be used in simulations. MSL0, one of the Skyrme parameter sets which best satisfy the current understanding of the physics of nuclear matter over a wide range of applications [46], is used in the following calculations.
According to the above analysis and the other studies of NNSC, the free NNCS is modified in this work according to
$ \sigma^{\rm{*}}_{\rm{tot}} = \sigma^{\rm{free}}_{\rm{in}}+\sigma^*_{\rm{el}} = \sigma^{\rm{free}}_{\rm{in}}+F(u, \delta, p)\sigma^{\rm{free}}_{\rm{el}}. $

(9) Here,
$ \sigma^{\rm{free}}_{\rm{el}} $ and$ \sigma^{\rm{free}}_{\rm{in}} $ are the free isospin dependent elastic and inelastic cross-sections, respectively. The form of the medium correction factor is the same as proposed by Q. Li et al. in Refs. [22-24]. The$ F(u, \delta, p) = F_{\delta}^{p} \cdot F_{u}^{p} $ depends on the reduced nuclear density$ u = \rho/\rho_0 $ , the isospin asymmetry$ \delta = (\rho_{{\rm n}}-\rho_{{\rm p}})/(\rho_{{\rm n}}+\rho_{{\rm p}}) $ and the momentum. Here,$ F_u = \lambda+(1-\lambda)\exp(-u/\zeta), $

(10) $ F_{\delta} = 1-\tau_{ij} A(u)\delta,\ \ \ \ A(u) = \frac{0.85}{1+3.25u}. $

(11) For
$ i = j = n, \tau_{ij} = -1; i = j = p, \tau_{ij} = +1; i\ne j, \tau_{ij} = 0 $ . The$ F_{\delta}^{p} $ and$ F_{u}^{p} $ factors can be expressed in a single formula as,$ F_{\delta, u}^{p} = \left\{ \begin{array}{lr} f_0, & p_{\rm{NN}}> 1\ {\rm GeV}/{c}, \\ \displaystyle\frac{F_{\delta, u}-f_0}{1+(p_{\rm{NN}}/p_0)^{\kappa}}+f_0, & p_{\rm{NN}} \leqslant 1 \ {\rm GeV}/{c}, \end{array} \right. $

(12) where
$ p_{\rm{NN}} $ is the relative momentum in the NN center-of-mass system. By varying the parameters$ \lambda $ ,$ \zeta $ ,$ f_0 $ ,$ p_0 $ and$ \kappa $ one can obtain different medium corrections for NNECS. The parameter sets used in this work are listed in Table 1 and 2. Among these parameter sets, FU1-3 and FP1-5 are taken from Refs. [22-24], FU4 and FP6 are obtained in this work.set $\lambda$ 

$\zeta$ 

FU1 1/3 0.54568 FU2 1/4 0.54568 FU3 1/6 1/3 FU4 1/5 0.45 Table 1. Parameter sets used for the density dependent correction factor Fu.
set $f_0$ 

$p_0 /({\rm GeV}/c)$ 

$\kappa$ 

FP1 1 0.425 5 FP2 1 0.225 3 FP3 1 0.625 8 FP4 1 0.3 8 FP5 1 0.34 12 FP6 1 0.725 10 Table 2. Parameter sets used for the momentum dependence of the correction factor Fu, δ.
The medium correction factor
$ F_u $ as function of the reduced density$ u $ and the momentum dependence of$ F_u $ with FU4 at$ \rho/\rho_0 = 0.5 $ are represented in Fig. 2.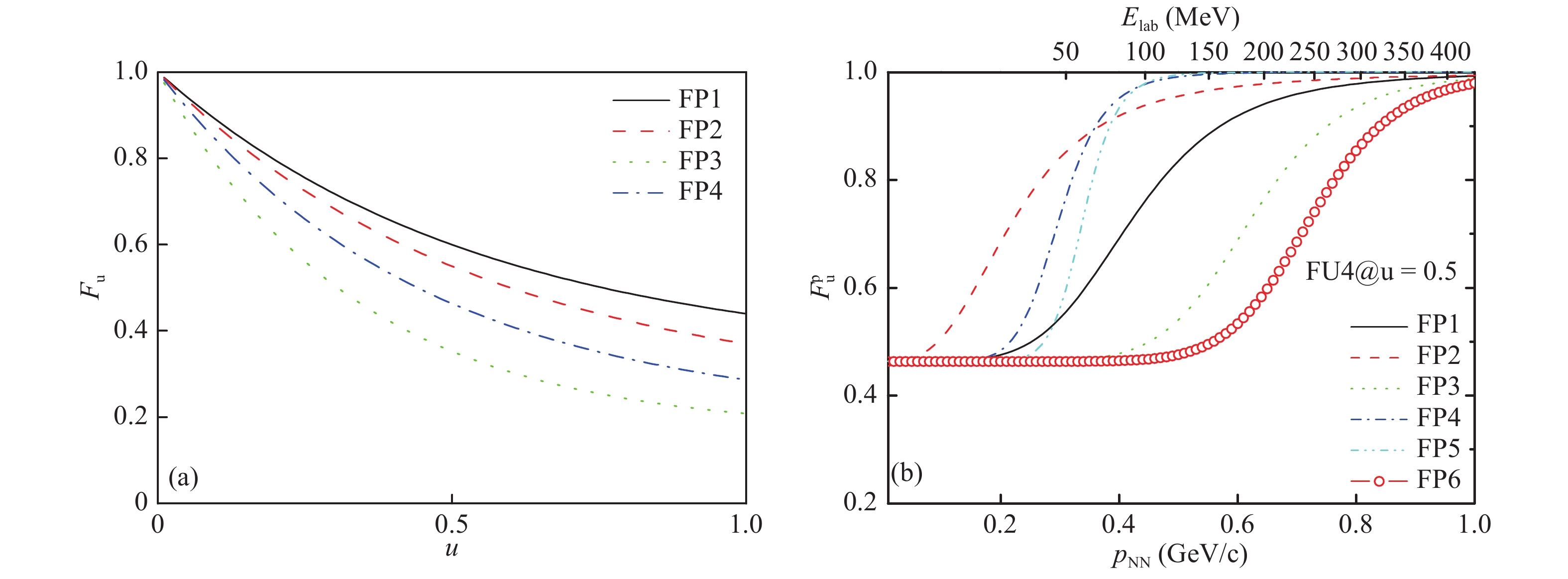
Figure 2. (color online) (a) The density dependence of
$F_u$ ; (b) the momentum dependence of$F_u$ with FU4 at$\rho/\rho_0 = 0.5$ .From this figure, one can see the character of the correction factor for NNECS, since with the increase of density the in-medium NNECS decreases. For a certain set of density values, the in-medium NNECS may be enhanced with increasing momentum.
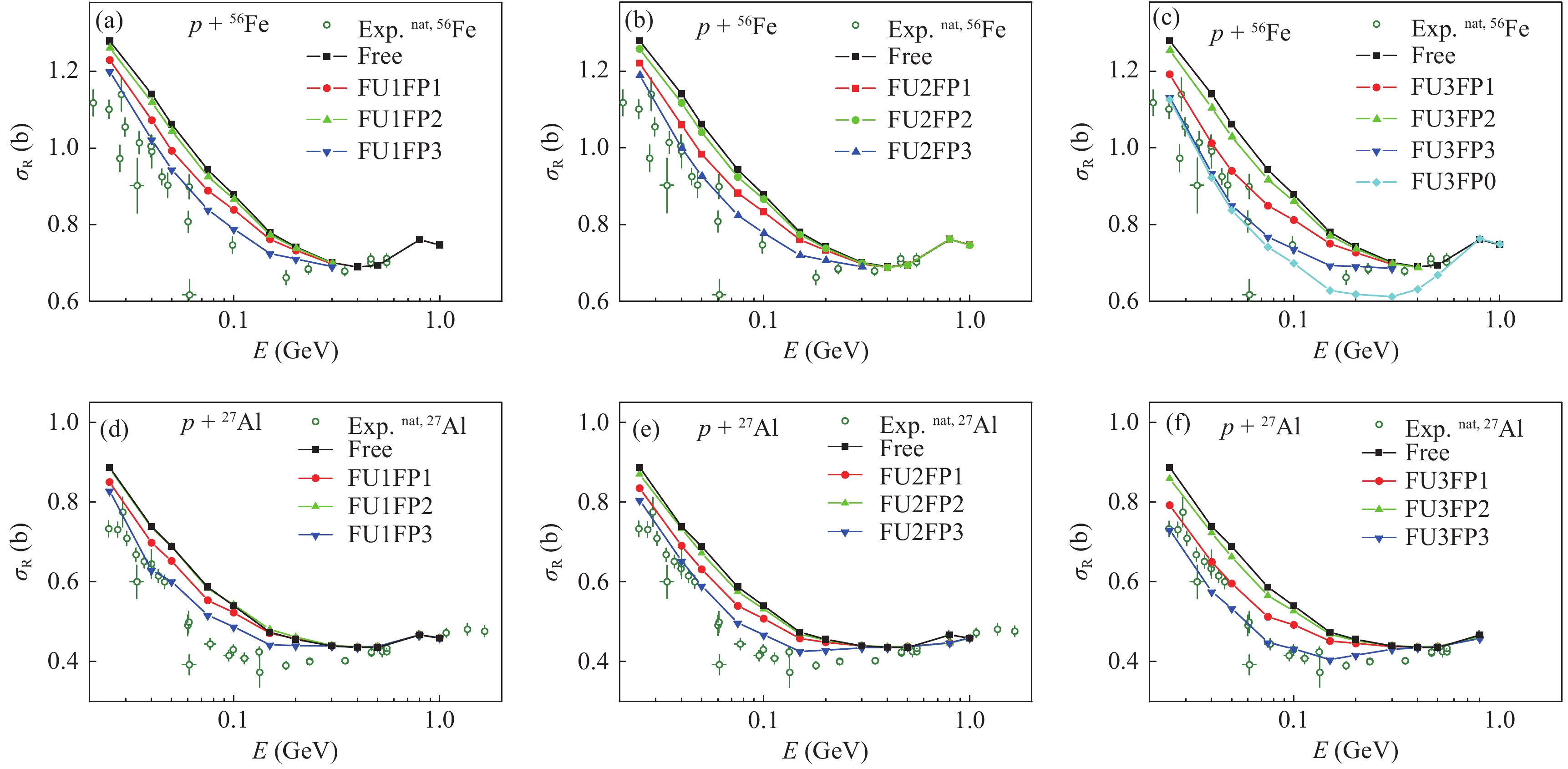
The various in-medium NNECS obtained from combinations of parametrization FU1, FU2, FU3 and FP1, FP2, FP3 are first tested for the excitation function of RCS for
$ {\rm p}+^{56} $ Fe, and$ {\rm p}+^{27} $ Al, as shown in Fig. 3.By using the in-medium NNECS, the description of the excitation function of RCS is greatly improved. However, none of the parametrizations reproduces the experimental data for
$ {\rm p}+ $ Fe and$ {\rm p}+ $ Al simultaneously. The combinations of FU2+FP3 and FU3+FP3 give best results. FU2+FP3 overestimates the data overall; FU3+FP3 underestimates the data at low energies, especially for the case of Al. Hence, it is necessary to propose a new parameter set for the in-medium NNECS. According to the momentum dependence of the in-medium NNECS$ F_u^p $ shown in Fig. 2(b), the enhancement effect of momentum correction does not appear at such low energies if FP3 is adopted. As a test, the excitation function of RCS calculated with FU3 and without momentum correction is shown in subfigure 3(c) , marked by FU3FP0. One can see that the momentum correction does not visibly affect the results below 50 MeV, while the RCSs at high energies are underestimated if the momentum correction is absent. This proves our assumption and implies that the depressive effect provided by FU3 is too strong while the one provided by FU2 is too weak.By varying the parameters
$ \lambda $ (0.18−0.22),$ \zeta $ (0.35−0.50),$ p_0 $ (0.675−0.775) and$ \kappa $ (9.0−11.0), more than a dozen combinations of$ F_u $ and$ F^p $ were tested for the experimental data of$ {\rm p}+ $ Fe and$ {\rm p}+ $ Al. A parameter set FU4, is found to provide a reasonable correction effect. For the density correction parameter set FU4, the corresponding momentum correction parameter FP6 is obtained by fitting the experimental data for RCS at higher energies. In Fig. 4, the excitation functions of RCS for$ {\rm p}+ $ Fe and$ {\rm p}+ $ Al, calculated with the combination FU4+FP6, are presented. The results calculated with the combinations FU2+FP3 and FU3+FP3 are also presented for comparison. One can see that the combination FU4+FP6 globally reproduces the experimental data well.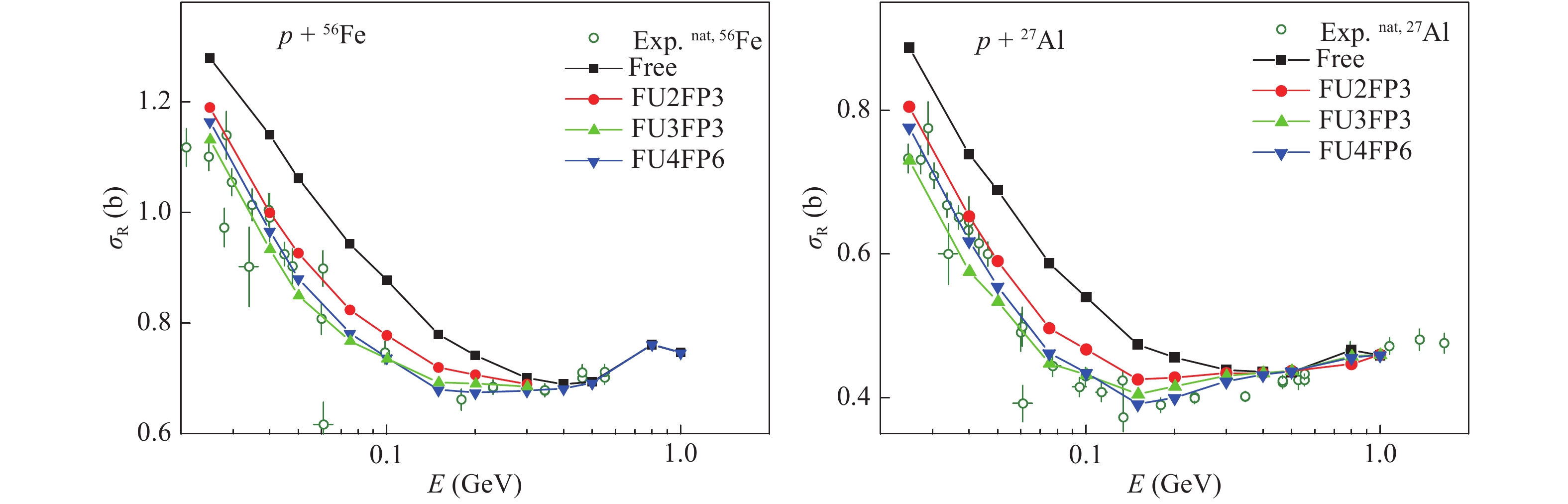
Figure 4. (color online) Same as Fig. 3 but with the results of FU4+FP6 added.
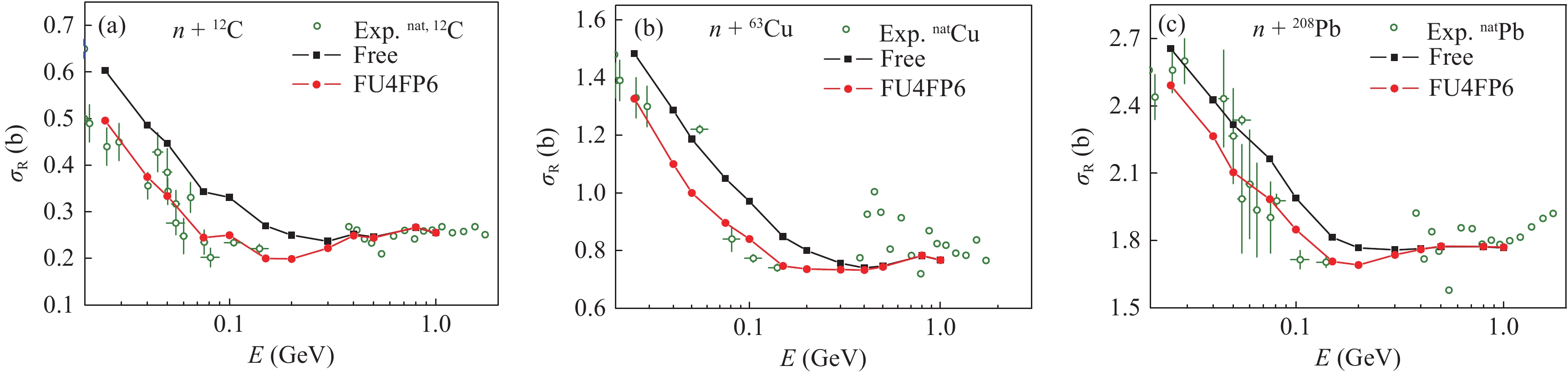
With the obtained in-medium NNECS given by FU4FP6, several reaction systems were calculated and compared to the experimental data. For the light to heavy targets A, proton induced reactions on 12C, 27Al, 40, 48Ca, 90Zr, 118Sn, 208Pb were simulated. The excitation functions of RCS for
$ {\rm p}+ $ A calculated with the in-medium NNECS, are compared with the experimental data in Fig. 5.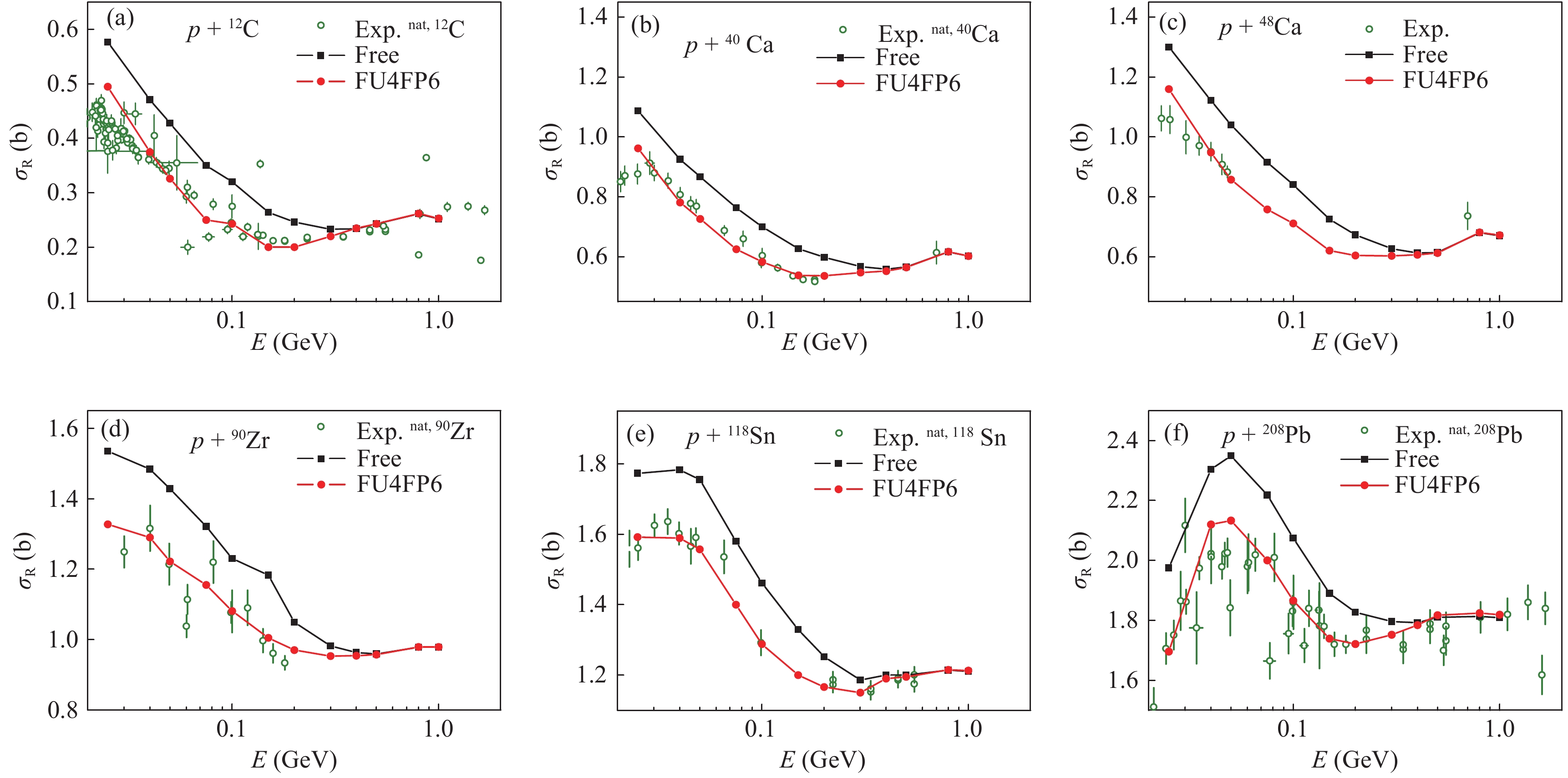
Figure 5. (color online) Excitation functions of RCS for
${\rm p}+$ A calculated with FU4+FP6 compared with the experimental data. Results calculated with free NNECS are also represented for reference. The experimental data are taken from Refs. [45, 47-50] for C, [45, 50] for Ca, [45, 47] for Sn, [45, 49] for Zr, and [45, 47, 50] for Pb targets, respectively.One can see that all experimental data are reproduced quite well. This demonstrates that the in-medium NNECS given by FU4FP6 is reasonable. In particular, not only are the excitation functions of RCS for the targets along the
$ \beta $ -stable line well described, but the excitation function of RCS for 48Ca, which is far away from the$ \beta $ -stable line, is also well reproduced. Beside the proton induced reactions, the neutron induced reactions are also used to test the in-medium NNECS.As seen in the results presented in Fig. 6, the excitation functions of RCS for
$ {\rm n}+ $ A calculated with FU4FP6 are in good agreement with the experimental data, which means that the medium correction of the isospin dependence of NNECS is reasonably reproduced. -
By using the improved quantum molecular dynamics model, the nucleon induced reactions on various targets with incident energies from 25 MeV to 1 GeV are investigated. The reaction cross-section is found to be very sensitive to the nucleon-nucleon cross-sections. By comparing the excitation functions of reaction cross-sections given by ImQMD model calculations with the experimental data, the medium modifications of the free nucleon-nucleon elastic cross-sections are investigated. Isospin, density, and momentum dependence of the medium correction factors of the free nucleon-nucleon elastic cross-sections are obtained. The parametrized formula is simple to use and gives reliable results for the nuclear reactions systems below the saturation density.
In-medium nucleon-nucleon elastic cross-sections determined from the nucleon induced reaction cross-section data
- Received Date: 2018-12-13
- Available Online: 2019-04-01
Abstract: Within the framework of the improved quantum molecular dynamics model, the medium modifications of the free nucleon-nucleon elastic cross-sections are investigated. By using various in-medium nucleon-nucleon elastic cross-sections in the model, the nucleon induced reactions on various targets are simulated, and the excitation functions of reaction cross-sections in the energy range from 25 MeV to 1 GeV are calculated. By comparing the calculations with the experimental data, the isospin, density, and momentum dependence of the medium correction factors of free nucleon-nucleon elastic cross-sections are determined.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: