-
A major purpose of relativistic heavy-ion collisions (HIC) performed at the RHIC [1–4] and the LHC [5–7] is to study the formation and map the properties of Quark-Gluon Plasma (QGP), a new kind of matter with de-confined quarks and gluons. An optimal probe of the creation and properties of the QGP is the jet quenching, a phenomenon indicating that an energetic parton propagating in the dense QCD medium suffers multiple scattering with other partons in the medium and subsequently loses a significant amount of its energy [8–10]. By indirectly quantifying the loss of the parton's energy in the medium by theoretical estimations and experimental data of final-state observables at large transverse momentum, such as leading hadron production, we can infer the transport properties of the QCD medium created in HIC [11–18].
An essential part of the jet quenching theory is the flavor dependence of the parton energy loss, i.e., the difference between energy loss patterns of quarks and gluons [9, 19]. In most perturbative QCD models of jet quenching, it is shown that an energetic gluon may lose more energy than a quark, which yields
$\Delta E_g/ \Delta E_q = $ $ (C_A/C_F) $ for asymptotic high-energy partons. However, in other models, the flavor pattern of energy loss may be different. For example, a hybrid strong/weak coupling model [20] utilizing parton energy loss results in a strongly coupled plasma described by the string theory, with$ \Delta E_g/ \Delta E_q = (C_A/C_F)^{1/3} $ . The difference in the energy loss of quarks and gluons may change the parton fraction in HIC relative to that in elementary proton-proton collisions, and thus modify the hadron chemistry [19, 21–24]. A deep understanding of the flavor dependence of parton energy loss is indispensable to solve the baryon anomaly, which remains an open question [21, 22, 25]. Another topic on the flavor dependence of parton energy loss is the mass dependence of the heavy quark energy loss. Refs. [26–31] provide further discussion on the mass hierarchy of jet quenching.Since the start of heavy-ion programs with the unprecedented colliding energies available at the LHC, full jet observables in HIC have attracted intense interests in terms of both theory and experiment [20, 32–50]. Jet observables could provide complementary information besides leading hadron productions, and they have been widely accepted as another excellent probe to investigate the properties of QGP. It is of great interest to study jet observable, which is sensitive to the pattern of gluon versus quark energy loss, and thus can help make further constrains in the jet quenching mechanism by utilizing the large amount data on jet measurements at the LHC and at the RHIC. One such kind of jet observables is the averaged jet charge [51–53], which yields the electric charge distribution in a reconstructed jet. The measurement of jet charge in HIC is expected to shed light on the flavor dependence of jet quenching [54].
In the present study, we present the first numerical calculations of medium modification on the averaged jet charge in Pb+Pb collisions at the LHC. PYHHIA6 [55] is used to simulate the particle production in p+p collisions. PYQUEN and JEWEL are used to simulate the parton energy loss in Pb+Pb collisions. Compared to p+p collisions, the averaged jet charge is found to be significantly suppressed because of the participation of neutrons in heavy-ion collisions. However, with the input that the gluon loses more energy than the quark, the fraction of quarks at large transverse
$ p_T $ will be increased to a large extent, and it is shown that$ R_{CP} $ , the ratio of averaged jet charge in central collisions to that in peripheral collisions, should be larger than unity across the entire range of jet transverse momenta. We demonstrate that the behavior of the central-to-peripheral ratio is particularly sensitive to the difference of the gluon and quark jet-medium interaction strength. -
We discuss our analysis framework of averaged jet charge from p+p to Pb+Pb collisions. The momentum-weighted jet charge is defined as [52, 53]:
$ Q^{\kappa} = \sum\limits_{i\in{\rm jet}}z_h^{\kappa}Q_{i} $

(1) with
$ z_h = {p^{i}_{T}}/{p^{\rm{jet}}_{T}} $ . Here,$ p^{i}_{T} $ depicts the transverse momentum of the hadron i inside jet,$ p^{\rm{jet}}_{T} $ is the transverse momentum of the jet,$ Q_{i} $ is the electric charge of the hadron. A power parameter κ, which satisfies$ \kappa\in(0.1,1) $ is used to adjust the contribution bias of jet constituents with different transverse momenta.The energy and and jet-size dependence of moments of jet-charge distributions in p+p can be calculated in perturbative QCD [52, 53]. In this study, we employ the Monte Carlo event generator PYTHIA with Perugia 2012 tune [56] to simulate particle production in p+p collisions, which gives us more leverage power to impose different kinematic cuts. The FastJet package [57] is used to construct final state jets for jet charge calculation. In the ATLAS Collaboration measurement, jets are reconstructed by the anti-
$ k_{T} $ algorithm with a radius$ R = 0.4 $ , and events are required to include at least two jets with$ p_{T}>50 $ GeV in the central rapidity region$ \left|\eta_{1,2}\right|<2.1 $ . Only the leading two jets with$p^{\rm{leading}}_{T}/ $ $ p^{\rm{subleading}}_{T}<1.5 $ are employed in the jet charge calculations. Fig. 1 shows our results for the jet charge at$ \sqrt{s} = 8 $ TeV in p+p collisions from PYTHIA+FastJet compared with recent ATLAS data [58]. Our MC results provide good descriptions for experimental data. We may calculate the jet charge at$ \sqrt{s} = 2.76 $ TeV p+p collisions using the same method, which provides a good baseline for the calculation in heavy-ion collisions.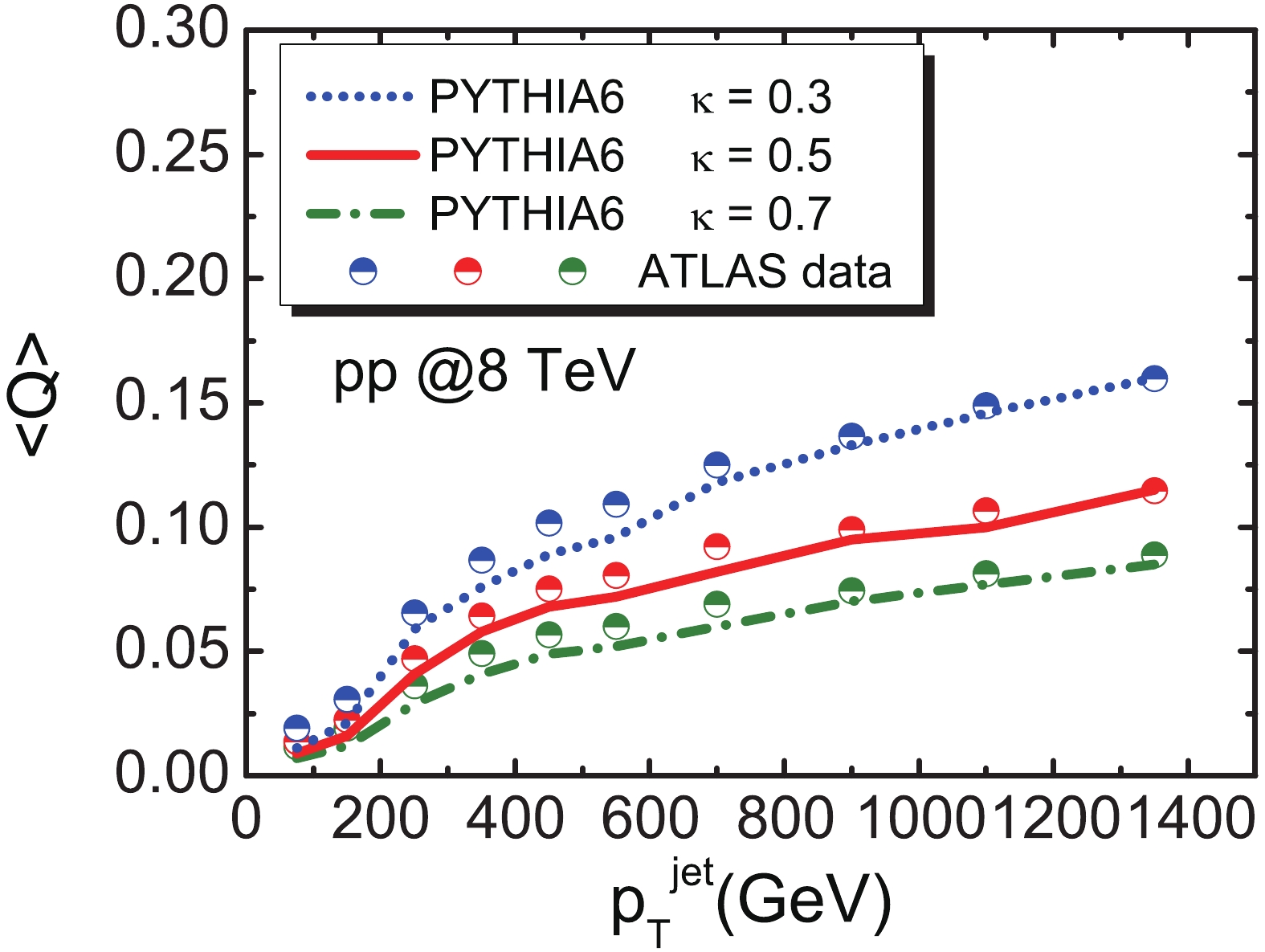
Figure 1. (color online) Average value of jet charge distribution for leading jet in dijet events, as a function of jet transverse momenta at
$\sqrt{s}=8.0$ TeV in p+p collisions, as compared with ATLAS data.We show the jet charge for the quark and gluon jets in Fig. 2. The distinct features of the jet charge between quark and gluon jets can be observed. The averaged complete jet charge is given by the combination of quark and gluon jets with their relative fractions. The fraction of quark jets increases with rising transverse momenta. The averaged jet charge may increase gradually with the jet transverse momentum
$ p_T^{\rm{jet}} $ , as shown in Fig. 1 and Fig. 2. Moreover, even for pure quark jets, the value of the averaged jet charge is increased. The hadronization effect decreases with the higher jet$ p_T^{\rm{jet}} $ , thus the out-of-cone contributions of electric charge and energy at high$ p_T^{\rm{jet}} $ jet should be suppressed as compared to those at low$ p_T^{\rm{jet}} $ .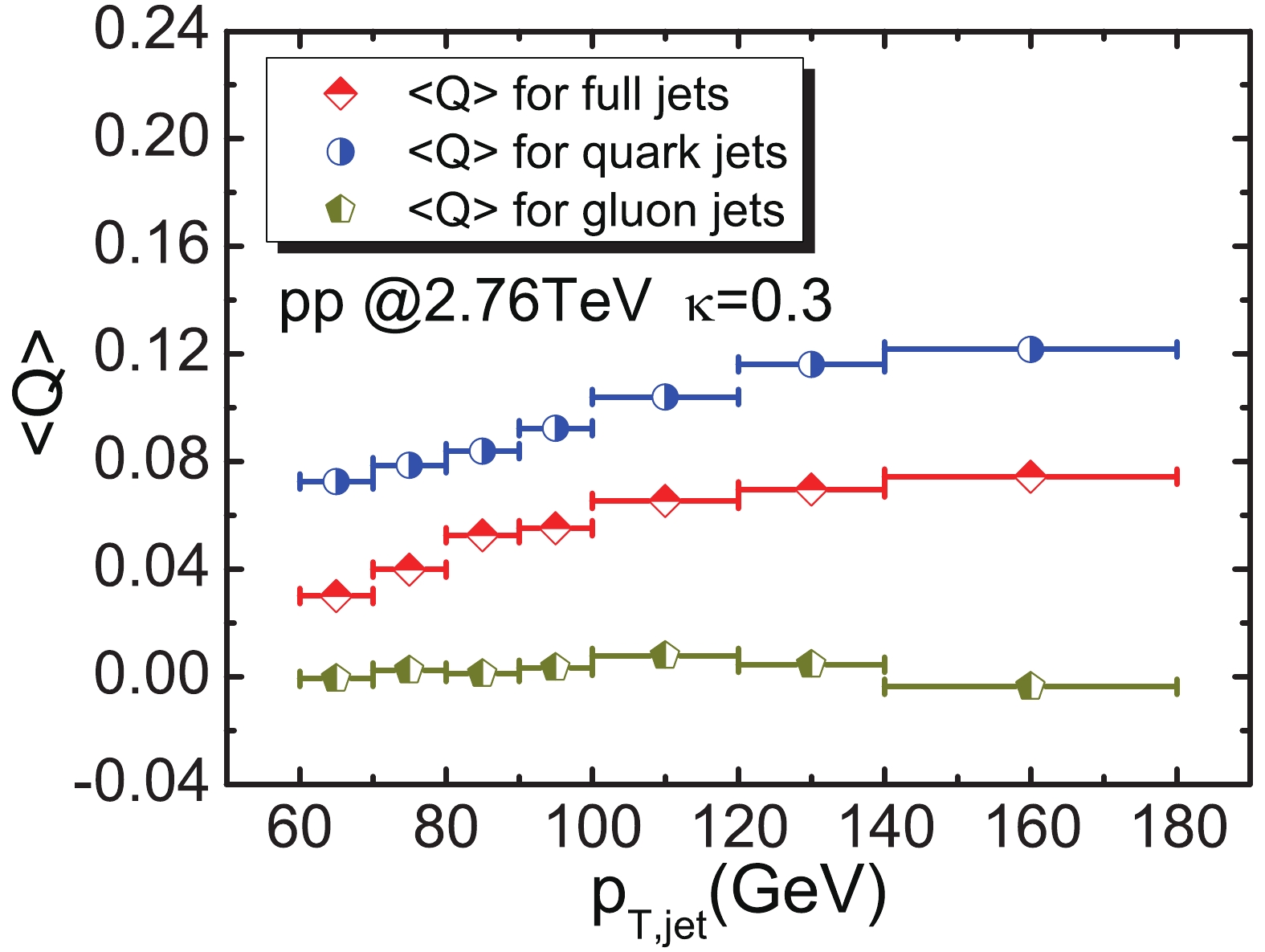
Figure 2. (color online) Average value of jet charge for quark and gluon jets at
$\sqrt{s}=2.76$ TeV in p+p collisions.We subsequently proceed to the calculations of jet charge in heavy-ion collisions at the LHC, where both the initial-state cold nuclear matter (CNM) effects and final-state hot nuclear matter effects are taken into account. For CNM effects, the EPPS16 parameterization set [59] was employed in our calculations. The total averaged jet charge originally arises from the electric charge of colliding participants. In Pb+Pb collisions at the LHC, besides proton-proton collisions, proton-neutron and neutron-neutron collisions may also occur. With the approximation that the cross-sections of these three types of collisions are almost the same, the probability of these collisions is determined by the number of fractions of colliding participants. Eventually, the averaged jet charge in Pb+Pb can be given as:
$ \begin{split} \langle Q^{\kappa}_{\rm PbPb} \rangle = & \left(\frac{N_{p}}{208}\right)^{2}\langle Q^{\kappa}_{pp}\rangle+\left(\frac{N_{p}}{208}\frac{N_{n}}{208}\right)\langle Q^{\kappa}_{pn}\rangle {} \\ &+\left(\frac{N_{n}}{208}\right)^{2}\langle Q^{\kappa}_{nn}\rangle , \end{split} $

(2) where
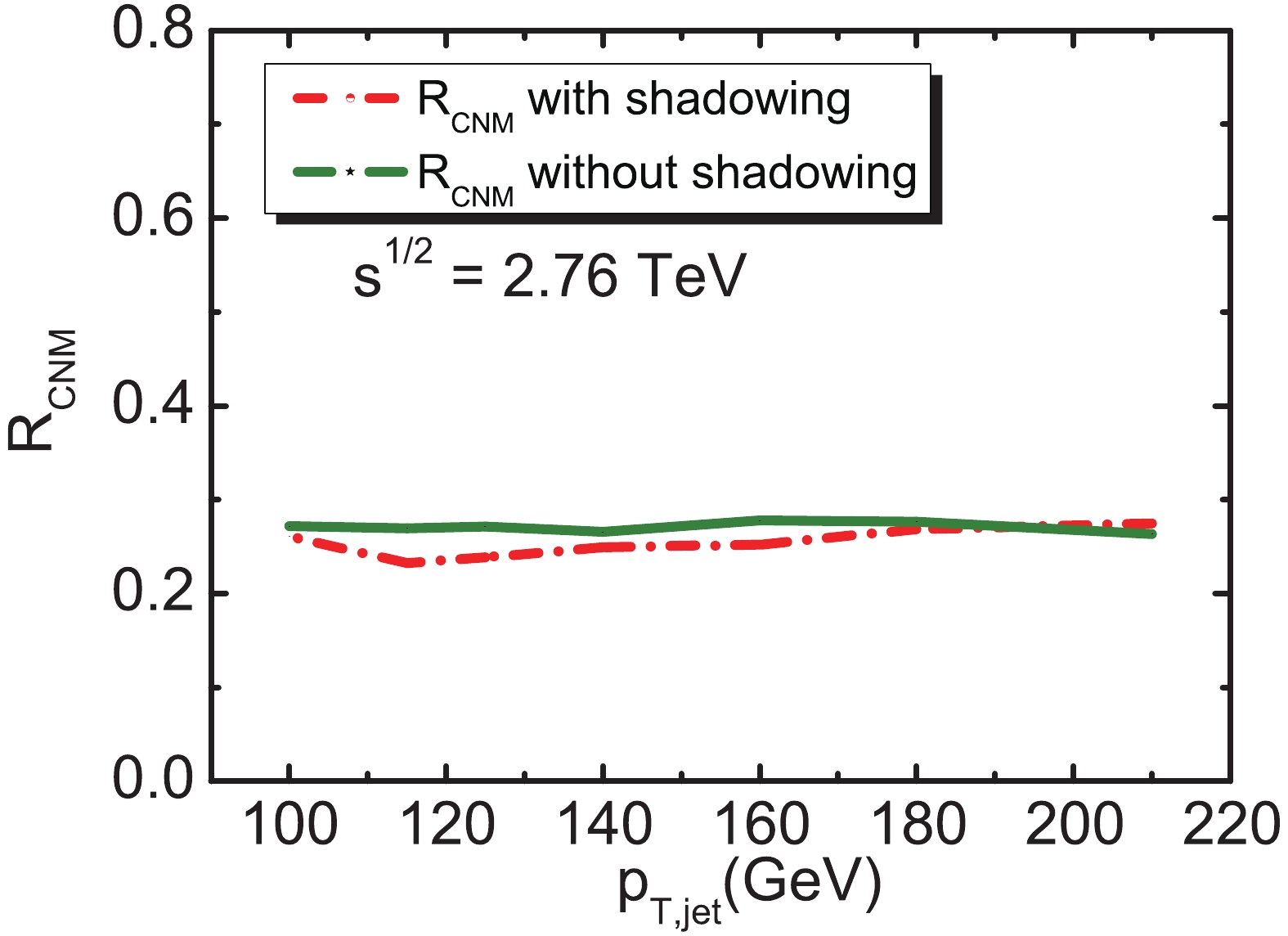
$ N_{p} $ and$ N_{n} $ represent the number of protons and neutrons in the lead nucleus, respectively. Eq. (2) calculates the averaged jet charge in Pb+Pb collisions without the final-state jet quenching effect, as shown in Fig. 3. The CNM modification ratio is expressed as:
Figure 3. (color online) Average jet charge distribution for leading jet in dijet events as a function of jet transverse momenta in pp, pn, and nn collisions.
$ R_{\rm{CNM}} = \frac{\langle Q_{AA}^{\rm{CNM}} \rangle}{\langle Q_{pp} \rangle} . $

(3) The CNM modification ratio as a function of
$ p^{\rm jet}_{T} $ is illustrated in Fig. 4. The averaged jet charge with CNM effects is significantly suppressed relative to that in p+p due to the participation of neutrons with zero electric charge during nuclear collisions.Previous studies have shown that energetic partons should lose energy when traversing the QCD medium due to elastic and inelastic processes. In this study, we employ PYQUEN and JEWEL models to simulate the parton energy loss in the QGP medium. PYQUEN [60–62] is one of the Monte Carlo event generators of jet quenching, built as a modification of jet events obtained for hadronic collisions with PYTHIA 6.4. Details on the employed physical model and simulation procedure can be found in [60]. The model has to include both radiative and collisional energy loss of hard partons, as well as the realistic nuclear geometry. To investigate jet observables, another key element of PYQUEN is the angular spectrum of medium-induced gluon radiation. The "wide-angle" radiation scenario was found to provide a better description for experimental measurements on full jets observables in the PYQUEN model [63], which is also adopted in the calculations of this paper.
The JEWEL event generator provides a good description of the jet evolution in QCD medium, created in ultra-relativistic heavy-ion collisions. This was tested for a large set of jet quenching measurements, including jet
$ R_{AA} $ , dijet asymmetry$ A_{J} $ , bosons tagged jet, as well as jet substructure observables, which are more sensitive to the jet-medium interaction [39, 44, 64–67]. In JEWEL, the recoiling scattering centers can be traced, and in principle they could be subjected to further interactions. To deal with the medium response, JEWEL provides the option that thermal partons are kept recoiling against interactions with the jet partons and then fragmented into hadrons along with the jet partons. This option is employed in the following simulations. -
Based on the framework established in the previous section, we calculate the average value of the jet charge distribution as function of the jet transverse momentum in HIC at the LHC. The CNM effect modified partonic jets are generated by PYTHIA+EPPS16 with Perugia 2012 tune [56], and suffer jet quenching with simulations of PYQUEN and JEWEL models, after which they are fragmented into final-state hadrons. The candidate particles used to reconstruct jets are required to have
$ p_T\geq 1 $ GeV to reduce the influence from the heavy-ion background. We note that background effects are significant in jet measurements [68, 69], and it is of interest to study in detail how the heavy-ion background affects medium-modifications of the jet charge in the future. Jets are reconstructed by using the anti-$ k_{t} $ jet finding algorithm [57] with the cone size$ R = 0.4 $ implemented in FastJet. Events are required to have two leading jets with$ p^{\rm{leading}}_{T}>100 $ GeV,$ p^{\rm{subleading}}_{T}>50 $ GeV, and$ |\eta|<2.1 $ , where$ p^{\rm{leading}}_{T} $ and$ p^{\rm{subleading}}_{T} $ are the transverse momenta of the two leading jets. To demonstrate the nuclear modification of the averaged jet charge in Pb+Pb collisions, the nuclear modification factor is given by:$ R_{AA} = \frac{\langle Q_{AA} \rangle}{\langle Q_{pp} \rangle} . $

(4) Fig. 5 shows our predictions for the jet charge
$ R_{AA} $ and their comparison with the cold nuclear modification ratio in central (0%–10%) Pb+Pb collisions. The nuclear modification factor for the jet charge may be observed to increase considerably by the jet quenching effect for both PYQUEN and JEWEL. To provide a clearer description of this phenomenon and suppress the initial-state isospin effect (the electronic charge difference between protons and neutrons), we study the central-to-peripheral ratio of the averaged jet charge in Pb+Pb collisions$ R_{CP} $ , while the jet quenching effect is significantly stronger in central collisions than that in the peripheral ones. The central-to-peripheral ratio$ R_{CP} $ is defined as:
Figure 5. (color online) Nuclear modification factor for averaged jet charge and their comparison with cold nuclear modification ratio in Pb+Pb collisions with
$\sqrt{s_{NN}}=2.76$ TeV.$ R_{CP} = \frac{\langle Q_{AA}^{\rm{central}} \rangle}{\langle Q_{AA}^{\rm{peripheral}} \rangle}. $

(5) In Fig. 6, we plot the
$ R_{CP} $ as a function of the jet transverse momentum for the averaged jet charge from 0–10% centrality ($ b\in(0,3.478) $ ) and 60%–80% centrality ($b\in(12.05, $ $ 13.91) $ ) Pb+Pb collisions. It is shown that$ R_{CP} $ is significantly larger than in the entire range of jet transverse momenta due to the jet quenching effect both from PYQUEN and JEWEL. We emphasize the behavior that$ R_{CP}>1 $ for the jet charge comes mainly from the increasing fraction of quark jet with$ p_T^{\rm{jet}} $ due to the jet quenching effect in both PYQUEN and JEWEL models, where$ \Delta E_{g}/$ $\Delta E_{q} = C_{A}/C_{F} = 9/4 $ has been implemented. In these models, because gluon loses more energy than quarks, the quark fraction will increase, whereas the gluon fraction will decrease. However, as we discussed before, the averaged jet charge for the gluon jet approaches zero. Therefore, the jet quenching model with gluon losing significantly more energy than quark naturally results in a$ R_{CP} $ that is larger than unity.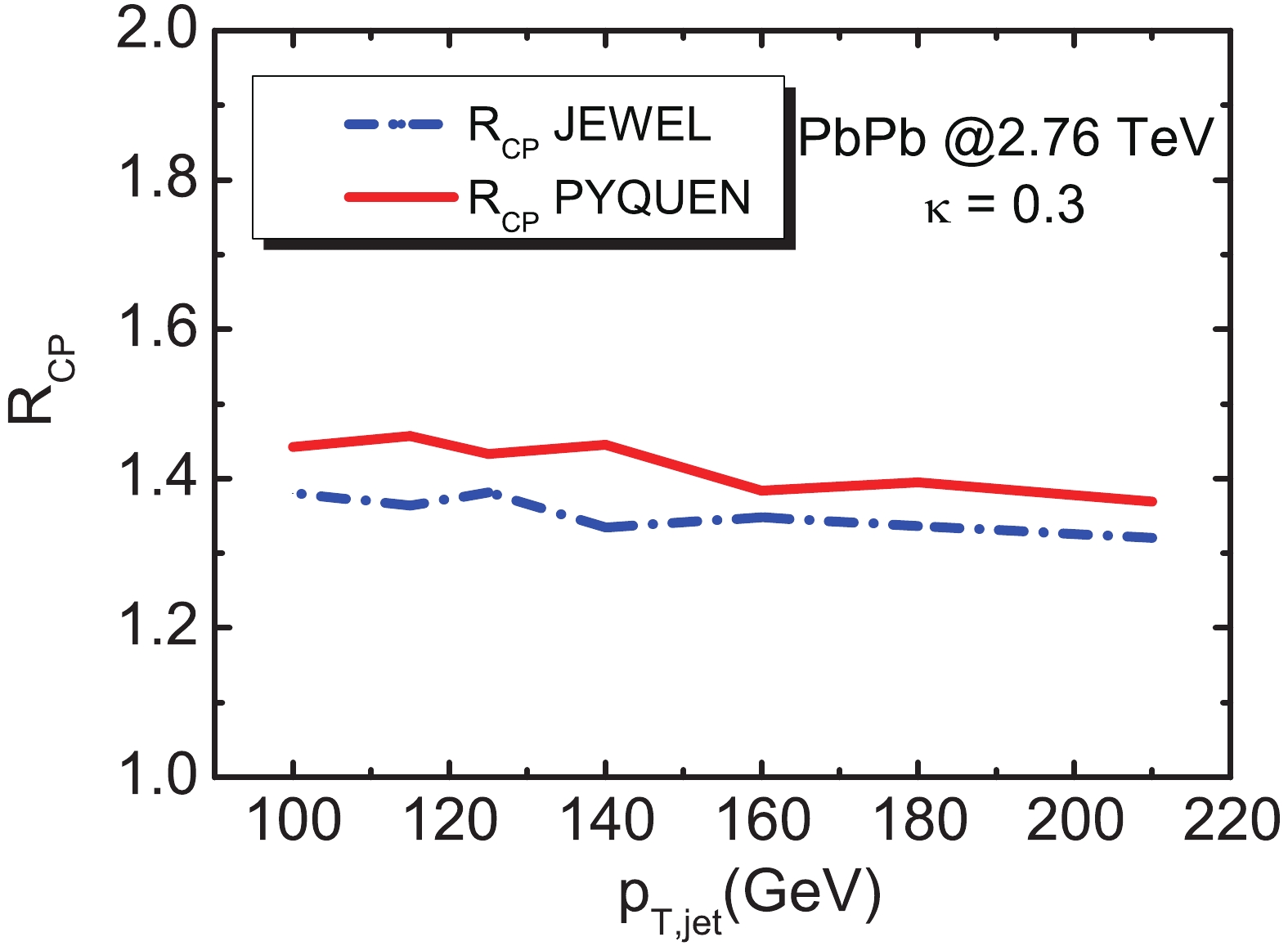
Figure 6. (color online) Central-to-peripheral ratio
$R_{CP}$ of averaged jet charge in Pb+Pb collisions with$\sqrt{s_{NN}}=2.76$ TeV.To clarify this, we numerically investigate the central-to-peripheral ratio (
$ R^{q,{\rm jet}}_{CP} $ ) for the averaged quark jet charge. The value of$ R^{q,{\rm j}et}_{CP} $ and their comparison with full jets is shown in Fig. 7. We observe that$ R^{q,{\rm j}et}_{CP}\sim 1 $ , which implies that the jet quenching effect has a rather modest impact of the pure quark jet charge. The difference between full charge in central and peripheral collisions mainly results from the decreasing fraction of gluon jet with an energy loss effect in the hot QCD medium.To further investigate the sensitivity of medium modifications of the jet charge in HIC to the flavor dependence of parton energy loss, we calculate
$ R_{CP} $ in jet quenching models with different values of:$ r = \Delta E_{g}/\Delta E_{q} . $

(6) We consider two scenarios: Scenario (I), where we have
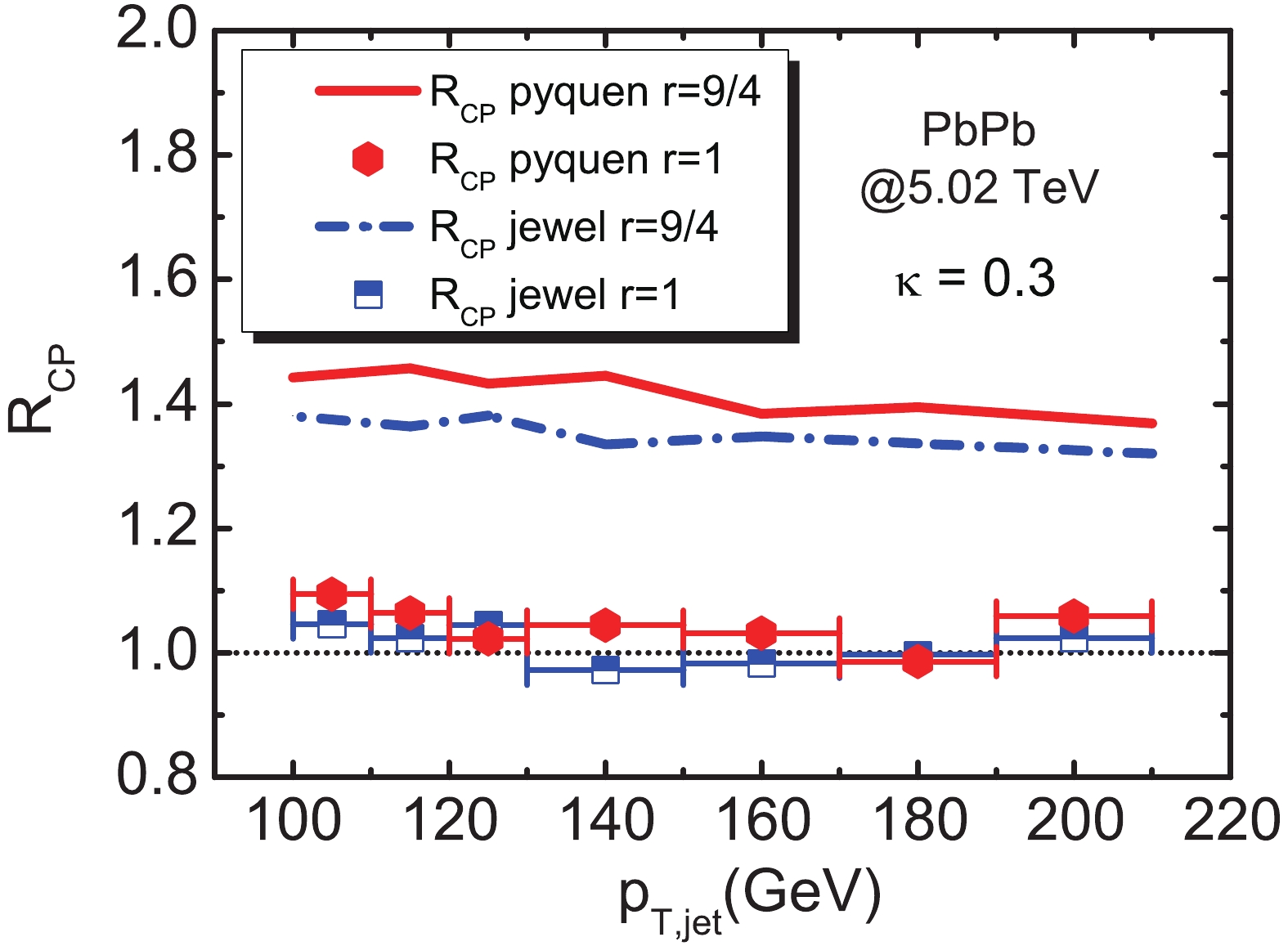
$ r = 9/4 $ for the conventional jet quenching model, and Scenario (II) with$ r = 1 $ . The different choices of r may alter the hadron chemistry, such as the$ p^{+}/\pi^{+} $ ratio in A+A collisions [22].In Fig. 8 and Fig. 9 we illustrate
$ R_{CP} $ for the average jet charge and quark jet fraction$ f_{\rm{quark}} $ in these two scenarios of flavor dependence of the parton energy loss model$ r = 9/4 $ and$ r = 1 $ , respectively. In Scenario (II) with$ r = 1 $ , the central-to-peripheral ratio$ R_{CP} $ is about 1, and a very small difference of quark jet fraction between central and peripheral Pb+Pb collisions is observed. This striking distinction between the results of Scenario (I) and Scenario (II) demonstrate convincingly the sensitivity of the jet charge to the energy loss pattern between quark and gluon jets in heavy-ion collisions. By measuring the jet charge in HIC and comparing the data with the theoretical results from different jet quenching models, we can form stringent constraints on the jet quenching mechanism. -
We present the first numerical results for the nuclear modification of the averaged jet charge in HIC at the LHC. In p+p collisions, PYTHIA6 is used to simulate final state hadron productions. The jet charge for quarks is shown to increase with rising jet transverse momenta, while the gluon jet charge is approximately zero across the entire range of
$ p_{T} $ , because the gluon carries no electric charge. In Pb+Pb collisions, the EPPS16 parameter set is used to investigate cold nuclear effects. We employ the MC event generators PYQUEN and JEWEL to simulate the parton energy loss in QCD medium. We found that during nuclear collisions, the averaged jet charge with cold nuclear matter influences is significantly suppressed by isospin effects. This is because neutrons with zero electric charge account for a large proportion of the collisions. To study the medium modification for jet charge by jet quenching effects and suppression of the isospin effect, we calculate the central-to-peripheral ratio for the jet charge in Pb+Pb collisions. The value of the averaged jet charge in central Pb+Pb collisions is enhanced relative to peripheral collisions, since the jet quenching effect is significantly stronger in central collisions. In conventional jet quenching calculations, a fast gluon will lose more energy in the QGP than a fast quark due to its large color-charge ($ \Delta E_{g}/\Delta E_{q} = C_{A}/C_{F} = 9/4 $ ), hence more quarks with an electric charge may survive in central collisions as compared with those in peripheral Pb+Pb collisions. The fraction of quark jet should be increased, which results in a larger jet charge in central collisions than in peripheral reactions. We found the central-to-peripheral ratio of the averaged jet charge is particularly sensitive to flavor dependence of parton energy loss, which may provide a very powerful tool to constrain the energy loss pattern between quark and gluon jets in heavy-ion collisions.
Jet charge in high-energy nuclear collisions
- Received Date: 2019-08-21
- Accepted Date: 2019-10-23
- Available Online: 2020-02-01
Abstract: The averaged jet charge characterizes the electric charge of the initiating parton and provides a powerful tool to distinguish quark jets from gluon jets. We predict, for the first time, the medium modification of the averaged jet charge in the heavy-ion collisions at the LHC, where jet productions in p+p collisions are simulated by PYTHIA6, and the parton energy loss in QGP is calculated with two Monte Carlo models of jet quenching: PYQUEN and JEWEL. We found that the distribution of averaged jet charge is significantly suppressed by initial state isospin effects due to the participation of neutrons with zero electric charge during nuclear collisions. The considerable enhancement of the averaged jet charge in central Pb+Pb collisions is observed relative to peripheral collisions, since the jet quenching effect is more pronounced in central collisions. The distinct feature of the averaged jet charge between quark and gluon jets, along with the sensitivity of medium modifications on the jet charge to flavor dependence of the parton energy loss, could be very useful to discriminate the energy loss pattern between quark and gluon jets in heavy-ion collisions.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: