-
It is well known that a black hole as a thermodynamic system has many interesting properties. It sets a fundamental connection between the laws of classical thermodynamics, quantum mechanics and general relativity. The thermodynamic properties of black holes have been extensively investigated since the first studies of Bekenstein and Hawking [1-6]. As thermodynamic systems, black holes have many similarities with general thermodynamic systems. For black holes in the AdS space, these similarities become more obvious and precise. Hawking and Page have pioneered the study of the phase transition between the Schwarzschild-AdS black hole and the thermal AdS space [7], and Chamblin and Emparan found the relation between the charged AdS black hole and the Van der Waals liquid-gas system [8, 9].
Recently, black hole thermodynamics in the AdS space has been intensively studied in the extended phase space where the cosmological constant is considered as the thermodynamic pressure
$ P = -\frac{\Lambda}{8\pi}, $

(1) and its conjugate quantity as the thermodynamic volume [10, 11]
$ V = {\Big(\frac{\partial M}{\partial P}\Big)}_{S,Q,J}, $

(2) which can enrich the AdS black hole thermodynamics. Further studies have shown that the charged AdS black hole is similar to the Van der Waals liquid-gas in the extended phase space [12], and that the
$ P-V $ criticality of the black hole system behaves similarly to the Van der Waals system [12-31]. In [32-35], it was found that black holes have second-order and third-order phase transitions, in addition to the Van der Waals-like phase transition.Apart from phase transitions and critical phenomena, the thermodynamic analogy between the AdS black hole and the Van der Waals system has been creatively generalized to the well known Joule-Thomson expansion process. In classical thermodynamics, the Joule-Thomson expansion means that a fluid passes at high pressure through a porous plug into a region of low pressure, such that its enthalpy is constant. In [36], Ökcü and Aydıner investigated the Joule-Thomson expansion of the charged RN-AdS black hole in the extended phase space, and obtained the inversion and isenthalpic curves and the heating-cooling regions in the
$ T-P $ plane. Subsequently, this pioneering work has been generalized to other kinds of black holes, such as the quintessence charged AdS black hole [37], the Kerr-AdS black hole [38], d-dimensional charged AdS black holes [39], holographic super-fluids [40], charged AdS black hole in$ f(r) $ gravity [41], AdS black hole with a global monopole [42], AdS black holes in Lovelock gravity [43], charged Gauss-Bonnet black holes [44], AdS black hole in Einstien-Maxwell axion theory and the AdS black hole in massive gravity [45] and [46-51].However, the above mentioned Joule-Thomson expansion processes are only applicable to the AdS black holes with singularities. For the regular black hole without singularity, the Joule-Thomson expansion has not been discussed so far. Bardeen has obtained the first solution of the regular black hole with nonsingular geometry satisfying the weak energy condition [52]. Subsequently, Ayón-Beato and García proved that the Bardeen black hole can be interpreted as a gravitationally collapsed magnetic monopole arising from a specific form of non-linear electrodynamics [53]. The stability of the Bardeen-like regular black holes was studied by Moreno and Sarbach [54], and the thermodynamic properties of these black holes were discussed in [55-63]. Recently, Tzikas found the Bardeen-AdS black hole thermodynamic system criticality and the first order small/large black hole phase transition, with critical exponents that are exactly the same as those of the Van der Waals gas [64]. Obviously, the phase transition and the
$ P-V $ criticality of the AdS black hole are independent of the spacetime with or without singularity. In this paper, taking the regular (Bardeen)-AdS black hole as an example, we attempt to find the dependence of the spacetime without singularity on the Joule-Thomson expansion.The paper are organized as follows. In Sec. 2, we review the thermodynamic properties of the Bardeen-AdS black hole in the extended phase space, and obtain the state equation of the black hole. In Sec. 3, we apply the Joule-Thomson expansion of the Van der Waals fluid and the Bardeen-AdS black hole, and plot the inversion and isenthalpic curves to determine the cooling and heating regions in the
$ T-P $ plane. The conclusions are given in Sec. 4. We use the units$ G_{N} = \hbar =$ $ \kappa_{B} = c = 1 $ . -
In this section, we briefly review the thermodynamic properties of the Bardeen-AdS black hole in the extended phase space. The physical interpretation of the Bardeen metric was given Ayon-Beato and García, describing a black hole with a nonlinear magnetic monopole which results in a solution of the Einstein equations coupled to nonlinear electrodynamics [53]. The corresponding action with a negative
$ \Lambda $ term is expressed as [64]$ {\cal{S}} = \frac{1}{16\pi}\int {\rm d}^{4}x \sqrt{-g}\left(R+\frac{6}{l^{2}}-4{\pounds}(F)\right), $

(3) where R and g are the Ricci scalar and the determinant of the metric tensor. l is the positive AdS radius, which is related to
$ \Lambda $ by the relation$ \Lambda = -3/l^{2} $ .$ \pounds(F) $ is the Lagrangian density of the electromagnetic field, with$ F = \frac{1}{4}F^{\mu\nu}F_{\mu\nu} $ , which can be expressed by [63, 64]$ \pounds(F) = \frac{3}{2s q^2}{\left(\frac{\sqrt{2q^2 F}}{1+\sqrt{2q^2 F}}\right)}^{\frac{5}{2}}, $

(4) where the parameter s is
$ \frac{q}{2M} $ , and q and M correspond to the magnetic charge and mass of the black hole. The field strength of the non-linear electrodynamics$ F_{\mu\nu} $ is given by [63]$ F_{\mu\nu} = 2(\nabla_\mu \triangle_\nu-\nabla_\nu \triangle_\mu). $

(5) The field equations-of-motion derived from the action in Eq. (3) is given by [63-65]
$ \begin{split} {G_{\mu \nu }} + \Lambda {g_{\mu \nu }} =& 2\left(\frac{{\partial \pounds(F)}}{{\partial F}}{F_{\mu \nu }}F_\nu ^\lambda - {g_{\mu \nu }}\pounds(F)\right),\\ {\nabla _\mu }\left(\frac{{\partial \pounds(F)}}{{\partial F}}{F^{\mu \nu }}\right) =& 0,\\ {\nabla _\mu }(*{F^{\nu \mu }}) =& 0, \end{split}$

(6) where
$ G_{\mu \nu} $ is the well known Einstein tensor.The line element of the Bardeen-AdS black hole is then given by [64]
$ {\rm d}s^{2} = -{\Big(1-\frac{2m(r)}{r}\Big)}{\rm d}t^{2}+{\Big(1-\frac{2m(r)}{r}\Big)}^{-1}{\rm d}r^{2}+r^{2}{{\rm d}\Omega}^{2}, $

(7) where
$ {{\rm d}\Omega}^{2} = {{\rm d}\theta}^{2}+{\sin}^{2}{\theta}{{\rm d}\phi}^{2} $ . From Eq. (7), and with the help of Eq. (6), one finds [65]$ F_{\mu \nu} = 2 \delta^{\theta}[_{\mu}\delta^{\phi}_{\nu}]q(r)\sin \theta. $

(8) The condition
$ {\rm d}F = \frac{{\rm d}q}{{\rm d}r}\sin \theta {\rm d}r \bigwedge {\rm d}\theta \bigwedge {\rm d}\phi = 0 $ leads to the conclusion that$ q(r) = {\rm con}st. = q $ . Hence, the magnetic field strength is given by [66]$ F_{\theta \phi} = q \sin \theta, $

(9) and
$ F = \frac{q^2}{4 r^4}. $

(10) By substituting F from Eq. (10) into Eq. (4), one obtains [64-66]
$ \pounds(F) = \pounds(r) = \frac{3M q^2}{({r^2+q^2)}^{\frac{5}{2}}}. $

(11) The above field motion equations yield a solution for
$ m(r) $ that reads$ m(r) = \frac{Mr^{3}}{{(q^{2}+r^{2})}^{\frac{3}{2}}}-\frac{r^{3}}{2l^{2}}. $

(12) The Bardeen-AdS metric potential can be expressed as [65]
$ f(r) = 1-\frac{2 M r^{2}}{{(q^{2}+r^{2})}^{\frac{3}{2}}}+\frac{r^{2}}{l^{2}}. $

(13) The event horizon
$ r_h $ of the black hole can be obtained as the largest root of$ f(r_{h}) = 0 $ . From Eq. (13), the mass M of the black hole can be written as$ M = \frac{(l^{2}+{r^2_{h}}){(q^{2}+{r^2_{h}})}^{\frac{3}{2}}}{2l^{2}{r^2_{h}}}. $

(14) In the extended phase space, the cosmological term defines the pressure of the system Eq. (1) along with its conjugate quantity [10, 13], so that the black hole pressure is expressed as
$ P = \frac{3}{8\pi l^{2}}. $

(15) According to the area law, the entropy is given by [1, 2, 4]
$ S = \frac{A}{4} = \pi r^2_h. $

(16) We consider the mass M of the black hole as a function of entropy S, pressure P and charge q, i.e.
$ M = M(S,P,q) $ (see Eqs. (14), (15) and (16)), so that the mass M of the black hole can be reformulated as$ M = \frac{(\pi q^2+S)^{3/2}(3+8PS)}{6\sqrt{\pi}S}. $

(17) The first law of thermodynamics of the black hole is given by
$ {\rm d}M = T{\rm d}S+V{\rm d}P+{\varphi}{{\rm d}q}, $

(18) and all thermodynamic variables defined above can be obtained as follows
$ T = \Big(\frac{\partial M}{\partial S}\Big)_{P,q},\; \;\; V = \Big(\frac{\partial M}{\partial P}\Big)_{S,q},\; \;\; \varphi = {\Big(\frac{\partial M}{\partial q}\Big)}_{S,P}. $

(19) According to Eqs. (17) and (19), the temperature of the black hole is
$ T = \frac{\sqrt{q^2+S/\pi}(S+8PS^2-2\pi q^2)}{4S^2}. $

(20) In fact, for regular black holes, there is an inconsistency between the first law and the area law. When studying the thermodynamic properties of these black holes, one has to abandon one in order for the other to work [60, 63, 67-73]. Here, we choose the Bekenstein-Hawking area law, and abandon the first law of black hole thermodynamics [68-70]. The black hole volume is given by
$ V = \frac{4\pi}{3}\left(q^2+\frac{S}{\pi}\right)^{\frac{3}{2}}. $

(21) Similarly, we have
$ {\varphi} = \frac{\pi q(3+8PS)\sqrt{q^2+S/\pi}}{2S}. $

(22) One can combine these thermodynamical quantities to obtain the Smarr relation, which can be expressed as
$ M = 2TS-2PV+\varphi q. $

(23) Moreover, combining the expressions for thermodynamic pressure Eq. (15), entropy Eq. (16) and temperature Eq. (20), we get the equation-of-state of the black hole as follows
$ P = \frac{T}{2\sqrt{q^2+r^2_{h}}}-\frac{1}{8 \pi r^2_{h}}+\frac{q^{2}}{4\pi {r^4_{h}}}. $

(24) At the critical point, we have [13]
$ \frac{\partial P}{\partial r_{h}} = \frac{{\partial}^{2} P}{{\partial}{r^2_{h}}} = 0, $

(25) and the critical temperature
$ T_{\rm c} $ is obtained as$ T_{\rm c} = \frac{25(31+13\sqrt{10})}{432(5+2\sqrt{10})^{\frac{3}{2}}\pi q}. $

(26) In this section, we have presented some thermodynamic quantities of the Bardeen-AdS black hole in the extended space. In the next section, we use these quantities to investigate the Joule-Thomson expansion of the black hole.
-
In this section, we study the Joule-Thomson expansion of the Bardeen-AdS black hole and compare it with the well known expansion of the Van der Waals fluid. The Joule-Thomson expansion is a classic physical process with the important property that the temperature changes with pressure and enthalpy are constant during the expansion process [74]. Hence, the Joule-Thomson expansion of a black hole is an isenthalpy process in the extended phase space. The Joule-Thomson coefficient
$ \mu $ , whose sign can be used to determine whether heating or cooling occurs, is defined via the change of temperature with respect to pressure as$ \mu = {\Big(\frac{\partial T}{\partial P}\Big)}_{H}. $

(27) Since the pressure always decreases during the expansion process, the change of pressure is negative, which may cause the temperature to decrease or increase during the process. Therefore, the change of temperature determines the sign of
$ \mu $ . If$ \mu $ is negative (positive), heating (cooling) occurs, and the fluid warms (cools). In the extended phase space, we compare a black hole system to a Van der Waals fluid with a fixed number of particles, so that we should consider the canonical ensemble with a fixed charge q. The Joule-Thomson coefficient is then given by [36]$ \mu = {\Big(\frac{\partial T}{\partial P}\Big)}_{M} = \frac{1}{C_p}\Big[T\Big({\frac{\partial V}{\partial T}}\Big)_P-V\Big]. $

(28) Setting
$ \mu = 0 $ , we can obtain the inversion temperature, i.e.$ T_{i} = V {\Big(\frac{\partial T}{\partial V}\Big)}_{P}. $

(29) In the next subsection, we use the Joule-Thomson coefficient Eqs. (27) and (28) to determine the inversion curves for the Van der Waals fluid and the Bardeen-AdS black hole in the extended phase space. The inversion temperatures are also obtained from Eq. (29).
-
It is well known that the Van der Waals equation is an improvement of the ideal gas equation, and is obtained by taking into account the size of the gas molecules and the interactions between them, which are ignored in the ideal gas. Hence, the gas-liquid phase transition behavior of the actual fluids is better described [74, 75]. The Van der Waals equation is given as [75]
$ P = \frac{k_{B}T}{\nu-b}-\frac{a}{\nu^{2}}, $

(30) and the Joule-Thomson expansion of the Van der Waals system is obtained in [36]. The inversion temperature of the Van der Waals system is obtained as
$ T_{i} = \frac{2(5a-3b^{2}P_{i}\pm 4\sqrt{a^{2}-3ab^{2}P_{i}})}{9bk_{B}}, $

(31) and the inversion curves for the Van der Waals system is plotted in Fig. 1. Moreover, the minimum and maximum inversion temperatures can be obtained as
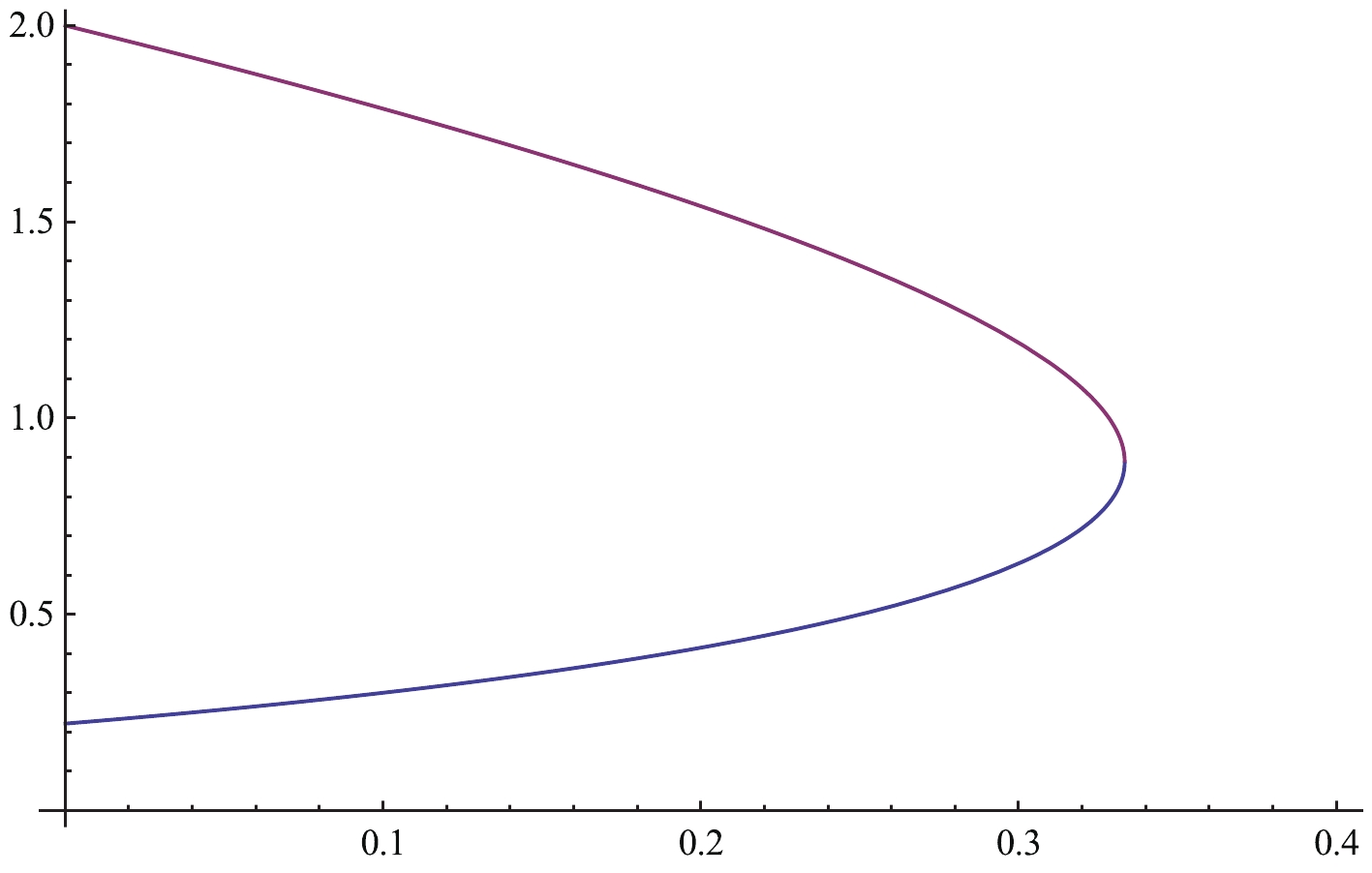
Figure 1. (color online) The inversion curves for the Van der Waals fluid. The red(blue) line corresponds to the lower(upper) inversion curve.
$ T^{\rm min}_i = \frac{2a}{9bk_{B}},\; \; \; T^{\rm max}_i = \frac{2a}{bk_{B}}. $

(32) The critical temperature of the Van der Waals fluid is given by
$ T_{\rm c} = 8a/(27bk_B) $ , and the ratio between the inversion temperature and the critical temperature is$ \frac{T^{\rm min}_i}{T_{\rm c}} = \frac{3}{4},\; \; \; \frac{T^{\rm max}_i}{T_{\rm c}} = \frac{27}{4}. $

(33) -
In this subsection, we investigate the Joule-Thomson expansion of the Bardeen-AdS black hole in the extended phase space. The characteristic feature of the expansion is that the temperature changes with pressure, while enthalpy remains constant during the expansion process. We know from [13] that the mass of the black hole is determined as the enthalpy in the AdS space, so that the mass of the black hole remains constant during the expansion process. In our case, by observing carefully the expressions for these thermodynamic quantities, we find a simpler method to derive the Joule-Thomson coefficient
$ \mu $ . From Eqs. (14) and (15), the pressure P can be rewritten as a function of$ {M} $ and$ r_h $ , i.e.$ P({M},{r}_{h}) = \frac{6M{r^2_{h}}-3{(q^{2}+{r^2_{h}})}^{\frac{3}{2}}}{8\pi{r^2_{h}}(q^{2}+r^2_h)^{\frac{3}{2}}}, $

(34) and substituting
$ P(M,r_h) $ into Eq. (20) for temperature yields$ T({M},{r}_{h}) = \frac{3Mr^4_h-(q^2+r^2_h)^{\frac{5}{2}}}{2\pi r^4_h(q^2+r^2_h)}. $

(35) From the relations between the Joule-Thomson coefficient
$ \mu $ , pressure$ P({M},{r}_{h}) $ and temperature$ T({M},{r}_{h}) $ , one can obtain a simple expression$ \mu = {\Big(\frac{\partial T}{\partial P}\Big)}_{M} = {\Big(\frac{\partial T}{\partial {r_{h}}}\Big)}_{M}{\Big(\frac{\partial {r_{h}}}{\partial P}\Big)}_{M} = \frac{\Big(\partial T/\partial {r_{h}\Big)}_{M}}{\Big(\partial P/\partial {r_{h}}\Big)_{M}}. $

(36) Then, setting
$ \mu = 0 $ in Eq. (36), one can get$ 8\pi P_{i}r^6_h+2r^4_h-5q^2r^2_h-4q^4 = 0. $

(37) By solving Eq. (37) for
$ r_h(P_i) $ , one can get a positive and real root which has a physical meaning, and the corresponding pressure$ P_i $ in the root is the inversion pressure. Substituting the root into Eq. (20) for temperature, one can obtain the inversion temperature$ T_i $ . Since these expressions are too complex, they are not explicitly given here.From the expression for the inversion temperature
$ T_i $ , we obtain the inversion temperature curves for the Bardeen-AdS black hole shown in Fig. 2. The curves are shown for different values of charge q. It can be seen that the inversion temperature for a given pressure increases with q. Compared with the inversion curve for the Van der Waals fluid, we also see that the inversion curves for the black hole are not closed, as there are only lower inversion curves. This means that during the Joule-Thomson expansion process, the black hole always cools above the inversion curve, as previously described in [36-51].
Figure 2. (color online) The inversion curves for the Bardeen-AdS black hole in the
$T-P$ plane. From bottom to top, the inversion curves correspond to$q = 1,2,3,4$ .If we set the inversion pressure
$ P_i $ to zero, the minimum inversion temperature is given by$ {T_{i}}^{\rm min} = \frac{\sqrt{9+\sqrt{57}}(\sqrt{57}-3)}{2(5+\sqrt{57})^2 \pi q}. $

(38) The ratio between the minimum inversion temperature and the critical temperature is given by
$ \frac{{T_{i}}^{\rm min}}{T_{\rm c}}{\approx} 0.536622. $

(39) The ratio between the minimum inversion temperature and the critical temperature for the Bardeen-AdS black hole is smaller than for the Van der Waals fluid (0.75), but is larger than any known ratio for the singular black hole. The large ratio is universal for the regular black hole, in contrast to the singular black hole, and it should therefore be related to some specific property of the regular black hole. In fact, there is a repulsive de Sitter core near the origin of the regular black hole, which is not present in the singular black hole (see in Sec. 4).
In Fig. 3, we plot the isenthalpic (constant mass) and inversion curves for different values of charge q in the
$ T-P $ plane. We can see that the inversion curves divide the plane into two regions. The region above the inversion curves corresponds to the cooling region, while the region below the inversion curves corresponds to the heating region. In fact, the heating and cooling regions are determined by the sign of the slope of the isenthalpic curves. It is positive in the cooling region and negative in the heating region. The inversion curve acts as a boundary between the two regions, and neither cooling nor heating occurs on the inversion curve itself.
Figure 3. (color online) The inversion and isenthalpic (constant mass) curves for the Bardeen-AdS black hole. The blue (black) lines are the inversion (isenthalpic) curves. From bottom to top, the isenthalpic curves correspond to an increasing mass
${M}$ of the black hole. Top left:$q = 1$ and$M = 2,2.5,3,3.5$ . Top right:$q = 2$ and$M = 5,5.5,6,6.5$ . Bottom left:$q = 3$ and$M = 8,8.5,9,9.5$ . Bottom right:$q = 4$ and$M = 12,12.5,13,13.5$ .Finally, we list the ratio between the minimum inversion temperature and the critical temperature for various black holes in Table 1. We easily see that the ratio for the Bardeen-AdS black hole is higher than for the singular black holes.
type ratio literature ${\rm van-der-Waals-fluid}$ 

0.75 [36] ${\rm RN-AdS}$ 

0.5 [36] ${\rm quintessence-AdS}$ 

$0.5$ 

[37] ${\rm Kerr-AdS}$ 

0.5 [38] ${\rm d-dimensional-AdS}$ 

<0.5 [39] ${\rm holographic-super-fluids}$ 

0.4864 [40] $f(r)-{\rm gravity}$ 

0.5 [41] ${\rm global-monopole}$ 

0.5 [42] ${\rm Lovelock-gravity}$ 

<0.4389 [43] ${\rm Gauss-bonnet}$ 

0.4765 [44] ${\rm Einstien-Maxwell-axions-theory}$ 

0.5 [45] ${\rm massive-gravity}$ 

0.4626 [46] ${\rm Bardeen}$ 

0.536622 Table 1. The ratio between the minimum inversion temperature and the critical temperature for various black holes.
-
In this paper, we investigated the Joule-Thomson expansion of the Bardeen-AdS black hole in the extended phase space, where the cosmological constant is viewed as pressure and the black hole mass as enthalpy. We first reviewed the thermodynamic properties of the Bardeen-AdS black hole in the extended phase space and obtained its equation-of-state. We then plotted for the Joule-Thomson expansion of the Van der Waals fluid, the inversion curves and determined the cooling and heating regions in the
$ T-P $ plane. We also investigated the Joule-Thomson expansion of the Bardeen-AdS black hole, and plotted the related inversion curves. In contrast to the Van der Waals fluid, the inversion curves for the Bardeen-AdS black hole are not closed, and there only exists a lower inversion curve. In addition, we have plotted the inversion and isenthalpic curves for the Bardeen-AdS black hole in the$ T-P $ plane, and determined the cooling and heating regions for various values of charge q and mass M. It was shown that the isenthalpic curves have positive slope above the inversion curves where cooling occurs, while the sign of the slope is negative below the inversion curves where heating occurs.The ratio between the minimum inversion temperature and critical temperature for the Bardeen-AdS black hole is smaller than for the Van der Waals fluid (0.75), but is larger than any known ratio for the singular black hole. The large ratio is universal for the regular black hole, in contrast to the singular black hole, and it should therefore be related to a specific property of the regular black hole. In fact, for large distances (
$ r\gg q $ ), the Bardeen-AdS black hole coincides with the conventional Schwarzschild-AdS black hole with$ f(r)\approx 1-\frac{2M}{r}+\frac{r^2}{l^2} $ . Near the origin ($ r\ll q $ ), the Bardeen-AdS black hole could be described by a line element where$ f(r)\approx 1-\Big(\frac{2Ml^2}{q^3}-1\Big)\frac{r^2}{l^2} $ . According to the metric potential, the origin can be seen as: i) a repulsive de Sitter core when$ 2Ml^2>q^3 $ ; ii) an attractive Anti de Sitter core when$ 2Ml^2<q^3 $ ; iii) a local Minkowski core with no gravitational interaction when$ 2Ml^2 = q^3 $ . Obviously, when the origin is an attractive Anti de Sitter core or a local Minkowski core, there is no horizon. Therefore, the Bardeen-AdS black hole exists only in the case of a repulsive de Sitter core at the origin. There is in any case a repulsive de Sitter core in a regular(Bardeen)-AdS black hole, in contrast to the singular black hole. Thus, we conclude that the large ratio for the regular(Bardeen)-AdS black hole may be due to the repulsive de Sitter core near the origin of the regular black hole. On the other hand, for the Van der Waals fluid, there exists a repulsive volume, in contrast to the ideal fluid, and studies have shown that in this case the ratio between the minimum inversion temperature and critical temperature is always larger than for the singular black hole. Therefore, it is reasonable to assume that a repulsive de Sitter core near the origin of the regular(Bardeen)-AdS black hole leads to the large ratio of these temperatures.After we have completed this paper, a similar study appeared in arXiv:1904.09548.
Joule-Thomson expansion of the regular(Bardeen)-AdS black hole
- Received Date: 2019-07-19
- Accepted Date: 2019-12-24
- Available Online: 2020-03-01
Abstract: We study the Joule-Thomson expansion of the regular black hole in an anti-de Sitter background, and obtain the inversion temperature for the Bardeen-AdS black hole in the extended phase space. We investigate the isenthalpic and inversion curves for the Bardeen-AdS black hole in the T-P plane and find that the intersection points between them are exactly the inversion points discriminating the heating from the cooling process. The inversion curve for the regular(Bardeen)-AdS black hole is not closed and there is only a lower inversion curve, in contrast to the Van der Waals fluid. Most importantly, we find that the ratio between the minimum inversion temperature and the critical temperature for the regular(Bardeen)-AdS black hole is 0.536622, which is larger than any known ratio for the singular black hole. The large ratio for the Bardeen-AdS black hole may be due to the repulsive de Sitter core near the origin of the regular black hole.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: