-
The principle of clustering is understood as a nuclear phenomenon in states around the cluster decay thresholds and in describing the nuclear structure [1–5]. A nuclear cluster might be characterized as a spatially located subsystem made out of strongly correlated nucleons, and it is described by intrinsic binding that is stronger than its external binding [6]. It is then conceivable to think about the cluster as a solitary unit, and to depict its conduct without reference to its interior structure. One of the most dominant cluster nuclei that have been used to study the nuclear structure of heavy nuclei is the α-cluster nucleus because of its high accuracy experimental measurements and the availability of its microscopic theory [7–9]. During the α or heavier cluster decay process, nucleons in the parent nucleus spend part of their time as clusters, in the nuclear surface [10, 11]. The strongly correlated nucleons in the parent nucleus can condense to form a cluster [12]. Thus, two neutrons and two protons can condense to form an α cluster, which then oscillates within the surface of the nucleus with certain quantum numbers on a shell model base. The formation probability of the condensed nucleons within the nuclear surface is determined by the preformation spectroscopic factor (
$ S_{\alpha(c)} $ ). Once formed, the light cluster will attempt to tunnel through the cluster-core Coulomb barrier, by knocking against it with an extremely large frequency, leaving the daughter behind. The quantum tunneling effect takes place in this stage through the penetration probability (P) and the assault frequency ($ \nu $ ). Both the preformation and the penetration probabilities can be numerically obtained from the incident and transmitted wave functions of the system, which are obtained from the numerical solution of the time-independent Schrödinger equation for a certain α- or heavier cluster-decay. The assault frequency is defined as the inverse of the time taken for the formed cluster to make one oscillation within the internal pocket region of the potential. Thereafter, the half-life can be estimated in terms of the preformation probability, assault frequency, and penetration probability.In general, the probability of forming the emitted particle from strongly correlated surface nucleons in the parent nucleus is called the preformation probability or the preformation factor. In the literature, it may also be referred to as the cluster-formation probability, the spectroscopic factor, or the amount of clustering. The cluster preformation probability is a very important quantity, as it reflects information about the nuclear structure. For instance, it is a good indicator of the deformation in the nuclei participating in the decay process. The preformation probability increases if the cluster is formed from the nucleons belonging to the last open shells, which lead to deform the nuclear surface [13]. In addition to its model dependence, the uncertainty in the estimated preformation probability increases when the involved nuclei are deformed in their ground states or have larger isospin asymmetry [14, 15]. Microscopically, the preformation probability can be calculated in terms of the formation amplitude of the amount of clustering of the emitted and daughter nuclei as two distinguishable entities inside the parent nucleus [16]. The formation amplitude represents the projection of the parent wave function with respect to the anti-symmetrized product of the identified wave functions of the cluster and core fragments. Using the R-matrix description [17], the formation amplitude of the α-cluster in 212Po has been calculated using high configuration mixing of harmonic-oscillator bases [18]. The calculations of the formation amplitude were improved using the multistep shell model method including pairing and mutual interactions between the valence nucleons [16, 17], as well as considering the high-lying states. The dimensions of matrix elements were reduced using surface delta interaction in truncated model space [16]. The existence of α-core structure has been confirmed in the framework of both the shell model and the cluster model within bases of large dimensions, and using Gaussian-bases and large number of configurations [19, 20]. Moreover, the α clustering has been described in numerous cluster-formation states [21].
The emitted light nucleus is most probably clustered appropriately distant from the center of the core nucleus, near the surface of the parent nucleus, due to Pauli blocking impacts from the core density [10, 12, 22, 23]. In the present work, we will investigate the location of forming the emitted cluster inside the parent nucleus. We shall use the relative motion wave function of the cluster-core system that obtained from the time-independent Schrödinger wave equation to estimate the distance, from the center of the parent nucleus, at which the cluster is formed with a reasonable preformation probability.
-
The interaction potential between the emitted cluster and daughter nucleus is a basic ingredient to study the decay process of a certain nucleus. After constructing the cluster-core interaction potential, it can be implemented in the time-independent Schrödinger wave equation to determine the incident and transmitted wave functions of the cluster-core system. Based on the Skyrme energy density functionals, the nuclear interaction potential, as a function of the separation distance r(fm) between the centers of mass of the interacting nuclei, is obtained by the difference between the energy expectation value E of the composite system at a finite separation distance r and that of individual separated nuclei at
$ r = \infty $ [21, 24, 25],$ \begin{split} V_N(r) =& E(r) - E(\infty) \\ =& \int \left\lbrace {\cal{H}}\left[ \rho_{pc}(\vec{x}) + \rho_{pD}(r, \vec{x}), \, \rho_{nc}(\vec{x}) + \rho_{nD}(r, \vec{x}) \right] \right. \\ & \left. - {\cal{H}}_c\left[ \rho_{pc}(\vec{x}) , \, \rho_{nc}( \vec{x}) \right] - {\cal{H}}_D\left[ \rho_{pD}(\vec{x}) , \, \rho_{nD}( \vec{x}) \right] \right\rbrace {\rm d}\vec{x}. \end{split} $

(1) $ {\cal{H}} $ ,$ {\cal{H}}_c $ , and$ {\cal{H}}_D $ in Eq. (1) define the energy density functionals of the composite system, the formed cluster, and the daughter nucleus, respectively.$ \rho_{ij}(i = p,n;j = c = D) $ represent the proton (p) and neutron (n) density distributions of both the emitted cluster (c) and the daughter nucleus (D). The Skyrme energy functional includes the kinetic and the nuclear (Sky) contributions,$\begin{split} {\cal{H}} \left( \rho_i, \tau_i, \vec{J}_i\right) =& \frac{\hbar^2}{2m}\sum\limits_{i = n,p}\tau_i\left(\rho_i,\vec{\nabla}\rho_i, \nabla^2 \rho_i \right) \\&+ {\cal{H}}_{\rm Sky}\left( \rho_i, \tau_i, \vec{J}_i\right) + {\cal{H}}_{\rm C}^{\rm exch}\left( \rho_p\right). \end{split} $

(2) Here,
$ \tau_i $ and$ \vec{J}_i $ respectively define the kinetic energy and the spin-orbit densities [21, 26, 27]. Regarding the nuclear part of the energy-density functional, we shall use the Skyrme-SLy4 parameterization [28] of the effective nucleon-nucleon, which includes zero- and finite-range, density-dependent, effective-mass, spin-orbit, tensor, and surface gradient terms. The last term in Eq. (2) considers the exchange Coulomb energy [13, 29]. The direct part of the Coulomb potential can be obtained by folding the proton-proton Coulomb interaction through the proton density distributions of the interacting nuclei [14],$ V_{\rm C}(r) = \int {\rm d}\vec{r}_1 \int {\rm d}\vec{r}_2 \frac{e^2}{|\vec{r} + \vec{r}_2 - \vec{r}_1|} \, \rho_{pc}(\vec{r}_1) \, \rho_{pD}(\vec{r}_2). $

(3) More details concerning the method of calculating the Coulomb and nuclear parts of the interaction potential can be found in Refs. [15, 21, 30]. The neutron (proton) density distribution of the involved nuclei heavier than α-particle can be expressed in the two-parameter Fermi form,
$ \rho_{n(p)} (r) = \frac{\rho_{0n(p)}}{1+ \exp\left[ {\dfrac{\left(r-R_{n(p)}\right)}{a_{n(p)}}}\right] } . $

(4) Based on a fit to a huge number of nuclear density distributions, which are obtained using Hartree-Fock calculations in terms of the Skyrme-SLy4 NN interaction, the half-density radii (
$ R_{n(p)} $ ) and diffuseness$ a_{n(p)} $ of finite nuclei have been parameterized as [31],$ \begin{split} & R_n ({\rm{fm}}) = 0.953\, N^{1/3} + 0.015\, Z + 0.774, \\ & R_p ({\rm{fm}}) = 1.322\, Z^{1/3} + 0.007\, N + 0.022, \\ & a_n ({\rm{fm}}) = 0.446 + 0.072 \, {N}/{Z}, \\ & a_p ({\rm{fm}}) = 0.449 + 0.071 \, {Z}/{N}. \end{split} $

(5) The saturation density
$ \rho_{0n(p)} $ is evaluated by normalizing the density to the corresponding nucleon number. This parameterization takes advantage of considering the isospin asymmetry dependence of the nuclear density distributions by giving the proton (neutron) density distribution as a function of both Z and N together. The α-particle density is usually taken as Gaussian distribution that is parameterized via electron scattering data [32]. For the favored decay modes with no angular momentum transferred by the emitted light cluster, we sum the nuclear and Coulomb potentials to construct the total potential,$ V_{\rm T}(r) = V_N(r) + V_{\rm C}(r). $

(6) The total potential
$ V_{\rm T}(r) $ is characterized by three classical turning points,$ r_{i = 1,2,3} $ (fm), at which$ V_{\rm T}(r_i) $ equals the Q-value ($ Q_{\rm C} $ ) of the decay process. Once we construct the total interaction potential, we implement it in the radial Schrödinger wave equation for the cluster-core dinuclear system,$ -\frac{\hbar^2}{2\mu}\frac{{\rm d}^2}{{\rm d}r^2} u_l(r) \,+\, \left( V_{\rm T}(r) + \frac{l(l+1) \hbar^2}{2\mu r^2} \right) u_{l}(r) = E \, u_{l}(r). $

(7) Here,
$ \mu = m_c m_D/(m_c + m_D) $ is the reduced mass of the cluster ($ m_c $ )-daughter ($ m_D $ ) system.$ u_l(r) $ represents the radial wave function,$ \psi = Y_{lm}(\theta,\phi) u_l(r)/r $ , that can be obtained by numerically solving Eq. (7). On the time scale, the half-lives in comparison to the observed α-decays of radioactive nuclei (1 μs – billions of years) are significantly longer than the times of standard nuclear motions (10-21 s). Then, the mean time before decay is in the range of 1015 – 1028 nuclear periods. Within this long time, the nucleus has numerous opportunities to set a pattern of motion, or to get clustered and emit the formed light cluster. These states can be safely considered to be quasi-stationary [33]. Another factor supporting the quasi- stationary state description of α and cluster decays is that all observed decay widths of heavy nuclei are significantly smaller than the corresponding Q-values by numerous orders of magnitude. This makes the decaying state almost a bound state [34], and subsequently the cluster decaying state is specified by a narrow resonant solution, including only outgoing components [35, 36]. The wave functions of the quasi-stationary decaying states, which are obtained by solving time-independent Schrödinger equations as an excellent approximation, are successfully used to study the α and heavier cluster decays in numerous studies [16, 34-42].After determining the normalized incident (
$ u_{li} $ ) and transmitted ($ u_{lt} $ ) wave functions at both sides of the Coulomb barrier, we can calculate the penetration probability in terms of their squared amplitudes [16, 17],$P = \frac{|A(u_{lt}(r>>r_3))|^2}{|A(u_{li}(r_2))|^2}. $

(8) The amplitude of the transmitted wave function in Eq. (8) is calculated at a sufficiently large distance [17], where the amplitude becomes constant. The assault frequency at which the formed cluster hits the Coulomb barrier can be obtained using the Wentzel-Kramers-Brillouin (WKB) approximation as the inverse of the time taken by the cluster to make one oscillation within the internal pocket of the interaction potential, between
$ r_1 $ and$ r_2 $ [19, 20],$ \nu = \left[ \int_{r_1}^{r_2} \frac{2\mu}{\hbar k(r)} {\rm d}r \right]^{-1}.$

(9) The wave number k in Eq. (9) is determined as
$ k(r) = \sqrt{ 2 \mu |V_{\rm T}(r)-Q_c|/ \hbar^2} $ . The half-life of the nucleus can be obtained in terms of P,$ \nu $ , and the preformation probability (S) of the formed cluster as$ T_{1/2} = \frac{\ln 2}{S\, \nu \, P}. $

(10) The emitted cluster must be formed before beginning its trials to penetrate the barrier. The preformation probability can be then defined as the quantum mechanical probability of finding the cluster-core as distinguished dinuclear system at a point near to the first turning point of the relative motion. As the obtained wave function is normalized to unity, then this probability can be estimated by integrating the squared incident wave function from the origin to a certain distance
$ R_0 $ , from the center of the parent nucleus, at which the cluster is expected to be formed [16]. This standard quantum mechanical probability indicates the weight of the cluster-core configuration, as distinguishable entities in the ground state, at$ R_0 $ . To find the expected value of the formation distance$ R_0 $ , we can employ an iterative procedure in terms of the experimentally observed half-life and the calculated penetration probability and assault frequency through the relation,$ \int\limits_{0}^{R_0} |u_{li}(r)|^2 \, {\rm d}r = \frac{\ln(2)}{P \, \nu \, T_{1/2}^{\rm exp}}. $

(11) -
Within the preformed cluster model, we attempt to estimate the most probable distance (
$ R_0 $ ) from the center of the parent nucleus, at which the emitted light nucleus is formed. To this end, we use the Skyrme-SLy4 nucleon-nucleon (NN) interaction to construct the total interaction potential for the cluster-daughter system, in the framework of the Hamiltonian energy density formalism for the nuclear part of the potential and the folding procedure for its Coulomb part. We implement the total interaction potential into the relative motion Schrödinger wave equation accompanied with the Bohr-Sommerfeld quantization condition. We numerically solve the time-independent Schrodinger wave equation of the decaying system, to extract the radial wave function ($ u_l(r) $ ) of the quasi-bound state. For the considered ground state to ground state favorite decays, the calculations are performed at l = 0. The formation distance, from the parent nucleus center, will be iteratively estimated using Eq. (11).We start our investigation of the estimated formation distance by the preformation of the α-particle inside the
$ ^{105-109} {\rm{Te}}$ isotopes, which exhibit ground state (g.s.) to ground state favorite α-decay modes. Here, the produced daughter isotopes (101-105Sn) are close to the double magic number and have similar numbers of neutrons and protons that occupy similar energy levels. As an example, we show in Fig. 1(a) the total interaction potential [$ V_{\rm T} $ =$ 0.922 $ $ V_N $ (Skyrme-SLy4) +$ V_{\rm C} $ ] between the α particle and the 103Sn daughter nucleus, which are involved in the α-decay of 107Te. The nuclear part of the shown potential is normalized by applying the Bohr-Sommerfeld quantization condition [16, 19]. Also displayed in Fig. 1(a) shows the internal and external real parts of the quasi-bound wave function ($ u_{l = 0} $ ) for the 107Te (103Sn, α) system, which are numerically obtained by solving the Schrödinger equation given by Eq. (7). Fig. 1(b) shows the variation of the formation distance$ R_0 $ from the centers of the Tellurium isotopes, as estimated using Eq. (11), in terms of the parent mass number. The proton ($ R_p $ ) and neutron ($ R_n $ ) half-density radii of the parent nuclei, which are given by Eq. (5), are shown in Fig. 1(b). In Fig. 1(c), we display the corresponding evaluated values of the α-preformation probability at the estimated distances, Eq. (11). The estimated preformation probability in Fig. 1(c) coincides with that obtained in different previous studies [7, 43, 44]. Figure 1(b) shows that the α-particle is formed within the region around the proton and neutron half-density radii of the parent nucleus. While the average proton and neutron half-density radii of the investigated Te isotopes are 5.34 fm and 5.18 fm, respectively, the average formation distance inside them is about 4.87 fm, which is smaller than the average$ R_p $ and$ R_n $ by about 0.47 fm and 0.3 fm. We find that the behavior of the calculated preformation probability with$ A_P $ resembles that of the estimated formation distance. The preformation probability increases when the α-particle is indicated to be formed at larger distance from the center of the parent nucleus, within its surface region. The smaller preformation probability refers to a shorter indicated formation distance. We recall here that different α-daughter systems are in question and not only different wave functions.
Figure 1. (color online) (a) Internal and external (magnified by 108) real part of quasi-bound wave function (
$ u_{l = 0} $ ) for 107Te (103Sn, α) system, as obtained by solving the Schrödinger equation (Eq. (7)). The 103Sn+α total interaction potential based on the Skyrme-SLy4 NN force [$ V_{\rm T} = 0.922 V_N $ (Skyrme-SLy4) +$ V_{\rm C} $ ], which is normalized using the Bohr-Sommerfeld quantization condition, is shown by the red line.$ R_B $ indicates the position of the Coulomb barrier. (b) Variation of the indicated α-formation distance$ R_0 $ (Eq. (11)) from the center of the parent nucleus for the favorite g.s. to g.s. α-decay modes of Tellurium isotopes, and the proton ($ R_p $ ) and neutron ($ R_n $ ) half-density radii (Eq. (5)) of parent Te isotopes. (c) Evaluated values of the α-preformation probability$ S_{\alpha} $ at the indicated$ R_0 $ (Eq. (11)), in terms of the parent mass number.The total potential based on the Skyrme NN interaction belongs to the type of potentials characterized by an automatic physical internal pocket. The folding potential improved by adding a repulsive term due to the change of the internal kinetic energy (
$ E_K $ ) in the large-overlap region of nuclear density can physically simulate this internal pocket. Based on the$ E_K $ +$ V_N $ (CDM3Y-230-Paris) [16] potential, the obtained values of the formation distance inside the$ ^{105-109} {\rm{Te}}$ isotopes range between 4.94 fm and 5.63 fm, which remain below or around their half-density radii, and within their pre-surface region. The other types of potentials that have no internal pockets, or an artificial one, fail to indicate realistic formation distance, where they provide an improbable claim that the formation of the cluster takes place near the center of the parent nucleus [16].Now we come to the favorite g.s. to g.s. decays of the even-even and even-odd
$ ^{190,191,194-202,204-208,210,212-216,218,219} {\rm{Po}}$ nuclei, which are heavier and exhibit larger isospin asymmetry than the Te isotopes. Fig. 2(a) shows the variation of the estimated formation distance and the proton and neutron half-density radii of the parent nuclei, as functions of the parent mass number. The estimated values of the preformation probability, based on the numerical solution of the time-independent Schrödinger equation of the α + Pb systems, are shown in Fig. 2(b). Fig. 2(b) shows the values of the preformation probability as extracted from different studies [21, 45-48] from the experimental half-lives and calculated decay widths based on different models. Figure 2(b) shows that the systematics of the preformation factor in the Polonium isotopes as estimated in the present study are consistent with that of the extracted values in previous studies [21, 45-48]. This clearly appears in the paining signatures for the even(Z)-even(N) Po isotopes and in the closed shell signature for 210Po (N = 126), which yields the smallest preformation probability. While the average proton and neutron half-density radii of the investigated Polonium isotopes in Fig. 2(a) are 6.65 fm and 6.73 fm, respectively, the average formation distance from their centers is about 5.22 fm, which is smaller than the average$ R_p $ and$ R_n $ by about 1.43 fm and 1.51 fm. This means that the α-particle is formed at a slightly deeper region inside the Po isotopes relative to the formation distance inside the Te isotopes. This is due to that the Po isotopes are of larger isospin asymmetry than the Te isotopes. Again, we see that the behavior of the preformation probability with$ A_P $ simulates that of the formation distance, where the shorter formation distance reflects less preformation probability. The formation region is deeper inside the Po isotopes of neutron numbers near the 126-neutron closed shell. Figure 2(c) shows the variation of the α-decay half-lives of the Po isotopes and the corresponding formation distances inside them. As shown in Fig. 2(c), the behavior of the formation distance with$ A_P $ inversely reflect that of the half-life, where the shorter formation distance indicates a more stable nucleus.
Figure 2. (color online) ((a) and (b)) Same as in Figs. 1(b) and 1(c), respectively, for the favorite g.s. to g.s. α-decay modes of Polonium isotopes. The preformation probabilites extracted from previous studies [21, 45-48], based on different models are added to panel (b) for comparison. (c) Variation of the α-decay half-lives of Po isotopes and corresponding formation distances, in terms of the parent mass number.
The estimated formation distance and the calculated preformation probability for the favorite g.s. to g.s. decays odd-even and odd-odd
$ ^{204,207,209,211,213-219}{\rm{At}} $ isotopes are displayed in Figs. 3(a) and 3(b), respectively. These Astatine isotopes have an isospin asymmetry comparable to (larger than) that of the Polonium (Tellurium) isotopes. The estimated values of$ S_{\alpha} $ in Fig. 3(b) come to an agreement with those yielded in other studies [48-50]. The average proton and neutron half-density radii of the Astatine isotopes presented in Fig. 3(a) are 6.73 fm and 6.85 fm, respectively. The average formation distance from their centers is about 5.31 fm. The average formation distance is then smaller than the average$ R_p $ and$ R_n $ by about 1.42 fm and 1.54 fm. This shows that the emitted α-particle is formed within the same pre-surface region pointed out for the Polonium isotopes.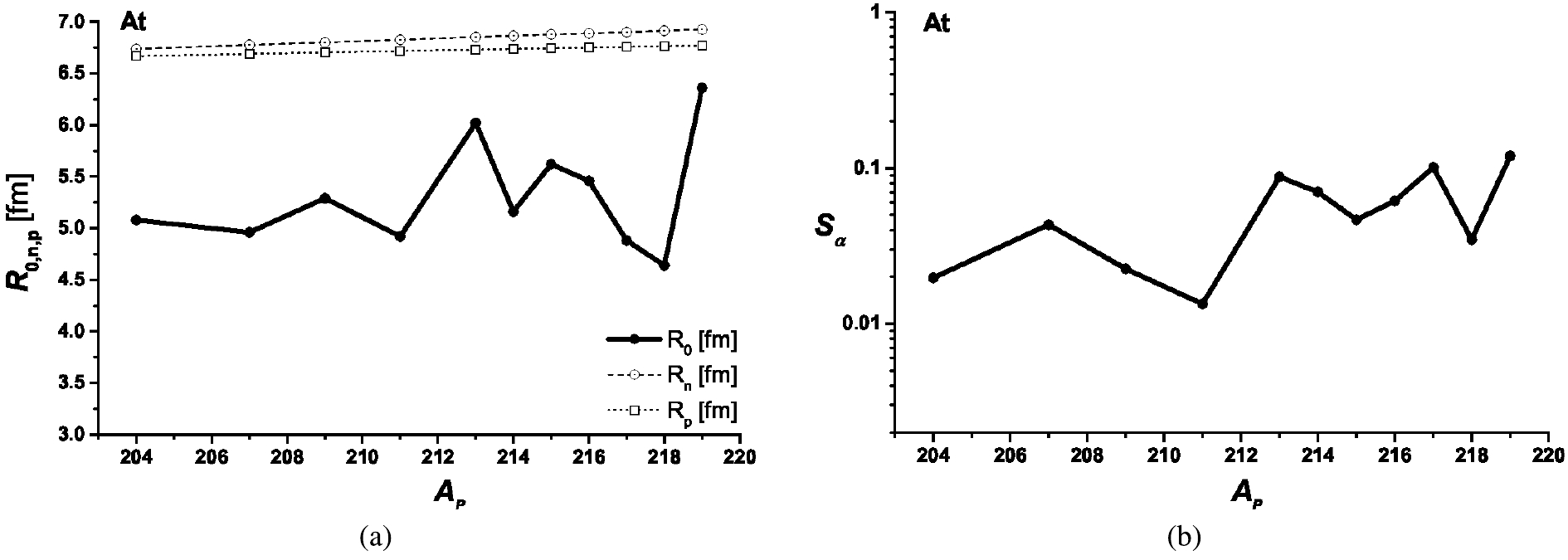
Figure 3. ((a) and (b)) Same as in Figs. 1(b) and 1(c), respectively, for the favorite g.s. to g.s. α-decay modes of Astatine isotopes.
We turn now to the emitted nuclei heavier than the α-particle. One of the heavy nuclei that are observed to emit heavy clusters is the 238Pu nucleus, which emits 28,30Mg and 32Si nuclei with branching ratios of about 6 × 10−15% and 1.4 × 10−14%, respectively, in addition to its principal α-decay mode (
$ \approx $ 100%) [51]. Fig. 4(a) shows the estimated formation distance and observed half-life as functions of the mass number of the formed cluster ($ A_c $ ). Fig. 4(b) shows the estimated values of the preformation probability based on the numerical solution of the time-independent Schrödinger equation of the α + 234U ($ Q_{\alpha} $ = 5.593 MeV), 28Mg + 210Pb ($ Q_{(^{28}{\rm{Mg}})} $ = 75.912 MeV), 30Mg + 208Pb ($ Q_{(^{30}{\rm{Mg}})} $ = 76.797 MeV), and 32Si + 206Hg ($ Q_{(^{32}{\rm{Si}})} $ = 91.188 MeV) systems. Figure 4(a) shows that the formation distance inside the nucleus does not vary significantly with increasing mass numbers of the formed cluster. However, the formation distance of the heavy clusters increases with increasing isospin asymmetry of the formed cluster. For instance, the α and 28Si clusters, which have isospin asymmetry parameter$ I = (N-Z)/A = 0 $ and$ I = 0.067 $ , respectively, are estimated to be formed at the short distance of 6.12 fm and 6.15 fm, from the center of the 238Pu nucleus. In contrast, the 28Mg($ I = 0.143 $ ) and 30Mg($ I = 0.2 $ ) clusters are estimated to be formed at larger distances of 6.49 fm and 6.53 fm, respectively. We recall here that the local isospin asymmetry increases on the surface and tail regions of the nucleus. Then, the binding energy of the surface and tail nucleons become less than that of those in the interior region, where the energy per nucleon decreases with increasing the isospin asymmetry [21]. This, in addition to the Pauli blocking effects from the saturated core density [10, 12, 22], endorses the formation of the cluster near the surface nuclear region. In addition to its$ A_c $ dependence, the observed partial half-lives of 238Pu in terms of its cluster-decay modes also increase with increasing the isospin asymmetry of the emitted cluster, as shown in Fig. 4(a). Figure 4(b) shows the cluster preformation probability that is microscopically estimated based on Eq. (11) and that calculated using the phenomenological formula of Blendowske and Walliser (BW),$ S_c = (S_{\alpha})^{\frac{A_c-1}{3}} $ [52, 53], in terms of the microscopically estimated α preformation probability. As seen in Fig. 4(b), the microscopically obtained preformation probability approves its$ A_c $ dependence given by the BW relation.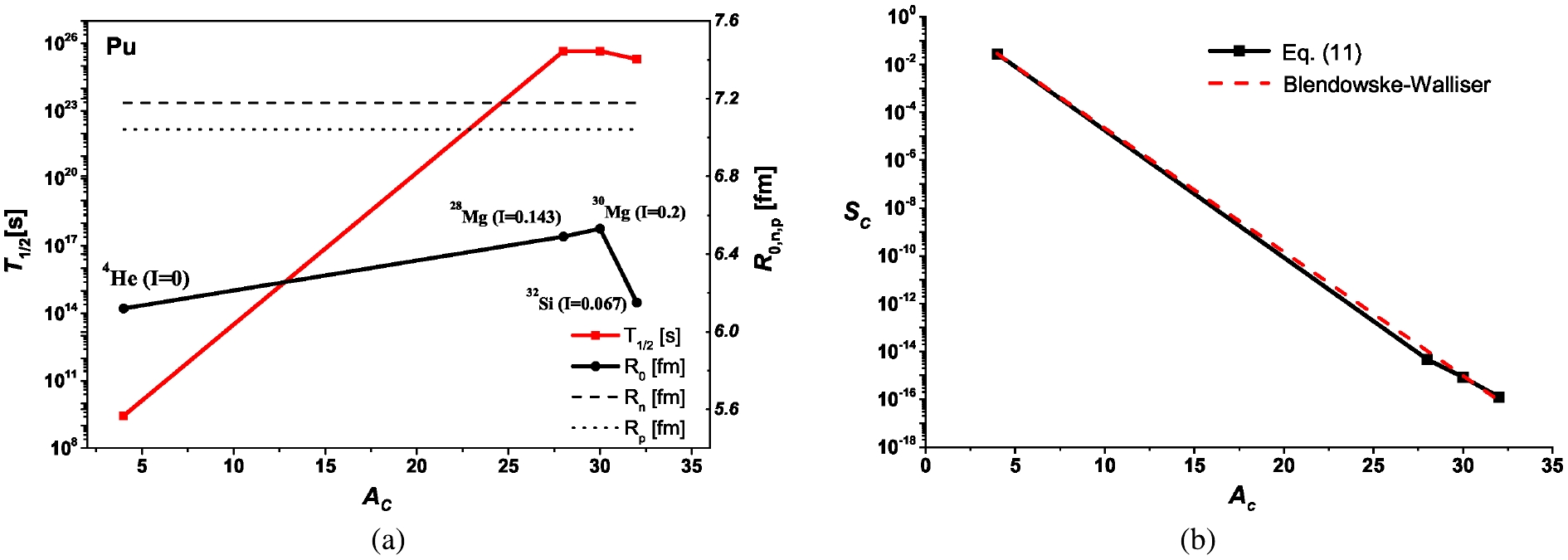
Figure 4. (color online) (a) Variation of indicated formation distance
$ R_0 $ from the center of the 238Pu parent nucleus in its α, 28,30Mg and 32Si decay modes, proton and neutron half-density radii of 238Pu, and corresponding observed partial half-lives, with respect to the mass number of the emitted cluster. (b) Microscopically estimated cluster-preformation probability$ S_C $ in 238Pu. The red dashed line depicts the Blendowske-Walliser behavior of$ S_C $ (238Pu) in terms of the microscopically estimated$ S_{\alpha} $ . -
Employing the wave functions obtained by the numerical solution of the stationary Schrödinger wave equation for the decaying system, we investigated the formation distance from the center of the parent nucleus at which the emitted cluster is formed. The results confirm that the emitted cluster is often formed at the pre-surface region of the parent nucleus under the effect of Pauli blocking from the saturated core density. While the estimated preformation probability of the α-particle mimics the behavior of its formation distance with the mass number of the parent nucleus, the observed half-life inversely reflex this behavior. Thus, the deeper α-formation distance inside the parent nucleus leads to lower preformation probability and a longer partial half-life. Further, the α-cluster tends to be formed at a slightly deeper sub-saturation density region in the nuclei of larger isospin asymmetry and in the closed shell nuclei. In contrast, we found that the cluster-formation distance increases by increasing the isospin asymmetry of the formed cluster, but not by increasing the cluster mass number. However, for a certain cluster-decay mode, the partial half-life increases with both the mass number of the emitted cluster and its isospin asymmetry.
Formation region of emitted α and heavier particles inside radioactive nuclei
- Received Date: 2020-01-16
- Available Online: 2020-07-01
Abstract: We investigate the formation distance (R0) from the center of the radioactive parent nucleus at which the emitted cluster is most probably formed. The calculations are performed microscopically starting with the solution to the time-independent Schrödinger wave equation for the cluster-core system, using nuclear potentials based on the Skyrme-SLy4 nucleon-nucleon interactions and folding Coulomb potential, to determine the incident and transmitted wave functions of the system. Our results show that the emitted cluster is mostly formed in the pre-surface region of the nucleus, under the effect of Pauli blocking from the saturated core density. The deeper α-formation distance inside the nucleus allows less preformation probability and indicates a more stable nucleus for a longer half-life. Furthermore, the α-particle tends to be formed at a slightly deeper region inside the nuclei, with larger isospin asymmetry, and in the closed shell nuclei. Regarding the heavy clusters, we observed that the formation distance of the emitted clusters heavier than α-particle increased via increasing the isospin asymmetry of the formed cluster rather than by increasing its mass number. The partial half-life of a certain cluster-decay mode increased with increase of either the mass number or the isospin asymmetry of the emitted cluster.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: