-
The global optical model potential (OMP) is an important and versatile tool for the analysis of the nucleus-nucleus elastic scattering process. It is widely applied for the analysis of various measured cross sections, such as elastic and inelastic scattering cross sections. In terms of understanding reaction mechanisms, the global OMP may also provide insight into underlying reaction processes and reaction mechanisms and further predict those reactions for nuclei away from stability.
Large scale analyses of global OMPs have been performed for elastic scattering involving light projectiles, namely neutrons, protons, deuterons, helium-3, tritons, and alpha-particles [1-6]. For heavy-ion elastic scattering, the study of OMPs is still in a developing stage and far from satisfactory. On the one hand, the experimental data on elastic scattering for reactions induced by heavy ions are insufficient. On the other hand, the exhibited angular distributions involving heavy-ion elastic scattering and the resultant optical model parameters are quite different from those observed for light ions. This is because the composite nature of the system makes the nuclear reaction mechanism more complicated as the result of mutual excitations, such as breakup or transfer reactions [7, 8].
In particular, the 12C nucleus is one of the most important and interesting nuclei for nuclear structure and nuclear reaction physics. To date, all the existing OMPs for 12C have been constructed for individual targets and few energy points. They are only applicable to special reactions and cannot predict other reactions, for which there are no experimental data available. Systematic analyses of a large body of scattering data have enabled us to find systematic behavior of the potential parameters according to variations in the mass and charge of the target nucleus as well as the incident energy. In recent years, experimental facilities have been intensively developed, and a larger quantity of experimental data has been analyzed for reactions induced by 12C. It is therefore crucial to establish a reliable global OMP over wide energy and mass ranges to survey the unknown properties of nuclear reactions and nuclear structure mechanisms for 12C.
In the present study, we analyze the elastic-scattering angular distributions together with the total reaction cross section data for reactions induced by 12C over a wide range of incident energies and target masses to obtain the 12C global phenomenological OMP. The new global OMP is constructed with the aim of systematically describing the elastic scattering of 12C.
The paper is organized as follows. In Sec. 2, we present the method and formalism used in the present work. The new global OMP is further determined and discussed. In Sec. 3, a comparison between the results and experimental data is performed, and a detailed analysis is provided. Sec. 4 contains the main conclusions.
-
The optical model potential is generally composed of a real part, an imaginary part, and a Coulomb potential:
$ \begin{array}{l} V(r,E) = V_{\rm R}(r,E)+{\rm i}[W_{\rm S}(r,E)+W_{\rm V}(r,E)]+V_{\rm C}(r), \end{array} $

(1) where
$ V_{\rm R} $ is the real part potential, and$ W_{\rm S} $ and$ W_{\rm V} $ are the surface and volume absorption imaginary part potentials, respectively, and$ V_{\rm C}(r) $ is the Coulomb potential. As discussed in a previous work [9], only the central components have been included in the optical potential because spin-orbit and other high-order spin-dependent couplings have been shown to have little or no influence on the shape of the elastic-scattering angular distributions and reaction cross sections analyzed in the present study.The Woods-Saxon form factor is adopted in our analyses for both the real and imaginary parts of the global OMP. The real part and the surface absorption and volume absorption imaginary parts of the OMP are respectively expressed as
$ \begin{array}{l} V_{\rm R}(r,E) = -\dfrac{V_{\rm R}(E)}{1+\exp[(r-R_{\rm R})/a_{\rm R}]}, \end{array} $

(2) $ \begin{array}{l} W_{\rm S}(r,E) = -4W_{\rm S}(E)\dfrac{\exp[(r-R_{\rm S})/a_{\rm S}]}{\{1+\exp[(r-R_{\rm S})/a_{\rm S}]\}^{2}}, \end{array} $

(3) $ \begin{array}{l} W_{\rm V}(r,E) = -\dfrac{W_{\rm V}(E)}{1+\exp[(r-R_{\rm V})/a_{\rm V}]}, \end{array} $

(4) where
$ R_{\rm i} $ and$ a_{\rm i} $ , with$ {\rm i = R, S, V} $ , are the radius parameters and diffuseness parameters corresponding to the real and surface and volume absorption imaginary parts of the potential, respectively. The radius parameter is expressed as$ R_{\rm i} = r_{\rm i}A^{1/3} $ , and A is the target mass number. The radius parameter of the real part potential can be further given by$ r_{\rm R} = r_{{\rm R}_{0}}+r_{{\rm R}_{1}}A^{1/3} $ .The energy-dependent potential depths
$ V_{\rm R}(E) $ ,$ W_{\rm S}(E) $ , and$ W_{\rm V}(E) $ are parameterized as$ \begin{array}{l} V_{\rm R}(E) = V_{0}+V_{1}E+V_{2}E^{2}, \end{array} $

(5) $ \begin{array}{l} W_{\rm S}(E) = W_{0}+W_{1}E, \end{array} $

(6) $ \begin{array}{l} W_{\rm V}(E) = U_{0}+U_{1}E. \end{array} $

(7) The Coulomb potential
$ V_{\rm C} $ is taken as that for a uniformly charged sphere of radius$ R_{\rm C} = r_{\rm C}A^{1/3} $ and has the form$ \begin{array}{l} V_{\rm C}(r) = \left\{ \begin{aligned} & \dfrac{zZe^{2}}{2R_{\rm C}}\left(3-\dfrac{r^{2}}{R^{2}_{\rm C}}\right) &\quad r<R_{\rm C}, \\ & \dfrac{zZe^{2}}{r} & \quad r\geqslant R_{\rm C}, \end{aligned} \right. \end{array} $

(8) where Z and z are the charge of the target and projectile, respectively.
-
Experimental data for 12C elastic scattering for nuclei from 24Mg to 209Bi below 200 MeV are analyzed in the present work. All the data were obtained from the nuclear database EXFOR at www-nds.iaea.org/exfor/exfor.htm. Details of these data are listed in Table 1.
target ELab /MeV Ref. 24Mg 16.0,17.0,18.5,19.5,22.0,23.5,24.0 [13] 40.0 [14] 28Si 25.0,29.0,30.0,32.0,34.0,36.0,40.0,46.0 [15] 49.3,70.0,83.5 [16] 59.0,66.0 [17] 186.4 [18] 19.0,21.0,23.0 [19] 27.0 [20] 23.0,24.0,25.0,27.0,28.0,29.0,29.86,31.29 [21] 32S 16.86,17.86,18.86,19.86,20.87,21.87,22.87 [22] 35.78 [23] 39K 54.0,63.0 [24] 40Ca 50.96 [25] 180.0 [26] 42Ca 49.89 [25] 48Ca 47.13 [25] 50Cr 65.0,73.5,140.0 [27] 56Fe 60.0 [28] nat.Fe 124.5 [29] 58Ni 26.0,27.0,27.5,28.0,28.5 [30] 60.0 [31] nat.Ni 124.5 [29] 64Ni 48.0 [32] 90Zr 66.0 [33] 90.0 [34] 120.0,180.0 [26] 91,94,96Zr 66.0 [33] 92Zr 66.0 [35] 92Mo 60.0,90.0 [34] 116-120,122,124Sn 66.0 [33] 194,198Pt 73.5 [36] 208Pb 54.5,55.5,56.0,56.5,57.0 [30] 58.9,60.9,62.9,64.9,69.9,74.9,84.9 [37] 118.0 [38] 180.0 [26] 209Bi 58.9,59.9,60.9,61.9,62.9,63.9,65.9,69.9,74.9,87.4 [39] 118.0 [38] Table 1. The elastic-scattering angular distributions database for 12C projectiles. E is the incident energy for different targets in the laboratory system.
As noted in our previous works [9-11], all these elastic scattering data are fitted simultaneously using the improved APMN code [12]. The 12C OMP parameters are optimized by minimizing
$ \chi^{2} $ , which is defined as follows:$ \begin{array}{l} \chi^{2} = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^{N}\left[\dfrac{\sigma_{i}^{\rm th}-\sigma_{i}^{\rm ex}}{\Delta\sigma_{i}^{\rm ex}}\right]^{2}, \end{array} $

(9) where N is the number of data points.
$ \sigma_{i}^{\rm th} $ ,$ \sigma_{i}^{\rm ex} $ , and$ \Delta\sigma $ are the theoretical and experimental differential cross sections and the corresponding experimental error, respectively. In searching for the parameters, we first give all the potential parameter reasonable boundaries in the varied region using some physical limitation. The uncertainty in the experimental data was also taken from the EXFOR nuclear database. Details of applying the method used here to obtain the best OMP parameters can be found in Refs. [9-11]. The final fifteen optical potential parameters, including the strength, radius, and diffuseness of the real and imaginary potentials, are presented in Table 2.parameter value unit $ V_{0} $ 

277.772 MeV $ V_{1} $ 

−0.278 $ V_{2} $ 

−0.0001 MeV−1 $ W_{0} $ 

56.059 MeV $ W_{1} $ 

−0.0546 $ U_{0} $ 

5.0 MeV $ U_{1} $ 

0.279 $ r_{\rm R_{0}} $ 

1.158 fm $ r_{\rm R_{1}} $ 

0.0273 fm $ r_{\rm S} $ 

1.161 fm $ r_{\rm V} $ 

1.627 fm $ r_{\rm C} $ 

1.1 fm $ a_{\rm R} $ 

0.770 fm $ a_{\rm S} $ 

0.851 fm $ a_{\rm V} $ 

0.545 fm Table 2. Global OMP parameters for 12C projectiles
-
The elastic-scattering angular distributions of the reactions induced by 12C are calculated using the present global OMP and are systematically analyzed by comparing the theoretical results with the corresponding experimental data. For light heavy ion systems, the total mass number of the projectile and target is usually less than fifty (
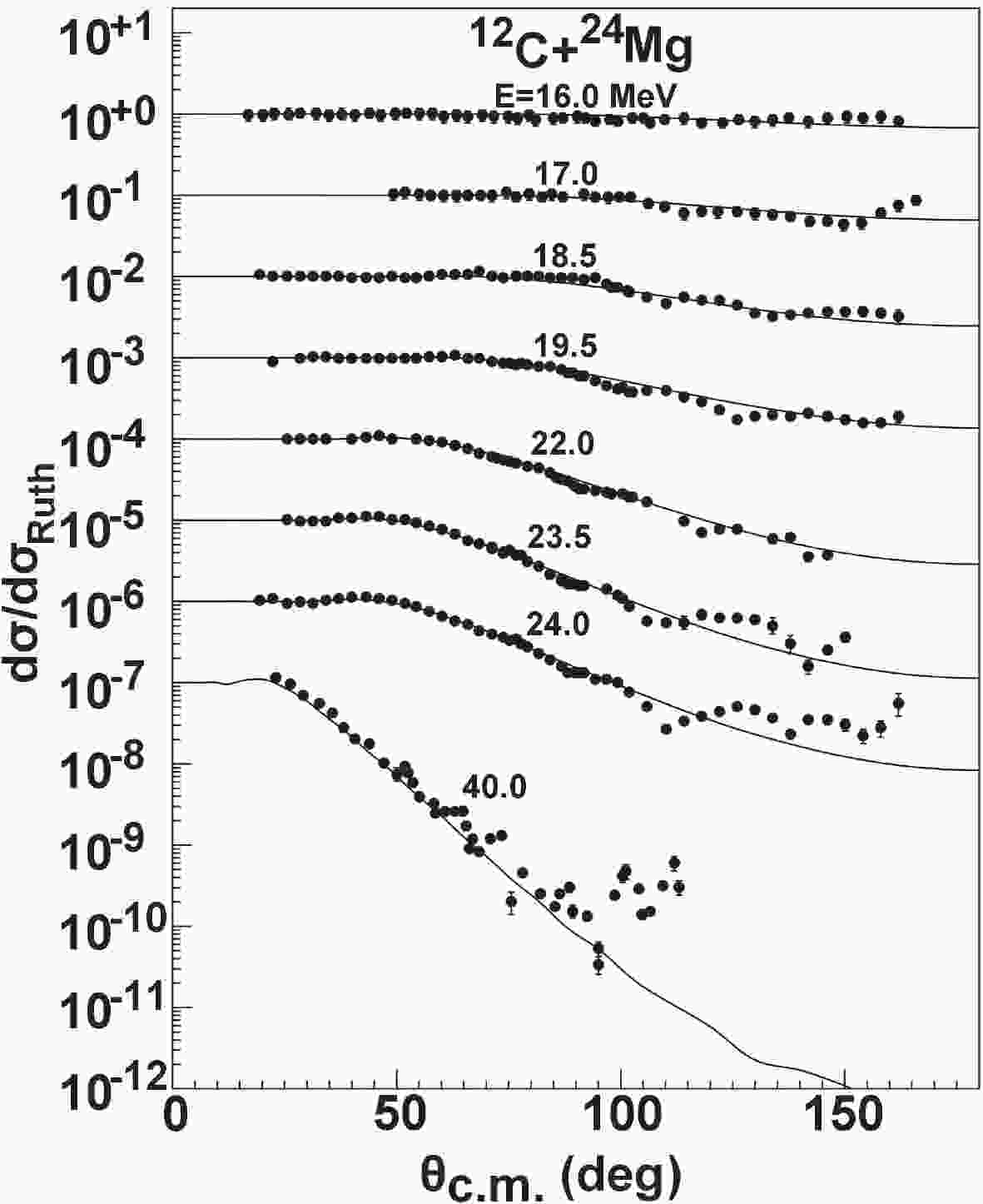
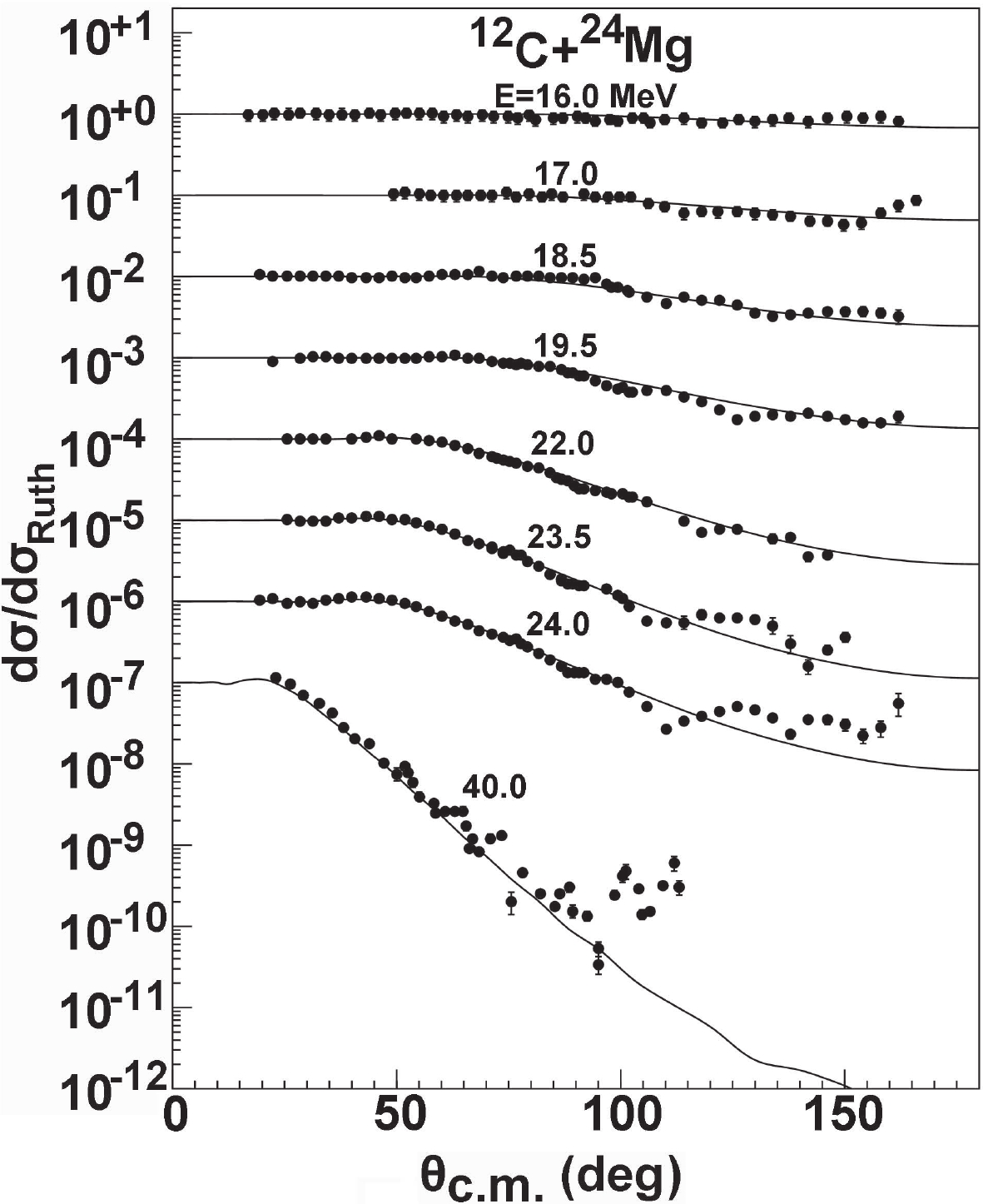
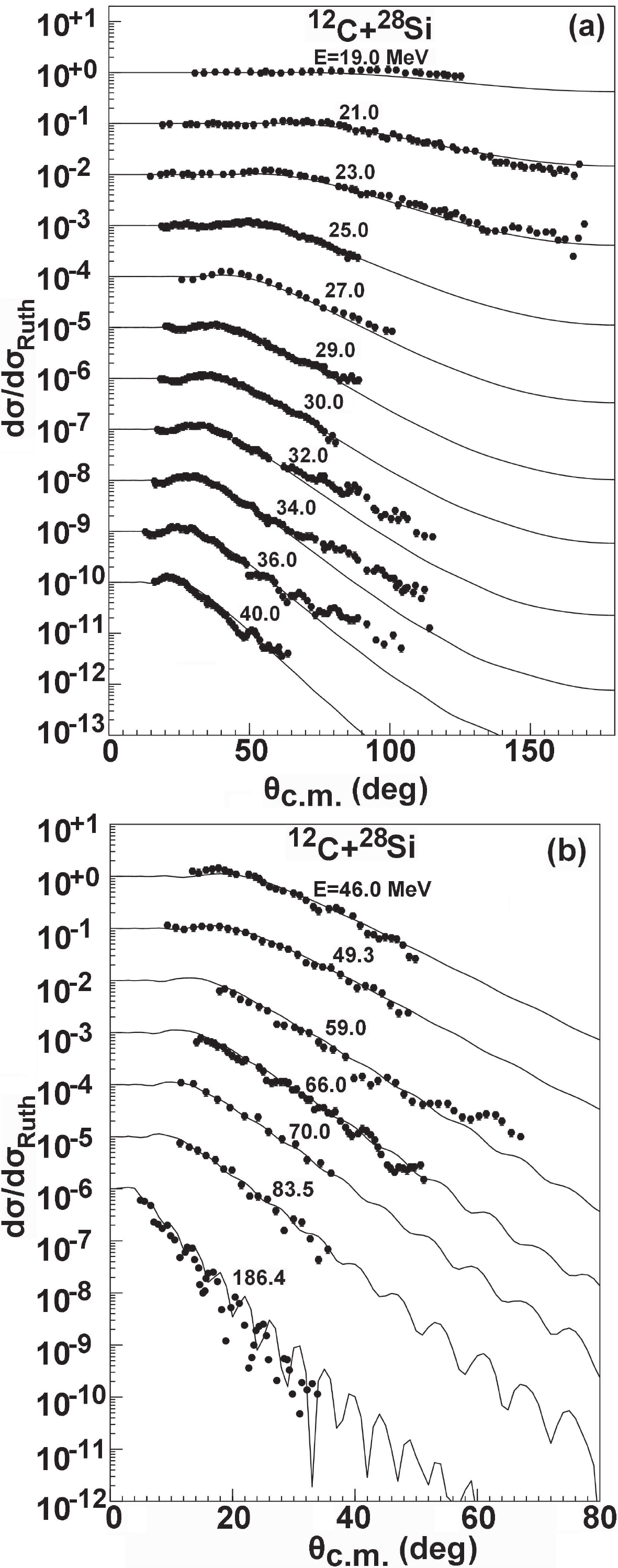
$ A_{ p} $ +$ A_{ T} $ $ < $ 50). The behavior of the elastic-scattering angular distribution is strikingly different from that of the heavier targets at energies near the Coulomb barrier. It presents a clear oscillatory pattern because of its sensitivity to the nuclear interior. The elastic-scattering angular distributions for 24Mg targets are compared with measurements [13, 14] from the same experiment at incident energies from 16.0 to 40.0 MeV. The results fit the experimental data well below$ 100^{\circ} $ and produce the average at the backward-angle, where the data present a strong oscillatory pattern. We also predict the angular distribution of 12C + 27Al and compare it with the existing experimental data [40-43]. Similarly, agreement is found for the forward-angles, where there is no oscillatory pattern, while the results produce an average description for backward-angles. The comparison between the calculations and the corresponding experimental data for 24Mg is presented in Fig. 1.For the 12C + 28Si system, the OMP calculations of the elastic-scattering angular distribution are also compared with different experimental data [15-20], as shown in Fig. 2. It is clear that the experimental angular distributions are smooth below 30.0 MeV. Moreover, no oscillation is observed at the incident energies of 21.0 and 23.0 MeV, especially for backward-angles [19]. The results calculated by the global OMP thus reproduce the experimental data well. However, between 32.0 and 40.0 MeV, the experimental data for the angular distributions exhibit an upward trend above
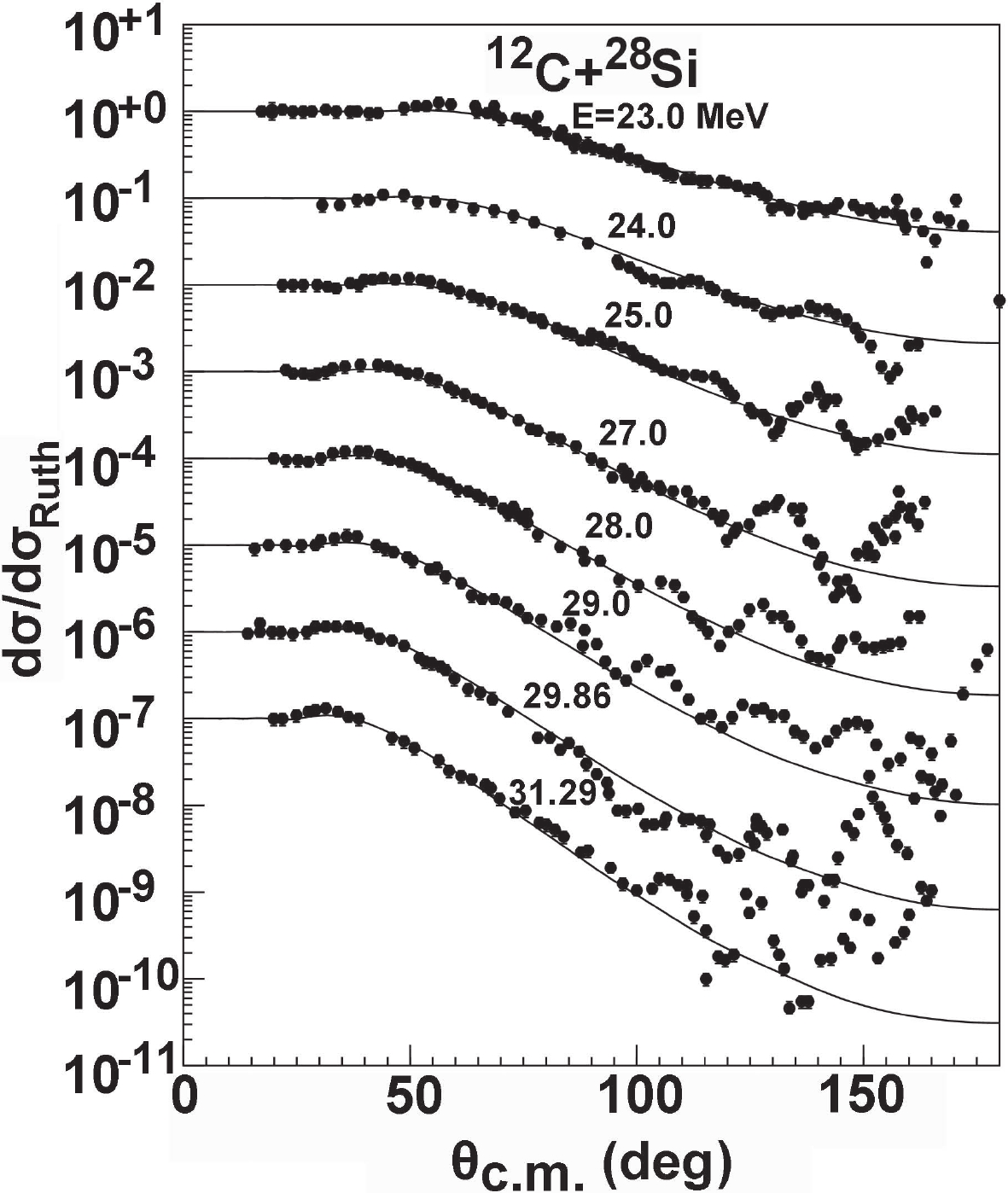
$ 60^{\circ} $ , for which the calculations of the optical model do not provide a good fit [15]. In the energy range from 48.0 to 186.4 MeV, there is good agreement between the calculations and the experiment values except for individual energies, for which occasional irregular structures are apparent at some scattering angles. The elastic angular distributions between 23.0 and 31.92 MeV were also measured [21]; from 25.0 to 31.92 MeV, they exhibit strong diffraction oscillations above$ 100^{\circ} $ . It is known that results calculated using the global OMP can describe the overall pattern of the elastic cross section well, but they have no oscillating behavior in the backward-angle range, where the oscillating behavior may be explained by introducing Regge-pole form terms in the optical model S-matrix [21, 44]. Comparisons between the calculations and the experimental data are displayed in Fig. 3. It can be seen that there are some discrepancies between the calculations and the measurements. In particular, strong diffraction oscillations in the backward-angle will be studied in our next work to obtain the local OMPs of these light heavy ion systems.The results of our global OMP analysis of the elastic-scattering angular distribution for 32S are shown in Fig. 4. The data in Ref. [22] are only for the angular distributions in the range from
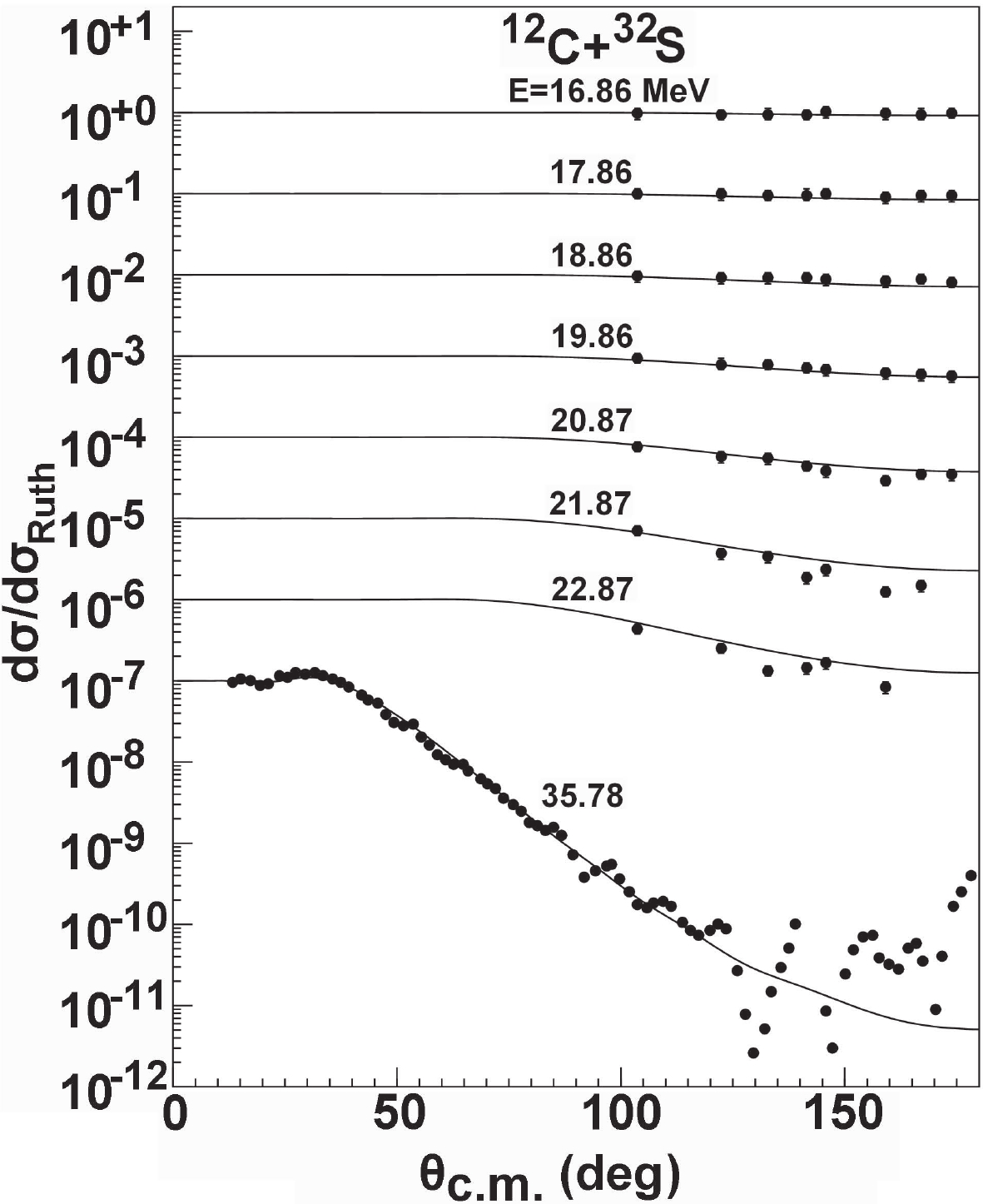
$ 72^{\circ} $ to$ 170^{\circ} $ . Compared with the experimental data [22], the calculations agree well with the measurements below 20.87 MeV. At energies of 21.87 and 22.87 MeV, the experimental elastic scattering cross sections exhibit smooth oscillations, and the calculations are slightly larger than the data above$ 120^{\circ} $ . Moreover, below 120°, the global OMP also gives a good description of the data [23] at 35.78 MeV. Above$ 120^{\circ} $ , it only produces an average of the cross sections where the data exhibit a strong oscillation pattern.In general, a similarity among the experimental measurements is that weak and strong oscillations and occasional irregular structures are clearly exhibited for the light targets 24Mg, 27Al, 28Si, and 32S at different incident energies. The global OMP cannot reasonably describe oscillating behaviors in backward-angles since these light nuclei are considered to exhibit significant
$ \alpha $ clustering. In particular, for the 12C + 24Mg system, oscillating behavior in the backward-angle is evident even at energies under the Coulomb barrier, while for the 12C + 28Si system at the same energy, the data are smooth and non-oscillating. The reason may be related to the fact that 24Mg and 28Si have quite different cluster properties [19]. For these targets, the global OMP can give a good description of the elastic-scattering angular distribution in forward-angles (below approximately$ 100^{\circ} $ ), although there are discrepancies between the calculations and the experimental data for backward-angles. In future work, we will focus on the oscillating behavior of these heavy-ion systems by considering other reaction mechanisms to improve the present calculations.Figure 5 presents the fit of the calculations to the experimental data [25, 26] for 40Ca at incident energies of 50.96 and 180.0 MeV and compares the predictions and experimental data [26] at 300.0 and 420.0 MeV. Finally, it provides comparisons for isotopes,
$ ^{42,48} $ Ca, at incident energies of approximately 50 MeV. The calculations fit the data well for 40Ca at incident energies of 180.0, 300.0, and 420.0 MeV and for 48Ca at 47.13 MeV. However, a pronounced oscillation superimposed on this overall shape is observed for 40Ca at 50.96 MeV in the backward-angle range. For 42Ca, a weak oscillation can also be seen at 49.89 MeV. Nevertheless, the results calculated using the global OMP can give a reasonable fit for these targets.The calculations of the elastic angular distributions for 39K, 50Cr, and 56Fe are shown in Fig. 6. This comparison indicates that a reasonable fit with the experimental data [24, 27-29] is obtained using the global OMP except for 56Fe at the incident energy of 60.0 MeV, for which the calculations are slightly larger than the measurements [28]. In Fig. 7, we compare the elastic angular distribution calculated using the obtained global OMP with the corresponding experimental data [29-31] at different incident energies for the reaction of 12C + 58Ni. A good description of the elastic scattering cross section data is obtained at the incident energies of 26.0, 27.0, 27.5, 28.0, 28.5, and 124.5 MeV, while the calculation at 60.0 MeV is smaller than the data in Ref. [31].
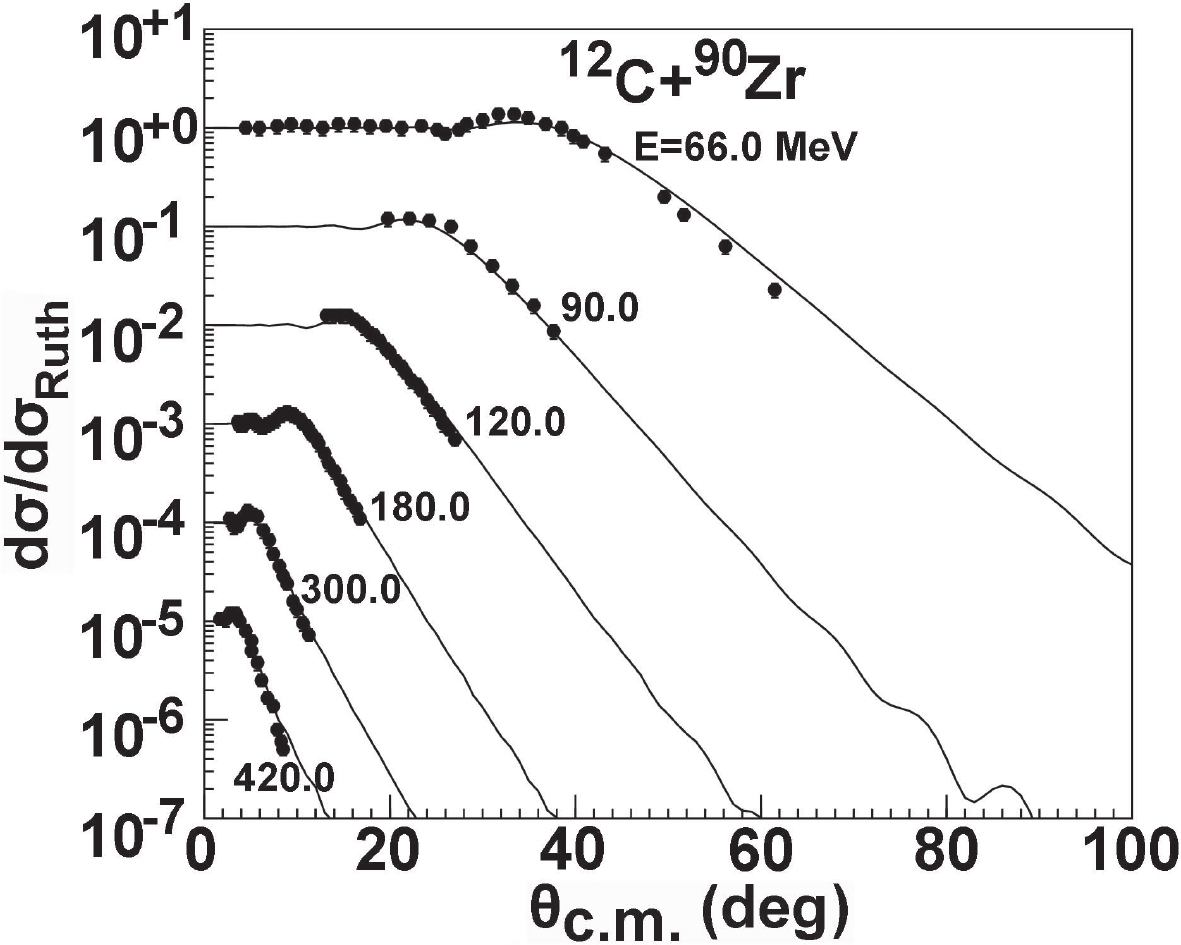
The elastic-scattering angular distributions are also calculated using the obtained global OMP for some medium mass targets. For the 12C + 90Zr system, the calculations are compared with the corresponding experimental data [26, 33, 34], and they are in good agreement with the existing experimental data at all incident energies. These results are presented in Fig. 8.
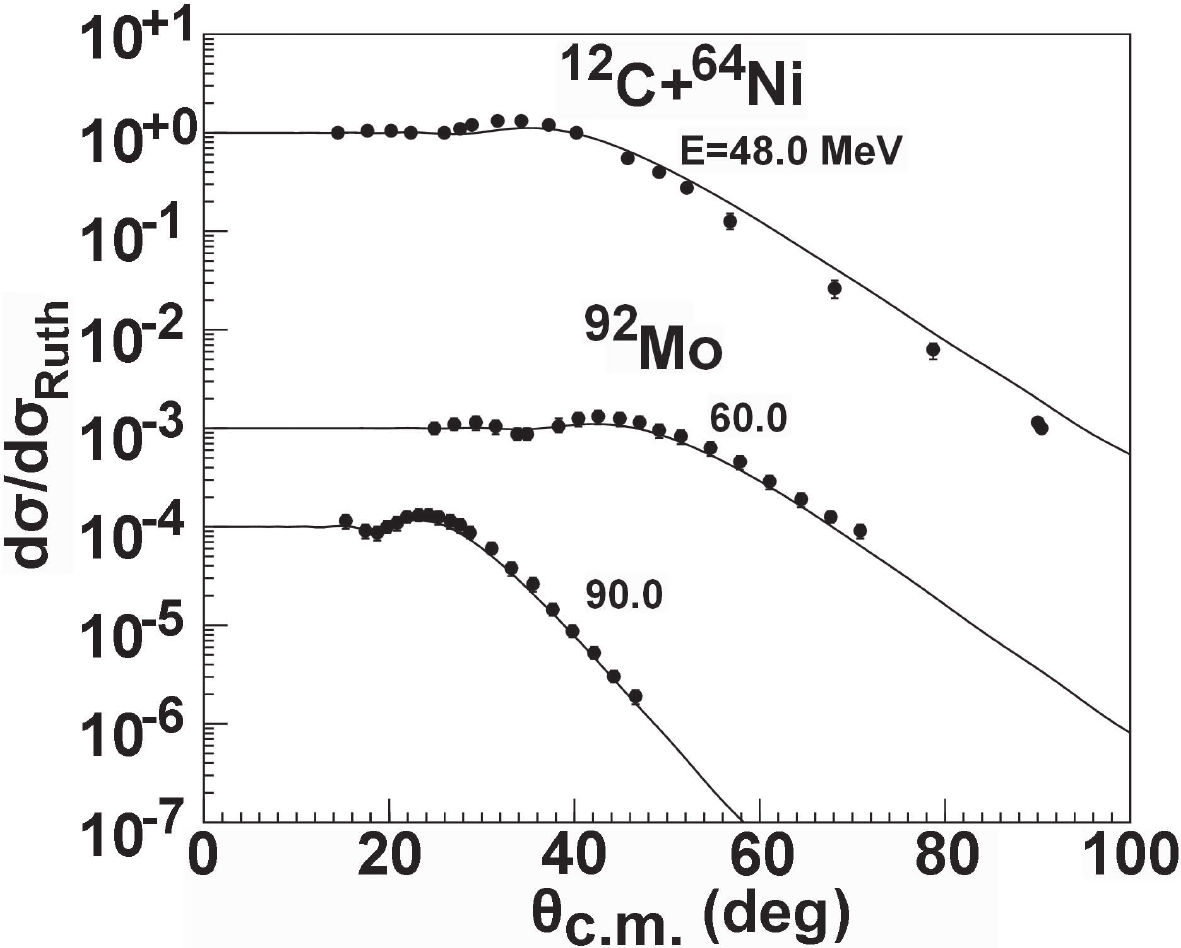
For 64Ni targets, the elastic-scattering angular distributions were only measured at one energy point. Figure 9 presents the comparison between the calculations and the measurements [32] at 48.0 MeV. Good agreement on the elastic angular distribution is obtained between them. We compare the elastic angular distributions of 92Mo with the data [34] in Fig. 9. The calculations are very consistent with the corresponding experimental data at 60.0 and 90.0 MeV.
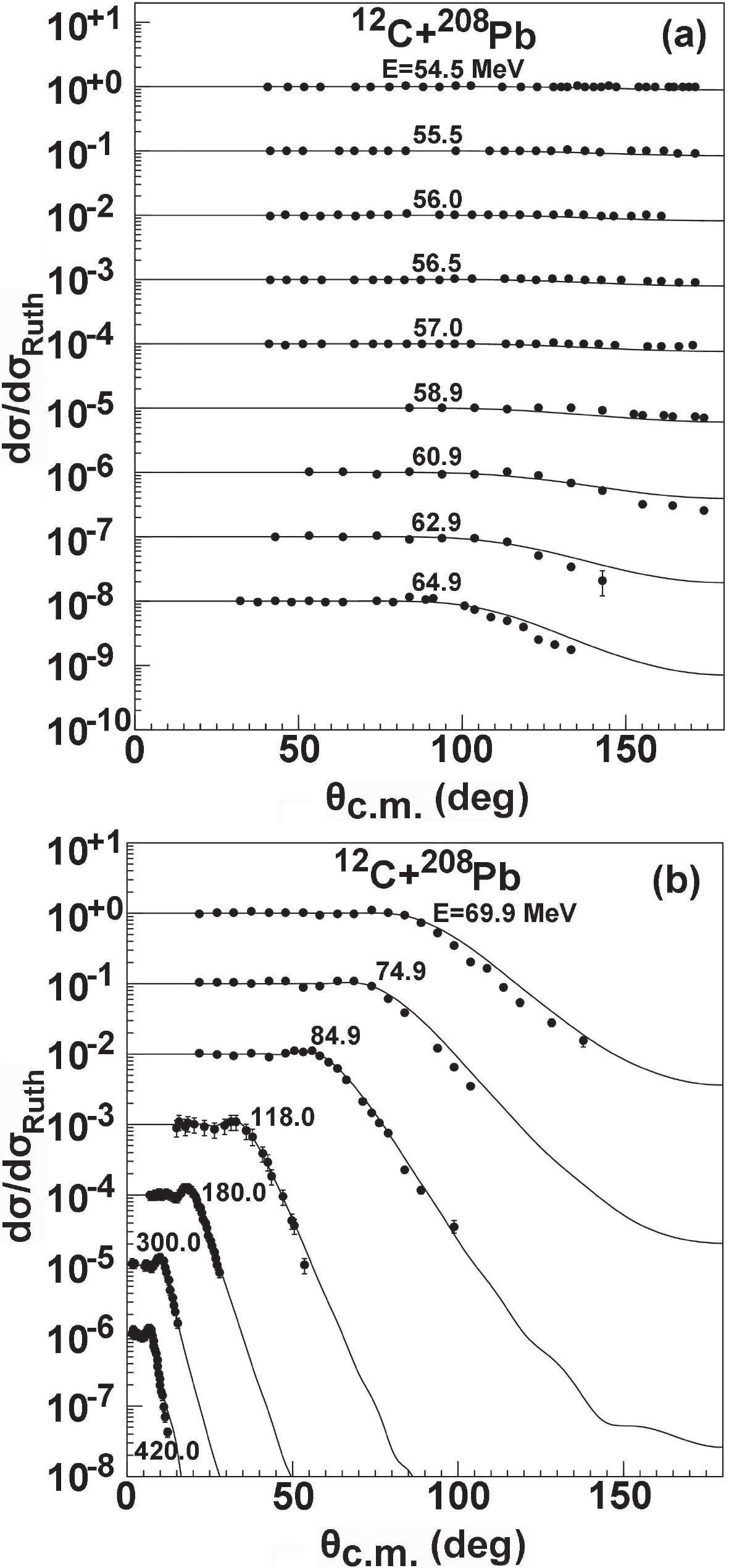
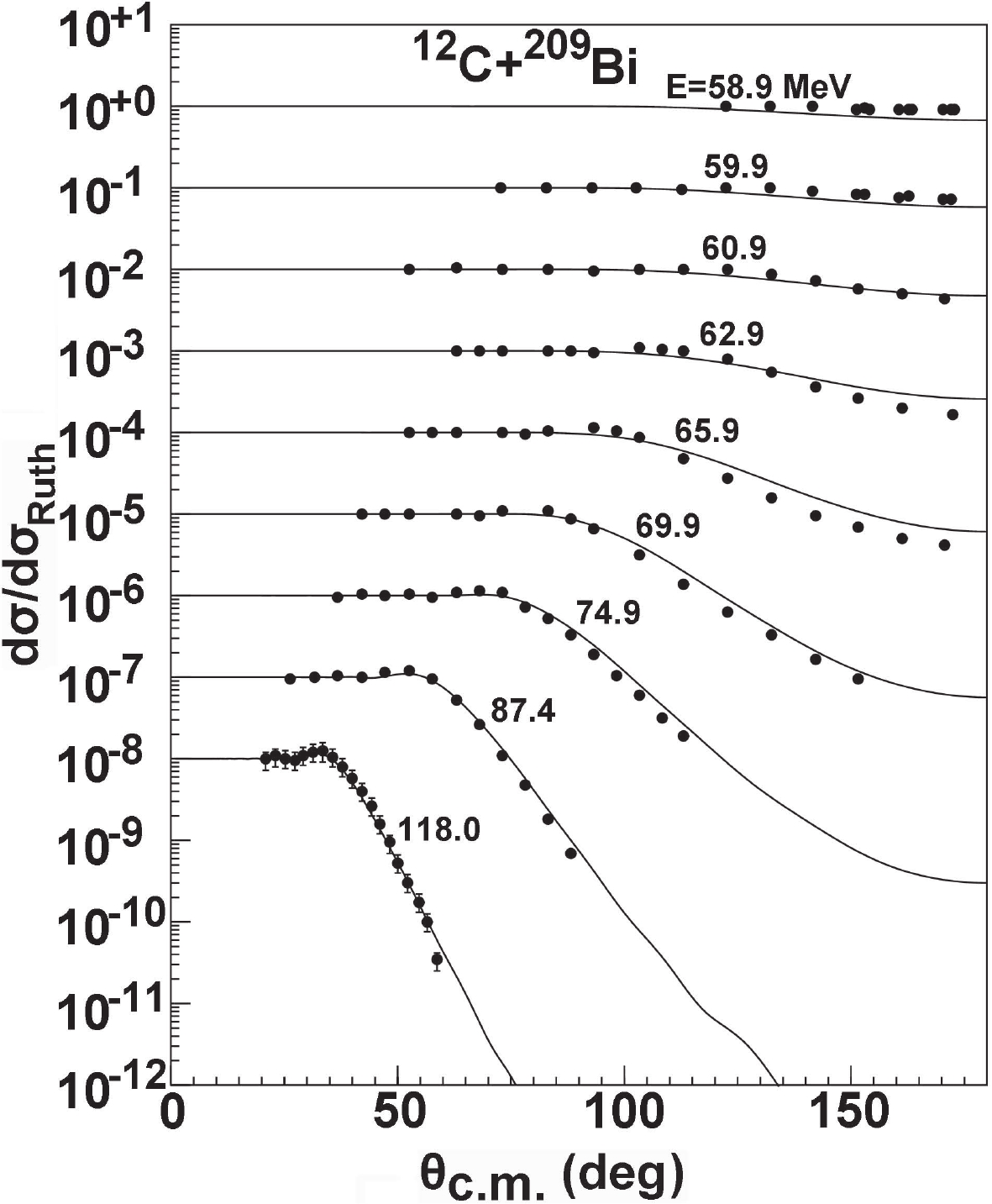
For heavier targets, the angular distributions are also calculated from the global OMP. Figure 10 provides comparisons of the calculations with the corresponding experimental data for 208Pb [26, 30, 37, 38] at incident energies from 54.5 to 420 MeV. Across this energy range, the global OMP gives a good approximation to these data. Similarly, for 209Bi, the agreement between the calculations and the experimental data [38, 39] is very good from 58.9 to 118.0 MeV. This result is displayed in Fig. 11.
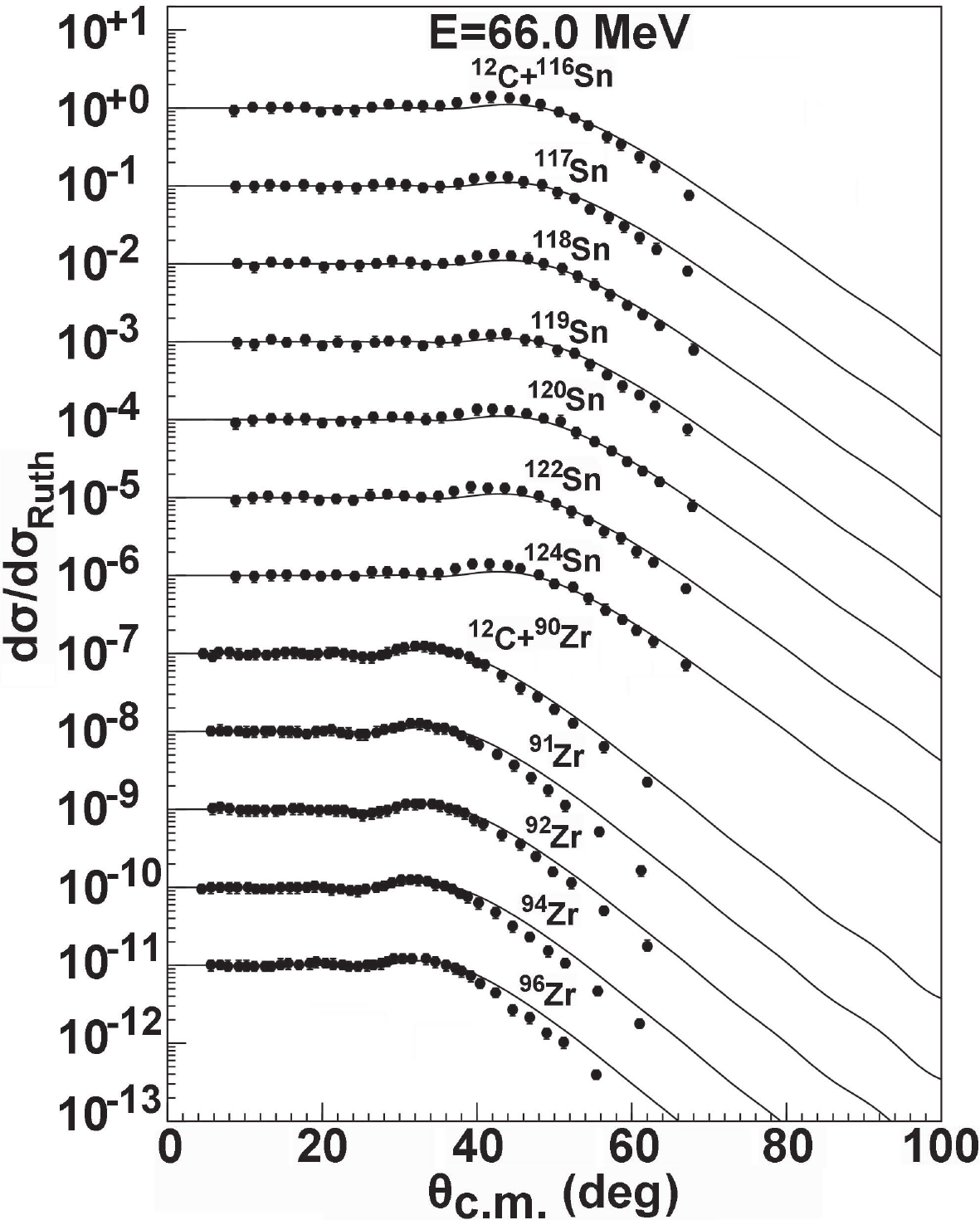
The angular distributions of the elastic scattering for different targets are also measured at the same incident energy. The full curves in Fig. 12 illustrate the comparison between the global OMP calculations and the data [33, 35] at an incident energy of 66.0 MeV for the isotopic chains of
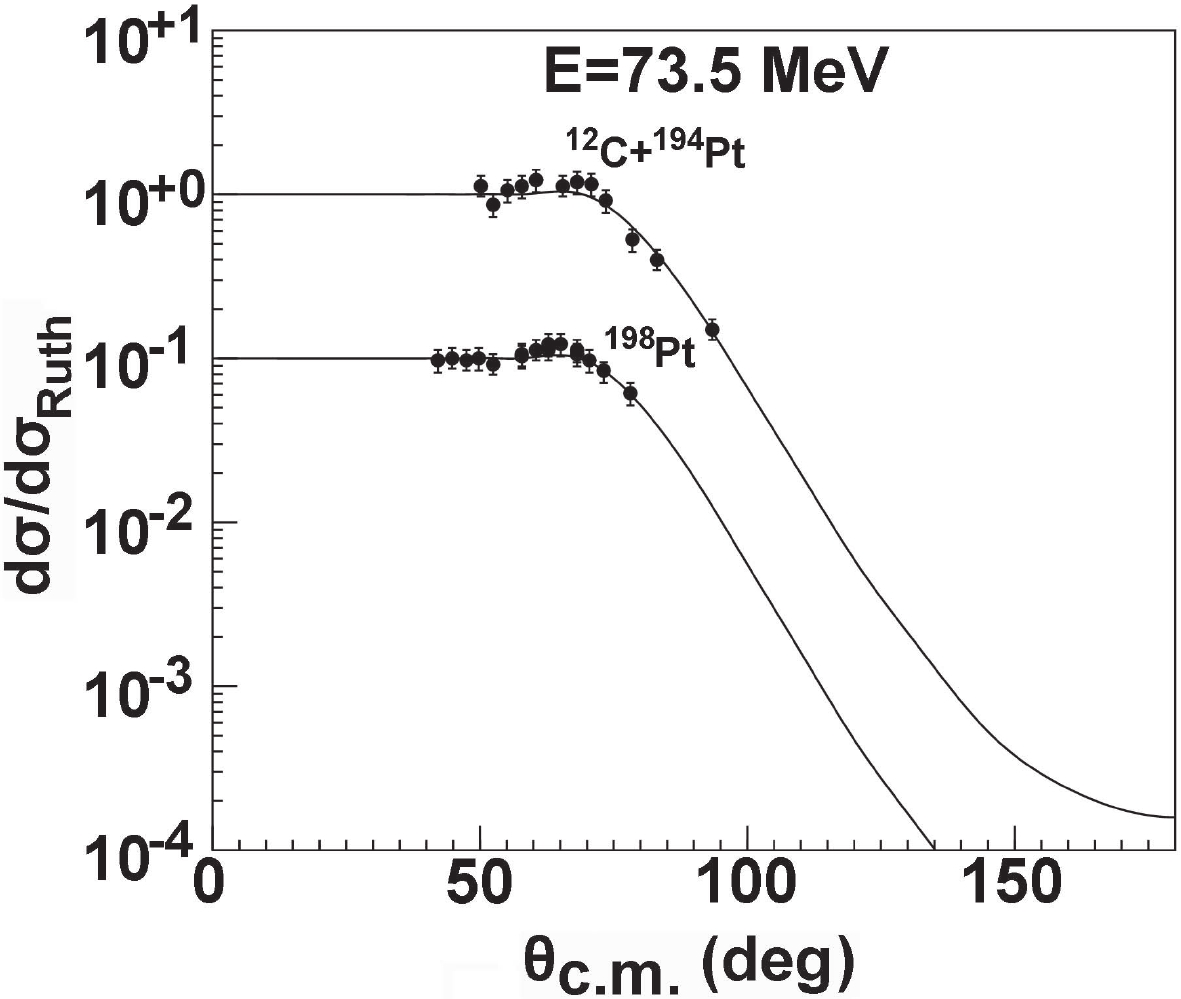
$ {\rm Sn} $ and$ {\rm Zr} $ . The overall agreement is also very good for these isotopes. In Fig. 13, the elastic-scattering angular distributions at incident energies of 73.5 MeV are compared with the experimental data [36] for$ ^{194,198} $ Pt targets. Good agreement is again achieved.The elastic scattering of 12C ions by
$ ^{\rm nat.} $ Al,$ ^{\rm nat.} $ Si, and$ ^{\rm nat.} $ Ti is also investigated at a backscattering angle of$ 170^{\circ} $ below 30 MeV [45]. The experimental data are not included in the fitting data. We compare the results predicted by the global OMP with the data and obtain perfect agreement between them, as shown in Fig. 14.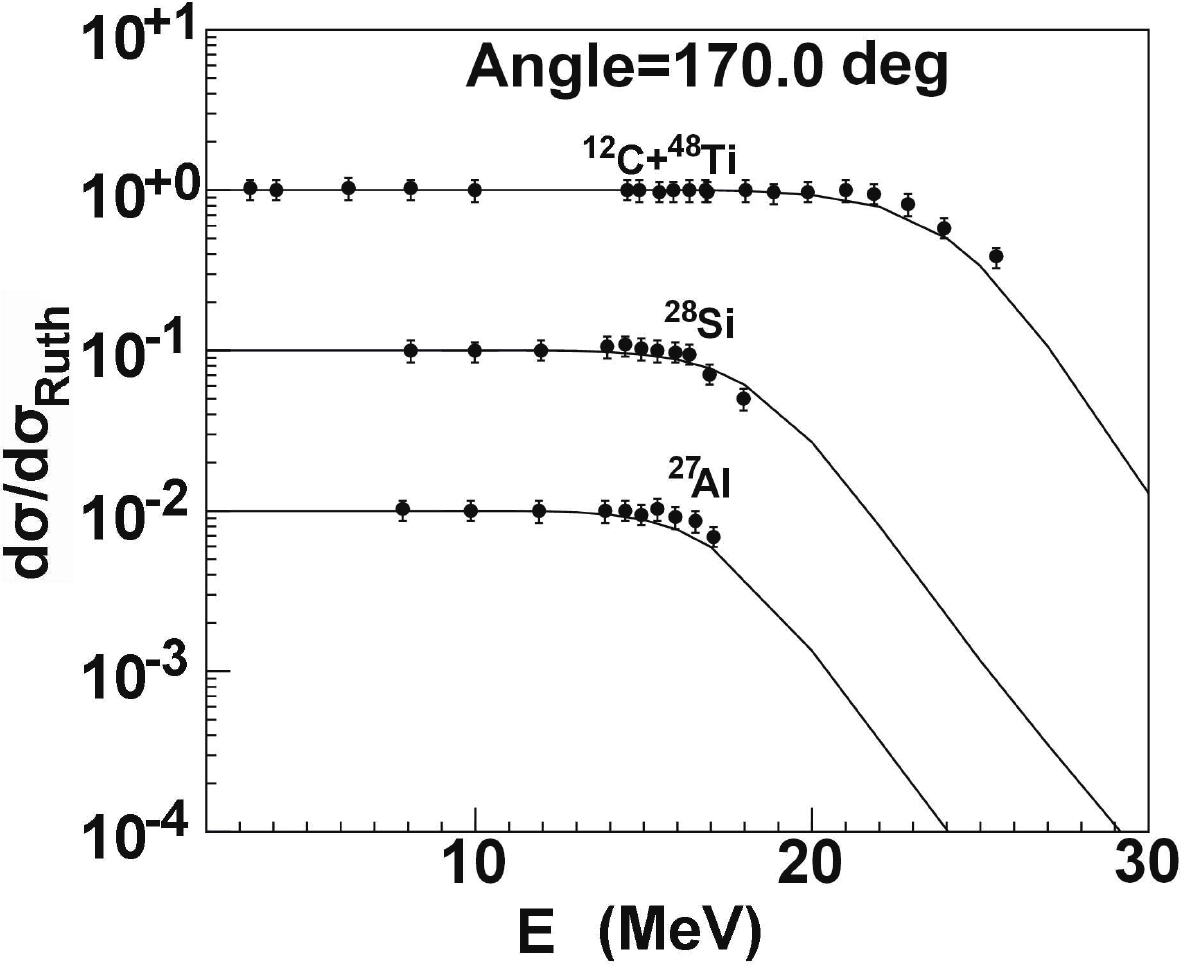
Figure 14. Calculated elastic-scattering angular distributions at the same incident angle compared with the experimental data [38] for different targets.
For the 12C + 197Au system, the quasi-elastic scattering angular distributions are also measured in the energy range from 56 to 82 MeV [46]. A comparison between the predictions and the existing experimental data is presented in Fig. 15. It is found that the calculations agree well with the experimental values except for those at 82 MeV. Moreover, the experimental data of quasi-elastic scattering angular distributions include elastic scattering and contributions from inelastic scattering and neutron transfer.
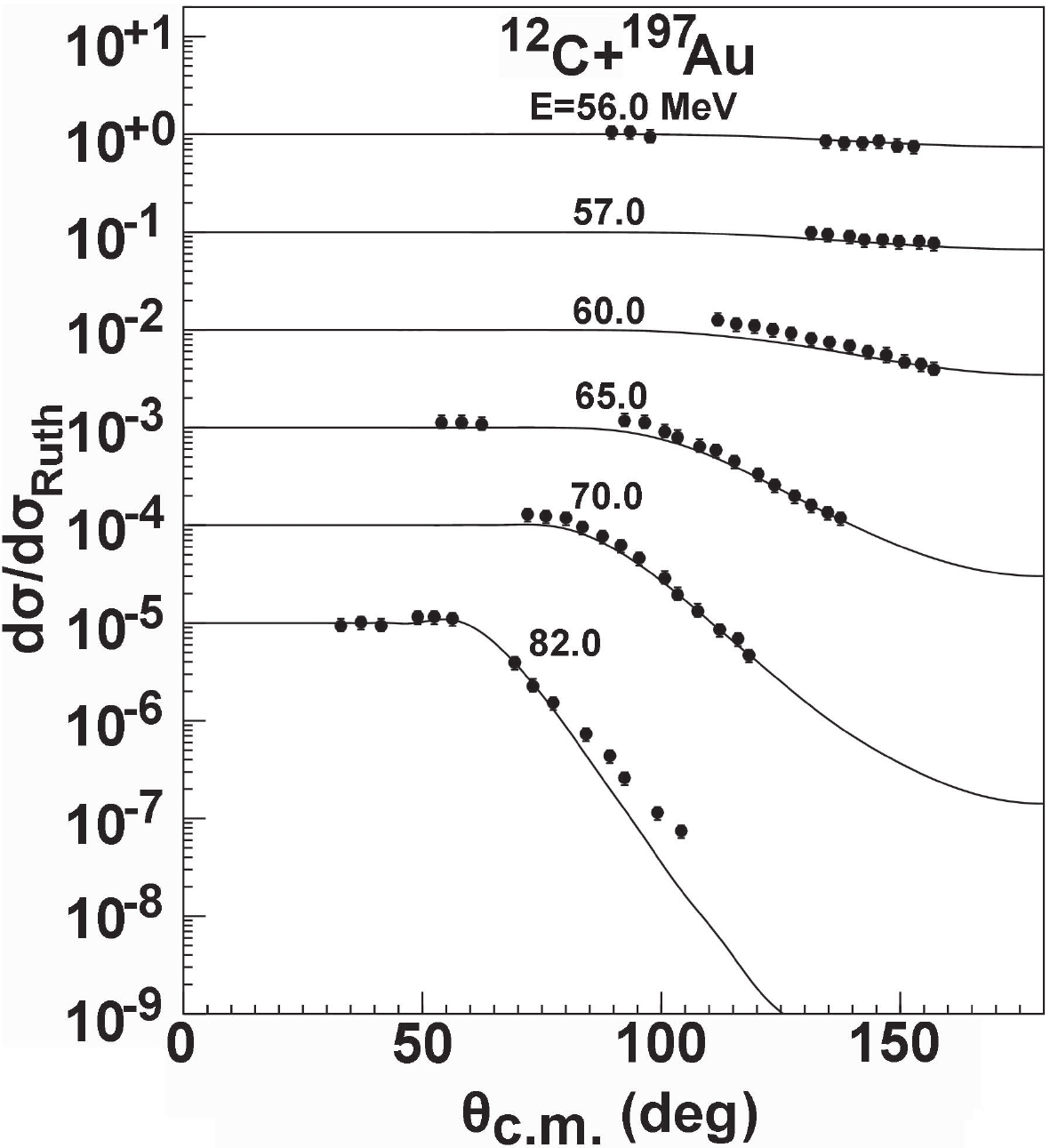
Figure 15. Comparison between the predictions of the optical model and the experimental data for the quasi-elastic scattering angular distributions of 197Au [46].
The angular distributions for actinides are also predicted and compared with the corresponding experimental data. The results for 236U are shown in Fig. 16. As can be seen from the figure, a good theoretical fit to the experimental data [47] is obtained.
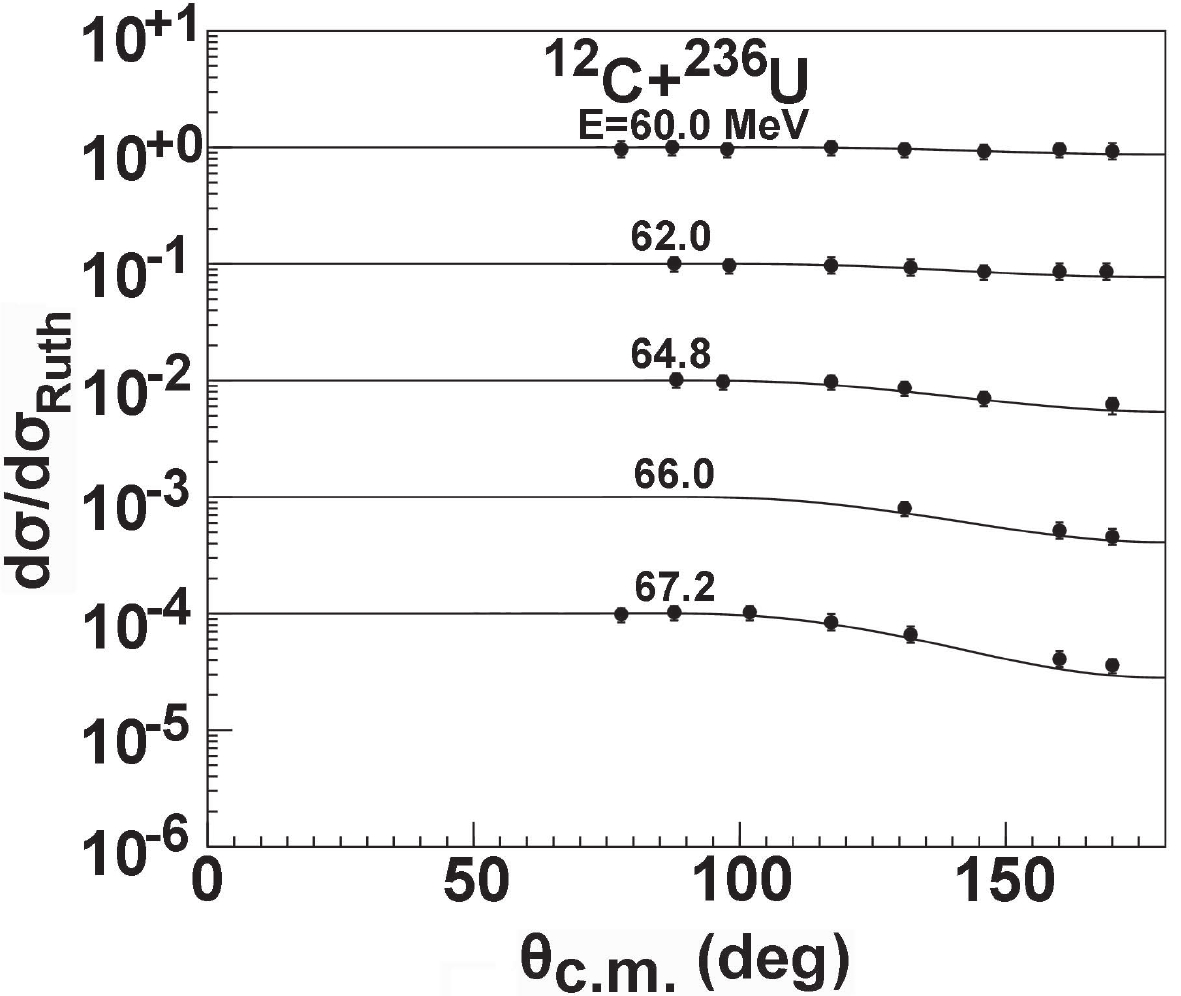
Figure 16. Comparison between the predictions of the optical model and the experimental data for the elastic scattering angular distributions of 236U [47].
-
The total reaction cross section is also an important observable in the optical model and is further investigated using the global OMP. The total reaction cross sections for 27Al and 28Si are predicted and compared with the existing experimental data; the predicted results are consistent with almost all of the data [48-52]. The total reaction cross sections for 40Ca and 56Fe are also calculated using the global OMP. Compared with the corresponding experimental data [26, 48], the calculations fit the data well in the error range for these targets. The results for 28Si and 40Ca are shown in Fig. 17.
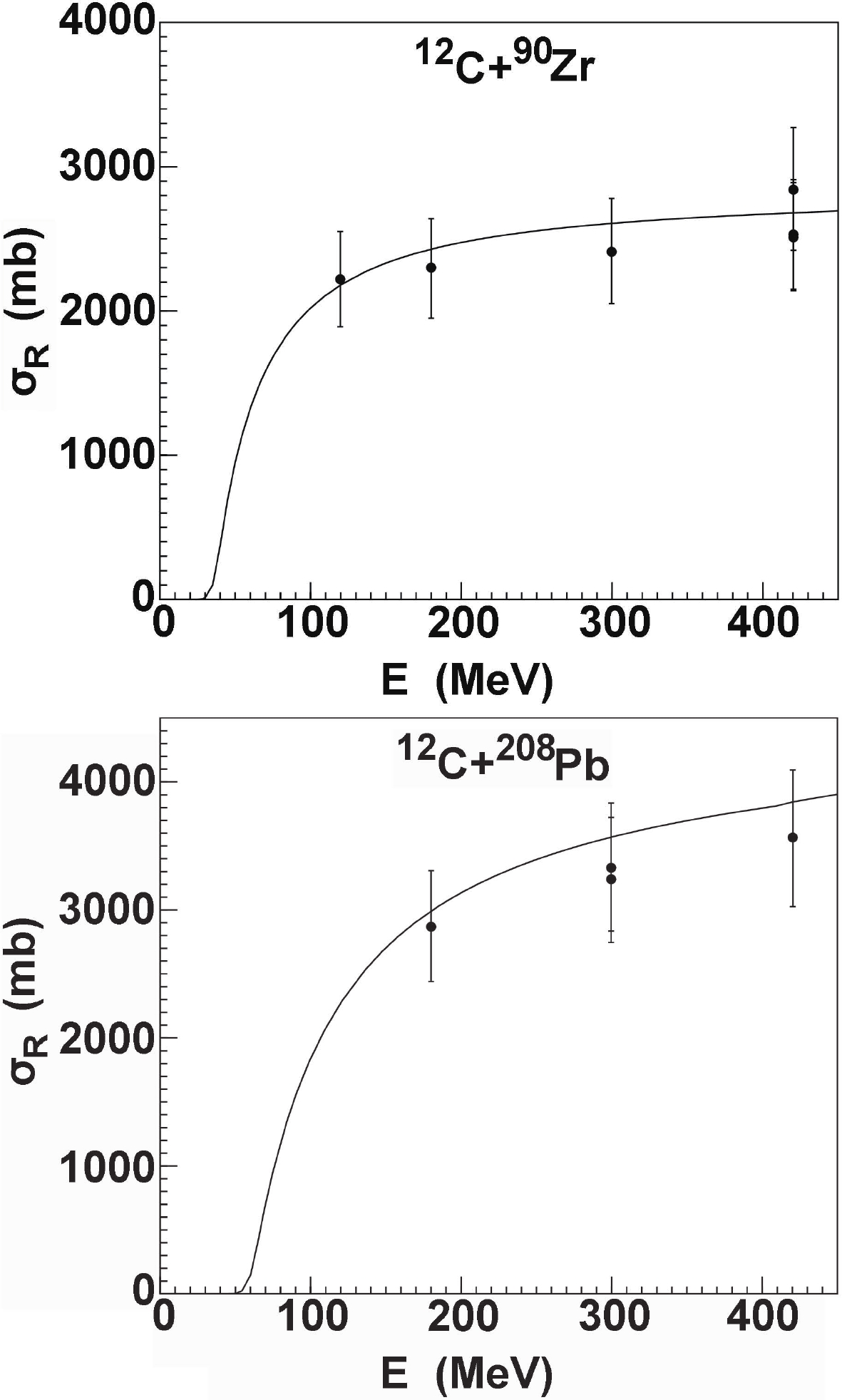
For copper targets, the total reaction cross sections are measured for
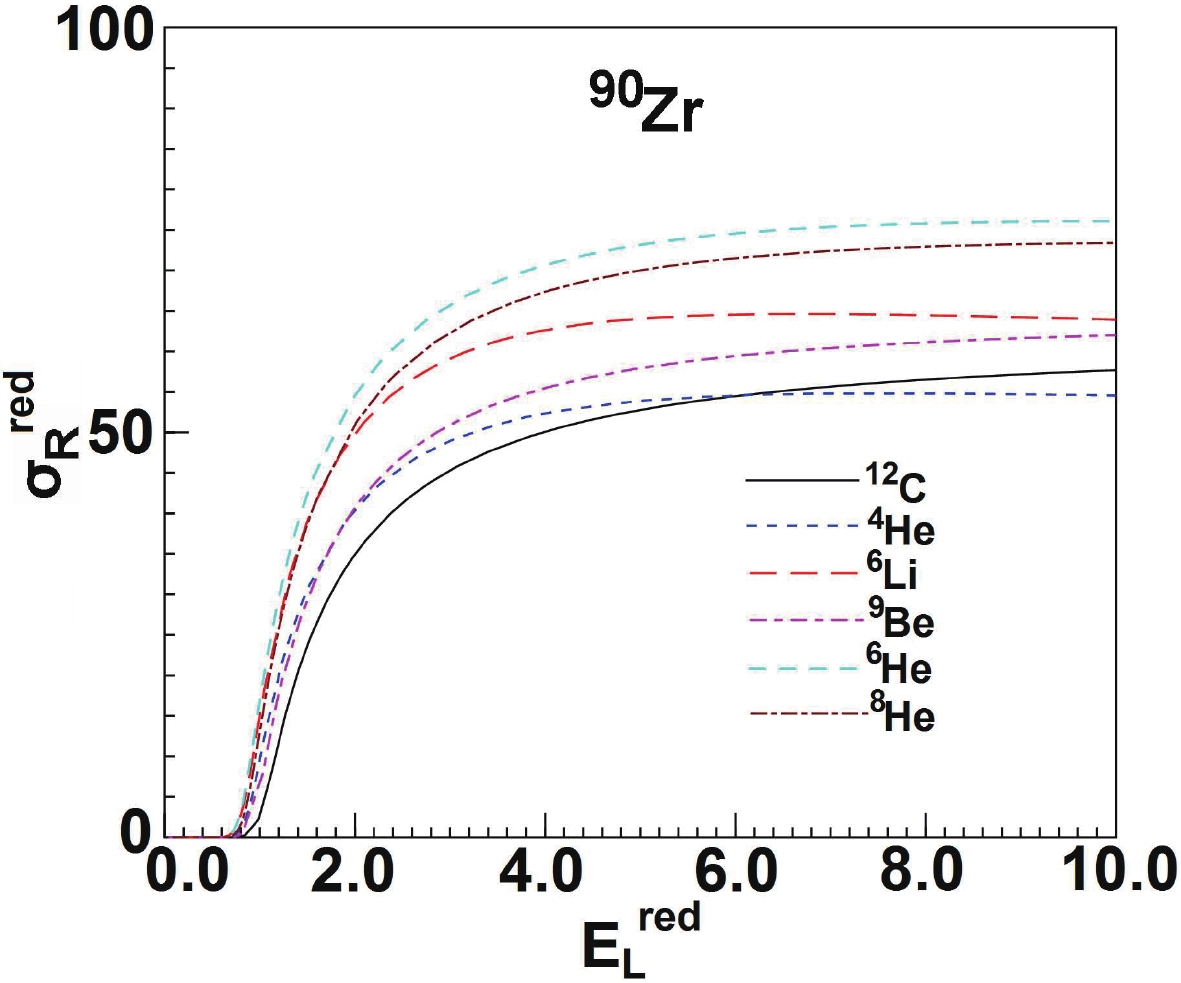
$ ^{\rm nat.} $ Cu above 200 MeV [53]. We compare the theoretical results of$ ^{63,65} $ Cu with the existing experimental data [53] and find that reasonable agreement is achieved between them. Similarly, the calculations for 64Zn are in good agreement with the experimental data [48]. For 90Zr and 208Pb, there are also data for the total reaction cross sections [26], which are extracted from the measured angular distributions of the elastic scattering process. The model calculations are in good agreement with these data. The results are shown in Fig. 18.To further investigate the structure of 12C, we compare the total reaction cross sections calculated for different systems. Among these systems are combinations of stable and unstable weakly bound nuclei 9Be [9] and 6Li [10], halo nuclei 6,8He [54], and
$ \alpha $ cluster structure nuclei 12C and 4He [6] on the same medium mass target 90Zr. As in Ref. [55], suitable scaling of the results is achieved by dividing the cross sections by the factor$ (A_{p}^{1/3}+ A_{T}^{1/3})^{2} $ and the energy by the factor$ Z_{p}Z_{T}/(A_{p}^{1/3}+A_{T}^{1/3}) $ , where$ Z_{p}(Z_{T}) $ and$ A_{p}(A_{T}) $ are the charge and mass number of the projectile (target), respectively. The results for the total reaction cross sections for the different systems are shown in Fig. 19. It is evident that the total reaction cross sections for the systems involving halo nuclei$ ^{6,8} $ He are highest among the investigated systems. The reason is that the Coulomb polarization favors the neutrons in the halo residing in the region between the core and the target, which then enhances the reaction probabilities [56]. The total reaction cross sections involving the weakly bound nuclei 9Be and 6Li are higher compared to those involving the cluster projectiles 12C and 4He. The extra contribution to the total reaction cross sections must come from the weakly bound nature of the nuclei as the breakup channel is one of the dominant reaction channels [57]. For the$ \alpha $ cluster structure nuclei 12C and 4He, the total reaction cross sections are the smallest among the investigated systems. -
Through the detailed study of the energy dependence of the optical potential of 12C projectiles, a set of global OMP parameters is developed by simultaneously fitting the experimental data of the elastic-scattering angular distributions and the reaction cross sections for the mass range of target nuclei from 24 to 209, below 200 MeV. Comparisons between the calculated and experimental data reveal that the elastic-scattering angular distributions are in very good agreement with the experimental values, with the exception of those for some light systems at backward angles, for which there are strong oscillations in the differential cross sections. The comparisons suggest that other reaction mechanisms, such as transfer processes, need to be considered in the calculations. In our future work, the local OMPs for the reactions of 12C induced lighter targets will be specifically studied. In this work, the elastic-scattering angular distributions and reaction cross sections are also predicted above 200 MeV, and the predictions are in good agreement with the corresponding experimental data. In the present work, the elastic scattering obseverables above 200 MeV are only tentative predictions, and most of the existing experimental angular distributions were measured at forward angles. The reliability of the 12C global OMP that is extrapolated towards higher-energy regions thus needs further verification with more experimental data. The results of the elastic-scattering angular distributions for some small deformed actinides are also predicted and give a satisfactory description of the existing experimental data. The calculations performed in this work show that the global OMP can be helpful to investigators who are conducting systematic studies for nuclear model calculations and experimental analysis involving 12C projectiles.
Global optical model potential describing 12C-nucleus elastic scattering
- Received Date: 2020-07-13
- Available Online: 2020-12-01
Abstract: We construct a new global optical model potential to describe the elastic scattering of 12C. The experimental data of elastic-scattering angular distributions and total reaction cross sections for targets from 24Mg to 209Bi are considered below 200 MeV within the framework of the optical model. The results calculated using the derived global optical potential are then compared with the existing experimental data. The reliability of the global optical potential is further tested by predicting the elastic scattering data out of the mass and energy ranges, within which the global potential parameters are determined, and reasonable results are also obtained.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: