-
The pioneering work [1, 2] of Hawking and Bekenstein makes it possible to study black holes from the perspective of thermodynamics. Since the four laws of black hole mechanics were established [3], much attention has been paid to reveal the deep and fundamental relationships between the laws of general relativity, quantum field theory and thermodynamics [4-7]. In view of the key role played in quantum gravity research [8], the study of black holes has led to many ideas colliding and new insights which have extensively enriched our understanding of the universe, including holographic superfluids and superconductors [8-11], the quantum version of condensed matter theory [12-15], and so on.
Hawking and Page showed the phase transition between Schwarzschild AdS black holes and thermal AdS space [16]. It has been shown that black holes in AdS space share common properties with general thermodynamic systems. This relation has been further enhanced in the extended phase space [17], where the cosmological constant and its conjugate quantity are treated as the thermodynamic pressure and volume, respectively:
$ P = -\frac{\Lambda }{8\pi } = \frac{(D-1)(D-2)}{16 \pi l^2},\ \ \ V = \left( \frac{\partial M}{\partial P}\right) _{S,Q}, $

(1) where l is the AdS space radius and the black hole mass M is understood as the enthalpy [18]. A number of papers then explored various thermodynamic aspects of black holes, such as phase transitions [19, 20], heat engine efficiency [21, 22], compressibility [23, 24], the critical phenomenon [25-27], and the weak cosmic censorship conjecture [28, 29]. A brief review is given in Ref. [18].
Non-linear electrodynamics (NLED) is the natural extension of Maxwell's theory in extreme conditions such as high field and small length scale. In recent years, NLED has been widely investigated in the context of black hole physics, for its promising construction of regular black hole solutions. Among the NLED theories, Born-Infeld electrodynamics has attracted a lot of attention and aroused much research interest. Born-Infeld electrodynamics encodes the low-energy dynamics of D-branes, incorporating maximal electric fields and smoothing out the divergence of the electrostatic self-energy of point-like charges. The Born-Infeld AdS black hole solution was first obtained in Ref. [30]. The thermodynamic behaviors and phase transitions of these black holes have been studied both in the canonical [31] and the grand canonical ensembles [32]. Moreover, we can consider string corrections to the thermodynamic properties of charged AdS black holes by introducing the Born-Infeld action [33-36]. Due to its intimate connection with string theory, a candidate theory of quantum gravity, we believe such an extension could bring new insights when it comes to the quantum regime.
The Joule-Thomson expansion of black holes was first investigated in Ref. [37]. Subsequently, this subject was comprehensively studied in Refs. [38-59]. The inversion curves that separate heating-cooling regions in the
$ T-P $ plane for isenthalpic curves with different parameters were presented. The results of these papers show that the inversion curves$ T (P) $ for different black hole systems are similar. In this paper, we would like to generalize the current research into Joule-Thomson expansion to the case of Born-Infeld AdS black holes.This paper is organized as follows. In Sec. II we briefly review the thermodynamics of Born-Infeld AdS black holes in D-dimensional spacetime. Then in Sec. III we discuss the Joule-Thomson expansion of a Born-Infeld AdS black hole in D-dimensional spacetime, including the Joule-Thomson coefficient, the inversion curves and the isenthalpic curves. Furthermore, we compare the critical temperature and the minimum of inversion temperature. The influence of the NLED parameters and the charge Q on inversion curves is also discussed. Finally, we give our conclusion in Sec. IV. Throughout the paper, we use the units
$ G = \hbar = k_{\rm B} = c = 1 $ . -
The Einstein-Hilbert-Born-Infeld action for D-dimensional (
$ D\geqslant 4 $ ) spacetime can be described as follows:$ S = \frac{1}{16\pi }\int {\rm{d}}^{D}x\sqrt{-g}(R-2\Lambda +{\cal L}(F)), $

(2) where the cosmological constant is related to the AdS space radius l by
$ \Lambda = -\frac{(D-1)(D-2)}{2l^{2}}. $

(3) This action is a nonlinear generalization of the Maxwell action in string theory [33, 34]:
$ {\cal L}(F) = 4\beta ^{2}\left( 1-\sqrt{1+\frac{F^{2}}{2\beta ^{2}}}\right) , $

(4) where the parameter
$ \beta \sim 1/2\pi \alpha ^{\prime } $ relates to the Regge slope. In the zero-slope limit ($ \beta\to\infty $ ), the action degenerates into Einstein-Maxwell theory,$ {\cal L}(F) = -F^{2}+{\cal O}\left( \frac{1}{\beta }\right) . $

(5) The metric of a D-dimensional Born-Infeld AdS black hole is [30, 31, 60]:
$ {\rm{d}}s^{2} = -f(r){\rm{d}}t^{2}+\frac{{\rm{d}}r^{2}}{f(r)}+r^{2}{\rm{d}}\Omega _{D-2}^{2}, $

(6) with
$ \begin{aligned}[b] \ f(r) =& 1-\frac{m}{r^{D-3}}+\frac{r^{2}}{l^{2}}+\frac{4\beta ^{2}r^{2}}{ (D-1)(D-2)}\\&\times \left( 1-\sqrt{1+\frac{(D-2)(D-3)q^{2}}{2\beta ^{2}r^{2D-4} }}\right) +\frac{2(D-2)q^{2}}{(D-1)r^{2D-6}}\\&\times {}_{2}F_{1}\left[ \frac{D-3}{2D-4}, \frac{1}{2},\frac{3D-7}{2D-4},-\frac{(D-2)(D-3)q^{2}}{2\beta ^{2}r^{2D-4}} \right] , \end{aligned} $

(7) where
$ _{2}F_{1}(a,b,c,z) $ is the hypergeometric function. The parameters m and q are related to the black hole mass and charge respectively as [30]:$ M = \frac{(D-2) \Omega_{D-2}}{16\pi }m\;, $

(8) $ Q = \sqrt{2(D-2)(D-3)}\frac{\Omega_{D-2}}{8\pi }q. $

(9) The event horizon
$ r_{+} $ is the solution of$ f(r_{+}) = 0 $ . The mass can be rewritten as:$ \begin{aligned}[b] M =& \frac{(D-2) \Omega_{D-2}}{16 \pi} r_{+}^{D-3}\left\{1+\frac{r_{+}^{2}}{l^{2}}+\frac{4 \beta^{2} r_{+}^{2}}{(D-1)(D-2)}(1-\sqrt{1-z})\right.\\& \left.+\frac{2(D-2) q^{2}}{(D-1) r_{+}^{2 D-6}} {}_{2}F_{1} \left[\frac{D-3}{2 D-4}, \frac{1}{2}, \frac{3 D-7}{2 D-4}, z\right]\right\}, \end{aligned} $

(10) where
$ z = -\frac{(D-2)(D-3)q^{2}}{2\beta ^{2}r_+^{2D-4}}. $

(11) The first law of black hole thermodynamics reads:
$ {\rm{d}}M = T{\rm{d}}S+\Phi {\rm{d}}Q+V{\rm{d}}P. $

(12) The connected Smarr relation is:
$ M = 2(TS-VP)+\Phi Q, $

(13) where the electric potential is:
$ \Phi = \sqrt{\frac{D-2}{2\left( D-3\right) }}\frac{q}{r_{+}^{D-3}}{}_{2}F_{1} \left[ \frac{D-3}{2D-4},\frac{1}{2},\frac{3D-7}{2D-4},z\right] , $

(14) and the Hawking temperature T, entropy S, thermodynamic volume V are given by [30, 60, 61]:
$ T = \frac{1}{4\pi }\left[ \frac{ (D-1)r_{+}}{l^{2}}+\frac{D-3}{r_{+}}+\frac{4\beta ^{2}r_{+}}{(D-2)}\times \left( 1-\sqrt{1-z}\right) \right], $

(15) $ S = \frac{\Omega_{D-2}}{4}r_{+}^{D-2}\;, \;\;\;\;\;V = \frac{\Omega_{D-2}}{D-1} r_{+}^{D-1}. $

(16) Substituting Eqs. (1) and (3) into Eq. (15), one obtains the equation of state:
$ P(V,T) = \frac{D-2}{4r_{+}}\left\{ T-\frac{D-3}{4\pi r_{+}}-\frac{\beta ^{2}r_{+}}{\pi (D-2)}\times \left( 1-\sqrt{1-z}\right) \right\} . $

(17) The critical point
$ r_{\rm c} $ obeys$ \frac{\partial P}{\partial r_{+}}{\big |}_{r = r_{\rm c}} = \frac{\partial ^{2}P}{\partial r_{+}^{2}}{\big |}_{r = r_{\rm c}} = 0, $

(18) which can be exactly solved in
$ D = 4 $ case:$ T_{\rm c} = \frac{1}{2 \pi r_{\rm c}} - \frac{Q^2}{\pi r_{\rm c}^3} \frac{1}{\sqrt{1+ Q^2/\beta^2 r_{\rm c}^4}}, $

(19) $ P_{\rm c} = \frac{1}{8\pi r_{\rm c}^2} - \frac{Q^2}{2\pi r_{\rm c}^4} \frac{1}{\sqrt{1+ Q^2/\beta^2 r_{\rm c}^4}} - \frac{\beta^2}{4 \pi} \left( 1-\sqrt{1+\frac{ Q^{2}}{\beta^{2} r_{\rm c}^{4}}} \right).$

(20) We plot the critical temperature with varying
$ \beta $ and Q in Fig. 1. We find that it is cut as$ \beta Q $ is$ \sqrt{2}/4 $ , which is in agreement with the result of Ref. [62]. Furthermore, one can easily go back to the RN-AdS case, as in Ref. [37], by simply taking the limit$ \beta\to\infty $ .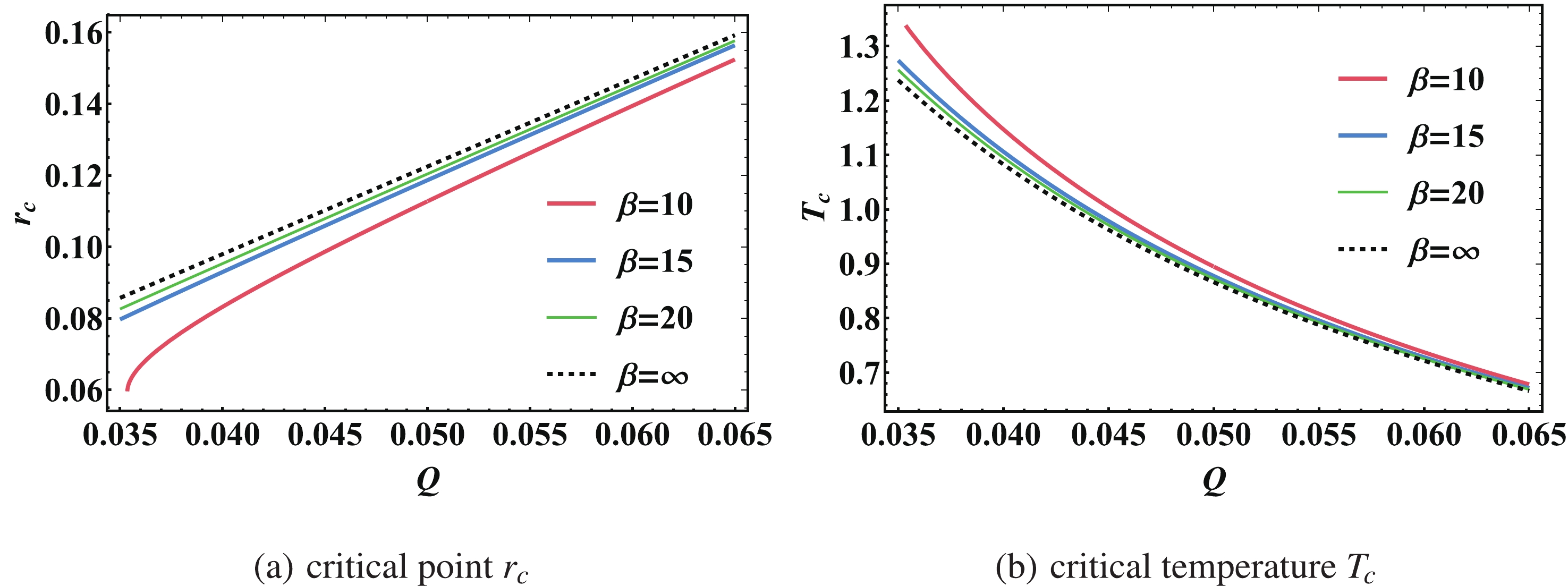
Figure 1. (color online) Critical point
$ r_{\rm c} $ and critical temperature$ T_{\rm c} $ versus charge Q for$ D=4 $ . From bottom to top, the curves correspond to$ \beta= $ 10, 15, 20,$ \infty $ .Unlike RN-AdS black holes [39], for
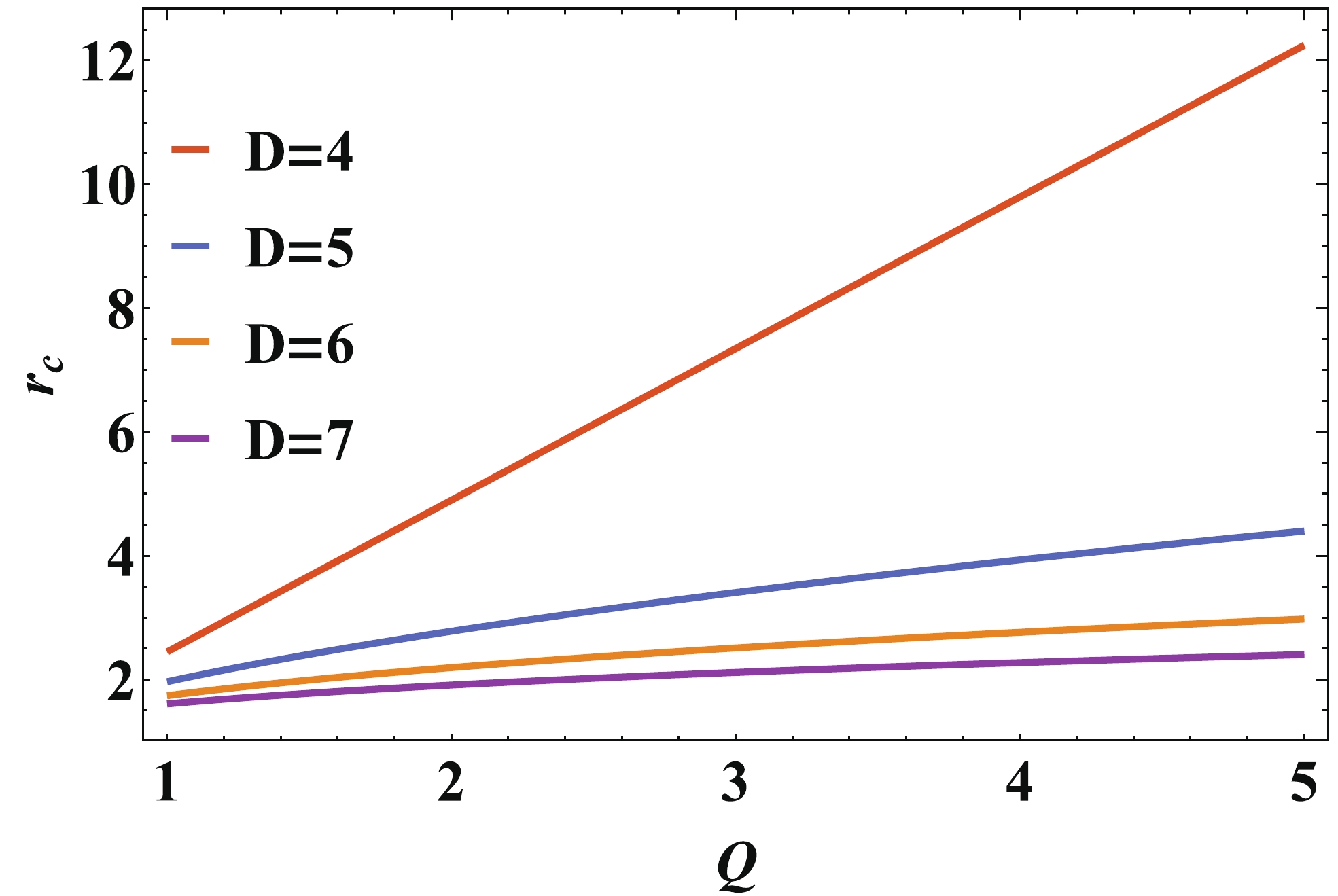
$ D>4 $ it is very difficult to obtain an exact solution of the critical radius for Born-Infeld AdS black holes. We thus solve Eq. (18) numerically. The result, as plotted in Fig. 2 shows that the critical radius is greatly suppressed by the spatial dimensionality. -
In Joule-Thomson expansion, gas at a high pressure passes through a porous plug or small valve while staying thermally insulated so that no heat is exchanged with the environment. One can describe the temperature change by the Joule-Thomson coefficient
$ \mu = \left( \frac{\partial T}{\partial P}\right) _{H} = \frac{1}{C_{P}}\left[ T\left( \frac{\partial V}{\partial T}\right) _{P}-V\right], $

(21) whose sign determines whether cooling or heating will occur.
$ \mu = 0 $ gives the inversion temperature$ T_{i} = V\left( \frac{\partial T}{\partial V}\right) _{P}. $

(22) -
The van der Waals equation,
$ P = \frac{T}{v-b} - \frac{a}{v^{2}}, $

(23) generalizes the ideal gas equation, and is regarded as an appropriate description of real fluids.
$ v = V/N $ is the specific volume and$ a,b $ measure the attraction between particles and molecule volume, respectively. The enthalpy is given by:$ H(T,v) = \frac{3}{2} T + \frac{Tv}{v-b} - \frac{2 a}{v}. $

(24) The inversion temperature as a function of inversion pressure is:
$ T_{i} = \frac{2\left( 5a-3b^{2}P_{i}\pm 4\sqrt{a^{2}-3ab^{2}P_{i}}\right) }{9b}. $

(25) With Eqs. (23) and (24) in hand, we can plot the isenthalpic curves in the
$ T-P $ plane, as shown in Fig. 3. The slopes of the isenthalpic curves are positive in the cooling region and negative in the heating region, and change signs when crossing the inversion curves.
Figure 3. (color online) The colored isenthalpic curves from bottom to top correspond to H starting from
$ 1 $ to$ 6.5 $ with an interval of$ 0.5 $ . Black empty diamonds mark the maximum value points. The purple solid curve together with dashed orange curve separates the cooling region and the heating region. We have set the parameters$ a=b=1 $ . -
Now we consider Joule-Thomson expansion of a
$ 4D $ Born-Infeld AdS black hole. Thermodynamic quantities can be acquired with the relations Eqs. (12), (13), (15) and (16), and the heat capacity at constant pressure is:$\begin{aligned}[b] C_{P} =& T \left(\frac{\partial S}{\partial T}\right)_{P,Q,\beta} \\=& \frac{2\pi r_{+}^{4} (8\pi Pr_{+}^{2}+1+2\beta^{2}r_{+}^{2}(1-\sqrt{1-z_4}))}{8\pi P r_{+}^{4} -r_{+}^{2}+2\beta^{2}r_{+}^{4}(1-\sqrt{1-z_4})+4Q^2/\sqrt{1-z_4}}, \end{aligned}$

(26) where
$ z_4 = z(D = 4) = -\frac{Q^2}{\beta^2 r_{+}^4}, $

(27) and one can derive:
$ \begin{aligned}[b] \mu =& \frac{1}{C_{P}}\left[ T\left( \frac{\partial V}{\partial T}\right) _{P,\beta}-V\right] \\=& \frac{8 r_{+}^2+32 \pi P r_{+}^4-8 Q^2/\sqrt{1-z_4}+8 \beta ^2 r_{+}^4 \left(1-\sqrt{1-z_4}\right)}{3r_{+} \left(1+8 \pi P r_{+}^2+2 \beta^2 r_{+}^2 \left(1-\sqrt{1-z_4}\right)\right)}. \end{aligned}$

(28) The Joule-Thomson coefficient
$ \mu $ versus the horizon$ r_+ $ is shown in Fig. 4. We fix$ \beta = 20 $ , the pressure$ P = 1 $ and the charge Q as 1, 2, 10. There exist both a divergence point and a zero point for different Q. By comparing these two plots, we can easily see that the divergence point of the Joule-Thomson coefficient is consistent with the zero point of Hawking temperature. The divergence point here reveals the Hawking temperature and corresponds to extremal black holes.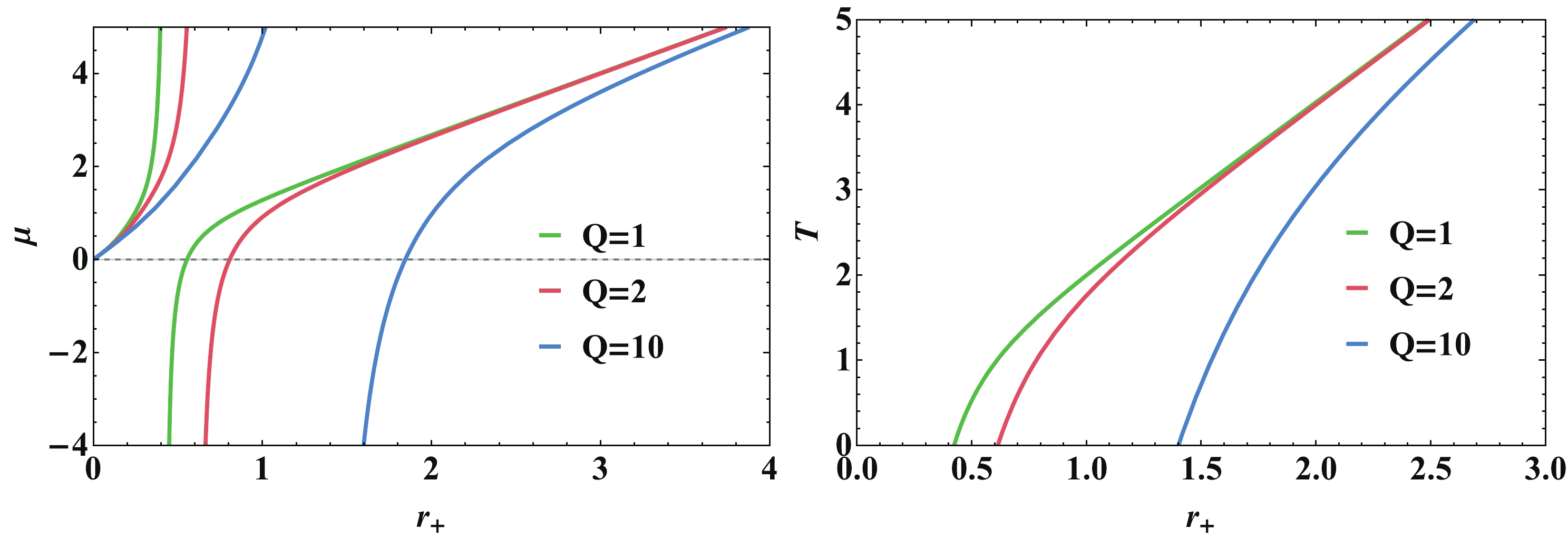
Figure 4. (color online) (left) Joule-Thomson coefficient
$ \mu $ and (right) Hawking temperature T versus the event horizon$ r_+ $ . Here$ \beta=20 $ , P=1, and from left to right, the curves correspond to Q = 1, 2, 10.Taking
$ D = 4 $ in Eq. (17), one obtains the equation of state:$ T = 2r_{+}P+\frac{1}{4\pi r_{+}}+\frac{\beta ^{2}r_{+}}{2\pi }\left( 1-\sqrt{1-z_4}\right) , $

(29) and the inversion temperature is given by
$ \begin{aligned}[b] T_{i} =& V\left( \frac{\partial T}{\partial V}\right)_{P}\\=& \frac{r_{+}}{3} \left\{ \frac{\beta ^{2}}{2\pi }\left( 1-\sqrt{1-z_4}\right) +\frac{Q^{2}}{\pi r_{+}^{4}\sqrt{1-z_4}}+2P-\frac{1}{4\pi r_{+}^{2}}\right\} . \end{aligned}$

(30) Plugging Eq. (30) into Eq. (29) at
$ P = P_{i} $ gives:$ P_i = -\frac{1}{4 \pi r_{+}^2}-\frac{\beta^2}{4\pi}+\frac{Q^2}{2\pi r_{+}^4 \sqrt{1-z_4}}+\frac{\beta^2}{4\pi} \sqrt{1-z_4} , $

(31) $ T_i = -\frac{1}{4\pi r_{+}}+\frac{Q^2}{2\pi r_{+}^3 \sqrt{1-z_4}}. $

(32) Equations (31) and (32) make up the parameter equation of the inversion curve. Since Eqs. (31) and (32) may have no analytical solution, we use numerical solutions to plot inversion curves in the
$ T-P $ plane.The inversion curves for different values of
$ \beta $ and Q are shown in Fig. 5. The inversion temperature increases monotonically with the inversion pressure, but the slope of the inversion curve decreases with the inversion pressure. Moreover, the inversion temperature increases with the charge Q and parameter$ \beta $ . We can go back to the case of the RN-AdS black hole as$ \beta\to\infty $ . Comparing with the van der Waals fluids, we see from Fig. 5 that the inversion curve is not closed, and there exists only one inversion curve that corresponds to the lower dashed orange curve in Fig. 3. Such a difference motivates us to explore the essence of AdS black holes from the perspective of thermodynamics. The existence of an inversion temperature results from the competition of attractive and repulsive interactions between real molecules. However, if we regard the AdS black hole as a thermodynamic system of certain molecules, the dominant interaction is attractive, although the electromagnetic interaction is repulsive (details are given in the Appendix). As a result, the Joule-Thomson coefficient is positive above the inversion curves and cooling occurs inside this region. This means that Born-Infeld AdS black holes always cool above the inversion curve during Joule-Thomson expansion, which is similar to the case of the RN-AdS black hole [37], Kerr-AdS black hole [38] and other AdS black holes examined in previous works.
Figure 5. (color online) Inversion curves for Born-Infeld AdS black holes in the
$ T-P $ plane. From bottom to top, the curves in the left-hand panel correspond to$ Q=1 $ and$ \beta $ = 10, 15, 20,$ \infty $ . Those in the right-hand panel correspond to$ \beta=20 $ and Q = 1, 2, 10, 20.Now we study the minimum of the inversion temperature, which can be obtained from Eq. (32),
$ T_{i}^{\min } = -\frac{1}{4\pi r_{+}^{\min }}+\frac{Q^{2}}{2\pi r_{+}^{\min 3}}\frac{1}{\sqrt{1+\dfrac{Q^{2}}{\beta ^{2}r_{+}^{\min 4}}}}, $

(33) where
$ r_{+}^{\min} $ is obtained by setting$ P_{i} = 0 $ in Eq. (31). The minimum of the inversion temperature can be obtained numerically. We then calculate the Q dependence of the minimum of the inversion temperature with different$ \beta $ in Fig. 6(a). We can also return to the case of RN-AdS black holes as$ \beta\to\infty $ . It is significant to calculate the ratio between the minimum of the inversion temperature$ T_i^{\min} $ and the critical temperature$ T_{\rm c} $ . Previous work shows that this ratio turns out to be$ \dfrac{1}{2} $ [37]. The minimum of the inversion temperature and the critical temperature can be obtained numerically and are displayed in Fig. 1 and Fig. 6(a). The Q dependence of the ratio$ T_i^{\min}/T_{\rm c} $ with different$ \beta $ is shown in Fig. 6(b). We can see that the ratio is not always$ \dfrac{1}{2} $ . The curves show that the ratio tends to$ \dfrac{1}{2} $ as Q increases. When$ \beta\to\infty $ , it degenerates into RN-AdS black holes again and the ratio is always$ \dfrac{1}{2} $ .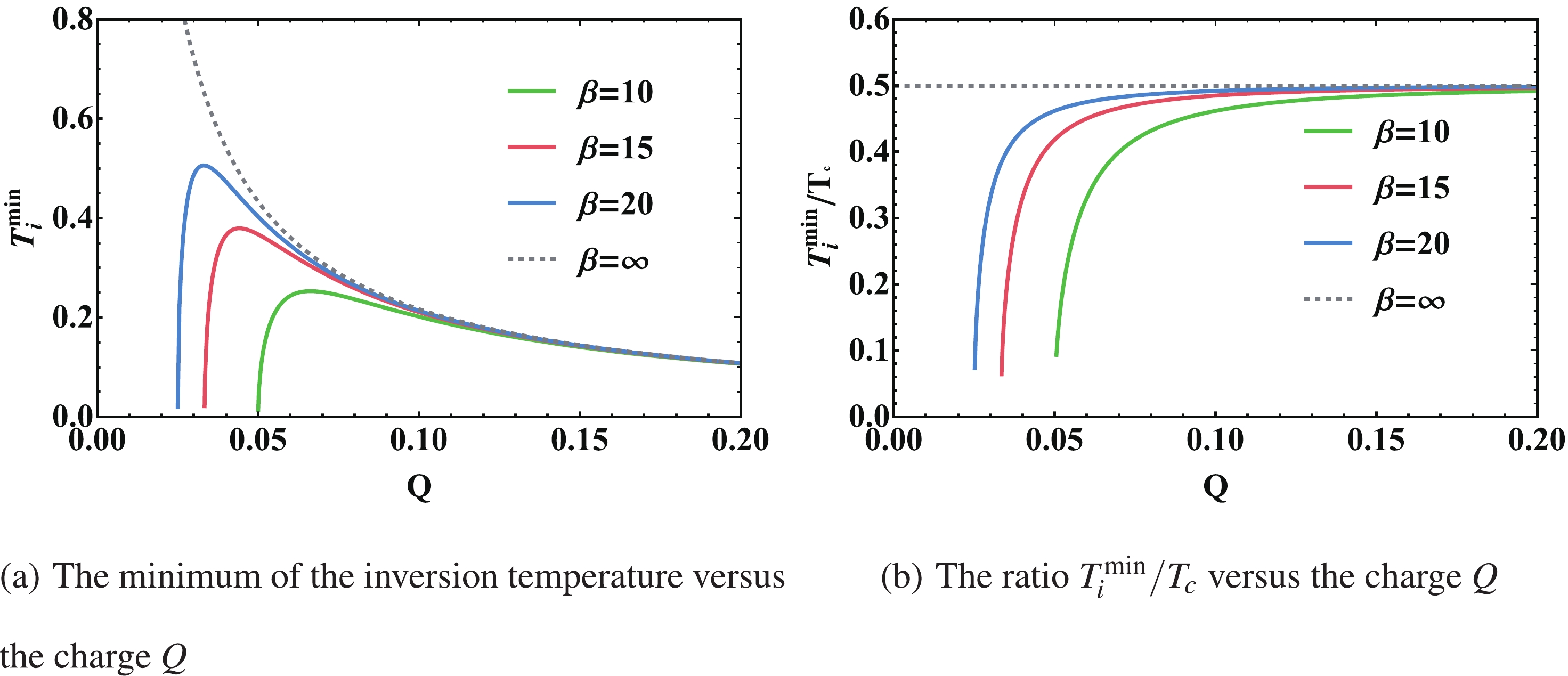
Figure 6. (color online) Minimum of inversion temperature and the ratio
$ T_i^{\min}/T_{\rm c} $ versus charge Q. From bottom to top, the curves correspond to$\beta = 10,\; 15,\; 20,\; \infty$ .Other thermodynamic quantities can be calculated using Eqs. (12) and (13). Using Eq. (10), we can get the mass of this black hole in terms of
$ r_{+} $ in$ D = 4 $ :$\begin{aligned}[b] M =& \frac{r_{+}}{2}\left\{ 1+\frac{8\pi P r_{+}^{2}}{3}+\frac{2\beta ^{2}r_{+}^{2}}{3}\left( 1-\sqrt{1-z_4}\right) \right.\\&\left.+\frac{4Q^{2}}{3r_{+}^{2}} {}_{2}F_{1}\left[ \frac{1}{4},\frac{1}{2},\frac{5}{4},z \right] \right\} . \end{aligned}$

(34) Since the Joule-Thomson expansion is an isenthalpic process, it is significant to study the isenthalpic curves of Born-Infeld AdS black holes. In the extended phase space, the mass can be interpreted as enthalpy. We can therefore plot isenthalpic curves in the
$ T-P $ plane by fixing the mass of the black hole. The isenthalpic curves are given by Eq. (29), with$ r_{+} $ being the larger root of Eq. (34) at given M. We show the isenthalpic curves and the inversion curves of Born-Infeld AdS black holes in Fig. 7. This result is consistent with that in Fig. 5. The inversion curve is the dividing line between heating and cooling. The isenthalpic curve has a positive slope above the inversion curve, so there is cooling above this inversion curve. Conversely, the sign of the slope changes and heating occurs below the inversion curve.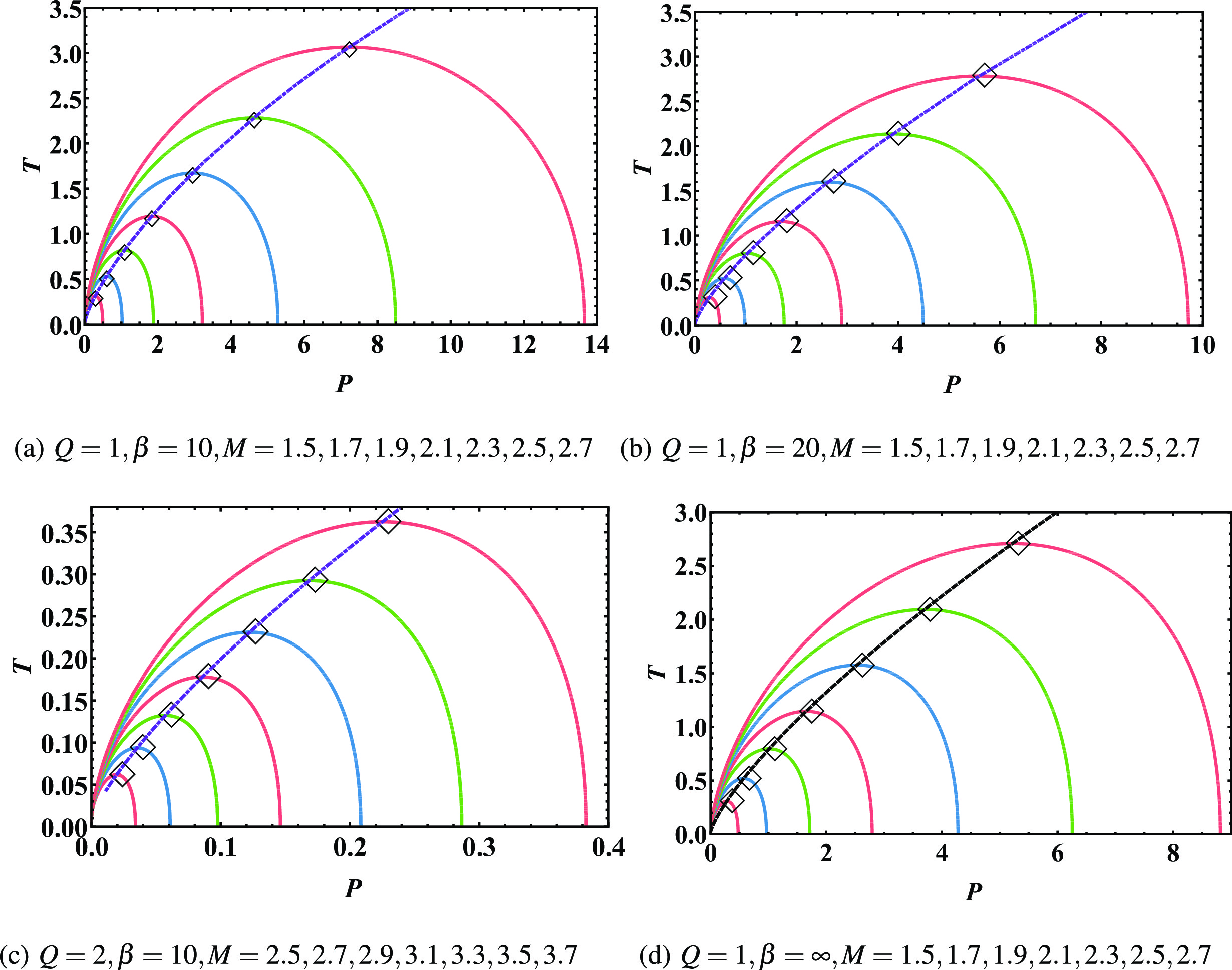
Figure 7. (color online) The different solid lines are isenthalpic curves with parameters given below the figures. Black empty diamonds mark the maximum value points, and purple dot-dashed lines are the inversion curves. The lower right panel denotes the RN-AdS case.
Finally, we give a brief extension of the discussion above to arbitrary dimension
$ D>4 $ . The critical pressure and temperature can be obtained from Eq. (18)$ \begin{aligned}[b] P_{\rm c} = & \frac{(D-2)(D-3)}{16\pi r_{\rm c}^2} + \frac{\beta^2 (D-2) z}{4 \pi \sqrt{1-z}} - \frac{\beta^2 \left(1-\sqrt{1-z}\right)}{4 \pi},\\\\ T_{\rm c} =& \frac{D-3}{2\pi r_{\rm c}} + \frac{\beta^2 z r_{\rm c}}{\pi \sqrt{1-z}}. \end{aligned}$

(35) One should not forget that z is a function of
$ r_{+} $ , and in the equations above should take$ r_{+} = r_{\rm c} $ . However, the critical radius may have no analytical solution, and we have to resort to a numerical method. The results are shown in Fig. 2. On the other hand, the inversion pressure and temperature are:$ \begin{aligned}[b] P_{i} =& -\frac{D(D-3)}{16\pi r_{+}^2} - \frac{\beta^2 z}{4\pi \sqrt{1-z}} - \frac{\beta^2 \left(1-\sqrt{1-z}\right)}{4 \pi},\\ \\T_{i} =& -\frac{D-3}{2(D-2)\pi r_{+}} - \frac{\beta^2 z r_{+}}{(D-2)\pi \sqrt{1-z}}. \end{aligned} $

(36) The two equations above define the parameter equations of the inversion curve
$ T(P) $ . We then study the inversion curves numerically in various dimensions and the result is presented in Fig. 8.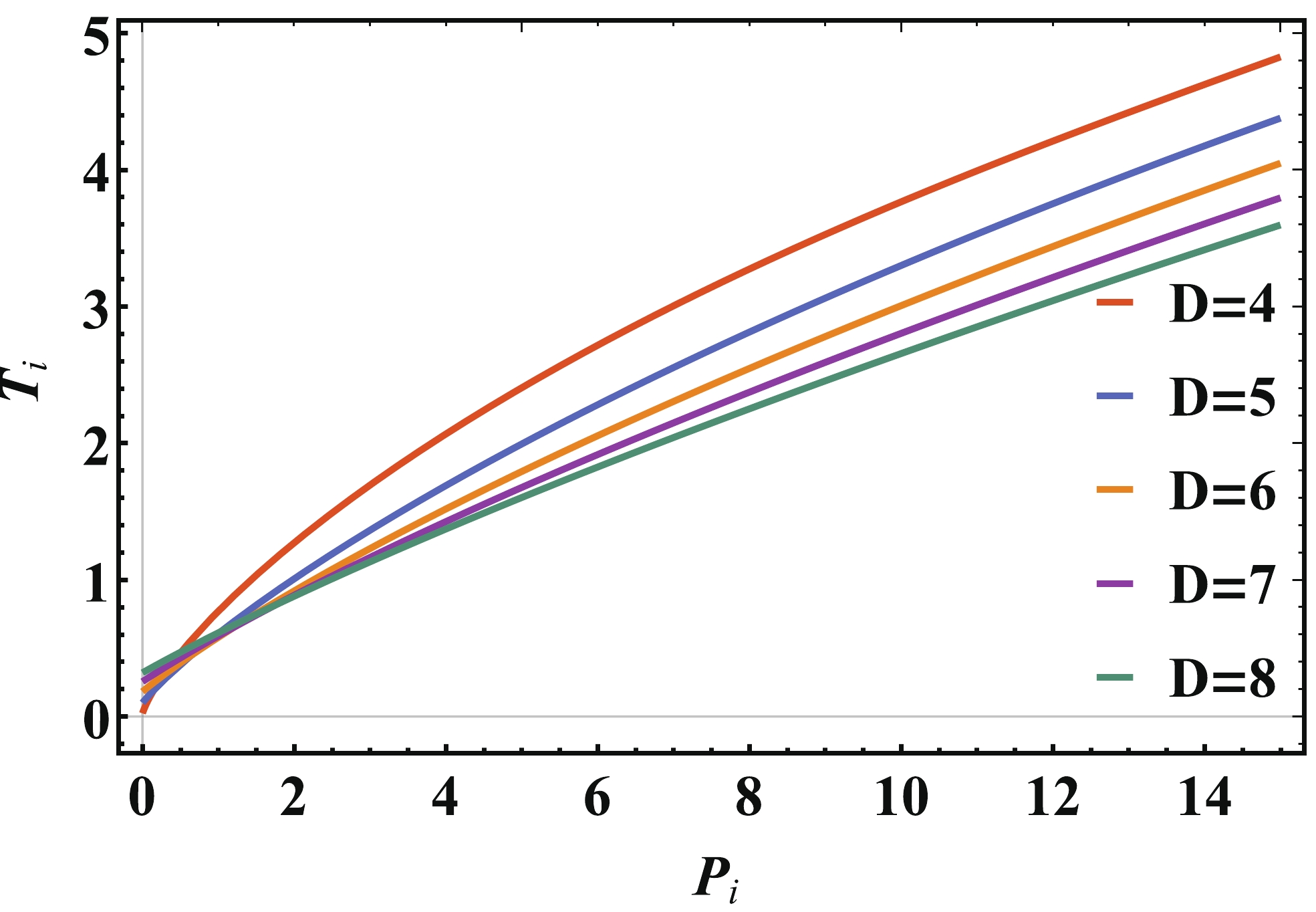
Figure 8. (color online) Inversion curves for
$ D=4,5,6,7,8 $ , from top to bottom. We set$ Q=1 $ and$ \beta=10 $ .A similar effect of dimensionality is demonstrated. At low pressure, the inversion temperature shows a small increase with dimension D, while at high pressure it is suppressed.
To confirm our result we further show the isenthalpic curves in five- and six-dimensional spacetimes, respectively. As shown below, the inversion curves pass through the maximum points and separate the cooling and heating regions. The ratio between
$ T_{i}^{\min} $ and$ T_{\rm c} $ is also calculated numerically . In previous work [39], the ratios for RN-AdS black holes in arbitrary dimension were obtained. We compare our results and those for RN-AdS black holes in Fig. 10. The dashed lines are the ratios for Born-Infeld black holes and the solid lines are those for RN-AdS black holes. When Q increases, the ratios asymptotically reach the predicted results given in Ref. [39]. However, string effects lead to obvious differences between the Born-Infeld and RN-AdS cases in the small Q regime. -
In this paper, we have studied the Joule-Thomson expansion for Born-Infeld AdS black holes in the extended phase space, where the cosmological constant is identified with the pressure. We focused mainly on the
$ D = 4 $ dimension, with extensions to higher dimensions also presented. Since the black hole mass is interpreted as enthalpy, it is the mass that does not change during the Joule-Thomson expansion. The Joule-Thomson coefficient$ \mu $ versus the horizon$ r_+ $ was shown in Fig. 4. There exist both a divergence point and a zero point in different$ \beta $ . We can easily see that the divergence point of the Joule-Thomson coefficient is consistent with the zero point of Hawking temperature, which corresponds to the extremal black holes. In addition, one can easily go back to the RN-AdS case as in Refs. [37, 39] by taking the limit$ \beta\to\infty $ .The inversion curves depending on the charge Q and parameter
$ \beta $ were investigated in Born-Infeld AdS black holes. The results were depicted in Fig. 5. We also showed the isenthalpic curves and the inversion curves in Fig. 7. Such results were reproduced in higher dimensions as demonstrated in Figs. 8 to 10. The results show that the inversion curve always has a positive slope, which is consistent with previous work [37, 39]. This means that Born-Infeld AdS black holes always cool above the inversion curve during expansion. We can use the inversion curve to distinguish the cooling and heating regions for different values of$ \beta $ and Q. Furthermore, we checked the ratio of the critical temperature and the minimum of the inversion temperature in Fig. 6, which shows that the ratio is asymptotically$ 1/2 $ as Q increases or$ \beta\to\infty $ in$ D = 4 $ , and those limit values of the RN-AdS case in arbitrary dimension.
Figure 10. (color online) The ratio
$ T_i^{\min}/T_{\rm c} $ versus the charge Q. We set$ \beta=10 $ . From top to bottom the dashed lines and their asymptotic lines correspond to$ D=4,\,5,\,6,\,7 $ .
Figure 9. (color online) The red, blue, and green solid lines are isenthalpic curves in (a) D=5 and (b) D=6 dimensions. The black diamonds denote the maxima of the isenthalpic lines and the purple dashed lines represent the inversion curves.
Finally, we would like to stress that in the present work we only focus on Joule-Thomson expansion for Born-Infeld AdS black holes. These results are related to many other interesting problems which deserve future study. For example, nontrivial charged black hole solutions can be obtained within the nonlinear massive gravity theory [63], and black holes may present more structure when higher order corrections have been taken into account, such as asymptotically safe gravity [64], or quadratic gravity [65]. It would be interesting to consider whether Joule-Thomson expansion can be applied to these theoretical paradigms. However, we leave such a study for future investigation.
-
We are grateful to thank Bo Ning, Peng Wang and Wei Hong for useful discussions.
-
In this appendix, we give a quantitative discussion on the non-existence of maximum inversion temperature for Born-Infeld AdS black holes. To make it concrete, let us compare van der Waals fluids and Born-Infeld AdS black holes. First, we take the virial expansion for the state equation of van der Waals fluid to the second order [66]:
$ \tag{A1} \frac{PV}{T} = 1+\frac{1}{V}B_{2}(T), $

where the second virial coefficient
$ {B_2}(T) = b-\dfrac{a}{T} $ . The modification term$ \dfrac{1}{V}{{B}_{2}}(T) \ll 1 $ and we can apply the zero-order approximation$ \dfrac{1}{V} = \dfrac{P}{T} $ (high temperature and low pressure limit). The modified volume is$ V = \dfrac{T}{P}+{{B}_{2}}(T) $ . Bringing the expression above into the Joule-Thomson coefficient, we get:$\tag{A2} \mu = \frac{1}{C_{P}}\left( T\frac{{\rm{d}}{{B}_{2}}}{{\rm{d}}T}-{{B}_{2}} \right) = \frac{1}{C_{P}}\left( \frac{2a}{T}-b \right). $

At low temperature, the attractive interaction is dominant and
$ {B}_{2} $ is negative. We thus have$ \mu>0 $ . When the temperature is high enough, the repulsive interaction is dominant and$ {B}_{2} $ is positive, so$ \mu $ may be less than zero. The competition of attractive and repulsive interaction results in the inversion temperature. Such a simple argument also gives the right$ T_{i}^{\max} = 2a/b $ . The analysis is suitable in the high temperature and low-pressure limit.Now we turn to Born-Infeld AdS black holes. The equation of state is:
$ \tag{A3} \begin{aligned}[b]P(V,T) =& \frac{D-2}{4r_{+}}\Bigg\{ T-\frac{D-3}{4\pi r_{+}}-\frac{\beta ^{2}r_{+}}{\pi (D-2)}\\&\times \left( 1-\sqrt{1-z}\right) \Bigg\} . \end{aligned} $

We see that the second virial coefficient
$ {{B}_{2}}(T) \sim -\dfrac{D-3}{4\pi T} $ is always negative in an arbitrary dimension, which means that the attractive interaction is dominant. Thus, the Joule-Thomson coefficient is approximately:$\tag{A4} \mu = \frac{1}{C_{P}}\left( T\frac{{\rm{d}}{{B}_{2}}}{{\rm{d}}T}-{{B}_{2}} \right) = \frac{1}{C_{P}}\times \frac{1}{2\pi T}, $

We see that in the high temperature and low-pressure limit, the Joule-Thomson coefficient is always positive, and there is no maximum inversion temperature.
Joule-Thomson expansion of Born-Infeld AdS black holes
- Received Date: 2020-06-18
- Available Online: 2021-02-15
Abstract: In this paper, the Joule-Thomson expansion of Born-Infeld AdS black holes is studied in the extended phase space, where the cosmological constant is identified with the pressure. The Joule-Thomson coefficient, the inversion curves and the isenthalpic curves are discussed in detail using a 4-dimensional black hole. The critical point of a Born-Infeld black hole is depicted with varying parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: