-
Since Stephen Hawking proved that black holes emit quantum radiation with a temperature
$ T = \dfrac{\kappa}{2\pi} $ [1], it has been believed that a black hole can be treated as a thermodynamic system. Until now, there has been much work on the thermodynamics of black holes, such as the four laws of thermodynamics [2, 3], phase transitions [4] and quantum effects [5, 6]. In general, the first law of thermodynamics of a black hole is written as:$ {\rm d}M = T{\rm d}S+\varPhi {\rm d}Q , $

(1) where M is the mass, T is the Hawking temperature of the black hole, S is the entropy,
$ \varPhi $ is the electric potential and Q is the electric charge. The mass is usually interpreted as the enthalpy [7]. It is clear that there is no$P{\rm d}V$ term in Eq. (1), which corresponds to the change in volume under pressure P. When the cosmological constant,$ \varLambda $ , is treated as the pressure of the black hole [8-13] and the volume of the black hole is defined as the thermodynamic variable conjugate to the pressure [14], Eq. (1) is modified as:$ {\rm d}M = T{\rm d}S+V{\rm d}P+\varPhi {\rm d}Q. $

(2) The relations between P,
$ \varLambda $ and V are$P = -\dfrac{\varLambda}{8\pi}$ ,$V = \left(\dfrac{\partial M}{\partial P}\right)_{S,Q}$ . High-precision observations have recently confirmed the existence of a gravitationally repulsive interaction at a global scale (cosmic dark energy) [15]. It is found that one type of dark energy model produces some gravitational effect when it surrounds black holes. For this type of dark energy, the equation of state parameters is in the interval$\left [-1,-\dfrac{1}{3}\right] $ [16]. This type of dark energy model is called quintessence dark energy, or quintessence for short. In this case, the first law of thermodynamics is given by [17]$ {\rm d}M = T{\rm d}S+V{\rm d}P+\varPhi {\rm d}Q-\frac{1}{2r_{+}^{3\omega_{q}}}{\rm d}\alpha, $

(3) where
$ \alpha $ is a positive normalization factor. There has been much interest in studying the physics of black holes surrounded by quintessence [18-35].According to string theory, nature can be represented by a set of extended objects (such as one-dimensional strings) rather than point particles. Therefore, understanding the gravitational effects caused by a set of strings is necessary. This can be achieved by solving Einstein's equations with a finite number of strings. The results obtained by Letelier show that the existence of a cloud of strings will produce a global origin effect related to a solid deficit angle. Moreover, the solid deficit angle depends on the parameters that determine the existence of the cloud [36]. Therefore, the existence of a cloud of strings will have an impact on black holes. When we consider the existence of the cloud of strings, the first law of thermodynamics takes the form:
$ {\rm d}M = T{\rm d}S+V{\rm d}P+\varPhi {\rm d}Q-\frac{r_{+}}{2}{\rm d}a, $

(4) where a is the state parameter of cloud of strings. The effect of the cloud of strings on black holes has been explored for various black holes [37-42]. As noted in Ref. [43], if the parameters related to the cloud of string and quintessence are considered as extensive thermodynamic parameters, the first law of thermodynamics of black holes is modified as:
$ {\rm d}M = T{\rm d}S+V{\rm d}P+\varPhi {\rm d}Q-\frac{1}{2r_{+}^{3}\omega_{q}}{\rm d}\alpha-\frac{r_{+}}{2}{\rm d}a. $

(5) There has been much interest in deducing and discussing the physical properties of various black holes when they are surrounded by cloud of strings and quintessence [43-50].
An important feature of a black hole is its horizon, no matter what matter can escape through it. There is a gravitational singularity at the center of the black hole, which is hidden by the event horizon. At the singularity, all the laws of physics break down. In order to avoid this phenomenon, Penrose proposed the weak cosmic censorship conjecture (WCCC) in 1969 [51, 52]. The WCCC claims that the singularity is always hidden by the event horizon and cannot be seen by an observer at infinite distance. Although the WCCC's correctness is widely accepted, there is no complete evidence to prove it and only its validity can be tested. Gedanken experiments are an effective method of testing the validity of the WCCC [53]. In these thought experiments, a test particle with sufficient energy, charge and angular momentum is thrown into the black hole. After the black hole absorbs the test particle, if the horizon is destroyed, the singularity becomes a naked singularity. In this case, the black hole is overcharged and the WCCC is violated. Conversely, if the horizon is not destroyed, the singularity is surrounded by the horizon. Consequently, the black hole is not overcharged and the WCCC is valid. The validity of the WCCC has been tested in this way for various black holes [54-74]. Recently, Sorce and Wald proposed a new version of the gedanken experiment to examine the WCCC for Kerr-Newman black holes [75]. The result of this experiment shows that the event horizon of a Kerr-Newman black hole cannot be destroyed. After that, using this experiment, the WCCC was found to be valid for a series of black holes [76-79]. Another way of destroying the event horizon of a black hole to test the validity of the WCCC is to use test fields to replace test particles in the gedanken experiment [80], a method which has been further developed in Refs. [81-92].
In this paper, we investigate the thermodynamics and overcharging problem in a RN-AdS black hole with a cloud of strings and quintessence, by charged particle absorption in extended phase space. Due to the existence of the cloud of strings and quintessence, the constants related to them are also taken into account in the calculation. The structure of this paper is as follows. In Section II, we review the thermodynamics of a RN-AdS black hole with a cloud of strings and quintessence. In Section III, the absorptions of scalar particles and fermions are discussed. In Section IV, the first and second laws of thermodynamics are investigated in extended phase space. In Section V, the overcharging problem is tested in near-extremal and extremal black holes. Our results are summarized in Section VII.
-
The metric of a RN-AdS black hole surrounded by a cloud of strings and quintessence in 4-dimensional space-time is given by [18, 44, 47]
$ {\rm d}s^{2} = f(r){\rm d}t^{2}-\frac{1}{f(r)}{\rm d}r^{2}-r^{2}\left({\rm d}\theta^{2}+\sin^{2}\theta {\rm d}\phi^{2}\right), $

(6) with
$ f(r) = 1-a-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}-\frac{\alpha}{r^{3\omega_{q}+1}}-\frac{\Lambda r^{2}}{3}.$

(7) In the above equation,
$ \Lambda $ is the cosmological constant related to the AdS space radius l by$ \Lambda = -3/l^{2} $ , and M and Q are the mass and charge of the black hole, respectively. a is the integral constant caused by the cloud of strings and$ \alpha $ is a normalization constant related to the quintessence, with density$ \rho_{q} $ $ \rho_{q} = -\frac{\alpha}{2}\frac{3\omega_{q}}{r^{3(\omega_{q}+1)}}. $

(8) In Fig. 1, the graphs of the function
$ f(r) $ are shown for different values of the parameters a,$ \alpha $ and$ \omega_{q} $ , which represent the presence of the cloud of strings and the quintessence.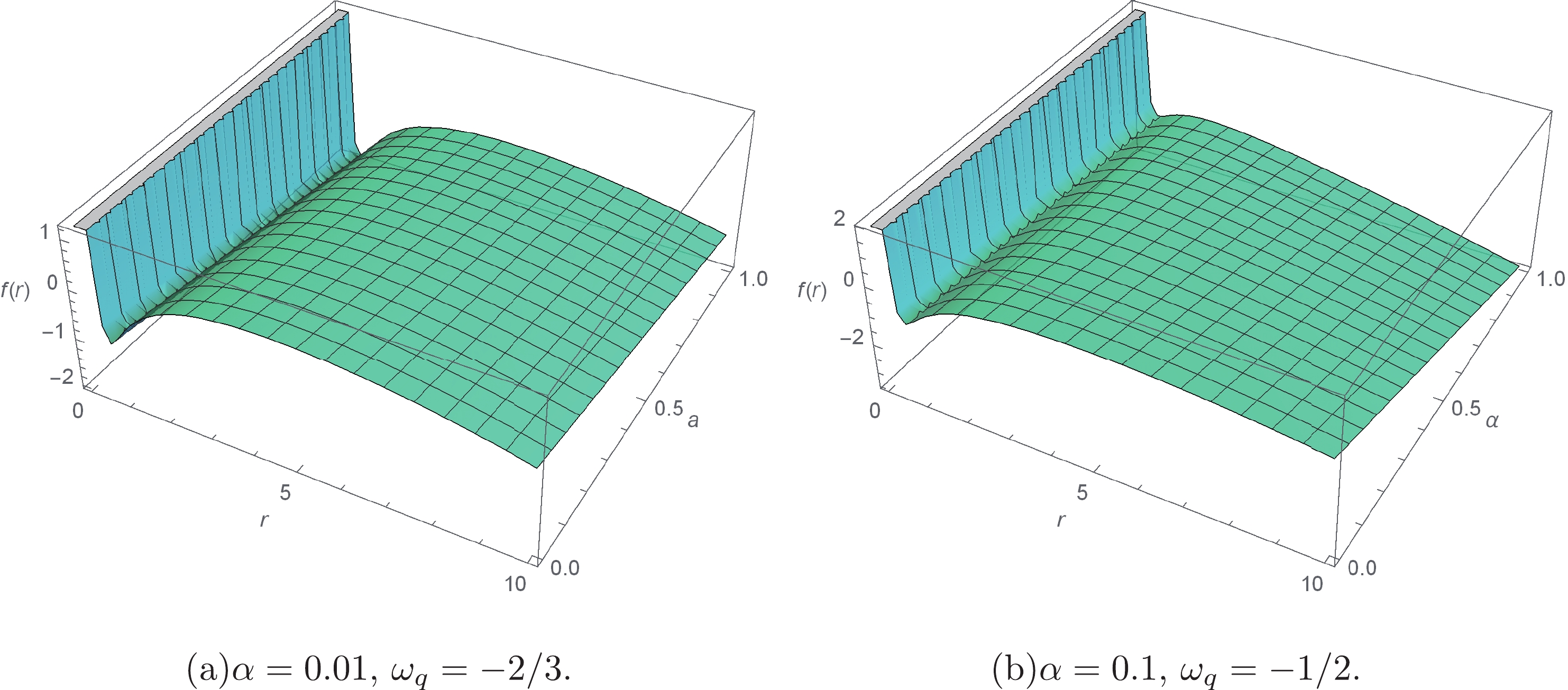
Figure 1. (color online) The function
$ f(r) $ for different values of a,$ \alpha $ and$ \omega_{q} $ . We choose$ M = 1 $ and$ Q = 0.8 $ .For a non-extremal black hole, the equation
$ f(r) = 0 $ has two positive real roots,$ r_+ $ and$ r_- $ .$ r_+ $ represents the radius of the event horizon. For an extremal black hole,$ f(r) = 0 $ has only one root,$ r_+ $ . The mass of the black hole can be represented by:$ M = \frac{1}{2}\left(r-ar+\frac{Q^{2}}{r^{2}}-\frac{\alpha}{r^{3\omega_{q}}}+\frac{r^{3}}{l^{2}}\right). $

(9) The Hawking temperature takes the form:
$ T = \frac{f^{\prime}(r_{+})}{4\pi} = \frac{1}{4\pi}\left(\frac{2M}{r_{+}^{2}}-\frac{2Q^{2}}{r_{+}^{3}}+\frac{(3\omega_{q}+1)\alpha}{r_{+}^{3\omega_{q}+2}}+\frac{2r_{+}}{l^{2}}\right). $

(10) The entropy and the potential of the black hole are:
$ S = \pi r_{+}^{2}, $

(11) $ \Phi = -A_{t}\left(r_{+}\right) = \frac{Q}{r_{+}}. $

(12) In previous studies, the cosmological constant was treated as a constant. Recently, however, the thermodynamic pressure of the black hole has been introduced into the laws of thermodynamics, and the cosmological constant treated as a variable related to pressure. The relationship between the cosmological constant and pressure is [8-13]
$ P = -\frac{\Lambda}{8\pi} = \frac{3}{8\pi l^{2}}. $

(13) The first law of thermodynamics in the extended phase space is written as:
$ {\rm d}M = T{\rm d}S+V{\rm d}P+\varphi {\rm d}Q+\gamma {\rm d}\alpha +\varkappa {\rm d}a, $

(14) where
$ \gamma = -\frac{1}{2r_{+}^{3\omega_{q}}},\varkappa = -\frac{r_{+}}{2}. $

(15) In the above equation, the volume is given by:
$ V = \left(\frac{\partial M}{\partial P}\right)_{S,Q} = \frac{4\pi r_{+}^{3}}{3}. $

(16) The mass of the black hole M is defined as its enthalpy. Hence, the relationship between enthalpy, internal energy and pressure is [7, 10]:
$ M = U+PV. $

(17) -
In curved space-time, the motion of a charged scalar particle satisfies the Klein-Gordon equation:
$ \frac{1}{\sqrt{-g}}\left(\frac{\partial}{\partial x^{\mu}}-\frac{{\rm i}q}{\hbar}A_{\mu}\right)\left[\sqrt{-g}g^{\mu\nu}\left(\frac{\partial}{\partial x^{\nu}}-\frac{{\rm i}q}{\hbar}A_{\nu}\right)\right]\Psi_{S}-\frac{m^{2}}{\hbar^{2}}\Psi_{S} = 0, $

(18) where
$ \Psi_{S} $ is the scalar field, and m and q are the mass and charge of the particle, respectively. Using the WKB approximation [93-95], the wave function is written as$ \Psi_{S} = \exp\left(\frac{\rm i}{\hbar}I+I_{1}+\mathcal{O}(\hbar)\right). $

(19) Inserting Eq. (19) and the contravariant metric components of the 4-dimensional black hole into the Klein-Gordon equation, we obtain:
$ f^{-1}(\partial_{t}I-qA_{t})^{2}-f(\partial_{r}I)^{2}-\frac{1}{r^{2}}(\partial_{\theta}I)^{2}-\frac{1}{r^{2}\sin^{2}\theta}(\partial_{\varphi}I)^{2}+m^{2} = 0. $

(20) Considering the symmetry of space-time, it is necessary to carry out the separation of variables in the action
$ I = -\omega t+W(r)+S(\theta,\varphi), $

(21) where
$ \omega $ is the energy of the absorbed scalar particle. Substituting the above separated action into Eq. (20) and simplifying it yields:$ \partial_{r}W = \pm\dfrac{\sqrt{\left(\omega-\dfrac{4qQ}{r}\right)^{2}+\left[m^{2}-\dfrac{1}{r^{2}}(\partial_{\theta}S)^{2}-\dfrac{1}{r^{2}\sin^{2}\theta}\left(\partial_{\varphi}S\right)^{2}\right]f}}{f}. $

(22) In the above equation,
$ +(-) $ indicates the situation of ingoing (outgoing) particles. Since we suppose that the particles are completely absorbed by the black hole, the negative sign is ignored [96]. Defining$ p^{r} = \partial_{r}I = \partial_{r}W $ , the above equation is modified as:$ \begin{aligned}[b] p^{r}\ & = g^{rr}p_{r} \\ &= \sqrt{\left(\omega-\frac{4qQ}{r}\right)^{2}+\left[m^{2}-\frac{1}{r^{2}}(\partial_{\theta}S)^{2}-\frac{1}{r^{2}\sin^{2}\theta}(\partial_{\varphi}S)^{2}\right]f}. \end{aligned}$

(23) Here we consider the situation of absorbed particles near the horizon, which means
$ f(r)\rightarrow0 $ . Then Eq. (23) is simplified to$ p^{r} = \omega-q\Phi, $

(24) where
$\Phi = \dfrac{Q}{r_{+}}$ is the electric potential. Equation (24) is the relationship between the momentum, the energy and the charge of the ingoing particle. When$ \omega < q\Phi $ , the energy of the black hole flows out from the event horizon and superradiation happens. When$ \omega = q\Phi $ , the energy of the black hole does not change. In this paper, it is assumed that$ \omega \geqslant q\Phi $ , which implies superradiation does not occur. Equation (24) plays an important role in the discussion of black hole thermodynamics, and is recovered by fermion absorption in the next section. -
In curved space-time, the motion of a charged fermion obeys the Dirac equation:
$ {\rm i}\gamma^{\mu}\left(\partial_{\mu}+\Omega_{\mu}-\frac{\rm i}{\hbar}qA_{\mu}\right)\Psi_{F}+\frac{m_0}{\hbar}\Psi_{F} = 0, $

(25) where m and q are the mass and charge of the fermion, respectively.
$\Omega_{\mu}\equiv\dfrac{\rm i}{2}\omega_{\mu}{}^{ab}\varSigma_{ab}$ ,$ \omega_{\mu}^{ab} $ is the spin connection defined by the normal connection and the tetragonal$ { e^{\lambda}}_{b} $ . The relation between the spin connection, the normal connection and the tetragonal is$ { { \omega_{\mu}}^{a}}_{b} = e_{\nu}{ ^{a}}e^{\lambda}{ _{b}}\Gamma_{\mu\lambda}^{\nu}-{ e^{\lambda}}_{b}\partial_{\mu}e_{\lambda}{ ^{a}}. $

(26) The Greek index rises and falls with the curved metric
$ g_{\mu\nu} $ . The Latin index is dominated by the flat metric$ \eta_{ab} $ . To construct the tetrad, the following definition is needed:$ g_{\mu\nu} \ =\ e_{\mu}{ ^{a}}e_{\nu}{ ^{b}}\eta_{ab}, \eta_{ab} \ =\ g_{\mu\nu}{ e^{\mu}}_{a}{ e^{\nu}}_{b}, { e^{\mu}}_{a}e_{\nu}{ ^{a}} \ =\ \delta_{\nu}^{\mu}, { e^{\mu}}_{a}e_{\mu}{ ^{b}} \ =\ \delta_{a}^{b}. $

(27) The Lorentz spinor generators are defined by:
$ \varSigma_{ab} = \frac{\rm i}{4}[\gamma^{a},\gamma^{b}], \{\gamma^{\mu},\gamma^{\nu}\} = 2\eta^{ab}. $

(28) Then the
$ \gamma^{\mu} $ is constructed in curved space-time as:$ \gamma^{\mu} = { e^{\mu}}_{a}\gamma^{a}, \{\gamma^{\mu},\gamma^{\nu}\} = 2g^{\mu\nu}. $

(29) For a fermion with a spin of 1/2, its wave function must be described as both spin-up and spin-down. We first describe the spin-up wave function. The wave function takes the form:
$ \Psi_{F\uparrow} = \left(\begin{array}{c} A\\ 0\\ B\\ 0 \end{array}\right)\exp\left(\frac{\rm i}{\hbar}I_{\uparrow}(t,r,\theta,\varphi)\right). $

(30) where A, B and I are functions of t, r,
$ \theta $ ,$ \phi $ . For the metric (6), we choose:$ e_{\mu}{}^{a} = {\rm diag}\left(\sqrt{f},1/\sqrt{f},r,r\sin\theta\right). $

(31) Then the
$ \gamma^{\mu} $ matrices are written as:$\begin{aligned}[b] &{\gamma ^t} = \frac{1}{{\sqrt {f\left( r \right)} }}\left( {\begin{array}{*{20}{c}} i&0\\ 0&{ - i} \end{array}} \right),{\gamma ^\theta } = r\left( {\begin{array}{*{20}{c}} 0&{{\sigma ^1}}\\ {{\sigma ^1}}&0 \end{array}} \right),\\ &{\gamma ^r} = \sqrt {f\left( r \right)} \left( {\begin{array}{*{20}{c}} 0&{{\sigma ^3}}\\ {{\sigma ^3}}&0 \end{array}} \right),{\gamma ^\varphi } = r\sin\theta \left( {\begin{array}{*{20}{c}} 0&{{\sigma ^2}}\\ {{\sigma ^2}}&0 \end{array}} \right), \end{aligned}$

(32) where
$ \sigma^{i} $ are the Pauli matrices, which are given by:$ \sigma^{1} = \left(\begin{array}{cc} 0 & 1\\ 1 & 0 \end{array}\right),\sigma^{2} = \left(\begin{array}{cc} 0 & -i\\ i & 0 \end{array}\right),\sigma^{3} = \left(\begin{array}{cc} 1 & 0\\ 0 & -1 \end{array}\right). $

(33) Inserting the spin connection, wave function and gamma matrices into the Dirac equation, we obtain:
$ -{\rm i}A\frac{1}{\sqrt{f}}\left(\partial_{t}I_{\uparrow}-qA_{t}\right)-B\sqrt{g}\partial_{r}I_{\uparrow}+Am_{0} = 0, $

(34) $ -{\rm i}B\frac{1}{\sqrt{f}}\left(\partial_{t}I_{\uparrow}-qA_{t}\right)-A\sqrt{g}\partial_{r}I_{\uparrow}+Bm_{0} = 0, $

(35) $ A\left[r\partial_{\theta}I_{\uparrow}+{\rm i}r\sin\theta\partial_{\varphi}I_{\uparrow}\right] = 0, $

(36) $ B\left[r\partial_{\theta}I_{\uparrow}+{\rm i}r\sin\theta\partial_{\varphi}I_{\uparrow}\right] = 0. $

(37) Equations (36) and (37) are simplified to one equation and yield
$r^{2}\left(\partial_{\theta}I_{\uparrow}\right)^{2}+r^{2}\sin^{2}\theta\left(\partial_{\varphi}I_{\uparrow}\right)^{2} = 0$ . In previous studies, the contribution of the angular part did not affect the results of tunneling radiation when the quantum gravity effects were not considered [97]. Since the radial action is determined by the first two of the above four equations, we mainly focus on them. To solve the question we are addressing, it is necessary to use the separation of variables:$ I_{\uparrow} = -\omega t+W\left(r\right)+\varTheta\left(\theta,\varphi\right). $

(38) In the above equation,
$ \omega $ is the energy of the ingoing fermion. Inserting Eq. (38) into Eqs. (34) and (35) yields:$ f^{2}\left(\partial_{r}W\right)^{2}-\left(\omega-\frac{4qQ}{r}\right)^{2}-m_{0}^{2}f = 0. $

(39) Simplifying Eq. (39), we have:
$ \partial_{r}W = \pm\dfrac{\sqrt{\left(\omega-\dfrac{4qQ}{r}\right)^{2}+m_{0}^{2}f}}{f}, $

(40) where the
$ +/- $ corresponds to the cases of the ingoing/outgoing fermion. In the work of Gwak [96], the positive sign in the above equation was selected. Thus, we get$ p^{r} = g^{rr}p_{r} = \sqrt{\left(\omega-\frac{4qQ}{r}\right)^{2}+m_{0}^{2}f}. $

(41) Near the event horizon,
$ f\rightarrow0 $ . The above equation is modified as$ p^{r} = \omega-q\Phi, $

(42) Therefore, Eq. (24) can be recovered by fermion absorption. The above discussion calculates the spin-up state. For the spin-down state, the result is the same as the spin-up state. It is clear that the results obtained by scalar particle absorption and fermion absorption are the same.
-
Recently, an interesting method has been adopted to treat the cosmological constant as a thermodynamic variable. From this point of view, the cosmological constant is not a fixed value but a thermodynamic variable, and represents quite consistent behaviors with other thermodynamic variables [8, 14]. In this extended thermodynamics, the cosmological constant plays the role of pressure P
$ P = -\frac{\Lambda}{8\pi} = \frac{3}{8\pi l^{2}}. $

(43) In this case, the mass of the black hole is no longer equivalent to the internal energy, but is seen as a gravitational version of the chemical enthalpy. The thermodynamic volume of the black hole is:
$ V = \frac{\partial M}{\partial P} = \frac{4\pi r_{+}^{3}}{3}. $

(44) In order to satisfy the Smarr relation, we need to further expand the phase space by elevating any dimensional parameter of the theory to a thermodynamic variable and introducing the associated conjugate [98, 99]. These parameters and their conjugations add additional terms to the first law of thermodynamics. In particular, the parameters related to the cloud of strings and quintessence are considered to be thermodynamic phase space variables, and the associated conjugates are:
$ \gamma = \frac{\partial M}{\partial\alpha} = -\frac{1}{2r_{+}^{3\omega_{q}}},\varkappa = \frac{\partial M}{\partial a} = -\frac{r_{+}}{2}. $

(45) The quintessence parameters
$ \gamma $ and$ \alpha $ are playing the same role as pressure and volume in the first law to make it consistent with the Smarr relation. The same is true for the parameters related to the cloud of strings, i.e.$ \varkappa $ and a. As shown in Ref. [44], for a 4-dimensional RN-AdS black hole surrounded by a cloud of strings and quintessence, all these quantities satisfy the following generalized Smarr formula:$ M = 2TS-2VP+\varPhi Q+\left(3\omega_{q}+1\right)\gamma\alpha. $

(46) When the black hole absorbs a particle, the changes in the internal energy and charge of the black hole are equal to the energy and charge of the particle, which take the form:
$ \omega = {\rm d}U = {\rm d}(M-PV),~ q = {\rm d}Q, $

(47) where
$ M-PV $ is the internal energy of the black hole in the extended phase space. Therefore, Eq. (42) is written as:$ {\rm d}U = \frac{Q}{r_{+}}{\rm d}Q+p^{r}. $

(48) Thus, after a charged particle with energy
$ \omega $ and charge q enters the black hole horizon, the black hole changes from the initial state$ (M,Q,P,a,\alpha,r_{+}) $ to the final state$(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha,r_{+}+{\rm d}r_{+})$ . The functions$ f(M,Q,P,a,\alpha,r_{+}) $ and$f(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P, a+{\rm d}a,\alpha+{\rm d}\alpha,r_{+} + {\rm d}r_{+})$ satisfy$ \begin{aligned}[b]f(M,Q,P,a,\alpha,r_{+}) =\ & f(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,a\\ &+{\rm d}a,\alpha+{\rm d}\alpha,r_{+}+{\rm d}r_{+}) = 0. \end{aligned}$

(49) The relation between the functions
$ f(M,Q,P,a,\alpha,r_{+}) $ and$f(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha,r_{+}+{\rm d}r_{+})$ is$ \begin{aligned}[b] & f(M\!+\!{\rm d}M,Q\!+\!{\rm d}Q,P\!+\!{\rm d}P,a\!+\!{\rm d}a,\alpha\!+\!{\rm d}\alpha,r_{+}\!+\!{\rm d}r_{+})\\ = & f(r) + \frac{\partial f}{\partial M}\Biggr|_{r = r_{+}}{\rm d}M\!+\!\frac{\partial f}{\partial Q}\Biggr|_{r = r_{+}}{\rm d}Q\!+\!\frac{\partial f}{\partial r}\Biggr|_{r = r_{+}}{\rm d}r_{+} \\ & +\frac{\partial f}{\partial P}\Biggr|_{r = r_{+}}{\rm d}P\!+\!\frac{\partial f}{\partial a}\Biggr|_{r = r_{+}}{\rm d}a\!+\!\frac{\partial f}{\partial\alpha}\Biggr|_{r = r_{+}}{\rm d}\alpha , \end{aligned} $

(50) where
$ \begin{aligned}[b] &\frac{\partial f}{\partial M}\bigg|_{r = r_{+}} = -\frac{2}{r_{+}}, ~~ \frac{\partial f}{\partial Q}\bigg|_{r = r_{+}} = \frac{2Q}{r_{+}^{2}}, ~~ \frac{\partial f}{\partial r}\bigg|_{r = r_{+}} = 4\pi T,\\ &\frac{\partial f}{\partial P}\bigg|_{r = r_{+}} = \frac{8\pi r_{+}^{2}}{3}, ~~ \frac{\partial f}{\partial\alpha}\bigg|_{r = r_{+}} = -\frac{1}{r_{+}^{3\omega_{q}+1}}, ~~ \frac{\partial f}{\partial a}\bigg|_{r = r_{+}} = -1.\end{aligned} $

(51) Using Eqs. (49), (50) and (51) yields
$ {\rm d}r_{+} = \frac{2p^{r}+r_{+}{\rm d}a+r_{+}^{-3\omega_{q}}{\rm d}\alpha}{4\pi r_{+}(T-2Pr_{+})}. $

(52) Then the variation of the entropy and volume is written as
$ {\rm d}S = \frac{2p^{r}+r_{+}{\rm d}a+r_{+}^{-3\omega_{q}}{\rm d}\alpha }{2T-4Pr_{+}}, $

(53) and
$ {\rm d}V = \frac{2r_{+}p^{r}+r_{+}^{2}{\rm d}a+r_{+}^{-3\omega_{q}+1}{\rm d}\alpha}{T-2Pr_{+}}. $

(54) From Eqs. (10), (53), (13) and (54), we obtain:
$ T{\rm d}S-P{\rm d}V = p^{r}+\frac{r_{+}}{2}{\rm d}a+\frac{r_{+}^{-3\omega_{q}}}{2}{\rm d}\alpha. $

(55) Moreover, substituting Eqs. (12), (47) and (48) into Eq. (55), the relation between the internal energy and enthalpy is simplified to
$ {\rm d}M = T{\rm d}S+V{\rm d}P+\varPhi {\rm d}Q+\mathcal{\gamma}{\rm d}\alpha+\varkappa {\rm d}a, $

(56) where
$ \gamma $ and$ \varkappa $ are physical quantities conjugated to the parameters$ \alpha $ and a, respectively. They satisfy$ \gamma = -\frac{1}{2r_{+}^{3\omega_{q}}},\varkappa = -\frac{r_{+}}{2}. $

(57) Hence, the first law of thermodynamics is still satisfied.
For an extremal black hole, the temperature is zero. Then Eq. (53) is modified as:
$ {\rm d}S = -\frac{2p^{r}+r_{+}{\rm d}a+r_{+}^{-3\omega_{q}}{\rm d}\alpha }{4Pr_{+}}. $

(58) If
${\rm d}\alpha > 0$ and${\rm d}a > 0$ , dS is less than zero and the entropy of the extremal black hole decreases over time. If${\rm d}\alpha < 0$ and${\rm d}a < 0$ , dS could be greater than zero. Therefore, the second law of thermodynamics is indefinite for an extremal black hole in the extended phase space.For a near-extremal black hole, we analyse the change of entropy numerically to intuitively understand the changes in entropy. We set
$ M = 0.5 $ and$ l = p^{r} = 1 $ . For the case$ \omega_{q} = -2/3 $ ,$ a = 0.01 $ and$ \alpha = 0.01 $ , the extremal charge is$ Q_e = 0.465706962 $ . When the charge is less than the extremal charge, the value of entropy changes when the value of charge changes. The values of$ r_+ $ and dS corresponding to different values of charge are listed in Table 1.Q r+ dS da ${\rm d}\alpha$ 

0.465706962 0.388699 −12.1128 0.465706 0.389388 −12.2765 0.46 0.440516 −61.7333 0.44 0.495002 35.3525 0.42 0.495002 20.7666 0.5 0.1 0.40 0.550912 17.2452 0.30 0.623442 12.1402 0.20 0.661300 10.9798 0.10 0.680975 10.5455 Table 1. The relation between dS, Q and r+.
From Table 1, it can be seen that the event horizon of the black hole and the variation of entropy increases when the charge of the black hole decreases. It is obvious that there exists a phase transition point that divides the value of dS into positive and negative regions.
In order to explore whether the values of state parameters of the cloud of strings and quintessence affect the second law of thermodynamics, we test the validity of the second law when the values of a,
$ \alpha $ and$ \omega_{q} $ change. In Table 2, we set$ a = 0.1 $ , with the values of the other variables the same as in Table 1. The extremal charge is$ Q_e = 0.480782137 $ . The values of$ r_+ $ and dS corresponding to different charge values are summarized in Table 2.Q r+ dS da ${\rm d}\alpha$ 

0.480782137 0.407715 −11.5960 0.480782 0.407979 −11.6471 0.48 0.427511 −16.6251 0.47 0.479200 −109.927 0.45 0.524836 45.8092 0.5 0.1 0.40 0.587213 19.7015 0.30 0.653150 14.1111 0.20 0.688780 12.6902 0.10 0.707491 12.1425 Table 2. The relation between dS, Q and r+.
In Table 3, we set
$ \omega_{q} = -1/2 $ ,$ a = 0.1 $ ,$ \alpha = 0.1 $ , with the values of other variables the same as in Table 1. The extremal charge is$ Q_e = 0.491516500 $ . The values of$ r_+ $ and dS corresponding to different charge values are summarized in Table 3.Q r+ dS da ${\rm d}\alpha$ 

0.491516500 0.424248 −12.5738 0.491516 0.424762 −12.6769 0.49 0.452203 −20.8312 0.47 0.525092 121.255 0.45 0.560603 37.4749 0.5 0.1 0.40 0.616308 20.7626 0.30 0.678621 15.3953 0.20 0.712972 13.8958 0.10 0.731128 13.3019 Table 3. The relation between dS, Q and r+.
In order to more intuitively observe the impact of a and
$ \alpha $ on dS, a function graph is used to express the relationship between dS and$ r_+ $ in different situations, which is shown in Fig. 2. From Fig. 2, it is clear that there is indeed a phase change point that divides dS into positive and negative regions. If the charge of the black hole is less than the extreme value of the charge, the value of dS is negative and entropy decreases. If the charge is greater than the extreme charge, the value of dS is positive and the entropy increases. Thus, the second law of thermodynamics is indefinite for a black hole in the extended phase space. From Tables 1, 2 and 3, we find that when the value of the state parameter of the cloud of strings or quintessence increases, the extremal charge$ Q_e $ and its corresponding$ r_+ $ also increase. Moreover, for the same value of$ r_+ $ , the value of dS increases when values of a,$ \alpha $ and$ \omega_q $ increase. The values of the parameters do affect the second law of thermodynamics, but the parameters do not determine whether the second law of thermodynamics is ultimately violated.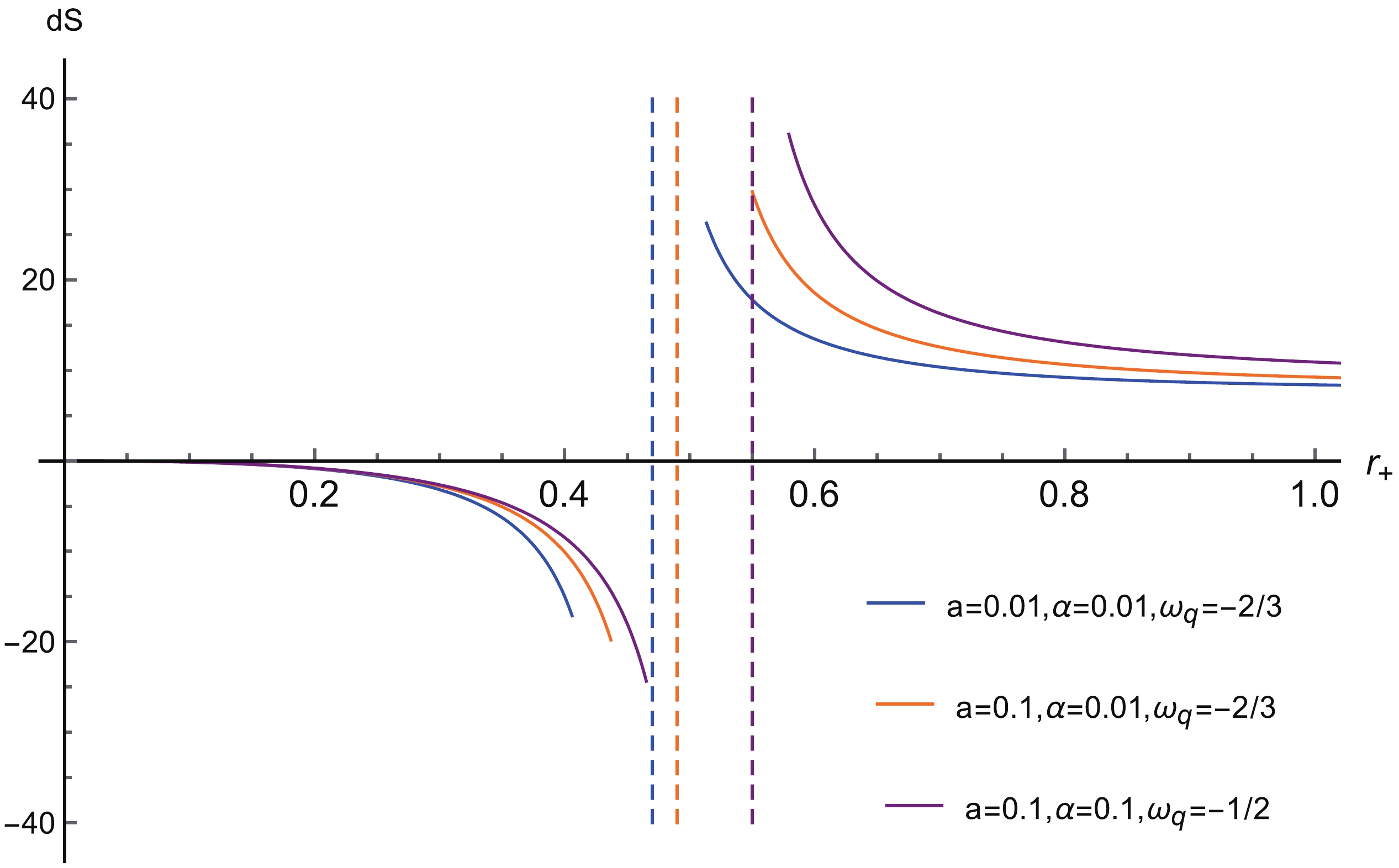
Figure 2. (color online) The relation between dS and
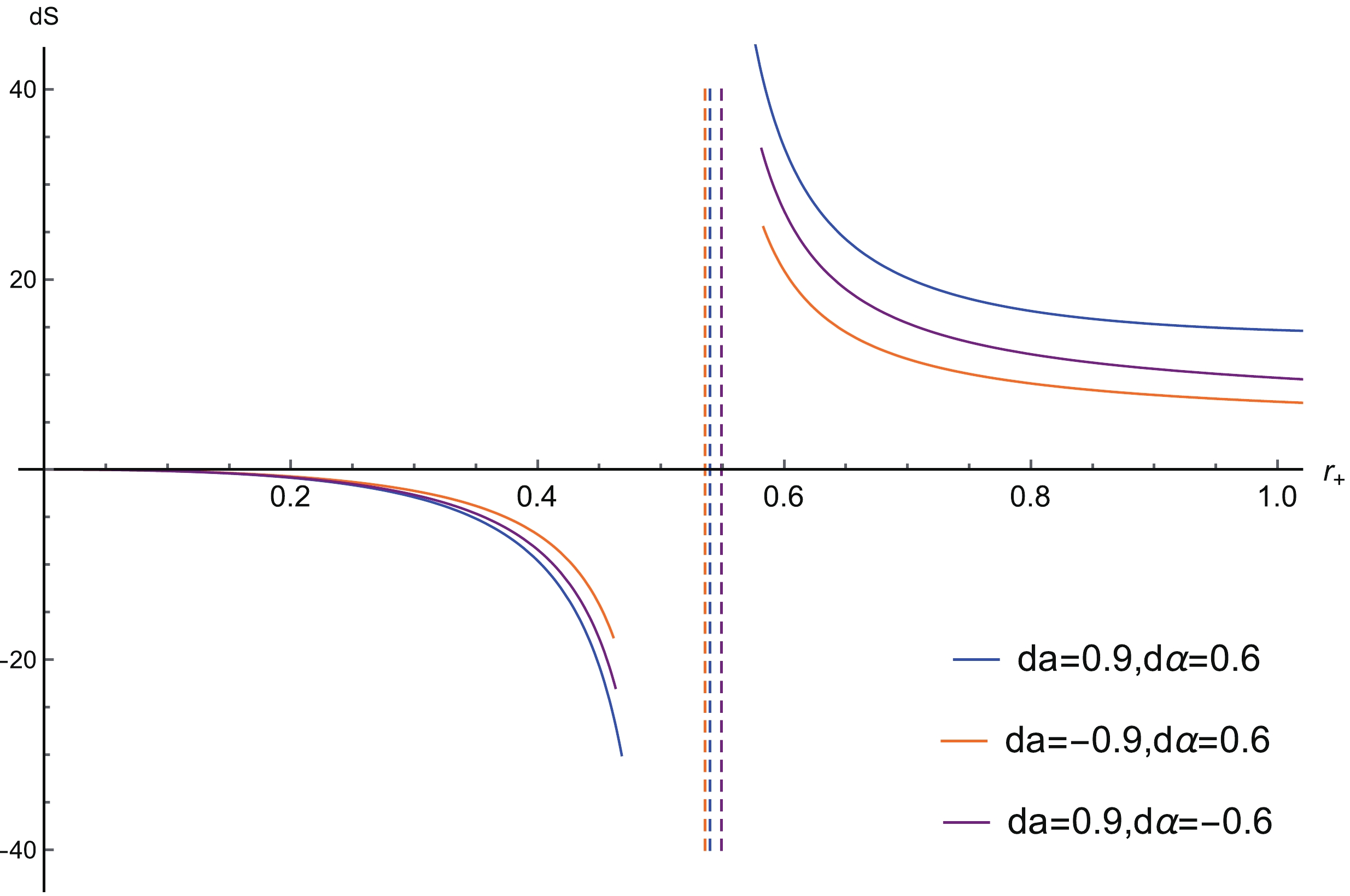
$ r_+ $ , with parameter values$ M = 0.5 $ ,$ l = p^{r} = 1 $ ,$ {\rm d}a = 0.5 $ , and$ {\rm d}\alpha = 0.1 $ .Furthermore, da and
${\rm d}\alpha$ also affect dS. Changing da and${\rm d}\alpha$ , we analyze the change in dS numerically and plot it as shown in Fig. 3. Ultimately, it can be concluded that the second law of thermodynamics is not always valid for near-extremal black holes in the extended phase space. -
In this section, the validity of the WCCC for extremal and near-extremal black holes is discussed by considering the absorptions of the scalar particle and fermion. An effective way to test the validity of the WCCC is to check whether the event horizon exists after the black hole absorbs the particles. The event horizon is determined by the function
$ f(r) $ . In the initial state, the minimum value of$ f(r) $ is negative or zero and$ f(r) = 0 $ has real roots. This means the event horizon exists. When the black hole absorbs a particle, the mass and charge of the black hole change during the infinitesimal time interval${\rm d}t$ and the minimum value of$ f(r) $ also changes. If the minimum value of$ f(r) $ is negative or equal to zero, the event horizon exists. Therefore, the WCCC is valid. Otherwise, the minimum value of$ f(r) $ is positive, and the event horizon does not exist. Consequently, the black hole is overcharged and the WCCC is not valid.The sign of the minimum value in the final state can be obtained in term of the initial state [100]. We assume
$ (M,Q,P,r_0,a,\alpha) $ and$(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,r_0+{\rm d}r_0, a+{\rm d}a,\alpha+{\rm d}\alpha)$ represent the initial state and the final state, respectively. At$r = r_0+{\rm d}r_0$ ,$f(M+{\rm d}M,Q+{\rm d}Q, P+{\rm d}P,r_0+{\rm d}r_0,a+ {\rm d}a,\alpha+{\rm d}\alpha)$ is written as:$ \begin{aligned}[b] &f\left(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha ,{\rm d}r_{0}+r_{0}\right) \\ =& \delta+\frac{\partial f}{\partial M}\Biggr|_{r = r_{0}}{\rm d}M+\frac{\partial f}{\partial Q}\Biggr|_{r = r_{0}}{\rm d}Q+\frac{\partial f}{\partial P}\Biggr|_{r = r_{0}}{\rm d}P\\ &+\frac{\partial f}{\partial a}\Biggr|_{r = r_{0}}{\rm d}a+\frac{\partial f}{\partial\alpha}\Biggr|_{r = r_{0}}{\rm d}\alpha +\frac{\partial f}{\partial r}\Biggr|_{r = r_{0}}{\rm d}r,\end{aligned} $

(59) where
$ \begin{aligned}[b]&\frac{\partial f}{\partial r}\bigg|_{r = r_{0}} = 0, ~~ \frac{\partial f}{\partial M}\bigg|_{r = r_{0}} = -\frac{2}{r_{0}}, ~~ \frac{\partial f}{\partial Q}\bigg|_{r = r_{0}} = \frac{2Q}{r_{0}^{2}},\\ &\frac{\partial f}{\partial P}\bigg|_{r = r_{0}} = \frac{8\pi r_{0}^{2}}{3}, ~~ \frac{\partial f}{\partial a}\bigg|_{r = r_{0}} = -1, ~~ \frac{\partial f}{\partial\alpha}\bigg|_{r = r_{0}} = -\frac{1}{r_{0}^{3\omega_{q}+1}}.\end{aligned} $

(60) At
$ r = r_0 $ , we have$ f\left(M,Q,P,a,\alpha,r_{0}\right)\equiv f_{0} = \delta\leqslant 0, $

(61) and
$ \partial_{r}f\left(M,Q,P,a,\alpha,r_{0}\right)\equiv f_{\min}^{\prime} = 0. $

(62) From Eqs. (59), (60), (47), (48) and (54), we obtain:
$ \begin{aligned}[b]f\left(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha ,r_{0}+{\rm d}r_{0}\right) =& \delta-\frac{2Tp^{r}}{r_{0}\left(T-2Pr_{+}\right)}-\frac{2qQ}{r_{0}}\left(\frac{1}{r_{+}}-\frac{1}{r_{0}}\right)+\frac{8\pi}{3r_{0}}\left(r_{+}-r_{0}\right){\rm d}P\\& +\frac{Tr_{0}^{-3\omega_{q}}+2Pr_{+}\left(r_{+}^{-3\omega_{q}}-r_{0}^{-3\omega_{q}}\right)}{r_{0}\left(T-2Pr_{+}\right)}{\rm d}{\alpha}+\frac{Tr_{0}+2Pr_{+}(r_{+}-r_{0})}{r_{0}\left(T-2Pr_{+}\right)}{\rm d}a.\end{aligned} $

(63) When the initial black hole is an extremal black hole,
$ r_{0} = r_{+} $ ,$ T = 0 $ and$ \delta = 0 $ . Then we can obtain$f_{\min} = \delta = 0$ and$f_{\min}^{\prime} = 0$ . Hence, Eq. (63) is written as:$ f\left(M\!+\!{\rm d}M,Q\!+\!{\rm d}Q,P\!+\!{\rm d}P,a\!+\!{\rm d}a,\alpha\!+\!{\rm d}\alpha ,{\rm d}r_{0}\!+\!r_{0}\right) \!=\! 0. $

(64) When the initial black hole is a near-extremal black hole,
$ r_0 $ and$ r_+ $ do not coincide. In Eq. (63), the first term in the second line satisfies Eq. (61) and the second term is only suppressed by the test particle limit. However, the other terms are suppressed by the approaching extreme value limit and the test particle limit. Therefore, they can be ignored. Hence, Eq. (63) is modified as:$ \begin{aligned}[b]&f\left(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha ,r_{0}+{\rm d}r_{0}\right) \\ =& \delta-\frac{2Tp^{r}}{r_{0}\left(T-2Pr_{+}\right)}<0. \end{aligned} $

(65) Hence, the near-extremal black hole stays near-extremal after absorbing a charged particle. The WCCC is satisfied for both extremal and near-extremal black holes in extended phase space.
-
Recent studies of thermodynamics and the WCCC in extended phase space have attracted a lot of attention, but also aroused controversy. The controversy primarily focuses on the following point: when a particle with energy E is thrown into the black hole, the energy of the particle changes the internal energy of the black hole, i.e.,
$E = {\rm d}U$ , or the energy of the particle changes the enthalpy of the black hole, i.e.,$E = {\rm d}M$ . In Ref. [57], the authors assume$E = {\rm d}M$ and find the second law of thermodynamics is valid. In our work, we assume$E = {\rm d}U$ and find the second law of thermodynamics is indefinite. When we assume$E = {\rm d}M$ , we find the variation in the entropy of a RN-AdS black hole with cloud of strings and quintessence is:$ {\rm d}S = \frac{2p^{r}+2r_{+}^{3}l^{-3}{\rm d}l+r_{+}{\rm d}a+r_{+}^{-3\omega_{q}}{\rm d}\alpha }{2T}. $

(66) When
${\rm d}\alpha > 0$ and${\rm d}a > 0$ , the variation in the entropy is positive, though approaching zero in the extremal limit. When${\rm d}\alpha < 0$ and${\rm d}a < 0$ , the variation in the entropy could decrease. Hence, the second law of thermodynamics is not always valid. Furthermore, we find when we assume$E = {\rm d}M$ ,$f(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,r_0+{\rm d}r_0,a+{\rm d}a,\alpha+ {\rm d}\alpha)$ is rewritten as$ \begin{aligned}[b] &f\left(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha ,r_{0}+{\rm d}r_{0}\right) \\ =& \delta-\frac{2p^{r}}{r_{0}}-\frac{2qQ}{r_{0}}\left(\frac{1}{r_{+}}-\frac{1}{r_{0}}\right)+\frac{8\pi r_{0}^{2}}{3}{\rm d}P-{\rm d}{\alpha}-\frac{1}{r_{0}^{3\omega_{q}+1}}{\rm d}a<0. \end{aligned}$

(67) Therefore, both extremal and near-extremal black holes cannot be overcharged after absorbing a charged particle. In future work, we plan to further study these two methods for various black holes.
-
We have investigated the first and second laws of thermodynamics and the overcharging problem in a RN-AdS black hole with a cloud of strings and quintessence, via the absorption of scalar particles and fermions in extended phase space. The cosmological constant is treated as a function of thermodynamic pressure P. Moreover, the state parameters of cloud of strings and quintessence are treated as variables. To study the variations of the thermodynamic quantities of the black hole after absorbing a charged particle, we calculated the absorption of scalar particles and fermions. We found they finally simplified to the same relation
$ p^{r} = \omega-q\Phi $ . This relation is exactly the same as that obtained by the Hamilton-Jacobi equation. The reason is that the Hamilton-Jacobi equation can be obtained by inserting the wave function (19) into the Klein-Gordon equation (18). The Hamilton-Jacobi equation takes the form:$ \left(\partial^{\mu}I+eA^{\mu}\right)\left(\partial_{\mu}I+eA_{\mu}\right)-m^{2} = 0. $

(68) In addition, the Hamilton-Jacobi equation can be obtained from the Dirac equation [101, 102]. The multiplication of Eq. (25) gives a second-order partial derivative equation. The wave function is written as
$ \varPsi_{F} = \varPsi_{0}e^{\frac{i}{h}I} $ , where$ \varPsi_{0} $ is a position-dependent spinor. By inserting the function into the second-order partial derivative equation and keeping only the first-order term in$ \hbar $ , the Hamilton-Jacobian equation can be obtained.Usually, the thermodynamics and overcharging problem are discussed via absorbing a charged and/or rotating particle. However, a black hole can also absorb an uncharged particle and the thermodynamic properties of the black hole can be discussed in this way [103]. When the black hole absorbs an uncharged particle, only the mass of the black hole increases. Then there will be no case where the charge of the black hole is greater than the mass, the black hole cannot be overcharged and the WCCC is always satisfied. The following calculation also proves that this conclusion is correct. After the black hole absorbs an uncharged particle,
$ q = 0 $ . The Klein-Gordon equation is written as$ \frac{1}{\sqrt{-g}}\frac{\partial}{\partial x^{\mu}}\left[\sqrt{-g}g^{\mu\nu}\frac{\partial}{\partial x^{\nu}}\right]\Psi_{S}-\frac{m^{2}}{\hbar^{2}}\Psi_{S} = 0. $

(69) The Dirac equation is modified as:
$ i\gamma^{\mu}(\partial_{\mu}+\Omega_{\mu})\Psi_{F}+\frac{m_{0}}{\hbar}\Psi_{F} = 0. $

(70) Then Eqs. (24) and (42) become
$ p^{r} = \omega. $

(71) Accordingly, the changes of the internal energy and charge of the black hole are written as
$ {\rm d}U = p^{r},~~{\rm d}Q = 0. $

(72) At
$r_{+}+{\rm d}r_{+}$ , the final state of the black hole is represented by$(M+{\rm d}M,P+{\rm d}P,r_{+}+{\rm d}r_{+})$ . Therefore, the first law of thermodynamics is:$ {\rm d}M = T{\rm d}S+V{\rm d}P+\mathcal{\gamma}{\rm d}\alpha+\varkappa {\rm d}a, $

(73) where
$ \gamma = -\frac{1}{2r_{+}^{3\omega_{q}}},\varkappa = -\frac{r_{+}}{2}. $

(74) The first law of thermodynamics is the basic equation of the black hole system, and has nothing to do with whether or not particles are absorbed. We can derive this formula in this special way. The above equation is a special form of Eq. (56). The variation of the entropy is still
$ {\rm d}S = \frac{2p^{r}+r_{+}{\rm d}a+r_{+}^{-3\omega_{q}}{\rm d}\alpha }{2T-4Pr_{+}}. $

(75) When the black hole is extremal,
${\rm d}\alpha > 0$ and${\rm d}a > 0$ , the value of dS is negative and the entropy of the black hole decreases. Hence, the second law of thermodynamics is violated.Furthermore, at
$r = r_0+{\rm d}r_0$ ,$f\left(M+{\rm d}M,P+{\rm d}P,a+{\rm d}a, \alpha+ {\rm d}\alpha ,r_{0}+ {\rm d}r_{0}\right)$ is written as$ \begin{aligned}[b] f\left(M+{\rm d}M,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha ,r_{0}+{\rm d}r_{0}\right) =\ & \delta-\frac{2Tp^{r}}{r_{0}\left(T-2Pr_{+}\right)}-\frac{8\pi}{3r_{0}}\left(r_{+}^{3}-r_{0}^{3}\right){\rm d}P\\ &-\frac{Tr_{0}^{-3\omega_{q}}+2Pr_{+}\left(r_{+}^{-3\omega_{q}}-r_{0}^{-3\omega_{q}}\right)}{r_{0}\left(T-2Pr_{+}\right)}{\rm d}{\alpha}-\frac{Tr_{0}+2Pr_{+}(r_{+}-r_{0})}{r_{0}\left(T-2Pr_{+}\right)}{\rm d}a. \end{aligned} $

(76) For an extremal black hole,
$ \delta = 0 $ ,$ r_0 = r_+ $ and$ T = 0 $ . Then Eq. (56) is written as:$ f\left(M+{\rm d}M,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha ,r_{0}+{\rm d}r_{0}\right) = 0. $

(77) Therefore, extremal black holes cannot be overcharged.
For a near-extremal black hole, we define
$ r_{+} = r_0+\epsilon $ , where$ 0<\epsilon\ll1 $ . Then Eq. (56) is written as:$ \begin{aligned}[b] f\left(M+{\rm d}M,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha ,r_{0}+{\rm d}r_{0}\right) =\ & \delta-\frac{2Tp^{r}}{r_{0}\left(T-2P\left(r_{0}+\epsilon\right)\right)}-8\pi r_{0}\epsilon {\rm d}P\\ &-\frac{Tr_{0}^{-3\omega_{q}}+2Pr_{0}\epsilon\left(-3\omega_{q}\right)r_{0}^{-3\omega_{q}-1}}{r_{0}\left(T-2P\left(r_{0}+\epsilon\right)\right)}{\rm d}{\alpha}-\frac{Tr_{0}+2Pr_{0}\epsilon}{r_{0}\left(T-2P\left(r_{0}+\epsilon\right)\right)}{\rm d}a+O\left(\epsilon^{2}\right). \end{aligned} $

(78) When the initial black hole is near-extremal, we have
${\rm d}P\sim\epsilon$ ,${\rm d}a\sim\epsilon$ and${\rm d}\alpha\sim\epsilon$ . Hence, the above equation leads to$ \begin{aligned}[b] &f\left(M+{\rm d}M,P+{\rm d}P,a+{\rm d}a,\alpha+{\rm d}\alpha ,r_{0}+{\rm d}r_{0}\right) \\ =& \delta-\frac{2Tp^{r}}{r_{0}\left(T-2Pr_{+}\right)}<0. \end{aligned} $

(79) Therefore, near-extremal black holes cannot be overcharged after absorbing an uncharged particle. Moreover, an extremal black hole stays extremal and a near-extremal black hole stays near-extremal.
We used the relation
$ p^{r} = \omega-q\Phi $ to recovered the first law of thermodynamics and discussed the validity of the second law of thermodynamics and the WCCC. During the discussion, the final state of the black hole was considered to be still a black hole. The first law of thermodynamics is recovered and the second law of thermodynamics is indefinite. Since we treated the parameters related to the cloud of strings and quintessence as variables, there are two more terms,$-\dfrac{1}{2r_{+}^{3\omega_{q}}} {\rm d}\alpha$ and$-\dfrac{r_{+}}{2} {\rm d}a$ , in the formula of the first law of thermodynamics. The detailed formulas of the first law of thermodynamics for black holes and black holes surrounded by clouds and quintessence are shown in Table 4.Type of black hole 1st law in extended phase space RN-AdS BH ${\rm d}M=T{\rm d}S+V{\rm d}P+\varphi {\rm d}Q$ 

RN-AdS BH with cloud of strings and quintessence ${\rm d}M=T{\rm d}S+V{\rm d}P+\varphi {\rm d}Q-\dfrac{1}{2r_{+}^{3}\omega_{q} }{\rm d}\alpha-\dfrac{r_{+} }{2}{\rm d}a$ 

Table 4. Results for the first thermodynamic law under different conditions in extended phase space.
When testing the validity of the second law of thermodynamics, we found there exists a phase change point that divides the value of dS into positive and negative value regions. The change in the values of the state parameters related to the cloud of strings and quintessence will affect the value of
$ r_+ $ ,$ Q_e $ and dS. As shown in Fig. 2, the parameters do affect the second law of thermodynamics, but the parameters do not determine whether the second law of thermodynamics is ultimately violated. Moreover, the values of da and${\rm d}\alpha$ also affect the values of$ Q_e $ and dS. Furthermore, the WCCC has been proven to be valid all the time for extremal and near-extremal black holes. The validity of the WCCC was tested by checking the sign of the minimum value of$ f(r) $ . Compared with black holes without a cloud of strings and/or quintessence, the minimum value of$ f(r) $ becomes larger after absorbing particles with energy and charge. However, the minimum value of$ f(r) $ remains the original positive and negative. Therefore, neither extremal black holes or near-extremal black holes will be overcharged. Our results are shown in Table 5.1st law Satisfied 2nd law Indefinite WCCC Satisfied for extremal and near-extremal black holes.
Extremal/near-extremal black holes stay extremal/
near-extremal after charged test particle absorptionTable 5. Results for the first and second laws of thermodynamics and the WCCC, tested for a RN-AdS black hole with cloud of strings and quintessence via charged test particle absorption.
In this paper, to satisfy the Smarr relation, the parameters associated with cloud of strings and quintessence are consider as variables. In previous studies, another approach was also taken. The parameters related to the cloud of strings and quintessence were considered as constants and the thermodynamic properties of black holes investigated [58]. When the terms related to a and
$ \alpha $ are turned off, in the extended phase space, the cosmological constant is treated as a variable and the parameters related to the cloud of strings and quintessence are treated as constants. The first law of thermodynamics is:$ {\rm d}M = T{\rm d}S+\varphi {\rm d}Q+V{\rm d}P. $

(80) The variation of the entropy is:
$ {\rm d}S = \frac{2p^{r}}{2T-4Pr_{+}}. $

(81) The denominator of dS has a negative value for an extremal black hole, which means the entropy of the black hole decreases at least in the extreme case. Hence, the second law of thermodynamics is violated.
Furthermore, at
$r_0+{\rm d}r_0$ ,$f(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P, r_{0}+ {\rm d}r_{0})$ is:$\begin{aligned}[b]& f\left(M+{\rm d}M,Q+{\rm d}Q,P+{\rm d}P,r_{0}+{\rm d}r_{0}\right) \\ =& \delta-\frac{2Tp^{r}}{r_{0}\left(T-2Pr_{+}\right)}-\frac{2qQ}{r_{0}}\left(\frac{1}{r_{+}}-\frac{1}{r_{0}}\right)-\frac{8\pi}{3r_{0}}\left(r_{+}^{3}-r_{0}^{3}\right){\rm d}P < 0.\end{aligned} $

(82) Therefore, both extremal and near-extremal black holes cannot be overcharged.
-
We are grateful to Peng Wang, Haitang Yang, Deyou Chen and Xiaobo Guo for useful discussions.
Thermodynamics and overcharging problem in extended phase space of charged AdS black holes with cloud of strings and quintessence under charged particle absorption
- Received Date: 2000-09-09
- Available Online: 2021-02-15
Abstract: The thermodynamics and overcharging problem in RN-AdS black holes with a cloud of strings and quintessence are investigated by the absorption of scalar particles and fermions in extended phase space. The cosmological constant is treated as the pressure of the black hole. The parameters related to quintessence and the cloud of strings are treated as thermodynamic variables. We find that the first law of thermodynamics is satisfied and the second law of thermodynamics is indefinite. Furthermore, we find that near-extremal and extremal black holes cannot be overcharged.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: