Phase transition and quasinormal modes for charged black holes in 4D Einstein-Gauss-Bonnet gravity

During the past few decades, higher order derivative curvature gravities, as effective models of gravity in the low-energy limits of string theories, have attracted considerable interest. Among these higher order derivative curvature gravities, the most widely studied theory is Gauss-Bonnet gravity. In this theory, Einstein's theory is generalized to higher dimensions, and except for the linear dependence of the Riemann tensor, all the characteristics of usual general relativity can be kept [1-4]. Unfortunately, the variation in the Gauss-Bonnet (GB) term is a total derivative in four-dimensional spacetime, which has no contribution to the gravitational dynamics. Therefore, one requires $ D\geqslant 5 $ for non-trivial gravitational dynamics. Recently, Glavan and Lin [5] suggested a novel theory of gravity in four-dimensional spacetime called “4D Einstein-Gauss-Bonnet gravity”(EGB). By rescaling the GB coupling constant $ \alpha \to \alpha/ (D-4) $, with D the number of spacetime dimensions, and defining the four-dimensional theory as the limit $ D\to 4 $, the GB term gives rise to non-trivial dynamics. Furthermore, spherically symmetric black hole solutions were also constructed in their paper. Generalizations to other black holes have also appeared, including charged AdS [6], Lovelock [7, 8], rotating [9, 10], Born-Infeld [11], Bardeen [12], and Hayward [13] black holes. Some important properties of the related 4D EGB black holes have also been studied, such as a spinning test particle in the black hole [14], causality [15], stability, and shadows [16, 17].

In black hole physics, the thermodynamical phase transition of a black hole is always a hot topic. Due to the AdS/CFT correspondence [18-21], a lot of attention has been paid to the phase transitions of black holes in anti-de Sitter (AdS) space. Recently, the thermodynamics of AdS black holes has been studied in the extended phase space where the cosmological constant is treated as the pressure of the system [22, 23]. It has been found that a first order phase transition between small and large black holes is allowed and that the $ P-V $ isotherms are analogous to the van der Waals fluid. There has also been discussion on reentrant phase transitions and more general van der Waals behavior in this direction [24-35]. On the other hand, the quasinormal modes (QNMs) of dynamical perturbations are considered as the characteristic sounds of black holes. The QNMs of the dynamical perturbations are expected to reflect the black hole phase transitions in their surrounding geometries through the frequencies and damping times of the oscillations. In fact, the thermodynamic phase transition of an AdS black hole in dual field theory corresponds to the beginning of instability of a black hole. With a lot of research on this issue, more and more evidence has been found of the connections between the QNMs of black holes and the thermodynamic phase transitions [36-46].

The above-mentioned $ P-V $ phase transition for various black holes in 4D GB gravity has been studied in Refs. [47-54]. Among these studies, the van der Waals-like (SBH/LBH) phase transition has been found in 4D neutral AdS EGB [51, 52], charged AdS [53], and Bardeen AdS black holes [54]. The QNMs of dynamical perturbation for black holes have also been reported for 4D neutral EGB [55, 56], neutral dS [57], and regularized black holes [58]. Motivated by these results and by the importance of AdS/CFT correspondence, the aim of this paper is to study whether the signature of the van der Waals-like SBH/LBH phase transition of charged AdS black holes in 4D EGB gravity can be reflected by dynamical QNM behavior with a massless scalar perturbation.

The paper is organized as follows. In Sec. II, we first discuss the phase transition of (charged) AdS black holes in four-dimensional EGB gravity in the extended phase space. Then, we discuss the QNM frequencies under test scalar field perturbations in Sec. III, and show that the phase transition can be reflected by the QNM frequencies of dynamical perturbations. We end the paper with some closing remarks.

As mentioned above, by rescaling the GB coupling parameter $ \alpha \to \alpha/(D-4) $ and then taking the limit $ D\to 4 $, Glavan and Lin [5] obtained a non-trivial 4D black hole solution. The static and spherically symmetric charged AdS black hole solution in 4D Einstein-Gauss-Bonnet (EGB) gravity is given by [6]

where M and Q are the mass and charge of the black hole, and $ \alpha $ is the Gauss-Bonnet coefficient with dimension $ (length)^2 $. When $ \alpha\to 0 $, $ f(r) $ reduces to the solution of a RN AdS black hole in general relativity. Fernandes has further investigated the related thermodynamic properties of this charged AdS black hole in Ref. [6].

Now we reconsider the thermodynamics of this 4D charged AdS black hole in the so-called extended phase space. In the extended phase space, the cosmological constant $ \Lambda $ is usually regarded as the thermodynamic pressure $ P = -\dfrac{\Lambda}{8\pi} $ in the geometric units $ G_N = \hbar = c = k = 1 $. Then, the mass M, Hawking temperature T and entropy S of 4D charged EGB-AdS black holes in the extended phase space can be written as

From the Hawking temperature (5), the equation of state can be obtained as

As usual, a critical point is determined as the inflection point of P,

Then we can obtain the corresponding critical temperature and critical pressure:

where the subscript “c” represents the critical values of the physical quantities. The critical horizon radius has two values:

When the GB coefficient $ \alpha $ is positive, the critical radius $ r_{c2} $ is always imaginary and the critical radius $ r_{c1} $ is always positive. From Eq. (8) to Eq. (10), we can verify that the critical temperature and pressure stay positive ($ T_{c1}>0 $ and $ P_{c1}>0 $) for arbitrary parameters $ \alpha>0 $. The system admits only one physical critical point ($ r_{c1} $, $ T_{c1} $ and $ P_{c1} $). Therefore we can tell that the system always allows a van der Waals phase transition when $ \alpha $ takes positive values. Now we consider the negative GB coefficient ($ \alpha<0 $). We find that the system allows two positive critical points ($ r_{c1}, T_{c1}, P_{c1} $ and $ r_{c2}, T_{c2}, P_{c2} $) when the charge Q and GB coefficient $ \alpha $ satisfy the constraint $ Q>2\sqrt{-\alpha} $. For example, when $ \alpha = -0.01,\; Q = 0.21 $, we can obtain $ r_{c1} = 0.3256,\; T_{c1} = 0.4017, \;P_{c1} = 0.2459 $ and $ r_{c2} = 0.1965, \;T_{c2} = 1.1205, \;P_{c2} = 1.2539 $. The so-called reentrant phase transition (RPT) will appear under this constraint. If we take the constraint $ 0<Q\leqslant 2\sqrt{-\alpha} $, the system has no physical critical point. In this paper, our main aim is to study whether the signature of a van der Waals-like SBH/LBH phase transition of charged AdS black holes in 4D EGB gravity can be reflected by the dynamical QNM behavior with the massless scalar perturbation. As mentioned above, when $ \alpha $ takes a negative value, the system can only allow the reentrant phase transition, which is hard to be reflected by the dynamical QNM behavior. Therefore we only consider the positive GB coefficient ($ \alpha>0 $) in the subsequent paragraph.

For instance, we can obtain a critical point with $ r_c = 0.4387 $, $ T_c = 0.219 $ and $ P_c = 0.0904 $ by fixing $ \alpha = 0.01 $ and $ Q = 0.1 $. Moreover, in the uncharged case, Eq. (8)-Eq. (10) can be written as:

For example, we can get a critical point with $ r_c = 0.3596 $, $ T_c = 0.2556 $ and $ P_c = 0.1264 $ by fixing $ \alpha = 0.01 $. We plot the $ P-r_+ $ isotherm diagram around the critical temperature $ T_c $ for this charged and uncharged AdS black hole in Fig. 1. The dotted line with $ T>T_c $ corresponds to the “ideal gas” phase behavior, and when $ T<T_c $ the van der Waals-like small/large black hole phase transition will appear.

Figure 1.  (color online) P-$ r_+ $ diagram of charged and uncharged AdS black holes with $ \alpha = 0.01 $.

The thermodynamic phase transition is determined by the behavior of the Gibbs free energy G, which obeys the thermodynamic relation $ G = M-TS $, with

Here $ r_+ = r_+(P,T) $ is understood as a function of the pressure and temperature, via the equation of state (6).

We plot the G-T and P-T figures for the charged and uncharged AdS black hole in Fig. 2 and Fig. 3 respectively. In the left-hand panel of Figs. 2 and 3, the swallow tail behavior of the Gibbs free energy G shows that the system contains a van der Waals-like first order phase transition. The coexistence line in the ($ P,T $) plane is plotted in the right-hand panels of Figs. 2 and 3. This curve shows where the small and large black holes have the same Gibbs free energy and temperature. We find that the coexistence line is very similar to that of the van der Waals fluid. At the end of the coexistence line the small circle indicates the critical point. When $ T<T_c $, the small-large black hole phase transition occurs.

Figure 2.  (color online) The Gibbs free energy G (left) and coexistence line of small/large black hole phase transition (right) with $ \alpha = 0.01 $ and $ Q = 0.1 $.

Figure 3.  (color online) The Gibbs free energy G (left) and coexistence line of small/large uncharged black hole phase transition (right) with $ \alpha=0.01 $ and $ Q=0. $

For the van der Waals liquid-gas system, the liquid-gas structure will undergo a second order phase transition, which does not suddenly change at the critical point $ (V = V_c,\; T = T_c, \;P = P_c) $. This phenomenon can be described by Ehrenfest's description [59, 60], which contains the first and second Ehrenfest equations [61, 62]:

In a genuine second order phase transition, the two equations have to be satisfied simultaneously. Here $ \kappa_T $ and $ \zeta $ represent the isothermal compressibility coefficients and the volume expansion of the system respectively:

Following the method in Ref. [63], we find that Ehrenfest’s equations are satisfied, which means that in the four-dimensional charged/neutral EGB-AdS black hole, this phase transition at the critical point is second order. It has the same nature as the liquid-gas phase transition at the critical point.

In order to reflect the thermodynamical stabilities in dynamical perturbations, we can study the evolution of a massless scalar field perturbation around this 4-dimensional EGB-AdS black hole.

A massless scalar field, $ \Phi(r,t,\Omega) = \phi(r){\rm e}^{-{\rm i}\omega t}Y_{lm}(\Omega) $, obeys the Klein-Gordon equation:

Then the radial equation for the function $ \phi(r) $ is obtained as

where $ \omega $ are complex numbers $ \omega = \omega_r + {\rm i}\omega_{im} $, corresponding to the QNM frequencies of the oscillations describing the perturbation.

Near the horizon $ r_+ $, we can impose the boundary condition of the scalar field, $ \phi(r)\to (r-r_+)^\frac{{\rm i}\omega}{4\pi T} $. Then we define $ \phi(r) $ as $\varphi(r){\rm exp}\left[-{\rm i}\displaystyle\int\dfrac{\omega}{f(r)}{\rm d}r\right]$. Where ${\rm exp}\left[-{\rm i}\displaystyle\int\dfrac{\omega}{f(r)}{\rm d}r\right]$ asymptotically approaches the ingoing wave near the horizon, we can rewrite Eq. (20) as

For Eq. (21), we have $ \varphi(r) = 1 $ in the limit of $ r\rightarrow r_+ $. At the AdS boundary $ (r\rightarrow\infty) $, we need $ \varphi(r) = 0 $. Under these boundary conditions, we will numerically solve Eq. (21) to find the QNM frequencies by adopting the shooting method.

In the left-hand panel of Fig. 4, we plot the T-$r_+ $ diagram of charged AdS black holes with fixed pressure $ P = 0.06< P_c = 0.219 $ in four-dimensional EGB gravity. When the pressure $ P<P_c $, there is an inflection point and the behavior of the system is similar to a van der Waals system. The critical point can be obtained from

Figure 4.  (color online) T-$r_+ $ (left) and G-T (right) diagrams of 4D EGB AdS black holes with $\alpha = 0.01, \;Q = 0.1$ and $ P\simeq0.06 $.

The right-hand panel of Fig. 4 shows the behavior of the Gibbs free energy. In this figure we mark the crossing point “5” between the solid line as “1-5” and and the solid line as “4-5”. The crossing point means the Gibbs free energy G and pressure P coincide for small and large black holes. In the left-hand panel of Fig. 4, we separate the point “5” into “L5” and “R5” for the same Gibbs free energy and the chosen $ T_*\approx0.18946 $, which represents where the small and large black hole can coexist. Moreover, between points “1-5” or “1-L5” the marked physical phase corresponds to the small black hole, while between points “5-4” or “R5-4” the indicated physical phase denotes the large black hole.

Table 1 lists the QNM frequencies of massless scalar perturbation ($ l = 0 $ and $ 1 $) for small and large charged black holes near the SBH/LBH phase transition point. When the temperature decreases from the phase transition temperature $ T_* $, the radius of the black hole becomes smaller and smaller, which corresponds to the small black hole phase. We find that the absolute values of the imaginary part of QNM frequencies decrease in this process, while the real parts of the frequencies change very little. On the other hand, the black hole will get larger when the temperature for the large black hole phase increases from the phase transition temperature $ T_* $. We also see that both the real part and the absolute value of the imaginary part increase, which means that despite the massless scalar perturbation outside the black hole oscillates even more, but decays faster. These results are similar to the discussions reported in Refs. [45, 46]. Figures 5 and 6 respectively illustrate the QNM frequencies with $ l = 0 $ and $ l = 1 $ for small and large black hole phases. The arrows indicate the direction of increasing black hole size.

T	$ r_+ $	$ \omega\; (l=0) $	$ \omega\; (l=1) $
0.1855	0.24719	1.67171-0.342286I	3.30238-0.488428I
0.186	0.24833	1.67141-0.343580I	3.30097-0.491701I
0.187	0.25072	1.67077-0.346294I	3.29793-0.498354I
0.188	0.25325	1.67009-0.349273I	3.29450-0.505050I
0.189	0.25594	1.66937-0.352404I	3.29115-0.512268I
0.190	0.91129	2.72028-0.982813I	4.02092-0.993442I
0.191	0.93516	2.74446-0.992160I	4.05526-1.003787I
0.192	0.95733	2.76751-1.001339I	4.08825-1.013420I
0.193	0.97819	2.78981-1.010033I	4.11994-1.022668I
0.194	0.99800	2.81150-1.018480I	4.15075-1.031497I

Table 1.  The QNM frequencies of massless scalar perturbation with the change of black hole temperature, with $ \alpha=0.01 $ and $ Q=0.1 $. The upper part, above the horizontal line, is for the small black hole phase, while the lower part is for the large black hole phase.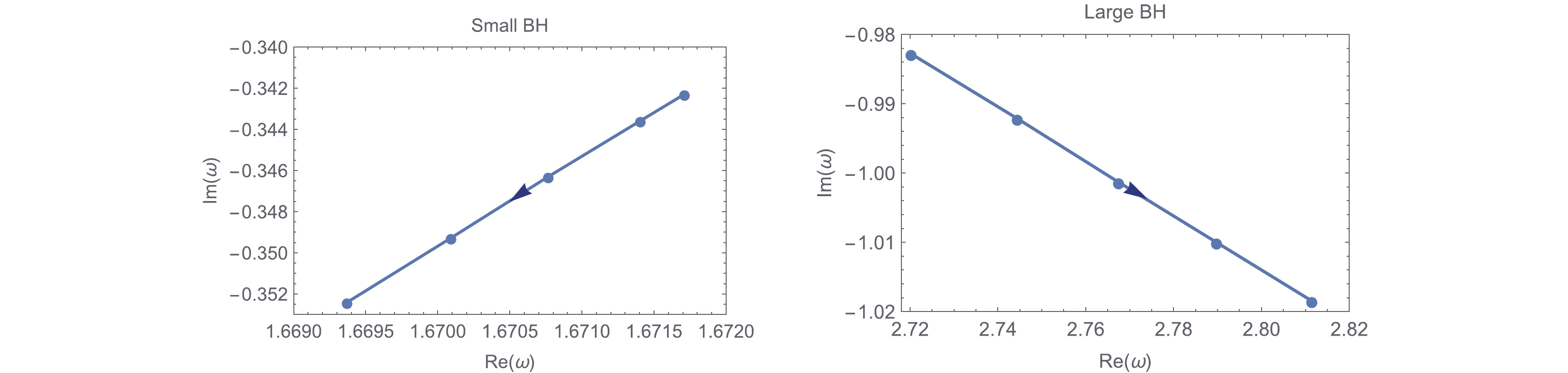

Figure 5.  (color online) The behavior of QNMs for large and small black holes in the complex-$ \omega $ with $ Q = 0.1 $ and $ l = 0 $. The arrow indicates the increase of black hole horizon.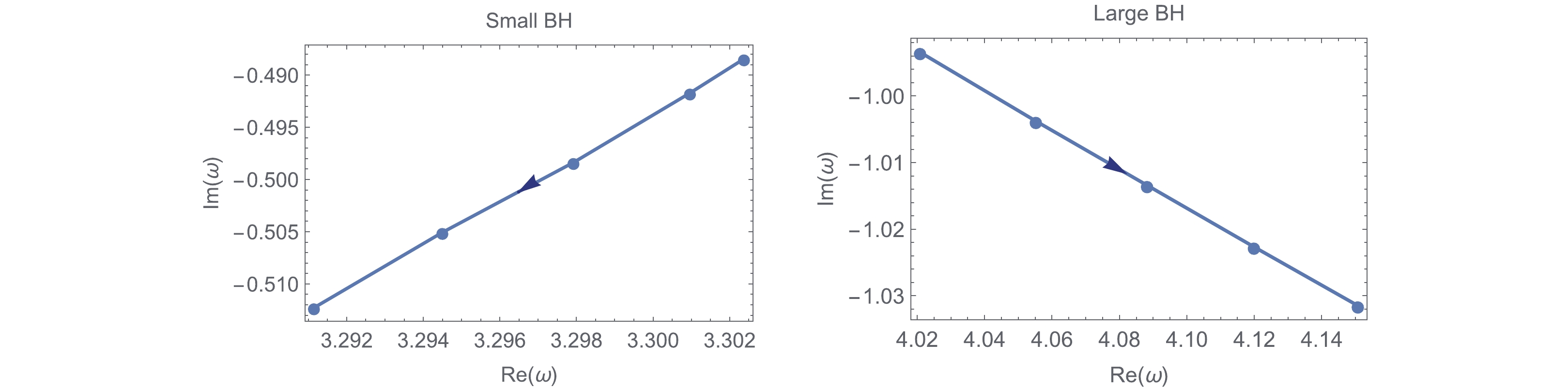

Figure 6.  (color online) The behavior of QNMs for large and small black holes in the complex-$ \omega $ with $ Q = 0.1 $ and $ l = 1 $. The arrow indicates the increase of black hole horizon.

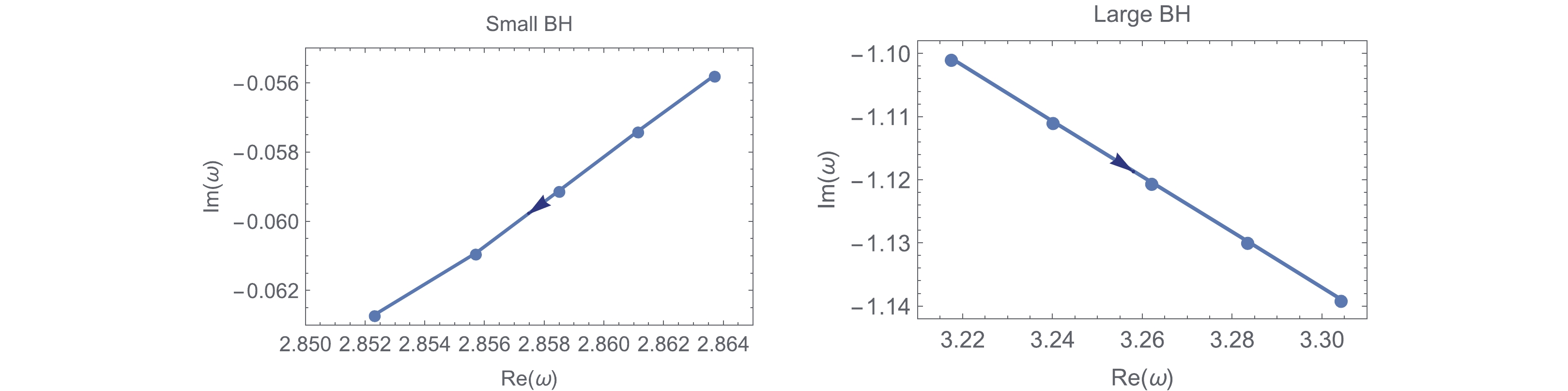
Moreover, at the critical position $ P = P_c $, with $ P_c\simeq0.06 $, a second-order phase transition occurs. The QNM frequencies of the small and large black hole phases (for $ l = 0 $ and $ l = 1 $) are shown in Fig. 7. We can see that at the critical point the QNM frequencies of these two black hole phases have the same behavior when the black hole horizon increases.

Figure 7.  (color online) The behavior of QNM frequencies for large (dashed) and small (solid) black holes in the complex-$ \omega $ with $ Q = 0.1 $. The arrow indicates the increase of black hole horizon.

In the neutral case, we can obtain similar T-$r_+ $ and G-T diagrams to the charged case. For instance, the coexistence temperature $ T_* $ equals $ 0.21860 $ when the pressure $ P = 0.08<P_c = 0.1264 $. The QNM frequencies of massless scalar perturbation (for $ l = 0 $ and $ 1 $) around small and large uncharged black holes for first order SBH/LBH phase transitions are listed in Table 2, showing a similar behavior to the charged case. The QNM frequencies with $ l = 0 $ and $ l = 1 $ for small and large uncharged black hole phases are shown in Fig. 8 and Fig. 9 respectively. Moreover, at the critical position, the corresponding QNM frequencies of the small and large uncharged black hole phases are also qualitatively similar to the charged case.

T	$ r_+ $	$ \omega\; (l=0) $	$ \omega\; (l=1) $
0.214	0.18938	1.97357-0.340401I	2.86372-0.0557742I
0.215	0.19088	1.97273-0.342787I	2.86116-0.0573858I
0.216	0.19245	1.97185-0.345297I	2.85852-0.0591034I
0.217	0.19408	1.97093-0.347917I	2.85572-0.0609143I
0.218	0.19579	1.96997-0.350686I	2.85233-0.0626936I
0.219	0.79874	2.42426-1.100808I	3.21754-1.100784I
0.220	0.81586	2.44275-1.111345I	3.24017-1.110794I
0.221	0.83201	2.46057-1.121425I	3.26214-1.120424I
0.222	0.84739	2.47780-1.131115I	3.28349-1.129773I
0.223	0.86211	2.49461-1.140502I	3.30429-1.138959I

Table 2.  The QNM frequencies of massless scalar perturbation with the change of black hole temperature, with $ \alpha=0.01 $ and $ Q=0 $. The upper part, above the horizontal line, is for the small black hole phase, while the lower part is for the large black hole phase.

Figure 8.  (color online) The behavior of QNMs for large and small black holes in the complex-$ \omega $ with $ Q = 0 $. The arrow indicates the increase of black hole horizon.$ Q = 0, \;l = 0 $.

Figure 9.  (color online) The behavior of QNMs for large and small black holes in the complex-$ \omega $ with $ Q = 0 $. The arrow indicates the increase of black hole horizon.$ Q = 0,\; l = 1 $.

In four-dimensional Einstein-Gauss-Bonnet gravity, we have studied the P-V criticality and phase transition of AdS black holes in the extended phase space. We have demonstrated that the system allows two physical critical points corresponding to the reentrant phase transition when the GB coefficient is negative and the charge satisfies the constraint $ Q>2\sqrt{-\alpha} $. For arbitrary positive parameter $ \alpha $ and Q, the van der Waals-like SBH/LBH phase transition always happens both in the charged and neutral cases. We further calculated the QNMs of massless scalar perturbations in four situations (charged/uncharged and $ l = 0 $ or $ 1 $). These results reveal that the slopes of the QNM frequency change are drastically different in the small and large black hole phases as the horizon radius $ r_+ $ increases, when the van der Waals-like SBH/LBH phase transition happens in the extended phase space. This clearly demonstrates the signature of the phase transition between small and large black holes. In addition, at the critical isobaric phase transitions, the QNM frequencies for both small and large black holes share the same behavior, showing that QNMs are not appropriate to probe the black hole phase transition in the second order.

This is one more example which shows that QNMs can provide a dynamical physical probe of the thermodynamic phase transition of black holes in 4D EGB gravity, since QNMs are expected to be detected and are of strong astrophysical interest. The ability of QNMs to reflect the thermodynamic phase transition is interesting, and is expected to give an observational signature of the thermodynamic phase transition.