-
One of the primary objectives of relativistic heavy-ion collision experiments is to unravel the Quantum Chromodynamics (QCD) phase structure. At low
$ \mu_{B} $ , the lattice QCD calculations predict a smooth crossover from hadronic to quark-gluon degrees of freedom [1]. QCD-based models suggest that the transition from Quark-Gluon Plasma (QGP) to hadronic matter is of the first order at large baryon chemical potentials [2-4]. The endpoint of the first-order phase transition line towards low$ \mu_{B} $ is the so-called QCD Critical Point (CP). Although numerous studies have been conducted both theoretically [5-14] and experimentally [15-20], the location of the CP remains unsettled. The experimental validation of the CP would be a breakthrough for the exploration of the QCD phase structure. For this reason, the Beam Energy Scan program at RHIC has been operating since 2010 to map out the phase diagram as a function of baryon chemical potential ($ \mu_{B} $ ) and temperature ($ T $ ) [21].For heavy-ion collisions, one of the foremost methods for the critical point search is measurement of the higher-order cumulants of conserved quantities, such as the net-baryon, net-charge, and net-strangeness numbers. Theoretically, it is expected that the higher-order cumulants of conserved charges will be sensitive to the correlation length (
$ \xi $ ) of the system, which will diverge near the critical point [22-26]. As a result, non-monotonic variation of higher-order cumulant ratios from their baseline values is expected in existence of the critical point. Furthermore, theoretical calculation suggests that the ratio of the sixth and second order cumulants ($ C_6/C_2 $ ) is sensitive to the phase transition and that it will become negative when the chemical freeze-out is close to the chiral phase transition boundary [27, 28]. Thus, the sixth order fluctuation could serve as a sensitive probe of the signature of the QCD phase transition [29]. Experimentally, due to the detection inefficiency of neutral particles and multi-strange baryons, the net-proton and net-kaon are used as experimental proxies of the net-baryon and net-strangeness, respectively. In the last few years, the measurement of second, third, and fourth order cumulants of net-charge [17, 30], net-proton [15, 16, 20, 31, 32], and net-kaon [18] multiplicity distributions have been conducted by the STAR and PHENIX experiments in the first phase of the beam energy scan (BES-I, 2010-2017) program at the Relativistic Heavy Ion Collider (RHIC). The measurement of the second order mixed cumulant has also been reported [33]. Recently, the HADES experiment published the proton number fluctuations in fixed target Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 2.4 GeV [34]. Within current statistical uncertainties, the cumulants of the net-charge and net-kaon distributions are found to have either modest or monotonic dependence on the beam energy, whereas the fourth order cumulant ratio ($ C_4/C_2 $ ) of the net-proton distributions exhibits non-monotonic behaviors as a function of$ \sqrt {{s_{{{NN}}}}}\; $ , with a 3.1$ \sigma $ significance [20]. To confirm these non-monotonic behaviors, it is important to perform high precision fluctuation measurements at higher$\mu_B$ regions. To fulfill this goal, RHIC started the second phase of the beam energy scan program (BES-II) in 2018, focusing on collision energies below 27 GeV. From 2018 to 2020, the STAR experiment collected data on high statistics Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 9.2, 11.5, 14.6, 19.6, and 27 GeV (collider mode) and$ \sqrt {{s_{{{NN}}}}}\; $ = 3.0 – 7.7 GeV (fixed target mode). Conversely, to understand the various background contributions from different physics processes, model (without CP) studies are important in that they can provide baselines for the experimental search of the QCD critical point. These background contributions may arise from the limited detector acceptance/efficiency, initial volume fluctuation, autocorrelation and centrality resolution, centrality width, baryon number conservation, and resonance decay. Some of these effects have been studied previously [35-44] but remain to be understood properly before solid physics conclusions can be attained.In this paper, we studied the effects of centrality fluctuation and deuteron formation on the proton cumulant and correlation functions up to the sixth order in the most central Au+Au collisions at
$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV using the JAM model. The paper is organized as follows. In Sec. II, we briefly discuss the JAM model used for this analysis. In Sec. III, we introduce the observables used for the present study. In Sec. IV, we present the cumulants up to the sixth order of the proton multiplicity distribution at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV with the JAM model and discuss the effect of centrality fluctuation and deuteron formation. The article is summarised in Sec. V. -
JAM (Jet AA Microscopic Transport Model) is a non-equilibrium microscopic transport model contracted on resonance and string degrees of freedom [45, 46]. In the JAM model, hadrons and their excited states have explicit space and time propagation by the cascade method. Inelastic hadron-hadron collisions with resonance are applied at low energy, whereas the string picture and hard parton-parton scattering are modeled at intermediate and high-energy, respectively. The nuclear mean-field is applied based on the simplified version of the relativistic quantum molecular dynamics (RQMD) approach [47]. Previously, the JAM model has been used to compute several cumulants and to study different effects on particle number fluctuations in heavy-ion collision phenomenology [42, 48]. Greater detail about the JAM model can be found in Refs. [46, 48, 49]. In this study, we analyzed around 25 million central events for the Au+Au system at
$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV generated using the JAM model with a nuclear mean field. Using the simulated events, we calculated up to sixth order cumulants and correlation functions of event-by-event proton multiplicity distributions. The light nuclei are not generated directly in the JAM model; rather, they are produced with an afterburner code along the coalescence of nucleons with the phase space obtained from the JAM model [50]. The coalescence process is then treated stochastically. The phase space density of the nucleon is obtained when the simulation process is stopped at a certain time (50 fm/c in our simulation). The coalescence conditions are constrained by the relative distance ($ \Delta R $ ) and relative momentum ($ \Delta P $ ) in the two body center of mass frame. When the relative distance and momentum of any two nucleons are less than the given parameters ($ R_{0},P_{0} $ ), the light nuclei are considered to be formed [50-53]. Based on the charge rms radius of the wave function for deuterons, we fixed the coalescence parameters of the deuteron at$ R_0 = 4 $ fm and$ P_0 = 0.3 $ GeV/c. -
Higher-order multiplicity fluctuations can be characterized by different order cumulants (
$ C_{n} $ ). The$ n^{\rm th} $ order cumulant is expressed via a generating function [54] as$ C_{n} = \frac{\partial^{n}}{\partial \alpha^{n}} K(\alpha)|_{\alpha = 0}, $

(1) where
$ K(\alpha) $ is the cumulant generating function, which is logarithm of the moment generating function ($ K(\alpha) = $ $ \ln(M(\alpha)) $ ). From event-by-event multiplicity distributions, the various order cumulants can be expressed in terms of the central moment as follows:$ C_{1} = \langle N \rangle, $

(2) $ C_{2} = \langle (\delta N)^{2} \rangle, $

(3) $ C_{3} = \langle (\delta N)^{3} \rangle, $

(4) $ C_{4} = \langle (\delta N)^{4} \rangle - 3\langle (\delta N)^{2} \rangle^{2}, $

(5) $ C_{5} = \langle (\delta N)^{5} \rangle - 10\langle (\delta N)^{2} \rangle \langle (\delta N)^{3} \rangle, $

(6) $ \begin{aligned}[b] C_{6} = & \langle (\delta N)^{6} \rangle - 15\langle (\delta N)^{4} \rangle \langle (\delta N)^{2} \rangle - 10\langle (\delta N)^{3} \rangle^{2}\\& + 30\langle (\delta N)^{2} \rangle^{3}, \end{aligned} $

(7) where
$ N $ is the event-by-event particle number and$ \delta N = N - \langle N \rangle $ represents the deviation of$ N $ from its mean.$ \left\langle \ldots \right\rangle $ represents an average over the event sample. The$ n $ -th order cumulant$ C_{n} $ is connected to the thermodynamic number susceptibilities of a system at thermal and chemical equilibrium:$ C_{n} = VT^{3} \chi_{n}, $

(8) where
$ V $ is the system volume, which is difficult to measure in heavy-ion collisions. To cancel out the volume dependence, different order cumulant ratios are measured as experimental observables, which are related to the ratios of thermodynamic susceptibilities [24, 55]:$ \begin{aligned}[b] \frac{C_{2}}{C_{1}} =& \frac{\chi_{2}}{\chi_{1}} = \frac{\sigma^{2}}{M},\;\;\;\; \frac{C_{3}}{C_{2}} = \frac{\chi_{3}}{\chi_{2}} = S\sigma, \\ \; \frac{C_{4}}{C_{2}} =& \frac{\chi_{4}}{\chi_{2}} = \kappa\sigma^{2},\; \;\;\;\frac{C_{5}}{C_{1}} = \frac{\chi_{5}}{\chi_{1}},\;\;\;\; \frac{C_{6}}{C_{2}} = \frac{\chi_{6}}{\chi_{2}}, \end{aligned} $

(9) where
$ M $ ,$ \sigma $ ,$ S $ , and$ \kappa $ are the mean, sigma, skewness, and kurtosis of the multiplicity distribution, respectively. Moreover, the multi-particle correlation function$ \kappa_{n} $ (or factorial cumulant) can also be expressed in terms of single particle cumulants [56, 57]:$ \kappa_{1} = C_{1}, $

(10) $ \kappa_{2} = -C_{1} + C_{2}, $

(11) $ \kappa_{3} = 2C_{1} - 3C_{2} + C_{3}, $

(12) $ \kappa_{4} = -6C_{1} + 11C_{2} - 6C_{3} + C_{4}, $

(13) $ \kappa_{5} = 24C_{1} - 50C_{2} + 35C_{3} - 10C_{4} + C_{5}, $

(14) $ \begin{aligned}[b] \kappa_{6} = & -120C_{1} + 274C_{2} - 225C_{3} + 85C_{4}\\& - 15C_{5} + C_{6}. \end{aligned} $

(15) For the Poisson distribution, the higher-order correlation functions
$ \kappa_{n} (n > 2) $ are equal to zero. Thus,$ \kappa_{n} $ can also be used to quantify deviations from the Poisson distribution.In this study, we analyzed approximately 25 million central events (b < 3 fm) for an Au+Au system generated using the JAM model. We studied the effect of centrality fluctuation and deuteron formation up to the sixth order cumulant of the proton multiplicity distribution in different acceptance windows.
In heavy-ion collision experiments, the collision centralities are usually defined by using charged particle multiplicities (
$ N_{\rm ch} $ ) around mid-rapidity in which the smallest centrality bin is a single multiplicity value. To avoid autocorrelation effects, protons are excluded from$ N_{\rm ch} $ within$ |\eta| < 1 $ for centrality selection. This centrality definition is called Refmult3 [16]. For better statistical accuracy, the cumulant values are reported in wider centrality bins. Therefore, the centrality bin width correction (CBWC) is necessary to suppress volume fluctuations in a wide centrality bin [35]. Conventionally, the CBWC is performed by calculating cumulants in each Refmult3 bin [39]. However, for such a low energy due to the greatly reduced final state particle multiplicity, even a single multiplicity bin may correspond to a wider initial volume fluctuation. We discuss this effect below by comparing the results of the Refmult3-CBWC with the impact parameter (b) CBWC. In CBWC techniques, as shown in Eq. (16), the nth order cumulants ($ C_n $ ) are first calculated in each bin$ i $ and then are weighted by the number of events in each bin ($ n_{i} $ ),$ C_n^{i} = \frac{\sum\nolimits_{i}n_{i}C_n^{i}}{\sum\nolimits_{i}n_{i}}, $

(16) where
$ C_n^{i} $ is the nth order cumulant in the i-th bin (either in the b = 0.1 fm bin or in each Refmult3 bin) and ($ \sum\nolimits_{i}n_{i} $ ) represents the total number of events. The uncertainties reported in the results are statistical due to the finite size of the event sample, and they are obtained using a standard error propagation method called the Delta theorem [58-60]. Generally, the uncertainty on cumulant measurement is inversely proportional to the number of events and proportional to the certain power of the width of the proton multiplicity distributions. -
We start by discussing the proton
$ {\rm d}N/{\rm d}y $ distribution. Figure 1 shows the$ {\rm d}N/{\rm d}y $ distribution of protons and deuterons in the most central Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV in the JAM model. The central Au+Au collisions are chosen with an impact parameter of less than 3 fm. The deuteron formation probability is proportional to the initial proton yield in that event according to coalescence after the kinetic freeze-out [61-63]; i.e.,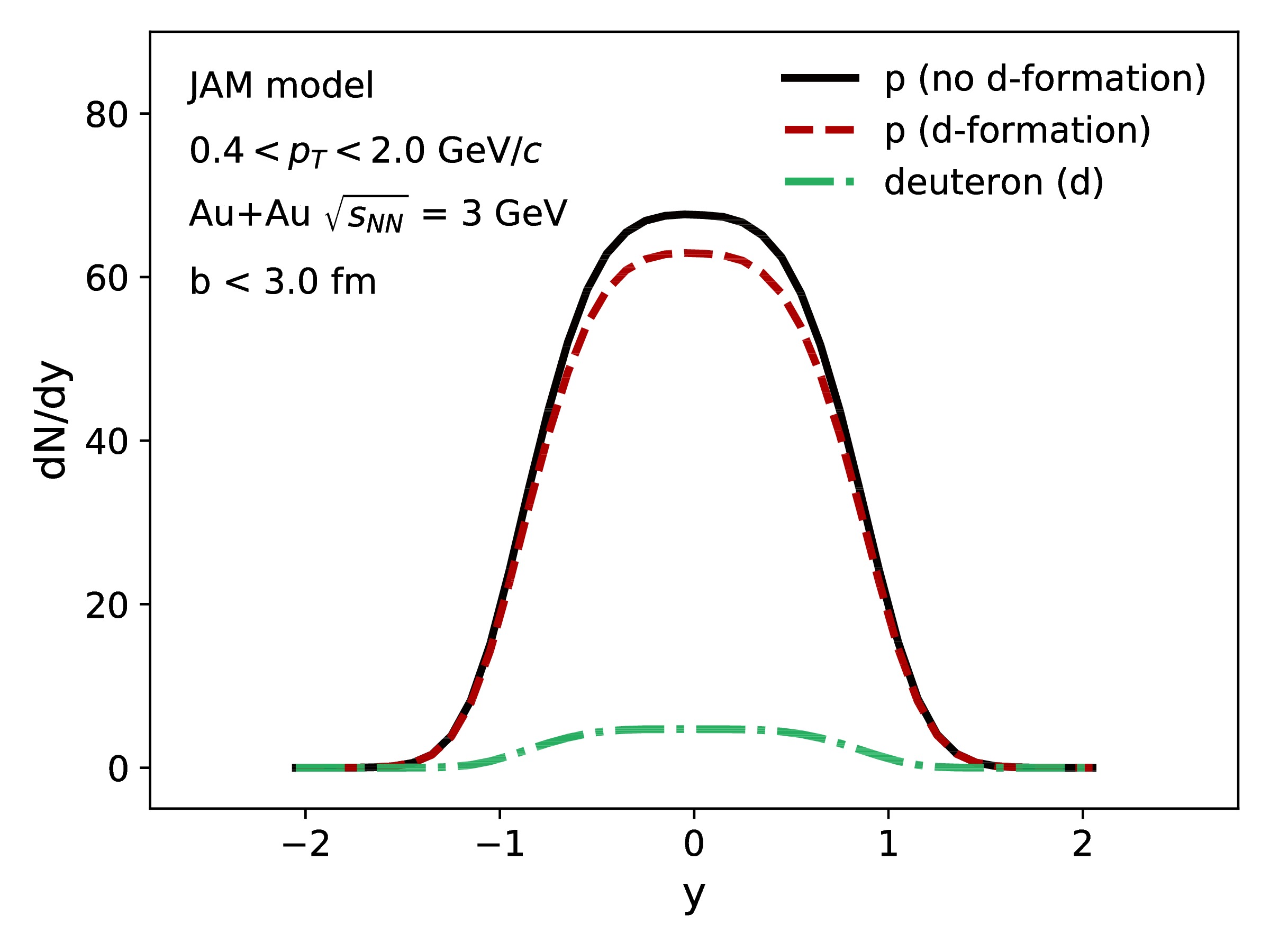
Figure 1. (color online) Rapidity (
${\rm d}N/{\rm d}y$ ) distributions for protons with and without deuteron formation in the most central (b < 3 fm) Au+Au systems at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV in the JAM model.$ \lambda_{d} = Bn_{p_{i}}^{2}, $

(17) where we assume that the neutron yield is proportional to the proton yield in each event. However, the additional checks have been performed assuming that the neutron and protons are uncorrelated [63].
$ B $ and$ n_{p_{i}} $ represent the coalescence parameter and initial proton number, respectively. The above assumption is valid where the volume fluctuation is minimal [64]. The initial proton number (p without d-formation) can thus be approximated by adding the observed proton and deuteron numbers as shown in Fig. 1 and also discussed in an earlier work [64],$ \frac{{\rm d}N_{p_{i}}}{{\rm d}y} = n_{p_{i}} = n_{p} + n_{d}. $

(18) Figure 2 shows the event-by-event proton number distribution in the most central Au+Au collision at
$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV with and without deuteron formation in the JAM model. The distributions are obtained by counting protons within$ 0.4<p_{T}<2.0 $ GeV/c, and the distributions presented in Fig. 2 are not corrected by centrality bin width as described in previous section.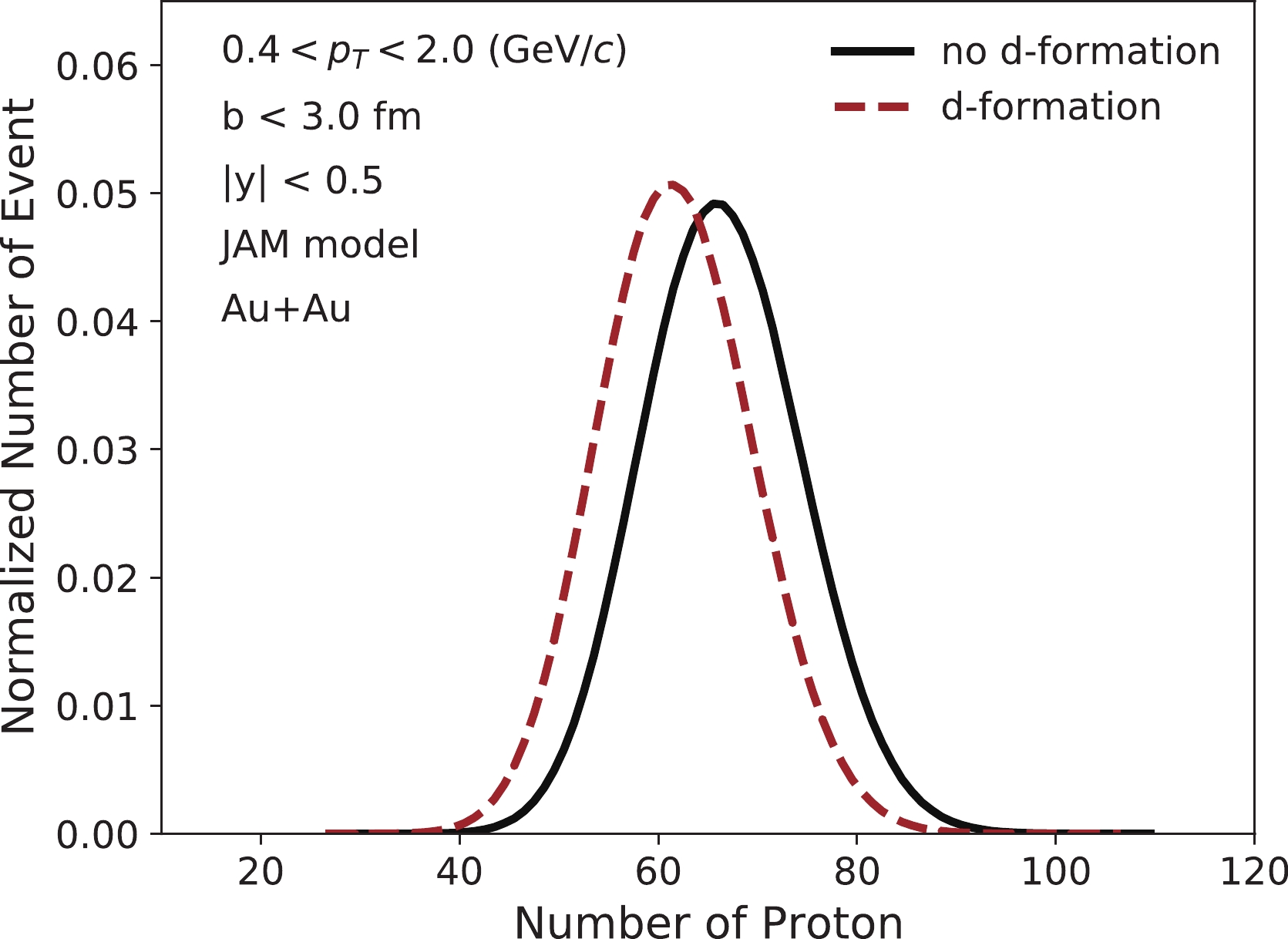
Figure 2. (color online) Normalized event-by-event proton multiplicity distributions in the most central (b < 3 fm) Au+Au collisions at
$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV with and without deuteron formation in the JAM model.We first discuss the validity of centrality bin width correction using Refmult3 at
$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. As we discussed in the previous section, at very low energies, even a single multiplicity bin corresponds to a wide initial volume fluctuation, as demonstrated in Fig. 3. Figure 3(a) shows the two-dimensional correlation plot between Refmult3 and the impact parameter at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. We can observe that at 3 GeV, no strong negative correlation is found between charged particles at the mid-rapidity region (Refmult3) and the impact parameter in contrast to observations for higher energies [39]. This indicates that at low energies the charged particles in the mid-rapidity region are insensitive to the initial collision geometry and have poor centrality resolution. Figure 3(b) shows the b-distributions for two different fixed Refmult3 values, 67 (the peak value of the Refmult3 distribution with maximum weight) and 60. We can clearly see that even a fixed Refmult3 corresponds to all the impact parameter values from 0-3 fm with a weight that is similar to that of the unbiased b-distribution.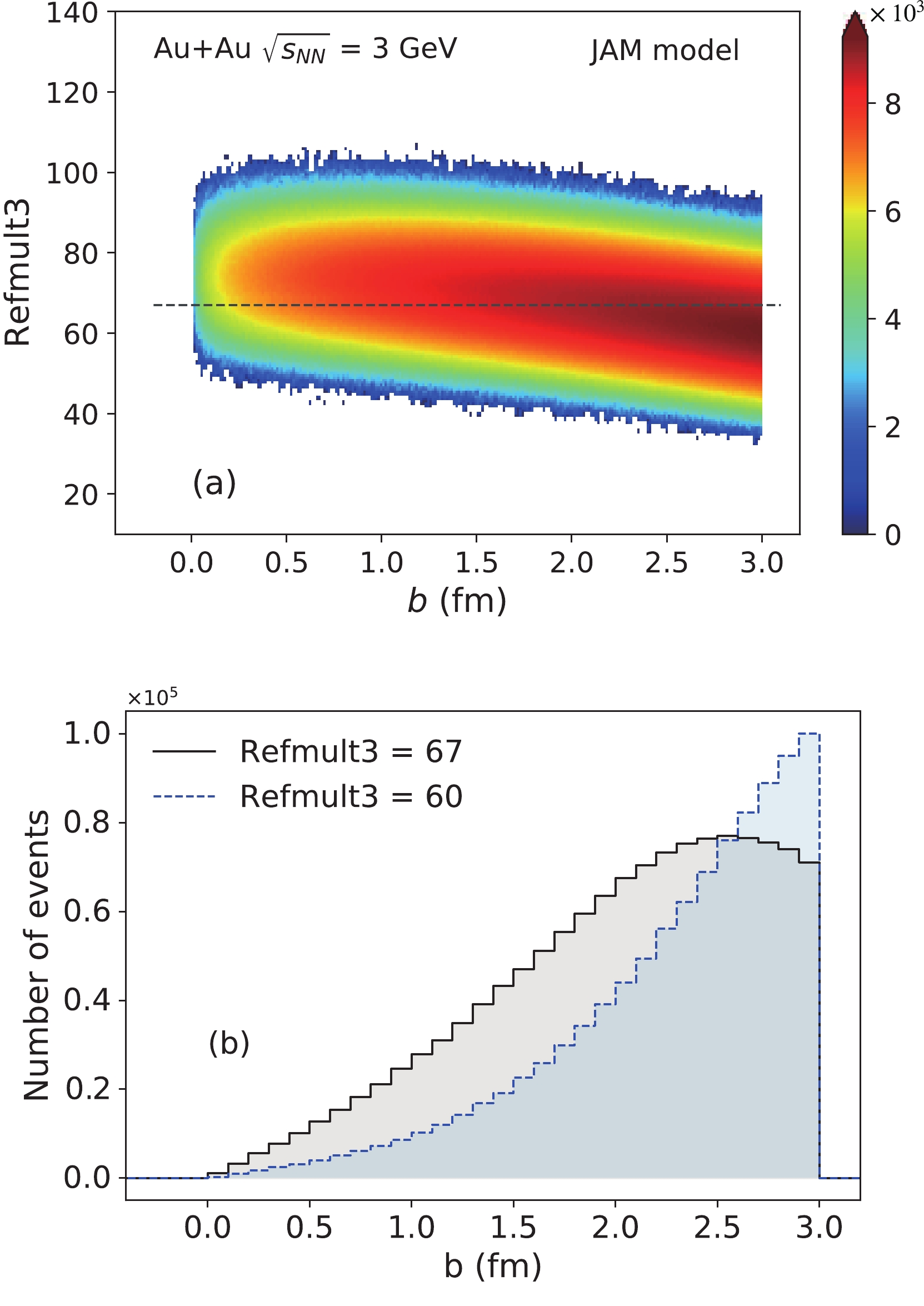
Figure 3. (color online) (a) Correlation between Refmult3 (charged particles excluding protons within
$|\eta|$ < 1) and the impact parameter in top central (b< 3 fm) Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. (b) Impact parameter distributions for fixed Refmult3 values.Figures 4 and 5 show the rapidity acceptance dependence for the cumulants and cumulant ratios of the proton multiplicity distributions for two different centrality definitions in Au+Au collisions at
$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV from the JAM model simulation. The results are also compared with the cumulants calculated without the CBWC. We observed that both the cumulants and cumulant ratios obtained from the Refmult3-CBWC have a large deviation from the impact parameter CBWC at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. We used 0.1 fm bins for the impact parameter based CBWC. As for the rapidity acceptance dependence, we also studied the CBWC effect with different tranverse momentum acceptance for the cumulants and cumulant ratios in Figs. 6 and 7, respectively. For this study, we fixed the rapidity acceptance to$ |y|<0.5 $ and the lower limit of transverse momentum to$ {p_{{T}_{\rm min}}} $ = 0.4 GeV/c. We varied the upper limit of transverse momentum ($ {p_{{T}_{\rm max}}} $ ) acceptance up to 2.4 GeV/c. We observed that the cumulants are saturated after$ {p_{{T}_{max}}}\sim $ 1.5-1.6 GeV/c due to the saturation of the proton yield. Based on this comparison, we can conclude that unlike at higher collision energies, the CBWC using charged-particle multiplicity bins cannot effectively suppress initial volume fluctuations in Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV [39]. New methods for classifying events at low energy heavy-ion collisions are therefore needed to determine the collision centralities. Recently, in Refs. [65, 66], machine learning has been proposed to determine the collision centrality with high resolution in heavy-ion collisions. This might be able to address the centrality fluctuation effect on cumulant analysis at low energies. In the subsequent sections, we use the b-CBWC to understand the effect of deuteron formation on the proton number cumulant and correlation functions.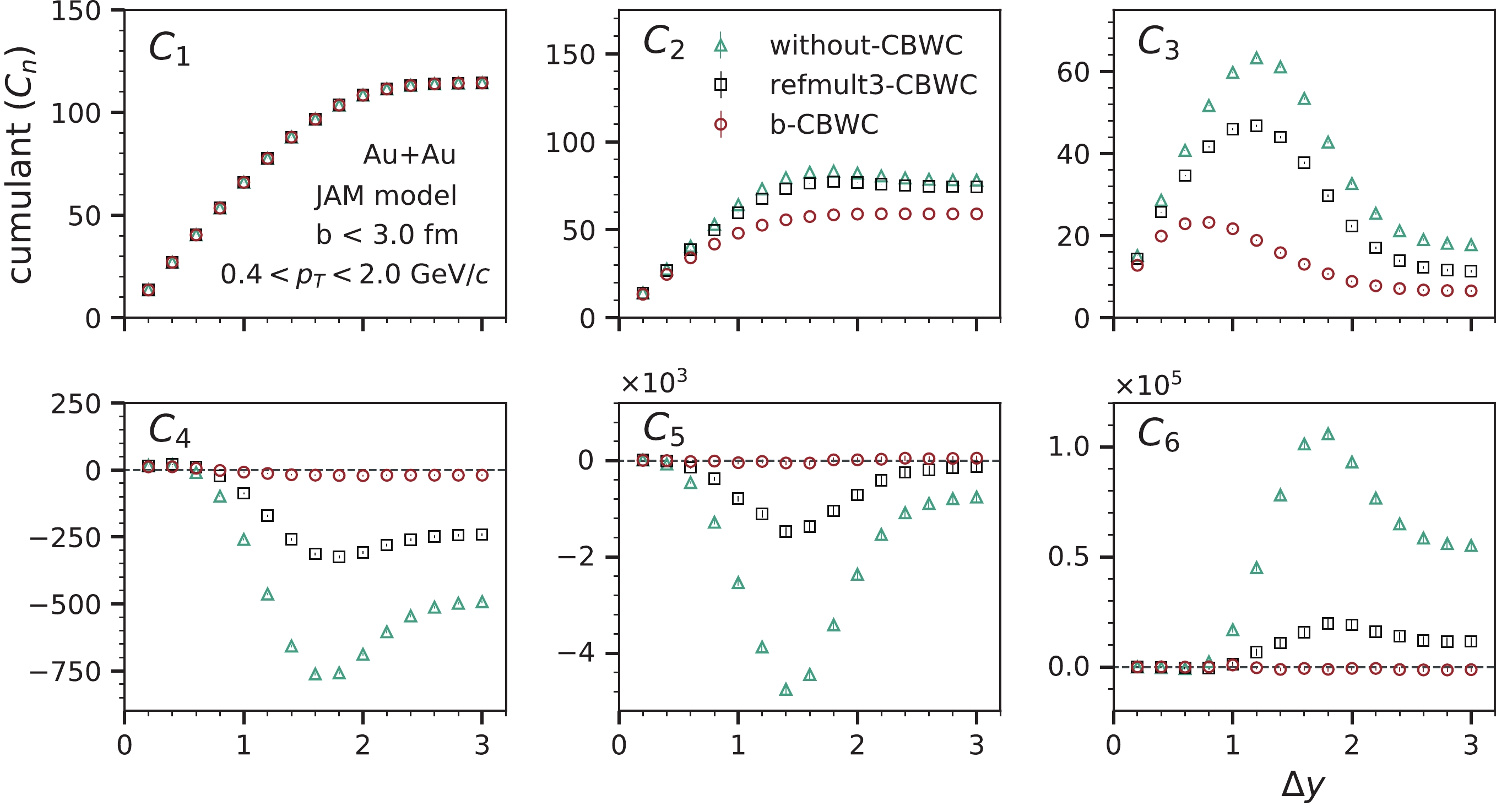
Figure 4. (color online) Rapidity acceptance dependence cumulants of proton multiplicity distributions in top central (
$ b $ < 3 fm) Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. The centrality bin width correction is performed with (a) each Refmult3-bin (black squares) and (b) a 0.1 fm impact parameter bin (red circles). The results are also compared with the cumulants calculated without the CBWC (green triangles).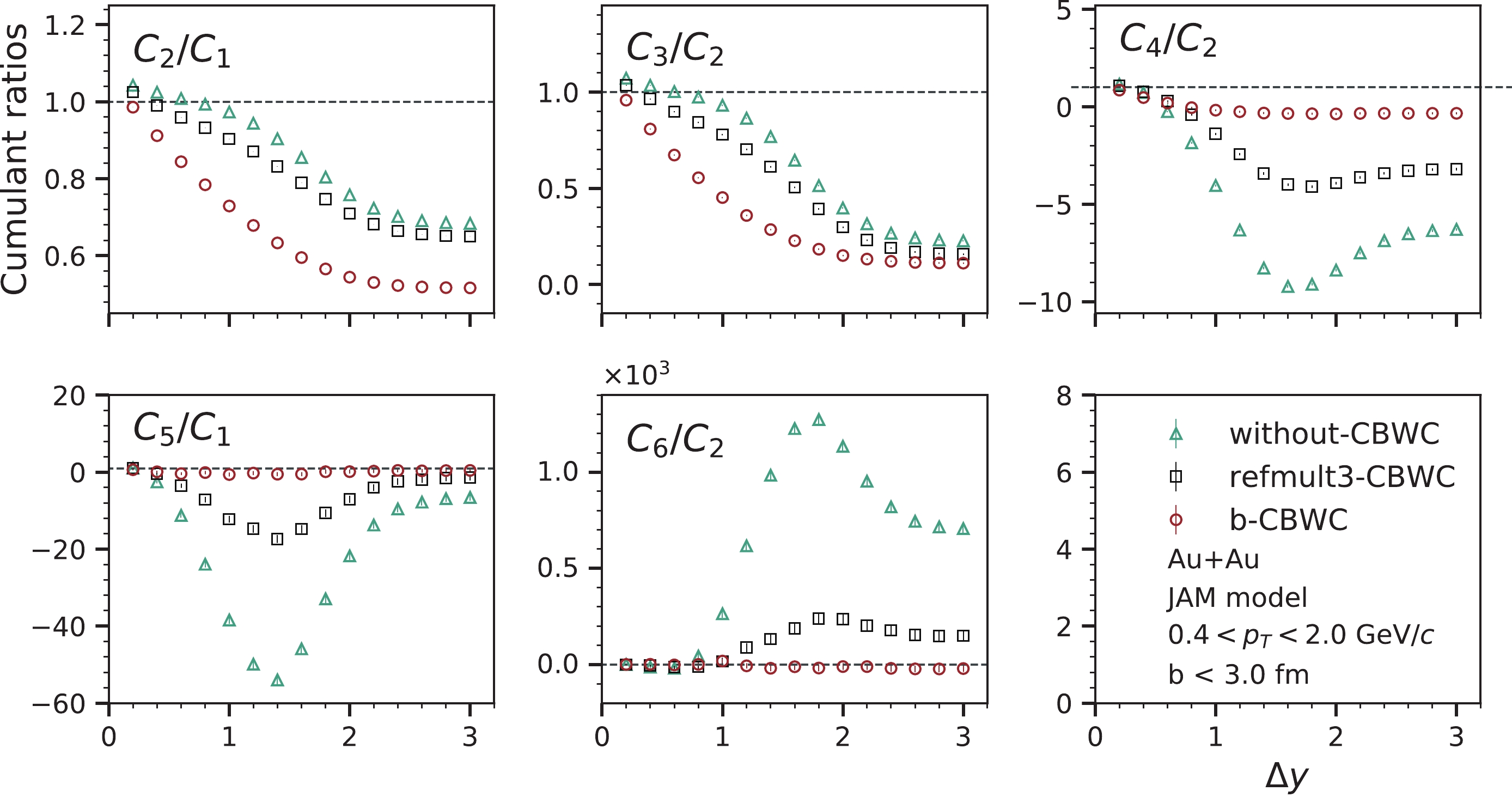
Figure 5. (color online) Rapidity acceptance dependence cumulant ratios of proton multiplicity distributions in top central Au+Au collisions at
$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. The centrality bin width correction is performed with (a) each Refmult3-bin (black squares) and (b) a 0.1 fm impact parameter bin (red circles). The results are also compared with the cumulants calculated without the CBWC (green triangles).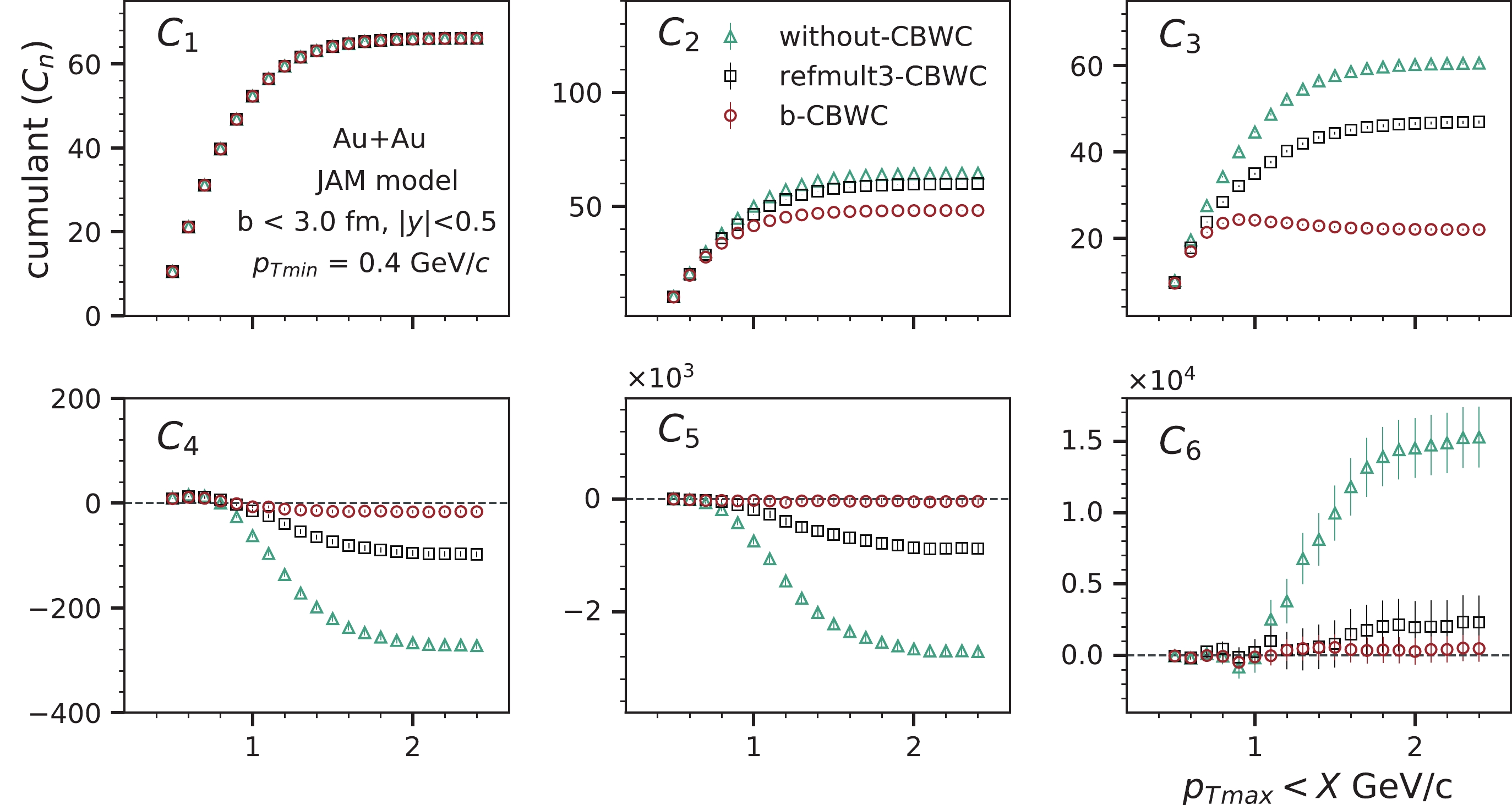
Figure 6. (color online) Transverse momentum acceptance dependence cumulants of proton multiplicity distributions in top central (
$ b $ < 3 fm) Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. The centrality bin width correction is performed with (a) each Refmult3-bin (black squares) and (b) a 0.1 fm impact parameter bin (red circles). The results are also compared with the cumulants calculated without the CBWC (green triangles).
Figure 7. (color online) Transverse momentum acceptance dependence cumulant ratios of proton multiplicity distributions in top central Au+Au collisions at
$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. The centrality bin width correction is performed with (a) each Refmult3-bin (black squares) and (b) a 0.1 fm impact parameter bin (red circles). The results are also compared with the cumulants calculated without the CBWC (green triangles).Theoretically, it was predicted that the rapidity window dependence of proton cumulants is an important observable when searching for the QCD critical point and for understanding the non-equilibrium effects of dynamical expansion on fluctuations in heavy-ion collisions [57]. It is expected that the proton cumulant and correlation functions will exhibit power law dependence with the rapidity acceptance and number of protons since
$ C_{n},\kappa_{n} \propto (\Delta y)^{n} \propto (N_{p})^{n} $ due to the long range correlation close to the critical point. This relationship holds when the rapidity acceptance is less than the typical correlation length near the critical point ($ \Delta y < \xi $ ) [42, 57]. On the other hand, if the rapidity acceptance is large enough relative to the correlation length ($ \Delta y \gg \xi $ ), the proton cumulant and multi-particle correlation function will be dominated by statistical fluctuations since$ C_{n},\kappa_{n} \propto \Delta y \propto N_{p} $ . However, if the rapidity acceptance is further enlarged, the baryon number conservation effect will dominate the statistical fluctuations.Figure 8 shows the variation of the cumulants
$ C_{n} $ with the rapidity acceptance ($ -y_{\rm max} < y < y_{\rm max}, \; \Delta y $ = 2$ y_{\rm max} $ ) of proton multiplicity distributions in the most central Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. The measurements were conducted within the transverse momentum range of 0.4 to 2.0 GeV/c. All cumulants are saturated around$ \Delta y \sim 2.2 $ , which is the acceptance up to beam rapidity ($ y_{\rm beam} = 1.039 $ at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV) [39].$ C_{1} $ and$ C_{2} $ increase linearly as a function of rapidity acceptance up to$ 2y_{\rm beam} $ due to an increase in the proton number with acceptance. We observed an approximately 7% reduction in the mean value of the number of protons in the case including deuteron formation.$ C_{3} $ increases in low rapidity acceptance, exhibits a peak around$ \Delta y \sim $ 0.7-0.8, and then decreases. The fourth order proton cumulant ($ C_4 $ ) values are negative above$ \Delta y \sim $ 0.6, whereas the fifth and sixth order proton cumulants ($ C_5 $ and$ C_6 $ ) are consistent with zero with large statistical uncertainties. To better understand the effect of deuteron formation, we randomly reduced the total proton number by 7% in each event using binomial sampling. Although the values are not identical, we found that the effect of randomly dropping 7% of protons was very similar to the case including deuteron formation.
Figure 8. (color online) Rapidity acceptance dependence cumulants (
$ C_{1} \sim C_{6} $ ) of proton multiplicity distributions in top central ($ b < 3 $ fm) Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. The results were obtained with/without deuteron formation in the JAM model. The blue cross markers indicate the random reduction of 7% of the protons in each event.Figure 9 shows the rapidity acceptance dependence of the correlation function
$ \kappa_{n} $ of protons in the most central Au+Au collisions at$ \sqrt {s_{NN}}\; $ = 3 GeV within the$ p_{T} $ range 0.4 to 2.0 GeV/c. Different orders of correlation function values are saturated at approximately$ \Delta y \sim $ 2.2 around mid-rapidity.$ \kappa_{1} $ increases as a function of the rapidity window. The two particle correlation function ($ \kappa_{2} $ ) of protons is found to be negative, and it decreases monotonically up to$ \Delta y \sim 2.2 $ . The three particle correlation function ($ \kappa_{3} $ ) of protons increases with$ \Delta y \sim $ acceptance. The fourth, fifth, and sixth order correlation functions of protons ($ \kappa_{4} $ ,$ \kappa_{5} $ , and$ \kappa_{6} $ , respectively) are found to be close to zero up to$ \Delta y \sim 1 $ ; they start to deviate from zero when further enlarging the rapidity acceptance. Interestingly, the odd order correlation functions are found to be positive while the even order correlation functions show negative values up to the sixth order at large rapidity acceptance at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. The strong rapidity acceptance dependence is mainly attributed to the effects of baryon number conservation [67-70]. In addition, we observed that when we randomly drop 7% of the protons in each event, the cumulants are close to the deuteron formation case.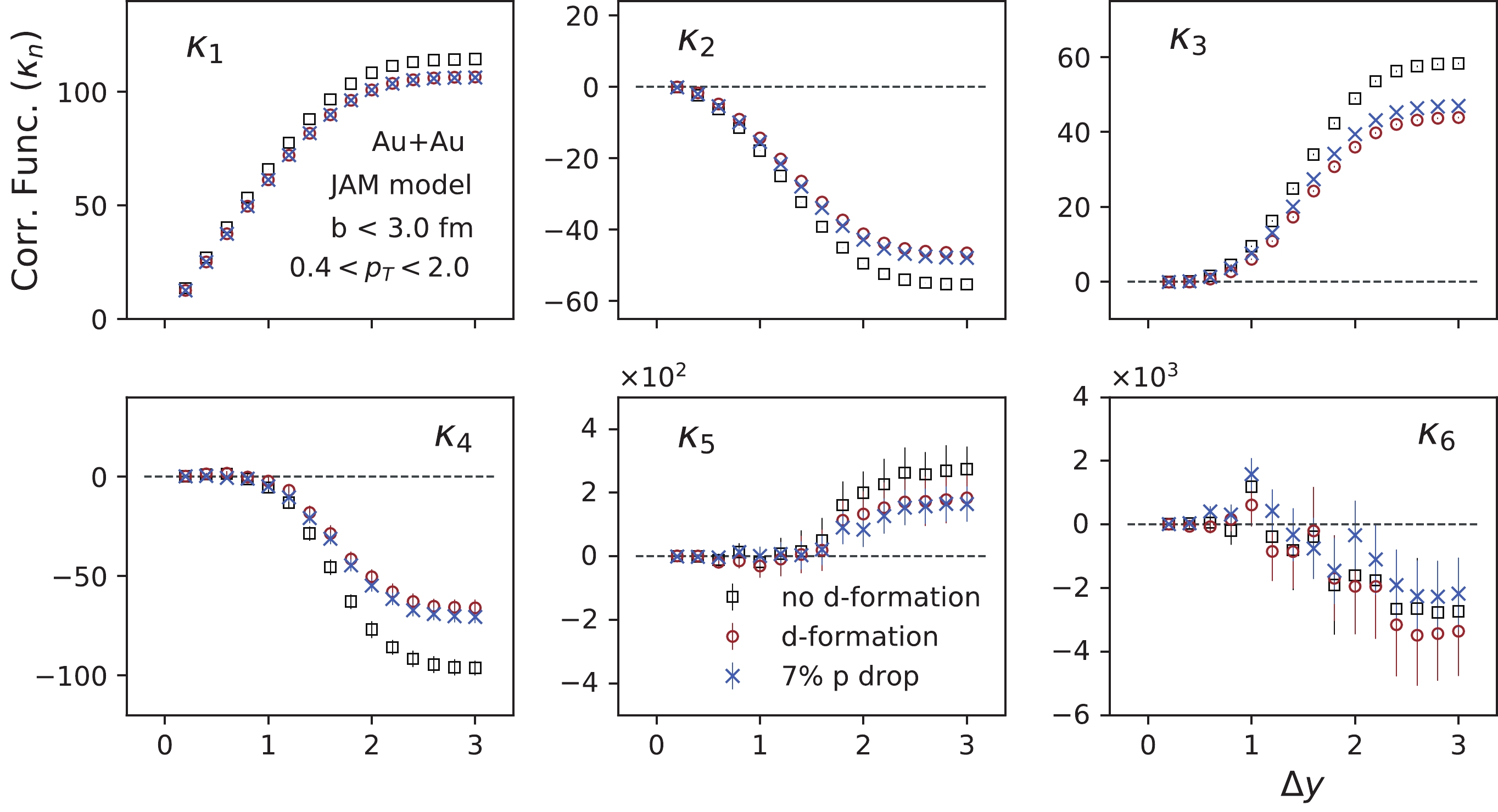
Figure 9. (color online) Rapidity acceptance dependence of the correlation functions (
$ \kappa_{1} \sim \kappa_{6} $ ) of the proton multiplicity distribution in top central ($ b < 3 $ fm) Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV with/without deuteron formation. The blue crosses represent the random dropping of 7% of the protons in each event.Figure 10 shows the rapidity acceptance dependence of cumulant ratios
$ C_{2}/C_{1} $ ,$ C_{3}/C_{2} $ ,$ C_{4}/C_{2} $ ,$ C_{5}/C_{1} $ and$ C_{6}/C_{2} $ of the proton multiplicity distributions in Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. At small rapidity acceptance values, the cumulant ratios follow statistical (Poisson) baseline fluctuations, and the values are close to unity ($ C_{m}/C_{n} \sim 1 $ ).$ C_{2}/C_{1} $ and$ C_{3}/C_{2} $ decrease smoothly with$ \Delta y $ and saturate around$ \Delta y \sim 2 $ . The values of$ C_{4}/C_{2} $ and$ C_{5}/C_{1} $ are positive for small rapidity acceptance, change sign around$ \Delta y \sim 0.6 $ , and then further decrease up to$ \Delta y \sim 1 $ .$ C_{6}/C_{2} $ is close to 1 within statistical uncertainty at smaller rapidity acceptance and exhibits negative values at larger acceptance values. We observed good agreement between the cumulant ratios for deuteron formation and the case in which random protons were dropped.
Figure 10. (color online) Rapidity acceptance dependence cumulant ratios (
$ C_{2}/C_{1} $ ,$ C_{3}/C_{2} $ ,$ C_{4}/C_{2} $ ,$ C_{5}/C_{1} $ , and$ C_{6}/C_{2} $ ) of the proton multiplicity distributions in the most central ($ b < 3 $ fm) Au+Au collisions at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. The results were obtained with/without deuteron formation in the JAM model. The blue crosses indicate the random dropping of 7% of the protons in each event. -
In this work, we studied the effects of centrality fluctuation and deuteron formation on the cumulant and correlation functions of protons up to the sixth order in the most central Au+Au collisions at
$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV using the JAM model. We presented the results as a function of the rapidity acceptance within the transverse momentum range of$ 0.4<p_{T}<2 $ GeV/c. The proton cumulants$ C_{1} $ and$ C_{2} $ increase linearly as a function of the rapidity acceptance up to$ \Delta y \sim 2y_{\rm beam} $ . This also leads to the suppression of$ C_3 $ and$ C_{4} $ in the larger rapidity acceptance window ($ \Delta y > 0.6 $ ). The cumulants are saturated after$ {p_{T}}_{\rm max}\sim $ 1.5-1.6 GeV/c due to the saturation of the proton yield in a fixed rapidity acceptance. Further, we found the odd order correlation functions to be positive, whereas the even order correlation functions were found to be negative up to the sixth order for larger rapidity acceptance at$ \sqrt {{s_{{{NN}}}}}\; $ = 3 GeV. This is mainly due to the effects of baryon number conservation in heavy-ion collisions. The results obtained by the centrality bin width correction (CBWC) using charged reference particle multiplicities were compared with the CBWC using finer impact parameter bins. We observed that the centrality resolution for determining the collision centrality using charged particle multiplicities cannot effectively reduce the centrality fluctuations in heavy-ion collisions at low energies. This presents a challenge when conducting cumulant measurements in low energy heavy-ion collisions. New methods, such as machine learning techniques, need to be developed and applied to determine the collision centrality with high resolution. This will be crucial for precisely measuring the higher-order cumulants in heavy-ion collisions at low energies. We also discussed the effect of deuteron formation on the cumulant and correlation functions of protons and found that it is similar to the binomial efficiency effect due to the loss of protons via deuteron formation. This work can serve as a non-critical baseline for the future QCD critical point search in heavy-ion collisions at high baryon density regions. -
X. Luo is grateful for the stimulating discussion with Dr. Jiangyong Jia and Dr. Nu Xu.
Effects of centrality fluctuation and deuteron formation on the proton number cumulant in Au+Au collisions at ${ \sqrt {{{ s}_{{{NN}}}}}\; } $ = 3 GeV from the JAM model
- Received Date: 2021-02-08
- Available Online: 2021-06-15
Abstract: We studied the effects of centrality fluctuation and deuteron formation on the cumulant (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: