-
The BESIII experiment [1] was designed to study physics in the
$ \tau $ -charm energy region (2.0 – 4.9 GeV) [2] through$ e^+e^- $ annihilations produced by the BEPCII storage ring [3]. Since it started running in 2008, a variety of data samples have been collected at different center-of-mass (CM) energies for the study of light hadron spectroscopy, charmonium and charmoniumlike states (also called${XYZ}$ states), charm physics,$ \tau $ physics, various QCD-related studies, and the search for new physics beyond the standard model [4].The Beam Energy Measurement System (BEMS) [5] was designed to precisely measure BESIII CM energies (
$ E_{{\rm{cm}}} $ ) using a method based on Compton back-scattered photons. However, its capability at high energy ($ E_{{\rm{cm}}} $ above 4 GeV) is degraded by its detection efficiency and limited calibration sources for high-energy gamma rays. Therefore, an alternative algorithm was developed to measure the$ E_{{\rm{cm}}} $ for data samples above 4 GeV. This method uses the well-understood QED process$e^+e^-\to $ $ (\gamma_{\rm ISR/FSR}) \mu^+\mu^-$ (the di-muon process), where$ \gamma_{\rm ISR/FSR} $ is a radiative photon due to initial state radiation (ISR) and/or final state radiation (FSR). Using this method, a precision of 0.8 MeV was previously achieved for data from 2011 to 2014 [6].In this paper, we present the
$ E_{\rm cm} $ measurement for the${{XYZ}}$ data samples taken at BESIII from 2017 to 2019. The method used in Ref. [6] is followed, but the precision of the momentum calibration is improved, and the$ E_{{\rm{cm}}} $ is measured with an uncertainty of 0.6 MeV.Using the selected di-muon events,
$ e^+e^-\to (\gamma_{\rm ISR/FSR}) $ $ \mu^+\mu^- $ , we determine$ E_{{\rm{cm}}} $ using$ E_{{\rm{cm}}} = (M_{\rm p}( \mu^+\mu^-) + \Delta M_{\rm ISR/FSR} + \Delta M_{\rm cal})\times c^{2},$

(1) where
$ M_{\rm p}( \mu^+\mu^-) $ is the peak position of the$ \mu^+\mu^- $ invariant mass of selected di-muon events;$ \Delta M_{\rm ISR/FSR} $ is the mass shift due to the emission of ISR or FSR photons, estimated from Monte Carlo (MC) simulation of the di-muon process by turning the ISR/FSR processes on and off in MC generation; and$ \Delta M_{\rm cal} $ is the correction introduced by the momentum calibration of the$ \mu^+\mu^- $ tracks, obtained from an analysis of the process$ e^+e^-\to \gamma_{\rm ISR} J/\psi $ . -
The BESIII detector is described in detail in Ref. [1]. The cylindrical core of the detector covers 93% of the full solid angle and consists of a helium-based multilayer drift chamber (MDC), a plastic scintillator time-of-flight system (TOF), and a CsI(Tl) electromagnetic calorimeter (EMC), all of which are enclosed in a superconducting solenoidal magnet providing a 1.0 T magnetic field. The solenoid is supported by an octagonal flux-return yoke with resistive plate counter muon identification modules interleaved with steel. The charged-particle momentum resolution at
$ 1\; {\rm GeV}/c $ is$ 0.5% $ , and the${\rm d}E/{\rm d}x$ resolution is$6\%$ for electrons from Bhabha scattering. The EMC measures photon energies with a resolution of$2.5\%$ ($5\%$ ) at$ 1 $ GeV in the barrel (end cap) region. The time resolution in the TOF barrel region is 68 ps, and that in the end cap region is 60 ps [7-9].The data samples analyzed in this work are listed in Table 1. They include 16 different CM energies from 4.13 to 4.44 GeV and were collected in two running years: from December 2016 to May 2017 (labelled as "2017XYZ" hereafter, the integrated luminosities are measured using the Bhabha events in Ref. [10]) and from February 2019 to June 2019 (labelled as "2019XYZ" hereafter, the integrated luminosities are estimated by using online monitoring information). The column "Sample" lists the nominal CM energy in MeV used during online data collecting. The true CM energy is generally within a few MeV of the nominal value. Run numbers are used to divide the data into subsamples. Other columns, such as
$ \mathcal{L} $ ($ \rm{pb^{-1}} $ ), areillustrated below. Sample Run Number $ {\cal{L}} $ /

$ \rm{pb^{-1}} $ 

$ M^{\rm cor}(J/\psi) $ 

$ M_{\rm p}(\mu^{+}\mu^{-}) $ 

$ E_{\rm cm} $ /MeV

4130 $ ^2 $ 

59163-59573 400 $ 3100.55\pm0.30 $ 

$ 4130.23\pm0.05 $ 

$ 4128.78\pm0.05\pm0.36 $ 

4160 $ ^2 $ 

59574-59896 400 $ 3100.18\pm0.29 $ 

$ 4158.89\pm0.05 $ 

$ 4157.83\pm0.05\pm0.34 $ 

4190 $ ^1 $ 

47543-48170 $ 526.70\pm2.16 $ 

$ 3097.89\pm0.28 $ 

$ 4187.90\pm0.05 $ 

$ 4189.12\pm0.05\pm0.34 $ 

4200 $ ^1 $ 

48172-48713 $ 526.60\pm2.05 $ 

$ 3098.17\pm0.27 $ 

$ 4198.20\pm0.05 $ 

$ 4199.15\pm0.05\pm0.34 $ 

4210 $ ^1 $ 

48714-49239 $ 517.10\pm1.81 $ 

$ 3097.41\pm0.29 $ 

$ 4207.67\pm0.06 $ 

$ 4209.39\pm0.06\pm0.34 $ 

4220 $ ^1 $ 

49270-49787 $ 514.60\pm1.80 $ 

$ 3097.51\pm0.26 $ 

$ 4217.31\pm0.05 $ 

$ 4218.93\pm0.06\pm0.32 $ 

4237 $ ^1 $ 

49788-50254 $ 530.30\pm2.39 $ 

$ 3097.36\pm0.24 $ 

$ 4233.99\pm0.04 $ 

$ 4235.77\pm0.04\pm0.30 $ 

4246 $ ^1 $ 

50255-50793 $ 538.10\pm2.69 $ 

$ 3097.35\pm0.24 $ 

$ 4242.18\pm0.04 $ 

$ 4243.97\pm0.04\pm0.30 $ 

4270 $ ^1 $ 

50796-51302 $ 531.10\pm3.13 $ 

$ 3098.09\pm0.26 $ 

$ 4265.74\pm0.04 $ 

$ 4266.81\pm0.04\pm0.32 $ 

4280 $ ^1 $ 

51305-51498 $ 175.70\pm0.97 $ 

$ 3097.55\pm0.48 $ 

$ 4277.73\pm0.04 $ 

$ 4277.78\pm0.11\pm0.52 $ 

4290 $ ^2 $ 

59902-60363 500 $ 3100.07\pm0.28 $ 

$ 4289.33\pm0.06 $ 

$ 4288.43\pm0.06\pm0.34 $ 

4315 $ ^2 $ 

60364-60805 500 $ 3099.97\pm0.30 $ 

$ 4313.46\pm0.06 $ 

$ 4312.68\pm0.06\pm0.35 $ 

4340 $ ^2 $ 

60808-61242 500 $ 3099.71\pm0.29 $ 

$ 4338.45\pm0.06 $ 

$ 4337.93\pm0.06\pm0.35 $ 

4380 $ ^2 $ 

61249-61762 500 $ 3099.68\pm0.30 $ 

$ 4378.35\pm0.06 $ 

$ 4377.88\pm0.06\pm0.35 $ 

4400 $ ^2 $ 

61763-62285 500 $ 3100.61\pm0.31 $ 

$ 4398.21\pm0.06 $ 

$ 4396.83\pm0.06\pm0.36 $ 

4440 $ ^2 $ 

62286-62823 570 $ 3099.73\pm0.29 $ 

$ 4437.59\pm0.06 $ 

$ 4437.10\pm0.06\pm0.35 $ 

Table 1. Summary of the data samples, including run numbers, integrated luminosity
$ {\cal L} $ [10], the measured$ J/\psi $ mass after FSR correction$ M^{\rm cor}( J/\psi) $ (in MeV/$ c^2 $ ),$ M_{\rm p}( \mu^+\mu^-) $ (in MeV/$ c^2 $ ), and$ E_{{\rm{cm}}} $ . Superscripts represent data from different periods: "1" denotes 2017XYZ data, and "2" denotes 2019XYZ data. The first uncertainties are statistical and the second systematic.A GEANT4 [11] based detector simulation package is developed to model the detector response for MC events. In our analysis, the di-muon sample is generated with BABAYAGA3.5 [12], and the
$ e^+e^-\to \gamma_{\rm ISR}J/\psi $ sample is generated with KKMC [13, 14]. One million events are generated for each process at each CM energy. -
The di-muon process
$ e^+e^-\to (\gamma_{\rm ISR/FSR}) \mu^+\mu^- $ is selected by requiring two oppositely charged tracks in the detector, each positively identified as a muon. Both charged tracks are reconstructed from hits in the MDC within the polar angle range$ |\cos\theta|<0.8 $ and their extrapolations to the interaction point (IP) within 10 cm along the beam direction and 1 cm in the plane perpendicular to the beam. The energy deposition in the EMC for each charged track is required to be less than 0.4 GeV to suppress backgrounds from radiative Bhabha events.The sample after these selections includes di-muon events with no photon emission or with very low-energy radiative photons, ISR
$ J/\psi $ with$ J/\psi\to \mu^+\mu^- $ , and ISR$ \mu^+\mu^- $ events with a smooth$ \mu^+\mu^- $ invariant mass ($ M( \mu^+\mu^-) $ ) distribution. The events in the$ J/\psi $ mass region are used for track momentum calibration and those with high invariant mass are used to measure the$ E_{{\rm{cm}}} $ after additional selection criteria are applied, as described below.To suppress di-muon events with high energy radiative photons, a requirement on the cosine of the opening angle between the two tracks,
$ \cos\theta_{ \mu^+\mu^-} < -0.9997 $ is applied. To further remove cosmic ray events, the TOF time difference between the two tracks is required to be$ |\Delta t| < 2 $ ns. The background contribution after these selection criteria is less than 0.1% compared with the signal and is therefore neglected in the following analysis.The
$ M( \mu^+\mu^-) $ distribution for the 4190 data sample is shown in Fig. 1 as an example. The distributions of the other samples are very similar. The distribution is a Gaussian due to the momentum resolution of the$ \mu^+\mu^- $ , though it is distorted by ISR and FSR effects, producing a tail on the left side of the peak. The central part of the distribution can be approximated with a Gaussian function. We measure the peak position of the distribution ($ M_{\rm p}( \mu^+\mu^-) $ ) by fitting it with a Gaussian function in the range of$ (-1\sigma,\; +1.5\sigma) $ around the peak, where$ \sigma $ is the standard deviation of the Gaussian. If the goodness of the fit,$ \chi^2/ndf>2.0 $ ($ ndf $ is the number of degrees of freedom of the fit), the fit range is slightly reduced until$ \chi^2/ndf<2.0 $ , guaranteeing a good fit quality. The fit result for the 4190 data sample is shown in Fig. 1. The values of$ M_{\rm p}( \mu^+\mu^-) $ for the other data samples are obtained using a similar method and are listed in Table 1.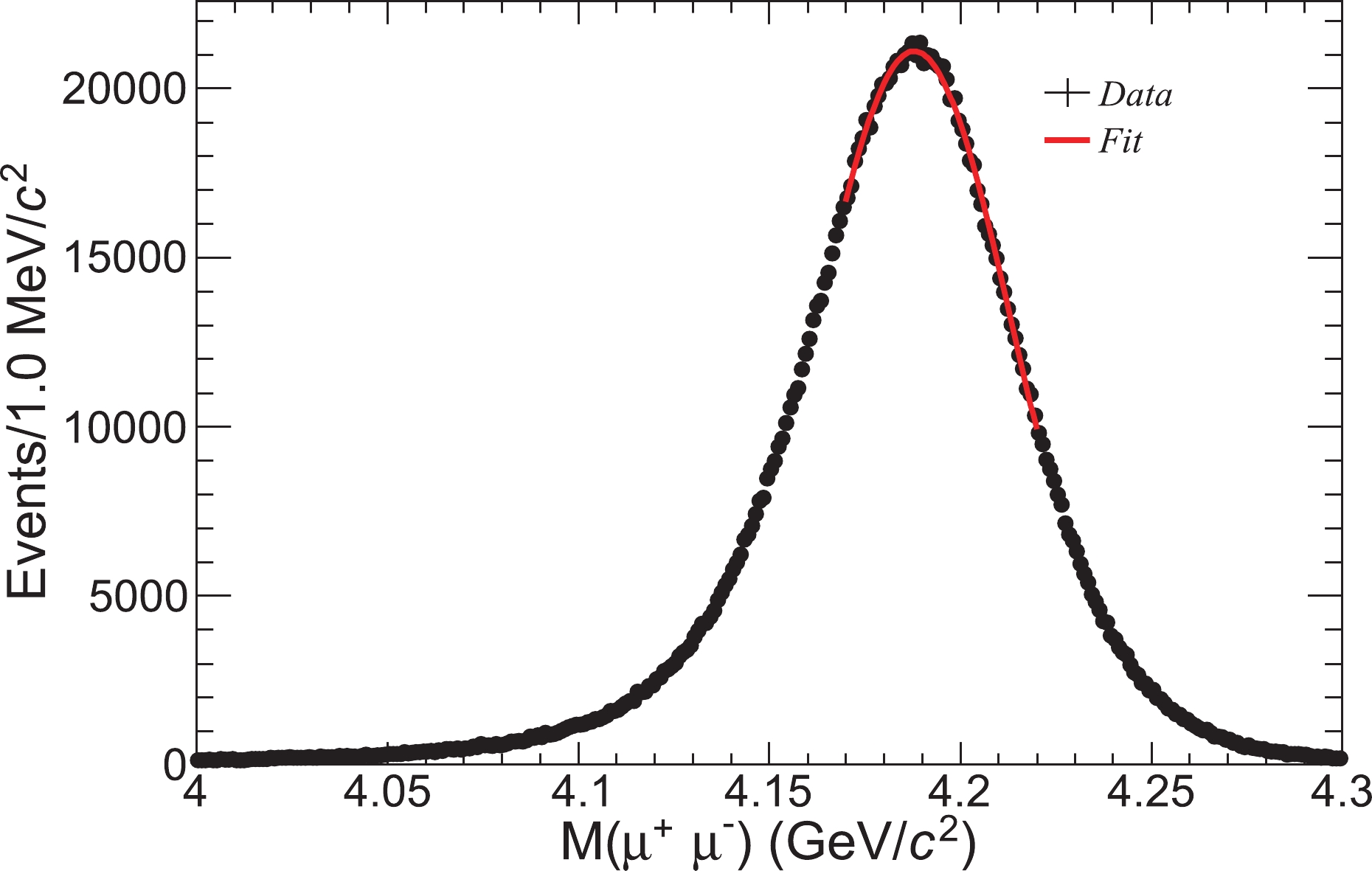
Figure 1. (color online) The
$ \mu^+\mu^- $ invariant mass distribution and the fit result of the 4190 sample. Dots with error bars are data, and the solid red curve is the fit.To examine the stability of the
$ E_{{\rm{cm}}} $ over the data-taking period for each data sample, the fit procedure is repeated for each run of the data sample. The measured peak values of the$ \mu^+\mu^- $ invariant mass distribution versus run number for all 16 samples are shown in Fig. 2. There are small jumps of less than 1 MeV in the 4130, 4200, 4210, 4246, 4380, and 4400 samples. Before and after the jumps, the energy is stable. We fit each stable part of the distribution with a linear function and Table 2 summarizes the average,$ M^{\rm ave}( \mu^+\mu^-) $ , for each period of time. The deviation of$ M^{\rm ave}( \mu^+\mu^-) $ from the peak position obtained in the full data sample is considered as one source of systematic uncertainty.
Figure 2. (color online) Measured run-by-run values for the
$ M_{\rm p}( \mu^+\mu^-) $ of di-muon events in each data sample. The red solid lines show the fit results for the data samples of each stable period of time. The green dotted lines are the fit results of the entire sample when there is an energy jump.Sample Run Number $ M^{\rm ave}( \mu^+\mu^-) $ 

Run Number $ M^{\rm ave}( \mu^+\mu^-) $ 

4130 59163-59190 $ 4131.44\pm0.36 $ 

59191-59573 $ 4130.02\pm0.05 $ 

4160 59574-59896 $ 4158.49\pm0.05 $ 

4190 47543-48170 $ 4187.52\pm0.06 $ 

4200 48172-48290 $ 4197.14\pm0.12 $ 

48291-48713 $ 4198.07\pm0.06 $ 

4210 48174-49065 $ 4206.75\pm0.06 $ 

49066-49239 $ 4207.49\pm0.09 $ 

4220 49270-49787 $ 4216.33\pm0.05 $ 

4237 49788-50254 $ 4233.21\pm0.04 $ 

4246 50255-50520 $ 4241.01\pm0.08 $ 

50521-50793 $ 4241.55\pm0.05 $ 

4270 50796-51302 $ 4265.20\pm0.06 $ 

4280 51305-51498 $ 4275.34\pm0.09 $ 

4290 59902-60363 $ 4288.91\pm0.05 $ 

4315 60364-60805 $ 4312.79\pm0.04 $ 

4340 60808-61242 $ 4337.93\pm0.05 $ 

4380 61249-61400 $ 4378.23\pm0.09 $ 

61401-61762 $ 4377.61\pm0.06 $ 

4400 61763-61980 $ 4397.51\pm0.08 $ 

61981-62285 $ 4398.06\pm0.07 $ 

4440 62286-62823 $ 4437.01\pm0.05 $ 

Table 2. Average value
$ M^{\rm ave}( \mu^+\mu^-) $ (in MeV/$ c^{2} $ ) for each stable data-taking period within each data sample. -
The momentum measurement of the muon tracks is validated with
$ J/\psi \to \mu^+\mu^- $ candidates produced via the process$ e^+e^-\to \gamma_{\rm ISR} J/\psi $ selected in the previous section. The distribution of$ M( \mu^+\mu^-) $ for each sample is fitted with a crystal-ball function [15] for the$ J/\psi $ signal and a linear function to model the background from continuum production of$ e^+e^-\to \gamma \mu^+\mu^- $ . Figure 3(a) shows the fit result for the 4190 data sample as an example. The peak position of the$ J/\psi $ signal,$ M^{\rm obs}(J/\psi) $ , is used to calibrate the momentum measurement of the muon tracks.
Figure 3. (color online) (a) Fit to the
$ M(\mu^{+}\mu^{-}) $ distribution in the$ J/\psi $ signal region for the 4190 data sample. Black dots with error bars are data, the red curve shows the fit result, the blue curve indicates the signal, and the green dashed line indicates the background. (b) The difference between$ M^{\rm cor}(J/\psi) $ and the world average mass of$ J/\psi $ [16],$ \Delta M^{\rm cor}(J/\psi) $ for each data sample.Due to FSR,
$ J/\psi\to \mu^+\mu^-\gamma_{\rm FSR} $ , the measured$ M^{\rm obs}(J/\psi) $ is slightly lower than the world average$ J/\psi $ mass ($ m_{ J/\psi} $ ) given by the PDG [16]. The mass shift due to the FSR photon(s)$ \Delta M^{\gamma J/\psi}_{\rm FSR} $ of the process$ e^+e^-\to \gamma_{\rm ISR}J/\psi $ at each$ E_{{\rm{cm}}} $ is obtained by using the generator PHOTOS [17] with FSR turned on or off. The shift is around 0.3 MeV/$ c^2 $ with minimal dependence on the CM energy of the data sample.Comparing the
$ M^{\rm cor}(J/\psi) = M^{\rm obs}(J/\psi)+\Delta M^{\gamma J/\psi}_{\rm FSR} $ (as shown in Table 1) with the world-average$ J/\psi $ mass value$ m_{ J/\psi} $ in the Particle Data Book (PDG), we measure the bias in the$ J/\psi $ mass measurement ($ \Delta M^{\rm cor}(J/\psi) $ ) due to the muon track momentum calibration, as shown in Fig. 3(b). It can be seen that the bias in the$ J/\psi $ invariant mass is stable throughout one running year, but is quite different in the 2017XYZ and 2019XYZ samples. This may indicate that the calibrations in these two periods of time have significant differences.Through MC simulation we find that the bias in the
$ M_{\rm p}( \mu^+\mu^-) $ measurement depends linearly on$ M( \mu^+\mu^-) $ (see Fig. 4), and there exists$ E_{{\rm{cm}}} = M( \mu^+\mu^-) $ with no radiation, so the correction to the$ M_{\rm p}( \mu^+\mu^-) $ due to calibration is expressed as
Figure 4. (color online) (a) The distribution of
$ \Delta M^{\rm cal}(J/\psi) $ of different$ E_{\rm cm} $ for the MC simulation of$ \gamma_{\rm ISR}J\psi $ process without FSR. The average value is$ 1.67\pm0.01 $ MeV/$ c^{2} $ . (b)$ \Delta M $ is the difference between the reconstructed and generated center-of-mass energy ($ E_{\rm cm} $ ) reported as a function of$ M( \mu^+\mu^-) $ ($ M( \mu^+\mu^-) $ is equal to$ E_{\rm cm} $ for events without radiation). The di-muon events are generated without radiation emission. The bias at$ J/\psi $ mass given from (b) is$ 1.67\pm0.24 $ MeV/$ c^{2} $ , which is consistent with the result provided in (a). The linear fit to the points provides the dependence of the bias on$ M_{\rm p}( \mu^+\mu^-) $ (slope$ k $ ) due to track momentum calibration, which is assumed to be the same for data and simulation.$ \Delta M_{\rm cal} = -(k \times ( E_{{\rm{cm}}} - m_{ J/\psi}) + \Delta M^{\rm cor}(J/\psi)) (\rm{MeV}), $

(2) where the slopes
$ k = (7.11\pm 0.50)\times $ $ 10^{-4} $ and$(7.04\pm $ $ 0.57)\times 10^{-4}$ correspond to the 2017XYZ and 2019XYZ samples, respectively. They agree within the statistical uncertainties of the MC samples, which indicates that the momentum dependence of the calibration constants is very similar in the 2017XYZ and 2019XYZ samples. -
$ E_{{\rm{cm}}} $ of the initial$ e^+e^- $ pair is measured via the di-muon process$ e^+e^-\to (\gamma_{\rm ISR/FSR}) \mu^+\mu^- $ . However, due to the emission of radiative photons, the invariant mass of the$ \mu^+\mu^- $ pair is smaller than$ E_{{\rm{cm}}} $ by$ \Delta M_{\rm ISR/FSR} $ . This correction is estimated with MC simulation using BABAYAGA3.5 [12].We generate one million di-muon events for each sample with ISR/FSR turned on or off, apply the same event selection criteria to the di-muon events as in the data (described in Sec. III), and fit the distributions of
$ M( \mu^+\mu^-) $ from the samples with ISR/FSR on and off with a Gaussian function in the range around the peak (same as in Sec. III). The difference in$ M_{\rm p}( \mu^+\mu^-) $ is taken as the mass shift$ \Delta M_{\rm ISR/FSR} $ caused by ISR or FSR.$ \Delta M_{\rm ISR/FSR} $ versus$ E_{{\rm{cm}}} $ shown in Fig. 5 indicates that the ISR/FSR effect depends linearly on$ E_{{\rm{cm}}} $ . The data are fitted with a linear function to provide an improved precision measurement of the correction. From the fit,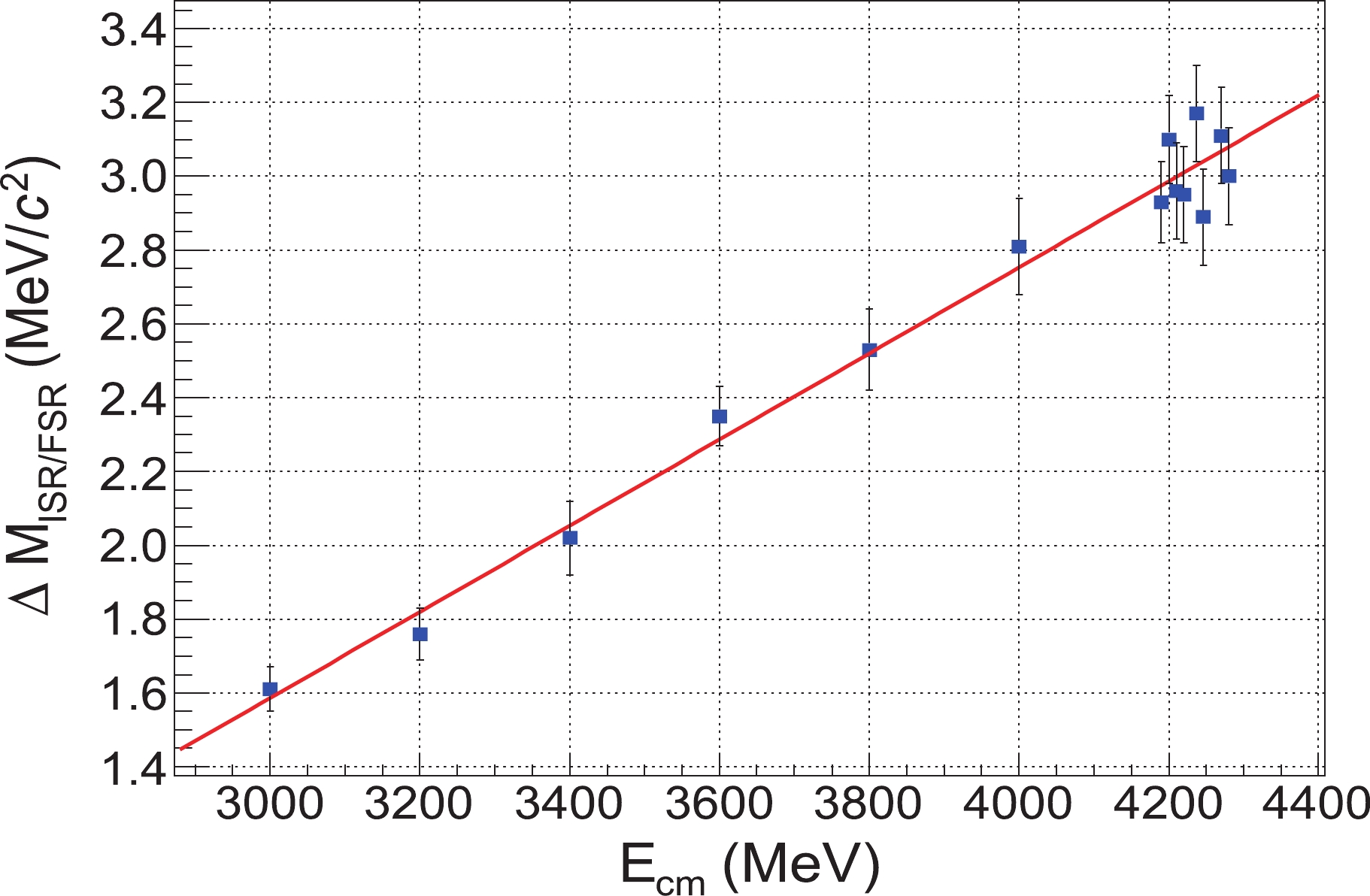
Figure 5. (color online) Mass shift
$ \Delta M_{\rm ISR/FSR} $ versus CM energy for$ e^+e^-\to (\gamma_{\rm ISR/FSR}) \mu^+\mu^- $ MC samples. The solid red line is the linear fit.$ \Delta M_{\rm ISR/FSR} = ( 1.17\pm 0.05)\times 10^{-3}\times E_{{\rm{cm}}} + (-1.91\pm 0.20) (\rm{MeV}) $

(3) with a correlation factor of
$ -0.99 $ between the slope and the intercept, and the goodness of the fit is$ \chi^2/ndf = $ $ 6.2/12 $ . -
The systematic uncertainty in
$ E_{{\rm{cm}}} $ is from the momentum calibration of$ \mu^{\pm} $ , the estimation of the mass shift$ \Delta M_{\rm ISR/FSR} $ due to ISR/FSR, the open angle cut of$ \cos\theta_{ \mu^+\mu^-} $ , the corresponding fit procedure, and the generator. The bias of the momentum measurement of$ \mu^{\pm} $ and the estimation of the mass shift$ \Delta M_{\rm ISR/FSR} $ due to ISR/FSR both have a linear relationship with$ E_{{\rm{cm}}} $ , and the uncertainty produced by the uncertainty of the parameters is regarded as the systematic uncertainties.To reduce the influence of the events with high radiation, we required
$ \cos\theta_{ \mu^+\mu^-}<-0.9997 $ . Different cut values will give different$ M_{\rm p}( \mu^+\mu^-) $ and corresponding radiation correction values$ \Delta M_{\rm ISR/FSR} $ . The changes in these two parts cancel each other out. The largest difference comes from the data between$ -0.9997 $ and$ -0.99975 $ , and is$ 0.12\pm 0.02 $ MeV. We take 0.14 MeV as the uncertainty due to this requirement.$ M_{\rm p}( \mu^+\mu^-) $ is measured by fitting with a Gaussian function in the range of$ (-1\sigma,\; +1.5\sigma) $ around the peak with fit quality$ \chi^2/ndf < 2.0 $ . If the fit range is smaller than the standard range, the difference in the fit results is less than 0.1 MeV. We take this as the uncertainty due to the fit method.The contribution to the systematic uncertainty of the ISR/FSR correction from the generator is negligibly small, as claimed in Ref. [12]. The uncertainties from other sources, such as background and other event selection criteria, are negligible.
Assuming all sources of systematic uncertainty are independent, the total systematic uncertainty is obtained by adding all the items in quadrature, which is listed in Table 1. The uncertainty is smaller than 0.6 MeV for all data samples.
-
The center-of-mass energies,
$ E_{{\rm{cm}}} $ , of the data samples are obtained using Eq. (1), with the correction factors in Eqs. (2) and (3). The final results are listed in Table 1, including the statistical and systematic uncertainties. The corresponding statistical uncertainty is very small, and the systematic uncertainty is less than 0.36 MeV everywhere, with the exception of the point at 4280 MeV, where the error on$ \Delta M^{\rm cor} $ is much larger than the rest. The stability of$ E_{{\rm{cm}}} $ over time for the data samples is also examined.The results presented in this work are essential for the discovery of new states and the investigation of the transitions of charmonium and charmoniumlike states [18] using the BESIII data. Some of the analyses have been presented in Refs. [19-24].
-
The BESIII collaboration thanks the staff of BEPCII and the IHEP computing center for their strong support.
Measurements of the center-of-mass energies of ${{\boldsymbol e^+}{\boldsymbol e^-}} $ collisions at BESIII
- Received Date: 2020-12-29
- Available Online: 2021-10-15
Abstract: During the 2016-17 and 2018-19 running periods, the BESIII experiment collected 7.5 fb







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: