-
There is a general consensus that the next large high-energy project after the Large Hadron Collider would be a linear collider. As a potential extension to the positron-electron (
$ e^+e^- $ ) collision mode, the photon-photon (γγ) collision [1, 2] at the International Linear Collider (ILC), i.e., the Photon Linear Collider (PLC), can help us to better understand the electroweak symmetry breaking and search for new physics beyond the standard model (BSM), such as supersymmetry, quantum gravity, extra dimensions, etc. Although the photon beam luminosity of PLC [3-5] can reach only approximately 80% of the electron beam luminosity at the ILC, the production rate of any charged particle pair in the γγ collision is typically about one order of magnitude higher than that in the$ e^+e^- $ collision. Therefore, the PLC provides a promising platform to test the standard model and search for BSM physics at the terascale [6–8].According to the "ILC Higgs White Paper" [2], the incoming photons at the high-energy PLC are produced via the backward Compton scattering (BCS) of the laser light off the linear electron beams [9, 10], which benefit from the monochromatic characteristic (concentrated at high energies in a narrow energy spread) and adjustable polarization mode. The γγ collision is known to have two polarization configurations:
${{J}} = 0$ and${{J}} = 2$ , where$ J $ denotes the total helicity of the two incoming photons. As is well known,$ \gamma\gamma \rightarrow l^+l^- $ is the most promising channel for calibrating the photon beam luminosity of PLC [1, 4, 9, 11], and the precision predictions for the light fermion-antifermion pair production via γγ scattering up to the electroweak (EW) next-to-leading order (NLO) were given in [12, 13]. However, such a reaction is incapable of determining the luminosity of${{J}} = 0$ polarized incoming photon beams, because the production rate of this channel is suppressed by a factor of$ m_{l}^2/\hat{s} $ in the${{J}} = 0$ polarization configuration [14]. On the other hand, as the${{J}} = 0$ polarization mode is preferred by Higgs physics due to the unique channel$ \gamma\gamma \rightarrow H^0 \rightarrow X $ ($ H^0 $ is any neutral scalar/pseudoscalar particle) in searching for BSM signals [15], the related high precision studies at γγ colliders are indispensable correspondingly. The$ \gamma\gamma \rightarrow W^+W^- $ process is also proposed for measuring the photon luminosity of PLC [11], but it can only work for the circumstance with colliding energy exceeding the threshold of W-boson pair, and its cross section has to be measured precisely at first because such reaction could be accompanied by some BSM effects. Although the cross section for the$ \gamma\gamma \rightarrow l^+l^-l^+l^- $ process is large and insensitive to the beam polarization, it is, unfortunately, rather small at large scattering angle where the lepton momenta can be measured precisely [3, 16].Compared to the
$ \gamma\gamma \rightarrow l^+l^- $ process, the lepton pair production in association with an extra photon via γγ scattering is suppressed by an additional fine structure constant, but free from the helicity suppression due to the radiated spin-1 photon in the final state. Consequently, the$ \gamma\gamma \rightarrow l^+l^-\gamma $ process can be adopted to measure the photon luminosity of the${{J}} = 0$ γγ collision mode, and the precision theoretical predictions for$ \gamma\gamma \rightarrow l^+l^-\gamma $ are necessary. Since the incoming photon beams at the PLC are only partially polarized, the ratio of the cross section for the$ l^+l^-\gamma $ production via the${{J}} = 0$ γγ scattering to that via${{J}} = 2$ γγ scattering should be sufficiently high to calibrate the${{J}} = 0$ γγ collision precisely. The dependences of the cross section for$ \gamma\gamma \rightarrow l^+l^-\gamma $ on the helicity and colliding energy of the two incoming photons, as well as the kinematic cuts on the final state, have already been analyzed at the lowest order [17, 18]. Careful and detailed studies show that the$ \gamma\gamma \rightarrow l^+l^-\gamma $ process is a unique channel in measuring the photon luminosity together with the$ \gamma\gamma \rightarrow l^+l^- $ process. In addition, the$ e^+e^- \rightarrow l^+l^- $ and$ e^+e^- \rightarrow l^+l^-\gamma $ processes also garner attention for determining the luminosity of the positron-electron collision mode at the ILC, and the related investigations at the EW NLO accuracy have been accomplished in [19, 20].In this study, we calculate the complete NLO EW radiative corrections to the
$ e^+e^-\gamma $ production in γγ collision, and provide the integrated cross sections and some kinematic distributions of final particles for both${{J}} = 0$ and${{J}} = 2$ polarization configurations. In Sec. II, we describe in detail the analytical calculation strategy, and then present the numerical results and discussion for the integrated and differential cross sections in both inclusive and exclusive event selection schemes in Sec. III. Finally, a short summary is provided in Sec. IV. -
We consider the process
$ \gamma_{\lambda_1}(q_1) + \gamma_{\lambda_2}(q_2) \rightarrow e^+_{h_1}(p_1) + e^-_{h_2}(p_2) + \gamma_{\lambda_3}(q_3), $

(1) where
$ \lambda_i = \pm $ and$ q_i = ( q_i^0 \equiv \vert \vec{q}_i \vert\,,\; \vec{q}_i ) $ $ (i = 1,\, 2,\, 3) $ are the helicities and four-momenta of the incoming and outgoing photons, while$ h_j = \pm $ and$ p_j = ( p_j^0 \equiv \sqrt{\vert \vec{p}_j \vert^2 + m_e^2}\,,\; \vec{p}_j ) $ $ (j = 1,\, 2) $ are the helicities and four-momenta of the two final-state fermions (positron and electron). Then, the total helicity of the two incoming photons is given by${ {J}} = \vert \lambda_1 - \lambda_2 \vert$ . We denote the differential cross section in the center-of-mass (c.m.) frame of the initial-state γγ system as$ d \hat{\sigma}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) $ . If the two incoming photon beams are partially polarized, the differential cross section for the unpolarized$ e^+e^-\gamma $ production (i.e., the polarizations of the final-state$ e^+ $ ,$ e^- $ and γ are not measured) in γγ collision is given by [21]$\begin{aligned}[b]& d \hat{\sigma}({\cal {P}}_1,\, {\cal {P}}_2;\, \vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) \\=& \frac{1}{4} \sum\limits_{\lambda_{1,2} = \pm} \left( 1 + \lambda_1 {\cal{P}}_1 \right) \left( 1 + \lambda_2 {\cal{P}}_2 \right) d \hat{\sigma}^{\lambda_1 \lambda_2}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3), \end{aligned}$

(2) where
$ {\cal{P}}_1 $ and$ {\cal{P}}_2 $ represent the degrees of polarization of the two incoming photon beams①, respectively, and$\begin{aligned}[b]& d \hat{\sigma}^{\lambda_1 \lambda_2}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) \\=& \sum\limits_{\lambda_3, h_{1,2} = \pm} d \hat{\sigma}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3).\end{aligned} $

(3) The tree-level Feynman diagrams for
$ \gamma\gamma \rightarrow e^+e^-\gamma $ are depicted in Fig. 1. By using$ {\cal{C}} $ ,$ {\cal{P}} $ ,$ {\cal{CP}} $ , and$ Bose $ symmetries [18], we obtain$ \begin{aligned}[b]& {\cal{C}}:\quad d \hat{\sigma}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}_{\rm{LO}}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) = d \hat{\sigma}^{\lambda_1 \lambda_2 h_2 h_1 \lambda_3}_{\rm{LO}}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_2,\, \vec{p}_1,\, \vec{q}_3) \\& {\cal{P}}: \quad d \hat{\sigma}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}_{\rm{LO}}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) = d \hat{\sigma}^{-\lambda_1 -\lambda_2 -h_1 -h_2 -\lambda_3}_{\rm{LO}}(-\vec{q}_1,\, -\vec{q}_2;\, -\vec{p}_1,\, -\vec{p}_2,\, -\vec{q}_3) \\& {\cal{CP}}: \quad d \hat{\sigma}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) = d \hat{\sigma}^{-\lambda_1 -\lambda_2 -h_2 -h_1 -\lambda_3}(-\vec{q}_1,\, -\vec{q}_2;\, -\vec{p}_2,\, -\vec{p}_1,\, -\vec{q}_3) \\ & Bose: \quad d \hat{\sigma}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) = d \hat{\sigma}^{\lambda_2 \lambda_1 h_1 h_2 \lambda_3}(\vec{q}_2,\, \vec{q}_1;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) \end{aligned} $ 
(4) It should be noted that
$ {\cal{C}} $ and$ {\cal{P}} $ are simply the Born-level symmetries for the$ \gamma\gamma \rightarrow e^+e^-\gamma $ process, because$ \gamma\gamma \rightarrow e^+e^-\gamma $ is a pure QED scattering process at the lowest order, and the weak interaction is only involved in the high-order radiative corrections. From Eq. (4), we obtain$ \begin{aligned}[b]& {\cal{CP}}+Bose:\\& \begin{array} {l} d\hat{\sigma}^{--}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) = d \hat{\sigma}^{++}(-\vec{q}_2,\, -\vec{q}_1;\, -\vec{p}_2,\, -\vec{p}_1,\, -\vec{q}_3) \\ d \hat{\sigma}^{+-}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) = d \hat{\sigma}^{+-}(-\vec{q}_2,\, -\vec{q}_1;\, -\vec{p}_2,\, -\vec{p}_1,\, -\vec{q}_3) \end{array} \end{aligned} $

(5) This clearly demonstrates that the differential distributions, as well as the integrated cross section for
$ \gamma_-\gamma_- $ collisions, can be obtained directly from the corresponding ones for$ \gamma_+\gamma_+ $ collisions. Therefore, in the following discussion, we only consider the$ \gamma_+\gamma_+ \rightarrow e^+e^-\gamma $ and$ \gamma_+\gamma_- \rightarrow e^+e^-\gamma $ channels for${{J}} = 0$ and${{J}} = 2$ polarization configurations of the γγ system, respectively. Moreover, we can conclude that the final-state electron and positron in the${{J}} = 2$ collision mode should have identical kinematic behaviors from Eq. (5), while there is no such coincidental feature in the${{J}} = 0$ collision mode.The leading order (LO) differential cross section for
$ \gamma_{\lambda_1}(q_1) + \gamma_{\lambda_2}(q_2) \rightarrow e^+_{h_1}(p_1) + e^-_{h_2}(p_2) + \gamma_{\lambda_3}(q_3) $ can be expressed as$\begin{aligned}[b]& d \hat{\sigma}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}_{\rm{LO}}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3)\\ =& \dfrac{1}{2 \hat{s}} \left| {\cal{M}}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}_{{\rm LO}}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) \right|^2 d\Phi_{3}(\vec{p}_1,\, \vec{p}_2,\, \vec{q}_3), \end{aligned}$

(6) where
$ \hat{s} = (q_1 + q_2)^2 $ ,$ {\cal{M}}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}_{\rm{LO}}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) $ is the LO helicity amplitude that can be acquired by applying the Weyl-van-der-Waerden spinor technique [14, 22, 23], and$ d\Phi_{3}(\vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) $ represents the$ e^+e^-\gamma $ final-state phase-space element, which is given by$\begin{aligned}[b] d\Phi_{3}(\vec{p}_1,\, \vec{p}_2,\, \vec{q}_3) =& (2 \pi)^4 \delta^{(4)}(p_1+p_2+q_3-q_1-q_2)\\&\times \dfrac{d^3\vec{p}_1}{(2 \pi)^3 2 p_1^0} \dfrac{d^3\vec{p}_2}{(2 \pi)^3 2 p_2^0} \dfrac{d^3\vec{q}_3}{(2 \pi)^3 2 q_3^0}.\end{aligned} $

(7) In the limit of
$ m_e \rightarrow 0 $ ,$ {\cal{M}}^{\lambda_1 \lambda_2 h_1 h_2 \lambda_3}_{\rm{LO}} = 0 $ , if$ h_1 = h_2 $ or$ \lambda_1 = \lambda_2 = -\lambda_3 $ . All the non-vanishing LO helicity amplitudes can be obtained from$ {\cal{M}}_{\rm{LO}}^{+--++} $ by using$ {\cal{C}} $ ,$ {\cal{P}} $ , and Bose symmetries in Eq. (4), and the crossing symmetry between the initial and final photons [18]. By adopting the helicity amplitude method [22], we obtain$\begin{aligned}[b]& \big|{\cal{M}}^{+--++}_{\rm{LO}}(\vec{q}_1,\, \vec{q}_2;\, \vec{p}_1,\, \vec{p}_2,\, \vec{q}_3)\big|^2 \\=& 4 e^6 \dfrac{(p_1 \cdot p_2) (p_2 \cdot q_2)^2}{(p_1 \cdot q_1) (p_1 \cdot q_3) (p_2 \cdot q_1) (p_2 \cdot q_3)}\,.\end{aligned} $

(8) -
We employ the modified FeynArts-3.7+FormCalc-7.3+LoopTools-2.8 packages [24-26] to generate Feynman diagrams, simplify Feynman amplitudes, and perform loop and phase-space integrations. The one-loop EW virtual correction to
$ \gamma \gamma \rightarrow e^+e^-\gamma $ includes 960 Feynman diagrams, which can be categorized into self-energy (36), triangle (438), box (414), pentagon (42) and counterterm (30) diagrams. Some representative box and pentagon Feynman diagrams for$ \gamma\gamma \rightarrow e^+e^-\gamma $ are depicted in Fig. 2. It can be seen that the loop diagram in Fig. 2(2) may induce Z resonance in the vicinity of$ M_{e^+e^-} = m_Z $ , where$ M_{e^+e^-} $ is the invariant mass of the final-state$ e^+e^- $ system due to the possible on-shell Z propagator. To avoid the numerical divergence in loop calculation, we replace the Z propagator$ 1/(p^2 - m_Z^2) $ by$1/(p^2 - m_Z^2 - $ $ {\rm i} m_Z \Gamma_Z)$ , where the contribution from the imaginary part is beyond the EW NLO and can therefore be ignored. We adopt the dimensional regularization (DR) scheme [27] to regularize the ultraviolet (UV) divergences. In the DR scheme, the dimensions of spinor and space-time manifolds are all extended to$ D = 4 - 2 \epsilon $ . The 5-point loop integrals are decomposed into 4-point loop integrals by adopting the Denner-Dittmaier method [28], and all the N-point ($ N \leqslant 4 $ ) tensor integrals are reduced to scalar integrals recursively by adopting the Passarino-Veltman reduction algorithm [29]. In the calculation of 4-point scalar integrals, numerical instability would occur at some phase-space regions with small Gram determinants. Generally, this problem can be solved by adopting the quadruple precision arithmetic proposed in [30].
Figure 2. Representative box and pentagon Feynman diagrams for
$ \gamma\gamma \rightarrow e^+e^-\gamma $ .The renormalized electric charge is defined by
$ e^{(B)} = ( 1 + \delta{Z_e} ) e $ , where$ e^{(B)} $ is the bare electric charge and$ \delta Z_e $ is the corresponding renormalization constant. We adopt the$ \alpha(0) $ scheme to renormalize the electric charge, in which the fine structure constant is set to its Thomson limit$ \alpha(0) $ and the electric charge renormalization constant$ \delta Z^{\alpha(0)}_e $ is given by [31]$\begin{aligned}[b] \delta Z^{\alpha(0)}_e =& -\dfrac{1}{2} \delta Z_{AA} - \dfrac{1}{2} \tan\theta_W \delta Z_{ZA} \\=& \dfrac{1}{2} \dfrac{\partial \displaystyle\sum\nolimits^{AA}_T(p^2)}{\partial p^2}\bigg{|}_{p^2 = 0} - \tan\theta_W \dfrac{\displaystyle\sum\nolimits^{AZ}_T(0)}{m^2_Z},\end{aligned} $

(9) where
$ \theta_W $ is the weak mixing angle and$ \sum^{ab}_T $ represents the transverse part of the unrenormalized self-energy of the$ a \rightarrow b $ transition. For the field and mass renormalization, we employ the on-mass-shell scheme. The definitions and expressions of the relevant renormalization constants in the on-mass-shell scheme can be found in [31]. After performing the renormalization procedure, all the UV singularities are canceled, and thus, the virtual correction is UV finite.The virtual photon in loops can induce soft and quasi-collinear infrared (IR) divergences. We introduce an infinitesimal fictitious photon mass to regularize IR divergences. According to the Kinoshita-Lee-Nauenberg (KLN) theorem [32, 33], we should consider the contribution from the real photon emission process
$\gamma\gamma \rightarrow $ $ e^+e^-\gamma\gamma$ to obtain IR-safe observables at the EW NLO. The IR divergences of the virtual correction can be canceled exactly by those of the real photon emission correction. We extract the IR singularities from the real emission correction by employing the dipole substraction (DS) method [34-37] and combine them with the virtual correction. In the DS method, a parameter$ \alpha \in (0, 1] $ is introduced to control the subtraction region [38, 39] ,but the total cross section is independent of α. We also employ the two cutoff phase space slicing (TCPSS) method [40] to deal with the real photon emission process for comparison, and find that the integrated cross sections obtained by using the DS and TCPSS methods agree well with each other within the calculation errors. -
Among all the methods of
$ e \rightarrow \gamma $ conversion, the best one is BCS of laser light on high energy electrons. The photons after BCS have an energy close to that of the initial electrons and follow their directions with some small angular spread. Given that the photon beams at the PLC are generated via BCS mechanism,$\gamma\gamma \rightarrow e^+e^-\gamma$ can be regarded as the subprocess of$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ . The production cross section for the parent process$ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma$ can be obtained by folding the cross section for$ \gamma\gamma \rightarrow e^+e^-\gamma $ with the photon luminosity, i.e.,$ \begin{aligned}[b]&\sigma(ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma;\, s) \\=& \int_{2 m_e/\sqrt{s}}^{x_{\rm{max}}} {\rm d}z \frac{{\rm d}{\cal{L}}_{\gamma\gamma}}{{\rm d}z}(z) \hat{\sigma}(\gamma\gamma \rightarrow e^+e^-\gamma;\, \hat{s} = z^2 s),\end{aligned} $

(10) where
$ \sqrt{s} $ and$ \sqrt{\hat{s}} $ are the c.m. colliding energies of ee and γγ systems, respectively. The photon luminosity is given by$ \frac{{\rm d}{\cal{L}}_{\gamma\gamma}}{{\rm d}z}(z) = 2 z \int_{z^2/x_{\rm{max}}}^{x_{\rm{max}}} \frac{{\rm d}x}{x}\phi_{\gamma/e}(x) \phi_{\gamma/e}(z^2/x), $

(11) where
$ \phi_{\gamma/e}(x) $ denotes the photon structure function, and x is the fraction of the energy of the incident electron carried by the back-scattered photon. As is well known, the degree of polarization of the back-scattered photon$ {\cal{P}}_{\gamma} $ is also a function of the energy fraction x. Both$ \phi_{\gamma/e} $ and$ {\cal{P}}_{\gamma} $ depend on the degrees of polarization of the incident electron and laser light. In the numerical treatment, the structure function$ \phi_{\gamma/e}(x) $ , the polarization degree function$ {\cal{P}}_{\gamma}(x) $ , and the maximum energy fraction$ x_{\rm{max}} $ of the back-scattered photon are all obtained from CompAZ [5], whose parametrization is based on a realistic TESLA prototype [41].Finally, the NLO EW corrected cross section for
$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ is given by$ \begin{aligned}[b]\sigma_{\rm{NLO}} =& \sigma_{\rm{LO}} \left( 1 + \delta_{\rm{EW}} \right)\,, \\\delta_{\rm{EW}} =& \frac{\Delta \sigma_{\rm{vir}} + \Delta \sigma_{\rm{real}}}{\sigma_{\rm{LO}}},\end{aligned} $

(12) where the NLO EW relative correction
$ \delta_{\rm{EW}} $ can be decomposed into QED and genuine weak relative corrections, i.e.,$ \delta_{\rm{EW}} = \delta_{\rm{QED}} + \delta_{\rm{W}} $ . The same definitions also hold for$ \gamma\gamma \rightarrow e^+e^-\gamma $ by substituting σ with$ \hat{\sigma} $ . In the following discussion on the$ \gamma\gamma \rightarrow e^+e^-\gamma $ channel, the superscript "^" in$ \hat{\sigma} $ will be omitted only for convenience. -
In this section, we provide the total cross sections and kinematic distributions of final particles for
$ \gamma\gamma \rightarrow e^+e^-\gamma $ up to the EW NLO for both${{J}} = 0$ and${{J}} = 2$ photon beam polarization configurations. Some kinematic cuts are imposed on the final state to exclude inevitable infrared divergences and fulfil the experimental requirement in the luminosity measurement. -
At the EW NLO, both
$ \gamma\gamma \rightarrow e^+e^-\gamma $ and$ \gamma\gamma \rightarrow e^+e^-\gamma \gamma $ channels are involved in the production of$ e^+e^-\gamma $ at the PLC. When generating$ e^+e^-\gamma $ event samples and calculating cross sections at the LO, the following set of kinematic and geometric acceptance requirements are applied on the final-state electron, positron and photon as event selection cuts:$ \begin{array}{*{20}{l}} {\rm{energies:}} & E_{e^{\pm}},\, E_{\gamma} \, \geqslant \, 10\; {\rm{GeV}} \\ {\rm{scattering\;angles:}} & \theta_{e^{\pm}},\, \theta_{\gamma} \, \in \, \left[ 10^{\circ},\, 170^{\circ} \right] \\ {\rm{opening\;angles:}} &\theta_{e^{\pm}\gamma} ,\, \theta_{e^+e^-} \, \geqslant \, 10^{\circ} \end{array} $

(13) where
$ \theta_{i}\; (i = e^{\pm},\, \gamma) $ denotes the scattering angle of the final-state particle i with respect to the incoming "+"-polarized photon beam direction, and$ \theta_{ij}\; (ij = e^{\pm}\gamma,\, e^+e^-) $ represents the opening angle between i and j in the c.m. frame of the initial-state γγ system. This set of kinematic cuts can also guarantee the IR safety at the LO, and all the final-state particles are well separated.For the
$ \gamma\gamma \rightarrow e^+e^-\gamma\gamma $ channel, the two tracks of the γγ- or$ \gamma e^{\pm} $ -pair will be recombined as a quasi-particle if they are sufficiently collinear ($ \theta_{\gamma\gamma}\; {\rm{or}}\; \theta_{e^{\pm}\gamma} \leqslant 10^{\circ} $ ), and the final state is regarded as an$ e^+e^-\gamma $ event; otherwise, it is categorized as an$ e^+e^-\gamma\gamma $ event. In this study, we adopt both inclusive and exclusive event selection schemes in the numerical calculations. In the inclusive event selection scheme (denoted by scheme-I), only the baseline event selection cuts in Eq. (13) are applied on the$ e^+e^-\gamma $ and$ e^+e^-\gamma\gamma $ events. It should be noted that only one of the two final-state photons needs to satisfy the kinematic constraints in Eq. (13) for an$ e^+e^-\gamma\gamma $ event. Hence, the events with two energetic and well separated photons are accepted in the inclusive event selection scheme. In contrast, an$ e^+e^-\gamma\gamma $ event will be rejected in the exclusive event selection scheme (denoted by scheme-II) if both final-state photons can pass the kinematic cuts in Eq. (13). -
The SM input parameters used in this paper are taken as [42]
$ \begin{array}{*{20}{l}} m_e = 0.5109989461\; {\rm{MeV}} & m_{\mu} = 105.6583745\; {\rm{MeV}} \\ m_{\tau} = 1776.86\; {\rm{MeV}} & m_u = 62\; {\rm{MeV}} \\ m_c = 1.5\; {\rm{GeV}} & m_t = 172.76\; {\rm{GeV}} \end{array} $

$ \begin{array}{*{20}{l}} m_d = 83\; {\rm{GeV}} & m_s = 215\; {\rm{MeV}}\\ m_b = 4.7\; {\rm{GeV}} & m_W = 80.379\; {\rm{GeV}}\\ m_Z = 91.1876\; {\rm{GeV}} & \Gamma_Z = 2.4952\; {\rm{GeV}} \\ \alpha(0) = 1/137.035999084 \end{array} $

(14) where the masses of light quarks can reproduce the hadronic contribution to the photon vacuum polarization [43], and
$ \alpha(0) $ is the fine structure constant in the Thomson limit.Normally, there exists mass-singular terms
$ \log(m_f^2/\mu^2) $ in both the electric charge renormalization constant and the photon wave-function renormalization constant. If the number of external photons equals that of the EW couplings in the tree-level amplitude, the full NLO EW correction is free of these unpleasant large logarithms because of the exact cancellation between the logarithms in the vertex counterterm and in the photon wave-function counterterm. Therefore, it is reasonable to adopt the$ \alpha(0) $ scheme for all the EW couplings involved in the$ \gamma\gamma \rightarrow e^+e^-\gamma $ process. -
In order to verify the correctness of our numerical calculations for the integrated cross section, we perform the following checks:
● We calculate the LO cross section for
$ \gamma\gamma \rightarrow e^+e^-\gamma $ in${{J}} = 0$ collision at$ \sqrt{\hat{s}} = 500\; {\rm{GeV}} $ by employing our developed FeynArts-3.7+FormCalc-7.3+LoopTools-2.8 and MadGraph5-2.3.3 [44] packages, respectively, and obtain$\begin{aligned}&{\sigma _{{\rm{LO}}}}\;[{\rm{pb}}] =\\& \left\{ {\begin{array}{*{20}{l}} {0.042817(5)}&{(\rm FeynArts+FormCalc+LoopTools)}\\ {0.04279(1)}&{(\rm MadGraph)} \end{array}} \right. \end{aligned}$

(15) These two results agree well with each other.
● We numerically verify the independence of the full NLO EW corrected cross section on the fictitious photon mass
$ m_{\gamma} $ in the range of$ 10^{-15} \leqslant m_{\gamma}/{\rm{GeV}} \leqslant 1 $ .● We calculate the NLO EW corrected cross section for
$ \gamma\gamma \rightarrow e^+e^-\gamma $ in${{J}} = 0$ collision at$ \sqrt{\hat{s}} = 250,500, $ $ 1000\; {\rm{GeV}} $ in scheme-I by adopting the DS (with$ \alpha = 0.1 $ ) and TCPSS (with$ \delta_s = \delta_c = 0.001 $ ) methods separately, and find that the numerical results (shown in Table 1) are coincident with each other within the calculation errors.$\sqrt{\hat{s} }/{\rm{GeV} }$ 

250 500 1000 $\sigma_{\rm{NLO} }^{\rm{(I)} }/{\rm{pb} }$ 

DS 0.15534(4) 0.04261(2) 0.01090(1) TCPSS 0.15525(9) 0.04260(3) 0.01092(2) Table 1. NLO EW corrected cross sections for
$ \gamma\gamma \rightarrow e^+e^-\gamma $ in${{J}} = 0$ collision at$ \sqrt{\hat{s}} = 250,500, 1000\; {\rm{GeV}} $ in the inclusive event selection scheme obtained by using the DS and TCPSS methods separately.In further numerical calculations, we adopt only the DS method with
$ \alpha = 0.1 $ , and fix the fictitious photon mass as$ m_{\gamma} = 10^{-2}\; {\rm{GeV}} $ . For brevity, the NLO EW corrected cross sections and the corresponding EW and pure QED relative corrections in the inclusive and exclusive event selection schemes are denoted by$ \sigma_{\rm{NLO}}^{\rm{(I, II)}} $ ,$ \delta_{\rm{EW}}^{\rm{(I, II)}} $ and$ \delta_{\rm{QED}}^{\rm{(I, II)}} $ , respectively. Since the colliding energy dependence of the NLO EW corrected integrated cross section and differential distributions in scheme-I are almost the same as the LO predictions, we only depict the integrated and differential cross sections in scheme-II in the following discussion.In Figs. 3 (a) and (b), we present the integrated cross sections
$ \sigma_{\rm{LO}} $ ,$ \sigma^{\rm{(II)}}_{\rm{NLO}} $ (in upper panels) and the corresponding EW relative corrections$ \delta_{\rm{EW}}^{\rm{(I, II)}} $ (in lower panels) as functions of the γγ c.m. colliding energy for the$ e^+e^-\gamma $ production in${{J}} = 0$ and${{J}} = 2$ γγ collisions, respectively. As illustrated in this figure, the LO and NLO EW corrected cross sections for$ \gamma\gamma \rightarrow e^+e^-\gamma $ in both${{J}} = 0$ and${{J}} = 2$ γγ collision modes decrease quickly as$ \sqrt{\hat{s}} $ increases from$ 120\; {\rm{GeV}} $ to$ 1\; {\rm{TeV}} $ . The EW relative correction is sensitive to the γγ colliding energy. In the inclusive event selection scheme, it increases in the low colliding energy region, reaches its maximum at$ \sqrt{\hat{s}} \sim 300 $ and$ 160\; {\rm{GeV}} $ for the${{J}} = 0$ and${{J}} = 2$ collision modes, respectively, and then decreases gradually as increase of$ \sqrt{\hat{s}} $ . In the exclusive event selection scheme, the EW relative correction is negative in the plotted$ \sqrt{\hat{s}} $ region. It decreases monotonically from −2.30% to −9.20% and from −2.36% to −10.65% for${{J}} = 0$ and${{J}} = 2$ , respectively, as$ \sqrt{\hat{s}} $ varies from$ 120\; {\rm{GeV}} $ to$ 1\; {\rm{TeV}} $ .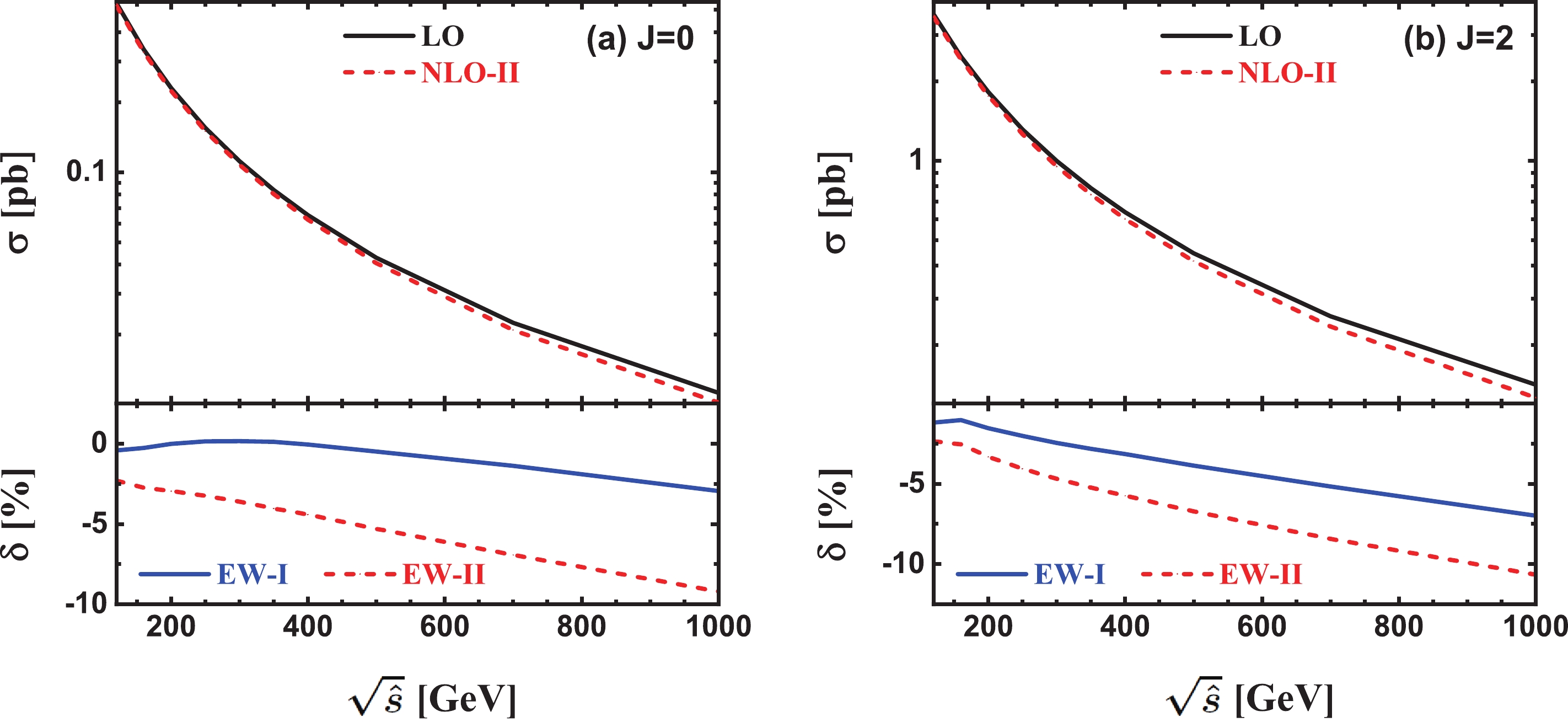
Figure 3. (color online) LO, NLO EW corrected integrated cross sections in scheme-II and the EW relative corrections in both scheme-I and -II as functions of
$ \sqrt{\hat{s}} $ for the$ e^+e^-\gamma $ production in (a)${{J}} = 0$ and (b)$ {\rm{J}} = 2 $ γγ collisions.To analyze the constituents of the NLO EW correction more clearly, we depict the dependence of the pure QED and genuine weak relative corrections in both inclusive and exclusive event selection schemes on the γγ colliding energy for the
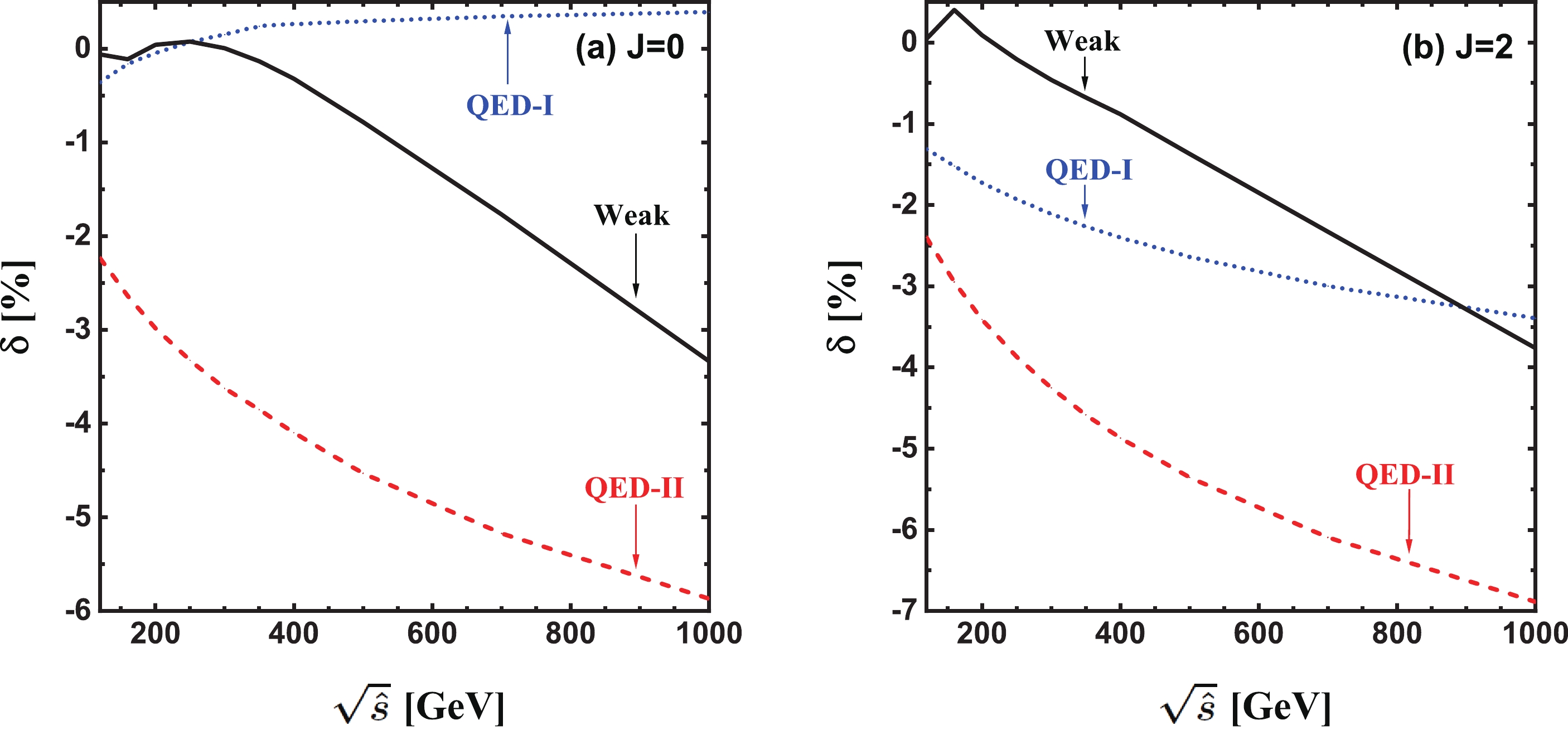
$ e^+e^-\gamma $ production in${{J}} = 0$ and${{J}} = 2$ γγ collisions in Figs. 4 (a) and (b) separately②. In the exclusive event selection scheme, both QED and genuine weak relative corrections strongly depend on the γγ colliding energy, and the full NLO EW correction is dominated by the QED correction. As$ \sqrt{\hat{s}} $ increases from$ 120\; {\rm{GeV}} $ to$ 1\; {\rm{TeV}} $ , the pure QED relative correction decreases consistently from −2.23% to −5.87% for the J = 0 collision mode, and from −2.40% to −6.89% for the${{J}} = 2$ collision mode. Compared to the QED relative correction, the weak relative correction is not a monotonically decreasing function of$ \sqrt{\hat{s}} $ . It can be seen from Fig. 4(b) that there is a small peak at$ \sqrt{\hat{s}} \simeq 2 m_W \simeq $ $ 160\; {\rm{GeV}} $ in the colliding energy distribution of the weak relative correction to the$ e^+e^-\gamma $ production via${{J}} = 2$ γγ collision, which corresponds to the W-pair resonance induced by the triangle loop in Fig. 2 (1). For both the${{J}} = 0$ and${{J}} = 2$ collision modes, the weak relative correction is small ($ \left| \delta_{\rm{W}} \right| $ < 0.5% ) when$ \sqrt{\hat{s}} < 300\; {\rm{GeV}} $ , while it becomes relatively remarkable in the high energy region due to the Sudakov logarithms induced by the virtual exchange of soft or collinear massive weak gauge bosons [45, 46]. At$ \sqrt{\hat{s}} = 1\; {\rm{TeV}} $ ,$ (\delta_{\rm{W}},\, \delta_{\rm{EW}}^{\rm{(II)}}) $ = (−3.33%, −9.20%) and (−3.76%, −10.65%) for${{J}} = 0$ and${J} = 2$ , respectively. It clearly indicates that the full EW relative correction to$ e^+e^-\gamma $ production in the exclusive event selection scheme can reach and even exceed −10% at a TeV PLC. In the inclusive event selection scheme, the QED relative correction contributed by$ e^+e^-\gamma\gamma $ events, i.e.,$ \delta_{\rm{QED}}^{\rm{(I)}} - \delta_{\rm{QED}}^{\rm{(II)}} $ , is sizable, especially in the high energy region. It increases gradually from 1.88% to 6.26% and from 1.09% to 3.49% for${{J}} = 0$ and${{J}} = 2$ , respectively, as$ \sqrt{\hat{s}} $ increases from$ 120\; {\rm{GeV}} $ to$ 1\; {\rm{TeV}} $ . -
The LO, NLO EW corrected energy distributions of the final-state positron in scheme-II and the corresponding EW relative corrections in both scheme-I and -II for the
$ e^+e^-\gamma $ production in${{J}} = 0$ and${{J}} = 2$ collisions at$ \sqrt{\hat{s}} = 500\; {\rm{GeV}} $ PLC are presented in Figs. 5(a) and (b), respectively. As$ \sqrt{\hat{s}} $ increases, the LO and NLO EW corrected$ E_{e^+} $ distributions for${{J}} = 0$ γγ collision mode decrease gradually, reach their minima at$ \sqrt{\hat{s}} \sim 160\; {\rm{GeV}} $ , and then increase rapidly to their maxima at$E_{e^+} \sim $ $ \sqrt{\hat{s}}/2 - E_{\gamma, \min} = 240\; {\rm{GeV}}$ , which corresponds to the minimum-energy photon emitted from positron, while the$ E_{e^+} $ distributions for${ {J}} = 2$ collision mode increases monotonically before reaching their maxima at$ \sqrt{\hat{s}} \sim 240\; {\rm{GeV}} $ . The LO, NLO EW corrected scattering angle distributions of the final-state positron and the corresponding EW relative corrections are depicted in Figs. 5(c) and (d). For the${ {J}} = 0$ collision mode, both${\rm d}\sigma_{\rm{LO}}/{\rm d}\cos\theta_{e^+}$ and${\rm d}\sigma_{\rm{NLO}}^{\rm{(I, II)}}/ $ $ {\rm d}\cos\theta_{e^+}$ are symmetric with respect to$ \cos\theta_{e^+} = 0 $ ③. The corresponding EW relative correction increases from −1.3% to −0.3% as$ \cos\theta_{e^+} $ varies from 0 to$ \cos 10^{\circ} = $ $ 0.985 $ in the inclusive event selection scheme, while it is steady at around −5.5% for$ \left| \cos\theta_{e^+} \right| < 0.9 $ in the exclusive event selection scheme. For the${ {J}} = 2$ collision mode, although the LO$ \cos\theta_{e^+} $ distribution is also symmetric with respect to$ \cos\theta_{e^+} = 0 $ , the NLO EW correction breaks this forward-backward symmetry. In the exclusive event selection scheme, the EW relative correction is negative and notable ($ | \delta_{\rm{EW}}^{\rm{(II)}} | $ > 5%), and can reach about −10% at$ \cos\theta_{e^+} \sim 0.5 $ . The lineshape of the EW relative correction in the inclusive event selection scheme is the same as the exclusive event selection scheme. The QED relative correction contributed by$ e^+e^-\gamma\gamma $ events is steady at around 2.8%.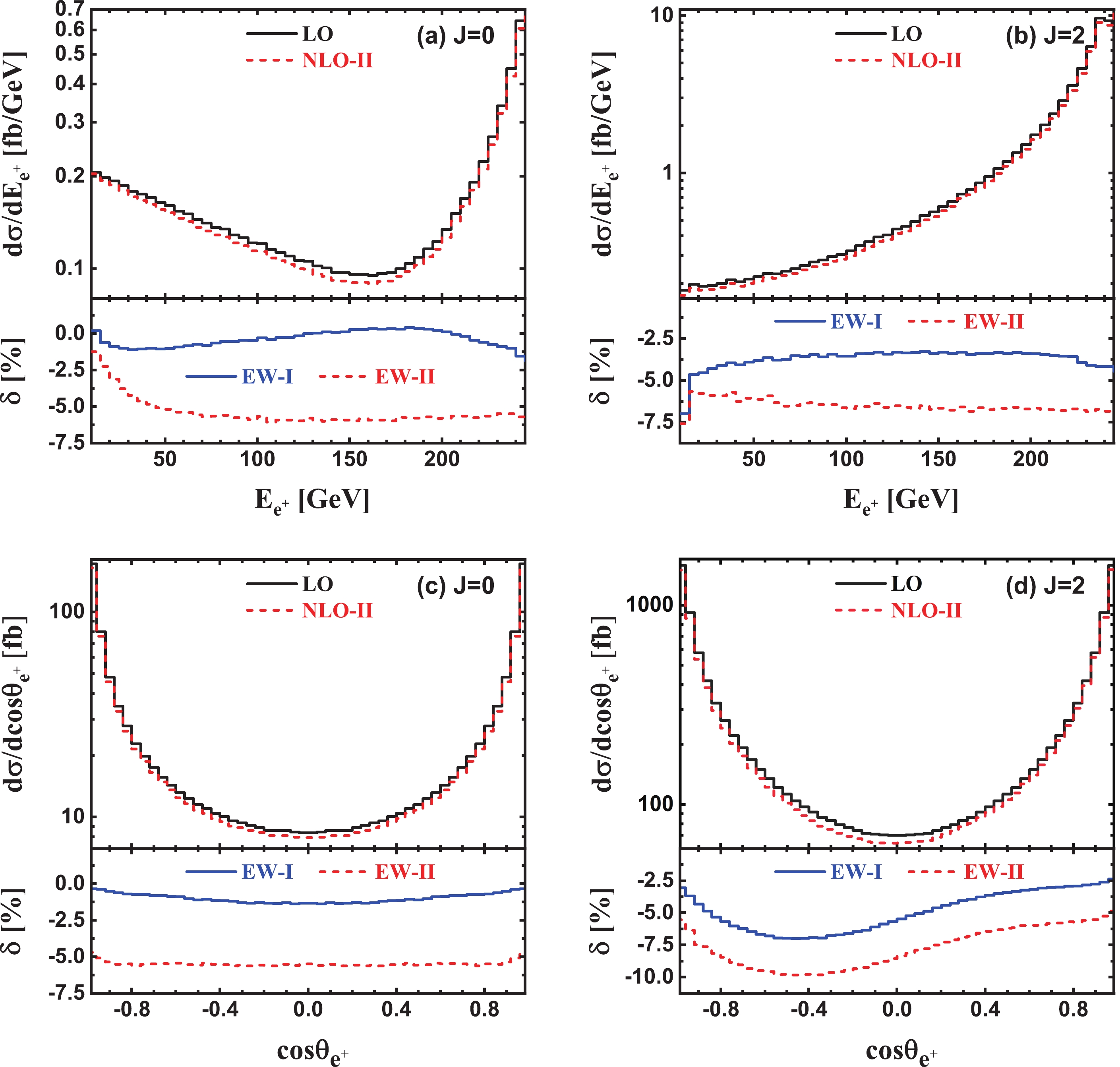
Figure 5. (color online) LO, NLO EW corrected differential distributions of the final-state positron and the corresponding EW relative corrections for the
$ e^+e^-\gamma $ production at$ \sqrt{\hat{s}} = 500\; {\rm{GeV}} $ PLC. (a), (b), (c) and (d) are for the energy and scattering angle distributions in${{J}} = 0$ and${{J}} = 2$ collision modes, respectively.The LO, NLO EW corrected energy and scattering angle distributions of the final-state electron, as well as the corresponding EW relative corrections for the
$ e^+e^-\gamma $ production in${{J}} = 0$ and${{J}} = 2$ collisions at$ 500\; {\rm{GeV}} $ PLC are plotted in Figs. 6(a)−(d). As expected, all the kinematic distributions of the final-state electron are the same as the corresponding ones of the final-state positron for both$ \gamma_+\gamma_+ \rightarrow e^+e^-\gamma $ (J = 0) and$ \gamma_+\gamma_- \rightarrow e^+e^-\gamma $ (J = 2) channels at the LO, due to the charge symmetry. However, it should be noted that the charge conjugation is only a Born-level symmetry operation for the$ e^+e^-\gamma $ production at the PLC since$ \gamma\gamma \rightarrow e^+e^-\gamma $ is a pure QED process at the lowest order, and the charge symmetry will be broken at the EW NLO by weak correction. Consequently, the EW relative corrections to the kinematic distributions of electron differ from the corresponding ones of the positron for the$ e^+e^-\gamma $ production in the${{J}} = 0$ γγ collision, as illustrated in the lower panels of Figs. 5(a, c) and Figs. 6(a, c). As stated in Sec. II.A, the kinematic behaviors of the final-state electron should be the same as positron for${{J}} = 2$ γγ collision mode due to the$ {\cal{CP}} + Bose $ symmetry. It can be concluded from Eq. (5) that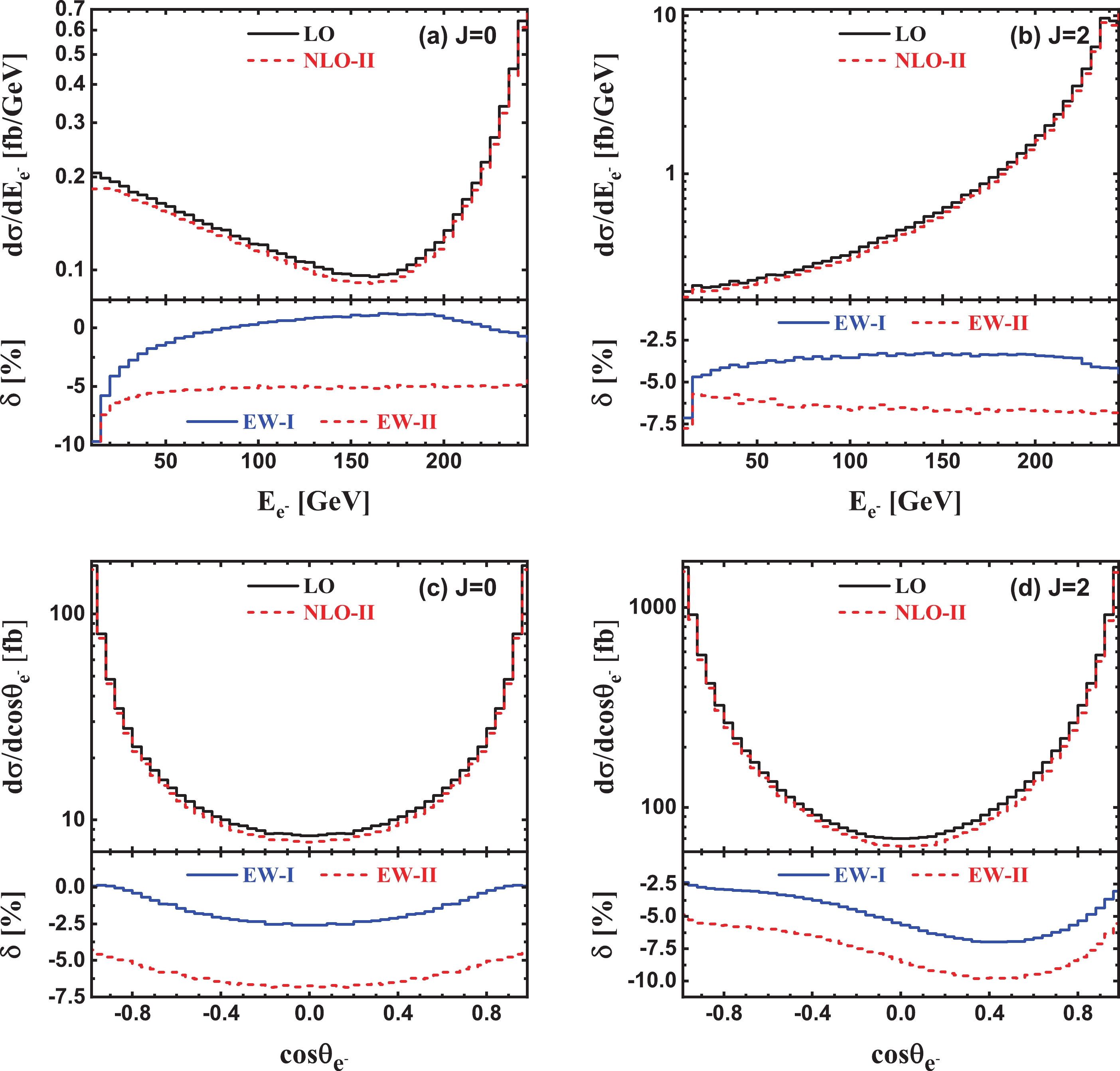
Figure 6. (color online) Same as Fig. 5, but for the final-state electron.
${\left. {\frac{{{\rm d}\sigma }}{{{\rm d}{E_{{e^ - }}}}} = \frac{{{\rm d}\sigma }}{{{\rm d}{E_{{e^ + }}}}}} \right|_{{E_{{e^ + }}} \to {E_{{e^ - }}}}}\quad {\rm{and}}\quad \frac{{{\rm d}\sigma }}{{{\rm d}\cos {\theta _{{e^ - }}}}} = {\left. {\frac{{{\rm d}\sigma }}{{{\rm d}\cos {\theta _{{e^ + }}}}}} \right|_{{\theta _{{e^ + }}} \to \pi - {\theta _{{e^ - }}}}}$

(16) at both LO and EW NLO. By comparing Figs. 6(b, d) with Figs. 5(b, d), it can be seen that the numerical results for
$ E_{e^{\pm}} $ and$ \cos\theta_{e^{\pm}} $ distributions of the$ \gamma_+\gamma_- \rightarrow e^+e^-\gamma $ production channel satisfy Eq. (16) exactly. The consistency of our numerical results with the$ {\cal{CP}} + Bose $ symmetry for the$ e^+e^-\gamma $ production in${{J}} = 2$ γγ collision also verifies the correctness of our calculations.For an
$ e^+e^-\gamma\gamma $ event collected in the inclusive event selection scheme, the two photons are called leading and sub-leading photons, respectively, according to their energies in decreasing order (The photon of an$ e^+e^-\gamma $ event can also be named as a leading photon). In the upper panels of Figs. 7(a)-(d), we depict the energy and scattering angle distributions of the leading photon for$ e^+e^-\gamma $ production in${{J}} = 0$ and${{J}} = 2$ γγ collisions at$ \sqrt{\hat{s}} = 500\; {\rm{GeV}} $ PLC, at both LO and EW NLO. The corresponding EW relative corrections are provided in the lower panels. As illustrated in Figs. 7(a) and (b), the LO and NLO EW corrected energy distributions of the leading photon in scheme-II increase consistently as$ \sqrt{\hat{s}} $ increases from 10 to$ 240\; {\rm{GeV}} $ for the${{J}} = 0$ polarization configuration of the incoming photon beams, while decrease gradually as$ \sqrt{\hat{s}} $ increases in the most plotted$ E_{\gamma} $ region for${{J}} = 2$ γγ collision mode. The peak structure at$ \sqrt{\hat{s}} \sim 240\; {\rm{GeV}} $ in the EW relative corrections in both inclusive and exclusive event selection schemes can be attributed to the Z resonance effect induced by the loop diagram in Fig. 2(2). At the Z resonance,$ M_{e^+e^-} = m_Z $ , and thus$ E_{\gamma} = (\hat{s} - m_Z^2)/(2 \sqrt{\hat{s}}) $ $ \sim 240\; {\rm{GeV}} $ , which corresponds to a photon recoiling against an on-shell Z boson. From Figs. 7(c) and (d), it can be seen that both the LO$ \cos\theta_{\gamma} $ distribution and the NLO EW correction are symmetric with respect to$ \cos\theta_{\gamma} = 0 $ , and the differential distribution increases rapidly as the increase of$ \left| \cos\theta_{\gamma} \right| $ . It implies that the leading photon prefers to be produced along the incoming photon beam directions. In the exclusive event selection scheme, the EW relative correction is negative and sizable. It can exceed −6% for${{J}} = 0$ and −7% for${{J}} = 2$ , respectively, when the final-state leading photon is produced centrally ($ \left| \cos\theta_{\gamma} \right| < 0.5 $ ).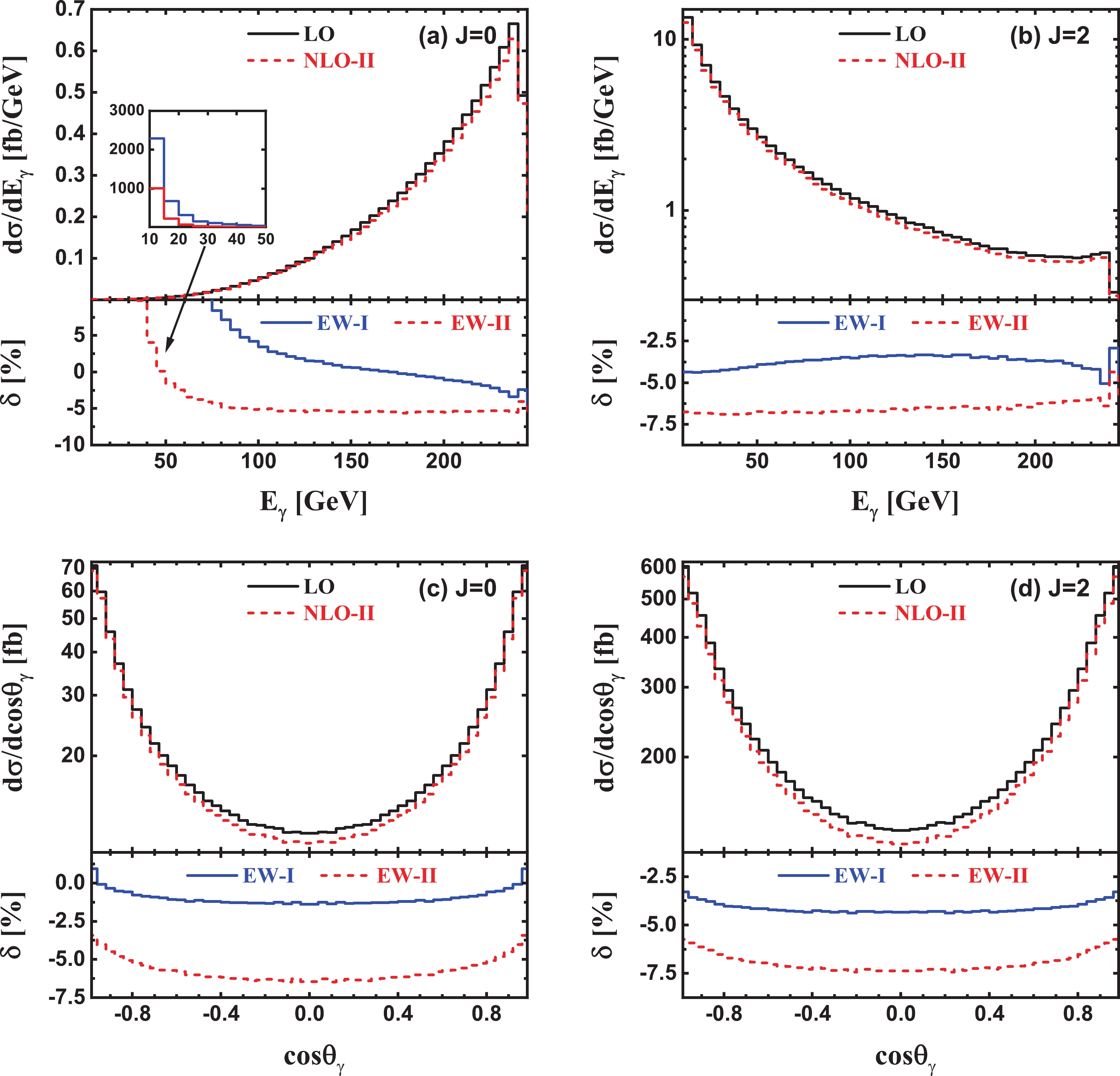
Figure 7. (color online) Same as Fig. 5, but for the final-state leading photon.
The LO, NLO EW corrected invariant mass and opening angle distributions of the final-state
$ \gamma e^+ $ system (or more strictly speaking, the final-state leading photon and positron) and the corresponding EW relative corrections for$ e^+e^-\gamma $ production via$ \gamma_+\gamma_+ $ and$ \gamma_+\gamma_- $ collisions at$ \sqrt{\hat{s}} = 500\; {\rm{GeV}} $ PLC are presented in Figs. 8(a)-(b) separately. For${{J}} = 0$ (i.e.,$ \gamma_+\gamma_+ $ ) collision mode, the invariant mass distribution of the$ \gamma e^+ $ system increases sharply in the low$ M_{\gamma e^+} $ region, reaches its maximum at$ \sqrt{\hat{s}} \sim 70\; {\rm{GeV}} $ , and then decreases gradually as$ M_{\gamma e^+} $ increases to about$ 260\; {\rm{GeV}} $ . Subsequently, the invariant mass distribution increases rapidly as$ M_{\gamma e^+} $ increases. The EW relative correction in the exclusive event selection scheme is steady at around –5% in most of the$ M_{\gamma e^+} $ region. For${{J}} = 2$ (i.e.,$ \gamma_+\gamma_- $ ) collision mode, there are two sharp peaks located at$ M_{\gamma e^+} \sim 20\; {\rm{GeV}} $ and$ M_{\gamma e^+} \sim 100\; {\rm{GeV}} $ in the$ \gamma e^+ $ invariant mass distribution. As we know, the invariant mass of the final-state$ \gamma e^+ $ system is given by
Figure 8. (color online) LO, NLO EW corrected invariant mass and opening angle distributions of the final-state
$ \gamma e^+ $ system and the corresponding EW relative corrections for the$ e^+e^-\gamma $ production in${{J}} = 0$ and${{J}} = 2$ γγ collisions at$ \sqrt{\hat{s}} = 500\; {\rm{GeV}} $ PLC.$ M_{\gamma e^+} \approx M_{\gamma e^+}^{\rm{(LO)}} = \sqrt{\hat{s} + m_e^2 - 2 E_{e^-} \sqrt{\hat{s}}}, $

(17) where
$ M_{\gamma e^+}^{\rm{(LO)}} $ is the lowest-order approximation of$ M_{\gamma e^+} $ . From Eq. (17), it can be seen that$ M_{\gamma e^+} \sim 20\; {\rm{GeV}} $ and$ M_{\gamma e^+} \sim 100\; {\rm{GeV}} $ are equivalent to$ E_{e^-} \sim 250\; {\rm{GeV}} $ and$ E_{e^-} \sim 240\; {\rm{GeV}} $ , respectively. It is evident that these two peaks in the$ \gamma e^+ $ invariant mass distribution can be attributed to the highest-energy electron ($ E_{e^-} \sim \sqrt{\hat{s}}/2 $ ) and a minimum-energy photon emitted from an electron ($E_{e^-} \sim $ $ \sqrt{\hat{s}}/2 - E_{\gamma, \min}$ ), respectively. Moreover, it can be deduced from the upper plots of Figs. 8(c) and (d) that the angular distributions of the final-state positron and leading photon are highly correlated. The positron and leading photon prefer to be produced back-to-back in the${{J}} = 0$ γγ collision, while tend to be produced in the same direction or back-to-back in the${{J}} = 2$ γγ collision. It is worth mentioning that the EW relative correction in the exclusive event selection scheme is relatively stable in the entire$ \theta_{\gamma e^+} $ region, especially for the${{J}} = 2$ collision mode.The differential cross sections with respect to the invariant mass and opening angle of the final-state
$ \gamma e^- $ system, as well as the corresponding EW relative corrections, are also provided in Figs. 9(a)-(d) for comparison. As expected, the invariant mass and opening angle distributions of the final-state$ \gamma e^- $ system are exactly the same as the corresponding ones of$ \gamma e^+ $ system at the LO due to the charge conservation in the electromagnetic interaction. For the$ \gamma_+\gamma_+ \rightarrow e^+e^-\gamma $ (i.e.,${{J}} = 0$ ) production channel, the EW relative corrections to$ M_{\gamma e^-} $ and$ \cos\theta_{\gamma e^-} $ distributions significantly differ from the EW relative corrections to$ M_{\gamma e^+} $ and$ \cos\theta_{\gamma e^+} $ distributions, as illustrated in the lower panels of Figs. 8(a, c) and Figs. 9(a, c), due to the charge symmetry violation in the weak interaction. In contrast, the EW relative corrections to the kinematic distributions of$ \gamma e^- $ and$ \gamma e^+ $ systems are exactly the same for the$\gamma_+\gamma_- \rightarrow $ $ e^+e^-\gamma$ (i.e.,${{J}} = 2$ ) production channel, as illustrated in the lower panels of Figs. 8(b, d) and Figs. 9(b, d), because of the$ {\cal{CP}} + Bose $ symmetry. The numerical consistency between the kinematic distributions of the final-state$ \gamma e^- $ and$ \gamma e^+ $ systems in the$ \gamma_+\gamma_- $ collision reconfirms the conclusion declared in Sec. II.A.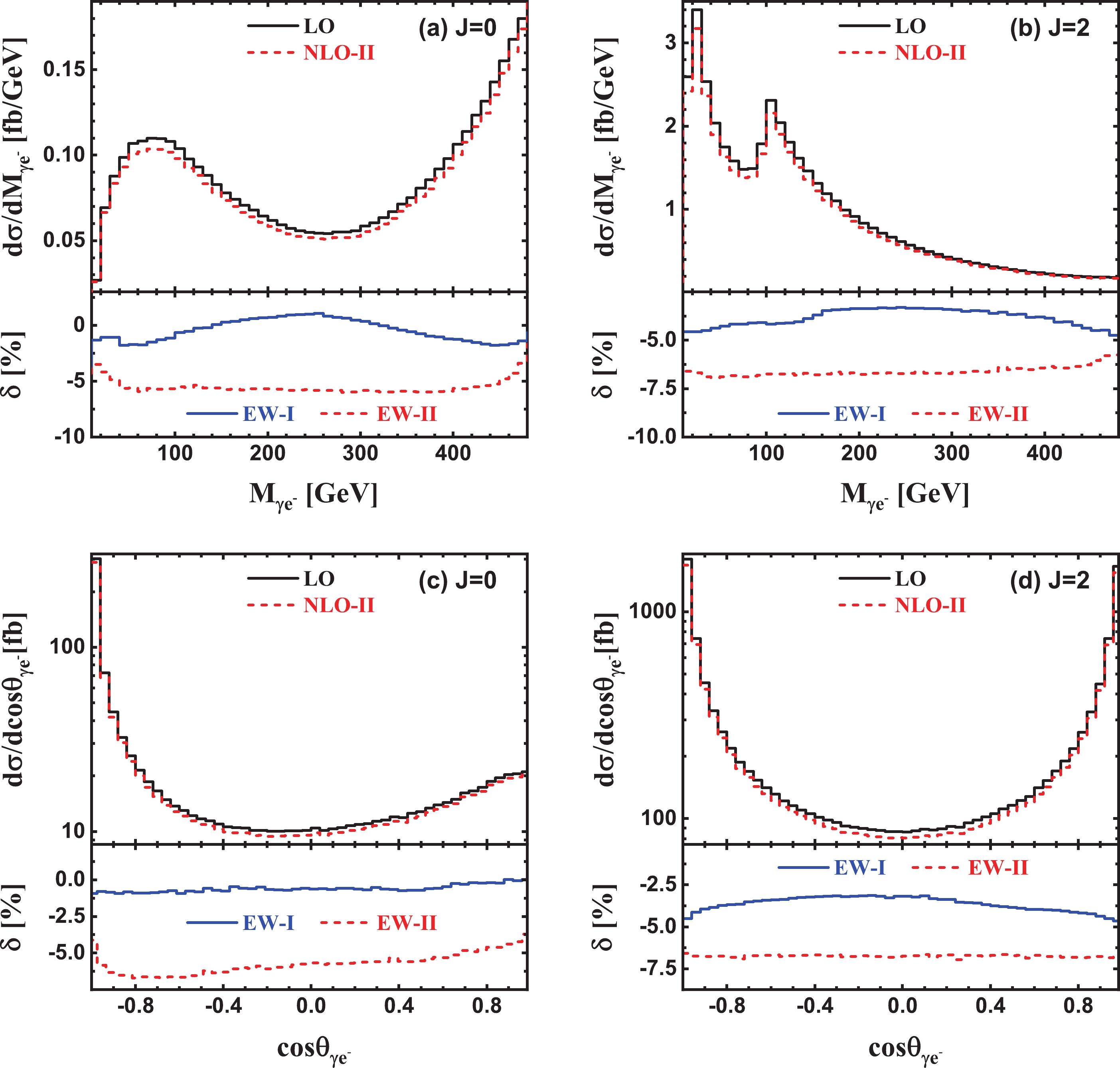
Figure 9. (color online) Same as Fig. 8, but for the final-state
$ \gamma e^- $ system. -
Now, we turn to the discussion of the parent process
$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ . The differential cross section for$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ with respect to a kinematic variable ζ can be expressed as$ \frac{{\rm d} \sigma}{{\rm d} \zeta} = \frac{{\rm d} \sigma^{(0)}}{{\rm d} \zeta} + \frac{{\rm d} \sigma^{(2)}}{{\rm d} \zeta}, $

(18) where
${\rm d} \sigma^{(0)}/{\rm d} \zeta$ and${\rm d} \sigma^{(2)}/{\rm d} \zeta$ represent the contributions from${{J}} = 0$ and${{J}} = 2$ γγ collision modes, respectively. Considering that the two back-scattered photon beams are partially polarized,${\rm d}\sigma^{(0)}/{\rm d} \zeta$ and${\rm d}\sigma^{(2)}/{\rm d} \zeta$ are calculated by$ \begin{aligned}[b] \frac{{\rm d} \sigma^{\rm{(J)}}}{{\rm d} \zeta}(s) =& \displaystyle\sum\limits_{\lambda_1 = (-1)^{\frac{{\rm{J}}}{2}} \lambda_2} \displaystyle\int_{2 m_e/\sqrt{s}}^{x_{\rm{max}}} \frac{z {\rm d}z}{2} \int_{z^2/x_{\rm{max}}}^{x_{\rm{max}}} \frac{{\rm d}x}{x} \phi_{\gamma/e}(x) \phi_{\gamma/e}(z^2/x) \\ & \times \Big[ 1 + \lambda_1 {\cal{P}}_{\gamma}(x) \Big] \Big[ 1 + \lambda_2 {\cal{P}}_{\gamma}(z^2/x) \Big] \frac{{\rm d} \hat{\sigma}^{\lambda_1\lambda_2}}{{\rm d} \zeta}(\hat{s} = z^2 s)\,,\\&({ {J}} = 0,\, 2) \end{aligned} $

(19) When discussing the angular distributions of final particles in the c.m. frame of the initial ee system, the reference direction can be chosen as either of the two electron beam directions due to the forward-backward symmetry.
In Figs. 10 (a) and (b), we depict the LO, NLO EW corrected integrated cross sections from the
${{J}} = 0$ and${{J}} = 2$ γγ collisions in the exclusive event selection scheme, as well as the corresponding EW relative corrections in both inclusive and exclusive event selection schemes as functions of the ee c.m. colliding energy for$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ . The integrated contributions from${{J}} = 0$ and${{J}} = 2$ γγ collisions increase at first, reach their maxima at$ \sqrt{s} \sim 140 $ and$ 200\; {\rm{GeV}} $ , respectively, and then decrease rapidly as$ \sqrt{s} $ increases. In the exclusive event selection scheme, the EW relative correction to the integrated cross section from the${{J}} = 0$ γγ collision is relatively stable as$ \sqrt{s} \in [400,\, 1000]\; {\rm{GeV}} $ , varying in the range of [−3.2%, −2.7%]. Compared to${{J}} = 0$ , the EW relative correction to the integrated cross section from${{J}} = 2$ γγ collision is more sensitive to the ee c.m. colliding energy. It decreases approximately linearly from about −2.5% to about −3.8% as$ \sqrt{s} $ increases from$ 400\; {\rm{GeV}} $ to$ 1\; {\rm{TeV}} $ . Similar to the discussion on$ \gamma\gamma \rightarrow e^+e^-\gamma $ , we also separately provide weak and QED relative corrections to the parent process$ ee \rightarrow \gamma\gamma \rightarrow $ $ e^+e^-\gamma $ for both${{J}} = 0$ and${{J}} = 2$ polarization configurations of the Compton back-scattered photons. As illustrated in Figs. 11(a) and (b), the weak relative correction is small ($ \left| \delta_{\rm{W}} \right| $ < 0.5%) and the full NLO EW correction is dominated by the negative QED correction for both polarization modes of the back-scattered photons in the entire plotted$ \sqrt{s} $ region ($ 120\; {\rm{GeV}} < \sqrt{s} < 1000\; {\rm{GeV}} $ ). In the exclusive event selection scheme, the QED relative correction reaches its maximum of about −1.9% at$ \sqrt{s} \sim 150\; {\rm{GeV}} $ and is roughly steady at −2.9% as$ \sqrt{s} \in [500,\, 1000]\; {\rm{GeV}} $ for the${{J}} = 0$ polarization of the back-scattered photons, while it decreases gradually from its maximum of approximately −1.9% to approximately −3.4% as$ \sqrt{s} $ increases from$ 180\; {\rm{GeV}} $ to$ 1\; {\rm{TeV}} $ for the${{J}} = 2$ γγ polarization mode. As is well known, the maximum energy fraction of the back-scattered photon is given by [5]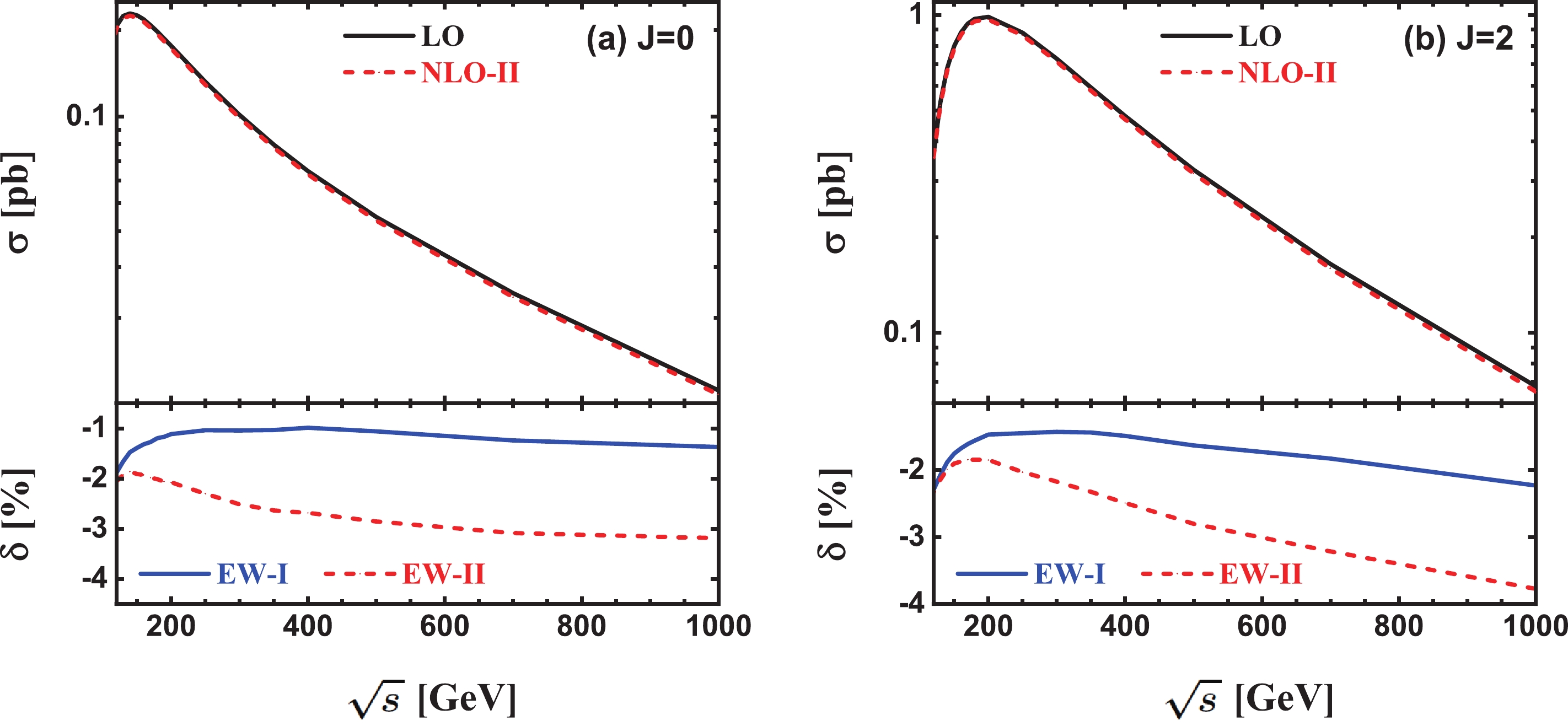
Figure 10. (color online) LO, NLO EW corrected integrated cross sections from (a)
${{J}} = 0$ and (b)${{J}} = 2$ γγ collisions in scheme-II and the corresponding EW relative corrections in both scheme-I and -II as functions of$ \sqrt{s} $ for$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ .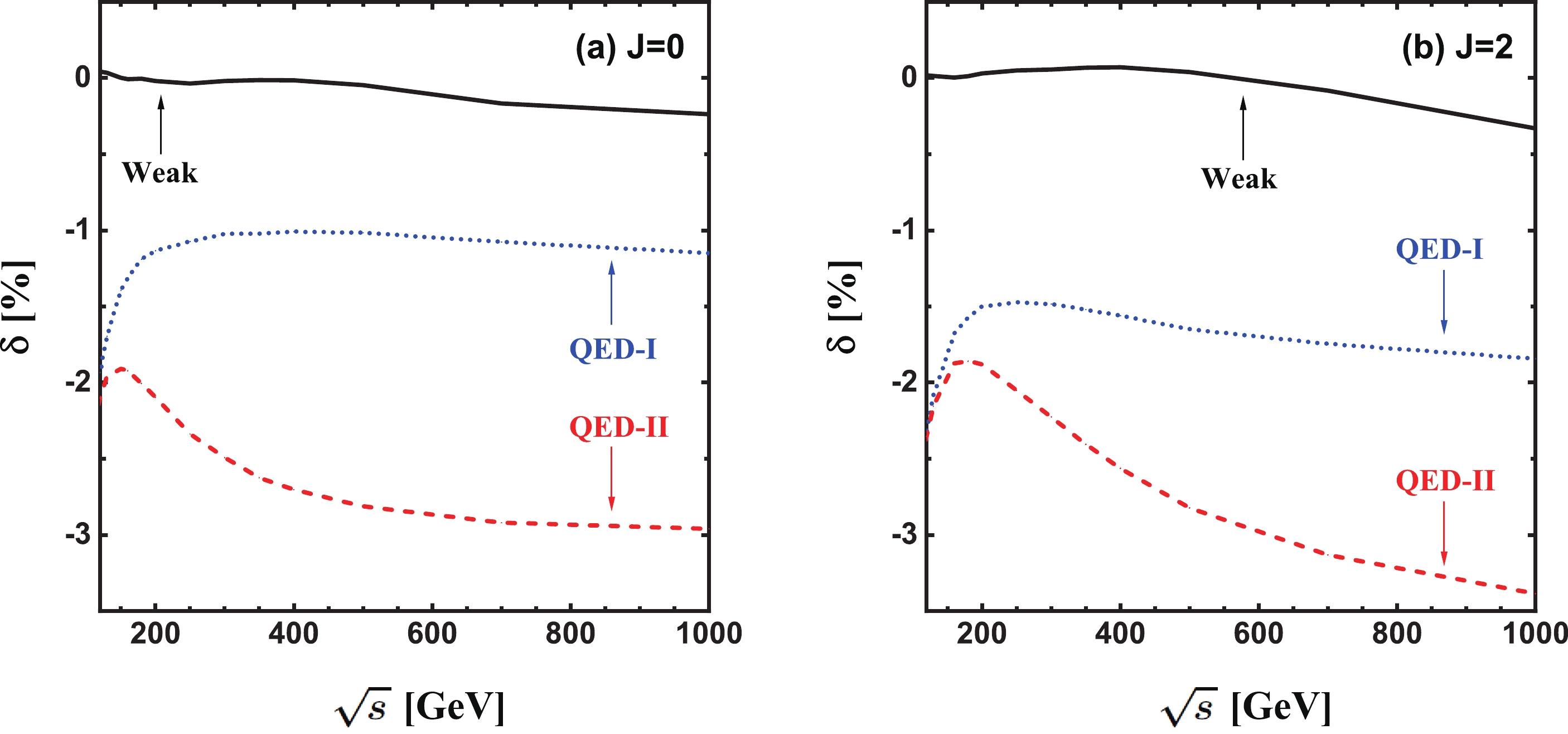
Figure 11. (color online) QED and weak relative corrections to the integrated cross sections from (a)
${{J}} = 0$ and (b)${{J}} = 2$ γγ collisions in both scheme-I and -II as functions of$ \sqrt{s} $ for$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ .$ x_{\rm{max}} = \frac{4E_e E_0}{4E_e E_0 + m_e^2}, $

(20) where
$ E_e $ represents the electron beam energy and$ E_0 $ denotes the energy of the laser photon. In this study, we take$ E_0 = 1.17\; {\rm{eV}} $ (i.e., the laser wave length$\lambda = 1.06\; \mu{\rm{m}}$ ). At$ \sqrt{s} = 120\; {\rm{GeV}} $ , the maximum c.m. colliding energy of the back-scattered photon beams is only approximately$ 60\; {\rm{GeV}} $ , thus the NLO QED contribution of the$e^+e^-\gamma\gamma $ events is too tiny to be ignored due to the small phase space of the$ e^+e^-\gamma\gamma $ four-body final state. As$ \sqrt{s} $ increases, the QED relative correction contributed by$ e^+e^-\gamma\gamma $ events (i.e.,$ \delta_{\rm{QED}}^{\rm{(I)}} - \delta_{\rm{QED}}^{\rm{(II)}} $ ) becomes more and more notable and compensates the negative EW correction from$ e^+e^-\gamma $ events. While$ \sqrt{s} \in [600,\, 1000]\; $ $ {\rm{GeV}} $ , the QED relative correction in the inclusive event selection scheme is steady at around −1.1% and −1.8% for${{J}} = 0$ and${{J}} = 2$ , respectively. Finally, in Table 2 and Table 3, we present in detail the production cross sections and the corresponding NLO relative corrections for$ee \rightarrow \gamma\gamma \rightarrow $ $ e^+e^-\gamma$ at$ \sqrt{s} = 250 $ , 500, and$ 1000\; {\rm{GeV}} $ , which correspond to the three stages of the ILC [2]. For more details on the kinematic distributions of final products of$ ee \rightarrow $ $ \gamma\gamma \rightarrow e^+e^-\gamma $ , refer to the Appendix section of this article.$\sqrt{s}/{\rm{GeV} }$ 

$\sigma_{\rm{LO} }/{\rm{fb} }$ 

$\sigma_{\rm{NLO} }^{\rm{(I)} }/{\rm{fb} }$ 

$\sigma_{\rm{NLO} }^{\rm{(II)} }/{\rm{fb} }$ 

$\delta_{\rm{EW} }^{\rm{(I)} }/(\%)$ 

$\delta_{\rm{EW} }^{\rm{(II)} }/(\%)$ 

$\delta_{\rm{QED} }^{\rm{(I)} } /(\%)$ 

$\delta_{\rm{QED} }^{\rm{(II)} } (\%)$ 

$\delta_{\rm{W} }/(\%)$ 

250 131.93 130.46 128.80 −1.11 −2.37 −1.05 −2.31 −0.06 500 44.729 44.260 43.452 −1.05 −2.85 −1.01 −2.81 −0.04 1000 11.195 11.041 10.838 −1.38 −3.19 −1.14 −2.95 −0.24 Table 2. LO, NLO EW corrected cross sections and the corresponding NLO relative corrections for
$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ via${{J}} = 0$ collision of Compton back-scattered photons at$ \sqrt{s} = 250 $ , 500 and$ 1000\; {\rm{GeV}} $ .$\sqrt{s}/{\rm{GeV} }$ 

$\sigma_{\rm{LO} }/{\rm{fb} }$ 

$\sigma_{\rm{NLO} }^{\rm{(I)} }/{\rm{fb} }$ 

$\sigma_{\rm{NLO} }^{\rm{(II)} }/{\rm{fb} }$ 

$\delta_{\rm{EW} }^{\rm{(I)} }/(\%)$ 

$\delta_{\rm{EW} }^{\rm{(II)} } /(\%)$ 

$\delta_{\rm{QED} }^{\rm{(I)} } /(\%)$ 

$\delta_{\rm{QED} }^{\rm{(II)} }/(\%)$ 

$\delta_{\rm{W} }/(\%)$ 

250 880.36 867.61 862.51 −1.45 −2.03 −1.48 −2.06 +0.03 500 326.15 320.84 317.01 −1.63 −2.80 −1.63 −2.80 +0.00 1000 67.879 66.366 65.319 −2.23 −3.77 −1.86 −3.40 −0.37 Table 3. Same as Table 2, but for
${{J}} = 2$ collision mode of back-scattered photons. -
$ \gamma\gamma \rightarrow l^+l^-\gamma $ as well as$ \gamma\gamma \rightarrow l^+l^- $ is an ideal channel for calibrating the beam luminosity of the Photon Linear Collider, especially for the${{J}} = 0$ polarization of the incident photon beams. In this paper, we present the full$ {\cal{O}}(\alpha) $ EW corrected integrated cross sections and some kinematic distributions of final products for the$ e^+e^-\gamma $ production in γγ collision. The production rate of$ e^+e^-\gamma $ in${{J}} = 2$ γγ collision is significantly larger than that in${{J}} = 0$ collision mode. In the exclusive event selection scheme, the NLO EW correction is dominated by the QED contribution; the full EW relative correction is sensitive to the γγ c.m. colliding energy and can exceed −10% at a TeV PLC for both${{J}} = 0$ and${{J}} = 2$ polarization configurations of photon beams. The kinematic behaviors of the final products in$ {\rm{J}} = 0 $ γγ collision are quite different from those in the${{J}} = 2$ collision. At$ \sqrt{\hat{s}} = 500\; {\rm{GeV}} $ , the EW relative correction is about −7% ~ −5% in most of the final-state phase space and can even reach around −10% in some specific phase-space regions. We can conclude that the NLO EW correction exerts important impact on both integrated and differential cross sections, and thus is significant in the precise determination of incoming photon beam luminosity at PLC. -
In Figs. A1–A5, we present the LO, NLO EW corrected kinematic distributions of the final-state positron, electron and leading photon as well as the corresponding EW corrected corrections for
$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ via${{J}} = 0$ and${{J}} = 2$ collisions of Compton back-scattered photons at$ \sqrt{s} = 500\; {\rm{GeV}} $ separately. As expected, the kinematic distributions of$ e^- $ and$ \gamma e^- $ system are the same as the corresponding ones of$ e^+ $ and$ \gamma e^+ $ system at both LO and EW NLO within the calculation errors for the${{J}} = 2$ polarization configuration of back-scattered photons.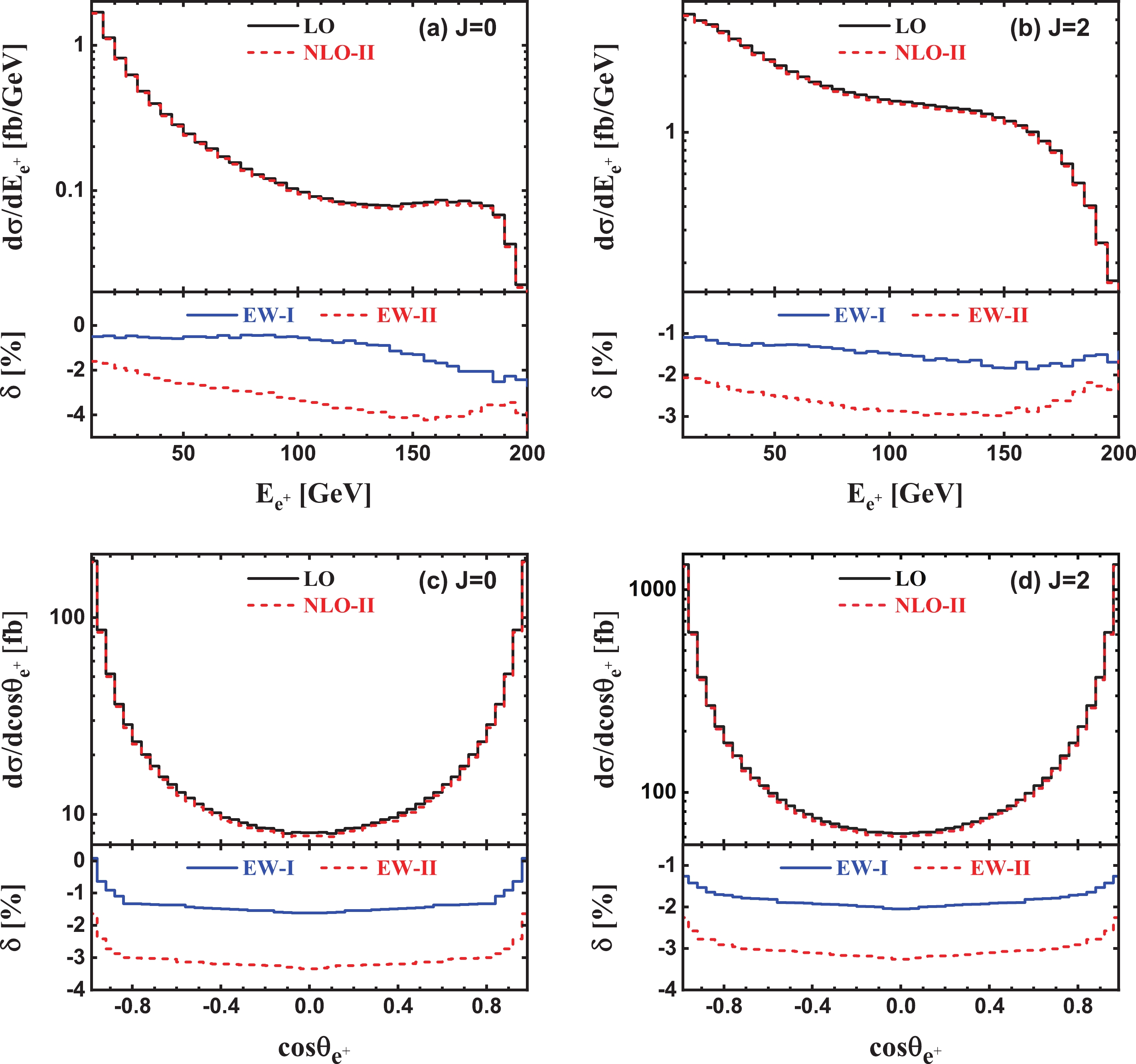
Figure A1. (color online) LO, NLO EW corrected energy and angular distributions of the final-state positron and the corresponding EW relative corrections for
$ ee \rightarrow \gamma\gamma \rightarrow e^+e^-\gamma $ via${{J}} = 0$ and${{J}} = 2$ collisions of Compton back-scattered photons at$ \sqrt{s} = 500\; {\rm{GeV}} $ .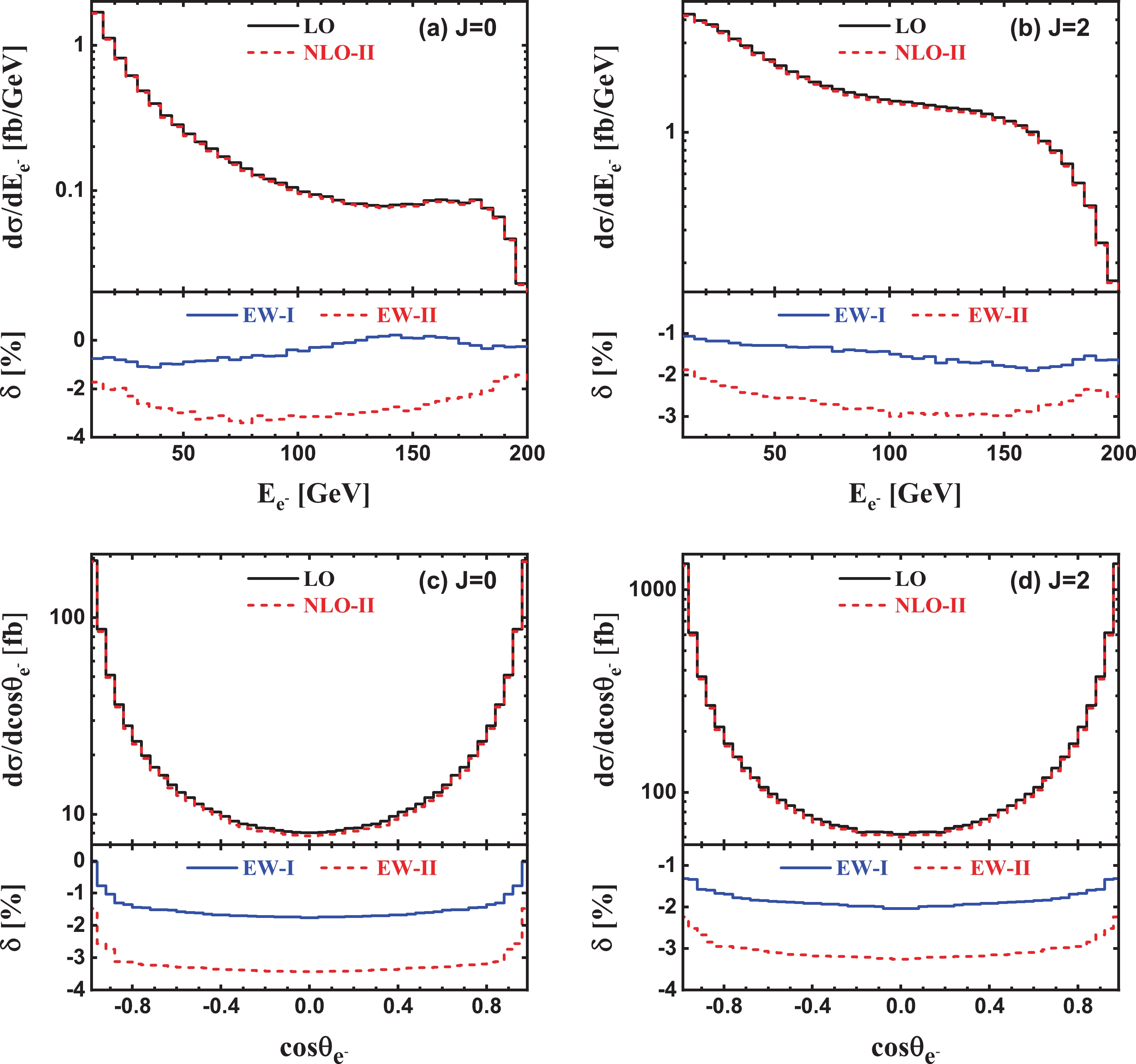
Figure A2. (color online) Same as Fig. A1, but for the final-state electron.
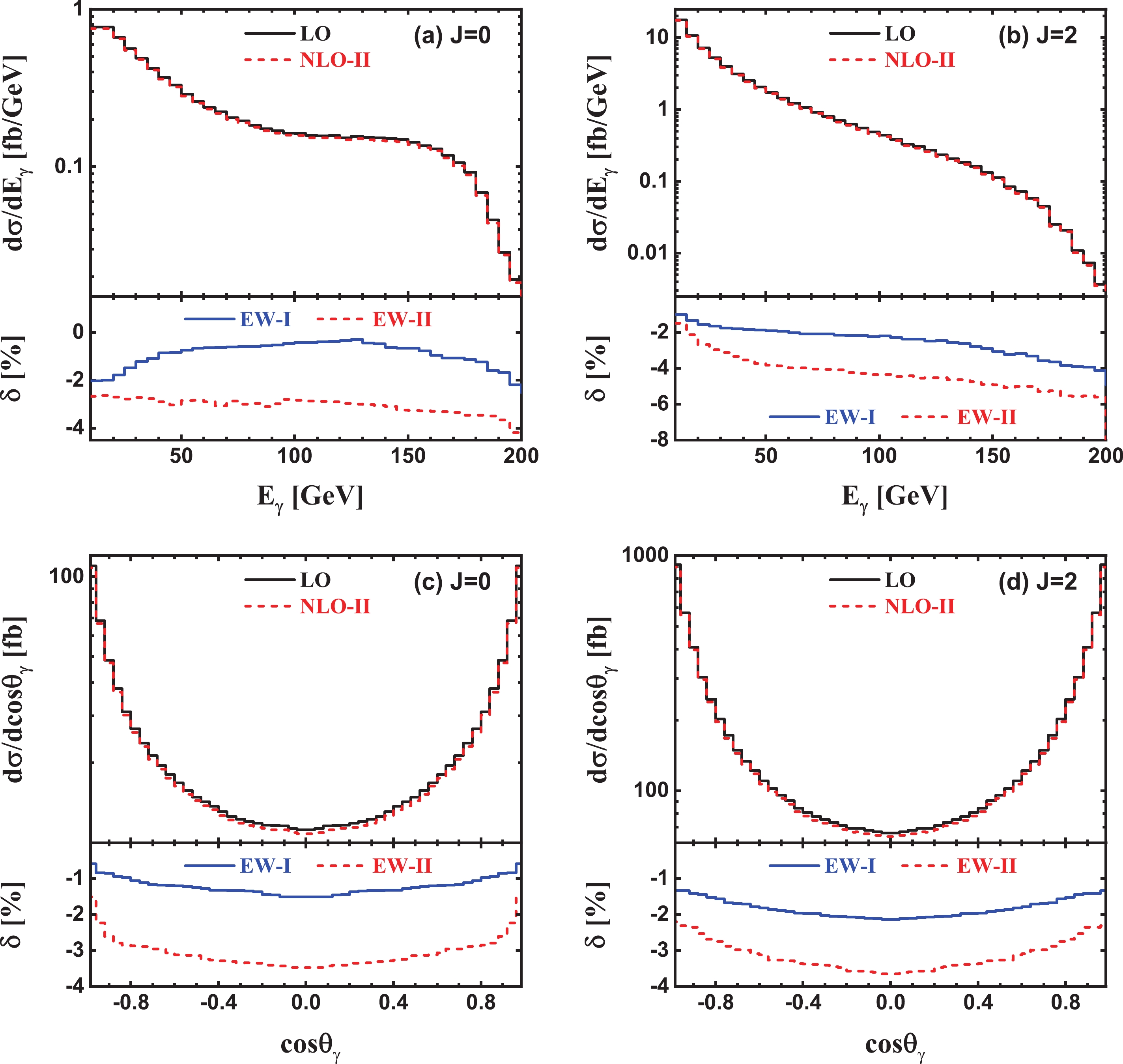
Figure A3. (color online) Same as Fig. A1, but for the final-state leading photon.
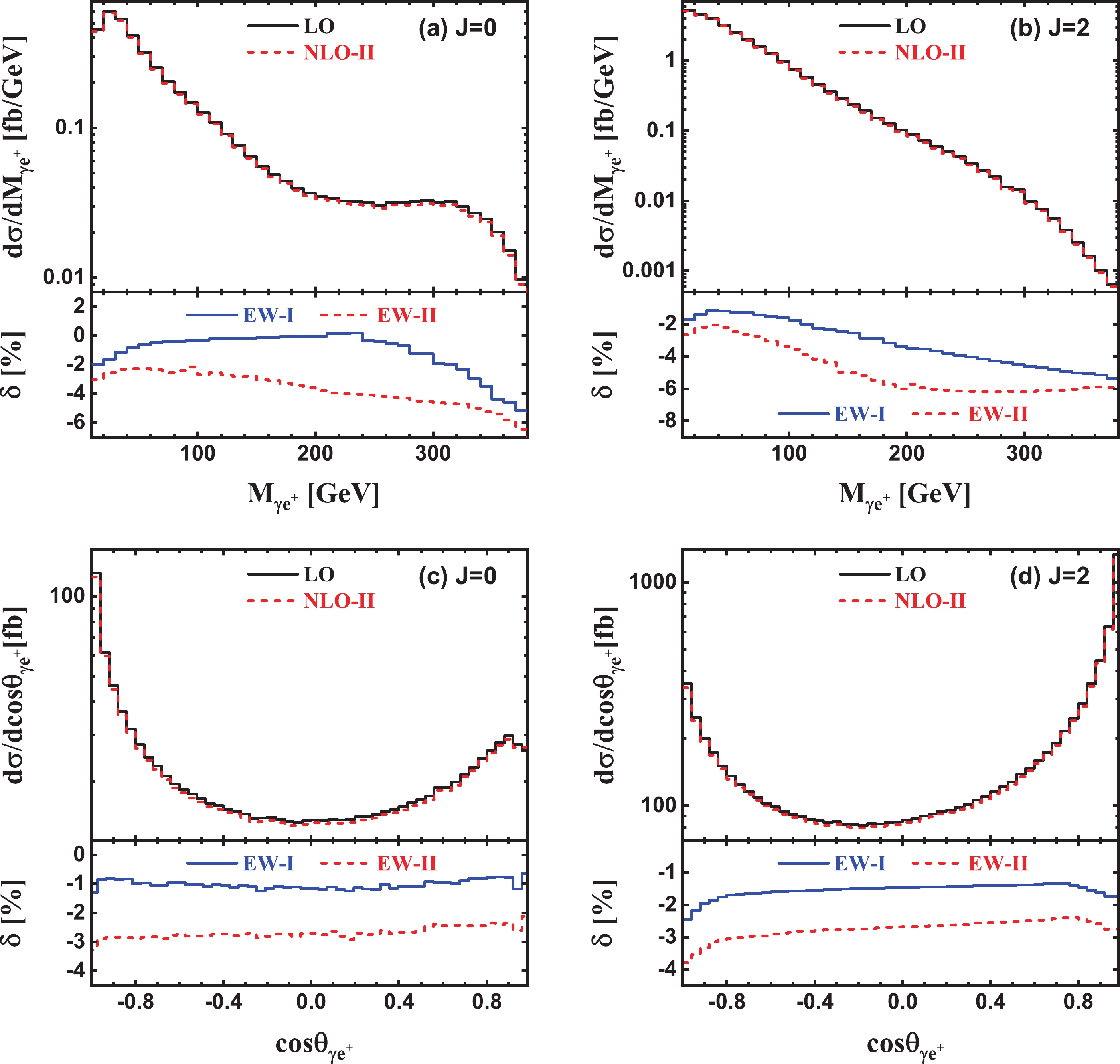
Figure A4. (color online) LO, NLO EW corrected invariant mass and opening angle distributions of the final-state
$\gamma {e^+}$ system and the corresponding EW relative corrections for$ee \to \gamma \gamma \to {e^ + }{e^ - }\gamma $ via${{J}} = 0$ and${{J}} = 2$ collisions of Compton back-scattered photons at$\sqrt s \; = \;{\rm{500}}\;{\rm{GeV}}$ .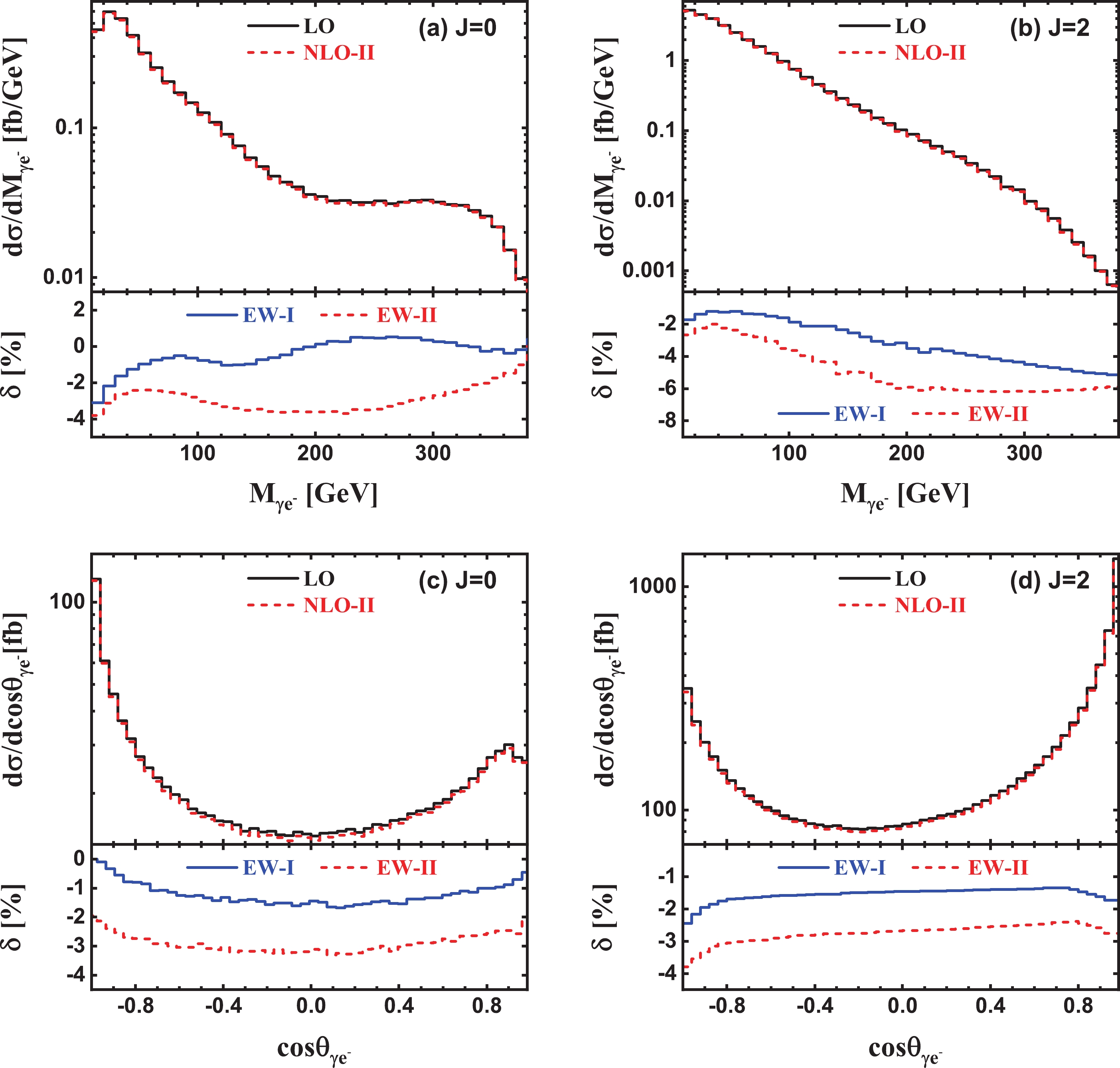
Figure A5. (color online) Same as Fig. A4, but for the final-state
$\gamma {e^ - }$ system.
e+e−γ production at photon-photon colliders at complete electroweak NLO accuracy
- Received Date: 2021-06-09
- Available Online: 2022-04-15
Abstract: We present the NLO electroweak radiative corrections to the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: