-
Since the energy per baryon decreases with incresing degrees of freedom, Witten speculated in 1984 that the 3-flavor strange quark matter (SQM) might be more stable than the 2-flavor nuclear matter, i.e., the true ground state of strong interactions [1]. It was demonstrated that SQM plays an important role in several interesting fields. For example, SQM can accommodate many abnormal astronomical phenomena in compact stars [2, 3]. In particular, the presence of SQM may be essential to understand the r-mode instability of compact stars [4] in the multi-messenger era of astronomy [5]. The droplets of SQM, namely strangelets or slets [6-9], could serve as a unique signature for the formation of quark gluon plasma (QGP) in relativistic heavy-ion collisions. A through investigation on the properties of SQM is thus crucial for us to understand various astrophysical phenomena and the QCD phase transition mechanisms [10-14].
In principle, the properties of quark matter can be described accurately by quantum chromodynamics (QCD). However, because of the non-perturbative nature at small densities and the sign problem in lattice simulations, QCD cannot be solved by the first principle. Effective models reflecting QCD characteristics are widely used to study the stability and properties of SQM, e.g., the Nambu-Jona-Lasinio model [15], perturbation model [16], field correlator method [17], quark-cluster model [18, 19], and other models [20-29]. Most of the effective models adopt quark masses that vary with density (chemical potential) and/or temperature [30-39], where we refer to those with density-dependent quark masses as quark mass-density-dependent models [26, 40-42].
The objective of this work is to investigate the properties of SQM at finite temperature and density, where a baryon density-dependent quark mass model, including both the confinement and first-order perturbative interactions is adopted. The remainder of this paper is organized as follows. In Sec. II, we discuss self-consistent thermodynamic treatment. In Sec. III, we present the quark mass scale for strange quarks at finite temperatures, considering both confinement and perturbation interactions. In Sec. IV, we present the numerical results for the properties of strange quark matter. In Sec. V, we provide numerical results for the properties of strange stars. Finally, a summary is given in Sec. VI.
-
One important aspect for the baryon density-dependent quark mass model is the thermodynamic self-consistency, where the fundamental thermodynamic relationship needs to be satisfied, e.g., the pressure at the minimum free-energy per baryon should be exactly zero. A detailed investigation on thermodynamic self-consistent treatments was carried out in Ref. [43], where the quark masses depend on the density and/or temperature [44]. The basic thermodynamic differential relationship of free energy
$ \overline{F} $ is expressed:$ \begin{equation} \mathrm{d}\overline{F} = -\overline{S}\mathrm{d}T-P\mathrm{d}V+\sum\limits_{i}\mu_{i}\mathrm{d}{N_{i}}, \end{equation} $

(1) where
$ \overline{S} $ , T, P, V,$ \mu_{i} $ , and$ N_{i} $ represent the entropy, temperature, pressure, volume, chemical potential, and particle number of the system, respectively. For a uniform system, one can define the free energy density$ F = \overline{F}/V $ , entropy density$ S = \overline{S}/V $ , and particle number density$ n_{i} = N_{i}/V $ . Substituting those into Eq. (1), we have$ \begin{aligned}[b] \mathrm{d}F = -S\mathrm{d}T+\left(-P-F+\sum\limits_{i}\mu_{i}n_{i}\right)\frac{\mathrm{d}V}{V} +\sum\limits_{i}\mu_{i}\mathrm{d}n_{i}. \end{aligned} $

(2) For a system comprising noninteracting particles, the free energy density is connected to the thermodynamic potential density
$ \Omega_{0}(T,\{\mu_{i}\},\{m_{i0}\}) $ by$ \begin{equation} F = \Omega_{0} + \sum\limits_{i}\mu_{i}n_{i}. \end{equation} $

(3) Note that the masses
$ m_{i0} $ of quark flavor i take constant values in these equations. To account for the strong interaction among quarks and gluons, the masses are replaced with the equivalent ones$ m_{i} = m_{i}(n_{u},n_{d},n_{s},T) = m_{i0}+ $ $ m_\mathrm{I}(n_{u},n_{d},n_{s},T) $ , where$ m_{i0} $ denotes the current mass of quarks. In such cases, as the mass varies with the state variables T and$ n_{i} $ , expressions for other quantities, such as the entropy, pressure, and chemical potential, should be carefully derived to maintain thermodynamics consistency [43, 44]. Here, we consider the temperature T, volume V, and quark number densities$ n_{i} $ as independent state variables, while the free energy density F corresponds to the characteristic thermodynamic function. The free energy density takes the same form as the free particle system with the quark masses replaced by the equivalent ones in Eq. (3), i.e.,$ \begin{aligned}[b] F = F(T,\{n_{i}\},\{m_{i}\}) = \Omega_{0}(T,\{\mu_{i}^{*}\},\{m_{i}\})+\sum\limits_{i}\mu_{i}^{*}n_{i}, \end{aligned} $

(4) where the chemical potential
$ \mu_i $ is replaced with the effective one$ \mu_i^* $ . The differential relationship then becomes$ \begin{aligned}[b] \mathrm{d}F = & \frac{\partial\Omega_{0}}{\partial T}\mathrm{d}T+\sum\limits_{i}\left(\frac{\partial\Omega_{0}}{\partial \mu_{i}^{*}}\mathrm{d}\mu_{i}^{*}+\mu_{i}^{*}\mathrm{d}n_{i}+n_{i}\mathrm{d}\mu_{i}^{*}\right)\\ & +\sum\limits_{i}\frac{\partial\Omega_{0}}{\partial m_{i}}\left(\sum\limits_{j}\frac{\partial m_{i}}{\partial n_{j}}\mathrm{d}n_{j}+\frac{\partial m_{i}}{\partial T}\mathrm{d}T\right) \\ = & \left[ \frac{\partial \Omega_0}{\partial T} + \sum\limits_i \frac{\partial \Omega_0}{\partial m_i} \frac{\partial m_i}{\partial T} \right]\rm{d}T \\ & + \sum\limits_i \left[ \mu_i^* + \sum\limits_j\frac{\partial \Omega_0}{\partial m_j}\frac{\partial m_j}{\partial n_i} \right] \rm{d} n_i. \end{aligned} $

(5) Comparing Eq. (2) with Eq. (5), one immediately obtains the thermodynamic quantities
$ S = -\frac{\partial\Omega_{0}}{\partial T}-\sum\limits_{i}\frac{\partial m_{i}}{\partial T}\frac{\partial\Omega_{0}}{\partial m_{i}}, $

(6) $ P = -F+\sum\limits_i \mu_{i} n_i , $

(7) $ \mu_{i} = \mu_i^* + \sum\limits_j\frac{\partial \Omega_0}{\partial m_j}\frac{\partial m_j}{\partial n_i}. $

(8) The particle number densities
$ n_{i} $ and the energy density are given by$ n_{i} = -\frac{\partial\Omega_{0}}{\partial \mu_{i}^{*}}, $

(9) $ E = F+TS = \Omega_{0}+\sum\limits_{i}\mu_{i}^{*}n_{i}+TS. $

(10) -
Another important issue for the baryon density-dependent quark mass model concerns the quark mass scaling, i.e., how to parameterize the density and/or temperature dependent particle masses. The equivalent quark masses
$ m_i $ usually comprise two parts, i.e.,$ \begin{equation} m_i = m_{i0}+m_\mathrm{I}, \end{equation} $

(11) where
$ m_{i0} $ represents the current mass ($ m_{u0} = 5\ \mathrm{MeV} $ ,$ m_{d0} = 10\ \mathrm{MeV} $ , and$ m_{s0} = 100\ \mathrm{MeV} $ ), and$ m_\mathrm{I} $ accounts for the strong interaction. Considering the fact that quark confinement dominates at low densities, based on MIT bag model, the interaction part$ m_\mathrm{I} $ was initially parameterized as an inverse proportion to the baryon number density [40, 45-47], i.e.,$ \begin{equation} m_\mathrm{I} = \frac{B}{3n_\mathrm{b}}, \end{equation} $

(12) where B denotes the bag constant. The contribution from temperature can be considered in an expansion form [48]
$ \begin{equation} m_\mathrm{I} = \frac{B}{3n_\mathrm{b}}\left[1-\left(\frac{T}{T_{\rm c}}\right)^{2}\right]. \end{equation} $

(13) An inverse cubic scaling was later derived, considering the in-medium quark condensate and linear confinement [26, 49], i.e.,
$ \begin{equation} m_\mathrm{I} = \frac{D}{n_\mathrm{b}^{1/3}}, \end{equation} $

(14) where D represents the quantity reflecting the confinement strength. This mass scaling was extended to the finite temperature as [28]
$ \begin{equation} m_\mathrm{I} = \frac{D}{n_\mathrm{b}^{1/3}}\left[1-\frac{8T}{\lambda T_{\rm c}}\mathrm{exp}\left(-\frac{\lambda T_{\rm c}}{T}\right)\right], \end{equation} $

(15) where
$ \lambda = 1.6 $ is a constant, and$ T_{\rm c} = 175 $ MeV is the critical temperature for the transition of the hadronic matter into QGP. This quark mass scaling is consistent with the temperature dependence of the string tension. However, it becomes negative at temperatures above the critical value$ T_\mathrm{\rm c} $ , while we expect$ m_\mathrm{I}\rightarrow 0 $ at large temperatures. The inverse cubic scaling can be extended to include the one-gluon-exchange interaction [50, 51]. To account for the first-order perturbative interactions at larger densities, an additional term proportional to the cube root of baryon number density was obtained in Ref. [43], i.e.,$ m_\mathrm{I} = \frac{D}{n_\mathrm{b}^{1/3}}+Cn_\mathrm{b}^{1/3}, $

(16) where C represents the strength of perturbative interactions. If C takes negative values, the one-gluon-exchange interaction is effectively included [50]. The interaction mass
$ m_\mathrm{I} $ in Eq. (16) is later extended to include the finite temperature effect for the$ ud $ quark matter [52], i.e.,$ m_\mathrm{I} = \frac{D}{n_\mathrm{b}^{1/3}}\left(1+\frac{8T}{\Lambda}{\rm e}^{-{\Lambda}/{T}}\right)^{-1} +Cn_\mathrm{b}^{1/3}\left(1+\frac{8T}{\Lambda}{\rm e}^{-{\Lambda}/{T}}\right) $

(17) with
$ \Lambda = 280 $ MeV. Unlike the scaling in Eq. (15), here, the interaction mass tends to zero when the temperature approaches$ T_{\rm c} $ . We thus adopt the$ m_\mathrm{I} $ expression to further investigate the properties of SQM at finite temperatures. To be consistent with the conventional nuclear physics and simultaneously ensure that strange stars exist stably in the Universe, the perturbative parameter C and confinement parameter D should satisfy the condition that the minimum energy per baryon of the strange quark matter is less than$ 930\ \mathrm{MeV} $ at zero temperature while that of the$ ud $ quark matter is larger than$ 930\ \mathrm{MeV} $ . According to our previous study, a stability window exists for various combinations of perturbative parameter C and confinement parameter$ D^{1/2} $ [33], where the parameter sets within are adopted in this work. In this work, we adopt the parameter sets (C,$ \sqrt D $ in MeV) as (0.7,129), (0.6,160), (0.4,160), (0,160), (0.4,140), and (0.4,129). Note that the sets (0.7,129), (0,160), and (0.4,140) lie within the stability window.At large temperatures, one needs to also consider the contribution of gluons. The gluon's equivalent mass is given by
$ (m_{\rm g}/T)^{2} = \eta\alpha\theta(T-T_{\rm c}), $

(18) with
$ T_{\rm c} = 175 $ MeV and$ \eta = 15 $ [52]. For the running coupling constant α, we use a rapidly convergent expansion [53]$ \begin{equation} \alpha = \frac{\beta_{0}}{\beta_{0}^{2}\ln{(u/\Lambda_{T})}+\beta_{1}\ln\ln(u/\Lambda_{T})}, \end{equation} $

(19) where
$ \beta_{0} = 11/2-N_{\mathrm{f}}/3 $ ,$ \beta_{1} = 51/4-(19/12)N_{\mathrm{f}} $ , and$ N_{\mathrm{f}} = 3 $ . To include the non-perturbative effects, we assume that the renormalization scale varies linearly with temperature as:$ \begin{equation} u/\Lambda_{T} = c_{0}+c_{1}x, \end{equation} $

(20) with
$ c_{0} = 1 $ ,$ c_{1} = 1/2 $ ,$ x = T/T_{\rm c} $ .The respective partial derivative with respect to density and temperature are easily obtained from relevant expressions
$ \frac{\partial m_{q}}{\partial n_{\rm b}} = -\frac{D}{3n_{\rm b}^{4/3}}\left(1+\frac{8T}{\Lambda}{\rm e}^{-\Lambda/T}\right)^{-1}+\frac{C}{3n_{\rm b}^{2/3}}\left(1+\frac{8T}{\Lambda}{\rm e}^{-\Lambda/T}\right), $

(21) $ \begin{aligned}[b] \frac{\partial m_{q}}{\partial T} = & -\frac{8D}{\Lambda n_{\rm b}^{1/3}} \left(1+\frac{\Lambda}{T}\right) \frac{{\rm e}^{-\Lambda/T}}{\left(1+\dfrac{8T}{\Lambda}{\rm e}^{-\Lambda/T}\right)^{2}} \\ & +8Cn_{\rm b}^{1/3}\left(\frac{1}{T}+\frac{1}{\Lambda}\right){\rm e}^{(-\Lambda/T)}, \end{aligned} $

(22) $ \frac{\mathrm{d}m_g}{\mathrm{d}T} = \frac{m_g}{T}\left(1+\frac{x}{2}\frac{\mathrm{d}\ln \alpha}{\mathrm{d}x}\right), $

(23) and
$ \begin{equation} \frac{\mathrm{d}\ln \alpha}{\mathrm{d}x} = -\frac{c_{1}\alpha}{c_{0}+c_{1}x}\left[\beta_{0}+\frac{\beta_{1}}{\beta_{0}}\frac{1}{\ln(c_{0}+c_{1}x)}\right]. \end{equation} $

(24) Finally, it is important to mention that there are other forms of quark mass scalings in the literature, e.g., an explicit isospin dependent term was introduced to include the quark matter symmetry energy [54, 55], the asymptotic freedom of strong interaction was considered explicitly through a Wood-Saxon factor [56]. In this study, we investigate the properties of SQM at finite temperatures, adopting the quark mass scaling with an interaction part in Eq. (17), where both quark confinement and first-order perturbation interactions are included. Note that only valence quarks are considered in the quark mass scaling while the baryon density is defined by
$ n_{b} = \sum_{i}{(n_{i}^{+}-n_{i}^{-})/3} $ . The contributions of antiquarks and gluons are accounted for by further considering the temperature dependence, as indicated in the quark and gluon mass scalings in Eq. (17) and Eq. (18). -
For simplicity, we assume that the system comprises quarks, electrons, their antiparticles, and gluons at finite temperatures. According to the equivalent mass model, the contribution of free particles to the thermodynamic potential density can be written as
$ \begin{equation} \Omega_{0} = \Omega_{0}^++\Omega_{0}^-+\Omega_{0}^{g}. \end{equation} $

(25) The contributions of the equivalent particle (+) and antiparticle (-) are
$ \Omega_{0}^{\pm} = \sum\limits_{i}-\frac{d_{i}T}{2\pi^{2}}\int_{0}^{\infty}\ln\left[1+{\rm e}^{-\big(\sqrt{p^{2}+m_{i}^{2}}\mp\mu_{i}^{*}\big)/T}\right]p^{2}\mathrm{d}p. $

(26) $ \Omega_{0}^{g} = \frac{d_{g}T}{2\pi^{2}}\int_{0}^{\infty}\ln\left[1-{\rm e}^{-\sqrt{p^{2}+m_{g}^{2}}/T}\right]p^{2}\mathrm{d}p, $

(27) where
$ i = q $ ($ q = u,d,s $ ),$d_{q} = 3(\rm colors)\times2(\rm spins) = 6$ and$ i = e $ ,$ d_ {e} = 2 $ and$ i = g $ ,$d_{g} = 8(\rm colors)\times2(\rm spins) = 16$ .Substituting this thermodynamic potential into Eqs. (6)-(10), we obtain the thermodynamic density of each particle at a finite temperature. The number density of particle and anti-particle is expressed as:
$ \begin{equation} n_{i}^{\pm} = \frac{d_{q}}{2 \pi^{2}}\int_{0}^{\infty}\frac{p^{2}\mathrm{d}p}{{\rm e}^{\big(\sqrt{p^{2}+m_{i}^{2}}\mp \mu_{i}^{*}\big)/T}+1}, \end{equation} $

(28) The chemical potentials are obtained with Eq. (8), where the derivative terms with respect to equivalent masses are:
$ \begin{aligned}[b] \frac{\partial \Omega_{0}}{\partial m_{q}} = &\frac{d_{q} m_{q}}{2\pi^{2}}\int_{0}^{\infty}\left[\frac{1}{{\rm e}^{\big(\sqrt{p^{2}+m_{q}^{2}}-\mu_{q}^{*}\big)/T}+1}\right.\\ &\left.+\frac{1}{{\rm e}^{\big(\sqrt{p^{2}+m_{q}^{2}}+\mu_{q}^{*}\big)/T}+1}\right]\frac{p^{2}\mathrm{d}p}{\sqrt{p^{2}+m_{q}^{2}}}. \end{aligned} $

(29) $ \begin{equation} \frac{\partial \Omega_{0}}{\partial m_{g}} = \frac{d_{g} m_{g}}{2\pi^{2}}\int_{0}^{\infty}\frac{1}{{\rm e}^{\sqrt{p^{2}+m_{g}^{2}}/T}-1}\frac{p^{2}\mathrm{d}p}{\sqrt{p^{2}+m_{q}^{2}}}. \end{equation} $

(30) To obtain the properties of SQM inside compact stars, we introduce an electron e; hence, condition of charge neutrality can be fulfilled. In addition, owing to the weak reactions such as d,
$ s \leftrightarrow u + e + \overline{\nu}_{e} $ and$ s + u \leftrightarrow u + d $ , the chemical potential$ \mu_{i} $ ($ i = u, d, s, e $ ) needs to satisfy weak equilibrium conditions (where we have assumed vanishing neutrino chemical potentials for simplicity).$ \begin{equation} \mu_{u}^{*}+\mu_{e}^{*} = \mu_{d}^{*} = \mu_{s}^{*}, \end{equation} $

(31) and the charge neutrality condition is
$ \begin{equation} 2n_{u}^+-n_{d}^+-n_{s}^+-3n_{e}^+-(2n_{u}^--n_{d}^--n_{s}^--3n_{e}^-) = 0, \end{equation} $

(32) and the quark number density satisfies the baryon number conservation condition
$ \begin{equation} n_{\rm b} = \sum\limits_{q = u,d,s}\frac{1}{3}\left(n_{q}^+-n_{q}^-\right). \end{equation} $

(33) In the framework of the thermodynamic treatment method given in Sec. II, we could connect the particle number density Eq. (28) with the effective chemical potential
$ \mu_{i}^{*} $ via the particle number density expression. Therefore, when we have a given baryon number density, the formula for Eqs. (31)-(33) comprises four effective chemical potential equations. Hence, we can get the effective chemical potential by solving these four equations. Eqs. (6)-(10) were adopted to determine other thermodynamic quantities. The real chemical potential$ \mu_ {i} $ connect with the effective chemical potential$ \mu_ {i} ^ {*} $ using formula Eq. (8).According to our quark mass scale, we present a curve of density as a function of the temperature when
$ n_\mathrm{b} = 0.5\ \mathrm{fm}^{-3} $ ,$ D^{1/2} = 160\ \mathrm{MeV} $ , and$ C = 0.6 $ in Fig. 1. The contributions of the confinement and perturbation are depicted by dashed and dash-dotted lines, respectively. We note that the quark mass constraint becomes less important than the perturbation term as the temperature increases.
Figure 1. Mass of quark as a function of temperature at
$n_{\rm b} = 0.5\ \mathrm{fm}^{-3}$ for$ D^{1/2} = 160\ \mathrm{MeV} $ and$ C = 0.6 $ .In Fig. 2, we consider the energy per baryon as a function of the baryon number density, where
$ T = 50$ ,$ 100 $ , and$ 150\ \mathrm{MeV} $ while$ D^{1/ 2} = 160\ \mathrm{MeV} $ and$ C = 0.6 $ are adopted. It is determined that, at small densities, the energy per baryon becomes infinite, as represented by quark confinement. At a higher baryon density, the energy per baryon also tends to increase because perturbation interactions become increasingly important.
Figure 2. Energy per baryon as a function of baryon number density at differently fixed temperature values of
$ T = 50 $ ,$ 100 $ ,$ 150\ \mathrm{MeV} $ .The temperature dependence of the energy per baryon and free energy per baryon is presented in Fig. 3. We notice that the energy per baryon increases with temperature. However, the free energy per baryon decreases with temperature and eventually becomes negative. This is understandable, considering the fact that
$ F = E-TS $ and the entropy term$ -TS $ are dominant at high temperatures.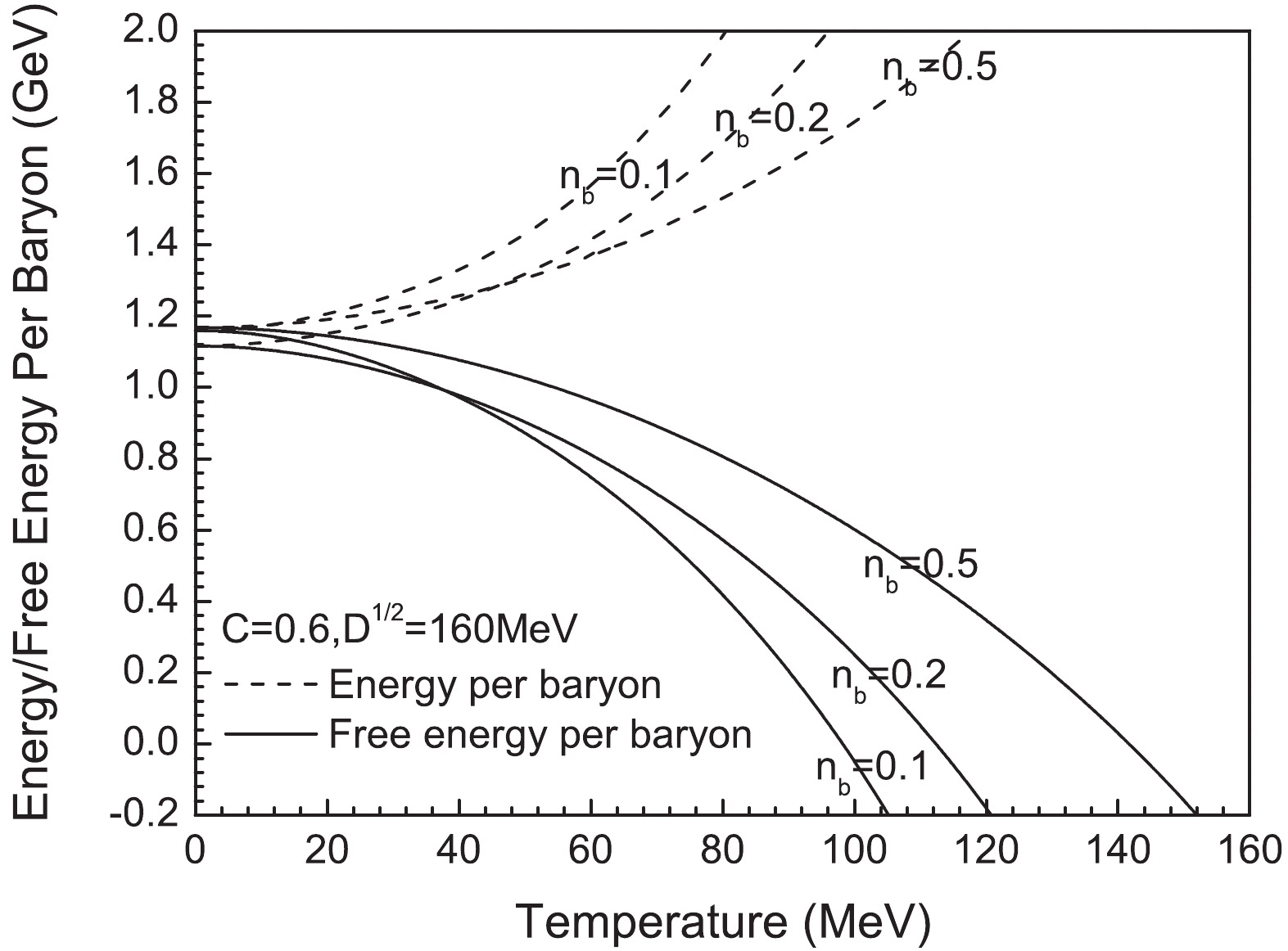
Figure 3. Energy (dashed line) and free energy (Solid line) per baron vary with temperature for baryon density
$ n_\mathrm{b} $ = 0.1, 0.2, and 0.5 fm$ ^{-3} $ .The obtained the equation of state (EOS) of matter of SQM inside compact stars is presented in Fig. 4. We determine that the slope of EOS increases with the increase in C and decrease in D.
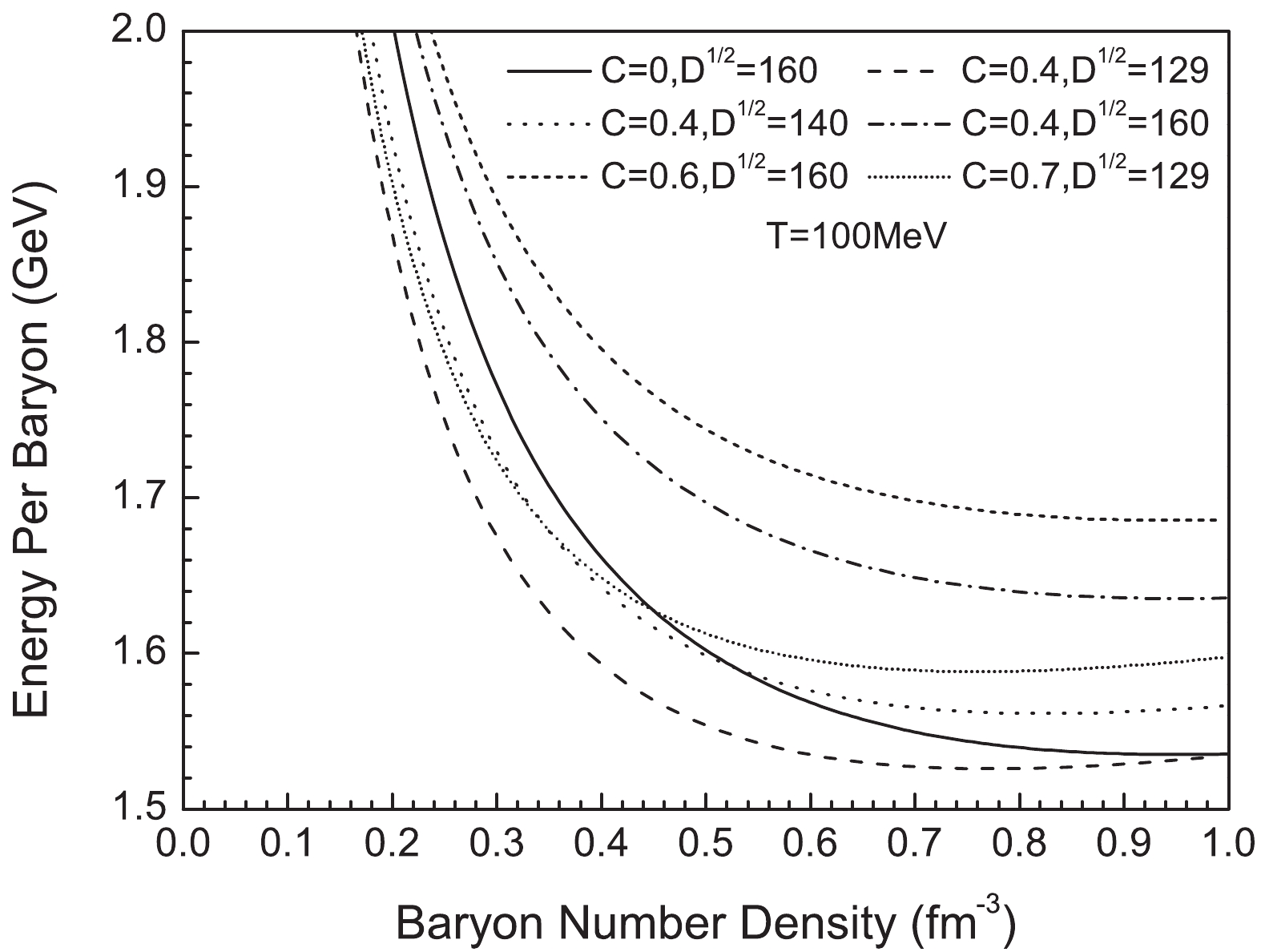
Figure 4. The relationship between the energy per baryon of strange quark matter and the baryon number density for
$ T = 100\ \mathrm{MeV} $ .Based on the EOS indicated in Fig. 4 and the sound velocity formula
$ \begin{equation} v = \sqrt{\frac{\mathrm{d}P}{\mathrm{d}E}}, \end{equation} $

(34) we calculate the sound velocity in a SQM at a fixed baryon number density. As illustrated in Fig. 5, the sound velocity increases with the baryon number density. In the case of high density, the curve corresponding to the larger C and D approximates the hyperelastic (
$ 1/\sqrt{3} $ ) slower. This is understandable because perturbation interactions still exist at higher densities.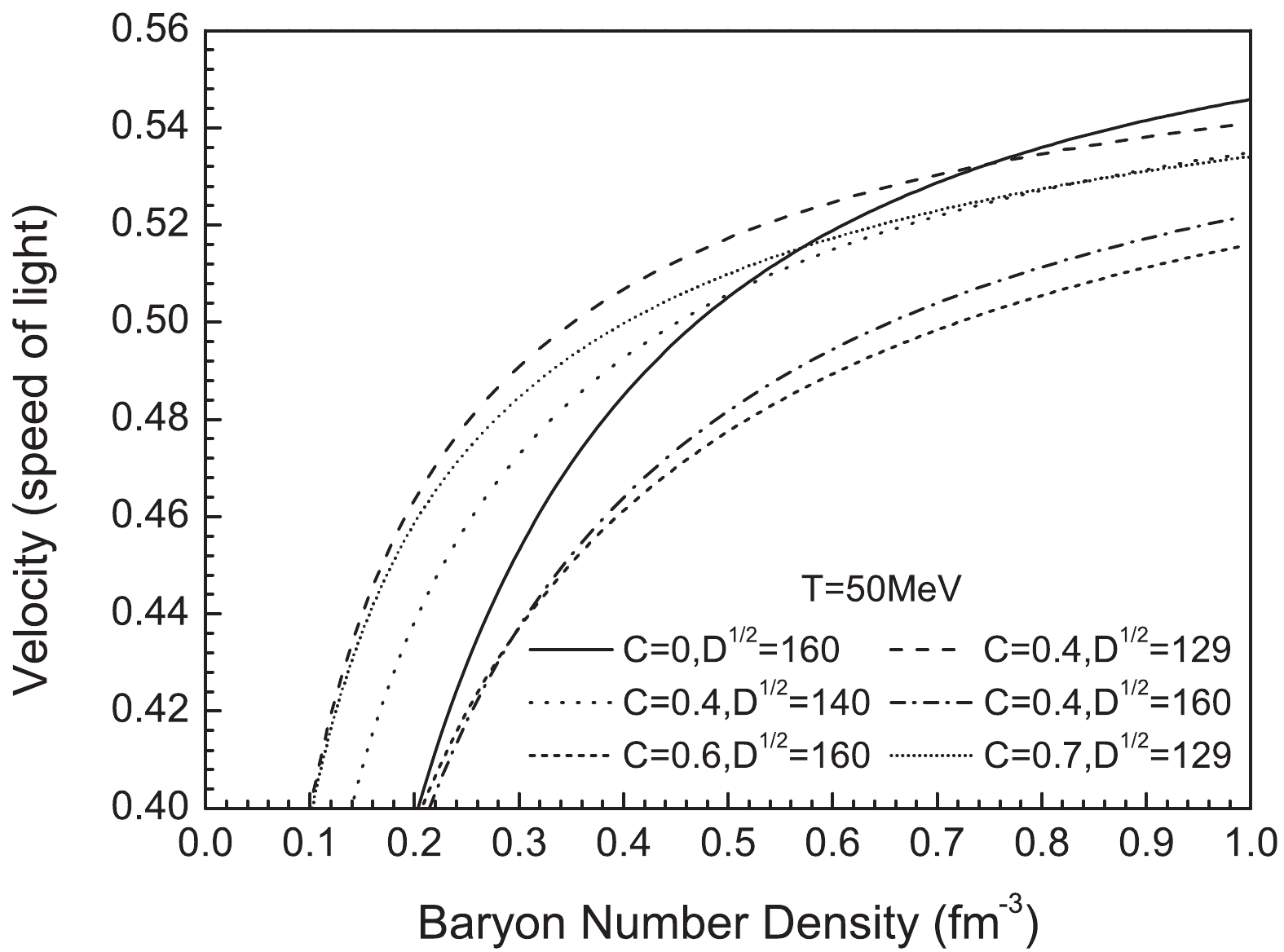
Figure 5. The sound velocity in SQM as a function of baryon number density at fixed temperature
$ T = 50\ \mathrm{MeV} $ .To check thermodynamic consistency and prove the influence of perturbation interaction, we plot the relationship between the free energy per baryon and energy per baryon and density at
$ T = 30\ \mathrm{MeV} $ in Fig. 6, where$ D^{1/2} = 160\ \mathrm{MeV} $ ,$ C = 0 $ ,$ C = 0.4 $ and$ C = 0.6 $ . The triangle is the minimum, and the open circles correspond to the zero pressure. We notice that the pressure happens to be zero in the case of the minimum free energy, which is a necessary condition for thermodynamic consistency.
Figure 6. Relationship between the free energy per baryon, energy per baryon and density at
$ T = 30\ \mathrm{MeV} $ . The triangle marks the minimum, and the open circles marks the zero pressure point.Additionally, Fig. 7 presents the pressure and the corresponding free energy per baryon at
$ T = 50\ \mathrm{MeV} $ . Evidently, when the density is less than the density with the lowest free energy, the pressure is negative. Otherwise it's going to be positive.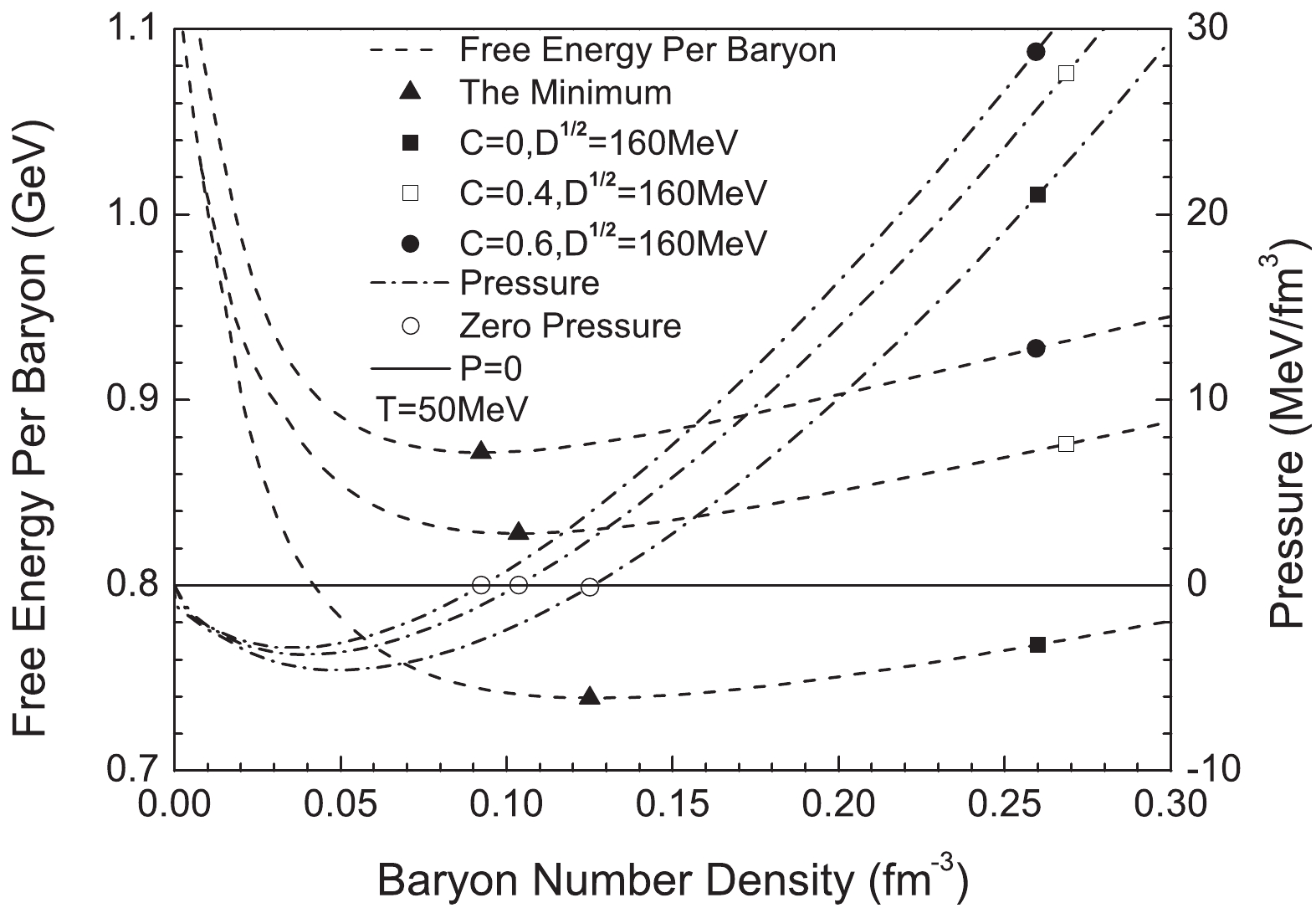
Figure 7. Relationship between the free energy per baryon, pressure and density at
$ 50\ \mathrm{MeV} $ for$ D^{1/ 2} = 160\ \mathrm{MeV} $ ,$ C = 0 $ ,$ C = 0.4 $ and$ C = 0.6 $ .To ensure the correctness of the results, we usually choose
$ \begin{equation} P-n^{2}\frac{\mathrm{d}}{\mathrm{d}n}\left(\frac{F}{n}\right) = 0, \end{equation} $

(35) to test thermodynamic self-consistency. Please refer to Ref. [26] for details of derivation.
Based on this formula, we can directly differentiate the average baryon free energy with respect to the baryon number density, to get the pressure. We note that the pressure at the lowest point of the energy per baryon is equal to zero, which is consistent with the most commonly used thermodynamic self-consistency test method.
Figure 8 shows the entropy per baryon as a function of temperature at different densities. It's an increasing function of temperature, whether the density is high or low, going to zero at zero temperature. This is guaranteed by

Figure 8. Entropy per baryon as a function of temperature at different baryon number densities, which increases with temperature, where
$ D^{1/ 2} = 160\ \mathrm{MeV} $ and$ C = 0.6 $ .$ \begin{equation} \lim\limits_{T\rightarrow 0}\partial m_{q} /\partial T = 0. \end{equation} $

(36) Interestingly, we did not require this in the derivation of the partial derivative of mass with respect to temperature. This ensures that at zero temperature, all quantities are restored to density-dependent models. In particular, as the temperature approaches zero, entropy naturally approaches zero, thus satisfying the third law of thermodynamics.
-
Quark stars are an interesting branch of nuclear physics, astrophysics, and other important fields. In the past two decades, several studiesa have been conducted on these astronomic bodies, such as Refs. [57-61].
In the earlier stages of strange star evolutions, the neutrinos are still trapped within the star; hence, the chemical equilibrium conditions become
$ \mu_{u}^{*}+\mu_{e}^{*}-\mu_{ve}^{*} = \mu_{d}^{*} = \mu_{s}^{*}, \mu_{\mu}^{*} = \mu_{e}^{*} $ and$ \mu_{v\mu}^{*} = \mu_{ve}^{*} $ and the lepton fraction$ Y_{l} = (n_{e}+n_{\mu}+ n_{ve}+ $ $ n_{v\mu})/n_{b} $ can reach 0.4, according to numerical simulations [62]. Based on the EOSs, we solve the Tolman-Oppenheimer-Volkov equation$ \begin{equation} \frac{\mathrm{d}P}{\mathrm{d}r} = -\frac{GmE}{r^{2}}\frac{(1+P/E)(1+4\pi r^{3}P/m)}{1-2Gm/r}, \end{equation} $

(37) with the subsidiary condition
$ \begin{equation} \mathrm{d}m = 4\pi Er^{2}\mathrm{d}r. \end{equation} $

(38) Then, the mass-radius relationship of the strange star corresponding to different parameters are obtained. The obtained results are presented in Fig. 9, where the most massive stars are represented by black dots. Generally, the maximum star mass increases with the confinement intensity parameter D, but decreases with the perturbative strength C. We can observe that relative to the previous quark mass scaling, the maximum star mass exceeds
$ 2\ M_{\odot} $ after considering the first-order perturbation interaction. In addition, we adjust the parameter space within our model to describe the recently discovered compact stars (MXB 1730-335, PSR J0030+0451, PSR J0348+0432, MSR J0740+ 6620 and PSR J2215+5135) as quark stars at different entropy per baryon. It can be observed that the results of the strange star with$ C = -0.1,0,0.6 $ and$ D^{1/2} = 160\ \mathrm{MeV} $ are consistent with the observational mass and radius of the Rapid Burster (MXB 1730-335) with$ M = 1.1\pm0.3\ M_{\odot} $ and$ R = 9.6\pm1.5\ {\rm km} $ [63]. The maximum star mass for the strange star with$ C = 0.4 $ and$ D^{1/2} = 140\ \mathrm{MeV} $ is consistent with the observations of the pulsars in the Rapid Burster (MXB 1730-335) and can describe the millisecond pulsar PSR J0030 + 0451 [64, 65]. The result of the maximum star mass of the strange star with$ C = 0.6 $ and$ D^{1/2} = 133\ \mathrm{MeV} $ can describe the millisecond pulsar PSR J0030 + 0451, PSR J0348 + 0432 with a mass of$ 2.01\pm0.04\ M_{\odot} $ [66] and the recently discovered massive pulsar MSR J0740 + 6620 ($ 2.14_{-0.18}^{+0.20}\ M_{\odot} $ at the$ 95.4\ $ % credibility interval) [67]. Furthermore, the result of the maximum star mass of the strange star with$ C = 0.7 $ and$ D^{1/2} = 129\ \mathrm{MeV} $ can describe massive pulsar MSR J0740 + 6620, PSR J0348 + 0432 and PSR J2215 + 5135 with a mass of$ 2.27_{-0.09}^{+0.10}\ M_{\odot} $ [68], but with the radii slightly larger than that of PSR J0030+0451.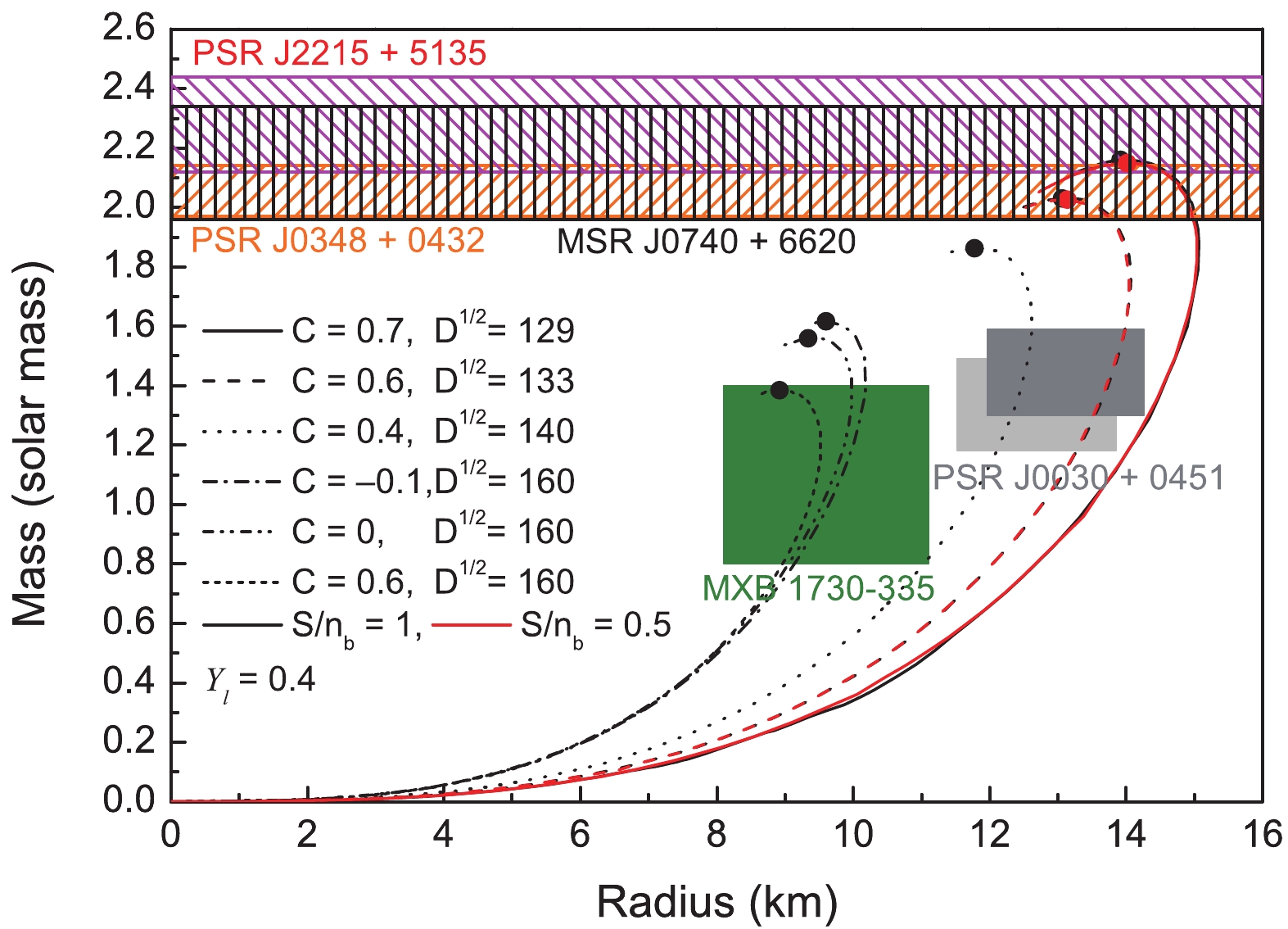
Figure 9. (color online) Mass-radius relationship for proto-quark stars with different baryon entropies at fixed lepton fraction. We have also included lower and upper limits of the masses and radii of MXB 1730-335 [63], PSR J0030+0451 [64, 65], PSR J0348+0432 [66], MSR J0740+6620 [67] and PSR J2215+5135 [68].
At fixed
$ S/n_{\rm b} $ and$ Y_{l} $ , we deduce that the star surface density could become negligible, or even lower than the normal nuclear saturation density when larger perturbation intensity parameters C and smaller quark confinement parameters D were adopted to generate a massive star. This might be a signal of phase transition to nuclear matter. Therefore, in the study of quark mass scale, it is necessary to further study the QCD phase diagram. To clearly illustrate this point, we chose four sets of parameters and drew the radial distribution diagram of the density corresponding to the central density of different stars, as illustrated in Fig. 10. The top curve of each subgraph is the central density corresponding to the maximum mass of the star, the third curve is the central density corresponding to the maximum radius of the star, and the horizontal line corresponds to the surface density of the star.We can observe that the surface density of the star becomes negligible, even lower than the normal nuclear saturation density when larger C and small D is used to produce a larger maximum mass. The panel (a) represents the parameter pair
$ (C,\sqrt{D}) = $ $ (0,160\ \mathrm{MeV}) $ . At this point, the central density of the baryon number corresponding to the maximum star mass (about 1.56$ M_\odot $ ) is 1.255$ \mathrm{fm}^{-3} $ . The surface density is 0.228$ \mathrm{fm}^{-3} $ . When the central density of baryon number is 0.64$ \mathrm{fm}^{-3} $ , the maximum radius of the star is about 9.98 km. The panel (b) is for the parameter pair$ (C,\sqrt{D}) = (0.4,140\ \mathrm{MeV}) $ . At this point, the central density of the baryon number corresponding to the maximum star mass (about 1.86$ M_\odot $ ) is 0.801$ \mathrm{fm}^{-3} $ . The surface density is 0.132$ \mathrm{fm}^{-3} $ . When the central density of the baryon number is 0.41$ \mathrm{fm}^{-3} $ , the maximum radius of the star is approximately 12.62 km. The panel (c) represents the parameter pair$ (C,\sqrt{D}) = (0.7,129\ \mathrm{MeV}) $ . The central density of the baryon number corresponding to the maximum star mass (about 2.16$ M_\odot $ ) is 0.610$ \mathrm{fm}^{-3} $ . The surface density is 0.091$ \mathrm{fm}^{-3} $ . When the central density of baryon number is 0.28$ \mathrm{fm}^{-3} $ , the maximum radius of the star is approximately 15.12 km. The panel (d) presents the parameter pair$ (C,\sqrt{D}) = $ $ (0.6,160\ \mathrm{MeV}) $ . At this point, the central density of baryon number corresponding to the maximum star mass (about 1.38$ M_\odot $ ) is 1.139$ \mathrm{fm}^{-3} $ . The surface density is 0.188$ \mathrm{fm}^{-3} $ . When the central density of baryon number is 0.59$ \mathrm{fm}^{-3} $ , the maximum radius of the star is approximately 9.52 km.In some cases, the maximum mass of the star increases; however, the surface density decreases, even below normal nuclear matter. This may obviously indicate a phase transition to nuclear matter. Therefore, further investigations on the QCD phase diagram are required to follow-up with the novel quark mass scaling.
-
We comprehensively studied the thermodynamic self-consistency of the equivalent mass model. Together with the novel quark mass scale, we studied the equation of state of strange quark matter at finite density and temperature. In particular, we studied the effects of quark confinement and first-order perturtabative interactions on strange quark matter. Based on the obtained equation of state, we calculated the velocity of sound in strange quark matter, the relationship between strange star and radius, which incluthe the fact that the maximum stellar mass varies with perturbation and constraint intensity parameters, and the relationship between the mass and radius of strange star whose surface density is lower than that of normal nuclear matter. We believe that this could be a signal for a phase transition to nuclear matter. The self-consistency of the model's thermodynamic treatment is verified by the relationship between pressure and free energy. Furthermore, we verified the third law of thermodynamics for strange quark matter under this model by adopting the entropy of the average baryon as a function of temperature.
In the next step, we plan to study the phase diagram of strongly interacting matter in the framework of the equivalent mass approach, and compare it with the phase diagram in the conventional MIT model. Then, we will proceed to the application of the model on the structure of hybrid stars, the properties of strangelets, and the formation of quark gluon plasma in relativistic heavy ion collisions, etc.
Strange quark matter and proto-strange stars in a baryon density-dependent quark mass model
- Received Date: 2021-09-16
- Available Online: 2022-05-15
Abstract: The properties of strange quark matter and the structures of (proto-)strange stars are studied within the framework of a baryon density-dependent quark mass model, where a novel quark mass scaling and self-consistent thermodynamic treatment are adopted. Our results indicate that the perturbative interaction has a significant impact on the properties of strange quark matter. It is determined that the energy per baryon increases with temperature, while the free energy decreases and eventually becomes negative. At fixed temperatures, the pressure at the minimum free energy per baryon is zero, suggesting that the thermodynamic self-consistency is preserved. Furthermore, the sound velocity v in quark matter approaches the extreme relativistic limit (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: