Resonances ρ(1450)⁺ and ρ(1700)⁺ in B → DKK decays

Three-body hadronic B meson decays provide us rich opportunities to explore CP violations in the relevant decay channels and to study intermediate resonance structures for the final states. Resonance contributions for the kaon pair in three-body B decays have been extensively studied experimentally [1-11] and theoretically [12-28] in recent years. Nevertheless, the contributions from $ \rho(770) $ and its excited states $ \rho(1450) $ and $ \rho(1700) $ for the kaon pair in the final states of these decays were considered to be small and have been ignored in most cases.

Recently, an unexpected fit fraction of approximately$ 30\% $ for the $ K^+K^- $ pair from resonance $ \rho(1450) $ in the decays $ B^\pm \to \pi^\pm K^+K^- $was reported by the LHCb Collaboration in Ref. [29]. This fit fraction is unreliable when it is compared with the proportion contributed by the same state $ \rho(1450) $ for the pion pair in $ B^\pm \to \pi^\pm \pi^+\pi^- $ decays [30,31]. In [32], the perturbative QCD (PQCD) [33-36] prediction for the branching fraction of $B^\pm \to \pi^\pm \rho(1450)^0 \to \pi^\pm K^+K^-$ is much smaller than LHCb's result in [29], even taking the contribution from the Breit-Wigner (BW) tail of $ \rho(770) $ into account. The calculation within the light-cone sum rule approach [37] does not support the result for $ \rho(1450)^0\to K^+K^- $ from LHCb [29] either. In Ref. [38], the authors claimed the unsettled state $ f_X(1500) $ is the vector $ \rho(1450) $ reported by LHCb. A broad resonance $ \rho_X(1500) $ has also been promoted to describe this broad resonance around the mass region of $ 1.5\; {\rm{GeV}} $ [39].

The vector resonance $ \rho(770) $ has been well established. However, the properties of its excited states $ \rho(1450) $ and $ \rho(1700) $ are not yet entirely clear. It has been shown that the neutral intermediate resonances $ \rho(1450)^0 $ and $ \rho(1700)^0 $ contribute the $ K\bar{K} $ pair in the processes $ \bar{p} p \to K^+K^-\pi^0 $ [40-42], $ e^+e^- \to K^+K^- $ [43-49], $ e^+ e^- \to K^0_{S}K^0_{L} $ [50-54], and $ J/\psi \to K^+K^-\pi^0 $ [55-59]. To capture the information on $ \rho(1450) $ and $ \rho(1700) $ clearly, the investigation on the charged excited rho mesons in $ K^+\bar{K}^0/K^-K^0 $ channels can be a good choice. The typical decay, $ \tau^- \to K^-K_S\nu_\tau $, has been measured by CLEO [60], Belle [61], and BABAR [62] Collaborations, and theoretical analyses have been performed by including the contributions of the ρ family [63-66]. The pole mass of $ m_{\rho(1700)} $ is close to the mass of the τ lepton; moreover, the full width for $ \rho(1700) $ is broad [67], so it is clearly unrealistic to find a complete curve of the intermediate resonance $ \rho(1700) $ in the $ K^\pm K_S $ distribution in the τ decay. Within the QCD factorization approach, the theoretical description for the decays $ B_c^+ \to J/\psi K^+K_S $ and $ B_c^+ \to \psi(2S) K^+K_S $ including the resonances $ \rho(1450)^+ $ and $ \rho(1700)^+ $ has been presented in Ref. [68]. In this work, we shall study the charged $ \rho(1450) $ and $ \rho(1700) $ in the three-body decays $ B^+ \to \bar{D}^0 K^+ \bar{K}^0 $, $ B^0 \to D^- K^+ \bar{K}^0 $, and $ B_s^0 \to D_s^-K^+ \bar{K}^0 $ with the corresponding quasi-two-body processes.

The decay $ B_s^0\to D_s^- R \to D_s^-K^+ \bar{K}^0 $ is contributed solely by the color-allowed emission diagrams as shown in Fig. 1(a). The decay amplitude is given by $ \mathcal{A}_{B_s} \propto [(C_2+C_1/3)F_{eD}^{LL}+C_1M_{eD}^{LL}] $, where $ F_{eD}^{LL} $ and $ M_{eD}^{LL} $ represent the amplitudes for factorizable and nonfactorizable parts respectively. Evidently, the relevant factorizable amplitude is dominant and can be expressed as $ <K^+ \bar{K}^0|(\bar{u}d)_{V-A}|0><D_s^-|(\bar{b}c)_{V-A}|B_s^0> $. Considering the $ K^+ \bar{K}^0 $ can only be produced by the vector current, the ρ family resonances with $ J^P = 1^- $ should be prominent in the $ KK $ system of $ B_s^0 \to D_s^-K^+ \bar{K}^0 $. For the other two decays, in addition to the color-allowed emission cases, the diagrams with the emission of a D meson and the annihilation diagrams as presented in Fig. 1 (b), (c) will also contribute to the decays $ B^+ \to\bar{D}^0 R\to \bar{D}^0 K^+ \bar{K}^0 $ and $ B^0 \to D^- R\to D^- K^+ \bar{K}^0 $, respectively, but they are both color-suppressed. It means that the decay amplitudes for these two decays should also be contributed mainly by the Feynman diagrams with the resonances emitted, and the ρ mesons can also be crucial in the $ KK $ distribution of the corresponding three-body B decays. Moreover, the concerned quasi-two-body decays are CKM-favored processes, which should have relatively large branching ratios and the potential to be measured by experiments.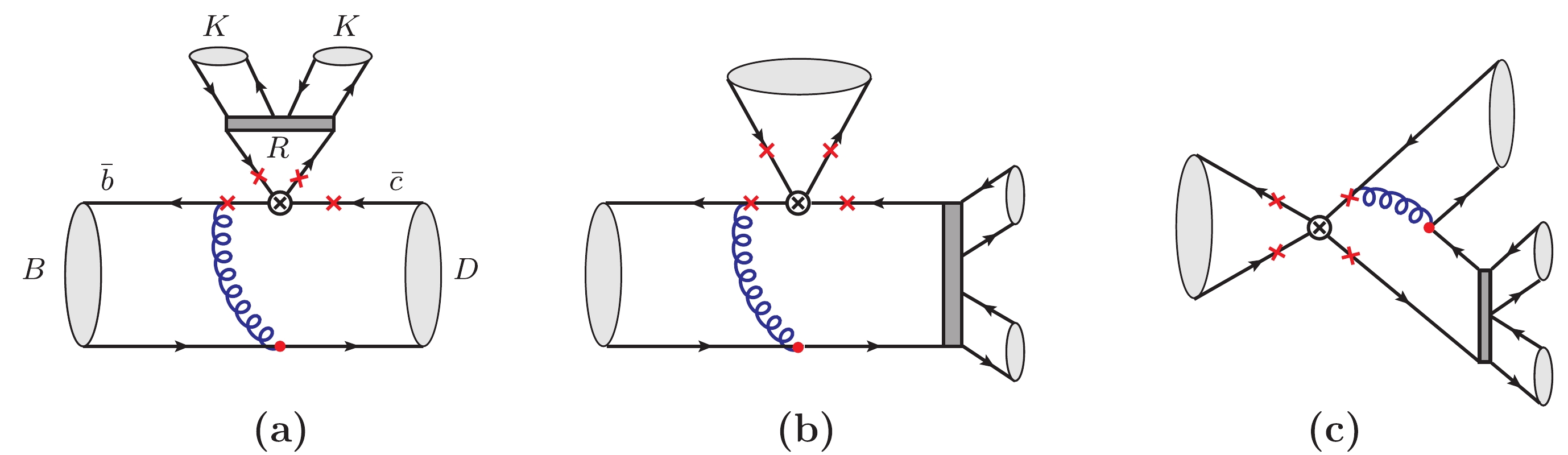

Figure 1.  (color online) Typical Feynman diagrams for the quasi-two-body decays $ B\to DR \to D KK $, in which D and R represent the D meson with $ \bar{c}q $ and the intermediate resonances, respectively. The symbol $ "\times" $ denotes the possible attachments for hard gluons, and $ "\otimes" $ represents the insertion of the four-fermion vertices in the effective theory.

In the past, the resonance contributions from various intermediate states for the three-body decays $ B \to D h_1h_2 $ ($ h_{1,2} $ represents pion or kaon) have been studied within the PQCD approach [24,25,69-77]. In the recent work, we studied the virtual contributions for the kaon pair from the tail of $ \rho(770) $ in the three-body decay $ B \to D K\bar{K} $ [78]. Faced with the huge disparities between the coefficients for the excited states of $ \rho(770) $, $ \omega(782) $, and $ \phi(1020) $ in the kaon vector timelike form factor fitted in different studies [63,79,80], a detailed discussion was provided in Ref. [81], and the contributions for the kaon pair from $ \rho(770,1450,1700) $ and $ \omega(782,1420,1650) $ in the $ B\to K\bar K h $ decay have also been studied systematically.

The rest of this article is structured as follows. In Sec. II, we provide a brief review of the PQCD framework for the concerned quasi-two-body decays. In Sec. III, we present the numerical results and the phenomenological analyses. Finally, we provide a short summary in Sec. IV.

Under the quasi-two-body approximation, the PQCD factorization formula for the decay amplitude $ {\mathcal A} $ of the decay $ B\to D R \to D KK $ can be expressed as the convolution of a calculable hard kernel H with the universal light-cone distribution amplitudes [82,83]

in which $ \Phi_B $ and $ \Phi_{D} $ are the distribution amplitudes for the B and D mesons, respectively. The distribution amplitude $ \Phi_{KK} $ is introduced to describe the interactions between the kaon pair originating from the resonance R.

In the PQCD approach, the distribution amplitudes for the initial and final states are crucial inputs. In this work, we employ the same forms of $ \Phi_B $ and $ \Phi_{D} $ as those widely adopted in PQCD; one can find their explicit expressions and parameters in Ref. [69] and the references therein. For the P-wave $ KK $ system along with the subprocesses $ \rho^+ \to KK $, the distribution amplitudes are organized into [28,32]

where z is the momentum fraction for the spectator quark, s is the squared invariant mass of the kaon pair, and $ \epsilon_L $ and p are the longitudinal polarization vector and momentum for the resonances, respectively. The twist-2 and twist-3 distribution amplitudes $ \phi^{0} $, $ \phi^{s} $, and $ \phi^{t} $ are chosen as

with the Gegenbauer polynomial $ C^{3/2}_2(t) = 3\left(5t^2-1\right)/2 $ and the Gegenbauer moments $ a_2^{0} = 0.25\pm0.10 $, $ a_2^s = 0.75\pm0.25 $, and $ a_2^t = -0.60\pm0.20 $ [32,84]. The vector time-like form factors $ F^s_K(s) $ and $ F^t_K(s) $ for the twist-$ 3 $ distribution amplitudes are deduced by the assumption $ F^{s,t}_K(s)\approx (f^T_{\rho}/f_{\rho})F_K(s) $ [81,84] with $ f_\rho = 0.216 $ GeV and $ f^T_\rho = 0.165 $ GeV [85].

For the P-wave $ K^+K^- $ and $ K^0\bar{K}^0 $ systems, the kaon form factors are generally saturated by $ \rho(770) $, $ \omega(782) $, $ \phi(1020) $, and their radial excitations. When it comes to the $ K^+ \bar{K}^0 $ case, only the ρ family states contribute, and the vector timelike form factors can be simply expressed as [63,78,81]

where the symbol $ \rho_i $ indicates the resonance $ \rho(770) $ and its excited states. For the normalization factors for $ \rho(1450) $ and $ \rho(1700) $, we take $ c^K_{\rho(1450)} = -0.156\pm0.015 $ and $c^K_{\rho(1700)} = -0.083\pm0.019$ as discussed in detail in Ref. [81]. The resonance shape for $ \rho(1450,1700) $ is described by the KS version of the BW formula [63,86]:

where the mass-dependent width $\Gamma_{\rm tot}(s)$ can be found in Refs. [87,88].

By combining various of contributions from the relevant Feynman diagrams as shown in Fig. 1, the total decay amplitudes for the concerned quasi-two-body decays are written as

where$ G_F = 1.16638 \times $$ 10^{-5}\; {\rm{GeV}}^{-2} $ is the Fermi coupling constant, $ V_{cb,ud} $ are the CKM matrix elements, and $ a_1 = C_1+ C_2/3 $ and $ a_2 = C_2+ C_1/3 $ are the Wilson coefficients. The PQCD calculations of individual amplitudes $ F^{LL}_{eD,e\rho,a\rho} $ and $ M^{LL}_{eD,e\rho,a\rho} $ for the factorizable and nonfactorizable Feynman diagrams are carried out in the frame with the B meson at rest. Because of the same quark composition, the decay amplitudes for the considered decays with the intermediate resonances $ \rho(1450,1700) $ are the same as those with $ \rho(770) $, and the explicit expressions, together with the definitions of related momenta in the light-cone coordinates, have been presented in Ref. [78]. For the sake of simplicity, we shall not present them in this work.

The masses for the initial and final particles, the full widths for the resonance states, and the decay constants for B and D mesons are summarized as follows (in units of GeV) [67]:

In addition, the mean lifetimes $ \tau_{B^\pm/B^0/B^0_s} = 1.638/ $$ 1.519/1.515 $ ps, and the Wolfenstein parameters for the CKM matrix $ A = 0.790^{+0.017}_{-0.012} $, $ \lambda = 0.22650\pm0.00048 $, $ \bar{\rho} = 0.141^{+0.016}_{-0.017} $, and $ \bar{\eta} = 0.357\pm0.011 $ are also adopted as in Ref. [67].

For the considered $ B \to D \rho(1450)^+ \to D K^+ \bar{K}^0 $ decays, the PQCD predictions for the branching ratios of each case are the following:

while the predicted branching ratios of same decays with the intermediate resonance $ \rho(1700) $ are

All the results above are given in the energy range with the invariant mass of the $ K^+ \bar{K}^0 $ pair varying between $ m_{K^+}+m_{\bar{K}^0} $ and $ m_B-m_D $. The first two theoretical errors come from the uncertainties of the parameters $ \omega_{B_{(s)}} = 0.40 \pm 0.04\; (0.50 \pm 0.05) $ and $ C_{D_{(s)}} = 0.5\pm 0.1\; $$ (0.4\pm0.1) $ in the distribution amplitudes for the B and D mesons, respectively; the errors from the uncertainties of Gegenbauer moments $ a^0_2 = 0.25\pm0.10 $, $ a^s_2 = 0.75\pm0.25 $, and $ a^t_2 = -0.60\pm0.20 $ in the two-kaon system are added together as the third error; and the last one is due to the coefficient $ c^K_{\rho(1450)} = -0.156\pm0.015 $ or $c^K_{\rho(1700)} = -0.083\pm $$ 0.019$ in the kaon timelike form factor. The errors from the uncertainties of other parameters are relatively small and have been neglected.

From the calculations and the numerical results, one can conclude the following:

(1) The branching ratios of the considered quasi-two-body decays, which are expected to be large and measurable, are predicted to be in the order of $ 10^{-5} $ numerically in the PQCD approach. We also test the contributions from the color-suppressed emission diagrams for $ B^+ \to {\bar{D}^0} [\rho(1450)^+\to] K^+ \bar{K}^0 $ and the annihilation diagrams for $ B^0 \to {D^-} [\rho(1450)^+ \to] K^+ \bar{K}^0 $, and the corresponding branching ratios are obtained to be $ 2.18 \times 10^{-6} $ and $ 1.06 \times 10^{-6} $, while the results become $ 6.92\times 10^{-5} $ and $ 6.45\times 10^{-5} $, respectively, when considering only the color-allowed emission diagrams for those two decays. Although the interference between the different types of Feynman diagrams for each decay are non-negligible, the contributions from the diagrams with the emission of a kaon pair are still dominant as expected.

(2) The PQCD predicted branching ratios of the decay modes with the subprocess $ \rho(1700)^+\to K^+ \bar{K}^0 $ are not much smaller than the corresponding ones with the intermediate state $ \rho(1450)^+ $. This is because the latter are suppressed in the phase space when considering the mass of the kaon pair $ m_{K^+}+m_{\bar{K}^0} $ is very close to $ m_{\rho(1450)}-\Gamma_{\rho(1450)} $ but considerably less than $ m_{\rho(1700)}-\Gamma_{\rho(1700)} $ in comparison. In contrast, the situation is quite different in the same B meson decays with the subprocesses $ \rho(1450) \to \pi\pi $ and $ \rho(1700) \to \pi\pi $ [70,89-93] on account of the impact on the phase space arising from the difference between the mass of the pion and kaon.

(3) In the measurement by the Belle Collaboration [1], the branching fraction of the $ B^+ \to \bar{D}^0 K^+ \bar{K}^0 $ decay was determined to be $ (5.5\pm1.4\pm 0.8)\times 10^{-4} $. Meanwhile, they also gave a branching ratio for $ B^0\to D^-K^+ \bar{K}^0 $ of $ (1.6\pm0.8\pm 0.3)\times 10^{-4} $ and set an upper limit as $ 3.1\times 10^{-4} $ at $ 90\% $ confidence level. With the center values of our predictions in Eqs. (11)–(12), we obtain the ratios

and

Similarly, the ratios become $ 31.38\% $ and $ 25.00\% $ for the $ B^0 \to D^- K^+ \bar{K}^0 $ decay mode. Since there are still large uncertainties in the branching fraction of $ B^0 \to D^- K^+ \bar{K}^0 $ presented by Belle, more precise measurements for this three-body channel are needed. Nevertheless, the above results indicate that the contributions from charged $ \rho(1450) $ and $ \rho(1700) $ can be important in the relevant three-body B meson decays.

(4) In our previous work [78], the virtual contribution for $ \rho(770) $ in $ B\to DKK $ was studied, and the center values of the branching ratios for the decays $ B^+ \to {\bar{D^0}} \rho(770)^+ $, $ B^0 \to {D^-} \rho(770)^+ $, and $ B_s^0 \to {D_s^-} \rho(770)^+ $ with the subprocess $ \rho(770)^+\to K^+ \bar{K}^0 $ are predicted to be $ 1.18 \times 10^{-4} $, $ 7.93 \times 10^{-5} $, and $ 6.06 \times 10^{-5} $, respectively. Comparing those results with the numerical results in this study, two conclusions can be obtained. On the one hand, the contribution from the tail of $ \rho(770) $ is still large and cannot be ignored in the P-wave $ K^+ \bar{K}^0 $ system. On the other hand, limited by the phase space for $ KK $ production in the decay of the $ \rho(770) $ meson, the contributions for $ KK $ pair from the excited states $ \rho(1450) $ and $ \rho(1700) $ are more close to that of $ \rho(770) $ compared with the corresponding ones in the $ \pi\pi $ system. Therefore, it is possible to find the resonances $ \rho^+(1450) $ and $ \rho^+(1700) $ in the $ KK $ channel, and the concerned $ B\to DKK $ decays can be employed to study the properties of those excited ρ mesons. Interestingly, the $ KK_S $ invariant mass spectrum for the $ B^+ \to \bar{D}^0 K^+ K^0_S $ decay presented by Belle showed a peak around $ 1.2 $ GeV [1]. It indicates that other possible resonances, such as $ a_0(980) $ and $ a_2(1320) $, will contribute to this region in addition to $ \rho(770) $ and $ \rho(1450) $. Moreover, the interference between $ \rho(770) $ and $ \rho(1450) $ can increase or decrease the total contributions from these two resonances. We leave these possible contributions for the kaon pair to future studies due to the lack of precise parameters of the kaon time-like form factor, and more accurate measurements for this decay will help to test the $ KK $ distribution close to the threshold determined by Belle.

In this work, we studied the resonance contributions for $ \rho(1450)^+ $ and $ \rho(1700)^+ $ in the $ B^+ \to \bar{D}^0 K^+ \bar{K}^0 $, $ B^0 \to D^- K^+ \bar{K}^0 $, and $ B_s^0 \to D_s^-K^+ \bar{K}^0 $ decays. The branching ratios of the concerned quasi-two-body B meson decays are predicted to be in the order of $ 10^{-5} $ numerically within the PQCD approach. The contributions from the intermediate states $ \rho(1450) $ and $ \rho(1700) $ are $ 16.35\% $ and $ 15.05\% $ of the data for the $ B^+ \to \bar{D}^0 K^+ \bar{K}^0 $ decay presented by Belle. The similar ratios become $ 31.38\% $ and $ 25.00\% $ for $ B^0 \to D^- K^+ \bar{K}^0 $, where the total three-body branching fraction still has large errors and needs further measurements. It shows that the contributions from charged $ \rho(1450) $ and $ \rho(1700) $can be important in the relevant three-body B meson decays, and all these PQCD predictions will be tested in the LHCb and Belle-II experiments in the future.