-
$ \alpha $ decay is a fundamental nuclear decay mode. Research on$ \alpha $ decay has long been focused in the vicinities of doubly magic nuclei$ ^{208} $ Pb ($ Z = 82,\; N = 126 $ ) and$ ^{298} $ Fl ($ Z = 114, \;N = 184 $ ) because$ \alpha $ decay can be a probe to study unstable nucleus structures, and can be the only way to identify new synthesized superheavy nuclei [1–27]. Over the past two decades,$ \alpha $ emitters around the self-conjugate doubly magic nucleus$ ^{100} $ Sn ($ Z = N = 50 $ ) at the opposite end of the mass table have also received a lot of attention and become a hot topic in nuclear physics [18, 28–35]. In particular, there is the fastest$ \alpha $ emitter$ ^{104} $ Te near doubly magic nucleus$ ^{100} $ Sn [34]. Since the$ \alpha $ emitters near self-conjugate doubly magic nucleus$ ^{100} $ Sn are close to the$ N = Z $ line, the nuclear force is extremely sensitive to isospin. Therefore, it is a great chance to study the unique neutron-deficient nuclear structure and examine various$ \alpha $ decay theoretical models. Moreover, cluster radioactivity was also predicted as one of the decay modes of nuclei in the$ ^{100} $ Sn region [36–39]. Further interest in the decay rates of nuclei around doubly magic nucleus$ ^{100} $ Sn comes from research into astrophysical processes, for which this region has been considered as the end of the rapid proton capture process due to the Sn–Sb–Te cycle [33, 40, 41].In addition, in the neutron-deficient Te, Xe, and Ba isotopes near
$ ^{100} $ Sn, one would expect that interactions between protons and neutrons occupying similar single-particle orbitals could enhance the$ \alpha $ -particle preformation factors, and together with the significantly reduced$ \alpha $ -widths compared to the analogous nuclei just above doubly magic nucleus$ ^{208} $ Pb, can result in the so-called "superallowed"$ \alpha $ decay [42]. This effect would be expected to be strongest for$ N = Z $ self-conjugate nuclei [42]. Recently,$ \alpha $ radioactivity to a heavy self-conjugate nucleus was observed for the first time on the$ ^{108} $ Xe$ \to $ $ ^{104} $ Te$ \to $ $ ^{100} $ Sn$ \alpha $ decay chain [34], including the measurements of the$ \alpha $ -particle kinetic energy and$ \alpha $ decay half-lives of the$ \alpha $ emitters$ ^{108} $ Xe [$ E_{\alpha} = 4.4(2) $ MeV,$ T_{1/2} = 58^{+106}_{-23} $ μs] and$ ^{104} $ Te [$ E_{\alpha} = 4.9(2) $ MeV,$ T_{1/2}<18 $ ns]. The authors of this article suggested that the$ \alpha $ -reduced width for$ ^{108} $ Xe or$ ^{104} $ Te is more than a factor of 5 larger than that for$ ^{212} $ Po [34].It is well known that
$ ^{104} $ Te, near the proton drip line, and$ ^{212} $ Po, near the$ \mathcal{\beta}- $ stability line, are the only two existing$ \alpha $ emitters decaying to doubly magic nuclei. In recent years, researchers adopted different models such as the density dependent cluster model (DDCM) [28, 43–45], the generalized liquid drop model (GLDM) [46, 47], the preformed cluster model (PCM) [48], etc. to study the$ \alpha $ decay of nuclei around doubly magic$ ^{208} $ Pb and$ ^{100} $ Sn, and provide some important insights on the$ \alpha $ -particle preformation factor. In this letter, we focus on the$ \alpha $ -particle preformation factors of nuclei near self-conjugate doubly magic nucleus$ ^{100} $ Sn, and compare them to those of analogous nuclei just above the doubly magic nucleus$ ^{208} $ Pb, based on the available experimental data of$ \alpha $ decay [34, 49–59] within the generalized liquid drop model (GLDM) [60–66]. These$ \alpha $ emitters have different isospins and mass numbers as well as different proton and neutron closed shells. We want to reveal some new behaviors of$ \alpha $ -particle preformation factors for extremely neutron-deficient nuclei near self-conjugate doubly magic nucleus$ ^{100} $ Sn, in order to understand the roles of proton–neutron correlation and the single-particle orbitals occupied by protons and neutrons in the preformation of$ \alpha $ -clusters, as well as the physical mechanism of superallowed$ \alpha $ decay.The GLDM can deal well with proton radioactivity [67], cluster radioactivity [68], fusion [69], fission [70], and the
$ \alpha $ decay process [22, 60–66, 71] by introducing the quasimolecular shape mechanism [60], which can describe the complex deformation process from the parent nucleus through continuous transition to the appearance of a deep and narrow neck, finally resulting in two tangential fragments, and adding the proximity energy, including an accurate radius and mass asymmetry. In previous works [60–66], the GLDM has been introduced in detail. The$ \alpha $ decay half-life can be obtained by$ T_{1/2} = \frac{\ln{2}}{\lambda} , $

(1) with the
$ \alpha $ decay constant$ \mathcal{\lambda} $ being expressed as$ \begin{array}{l} \ \lambda = P_{\alpha}{\nu}P , \end{array} $

(2) where the assault frequency
$ \mathcal{\nu} $ is obtained using the classical method with the kinetic energy of the$ \alpha $ -particle. The barrier-penetrating probability$ P $ is determined by tunneling the GLDM potential barriers [60–66] with the Wentzel–Kramers–Brillouin (WKB) approximation.The experimental
$ \alpha $ -particle preformation factor$ P_{\alpha}^{\rm{Exp}} $ can be extracted from the ratios of the theoretical decay half-life$ T_{1/2}^{\rm{Cal1}} $ , calculated by assuming the$ \alpha $ -particle preformation factor is a constant$ P_{\alpha} = 1 $ , to experimental decay half-life [65, 72–75]. This is expressed as$ P_{\alpha}^{\rm{Exp}} = \frac{T_{1/2}^{\rm{Cal1}}}{T_{1/2}^{\rm{Exp}}} . $

(3) To examine the experimental
$ \alpha $ decay half-life data, the analytic formula for estimating the$ \alpha $ -particle preformation factor is also adopted, which was put forward in our previous works [66, 71]. It is expressed as$ \begin{aligned}[b] \log_{10}P_{\alpha}^{\rm{Eq}} =& a+bA^{1/6}\sqrt{Z}+c\frac{Z}{\sqrt{Q_{\alpha}}}-d\chi^{\prime}\\&-e\rho^{\prime}+f\sqrt{l(l+1)} , \end{aligned} $

(4) where
$ \chi^{\prime} = Z_1Z_2\sqrt{\dfrac{A_1A_2}{(A_1+A_2)Q_{\alpha}}} $

and
$\rho^{\prime} = \sqrt{\dfrac{A_1A_2}{A_1+A_2}Z_1Z_2\left(A_1^{1/3}+A_2^{1/3}\right)}. $

$ A $ ,$ Z $ , and$ Q_{\alpha} $ represent mass number, proton number, and$ \alpha $ decay energy of the parent nucleus.$ A_1 $ ,$ Z_1 $ ,$ A_2 $ , and$ Z_2 $ denote the mass and proton numbers of the$ \alpha $ -particle and daughter nucleus.$ l $ is the angular momentum carried by the$ \alpha $ -particle. The parameters values are listed in Ref. [66].The calculated
$ \alpha $ decay half-lives for nuclei above doubly magic nuclei$ ^{100} $ Sn and$ ^{208} $ Pb are presented in Tables 1 and 2, respectively. In these two tables, the first four columns represent the$ \alpha $ transition, the experimental kinetic energy of the$ \alpha $ -particle, the experimental$ \alpha $ decay energy, and the minimum angular momentum carried by the$ \alpha $ -particle. The fifth column is the experimental$ \alpha $ decay half-life. The sixth column denotes the calculated$ \alpha $ decay half-life$ T_{1/2}^{\rm{Cal1}} $ within the GLDM with$ P_{\alpha} = 1 $ . The seventh column gives the calculated$ \alpha $ decay half-life$ T_{1/2}^{\rm{Cal2}} $ within the GLDM with the estimated$ \alpha $ -particle preformation factor from Eq. (4). The eighth column shows the extracted experimental$ \alpha $ -particle preformation factor by using Eq. (3) with$ T^{\rm{Cal1}}_{1/2} $ and$ T^{\rm{Exp}}_{1/2} $ . The last two columns express the calculated proton–neutron correlation energy$ E_{p-n} $ and two protons–two neutrons correlation energy$ E_{2p-2n} $ determined by Eqs. (6) and (7). From these two tables, it can be seen immediately that the calculated$ \alpha $ decay half-lives$ T_{1/2}^{\rm{Cal2}} $ can accurately reproduce the experimental data including the newly observed self-conjugate nuclei$ ^{104} $ Te and$ ^{108} $ Xe [34]. Note that the calculations provide support for recent experimental observation data in Ref. [34]. In Table 1, for$ ^{110} $ Te, the calculated$ \alpha $ -particle preformation factor using Eq. (4) is an order of magnitude larger than the extracted value from the experimental$ \alpha $ decay half-life data. This is because the$ \alpha $ decay branch ratio of$ ^{110} $ Te is very small, only 0.00067% [28], and the microscopic calculation of the$ \alpha $ -particle preformation factor is very complicated, while Eq. (4) mainly considers the$ \alpha $ decay energy, proton number, and mass number when calculating the$ \alpha $ -particle preformation factor. This leads to a deviation between the theoretically calculated$ \alpha $ -particle preformation factors and the experimental data for nuclei with extremely low$ \alpha $ decay branch ratios such as$ ^{110} $ Te.$ \alpha $ transition

$ E_{\alpha} $ 

/MeV$ Q_{\alpha} $ 

/MeV$ l_{\rm min} $ 

$ T^{\rm{Exp}}_{1/2} $ 

/s$ {T_{1/2}^{\rm{Cal1}}} $ 

/s$ {T_{1/2}^{\rm{Cal2}}} $ 

/s$ {P_{\alpha}^{\rm{Exp}}} $ 

$ E_{p-n} $ 

/MeV$ E_{2p-2n} $ 

/MeV$ ^{104} $ Te

$ \to^{100} $ Sn

4.9
[34]5.1 0 $<1.80\times10^{-8} $ 

[34]$ 1.47\times10^{-8} $ 

$ 7.29\times10^{-8} $ 

$>0.81 $ 

1.26 $ {^a} $ 

3.64 $ {^a} $ 

$ ^{106} $ Te

$ \to^{102} $ Sn

4.128
[51]4.29 0 $ 7.00\times10^{-5} $ 

[50–52]$ 2.52\times10^{-5} $ 

$ 8.38\times10^{-5} $ 

0.36 0.56 $ {^b} $ 

1.84 $ {^a} $ 

$ ^{108} $ Te

$ \to^{104} $ Sn

3.314
[54]3.44 0 $ 4.30\times10^{0} $ 

[51, 53, 54]$ 9.30\times10^{-1} $ 

$ 1.68\times10^{0} $ 

0.22 1.06 $ {^b} $ 

1.83 $ {^b} $ 

$ ^{110} $ Te

$ \to^{106} $ Sn

2.624
[55]2.72 0 $ 2.78\times10^{6} $ 

[55, 56]$ 3.32\times10^{5} $ 

$ 2.87\times10^{5} $ 

0.12 0.71 $ {^b} $ 

1.73 $ {^b} $ 

$ ^{108} $ Xe

$ \to^{104} $ Te

4.32
[34, 49]4.49 0 $ 5.80\times10^{-5} $ 

[34]$ 3.70\times10^{-5} $ 

$ 1.10\times10^{-4} $ 

0.64 1.10 $ {^a} $ 

3.35 $ {^a} $ 

$ ^{110} $ Xe

$ \to^{106} $ Te

3.72
[50]3.86 0 $ 1.48\times10^{-1} $ 

[50]$ 5.00\times10^{-2} $ 

$ 1.07\times10^{-1} $ 

0.34 0.73 $ {^b} $ 

2.02 $ {^a} $ 

$ ^{112} $ Xe

$ \to^{108} $ Te

3.216
[51]3.34 0 $ 3.38\times10^{2} $ 

[51, 53]$ 1.01\times10^{2} $ 

$ 1.53\times10^{2} $ 

0.30 1.13 $ {^b} $ 

1.66 $ {^b} $ 

$ ^{114} $ Ba

$ \to^{110} $ Xe

3.48
[50]3.61 0 $ 4.20\times10^{1} $ 

[50]$ 2.60\times10^{1} $ 

$ 4.19\times10^{1} $ 

0.62 0.66 $ {^b} $ 

1.96 $ {^a} $ 

a Calculated by using nuclear mass data in the WS4+ mass model [76].
b Calculated using nuclear mass data in the evaluated atomic mass table AME2016 [58, 59].Table 1. Calculations of
$ \alpha $ -particle preformation factor,$ \alpha $ decay half-lives, and the proton–neutron correlation energy$ E_{p-n} $ and two protons–two neutrons correlation energy$ E_{2p-2n} $ of even–even Te, Xe, and Ba isotopes near$ ^{100} $ Sn.$ \alpha $ transition

$ E_{\alpha} $ 

/MeV$ Q_{\alpha} $ 

/MeV$ l_{\rm min} $ 

$ T^{\rm{Exp}}_{1/2} $ 

/s$ {T_{1/2}^{\rm{Cal1}}} $ 

/s$ {T_{1/2}^{\rm{Cal2}}} $ 

/s$ {P_{\alpha}^{\rm{Exp}}} $ 

$ E_{p-n} $ 

/MeV$ E_{2p-2n} $ 

/MeV$ ^{212} $ Po

$ \to^{208} $ Pb

8.79 8.95 0 $ 2.95\times10^{-7} $ 

$ 1.00\times10^{-8} $ 

$ 1.48\times10^{-7} $ 

0.03 0.87 1.44 $ ^{214} $ Po

$ \to^{210} $ Pb

7.69 7.83 0 $ 1.64\times10^{-4} $ 

$ 1.14\times10^{-5} $ 

$ 1.23\times10^{-4} $ 

0.07 0.70 1.28 $ ^{216} $ Po

$ \to^{212} $ Pb

6.78 6.91 0 $ 1.45\times10^{-1} $ 

$ 1.39\times10^{-2} $ 

$ 1.09\times10^{-1} $ 

0.10 0.51 1.11 $ ^{218} $ Po

$ \to^{214} $ Pb

6.00 6.12 0 $ 1.86\times10^{2} $ 

$ 1.93\times10^{1} $ 

$ 1.09\times10^{2} $ 

0.10 0.38 1.09 $ ^{212} $ Rn

$ \to^{208} $ Po

6.26 6.38 0 $ 1.43\times10^{3} $ 

$ 1.40\times10^{1} $ 

$ 6.86\times10^{2} $ 

0.01 0.23 0.57 $ ^{214} $ Rn

$ \to^{210} $ Po

9.04 9.21 0 $ 2.70\times10^{-7} $ 

$ 1.08\times10^{-8} $ 

$ 1.85\times10^{-7} $ 

0.04 0.67 1.24 $ ^{216} $ Rn

$ \to^{212} $ Po

8.05 8.20 0 $ 4.50\times10^{-5} $ 

$ 4.99\times10^{-6} $ 

$ 6.56\times10^{-5} $ 

0.11 0.70 1.33 $ ^{218} $ Rn

$ \to^{214} $ Po

7.13 7.26 0 $ 3.38\times10^{-2} $ 

$ 4.23\times10^{-3} $ 

$ 4.15\times10^{-2} $ 

0.13 0.58 1.29 $ ^{220} $ Rn

$ \to^{216} $ Po

6.29 6.41 0 $ 5.56\times10^{1} $ 

$ 8.33\times10^{0} $ 

$ 5.92\times10^{1} $ 

0.15 0.52 1.18 $ ^{222} $ Rn

$ \to^{218} $ Po

5.49 5.59 0 $ 3.30\times10^{5} $ 

$ 5.71\times10^{4} $ 

$ 2.79\times10^{5} $ 

0.17 0.51 1.15 $ ^{214} $ Ra

$ \to^{210} $ Rn

7.14 7.27 0 $ 2.44\times10^{0} $ 

$ 3.25\times10^{-2} $ 

$ 1.53\times10^{0} $ 

0.01 0.22 0.65 $ ^{216} $ Ra

$ \to^{212} $ Rn

9.35 9.53 0 $ 1.82\times10^{-7} $ 

$ 8.41\times10^{-9} $ 

$ 1.70\times10^{-7} $ 

0.05 0.52 1.14 $ ^{218} $ Ra

$ \to^{214} $ Rn

8.39 8.55 0 $ 2.52\times10^{-5} $ 

$ 2.44\times10^{-6} $ 

$ 3.88\times10^{-5} $ 

0.10 0.58 1.21 $ ^{220} $ Ra

$ \to^{216} $ Rn

7.45 7.59 0 $ 1.79\times10^{-2} $ 

$ 1.93\times10^{-3} $ 

$ 2.34\times10^{-2} $ 

0.11 0.68 1.35 $ ^{222} $ Ra

$ \to^{218} $ Rn

6.56 6.68 0 $ 3.36\times10^{1} $ 

$ 4.46\times10^{0} $ 

$ 3.92\times10^{1} $ 

0.13 0.44 1.34 $ ^{224} $ Ra

$ \to^{220} $ Rn

5.69 5.79 0 $ 3.14\times10^{5} $ 

$ 4.97\times10^{4} $ 

$ 2.99\times10^{5} $ 

0.16 0.41 1.25 $ ^{226} $ Ra

$ \to^{222} $ Rn

4.78 4.87 0 $ 5.05\times10^{10} $ 

$ 1.10\times10^{10} $ 

$ 4.00\times10^{10} $ 

0.22 0.40 1.23 Table 2. Same as Table 1, but for even–even Po, Rn, and Ra isotopes near
$ ^{208} $ Pb. The experimental$ \alpha $ decay half-lives are taken from the evaluated nuclear properties table NUBASE2016 [57]. The experimental$ \alpha $ decay energy are taken from the evaluated atomic mass table AME2016 [58, 59]. The$ E_{p-n} $ and$ E_{2p-2n} $ energies are calculated using the nuclear mass data in the AME2016 [58, 59].To measure the agreement between the calculated
$ \alpha $ decay half-lives$ T^{\rm{Cal2}}_{1/2} $ and experimental data$ T^{\rm{Exp}}_{1/2} $ , the standard deviations are calculated by$ \begin{array}{l} \sigma = \sqrt{\frac{1}{n}\sum ({\log_{10}T_{1/2}^{\rm{Cal2}}-\log_{10}T_{1/2}^{\rm{Exp}}})^2} . \end{array} $

(5) For nuclei in Tables 1 and 2, the results of standard deviations
$ \sigma_1 = 0.47 $ and$ \sigma_2 = 0.16 $ are satisfactory, showing that$ T^{\rm{Cal2}}_{1/2} $ can accurately reproduce$ T^{\rm{Exp}}_{1/2} $ within factors of$ 10^{0.47} = 2.95 $ and$ 10^{0.16} = 1.45 $ , respectively. This demonstrates that the GLDM can be applied to extract the experimental$ \alpha $ -particle preformation factors for studying the structure information of nuclei in these two regions.Furthermore, Tables 1 and 2 show that the extracted experimental
$ \alpha $ -particle preformation factors$ P_{\alpha}^{\rm{Exp}} $ of nuclei near$ ^{100} $ Sn are larger than$ P_{\alpha}^{\rm{Exp}} $ of nuclei near$ ^{208} $ Pb, and in particular, larger than$ P_{\alpha}^{\rm{Exp}} $ of analogous nuclei just above$ ^{208} $ Pb. The analogous nuclei refer to the two nuclei with the same valence proton and valence neutron located above doubly magic cores$ ^{100} $ Sn and$ ^{208} $ Pb, respectively. The valence protons$ N_p $ and valence neutrons$ N_n $ are defined as$ N_p = Z-Z_0 $ and$ N_n = N-N_0 $ with$ Z_0 = 50 $ and 82,$ N_0 = 50 $ and 126, being the magic numbers of protons and neutrons in the corresponding nuclear region. For example,$ ^{104} $ Te is analogous to$ ^{212} $ Po because they both have two valence protons and two valence neutrons outside of the doubly magic nuclei$ ^{100} $ Sn and$ ^{208} $ Pb, respectively.The extracted experimental
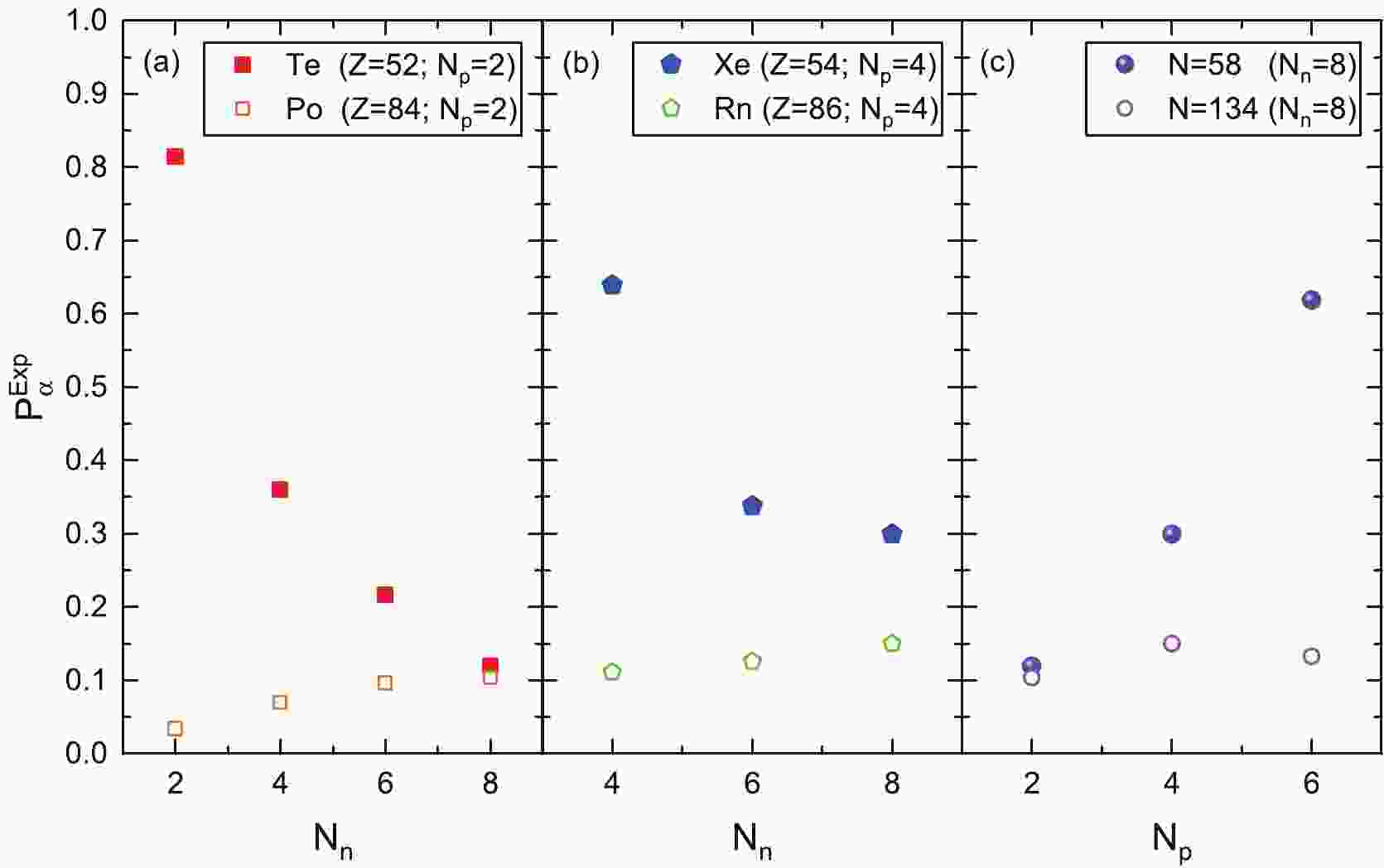
$ \alpha $ -particle preformation factors$ P_{\alpha}^{\rm{Exp}} $ for nuclei above$ ^{100} $ Sn and for analogous nuclei just above$ ^{208} $ Pb are shown as functions of valence protons and valence neutrons in Fig. 1 (a), (b), and (c), respectively. In this figure, one can see that$ P_{\alpha}^{\rm{Exp}} $ for nuclei above$ ^{100} $ Sn are significantly larger than those of analogous nuclei just above$ ^{208} $ Pb. Furthermore, Fig. 1 (a) shows the variations of$ P_{\alpha}^{\rm{Exp}} $ for Te ($ Z = 52 $ ) and Po ($ Z = 84 $ ) isotopes, whose valence protons are$ N_p = $ $ Z-Z_0 = 2 $ , against valence neutrons$ N_n $ . It is clear that for Te isotopes$ P_{\alpha}^{\rm{Exp}} $ exhibits an increasing trend when the nucleus moves towards the$ N = Z $ line, but Po isotopes do not show similar patterns due to the large asymmetry between neutrons and protons. Figure 1 (b) displays the variations of$ P_{\alpha}^{\rm{Exp}} $ for Xe ($ Z = 54 $ ) and Rn ($ Z = 86 $ ) isotopes, whose valence protons are$ N_p = Z-Z_0 = 4 $ , against valence neutrons$ N_n $ . We find that for Xe isotopes$ P_{\alpha}^{\rm{Exp}} $ also increases as the nucleus moves towards the$ N = Z $ line. However, Rn isotopes still do not show a similar trend of change. Figure 1 (c) plots$ P_{\alpha}^{\rm{Exp}} $ as a function of valence protons$ N_p $ for$ N = 58 $ and$ N = 134 $ isotones, whose valence neutrons are$ N_n = N-N_0 = 8 $ .$ P_{\alpha}^{\rm{Exp}} $ for$ N = 58 $ isotopes also show an increasing tendency as the nuclei move towards the$ N = Z $ line, but this phenomenon does not occur in the analogous$ N = 134 $ isotopes just above$ ^{208} $ Pb. This indicated that$ P_{\alpha}^{\rm{Exp}} $ is enhanced when a nucleus moves towards the$ N = Z $ line, resulting in the superallowed$ \alpha $ decay near doubly magic nucleus$ ^{100} $ Sn. In recent work, Clark et al. adopted a very different model and studied the$ \alpha $ -particle preformation factors of nuclei in these two regions [31]. A similar conclusion was obtained, though the$ \alpha $ -particle preformation factors of nuclei near doubly magic nuclei$ ^{100} $ Sn and$ ^{208} $ Pb are in orders of$ 10^{-2} $ and$ 10^{-3} $ , respectively.
Figure 1. (color online) Variations of extracted experimental
$\alpha$ -particle preformation factors$P_{\alpha}^{\rm{Exp}}$ from Eq. (3) against the valence neutrons for$Z = 52$ and$Z = 84$ isotopes (left), and against the valence neutrons for$Z = 54$ and$Z = 86$ isotopes (middle), and against the valence protons for$N = 58$ and$N = 134$ isotones (right), respectively.To investigate the effects of the proton–neutron interaction and the two protons–two neutrons interaction on
$ \alpha $ -particle preformation, we calculate the proton–neutron correlation energy$ E_{p-n} $ and two protons–two neutrons correlation energy$ E_{2p-2n} $ using$ \begin{aligned}[b] E_{p-n} =& B(A, Z)+B(A-2, Z-1)\\&-B(A-1, Z-1)-B(A-1, Z) , \end{aligned} $

(6) $ \begin{aligned}[b] E_{2p-2n} =& B(A, Z)+B(A-4, Z-2)\\&-B(A-2, Z-2)-B(A-2, Z) . \end{aligned} $

(7) Equations (6) and (7) were proposed in Ref. [77] and used to determine the experimental pairing energy of the nucleons [78].
$ B(A, Z) $ is the binding energy of a nucleus with the mass number$ A $ and proton number$ Z $ . The results of$ E_{p-n} $ energy and$ E_{2p-2n} $ energy are listed in the last two columns of Tables 1 and 2. In these two tables, it can be found that the$ E_{p-n} $ and$ E_{2p-2n} $ energies of nuclei above doubly magic nucleus$ ^{100} $ Sn are larger than those of analogous nuclei just above$ ^{208} $ Pb. This, in turn, leads to significant enhancement of$ P_{\alpha}^{\rm{Exp}} $ for nuclei near$ ^{100} $ Sn. The results for the$ E_{p-n} $ and$ E_{2p-2n} $ energies are plotted in Fig. 2. In this figure, the$ E_{p-n} $ and$ E_{2p-2n} $ energies of nuclei above$ ^{100} $ Sn are strengthened when compared to analogous nuclei just above$ ^{208} $ Pb. For$ Z = 52 $ isotopes, the$ E_{p-n} $ and$ E_{2p-2n} $ energies increase rapidly in$ N_n = 2 $ . Similarly, for$ Z = 54 $ isotopes, the$ E_{p-n} $ and$ E_{2p-2n} $ energies rise fast in$ N_n = 4 $ . However, the$ E_{p-n} $ and$ E_{2p-2n} $ energies of analogous nuclei just above$ ^{208} $ Pb change slowly. Therefore, it is demonstrated that the$ \alpha $ -particle is more likely to form in self-conjugate nuclei, resulting in the superallowed$ \alpha $ decay. In addition, the$ E_{2p-2n} $ energy appears an increased tendency, the same as$ P_{\alpha}^{\rm{Exp}} $ , when the nucleus moves towards the$ N = Z $ line, implying that the two protons–two neutrons interaction plays a more significant role than one proton–one neutron interaction in$ \alpha $ -particle preformation.
Figure 2. (color online) Proton–neutron
$E_{p-n}$ correlation energy and two protons–two neutrons correlation energy$E_{2p-2n}$ for nuclei above$^{100}$ Sn (denoted as solid symbols) and analogous nuclei above$^{208}$ Pb (denoted as open symbols).The extracted experimental
$ \alpha $ -particle preformation factors$ P_{\alpha}^{\rm{Exp}} $ for nuclei above$ ^{100} $ Sn and$ ^{208} $ Pb are shown as functions of$ ({N_pN_n})/({Z_0+N_0}) $ in Fig. 3 (a) and (b), respectively. In Fig. 3 (b), one can see that the closer$ ({N_pN_n})/({Z_0+N_0}) $ is to zero, representing the proton and/or neutron numbers approaching closed shells, the smaller is$ P_{\alpha}^{\rm{Exp}} $ . When$ ({N_pN_n})/({Z_0+N_0}) $ is far from zero,$ P_{\alpha}^{\rm{Exp}} $ will increase. This indicates that the closer the proton and/or neutron number is to the magic number, the more difficult it is for an$ \alpha $ -particle to form inside its parent nucleus. We find that$ P_{\alpha}^{\rm{Exp}} $ is linearly dependent on$ ({N_pN_n})/({Z_0+N_0}) $ for nuclei above$ ^{208} $ Pb. This is consistent with the conclusions deduced by adopting different models, in which the$ \alpha $ -particle preformation factors are extracted from the ratios between theoretical$ \alpha $ decay half-lives calculated by adopting the different models to experimental data [15, 79, 80], or calculated using the differences of binding energy between the$ \alpha $ decaying parent nucleus and its neighboring nuclei within the cluster-formation model [81]. It is shown that the nuclear shell effects and the nucleon configurations play key roles in$ \alpha $ -cluster preformation for$ \alpha $ -particle emitters around doubly magic$ ^{208} $ Pb. However, in Fig. 3 (a) this phenomenon is broken in the$ ^{100} $ Sn region. The values of$ P_{\alpha}^{\rm{Exp}} $ for nuclei above$ ^{100} $ Sn are linearly independent of$ ({N_pN_n})/({Z_0+N_0} )$ and show a new behavior. When the nucleus is close to shell closure,$ P_{\alpha}^{\rm{Exp}} $ for nuclei near$ ^{100} $ Sn does not decrease like that for nuclei near$ ^{208} $ Pb, but rather increases. In addition, we can find that the maximum values of$ P_{\alpha}^{\rm{Exp}} $ in Fig. 3 (a) correspond to$ ^{104} $ Te,$ ^{108} $ Xe, and$ ^{114} $ Ba. In particular,$ P_{\alpha}^{\rm{Exp}} $ is significantly enhanced along the N = Z line, which results in$ P_{\alpha}^{\rm{Exp}} $ for nuclei above$ ^{100} $ Sn not being linearly dependent on$({N_pN_n})/({Z_0+N_0}) $ .
Figure 3. (color online) Variations of extracted experimental
$\alpha$ -particle preformation factors$P_{\alpha}^{\rm{Exp}}$ from Eq. (3) against$({N_pN_n})/({Z_0+N_0})$ for nuclei above$^{100}$ Sn (left) and for nuclei above$^{208}$ Pb (right).In 2014 and 2017, Wang et al. and Seif et al. adopted the generalized liquid drop model (GLDM) [46, 47] and the preformed cluster model (PCM) [48], respectively, to study the
$ \alpha $ decay of even–even, odd-$ A $ , and doubly odd nuclei around doubly magic$ ^{100} $ Sn. In these works [46–48], the calculated$ \alpha $ decay half-lives can accurately reproduce the experimental data, and the$ \alpha $ -particle preformation factors evidently depend on the odd–even effect. In addition, in these works [46–48], the calculated$ \alpha $ -particle preformation factors of nuclei near doubly magic nucleus$ ^{100} $ Sn are of the order of$ 10^{-1} $ , larger than ones of nuclei around doubly magic nucleus$ ^{208} $ Pb. These works [46–48] also find that the proton–neutron interaction plays an important role in the formation of an$ \alpha $ cluster. These important insights support this present work. However, our research further shows that the$ \alpha $ -particle preformation factors of nuclei near self-conjugate doubly magic$ ^{100} $ Sn are significantly larger than those of analogous nuclei just above$ ^{208} $ Pb, and they will be enhanced as the nuclei move towards the$ N = Z $ line. Furthermore, our research finds that the linear relationship between$ \alpha $ -particle preformation factors and the product of valence protons and valence neutrons for nuclei around$ ^{208} $ Pb is broken in the$ ^{100} $ Sn region because the$ \alpha $ -particle preformation factor is enhanced when the nucleus near$ ^{100} $ Sn moves towards the$ N = Z $ line.In general,
$ \alpha $ decay is approximatively treated as a quasi-stationary-state problem that is characterized by the orbital angular momentum$ l $ and the global quantum number$ G $ . Based on the Wildermuth rule, the global quantum number$ G = 2n_r+l $ denotes the principal quantum number with the radial quantum number$ n_r $ and angular momentum quantum number$ l $ . For$ \alpha $ decay [82],$ G $ can be obtained by$ \begin{array}{l} \ G = 2n_r+l = \left\{\begin{array}{lll} 18,\;\;\; {N} \leq82,\\ 20,\;\;\;82< {N} \leq126,\\ 22,\;\;\; {N} >126. \end{array}\right. \end{array} $

(8) In the different major proton and neutron closed shells, the different global quantum numbers
$ G $ describe the different$ \alpha $ -core relative motion for$ \alpha $ decay near$ ^{100} $ Sn and$ ^{208} $ Pb, which maybe can also influence the$ \alpha $ -particle preformation. In the cluster model [7, 28, 43–45, 82], the quantum effect can be taken into account by the Bohr–Sommerfeld quasiclassical condition. However, the GLDM is a macroscopical model, which doesn't take into account the$ \alpha $ -core relative motion. Therefore, the GLDM will need to be improved to introduce the$ \alpha $ -core relative motion in the future.In summary, we have systematically studied the
$ \alpha $ -particle preformation factors$ P_{\alpha}^{\rm{Exp}} $ of nuclei above doubly magic nuclei$ ^{100} $ Sn and$ ^{208} $ Pb, which are extracted from the ratios between the theoretical$ \alpha $ -decay half-lives within the GLDM and the experimental data. The results show that$ P_{\alpha}^{\rm{Exp}} $ for nuclei near self-conjugate doubly magic$ ^{100} $ Sn are significantly larger than those of analogous nuclei just above$ ^{208} $ Pb, and they will be enhanced when the nucleus moves towards the$ N = Z $ line. The proton–neutron correlation energy$ E_{p-n} $ and two protons–two neutrons correlation energy$ E_{2p-2n} $ for nuclei near$ ^{100} $ Sn are also larger than those of analogous nuclei just above$ ^{208} $ Pb. This indicates that the interactions between protons and neutrons occupying similar single-particle orbitals could enhance$ P_{\alpha}^{\rm{Exp}} $ and result in the superallowed$ \alpha $ decay near doubly magic nucleus$ ^{100} $ Sn. Furthermore, as the nucleus moves towards the$ N = Z $ line, the$ E_{2p-2n} $ energy shows an increased tendency which is the same as that of$ P_{\alpha}^{\rm{Exp}} $ , while the$ E_{p-n} $ energy doesn't follow this pattern, indicating that the$ E_{2p-2n} $ energy plays a more important role than$ E_{p-n} $ energy in$ \alpha $ -particle preformation of superallowed$ \alpha $ decay. The linear relationship between$ P_{\alpha}^{\rm{Exp}} $ and the product of valence protons and valence neutrons$ ({N_pN_n})/({Z_0+N_0}) $ for nuclei above$ ^{208} $ Pb is broken in the$ ^{100} $ Sn region because$ P_{\alpha}^{\rm{Exp}} $ is enhanced when the nucleus near$ ^{100} $ Sn moves towards the$ N = Z $ line. Also, the calculated$ \alpha $ decay half-lives can accurately reproduce experimental data including the newly observed self-conjugate nuclei$ ^{108} $ Xe and$ ^{104} $ Te. This letter also provides evidence of the significant role of the proton–neutron interaction on$ \alpha $ -particle preformation, which can shed some new light on$ \alpha $ decay and$ \alpha $ -particle preformation factors in nuclear physics research in the future.
New behaviors of α-particle preformation factors near doubly magic 100Sn
- Received Date: 2021-12-06
- Available Online: 2022-06-15
Abstract: The





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
























 DownLoad:
DownLoad: