-
As a charmonium ground state, the
$J/\psi $ offers a unique laboratory for studying light hadron spectroscopy. In particular,$J/\psi $ decays can be used to search for exotic hadrons composed of light quarks and gluons, which are key to a more comprehensive understanding of the nature of the strong interaction.Many important results in light hadron spectroscopy [1] have been reported based on
$ (1310.6 \pm 7.0)\times 10^6 $ $J/\psi $ events collected by the BESIII experiment [2] in 2009 and 2012. An additional large sample of$J/\psi $ events was collected by BESIII during 2017–2019 to improve the precision of the measurements and search for new processes. The three data samples of$J/\psi$ events collected at BESIII are summarized in Table 1.Data set $\sqrt{s}$ 

$ {\mathcal{L}}_\text{online}$ 

Date (duration) (YYYY-MM-DD) $J/\psi $ 

3.097 GeV $2678$ pb

$^{-1}$ 

2017-08-12 – 2019-06-02 QED1 3.08 GeV $48$ pb

$^{-1}$ 

2018-04-12 – 2018-04-14 QED2 3.08 GeV $88$ pb

$^{-1}$ 

2019-02-07 – 2019-02-11 $\psi(3686)$ 

3.686 GeV $25$ pb

$^{-1}$ 

2018-05-20 $J/\psi $ 

3.097 GeV $323$ pb

$^{-1}$ 

2012-04-10 – 2012-05-22 QED1 3.08 GeV $13$ pb

$^{-1}$ 

2012-04-08 QED2 3.08 GeV $17$ pb

$^{-1}$ 

2012-05-23 – 2012-05-24 $\psi(3686)$ 

3.686 GeV $7.5$ pb

$^{-1}$ 

2012-05-26 J/ψ 3.097 GeV $82$ pb

$^{-1}$ 

2009-06-12 – 2009-07-28 QED 3.08 GeV $0.3$ pb

$^{-1}$ 

2009-06-19 $\psi(3686)$ 

3.686 GeV $150$ pb

$^{-1}$ 

2009-03-07 – 2009-04-14 Table 1. Data samples used in the determination of the number of
$J/\psi $ events.$\psi(3686)$ and QED samples (continuum data samples at$\sqrt{s} = 3.08$ GeV) are taken in close chronological order to each$J/\psi $ sample with only different c.m. energies to make sure the efficiency and background estimation reliable.This paper reports a precise determination of the total number of
$J/\psi $ events. The number of$J/\psi $ events for the new samples collected in 2017–2019 was determined with an inclusive method as the one used in the previous measurements [3, 4]. In addition, in this analysis we also recalculate the number of$J/\psi $ events for the two data samples taken in 2009 and 2012, reconstructed using the latest BESIII software [5, 6]. The number of$J/\psi $ events,$N_{J/\psi}$ , was calculated as$ \begin{eqnarray} N_{ J/\psi}=\frac{N_{\rm{sel}}-N_{\rm{bg}}}{\epsilon_{\rm{trig}} \times \epsilon^{\psi(3686)}_{\rm{data}} \times f_{\rm{cor}}}, \end{eqnarray} $

(1) where
$ N_{\rm{sel}} $ is the number of inclusive$J/\psi$ decays selected from the$J/\psi $ data;$ N_{\rm{bg}} $ is the number of background events estimated with continuum data taken at$ \sqrt{s} = $ 3.08 GeV;$ \epsilon_{\rm{trig}} $ is the trigger efficiency;$ \epsilon^{\psi(3686)}_{\rm{data}} $ is the inclusive$J/\psi $ detection efficiency determined experimentally using the$J/\psi $ sample from the reaction$\psi(3686) \rightarrow \pi^+ \pi^- J/\psi$ .$ f_{\rm{cor}} $ is a correction factor that accounts for the difference in the detection efficiency between the$J/\psi $ events produced at rest and those produced in$\psi(3686)\rightarrow \pi^+ \pi^- J/\psi$ .$ f_{\rm{cor}} $ is expected to be approximately unity and is determined by the Monte Carlo (MC) simulation sample with$ \begin{eqnarray} f_{\rm{cor}} = \frac {\epsilon^{J/\psi}_{\rm MC}} {\epsilon^{\psi(3686)}_{\rm{MC}}}, \end{eqnarray} $

(2) where
$\epsilon^{J/\psi}_{\rm{MC}}$ is the detection efficiency of inclusive$J/\psi $ events determined from the MC sample of$ J/\psi $ events produced directly in electron-positron collisions, and$ \epsilon^{\psi(3686)}_{\rm{MC}} $ is that from the MC sample of$\psi(3686)\to \pi^+\pi^- J/\psi $ . For the number of$ J/\psi $ events determined with Eq. (1), only$ f_{\rm{cor}} $ depends on MC simulation. According to Eq. (2), the uncertainties related to MC simulation (including generator, detector response, etc.) almost cancel out because they impact both the numerator and denominator, which improves the precision of the number of$J/\psi $ events. In the MC simulation, the production of$J/\psi $ and$ \psi(3686) $ resonances was simulated with a GEANT4-based [7] MC software, which includes the geometric description of the BESIII detector and the detector response. The simulation models the beam energy spread and initial state radiation (ISR) in the$ e^+e^- $ annihilations with the generator KKMC [8]. The known decay modes were modeled with EVTGEN [9, 10] using branching fractions taken from the Particle Data Group [11], and the remaining unknown charmonium decays were modeled with LUNDCHARM [12, 13]. -
Candidate events must contain two or more charged tracks that must have a momentum less than 2.0 GeV/c and to be within a polar angle (θ) range of
$ |\cos \theta| < 0.93 $ , where θ is defined with respect to the axis of the Main Drift Chamber (MDC). The distance of closest approach to the interaction point (IP) must be less than 15 cm along the z-axis,$ |V_z| $ , and less than 1 cm in the transverse plane,$ V_r $ . Photon candidates were identified using isolated showers in the electromagnetic calorimeter (EMC). The deposited energy of each shower must be more than 25 MeV in the barrel region ($ |\cos\theta| < 0.83 $ ) and more than 50 MeV in the end cap region ($ 0.86< |\cos\theta| < 0.93 $ ). To suppress electronic noise and showers unrelated to the event, the difference between the EMC time and the event start time is required to be within [0, 700] ns.To suppress events from Quantum Electrodynamics (QED) processes (i.e., Bhabha and dimuon events), from cosmic rays, beam-induced backgrounds, and electronic noise, a series of selection criteria were applied to the candidate events.
The sum of charged particle energies computed from the track momenta assuming a pion mass and the neutral shower energies deposited in the EMC,
$ E_{\rm{vis}} $ , is required to be greater than 1.0 GeV. Fig. 1 shows a comparison of the$ E_{\rm{vis}} $ distribution between the$J/\psi $ data, the data taken at$ \sqrt{s} = 3.08 $ GeV, and the inclusive$J/\psi $ MC sample. The requirement$ E_{\rm{vis}} > 1.0\; {\rm{GeV}} $ removes one third of the background events while retaining$ 99.5\% $ of the signal events.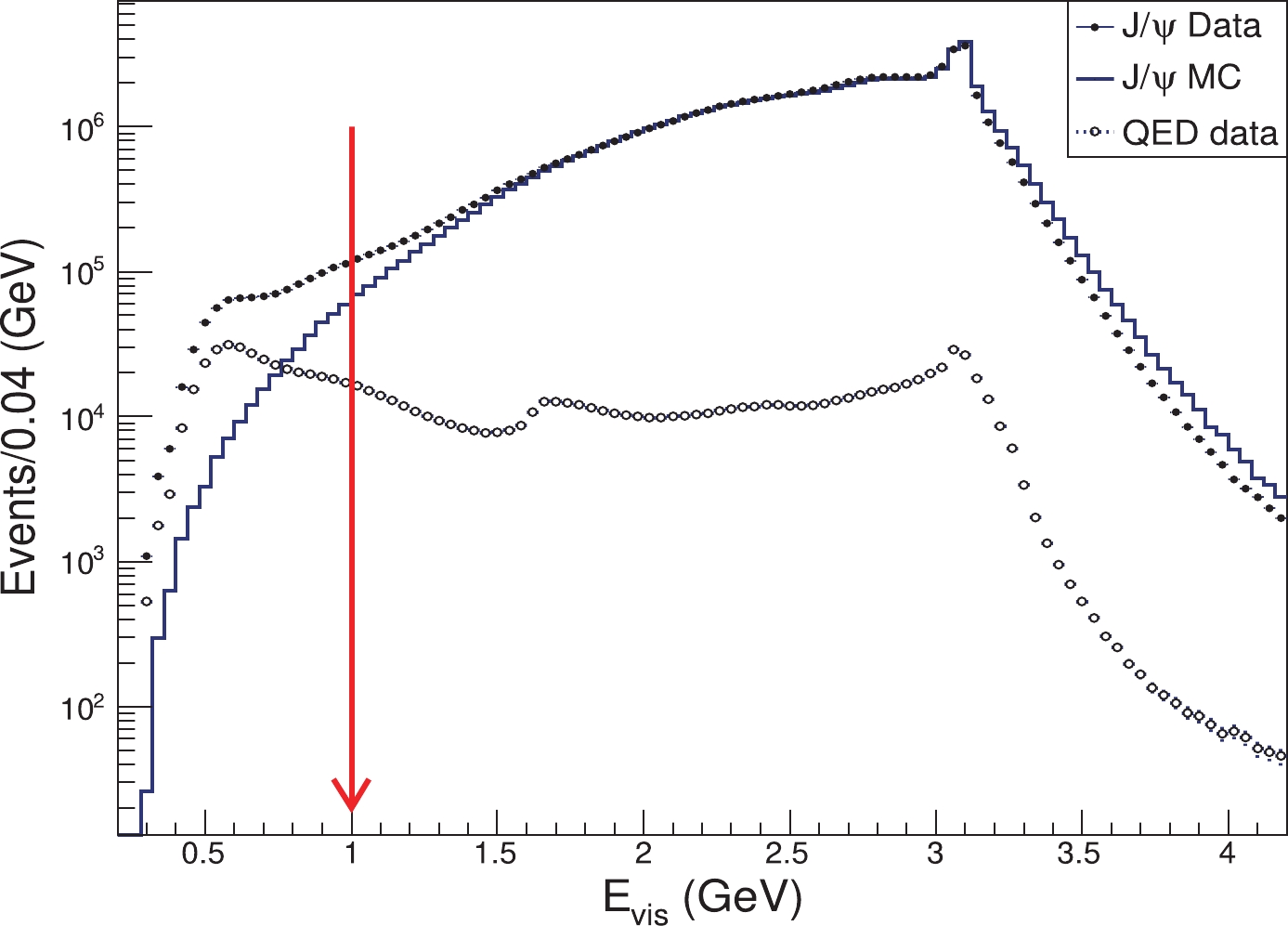
Figure 1. (color online) Distributions of the visible energy
$E_\text{vis}$ for$J/\psi $ data (dots with error bars), continuum data at$\sqrt{s}=3.08$ GeV (open circles with error bars, normalized to the integrated luminosity of$J/\psi $ data) and MC simulation of inclusive$J/\psi $ events (blue solid line). The arrow indicates the minimum$E_\text{vis}$ required to select inclusive events.For events with only two charged tracks, the momentum of each track is required to be less than 1.5 GeV/c to exclude Bhabha and dimuon events. Fig. 2 shows a scatter plot of the momenta of the two charged tracks, and the solid lines depict the momentum requirement. Fig. 3 displays the distribution of energy deposited by the charged particles in the EMC; a significant peak around 1.5 GeV is from Bhabha events, which can be rejected by requiring the energy deposited in the EMC to be less than 1 GeV for each charged track.
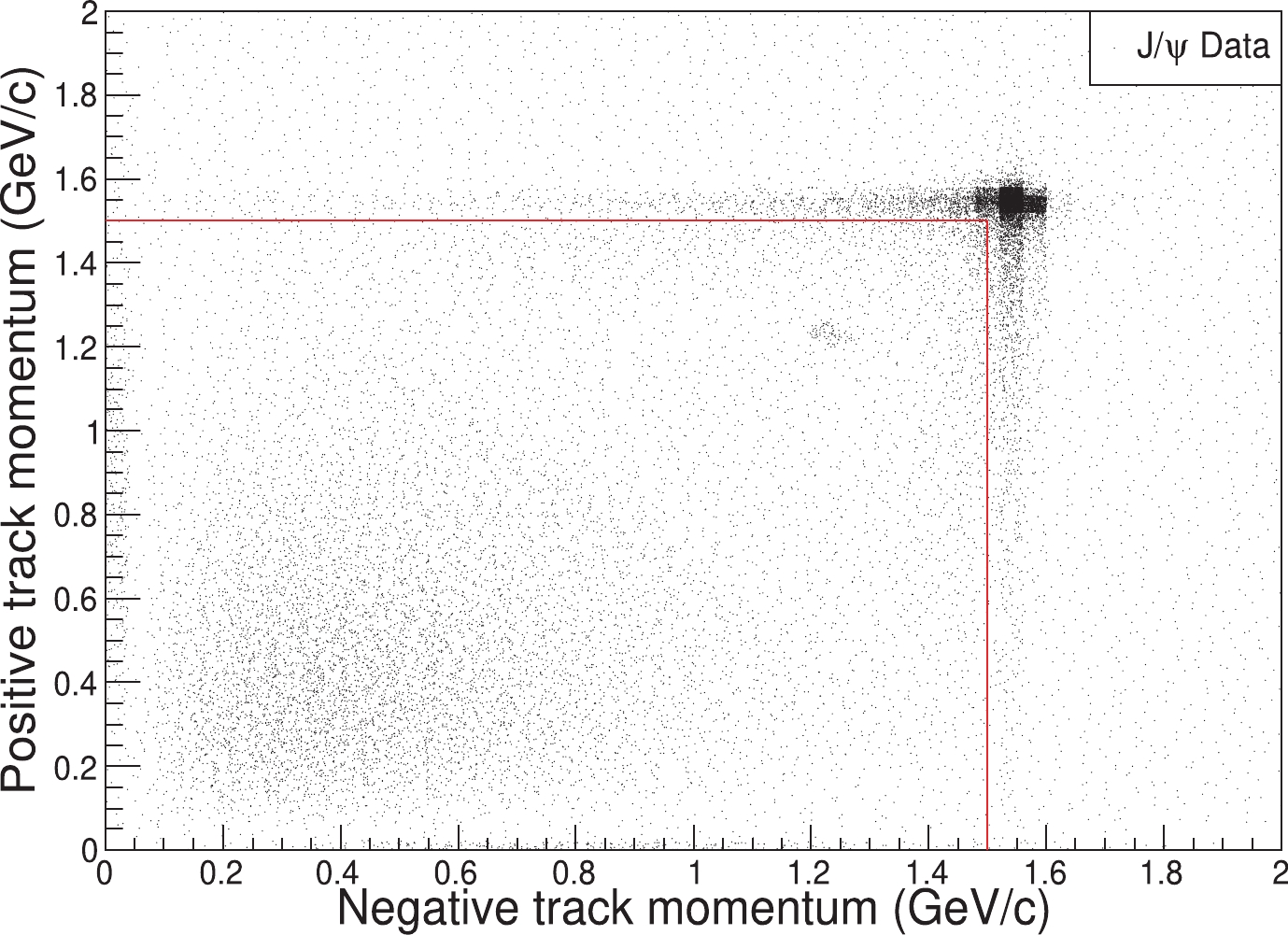
Figure 2. (color online) Distribution of the momenta of the charged tracks for 2-prong events in data. The cluster around 1.55 GeV/c corresponds to the contribution from lepton pairs, and the cluster at 1.23 GeV/c comes from
$J/\psi \rightarrow p\bar{p}$ . Most of lepton pairs are removed with the requirements on the two charged tracks,$p_1<1.5$ GeV/c and$p_2<1.5$ GeV/c, as indicated by the solid lines.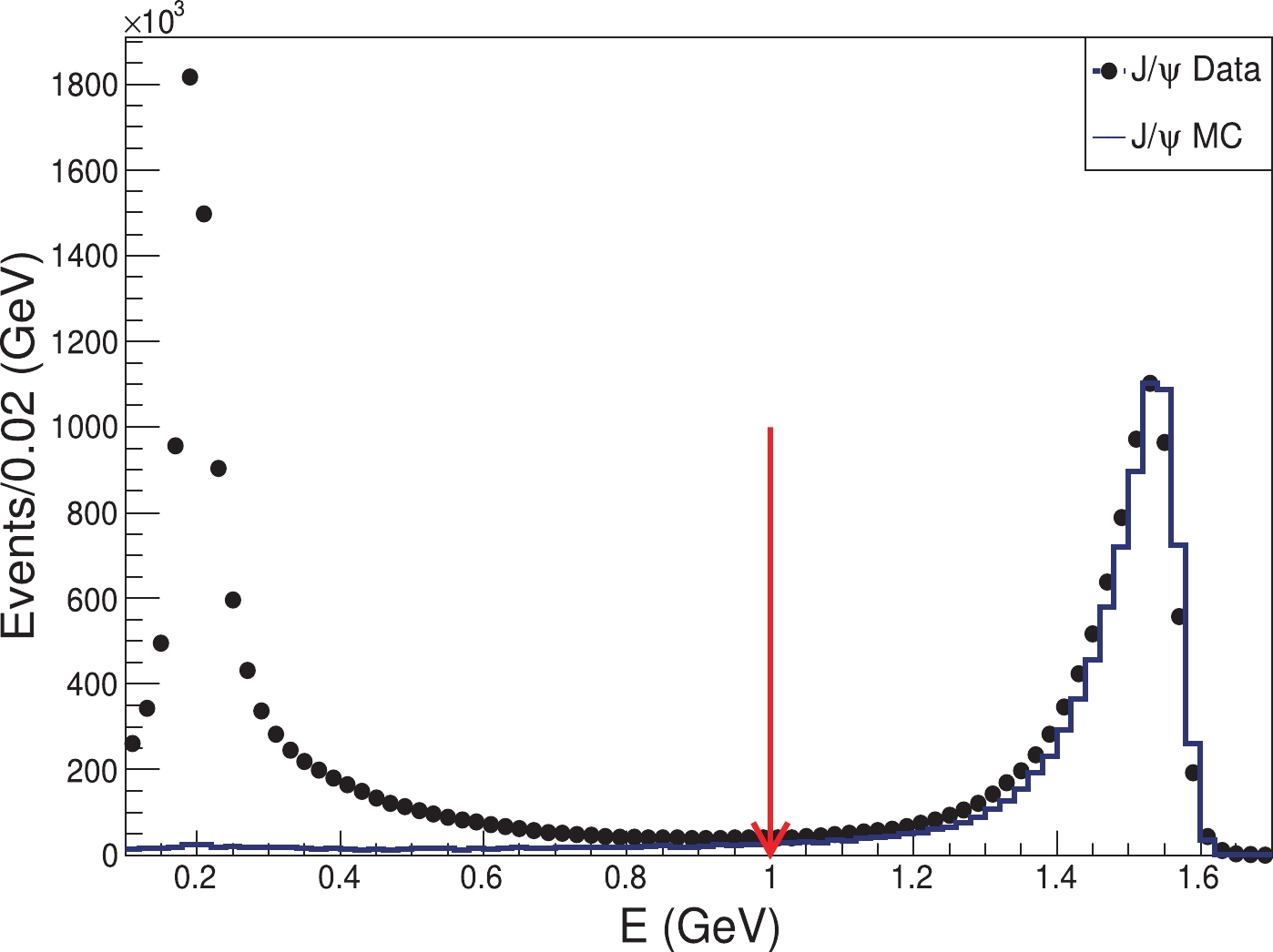
Figure 3. (color online) Distributions of deposited energy in the EMC for the charged tracks of 2-prong events for
$J/\psi $ data (dots with error bars) and for the combined, normalized MC simulations of$ e^+e^-\rightarrow e^+e^-(\gamma)$ and$ J/\psi\rightarrow e^+e^-(\gamma)$ (blue solid line).After the above requirements,
$N_{\rm{sel}} = (6912.03 \pm 0.08)\times 10^{6}$ candidate events were selected from the$J/\psi $ data taken in 2017–2019. The distributions of the track parameters of closest approach along the beam line and in radial direction ($ V_z $ and$ V_r $ ), the polar angle ($ \cos\theta $ ), and the total energy deposited in the EMC ($ E_{\rm{EMC}} $ ) after subtracting background events estimated with the continuum data taken at$ \sqrt{s} = 3.08 $ GeV (see Sec. III for details) are illustrated in Fig. 4. The multiplicity of charged tracks ($ N_{\rm{good}} $ ) is shown in Fig. 5, where the MC sample generated according to the standard MC model agrees very well with the data while the MC sample generated with an 'incomplete' MC model deviates from the data. The standard MC model includes the known decay processes listed in the PDG and the unknown ones modeled with LUNDCHARM [12, 13], while the incomplete MC model only includes the known decay modes listed in the PDG. The MC sample generated with the incomplete MC model was used to test the effect of this discrepancy on the determination of the number of$J/\psi $ events, which is small as described in Sec. VI.
Figure 4. (color online) Comparison of distributions between J/ψ data (dots with error bars) and MC simulation of inclusive
$J/\psi $ (blue solid line): (a)$V_z$ , (b)$V_r$ , (c)$\cos\theta$ of charged tracks, (d) total energy deposited in the EMC.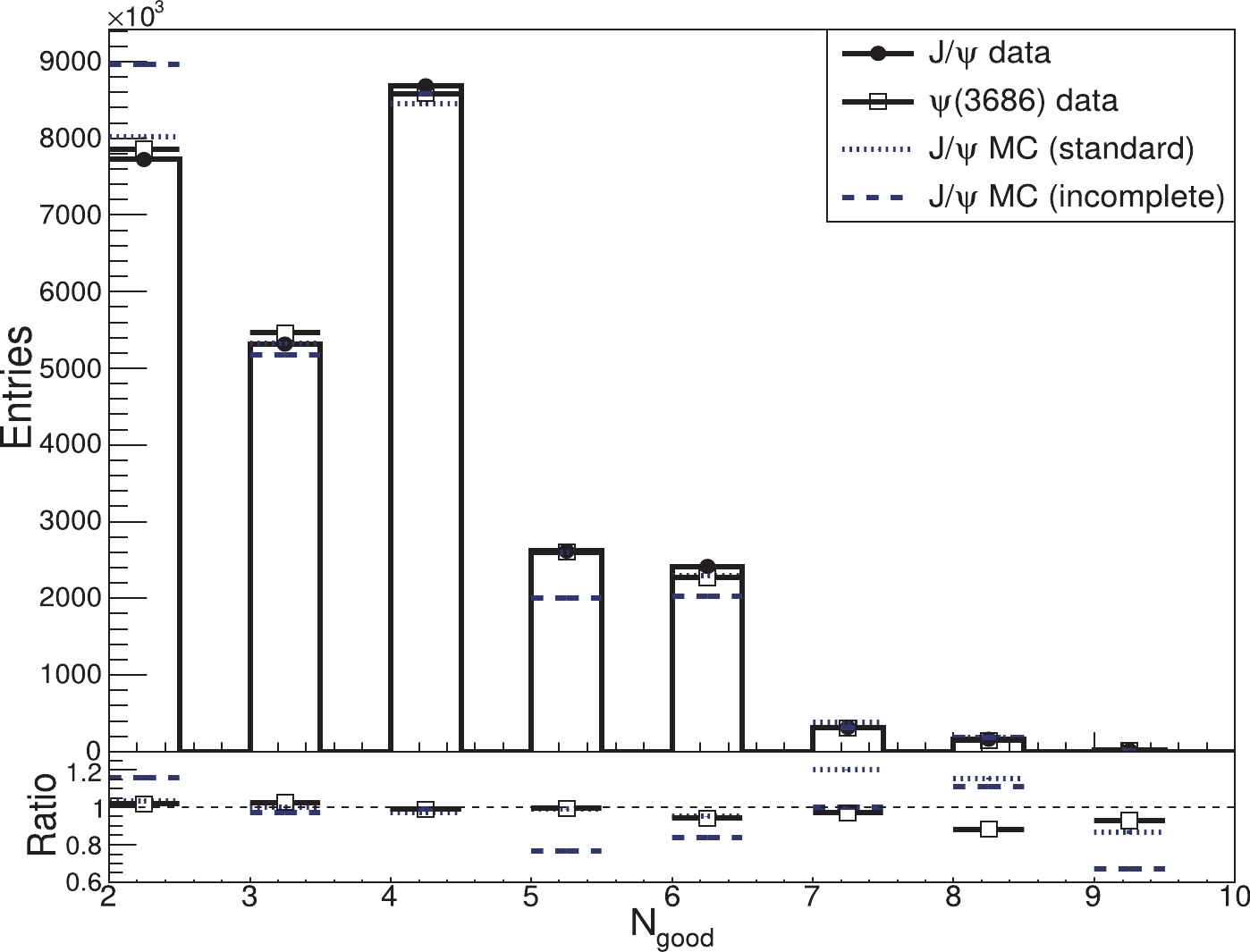
Figure 5. (color online) Distributions of the reconstructed charged track multiplicity in inclusive
$J/\psi $ events for$J/\psi $ data (dots with error bars) and$\psi(3686)$ data (squares with error bars) and MC simulation generated using standard and incomplete MC model (short-dashed and long-dashed lines, respectively). -
In this analysis, the potential background sources include QED processes, beam-induced background, cosmic rays, and electronic noise. The continuum data samples at
$ \sqrt{s}=3.08 $ GeV were taken in close chronological order to each$J/\psi $ sample to estimate these backgrounds.The integrated luminosity was determined using the process
$e^+e^-\rightarrow \gamma\gamma$ . The candidate events were selected by requiring at least two showers in the EMC within$ |\cos\theta | < 0.8 $ and with the energy of the second most energetic shower between 1.2 and 1.6 GeV. The number of signal events was determined from the number of events in the signal region$ |\Delta \phi| < 2.5^\circ $ , and the background was estimated from those in the side-band region$ 2.5^\circ < |\Delta \phi| < 5^\circ $ , where$ \Delta \phi = |\phi_{\gamma1} - \phi_{\gamma2}| - 180^\circ $ and$ \phi_{\gamma1/2} $ are the azimuthal angles of the two photon candidates. Taking into account the detector efficiency obtained from the MC simulation and the cross section of the QED process$e^+e^- \rightarrow \gamma\gamma$ , the integrated luminosities of the$J/\psi $ data sample and the sample taken at$ \sqrt{s}=3.08 $ GeV in 2017–2019 were determined to be$ (2568.07 \pm 0.40) \;{\rm{pb}}^{-1} $ and$ (136.22 \pm 0.09)\;{\rm{pb}}^{-1} $ , respectively, where the errors are statistical only.After applying the same selection criteria as for the
$J/\psi $ data,$ N_{3.08}=6,363,941 \pm 2,523 $ events were selected from the continuum data taken at$ \sqrt{s} = 3.08 $ GeV. Assuming the same detection efficiency at$ \sqrt{s} = 3.08 $ GeV as for the$J/\psi $ peak and taking into account the energy-dependent cross section of the QED processes, the number of background events for the$J/\psi $ sample,$ N_{\rm{bg}} $ , was estimated to be$ \begin{eqnarray} N_{\rm{bg}}=N_{3.08}\times \frac{ {\mathcal{L}}_{J/\psi}}{ {\mathcal{L}}_{3.08}} \times \frac{s_{3.08}}{s_{J/\psi}}=(118.66 \pm 0.05)\times 10^{6} , \end{eqnarray} $

(3) where
$ {\mathcal{L}}_{ J/\psi} $ and$ {\mathcal{L}}_{3.08} $ are the integrated luminosities for the$J/\psi $ data sample and the data sample taken at$ \sqrt{s}=3.08 $ GeV, and$s_{ J/\psi}$ and$ s_{3.08} $ are the corresponding squares of the center-of-mass energies. The background was calculated to be$ (1.717 \pm 0.002)\% $ of the number of selected inclusive$J/\psi $ events taken in 2017–2019. -
In this analysis, the detection efficiency was determined experimentally using a sample of
$J/\psi $ events from the reaction$\psi(3686) \rightarrow \pi^+ \pi^- J/\psi$ to reduce the uncertainty related to any discrepancies between the MC simulation and the data. To ensure that the beam conditions and detector status are similar to those of the sample collected at the$J/\psi $ peak, a dedicated$ \psi(3686) $ sample taken on May 20, 2018 was used for this study.For a candidate
$ \psi(3686) \rightarrow \pi^+\pi^- J/\psi $ event, there must be at least two soft pions with opposite charge detected in the MDC with$ |\cos\theta| < 0.93 $ . Each candidate pion is required to have a momentum less than$ 0.4\;{\rm{GeV}}/c $ , and the distance of closest approach to the IP must satisfy$ |V_z|<15 $ cm and$ V_r<1 $ cm. No further selection criteria on the remaining charged tracks or showers are required. The distribution of the invariant mass recoiling against all possible soft$ \pi^+\pi^- $ pairs is shown in Fig. 6. A prominent peak around$ 3.1\;{\rm{GeV}}/c^2 $ , corresponding to the decay of$ \psi(3686) \rightarrow \pi^+\pi^- J/\psi $ is observed over a smooth background. The number of inclusive$J/\psi $ events,$ N_{\rm{inc}} = (3538.5 \pm 3.6)\times 10^{3} $ , was obtained by fitting a double-Gaussian function for the$J/\psi $ signal plus a second-order Chebychev polynomial for the background to the$ \pi^+ $ $ \pi^- $ recoil mass spectrum.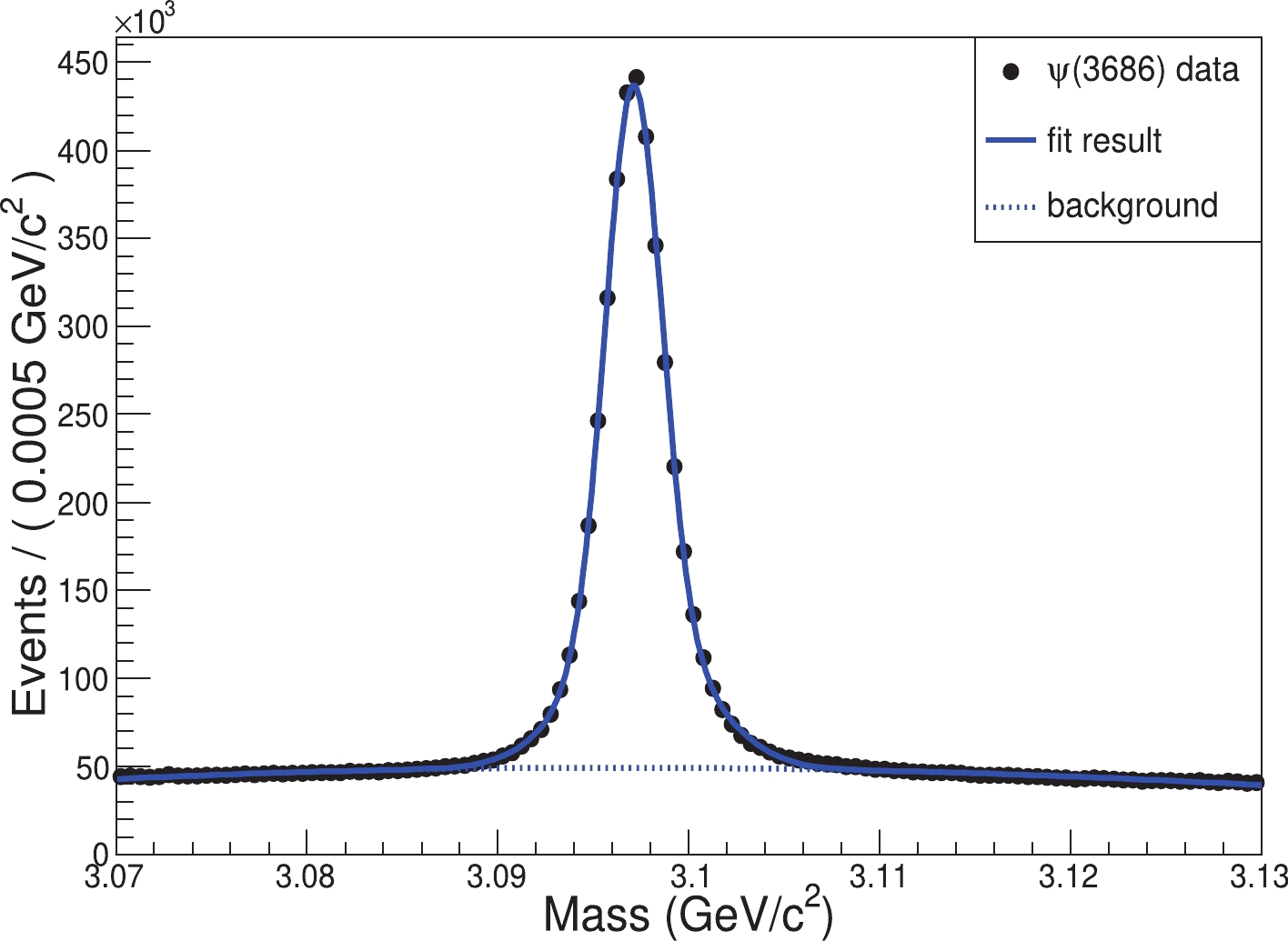
Figure 6. (color online) Invariant mass recoiling against selected
$ \pi^+\pi^- $ pairs for the${\rm{ \mathsf{ ψ} }}(3686)$ data sample. The curves are the results of the fit described in the text.To measure the detection efficiency of inclusive
$J/\psi $ events, the same selection criteria as described in Sec. II were applied to the remaining charged tracks and showers. The number of selected inclusive$J/\psi $ events,$ N_{\rm{inc}}^{\rm{sel}} $ , was determined to be$ (2717.6 \pm 3.4)\times 10^{3} $ using a fit to the recoil mass distribution of the selected events with the same function as described above. The detection efficiency of inclusive$J/\psi $ events,$ \epsilon^{ \psi(3686)}_{\rm{data}} = (76.80 \pm 0.05)\% $ , was calculated from the ratio of the number of inclusive$J/\psi $ events with and without the inclusive$J/\psi $ event selection criteria applied.To account for the efficiency difference between the
$J/\psi $ produced at rest and the$J/\psi $ from the decay$ \psi(3686) \rightarrow \pi^+\pi^- J/\psi $ , a correction factor, defined in Eq. (2), was used. Two large statistics MC samples, inclusive$ \psi(3686) $ and inclusive$J/\psi $ events, were produced and subjected to the same selection criteria as the data samples. The detection efficiencies of inclusive$ J/\psi $ events were determined to be$ \epsilon^{\psi(3686)}_{\rm{MC}} = (76.93 \pm 0.02) $ % and$ \epsilon^{J/\psi}_{\rm{MC}}=(77.56 \pm 0.01) $ % for the two inclusive MC samples, respectively. The correction factor$ f_{\rm{cor}} $ for the detection efficiency was therefore taken as$ \begin{eqnarray} f_{\rm{cor}} = \frac {\epsilon^{J/\psi}_{\rm{MC}}} {\epsilon^{\psi(3686)}_{\rm{MC}}}=1.0082 \pm 0.0007, \end{eqnarray} $

(4) where the error is statistical only.
-
With Eq. (1) and the corresponding parameter values summarized in Table 2, the number of
$J/\psi $ events collected in 2017-2019 was determined to be$ (8774.0 \pm 0.2) \times 10^6 $ . The trigger efficiency of the BESIII detector was taken to be 100%, based on a study of various reactions [14]. With the same procedure, the numbers of$J/\psi $ events taken in 2012 and 2009 were recalculated to be$ (1088.5 \pm 0.1) \times 10^6 $ and$ (224.0 \pm 0.1) \times 10^6 $ , respectively, where the uncertainties are statistical only. The statistical uncertainties of$ N_{\rm{bg}} $ were taken into account as part of the systematic uncertainty (see Sec. VI.D). The systematic uncertainties from different sources are discussed in detail in Sec. VI.Item 2017–2019 2012 2009 $N_\text{sel}(\times 10^6)$ 

$6912.03 \pm 0.08$ 

$860.59 \pm 0.03$ 

$180.84 \pm 0.01$ 

$\epsilon_\text{trig}$ 

1.00 1.00 1.00 $N_\text{QED} (\times 10^3)$ 

$6363.9 \pm 2.5$ 

$1616.6 \pm 1.3$ 

$24.6 \pm 0.2$ 

$N_\text{bg}(\times 10^6)$ 

$118.66 \pm 0.05$ 

$15.32 \pm 0.02$ 

$6.89 \pm 0.04$ 

$\epsilon^{\psi(3686)}_\text{data}$ 

$\dfrac{(2717.6 \pm 3.4) \times 10^3 }{(3538.5 \pm 3.6) \times 10^3} =0.7680 \pm 0.0005$ 

$\dfrac{(981.6 \pm 2.0) \times 10^3 }{(1274.9 \pm 2.1) \times 10^3} =0.7699 \pm 0.0005$ 

$\dfrac{(17048.6 \pm 8.9) \times 10^3}{(22120.0 \pm 9.4) \times 10^3} =0.7707 \pm 0.0001$ 

$\epsilon^{\psi(3686)}_\text{MC}$ 

$\dfrac{(4450.2 \pm 3.2) \times 10^3 }{(5784.7 \pm 3.5) \times 10^3}=0.7693 \pm 0.0002$ 

$\dfrac{(4668.8 \pm 3.1) \times 10^3}{(6056.3 \pm 3.4) \times 10^3} =0.7709 \pm 0.0002$ 

$\dfrac{(4626.8 \pm 3.3) \times 10^3}{(5991.4 \pm 3.4) \times 10^3}=0.7723 \pm 0.0002$ 

$\epsilon^{J/\psi}_\text{MC}$ 

$\dfrac{(6747.59 \pm 0.04) \times 10^6}{8700 \times 10^6}=0.7756 \pm 0.0001$ 

$\dfrac{(7775.5 \pm 1.4) \times 10^3}{10^7} =0.7776 \pm 0.0001$ 

$\dfrac{(174.26 \pm 0.02) \times 10^6}{ 224 \times 10^6}=0.7780 \pm 0.0001 $ 

$f_\text{cor}$ 

$1.0082 \pm 0.0007$ 

$1.0086 \pm 0.0008$ 

$1.0074 \pm 0.0003$ 

$N_{J/\psi}(\times 10^6)$ 

$8774.0 \pm 0.2$ 

$1088.5 \pm 0.1$ 

$224.0 \pm 0.1$ 

Table 2. The values used in the calculation, and the resulting number of
$J/\psi $ events, where the uncertainties are statistical. -
The sources of systematic uncertainties, including the MC model, track reconstruction efficiency, fit to the
$J/\psi $ peak, background estimation, random trigger mixing and the efficiency of selecting the two soft pions recoiling against$J/\psi $ , are investigated in detail below, and the corresponding contributions are summarized in Table 3.Sources 2017–2019(%) 2012 (%) 2009(%) MC model uncertainty 0.18 $^*$ 

0.18 $^*$ 

0.27 $^*$ 

Tracking efficiency 0.02 $^*$ 

0.03 $^*$ 

0.31 Fit to $J/\psi $ peak

0.10 0.21 0.09 Background uncertainty 0.04 0.10 0.14 Noise mixing 0.06 0.02 0.12 $\epsilon_{\pi^+\pi^-}$ uncertainty

0.40 $^*$ 

0.27 $^*$ 

0.32 $^*$ 

Total 0.45 0.40 0.56 Table 3. Sources of systematic uncertainties and the corresponding contributions to the number of
$J/\psi $ events, where the superscript * indicates that the error is common for the same item in different data samples. -
There are some differences between experimental data and MC simulation as shown in Figs. 1, 3, 4 because only half of the
$J/\psi $ inclusive decays were measured, and the MC model cannot describe the$J/\psi $ inclusive decays exactly. In the measurement of the number of$J/\psi $ events, only the efficiency correction factor,$ f_{\rm{cor}} $ , depends on the MC simulation. To evaluate the uncertainty due to the MC model, MC samples were generated with the incomplete MC model, and the correction factor based on these samples was compared to its nominal value. As shown in Fig. 5, the charged track multiplicity distribution of the incomplete MC sample significantly deviates from the experimental data, indicating that this method will overestimate the systematic uncertainty. To be conservative, the change in the correction factor, 0.18%, was taken as the systematic uncertainty due to the MC model on the number of$J/\psi $ events collected in 2017–2019 (0.18% for 2012 and 0.27% for 2009). -
The charged track reconstruction efficiencies in MC simulation and experimental data were studied, and the disagreement between them was less than
$ 1 $ % for each charged track. In the analysis, the detection efficiency for inclusive$J/\psi $ decays was obtained using the$ \psi(3686) $ data sample. The consistency of charged track reconstruction efficiency between the MC and data samples in$ \psi(3686) $ decays was assumed to be the same as that in$J/\psi $ decays since the$ \psi(3686) $ data was taken in close chronological proximity to the$J/\psi $ sample. To evaluate the effect of a possible difference, the track reconstruction efficiencies in both$J/\psi $ and$ \psi(3686) $ MC samples were varied by$ -1\% $ to determine the uncertainty due to the MDC tracking. As expected, the change in the correction factor was very small at$ 0.02\% $ , and this value was taken as a systematic uncertainty ($ 0.03\% $ for 2012).In 2009, the
$J/\psi $ and$ \psi(3686) $ data samples were collected in different time periods, and there may be slight differences in the tracking efficiencies between the two data sets. Here, the difference between the MC/data consistencies in the$J/\psi $ and$ \psi(3686) $ samples was assumed to be 0.5%, half of the data/MC inconsistency, 1%. To estimate the corresponding systematic uncertainty, we modify the track reconstruction efficiency by$ -0.5\% $ in the$J/\psi $ MC sample, keeping it unchanged for the$ \psi(3686) $ MC sample. The resulting change in the correction factor,$ 0.31\% $ , was taken as a systematic uncertainty on the number of$J/\psi $ events in 2009. -
The
$ \psi(3686) $ data sample was used to measure the selection efficiency of inclusive$J/\psi $ events. The yield of$J/\psi $ events in$\psi(3686) $ decays was determined by fitting the$J/\psi $ peak in the mass spectrum recoiling against$ \pi^+ \pi^- $ . The uncertainties due to the fit were investigated.$ (a) $ The fit: we propagated the statistical uncertainties of the$J/\psi $ signal yield from the fit to the selection efficiency, and the resulting uncertainties, 0.07% and 0.03% for$ \epsilon^{\psi(3686)}_{data} $ and$ \epsilon^{\psi(3686)}_{MC} $ , respectively, are considered to be the uncertainties from the fit itself.$ (b) $ The fit range: the fit range on the$ \pi^+\pi^- $ recoil mass was changed from [3.07, 3.13] GeV/$ c^2 $ to [3.08, 3.12] GeV/$ c^2 $ , and the change of the result, 0.07%, was taken as the corresponding systematic uncertainty.$ (c) $ The signal description: we performed an alternative fit by describing the$J/\psi $ signal with a histogram (convolved with a Gaussian function) obtained from the recoil mass spectrum of$ \pi^+ \pi^- $ in$\psi(3686)\rightarrow \pi^+ \pi^- J/\psi$ ,$J/\psi \rightarrow \mu^+ \mu^- $ , and the resulting change, 0.01%, was considered to be the associated systematic uncertainty.$ (d) $ The background shape: the uncertainty due to the background shape, 0.03%, was estimated by replacing the second-order Chebychev polynomial with a first-order or third-order Chebychev polynomial. By assuming that all of the sources of systematic uncertainty are independent, the fit uncertainty for the 2017–2019$J/\psi $ sample, 0.10%, was obtained by adding all of the above effects in quadrature.The same sources of systematic uncertainty were considered for the
$J/\psi $ sample taken in 2012 (2009). The fit has an uncertainty of 0.07% (0.02%) for$ \epsilon^{\psi(3686)}_{\rm{data}} $ and 0.03% (0.03%) for$ \epsilon^{\psi(3686)}_{\rm{MC}} $ . The uncertainties from the fit range, signal function, and background shape are 0.08% (0.03%), 0.15% (0.06%), and 0.10% (0.04%), respectively. The total uncertainty from the fit for the 2012 (2009) data is 0.21% (0.09%). -
In this analysis, the events selected from the experimental data sample include the
$J/\psi $ events and background: QED processes, cosmic rays, beam-induced backgrounds, and electronic noise. The contribution of the background was estimated by normalizing the number of events in the continuum data sample taken at$ \sqrt{s} = 3.08 $ GeV according to Eq. (3). The uncertainty due to the background estimation mainly comes from the normalization method, the statistics of the continuum sample, the statistical uncertainty of the integrated luminosity, and the uncertainty due to beam associated backgrounds.The cosmic ray background, beam associated backgrounds and electronic noise can not be normalized properly with Eq. (3), since the number of cosmic rays is proportional to the time of data taking, while beam-associated backgrounds depend on the vacuum status and beam currents during data taking in addition to the time of data taking; the electronic noise also depends on the detector status. To estimate the associated systematic uncertainty, the difference in the estimated number of background events with and without the energy-dependent factor in Eq. (3) was used.
During 2017–2019, two data samples at
$ \sqrt{s} = 3.08 $ GeV were taken at different times during the$J/\psi $ data taking. They were compared to each other to estimate the uncertainty of the background related with the stability of the beam and vacuum status. Each of the two continuum data samples was used to estimate the background with Eq. (3), and the maximum difference to the nominal result, 0.03%, was taken as the related systematic uncertainty. The corresponding systematic uncertainty for the 2012 sample is 0.09%. Only one continuum data sample was taken for$J/\psi $ data in 2009. The selected background events from the continuum sample were compared to those from the$J/\psi $ data to estimate the corresponding uncertainty, as described in detail in Ref. [3].Assuming that all the above effects are independent, their contributions were added quadratically. The resulting uncertainties on the number of
$J/\psi $ events due to the background estimation were determined to be 0.04%, 0.10%, and 0.14% for the data taken in 2017–2019, 2012, and 2009, respectively. -
In the MC simulation, events recorded by a random trigger were mixed into the MC events to simulate the electronic noise and beam-induced background. In the
$ \psi(3686) $ MC sample, the random trigger events from the$ \psi(3686) $ data taking were replaced by the random trigger events from the$J/\psi $ data taking to estimate the effect of the different background levels. The change of the correction factor for the detection efficiency, 0.06%, was taken as the systematic uncertainty due to random trigger mixing for the number of$J/\psi $ events taken in 2017–2019. The corresponding uncertainties for the 2012 and 2009 samples are 0.02% and 0.12%, respectively. -
Study of the MC sample shows that the selection efficiency of soft pions,
$ \epsilon_{\pi^+ \pi^-} $ , recoiling against the$ J/\psi$ in$ \psi(3686)\rightarrow \pi^+ \pi^-J/\psi$ depends on the multiplicity of charged tracks in the$J/\psi $ decays. Differences between the data and MC samples may lead to a change in the number of$J/\psi $ events. The dependence of$ \epsilon_{\pi^+ \pi^-} $ in the data is obtained by comparing the multiplicity distribution of$J/\psi $ decays in the$ \psi(3686) \rightarrow \pi^+\pi^- J/\psi$ data sample to that of the$J/\psi $ data at rest. Then the efficiency of$ J/\psi $ in the$ \psi(3686) \rightarrow \pi^+ \pi^- J/\psi (J/\psi\rightarrow {\rm{inclusive}}) $ MC sample,$ \epsilon^{\psi(3686)}_{\rm{MC}} $ in Eq. (2), can be reweighted with the dependence of$ \epsilon_{\pi^+\pi^-} $ from the data sample. The resulting changes in the number of$ J/\psi $ events, 0.40%, 0.27%, and 0.32%, are taken as the uncertainties for the data taken in 2017–2019, 2012, and 2009, respectively. -
The systematic uncertainties from the different sources studied above are summarized in Table 3. The total systematic uncertainty for the number of
$J/\psi $ events in 2017–2019, 0.45%, is the quadratic sum of the individual uncertainties. Correspondingly, the uncertainties for 2012 and 2009 are 0.40% and 0.56%, respectively. -
Using the inclusive
$J/\psi $ decays, the number of$J/\psi $ events collected with the BESIII detector in 2017–2019 was determined to be$ (8774.0 \pm 39.4)\times10^{6}, $ where the uncertainty is completely dominated by systematics, and the statistical uncertainty is negligible. The numbers of$J/\psi $ events taken in 2009 and 2012 were recalculated to be$ (224.0 \pm 1.3)\times10^{6} $ and$ (1088.5 \pm 4.4)\times10^{6}, $ which are consistent with the previous measurements [4] but with improved precision.The total number of
$J/\psi $ events taken with BESIII detector was determined to be$N_{J/\psi}= (10087 \pm 44)\times10^{6}$ . Here, the total uncertainty was determined by adding the common uncertainties linearly and the independent ones in quadrature. -
The BESIII collaboration thanks the staff of BEPCII and the IHEP Computing Center for their strong support.
Number of J/ψ events at BESIII
- Received Date: 2021-11-17
- Available Online: 2022-07-15
Abstract: Using inclusive decays of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: