-
Recent decades have witnessed nickel isotopes, especially those with excess neutrons, receive special attention owing to their various applications in both theoretical and experimental nuclear physics [1, 2]. The chain of
$ N=40 $ neutron-rich isotones and 68Ni in particular, as well as other neighboring isotopes, present another case of an island of inversion — a region with significant changes in shell structure and abrupt transitions from spherical to deformed states of atomic nuclei, similar to an island of inversion in the$ N=20 $ region. Doubly magic 78Ni is of particular interest in terms of the studies on magic number conservation and shape co-existence. This is the only neutron-rich magic nuclide on the very edge of the nuclear chart that is currently available in experiments [3].Nuclei in the vicinity of 78Ni are crucial in astrophysics [4], serving as some of the initial isotopes produced in the r-process responsible for the production of nuclei with
$ Z>26 $ . The probability of the synthesis of different chemical elements along different neutron-rich isotope chains strongly depends on the shell structure of these isotopes.The spectroscopic studies of 78Ni and its neighbors are included in the program of all the next-generation RI-beam in-flight facilities such as the Radioactive Isotope Beam Factory (RIBF) in Japan, Facility for Rare Isotope Beams (FRIB) in USA, Facility for Antiproton and Ion Research (FAIR) in Germany. In just the past two decades, major progress was made in experimental studies in isotopes
$ ^{70-76} $ Ni [5–13]. A particular aspect broadly discussed is the conservation seniority number ν in these and other nuclei with$ j=9/2 $ filled shell [14, 15]. Earlier, a series of experiments (e.g. [16, 17]) was designed to verify the magicity of the$ N=40 $ shell closure in 68Ni and the isolation of$ \nu g_{9/2} $ . Accordingly, a hypothesis was made regarding the existence of excited states that should typically form as a consequence of pairing. These states should be isomeric to those well known in$ N=50 $ isotones [6]. However, detailed analysis showed that the magicity of the$ N=40 $ gap is less defined than the$ Z=40 $ gap [17]. Further accumulation of experimental data on nickel isotopes with greater neutron excess had us acknowledge the differences between the formation of low-lying excited states in$ \nu = 4 $ nuclei 72Ni, 74Ni, 94Ru, and 96Pd, as well as raise the question regarding the order of levels with the same value of$ J^\pi $ and different seniority [18]. Novel spectroscopic data on 72Ni and 74Ni allow us to examine this matter comprehensively [9, 10].We consider the spectra of excited states in neutron-rich
$ ^{70-76} $ Ni isotopes and$ N=50 $ isotones in a simplistic phenomenological approach. The seniority$ \nu=2 $ part of the spectrum is described using the δ-force approximation for interaction of two like nucleons on the$ j=9/2 $ shell. The only parameter in this case, which is the ground state multiplet (GSM) splitting, can be estimated using the mass relationship for pairing energy. States with higher seniority number can be then reproduced within the frame of seniority scheme. The advantages of such an approach lie with its simplicity and lack of free parameters. Earlier it was adopted to calculate the GSM in nuclei near 208Pb, where a feasible description of high momentum states was achieved [19, 20]. -
Nucleon pairing facilitates the formation of specific sets of excited states that constitute the ground state multiplet. In case of a pair of similar nucleons in j state, the spins of these states take on even values and are characterized by the isospin of the nucleon pair
$ T=1 $ and spin$ S=0 $ . In the seniority model, these excited states are degenerate [21, 22]. In 1950, Goeppert Mayer proposed the description of nucleon pairing δ-potential approximation [24]. In this case, the relative shift of the excited state J can be determined as [23, 25]:$ \begin{align} \frac{\Delta E_{J}}{\Delta E_{0}}=(2j+1) \begin{pmatrix} j& j& J\\ \dfrac{1}{2}& -\dfrac{1}{2}& 0 \end{pmatrix}^2. \end{align} $

(1) If we know the pairing energy
$ \Delta E_0=\Delta_{NN} $ , the energy of all GSM states$ E_J $ can be calculated as:$ \begin{align} E_J = \Delta_{NN}\left(1 - \frac{\Delta E_{J}}{\Delta E_{0}}\right). \end{align} $

(2) An illustration of the nucleon pairing depicted above is based on a description of a typical nucleus with two nucleons above the doubly magic core. On the example of two neutrons above the core
$ (N-2, Z) $ , the lack of pairing would result in equality between two neutron separation energy$ S_{nn}(N, Z) $ in the nucleus$ (N, Z) $ and double the separation energy$ S_n(N-1, Z) $ . Pairing correlations then result in a difference between these two values, and the corresponding energy of residual interaction can be found using the mass relation [26]:$ \begin{aligned}[b] \Delta_{nn}(N,Z) &= (-1)^{N} [S_{nn}(N,Z) - 2 \cdot S_n(N-1,Z)]\\ &= (-1)^{N} [B(N,Z) - 2 \cdot B(N-1,Z) + B(N-2,Z)]\\ &= (-1)^{N} [S_n(N,Z) - S_n(N-1,Z)]. \end{aligned} $

(3) Here,
$ B(N,Z) $ is the binding energy of (N, Z). In the case of protons, the n indexes are swapped for p and the relationship is based on masses or binding energies of isotones. Such an estimate requires the data on three neighboring nuclei. The question of correspondence between pairing energy and different mass relationships, related to even-odd staggering, was investigated thoroughly, e.g. in [27–30]. Earlier, we conducted the analysis of different mass relationships based on the masses of three or more isotopes [31]. Splitting of the GSM for two nucleons above the closed core and the pairing energy are strongly correlated.In [32], it was demonstrated that, for nuclei near the line of stability, the best fit between these values is obtained for the mass relationship from [29], based on five neighboring isotopes. The nickel isotopes under consideration in this study are located close to the neutron drip-line; hence, the use of additional data is undesirable, and thus, calculations of the GSM in neutron-rich nickel isotopes and
$ N=50 $ isotones were performed using the relationship [27]$ \begin{equation} \Delta_{nn}^{(4)}(N)=\frac{(-1)^N}{2}[-S_n(N+1)+2S_n(N)-S_n(N-1)], \end{equation} $

(4) which serves as an averaging of
$ \Delta_{nn}(N, Z) $ for two neighboring nuclei. All the data were taken from AME2020 [33].Figure 1 presents the experimental spectra in even neutron-rich nickel isotopes and isotones
$ N=50 $ for comparison. We should point out the distinct spectra of 90Zr and 68Ni as opposed to other nuclides in the chains: the first excited states$ 2^+ $ and$ 4^+ $ there lie higher than the corresponding states in the adjacent nuclei, although this effect is not as prominent as in other magic nuclei. The spectra of these and the rest of the isotopes demonstrate the trademark of the GSM originating from pairing similar nucleons on$ j=9/2 $ : even-spin states with a small splitting at approximately$ \; 100 $ keV between$ 8^+ $ and$ 6^+ $ . The values of$ \Delta_{\tau\tau}^{(4)} $ ($ \tau=n, p $ ) correspond to the position of state$ 8^+ $ and are approximately 0–250 keV above it; this is not only for 70Ni and 92Mo with the two nucleons above the closed shell but also for isotopes with more nucleons.
Figure 1. (color online) Experimental spectra: a) even isotopes
$^{68-76}$ Ni and b) even isotones$N=50$ with filled$j=9/2$ subshell. The dots represent the value of neutron pairing energy$\Delta_{nn}^{(4)}$ in nickel isotopes or proton pairing energy$\Delta_{pp}^{(4)}$ in isotones$N=50$ .This agrees well with the seniority scheme, where the total splitting of the GSM part with
$ \nu=2 $ (where ν is seniority number, the number of unpaired nucleons) remains constant from isotope to isotope, during the filling of the entire subshell. The possible values of the total angular momentum J for nuclei with N valence nucleons on the outer$ j=9/2 $ subshell, among which ν are unpaired, are presented in Table 1. As j grows, the sets of possible values of J for$ \nu>2 $ become more complex, one of the first such calculations for$ j>7/2 $ performed in [34].v Total angular momentum J $0$ 

$0$ 

$1$ 

$\frac92$ 

$2$ 

$2,4,6,8$ 

$3$ 

$\frac32,\frac52,\frac72,\frac92,\frac{11}{2},\frac{13}{2},\frac{15}{2},\frac{17}{2},\frac{21}{2}$ 

$4$ 

$0,2,3,4^2,5,6^2,7,8,9,10,12$ 

$5$ 

$\frac12,\frac52,\frac72,\frac92,\frac{11}{2},\frac{13}{2},\frac{15}{2},\frac{17}{2},\frac{19}{2},\frac{25}{2}$ 

Table 1. Summation of angular momenta
$j = \frac{9}{2}$ .In the seniority scheme, the states with higher seniority ν are also degenerate. The splitting occurs in calculations based on the non-degenerate set of
$ \nu=2 $ levels, which can either be found using different models or obtained from the experiment. The wave functions and energies of a three-nucleon system can be expressed as linear combinations and wave functions or energies of the system with two nucleons with an added third nucleon. For energies of the excited states for the three-nucleon system, the following formula holds [35]:$ \begin{align} E(J_3)=\sum_{J_2}[(jj)J_2 j J_3 |\} j^3 J_3]^2 E(J_2). \end{align} $

(5) Here,
$ [(jj)J_2 j J_3 |\} j^3 J_3] $ represent the fractional parentage coefficients (FPC). The calculated spectrum of the system of three nucleons can then be similarly used to determine the energies of the system with more nucleons on the given subshell via the iterative procedure. In our calculations, we used the FPC values from [22].The seniority scheme was first proposed by Racah and Flowers [21, 36, 37] for the cases
$ j \le 7/2 $ . However, the seniority number may not be necessarily conserved for higher values of j. Regarding the case of$ j=9/2 $ , there appear pairs of$ J=4 $ and$ J=6 $ states with$ \nu=4 $ , which may partly be mixed with corresponding$ \nu=2 $ states. Simultaneously, there remain two distinct$ J=4 $ and$ J=6 $ states, for which seniority remains an optimal quantum number, regardless of the form of nucleon-nucleon interaction [38–41]. Analytical and numerical studies in this regard showed that these states are indeed reproduced within Bayman's FPC scheme [22] with accuracies of 99% and above [42]. -
The seniority model together with the δ-force approximation for pairing was used to describe the GSM spectra in
$ ^{70-76} $ Ni, with 68Ni taken as the doubly magic nucleus ($ Z=28 $ ). The nuclei in this range of masses and neutron excess are commonly handled using the shell model configuration mixing taken into account. For isotopes studied in this study, such calculations within$ pfg_{9/2}d_{5/2} $ model space showed that the occupation of$ \nu g_{9/2} $ in 68Ni is affected on a rather negligible scale of around 4.7% compared to isotones$ N=40 $ [43]. Experimental data for$ ^{69-77} $ Ni also show that it is the$ \nu g_{9/2} $ single particle state that is primarily filled along this chain of isotopes. This is evident from the ground states of odd isotopes having the spin of$ J^\pi=9/2^+ $ , as well as from the observed ground state multiplets originating from pairing the neutrons on$ j=9/2 $ subshell. Hence, we treated the isotopes$ ^{70-76} $ Ni within the model space including just the subshell$ g_{9/2} $ . Similar calculations were performed in isotones$ N=50 $ with valence protons in$ g_{9/2} $ . -
Figure 2a presents the comparison between experimental and calculated spectra in isotopes 70Ni (76Ni) with 2 nucleons or (2 holes) in
$ 1g_{9/2} $ . Notably, higher momentum states$ 6^+ $ and$ 8^+ $ are reproduced most accurately within the approximation of δ-potential, the energies of$ 4^+ $ and$ 2^+ $ are overestimated by 250–300 keV and$ \sim $ 1 MeV, respectively. A similar situation is observed in the spectra of 92Mo and 96Cd (Fig. 2b).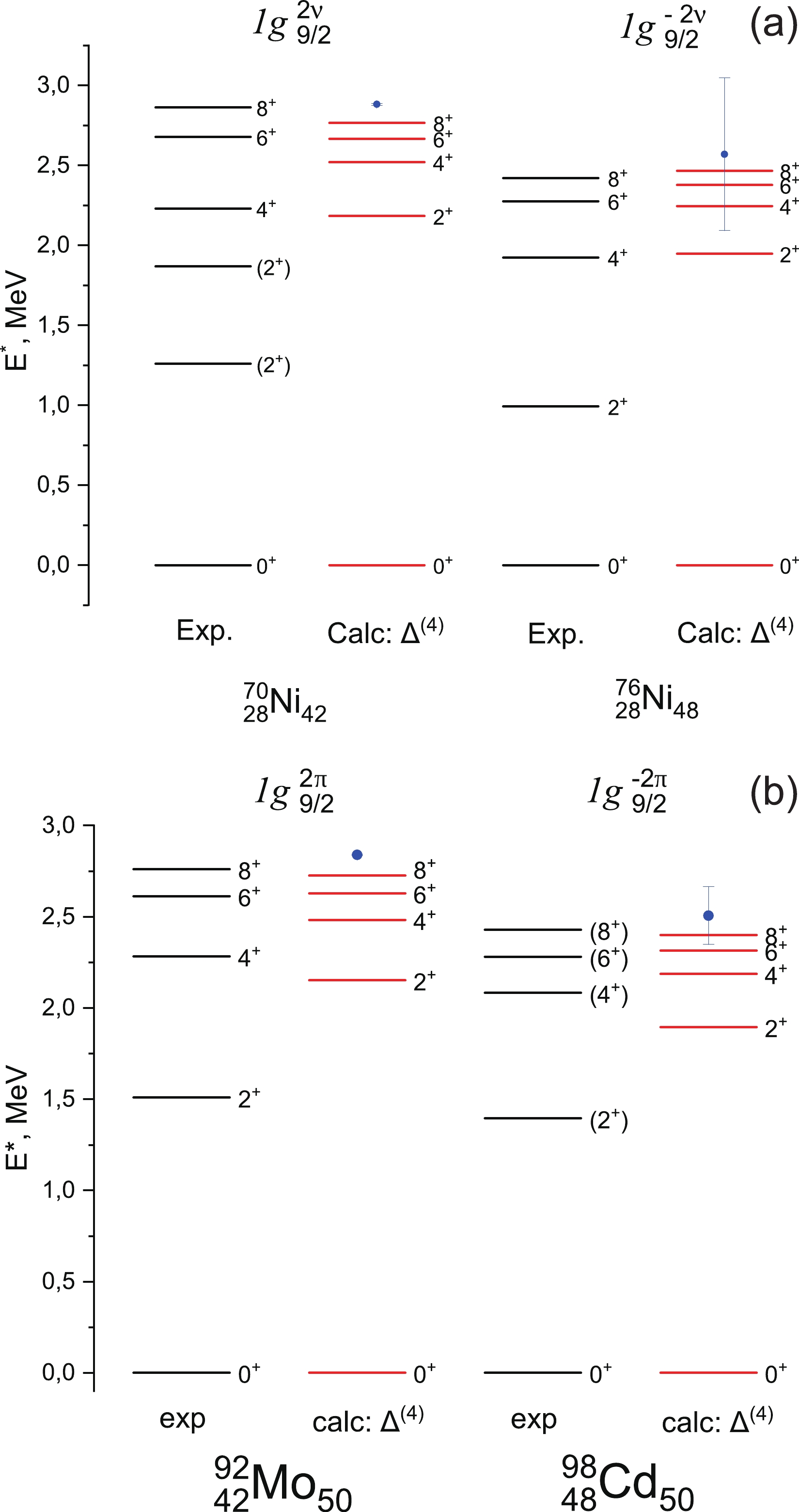
Figure 2. (color online) Experimental (Exp.) and calculated (Calc.) low-energy level schemes of nickel isotopes
$^{70,76}$ Ni (a) and$N=50$ isotones 92Mo, 98Cd (b). The dots represent the value of$\Delta_{nn}^{(4)}$ in nickel isotopes or$\Delta_{pp}^{(4)}$ in$N=50$ isotones. Experimental data are from [51] (70Ni), [52] (76Ni), [53] (92Mo), and [54] (98Cd). See text for details.It should be noted that in decomposition of residual interaction by Legendre polynomials
$ v(r_{12})=\sum\limits_l f_l(r_1,r_2)P_l(\cos \Theta_{12}), $

the values of coefficients
$ f_l $ for δ-interaction are of the form$ f_l = \delta(r_1-r_2)\frac{2l+1}{4\pi r_1^2}, $

which implies that larger values of
$ f_l $ correspond to larger l.Terms with lower l are responsible for long-ranged interaction and collective nuclear effects [44]. It is for this reason that δ-interaction works best when describing states with higher angular momentum. In contrast, for states
$ J^\pi=2^+ $ , the first of such a state in experimental spectra often lies at energies of approximately the BCS gap$ \Delta_\tau = \Delta_{\tau \tau}/2 $ , whereas in δ-approximation,$ E^*(2^+)/\Delta_{\tau \tau}^{(4)}=0.75 $ . In the region of medium and light nuclei, these states are often reproduced via configuration mixing.It should be noted that the first
$ 2^+ $ states lie below the value of$ \Delta_{\tau\tau}/2 $ in 70Ni and 76Ni. Specifically,$ E^*(2^+)/\Delta_{nn}^{(4)} = 0.44 $ for 70Ni and 0.39 for 76Ni. For protons, the corresponding value$ E^*(2^+)/\Delta_{pp}^{(4)} $ is higher: 0.53 for 92Mo and 0.56 for 98Cd. Later, we will see this resulting in significant differences in the structure of spectra with higher seniority. -
In accordance with seniority model, the spectrum of 72Ni with four neutrons on
$ 1g_{9/2} $ should include a set of$ \nu=2 $ states (observed in 70Ni) complemented by levels with$ \nu=4 $ . Considering the location of$ \nu=4 $ states depending on the energies of$ \nu=2 $ levels, it is important to verify the sensitivity of the former, in particular, to the energy of the$ J=2^+ (\nu=2) $ overestimated within the δ-potential approximation. The corresponding calculation is shown on Fig. 3 as the first spectrum. Hereafter, all$ \nu=4 $ states are depicted with colored lines. Notably, the energies of the second$ J^\pi=4_2^+, 6_2^+ $ states are overvalued by$ \sim $ 1 MeV. We assumed that this overestimation primarily emerges as a result of inaccuracies in the energy of$ J^\pi=2^+ (\nu=2) $ ; hence, we performed a calculation with the fixed energy value of this state taken from experiment. In fact, fixing this state results in the increase in the splitting of the$ \nu=4 $ spectrum. Furthermore, 72Ni observes the shift of$ J^\pi=4^+,6^+ (\nu=4) $ levels below the corresponding$ \nu=2 $ states. In other words, an inversion of excited states occurs as per the seniority model. Such an anomalous order of levels was described in [10], in which the authors drew conclusions on the structure of the spectra based on the intensity of transitions between different levels.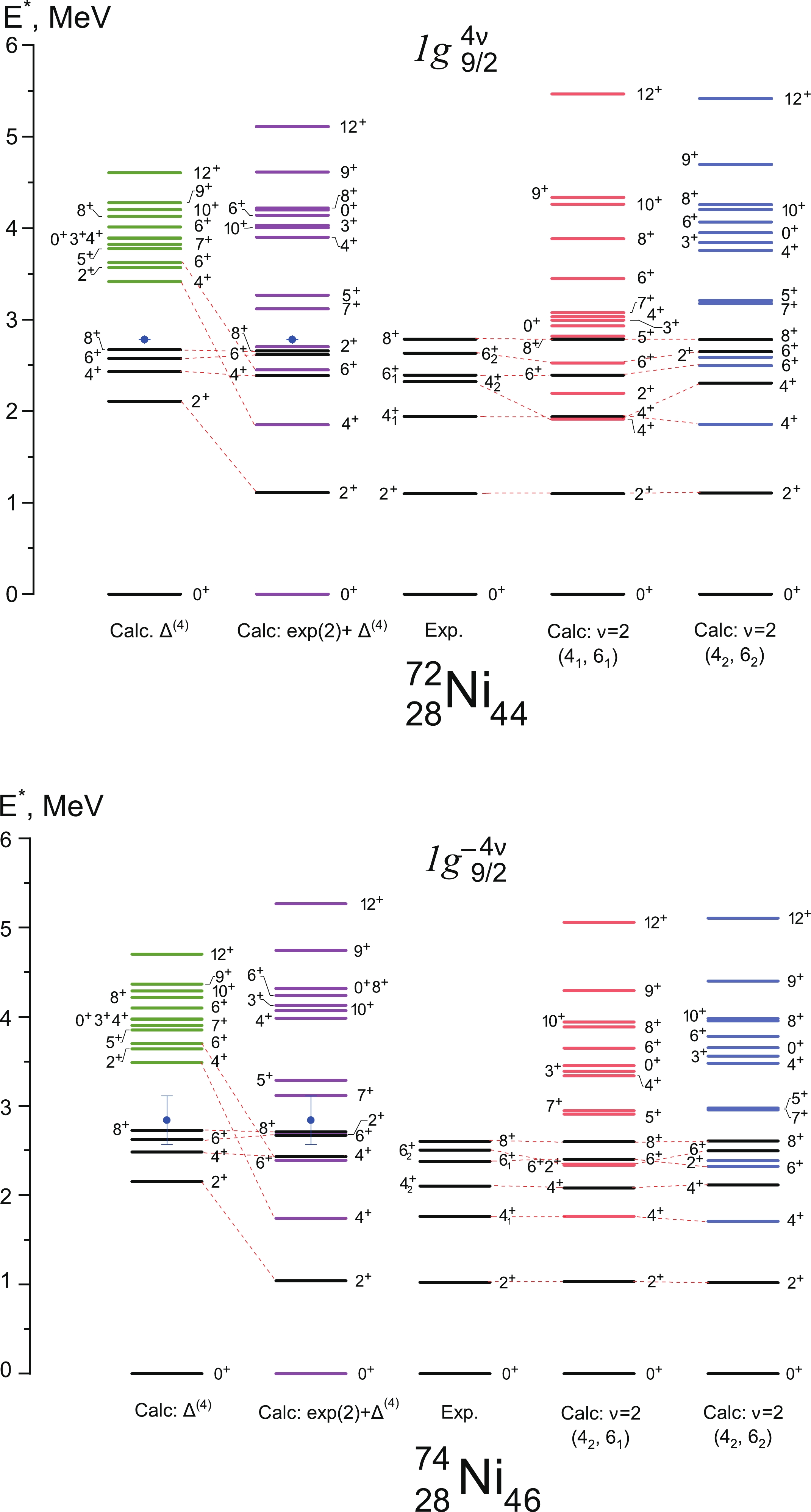
Figure 3. (color online) Low-energy level schemes of nickel isotopes 72Ni (top) and 74Ni (bottom). States with seniority
$\nu=2$ are shown in black, states$\nu=4$ — by colored lines. The experimental spectrum is shown in the center (data from [9, 10]). Left: first column — calculations in the δ-approximation based on$\Delta_{nn}^{(4)}$ (marked with a dot); the second one — the same using the experimental value$2^+$ . On the right are calculations using different experimental values$4^+$ and$6^+$ as states with seniority$\nu=2$ .To make more objective predictions regarding which experimental states (
$ 4_1 $ or$ 4_2 $ ,$ 6_1 $ or$ 6_2 $ ) correspond to seniority$ \nu=2 $ and$ \nu=4 $ , we performed several calculations with all the$ \nu=2 $ state energies fixed and taken from experimental data, for each of the combinations of states$ 4_i $ ,$ 6_j $ . Examples of such calculations are also presentd on Fig. 3 as the fourth and fifth spectra. Namely, the fourth spectrum was obtained in the assumption experimental states$ 4_1^+, 6_1^+ $ , which are characterized by seniority$ \nu=2 $ , and thus, their energy can be used to reproduce the spectrum$ \nu=4 $ ; similarly,$ 4_2^+, 6_2^+ $ levels were taken as$ \nu=2 $ on the fifth spectrum. The comparison of these spectra to the experiment shows that$ 4_2^+ $ should likely be the$ \nu=2 $ state, as discussed earlier. Data on decay of 72Ni support this claim. Simultaneously, it remains uncertain which of the$ 6_{1,2} $ belongs to$ \nu=2 $ part of the spectrum, as both calculations reproduce these levels.Similar calculations were carried out for 74Ni with four holes on
$ 1g_{9/2} $ . We drew similar conclusions for the$ 4^+ $ levels in this nucleus: the lower of the two is the$ \nu=4 $ state. The$ 6^+ $ states, on the other hand, can barely be resolved seniority-wise due to even smaller spacing between them. Furthermore, similar to the 72Ni case, the location of higher momentum levels also has a strong dependence on$ E(2^+, \nu=2) $ : in both of these nuclides, the energy of$ 12^+ $ is estimated at 5 – 6 MeV.The absence of data on the position of the levels with
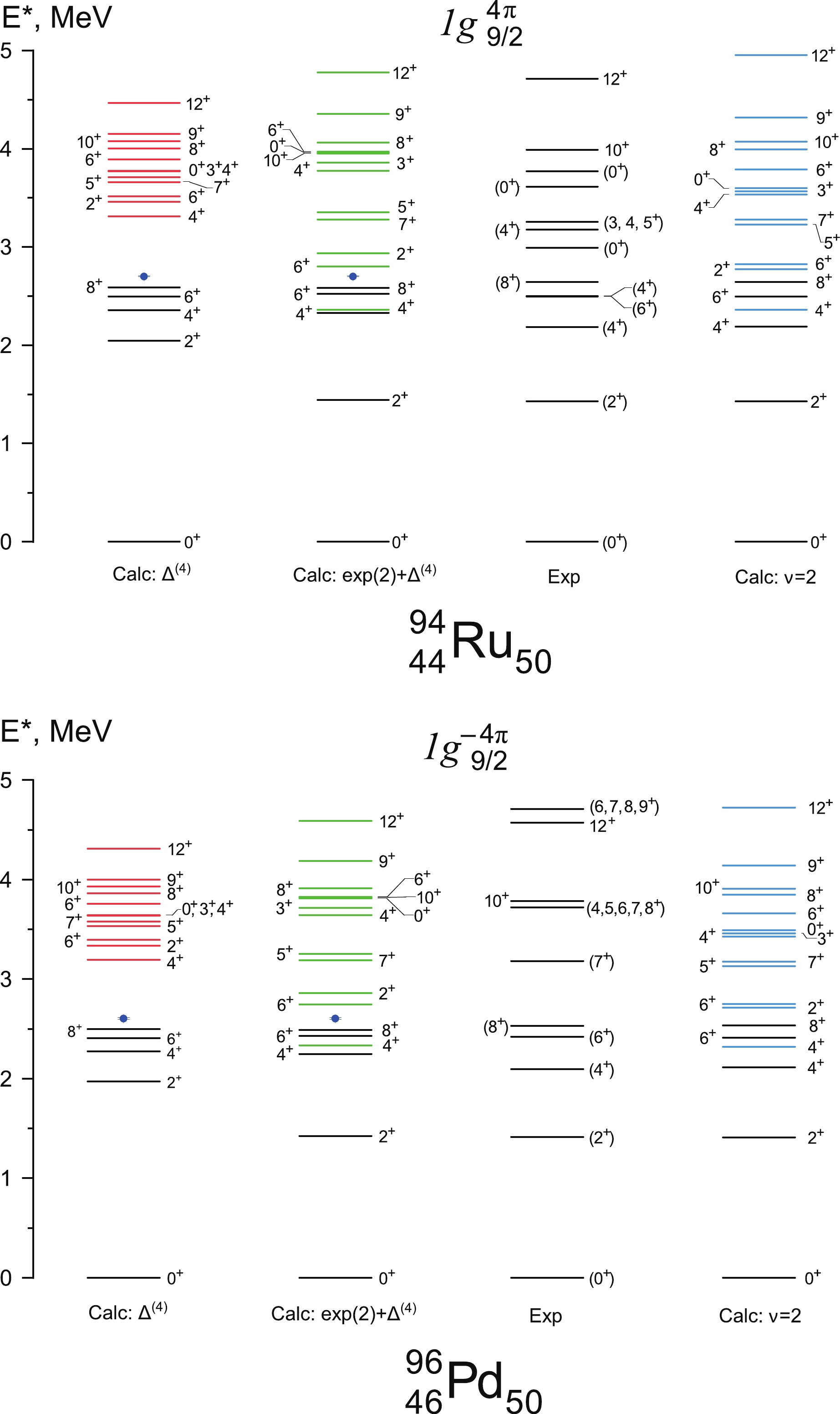
$J^{\max} = 12^+$ in the spectra of 72Ni and 74Ni does not allow us to compare the total splitting of the GSM with the experiment. From this perspective, it is all the more important to compare the corresponding calculations for isotones$ N=50 $ . Low energy spectra of semi-magic isotopes 94Ru and 96Pd exhibits the example of the dominance of isovector paring in accordance with the seniority scheme [14, 45].Experimental spectra of 94Ru and 96Pd are compared to our calculations on Fig. 4. The
$ \nu=4 $ spectra for protons in the$ N=50 $ isotone chain exhibit an important difference: there are still two$ 4^+ $ levels within the energy boundaries of the$ \nu=2 $ part of the GSM (energies up to$ 8_1^+ $ state), yet only one$ 6^+ $ level. Unlike nickel isotopes, in this case the first$ 4^+_1 $ state belongs to seniority$ \nu=2 $ , which turns out to be important in interpreting the observed E2 transitions properties in these isotopes [46]. Calculations of the δ-potential approximation showed that fixing just the energy of$ 2^+ $ is sufficient to reproduce the general order of excited states known experimentally and achieve a significantly better correspondence between the energies of particular levels, especially for high momentum states$ 12^+ $ and$ 10^+ $ .The correspondence between the
$ 0^+ - 2^+ $ splitting and location of$ (6^+, \nu=4) $ was discussed earlier, for example, in [48]. The authors of the article drew a connection with the differences between the cores 90Zr and 68Ni. The model assumes the presence of a closed core and is thus rather simplified in the given case, as neither 68Ni nor in 90Zr possesses a distinctly magic number of neutrons or protons (40 in this case). For example, in microscopic calculations within dispersive optical potential, the estimate of$ \nu g_{9/2} $ occupation in 68Ni is at 20% [49], the occupation of$ \pi g_{9/2} $ in 90Zr: 14% [50]. When describing Ni isotopes within shell model and comparing them to$ N=50 $ isotones, the authors of [48] point out the differences between the order of single particle states in the$ fp $ -shell and the differences between the spectra coming as a result. Nevertheless, our analysis shows that GSM spectra of nuclei with like nucleons on$ g_{9/2} $ may present an excellent opportunity to study the conservation of seniority for nucleons in$ j=9/2 $ state. -
The experimental spectra of odd nickel isotopes under consideration are also not well studied compared to those of more stable nuclides. The spectrum of 71Ni, for example, includes five states in the range of 1.3 MeV, whereas 8
$ \nu=3 $ states should be observable within the seniority scheme.The splitting of this GSM is equal to
$ 4/5\Delta_{nn} $ , which equals approximately 2.27 MeV for 71Ni, and the maximal spin is$J= {21}/{2}$ . Some impressive experimental data on 73Ni and 75Ni were recently obtaned on RIBF (RIKEN) [12,13] and NSCL (MSU) [11], including novel information on the state${13}/{2}^+$ .Earlier we demonstrated that the most accurate estimates on energies of
$ \nu=4 $ levels in even nuclei are attained via the combined use of δ-interaction approximation and the fixed experimental energy of the$ 2^+ $ state. Similar calculations can be performed in the case of odd isotopes if the energy value of$ J=2^+ $ state is taken from the neighboring even isotope. The corresponding calculated spectra are presented on Fig. 5.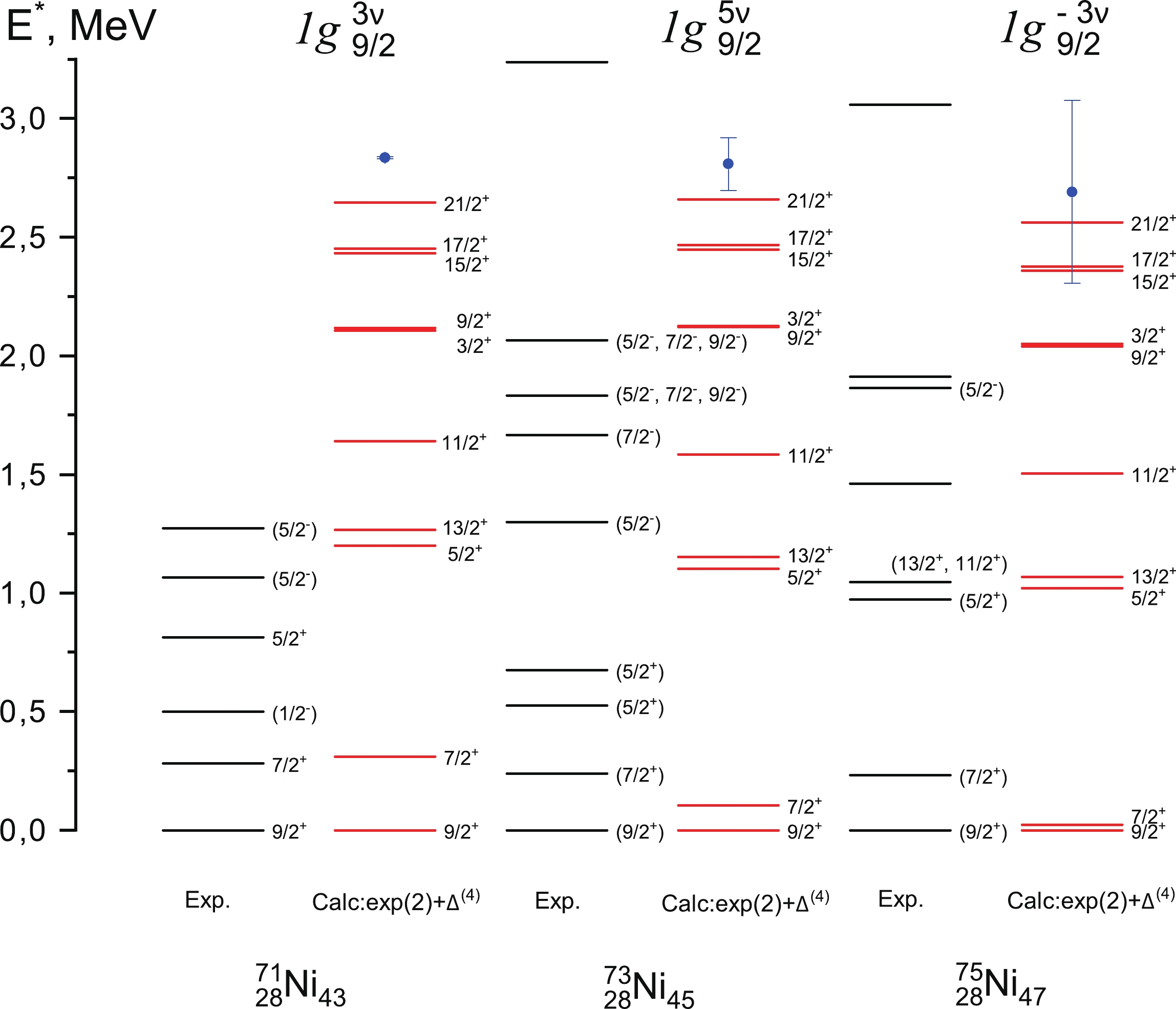
Figure 5. (color online) Experimental (Exp.) and calculated (Calc.) low-energy level schemes of nickel isotopes
$^{71,73,75}$ Ni. Experimental data taken from [47] (71Ni), [11] (73Ni), [13] (75Ni). The calculated states with$\nu=3$ were obtained in the δ-force approximation using the experimental energy value of the$2^+_1$ state in the neighboring even-even isotope in the spectrum of seniority$\nu=2$ .It seems most reasonable to base the calculations of
$ \nu=3 $ levels in 71Ni on the energy of level$ 2^+ $ in 70Ni as nucleus with two nucleons on the shell. In reality, there are two of such levels in the experimental spectrum of 70Ni which results in ambiguity as to which belongs to the GSM coming from pairing. Two separate calculations were performed for this reason, each based on the energy of either state$ 2_1^+ $ or$ 2_2^+ $ . We determined that the only known experimental states with positive parity in 71Ni,$ J=7/2^+, 5/2^+ $ , are best reproduced when the energy of$ J=2_1 $ is adopted, proving it's$ \nu=2 $ nature and affiliation with the GSM.The
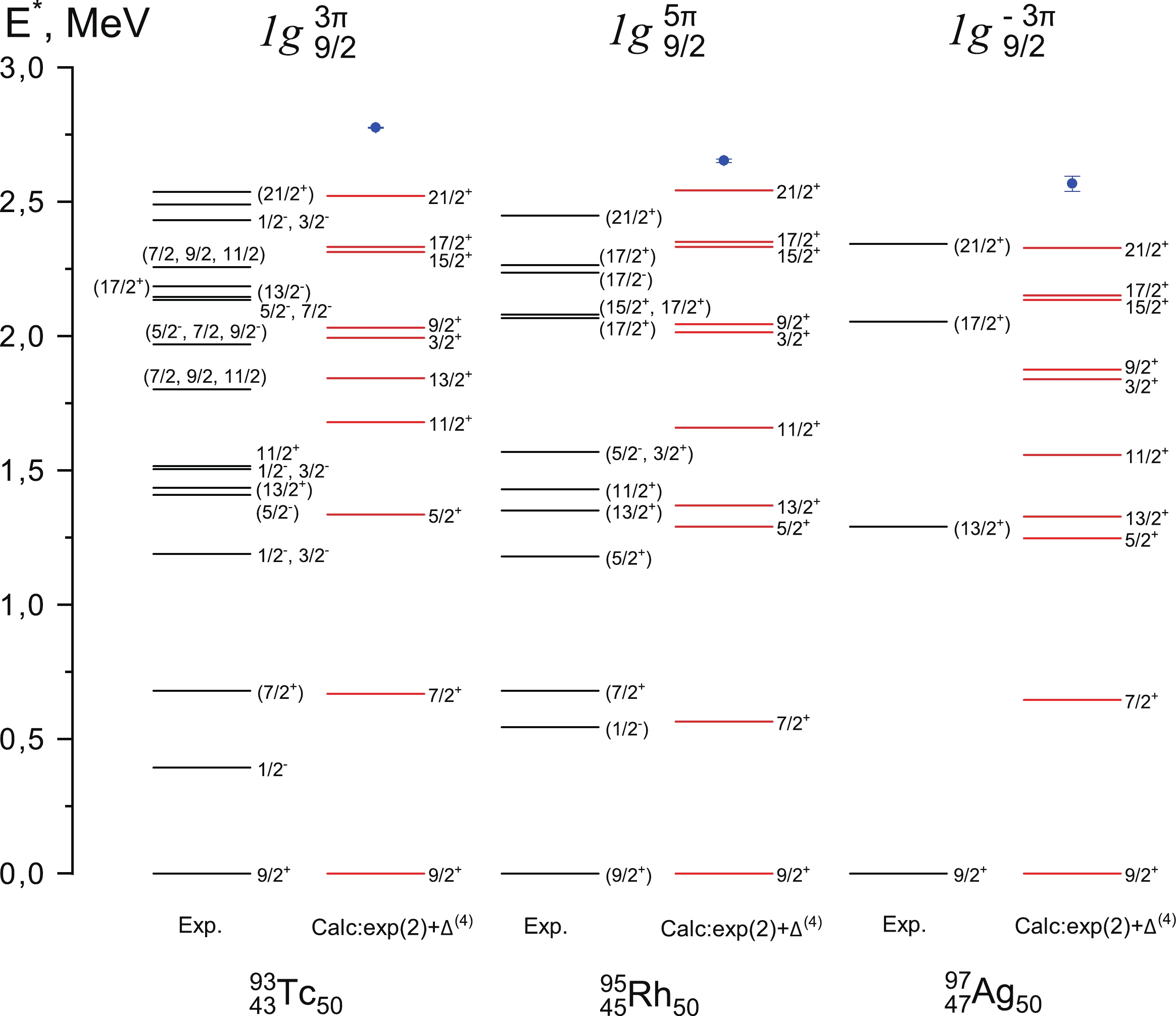
$ 1g_{9/2} $ subshell of 73Ni is half filled, and strictly speaking, its spectrum should be made up of$ \nu=1,3,5 $ levels. We chose to limit our calculations to seniority$ \nu=1,3 $ and use the experimental energy of the$ J=2 $ level in 72Ni. For 75Ni with three holes, similar calculations were based$ E(2^+) $ in 76Ni. Here, reasonable agreement was achieved for the states${5}/{2}^+, {13}/{2}^+$ .Analogous studies of the 93Tc, 95Rh and 97Ag spectra may also prove fruitful, as more experimental data on higher spin states are available for these nuclei (see Fig. 6). In comparison with our previous calculations [19], the use of the experimental value energy of the state
$ J^P=2^+ (\nu=2) $ from the spectrum of the neighboring even-even isotope made it possible to better reproduce both the position of${7}/{2}^+$ state and levels with J high value. It is worth noting the reliable reproduction of the overall splitting, also known as the energy of the$ J^\pi=21/2^+ $ state.As observed from our estimates for
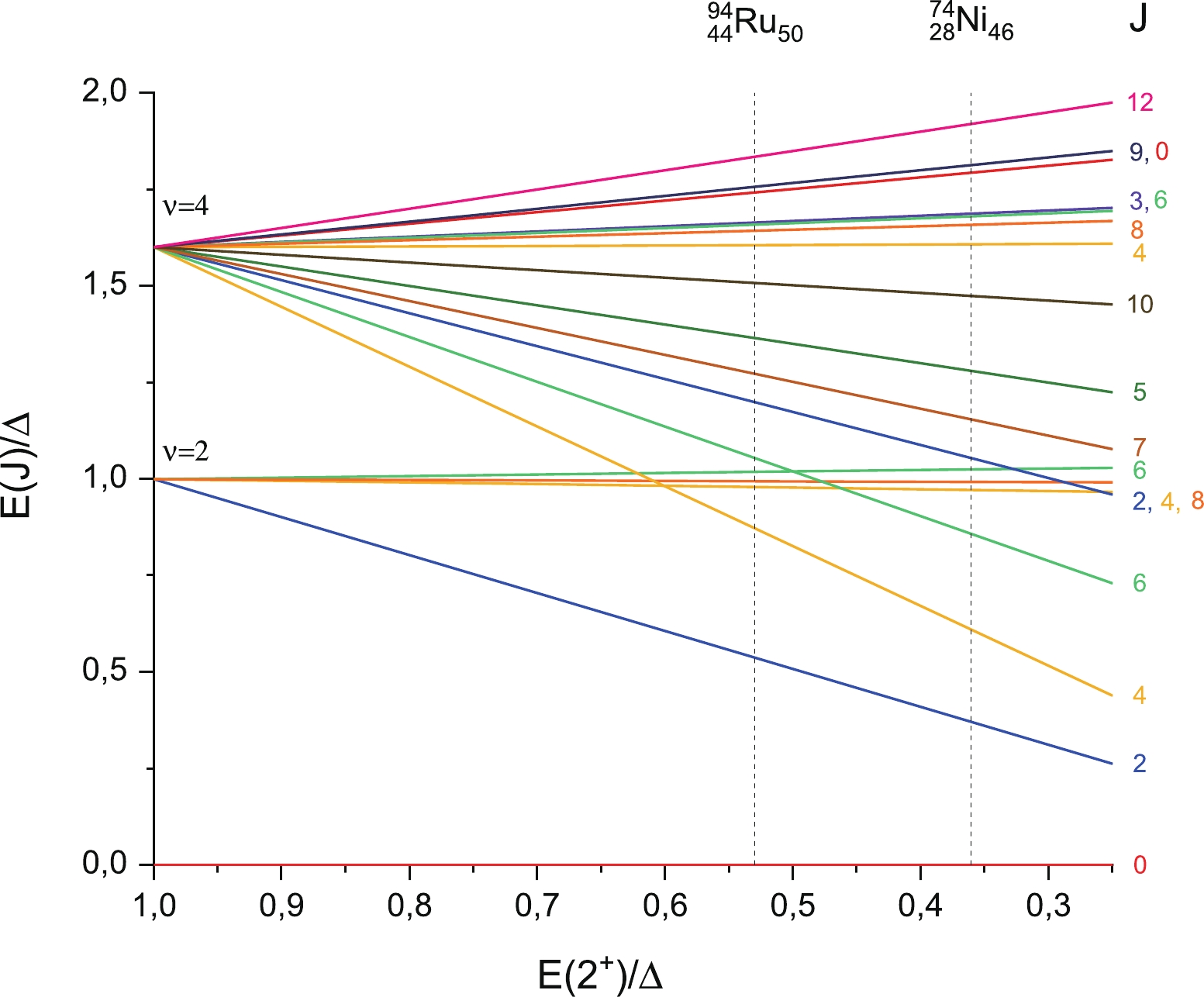
$ \nu=3,4 $ levels in various isotopes, GSM splitting can be very sensitive to the location of$ (J^\pi=2^+, \nu=2) $ . The structure of the entire$ \nu=0,2,4 $ spectrum as a function of$ E(2^+)/\Delta_{\tau \tau} $ is shown on Fig. 7. As observed from the graph, the relative energy of$ 2^+ $ has the strongest influence on$ 4^+ $ and$ 6^+ $ in$ \nu = 4 $ spectrum. The second$ 4^+, 6^+ $ has a negligibly small dependence on$ \nu=2 $ states and does not change its position, as neither does$ 8^+ $ , which implies that the seniority is an optimal quantum number for these levels. Among the odd-spin states,$ 3^+ $ is the least sensitive to the energy of$ (J=2,\nu=2) $ .The value of
$ E(2^+)/\Delta_{\tau \tau} $ also has a significant effect on the overall GSM splitting and the difference between the energies of high momentum levels$ 12^+ $ and$ 10^+ $ . Regarding the structure of the multiplet, we shall recall that the δ-force approximation yields the value of$ E^*(2^+)/\Delta_{\tau\tau}\approx 0.75 $ for the nucleons on$ j=9/2 $ shell — the value at which, in accordance with Fig. 7, no significant changes in the GSM structure occur. For both isotones 94Ru and 96Pd, this value is equal to approximately 0.53, which, as observed from the graph, results in$ (4^+ \nu=4) $ "dropping" below the pairing energy in the region of$ \nu=2 $ part of GSM. For the nickel isotopes, this value is even lower (at 0.39 MeV for 72Ni and 0.36 for 74Ni) - and indeed, the second$ 6^+ $ state also shifts down to$ \nu=2 $ energies. -
Pairing correlations exhibit a significant influence on the properties of atomic nuclei. The multiplet of excited states as one of its consequences depends on several factors including the form of residual interaction, shell structure of the nucleus and its deformation. Nevertheless, even a simplified model that does not take configuration mixing and long-ranged part of nucleon-nucleon interaction into account may provide a good understanding of the structure of low-lying excited states in a nucleus with an isolated subshell.
The approximation of δ-interaction for nucleon pairing was employed to handle the
$ \nu=2 $ part of GSM spectra in$ ^{70-76} $ Ni and isotones$ N=50 $ with valence nucleons on the$ g_{9/2} $ subshell. Mass relationships were shown to provide a feasible estimate for GSM splitting; ($ J^\pi=6^+,8^+ $ ,$ \nu=2 $ ) states in even nuclei were reproduced with an error of no more than 0.1 MeV and ($ J^\pi=4^+ $ ,$ \nu=2 $ ) were reproduced with an error of no more than 0.5 MeV. This approximation provides a significantly higher energy value$ E(2^+) $ owing to the presence of configuration mixing and a long-range part of nucleon interaction.A correct account of
$ (J^\pi=2^+ $ ,$ \nu=2) $ (whether through use of more realistic interaction or just direct fixing of experimental values) yields some remarkable effects. The remarkable dependence of$ \nu = 4 $ GSM splitting on the location of this state results in a shift of$ 12^+ $ in isotopes with 4 nucleons (or 4 holes) on the$ j=9/2 $ subshell to higher energies by 300–500 keV, which allows for a better description of this and other high momentum states, particularly, in 94Ru and 96Pd. In contrast, two states$ (J=4,6,\nu=4) $ drop down, and the shift is more significant when$ (J=2, \nu=2) $ is lower. This effect is especially remarkable in$ ^{72,74} $ Ni, where the very low (in relation to GSM splitting)$ 2_1 $ level triggers the inversion of the order of$ 4^+ $ states with different seniority. The presence of such an inversion is not significant for$ 6^+ $ states, and it is highly likely that seniority is not an optimal quantum number for these levels.
Seniority and ${ \left(\frac{\bf 9}{{\bf 2}}\right)^{\boldsymbol n} }$ configurations in neutron-rich Nickel isotopes
- Received Date: 2022-01-12
- Available Online: 2022-07-15
Abstract: Excited states in low-energy spectra of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: