-
One of the main scientific goals of relativistic heavy-ion collisions carried out at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) is to search for a new form of matter — Quark–Gluon Plasma (QGP) — and study its properties in laboratories [1–6].
$ J/\psi $ suppression, due to the color-screening effect in the hot medium, was proposed to be the signature of QGP formation in heavy-ion collisions [7]. Various measurements of$ J/\psi $ production in heavy-ion collisions have been performed so far at the CERN Super Proton Synchrotron (SPS), RHIC, and LHC [8–13]. These observations of$ J/\psi $ suppression in heavy-ion collisions can be interpreted as the interplay of the color-screening effect, the regeneration effect (recombination of charm quarks in the medium) [14] and cold nuclear matter (CNM) effects (nuclear shadowing, initial energy loss, breakup by co-movers etc.) [15].$ J/\psi $ can also be produced by the collision of the two electromagnetic fields of the relativistic heavy ions [16, 17]. For a fast-moving charged particle, the electric field vector points radially outward and the magnetic field circles it. The electromagnetic fields of relativistic heavy ions are highly Lorentz-contracted so that they can be considered as fields of quasi-real photons. When two nuclei pass by each other, the photon field of one nucleus could interact with the other nucleus, and produce a$ J/\psi $ by a photon–nucleus interaction. Most of these interactions are experimentally observed only without the accompaniment of hadronic processes, i.e., in so-called ultra-peripheral collisions (UPCs). In these collisions, the impact parameter b exceeds twice the nuclear radius ($ R_{A} $ ). Various measurements of$ J/\psi $ photoproduction have been performed in UPCs at RHIC and the LHC energies [18–23]. According to pQCD calculations [24–26], the photoproduction process of$ J/\psi $ is sensitive to the gluon density distribution, and the differential momentum transfer ($ |t| $ ) spectra of the process are determined by the production site in the target [27, 28], which provides information about the spatial distribution of gluons in the nucleus. So these measurements hopefully give insight to the gluonic structure of nuclei in Quantum Chromodynamics (QCD), which is also one of the key objectives of the physics program of a future Electron–Ion Collider [29, 30].Recently significant excesses with respect to expectations from purely hadronic production of
$ J/\psi $ yield at very low$ p_T $ (<0.3 GeV/c) have been observed by the ALICE [31] and STAR [32] collaborations in peripheral hadronic heavy-ion collisions (HHICs, b <$ 2R_A $ ). The excesses have the characteristics of coherent photoproduction, and could be qualitatively described by the coherent photonuclear production mechanism, which points to the evidence of coherent photon–nucleus interactions in HHICs.In facilities with heavy-ion collisions,
$ J/\psi $ signals are usually measured via the invariant mass distribution of dileptons, i.e.,$ e^+e^- $ and$ \mu^+\mu^- $ . The measured dilepton mass spectrum includes both the decay from$ J/\psi \rightarrow l^+l^- $ and$ J/\psi \rightarrow l^+l^-\gamma $ [33], which cannot be separated event by event. The invariant mass distribution of the dileptons from the latter decay channel usually has a long tail on the left-hand side. In order to keep the signal-to-background ratio at a reasonable level,$ J/\psi $ yields are usually counted in a limited mass window around the peak of$ J/\psi $ signals, instead of integrating over the entire mass range. The loss of$ J/\psi $ signals due to the mass cut can be corrected in the real data analysis. However, the$ p_T $ shift due to the missing radiated soft photon in$ J/\psi \rightarrow e^+e^-\gamma $ is usually ignored. The effect on the hadroproduced$ J/\psi $ should be negligible as the$ p_T $ shift is much smaller than the$ p_T $ of$ J/\psi $ . But the effect on coherent photoproduced$ J/\psi $ , whose$ p_T $ is on the order of tens of MeV/c, could be significant.In this article, we report calculations of
$ J/\psi $ photoproduction in hadronic Au+Au and U+U collisions at RHIC energy. We also take the$ J/\psi $ internal radiation effect into account and compare the calculations with experimental results with the expected hadronic contribution subtracted. -
$ J/\psi $ photoproduction can proceed via photon–Pomeron fusion, where the photons come from the electromagnetic field of one nucleus and the Pomeron or meson couples to the other. The calculation of the cross section of$ J/\psi $ photoproduction is approached by using a similar method to Ref. [34]. The probability distribution of$ J/\psi $ from coherent photoproduction in two-dimensional transverse momentum space can be calculated by performing a Fourier transformation to the amplitude in coordinate space, written as:$ \quad\frac{{\rm d}^{2} P}{{\rm d} p_{x} {\rm d} p_{y}} =\left|\frac{1}{2 \pi} \int {\rm d}^{2} \vec{x}_{\perp}\left(A_{1}\left(\vec{x}_{\perp}\right)+A_{2}\left(\vec{x}_{\perp}\right)\right) {\rm e}^{{\rm i} p_{\perp} \cdot \vec{x}_{\perp}}\right|^{2}, $

(1) where
$ \vec{x}_{\perp} $ is two-dimensional position vector, and$ A_{1}\left(\vec{x}_{\perp}\right) $ and$ A_{2}\left(\vec{x}_{\perp}\right) $ are the amplitude distributions in the transverse plane from the two colliding nuclei. Following Ref. [35], the production amplitude distribution for vector meson photoproduction is determined by the spatial photon flux and the corresponding$ \gamma A $ scattering amplitude$ \Gamma_{\gamma A \rightarrow V A} $ . According to the equivalent photon approximation [36], the spatial photon flux from a relativistic heavy ion is given by:$ \begin{aligned}[b] n\left(\omega_{\gamma}, \vec{x}_{\perp}\right) =&\frac{4 Z^{2} \alpha}{\omega_{\gamma}}\left|\int \frac{{\rm d}^{2} \vec{k}_{\gamma \perp}}{(2 \pi)^{2}} \vec{k}_{\gamma \perp} \frac{F_{\gamma}\left(\vec{k}_{\gamma}\right)}{\left|\vec{k}_{\gamma}\right|^{2}} {\rm e}^{{\rm i} \vec{x}_{\perp} \cdot \vec{k}_{\gamma \perp}}\right|^{2} \\ \vec{k}_{\gamma} =&\left(\vec{k}_{\gamma \perp}, \frac{\omega_{\gamma}}{\gamma_{c}}\right), \quad \omega_{\gamma}=\frac{1}{2} M_{J/\psi} {\rm e}^{\pm y}, \end{aligned} $

(2) where
$ \vec{k}_{\gamma \perp} $ is the two-dimensional momentum vector perpendicular to the beam direction, Z is the nuclear charge, α is the electromagnetic coupling constant,$ {\gamma_{c}} $ is the Lorentz factor of the nucleus,$ M_{J/ \psi} $ and y are the mass and rapidity of$ J/\psi $ , and$ F_{\gamma}\left(\vec{k}_{\gamma}\right) $ is the nuclear electromagnetic form factor.$ F_{\gamma}\left(\vec{k}_{\gamma}\right) $ is obtained via the Fourier transformation of the charge density in the nucleus. The nuclear density for a nucleus A at a distance r from its center is modeled with a Woods–Saxon distribution for symmetric nuclei:$ \rho_{A}(r)=\frac{\rho_{0}}{1+\exp \left[\left(r-R_{\rm{WS}}\right) / d\right]}, $

(3) where the radius
$ R_{\rm{WS}} $ and skin depth d are based on fits to electron-scattering data [35], and$ \rho_{0} $ is the normalization factor. The parameters of Au and U nuclei are listed in Table 1.$ A $ 

$ Z $ 

$R_{ws}/\rm fm$ 

$d /\rm fm$ 

Au 197 79 6.38 0.75 U 238 92 6.805 0.605 Table 1. Parameters of Au and U nuclei.
The scattering amplitude
$ \Gamma_{\gamma A \rightarrow V A} $ are found with a Glauber [37] and vector meson dominance (VMD) approach [38]:$\begin{aligned}[b] \Gamma_{\gamma A \rightarrow V A}\left(\vec{x}_{\perp}\right)=&\frac{f_{\gamma N \rightarrow V N}(0)}{\sigma_{V N}}\\&\times2\left[1-\exp \left(-\frac{\sigma_{V N}}{2} T^{\prime}\left(\vec{x}_{\perp}\right)\right)\right], \end{aligned}$

(4) where
$ f_{\gamma N \rightarrow V N}(0) $ is the forward-scattering amplitude for$ \gamma+N \rightarrow V+N $ when momentum transfer from the photon to the nucleon is 0, and$ \sigma_{V N} $ is the total V N cross section.$ f_{\gamma N \rightarrow V N}(0) $ can be determined from the measurements of the forward-scattering cross section, which is well parameterized from worldwide experimental measurements in Ref. [39]. To consider the coherent effect on the z direction, the modified thickness function is written as:$ \begin{aligned}[b] T^{\prime}\left(\vec{x}_{\perp}\right)=&\int_{-\infty}^{+\infty} \rho_{A}\left(\sqrt{\vec{x}_{\perp}^{2}+z^{2}}\right) {\rm e}^{{\rm i} q_{L} z} {\rm d} z,\\ q_{L}=&\frac{M_{V} {\rm e}^{y}}{2 \gamma_{c}}, \end{aligned} $

(5) where
$ q_{L} $ is the longitudinal momentum transfer required to produce a real vector meson. Using the optical theorem and VMD relation, the total cross section for$ V N $ scattering can be given by$ \sigma_{V N}=\frac{f_{V}}{4 \sqrt{\alpha} C} f_{\gamma N \rightarrow V N}, $

(6) where
$ f_{V} $ is the V-photon coupling and C is a correction factor for the nondiagonal coupling through higher mass vector mesons [40]. Finally, the production amplitude can be given by$ A\left(\vec{x}_{\perp}\right)=\Gamma_{\gamma A \rightarrow V A} \sqrt{n\left(\omega_{\gamma}, \vec{x}_{\perp}\right)}. $

(7) The
$ J / \psi $ ${\rm d} N / {\rm d} y$ in a certain centrality bin is related to the cross section$({\rm d} \sigma / {\rm d} y)$ via the following equation:$ \frac{{\rm d} \sigma}{{\rm d} y}(J / \psi)=\int_{b_{\min }}^{b_{\max }} 2 \pi b \frac{{\rm d} N}{{\rm d} y}(J / \psi, b) {\rm d} b. $

(8) In the coherent photoproduction case, the photon interacts with the entire nuclear target as one during the photon–nucleus interaction process, thus the
$ p_T $ of the photoproduced vector meson is constrained to be the level of the inverse of the nucleus size, which is about 60 MeV/c [41].Additionally, the incoherent photon–nucleus interaction contributes to the relatively high transverse momentum of
$ J/\psi $ production in heavy-ion collisions. In this case, the$ p_T $ of the produced$ J/\psi $ meson is constrained to the order of the inverse of the nucleon size, which is about approximately 300 MeV/c [41]. The cross section of incoherent$ J/\psi $ photoproduction$ \sigma_{\gamma A \rightarrow J/\psi A^{\prime}} $ is scaled to the cross section$ \sigma_{\gamma p \rightarrow V p} $ via the Glauber + VMD approach, where$ A^{\prime} $ is the nuclear state after the interaction, and it contains the products of the nuclear disintegration. So the cross section$ \sigma_{\gamma A \rightarrow J/\psi A^{\prime}} $ can be written as:$ \begin{aligned}[b] \quad\quad\sigma_{\gamma A \rightarrow J/\psi A^{\prime}} =&\sigma_{\gamma p \rightarrow V p} \int {\rm d}^{2} \vec{x}_{\perp} T\left(\vec{x}_{\perp}\right) {\rm e}^{-(1 / 2) \sigma_{V N}^{\rm{in}} T\left(\vec{x}_{\perp}\right)}, \\ \sigma_{V N}^{\rm{in}} =&\sigma_{V N}-\sigma_{V N}^{2} /\left(16 \pi B_{V}\right), \end{aligned} $

(9) where
$ T\left(\vec{x}_{\perp}\right) $ is the thickness function of the nucleus,$ \sigma_{V N}^{\rm{in}} $ is the inelastic vector meson–nucleon cross section and$ B_V $ is the slope of the t dependence of the$ \gamma p \rightarrow V p $ scattering [39].In the decay process
$ J/\psi \rightarrow e^+e^- $ , the lowest order decay width is$ \Gamma_{0}=\Gamma_{0}\left(J/\psi \rightarrow e^{+} e^{-}\right) $ . The radiative decay process is$ J/\psi \left(p_{0}\right) \rightarrow e^{-}\left(p_{1}\right)+e^{+}\left(p_{2}\right)+\gamma(k) $ , and the distribution in phase space is:$ \begin{aligned}[b] \frac{1}{\Gamma_{0}} \frac{{\rm d}^{2} \Gamma\left(J/\psi \rightarrow e^+ e^- \gamma\right)}{{\rm d} \varsigma {\rm d} \tau}=&P(\varsigma, \tau) \\ =&\frac{\alpha}{2 \pi}\left(\frac{1+\varsigma^{2}}{1-\varsigma}\right)\left(\frac{1}{\tau}+\frac{1}{1-\varsigma-\tau}\right) \\&- \frac{\alpha a}{4\pi}\left(\frac{1}{\tau^{2}}+\frac{1}{(1-\varsigma-\tau)^{2}}\right)-\frac{\alpha}{\pi}, \\ \varsigma=&\left(p_{1}+p_{2}\right)^{2} / M_{J/\psi}^{2}, \\ \tau=&\left(p_{0}-p_{1}\right)^{2} / M_{J/\psi}^{2}, \end{aligned} $

(10) where a=
$ 4 m_{e}^{2} / M_{J/\psi}^{2} $ , a ≤ ς ≤ 1 [33].In the rest frame of the decaying particle we have
$ \varsigma=1-2 E_{\gamma} / M_{J/\psi}^{2}, \tau=1-2 E_{1} / M_{J/\psi}^{2} $ and$ 1-\varsigma-\tau=1- 2 E_{2} / M_{J/\psi}^{2} $ , and in the center-of-mass system:$ \begin{aligned}[b] \tau=&1-\varsigma-\frac{1}{2}(1-\varsigma)\left(1-r \cos \theta_{1}\right) \\ {\rm { or }}\; \tau=&\frac{1}{2}(1-\varsigma)\left(1-{\rm{r}}\; \cos \theta_{2}\right), \end{aligned} $

(11) with
$ r=\sqrt{1-a / \varsigma} $ and$ \theta_{i} $ the angle between the photon and electron with momentum$ \vec{p}_{i} $ , obviously$ \theta_{1}=\pi-\theta_{2} $ . Variations of$ \theta_{2} $ from$ \theta_{2}=0 $ to$ \theta_{2}=\pi $ corresponds to$\begin{aligned}[b] \tau(0)=&\frac{1}{2}(1-\varsigma)(1-r), \\ \tau(\pi)=&\frac{1}{2}(1-\varsigma)(1+r). \end{aligned}$

By integrating
$ P(\varsigma, \tau) $ over the parameter τ:$ \begin{aligned}[b] \frac{1}{\Gamma_{0}} \frac{{\rm d} \Gamma\left(J/\psi \rightarrow e^+ e^- +\gamma\right)}{{\rm d} \varsigma}=&P(\varsigma) \\ =&\int_{\tau(0)}^{\tau(\pi)} P(\varsigma, \tau) {\rm d} \tau \\ =&\frac{\alpha}{\pi} \frac{1+\varsigma^{2}}{1-\varsigma}\left(\ln \frac{1+r}{1-r}-r\right), \end{aligned} $

(12) one can obtain the distribution
$ P(\varsigma) $ .The radiative photon emission causes a tail towards lower masses in the
$ J/\psi $ mass spectrum. The distribution$ P(m) $ of the dilepton mass after the$ J/\psi $ radiative decay from the calculation is defined as :$ \begin{aligned}[b]& \frac{1}{\Gamma_{0}} \frac{{\rm d} \Gamma\left(J/\psi \rightarrow e^+ e^- \gamma\right)}{{\rm d} m} =P(m) \\ =&\frac{\alpha}{\pi} \frac{2 m}{\left(M_{J/\psi}^{2}-m^{2}\right)}\left(1+\frac{m^{4}}{M_{J/\psi}^{4}}\right)\left(\ln \frac{1+r}{1-r}-r\right), \end{aligned} $

(13) where
$ r=\sqrt{1-4 m_{e}^{2} / m^{2}} $ . In the real data analysis a mass cut is commonly applied on the invariant mass of dilepton to reject backgrounds and improve the significance of$ J/\psi $ signals, so a similar cut is also used in the calculations. On the other hand, the photon also carries part of$ J/\psi $ mass, which introduces a transverse momentum shift for the dielectron pair. The effect on transverse momentum shift will be discussed in the following section. -
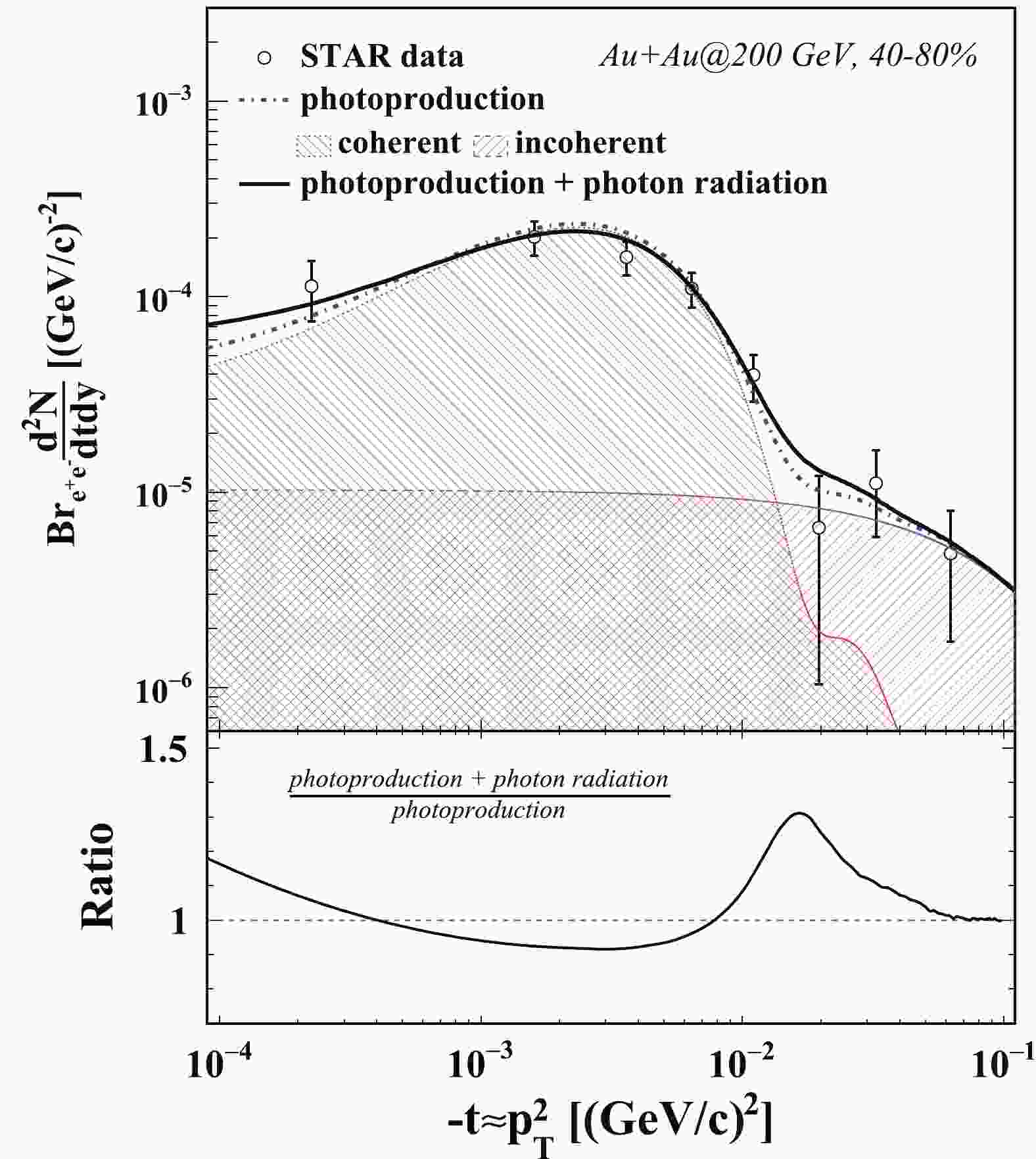
Figures 1 and 2 show the
$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ distribution from photoproduction in 40%–80% peripheral Au+Au collisions at 200 GeV and U+U collisions at 193 GeV, respectively. The Mandelstam variable t is approximately equal to$ -p_T^2 $ at RHIC top energy. The calculations are done in 40%–80% peripheral collisions and are compared with measurements from the STAR experiment, shown as a function of –t. On the top panel in Fig. 1 (Fig. 2), the dash-dotted line denotes the calculations on the photoproduced$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ distribution as a function of$ -t $ without taking the soft radiation effect into account. The contributions from coherent and incoherent photoproduction are represented as the shaded areas. The coherent photoproduction makes the dominant contribution at relatively low$ p_T $ , as discussed in the last section. The coherent contribution exhibits a peak structure, which agrees with the STAR measurements. In the coherent case, it is distinguishable between the photo-emitting nucleus and target nucleus. Thus the cross section of photoproduced$ J/\psi $ is the interference of the production from photo-emitting (target) nucleus and target (photo-emitting) nucleus. As$ J/\psi $ mesons have a negative parity, the cross section of coherent photoproduced$ J/\psi $ is influenced by destructive interference. In the relatively high$ p_T $ region, the photoproduced$ J/\psi $ are mainly from incoherent photoproduction, namely the photon–nucleon interaction. The solid line represents the calculations with the photon radiation effect. In the real data analysis, a$ J/\psi $ mass window cut is commonly applied to reject the background. A mass cut ($ M_{J/\psi} - m $ < 200 MeV) is used in this calculation to keep consistency with the measurements. The black circles represent the measurement from the STAR experiment,$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ with the expected hadronic contribution subtracted, acting as the estimation of the yield of photoproduced$ J/\psi $ . The vertical bar on each point shows the combination of the statistical uncertainty and the systematic uncertainty. The calculations in this study describe the results from the STAR experiment reasonably well. In the relatively high$ -t $ region, one can see that${\rm d}^2N/{\rm d}t{\rm d}y$ becomes larger with the internal radiation taken into account. For$ J/\psi $ with very low transverse momentum, it gains additional momentum, like being kicked by radiated photons. Thus$ J/\psi $ with very low transverse momentum are shifted toward higher values of$ -t $ . This result can be interpreted as a broadening in the t-distribution of$ J/\psi $ photoproduction with the soft radiation effect. On the bottom panel of Fig. 1, the black line shows the ratio of the calculation with the photon radiation effect over that without the photon radiation effect. The cross section decreases by about 10% at$ -t\approx0.04 $ (GeV/c)2 and increases toward high$ -t $ . This increment achieves its maximum at –$ t\approx0.16 $ (GeV/c)2.
Figure 1. (color online) Top: Photoproduced
$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ distributions in 40%–80% Au+Au collisions at 200 GeV. The dash-dotted line denotes the calculations on photoproduced$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ distribution as a function of$ -t $ , including contributions from coherent and incoherent photoproduction. The solid line represents the calculations with the photon radiation effect. Bottom: Ratio of the calculation with photon radiation effect over that without photon radiation effect.
Figure 2. (color online) Top: Photoproduced
$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ distributions in 40%–80% U+U collisions at 193 GeV. The dash-dotted line denotes the calculations on photoproduced$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ distribution as a function of$ -t $ , including contributions from coherent and incoherent photoproduction. The solid line represents the calculations with the photon radiation effect. Bottom: Ratio of the calculation with photon radiation effect over that without photon radiation effect.The soft radiation effect from different decay channels are also studied. Figure 3 (Fig. 4) shows the ratios of the calculation with the photon radiation effect over that without the photon radiation effect from both the dielectron and dimuon decay channels in 40%–80% Au+Au collisions at 200 GeV (U+U collisions at 193 GeV). The solid and dash-dotted lines show the ratios of the calculation on photoproduced
$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ in Au+Au 40%–80% with the photon radiation effect over that without the photon radiation effect from the dielectron and dimuon decay channels, respectively. There are no principal differences between these cases, except the level of the radiative effect. In the whole calculated$ -t $ region, the ratio from the dimuon decay channel is closer to unity than that from the dielectron decay channel. Muons have much larger rest mass, so they are less affected by the soft internal radiation effect.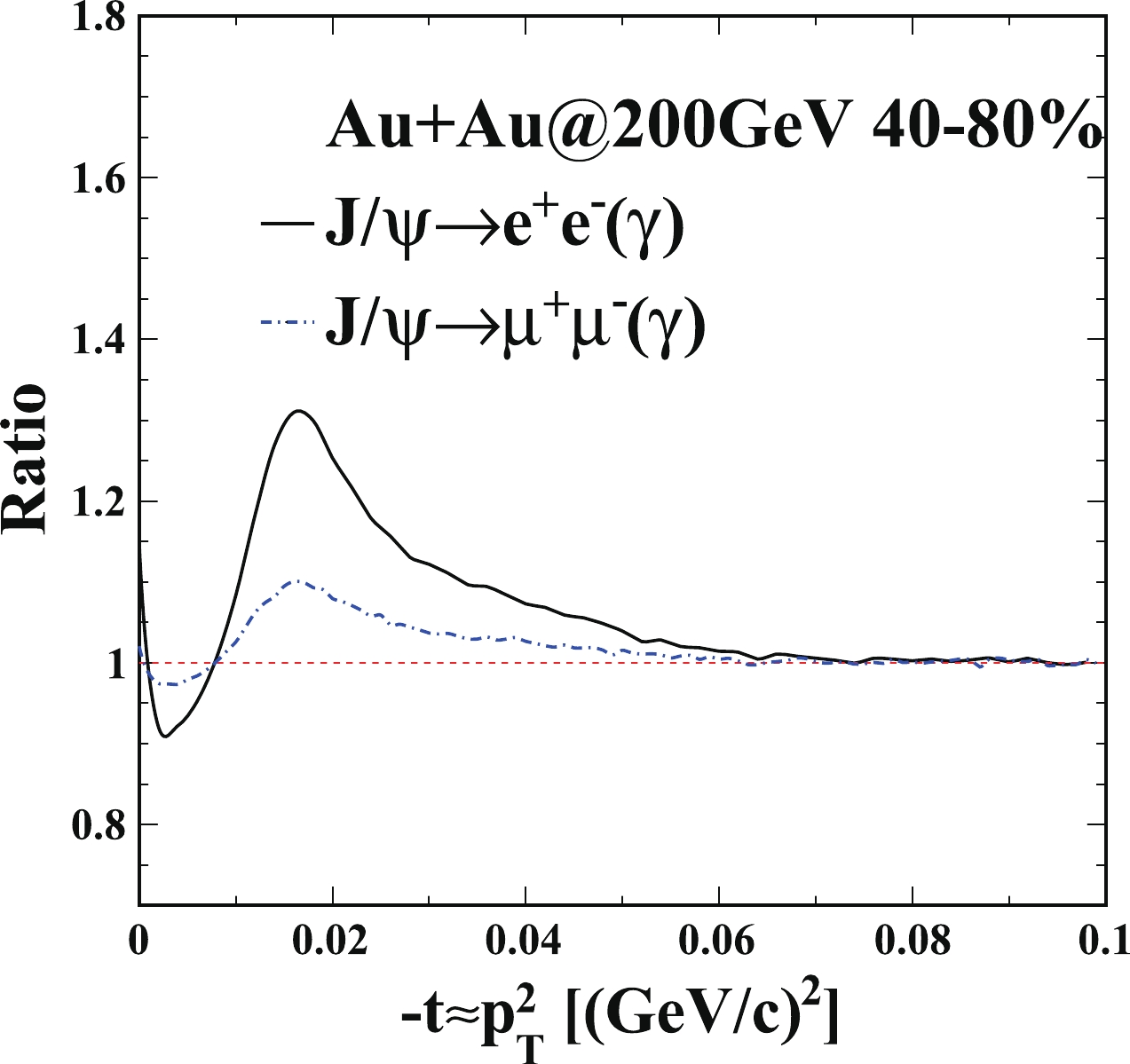
Figure 3. (color online) Ratio of the calculation for photoproduced
$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ in Au+Au 40%–80% with the photon radiation effect over that without the photon radiation effect from the dielectron (solid) and dimuon decay (dash-dotted) channels, respectively.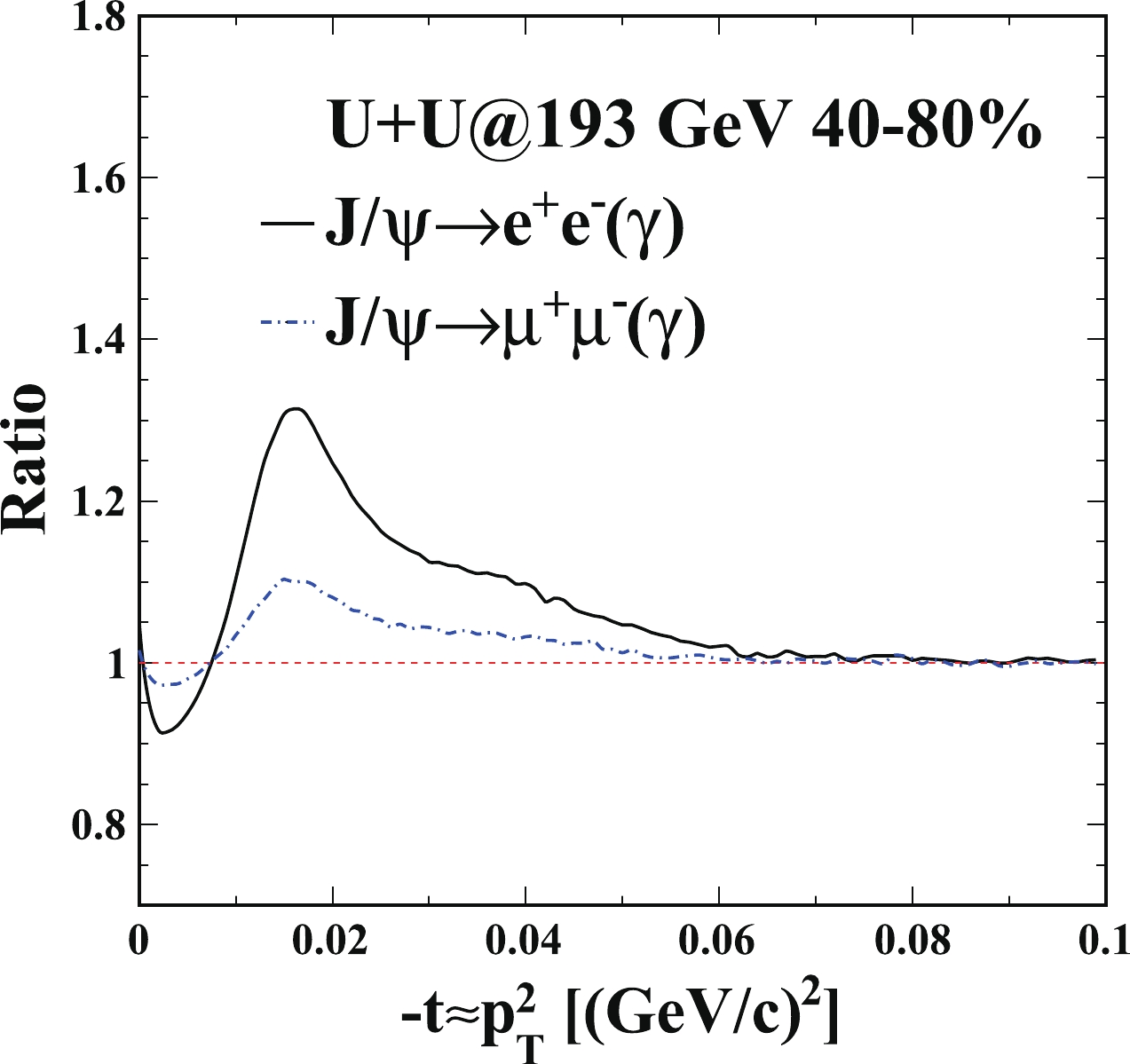
Figure 4. (color online) Ratio of the calculation for photoproduced
$ J/\psi $ ${\rm d}^2N/{\rm d}t{\rm d}y$ in 40%–80$ \% $ U+U collisions at 193 GeV with the photon radiation effect over that without the photon radiation effect from the dielectron (solid) and dimuon decay (dash-dotted) channels, respectively. -
In summary, we explored photoproduction in heavy-ion collisions and the effect of soft radiation on this interaction. The calculations of coherent and incoherent photoproduction in HHICs describe the experimental data from STAR reasonably well. The soft radiation effects in both the dielectron and dimuon decay channels are also taken into account on top of photoproduction. The cross section of photoproduced
$ J/\psi $ decreases about 10% at$ -t\approx0.04 $ (GeV/c)2 and increases toward high$ -t $ . The calculations also show that measurements via the dimuon channel are less affected by internal radiation than those from the dielectron decay channel. Meanwhile, leptons, especially electrons, also lose their energies through Bremsstrahlung radiation in the detector material, which has a similar effect on the reconstructed$ J/\psi $ signals and should be taken into consideration in the measurements as well.
Calculations of differential momentum transfer spectra for J/ψ photoproduction in heavy-ion collisions
- Received Date: 2021-12-30
- Available Online: 2022-07-15
Abstract: Understanding the gluonic structure in nuclei is one of the most important goals in modern nuclear physics, for which J/ψ photoproduction is suggested as a powerful tool to probe the gluon density distribution. The experimental investigation of the photoproduction process is conventionally studied in ultra-peripheral heavy-ion collisions, and has recently been extended to hadronic collisions. However, theoretical efforts in hadronic heavy-ion collisions are still lacking in the literature. In this paper, we build up a phenomenological framework to calculate the differential momentum transfer spectra for J/ψ photoproduction in hadronic heavy-ion collisions based on a vector meson dominance model. For the first time, we include the effect of internal photon radiation in the calculations, and we find that the results with internal photon radiation could describe the experimental measurements from STAR very well.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: