-
Fast radio bursts (FRBs) are short-duration and luminous radio transients occurring in the Universe; see, e.g., Refs. [1–4] for a recent review. In 2007, Lorimer et al. [5] reanalyzed the archive data of the Parkes 64 m telescope recorded in 2001 and found an extraordinary radio pulse, which is now named FRB 010724. This phenomenon did not attract much attention for a long time, until four other bursts were discovered several years later [6]. Thereafter, FRBs have attracted great interest within the astronomy community. The observed dispersion measures (DM) of most FRBs significantly exceed the contribution from the Milky Way, hinting that they occur at a cosmological distance. Their cosmological origin was further confirmed by identification of the host galaxy and direct measurements of redshifts [7–9]. There are, in general, two kinds of FRBs, i.e., the repeaters and non-repeaters. Most of the repeating sources found by the Canadian Hydrogen Intensity Mapping Experiment (CHIME) telescope were only repeated two or three times for each source [10]. There is one exception, FRB 121102, from which thousands of bursts have been observed by different telescopes [11–16]. Statistical analysis of FRB 121102 shows that the burst energies and waiting times follow the power-law distribution [17–19], hinting that the explosion of repeating FRBs may be a self-organized criticality process. Further analysis shows that the bursts of FRB 121102 can be more well fitted by the bent power-law and are scale-invariant [20], implying that there are some similarities between FRBs and soft gamma repeaters (SGRs) [21, 22]. As the FAST telescope detected extensively increased bursts from FRB 121102, a bimodal burst energy distribution was found [15]. Repeating FRBs usually have no regular period, but the CHIME/FRB Collaboration [23] found an unexpectedly long period of 16.35 days with an approximately 4-day active window for FRB 180916. J0158+65. The physical mechanism of FRBs is still under extensive debate. Several theoretical models have been proposed to explain the explosion of FRBs [24–32]. The most popular models involve one or two compact objects such as a neutron star and a magnetar in the center of the FRB source. The recently discovered burst FRB200428, which was associated with a Galactic magnetar, strongly supports the magnetar origin of at least some FRBs [33, 34].
FRBs are very luminous and they are expected to remain detectable in the most ideal case up to a redshift of
$ z\sim 15 $ for sensitive radio telescopes, such as the Five-hundred-meter Aperture Spherical radio Telescope [35]. Therefore, FRBs could be used as probes to study high-redshift cosmology. For example, Munoz et al. [36] pointed out that strongly lensed FRBs can be used to probe the compact dark matter in the Universe. Yu & Wang [37] showed that FRBs can be used to measure the cosmic proper distance. Li et al. [38] proposed that strongly lensed repeating FRBs can tightly constrain the Hubble constant and cosmic curvature. Walters et al. [39] showed that FRBs can be used to constrain the baryon matter density. Li et al. [40, 41] showed that FRBs can be used to constrain the fraction of baryon mass in the intergalactic medium (IGM). Xu & Zhang [42] proposed that FRBs can be used to probe the intergalactic turbulence. Wu et al. [43] proposed that FRBs can be used to measure the Hubble parameter model-independently. Qiang et al. [44] showed that FRBs can be used to test the possible cosmic anisotropy. Pagano & Fronenberg [45] pointed out that highly dispersed FRBs can be used to constrain the epoch of cosmic reionization. Pearson et al. [46] showed that strongly lensed repeating FRBs can be used as probes in searching for gravitational waves. In addition, FRBs can be used as probes for testing fundamental physics, such as constraining the Lorentz invariance violation, the weak equivalent principle and the photon mass [47–51].The applications of FRBs as probes for investigating the Universe often involve observation of the dispersion measure (DM, see next section for details), which depends on the electron distribution along the line of sight. The total DM of an extragalactic FRB consists of four parts: the Milky Way interstellar medium (ISM), the Milky Way halo, the IGM and the host galaxy. The electron distribution in the Milky Way ISM has been modelled from pulsar observations, for example, the TC93 model [52], NE2001 model [53], YMW16 model [54], and so on. The DM of the Milky Way halo can be reasonably estimated [55]. Therefore, the DM contributed by the Milky Way can be subtracted from the total DM. The IGM contribution is proportional to the electron density in IGM, which depends on the density and ionization rate of baryon matter in IGM. It is this part that contains information on the Universe and can be used to investigate the cosmology. The difficulty is that the host galaxy contribution to DM is hard to model. This is because, although there are some observations [56–58], we still have poor knowledge of the local environment of the majority of FRBs. Several factors may affect the DM of a host galaxy, such as the galaxy type, the inclination angle of the host galaxy, the mass of the host galaxy, the star-formation rate, the offset of the FRB site from the galactic center, just to name a few. FRBs have been observed in different types of galaxies, and there is no unique way to model the DM of the host galaxy. For example, Xu & Han [59] modelled the DM of the host galaxy by assuming that the host galaxies are similar to the Milky Way or M31. Luo et al. [60] assumed that the distribution of DM of the host galaxy follows the star-formation rate (SFR). Because there is a lack of direct DM measurements of host galaxies, reasonably extracting them from observation is of great importance. Yang & Zhang [61] pointed out that the average DM of a host galaxy can be obtained statistically from a large sample of FRBs with redshift measurements. However, this method requires the reconstruction of the first order derivative curves from discrete data points, which will introduce a large uncertainty.
Up to now, hundreds of FRBs have been reported [62, 63]. However, there are only 19 well-localized FRBs (except for the Galactic FRB200428) with directly identified host galaxies①. All of these 19 well-localized FRBs have a direct measurement of the redshift associated (either spectroscopic redshift or photometric redshift), which falls in the redshift range
$ z\in(0.0039,0.66) $ . The properties of the host galaxies, such as the stellar mass, age of galaxy, SFR, and half-light radius, have been observed in detail by follow-up observations. In this study, based on these well-localized FRBs, we investigate the DM of a host galaxy statistically. The rest of this paper is arranged as follows. In Sec. II, we search for the possible correlations between$DM_{\rm host} $ and the host galaxy properties. In Sec. III, assuming a constant value of$ DM_{\rm host} $ , we use well-localized FRBs to constrain the fraction of baryon mass in IGM. Finally, discussions and conclusions are given in Sec. IV. -
The propagation of electromagnetic waves in cold plasma leads to a frequency-dependent group velocity of light. Therefore, photons with different energies travelling over the same distance need different amounts of time. This plasma effect, although it is tiny, is detectable if accumulated over cosmological distances. The time delay between low- and high-energy photons propagating from a distant source to earth is proportional to a quantity called the dispersion measure (DM), which is the integral of the electron density along the photon path [64]. The plasma effect is negligible for visible light, but it is important for radio waves in, e.g., FRBs. The DM of an FRB can be obtained from a time-resolved spectrum. The observed DM of an extragalactic FRB consists of three parts: contributions from the Milky Way, intergalactic medium (IGM), and host galaxy [65, 66],
$ \begin{equation} DM_{\rm obs}= DM_{\rm MW}+ DM_{\rm IGM}+\frac{ DM_{\rm host}}{1+z}, \end{equation} $

(1) where
$DM_{\rm host}$ is the DM of the host galaxy in the source frame, z is the redshift of the host galaxy, and the factor$ 1+z $ accounts for cosmic dilation.The DM of the Milky Way can be divided into two components: contributions from the Milky Way interstellar medium (ISM) and Milky Way halo [55],
$ \begin{equation} DM_{MW}= DM_{\rm MW,\,ISM}+ DM_{\rm MW,\,halo}. \end{equation} $

(2) Given the sky position of an FRB,
$DM_{\rm MW,ISM}$ can be well constrained by modelling the electron distribution in the Milky Way ISM from pulsar observations, such as the NE2001 model [53] and the YMW16 model [54]. The Milky Way halo contribution is not well constrained yet, but it is expected to be in the range$ 50-100\; {\rm pc\; cm^{-3}} $ [55].The DM of IGM, assuming that both hydrogen and helium are fully ionized, can be written as [65, 67]
$ \begin{equation} { \overline{DM}_{\rm IGM}}(z)=\frac{21cH_0\Omega_b}{64\pi Gm_p}\int_0^z\frac{f_{\rm IGM}(z)(1+z)}{\sqrt{\Omega_m(1+z)^3+\Omega_\Lambda}}{\rm d}z, \end{equation} $

(3) where
$ m_p $ is the proton mass,$ f_{\rm IGM}(z) $ is the fraction of the baryon mass in IGM,$ H_0 $ is the Hubble constant, G is the Newtonian gravitational constant,$ \Omega_b $ is the normalized baryon matter density, and$ \Omega_m $ and$ \Omega_\Lambda $ are the normalized densities of matter (includes baryon matter and dark matter) and dark energy at present day, respectively. Note that Eq. (3) should be interpreted as the mean contribution from IGM. The actual value would deviate from Eq. (3) due to, e.g., fluctuations in baryon matter, an incomplete ionization of hydrogen or helium, etc.The DM of the host galaxy is difficult to model due to a lack of observations on the local environments of the FRB sources. However, given that the DM of the Milky Way is modeled, and the DM of IGM is predicted by a specific cosmological model, we can invert Eq. (1) to obtain the DM of the host galaxy,
$ \begin{equation} { DM_{\rm host}}=(1+z)({DM_{\rm obs}}-{DM_{\rm MW}}-{ DM_{\rm IGM}}). \end{equation} $

(4) The uncertainties of
$ DM_{\rm host} $ can be calculated using the standard error propagation formula,$ \begin{equation} \sigma_{\rm host}=(1+z)\sqrt{(\sigma_{\rm obs}^2+\sigma_{\rm MW}^2+\sigma_{\rm IGM}^2)}, \end{equation} $

(5) where the uncertainty on
$ DM_{\rm MW} $ is propagated from the uncertainties on$ DM_{\rm MW,\,ISM} $ and$ DM_{\rm MW,halo} $ ,$ \begin{equation} \sigma_{\rm MW}=\sqrt{\sigma_{\rm MW,ISM}^2+\sigma_{\rm MW,halo}^2}. \end{equation} $

(6) Note that the DM contribution from the host galaxy also consists of ISM and halo parts. Without other observations, these two parts are completely degenerated. Therefore, we do not distinguish them and treat them as one factor.
So far, there are in total 19 extragalactic FRBs that are well localized and have an identified host ②. From among these 19 FRBs, we omit FRB20200120E and FRB20190614D. The repeating burst FRB20200120E is localized in the direction of M81, and its redshift is measured to be
$ -0.0001 $ [68]. This burst is very close to the Milky Way, and its peculiar velocity dominates over the Hubble flow, so it is inappropriate to use it in the study of cosmology. The non-repeating burst FRB20190614D has a photometric redshift$ z\approx 0.6 $ [69], but there is a lack of detailed observations on the host galaxy. Therefore, we only consider the remaining 17 FRBs, whose properties are listed in Table 1. From among these 17 FRBs, 6 bursts are repeating and 11 bursts are non-repeating. All FRBs have a well-measured sky position (RA, Dec), an observed dispersion measure ($DM_{\rm obs}$ ), the spectroscopic redshift (z), the stellar mass of the host galaxy ($ M_{\star} $ ), the star formation rate (SFR), the mass-weighted age of the host galaxy (Age), the offset of FRB site from the galactic center (Offset), and the half-light radius of the host galaxy ($ R_{\rm eff} $ ). We calculate the DM of the Milky Way ISM using two different models, i.e., the NE2001 model and YMW16 model, and list the results in the fifth and sixth columns of Table 1, respectively.FRBs RA/
($ ^{\circ} $ )

Dec/
($ ^{\circ} $ )

$ DM_{\rm obs}/ $ 

($ {\rm pc\; cm^{-3}} $ )

NE2001/
($ {\rm pc\; cm^{-3}} $ )

YMW16/
($ {\rm pc\; cm^{-3}} $ )

z $ M_{\star}/ $ 

($ 10^9M_{\odot} $ )

SFR/
($ M_{\odot}/{\rm yr} $ )

Age/
MyrOffset/
kpc$ R_{\rm eff}/ $ 

kpcrepeat? References 20121102A $ 82.99 $ 

$ 33.15 $ 

557.00 157.60 287.62 0.1927 $ 0.14\pm0.07 $ 

$ 0.15\pm0.04 $ 

$ 257.7 $ 

$ 0.8\pm0.1 $ 

$ 2.05\pm0.11 $ 

Yes [8, 9, 11, 58, 70] 20180301A $ 93.23 $ 

$ 4.67 $ 

536.00 136.53 263.16 0.3305 $ 2.30\pm0.60 $ 

$ 1.93\pm0.58 $ 

$ 607.2 $ 

$ 10.8\pm3.0 $ 

$ 5.80\pm0.20 $ 

Yes [71] 20180916B $ 29.50 $ 

$ 65.72 $ 

348.80 168.73 319.42 0.0337 $ 2.15\pm0.33 $ 

$ 0.06\pm0.02 $ 

$ 154.9 $ 

$ 5.5\pm0.0 $ 

$ 3.57\pm0.36 $ 

Yes [56, 58, 72, 73] 20180924B $ 326.11 $ 

$ -40.90 $ 

362.16 41.45 27.28 0.3214 $ 13.20\pm5.10 $ 

$ 0.88\pm0.26 $ 

$ 383.4 $ 

$ 3.4\pm0.8 $ 

$ 2.75\pm0.10 $ 

No [56, 58, 74–76] 20181030A $ 158.60 $ 

$ 73.76 $ 

103.50 40.16 32.72 0.0039 $ 5.80\pm1.80 $ 

$ 0.36\pm0.10 $ 

$ 4800.0 $ 

$ – $ 

$ 2.60\pm0.00 $ 

Yes [77] 20181112A $ 327.35 $ 

$ -52.97 $ 

589.00 41.98 28.65 0.4755 $ 3.98\pm2.02 $ 

$ 0.37\pm0.11 $ 

$ 572.4 $ 

$ 1.7\pm19.2 $ 

$ 7.19\pm1.70 $ 

No [58, 75, 78] 20190102C $ 322.42 $ 

$ -79.48 $ 

364.55 56.22 42.70 0.2913 $ 3.39\pm1.02 $ 

$ 0.86\pm0.26 $ 

$ 55.6 $ 

$ 2.3\pm4.2 $ 

$ 5.00\pm0.15 $ 

No [55, 57, 58, 75, 76] 20190523A $ 207.06 $ 

$ 72.47 $ 

760.80 36.74 29.75 0.6600 $ 61.20\pm40.10 $ 

$ 0.09\pm0.00 $ 

$ 685.9 $ 

$ 27.2\pm22.6 $ 

$ 3.28\pm0.18 $ 

No [58, 79] 20190608B $ 334.02 $ 

$ -7.90 $ 

340.05 37.81 26.44 0.1178 $ 11.60\pm2.80 $ 

$ 0.69\pm0.21 $ 

$ 383.4 $ 

$ 6.5\pm0.8 $ 

$ 7.37\pm0.07 $ 

No [55–58, 75, 76] 20190611B $ 320.74 $ 

$ -79.40 $ 

332.63 56.60 43.04 0.3778 $ 0.75\pm0.53 $ 

$ 0.27\pm0.08 $ 

$ – $ 

$ 11.7\pm5.8 $ 

$ 2.15\pm0.11 $ 

No [55, 58, 76] 20190711A $ 329.42 $ 

$ -80.36 $ 

592.60 55.37 42.06 0.5217 $ 0.81\pm0.29 $ 

$ 0.42\pm0.12 $ 

$ 607.2 $ 

$ 3.2\pm2.1 $ 

$ 2.94\pm0.17 $ 

Yes [55, 57, 58, 76] 20190714A $ 183.98 $ 

$ -13.02 $ 

504.13 38.00 30.94 0.2365 $ 14.20\pm5.50 $ 

$ 0.65\pm0.20 $ 

$ 1593.2 $ 

$ 2.7\pm1.8 $ 

$ 3.94\pm0.05 $ 

No [57, 58] 20191001A $ 323.35 $ 

$ -54.75 $ 

507.90 44.22 30.67 0.2340 $ 46.40\pm18.80 $ 

$ 8.06\pm2.42 $ 

$ 639.7 $ 

$ 11.1\pm0.8 $ 

$ 5.55\pm0.03 $ 

No [57, 58, 80] 20191228A $ 344.43 $ 

$ -29.59 $ 

297.50 33.75 19.67 0.2432 $ 5.40\pm6.00 $ 

$ 0.03\pm0.01 $ 

$ – $ 

$ 5.7\pm3.3 $ 

$ 1.78\pm0.06 $ 

No [71] 20200430A $ 229.71 $ 

$ 12.38 $ 

380.25 27.35 26.33 0.1608 $ 2.10\pm1.10 $ 

$ 0.26\pm0.08 $ 

$ 689.5 $ 

$ 1.7\pm2.2 $ 

$ 1.64\pm0.53 $ 

No [58, 71] 20200906A $ 53.50 $ 

$ -14.08 $ 

577.80 36.19 38.37 0.3688 $ 13.30\pm3.70 $ 

$ 0.48\pm0.14 $ 

$ 1150.7 $ 

$ 5.9\pm2.0 $ 

$ 7.58\pm0.06 $ 

No [71] 20201124A $ 77.01 $ 

$ 26.06 $ 

413.52 126.49 204.74 0.0979 $ 16.00\pm1.00 $ 

$ 2.12\pm0.49 $ 

$ 5000.0 $ 

$ 1.3\pm0.1 $ 

$ – $ 

Yes [81–83] Table 1. Properties of host galaxies of 17 well-localized FRBs.
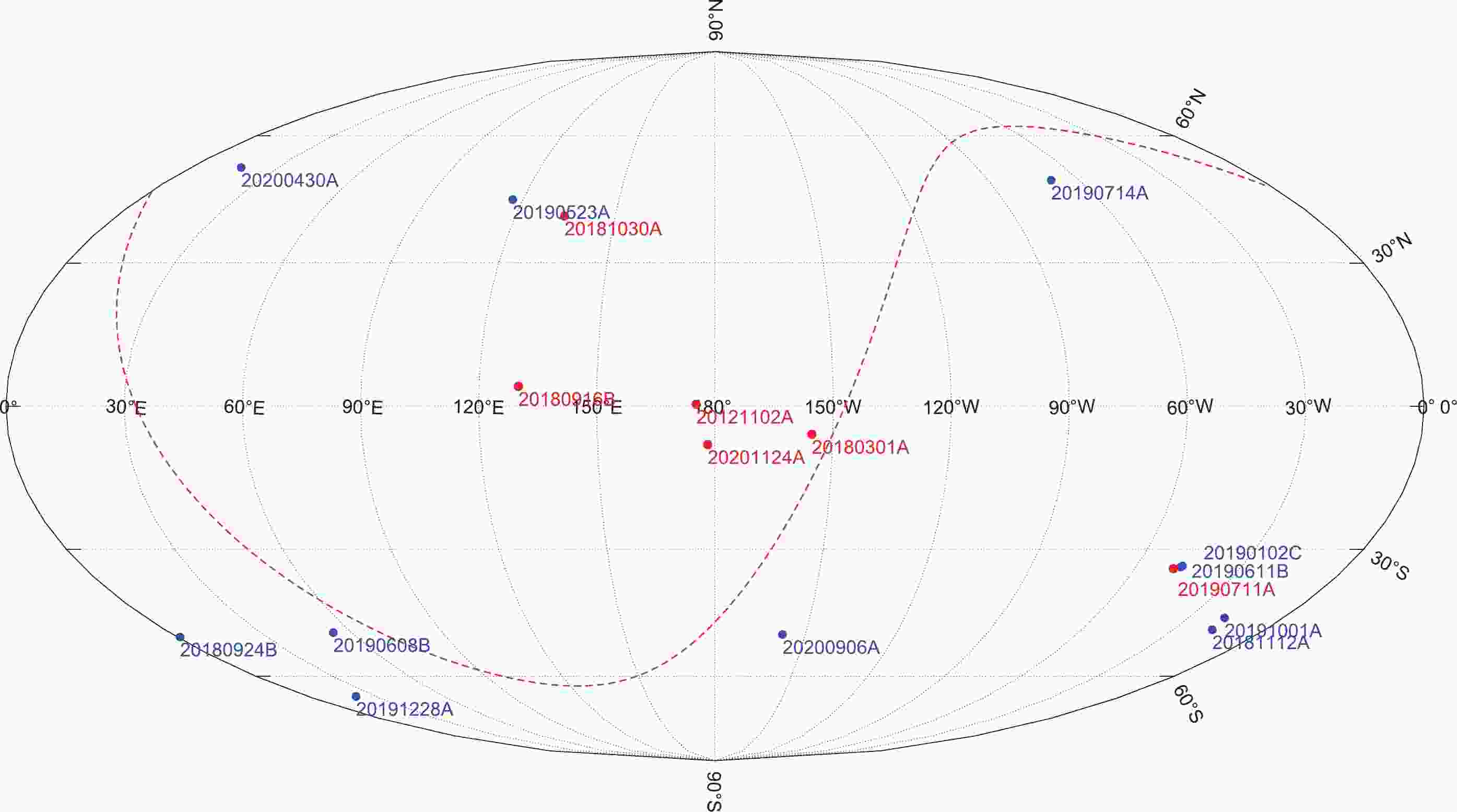
Figure 1 shows the sky positions of the 17 FRBs in Galactic coordinates. The repeaters and non-repeaters are denoted in red and blue dots, respectively. Four repeaters (FRB20121102A, FRB20180301A, FRB20180916B and FRB20201124A) are located at low Galactic latitudes, so the Milky Way ISM contribution to the DM is very large (see Table 1). The other 13 bursts are located at high Galactic latitudes (
$ |b|>30^{\circ} $ ), hence the Milky Way ISM contribution to the DM is relatively small, with mean values of$ \overline{DM}_{\rm MW,ISM}= 42 $ and 32$ {\rm pc\; cm^{-3}} $ for the NE2001 model and YMW16 model, respectively. Three bursts (FRB20190102C, FRB20190611B and FRB20190711A) have a very similar sky orientation; hence, their Milky Way ISM contributions to the DM are similar to each other. We note that$ DM_{\rm MW,ISM} $ strongly depends on the Milky Way electron models, especially for low-latitude FRBs. At a low Galactic latitude, the YMW16 model predicts a much larger value for$ DM_{\rm MW,ISM} $ than the NE2001 model. At a high Galactic latitude, on the contrary, the YMW16 model in general gives a smaller value of$ DM_{\rm MW,ISM} $ than the NE2001 model.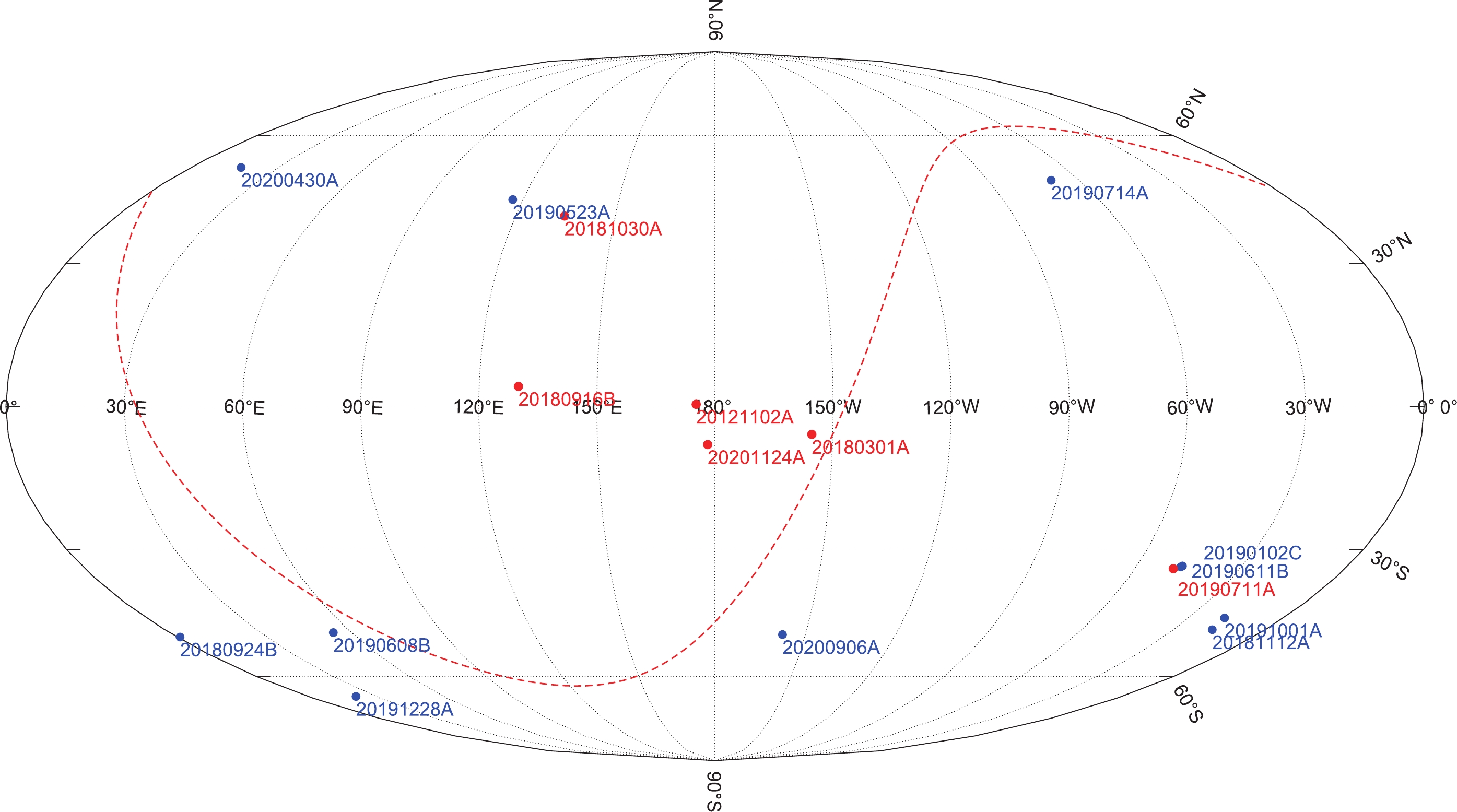
Figure 1. (color online) Sky positions of 17 well-localized FRBs in Galactic coordinates. The repeaters and non-repeaters are denoted in red and blue dots, respectively. The red-dashed line is the Equatorial plane.
We calculate the DM of the host galaxy,
$ DM_{\rm host} $ , by subtracting$ DM_{\rm MW} $ (including the Milky Way ISM and halo contributions) and$ DM_{\rm IGM} $ from the observed$ DM_{\rm obs} $ according to Eq. (4). The$ DM_{\rm IGM} $ term is calculated according to Eq. (3) using the Planck 2018 parameters,$ H_0=67.4 {\rm km\; s^{-1}\; Mpc^{-1}} $ ,$ \Omega_m=0.315 $ ,$ \Omega_\Lambda=0.685 $ and$ \Omega_{b0}=0.0493 $ [84]. The fraction of the baryon mass is assumed to be a constant,$ f_{\rm IGM}=0.84 $ [41, 67]. The uncertainty on$ DM_{\rm host} $ is calculated using Eq. (5). The$ DM_{\rm obs} $ can be tightly constrained by observing the time-resolved spectra of FRBs. According to the FRB catalog [62], the average uncertainty on$DM_{\rm obs} $ is only$ \sim 1.5 $ pc cm$ ^{-3} $ . Both the NE2001 model and the YMW16 model do not provide the uncertainty on$ DM_{\rm MW,ISM} $ . As these two models predict different values for$ DM_{\rm MW,ISM} $ , we take$ \sigma_{\rm MW,ISM} $ as the absolute value of the difference of$ DM_{\rm MW,ISM} $ calculated using these two models. This ensures that the two models give consistent results within$ 1\sigma $ uncertainty. For FRBs at a high Galactic latitude$ (|b|>10^\circ) $ , the value of$ \sigma_{\rm MW,ISM} $ is about 10 pc cm$ ^{-3} $ , while for low-latitude$ (|b|<10^\circ) $ FRBs it is at the order of magnitude 100 pc cm$ ^{-3} $ . The Milky Way halo contribution is assumed to be$ DM_{\rm MW,halo}= 50\; {\rm pc\; cm^{-3}} $ [55], and we add a 50% uncertainty to it. The$ DM_{\rm IGM} $ term has a large uncertainty due to density fluctuations in the large-scale structure [85]. Cosmological simulations show that the uncertainty on$ DM_{\rm IGM} $ increases with the redshift [86]. Here, we use the$ \sigma_{{\rm IGM}}(z) $ relation given in Ref. [40] to calculate the uncertainty.In Fig. 2, we plot the correlations between
$ DM_{\rm host} $ and the properties of the host galaxies. In all subfigures, the vertical axes are$ DM_{\rm host} $ , and the horizonal axes are the redshift, the stellar mass, the SFR, the mass-weighted age, the offset from the galactic center, and the half-light radius, respectively. In Table 2, we list the Spearman's correlation coefficients ρ of six correlations [87]. In general,$ |\rho|<0.3 $ ,$ 0.3<|\rho|<0.7 $ and$ |\rho|>0.7 $ imply that the correlation is weak, moderate and strong, respectively [88]. From Table 2, we see that there is no strong correlation between$ DM_{\rm host} $ and any of the host galaxy parameters, neither in the NE2001 model nor in the YMW16 model. From the upper-left panel of Fig. 2, we note that$DM_{\rm host} $ of the first 8 FRBs at$ z<0.24 $ is strongly linearly correlated with the redshift. The Spearman's correlation coefficients are 1.0 and 0.8 for the NE2001 model and the YMW16 model, respectively. The positive$ DM_{\rm host}-z $ correlation means that high-redshift FRBs generally have a larger host DM than low-redshift FRBs, which may imply that high-redshift galaxies have more diffuse gas than low-redshift galaxies. Due to the small FRB sample and the large uncertainty, it is unclear whether the$ DM_{\rm host}-z $ correlation is intrinsic or not. For high-redshift FRBs ($ z>0.24 $ ), however, the correlation disappears. Therefore, we suspect that the linear$ DM_{\rm host}-z $ correlation at$ z<0.24 $ might have happened by chance. From Table 2, we note that there is a moderate correlation between$ DM_{\rm host} $ and the stellar mass of the host galaxy. The positive$ DM_{\rm host}-M_\star $ correlation implies that a more massive galaxy usually contributes a larger$ DM_{\rm host} $ . This is because more massive galaxies in general contain more diffuse gas. In addition, some other factors, such as the age of the host galaxy may also moderately affect$ DM_{\rm host} $ . A larger FRB sample is required to confirm or falsify the$ DM_{\rm host}-M_\star $ correlation.
Figure 2. (color online) Correlations between
$DM_{\rm host}$ and the properties of the host galaxy. The DM of the Milky Way is calculated using two different electron models, i.e., the NE2001 model (red diamonds) and the YMW16 model (black circles).z $ M_{\star} $ 

SFR Age Offset $ R_{\rm eff} $ 

NE2001 −0.23 0.36 0.18 0.37 −0.17 0.37 YMW16 −0.04 0.54 0.21 0.43 −0.09 0.19 Table 2. Spearman's correlation coefficients between
$ DM_{\rm host} $ and parameters of the host galaxies.The central value of
$ DM_{\rm host} $ of FRB20190611B (galactic latitude$ b=-33.6^{\circ} $ , redshift$ z=0.3778 $ ) is somehow negative in both the NE2001 model and the YMW16 model, which implies that$ DM_{\rm MW,ISM} $ and/or$ DM_{\rm IGM} $ for this burst are/is overestimated. As the$ DM_{\rm MW,ISM} $ values of FRB 190611 calculated from both models are consistent with those of other FRBs located in similar directions (such as FRB20190102C and FRB 20190711A), the most likely possibility is that$ DM_{\rm MW,ISM} $ is accurate while$ DM_{\rm IGM} $ is overestimated. The overestimation of$ DM_{\rm IGM} $ may be caused by matter fluctuation. For FRB20180301A ($ b=-5.8^{\circ} $ ,$ z=0.3305 $ ) and FRB20180916B ($ b=4.0^{\circ} $ ,$ z=0.0337 $ ), the central values of$ DM_{\rm host} $ calculated from the YMW16 model are negative. This is because the YMW16 model may overestimate the Milky Way ISM contribution at a low Galactic latitude [ 89]. Excluding the unphysical negative values, the mean and standard deviation of$ DM_{\rm host} $ are$ ( \overline{DM}_{\rm host},\sigma_ {DM_{\rm host}})=(131.6, 92.0)\; {\rm pc\; cm}^{-3} $ for NE2001 model, and$ ( \overline{DM}_{\rm host},\sigma_{ DM_{\rm host}})=(120.1, 96.3) {\rm pc\; cm}^{-3} $ for the YMW16 model. -
The DM of IGM in Eq. (3) contains information on cosmology, which can be used to study the Universe. In this section, we use well-localized FRBs to constrain the fraction of the baryon mass in IGM, i.e., the parameter
$ f_{\rm IGM}(z) $ . To test if$ f_{\rm IGM} $ is redshift-dependent or not, we follow Li et al. [40] and parameterize it as a slowly evolving function of the redshift,$ \begin{equation} f_{\rm IGM}=f_{\rm IGM,0}\left(1+\frac{\alpha z}{1+z}\right), \end{equation} $

(7) where
$ f_{\rm IGM,0} $ is the fraction of the baryon mass in the IGM at the present day, and α is a constant.In the previous section, we have shown that there is no strong correlation between
$ DM_{\rm host} $ and any of the host galaxy parameters. Therefore, there is no reason to parameterize$ DM_{\rm host} $ as a function of one or some of the host galaxy parameters. The simplest and most straightforward assumption is that$ DM_{\rm host} $ is a constant. We introduce an uncertainty term$ \sigma_{ DM_{\rm host}} $ to account for possible deviations from the constant. The value of$ \sigma_{ DM_{\rm host}} $ is fixed to be the standard deviation of$ DM_{\rm host} $ , obtained in the previous section, i.e.,$ \sigma_{ DM_{\rm host}}=92.0 $ and 96.3$ {\rm pc\; cm}^{-3} $ in the NE2001 model and YMW16 model, respectively. This choice of$ \sigma_{ DM_{\rm host}} $ , rather than the value calculated from Eq. (5), avoids the double bias caused by the large uncertainty of$ DM_{\rm IGM} $ .By fitting the observed DM to the theoretical prediction, the cosmological parameters can be constrained. The likelihood function is given by
$ \begin{equation} \mathcal{L}({\rm Data}|{\mathit{\boldsymbol{\theta}}})=\prod\limits_{i=1}^N\frac{1}{\sqrt{2\pi}\sigma_{\rm total}}\exp\left(-\frac{1}{2}\chi^2\right), \end{equation} $

(8) where
$ \mathit{\boldsymbol{\theta}} $ is the set of free parameters and 'Data' represents the FRB sample, and$ \begin{equation} \chi^2=\frac{[ DM_{\rm obs}- DM_{\rm MW}- DM_{\rm IGM}-{ DM_{\rm host}/(1+z)}]^2}{\sigma_{\rm total}^2}, \end{equation} $

(9) where
$ DM_{\rm IGM} $ is calculated from Eq. (3), and the total uncertainty is given by [40]$ \begin{equation} \sigma_{\rm total}=\sqrt{\sigma_{\rm obs}^2+\sigma_{\rm MW}^2+\sigma_{\rm IGM}^2+\sigma_{ DM_{\rm host}}^2/(1+z)^2}. \end{equation} $

(10) The posterior probability density functions (PDFs) of the parameters are given by
$ \begin{equation} P({\mathit{\boldsymbol{\theta}}}|{\rm Data})\propto \mathcal{L}({\rm Data}|{\mathit{\boldsymbol{\theta}}})P_0({\boldsymbol\theta}), \end{equation} $

(11) where
$ P_0({\boldsymbol\theta}) $ is the prior of the parameters.We calculate the posterior PDFs of the parameters using the publicly available python package
$\textsf{emcee}$ ③ [90]. Note that$ f_{\rm IGM,0} $ is completely degenerated with the Hubble constant$ H_0 $ and the baryon density$ \Omega_{b} $ , hence we fix the latter two parameters to the Planck 2018 values, i.e.,$ H_0=67.4\; {\rm km\; s^{-1}\; Mpc^{-1}} $ and$ \Omega_{b}=0.0493 $ [84]. In addition,$ \Omega_m $ and$ \Omega_\Lambda $ depict the background Universe and they have been tightly constrained by the Planck data. Therefore, we also fix them to the Planck 2018 values, namely,$ \Omega_m=0.315 $ and$ \Omega_\Lambda=0.685 $ [84]. This leaves three free parameters$ (f_{\rm IGM,0},\alpha, DM_{\rm host}) $ . We use a flat prior on all free parameters:$ f_{\rm IGM,0}\in \mathcal{U}(0,1) $ ,$ \alpha\in \mathcal{U}(-2,2) $ and$ DM_{\rm host}\in \mathcal{U}(0,300)\; {\rm pc\; cm^{-3}} $ .The best-fitting parameters (
$ f_{\rm IGM,0}, \alpha, DM_{\rm host} $ ) are listed in Table 3, and the marginalized posterior PDFs and Fig. 3. FRBs with negative$ DM_{\rm host} $ values are excluded from the fitting. For the NE2001 model, we obtain$ f_{\rm IGM,0}= 0.78_{-0.19}^{+0.15} $ ,$ \alpha=0.20_{-1.14}^{+1.15} $ and$ DM_{\rm host}=141.3_{-55.8}^{+59.8} {\rm pc\; cm^{-3}} $ , where the uncertainties are given with a$ 1\sigma $ confidence level. For the YMW16 model, we obtain$ f_{\rm IGM,0}=0.78_{-0.19}^{+0.15}, $ $ \alpha= 0.29_{-1.18}^{+1.10} $ and$ DM_{\rm host}=135.8_{-60.4}^{+65.6}\; {\rm pc\; cm^{-3}} $ . In both models,$ f_{\rm IGM,0} $ and$ DM_{\rm host} $ can be tightly constrained. Although the constraint on α is loose, the best-fitting α prefers a positive value, which is consistent with the requirement that$ f_{\rm IGM} $ mildly increases with the redshift [40, 86]. The two Milky Way electron models give very consistent results within$ 1\sigma $ uncertainty, which is because high-latitude FRBs have much larger weights than low-latitude FRBs in the fitting, while both models give consistent$ DM_{\rm MW,ISM} $ values for high-latitude FRBs. Based on the limited number of FRBs and the large uncertainty, there is no evidence for a redshift evolution of the baryon mass fraction in IGM.$ f_{\rm IGM,0} $ 

α $DM_{\rm host} /{\rm pc\, cm^{-3} }$ 

NE2001 $ 0.78_{-0.19}^{+0.15} $ 

$ 0.20_{-1.14}^{+1.15} $ 

$ 141.3_{-55.8}^{+59.8} $ 

YMW16 $ 0.78_{-0.19}^{+0.15} $ 

$ 0.29_{-1.18}^{+1.10} $ 

$ 135.8_{-60.4}^{+65.6} $ 

Table 3. Best-fitting parameters (
$f_{\rm IGM,0}, \alpha, DM_{\rm host}$ ) by assuming a constant$DM_{\rm host}$ .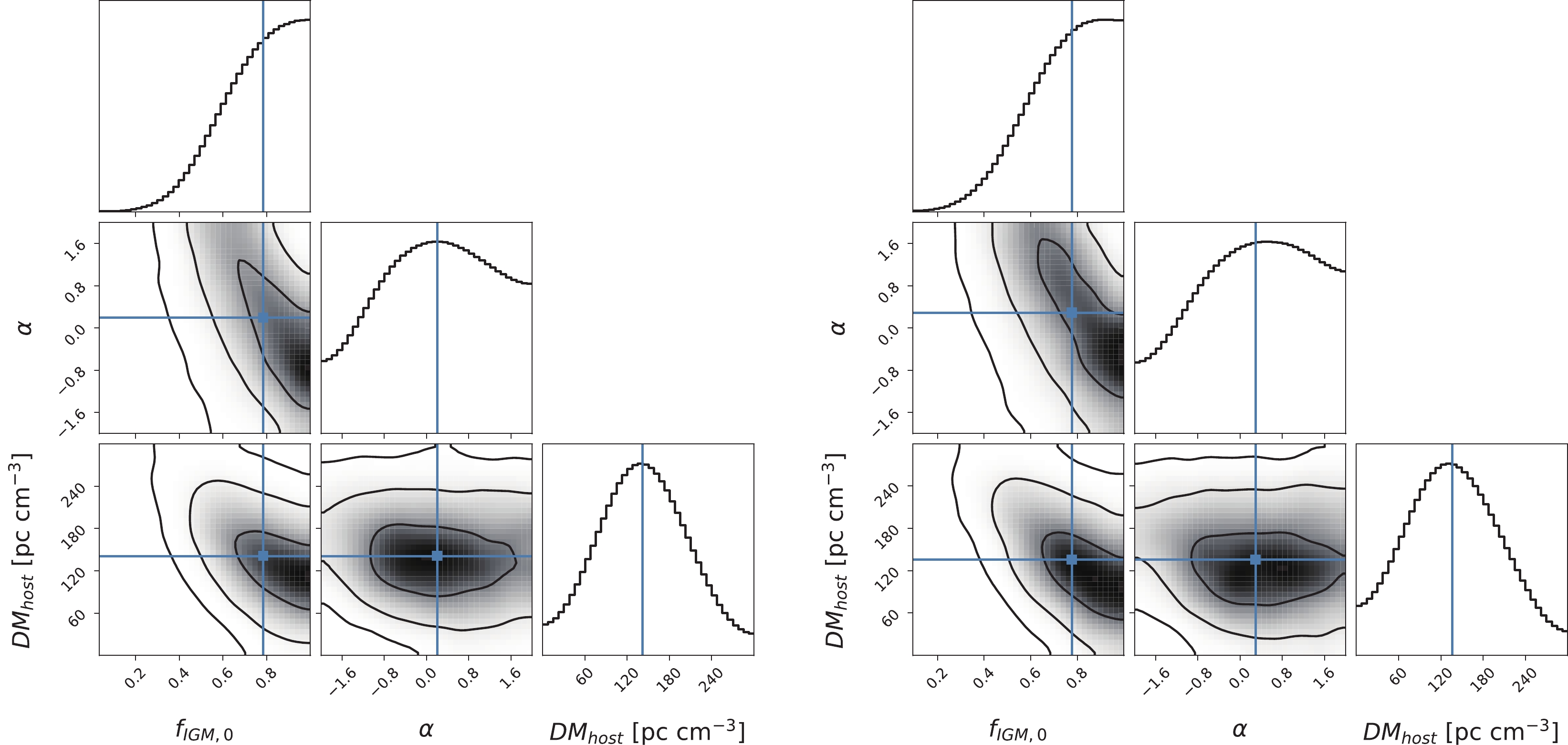
Figure 3. (color online) Posterior PDFs and confidence contours on the free parameters (
$ f_{\rm IGM,0}, \alpha, DM_{\rm host} $ ) when assuming a constant$ DM_{\rm host} $ . (left panel) NE2001 model; (right panel) YMW16 model.In fact,
$ { DM_{\rm host}} $ can vary significantly from burst to burst. Hence, it is not a good approximation to assume a constant$ { DM_{\rm host}} $ . A more reasonable way to deal with$ {DM_{\rm host}} $ is to model it as a probability distribution and marginalize over the free parameters. It is shown that$ { DM_{\rm host}} $ can be fitted with a log-normal distribution based on theory and cosmological simulations [55, 91, 92]. Therefore, instead of assuming a constant$ {DM_{\rm host}} $ , we model it as a log-normal distribution centered at$ { DM_{\rm host}} $ and refit the data. This is equivalent to using a log-normal prior on the parameter$ { DM_{\rm host}} $ in the MCMC fitting. The best-fitting results are listed in Table 4. The marginalized posterior PDFs and 2-dimensional marginalized confidence contours of the parameter space are plotted in Fig. 4. The best-fitting curves to the extragalactic DM$({ DM_E\equiv DM_{\rm obs}-DM_{\rm MW}=DM_{\rm IGM}+DM_{\rm host}}/(1+z))$ for the NE2001 model and the YMW16 model are plotted in the left and right panels of Fig. 5, respectively. Using log-normal prior, we obtain a larger$f_{\rm IGM}$ value (0.83 vs. 0.78) and a smaller$ DM_{\rm host}$ ($\sim 100$ vs.$\sim 140$ pc cm$^{-3}$ ) than those obtained using a flat prior. Using log-normal prior, the best-fitting$f_{\rm IGM}$ is more consistent with the fiducial value (0.84). This confirms that assuming a log-normal distribution for${DM_{\rm host}}$ is more reasonable than assuming a constant value.$ f_{\rm IGM,0} $ 

$ \alpha $ 

$DM_{\rm host} /{\rm (pc\, cm^{-3})}$ 

NE2001 $ 0.83_{-0.17}^{+0.12} $ 

$ 0.36_{-1.13}^{+1.02} $ 

$ 107.7_{-62.9}^{+65.3} $ 

YMW16 $ 0.83_{-0.17}^{+0.12} $ 

$ 0.44_{-1.15}^{+1.00} $ 

$ 94.0_{-59.1}^{+69.0} $ 

Table 4. Best-fitting parameters (
$ f_{\rm IGM,0}, \alpha, DM_{\rm host} $ ) by assuming a log-normal distribution for$ DM_{\rm host} $ .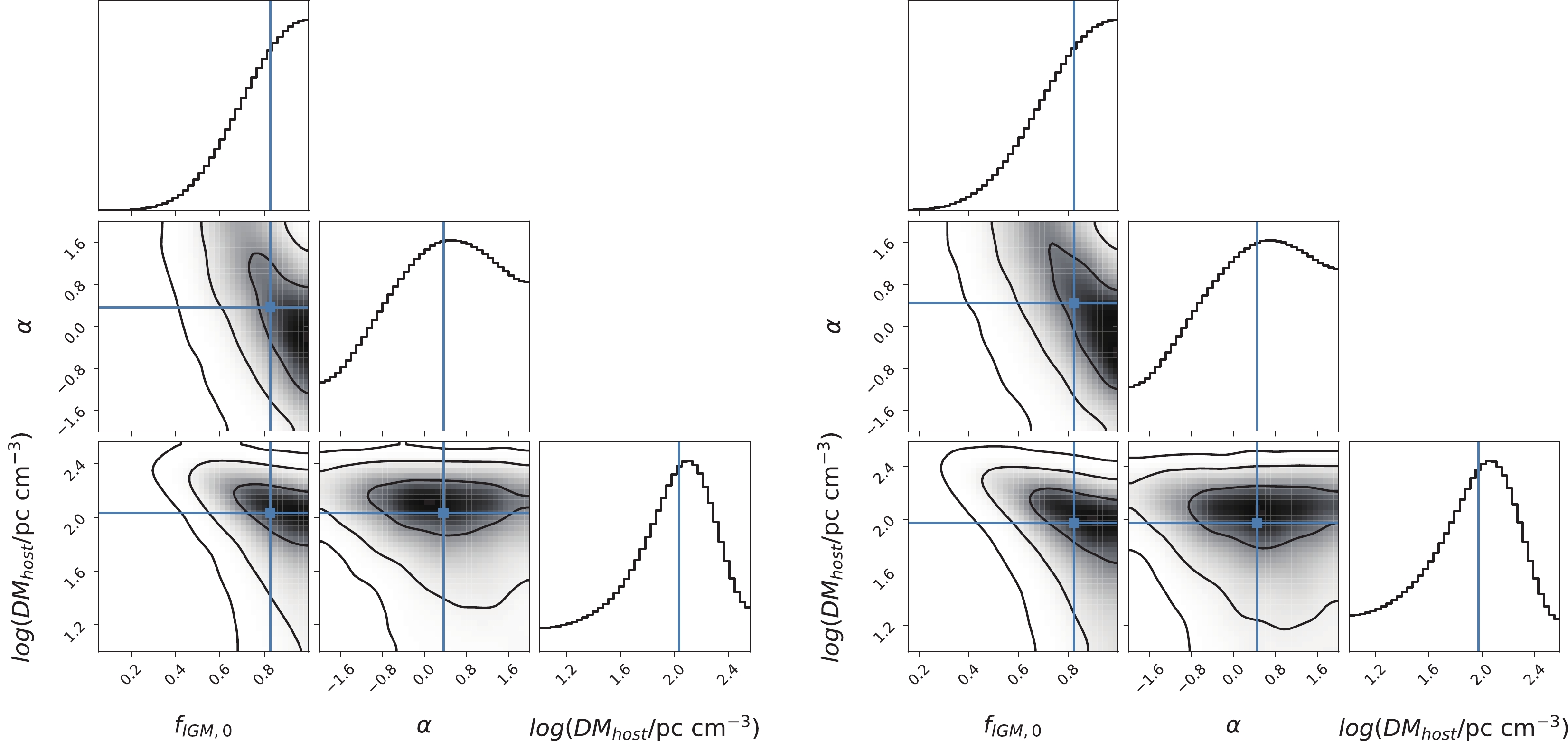
Figure 4. (color online) Posterior PDFs and confidence contours on the free parameters (
$ f_{\rm IGM,0}, \alpha, DM_{\rm host} $ ) by assuming a log-normal distribution for$DM_{\rm host} $ . (left panel) NE2001 model; (right panel) YMW16 model.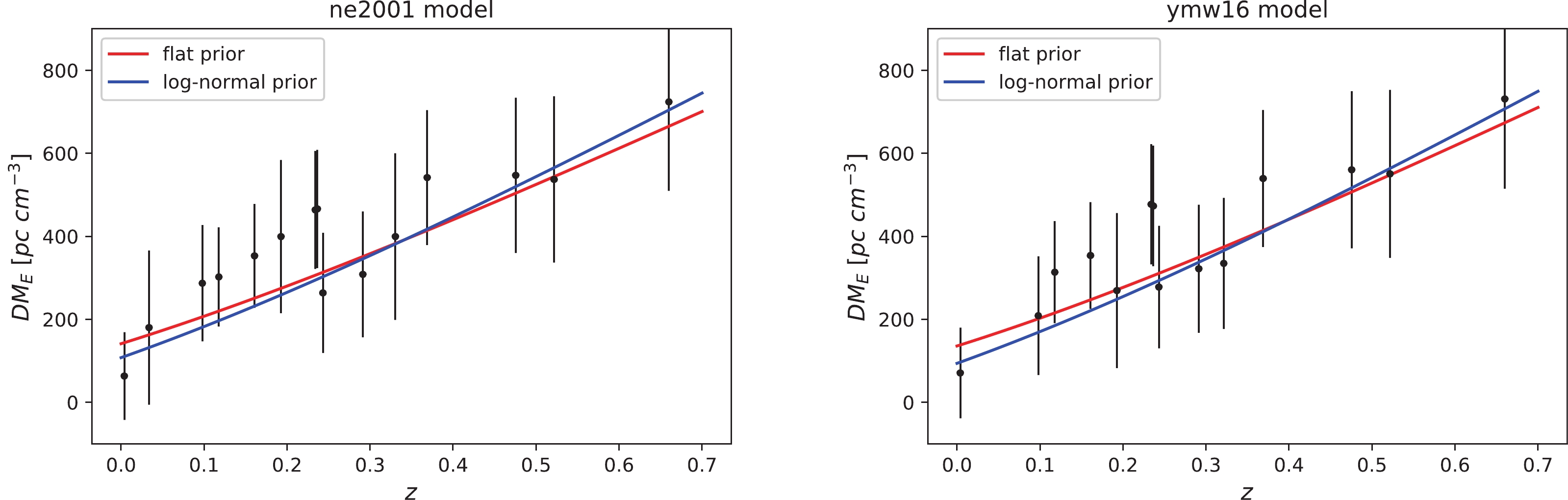
Figure 5. (color online) Best-fitting curves to the extragalactic DM for the NE2001 model (left) and YMW16 model (right). Black dots with
$ 1\sigma $ error bars are the data points, red and blue lines are the best-fitting curves assuming flat prior and log-normal prior for$DM_{\rm host}$ , respectively. -
In this paper, we investigated the host galaxy DM using well-localized FRBs. We tested the possible correlations between
$ DM_{\rm host} $ and six properties of the host galaxies: the redshift, the stellar mass, the star-formation rate, the age of galaxy, the offset of the FRB site from the galactic center, and the half-light radius. We found that there is no strong correlation between$ DM_{\rm host} $ and any of the parameters. Luo et al. [60] pointed out that$ DM_{\rm host} $ is proportional to the square-root of the SFR of the host galaxy. However, we found no correlation between them in the 17 well-localized FRBs. The host of FRB20191001A is an active galaxy, with$ {\rm SFR}=8.06\pm 2.42\; M_\odot\; {\rm yr}^{-1} $ . For the other 16 FRBs, the SFRs of the host galaxies are small ($ {\rm SFR}\lesssim 2\; M_\odot\; {\rm yr}^{-1} $ ). There is a big gap in the SFR range$ 2\sim 8\; M_\odot\; {\rm yr}^{-1} $ . We cannot exclude the possible existence of a correlation between$ DM_{\rm host} $ and SFR if the FRB sample is enlarged in the future.The FRB sample contains host galaxies with very different properties. For example, the galaxy types vary from burst to burst, the stellar masses of the host galaxies span a wide range from
$ 10^8M_\odot $ to$ 10^{11}M_\odot $ , and the galaxy ages range from decades Myr to thousands Myr. As the available FRB sample is very small, we have to combine all FRBs together to study the correlations. When studying the correlation between host DM and other properties (such as$ DM_{\rm host}-z $ correlation), it is better to choose FRBs whose other properties (such as galaxy type, stellar mass, SFR, etc.) are similar. Only in this way can we make a fair comparison. However, due to the small FRB sample, we cannot do this at present. An alternative way is to study the multi-dimensional correlations. But this also requires a large FRB sample. Thus multi-dimensional correlations are not considered here. If the host galaxy is a spiral galaxy, one of the main factors that may affect$ DM_{\rm host} $ is the inclination angle. A edge-on galaxy is expected to contribute a larger value of$ DM_{\rm host} $ than a face-on galaxy. Unfortunately, except for FRB20190608B [58], the other FRBs have no observation on inclination angle.The
$ DM_{\rm host} $ values obtained by subtracting the contributions of MW and IGM from the observed DM have a large uncertainty. The uncertainty for$ DM_{\rm host} $ is dominated by the uncertainty for$ DM_{\rm IGM} $ . For low-latitude FRBs, the$DM_{\rm MW,ISM}$ term also introduces a large uncertainty. Because both Milky Way electron models do not provide the uncertainty of$ DM_{\rm MW,ISM} $ directly, we simply adopt the difference between the$ DM_{\rm MW,ISM} $ values calculated from the two electron models as$ \sigma_{\rm MW,ISM} $ . This is reasonable for high-latitude FRBs, as both electron density models give consistent$ DM_{\rm MW,ISM} $ values. For low-latitude FRBs, however, the YMW16 model gives a much higher value of$ DM_{\rm MW,ISM} $ than the NE2001 model. Koch Ocker et al. [89] pointed out that the YMW16 model may overestimate$ DM_{\rm MW,ISM} $ at a low latitude. With more Galactic plane pulsars discovered by, e.g., the FAST telescope [93],$ DM_{\rm MW,ISM} $ at low latitude is expected to be modeled more accurately in the future. In addition, the FRB source may also contribute a non negligible DM value, thus introducing additional uncertainty. However, without independent observations, the FRB source contribution is indistinguishable from the host galaxy contribution. Therefore, we do not distinguish between them and treat them as one. Unless we can observe the DM of an FRB source directly in the future, this part can be separated and the uncertainty can be reduced. Of course, if we can observe the host DM directly (through, e.g., optical/UV observations) [58], the uncertainty for the$ DM_{\rm host} $ can be further reduced.We assumed a constant value of
$DM_{\rm host} $ for the FRBs and used it to constrain the fraction of baryon mass in IGM. We found no strong evidence for a redshift dependence of$ f_{\rm IGM} $ , and obtained a consistent constraint in both Milky Way electron models, i.e.,$ f_{\rm IGM,0}=0.78_{-0.19}^{+0.15} $ . Our results are consistent with that of Ref. [41], which used a small sample of localized FRBs to constrain the fraction of baryon mass in IGM, and obtained$ f_{\rm IGM,0}= 0.84_{-0.22}^{+0.16} $ from five FRBs, and$ f_{\rm IGM,0}=0.74_{-0.18}^{+0.24} $ from three non-repeating FRBs. The central value we obtained here ($ f_{\rm IGM,0}=0.78 $ ) is somewhat smaller than some previous observations, e.g.,$ f_{\rm IGM,0}\approx 0.83 $ [94], but they are still consistent within$ 1\sigma $ uncertainty. One reason why we obtain a smaller$ f_{\rm IGM,0} $ value may be that the posterior probability density function of$ f_{\rm IGM,0} $ is non-symmetric (see Fig. 3). From the posterior probability density function, we can see that the probability of$ f_{\rm IGM,0} $ being smaller than 0.78 is suppressed. The best fitting values of$ DM_{\rm host} $ we obtained are$ 141.3_{-55.8}^{+59.8} $ and$ 135.8_{-60.4}^{+65.6}\; {\rm pc\; cm^{-3}} $ for the NE2001 and YMW16 models, respectively. These values are consistent with Ref. [55], which obtained a range of$ DM_{\rm host}\in (20,200)\; {\rm pc\; cm^{-3}} $ for non-repeating FRBs. They are also consistent with the host DM of FRB20190608B obtained from optical/UV observations, i.e.,$ 137\pm 43 {\rm pc\; cm^{-3}} $ [58]. If we model$ DM_{\rm host} $ as a log-normal distribution instead of a constant, we obtained$ f_{\rm IGM,0}= 0.83_{-0.17}^{+0.12} $ , which is well consistent with the fiducial value. In this case, we obtained a smaller average$ DM_{\rm host} $ value in both Milky Way electron models, i.e.,$ DM_{\rm host}\sim 100 {\rm pc\; cm^{-3}} $ .From Eq. (3), we know that
$ f_{\rm IGM} $ and$ H_0 $ are completely degenerated, namely$ f_{\rm IGM} $ is inversely proportional to$ H_0 $ . Therefore, a larger$ H_0 $ value will lead to a smaller$ f_{\rm IGM} $ value. The$ H_0 $ value measured from local data ($ H_0=73.48\; {\rm km\; s^{-1}\; Mpc^{-1}} $ ) [95] is in tension with the Planck value ($ H_0=73.48\; {\rm km\; s^{-1}\; Mpc^{-1}} $ ) [84] at more than$ 3\sigma $ . If we use the local$ H_0 $ value, we obtain$ f_{\rm IGM,0}= 0.76_{-0.16}^{+0.11} $ , compared with$ f_{\rm IGM,0}=0.83_{-0.17}^{+0.12} $ obtained when the Planck value is used. We see that$ f_{\rm IGM,0} $ is sensitive to the$ H_0 $ value. A biased$ H_0 $ will lead to a biased estimation of$ f_{\rm IGM,0} $ . Therefore, an accurate$ H_0 $ value is required in order to accurately constrain$ f_{\rm IGM,0} $ .
Search for correlations between host properties and DMhost of fast radio bursts: constraints on the baryon mass fraction in IGM
- Received Date: 2022-01-31
- Available Online: 2022-07-15
Abstract: The application of fast radio bursts (FRBs) as probes for investigating astrophysics and cosmology requires proper modelling of the dispersion measures of the Milky Way (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: