-
The strong CP problem is a long standing puzzle in the Standard Model (SM), with a small value of
$ \bar{\theta} \lesssim 10^{-10} $ . Introducing additional spontaneously broken$ U(1) $ symmetry, which is also broken by an anomaly at the quantum level, can elegantly solve the strong CP problem [1, 2]. This mechanism predicts a light pseudo Nambu-Goldstone boson known as a quantum chromodynamics (QCD) axion [3, 4]. This axion is also a suitable candidate of cold dark matter. In the early universe, these particles were nonthermally produced via the misalignment mechanism or the decays of topological defects [5−9].The interactions between the axion and SM particles, such as photons, leptons, and nucleons, can be described by the effective operators. In QCD axion models, the axion mass and its couplings to the SM particles are related. From the experimental perspective, the search for a more general parameter space is well motivated. The corresponding particles have similar effective interactions as the QCD axion but do not require the solving of the strong CP problem. Such particles are known as axion-like particles (ALPs), the search for which is also well motivated within several new physics models beyond the SM, such as the string models [10−12].
ALPs have long been searched for in numerous laboratory and astrophysical experiments. If the ALP has a coupling to photons, the ALP and free photon may convert into each other in the external magnetic field [13]. The astrophysical magnetic fields on a large scale would induce a detectable ALP-photon oscillation effect. For an astrophysical source at a large distance, this effect would modify the measured photon spectrum [14, 15]. In literature, many studies have been performed to investigate this effect based on the observations of different sources [14−51]. However, because no ALP effect has been found, these analyses set limits on the ALP mass
$ m_a $ and ALP-photon coupling$ g_{a\gamma} $ parameter space.The ALP implication of the high energy γ-ray spectra of the blazars PKS 2155
$ - $ 304 and PG 1553+113, which are measured by H.E.S.S. and the Fermi Large Area Telescope (Fermi-LAT) [52] during the common operation time, is investigated in Ref. [43]. The ALP-photon conversion in the turbulent inter-cluster magnetic field$\sim {\cal{O}}(1)$ μG is considered. The ALP-photon conversion in the blazar jet magnetic field (BJMF) of Markarian 421 (Mrk 421) is explored in Ref. [45]. The Astrophysical Radiation with Ground-based Observatory at YangBaJing (ARGO-YBJ) and the Fermi-LAT results covering 10 phases of Mrk 421 [53] are combined to set the constraint on the ALP parameter space. Compared with the constraint derived from the individual phase, the combined constraint is significantly improved.In this study, we use the very high energy (VHE) γ-ray spectra of Mrk 421 and PG 1553+113 measured by the Major Atmospheric Gamma Imaging Cherenkov Telescopes (MAGIC) [54] to investigate the ALP-photon oscillation effect. In contrast to Ref. [43], we study the ALP-photon conversion in the BJMF of PG 1553+113 via analyses. Compared with the VHE measurements used in previous studies [43, 45], the MAGIC measurements cover more phases (15 phases for Mrk 421 and five phases for PG 1553+113) with high precision. Additionally, the γ-ray spectra of the blazars at lower energies (
$ \sim 0.1−100 \; {\rm{GeV}} $ ) can be well constrained by the observation of Fermi-LAT. We attempt to combine these results to search for the ALP-photon oscillation effect and set constraint on the ALP parameter space.This paper is structured as follows. In Sec. II, we briefly introduce the ALP-photon oscillation effect in the VHE astrophysical process and describe the propagation of the ALP-photon system in a blazar jet, extragalactic space, and the Milky Way. In Sec. III, we introduce data fitting and statistical methods for this analysis. In Sec. IV, we investigate the ALP implication in the MAGIC observations of Mrk 421 and PG 1553+113. The conclusion is given in Sec. V.
-
The Lagrangian of the ALP, including the effective ALP-photon interaction term, is
$ \begin{eqnarray} {\cal{L}}_{\rm{ALP}}&=\frac{1}{2}\partial^{\text{μ}} a\partial_{\text{μ}} a - \frac{1}{2}m_a^2a^2 -\frac{1}{4}g_{a\gamma}aF_{{\text{μ}}\nu}\tilde{F}^{{\text{μ}}\nu}, \end{eqnarray} $

(1) where a is the ALP,
$ m_a $ is its mass,$ g_{a\gamma} $ is the coupling between the ALP and photons, and$ F_{{\text{μ}}\nu} $ and$ \tilde{F}^{{\text{μ}}\nu} $ are the electromagnetic field tensor and its dual tensor, respectively. The ALP-photon system propagating along the$ x_3 $ direction is written as [21]$ \Psi = \left(A_1, A_2, a \right)^T $ , where$ A_1 $ and$ A_2 $ denote the linear polarization amplitudes of the photon in the perpendicular directions. The corresponding density matrix$ \rho=\Psi \otimes \Psi^\dagger $ satisfies the Von Neumann like equation [18]$ \begin{eqnarray} {\rm i}\frac{{\rm{d}}\rho(x_3)}{{\rm{d}}x_3}=\left[ \rho(x_3), \; {\cal{M}}_0 \right]. \end{eqnarray} $

(2) Assuming that
$ B_{\rm{T}} $ is the transversal magnetic field aligned along the direction of$ x_2 $ , the mixing matrix$ {\cal{M}}_0 $ can be described by [13, 17, 22]$ \begin{eqnarray} \begin{aligned} {\cal{M}}_0=\begin{pmatrix} \Delta_{\rm{pl }}+2\Delta_{\rm{QED }} & 0&0 \\ 0& \Delta_{\rm{pl }}+\dfrac{7}{2} \Delta_{\rm{QED }} & \Delta_{a \gamma} \\ 0&\Delta_{a\gamma} & \Delta_{aa} \end{pmatrix}, \end{aligned} \end{eqnarray} $

(3) with
$ \begin{eqnarray} \Delta_{\rm{pl}}&=&-\frac{\omega_{\rm{pl}}^2}{2E}\simeq -1.1 \times 10^{-4} \, {\rm{kpc}}^{-1} \, n_{{\rm{cm}}^{-3}}E_{\rm{GeV}}^{-1}, \end{eqnarray} $

(4) $ \begin{eqnarray} \Delta_{\rm{QED}}&=&\frac{\alpha E}{45\pi} \left( \frac{B_{\rm{T}}}{B_{\rm{cr}}}\right)^2 \simeq4.1\times 10^{-9}\, {\rm{kpc}}^{-1} \, E_{\rm{GeV}} B_{{\text{μ}} {\rm{G}}}, \ \ \end{eqnarray} $

(5) $ \begin{eqnarray} \Delta_{a\gamma}&=&\frac{1}{2}g_{a\gamma}B_{\rm{T}}\simeq 1.52 \times 10^{-2} \, {\rm{kpc}}^{-1} \, g_{11} B_{{\text{μ}} {\rm{G}}}, \end{eqnarray} $

(6) $ \begin{eqnarray} \Delta_{aa}&=&-\frac{m_a^2}{2E}\simeq -7.8 \times 10^{-2} \, {\rm{kpc}}^{-1} \, m_{\rm{neV}}^2 E_{\rm{GeV}}^{-1}, \end{eqnarray} $

(7) where
$ \omega_{\rm{pl}}= \sqrt{4\pi \alpha n_{\rm e}/m_{\rm e}} $ is the plasma frequency,$ n_{\rm e} $ is the number density of the free electrons, α is the fine-structure constant, and$ B_{\rm{cr}} \equiv m^2_{\rm e}/|e|\simeq4.4\times 10^{13} \rm \; G $ . The terms$ \Delta_{\rm{pl}} $ and$ \Delta_{\rm{QED}} $ represent the plasma and QED vacuum polarization effects, respectively. The notations$ n_{{\rm{cm}}^{-3}} \equiv n_{\rm e}/1 \rm {cm}^{-3} $ ,$ E_{\rm{GeV}} \equiv E /1 \; {\rm{GeV}} $ ,$ g_{11}\equiv g_{a\gamma}/10^{-11} \; {\rm{GeV}}^{-1} $ ,$ B_{\rm{{\text{μ}} G}} \equiv B_{\rm T} /1 {\text{μ}}{\rm{G}} $ , and$ m_{\rm{neV}} \equiv m_a/1 \; \rm {neV} $ are used in the above equations. The general mixing matrix$ {\cal{M}} $ depends on the angle ψ between the directions of$ B_{\rm{T}} $ and$ x_2 $ .ALP-photon conversion occurs in numerous regions with different magnetic field configurations. The final density matrix can be derived from the solution of Eq. (2) as
$ \begin{eqnarray} \rho\left(s\right)=T(s)\rho(0)T^\dagger(s). \end{eqnarray} $

(8) The entire transfer matrix
$ T(s) $ for the propagation distance s reads as$ \begin{eqnarray} T(s)=\prod^{n}_{i}{\cal{T}}_i, \end{eqnarray} $

(9) where
$ {\cal{T}}_i $ can be derived from the mixing matrix$ {\cal{M}}_i $ in the i-th region. For the initial unpolarized photon beam with$ \rho(0)=\rm {diag}(1, 1, 0)/2 $ , the photon survival probability after propagation is given by [21]$ \begin{eqnarray} P_{\gamma\gamma}={\rm{Tr}}\left(\left(\rho_{11}+\rho_{22}\right)T(s)\rho(0)T^\dagger(s)\right) \end{eqnarray} $

(10) with
$ \rho_{ii}={\rm{diag}}(\delta_{i1},\delta_{i2},0) $ .Subsequently, we describe the prorogation effect of the ALP-photon beam in three astrophysical regions with different magnetic field configurations, including the blazar jet, extragalactic space, and Milky Way [15, 28]. For the BL Lac objects considered in this study, we do not consider the effects in the blazar broad line region. The ALP-photon oscillation might occur significantly in the BJMF. There is evidence that the magnetic field of the BL Lac jet can be described by the poloidal (along the jet, with
$ B \propto r^{-2} $ ) and toroidal (perpendicular to the jet, with$ B \propto r^{-1} $ ) coherent components [55]. We take the BJMF model of the BL Lac sources as in Refs. [26, 35].The transverse magnetic field
$ B_{\rm{jet}}(r) $ reads [56, 57]$ \begin{eqnarray} B_{\rm{jet}}(r)=B_0\left(\frac{r}{r_{\rm{VHE}}}\right)^{-1}, \end{eqnarray} $

(11) where
$ r_{\rm{VHE}} $ is the distance between the central black hole and emission region. The density profile of the electrons$ n_{\rm{el}}(r) $ can be given by [58]$ \begin{eqnarray} n_{\rm{el}}(r)=n_0\left(\frac{r}{r_{\rm{VHE}}}\right)^{-2}. \end{eqnarray} $

(12) Note that the above profiles hold in the jet comoving frame. The energies of the photons in the laboratory frame
$ E_{\rm L} $ and comoving frame$ E_j $ are related by the Doppler factor$ \delta_{\rm{D}} $ through$ E_{\rm L} = E_j\cdot\delta_{\rm{D}} $ .The fit to the blazar spectra on the multi-wave bands with the synchrotron self-Compton model may determine the values of the BJMF parameters. In our analysis, these parameters for one source during all phases are assumed to be the same. We set
$ B_0 $ as$ 0.1 $ and$ 1.0\; {\rm{G}} $ for Mrk 421 and PG 1553+113, respectively, and take$ \delta_{\rm{D}} = 30 $ and$ n_0 = 3 \times 10^3 \; \rm {cm}^{-3} $ as the benchmark parameters. These values are consistent with the results derived in Refs. [53, 59]. In the region with$ r > 1\; \rm kpc $ , we assume that the magnitude of BJMF is zero. Note that among the BJMF parameters,$ r_{\rm{VHE}} $ is difficult to determine through the measurements. Its value might be in the range of$ {\cal{O}}(10^{16}) $ −${\cal{O}}(10^{17})\;{\rm{cm}}$ . Here, we adopt$ r_{\rm{VHE}}=10^{17}\;{\rm{cm}} $ as a benchmark parameter.When the ALP-photon system propagates in the host galaxy in which the blazar is located, the oscillation effect can be neglected [35, 60]. If the blazar is located in a cluster with a rich environment, the turbulent inter-cluster magnetic field
$\sim {\cal{O}}(1)$ μG may also induce a significant ALP-photon oscillation effect [28]. Because no definite evidence that the blazars Mrk 421 and PG 1553+113 are located in such an environment has been provided, this oscillation effect is not considered in our analysis.The oscillation in the extragalactic magnetic field on the largest cosmological scale is also neglected here. The magnitude of this magnetic field is not larger than
$ {\cal{O}}(1)\; \rm nG $ , although it has not yet been precisely determined [61]. For the VHE photons crossing extragalactic space, the attenuation effect caused by the extragalactic background light (EBL) through$ \gamma_{\rm{VHE}} + \gamma_{\rm{EBL}} \to e^+ + e^- $ should be considered. This effect is described by a suppression factor of$ {\rm e}^{-\tau} $ , where τ is the optical depth depending on the redshift of the source and the EBL density distribution. In this study, we take the EBL model provided by Ref. [62] as a benchmark. The redshift of Mrk 421 and PG 1553+113 are taken as$ z_0=0.031 $ and 0.45, respectively.Finally, we consider the effect in the magnetic field of the Milky Way, where the ALPs could be reconverted to photons. Only the regular component of the Galactic magnetic field is considered here, whereas the random component on the small scale is neglected. Details on this model can be found in Ref. [63].
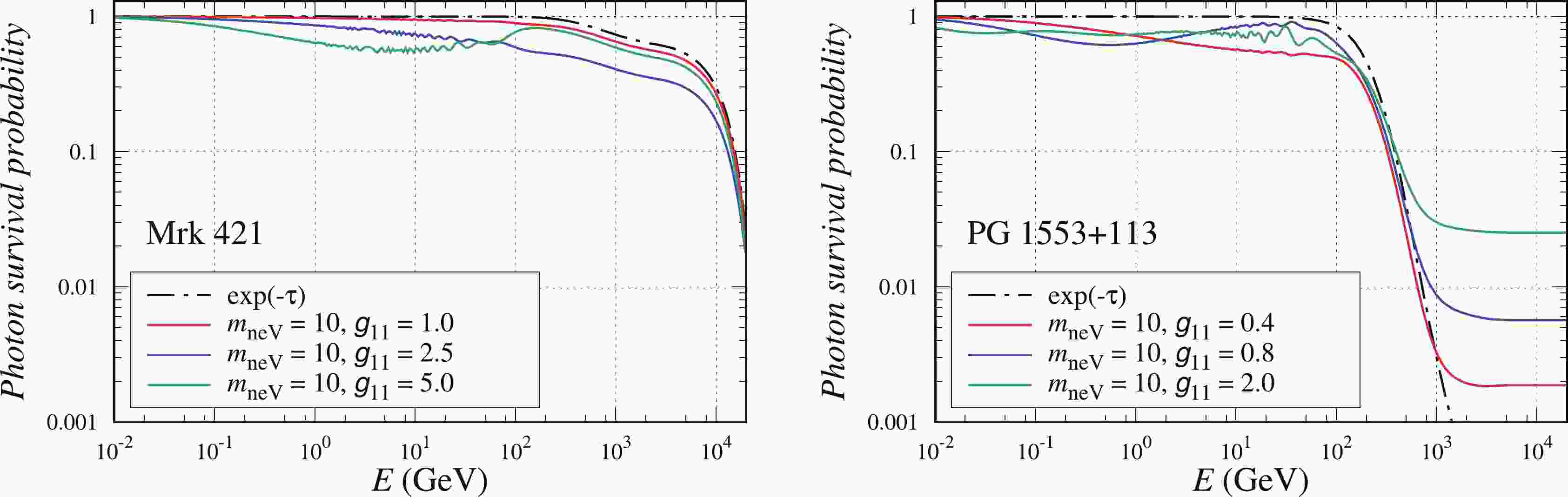
We show the photon survival probability
$ P_{\gamma\gamma} $ as a function of energy for the blazars Mrk 421 and PG 1553+113 in Fig. 1. It can be seen that the pure EBL attenuation effect described by the factor of$ {\rm e}^{-\tau} $ dramatically suppresses the photon energy spectrum at energies above${\cal{O}}(10^2)\;{\rm GeV}$ . The ALP-photon oscillation might affect the survival probability at lower energies compared with the EBL attenuation effect. However, for several ALP parameters, the ALP-photon conversion can compensate for the EBL attenuation effect in the VHE region and lead to a moderate photon survival probability. This compensation may be significant for PG 1553+113 at large redshifts, as shown in Fig. 1.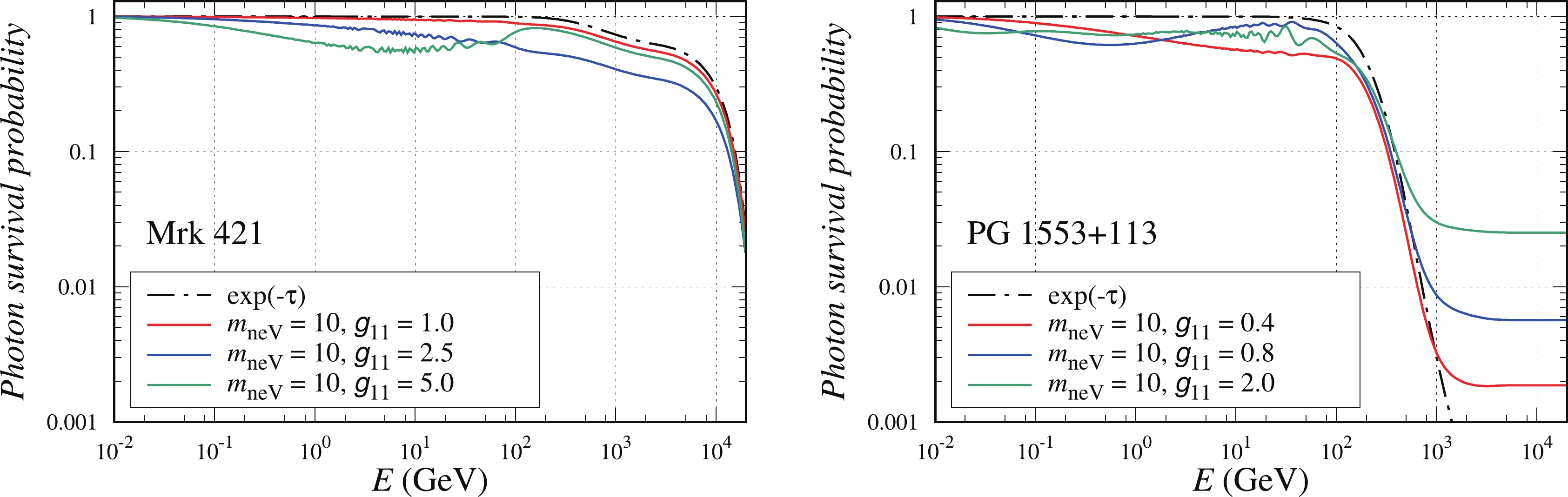
Figure 1. (color online) Photon survival probability as a function of energy for Mrk 421 (left) and PG 1553+113 (right). The black dotted dashed lines represent the survival probability with only the EBL attenuation effect. The solid lines represent the survival probability with both the EBL attenuation and ALP-photon oscillation effects for selected ALP parameters. The EBL model is taken from Ref. [62].
-
MAGIC [64, 65] is a system containing two imaging atmospheric Cherenkov telescopes located at the Roque de los Muchachos Observatory in Spain. These telescopes can detect extensive air showers in the stereoscopic mode and observe VHE γ-ray sources at energies above
$ 50\;{\rm GeV} $ [54]. In Ref. [54], the MAGIC collaboration reported 32 VHE γ-ray spectra from 12 blazars. All the data were collected during dark nights in good weather conditions. The γ-ray spectra at lower energies,$ \sim 0.1−100\;{\rm GeV} $ , during the common operation time observed by Fermi-LAT are also analyzed in Ref. [54]. Here, we use the MAGIC results of the BL Lac sources Mrk 421 and PG 1553+113 covering several activity phases to investigate the ALP-photon oscillation effects.We take expressions for the γ-ray blazar intrinsic energy spectra
$ \Phi_{\rm{int}} (E) $ as in Ref. [54].$ \Phi_{\rm{int}} (E) $ can be described using simple functions with three to five parameters, including the power law with exponential cut-off (EPWL), power law with superexponential cut-off (SEPWL), log parabola (LP), and log parabola with exponential cut-off (ELP). The functional expressions of$ \Phi_{\rm{int}} (E) $ are given as follows:● EPWL:
$ \begin{eqnarray} \Phi_{\rm{int}} ( E ) = F_0\left(\frac{E}{E_0}\right)^{-\Gamma}\exp\left(-\frac{E}{E_c}\right), \end{eqnarray} $

(13) ● SEPWL:
$ \begin{eqnarray} \Phi_{\rm{int}} ( E ) = F_0\left(\frac{E}{E_0}\right)^{-\Gamma}\exp\left(-\left(\frac{E}{E_c}\right)^d\right), \end{eqnarray} $

(14) ● LP:
$ \begin{eqnarray} \Phi_{\rm{int}} ( E ) = F_0\left(\frac{E}{E_0}\right)^{-\Gamma-b \log\left({E}/{E_0}\right)}, \end{eqnarray} $

(15) ● ELP:
$ \begin{eqnarray} \Phi_{\rm{int}} ( E ) = F_0\left(\frac{E}{E_0}\right)^{-\Gamma-b \log\left({E}/{E_0}\right)}\exp\left(-\frac{E}{E_c}\right), \end{eqnarray} $

(16) where
$ F_0 $ ,$ E_c $ , Γ, b, and d are free parameters. For EPWL and SEPWL,$ E_0 $ is taken to be 1 {$ {\rm GeV} $ }, whereas for LP and ELP,$ E_0 $ is also treated as a free parameter. Thus, these four functional expressions have 3, 4, 4, and 5 free parameters, respectively. For each phase, we choose the intrinsic energy spectrum with the minimum best-fit reduced$ \chi^2 $ under the null hypothesis. This is different from the analysis in Ref. [45], where the expression of the intrinsic energy spectrum is the same for all phases. The spectrum expressions for all the phases adopted in this analysis are listed in Table 1.Source [period] Tstart Tstop Spectrum $ {\chi}_{\rm{w/oALP}}^2 $ 

$ \chi^2_{\rm{min}} $ 

Effective d.o.f. $ \Delta\chi^2 $ 

Mrk 421 [20130410] 2013-04-09T12:00 2013-04-10T12:00 SEPWL 12.2 8.8 4.45 10.2 Mrk 421 [20130411] 2013-04-10T18:00 2013-04-11T06:00 ELP 16.2 10.1 6.85 13.9 Mrk 421 [20130412] 2013-04-11T18:00 2013-04-12T06:00 ELP 8.9 6.2 7.54 14.9 Mrk 421 [20130413a] 2013-04-12T12:00 2013-04-13T12:00 ELP 16.0 12.9 8.00 15.5 Mrk 421 [20130413b] 2013-04-12T12:00 2013-04-13T12:00 SEPWL 9.7 8.6 4.72 10.7 Mrk 421 [20130413c] 2013-04-12T12:00 2013-04-13T12:00 SEPWL 10.0 7.5 4.56 10.4 Mrk 421 [20130414] 2013-04-13T12:00 2013-04-14T12:00 ELP 22.4 13.7 9.22 17.2 Mrk 421 [20130415a] 2013-04-14T21:17 2013-04-15T04:13 ELP 5.8 4.8 5.23 11.4 Mrk 421 [20130415b] 2013-04-14T21:17 2013-04-15T04:13 SEPWL 13.4 10.0 5.02 11.1 Mrk 421 [20130415c] 2013-04-14T21:17 2013-04-15T04:13 SEPWL 5.1 4.0 4.71 10.6 Mrk 421 [20130416] 2013-04-15T12:00 2013-04-16T09:00 SEPWL 32.9 19.6 5.48 11.8 Mrk 421 [20130417] 2013-04-16T18:00 2013-04-17T06:00 SEPWL 26.1 11.2 4.99 11.1 Mrk 421 [20130418] 2013-04-17T12:00 2013-04-18T12:00 EPWL 13.3 9.0 5.56 12.0 Mrk 421 [20130419] 2013-04-18T12:00 2013-04-19T12:00 ELP 3.6 2.0 4.07 9.6 Mrk 421 [20140426] 2014-04-25T18:00 2014-04-26T06:00 ELP 25.8 15.2 6.19 12.9 PG 1553+113 [ST0202] 2012-02-28T12:00 2012-03-04T12:00 EPWL 2.3 0.9 3.52 8.7 PG 1553+113 [ST0203] 2012-03-13T12:00 2012-05-02T12:00 SEPWL 15.6 6.3 6.24 13.0 PG 1553+113 [ST0302] 2013-04-07T12:00 2013-06-12T12:00 SEPWL 5.4 1.3 4.50 10.3 PG 1553+113 [ST0303] 2014-03-11T12:00 2014-03-25T12:00 EPWL 10.2 5.9 6.73 13.7 PG 1553+113 [ST0306] 2015-01-25T12:00 2015-08-07T12:00 SEPWL 4.7 0.7 3.43 8.6 Combined Mrk 421 221.5 204.6 31.17 45.2 Combined PG 1553+113 38.2 20.5 8.94 16.9 Table 1. Best-fit values of
$ {\chi}_{\rm{w/oALP}}^2 $ under the null hypothesis and$ \chi^2_{\rm{min}} $ under the ALP hypothesis for all phases. The periods represent the corresponding MAGIC observations. The expressions for the intrinsic energy spectra, the effective$d.o.f.$ of the TS distributions, and$ \Delta{\chi}^2 $ at 95% C.L. are also listed. The last two rows denote the results of the combined analysis.Under the alternative hypothesis, including the ALP-photon oscillation effect, we obtain the expected photon spectrum as
$ \begin{eqnarray} \Phi_{\rm{w \; ALP}} ( E ) = P_{\gamma\gamma} \Phi_{\rm{int}} ( E ), \end{eqnarray} $

(17) where
$ P_{\gamma\gamma} $ is the photon survival probability. The detected photon flux in the energy bin of$ (E_1,E_2) $ is given by [35, 36]$ \begin{eqnarray} \Phi'=\frac{\int_0^{\infty}D(E', E_1, E_2)\Phi ( E' ){\rm{d}}E'}{E_2 - E_1}, \end{eqnarray} $

(18) where
$ D(E', E_1, E_2) $ is the energy dispersion function, and$ E' $ and$ \Phi(E') $ are the energy and spectrum of the photons before detection, respectively. The energy resolution of MAGIC is taken to be 16% [65].In Ref. [54], the Fermi-LAT spectra are provided in the form of spectral bow-ties rather spectral points. The bow-ties contain information on the flux and local spectrum index determined at the decorrelation energy; each one contributes two degrees of freedom in the fit. The
$ \chi^2 $ of the fit is defined as [54]$ \begin{aligned}[b] \chi^2 =& \left(\frac{\Phi'(E_{\rm{LAT}})-F_{\rm{LAT}}}{\Delta F_{\rm{LAT}}}\right)^2+ \left(\frac{\Gamma_{\rm{fit}}-\Gamma_{\rm{LAT}}}{\Delta \Gamma_{\rm{LAT}}}\right)^2 \\ &+ \sum_{i=1}^{N} \left(\frac{\Phi'(E_i) - \tilde{\phi}_i}{\delta_i}\right)^2, \end{aligned} $

(19) where
$ E_{\rm{LAT}} $ ,$ F_{\rm{LAT}} $ ,$ \Gamma_{\rm{LAT}} $ , and$ \Gamma_{\rm{fit}} $ are the central energy, flux, local spectral index, and expected spectral index for the Fermi-LAT results, respectively. N is the number of the MAGIC spectral points,$ \Phi'(E_i) $ is the expected flux of the photons,$ \tilde{\phi}_i $ is the detected photon flux, and$ \delta_i $ is the uncertainty of the MAGIC measurement.With the
$ \chi^2 $ values under the ALP hypothesis in the$ m_a-g_{a\gamma} $ plane, the constraint on the parameter space is set by requiring$ \chi^2 \leq \chi_{\rm{min}}^2 + \Delta{\chi}^2 $ , where$ {\chi}_{\rm{min}}^2 $ is the minimum best-fit$ {\chi}^2 $ under the ALP hypothesis. Because the modifications of the blazar spectra nonlinearly depend on the ALP parameters, the threshold value of$ \Delta{\chi}^2 $ at the particular confidence level should be derived from the Monte Carlo simulations rather than directly using Wilks' theorem [20, 34]. Based on the best-fit spectra to the data under the null hypothesis, for each phase, 400 sets of spectra in the pseudo-experiments are generated by Gaussian samplings. The test statistic (TS) value is defined as the difference between the best-fit$ {\hat{\chi}}^2 $ under the null and ALP hypotheses for each generated spectrum$ {TS}\equiv {\hat{\chi}_{\rm{null}}}^2 - {\hat{\chi}_{\rm{w \; ALP}}}^2 $ . In each phase, the distribution of the TS for all generated spectrum sets is derived. Such distribution can be described by the non-central$ \chi^2 $ distribution (see Appendix 6) with the non-centrality λ and effective degree of freedom ($ d.o.f. $ ). Although this TS distribution is derived under the null hypothesis, following Ref. [34], we take it as the approximation of the TS distribution under the ALP hypothesis and adopt the corresponding$ \Delta{\chi}^2 $ in the subsequent analysis. -
In this section, we investigate the implication of the ALP on the observations of MAGIC and Fermi-LAT. The best-fit
$ {\chi}_{\rm{w/oALP}}^2 $ under the null hypothesis and$ \chi_{\rm{w \; ALP}}^2 $ under the ALP hypothesis are given in Table 1. We calculate the TS distributions for all phases and obtain their non-centralities as$ \sim 0.01 $ . The corresponding effective$ d.o.f. $ and the values of$ \Delta{\chi}^2 $ at$ 95\%\; \rm C.L. $ are also given in Table 1.The best-fit photon spectra under the null and ALP hypotheses for all phases are shown in Fig. 2. We find that the null hypothesis can well fit the Mrk 421 observations. The corresponding best-fit reduced
$ \chi^2 $ have an average value of approximately 1.10. For most of the phases, introducing the ALP-photon oscillation does not significantly improve the fit. With the values of$ \Delta{\chi}^2 $ , the constraints on the ALP parameter space at 95% C.L. from the Mrk 421 observations are represented by the red contours in Fig. 3. We find that not all the observations of the single phase can be used to set the 95% C.L. constraint on the ALP parameter space. Following Ref. [36], we also perform an analysis combined the Mrk 421 results of the 15 phases. This approach can provide a more reliable implication. The combined$ \chi_{\rm{w \; ALP}}^2 $ in the$ m_a-g_{a\gamma} $ plane and the best-fit value are shown in Fig. 3 and Table 1, respectively. The red contour representing the combined upper limit at 95% C.L. is also shown.
Figure 2. (color online) Best-fit photon spectra for the 15 and five phases of Mrk 421 and PG 1553+113, respectively. The black and green lines represent the spectra under the null and ALP hypotheses, respectively. The values of the corresponding best-fit
$ \chi^2 $ are listed in Table 1. The spectral points and bow-ties represent the results from MAGIC and Fermi-LAT [54], respectively.
Figure 3. (color online)
$ \chi_{\rm{w \; ALP}}^2 $ values in the$ m_a-g_{a\gamma} $ plane for the 15 phases of Mrk 421. The$ \chi_{\rm{w \; ALP}}^2 $ values for the combined results are shown in the bottom right panel. The red contours represent the excluded regions at 95% C.L. The "#" symbol represents the best-fit ALP parameter points. The horizontal line represents the upper limit placed by CAST [66].In Fig. 4, the constraints on the ALP parameter space placed by CAST [66], the PKS 2155 - 304 observation of H.E.S.S. [23], and the NGC 1275 observation of Fermi-LAT [30] are shown for comparison. We also show the limits set by the analyses using the Mrk 421 observations of ARGO-YBJ and Fermi-LAT [45] and the PG 1553+113 observations of H.E.S.S. II and Fermi-LAT [43] in Fig. 4. Compared with the CAST constraint of
$g_{a\gamma} \lesssim 6.6\times 10^{-11}\, {\rm GeV}^{-1}$ [66], the combined limit at 95% C.L. set in this study excludes the ALP parameter region with the ALP-photon coupling of$g_{a\gamma} \gtrsim 2 \times 10^{-11}\, {\rm GeV}^{-1}$ for the ALP mass of$\sim 8\times 10^{-9} \lesssim m_a \lesssim 2\times 10^{-7}\; \rm eV$ . This combined constraint does not completely coincide with that derived from the observations of ARGO-YBJ and Fermi-LAT in Ref. [45]. A possible reason is that the spectral forms of the Fermi-LAT results are different in these two analyses. The spectral points of the Fermi-LAT results provide a large contributions to the final$ \chi^2 $ in Ref. [45]. In contrast, the Fermi-LAT results used in this analysis are in the form of bow-ties with two parameters. Therefore, the VHE data from MAGIC provide the dominant contributions to the final$ \chi^2 $ in this analysis. Additionally, the intrinsic energy spectra for all the phases are assumed to be same in Ref. [36], whereas they are separately chosen according to the fits for different phases in this analysis. This difference also induces different fitting results.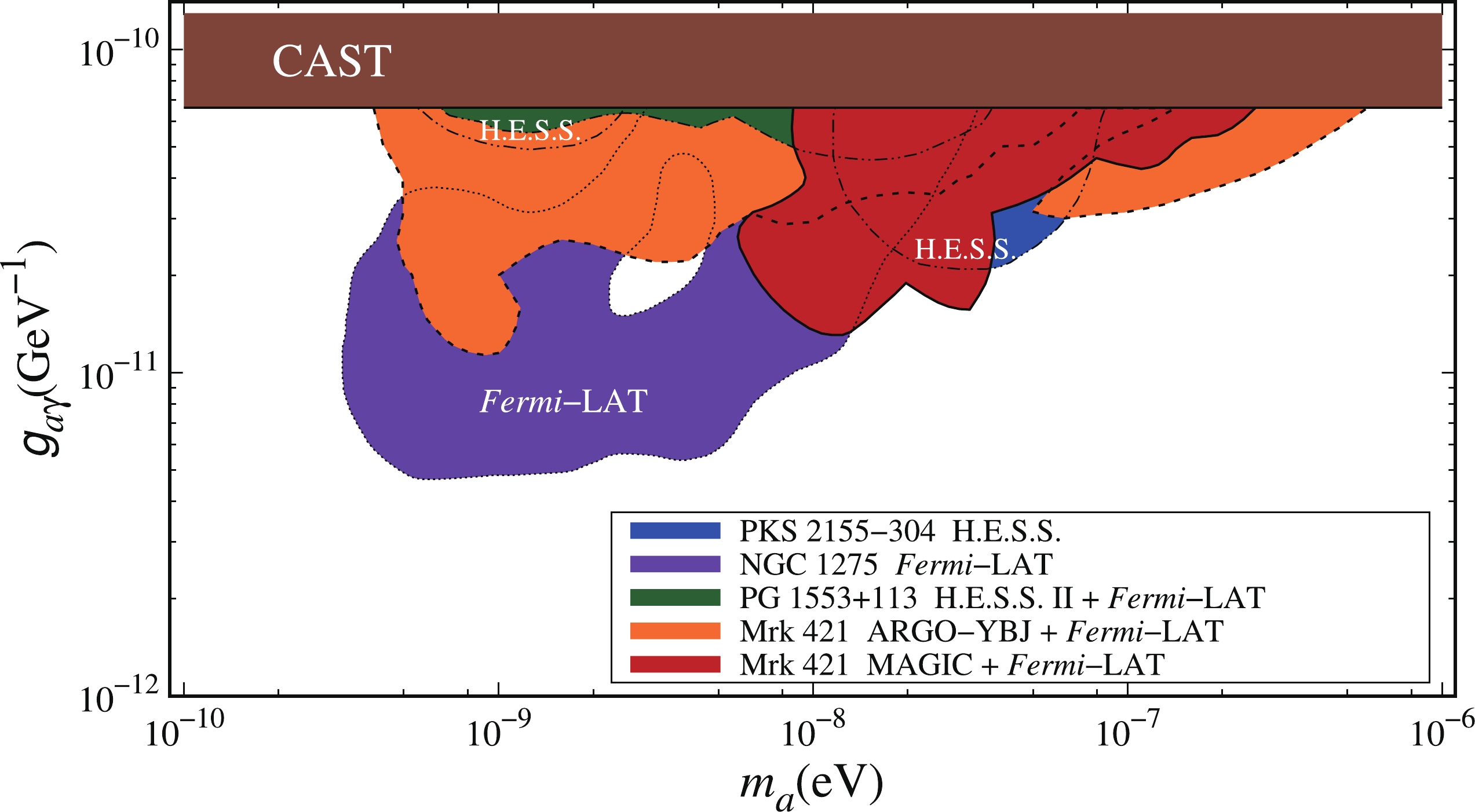
Figure 4. (color online) 95% C.L. upper limit (red contour) placed by the Mrk 421 observations of MAGIC and Fermi-LAT. The upper limits set by CAST [66], the PKS 2155 - 304 observation of H.E.S.S. [23], and the NGC 1275 observation of Fermi-LAT [30] are shown for comparison. The limits placed by the analyses using the Mrk 421 observations of ARGO-YBJ and Fermi-LAT [45] and the PG 1553+113 observations of H.E.S.S. II and Fermi-LAT [43] are also shown.
For PG 1553+113, the best-fit reduced
$ \chi^2 $ have an average value of approximately 1.23. For all phases except PG 1553+113 [ST0203], the ALP hypothesis does not significantly improve the fit. However, for PG 1553+113 [ST0203], the difference between the best-fit$ \chi^2 $ values under the null and ALP hypotheses is near the threshold$ \Delta \chi^2 $ at 95% C.L., as shown in Table 1. Combining all the results of the five phases, we find that this difference becomes larger than$ \Delta \chi^2 $ at 95% C.L. In this case, we only show the values of$ \chi^2 $ in the$ m_a-g_{a\gamma} $ plane in Fig. 5. We do not set the constraints on the ALP parameter space.
Figure 5. (color online)
$ \chi_{\rm{w \; ALP}}^2 $ values in the$ m_a-g_{a\gamma} $ plane for the five phases of PG 1553+113. The$ \chi_{\rm{w \; ALP}}^2 $ values for the combined results are shown in the bottom right panel. The "#" symbol represents the best-fit ALP parameter points. The horizontal line represents the upper limit placed by CAST [66].Here, we provide comments on these results. The ALP-photon oscillation effect strongly depends on the magnitude of the astrophysical magnetic field. For PG 1553+113, we take a relatively large value of
$ B_0=1\; {\rm{G}} $ , which directly enhances the oscillation effect. Because the ALPs do not interact with the EBL, the large oscillation effect may compensate for the attenuation effect and reduce the absorption of the VHE photons in the extragalactic space, especially for the astrophysical source at a large redshift suffering from a significant attenuation effect. Therefore, for PG 1553+113 at$ z_0\sim 0.45 $ , the oscillation effect might induce a relatively large photon flux in the VHE band compared with that in the null hypothesis. From Fig. 2, we can see that the ALP hypothesis improves the fit to the last one or two data points of the MAGIC measurements, which do not appear to drop dramatically compared with the previous data points. This behavior can be explicitly observed in the spectrum of the phase PG 1553+113 [ST0303], despite the relatively large uncertainties of this phase. Conversely, the spectrum of the phase PG 1553+113 [ST0203] has small uncertainties and can be used to reveal the oscillation effect.We emphasize that the results discussed above are affected by astrophysical uncertainties. The dominant uncertainties originate from the BJMF model. In the BJMF model used in this study, the magnitude of the magnetic field depends on the parameters
$ B_0 $ ,$ \delta_{\rm{D}} $ ,$ n_0 $ , and$ r_{\rm{VHE}} $ . As discussed in Refs. [28, 45], the distance between the VHE emission site and central black hole$ r_{\rm{VHE}} $ and the magnitude of the core magnetic field$ B_0 $ at$ r_{\rm{VHE}} $ significantly affect the final results. The parameter$ B_0 $ directly characterizes the magnitude of the BJMF. In principle, this parameter can be obtained from the fit to the blazar spectrum using the synchrotron self-Compton model. However, the value of$ r_{\rm{VHE}} $ is difficult to precisely determine.As discussed in Ref. [45], with the increasing value of
$ r_{\rm{VHE}} $ in the range of$ \sim 10^{16}-10^{18}\, {\rm{cm}} $ , the final constraint from the Mrk 421 observations also becomes more strict by an order of magnitude of$ 1-2 $ . The results for Mrk 421 in this analysis have a similar dependence on$ r_{\rm{VHE}} $ . For PG 1553+113, we perform an analysis for a small value of$ r_{\rm{VHE}} $ , that is,$ 3\times 10^{16}\, {\rm{cm}} $ . We find that the difference between the best-fit$ \chi^2 $ under the null and ALP hypotheses is 17.1, which is slightly larger than the threshold value at 95% C.L. of 16.6. In this case, because the ALP hypothesis is able to improve the fit, the constraint on the parameter space is not set. The corresponding$ \chi^2 $ values under the ALP hypothesis for PG 1553+113 are shown in Fig. 6. We can see that for a fixed$ m_a $ , the behavior of the change in$ \chi^2 $ for$ r_{\rm{VHE}}=3\times 10^{16}\, {\rm{cm}} $ is similar to that at smaller$ g_{a\gamma} $ for$ r_{\rm{VHE}}=10^{17}\, {\rm{cm}} $ .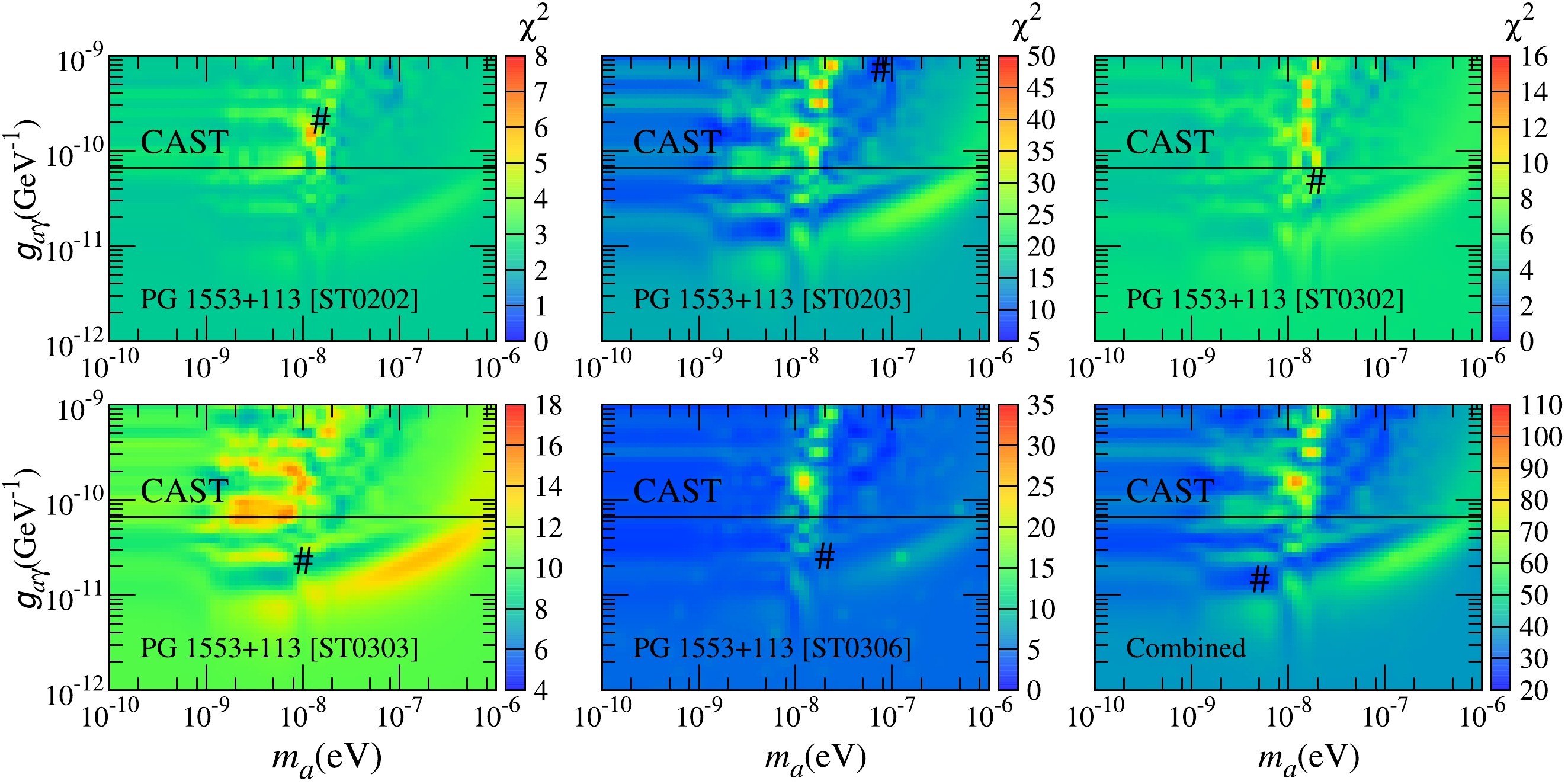
Figure 6. (color online) Same as Fig. 5 but for
$ r_{\rm{VHE}}=3 \times 10^{16}\, {\rm{cm}} $ . -
In this study, we analyze the ALP-photon oscillation effect in the spectra of the blazars Mrk 421 and PG 1553+113 measured by MAGIC and Fermi-LAT during the common operation time, which covers 15 and five activity phases, respectively. We find that not all the observations of these phases can be individually used to set the 95% C.L. limit on the ALP parameter space. For Mrk 421, we find that the constraint can be significantly improved if the results of all the 15 phases are combined. The combined Mrk 421 observations of MAGIC and Fermi-LAT exclude the ALP parameter region with the ALP-photon coupling of
$ g_{a\gamma} \gtrsim 2 \times 10^{-11}\, {\rm GeV}^{-1} $ for the ALP mass of$ \sim 8\times 10^{-9} \lesssim m_a \lesssim 2\times 10^{-7}\; \rm eV $ at 95% C.L. For PG 1553+113, the ALP hypothesis can slightly improve the fit to the data in certain parameter regions. However, because the anomalies of the intrinsic spectrum and EBL model may also induce a similar effect, we do not make a further ALP interpretation for the current observation.In the future, a new generation of VHE γ-ray observation sites, such as the Cherenkov Telescope Array [67], Large High Altitude Air Shower Observatory [68], High Energy cosmic-Radiation Detection facility [69], Gamma-Astronomy Multifunction Modules Apparatus [70], and Tunka Advanced Instrument for Gamma-ray and Cosmic ray Astrophysics-Hundred Square km Cosmic ORigin Explorer [71], will collect more data for high energy γ-ray sources at large distances from the Earth with high precision. With these precise γ-ray observations of several blazars, it will be possible to test the ALP-photon oscillation in the VHE band or set more stringent constraints on the ALP parameters.
-
The authors would like to thank Mireia Nievas Rosillo for providing the energy spectra of Mrk 421 and PG 1553+113 measured by MAGIC and Fermi-LAT in the common operation time. We also thank Jun-Guang Guo for helpful discussions and comments.
-
In this appendix, we briefly introduce the non-central
$ \chi^2 $ distribution. Usually, the distribution of the$ \chi^2 $ density function with the$ d.o.f. \nu $ can be described by$ \begin{eqnarray} f(x,\nu)=\frac{1}{2^{{\nu}/{2}}\Gamma({\nu}/{2})}x^{{\nu}/{2}-1}{\rm e}^{-{x}/{2}}, \end{eqnarray} \tag{A1}$

where
$ \Gamma(a) $ is the celebrated Gamma function$ \begin{eqnarray} \Gamma(a)=\int_0^{\infty}t^{a-1}{\rm e}^{-t}{\rm{d}}t. \end{eqnarray} \tag{A2}$

Then, we have the non-central
$ \chi^2 $ distribution described by the Poisson mixture of the$ \chi^2 $ density function$ \begin{eqnarray} f(x,\nu,\lambda)=\sum_{j=0}^\infty \frac{{\rm e}^{-{\lambda}/{2}}\left({\dfrac{\lambda}{2}}\right)^j}{j!}f(x,\nu+2j), \end{eqnarray} \tag{A3}$

with the non-centrality λ and
$d.o.f. \nu$ . Both the values of λ and ν can be derived by fitting the realistic TS distribution. An integer value is not required for the derived ν, which is often referred to as the effective$d.o.f$ . The cumulative distribution function is given by$ \begin{eqnarray} P(x,\nu,\lambda)=\int_0^x f(t,\nu,\lambda){\rm{d}}t. \end{eqnarray}\tag{A4} $

When considering a
$ 95\% $ limit for a given ν and λ, one can solve$ P(x_{95\%}, \nu, \lambda)=0.95 $ and take the corresponding$ x_{95\%} $ as the threshold value of$ \Delta \chi^2 $ at$ 95\% $ C.L.
Searching for axion-like particles with the blazar observations of MAGIC and Fermi-LAT
- Received Date: 2022-04-08
- Available Online: 2022-08-15
Abstract: In this study, we explore the axion-like particle (ALP)-photon oscillation effect in the γ-ray spectra of the blazars Markarian 421 (Mrk 421) and PG 1553+113, which are measured by the Major Atmospheric Gamma Imaging Cherenkov Telescopes (MAGIC) and Fermi Large Area Telescope (Fermi-LAT) with high precision. The Mrk 421 and PG 1553+113 observations of 15 and five phases are used in the analysis, respectively. We find that the combined analysis with all the 15 phases improves the limits of the Mrk 421 observations. For the selected blazar jet magnetic field and extragalactic background light models, the combined limit set by the Mrk 421 observations excludes the ALP parameter region with the ALP-photon coupling of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: