-
During relativistic heavy ion collisions at the relativistic heavy ion collider (RHIC) and large hadron collider (LHC), a hot and dense, strongly interacting medium named quark-gluon plasma (QGP) was created [1–3]. One of the main experimental signatures of QGP formation is the dissociation of heavy quarkonium [4]. They are expected to be created in the early stages of the collisions and provide significant information regarding the evolution of QGP. Previous research has indicated that the heavy quarkonium is suppressed due to the Debye screening induced by the high density of color charges in QGP. However, recent studies of charmonium (heavy quarks of charm and anticharm) revealed a puzzle: the charmonium suppression observed at RHIC (lower energy density) is stronger than that at LHC (larger energy density) [5, 6]. This clearly contradicts the Debye screening scenario [4] as well as the thermal activation through the impact of gluons [7, 8]. Some scholars believe this could be due to the recombination of the produced charm quarks into charmonium [9, 10].
However, recent research suggested [11] that the puzzle regarding the suppression of the charmonium can be a consequence of the nature of deconfinement. This argument is based on the lattice QCD results [12–15], indicating a large amount of entropy S associated with the heavy quark-antiquark pair (
$ Q\bar{Q} $ ) around the crossover region of QGP. In particular, this entropy, which grows with the inter-distance L between$ Q\bar{Q} $ , leads to the emergent entropic force [11]$ \begin{equation} \mathcal{F}=T\frac{\partial S}{\partial L}, \end{equation} $

(1) where T denotes the temperature of the plasma. It has been shown that the repulsive entropic force is responsible for dissociating the quarkonium, which could provide a solution to the above puzzle.
The AdS/CFT correspondence [16–18] or more general gauge/gravity duality provides a helpful tool to explore various properties of QGP [19, 20]. With this method, K. Hashimoto and D. Kharzeev first calculated the entropic force associated with
$ Q\bar{Q} $ for$ \mathcal N=4 $ SYM plasma [21]. It was found that the entropy increases with the inter-quark distance, and the peak of the entropy emerges when the U-shaped string stretched between the$ Q\bar{Q} $ touches the horizon of the black hole. Subsequently, there have many attempts to address the entropic force in this direction [22–31].In this paper, we extend the studies of [21] to the case of rotating plasma with chemical potential. In particular, we employ the AdS-Reissner Nordstrom (AdS-RN) black hole [32, 33] and extend it to a rotating case with planar horizon because there's the strong possibility that the QGP produced in (typical) noncentral heavy ion collisions may carry a nonzero angular momentum on the order of
$ 10^4 $ –$ 10^5\hbar $ with local angular velocity in the range of 0.01–0.1 GeV [34–38]. Although the major part of this angular momentum will be taken away by the spectator nucleons, some amount of angular momentum remains in the QGP [39–41], and this may give rise to significant observable effects. Meanwhile, the QGP produced in heavy ion collisions is assumed to carry a finite, albeit small, baryon number density, e.g., the Beam Energy Scan program at RHIC covers the beam energies of$ \sqrt{S_{NN}} $ = 200, 62.4, 54.4, 39, 27 GeV... corresponding to a region of the chemical potential$0.025\leq\mu_B\leq0.72 ~{\rm GeV}$ [42]. In this regard, it would be interesting to study the entropic force at finite temperature and density under rotation.This paper is organized as follows: In the next section, we briefly review the AdS-RN background and extend it to a rotating case. In section III, we investigate the behavior of the entropic force in this background and explore how the deconfinement transition can be viewed as entropic self-destruction. In section IV, we summarize our results and provide a concluding discussion.
-
From the AdS/CFT correspondence,
$ \mathcal N=4 $ SYM theory with non-zero chemical potential can be obtained by charging the black hole in the holographic dimension. The corresponding metric is the AdS-RN black hole [32, 33]$ \begin{equation} {\rm d}s^2 =-\frac{r^2}{R^2}f(r){\rm d} t^2+\frac{r^2}{R^2} {\rm d} \vec{x}^2+\frac{R^2}{r^2f(r)}{\rm d} r^2, \end{equation} $

(2) with
$ \begin{equation} f(r)=1-(1+Q^2)\left(\frac{r_h}{r}\right)^4+Q^2\left(\frac{r_h}{r}\right)^6, \end{equation} $

(3) where R is the curvature radius (for convenience, we set
$ R=1 $ for later discussion), Q denotes the charge of black hole, r refers to the radial coordinate with$ r=r_h $ the horizon, defined by$ f(r_h)=0 $ . The asymptotic boundary is at$ r=\infty $ . The string tension$ \dfrac{1}{2\pi\alpha^\prime} $ is related to the 't Hooft coupling constant λ by$ \dfrac{1}{\alpha^\prime}=\sqrt{\lambda} $ .Following [43–45], (2) can be extended to a rotating case from the static configuration through a local Lorentz boost in the
$ t-\phi $ plane$ \begin{equation} t\rightarrow \gamma(t+\omega l^2 \phi), \qquad \phi\rightarrow \gamma(\phi+\omega l^2 t), \end{equation} $

(4) with
$ \begin{equation} \gamma=\frac{1}{\sqrt{1-\omega^2l^2}}, \end{equation} $

(5) where ϕ is the angular coordinate describing the rotation, ω represents the angular velocity, and l is the radius of the rotating axis. In this work, we focus on the qualitative results; therefore, we simply set
$l=1 ~{\rm GeV}^{-1}$ as follows from [45].Accordingly, the rotating case of (2) is given by
$ \begin{aligned}[b] {\rm d}s^2=&-p(r){\rm d}t^2+r^2({\rm d}x^2+{\rm d}y^2)\\&+\frac{1}{r^2f(r)}{\rm d}r^2+q(r)({\rm d}\phi+m(r){\rm d}t)^2, \end{aligned} $

(6) with
$ \begin{aligned}[b] p(r)=&\frac{f(r)r^2(1-\omega^2)}{1-f(r)\omega^2},\\ q(r)=&(1-f(r)\omega^2)r^2\gamma^2, \\ m(r)=&\frac{\omega(1-f(r))}{1-f(r)\omega^2}. \end{aligned} $

(7) The temperature of the black hole reads
$ \begin{equation} T=\frac{r_h}{\pi}\sqrt{1-\omega^2}\left(1-\frac{Q^2}{2}\right). \end{equation} $

(8) where Q is in the range
$ 0\leq Q\leq\sqrt{2} $ .The chemical potential is expressed as [45]
$ \begin{equation} \mu=\sqrt{3}Qr_h\sqrt{1-\omega^2}. \end{equation} $

(9) It should be noted that the chemical potential implemented here is not the baryon chemical potential of QCD, but a chemical potential conjugated to the R-charge associated with SYM. However, in such a context, it could serve as a simple way of introducing finite density effect into the system [46].
-
We now proceed to study the entropic force in the rotating AdS-RN black hole (6) following the prescription of [21]. The Nambu-Goto action is given by
$ \begin{equation} S_{\rm NG}=-\frac{1}{2\pi\alpha^\prime}\int {\rm d}\tau {\rm d}\sigma\sqrt{-{\rm det}\, g_{\alpha\beta}}, \end{equation} $

(10) with
$ \begin{equation} g_{\alpha\beta}=g_{\mu\nu}\frac{\partial X^\mu}{\partial\sigma^\alpha} \frac{\partial X^\nu}{\partial\sigma^\beta}, \end{equation} $

(11) where
$ g_{\alpha\beta} $ represents the induced metric and parameterized by$ (\tau,\sigma) $ on the string world-sheet,$ g_{\mu\nu} $ is the metric, and$ X^\mu $ is the target space coordinate.As the transformation (4) is a boost in the
$ t-\phi $ plane, one may consider the$ Q\bar{Q} $ pair located at the$ x-y $ plane, e.g., one considers the$ Q\bar{Q} $ pair to be aligned in the x direction,$ \begin{equation} t=\tau, \quad x=\sigma, \quad y=0,\quad \phi=0, \quad r=r(\sigma). \end{equation} $

(12) Based on these assumptions, (10) becomes
$ \begin{equation} S_{\rm NG}=\frac{\mathcal{T}}{2\pi\alpha^\prime}\int_{-L/2}^{L/2} {\rm d}x \sqrt{A(r)+B(r)(\frac{{\rm d}r}{{\rm d}\sigma})^2}, \end{equation} $

(13) with
$ \begin{equation} A(r)=(p(r)-q(r)m^2(r))r^2,\qquad B(r)=\frac{p(r)-q(r)m^2(r)}{r^2f(r)}, \end{equation} $

(14) where
$ Q\bar{Q} $ are set at$ x=-L/2 $ and$ x=L/2 $ , respectively.As (13) does not depend on σ explicitly, a conserved quantity was obtained:
$ \begin{equation} \mathcal L-\frac{\partial\mathcal L}{\partial\dot{r}}\dot{r}=\rm constant. \end{equation} $

(15) Imposing the boundary condition (the deepest point of the U-shaped string)
$ \begin{equation} \dot{r}=0,\qquad r=r_c \qquad (r_h<r_c) , \end{equation} $

(16) gives
$ \begin{equation} \frac{{\rm d}r}{{\rm d}\sigma}=\sqrt{\frac{A^2(r)-A(r)A(r_c)}{A(r_c)B(r)}} , \end{equation} $

(17) with
$ A(r_c)=A(r)|_{r=r_c} $ .Integrating (17), the inter-distance of
$ Q\bar{Q} $ is found to be$ \begin{equation} L=2\int_{r_c}^{\infty}{\rm d}r\sqrt{\frac{A(r_c)B(r)}{A^2(r)-A(r)A(r_c)}} . \end{equation} $

(18) Meanwhile, the entropy is given by
$ \begin{equation} S=-\frac{\partial F}{\partial T}, \end{equation} $

(19) where F denotes the free energy of
$ Q\bar{Q} $ . Note that F has been studied at zero temperature [47] and finite temperature [48, 49] from holography. Generally, there are two situations:1. If
$ L>\dfrac{c}{T} $ (where c denotes the maximum value of$ LT $ ), some new configurations need to be considered; thus, there are several alternatives for F [50, 51]. If a configuration of two disconnected trailing drag strings is selected [52, 53], the corresponding free energy can be written as$ \begin{equation} F^{(1)}=\frac{1}{\pi\alpha^\prime}\int_{r_h}^{\infty}{\rm d}r, \end{equation} $

(20) leading to
$ \begin{equation} \mathcal{S}^{(1)}=\sqrt{\lambda}\theta\left(L-\frac{c}{T}\right) , \end{equation} $

(21) where
$\theta \left(L-\dfrac{c}{T}\right)$ is the Heaviside step function.2. If
$ x<\dfrac{c}{T} $ , the fundamental string is connected. Then F can be obtained from the on-shell action of the fundamental string in the dual geometry,$ \begin{equation} F^{(2)}=\frac{1}{\pi\alpha^\prime}\int_{r_c}^{\infty} {\rm d}r \sqrt{\frac{A(r)B(r)}{A(r)-A(r_c)}}. \end{equation} $

(22) Then from (8), (10), and (22), the following can be realized:
$ \begin{aligned}[b]& S^{(2)}=-\frac{\partial F^{(2)}}{\partial T}=-\frac{1}{2\alpha^\prime}\frac{1}{\sqrt{1-\omega^2}(1-\frac{Q^2}{2})}\int_{r_c}^{\infty} {\rm d}r\\&\frac{[A^\prime(r)B(r) + A(r)B^\prime(r)][A(r) - A(r_c)] - A(r)B(r)[A^\prime(r) - A^\prime(r_c)]}{\sqrt{A(r)B(r)[A(r) - A(r_c)]^3}} , \end{aligned} $

(23) with
$ \begin{aligned}[b] A^\prime(r)=&r^2(p^\prime-q^\prime m^2-2qmm^\prime), \\ B^\prime(r)=&\frac{(p^\prime-q^\prime m^2-2qmm^\prime)f-(p-qm^2)f^\prime}{r^2f^2},\\ p^\prime=&\frac{r^2(1-\omega^2)(f^\prime(1-f\omega^2)+\omega^2ff^\prime)}{(1-f\omega^2)^2},\\ q^\prime=&-r^2\gamma^2\omega^2f^\prime,\\ m^\prime=&\frac{\omega(-f^\prime(1-f\omega^2)+\omega^2(1-f)f^\prime)}{(1-f\omega^2)^2},\\ f^\prime=&-4(1+Q^2)r_h^3r^{-4}+6Q^2r_h^5r^{-6}, \end{aligned} $

(24) where
$A^\prime(r_c)\equiv A^\prime(r)|_{r=r_c},~ q\equiv q(r),~ m\equiv m(r),~ f\equiv f(r)$ , and the derivatives are with respect to$ r_h $ . This can be checked by setting$ \omega=0 $ and$ \mu=0 $ (or$ Q=0 $ ) in (23); the result of SYM [21] will be recovered.First, we analyzed how angular velocity affects the inter-distance of
$ Q\bar{Q} $ . Accordingly, we plotted$ LT $ as a function of$ \varepsilon\equiv r_h/r_c $ for various values of ω in Fig. 1, where the left panel is for$\mu=0.025~{\rm GeV}$ and the right is$\mu=0.1~{\rm GeV}$ (note that in all the plots, ω and μ are in GeV, which are not mentioned for the sake of brevity of the notation). In both panels from top to bottom,$\omega=$ 0.1, 0.3, and 0.5 GeV, respectively. From each panel, it is clear that by increasing ω,$ LT $ decreases. Namely, the inclusion of angular velocity reduces the inter-distance.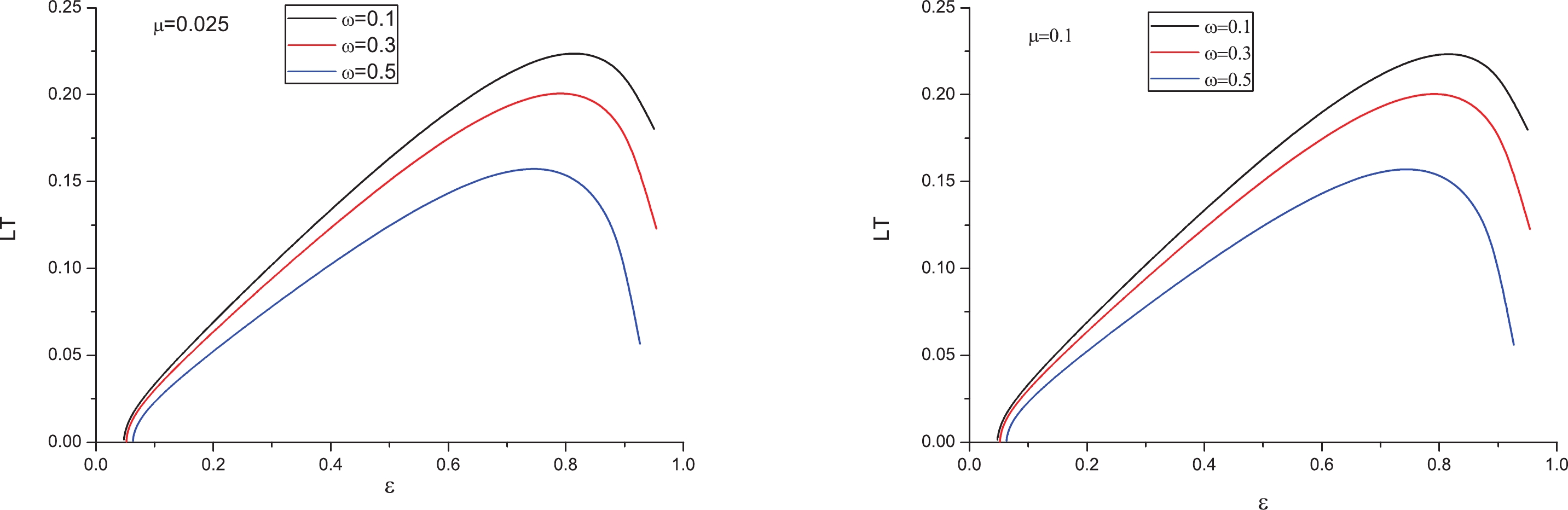
Figure 1. (color online)
$ LT $ versus ε for different ω. Left:$\mu=0.025~{\rm GeV}$ ; Right:$\mu=0.1~{\rm GeV}$ . In both panels from top to bottom$\omega=0,~0.1,~0.3~{\rm GeV}$ , respectively.Moreover, to see how angular velocity modifies the entropic force, we plotted
$ S^{(2)}/\sqrt{\lambda} $ versus$ LT $ for various cases in Fig. 2. Similarly,$\mu=0.025, \sim 0.1 \sim{\rm GeV}$ and$\omega= 0.1, \sim0.3,\sim0.5\sim{\rm GeV}$ were used in the calculations. From these figures, it is apparent that increasing ω leads to larger entropy at small distances. It is known that the entropic force (see Eq. (1)) depends on the growth of the entropy with the inter-distance and is responsible for dissociating the quarkonium. Therefore, the inclusion of angular velocity increases the entropic force, thus enhancing the quarkonium dissociation, which is in agreement with [31].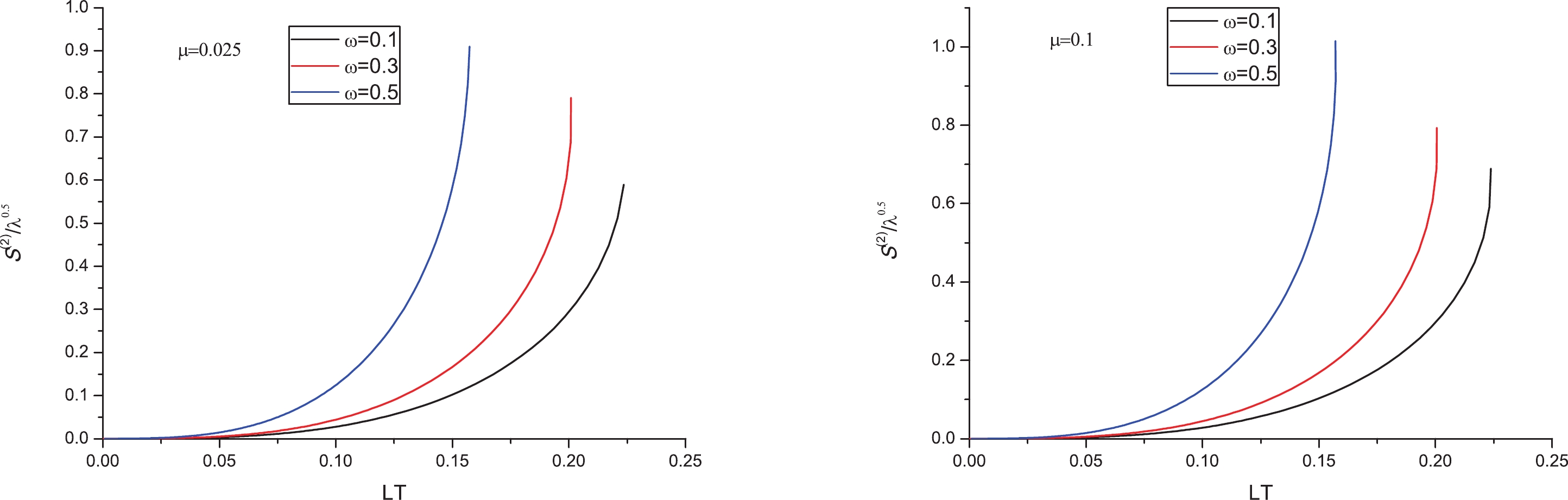
Figure 2. (color online)
$ S^{(2)}/\sqrt{\lambda} $ versus$ LT $ for different ω. Left:$\mu=0.025~{\rm GeV}$ ; Right:$\mu=0.1~{\rm GeV}$ . In both panels from right to left,$\omega=0,~0.1,~0.3~{\rm GeV}$ , respectively.Moreover, one can analyze the chemical potential dependence of the entropic force. For this purpose, we plotted
$ LT $ versus ε and$ S^{(2)}/\sqrt{\lambda} $ versus$ LT $ for different values of μ in Fig. 3. As a result, the presence of chemical potential also reduces the inter-distance and enhances the entropic force, which is consistent with [23]. The physical significance of these results will be discussed in the final section.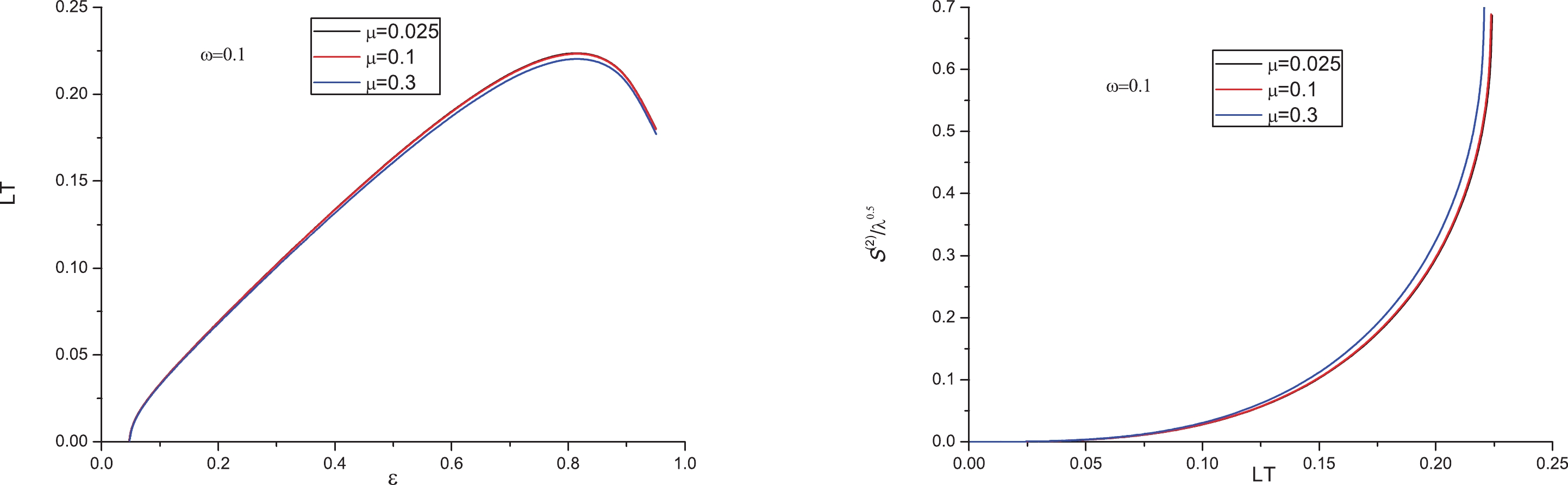
Figure 3. (color online) Left:
$ LT $ versus ε for different μ, from top to bottom$\mu=0.025,~0.1,~0.3~{\rm GeV}$ , respectively. Right:$ S^{(2)}/\sqrt{\lambda} $ versus$ LT $ for different μ, from right to left,$\mu=0.025,~0.1,~0.3~{\rm GeV}$ , respectively. In both cases we take$\omega=0.1~{\rm GeV}$ . -
Recent studies have shown [21] that the peak of the quarkonium entropy at the deconfinement transition can be related to the entropic force, which can destruct the heavy quarkonium. In this work, we extended the studies of [21] to the case of a rotating medium with chemical potential using AdS/CFT correspondence. It is shown that the inclusion of angular velocity increases the entropic force; thus, enhancing the quarkonium dissociation, while chemical potential has the same effect. Furthermore, the results imply that quarkonium dissociates easier in rotating medium compared with the static case.
Interestingly, the entropic force of a moving heavy quarkonium was investigated in [22], and the results show that the entropic force destroys the moving quarkonium more easily than in the static case. As motion is relative, their results can be understood as follows: quarkonium dissociates easier in moving medium compared with the static case. Comparing their results with ours, it may be inferred that translation and rotation have the same effect on quarkonium dissociation. In particular, quarkonium dissociates easier in moving or rotating medium compared with the static case.
However, there are some inadequacies in this research, e.g., the model we employed is not consistent. Considering the entropic force in some consistent models, e.g., [54–59], would be instructive. Meanwhile, the entropic force mechanism applies only to charmonium, but hardly applies to bottomonium (the mass of c quark is about 1.27 GeV, while b quark 4.2 GeV). It was argued [11] that most of the bottomonium states have smaller sizes, which are much less influenced by entropic force.
Finally, it is worth noting that rotating QGP can also be described using five-dimensional Kerr-AdS black hole [60]. Then, the entropic force can be evaluated in that rotating frame as well. This will be examined as a further study.
Entropic destruction of heavy quarkonium in a rotating hot and dense medium from holography
- Received Date: 2022-05-09
- Available Online: 2022-11-15
Abstract: Previous studies have indicated that the peak of the quarkonium entropy at the deconfinement transition can be related to the entropic force, which would induce the dissociation of heavy quarkonium. In this study, we investigated the entropic force in a rotating hot and dense medium using AdS/CFT correspondence. It was found that the inclusion of angular velocity increases the entropic force, thus enhancing quarkonium dissociation, while chemical potential has the same effect. The results imply that the quarkonium dissociates easier in rotating medium compared with the static case.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: