-
Fragmentation reactions play important roles in various scientific research fields. Firstly, the projectile fragmentation is one of the most important methods for the production of exotic nuclei. It has been widely used to produce the radioactive nuclei far from stability. Especially, it has proven to be a well suited reaction mechanism for producing heavy neutron-rich nuclei [1–3]. Secondly, it is a powerful means to produce the hypernuclei [4]. Thirdly, fragmentation reactions are often employed to investigate the structure and dynamics of the atomic nuclei [5] and constrain the equation of state of nuclear matter [6]. Fourthly, fragmentation has a crucial impact on the hadron therapy and the space radiation protection [7]. Last but not least, an accurate database of production cross sections is essential for the development of reliable cross section models, which play a crucial role in the design of radioactive ion beam experiments. For decades, several kinds of theoretical models and empirical formulas have been developed to describe fragmentation reactions, such as the abrasion-ablation model NUCFRG2 [8], modified statistical abrasion-ablation model ABRABLA [9], empirical parametrization EPAX as well as its extensions [10–12], and FRACS code [13–17]. During the development of these theories, large amounts of cross section data obtained in fragmentation reactions have been employed to benchmark and improve their predictive power. Therefore, the investigation of fragmentation reactions and measurement of the production cross sections are crucial. A state-of-art review of projectile fragmentation reaction studies can be found in Ref. [18].
In recent decades, most of the projectile fragmentation reaction studies employed medium or heavy projectiles, such as 80Kr, 136Xe, and 238U. Systematic studies of residual fragments produced with light projectiles are scarce. However, the fragmentation reaction studies using light projectiles are crucial. On the one hand, the peripheral reactions induced by light projectiles have been proved to be useful spectroscopic tools to investigate the structure of nuclei [19]. On the other hand, systematic studies of the residue fragments produced with light projectiles are important for radiotherapy and space exploration [7]. From a theoretical point of view, the theoretical complexity and limited data lead to a limited predictive power of the model descriptions of the fragmentation reactions induced by light projectiles. Therefore, the experimental data with light projectiles are requested for benchmarking the model calculations. It is also of interest to examine the validity of some widely-used empirical parametrizations (e.g., EPAX3 [12]) in describing the light nuclei.
In this manuscript, we report a set of production cross sections of isotopically separated residue nuclei produced in fragmentation reactions induced by 18O projectiles impinging on a carbon target at energies near 260 MeV/nucleon. This paper is structured as follows. The experimental setup is described in Sec. II. In Sec. III, we present the measured cross sections compared with existing data and the state-of-the-art model calculations. Finally, a summary of the present work is given in Sec. IV.
-
The experiment was conducted at the HIRFL-CSR facility [20, 21] in Lanzhou (China). The 18O primary beam was transported to the entrance of the second Radioactive Ion Beam Line in Lanzhou (RIBLL2) [22] to impinge on a primary Be target. The main purpose of the experiment was to study the neutron knock-out reactions of C isotopes produced by the fragmentation of 18O projectiles on a primary Be target, and desirable results have been obtained [23, 24]. In the experiment, we also took some measurements in which the primary Be target was removed, and the 18O primary beam was transported through the RIBLL2 beamline and delivered into the External Target Facility (ETF) where the reaction target was located. The details are described as follows.
Fig. 1 is a schematic layout of the RIBLL2 beamline and ETF terminal together with the employed detectors. During the experiment, an 18O beam with an intensity of approximately
$ 10^6 $ particles per second was accelerated to 280 MeV/nucleon and injected into the entrance of the RIBLL2 beamline. The RIBLL2 was tuned to transport the 18O beam through the F0 and F1 then reached the ETF to bombard a C target with a thickness of 900 mg/cm$^2 $ and a diameter of 50 mm. The 18O ions have an energy about 260 MeV/nucleon at the center of the C target. The projectile fragmentation reactions occurred and several detectors were utilized to measure the experimental information. At F1, a scintillator detector (i.e., SC1 in Fig. 1) was positioned. Another scintillator (see SC2 in Fig. 1) was located upstream of the reaction target at ETF. These two scintillators served as time-of-flight (TOF) detectors to measure the TOF of ions. Most of the detectors were installed at the ETF area. Upstream of the reaction target, a MUlti-Sampling Ionization Chamber (see MUSIC1 in Fig. 1) detector sandwiched by two multi-wire drift chambers (i.e., MWDC1 and MWDC2 in Fig. 1) were located. Downstream of the reaction target, a similar setup including another MUSIC detector (see MUSIC2 in Fig. 1) and two MWDCs (i.e., MWDC3 and MWDC4 in Fig. 1) were installed. The sensitive area of the MUSIC2 detector is sufficiently large to cover almost all outgoing residue particles. MUSIC1 and MUSIC2 were employed to measure the energy loss (ΔΕ) of ions upstream and downstream of the reaction target, respectively. MWDC1 and MWDC2 were used to measure the trajectories of the incoming particles. The particle identification (PID) for the incoming primary beam upstream of the reaction target was achieved by employing the ΔΕ-TOF method. Downstream of the C target, the trajectories of the outgoing ions were monitored by MWDC3 and MWDC4. Then, the ions were bent by a dipole magnet (see Dipole Magnet in Fig. 1), which has a large gap that can assure a nearly full acceptance of the fragment residues downstream of the reaction target. Downstream of the dipole magnet, an MWDC array [25] consisting of three MWDCs was positioned and a TOF wall (TOFW in Fig. 1) detector was installed at the end. The detailed description of the charged fragment detector system at the ETF can be found in Ref. [26]. With the experimental information obtained by SC2, MUSIC2, the dipole magnet, the MWDC array, and the TOFW, one can reconstruct the ion’s trajectory, derive the Bρ, and determine the TOF and ΔE. Therefore, the fragmentation residues induced by the 18O projectiles can be unambiguously identified with the so-called Bρ-ΔE-TOF method.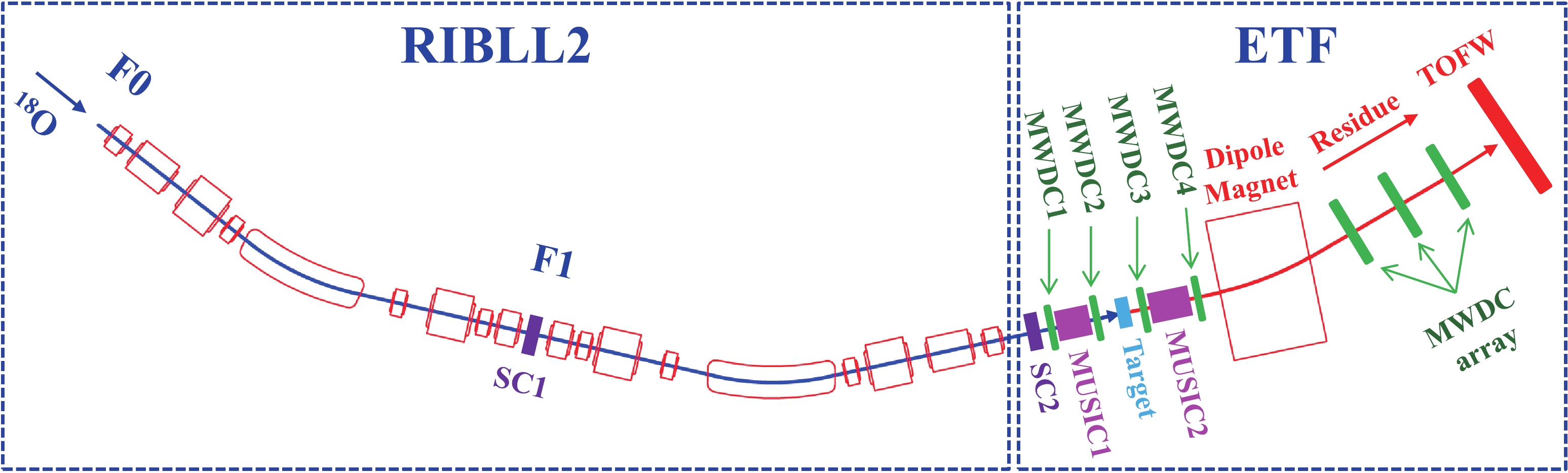
Figure 1. (color online) Schematic plot of RIBLL2 beam line and the ETF terminal. The detectors used in the experiment are also shown. See text for details.
Measurements without the reaction target were also conducted with the same beam conditions as the target-in runs. The target-out runs were employed to eliminate the contributions from reactions in the non-target material (e.g., the detection medium, the air gap between detectors). The final cross section was obtained by subtraction of the cross section obtained in the target-out run from that obtained in the target-in run. In order to eliminate the influence of reactions on the target frame, the size of the beam spot on the target was limited by applying a software gate in the off-line analysis.
-
Based on the ETF setup, a general data analysis framework including the data reduction and basic analysis procedures was developed by Y. Z. Sun et al. [27, 28]. We employed this framework and conducted a careful data analysis on an event-by-event basis. Particle identification for the ions upstream of the target was obtained. Fig. 2 displays the ion’s ΔΕ measured by MUSIC1 versus the ion’s TOF measured by SC1 and SC2. The main cluster corresponds to the 18O ions. Several spots with low statistics are other ion species, which were mainly produced from the interactions of 18O ions with the TOF stop detector, i.e., SC2 in Fig. 1.

Figure 2. (color online) Particle identification plot for the ions reached the ETF. The abscissa shows the ion’s time-of-flight from F1 to ETF, while the ordinate indicates the ion’s energy loss in the MUSIC1 detector.
For our purpose, the 18O ions upstream of the target were selected. Then, we examined the fragmentation reaction residues induced by the 18O projectiles on the C target. Fig. 3 displays the residue nuclei downstream of the C target. One can clearly see several kinds of ions in this cluster plot. The ion species with the largest intensity corresponds to the 18O ions that passed through the target. In the oxygen isotopic chain, 16O and 17O are also present. Concerning the N, C, and B isotopic chains, in total, there are more than ten isotopes that were produced and can be clearly identified. Beryllium isotopes were also seen in Fig. 3 but with very low statistics. The pileup in the ΔE direction is clearly visible in Fig. 3, especially for the 18O ions. Such pileup signals are attributed to one or multiple 18O ions accidentally intruding to the MUSIC2 detector during its processing of the present signal.

Figure 3. (color online) Cluster plot of ΔE versus A/Z for the fragmentation residues produced by the 18O ions bombarding on a carbon target at energies near 260 MeV/nucleon.
Once the PID for the ions downstream of the target was obtained, one can plot the mass distribution of fragmentation residues, as shown in Fig. 4. It is obvious that the neighboring isotopes are clearly separated, and there are three to four isotopes with relatively sufficient statistics in each isotopic chain.
The production cross section for the fragment residues is calculated as follows:
$ \begin{equation} \sigma(A,Z) = \dfrac{n_f}{n_pn_t\epsilon\eta r}, \end{equation} $

(1) where
$ n_f $ ,$ n_p $ , and$ n_t $ are the yields of residue fragments, number of projectiles, and number of target atoms per unit area, respectively. ϵ, η, and r are the geometric acceptance, PID efficiency, and pileup correction coefficient for residue nuclei, respectively. In the following paragraphs, the procedures for the determination of ϵ, η, and r are described.Concerning the geometric acceptance of the detector setup downstream of the reaction target, the acceptance in the horizontal direction is the main limitation, which is due to the relatively long distance between the TOFW and target. In order to investigate the acceptance of the setup, we carefully examined the ions' horizontal position in the TOF wall detector. It is found that some residue nuclei, namely 15,16,17N, 13,14C, and 11B, are well located within the acceptance range of the TOFW, which indicates that the present setup has a 100% geometric acceptance for these nuclei. However, several isotopes (i.e., 14N, 15C, 12C, 12,13B, and 10B) are not totally accepted by the TOFW. Following similar procedures described in Ref. [29], we fitted the ions' horizontal position distribution by a Gaussian function and used the fitted function to evaluate the missing part of the profile. Then, we calculated the geometric acceptance for each fragment residue.
Regarding the PID efficiency, the measurements using different C beams without the reaction target were employed. The PID efficiency was deduced by comparing the counts of ions that were identified upstream of the target and the number of outgoing ions that were correctly identified with the PID detectors downstream of the target (including MUSIC2, the big dipole, the MWDC array, and the TOF wall). The PID efficiency results are displayed in Fig. 5. It is evident that the PID efficiency of fragment residues ranges from 0.85 to 0.95. The typical efficiency for B isotopes is slightly smaller than that of C and N isotopes. The uncertainties of B isotopes are slightly large, which is mainly due to the low statistics.
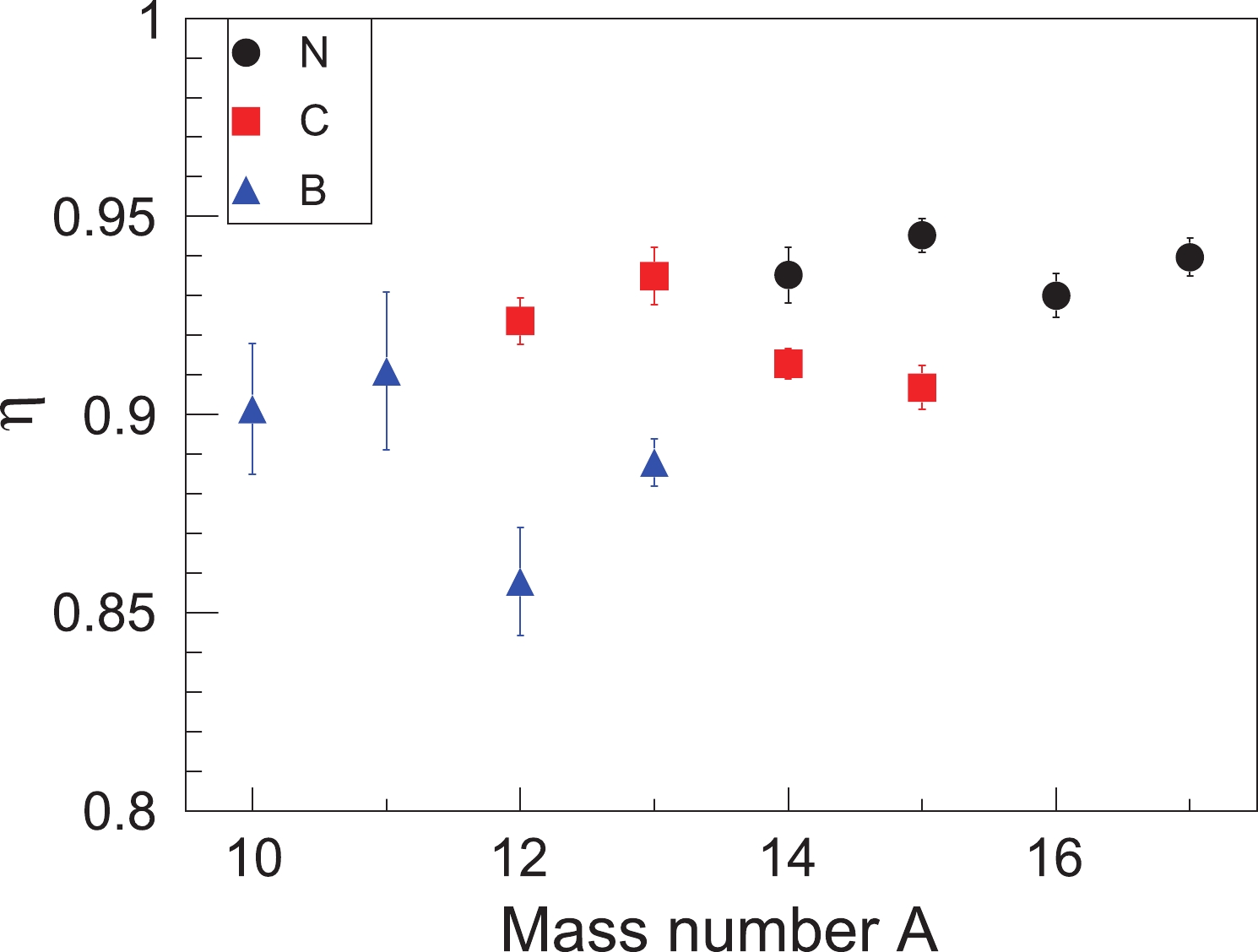
Figure 5. (color online) The PID efficiency of the setup downstream of the reaction target for N, C, and B isotopes.
In our data analysis, we assume that the pileup correction coefficient for all the ion species is the same. The measurement without the C target was employed to deduce the pileup correction coefficient. Given the fact that the 18O ions have the highest statistics downstream of the reaction target, the pileup correction coefficient is calculated as the ratio between the number of outgoing 18O ions with normal signal and the counts of total outgoing 18O ions.
Once the geometric acceptance, PID efficiency, and pileup correction coefficient are determined, one can calculate the isotopic production cross sections of fragment residuals using Eq. (1). Table 1 lists the cross section results for the N, C, and B fragments. The cross sections are of the order of several mb to several tens of mb. The uncertainties of measured cross sections include statistical and systematic contributions. It is found that the relative uncertainties of the cross sections are below 30% for most of the isotopes.
Z A σ/mb $ \Delta\sigma $ /mb

7 17 29.12 2.21 7 16 19.89 2.03 7 15 65.16 3.53 7 14 15.80 2.86 6 15 5.03 1.56 6 14 28.50 2.12 6 13 45.63 2.91 6 12 36.32 3.94 5 13 4.14 1.40 5 12 9.05 2.36 5 11 31.25 2.50 5 10 10.48 3.03 Table 1. Isotopic cross sections of nitrogen, carbon, and boron isotopes produced in the reactions of 18O projectiles impinging on a carbon target at energies near 260 MeV/nucleon. Final uncertainties including statistical and systematic uncertainties are also shown.
In order to compare our cross section results with the previous experimental data obtained from the 18O+12C fragmentation reactions as well as the theoretical model predictions, in Fig. 6, we plotted our data and existing data together with the predictions of EPAX3, FRACS, NUCFRG2, and ABRABLA. The black dots indicate the data obtained in the present experiment with 18O energy at 260 MeV/nucleon. The open squares show the data obtained from the previous experiment performed by Leistenschneider et al. with 18O energy at 573 MeV/nucleon [30], while the open triangles indicate the cross sections obtained by another experiment performed by Olsen et al. with 18O energy at 1700 MeV/nucleon [31]. The theoretical predictions for isotopic production cross section are displayed with different lines. The models used in the present work can be classified into two groups: empirical formulas (i.e., EPAX3 and FRACS) and abrasion-ablation models (i.e., ABRABLA and NUCFRG2). Here, we describe their main characteristics. EPAX3 [12] is the third version of EPAX parametrization [10]. It is a universal empirical formula for predicting the fragmentation cross sections in heavy-ion reactions. The parameters were determined by fitting the experimental cross-section data. The FRACS code [13] was developed on the basis of the EPAX parametrization with several modifications to improve the predictive power. The target and projectile energy dependencies were considered. Later, the odd-even staggering was further incorporated into the FRACS formula [14, 15]. Concerning the ABRABLA model [9], it describes the fragmentation reactions as a two-step process. The first step is the abrasion stage, in which the projectile interacts with the target at the overlapping region and the nucleons abraded from the projectile. In the ablation stage, the pre-fragments de-excite through the evaporation of the light particles. NUCFRG2 [8] is an updated version of the NUCFRG model [32], in which the collisions between projectile and target nuclei are also described by employing an abrasion-ablation picture. The collisions of nucleons are believed to depend on the nuclear density distribution, nucleon-nucleon cross sections, and surface deformation energy of the pre-fragment. This model assumes that the nuclei have uniform nuclear matter distributions. The features of the models described here are brief. A detailed review of these theoretical models can be found in Ref. [18]. In the following, firstly, we discuss the similarities and differences between the data sets displayed in Fig. 6. Then we compare the theoretical calculations with the data.
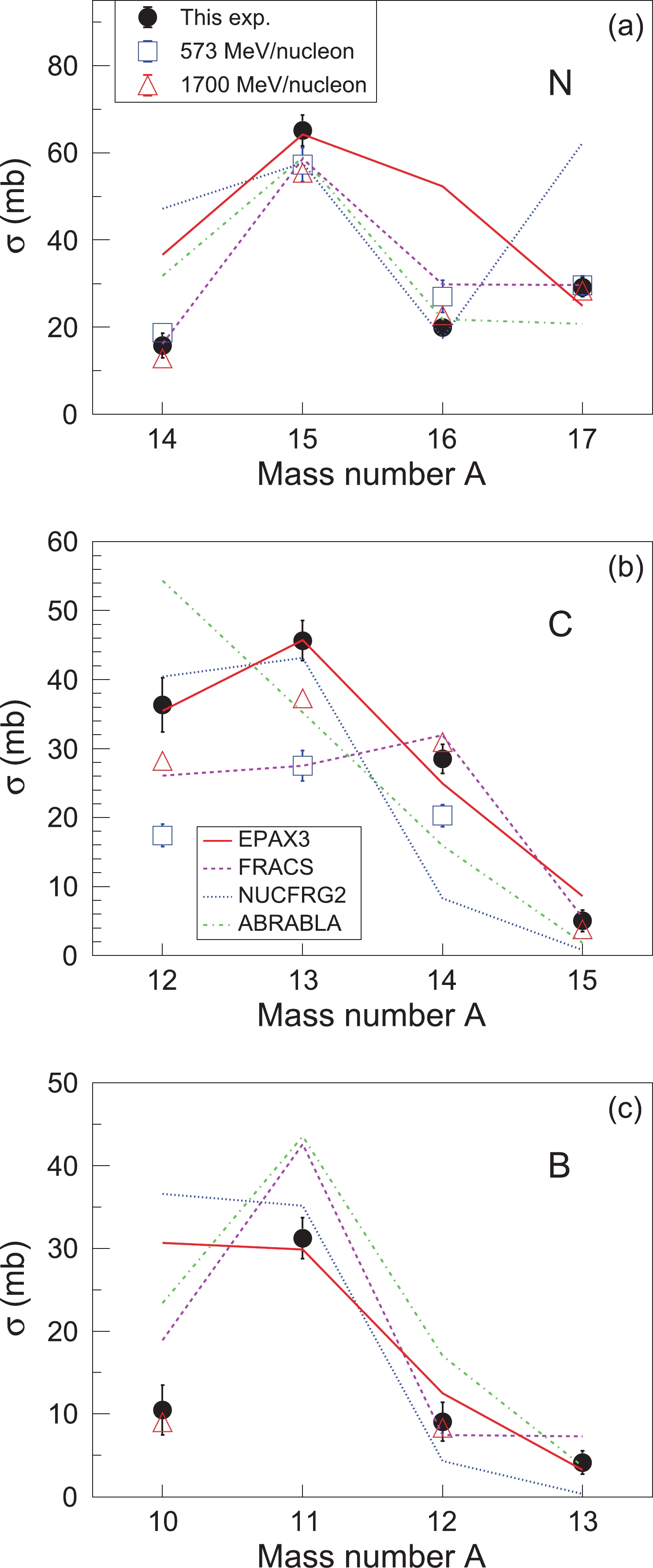
Figure 6. (color online) Isotopic production cross sections of nitrogen (a), carbon (b), and boron (c) isotopes produced by the 18O + 12C fragmentation reactions. Filled dots indicate the data obtained from the present work, while open squares and open triangles indicate those measured at 573 MeV/nucleon [30] and at 1700 MeV/nucleon [31], respectively. The solid, dashed, dotted, and dash-dotted lines depict the predictions of EPAX3, FRACS, NUCFRG2, and ABRABLA, respectively. See text for details.
For the N isotopes, the previous measurements at higher energies are in good agreement with our data. Only for 15N, we observe a small discrepancy, and the uncertainty of the present data is slightly large. Concerning the C isotopes, the situation is slightly complicated. Significant deviations are observed for the cross sections of 12,13C measured by three experiments at different energies. The production cross sections for these two nuclei seem to be energy dependent. This feature is not observed for N and B isotopes. It should be noted that the cross sections of 12,13C measured by the present work have slightly large uncertainties. Future measurements with high precision for the C isotopes are needed to examine the energy dependence and clarify this issue. As for the cross section of 14C, the data measured at 1700 MeV/nucleon beam energy agrees with our result remarkably, while the measurement at 573 MeV/nucleon beam energy provides a smaller value. The situation is similar for 15C, of which the data measured with 18O energy at 1700 MeV/nucleon is in harmony with the present data within uncertainties. Regarding the B isotopes, the present work measured the cross sections for 10−13B. Our 10,12B data are in quite good agreement with the previous measurement at 1700 MeV/nucleon beam energy. It is worth mentioning that a prominent feature of the isotopic cross section data shown in Fig. 6 is the odd-even staggering (OES), especially in the case of N residues.
Now, we compare the theoretical model predictions with the data in a qualitative manner. In Fig. 6(a), it is evident that all of the four theoretical predictions roughly reproduce the OES trend of the data. In particular, the FRACS presents an overall reasonable description of the OES strength between neighboring nitrogen isotopes. The calculations with ABRABLA reasonably reproduce the cross sections of 15,16N, while the predictions overestimate the cross section of 14N and underestimate the cross section of 17N. Similarly, the predictions of NUCFRG2 reproduce the 15,16N data but fail to describe the 14,17N data. The EPAX3 calculations reproduce our 15,17N data but strongly overestimate the cross sections of 14,16N. Regarding the model calculations for the cross sections of C isotopes, all of the four model predictions differ drastically, as shown in Fig. 6(b). EPAX3 provides an overall best description of our data with a small underestimation of the cross section for 14C. The NUCFRG2 predictions reproduce the cross sections of 12,13,15C obtained by our measurements within the uncertainties but underestimate the cross section of 14C. The ABRABLA predictions illustrate a monotonic decrease in cross sections and fail to describe the trend of data from 12C to 15C. FRACS provides a reasonable description of the cross sections for 14,15C but significantly underestimates the cross sections of 12,13C obtained by the present work. In Fig. 6(c), the EPAX3 and the NUCFRG2 predictions show a similar trend, which greatly overestimates the cross section of 10B and generally reproduces the cross sections of 11,12,13B. FRACS overestimates the cross sections of 10,11B but offers a reasonable description of the 12,13B data. ABRABLA provides a significant overestimation of the cross sections of 11,12,13B, while its prediction for 13B agrees well with the data.
-
Nuclide production cross sections were measured for a dozen of residues produced in the fragmentation of a 260 MeV/nucleon 18O beam on a C target. The measured cross sections of N and B isotopes are in good harmony with previous experimental data. The production cross sections of some C isotopes (especially 12,13C) seem to depend on the projectile energy. Future experiments and improved theoretical models are needed for better understanding of this phenomenon. The data are also compared to several theoretical model predictions. The similarities and differences between the data and calculations are qualitatively discussed.
-
The authors thank the staffs in the accelerator division of Institute of Modern Physics for providing stable beams.
Isotopic production cross sections of fragmentation residues produced by 18O ions on a carbon target near 260 MeV/nucleon
- Received Date: 2022-06-08
- Available Online: 2022-11-15
Abstract: The isotopic cross sections of residual nuclei produced in fragmentation reactions of 18O projectiles impinging on a carbon target at energies near 260 MeV/nucleon were measured at the HIRFL facility in Lanzhou (China). A full identification of atomic and mass numbers of fragments was achieved from the determination of their magnetic rigidity, energy loss, and time of flight. The production cross sections for a dozen of nitrogen, carbon, and boron isotopes were determined with uncertainties below 30% for most of the cases. The obtained cross sections for N and B isotopes show a rather good agreement with previous experimental data obtained with different projectile energies. The cross sections for some C isotopes seem to exhibit a dependence on the projectile energy. A comparison of the data and several theoretical model calculations are presented.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: