-
Theory of General Relativity (GR) is so far the most accepted theory of gravity. Recently, it has been verified by gravitational waves observed by LIGO [1]. The observation of the images of supermassive black hole shadows at the center of the nearby galaxy M87 and also at the center of our own galaxy by the Event Horizon Telescope (ETH) collaboration [2, 3] further confirms GR. However, there are still some unresolved issues such as the accelerated expansion of our Universe, which cannot be completely explained by the theory of GR. The presence of the cosmological constant in the field equations of GR may be a candidate to explain the accelerated expansion of the Universe [4−10]. Alternatives have so far been proposed to explain the behavior of dark energy, and of them, the quintessence matter field is a well-accepted alternative form of dark energy [11–13]. For example, Kiselev proposed a black hole solution with the quintessence represented by the equation of state
$ p = \omega_{q}\rho $ , where$ \omega_q $ is given in the range$ (-1;-1/3) $ [14] and$ (-1;-2/3) $ [15]. In contrast to the quintessence, the case of$ \omega_{q}=-1 $ corresponds to the vacuum energy represented by the cosmological constant Λ. In addition to the effect of string clouds, which are assumed as a collection of strings formed in the early era after the big-bang in the structuring of the Universe, due to the asymmetry breaking, has also been considered in the study of black hole spacetime [16]. The dynamics of test particles and photons in the vicinity of these stringy static black holes have been analyzed [17–19].Recent experiments associated with BlackHoleCam and the EHT have provided the shadows of the supermassive black hole that exists at the center of the M87 galaxy and milky way galaxy [2, 3]. Note that the black hole shadow reflects the gravitational lensing, and thus black hole shadows and gravitational lensing effects are of primary importance to test the GR and deeply understand the nature of the background geometry very near to the black hole horizon. Further, the study of black hole shadow and gravitational lensing may be helpful in constraining the parameters of different alternative theories of gravity. There exists a vast literature on these lines (see, for example, [20–36]). Gravitational lensing is currently the main astrophysical test in GR to provide information on the geometry of the compact objects. In this regard, gravitational lensing in both weak and strong field regimes has also become very important in understanding unexplored properties of gravitational compact objects. The strong gravitational lensing was proposed and considered by Virbhadra and Ellis [37]. Following that, an extensive body of work has been done in a wide variety of contexts [see, for example, [38–50]]. From an astrophysical point of view, all photons mostly go through a plasma medium. On the other hand, the plasma medium can affect angular positions of an equivalent image, thus giving various wavelengths in observations. Therefore, this is the most intriguing and important reason to consider the plasma medium in the analysis of gravitational lensing. Thus, a large amount of work has addressed the impact of plasma medium on the gravitational lensing effects in the weak field regime [51–64].
In this study, we use the method by Gibbons and Werner, who proposed a new methodology to calculate weak deflection angle using the Gauss-Bonnet theorem (GBT) of asymptotically flat spacetime [65]. Werner has applied it to stationary spacetimes using the Finsler-Randers type geometry [66]. Moreover, Ishihara et al. have extended the method of Gibbons and Werner to non-asymptotically flat spacetimes using the finite distance corrections of the source and the receiver [67, 68]. Further, Ono et al. have showed that it also works for the axisymmetric spacetimes [69]. Li et al. have studied the finite distance method using the massive particles and Jacobi-Maupertuis Randers-Finsler metric within the framework of the GBT [70, 71]. Crisnejo and Gallo have calculated the weak deflection angle in a plasma medium using GBT [72]. The study of gravitational lensing for black holes has also been reported [73–96]. In this study, we investigate the shadow and gravitational lensing in the weak field limit in the Schwarzschild black hole spacetime with the string cloud and quintessence background. We use the data released by the EHT collaboration for M87* and Sgr A* to restrict the string cloud parameter a and the quintessence parameter γ.
The rest of this paper is organized as follows. In Sec. II, we discuss the spacetime metric of the Schwarzschild black hole in the presence of string cloud in quintessential background. In Sec. III, we study the effects of the string clouds and quintessence on the shadow of the Schwarzschild black hole. In the same section, we also investigate the effects of string clouds and quintessence on the energy emission rate for the Schwarzschild black hole. We analyze the weak deflection angle of the photon beam by the Schwarzschild black hole in string clouds with the quintessential field in Sec. IV. Finally, in Sec. V, we conclude our work.
-
In this section, we derive the Kiselev black hole in the background of string clouds. The detailed solution has already been derived in the Refs. [96, 97].
Here the action can be represented as
$ \begin{equation} S=\frac{1}{2}\int{{\rm d}x^4\sqrt{-g}}(R - L_{m}), \end{equation} $

(1) where g stands for the determinant of the metric tensor
$ g_{\mu\nu} $ , R represents the scalar curvature, and$ L_{m} $ denotes the matter parts of the action. It should be mentioned that the matter part further consists of two parts, namely the string clouds and the quintessence, i.e.,$ L_m=L_s+L_q $ , and are defined below.The Lagrangian density for the string clouds is given by [97]
$ \begin{equation} L_s=k\left(-\frac{1}{2}\Sigma^{\mu\nu}\Sigma_{\mu\nu} \right), \end{equation} $

(2) where the constant k is related to the tension of the string and the bivector
$ \begin{equation} \Sigma^{\mu\nu}=\epsilon^{a\beta}\frac{\partial x^\mu}{\partial \lambda^{a}}\frac{\partial x^\nu}{\partial \lambda^{\beta}}. \end{equation} $

(3) In the last equation,
$ \epsilon^{a \beta} $ is the two-dimensional Levi-Civita tensor, and$ \lambda^{a} (\lambda^{a}=\lambda^0, \lambda^1) $ is used for the parameterization of the world sheet that is described by the string with the induced metric [97]$ \begin{equation} h_{a \beta}=g_{\mu\nu}\frac{\partial x^\mu}{\partial \lambda^{a}}\frac{\partial x^\nu}{\partial \lambda^{\beta}}. \end{equation} $

(4) The
$ \Sigma^{\mu \nu} $ describes the following identities [97, 98]:$ \begin{equation} \Sigma^{\mu [a}\Sigma^{\beta \sigma]}=0,\quad \nabla_\mu\Sigma^{\mu [a}\Sigma^{\beta \sigma]}=0, \quad \Sigma^{\mu a}\Sigma_{a\sigma}\Sigma^{\sigma \nu}={\boldsymbol h} \Sigma^{\nu\mu}, \end{equation} $

(5) where
$ {\boldsymbol h} $ denotes the determinant of$ h_{a \beta} $ . Varying the Lagrangian density with respect to$ g_{\mu\nu} $ , one obtains [98]$ \begin{equation} T^{\mu\nu}=\rho_s\frac{\Sigma^{\mu a}\Sigma^{\nu}_{a}}{\sqrt{-\boldsymbol h}}, \end{equation} $

(6) where
$ \rho_s $ stands for the string cloud density. Using the three identities given above in (5), one obtains$ \partial_\mu(\sqrt{-g}\Sigma^{\mu a})=0 $ . Therefore, for the spherically symmetric static spacetime, the non-zero components of the stress-energy-momentum tensor in the background of string clouds are [99, 100]$ T_{0}^0=T_{1}^1=-\frac{a}{r^2}\, , $

(7) $ T_{2}^2=T_{3}^3=0\, , $

(8) where the cloud of strings corresponds to the constant a. The line element is then given by [101]
$ \begin{eqnarray} {\rm d} s^2=-\left(1-a-\frac{R_s}{r}\right){\rm d}t^2+\left(1-a-\frac{R_s}{r}\right)^{-1}{\rm d}r^2 + r^2 {\rm d}\Omega^2. \end{eqnarray} $

(9) Throughout, we use
${\rm d}\Omega^2={\rm d}\theta^2 + \sin^2\theta {\rm d}\phi^2$ and$ R_s=2M $ , where M refers to the black hole mass. In the above metric, one can find the black hole horizon as follows:$ \begin{eqnarray} r_{H}=\frac{2M}{1-a}\, . \end{eqnarray} $

(10) From the above Eq. (10), one can see that the horizon radius increases/enlarges in the case when
$ a<1 $ . For our analysis, we focus on the case$ a<1 $ since it acts as an attractive gravitational charge. It is worth noting that the string cloud model has been proposed to explain the field theory that stems from distance interactions existing between particles. Accordingly, these interactions correspond to a particular behavior of a gravitational field. Hence, it is assumed that this gravitational field can be produced by the elements of strings. With this in mind, the abovementioned string cloud parameter a can be proposed to reveal a reasonable behaviour of such field theory. Thus, it is potentially important to understand more deeply the nature of string cloud parameter a to bring out its effect on the astrophysical phenomena, such as the black hole shadow and deflection angle of light.For the quintessence part we formulate [102]
$ \begin{equation} L_q=-\frac{1}{2}g^{\mu\nu}\partial_\mu\varphi \partial_\nu\varphi-V(\varphi), \end{equation} $

(11) where φ represents the quintessence field and
$ V(\varphi) $ stands for the potential term. The non-zero components of the stress-energy-momentum tensor of the matter fluid for the Kiselev black hole solution are given as [16, 97]$ \begin{eqnarray} T_{0}^0=T_{1}^1=\rho_{q}\, , \end{eqnarray} $

(12) $ \begin{eqnarray} T_{2}^2=T_{3}^3=-\frac{\rho_{q}}{2}(3\omega_q+1)\, , \end{eqnarray} $

(13) where
$ p_q $ and$ \rho_q $ denote, respectively, the pressure and density of the quintessence, and$ \omega_q $ represents the equation of state parameter for the quintessence. The Kiselev black hole line element is$ \begin{aligned}[b] {\rm d}s^2=&-\left(1-\frac{R_s}{r}-\frac{\gamma}{r^{3\omega_q+1}}\right){\rm d}t^2 \\ &+\left(1-\frac{R_s}{r}-\frac{\gamma}{r^{3\omega_q+1}}\right)^{-1}{\rm d}r^2 + r^2 {\rm d}\Omega^2\, , \end{aligned} $

(14) where the density
$ \begin{eqnarray} \rho_{q}=-\frac{\gamma}{2}\frac{3\omega_q}{r^{3\omega_q+1}}\, , \end{eqnarray} $

(15) and γ is used as the quintessence parameter.
The Kiselev black hole was then analyzed in the background of the string clouds [16]. It was assumed that the quintessence and the string clouds are not interacting and the surviving components of the total stress-energy-momentum tensor for the two matter-energy contents were obtained as [16]
$ \begin{eqnarray} T_{0}^0=T_{1}^1=\rho_{q}+\frac{a}{r^2}\, , \end{eqnarray} $

(16) $ \begin{eqnarray} T_{2}^2=T_{3}^3=-\frac{\rho_{q}}{2}(3\omega_q+1)\, . \end{eqnarray} $

(17) The Kiselev black hole with string clouds is given as [16, 96]
$ \begin{aligned}[b] {\rm d}s^2=&-\left(1-a-\frac{R_s}{r}-\frac{\gamma}{r^{3\omega_q+1}}\right){\rm d}t^2\\ &+\left(1-a-\frac{R_s}{r}-\frac{\gamma}{r^{3\omega_q+1}}\right)^{-1}{\rm d}r^2 + r^2 {\rm d}\Omega^2\, . \end{aligned} $

(18) Note that γ and
$ \omega_q $ , respectively, represent the quintessential field parameter and the equation of state parameter. The quintessence equation of state is given as$ p_q=\omega_{q}\rho_q $ , with$ \omega_q\in(-1;-1/3) $ . It is worth noting here that$ \omega_q=-1 $ refers to the matter field with the vacuum energy defined by the cosmological constant Λ, while$ \omega_q=-1/3 $ represents another matter field and corresponds to the frustrated network of cosmic strings (for detail see, for example, [103, 104]). With this in mind, we further restrict ourselves to the case$ \omega_q=-2/3 $ that implicitly describes the pure quintessential field. The above metric (18) reduces to the Schwarzschild metric in the case of$ a=0 $ and$ \gamma=0 $ . For the structure of the horizon of the metric represented by (18), see Ref. [16].Let us then introduce the black hole horizon. The horizon is located at the root of
$ \gamma r^2+r(a-1)+2M=0 $ , which solves to give$ \begin{eqnarray} r_{H}&&=\frac{1-a-\sqrt{a^2-2 a-4R_s \gamma+1}}{\gamma}\, , \end{eqnarray} $

(19) $ \begin{eqnarray} r_{q}&&=\frac{1-a+\sqrt{a^2-2 a-4R_s \gamma+1}}{\gamma}\, , \end{eqnarray} $

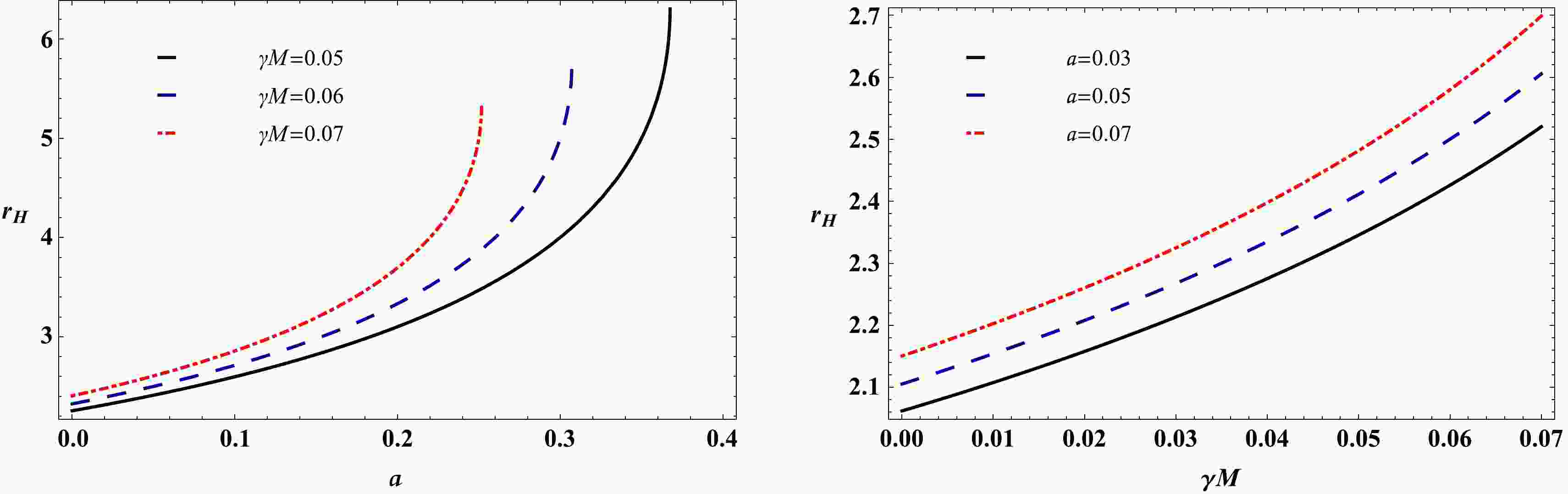
(20) where
$ r_h $ and$ r_q $ refer to the black hole horizon and the quintessential cosmological horizon, respectively. Interestingly, it turns out that the cosmological horizon never vanishes regardless of the fact that there exists no source. We note that the cosmological horizon is located at a distance far away from the black hole. In Fig. 1, we show the black hole horizon as a function of the string cloud parameter a and the quintessence parameter γ. From Fig. 1, we see that, as the parameters a and γ increase, the event horizon also increases. -
The Lagrangian for the spacetime metric (18) with
$ \omega_q={-2}/{3} $ is$ \begin{eqnarray} \mathcal{L}=m\bigg(-f(r)\frac{\dot{t}^{2}}{2}+\frac{\dot{r}^{2}}{2f(r)}+\frac{r^{2}}{2}(\dot{\theta}^{2}+\sin^{2}\theta \dot{\phi}^{2})\bigg), \end{eqnarray} $

(21) with
$ f(r)=1-a-\frac{R_s}{r}-\gamma r $ . For (21), there are two conserved quantities: the specific angular momentum$ \mathfrak{L} $ and the specific energy$ \mathcal{E} $ , given as [18]$ \begin{eqnarray} \dot{t}=-\mathcal{E}\left(f(r)\right)^{-1},\;\;\;\;\dot{\phi}=\frac{\mathfrak{L}}{r^{2}\sin^{2}\theta} .\end{eqnarray} $

(22) Restricting ourselves to the equatorial plane, we take
$ \theta=\dfrac{\pi}{2} $ , and (21) becomes$ \begin{equation} -f(r)\dot{t}^{2}+\frac{\dot{r}^{2}}{f(r)}+r^{2}\dot{\phi}^{2}=-\lambda, \end{equation} $

(23) where
$ \lambda=0 $ and$ \lambda=1 $ corresponds to the null and timelike geodesics, respectively. By using the normalization condition, the equation of motion becomes$ \begin{equation} \bigg(\frac{{\rm d}r}{{\rm d}\chi}\bigg)^{2}+ V_{\rm eff}(r)=\mathcal{E}^{2}, \end{equation} $

(24) where
$V_{\rm eff}(r)$ denotes the effective potential and expressed as$ \begin{equation} V_{\rm eff}(r)= f(r)\left(\lambda+\frac{{\mathfrak{L}}^2}{r^2}\right), \end{equation} $

(25) For the current analysis,
$ \mathcal{E}^2 $ and$ \mathfrak{L}^2 $ are expressed as [18]$ \begin{eqnarray} \mathcal{E}^{2}&&=\frac{2 r}{r^2 \left(-\dfrac{2}{r (a+\gamma r-1)+R_s}-\gamma\right)+R_s}, \end{eqnarray} $

(26) $ \begin{eqnarray} \mathfrak{L}^{2}=\frac{r^4 \left(\gamma - \frac{R_s}{r^2}\right)}{r^2 \left(-\dfrac{2}{r (a+\gamma r-1)+R_s}-\gamma\right)+R_s}. \end{eqnarray} $

(27) We then consider the photon orbit around the Schwarzschild black hole surrounded by quintessential field in the string cloud background. The photon orbit
$r_{\rm ph}$ can be derived from the standard condition${V}_{\rm eff}'=0$ with$ \lambda=0 $ and we can formulate the orbit$r_{\rm ph}$ as$ \begin{eqnarray} r_{\rm ph}&&=\frac{1-a-\sqrt{a^2-2 a-3R_s \gamma+1}}{\gamma}\, . \end{eqnarray} $

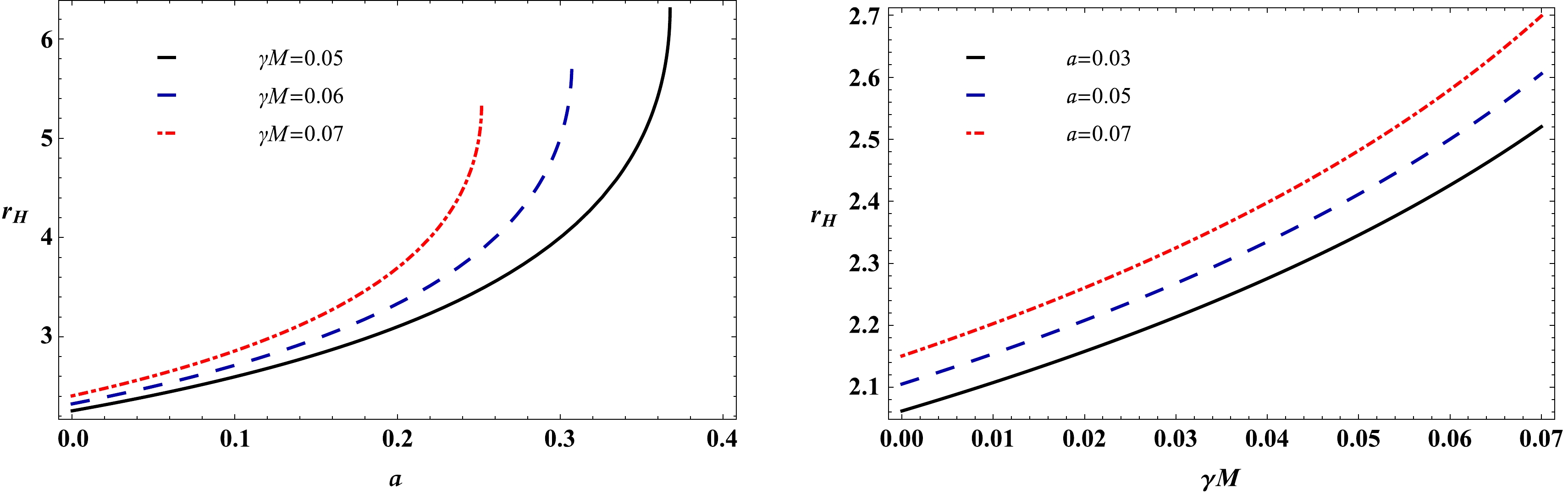
(28) From the above equation, it is easily seen that the photon orbit
$r_{\rm ph}$ reduces to the one for the Schwarzschild case when$ a\to0 $ and$ \gamma\to 0 $ . In Fig. 2, we show the radius of the photon sphere with respect to the quintessence parameter γ and string cloud parameter a. In Fig. 2, the left panel represents the effect of the string cloud parameter a on the radius of the photon sphere, while the right panel shows the impact of the quintessence parameter γ on the radius of the photon sphere. As can be seen from Fig. 2, the radius of the photon sphere shifts upward as a consequence of an increase in the values of both the parameters a and γ, thus resulting in an increase in the radius of the photon sphere. -
In string theory, the one-dimensional strings are considered to be the fundamental building blocks of nature instead of elementary particles. In gravity, the one-dimensional analogue of a cloud of dust is taken as a cloud of string [16] to investigate the possible measurable effects of these clouds on the strong gravitational fields of black holes. Letelier was the first to generalize the Schwarzschild black hole solution in the presence of spherically symmetric static cloud of string and has obtained some interesting features of the resulting black hole spacetime [101]. The Letelier generalization of the Schwarzschild black hole was in the sense that the metric of the black hole spacetime with clouds of strings corresponds locally to the geometry of the Schwarzschild spacetime with a solid deficit angle from the metric of the Schwarzschild black hole with clouds of strings and quintessence. From the above, one can infer that the string cloud parameter a is responsible for the solid deficit angle. The quintessence dark energy has its own role in the theory of gravity, especially in the surrounding of a black hole, as discussed in the first section above. Consequently, in this subsection, we explore the shadow of the Schwarzschild black hole in the string cloud background with quintessential dark energy. For the angular radius of the black hole shadow, we consider [105, 106]
$ \begin{eqnarray} \sin^2\alpha_{\rm sh}=\frac{h(r_{\rm ph})^2}{h(r_{\rm obs})^2}, \end{eqnarray} $

(29) where
$ \begin{eqnarray} h(r)^2=\frac{g_{22}}{g_{00}}=\frac{r^2}{f(r)}, \end{eqnarray} $

(30) $\alpha_{\rm sh}$ is the angular radius of the black hole shadow, and$r_{\rm obs}$ is the observe position. We assume that distant observer$r_{\rm obs}$ is located at the cosmological radius$ r_q $ , which is located at the distance far away from the black hole. It is worth noting that, in an astrophysical-realistic scenario, the quintessential field parameter γ is supposed to be constant in the Universe and extremely small, and thus, the cosmological horizon is supposed to be located at large distances. The quantity$r_{\rm ph}$ is the radius of the photon sphere as mentioned previously.Now we combine Eqs. (29) and (30), and for an observer, Eq. (29) takes the following form:
$ \begin{eqnarray} \sin^2 \alpha_{\rm sh}=\frac{r_{\rm ph}^2}{f(r_{\rm ph})}\frac{f(r_{\rm obs})}{r^2_{\rm obs}}. \end{eqnarray} $

(31) One can find the radius of black hole shadow for an observer at a large distance using Eq. (31) as [105]
$ \begin{eqnarray} R_{\rm sh}=r_{\rm obs} \sin \alpha_{\rm sh} = \frac{r_{\rm ph}}{\sqrt{f(r_{\rm ph})}}{\sqrt{f(r_{\rm obs})}}. \end{eqnarray} $

(32) Finally, Eq. (32) can explain the shadow of a static black hole. In order to discuss the size and the shape of the shadow of the Schwarzschild black holes surrounded by the clouds of string and quintessence, we may show black hole shadow plots using two celestial coordinates for the observer [20, 107], namely X and Y (where
$R_{\rm sh}=\sqrt{X^2+Y^2}$ ); using the above equation, black hole shadows are represented in Figs. 3, 4, 5, and 6.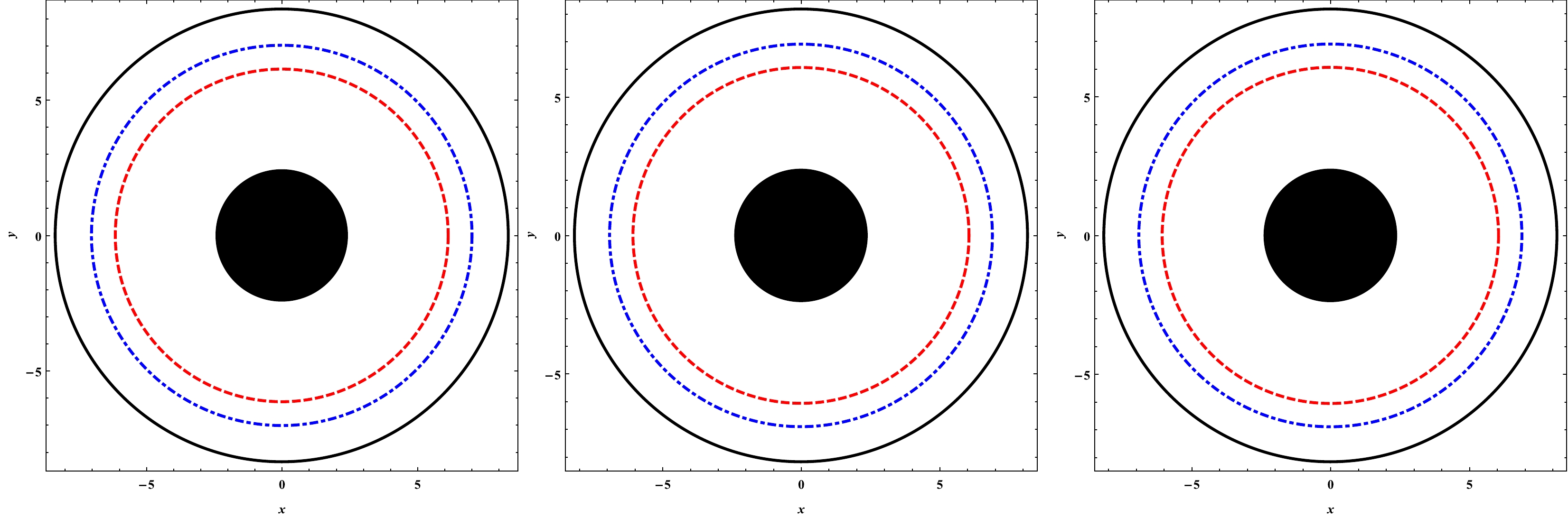
Figure 3. (color online) The shadows of black hole with
$ a=0.05 $ (left panel),$ a=0.03 $ (middle panel), and$ a=0.01 $ (right panel) for three different values of the quintessence parameter$ \gamma M=0.05 $ ,$ \gamma M=0.03 $ , and$ \gamma M=0.01 $ , from the outer circle to inner circle, respectively.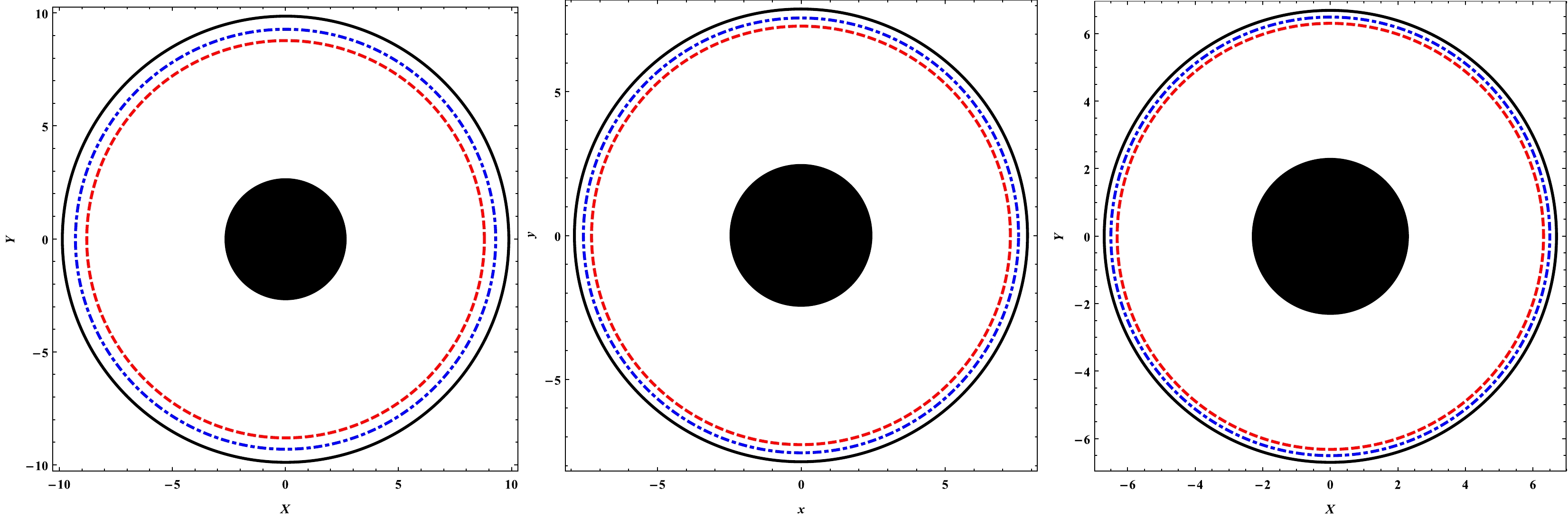
Figure 4. (color online) The shadows of black hole with
$ \gamma M=0.05 $ (left panel),$ \gamma M=0.03 $ (middle panel), and$ \gamma M=0.01 $ (right panel) for three different values of the string cloud parameter$ a=0.05 $ ,$ a=0.03 $ , and$ a=0.01 $ , from the outer circle to inner circle, respectively.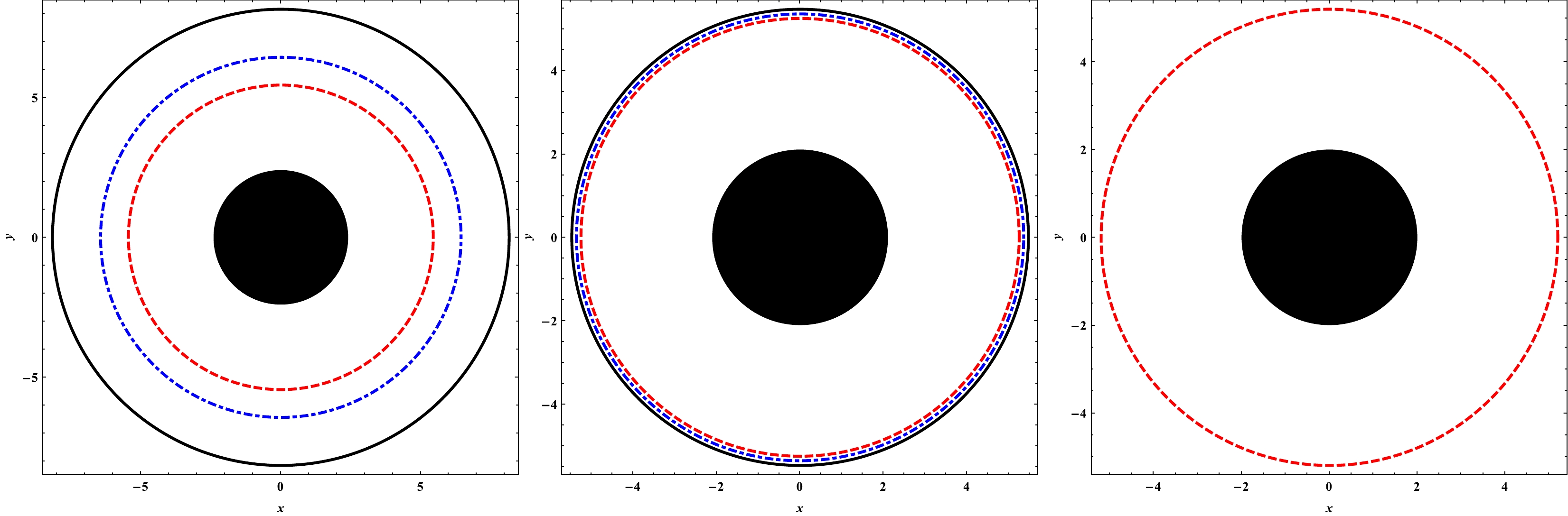
Figure 5. (color online) The shadows of black hole with
$ a=0.0 $ (left panel) for$ \gamma M=0.05 $ ,$ \gamma M=0.03 $ , and$ \gamma M=0.01 $ . Shadows of black hole with$ \gamma M=0.0 $ (right panel) for three different values of$ a=0.05 $ ,$ a=0.03 $ , and$ a=0.01 $ , from the outer circle to inner circle, respectively. The last panel shows the Schwarzschild black hole shadow.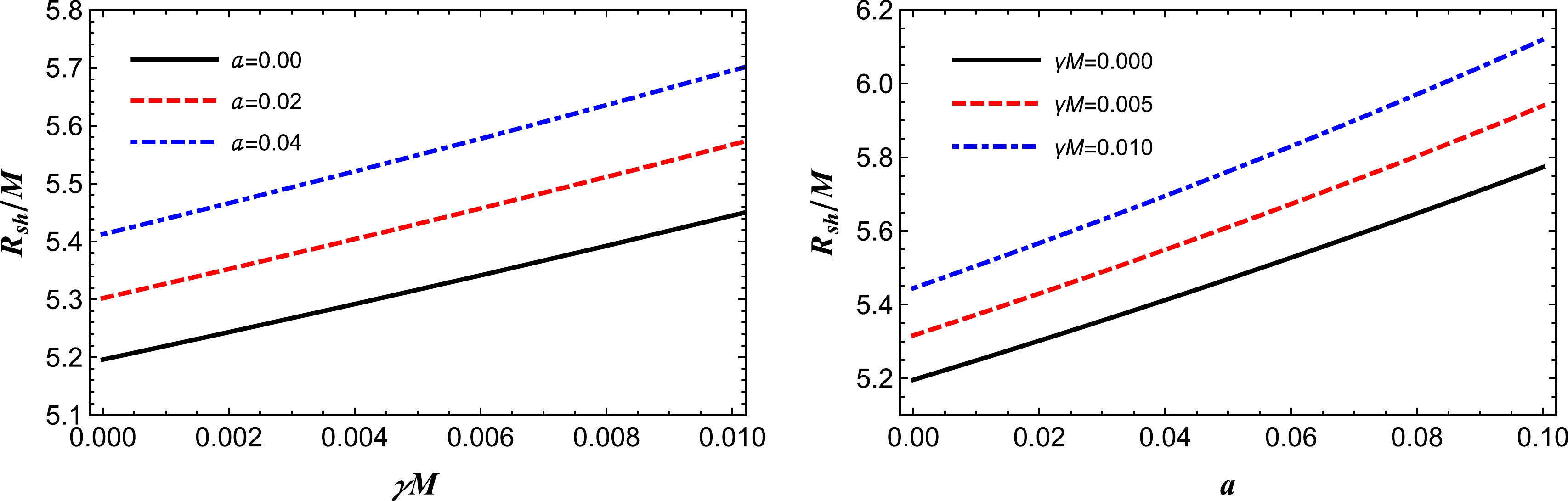
Figure 6. (color online) The dependence of the black hole shadow radius on the quintessential field parameter
$ \gamma M $ and the string cloud parameter a. Left panel: the shadow radius is plotted for various combinations of a. Right panel: the shadow radius is plotted for various combinations of$ \gamma M $ .From Fig. 3 below, we can see that, for a fixed value of the quintessence parameter γ, the effect of the string cloud parameter a on the radius of the black hole shadow is negligible. In the same figure, we can observe that the radius of the black hole shadow increases with the parameter γ. This suggest that the gravitational field becomes stronger in the presence of quintessence. This also confirms the repulsive nature of the quintessence dark energy. In Fig. 4, for increasing γ, we see an increase in the radius of the shadow of the black hole. In the same figure, we observe that the effect of the parameter a on the radius of the black hole shadow is nearly similar to that of the parameter γ. We see that the radius of the shadow increases as the value of the parameter a increases. This can be interpreted as an effect of string clouds strengthening the gravitational field. In Fig. 5, we notice that, if the parameter
$ a=0 $ , i.e., there are no string clouds, with a decrease in the parameter γ, the radius of the shadow shrinks. Similarly, if there is no quintessence, i.e.,$ \gamma=0 $ , as the parameter a decreases, the radius of the shadow also decreases. In the right panel of Fig. 5, we have the radius of the pure Schwarzschild black hole shadow. Here, we see in the absence of the string clouds and quintessence, i.e., when both the parameters$ a=0 $ and$ \gamma=0 $ , we have a smaller radius of the shadow. Hence, the presence of both the string clouds and the quintessence push the black hole shadow outwards, and therefore, the combined effect of both the quintessences and cloud of strings is attractive in nature and increases the strength of the gravitational field. The effect of both parameters is clearly shown in Fig. 6. This explicitly shows that$R_{\rm sh}$ increases with increasing a and γ. Further, we noticed that the size of the Schwarzschild black hole shadow is more sensitive to the quintessence parameter than the string cloud parameter.From a quantitative perspective, we try to theoretically explore the upper limits of parameters γ and a. For that, we constrain these two parameters using the observational data provided by the EHT collaboration for M87* and Sgr A* as a consequence of their shadows. For M87*, it is well known [2] that the angular diameter of the shadow, the distance from the Earth, and its mass have been reported as
$ \theta_{\rm{M87*}} = 42 \pm 3 \:\mu $ as,$ D = 16.8 $ Mpc, and$M_{\rm{M87*}} = 6.5 \pm 0.90 \times 10^9 \: M_\odot$ , respectively. For Sgr A*, the data have been provided in a recent EHT collaboration paper [108]. The abovementioned parameters for M87* in the case of Sgr A* are$ \theta_{\rm{Sgr A*}} = 48.7 \pm 7 \:\mu $ as (EHT),$ D = 8277\pm33 $ pc, and$M_{\rm{Sgr A*}} = 4.3 \pm 0.013 \times $ $ 10^6 \: M_\odot$ (VLTI) [108]. Based on the data, we are able to evaluate the diameter of the shadow size per unit mass using the expression [34]$ \begin{equation} d_{\rm{sh}} = \frac{D \theta}{M}\,. \end{equation} $

(33) One can then be allowed to obtain the shadow diameter theoretically via
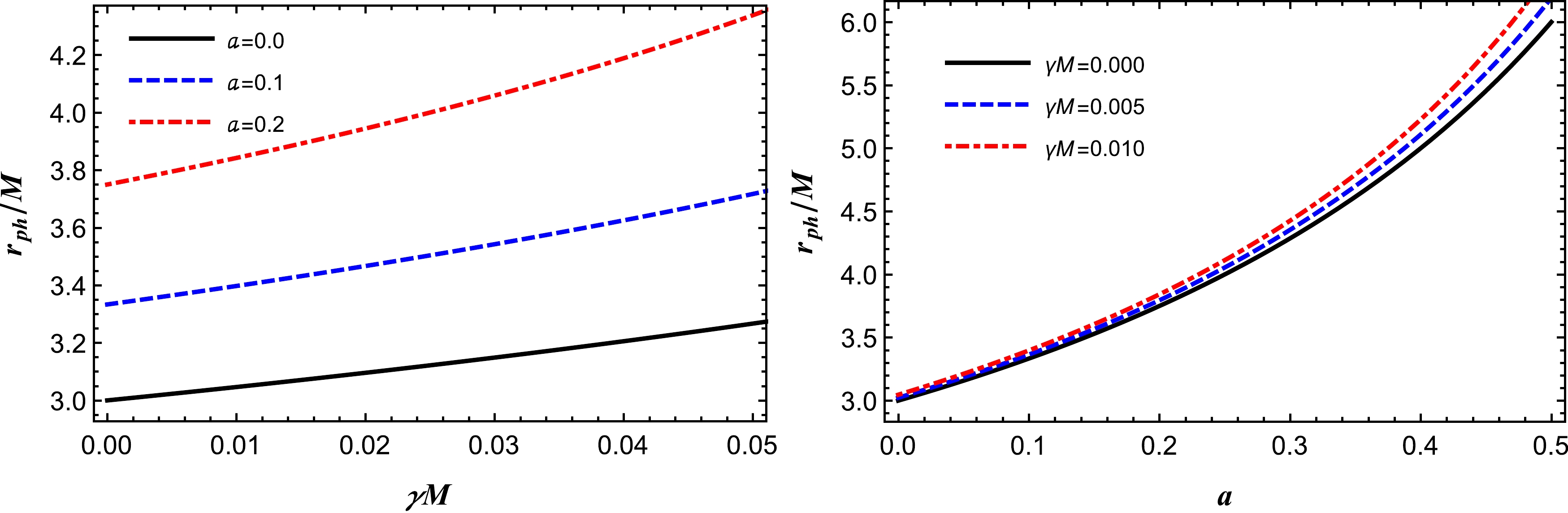
$ d_{\rm{sh}}^{\rm{theo}} = 2R_{\rm{sh}} $ . Following the literature [2, 34, 108], it is then straightforward to obtain the diameter of the shadow image as follows:$ d^{\rm{M87*}}_{\rm{sh}} = (11 \pm 1.5)M $ for M87* and$ d^{\rm{Sgr A*}}_{\rm{sh}} = (9.5 \pm 1.4)M $ for Sgr A*. Following the data results, we find the upper values of γ and a for the supermassive black holes in the galaxy M87 and Sgr A* and show these values in Table 1. Interestingly, we observe that the upper limit of the quintessential parameter γ decreases once the string cloud parameter a grows. From this, we can expect that the effect from the string cloud would be a bit larger on the geometry as compared to the one for the quintessential field. The behavior summarized in Table 1 is also demonstrated in Fig. 7. As can be seen from Fig. 7, the upper threshold value of γ would be larger for the supermassive black hole in the galaxy M87 as compered to Sgr A*.$a_{\rm M87*}$ 

$ 0.01 $ 

$ 0.02 $ 

$ 0.03 $ 

$ 0.04 $ 

$ 0.05 $ 

$\gamma_{\rm M87*}$ 

0.0329 0.0307 0.0284 0.0262 0.0239 $a_{\rm Sgr A*}$ 

$ 0.01 $ 

$ 0.02 $ 

$ 0.03 $ 

$ 0.04 $ 

$ 0.046 $ 

$\gamma_{\rm Sgr A*}$ 

0.0080 0.0058 0.0036 0.0015 0.0000 Table 1. The upper values of γ and a are tabulated for the supermassive black holes M87* and the Sgr A*. Note that we set
$ M=1 $ . -
Due to the quantum fluctuations in a black hole spacetime, the creation and annihilation of pairs of particles take place in the vicinity of the horizon of the black hole. During this process, particles having positive energy escape from the black hole through quantum tunneling. In the region where the Hawking-radiation takes place, the black hole evaporates in a definite period of time. In this subsection, we consider the associated rate of the energy emission. Near a limiting constant value
$\sigma_{\rm lim}$ , at a high energy, the cross section of absorption of a black hole modulates slightly. As a consequence, the shadow cast by the black hole causes the high energy cross section of absorption by the black hole for the observer located at finite distance$ r_0 $ . The limiting constant value$\sigma_{\rm lim}$ , which is related to the radius of the photon sphere is given as [106]$ \begin{equation} \sigma_{\rm lim} \approx \pi R_{\rm sh}^2, \end{equation} $

(34) where
$R_{\rm sh}$ denotes the radius of the black hole shadow. The equation for the rate of the energy emission of a black hole is [106]$ \begin{equation} \frac{{\rm d}^2 {\cal E}}{{\rm d}\omega {\rm d}t}= \frac{2 \pi^2 \sigma_{\rm lim}}{\exp[{\omega/T}]-1}\omega^3, \end{equation} $

(35) where
$ T=\kappa/2 \pi $ is the expression for the Hawking temperature and κ is the notation used for the surface gravity. Combining Eq. (34) with the Eq. (35), we arrive at an alternate form for the expression of emission energy rate as$ \begin{equation} \frac{{\rm d}^2 {\cal E}}{{\rm d}\omega {\rm d}t}= \frac{2\pi^3 R_{\rm sh}^2}{{\rm e}^{\omega/T}-1}\omega^3. \end{equation} $

(36) Variation in the energy emission rate with respect to the frequency of photon ω, for different values of the parameters a and γ is represented in Fig. 8. We see that, with an increase in the values of the parameters b and γ, the peak of the graph of the rate of the energy emission increases. This indicates that, for a higher energy emission rate, the evaporation of the black hole is high.
-
In this section, we study the effect of a string cloud on the weak deflection angle by the Schwarzschild black hole with quintessential energy. For this purpose, we will use the notion of the GBT.
First, we obtain the corresponding optical metric for the Schwarzschild black hole in the string cloud background with quintessential field given in 18 as follows:
$ \begin{equation} {\rm d} \sigma ^ { 2 } = g _ { i j } ^ { \mathrm { opt } } {\rm d} x ^ { i } {\rm d} x ^ { j } =\frac{1}{f(r)}\left(\frac{{\rm d} r^{2}}{f(r)}+r^2 {\rm d} \phi^{2}\right), \end{equation} $

(37) where
$ f(r)=\left(1-a-\dfrac{2 M}{r}-\dfrac{\gamma}{r^{3\omega_q+1}}\right) $ .We obtain the Gaussian curvature for the above optical metric as follows:
$ \begin{aligned}[b] \mathcal{K}\approx & \frac{9 a \gamma \omega _q}{2 r^3}-\frac{3 a \gamma \omega _q \log (r)}{r^3}+\frac{a \gamma}{r^3}+\frac{2 a M}{r^3}+\frac{6 \gamma M \omega _q}{r^4} \\&-\frac{9 \gamma M \omega _q \log (r)}{r^4}+\frac{3 \gamma M}{r^4}-\frac{9 \gamma \omega _q}{2 r^3} \\&+\frac{3 \gamma \omega _q \log (r)}{r^3}-\frac{\gamma}{r^3}-\frac{2 M}{r^3}, \end{aligned} $

(38) noting that there is a contribution from the cloud of strings on the Gaussian curvature. Then, we have
$ \begin{equation} \frac{{\rm d}\sigma}{{\rm d}\phi}\bigg|_{C_{R}}= \left( \frac {r^2 } { f ( R ) } \right) ^ { 1 / 2 }, \end{equation} $

(39) which has the following limit:
$ \begin{equation} \lim_{R\to\infty} \kappa_g\frac{{\rm d}\sigma}{{\rm d}\phi}\bigg|_{C_R}\approx 1\,. \end{equation} $

(40) At spatial infinity,
$ R\to\infty $ , and by using the straight light approximation$ r=b/\sin\phi $ , the GBT reduces to [65]$ \begin{equation} \int^{\pi+\alpha}_0 \left[\kappa_g\frac{{\rm d}\sigma}{{\rm d}\phi}\right]\bigg|_{C_R}{\rm d}\phi =\pi-\lim_{R\to\infty}\int^\pi_0\int^{\infty}_{\frac{b}{\sin\phi}}\mathcal{K} {\rm d} S. \end{equation} $

(41) We calculate the weak deflection angle in the weak limit approximation as follows:
$ \begin{aligned}[b] \alpha \approx & \frac{4 M}{b}+\frac{2 \gamma}{b}+\frac{a \gamma}{b}+\frac{2 a M}{b}+\frac{9 \gamma \omega _q}{b}+\frac{27 a^2 \gamma \omega _q}{8 b} \\&+\frac{3 a^2 \gamma}{4 b}+\frac{3 a^2 M}{2 b}+\frac{9 a \gamma \omega _q}{2 b}. \end{aligned} $

(42) Hence, we see the effect of the string cloud on the deflection angle in weak field limits using the GBT. As a result, the cloud of the string parameter a and quintessence parameter γ increase the deflection angle α, as can be seen from Eq. (42) for positive values of
$ \omega _q $ (similar to that in the paper [109]). However, for negative values of$ \omega _q $ , the deflection angle α decreases, as can be seen in Fig. 9.
Figure 9. (color online) The first panel shows the dependence of α on string cloud parameter a, for fixed
$ M=1 $ ,$ \omega_q=-2/3 $ and$ \gamma=0.01 $ , where it is compared with the Schwarzschild black hole case (plotted with a black solid line). The second panel shows the dependence of α on the parameter γ, for fixed$ a = 0.01 $ ,$ M=1 $ ,$ \omega_q=-2/3 $ , where it is compared with the Schwarzschild black hole case (plotted with a black solid line). -
In this study, we considered the Schwarzschild black hole in the background of string clouds and the quintessence field to observe the shadows and the gravitational deflection angle of photons. In Fig. 1, the black hole horizon radius is plotted against the string cloud parameter a and the quintessence parameter γ. We have seen that, with both a and γ, the horizon of the Schwarzschild black hole increases. From Fig. 2, we have concluded that the radius of the photon sphere for
$ \omega_q=-2/3 $ increases if a and γ increase. We observed the impacts of a and γ on both the shadow and the deflection angle in the Schwarzschild spacetime in the presence of the cloud of strings and quintessence dark energy. In Figs. 3, 4, 5, and 6, the dependencies of the shadows of the Schwarzschild black hole with quintessence and cloud of strings on the parameters a and γ are presented. In these graphs, we noticed that, with an increase in the values of the parameters a and γ, the radius of the shadow cast by the Schwarzschild black hole with quintessence and string clouds increases. We showed that, if$ a=0 $ and$ \gamma=0 $ , the black hole shadow is smaller when compared with the one obtained in the case of non-zero values of a and γ. This fact is evident from the right panel of Fig. 5. From this, it may be speculated that the black hole shadow can be bigger in the presence of string clouds and quintessence for spherically symmetric static black holes, and the effect of both the quintessence and string cloud is repulsive in this scenario. As the size of the shadow of the black hole increases, the intensity of the gravitational field of the Schwarzschild black hole increases in the presence of the string clouds and quintessence dark energy. Another observation is that the radius of the shadow of the black hole is more sensitive to the quintessence parameter γ as compared to the string cloud parameter a. We have used the observational data provided by the EHT collaboration for the shadows of the black holes at the center of the Messier 87 and the milky way galaxies, to obtain upper limits for the values of the parameters a and γ. These values are presented in Table 1.The evaporation of a black hole by Hawking radiation can be explained in terms of the emission rate of energy. Therefore, the emission rate of energy of a black hole attracts researchers and is linked with the radius of the black hole shadow. Therefore, in this study, we also considered the emission rate of energy for the Schwarzschild black hole with string clouds and quintessence. In Fig. 8, we have seen that with an increase in the the string cloud parameter a and quintessence parameter γ, the peak of the graph for the rate of energy emission increases. The peak of the graph indicates that, for a higher rate of energy emission, the rate of evaporation of the black hole is also high.
Lastly, we calculated the weak deflection angle using the GBT to probe the effect of the cloud of string parameter a and quintessence parameter γ on the weak deflection angle α. We showed that the deflection angle obtained in Eq. (42) increases with the cloud of string parameter a but decreases with the the quintessence parameter γ for negative values of
$ \omega _q $ , as shown in Fig. 9. -
This manuscript has no associated data; no data will be deposited (there are no observational data related to this article; the necessary calculations and graphic discussion can be made available on request).
-
G. Mustafa is very thankful to Prof. Gao Xianlong from the Department of Physics, Zhejiang Normal University, for his kind support and help during this research.
Shadows and gravitational weak lensing by the Schwarzschild black hole in the string cloud background with quintessential field
- Received Date: 2022-07-14
- Available Online: 2022-12-15
Abstract: In this study, we observe that, in the presence of the string cloud parameter a and the quintessence parameter γ, with the equation of state parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: