-
Recently, the Event Horizon Telescope (EHT) Collaboration et al. revealed the first images of the supermassive black hole at the centre of the giant elliptical galaxy M87 [1–7] and Milky Way Galaxy [8–13]. This is highly useful for black hole physics and astrophysics and has drawn an increasing number of researchers into the study of black hole images. An important element in a black hole image is the black hole shadow [14–17], which is a dark silhouette. A dark shadow appears because light rays close to the event horizon are captured by the black hole, thereby leaving a black shadow in the observer's sky. Because the fingerprints of the geometry around the black hole can be reflected in the shape and size of the shadow, research on black hole shadows plays a vital role in the study of black holes (constraining black hole parameters) [18–24], probing fundamental physics issues, including dark matter [25–29], and the verification of various gravity theories [30–36]. These shadows are a perfect black disk for Schwarzschild black holes, and they gradually become a D-shaped silhouette with an increase in the spin parameter for Kerr black holes [15]. In the space-time of a Kerr black hole with Proca hair and a Konoplya-Zhidenko rotating non-Kerr black hole, a cusp silhouette of black hole shadows emerges [37, 38]. Self-similar fractal structures appear in black hole shadows originating from chaotic lensing [39–48]. Many other black hole shadows with other parameters in various theories of gravity have been recently investigated in Refs. [49–91]. It is hoped that the information imprinted in black hole shadows can be captured in future astronomical observations, including the upgraded Event Horizon Telescope and BlackHoleCam [92], to study black holes and verify various gravity theories.
It is widely believed that a massive halo, ring, or other shell-like distributions of matter may be concentrated around the black hole in a galactic center. The first image of a Schwarzschild black hole with a thin accretion disk was announced by Luminet [16], revealing primary and secondary images of the thin accretion disk around a shadow. The superposition of a black hole and exterior matter will reorganize the space-time structure and induce a significant change to the black hole shadow. We previously researched the shadows of a Schwarzschild black hole surrounded by a Bach-Weyl ring [49] and found that the black hole shadow becomes an "8" shaped silhouette and possesses self-similar fractal structures. Cunha et al. [50] researched the shadows of a black hole surrounded by a heavy Lemos-Letelier accretion disk and found that the black hole shadow becomes more prolate with increasing accretion disk mass. In this paper, we consider a solution to the Einstein equations representing the superposition of a Schwarzschild black hole with a halo containing quadrupolar and octopolar contributions [93]. For this space-time, Vieira et al. detected the timelike geodesic orbits of test particles and found that the octopolar term could bring about chaotic motions [93]. Through further numerical analysis, they found that the quadrupolar term also gives rise to a chaotic behavior in addendum [94]. Dubeibe further investigated the effects of the quadrupole and octupole moments on the motion of a test particle using modern color-coded basin diagrams [95] and found that the final state of the test particle was highly affected. Therefore, the nonlinear superposition of a Schwarzschild black hole with a halo may also influence the null geodesic motions of photons, thus affecting the black hole shadow. In this paper, we investigate the effect of quadrupolar and octopolar terms on the Schwarzschild black hole shadow.
The paper is organized as follows: In Sec. II, we briefly review the space-time of a Schwarzschild black hole with a halo and reveal the influences of quadrupolar and octopolar terms on the surface geometry of the black hole. In Sec. III, we numerically present the shadows of a Schwarzschild black hole with a halo and analyze the new features of the black hole shadow arising from the quadrupolar and octopolar terms. Finally, we conclude the paper with a summary.
-
The space-time of a Schwarzschild black hole with a halo is vacuum static and axially symmetric; hence, it can be described by the Weyl metric
$ {\rm d}s^{2}=-{\rm e} ^{2\nu}{\rm d}t^{2}+{\rm e} ^{2\lambda-2\nu} ({\rm d}\rho^{2}+{\rm d}z^{2})+\rho^{2}{\rm e} ^{-2\nu}{\rm d}\phi^{2}, $

(1) where only ν and λ are the functions of ρ and z. The Einstein equations reduce to
$\nu_{,\rho\rho}+\frac{\nu_{,\rho}}{\rho}+\nu_{,zz}=0, $

(2) $\lambda_{,\rho}=\rho(\nu_{,\rho})^{2}-\rho(\nu_{,z})^{2},\;\;\;\;\;\;\lambda_{,z}=2\rho\nu_{,\rho}\nu_{,z}. $

(3) The function
$ \nu(\rho, z) $ satisfies the Laplace equation and behaves as the gravitational potential in Newtonian theory; thus, it can be linearly superposed. However, the function$ \lambda(\rho, z) $ does not exhibit such linear superposition. In the solution of a Schwarzschild black hole with a halo, the functions ν and λ for the entire system can be written as$\nu=\nu_{{\rm Schw}}+\nu_{{\rm halo}}$ and$\lambda=\lambda_{{\rm Schw}}+\lambda_{{\rm halo}}+\lambda_{{\rm int}}$ , respectively [96]. The functions$ \nu_{}, \lambda_{} $ are the solution of Schwarzschild space-time, expressed as$\nu_{{\rm Schw}}=\frac{1}{2}\ln\frac{d_{1}+d_{2}-2{M}}{ d_{1}+ d_{2}+2{M}}, $

(4) $\lambda_{{\rm Schw}}=\frac{1}{2}\ln\frac{(d_{1}+ d_{2})^{2}-4{M}^{2}}{4d_{1}d_{2}}, $

(5) where M is the mass of a Schwarzschild black hole, and
$d_{1,2}=\sqrt{\rho^{2}+(z\mp M)^{2}}$ . The functions$\nu_{{\rm halo}}, \lambda_{{\rm halo}}$ are the solution of the halo structure, and$\lambda_{{\rm int}}$ represents the interaction between the black hole and halo.In Schwarzschild coordinates, the space-time of a Schwarzschild black hole with a halo can be described by the metric [93]
$\begin{aligned}[b] {\rm d}s^{2}=&-\left(1-\frac{2M}{r}\right){\rm e}^{(\nu_{Q}+\nu_{O})}{\rm d}t^{2}+{\rm e}^{(\lambda_{Q}+\lambda_{O}+\lambda_{QO}-\nu_{Q}-\nu_{O})}\\&\times\bigg[\left(1-\frac{2M}{r}\right)^{-1}{\rm d}r^{2}+r^{2}{\rm d}\theta^{2}\bigg]+{\rm e}^{-(\nu_{Q}+\nu_{O})}r^{2}\sin^{2}\theta {\rm d}\phi^{2}, \end{aligned} $

(6) where
$ \begin{aligned}[b] \nu_{Q} =& ({\cal{Q}}/3)(3u^{2}-1)(3v^{2}-1),\\ \nu_{O} =& ({\cal{O}}/5)uv(5u^{2}-3)(5v^{2}-3),\\ \lambda_{Q} =& -4{\cal{Q}}u(1-v^{2})+({\cal{Q}}^{2}/2)[9u^{4}v^{4}-10u^{4}v^{2}\\ &-10u^{2}v^{4}+12u^{2}v^{2}+u^{4}+v^{4}-2u^{2}-2v^{2}+1],\\ \lambda_{O} =& -2{\cal{O}}\left[3u^{2}v-3u^{2}v^{3}+v^{3}-\frac{9}{5}v+\frac{4}{5}\right]+2{\cal{O}}^{2}\Bigg[\frac{75}{8}u^{6}v^{6}\\ &-\frac{117}{8}u^{6}v^{4}-\frac{117}{8}u^{4}v^{6}+\frac{45}{8}u^{6}v^{2}+\frac{45}{8}u^{2}v^{6}\\ & + \frac{189}{8}u^{4}v^{4}-\frac{387}{40}u^{4}v^{2}-\frac{387}{40}u^{2}v^{4}+\frac{891}{200}u^{2}v^{2}-\frac{3}{8}u^{6}\\ &-\frac{3}{8}v^{6}+\frac{27}{40}u^{4}+\frac{27}{40}v^{4}-\frac{81}{200}u^{2}-\frac{81}{200}v^{2}+\frac{21}{200}\Bigg],\end{aligned} $

$ \begin{aligned}[b] \lambda_{QO} =& 2{\cal{Q}}{\cal{O}}\Bigg[9u^{5}v^{5}-12u^{5}v^{3}+3u^{5}v-12u^{3}v^{5}+\frac{84}{5}u^{3}v^{3}\\&-\frac{24}{5}u^{3}v+3uv^{5}-\frac{24}{5}uv^{3}+\frac{9}{5}uv\Bigg], \end{aligned} $

(7) and
$ \begin{aligned}[b] u=&\frac{1}{2 M}\bigg[\sqrt{\rho^{2}+(z+M)^{2}}+\sqrt{\rho^{2}+(z-M)^{2}}\bigg],\\ v=&\frac{1}{2M}\bigg[\sqrt{\rho^{2}+(z+M)^{2}}-\sqrt{\rho^{2}+(z-M)^{2}}\bigg]. \end{aligned} $

(8) The transformation between the Schwarzschild coordinates (
$ r, \theta $ ) and Weyl coordinates ($ \rho, z $ ) is$ \rho=\sqrt{r(r-2M)}\sin\theta,\;\;\;\;\;\;\;\;z=(r-M)\cos\theta. $

(9) The exterior halo is a multipolar structure containing quadrupolar and octopolar terms, and
$ {\cal{Q}} $ and$ {\cal{O}} $ are the quadrupole and octopole strengths, respectively. The metric will reduce to a Schwarzschild solution when$ {\cal{Q}}={\cal{O}}=0 $ .The existence of a halo does not change the radial coordinate of the event horizon,
$r_{h}=2M$ ; however, the surface geometry of a Schwarzschild black hole with a halo would be affected by the quadrupole strength$ {\cal{Q}} $ and octopole strength$ {\cal{O}} $ . The event horizon of a Schwarzschild black hole with a halo can be described by the two-dimensional line element$ {\rm d}s_{h}^{2}=r_{h}^{2}{\rm e}^{(-\nu_{Q}-\nu_{O})}|_{r=r_{h}}({\rm d}\theta^{2}+\sin^{2}\theta {\rm d}\phi^{2}). $

(10) Embedding diagrams [97, 98] for the event horizon of a Schwarzschild black hole with a halo in Euclidean 3-space with different
$ {\cal{Q}} $ and$ {\cal{O}} $ are exhibited in Fig. 1. Because the event horizon in the ($ x,y $ ) plane is centrosymmetric, we only show the event horizon in the ($ x,z $ ) plane, where$ z=0 $ represents the equatorial plane. As shown in Fig. 1(a) with$ {\cal{O}}=0 $ , the event horizon is prolate at the quadrupole strength$ {\cal{Q}}<0 $ and may become more prolate via stretching along the vertical direction and squeezing along the horizontal direction as$ {\cal{Q}} $ decreases. However, at$ {\cal{Q}}>0 $ , the event horizon becomes more oblate in the opposite manner as$ {\cal{Q}} $ increases. As shown in Fig. 1(b) with$ {\cal{Q}}=0 $ , the octopolar term ($ {\cal{O}}\neq0 $ ) breaks the reflection symmetry of the event horizon with respect to the equatorial plane, whereas the event horizon in the equatorial plane does not change with$ {\cal{O}} $ . The event horizon stretches upward at$ {\cal{O}}<0 $ and downward at$ {\cal{O}}>0 $ . The two event horizons with opposite$ {\cal{O}} $ are symmetrical to each other about the equatorial plane. Figure 1(c) shows the joint effort of the quadrupole strength$ {\cal{Q}} $ and octopole strength$ {\cal{O}} $ on the event horizon at$ {\cal{O}}=0.1 $ and$ {\cal{Q}}=-0.1 $ , 0, 0.1. That is, the quadrupole term causes the Schwarzschild black hole to be prolate at$ {\cal{Q}}<0 $ and oblate at$ {\cal{Q}}>0 $ , and the octopole term causes the shadow to stretch upward at$ {\cal{O}}<0 $ and downward at$ {\cal{O}}>0 $ .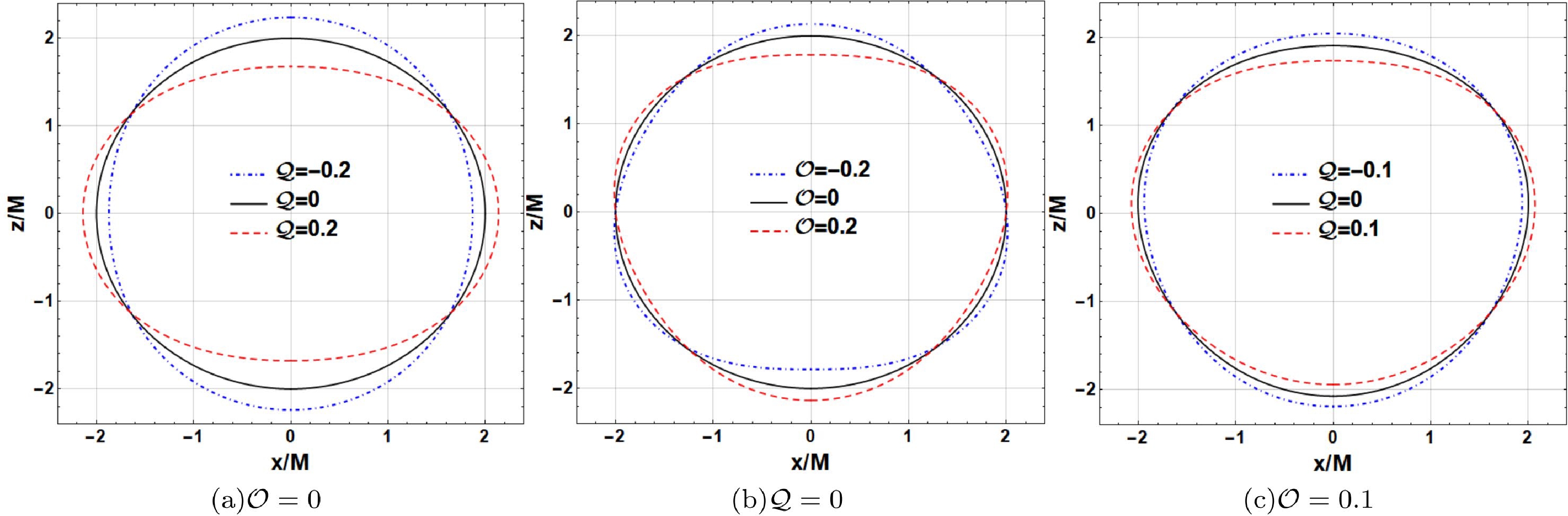
Figure 1. (color online) Embedding diagrams for the surface geometry of a Schwarzschild black hole with a halo in Euclidean 3-space with different quadrupole strengths
$ {\cal{Q}} $ and octopole strengths$ {\cal{O}} $ .To quantitatively illustrate the influences of the quadrupolar and octopolar terms on a Schwarzschild black hole with a halo, we compute the equatorial circumference
$ C_{\rm e} $ and polar circumference$ C_{\rm p} $ of the event horizon, which are given by$ C_{{\rm e}} = \int^{2\pi}_{0}\sqrt{g_{\phi\phi}}{\rm d}\phi\big|_{(r=r_{h},\theta=\frac{\pi}{2})}=\int^{2\pi}_{0}r_{h}{\rm e}^{-\frac{1}{2}(\nu_{Q}+\nu_{O})}\big|_{(r=r_{h},\theta=\frac{\pi}{2})}{\rm d}\phi, $

(11) $ C_{{\rm p}} = 2\int^{\pi}_{0}\sqrt{g_{\theta\theta}}{\rm d}\theta\big|_{r=r_{h}}=2\int^{\pi}_{0}r_{h}{\rm e}^{-\frac{1}{2}(\nu_{Q}+\nu_{O})}\big|_{r=r_{h}}{\rm d}\theta. $

(12) Figures 2(a) and (b) show the plots of the equatorial circumference
$C_{{\rm e}}$ and polar circumference$C_{{\rm p}}$ of the event horizon as a function of$ {\cal{Q}} $ . Here,$ 2\pi r_{h} $ is the circumference of the Schwarzschild black hole event horizon ($ {\cal{Q}}={\cal{O}}=0 $ ). With increasing$ {\cal{Q}} $ , we find that$C_{{\rm e}}$ increases and$C_{{\rm p}}$ decreases. The equatorial circumference$C_{{\rm e}}$ is independent of$ {\cal{O}} $ , which is consistent with the results in Fig. 1(b). The two polar circumferences$C_{{\rm p}}$ with opposite$ {\cal{O}} $ share the same value and increase as$ |{\cal{O}}| $ increases for fixed$ {\cal{Q}} $ . In addition, the change in$C_{{\rm p}}$ with$ {\cal{O}} $ is very small, which signifies that the octopole strength$ {\cal{O}} $ has little effect on the polar circumference$C_{{\rm p}}$ . The distortion parameter δ, defined as$(C_{{\rm e}}-C_{{\rm p}})/C_{{\rm e}}$ , can determine the departure of the event horizon from spherical symmetry. Figure 2(c) shows the behavior of the distortion parameter δ with$ {\cal{Q}} $ and$ {\cal{O}} $ . The distortion parameter δ almost depends only on$ {\cal{Q}} $ and is nearly less than$ 0 $ at$ {\cal{Q}}<0 $ , indicating a prolate event horizon, whereas$ \delta>0 $ indicates an oblate event horizon. The surface area A of the event horizon is given by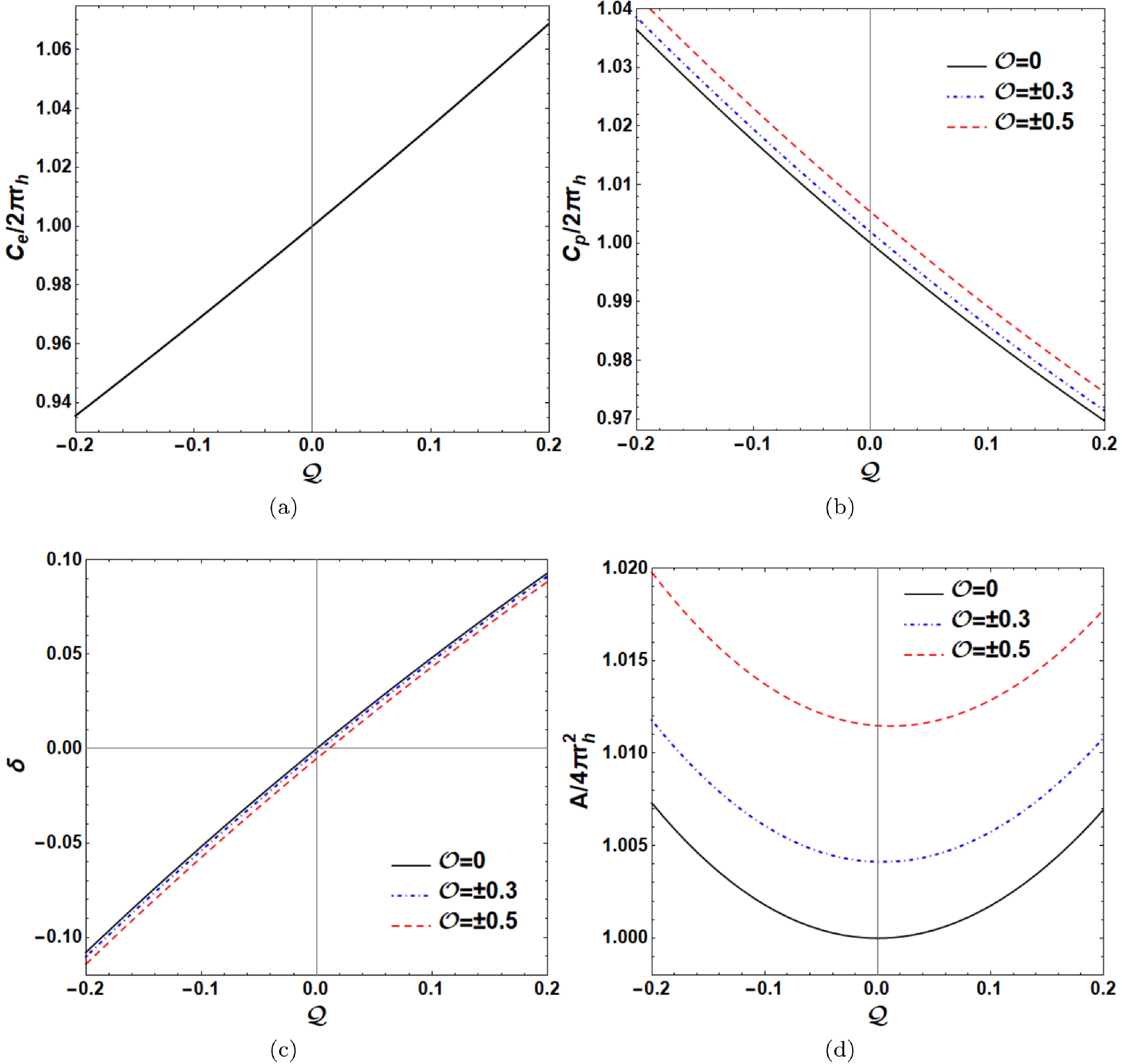
Figure 2. (color online) Change in the equatorial circumference
$C_{{\rm e}}$ , polar circumference$C_{{\rm p}}$ , distortion parameter δ, and surface area A of the event horizon with the quadrupole strength$ {\cal{Q}} $ for different octopole strengths$ {\cal{O}} $ . Here, we set the Schwarzschild black hole mass$ M=1 $ .$\begin{aligned}[b] A=&\int^{\pi}_{0}\int^{2\pi}_{0}\sqrt{g_{\phi\phi}g_{\theta\theta}}{\rm d}\theta {\rm d}\phi\big|_{r=r_{h}}\\=&\int^{\pi}_{0}\int^{2\pi}_{0}r_{h}^{2}\sin\theta {\rm e}^{-(\nu_{Q}+\nu_{O})}\big|_{r=r_{h}}{\rm d}\theta {\rm d}\phi. \end{aligned} $

(13) Figure 2(d) shows the change in the surface area A of the event horizon with
$ {\cal{Q}} $ and$ {\cal{O}} $ , where$ 4\pi r_{h}^{2} $ is the surface area of the Schwarzschild black hole. The surface area A first decreases and then increases with increasing$ {\cal{Q}} $ , which indicates that prolate and oblate event horizons both have large surface areas. The increase in the surface area A with$ |{\cal{O}}| $ means that the octopole term can also enlarge the surface area of the Schwarzschild black hole.The Hamiltonian
$ {\cal{H}} $ of photon propagation along null geodesics in the space-time of a Schwarzschild black hole with a halo (6) can be described as$ {\cal{H}}=g^{rr}p_{r}^{2}+g^{\theta\theta}p_{\theta}^{2}+V_{{\rm eff}}=0, $

(14) where the effective potential
$V_{{\rm eff}}$ is defined as$ V_{{\rm eff}}=g^{tt}E^{2}+g^{\phi\phi}L_{z}^{2}=E^{2}(g^{tt}+g^{\phi\phi}\eta^{2}). $

(15) E and
$ L_{z} $ are two constants of motion for null geodesics motion, that is, the energy and z-component of the angular momentum; therefore, the impact parameter$ \eta=L_{z}/E $ is also a constant of photon motion. The boundary of the shadow is determined using the photon sphere caused by unstable photon circular orbits. Light rays that enter the photon sphere are captured by the black hole; light rays that do not enter the photon sphere move away to infinity; and light rays that spiral asymptotically toward the photon sphere compose the boundary of the black hole shadow. Now, let us study the spherical photon orbits in the equatorial plane, which are also known as light rings. Light rings must satisfy$ \theta=\pi/2,\;\;\;\;\;\;\;\; V_{{\rm eff}}=0,\;\;\;\;\;\;\;\;\frac{\partial V_{{\rm eff}}}{\partial r}=0. $

(16) Moreover, a light ring with
$\partial^{2}V_{{\rm eff}}/\partial r^{2} < 0$ is unstable, whereas a light ring with$\partial^{2}V_{{\rm eff}}/\partial r^{2} > 0$ is stable. By solving Eq. (16), we find that the radius of light rings$ r_{LR} $ only depends on the quadrupole strength$ {\cal{Q}} $ , as shown in Fig. 3. There is a critical value of the quadrupole strength$ {\cal{Q}}_{c}\approx-0.0209445 $ for light rings in Fig. 3. Light rings do not exist in the space-time of a Schwarzschild black hole with a halo at$ {\cal{Q}}<{\cal{Q}}_{c} $ ; both unstable (red dashed line) and stable (black line) light rings exist at$ {\cal{Q}}_{c}<{\cal{Q}}<0 $ ; and only one unstable (red dashed line) light ring exists at$ {\cal{Q}}>0 $ . Our previous study [51] manifested that the existence of a stable light ring ensures that photons in stable orbits are always moving around the black hole and cannot enter the black hole or escape to infinity. The inexistence of light rings causes a panoramic (equatorial) shadow to appear [51, 52]. In this study, we only research the case in which light rings exist, and the halo structures could be considered a perturbation of a black hole. After this research, we decide to set the quadrupole strength$ {\cal{Q}} $ to the order of$ 10^{-4} $ and the quadrupole strength$ {\cal{O}} $ to the order of$ 10^{-6} $ . In this case, the halo structures are more in line with the actual astronomical situation. Moreover, the radius of stable light rings is larger than the radius$r_{{\rm obs}}$ of the observer we set (for$ {\cal{Q}}=-1\times10^{-4} $ ,$r_{LR}=70.7M > r_{{\rm obs}}=50M$ ), in which the observer directly observes the black hole shadow. -
Now, we study the shadow of the Schwarzschild black hole with a halo using the backward ray-tracing technique [39–45]. In this method, we assume that the static observer is located at (
$r_{{\rm obs}}, \theta_{{\rm obs}}$ ) in the zero-angular-moment-observers (ZAMOs) reference frame [15], and evolved light rays from the observer move backward in time. The shadow of a black hole is caused by light rays falling into the event horizon of the black hole. The coordinates of a photon image in the observer's sky can be expressed as [39–45]$ \begin{aligned}[b] x =& -r_{{\rm obs}}\frac{\sqrt{1-\dfrac{2M}{r}}L_{z}}{r\sin\theta {\rm e}^{(\frac{1}{2}\lambda_{Q}+\frac{1}{2}\lambda_{O}+\frac{1}{2}\lambda_{QO}-\nu_{Q}-\nu_{O})}\dot{r}}\bigg|_{(r_{{\rm obs}},\theta_{{\rm obs}})}, \\ y =& r_{{\rm obs}}\frac{\sqrt{r(r-2M)}\dot{\theta}}{\dot{r}}\bigg|_{(r_{{\rm obs}},\theta_{{\rm obs}})}. \end{aligned} $

(17) In Fig. 4, we show the influence of the quadrupole term on the Schwarzschild black hole shadow with different quadrupole strengths
$ {\cal{Q}} $ . Here, we set${M}=1$ and the static observer at$r_{{\rm obs}}=50$ with the inclination angle$\theta_{{\rm obs}}=\pi/2$ . In this paper, we set a light-emitting celestial sphere as the background light source marked by four different colored quadrants and brown grids as the longitude and latitude, which is the same as the celestial sphere in Refs. [39–41]. The shadow of a Schwarzschild black hole with only the quadrupole structure is symmetric about the equatorial plane. The shadow of a Schwarzschild black hole with a halo becomes more oblate by only stretching along the horizontal direction as$ {\cal{Q}} $ decreases at$ {\cal{Q}}<0 $ . However, at$ {\cal{Q}}>0 $ , the black hole shadow becomes more prolate by only squeezing along the horizontal direction as$ {\cal{Q}} $ increases. With increasing$ |{\cal{Q}}| $ , the Einstein ring, the white ring around the black hole shadow, is torn into an Einstein cross. In Fig. 5, we show the influence of the octopolar term on the Schwarzschild black hole shadow with different octopolar strengths$ {\cal{O}} $ . The black hole shadow shifts upward as$ {\cal{O}} $ decreases at$ {\cal{O}}<0 $ and downward as$ {\cal{O}} $ increases at$ {\cal{O}}>0 $ . The octopolar term also breaks the reflection symmetry of the Schwarzschild black hole shadow with respect to the equatorial plane; however, the two black hole shadows with opposite$ {\cal{O}} $ are symmetrical to each other about the equatorial plane. In Fig. 6, we show the joint effort of the quadrupole and octopole terms on the shadow of the Schwarzschild black hole. That is, the black hole shadow stretches and squeezes along the horizontal direction at$ {\cal{Q}}<0 $ and$ {\cal{Q}}>0 $ , respectively, and the black hole shadow shifts upward at$ {\cal{O}}<0 $ and downward at$ {\cal{O}}>0 $ . In Fig. 7, we present the light rays that form the shadow boundary to explain the emergence of the extraordinary patterns of the black hole shadow with quadrupole and octopole terms. Figures 7(a) and (b) show the light rays with$ {\cal{Q}}=-2\times10^{-4} $ and$ {\cal{Q}}=2\times10^{-4} $ , respectively, in the$ y=0 $ plane (the equatorial plane), where y is the celestial coordinate (17) in the observer's sky. As shown, the two light rays (red lines) propagate from the observer backward in time and spiral asymptotically toward the photon sphere. However, for the observer, the light rays propagate along the red dash lines, which determine the left and right margins of the black hole shadow, respectively. The black region on the x axis represent the black hole shadow on the celestial sphere, where x is the celestial coordinate (17). The angle between the two red dash lines, namely, the angular radius of the black hole shadow, is significantly larger for$ {\cal{Q}}=-2\times10^{-4} $ and significantly smaller for$ {\cal{Q}}=2\times10^{-4} $ , which results in the stretching and squeezing of the black hole shadow in the horizontal direction at$ {\cal{Q}}<0 $ and$ {\cal{Q}}>0 $ , respectively. Figures 7(c) and (d) show the light rays with$ {\cal{O}}=-2\times10^{-6} $ and$ {\cal{O}}=2\times10^{-6} $ , respectively, in the$ x=0 $ plane. We also present the light rays (red lines) spiraling asymptotically toward the photon sphere and their tangents (red dash lines) at the observer, which determine the upper and lower margins of the shadow. As shown, the tangents slope upward for$ {\cal{O}}=-2\times10^{-6} $ and downward for$ {\cal{O}}=2\times10^{-6} $ , which causes the shadow to shift upward and downward along the y axis of the celestial sphere at$ {\cal{O}}<0 $ and$ {\cal{O}}>0 $ , respectively.
Figure 4. (color online) Shadows of a Schwarzschild black hole with a halo for the quadrupole strength
${\cal{Q}}=-2\times10^{-4}, -1\times10^{-4}, $ $ ~ 0,~ 1\times10^{-4},~ 2\times10^{-4}$ , and octopolar strength$ {\cal{O}}=0 $ . Here, we set${M}=1$ and the static observer at$r_{{\rm obs}}=50$ with the inclination angle$\theta_{{\rm obs}}=\pi/2$ .
Figure 5. (color online) Shadows of a Schwarzschild black hole with a halo for the quadrupole strength
$ {\cal{Q}}=0 $ , and octopolar strength${\cal{O}}=-2\times10^{-6},~ -1\times10^{-6},~ 0, 1\times10^{-6},~ 2\times10^{-6}$ . Here, we set${M}=1$ and the static observer at$r_{{\rm obs}}=50$ with the inclination angle$\theta_{{\rm obs}}=\pi/2$ .
Figure 6. (color online) Shadows of a Schwarzschild black hole with a halo for the quadrupole strength
${\cal{Q}}=-2\times10^{-4}, $ $ -1\times10^{-4},~ 0, 1\times10^{-4},~ 2\times10^{-4}$ , and octopolar strength$ {\cal{O}}=-1\times10^{-6} $ . Here, we set${M}=1$ and the static observer at$r_{{\rm obs}}=50$ with the inclination angle$\theta_{{\rm obs}}=\pi/2$ .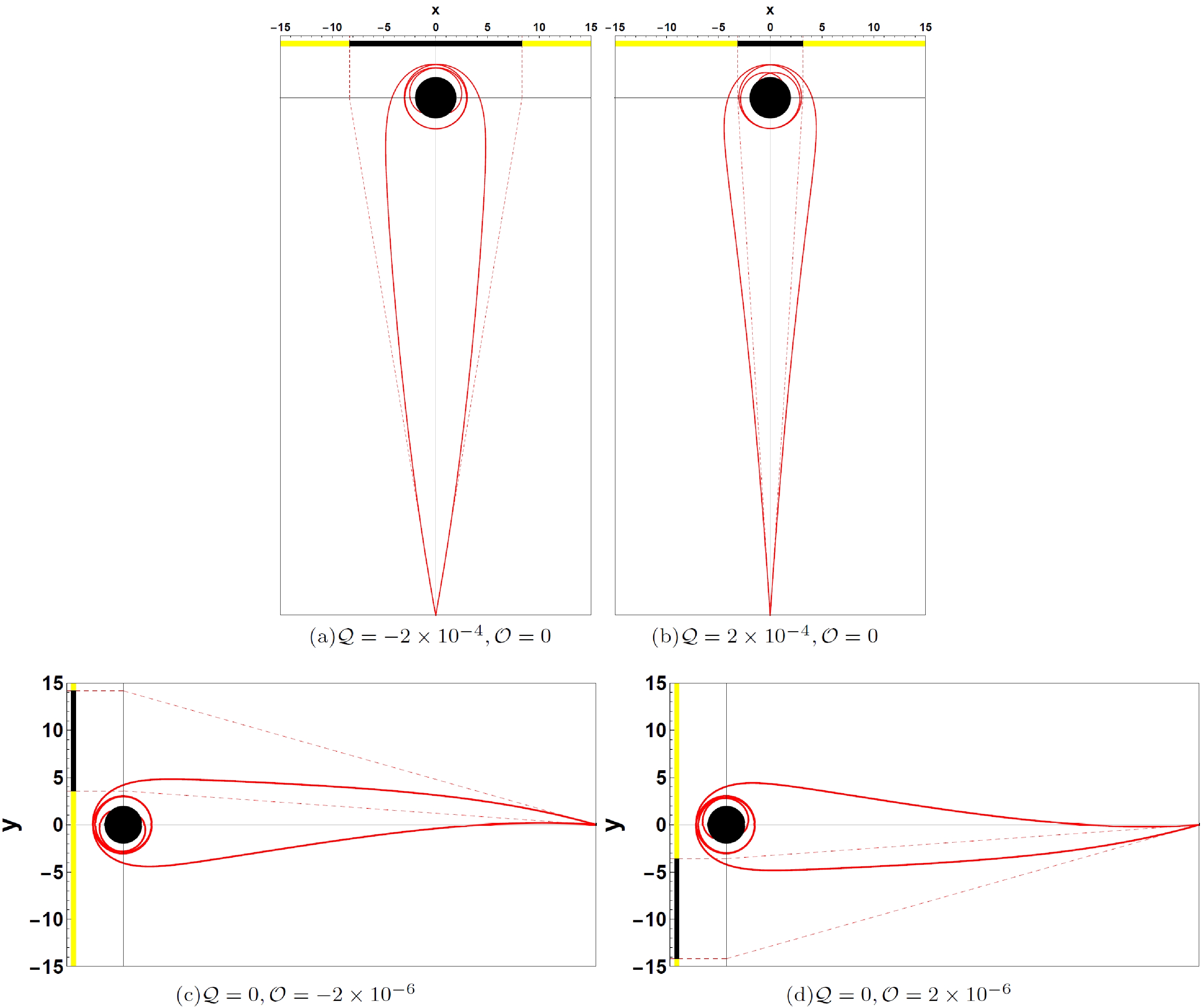
Figure 7. (color online) Light rays (red lines) spiraling asymptotically toward the photon sphere and their tangents (red dash lines) at the observer, which determine the boundary of the black hole shadow. The black hole shadow stretches and squeezes on the celestial sphere at
$ {\cal{Q}}<0 $ and$ {\cal{Q}}>0 $ , respectively, and shifts upward at$ {\cal{O}}<0 $ and downward at$ {\cal{O}}>0 $ .Black holes in the universe can be perturbed by a halo with quadrupole and octopolar terms; hence, we estimate several observables of the black hole shadow to determine the quadrupole strength
$ {\cal{Q}} $ and octopolar strength$ {\cal{O}} $ in astronomical observations. To characterize the shadow of a Schwarzschild black hole with a halo, we should first introduce four important points for the shadow: the leftmost point ($ x_{l} $ ,$ y_{l} $ ), rightmost point ($ x_{r} $ ,$ y_{r} $ ), topmost point ($ x_{t} $ ,$ y_{t} $ ), and bottommost point ($ x_{b} $ ,$ y_{b} $ ), as shown in Fig. 8. We can then define the observable values of the black hole shadow: the width$ W=(x_{r}-x_{l})/R_{s} $ , height$ H=(y_{t}-y_{b})/R_{s} $ , and oblateness$ K=W/H $ , where$ R_{s} $ is the radius of the Schwarzschild black hole shadow ($ {\cal{Q}}={\cal{O}}=0 $ ). Figure 9 shows the various widths W, heights H, and oblateness K of the black hole shadow with the quadrupole strength$ {\cal{Q}} $ for different octopolar strengths$ {\cal{O}} $ . As shown in Fig. 9(a), the width W of the black hole shadow decreases as$ {\cal{Q}} $ increases; almost all width values are larger than$ 2R_{s} $ at$ {\cal{Q}}<0 $ and less than$ 2R_{s} $ at$ {\cal{Q}}>0 $ . Moreover, the octopolar strength$ {\cal{O}} $ has little effect on the width W of the black hole shadow. This indicates that only the quadrupole term stretches and squeezes the black hole shadow along the horizontal direction at$ {\cal{Q}}<0 $ and$ {\cal{Q}}>0 $ , respectively. As shown in Fig. 9(b), the height H of the black hole shadow increases as$ {\cal{Q}} $ increases, but the change in height is considerably smaller than the change in width. Thus, the change in oblateness K of the black hole shadow with$ {\cal{Q}} $ is almost the same as the change in width W. The black hole shadow is oblate ($ K>1 $ ) at$ {\cal{Q}}<0 $ and prolate ($ K<1 $ ) at$ {\cal{Q}}>0 $ . In addition, the height H of the black hole shadow increases as$ |{\cal{O}}| $ increases for fixed$ {\cal{Q}} $ . The main effect of the octopolar strength$ {\cal{O}} $ is moving the black hole shadow along the vertical direction. Therefore, we define the center of the black hole shadow as$ (x_{c}, y_{c})=\Bigg(\dfrac{x_{l}+x_{r}}{2}, \dfrac{y_{t}+y_{b}}{2}\Bigg) $ and make use of$ Y_{c} $ ($ y_{c}/R_{s} $ ) to describe the deviation of the shadow away from the equatorial plane. In Fig. 10(a), we show various$ Y_{c} $ with the octopolar strength$ {\cal{O}} $ for different$ {\cal{Q}} $ . The deviation$ |Y_{c}| $ increases as$ |{\cal{O}}| $ increases, and$ Y_{c}>0 $ at$ {\cal{O}}<0 $ , whereas$ Y_{c}<0 $ at$ {\cal{O}}>0 $ . Furthermore, the deviation$ |Y_{c}| $ is larger at larger$ {\cal{Q}} $ . This indicates that a prolate shadow amplifies the deviation of the shadow, whereas an oblate shadow diminishes the deviation. Unfortunately, in actual observations of a black hole shadow, we cannot determine the coordinates of the shadow center$ (x_{c}, y_{c}) $ to estimate the value of$ {\cal{O}} $ . The octopolar term, meanwhile, can cause a slight distortion along the vertical direction in the black hole shadow that is$ y_{c} $ is not equal to$ y_{l} $ or$ y_{r} $ , as shown in Fig. 8. Hence, we can define a distortion parameter$ \delta_{c}=(y_{c}-y_{l})/R_{s} $ to describe the distortion caused by the octopolar term. Figure 10(b) shows the various values of the distortion parameter$ \delta_{c} $ with the octopolar strength$ {\cal{O}} $ for different$ {\cal{Q}} $ . The distortion parameter$ |\delta_{c}| $ increases as$ |{\cal{O}}| $ increases, and$ \delta_{c}<0 $ at$ {\cal{O}}<0 $ , whereas$ \delta_{c}>0 $ at$ {\cal{O}}>0 $ . In addition, the distortion parameter$ |\delta_{c}| $ is smaller at larger$ {\cal{Q}} $ . This indicates that a prolate shadow diminishes the distortion, whereas an oblate shadow amplifies the distortion. We hope that the Event Horizon Telescope and BlackHoleCam will observe the shadow of a black hole perturbed by a halo with quadrupole and octopolar terms in future astronomical observations.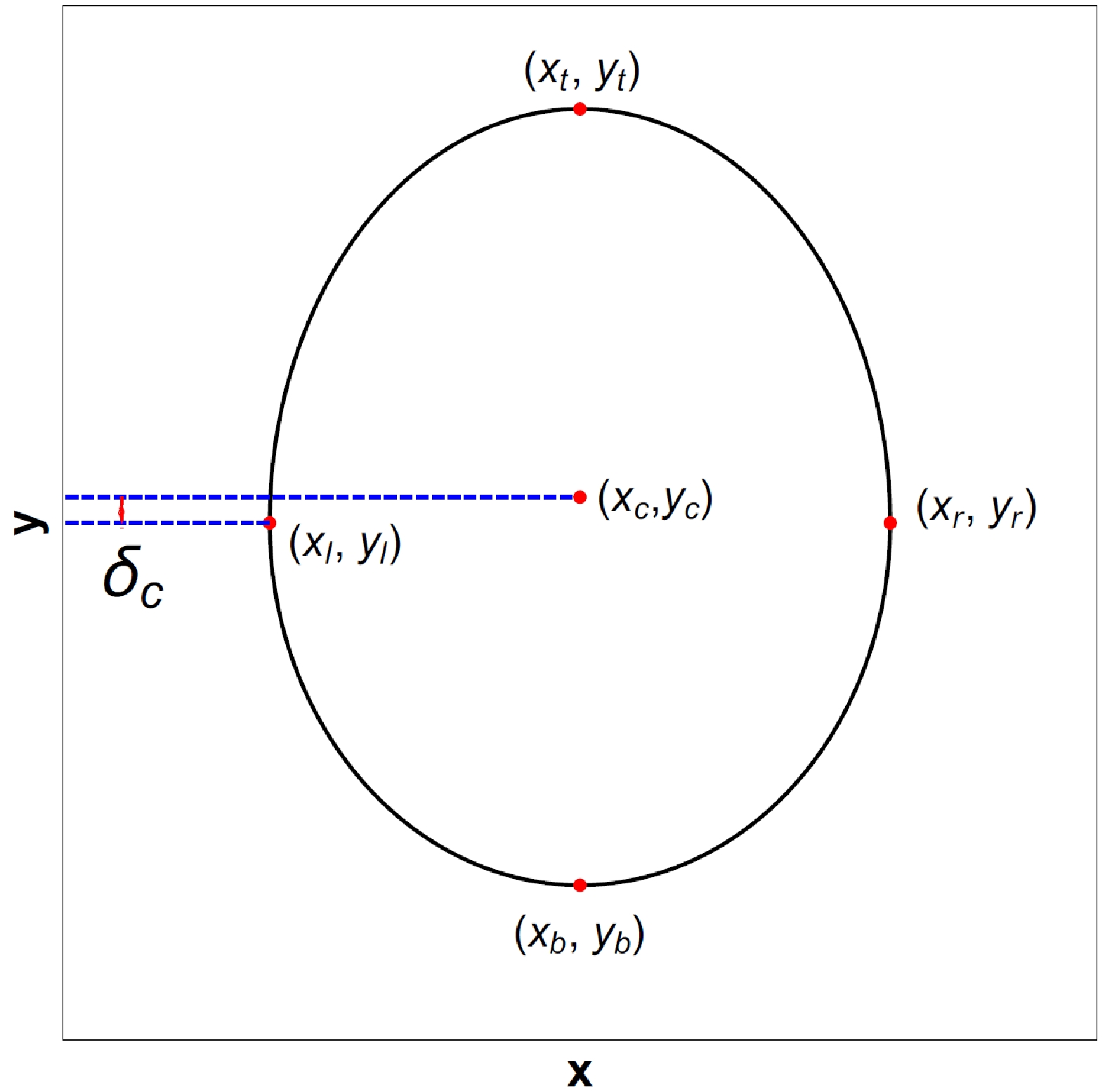
Figure 8. (color online) Leftmost point (
$ x_{l} $ ,$ y_{l} $ ), rightmost point ($ x_{r} $ ,$ y_{r} $ ), topmost point ($ x_{t} $ ,$ y_{t} $ ), bottommost point ($ x_{b} $ ,$ y_{b} $ ), and center$ (x_{c}, y_{c})=\left(\dfrac{x_{l}+x_{r}}{2},\dfrac{y_{t}+y_{b}}{2}\right) $ of the black hole shadow. The distortion parameter$ \delta_{c} $ is defined as$ (y_{c}-y_{l})/R_{s} $ , where$ R_{s} $ is the radius of the Schwarzschild black hole shadow ($ {\cal{Q}}={\cal{O}}=0 $ ).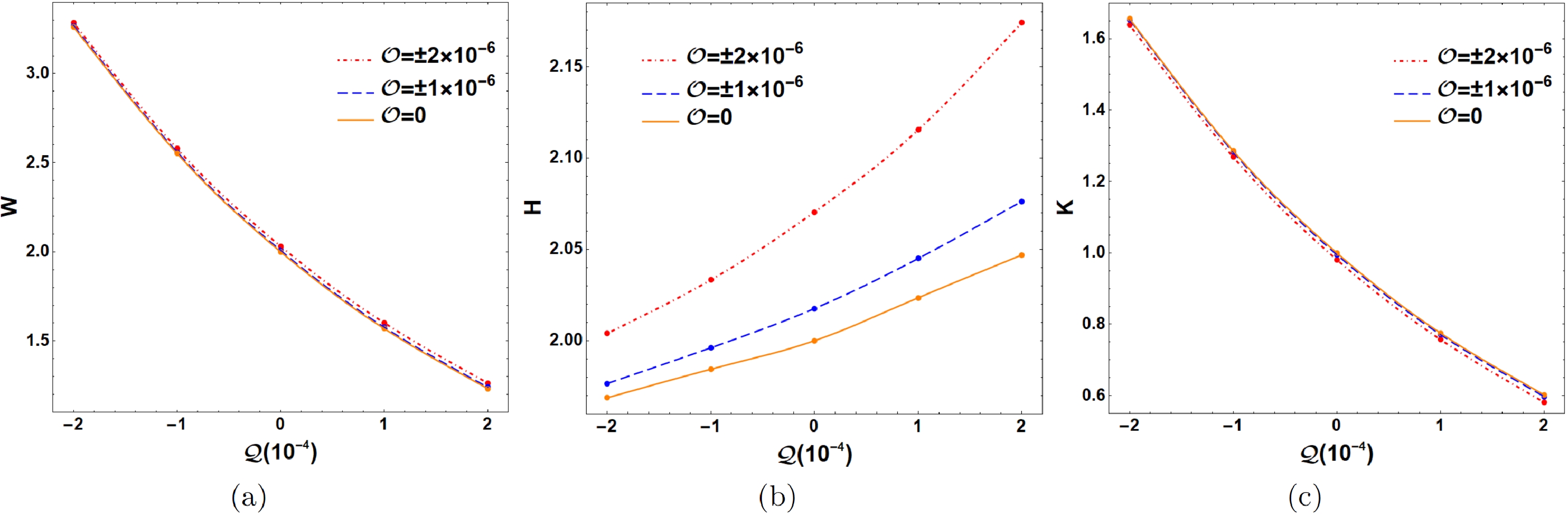
Figure 9. (color online) Various values of the width W, height H, and oblateness K of the black hole shadow with the quadrupole strength
$ {\cal{Q}} $ for different$ {\cal{O}} $ .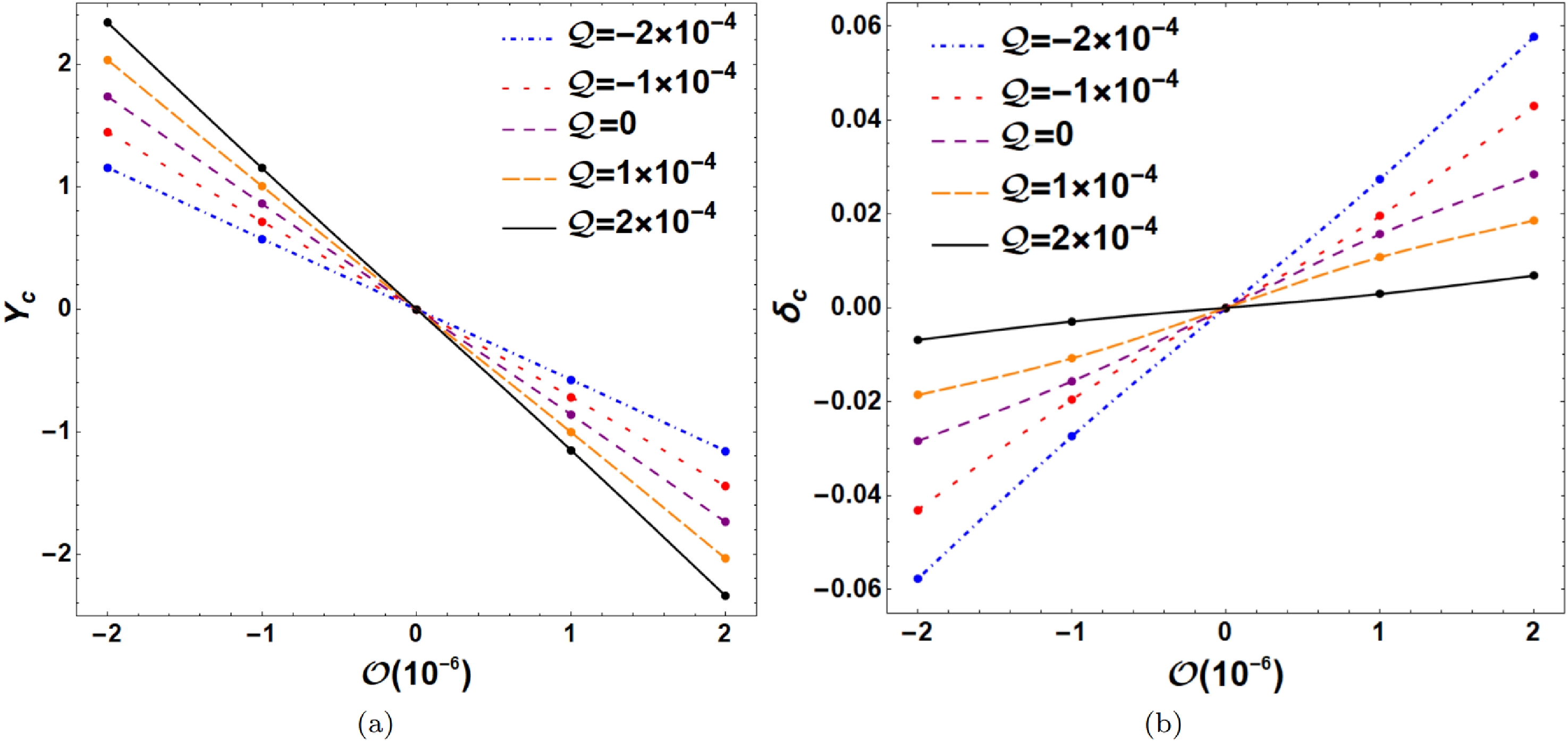
Figure 10. (color online) Various values of the deviation
$ Y_{c} $ and distortion parameter$ \delta_{c} $ of the black hole shadow with the octopolar strength$ {\cal{O}} $ for different$ {\cal{Q}} $ .In Figs. 11 and 12, we present the shadows of a Schwarzschild black hole with a halo for the observer inclination angle
$ \theta_{{\rm obs}}=0 $ and$ \pi/4 $ , respectively. As shown in Fig. 11, the black hole shadows are always circular with different$ {\cal{Q}} $ and$ {\cal{O}} $ at$ \theta_{{\rm obs}}=0 $ . However, interestingly, the black hole shadow becomes larger with increasing$ {\cal{Q}} $ or$ {\cal{O}} $ . Via a comparison with the Schwarzschild black hole shadow (Fig. 11(e) with$ {\cal{Q}}={\cal{O}}=0 $ ), we find that a negative$ {\cal{Q}} $ or$ {\cal{O}} $ causes the black hole shadow to shrink, whereas a positive$ {\cal{Q}} $ or$ {\cal{O}} $ causes the black hole shadow to expand. For the observer inclination angle$ \theta_{{\rm obs}}=\pi/4 $ (Fig. 12), the black hole shadow not only becomes more prolate but also shifts upward with increasing$ {\cal{Q}} $ or$ {\cal{O}} $ .
Figure 11. (color online) Shadows of a Schwarzschild black hole with a halo for the observer with the inclination angle
$\theta_{{\rm obs}}=0$ . Top row:$ {\cal{Q}}=-1\times10^{-4} $ ,${\cal{O}}=-1\times10^{-6},~ 0, 1\times10^{-6}$ . Middle row:$ {\cal{Q}}=0 $ ,${\cal{O}}=-1\times10^{-6},~ 0, 1\times10^{-6}$ . Bottom row:$ {\cal{Q}}=1\times10^{-4} $ ,$~{\cal{O}}=-1\times10^{-6},~ 0, 1\times10^{-6}$ .
Figure 12. (color online) Shadows of a Schwarzschild black hole with a halo for the observer with the inclination angle
$\theta_{{\rm obs}}=\pi/4$ . Top row:$ {\cal{Q}}=-1\times10^{-4} $ ,${\cal{O}}=-1\times10^{-6},~ 0, 1\times10^{-6}$ . Middle row:$ {\cal{Q}}=0 $ ,${\cal{O}}=-1\times10^{-6},~ 0, 1\times10^{-6}$ . Bottom row:$ {\cal{Q}}=1\times10^{-4} $ ,${\cal{O}}=-1\times10^{-6},~ 0, 1\times10^{-6}$ . -
We study the surface geometry and shadows of a Schwarzschild black hole with a halo. The exterior halo is a multipolar structure containing quadrupolar and octopolar terms. We find that the quadrupole term causes the Schwarzschild black hole to be prolate at quadrupole strength
$ {\cal{Q}}<0 $ and oblate at$ {\cal{Q}}>0 $ , and the octopole term causes the shadow to stretch upward at octopolar strength$ {\cal{O}}<0 $ and downward at$ {\cal{O}}>0 $ . The radius of the light rings$ r_{LR} $ only depends on$ {\cal{Q}} $ in the space-time of a Schwarzschild black hole with a halo. Light rings do not exist when$ {\cal{Q}} $ is larger than a critical$ {\cal{Q}}_{c} $ ; both unstable and stable light rings exist at$ {\cal{Q}}_{c}<{\cal{Q}}<0 $ ; and only one unstable light ring exists at$ {\cal{Q}}>0 $ . The shadow of a Schwarzschild black hole with a halo stretches and squeezes along the horizontal direction at$ {\cal{Q}}<0 $ and$ {\cal{Q}}>0 $ , respectively. Meanwhile, the black hole shadow shifts upward at$ {\cal{O}}<0 $ and downward at$ {\cal{O}}>0 $ . We show the light rays spiraling asymptotically toward the photon sphere and their tangents at the observer, which determine the margins of the shadow. The angle between the two tangents, namely, the angular radius of the black hole shadow, is larger at$ {\cal{Q}}<0 $ and smaller at$ {\cal{Q}}>0 $ , which results in the stretching and squeezing of the black hole shadow in the horizontal direction. The tangents slope upward at$ {\cal{O}}<0 $ , and downward at$ {\cal{O}}> $ , which causes the shadow to shift upward and downward in the vertical direction. From the observable width W, height H, oblateness K, and distortion parameter$ \delta_{c} $ of the black hole shadow, one can determine the value of$ {\cal{Q}} $ and$ {\cal{O}} $ of a Schwarzschild black hole with a halo. Black hole shadows are always circular and become larger as$ {\cal{Q}} $ or$ {\cal{O}} $ increases for the observer inclination angle$\theta_{{\rm obs}}=0$ . Black hole shadows not only become more prolate but also shift upward with increasing$ {\cal{Q}} $ or$ {\cal{O}} $ for$\theta_{{\rm obs}}=\pi/4$ . Our results show that the quadrupolar and octopolar terms yield a series of interesting patterns for the shadow of a Schwarzschild black hole with a halo.
Surface geometry and shadow of a Schwarzschild black hole with a halo
- Received Date: 2022-09-08
- Available Online: 2023-01-15
Abstract: We studied the surface geometry and shadows of a Schwarzschild black hole with a halo containing quadrupolar and octopolar terms. It was found that the quadrupole term causes a Schwarzschild black hole to be prolate at the quadrupole strength





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: