Binding energies of proton-rich nuclei determined from their mirror pairs

With the advent of the concept of isospin quantum number, the proton and neutron have been manifested as two states of the nucleon in view of the strong interaction, formalizing the charge symmetry or charge independence of the nuclear interaction [1]. A pair of mirror nuclei is then a natural laboratory for testing isospin symmetry, which leads to the existence of isobaric multiplets and analog states or resonances [2, 3]. Another conjecture, used in the present study, is that, if the nuclear interaction is charge independent, the mass differences of mirror nuclei would be dominantly determined by the Coulomb interaction [4, 5]. By employing the conventional liquid drop mass formula, this point can be readily verified through available experimental data on nuclear mass. Of course, there are still residual mass differences (RMDs) for mirror pairs after excluding the Coulomb interaction, which may be attributed to the broken isospin symmetry [6–8].

In turn, once the above RMDs can be effectively described for a better evaluation of the mass differences (MDs) of mirror nuclei, one of their masses can be predicted based on the other [9–11]. For many decades, this idea has been actualized in the prediction of the masses of proton-rich nuclei owing to the abundance of binding energy (BE) data in the partner (neutron-rich) side, especially in the recent years [12, 13, 14]. The MDs of mirror nuclei are also used in the modifications of mass formulas, such as in the Weizsäcker-Skyme (WS) model [15] and a combination of the Kelson-Garvey relationship [16]. The treatment of MDs in mirror nuclei can be classified into two main groups, namely, the refined Coulomb interaction energy [12, 13, 17] and empirical RMDs [10, 11, 14, 18]. Besides the traditional liquid drop model (LDM), density functional theory has been employed to improve the former quantity [12, 13]. As for the RMD case, a popular idea is based on the shell effect correction [14, 18], in which the differences between the proton and neutron mean-field approximations are considered along with their spin-orbit interactions. Within the valence correlation scheme (VCS), the (modified) valence nucleon product and the linear form of valence nucleon number have been used to reveal the remarkable similarity generated from complicated nuclei [1, 19]. With these in mind, this study aims to introduce the VCS into the RMD curve of mirror nuclei, serving as a more reasonable evaluation of the MDs of a mirror pair and the subsequent masses of involved nuclei.

Let us begin with a macroscopic-microscopic type mass formula,

Here, the macroscopic part corresponds to the conventional LDM, which is comprised of the volume, surface, Coulomb, symmetry, and pairing energies. Clearly, these terms, except the Coulomb energy, satisfy the charge independence of nuclear interactions, that is, their values are unchanged if the neutron and proton numbers are exchanged. The $ B_{\mathrm{mic}} $ part is only considered in terms of the shell correction in this study. This is consistent with the treatment in WS-type mass models [15], which also include the mirror nuclei constraint. Before proceeding to the VCS shell correction for mirror nuclei, it is interesting to check the validity of the MDs of mirror nuclei in the sole Coulomb energy.

As a starting point, the MD of a pair of mirror nuclei, namely, ($ Z,N $) and ($ N,Z $), is expressed via the BE,

where the convention of $ N>Z $ is used in this study. Following the traditional Bethe-Weizsäcker mass formula, i.e., the above $B (Z,N)$ equation, the $\Delta B (Z,N)$ value is determined by the Coulomb displacement energies,

where $ \Delta Z=N-Z $. Therefore, it is interesting to check the validity or reliability of the above formula, which is also somewhat related to the Nolen-Schiffer anomaly [17, 20]. By collecting the 106 pairs of mirror nuclei in the AME16 compilation [21], the quantity $ \Delta B/\Delta Z $ is plotted against$ A^{2/3} $ in Fig. 1. As expected, a linear relationship between the two former quantities is obtained, and the fixed $a_{{\rm C}}$ value is –0.715 MeV, which is comparable with the commonly-accepted value [9–11]. However, there is a sizable intercept for this linear line, which is beyond the capability of Eq. (3) (the expected value is zero). Of course, the aforementioned formula for Coulomb energy originates from the assumption of a uniformly charged nuclear sphere. If one considers the diffuseness modification, proton form-factor correction, and other effects [20, 22, 23], the Coulomb energy should be rewritten. Nonetheless, these corrections appear to not have the ability to reproduce the non-zero intercept value. Moreover, they cannot clearly enhance the accuracy of the evaluation of the Coulomb displacement energy, as shown in Ref. [18]. This unexpected deviation may contribute to the quantal correction to the empirical Coulomb energy via the so-called exchange energy [23, 24]. It is simply stated that the exchange (xC) term can be expressed as $E_{{\rm xC}}=\sum_{a,b}\langle ab|{\rm e}^2/r_{12}|ab-ba\rangle$, in which the double summation covers all single-proton states in the Fermi sea. The exchange term is then found to be proportional to $Z^2/\Omega k_{{\rm F}}^2$ within the Fermi gas model [25]. Because the Fermi momentum is related to the volume parameter via $k_{{\rm F}}\sim (Z/\Omega)^{1/3}$ and $ \Omega\sim A $, the Coulomb exchange potential is fixed as $a_{{\rm xC}}^{'}Z^{4/3}/A^{1/3}$. Through Taylor expansion to the first order, the total Coulomb displacement energy can be expressed as $\Delta B(Z,N)/\Delta Z= a_{{\rm C}}A^{2/3}+(2^{5/3}/3)a_{{\rm xC}}'=$ $a_{{\rm C}}A^{2/3}+a_{{\rm xC}}$, where the final constant is responsible for the non-zero intercept in Fig. 1. Moreover, it is found that the MDs of mirror nuclei can be reproduced more accurately after the introduction of exchange Coulomb energy. In addition, the Coulomb displacement energy should be responsible for the energy differences between isobaric states in mirror nuclei. As mentioned in Ref. [24], the fixed values of $a_{{\rm C}}$ and $a_{{\rm xC}}$ would be different from this case of MDs in mirror nuclei. This is worth further investigation and may be related to the Nolen-Schiffer anomaly.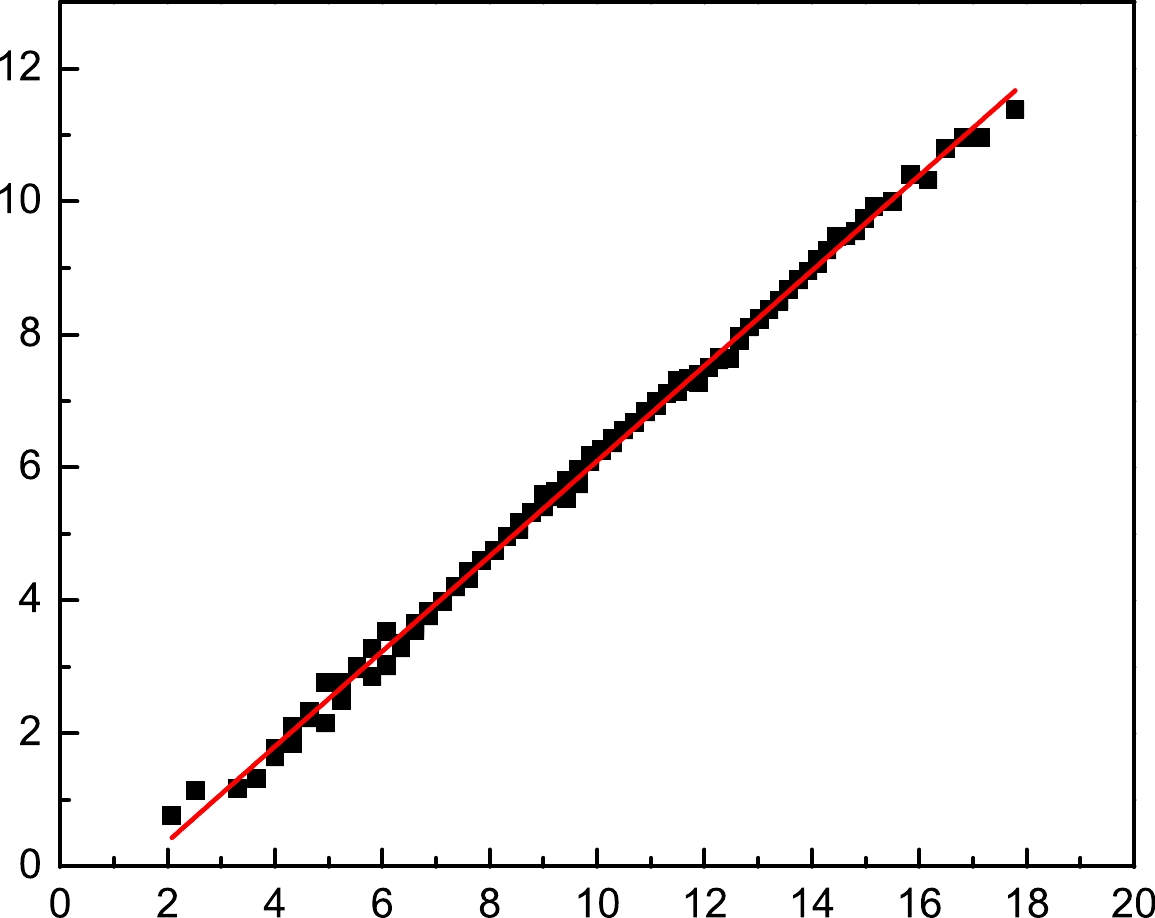

Figure 1.  (color online) Binding energy difference between mirror nuclei (divided by the difference in their proton numbers) versus the mass number quantity $A^{2/3}$. Despite the linear relationship, there is an intercept value at approximately –1.053 MeV, which is consistent with the analysis in Ref. [24].

Now, we investigate the RMDs between mirror nuclei after excluding the Coulomb displacement energy. As mentioned before, the RMDs are attributed to the shell correction in this case via the valence nucleon scheme. In the VCS, there are three types of Casten plots [1, 19, 26, 27], namely, $N_p N_n$, $\frac{N_ pN_n}{N_p+N_n}$, and $\alpha N_ p+\beta N_ n$, in which $N_ p$ ($N_ n$) is the difference between the proton (neutron) number and the nearest magic number for one given nucleus. The two former quantities have been widely used in the description of structural factors, such as the ratio of excitation energies $ E_{4_{1}^{+}}/E_{2_{1}^{+}} $ [1, 19], empirical shell corrections [24], and preformation probability of clustering in heavy nuclei [28–31]. However, these two quantities would be identical, even if the proton and neutron numbers are exchanged for mirror nuclei, implying that they are not suitable for mapping the RMDs of mirror pairs. In comparison, the last Casten factor, $\alpha N_ p+\beta N_ n$, would change for mirror nuclei. Moreover, this factor has shown its effectiveness in the evaluation of nucleon separation energies and decay energies [26, 27].

Keeping this in mind, the MDs of mirror nuclei can be expressed as

where the first term is the Coulomb displacement energy, and the residual terms correspond to the shell correction. By fitting the available experimental MDs in 106 pairs of mirror nuclei ($ 1\leq\Delta Z\leq5 $) from AME16 [21], the parameters are obtained as $a_{{\rm C}}=-0.7267$, $a_{{\rm xC}}=-1.207$, $ \alpha=0.0374 $, and $ \beta=-0.0134 $, with the standard deviation between theory and experiment $ \sigma=0.291 $ MeV. This fitting procedure is performed using the Levenberg-Marquardt iteration algorithm to obtain the parameters simultaneously. Better insight into the validity of the above formula can be found in Fig. 2. As shown, the deviation between the calculated $ \Delta B $ value and the measured value is generally in the range $ -0.75\sim 0.5 $ MeV, except for the pairs (1, 3) and (5, 10) with extreme neutron-proton ratios. As shown in Ref. [10], it is worth noting that, if mirror nuclei are divided into five groups according to the $ \Delta Z $ value and the respective fitting process for each group, the standard deviation σ would be clearly reduced for Eq. (4).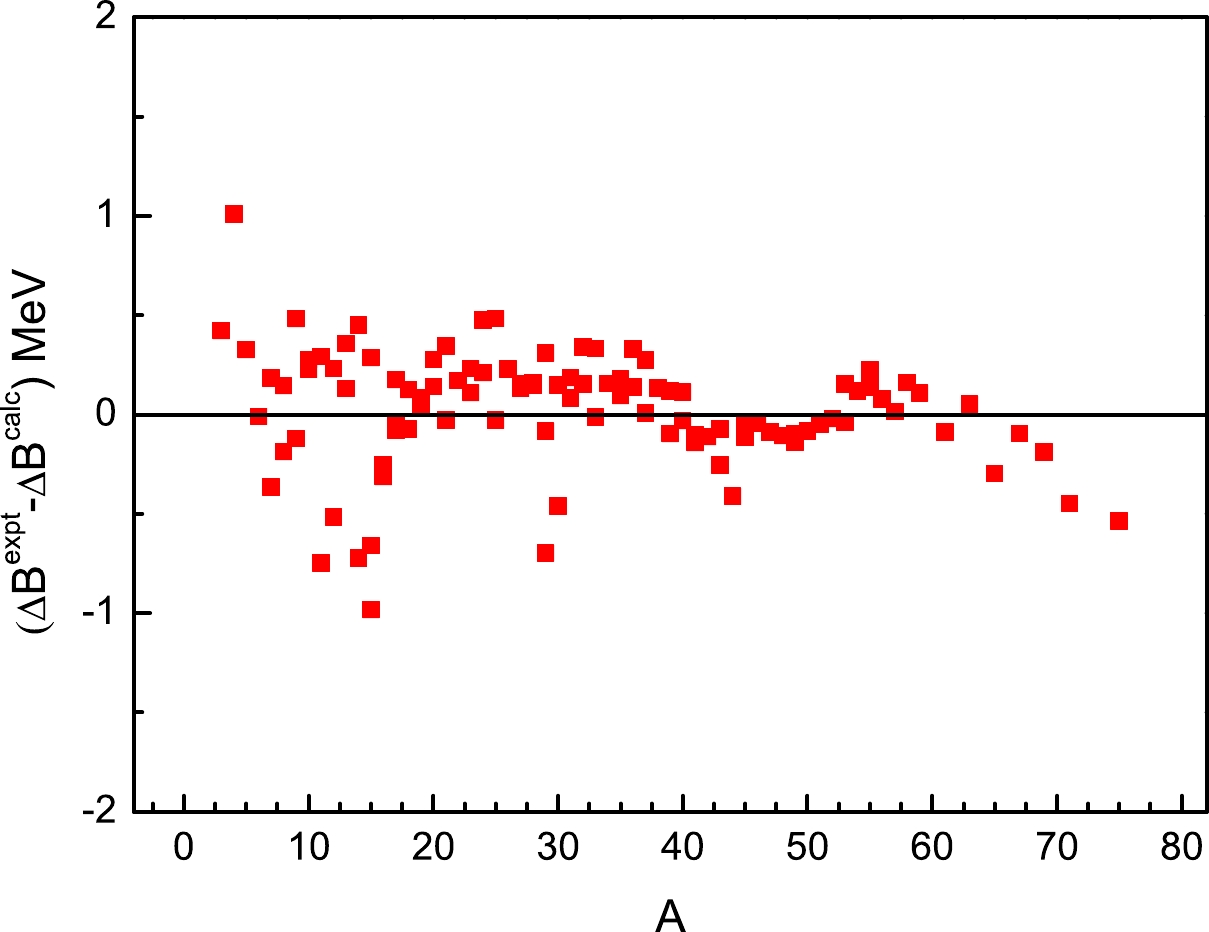

Figure 2.  (color online) Difference between the experimental $\Delta B$ value of mirror nuclei and the calculated value via Eq. (4) versus the mass number A. The zero line is to guide the eye.

However, the accuracy of the above formula appears to increase with increasing mass number, which corresponds to the different regions in the shell-model text, as discussed in Refs. [14, 32]. In fact, after these mirror pairs are classified into four groups via the magic number, that is, ($ 2 \sim 8 $), ($ 8 \sim 20 $), ($ 20 \sim 28 $), and ($ 28 \sim 50 $), the standard deviation of Eq. (4) is 0.315 MeV, 0.206 MeV, 0.093 MeV, and 0.098 MeV for these four regions, respectively, implying a decrease in the general σ value (0.291 MeV) and an improvement in the present approach. Of course, there are still clear fluctuations in the difference $ \Delta B^{\mathrm{expt}}-\Delta B^{\mathrm{calc}} $ in Fig. 2, which may correspond to the residual shell or another structural effect due to the few-body character for light nuclei. In this sense, the $\alpha N_ p+\beta N_ n$ term or its higher order term is not fully capable of covering the RMDs $\Delta B^{\mathrm{expt}}(Z,N)- (-a_{{\rm C}}A^{2/3}+ a_{{\rm xC}})\Delta Z$, although this VCS term is good at describing the separation energies and decay energies of heavier nuclei [26, 27]. This deserves further investigation, possibly from the perspective of nucleon-nucleon interactions. Moreover, the mass relationship between mirror nuclei introduces a possible method of predicting the BE of unknown nuclei. There are six new pairs of mirror nuclei with measured masses in the AME20 table [33] when compared to AME16 [21]. This provides us with a good opportunity to test the present formula for the MDs of mirror nuclei. Table 1 presents the predicted results for these new mirror pairs, where the deviation between the calculation and measurement is listed in the last column. Encouraged by these small deviations for mirror nuclei from both the AME16 and AME20 tables, the $ \Delta B $ formula, namely, Eq. (4), is applied to predict the BEs of several unknown proton-rich nuclei near the dripline.

Z	N	A	$\Delta B^{{\rm expt}}$ /MeV	$\Delta B^{{\rm calc}}$ /MeV	δ /MeV
24	20	44	31.177	31.346	0.169
25	21	46	32.472	32.486	0.014
26	22	48	33.615	33.611	−0.004
27	23	50	34.765	34.721	−0.044
28	24	52	35.989	35.817	−0.172
37	36	73	11.321	11.665	0.344

Table 1.  Detailed results of the six new pairs of mirror nuclei from AME20 [33]. The proton, neutron, and mass numbers are listed in columns one to three, respectively, and the experimental and evaluated $\Delta B$ values are shown in the fourth and fifth columns, respectively, along with their deviations in the last column.

By combining Eqs. (2) and (4), we find that, once the BE of one nucleus is obtained, the BE value of its pair can be readily found using $ B(N,Z)=B(Z,N)-\Delta B(Z,N) $. Owing to the abundance of data on $ B(Z,N) $ ($ N>Z $) in AME20 [33], we predict the BEs of 47 proton-rich nuclei in the ranges $ \Delta Z\leq 4 $ and $ A\leq 90 $, as displayed in Table 2. For comparison, other theoretical results from the finite-range droplet model (FRDM) [23] and WS type nuclear mass model [34] are listed in the last two columns of this table, indicating the consistency between our evaluations and these other results. Encouraged by this, it is hoped that the present formula for MDs in mirror nuclei and the corresponding predictions will be useful for future experiments.

Z	N	A	$BE {\rm pred}$ /MeV	$BE$[23] /MeV	$BE$[34] /MeV
19	15	34	261.400	260.47	260.845
21	17	38	295.083	295.55	294.640
23	19	42	328.862	330.39	328.978
30	26	56	454.493	454.04	453.505
30	27	57	469.609	469.12	469.477
31	27	58	468.137	467.25	468.102
31	28	59	486.080	485.68	485.697
31	29	60	500.078	498.77	499.433
32	28	60	487.179	486.45	485.767
32	29	61	501.501	500.08	500.568
32	30	62	517.745	516.37	516.983
33	29	62	499.845	498.48	498.654
33	30	63	516.333	515.52	515.408
33	31	64	530.259	529.23	529.267
34	30	64	517.424	516.52	515.862
34	31	65	531.386	530.51	530.468
34	32	66	547.888	547.09	547.727
35	31	66	529.516	529.15	528.139
35	32	67	546.019	547.97	545.482
35	33	68	560.034	559.90	559.381
36	32	68	547.153	546.97	545.923
36	33	69	561.080	561.11	560.733
36	34	70	577.933	577.98	578.011
37	34	71	575.747	576.48	576.162
37	35	72	589.934	590.57	590.122
38	35	73	590.884	591.42	591.701
38	36	74	608.076	608.68	609.167
39	36	75	606.206	607.29	607.094
39	37	76	621.100	621.78	621.302
39	38	77	637.394	638.12	637.758
40	37	77	621.336	622.53	622.315
40	38	78	638.649	639.75	639.567
40	39	79	652.477	653.22	652.961
41	39	80	651.481	652.11	651.293
41	40	81	667.360	667.97	667.829
42	39	81	651.482	652.34	652.081
42	40	82	668.883	669.06	669.469
42	41	83	682.607	682.34	682.731
43	40	83	666.396	667.23	666.965
43	41	84	681.403	681.62	680.950
43	42	85	697.666	698.02	698.024
44	42	86	699.264	699.47	699.641
44	43	87	713.011	713.16	713.703
45	43	88	711.770	712.05	711.897
45	44	89	728.857	728.35	728.869
46	44	90	729.934	730.18	730.807

Table 2.  Predicted binding energies of proton-rich nuclei near the dripline using the present mass relationship between mirror nuclei compared with other theoretical results from the FRDM [23] and WS-type [34] mass formulas.

To summarize, the MDs between mirror nuclei are initially ascribed to the Coulomb displacement energy by considering the charge-independent nucleon-nucleon interaction. After the systematic analysis of the experimental data of MDs for 106 pairs of mirror nuclei from AME16, the exchange Coulomb term is reconfirmed as essential for the reasonable description of Coulomb displacement energy in terms of both accuracy and physics. The RMDs of mirror pairs are then dependent on the valence nucleon number in the VCS picture. Considering the request of broken isospin symmetry, the linear formula of the valence proton (neutron) number, i.e., $\alpha N_{ p}+\beta N_{ n}$, is selected to obtain the MD formula for mirror nuclei. Besides the satisfactory agreement between theory and evaluation for AME16, the experimental MDs are well reproduced for six new pairs of mirror nuclei in AME20. A number of predictions are then made on the BEs of proton-rich nuclei using the available BE values of relatively neutron-rich nuclei from AME20 for use in future measurements.