-
Recently, a universal upper bound for a Lyapunov exponent of chaos in thermal quantum systems with a large number of degrees of freedom was proposed by Maldacena, Shenker, and Stanford [1]. The bound is given by a temperature dependent relation
$ \begin{eqnarray} \lambda \leq \frac{2\pi T}{\hbar}, \end{eqnarray} $

(1) where λ is the Lyapunov exponent, and T is the temperature of the systems, which is obtained by shock waves near black hole horizons [2, 3]. This bound argues through the physical input that certain time-ordered correlation functions approximately factorize and saturate in the Sachdev-Ye-Kitaev model [4–9]. This conjecture highlights a connection between black holes and quantum chaos. Since this seminal research was put forward, it has attracted considerable attention [10–65], and many studies have shown its correctness.
Motions of particles around black holes have been extensively researched. These motions convey important information on background spacetimes. For example, unstable circular geodesics affect the optical appearance of a gravitationally collapsed star and explain the star's luminosity [66]. Null geodesics are useful for explaining the quasinormal modes of a black hole for test fields [67–69]. Spins and mergers of black holes can be explained by the circular motions of particles [70]. When a particle is subjected to sufficiently strong external forces, it can be in unstable equilibrium and very close to a black hole without falling into it. This equilibrium may lead to chaos owing to small perturbations. Based on this, Hashimoto and Tanahashi studied the chaos bound by the radial motion of the particle [71]. They found that there is an upper bound for the Lyapunov exponent, and the bound is related to the surface gravity, that is,
$ \begin{eqnarray} \lambda \leq \kappa. \end{eqnarray} $

(2) where κ is the surface gravity. From the relation between the surface gravity and temperature, this result is completely consistent with Eq. (1).
There are cases in which the chaos bound is violated [72–76]. The chaos bound has also been studied via the motion of particles near horizons. When considering static equilibrium of a charged particle around a charged black hole, one can adjust the charge-to-mass ratio of the particle so that it is close to the event horizon. To take into account the contributions of the sub-leading terms in near-horizon expansion, Zhao, Li, and Lü expanded the exponent at the horizon [72]. They found that the bound was satisfied by Reissner-Nordström (RN) and RN anti-de Sitter (RN AdS) black holes and violated by a large number of black holes. In their research, the exponent was derived using the effective potential method, and the influence of the particle angular momenta was neglected. In fact, a particle's angular momentum affects not only the exponent's value, but also the location of the particle's equilibrium orbit. When the angular momentum was considered, the exponent of chaos for charged particles around charged rotating black holes was obtained. The violations of the bound were found in [74, 75]. In [50, 77, 78], two exponents for a rotating BTZ black hole were obtained by calculating out-of-time-order correlators, one of which obeys the bound, whereas the other violates it. Another method for deriving the exponent is to solve a determination of the eigenvalues of a Jacobian matrix in phase space. Using this method and considering the influence of the angular momentum, Lei and Ge first found the violations for the bound in the near-horizon regions of RN and RN AdS black holes [73]. Considering the expression for the exponent at any location of the radial coordinate, they extended their study to cases beyond near-horizon regions and found the violations. This study is meaningful and different from that in [72] because this is the first time the circular motion of RN (AdS) black holes has been found to violate the bound locally. Owing to the appearance of the particle angular momentum, the value of the exponent increases with increasing angular momentum. When the angular momentum approaches infinity, it describes the case of a photon [73]. This is a significant difference from static equilibrium.
In this paper, we investigate the Lyapunov exponent of chaos for a charged particle around Kerr-Newman-Taub-NUT black holes and find spatial regions where the chaos bound is violated. In our investigation, the exponent is obtained in the dragging coordinate by solving the eigenvalue of a Jacobian matrix and is not expanded at the event horizons. The angular momentum of the particle plays an important role in the investigation. It affects not only the value of the exponent, but also the position of an equilibrium orbit. To find the regions, we fix the particle's charge to mass ratio and the parameters of the black holes and change the angular momentum to calculate the values of the exponent at the different positions and surface gravity. These regions are significantly affected by the electric charge, NUT charge, and rotational parameter. The black holes and particle rotating in the same and opposite directions are taken into account. The thermodynamic properties of Kerr-Newman-Taub-NUT black holes have been studied in [79]. These black holes have four conserved charges: the Komar mass, electric charge, NUT charge, and angular momentum. One feature of the NUT charge is that it has both rotation-like and electromagnetic charge-like characteristics. This feature has a significant influence on the violation of the bound.
The paper is organized as follows. In the next section, we review the Kerr-Newman-Taub-NUT black hole geometry and derive the Lyapunov exponent in the dragging coordinate system. The influence of the angular momentum of the particle on the exponent is considered. In Sec. III, fixing the charge to mass ratio of the particle, we discuss the range of the angular momentum and spatial region where the chaos bound is violated for specific values of the electric charge, NUT charge, and rotational parameter. The last section is devoted to our conclusions.
-
We first review the Kerr-Newman-Taub-NUT black hole. Its metric is given by [80]
$ \begin{aligned}[b] {\rm d}s^2 =& -\frac{\Delta}{\rho^2}\left({\rm d}t-\chi {\rm d}\psi\right)^2 +\frac{\rho^2}{\Delta}{\rm d}r^2 + \rho^2 {\rm d}\theta^2 \\&+\frac{\sin^2\theta}{\rho^2}\left[a{\rm d}t -(r^2+a^2+n^2){\rm d}\psi\right]^2, \end{aligned} $

(3) with an electromagnetic potential
$ \begin{eqnarray} A_{\mu}{\rm d}x^{\mu}=\frac{Qr}{\rho^2}\left[{\rm d}t + \left(2n\cos\theta-a\sin^2\theta\right){\rm d}\psi\right], \end{eqnarray} $

(4) where
$ \begin{aligned}[b] \Delta =& r^2 -2Mr-n^2+a^2+Q^2, \\ \rho^2 =& r^2 + (n+a\cos\theta)^2,\\ \chi =& a\sin^2\theta -2n\cos\theta, \end{aligned} $

(5) where M, Q, and n are the Komar mass, electric charge, and NUT charge, respectively, and a is a rotational parameter representing the angular momentum per unit mass. When
$ a=0 $ , the metric describes a RN Taub-NUT black hole. When$ Q=0 $ , it is reduced to a Kerr-Taub-NUT black hole. When$ Q=a=0 $ , it describes Taub-NUT spacetime. There are two roots for$ \Delta =0 $ , which describe the event horizon$ r_+ $ and inner horizon$ r_- $ ,$ \begin{eqnarray} r_{\pm} = M \pm \sqrt{M^2+n^2-Q^2-a^2}. \end{eqnarray} $

(6) The surface gravity is
$ \begin{eqnarray} \kappa = \frac{r_+ - r_-}{2(r_+^2+a^2+n^2)}= \frac{r_+ - M}{r_+^2+a^2+n^2}. \end{eqnarray} $

(7) When the event and inner horizons coincide,
$ M^2+n^2 = Q^2 + a^2 $ and the surface gravity disappears. To facilitate the derivation of the Lyapunov exponent, we perform a coordinate transformation,$ \begin{eqnarray} {\rm d}\phi={\rm d}\psi- \frac{\chi\Delta - a(r^2 + a^2 + n^2)\sin^2\theta}{\chi^2\Delta - (r^2 + a^2 + n^2)^2 \sin^2\theta } {\rm d}t, \end{eqnarray} $

(8) on metric (3) and the electromagnetic potential (4). Then, metric (3) becomes
$ \begin{aligned}[b] {\rm d}s^2 =& -F(r){\rm d}t^2 + \frac{1}{N(r)}{\rm d}r^2 + C(r){\rm d}\theta^2 + D(r){\rm d}\phi^2, \\ =& -\frac{\rho^2 \Delta \sin^2\theta}{(r^2 + a^2 + n^2)^2\sin^2\theta - \chi^2\Delta}{\rm d}t^2 \\&+\frac{1}{\rho^2}\left[(r^2 + a^2 + n^2)^2 \sin^2\theta - \chi^2\Delta\right]{\rm d}\phi^2 \\ & + \frac{\rho^2}{\Delta}{\rm d}r^2 + \rho^2 {\rm d}\theta^2, \end{aligned} $

(9) and the electromagnetic potential takes the form
$ \begin{aligned}[b] A_{\mu}{\rm d}x^{\mu} =&\frac{(r^2+a^2+n^2)Qr\sin^2\theta }{(r^2+a^2+n^2)^2 \sin^2\theta - \chi^2\Delta}{\rm d}t \\&+ \frac{Qr}{\rho^2}\left(2n\cos\theta\ -a\sin^2\theta \right){\rm d}\phi. \end{aligned} $

(10) Clearly, the above metric is different from that of a general spherically symmetric black hole. When
$ a = 0 $ , metric (9) describes a spherically symmetric spacetime, and the electromagnetic potential is not zero in the ϕ-direction. -
We consider a charged particle moving around a Kerr-Newman-Taub-NUT black hole. Its Lagrangian is
$ \begin{eqnarray} \mathcal{L} =\frac{1}{2}g_{\mu\nu}\dot{x}^{\mu}\dot{x}^{\nu}-qA_{\mu}\dot{x^{\mu}}, \end{eqnarray} $

(11) where
$\dot{x}^{\mu} = \dfrac{{\rm d}{x}^{\mu}}{{\rm d}\tau}$ , and the particle mass is one unit. The Lagrangian calculated using metric (3) and potential (4) is fully consistent with that calculated using Eqs. (9) and (10). We adopt the latter to obtain this. When the particle moves in the equatorial plane of the black hole, where$\theta = \dfrac{\pi}{2}$ , the Lagrangian in the dragging coordinate system is$ \begin{eqnarray} \mathcal{L} = \frac{1}{2}\left(-F\dot{t}^2+\frac{\dot{r}^2}{N} +D\dot{\phi}^2\right) -qA_t\dot{t}-qA_{\phi}\dot{\phi}, \end{eqnarray} $

(12) where
$ \begin{aligned}[b] F =&\frac{(r^2+n^2)\Delta}{(r^2 + a^2 + n^2)^2 - a^2\Delta}, \quad N= \frac{\Delta}{r^2+n^2}, \quad A_{\phi}= - \frac{Qra}{r^2+n^2}, \\ D =& \frac{(r^2 + a^2 + n^2)^2 - a^2\Delta}{r^2+n^2}, \quad A_t = \frac{(r^2+a^2+n^2)Qr }{(r^2+a^2+n^2)^2 - a^2\Delta}. \end{aligned} $

(13) From the definition of the generalized momenta
$ \pi_{\mu}=\dfrac{\partial\mathcal{L}}{\partial\dot{x}} $ , we get$ \begin{eqnarray} \pi_t = -F\dot{t} -qA_t =E, \quad\quad \pi_r = \frac{\dot{r}}{N}, \quad\quad \pi_{\phi} = D \dot{\phi}-qA_{\phi} =L. \end{eqnarray} $

(14) In the above equation, E and L are the energy and angular momentum of the particle, respectively. The Hamiltonian of the particle is
$ \begin{aligned}[b] H =& \frac{1}{2}g^{\mu\nu}(\pi_{\mu}+qA_{\mu})(\pi_{\nu}+qA_{\nu}) \\ =& \frac{-(\pi_{t}+qA_{t})^2+\pi_r^2FN+ (\pi_{\phi}+qA_{\phi})^2D^{-1}F}{2F}. \end{aligned} $

(15) To investigate the chaos bound, we must find the equations of motion of the particle, which are obtained from the Hamiltonian,
$ \begin{aligned}[b] \dot{t} =& \frac{\partial H}{\partial \pi_t}=-\frac{\pi_t+qA_t}{F}, \quad \dot{\pi_t}= -\frac{\partial H}{\partial t} =0 , \quad \dot{r} = \frac{\partial H}{\partial \pi_r}= \pi_r N, \\ \dot{\pi_r} =& -\frac{\partial H}{\partial r} =-\frac{1}{2}\Bigg[\pi^2_r N^{\prime} -\frac{2qA^{\prime}_t(\pi_t+qA_t)}{F}\\&+\frac{(\pi_t+qA_t)^2F^{\prime}}{F^2} +\left(\frac{(\pi_{\phi}+qA_{\phi})^2}{D}\right)^{\prime}\Bigg], \\ \dot{\phi} =& \frac{\partial H}{\partial \pi_{\phi}}= \frac{\pi_{\phi}+qA_{\phi}}{D}, \quad \dot{\pi_{\phi}}= -\frac{\partial H}{\partial \phi} =0. \end{aligned} $

(16) In the above equations, "
$\prime$ " represents the derivative of r. We focus our attention to a two-dimensional phase space of the form$ (\pi_r, r) $ and obtain the radial equation at time t [81],$ \begin{aligned}[b] \frac{{\rm d}r}{{\rm d}t} =& \frac{\dot{r}}{\dot{t}} =-\frac{\pi_rFN}{\pi_t+qA_t}, \\ \frac{{\rm d}\pi_r}{{\rm d}t} =& \frac{\dot{\pi_r}}{\dot{t}} = -qA^{\prime}_t +\frac{1}{2}\Bigg[\frac{\pi^2_r FN^{\prime}}{\pi_t+qA_t}+\frac{(\pi_t+qA_t)F^{\prime}}{F}\\& +\frac{((\pi_{\phi}+qA_{\phi})^2D^{-1})^{\prime}F}{\pi_t+qA_t}\Bigg]. \end{aligned} $

(17) The normalization of the four-velocity of a particle is given by
$ g_{\mu\nu}\dot{x}^{\mu}\dot{x}^{\nu}=\eta $ , where$ \eta =0 $ describes the motion of a massless particle, and$ \eta =-1 $ corresponds to the motion of a massive particle. Because the particle is charged here, the normalization yields a constraint condition,$ \pi_t+qA_t= -\sqrt{F[1+ \pi_r^2N + (\pi_{\phi}+qA_{\phi})^2D^{-1}]} $ . We define$F_1= \dfrac{{\rm d}r}{{\rm d}t}$ and$F_2=\dfrac{{\rm d}\pi_r}{{\rm d}t}$ and use the constraint to rewrite the above equations as$ \begin{aligned}[b] F_1 =& \frac{\pi_rFN}{\sqrt{F[1+ \pi_r^2N + (\pi_{\phi}+qA_{\phi})^2D^{-1}]}}, \\ F_2 =& -qA^{\prime}_t -\frac{\pi^2_r (NF)^{\prime}+F^{\prime}+[(\pi_{\phi}+qA_{\phi})^2D^{-1}F]^{\prime}}{2\sqrt{F[1+ \pi_r^2N + (\pi_{\phi}+qA_{\phi})^2D^{-1}]}}. \end{aligned} $

(18) To derive the Lyapunov exponent using the matrix method in the phase space
$ (\pi_r, r) $ , we define a Jacobian matrix$ K_{ij} $ with the elements$ \begin{eqnarray} K_{11} =\frac{\partial F_1}{\partial r}, \quad K_{12}= \frac{\partial F_1}{\partial \pi_r}, \quad K_{21}= \frac{\partial F_2}{\partial r}, \quad K_{22} = \frac{\partial F_2}{\partial \pi_r} . \end{eqnarray} $

(19) In the phase space, an equilibrium position
$ r_0 $ for the particle must first be found. At this position, the radial momentum of the particle satisfies$ \begin{eqnarray} \pi_r=\frac{{\rm d}\pi_r}{{\rm d}t}=0 . \end{eqnarray} $

(20) Using Eq. (20), we obtain the equilibrium position, which satisfies
$ \begin{eqnarray} -qA^{\prime}_t -\frac{\pi^2_r (NF)^{\prime}+F^{\prime}+[(\pi_{\phi}+qA_{\phi})^2D^{-1}F]^{\prime}}{2\sqrt{F[1+ \pi_r^2N + (\pi_{\phi}+qA_{\phi})^2D^{-1}]}} = 0. \end{eqnarray} $

(21) From Eqs. (19) and (20), the Lyapunov exponent is obtained by calculating the eigenvalue of the matrix,
$ \begin{aligned}[b] \lambda^2 =& \frac{1}{4}\frac{N[F^{\prime}+(\pi_{\phi}+qA_{\phi})^2(D^{-1}F)^{\prime}]^2}{F[1+(\pi_{\phi}+qA_{\phi})^2D^{-1}]^2}\\&-\frac{N}{2}\frac{F^{\prime\prime}+[(\pi_{\phi}+qA_{\phi})^2D^{-1}F]^{\prime\prime}}{1+(\pi_{\phi}+qA_{\phi})^2D^{-1}}\\ &-\frac{qA_t^{\prime\prime}NF}{\sqrt{F(1+(\pi_{\phi}+qA_{\phi})^2D^{-1})}}. \end{aligned} $

(22) At the event horizon,
$ \Delta=0 $ . Using Eqs. (7), (13), and (22), we get$ \begin{eqnarray} \lambda^2 =\frac{N(F^{\prime})^2}{4F}=\kappa^2, \end{eqnarray} $

(23) which is saturated at the horizon. This result is consistent with that obtained for spherically symmetric black holes [72, 73].
The exponent has been derived using the effective potential and matrix methods in [72, 73, 81]. In [72, 73, 81], considering the constraint on the particle charge, the authors used the electromagnetic potential, radial momentum, and other physical quantities to express the charge q. Therefore, the exponent they obtained does not show the charge. To study the chaos bound in the near-horizon regions, they expanded the exponent at the horizon. In this paper, we fix the charge-to-mass ratio of the particle to investigate the influence of the particle's angular momentum and the parameters of the black holes on the exponent and find the range of the angular momentum and spatial region where the bound is violated. The particle charge is always fixed as a constant in the calculation, and the exponent obtained here is a special case of that derived in [72, 73, 81]. When
$ a=n=0 $ , metric (3) is reduced to the RN metric. Using the constraint on the particle charge, we can easily recover the exponent in [73]. Furthermore, when$ a=n=\pi_{\phi}=0 $ , the exponent in [72] is also recovered. -
We use a charged particle moving around Kerr-Newman-Taub-NUT black holes to investigate the Lyapunov exponent of chaos. The particle's balance is provided by the Lorentz and centrifugal forces. We can adjust the charge and angular momentum so that it is close to or away from the horizon. In [72, 73], the violation of the bound in the near-horizon regions of spherically symmetric black holes was studied. Here, we fix the charge of the particle and investigate the influence of the angular momentum on the exponent. Our interest is focused on the angular momentum's range and spatial regions where the bound is violated. Clearly, equilibrium positions are affected by the angular momentum.
We first use Eqs. (18) and (20) to find the equilibrium positions. The specific positions are obtained via numerical calculations and listed in Tables 1–9. The location of the event horizon is also calculated. In this section, we set
$ M=1 $ and$ q=10 $ . For an extremal black hole, its horizon is located at$ r_+ = 1 $ . If L and a have the same sign, this indicates that the particle and black hole rotate in same direction, whereas if they have different signs, they rotate in opposite directions. From the tables, we find that the equilibrium positions gradually move away from the horizon with an increase in the particle’s angular momentum when Q, n, and a are fixed. This implies that the spatial regions where the bound is discussed gradually move away from the horizon.L 0 1 2 3 5 10 20 $ r_0 $ 

Q=0.80 1.74330 1.74988 1.76837 1.79564 1.86320 2.02677 2.23111 Q=0.70 1.85440 1.86358 1.88868 1.92422 2.00662 2.18647 2.39078 Q=0.60 1.95162 1.96427 1.99773 2.04278 2.13984 2.33106 2.52986 Q=0.50 2.04720 2.06453 2.10828 2.16355 2.27325 2.46819 2.65458 Table 1. Equilibrium positions of the charged particle around the non-extremal Kerr-Newman-Taub-NUT black hole when
$ n=0.40 $ and$ a=0 $ . The event horizon is located at$ r_+ $ =1.72111 when$ Q=0.80 $ , at$ r_+ $ =1.81854 when$ Q=0.70 $ , at$ r_+ $ =1.89443 when$ Q=0.60 $ , and at$ r_+ $ =1.95394 when$ Q=0.50 $ .L -7 -5 -3 -1 0 1 3 5 7 $ r_0 $ 

a=0.80 1.61903 1.61221 1.60682 1.60310 1.60192 1.60124 1.60136 1.60347 1.60748 a=0.60 1.83297 1.82106 1.81143 1.80493 1.80309 1.80228 1.80384 1.80946 1.81856 a=0.40 1.99611 1.96983 1.94633 1.92955 1.92520 1.92419 1.93239 1.95155 1.97678 a=0.20 2.20595 2.14908 2.08754 2.03435 2.02127 2.02345 2.06732 2.13077 2.19163 Table 2. Equilibrium positions of the charged particle around the non-extremal Kerr-Newman-Taub-NUT black hole when
$ Q=n=0.40 $ . The event horizon is located at$ r_+ $ =1.60000 when$ a=0.80 $ , at$ r_+ $ =1.80000 when$ a=0.60 $ , at$ r_+ $ =1.91652 when$ a=0.40 $ , and at$ r_+ $ =1.97980 when$ a=0.20 $ .L −7 −5 −3 −1 0 1 3 5 7 $ r_0 $ 

Q=0.80 1.67216 1.65076 1.63119 1.61537 1.60963 1.60576 1.60457 1.61248 1.62801 Q=0.60 1.85376 1.83593 1.82056 1.80931 1.80580 1.80396 1.80562 1.81412 1.82807 Q=0.40 1.96099 1.94506 1.93196 1.92320 1.92089 1.92014 1.92340 1.93246 1.94599 Table 3. Equilibrium positions of the charged particle around the non-extremal Kerr-Newman-Taub-NUT black hole when
$ a=n=0.50 $ . The event horizon is located at$ r_+ $ =1.60000 when$ Q=0.80 $ , at$ r_+ $ =1.80000 when$ Q=0.60 $ , and at$ r_+ $ =1.91652 when$ Q=0.40 $ .L −7 −5 −3 −1 0 1 3 5 7 $ r_0 $ 

n=0.40 2.12730 2.08689 2.04712 2.01667 2.00963 2.01025 2.03279 2.07123 2.11304 n=0.30 2.09624 2.05503 2.01390 1.98175 1.97413 1.97468 1.99846 2.03855 2.08153 n=0.20 2.07315 2.03141 1.98933 1.95594 1.94789 1.94836 1.97305 2.01434 2.05813 n=0.10 2.05891 2.01686 1.97421 1.94007 1.93175 1.93217 1.95741 1.99942 2.04369 Table 4. Equilibrium positions of the charged particle around the non-extremal Kerr-Newman-Taub-NUT black hole when
$ Q=a=0.30 $ . The event horizon is located at$ r_+ $ =1.98995 when$ n=0.40 $ , at$ r_+ $ =1.95394 when$ n=0.30 $ , at$ r_+ $ =1.92736 when$ n=0.20 $ , and at$ r_+ $ =1.91104 when$ n=0.10 $ .L −7 −5 −3 −1 0 1 3 5 7 $ r_0 $ 

n=0.80 1.83035 1.82416 1.81922 1.81572 1.81456 1.81381 1.81359 1.81507 1.81821 n=0.60 1.64768 1.63763 1.62918 1.62282 1.62056 1.61899 1.61801 1.62001 1.62488 n=0.40 1.47634 1.46123 1.44774 1.43677 1.43255 1.42935 1.42641 1.42853 1.43564 n=0.20 1.32523 1.30421 1.28461 1.26769 1.26072 1.25502 1.24833 1.24911 1.25799 Table 5. Equilibrium positions of the charged particle around the non-extremal Kerr-Newman-Taub-NUT black hole when
$ Q=a=0.70 $ . The event horizon is located at$ r_+ $ =1.81240 when$ n=0.80 $ , at$ r_+ $ =1.61644 when$ n=0.60 $ , at$ r_+ $ =1.42426 when$ n=0.40 $ , and at$ r_+ $ =1.24495 when$ n=0.20 $ .n 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 $ r_0 $ 

L=0 1.19308 1.26072 1.34330 1.43255 1.52545 1.62056 1.71709 1.81456 L=20 1.36059 1.40682 1.46940 1.54084 1.61755 1.69796 1.78133 1.86730 L=50 1.61520 1.64587 1.69138 1.74684 1.80870 1.87473 1.94371 2.01503 L=105 1.82068 1.84869 1.89123 1.94412 2.00386 2.06789 2.13451 2.20272 Table 6. For
$ Q=a=0.70 $ , the equilibrium positions of the charged particle around the non-extremal Kerr-Newman-Taub-NUT black hole changes with increasing NUT charge. The event horizon is located at$ r_+ $ =1.17311 when$ n=0.10 $ , at$ r_+ $ =1.33166 when$ n=0.30 $ , at$ r_+ $ =1.51926 when$ n=0.50 $ , and at$ r_+ $ =1.71414 when$ n=0.70 $ .L −7 −5 −3 −1 0 1 3 5 7 $ r_0 $ 

$ Q^2= \dfrac{20}{25},\; a^2= \dfrac{21}{25} $ 

1.16772 1.14777 1.12730 1.10649 1.09608 1.08582 1.06708 1.05840 1.07011 $ Q^2= \dfrac{22}{25},\; a^2= \dfrac{19}{25} $ 

1.18192 1.16018 1.13773 1.11474 1.10316 1.09170 1.07060 1.06081 1.07452 $ Q^2= \dfrac{24}{25},\; a^2= \dfrac{17}{25} $ 

1.19652 1.17279 1.14811 1.12262 1.10971 1.09685 1.07307 1.06250 1.07912 Table 7. Equilibrium positions of the charged particle around the extremal Kerr-Newman-Taub-NUT black hole when
$ n=0.80 $ .L −7 −5 −3 −1 0 1 3 5 7 $ r_0 $ 

$ a^2= \dfrac{24}{25},\; n^2= \dfrac{8}{25} $ 

1.13421 1.11501 1.09555 1.07606 1.06648 1.05722 1.04156 1.03888 1.05354 $ a^2= \dfrac{22}{25},\; n^2= \dfrac{6}{25} $ 

1.14428 1.12279 1.10086 1.07874 1.06779 1.05713 1.03870 1.03468 1.05193 $ a^2= \dfrac{20}{25}, \;n^2= \dfrac{4}{25} $ 

1.15415 1.13000 1.10516 1.07989 1.06729 1.05492 1.03299 1.02679 1.04735 Table 8. Equilibrium positions of the charged particle around the extremal Kerr-Newman-Taub-NUT black hole when
$ Q=0.60 $ .L −7 −5 −3 −1 0 1 3 5 7 $ r_0 $ 

$ Q^2= \dfrac{16}{25},\; n^2= \dfrac{7}{25} $ 

1.18581 1.15827 1.12938 1.09929 1.08393 1.06855 1.03947 1.02463 1.04661 $ Q^2= \dfrac{13}{25},\; n^2= \dfrac{4}{25} $ 

1.17896 1.15016 1.11991 1.08839 1.07232 1.05623 1.02572 1.00933 1.03324 $ Q^2= \dfrac{10}{25},\; n^2= \dfrac{1}{25} $ 

1.17205 1.14168 1.10974 1.07651 1.05961 1.04272 1.01076 1.0000001 1.02023 Table 9. Equilibrium positions of the charged particle around the extremal Kerr-Newman-Taub-NUT black hole when
$ a=0.80 $ .Now, we numerically calculate the Lyapunov exponent and surface gravity using Eqs. (6), (13), (18), (21), and (22).
$ \lambda^2-\kappa^2<0 $ shows that the chaos bound obeys the conjecture put forward by Maldacena et al., whereas$ \lambda^2-\kappa^2>0 $ implies that the bound is violated. The relation between$ \lambda^2-\kappa^2 $ and L is plotted in Figs. 1–9.
Figure 1. (color online) Influence of the angular momentum of the particle around the non-extremal Kerr-Newman-Taub-NUT black hole on the Lyapunov exponent, where
$ n=0.40 $ and$ a=0 $ . The angular momentum's range where the chaos bound is violated is$ 2.27<L<16.11 $ (the corresponding spatial region is$ 1.03132r_+<r_0<1.25942r_+ $ ) when$ Q=0.80 $ . The bound is also violated in the region$ 2.70<L<10.76 $ ($ 1.05184r_+< $ $ r_0 < 1.21430 r_+ $ ) when$ Q=0.70 $ , and in the region$ 4.00<L<6.04 $ ($ 1.10411 r_+<r_0<1.15441 r_+ $ ) when$ Q=0.60 $ .
Figure 2. (color online) Influence of the angular momentum of the particle around the non-extremal Kerr-Newman-Taub-NUT black hole on the Lyapunov exponent, where
$ Q=n=0.40 $ . When$ a=0.20 $ , the angular momentum's range for the violation of the chaos bound is$ -49.98<L<49.71 $ , which corresponds to the spatial region$ 1.02095r_+<r_0<1.34220r_+ $ when the black hole and particle rotate in opposite directions, and to the region$ 1.02040r_+<r_0<1.34171r_+ $ when they rotate in the same direction.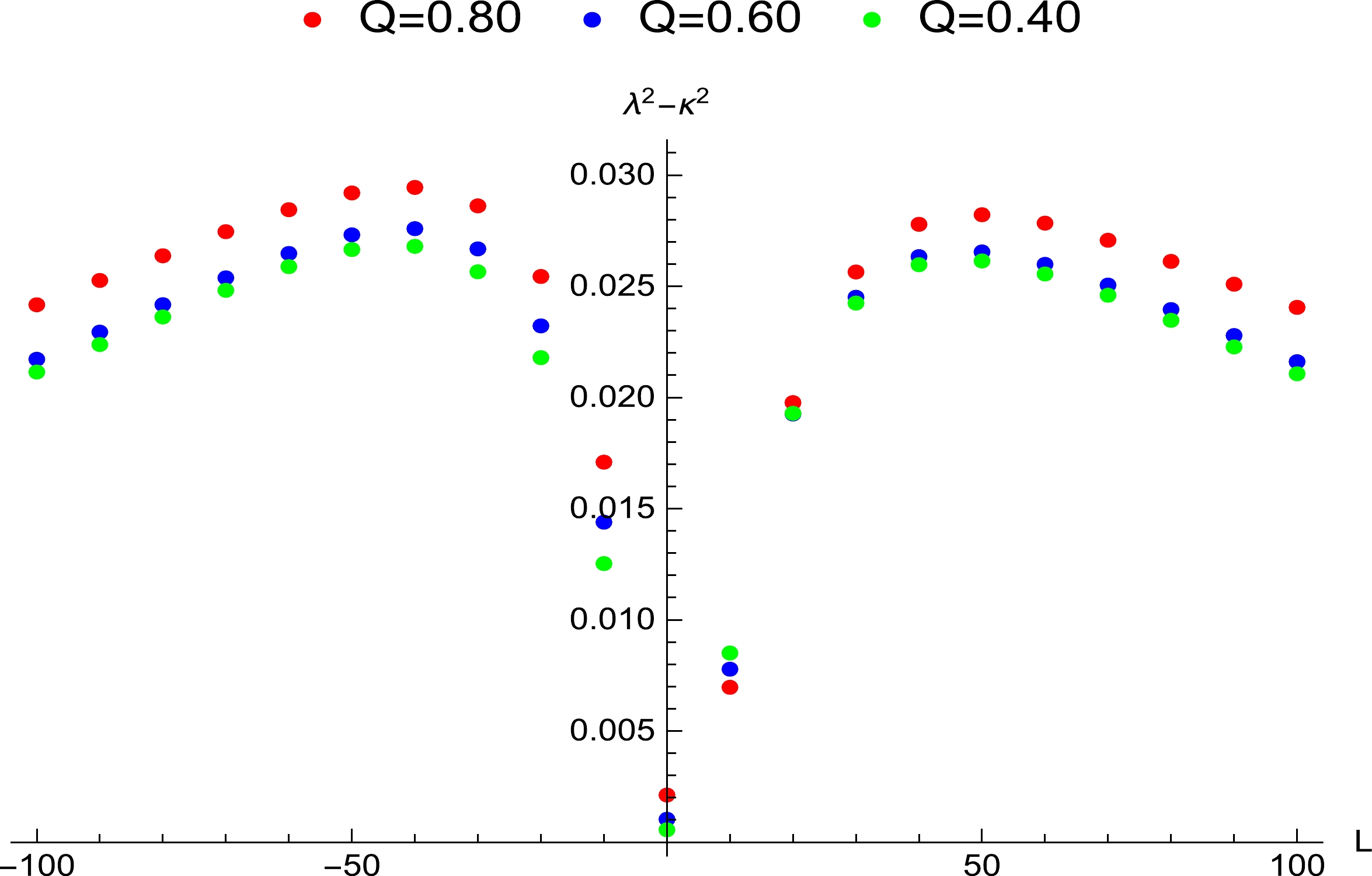
Figure 3. (color online) Influence of the angular momentum of the particle around the non-extremal Kerr-Newman-Taub-NUT black hole on the Lyapunov exponent, where
$ a=n= $ 0.50.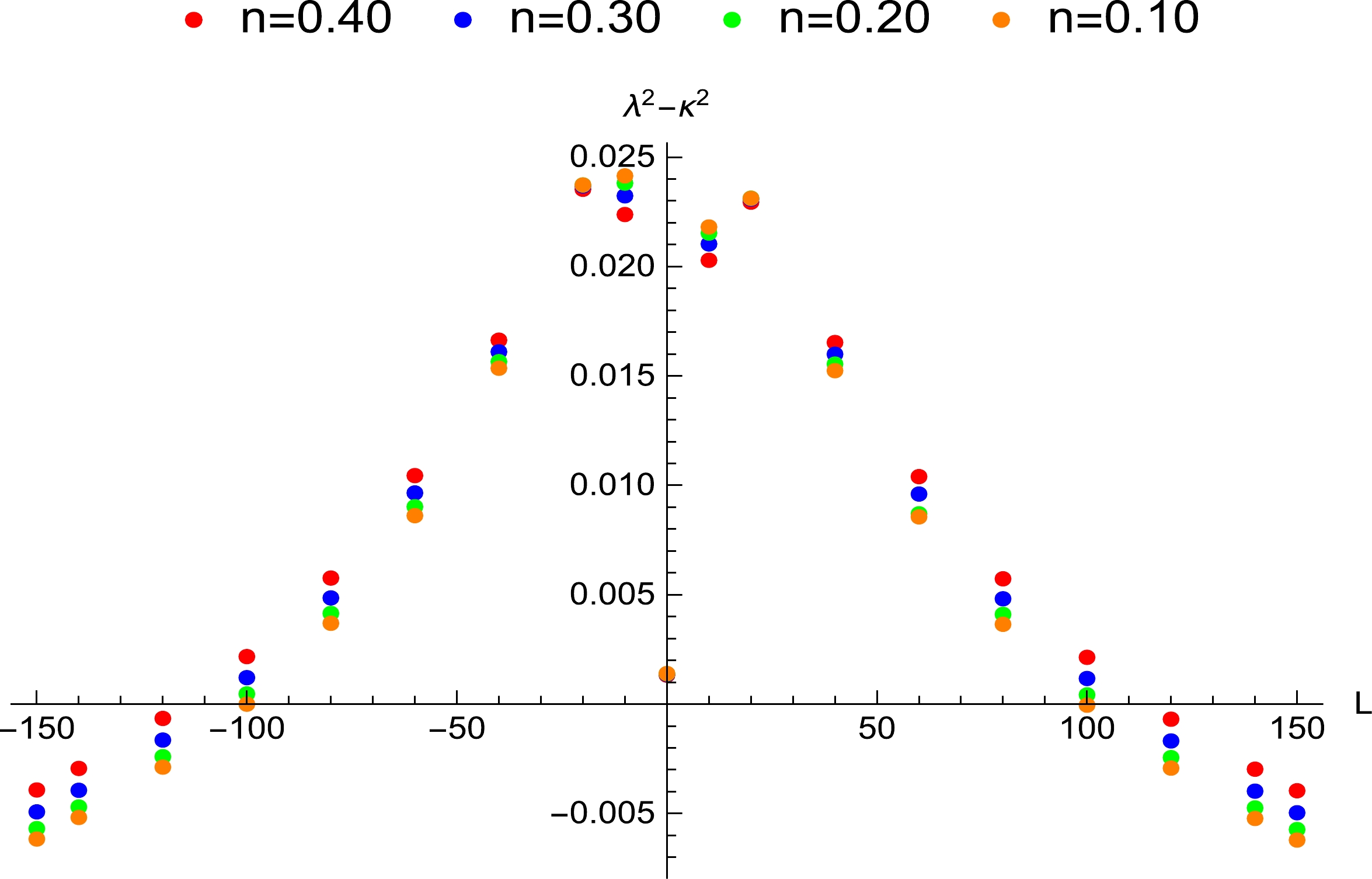
Figure 4. (color online) Influence of the angular momentum of the particle around the non-extremal Kerr-Newman-Taub-NUT black hole on the Lyapunov exponent, where
$ Q=a=0.30 $ . The angular momentum's range where the bound is violated is$ -114.97<L<114.72 $ when$ n=0.40 $ ,$ -107.97 < $ $ L < 107.65 $ when$ n=0.30 $ ,$ -102.97<L<102.65 $ when$ n=0.20 $ , and$ -99.99<L<99.72 $ when$ n=0.10 $ .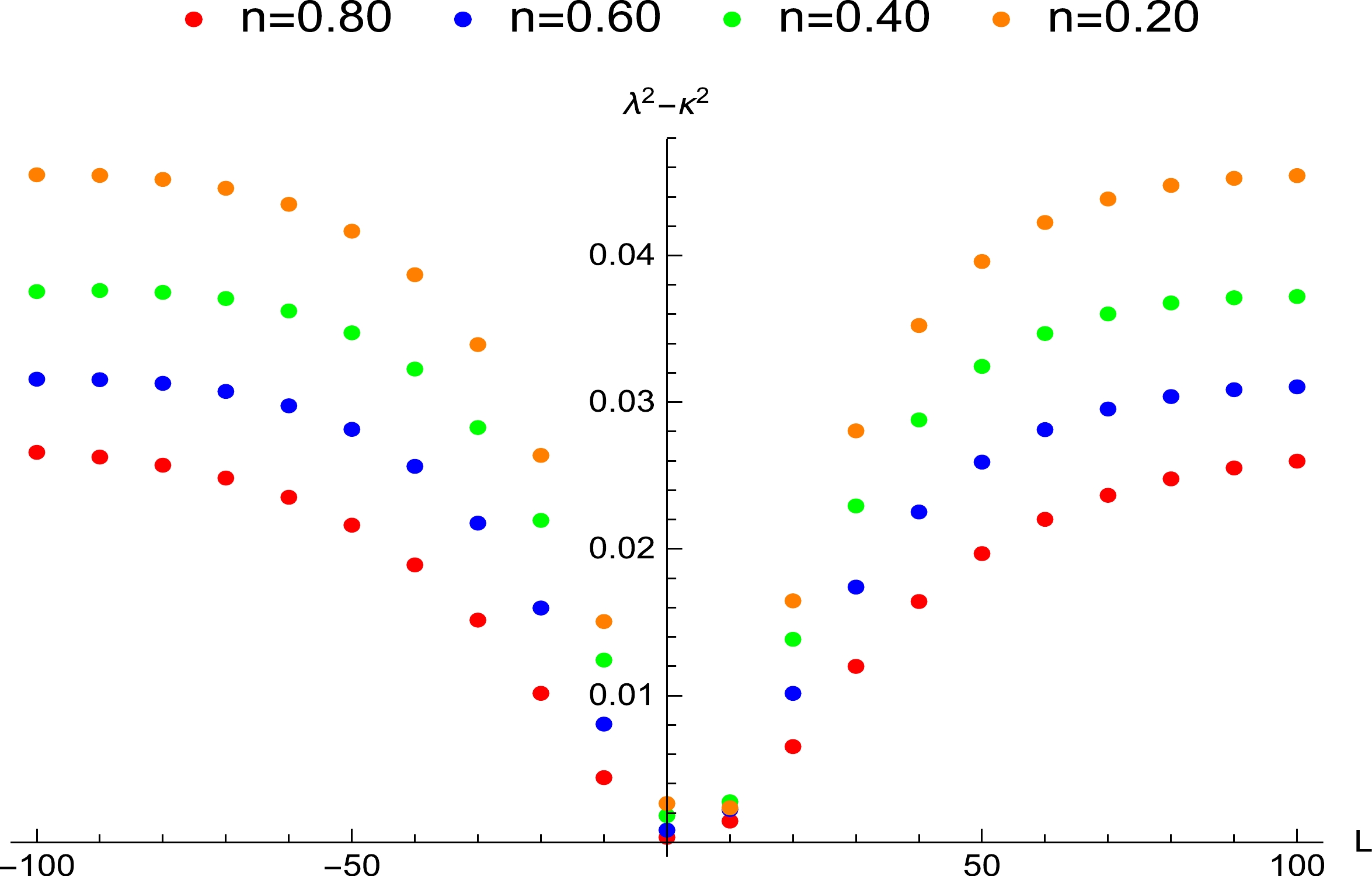
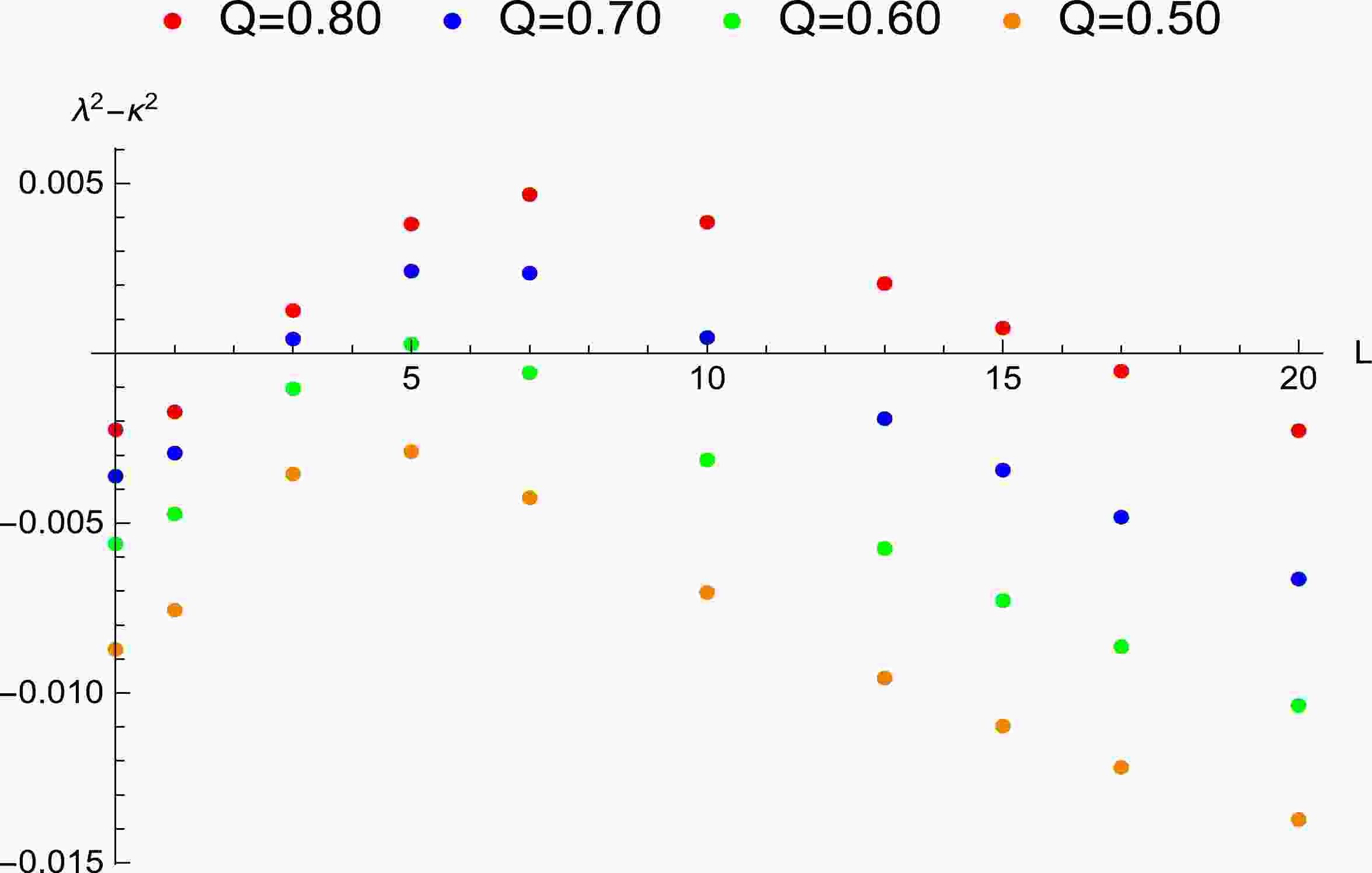
Figure 5. (color online) Influence of the angular momentum of the particle around the non-extremal Kerr-Newman-Taub-NUT black hole on the Lyapunov exponent, where
$ Q=a= $ 0.70.
Figure 6. (color online) Influence of the NUT charge of the particle around the non-extremal Kerr-Newman-Taub-NUT black hole on the Lyapunov exponent, where
$ Q=a=0.70 $ .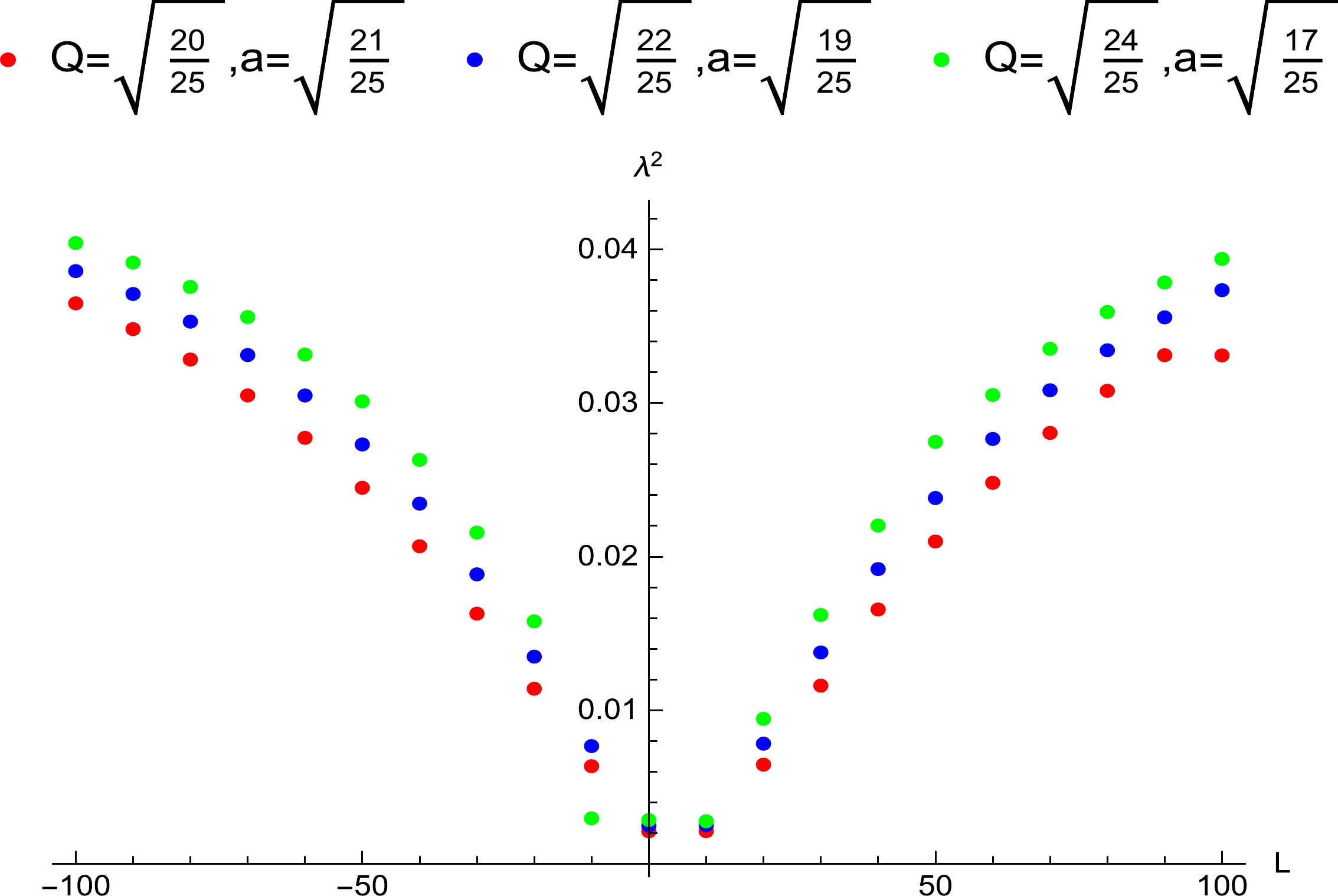
Figure 7. (color online) Influence of the angular momentum of the particle around the extremal Kerr-Newman-Taub-NUT black hole on the Lyapunov exponent, where
$ n=0.80 $ .
Figure 8. (color online) Influence of the angular momentum of the particle around the extremal Kerr-Newman-Taub-NUT black hole on the Lyapunov exponent, where
$ Q=0.60 $ .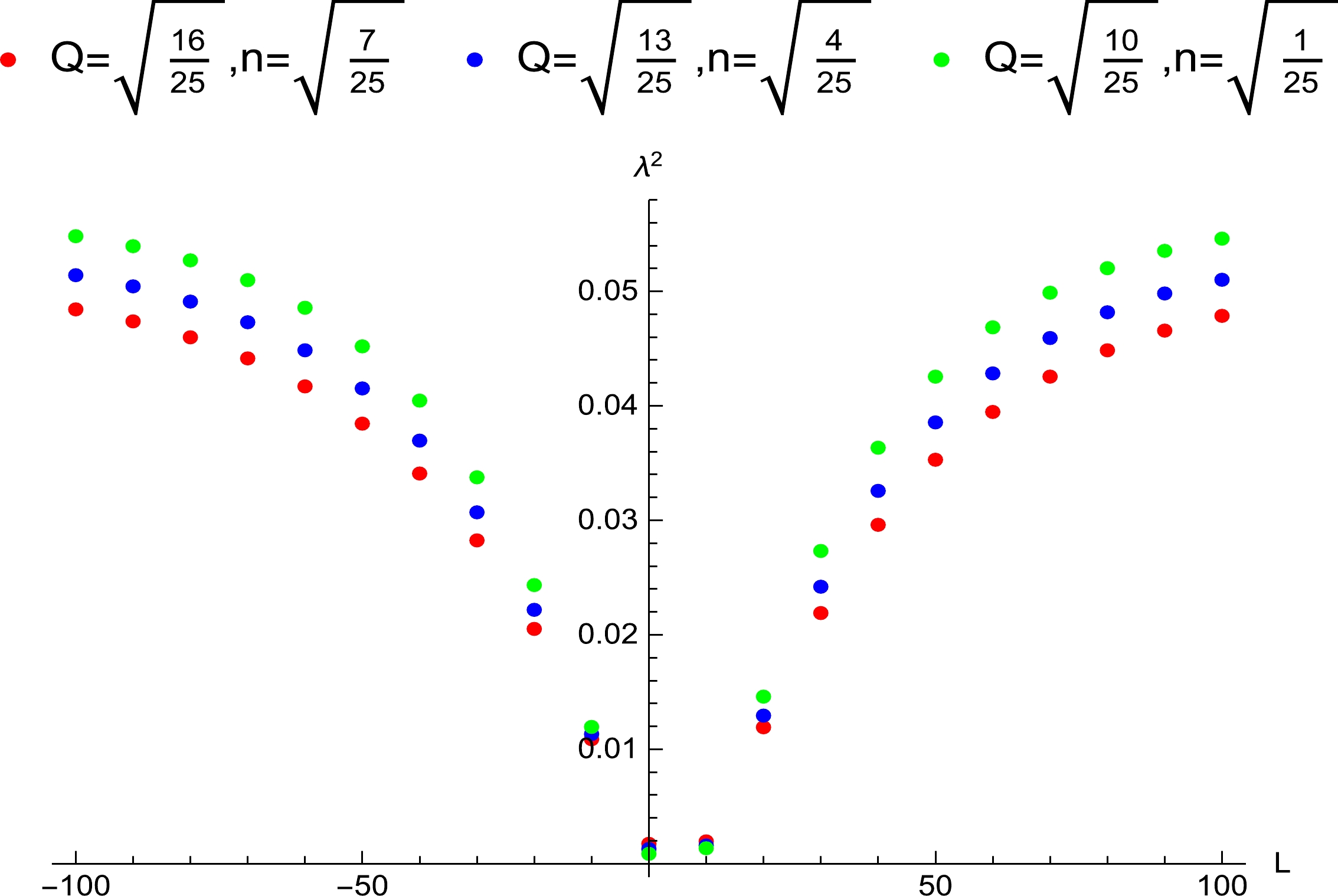
Figure 9. (color online) Influence of the angular momentum of the particle around the extremal Kerr-Newman-Taub-NUT black hole on the Lyapunov exponent, where
$ a=0.80 $ .When
$ a=0 $ , the Kerr-Newman-Taub-NUT metric is reduced to a charged Taub-NUT metric. The relation between the exponent and bound is plotted in Fig. 1. In this figure, the ranges of the angular momentum and spatial region for the violation of the bound increase with increasing electric charge when the NUT charge is fixed as$ n=0.40 $ . This indicates that the large electric charge is more likely to lead to violation of the chaos bound. The violation only occurs in a certain range of the angular momentum.In Fig. 2, the angular momentum range and spatial region for the violation of the bound are large when the rotation parameter is large, and a small rotational parameter can cause the violation. The violation does not appear when the angular momentum is large. The violation is also shown in Fig. 3. In Fig. 3, we fix
$ n=a=0.50 $ and change the angular momentum. The angular momentum's range and spatial region for the violation increase with increasing electric charge.In Fig. 4, the angular momentum's range where the violation appears is found. For
$ n=0.40 $ , the range is$ -114.97<L<114.72 $ , which corresponds to the spatial region$ 1.00989r_+<r_0<1.36857r_+ $ when the black hole and particle rotate in opposite directions, and to the region$ 1.00953r_+<r_0<1.36814r_+ $ when they rotate in the same direction. For$ n=0.30 $ , the range is$ -107.97<L<107.65 $ . The corresponding spatial region is$ 1.01030 r_+<r_0<1.36620 r_+ $ when they rotate in opposite directions, and$ 1.00992 r_+<r_0<1.36612 r_+ $ when they rotate in the same direction. For$ n=0.20 $ , the range is$ -102.97<L<102.65 $ , and the corresponding spatial regions are$ 1.01070 r_+<r_0<1.36425 r_+ $ and$ 1.01019 r_+< r_0<1.36377 r_+ $ . For$ n=0.10 $ , the range is$ -99.99<L< 99.72 $ , and the corresponding spatial regions are$ 1.01080 r_+<r_0<1.36312 r_+ $ and$ 1.01034 r_+<r_0< 1.36256 r_+ $ . This result implies that the range of the angular momentum and spatial region for the violation increase with increasing NUT charge when$ Q=a=0.30 $ . In Fig. 5, for$ n= 0.40 $ and$ 0.20 $ , owing to the increase in the values of Q and a, the range of the angular momentum and spatial region where the violation appears is obviously larger than that in Fig. 4.For all values of Q, a, and n in Figs. 2–5, we observe that
$ \lambda^2-\kappa^2>0 $ when$ L=0 $ . Meanwhile, we can obtain$ \lambda^2-\kappa^2<0 $ when the angular momentum increases to certain values, which reveals that the bound is satisfied for the non-extremal Kerr-Newman-Taub-NUT black hole when the angular momentum is sufficiently large. In Tables 1–5 and Figs. 1–5, we find the contributions of the parameters Q, n, and a to the exponent and equilibrium orbits. For fixed values of a and Q, when the value of n increases, the value of the exponent decreases, and the equilibrium orbit and event horizon position increase. For fixed values of Q and n, when the value of a increases, the value of the exponent decreases, and the equilibrium orbit and horizon position decrease. For fixed values of n and a, when the value of Q increases, the value of the exponent decreases, and the equilibrium orbit and horizon position decrease. In Ref. [73], the authors found that the bound is violated by RN black holes when$ 1<M/Q<1.1547 $ . In Ref. [74], the bound is violated by Kerr black holes when$ a^2/M^2 =4/5 $ . In Ref. [76], where the exponent is obtained using the effective potential method, the bound is violated when$ a/M=5/6 $ . In fact, when$ 5/6<a/M<1 $ , the bound is also violated. Therefore, when the bound is violated, the range of$ a/M $ is larger than that of$ Q/M $ . In the calculation of the exponent, we find that the range of$ Q/M $ is larger than that of$ n/M $ when$ a\to 0 $ ,$ n/M<1 $ , and the bound is violated.Based on the influences of these parameters on the exponent, we directly choose a large Q and a so that the bound is violated and plot in Fig. 6 to show that the exponent is affected by the NUT charge. In the figure, we observe that when the NUT charge increases, the value of the exponent gradually approaches the surface gravity. It is more likely to cause the violation for a small NUT charge, which can be also found in Figs. 4 and 5. For the same NUT charge, the exponent is far from the surface gravity with increasing angular momentum. The range of the NUT charge is relatively large in Fig. 6, which is due to the large values of Q and a. This shows that the influences of a and Q on the exponent are greater than that of n.
When the Kerr-Newman-Taub-NUT black hole is extremal, the surface gravity is zero and the horizon is located at
$ r_+ =1 $ . Then,$ \lambda^2 >0 $ implies violation of the bound. The values of the Lyapunov exponent are plotted in Figs. 7–9. From the figures, we find that there is violation for$ n=0.80 $ , or$ Q=0.60 $ , or$ a=0.80 $ . When this violation occurs, the range of the angular momentum is$ 0\leq L<\infty $ , and the spatial regions are given as follows:In Fig. 7, for
$ Q=\sqrt{\frac{20}{25}} $ and$ a=\sqrt{\frac{21}{25}} $ , the spatial region is$ 1.09608\leq r_0<2.85208 $ when the black hole and particle rotate in opposite directions, and$ 1.05834\leq r_0<2.85208 $ when they rotate in the same direction. For$ Q=\sqrt{\frac{22}{25}} $ and$ a=\sqrt{\frac{19}{25}} $ , the spatial region is$ 1.10316 \leq r_0<2.80376 $ ($ 1.06072\leq r_0<2.80376 $ ). For$ Q=\sqrt{\frac{24}{25}} $ and$ a=\sqrt{\frac{17}{25}} $ , the spatial region is$ 1.23027 \leq r_0<2.75435 $ ($ 1.06228\leq r_0<2.75435 $ ).In Fig. 8, for
$ a=\sqrt{\frac{24}{25}} $ and$ n=\sqrt{\frac{8}{25}} $ , the spatial region is$ 1.06648\leq r_0<2.84146 $ when they rotate in opposite directions, and$ 1.03744\leq r_0<2.84146 $ when they rotate in the same direction. For$ a=\sqrt{\frac{22}{25}} $ and$ n=\sqrt{\frac{6}{25}} $ , the spatial region is$ 1.06779 \leq r_0<2.77075 $ ($1.03326\leq r_0 < 2.77075$ ). For$ a=\sqrt{\frac{20}{25}} $ and$ n=\sqrt{\frac{4}{25}} $ , the spatial region is$ 1.06729 \leq r_0<2.69716 $ ($ 1.02563\leq r_0<2.69716 $ ).In Fig. 9, the spatial region is
$ 1.08393\leq r_0<2.62492 $ ($ 1.02453\leq r_0<2.62492 $ ) when$ Q=\sqrt{\frac{16}{25}} $ and$ n=\sqrt{\frac{7}{25}} $ ,$ 1.07232 \leq r_0<2.58884 $ ($ 1.00928\leq r_0<2.58884 $ ) when$ Q=\sqrt{\frac{13}{25}} $ and$ a=\sqrt{\frac{4}{25}} $ , and$ 1.05961 \leq r_0<2.55207 $ ($ 1.0000001\leq r_0<2.55207 $ ) when$ Q=\sqrt{\frac{10}{25}} $ and$ a=\sqrt{\frac{1}{25}} $ .Therefore, violation of the bound exists in non-extremal and extremal Kerr-Newman-Taub-NUT black holes. The values of the electric charge, NUT charge, and rotational parameter have significant influences on the violation. In Figs. 2–9, when the angular momentum of the particle is zero, the violation also exists.
-
In this paper, we investigate the influence of the angular momentum of a charged particle around non-extremal and extremal Kerr-Newman-Taub-NUT black holes on the Lyapunov exponent and find the ranges of the angular momentum and spatial regions where the chaos bound is violated. The exponent is obtained by solving the eigenvalue of the Jacobian matrix in the phase space. The angular momentum's ranges and spatial regions are found for certain values of Q, n, and a.
For specific values of Q, n, and a of the non-extremal black hole, a small angular momentum (even zero angular momentum) causes violation of the bound, and this violation disappears at a distance from the event horizon when the angular momentum increases to a certain value. The range of the angular momentum and spatial region where the violation appears decreases with a decrease in the value of the rotational parameter when
$ Q = n = 0.40 $ and increase with increasing NUT charge when$ Q=a=0.30 $ . However, for the same NUT charge, the spatial region when$ Q=a=0.70 $ is larger than that when$ Q=a=0.30 $ . For the extremal black hole, the violation always exists no matter how the angular momentum changes when Q, n, and a have specific values. Although the range of the angular momentum is very large, the corresponding spatial region is limited. For example, when$ n=0.80 $ ,$ Q=\sqrt{\frac{20}{25}} $ ,$ a=\sqrt{\frac{21}{25}} $ , and$ 0 \leq L<\infty $ , the spatial region is$ 1.09608\leq r_0 < 2.85208 $ .In Ref. [56], the authors considered the effects of minimal length on the chaotic motion of particles and found that the chaos bound is violated. They believed that their result does not necessarily imply the violation of the bound conjectured in [1], and the bound should be corrected by minimal length effects. In Ref. [73], Lei and Ge perceived that this violation should be related to the dynamical stability of the black hole. Therefore, it is necessary to further study the stability of black holes.
Chaos bound in Kerr-Newman-Taub-NUT black holes via circular motions
- Received Date: 2022-09-20
- Available Online: 2023-01-15
Abstract: In this study, we investigate the influence of the angular momentum of a charged particle around Kerr-Newman-Taub-NUT black holes on the Lyapunov exponent and find spatial regions where the chaos bound is violated. The exponent is obtained by solving the determination of the eigenvalues of a Jacobian matrix in the phase space. Equilibrium positions are obtained by fixing the charge-to-mass ratio of the particle and changing its angular momentum. For certain values of the black holes' electric charge, the NUT charge and rotational parameter, a small angular momentum of the particle, even with zero angular momentum, causes violation of the bound. This violation disappears at a certain distance from the event horizon of the non-extremal Kerr-Newman-Taub-NUT black hole when the angular momentum increases to a certain value. When the black hole is extremal, the violation always exists no matter how the angular momentum changes. The ranges of the angular momentum and spatial regions for the violation are found. The black holes and particle rotating in the same and opposite directions are discussed.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: