HTML
-
Fragmentation functions (FFs) encode essential information about the nonperturbative hadronization mechanism. According to the QCD factorization theorem [1], in a high-energy hadron collision experiment, the inclusive production rate of an identified hadron H at large transverse momentum is dominated by the fragmentation mechanism:
$ \begin{aligned}[b] {\rm d}\sigma[A+B\to H(P_\perp)+X] = &\sum\limits_i {\rm d}{\hat\sigma}[A+B\to i(P_\perp/z)+X]\\& \otimes D_{i \to H}(z,\mu)+{\mathcal O}(1/P_\perp^2), \end{aligned} $

(1) where A, B represent two colliding hadrons,
${\rm d}\hat{\sigma}$ denotes the partonic cross section, and the function$ D_{i \to H}(z) $ characterizes the fragmentation probability for the parton i to hadronize into a multi-hadron state that contains the specified hadron H carrying the fractional light-cone momentum z with respect to the parent parton. The sum in (1) is extended over all parton species ($ i=q,\bar{q},g $ ). Similar to PDFs, FFs are also nonperturbative yet universal objects, whose scale dependence is governed by the celebrated Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) equation:$ \begin{equation} {{\rm d} \over {\rm d} \ln \mu^2} D_{g \to H}(z,\mu) = \sum\limits_{i} \int_z^1 {{\rm d}\xi\over \xi} P_{i g} (\xi, \alpha_s(\mu)) D_{i \to H} \left({z\over \xi},\mu\right), \end{equation} $

(2) where we have taken the gluon fragmentation function as an explicit example, with
$ P_{ig}(\xi) $ the corresponding splitting kernel, and μ is usually referred to as the QCD factorization scale. The μ dependence of the fragmentation function is such that it compensates the μ dependence of${\rm d}\hat{\sigma}$ in (1), so that the physical production rate does not depend on this artificial scale. Once the FF is determined at some initial scale$ \mu_0 $ by some means, one can deduce its form at another scale μ by solving the evolution equation (2).Unlike fragmentation into light hadrons, the fragmentation function for a parton to a heavy quarkonium is not necessarily a truly nonperturbative object. Owing to the weak QCD coupling at the length scale
$ \sim 1/m $ (m represents the heavy quark mass) as well as the nonrelativistic nature of heavy quarkonium, the nonrelativistic QCD (NRQCD) factorization approach [2] may be invoked to refactorize the quarkonium FFs as the sum of products of short-distance coefficients (SDCs) and long-distance yet universal NRQCD matrix elements [3, 4]. To some extent, the profiles of the quarkonia FFs are solely determined by perturbative QCD, which renders the NRQCD approach a particularly predictive theoretical framework. Recently, equipped with the knowledge of various fragmentation functions evaluated in this fashion, some phenomenological predictions based on (1) have been made to account for the large-$ P_\perp $ $ J/\psi $ ,$ \chi_{cJ} $ and$ \psi^\prime $ data samples collected in LHC experiments [5, 6].The original computation of FFs for quark/gluon fragmentation into the S-wave quarkonium was initiated by Braaten and collaborators using the NRQCD approach [3, 4]. Since then, a number of fragmentation functions for quark/gluon into various quarkonium states, including P- and D-wave quarkonia, have been calculated via the NRQCD approach during the past two decades (for an incomplete list, see Refs. [7–25]; for a recent compilation of various quarkonia FFs, see Ref. [26]).
Most SDCs associated with quarkonium FFs were known only at LO in
$ \alpha_s $ , except for the simplest$ g\to {}^3S_1^{(8)} $ channel [16]. In 2014 the gluon fragmentation into the pseudoscalar ($ {}^1S_0^{(1)} $ ) quarkonium was computed to next-to-leading-order (NLO) in$ \alpha_s $ by Artoisenet and Braaten [20]. By that point, it is a rather challenging calculation, and the authors employed some complicated subtraction techniques to disentangle ubiquitous IR divergences. On the other hand, the NLO QCD correction to an analogous FF, i.e., gluon fragmentation into the S-wave spin-singlet color-octet Fock component of a charmonium,$ g\to c\bar{c}({}^1S_0^{(8)} $ ), remains unknown to date. The calculational challenge is expected to be comparable with Ref. [20]. While the$ g\to {}^1S_0^{(1)} $ fragmentation is useful for$ \eta_{c,b} $ production at large$ P_\perp $ , knowledge of the$ g\to {}^1S_0^{(8)} $ fragmentation function is essential to augment our understanding of$ h_{c,b} $ production at large$ P_\perp $ [25].The goal of this work is to evaluate the NLO QCD corrections to the fragmentation functions associated with both the gluon-to-
$ {}^1S_0^{(1,8)} $ quarkonia, yet at the lowest order in velocity expansion. We invoke some modern techniques widely used in the area of automated multi-loop computation, which are presumably much simpler than that used in Ref. [20].
-
According to the NRQCD factorization theorem [2], the gluon fragmentation function into charmonium H can be expressed as
$ \begin{aligned}[b] D_{g \to H}(z,\mu) =& {d_1(z,\mu)\over m^3} \langle 0\vert \mathcal{O}_1^{H}(^1S_0)\vert 0 \rangle \\&+ {d_8(z,\mu)\over m^3} \langle 0\vert \mathcal{O}_8^{H}(^1S_0)\vert 0 \rangle+\cdots, \end{aligned} $

(3) where
$ d_1(z,\mu) $ and$ d_8(z,\mu) $ are the desired SDCs, and the corresponding NRQCD production operators are defined by$ \mathcal{O}_1^{H}(^1S_0) = \chi^\dagger \psi \sum\limits_{X} |H+X\rangle \langle H+X| \psi^\dagger \chi, \tag{4a} $

$ \mathcal{O}_8^{H}(^1S_0) = \chi^\dagger T^a \psi \sum\limits_{X} |H+X\rangle \langle H+X| \psi^\dagger T^a \chi, \tag{4b}$

where ψ and
$ \chi^\dagger $ represent two-component spinor fields that annihilate a heavy quark and a heavy anti-quark respectively, and$ T^a $ ($ a=1,\ldots, N_c^2-1 $ ) represents the generators of the$S U(N_c)$ group in fundamental representation.The color-singlet and octet SDCs
$ d_{1,8} $ can be organized in an expansion in$ \alpha_s $ :$ d_{1,8}(z,\mu) = d_{1,8}^{\rm LO}(z,\mu) + \frac{\alpha_s(\mu)}{\pi} d_{1,8}^{\rm NLO}(z,\mu) + \cdots. $

(5) These SDCs at LO in
$ \alpha_s $ are well-known [4, 27]:$ d^{\rm LO}_1(z,\mu) = \frac{\alpha_s^2}{2N_c^2} \Big[ (1-z)\ln(1-z) + \frac{3}{2}z -z^2 \Big], \tag{6a} $

$ d^{\rm LO}_8(z,\mu) = \frac{\alpha_s^2}{2}\frac{N_c^2-4}{N_c(N_c^2-1)} \Big[ (1-z)\ln(1-z) + \frac{3}{2}z -z^2 \Big], \tag{6b} $

where
$ N_c=3 $ is the number of colors.We choose to evaluate the gluon fragmentation function in a Lorentz frame such that H has vanishing transverse momentum. It is customary to adopt light-cone coordinates in calculating FF. Any four-vector
$ A^\mu=(A^0,A^1, A^2,A^3) $ can be recast in the light-cone format$ A^\mu=(A^+,A^-, {\bf A}_\perp) $ , with$ A^\pm \equiv {1\over \sqrt{2}}(A^0\pm A^3) $ and${\bf A}_\perp \equiv (A^1,A^2)$ . The scalar product of two four-vectors A and B then becomes$ A\cdot B=A^+B^- + A^-B^+ - {\bf A}_\perp \cdot {\bf B}_\perp $ .To compute the NLO radiative correction to
$ d_{1,8}(z) $ , let us specialize to the gauge-invariant operator definition for the fragmentation functions as coined by Collins and Soper long ago [28]. Note that this definition was first employed by Ma to compute the quarkonium FFs in the NRQCD approach [8]. For the desired g-to-H fragmentation function, we start from the operator definition [28] (also see Refs. [17, 19]):$ \begin{aligned}[b] D_{g \to H}(z,\mu) = &\frac{-g_{\mu \nu}z^{D-3} }{ 2\pi k^+ (N_c^2-1)(D-2) } \int_{-\infty}^{+\infty} {\rm d}x^- \, {\rm e}^{-{\rm i} k^+ x^-} \\ & \times \langle 0 | G^{+\mu}_c(0) \Phi^\dagger(0,0,{\bf 0}_\perp)_{cb} \sum\limits_{X} |H(P)+X\rangle \langle H(P)\\&+X| \Phi(0,x^-,{\bf 0}_\perp)_{ba} G^{+\nu}_a(0,x^-,{\bf 0}_\perp) \vert 0 \rangle, \end{aligned} $

(7) where z denotes the fraction of the
$ + $ -momentum carried by H with respect to the gluon,$ D=4-2\epsilon $ signifies the space-time dimensions,$ G_{\mu\nu} $ is the matrix-valued gluon field-strength tensor in the adjoint representation of$ SU(N_c) $ , and$ k^+ = P^+/z $ is the$ + $ -component momentum injected by the gluon field strength operator. μ is the renormalization scale for this composite nonlocal operator. The insertion of the intermediate states implies that in the asymptotic future, one only needs to project out those states that contain a charmonium H carrying the definite momentum$ P^\mu $ , with additional unobserved hadrons labeled by the symbol X.The gauge link (eikonal factor)
$ \Phi(0,x^-,{\bf 0}_\perp) $ in Eq. (7) is a path-ordered exponential of the gluon field, whose role is to ensure the gauge invariance of the FF:$ \begin{equation} \Phi(0,x^-,{\bf 0}_\perp)_{ba} = \mathrm{P} \exp \left[ {\rm i} g_s \int_{x^-}^\infty {\rm d} y^- n\cdot A(0^+,y^-,{\bf 0}_\perp) \right]_{ba}, \end{equation} $

(8) where
$ \mathrm{P} $ implies the path-ordering,$ g_s $ is the QCD coupling constant, and$ A^\mu $ designates the matrix-valued gluon field in the adjoint representation.$ n^\mu =(0,1,{\bf 0}_\perp) $ is a reference null 4-vector.We proceed to calculate the SDCs
$ d_{1,8}(z) $ by the standard perturbative matching strategy, i.e., by replacing the physical charmonium H in (3) with the free$ c\bar{c} $ pair of quantum number$ ^1S_0^{(1,8)} $ . Computing the QCD side from (7) in perturbation theory, and using the following NRQCD matrix elements,$ \begin{equation} \langle 0\vert {\cal O}^{c\bar{c}}_1(^1S_0) \vert 0 \rangle = 2N_c, \qquad \langle 0\vert {\cal O}^{c\bar{c}}_8(^1S_0) \vert 0 \rangle = N_c^2-1, \end{equation} $

(9) one can readily solve for
$ d_{1,8}(z) $ order by order in$ \alpha_s $ .Since Eq. (7) is manifestly gauge-invariant, for simplicity we specialize to the Feynman gauge. Dimensional regularization, with spacetime dimensions
$ d=4-2\epsilon $ , is used throughout to regularize both UV and IR divergences. We wrote a private Mathematica interface to Qgraf [29] to automatically generate the left side of corresponding cut Feynman diagrams and generate the squared amplitudes that correspond to the perturbative fragmentation function defined in Eq. (7), by implementing the eikonal propagator and vertex [28] as well as those for conventional QCD propagators and vertices in the Qgraf model. Some typical Feynman diagrams for$ d_{1,8} $ through NLO in$ \alpha_s $ are shown in Fig. 1.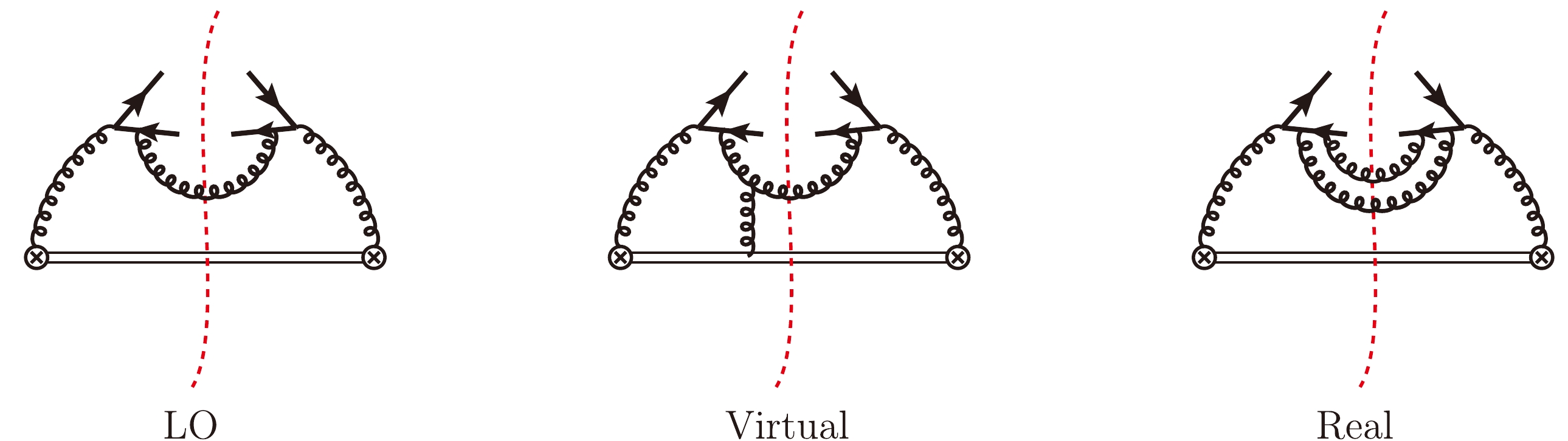
Figure 1. (color online) Representative cut diagrams for the gluon fragmentation function
$ d_{g\to c\bar{c}(^1S_0^{(1,8)})}(z) $ . The cap represents the gluonic field strength operator$ G_a^{+\nu} $ , and the double line signifies the eikonal line.To project the
$ c\bar{c} $ pair onto the intended spin/orbital/color states, it is convenient to employ the familiar covariant projector technique to expedite the calculation [30]:$ \Pi_1 = \frac{1}{\sqrt{8m^3}}\left({\not P\over 2}- m\right)\gamma_5 \left({\not P\over 2}+m\right) \otimes { \mathrm{1}_c \over \sqrt{N_c}}, \tag{10a} $

$ \Pi_8^a = \frac{1}{\sqrt{8m^3}}\left({\not P\over 2}- m\right)\gamma_5 \left({\not P\over 2}+m\right) \otimes \sqrt{2} T^a, \tag{10b}$

where
$ P^\mu $ designates the total momentum of the$ c\bar{c} $ pair, and$ \mathrm{1}_c $ is the$ N_c\times N_c $ -dimensional unit matrix. Since we are only interested in the LO contribution in velocity expansion, we have neglected in Ref. (10) the relative momentum between c and$ \bar{c} $ on both sides of the cut; consequently$ P^2=4m^2 $ .With the aid of the covariant projector (10), we utilize the packages FeynCalc/FormLink [31, 32] to conduct the Dirac/color trace operation. We also use the package Apart [33] to simplify the amplitude by the method of partial fractions, to make the loop integration in the next step easier.
A specific trait of the fragmentation function is its cut diagram structure, which results from the insertion of the asymptotic out states in (7). As a consequence, the corresponding cut-line phase space integration measure reads [17, 19]
$ {\rm d}\Phi_n = {8\pi m \over S_n} \delta\left(k^+-P^+-\sum\limits_{i=1}^n k_i^+\right) \prod\limits_{i=1}^n \frac{{\rm d}k^+_i}{2k_i^+}\frac{{\rm d}^{D-2}k_{i\perp}}{(2\pi)^{D-1}} \theta(k^+_i), $

(11) where
$ n=1 $ for the virtual and$ n=2 $ for the real corrections,$ k_i $ satisfying$ k_i^2=0 $ stands for the momentum of the i-th on-shell parton (gluon, light quark or antiquark in our case) that passes through the cut, and$ S_n $ is the statistical factor for n identical partons. For our purpose, it suffices to know$ S_n=2 $ for the process with two out-going gluons, and$ S_1=1 $ for the other cases. It is important to note that integration over$ k_i^+ $ can be transformed into a parametric integration in a finite interval, but the integration over the transverse momentum$ k_{i,\perp} $ is completely unbounded, i.e., from$ -\infty $ to$ +\infty $ . This feature may persuade us that integration over$ k_{i,\perp} $ could be regarded as loop integration in$ D-2 $ -dimensional spacetime.The real correction diagrams are featured by those in Fig. 1 with two gluons passing through the cut besides the
$ c\bar{c}({}^1S_0^{(1,8)}) $ , while the virtual correction diagrams are defined as those with only one additional gluon passing through the cut. For the former type of contribution, it has been recently shown in Ref. [24] that the integration-by-part (IBP) technique developed in the area of multi-loop calculation can be effectively invoked to reduce the integrand into the linear combination of a set of simpler master integrals, which can then be analytically ascertained. The gluon fragmentations into$ c\bar{c}({}^3S_1^{(1)}) $ and$ c\bar{c}({}^1P_1^{(1)}) $ have been analytically evaluated in this manner [24, 25].In this work, rather than utilize the IBP technique, we apply the influential sector decomposition method [34, 35] to evaluate both real and virtual correction diagrams. Consequently, we present our final results in an entirely numerical fashion. In our opinion, the approach used in this work appears to be more amenable to automated calculation, and yields more accurate numerical predictions than the subtraction approach adopted in Ref. [20].
The first step is to combine all the propagators in a cut amplitude using Feynman parametrization. For real correction contribution, it is straightforward to accomplish two-loop integration over
$ k_{1,2\,\perp} $ in$ D-2 $ -dimensional spacetime. We are then left with multi-fold integrals over Feynman parameters, which are ready and suitable for conducting sector decomposition with the help of the package FIESTA [36]. For virtual correction diagrams, the situation is somewhat more subtle. One cannot carry out the integration over loop momentum l in D-dimensional spacetime and the transverse momentum$ k_{1,\perp} $ in$ D-2 $ -dimensional spacetime simultaneously by following the standard Wick rotation and the Gaussian integration method due to the different integration dimensions. The key is to first integrate over l by the standard Gaussian method, and the resulting expression is still of quadratic form with respect to$ k_{1,\perp} $ , so we can continue to integrate over$ k_{1,\perp} $ using the Gaussian method, and end up with multi-fold integrals over Feynman parameters. This form is again suitable for conducting sector decomposition with the aid of FIESTA [36]. The role of the sector decomposition method [34, 35] is to disentangle various poles, typically with many finite multi-variable parametric integrals as output for the corresponding coefficients. We finally adopt the powerful integrators${\tt CubPack}$ [37] and${\tt ParInt}$ [38] to carry out those numerical integrations to high precision.Adding both real and virtual correction pieces, and implementing the contribution from the counterterm QCD Lagrangian (we renormalize the QCD coupling constant according to the
$ \overline{\rm MS} $ scheme), we find that the NLO SDCs in both color-singlet and octet channels are absent of IR poles, but still contain an extra single UV pole, whose coefficients are dependent on the momentum fraction z. This indicates that the fragmentation function still requires an additional operator renormalization [21, 28]:$ \begin{equation} D^{\overline{\rm MS}}_{g\to H}(z,\mu) = D_{g\to H}(z,\mu) - {1\over \epsilon}{\alpha_s\over 2\pi} \int_z^1 {{\rm d}y\over y}\, P_{gg}(y) D_{g\to H}(z/y,\mu), \end{equation} $

(12) where
$ P_{gg}(y) $ represents the Altarelli-Parisi splitting kernel for$ g\to g $ :$ \begin{equation} P_{gg}(y) = 2N_c \left[ \frac{y}{(1-y)_+} + \frac{1-y}{y} + y(1-y) \right] + \beta_0 \delta(1-y), \end{equation} $

(13) with
$ \beta_0=(11 N_c-2 n_f)/6 $ the one-loop QCD β function, and$ n_f=n_L+n_H $ signifies the number of active flavors. Here$ n_L $ denotes the number of light quarks, and$ n_H $ denotes the number of heavy quarks comprising the quarkonium. Note that in (12) the UV pole is subtracted in accordance with the$ \overline{\rm MS} $ procedure.Following the DGLAP renormalization procedure specified in (12), we then extract the intended finite SDCs
$ d^{\rm NLO}_{1,8}(z,\mu) $ through NLO in$ \alpha_s $ . It is convenient to divide them into several parts:$ \begin{aligned}[b] d^{\rm NLO}_{1,8}(z,\mu) =& c^{(1,8)}_0(z) \ln\frac{\mu}{m} + \alpha_s^2 \Big[ c^{(1,8)}_1(z) + n_L c^{(1,8)}_2(z) \\& + n_H c^{(1,8)}_3(z) \Big]. \end{aligned} $

(14) For clarity, we have separated the light-quark contributions from those of heavy quarks.
The coefficient function of
$ \ln \mu $ can be analytically deduced:$ \begin{aligned}[b] c^{(1,8)}_0(z) \equiv & \int_{z}^1 \frac{{\rm d}y}{y} \Big[ P_{gg}(y) + 2\beta_0 \delta(1-y) \Big] d_{1,8}^{\rm LO}(z/y) = 3\beta_0 d_{1,8}^{\rm LO}(z) + \frac{\alpha_s^2}{6z} {\mathcal F}^{(1,8)} \bigg\{ \left(-6 z^2-12 z\right) \text{Li}_2(z)+\left(6 z-6 z^2\right) \ln^2(1-z) \\& + \left(6 z^2-6 z\right) \ln(1-z) \ln z+\left(-9 z^3+6 z^2+3 z+3\right) \ln(1-z) + \left(3 z^3-12 z^2\right) \ln z +\pi ^2 \left(2 z^2+z\right) +1 -9 z +17 z^3-9 z^2 \bigg\}, \end{aligned} $

(15) with the color factors
$ \begin{aligned}[b] {\mathcal F}^{(1)} =&\frac{1}{N_c},\\ {\mathcal F}^{(8)} =& \frac{N_c^2-4}{N_c^2-1}. \end{aligned} $

(16) We notice that (15) diverges as
$ 1/z $ in the$ z\to 0 $ limit.It is impossible for our approach to deduce the analytical expressions for those non-logarithmic coefficient functions
$ c^{(1,8)}_{i}(z) $ ($ i=1,2,3 $ ). Nevertheless, for a given z, we can compute their numerical values to very high precision, within a relatively short time. For the reader's convenience, we have tabulated in Table 1 and Table 2 the values of$ c^{(1,8)}_{1,2,3}(z) $ for a number of representative values of z.z $c^{(1)}_1(z)$ 

$c^{(1)}_2(z)$ 

$c^{(1)}_3(z)$ 

z $c^{(1)}_1(z)$ 

$c^{(1)}_2(z)$ 

$c^{(1)}_3(z)$ 

0.05 −1.2635(2) 0.1932(2) 0.16065(8) 0.55 0.17598(9) 0.0825(2) 0.18142(8) 0.10 −0.46478(3) 0.2744(2) 0.24159(7) 0.60 0.1771(1) 0.0454(2) 0.15398(8) 0.15 −0.19605(4) 0.3106(2) 0.28783(7) 0.65 0.17507(8) 0.0119(2) 0.12961(8) 0.20 −0.05978(6) 0.3180(2) 0.31024(7) 0.70 0.17039(7) −0.0187(2) 0.10914(8) 0.25 0.02256(5) 0.3059(2) 0.31542(7) 0.75 0.1624(1) −0.0487(1) 0.09259(8) 0.30 0.07698(6) 0.2805(2) 0.30781(7) 0.80 0.1493(1) −0.0845(1) 0.07856(8) 0.35 0.11772(9) 0.2462(2) 0.29084(7) 0.85 0.12909(9) −0.1399(1) 0.06286(8) 0.40 0.14046(5) 0.2067(2) 0.26738(7) 0.90 0.09093(9) −0.2499(1) 0.03489(8) 0.45 0.15814(5) 0.1647(2) 0.23991(8) 0.95 −0.0102(1) −0.5280(1) −0.03512(8) 0.50 0.1694(1) 0.1227(2) 0.21061(8) 0.99 −0.4349(7) −1.3903(1) −0.20468(8) Table 1. Numerical values of non-logarithmic color-singlet coefficient functions
$ c_{1,2,3}^{(1)}(z) $ as introduced in (14). We caution that the actual values of$ c^{(1)}_2(z) $ and$ c^{(1)}_3(z) $ should be multiplied by a factor$ 10^{-2} $ .z $c^{(8)}_1(z)$ 

$c^{(8)}_2(z)$ 

$c^{(8)}_3(z)$ 

z $c^{(8)}_1(z)$ 

$c^{(8)}_2(z)$ 

$c^{(8)}_3(z)$ 

0.02 −6.928(3) 0.1976(4) 0.1568(5) 0.55 0.3105(3) 0.155(3) 0.34016(6) 0.05 −2.4747(3) 0.362(4) 0.30134(6) 0.60 0.3486(4) 0.085(3) 0.28871(6) 0.10 −1.0082(3) 0.515(4) 0.45336(6) 0.65 0.3845(3) 0.022(3) 0.24302(6) 0.15 −0.5161(3) 0.582(4) 0.53967(6) 0.70 0.4189(4) −0.035(3) 0.20464(7) 0.20 −0.2620(3) 0.596(4) 0.58170(6) 0.75 0.4522(3) −0.091(3) 0.17361(7) 0.25 −0.1020(3) 0.574(4) 0.59142(6) 0.80 0.4818(3) −0.158(2) 0.14731(7) 0.30 0.0109(3) 0.526(4) 0.57714(6) 0.85 0.5001(3) −0.262(2) 0.11787(7) 0.35 0.0964(3) 0.462(4) 0.54532(6) 0.90 0.4785(3) −0.469(2) 0.06541(7) 0.40 0.1644(3) 0.388(4) 0.50134(6) 0.95 0.2864(4) −0.990(2) −0.06585(7) 0.45 0.2200(5) 0.309(3) 0.44983(6) 0.98 −0.2839(3) −1.8829(1) −0.26181(6) 0.50 0.2681(5) 0.230(3) 0.3949(5) 0.99 −0.9373(9) −2.6068(2) −0.38376(6) Table 2. Numerical values of non-logarithmic color-octet coefficient functions
$ c_{1,2,3}^{(8)}(z) $ defined in (14). We caution that the actual values of$ c^{(8)}_2(z) $ and$ c^{(8)}_3(z) $ should be multiplied by a factor$ 10^{-2} $ .For numerical investigation, we take μ as twice the heavy quark mass, and adopt the following input parameters [39, 40]:
$ \begin{aligned}[b] m_c =& 1.68\,\text{GeV},\quad m_b=4.78\,\text{GeV},\\ \alpha_s(2m_c)=&0.242,\quad \alpha_s(2m_b)=0.180. \end{aligned} $

(17) We have taken
$ n_L=3,4 $ for charmonium and bottomonium, respectively, and sent$ n_H = 0 $ so$ n_f=n_L $ .The profiles of SDC
$ d_{1,8}(z) $ through the NLO in$ \alpha_s $ are displayed in Fig. 2, for gluon fragmentation into both charmonium and bottomonium. Apparently, the NLO QCD corrections have a significant impact on both channels, qualitatively changing the shape of LO fragmentation functions. It should be mentioned that our result for$ d_{1}^{\rm NLO}(z) $ disagrees with that in Ref. [20], especially in the low z region. Since we already know from (15) that our$ d_{1,8}^{\rm NLO}(z,\mu) $ divergences$ \propto 1/z $ in$ z\to 0 $ limit, we are thereby unable to present a finite prediction to the total fragmentation probability at NLO in$ \alpha_s $ .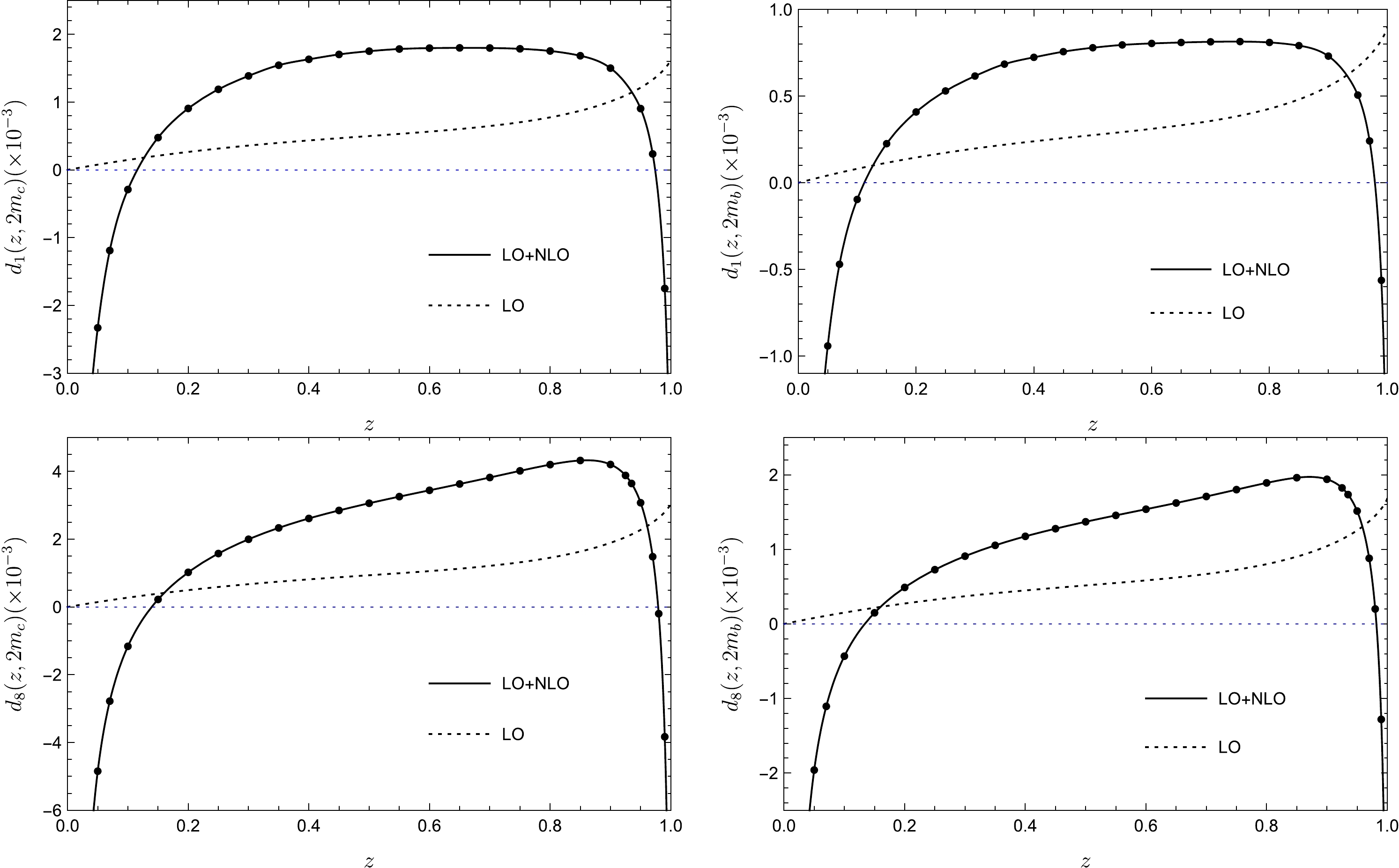
Figure 2. (color online) SDCs
$ d_{1,8}(z) $ associated with gluon fragmentation into quarkonium, including the NLO QCD corrections. The two figures in the top row correspond to$ d_1(z) $ for gluon fragmentation into the color-singlet charmonium and bottomonium, while the two figures in the lower panel correspond to$ d_8(z) $ for gluon into the color-octet charmonium and bottomonium.
-
In summary, in this work we have computed the NLO QCD corrections to the gluon fragmentation into both
$ {}^1S_0^{(1,8)} $ Fock components of quarkonium, at the LO in velocity expansion in NRQCD factorization. It is most transparent to start from Collins and Soper's operator definition of the fragmentation function when investigating the higher order radiative corrections. To facilitate the numerical evaluation of virtual and real correction contributions, we have employed an automated approach that is based crucially upon the sector decomposition technique. This method is found to be quite efficient and systematic, and a good numerical accuracy can be achieved with modest calculational expense.It is found that the NLO QCD corrections in both color-singlet and octet channels have an important impact, and qualitatively modify the profiles of the corresponding LO fragmentation functions.
Our results might be useful for strengthening understanding of large-
$ P_\perp $ production of$ \eta_{c,b} $ and$ h_{c,b} $ in LHC experiments.Note added. While we were finalizing the manuscript, a preprint has recently appeared, which also computes the NLO QCD corrections to the fragmentation function for gluon-to-
$ {}^1S_0^{(8)} $ quarkonium, yet using the FKS subtraction scheme [41]. Their numerical results appear to be compatible with ours. We also compare our NLO radiative corrections for both$ g\to {}^1S_0^{(1,8)} $ fragmentation functions at some typical values of z with a forthcoming paper [42], and find perfect agreement.







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: