-
High energy nucleus-nucleus collisions performed at the Relativistic Heavy-Ion Collider (RHIC) and Large Hadron Collider (LHC) suggest that novel color-deconfined QCD matter (quark-gluon plasma, known as QGP) is created in the reaction region. The azimuthal asymmetric flows (collective flow) of the observed hadrons in various collision systems [1–3] are important phenomena in the study of the strongly interacting nature of QGP, such as directed flow
$ v_{1} $ , elliptic flow$ v_{2} $ , and triangular flow$ v_3 $ . Collective flows have been successfully described by relativistic hydrodynamic models [4–24], and the shear viscosity ratio ($ \eta_{v}/s $ ) extracted from experimental data seems to be small [25, 26].Directed flow (
$ v_{1} $ ) is one of earliest observables for investigating collectivity properties in heavy ion collisions [27–29]. It is defined by the first-order Fourier coefficient of the final-hadron azimuthal distribution and has been widely investigated at both the RHIC and LHC [30–37]. Many studies have suggested that directed flow is generated at an early stage in nuclear collisions, whose typical time scale is nearly$ 2R/\gamma $ , where R and γ are the nuclear radius and Lorentz boost factor, respectively [6, 27, 38]. Such a time scale is even shorter than the production time of the elliptic flow$ v_{2} $ . Therefore, the directed flow$ v_1 $ could be a useful probe to investigate the medium distribution and nucleon flow at the initial stage of nucleus-nucleus collisions [4, 30, 38–43]. Various mechanisms may contribute to the directed flow of light hadrons. Model calculations suggest that$ v_1 $ may depend on the deformation of the initial fireball geometry, initial baryon density distribution, flow velocity field, equation of state of the QGP medium, external electromagnetic fields, and final hadronic rescatterings [40, 44–51], although their exact quantitative contributions are still unknown.The recent isobar run of the collisions of both
$ {^{96}_{44} \rm{Ru}} $ and$ {^{96}_{40} \rm{Zr}} $ ① at$\sqrt{s_{NN}}=200$ GeV by the STAR Collaboration at the RHIC [52] had a special motivation: to search for the chiral magnetic effect (CME) [53–56]. However, the isobar blind analysis did not provide a predefined CME signal but surprisingly found that Ru+Ru collisions provided higher particle yields than Zr+Zr collisions, as well as a larger elliptic flow ($ v_{2} $ ), albeit with a smaller triangular flow ($ v_{3} $ ) [57, 58]. The differences in the experimental results at STAR indicate a difference in nuclear structure (geometry shape), whose observable effects are seemingly larger than those induced by the difference of the electric charge between Ru and Zr [52] and have been investigated from nuclear structure analyses in many studies [57, 59–65]. Therefore, it is of great interest to conduct a detailed comparison between Ru and Zr within a uniform QGP evolution framework and identify the main features of the nuclear structure (or system size) that contribute to the directed flow$ v_{1} $ of identified final-state light hadrons.In this study, we utilize a (3+1)-D viscous hydrodynamic model (CLVisc) with a tilted initial condition [66–68] to investigate the origin of the directed flow of light hadrons produced in Au+Au and isobar collisions at
$\sqrt{s_{NN}}=200$ GeV, with nuclear structure parameters for Ru and Zr from energy density functional theory (DFT) calculations [69–71]. The correlation between the fireball structure of the initial state and the directed flow coefficient of the final state light hadrons is presented. Our numerical results indicate that the tilted initial energy density profile for different nuclei (Au, Ru, and Zr) yields different nonzero average pressure gradients$ -\langle \partial_x P\rangle $ at forward/backward space-time rapidity, which further induces a negative slope for the average flow velocity$ \langle v_x \rangle $ with respect to the space-time rapidity$ \eta_s $ and eventually the same size and sign of$ v_1 $ vs. η, which is consistent with experimental data on Au+Au and isobar collisions at$\sqrt{s_{NN}}=200$ GeV [52, 72, 73]. Our calculation shows a clear system size dependence for light hadron$ v_{1} $ across different collision systems. In the end, we compare the directed flows ($ v_{1} $ ) of three different nuclear structures with quadrupole deformation ($ \beta_{2} $ ) for Ru and Zr nuclei.The remainder of this article is organized as follows. In Sec. II, we present the rapidity-dependent energy density distributions in Au+Au and isobar collisions and their impacts on the pressure gradient and flow velocity with respect to time during hydrodynamic simulations. In Sec. III, we present the directed flow of light hadrons from our hydrodynamic calculation and study its dependence on the nuclear structure. We present a brief summary in Sec. IV.
-
To investigate the directed flow of light hadrons in Au+Au and isobar collisions, following our previous studies [74–77], we start with the initial energy density distributions of the nuclei Au, Ru, and Zr. Their impact on the pressure gradient and flow velocity with respect to time is investigated using the (3+1)-D hydrodynamic model CLVisc.
Based on the Woods-Saxon (WS) distribution, the nucleus thickness function is defined as
$ T(x,y)=\int_{-\infty}^{\infty} {\rm d} z\frac{n_{0}}{1+\exp\left[\dfrac{r-R_{0}(1+\beta_{2}Y^{0}_{2}(\theta))}{d}\right]}, $

(1) where
$ r=\sqrt{x^{2}+y^{2}+z^{2}} $ is the radial position,$ x,\; y,\; z $ are the space coordinates, θ is the polar angle in their rest frame, d is the surface diffusiveness parameter,$ \beta_{2} $ is the quadrupole deformity of the nucleus,$Y_{2}^{0}(\theta) = \dfrac{1}{4}\sqrt{\dfrac{5}{\pi}} \times (3\cos^{2}\theta-$ 1), and$ R_{0} $ is the radius of the nucleus, which depends on the nucleus species. The values of the parameters used for Au, Ru, and Zr in the current study are listed in Table 1. At present, the nuclear density distributions of Ru and Zr are not accurately confirmed because there are a number of setups for parameters ($ R_{0} $ , d, and$ \beta_{2} $ ) from different experiments and models. In this study, following the pioneering research [69–71] and STAR experiment [52], we first adopt the nuclei sets from recent calculations based on DFT [69–71, 78] to study light hadron directed flow. The other two sets are discussed later when we investigate the effect of nuclear structure on the directed flow$ v_1 $ of final light hadrons.Nucleus $ n_{0} $ /(1/fm

$ ^{3} $ )

$ R_{0} $ /fm

d/fm $ \beta_{2} $ 

$ ^{197}_{79} {\rm{Au}}$ 

0.17 6.38 0.535 0.0 $ ^{96}_{44} {\rm{Ru}}$ 

0.17 5.067 0.500 0.0 $ ^{96}_{40} {\rm{Zr}} $ 

0.17 4.965 0.556 0.0 Considering the projectile and target nuclei propagating along the
$ \pm \hat{z} $ direction with the impact parameter$\boldsymbol{b}$ , the corresponding thickness function can be written as$ \begin{array}{*{20}{l}} T_+(\boldsymbol{x}_{T})=T(\boldsymbol{x}_{T}-\boldsymbol{b}/2),\; \; \; \; T_-(\boldsymbol{x}_ {T})=T(\boldsymbol{x}_{T}+\boldsymbol{b}/2), \end{array} $

(2) where
$\boldsymbol{x}_{T}=(x,y)$ is the transverse plane coordinate. The density distributions of the participant nucleons are then given by$ T_{1}(\boldsymbol{x}_{T})=T_+(\boldsymbol{x}_{T})\left\{1-\left[1-\frac{\sigma_{NN} T_-(\boldsymbol{x}_{T})}{A}\right]^{A}\right\}, $

(3) $ T_{2}(\boldsymbol{x}_{T})=T_-(\boldsymbol{x}_{T})\left\{1-\left[1-\frac{\sigma_{NN} T_+(\boldsymbol{x}_{T})}{A}\right]^{A}\right\}, $

(4) where A is the nucleus mass number, and
$\sigma_{NN}$ = 42 mb is the inelastic nucleon-nucleon scattering cross section at$\sqrt{s_{NN}}=200$ GeV [79]. The centrality bins in different nuclear collisions are determined by the impact parameter$\boldsymbol{b}$ [79].Because the right/left-moving wounded nucleons (as shown in Fig. 1) are expected to emit more particles at forward/backward rapidity, we assume this can be constructed by introducing a deformation mechanism into the weight function
$W_ {N}$ [74], in which a tilted fireball is introduced to describe the observed charged particle directed flow in the RHIC and LHC energy region [74, 80]. In our earlier studies [74–76], a monotonic function ($ T_{1}(x,y)+ T_{2}(x,y) $ ) was modified to obtain the asymmetry between the forward and backward nuclei, as shown below.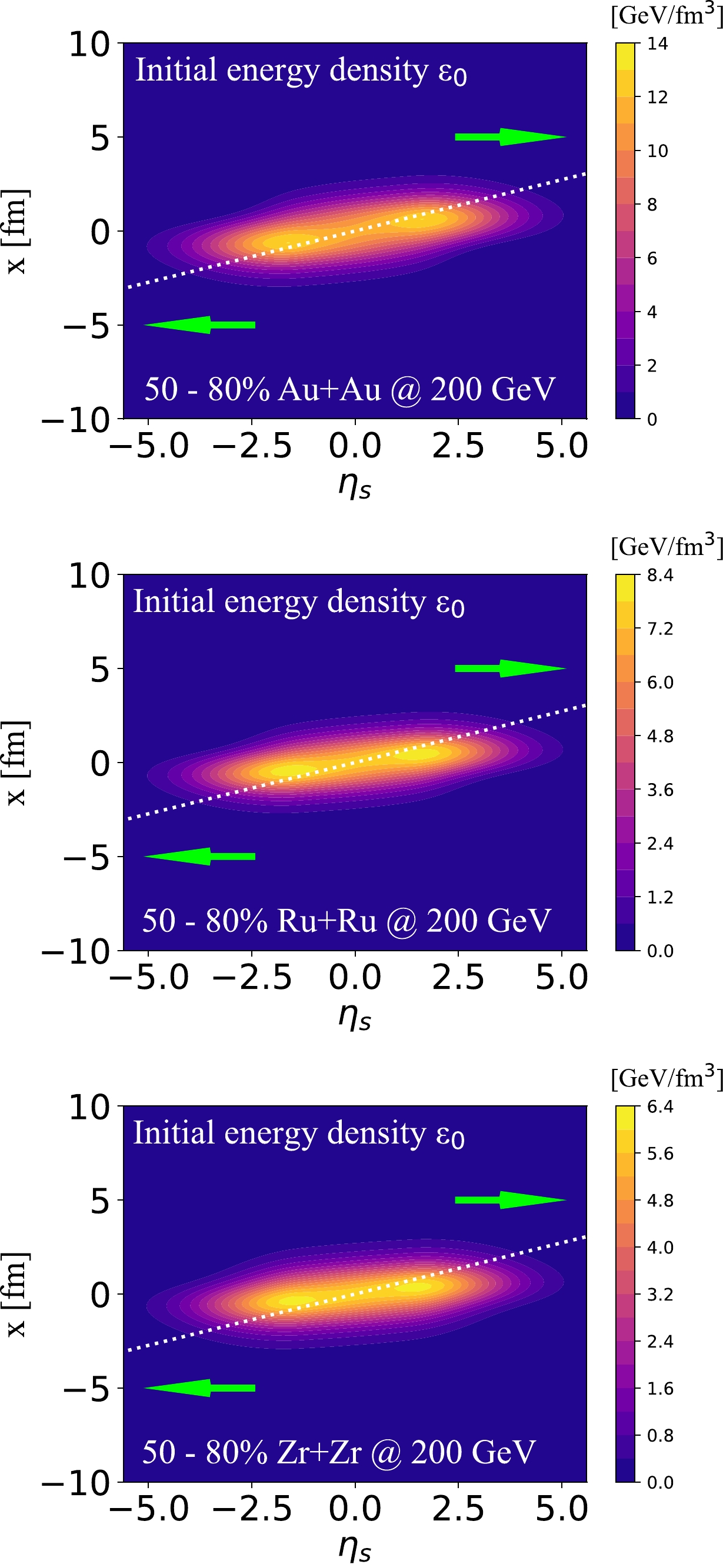
Figure 1. (color online) Tilted initial energy density on the
$ \eta_{s} $ -x plane at$ \tau_0 $ = 0.6 fm/c in 50%–80% Au+Au (b = 11.4 fm), Ru+Ru (b = 9.3 fm), and Zr+Zr (b = 9.6 fm) collisions at$\sqrt{s_ {NN}}=200$ GeV. The dotted line (white) shows the counter-clockwise tilted initial condition with respect to the$ x=0 $ axis in the$ \eta_{s} $ -x plane, and the arrow (green) indicates the motion at forward and backward rapidity.$ \begin{aligned}[b] W_{N}(x,y,\eta_{s})=&T_{1}(x,y)+T_{2}(x,y) \\& +H_{t}[T_{1}(x,y)-T_{2}(x,y)]\tan\left(\frac{\eta_{s}}{\eta_{t}}\right), \end{aligned} $

(5) where
$ H_{t} $ reflects the strength of imbalance at the forward and backward rapidities, the function$ \tan (\eta_{s}/\eta_{t}) $ produces the deformation of the initial energy density distribution along the longitudinal direction, and$ \eta_{t}=8.0 $ is utilized for all collision systems [74]. In different centrality classes, the baryon stopping effect is different; hence, the contribution from the forward and backward nuclei are imbalanced. In our model, the parameter$ H_{t} $ reflects the strength of the baryon stopping effect and depends on the centrality. The value of$ H_{t} $ is extracted from the experimental data.The total weight function
$ W(x,y,\eta_{s}) $ is defined as$ W(x,y,\eta_{s})=\frac{0.95 W_{N}(x,y,\eta_{s})+0.05 n_\text{BC}(x,y)}{\left[0.95 W_{N}(0,0,0)+0.05 n_\text{BC}(0,0)\right]|_{\boldsymbol{b}=0}}. $

(6) Here, the number of binary collisions
$ n_\text{BC}(x,y) $ is defined as [67, 79]$ \begin{array}{*{20}{l}} n_\text{BC}(x,y)=\sigma_{NN}T_+(x,y)T_-(x,y). \end{array} $

(7) The initial energy density
$ \varepsilon(x,y,\eta_{s}) $ is given by [67]$ \begin{array}{*{20}{l}} \varepsilon(x,y,\eta_{s})=K \cdot W(x,y,\eta_{s}) \cdot H(\eta_{s}), \end{array} $

(8) where K is a normalization factor and determined by the multiplicity density distribution (
${\rm d}N_{ \rm{ch}}/{\rm d}\eta$ ) of soft particles. The function$ H(\eta_{s})=\exp\left[-\frac{(|\eta_{s}|-\eta_{w})^{2}}{2\sigma^{2}_{\eta}}\theta(|\eta_{s}|-\eta_{w}) \right] $

(9) is introduced to describe the plateau structure of the rapidity distribution of emitted hadrons at mid-rapidity, in which
$ \eta_{w}=1.3 $ determines the width of the central rapidity plateau, whereas$ \sigma_{\eta}=1.5 $ determines the width (spread) of Gaussian decay from the plateau region [67].In Table 2, we summarize the parameters of the initial conditions that are tuned to provide reasonable descriptions of the charged particle yields in the most central collisions [67], as shown in Figure 6. These include the overall normalization factor (K), initial time of hydrodynamic evolution (
$ \tau_{0} $ ), impact parameters (b), and tilted parameters ($ H_{t} $ ).Parameters Au+Au Ru+Ru Zr+Zr K/(GeV/fm $ ^{3} $ )

35.5 23.0 23.0 $ \tau_{0} $ /(fm/c)

0.6 0.6 0.6 b/fm 2.4 2.1 2.1 $ H_{t} $ 

1.0 1.0 1.0 In present study, we set the initial fluid velocity in the transverse and space-time rapidity directions following the Bjorken approximation, that is,
$ v_{x} = v_{y} =0 $ and$ v_{z} = z/t $ . -
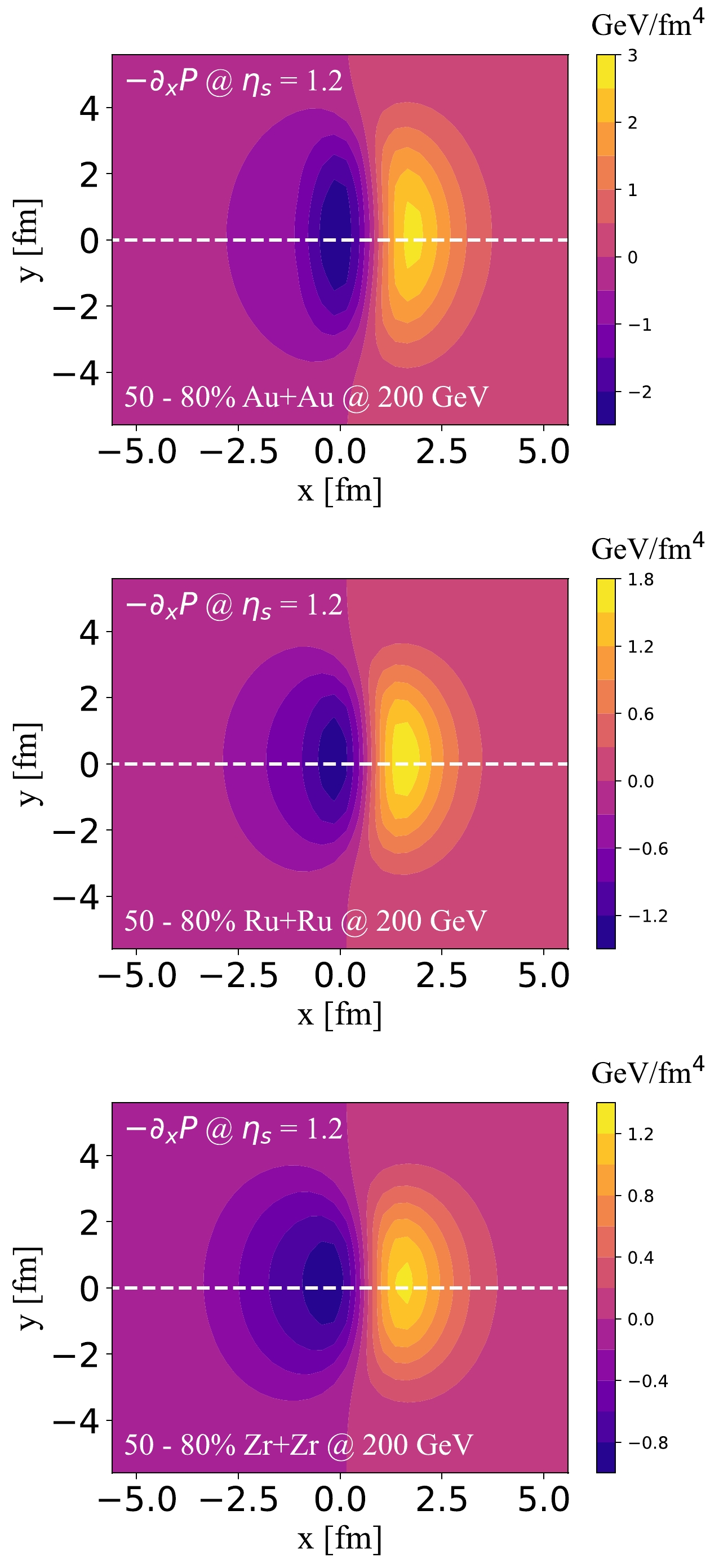
Using the tilted initial condition above, we first present the energy density profile for different nuclei (Au, Ru, and Zr). In Fig. 1, we show the energy density profile for 50%–80% Au+Au, Ru+Ru, and Zr+Zr collisions at
$\sqrt{s_{NN}} = 200$ GeV in the$ \eta_{s} - x $ plane. Here, the model parameter$ H_{t} = 4.5 $ is taken for the Au+Au collisions (top panel),$ H_{t} = 3.9 $ is taken for the Ru+Ru collisions (middle panel), and$ H_{t}=3.1 $ is taken for the Zr+Zr collisions (bottom panel).$ H_{t} $ is extracted from experimental data to describe the directed flow$ v_{1} $ of charged particles and protons/anti-protons. From Fig. 1, the energy density distribution for different nuclei is not only shifted in the forward/backward rapidity direction but is also tilted counter-clockwise with respect to$ x=0 $ [74, 80].To quantify the asymmetry strength of the initial energy density for different nuclei at the initial state, we first present the first-order eccentricity coefficient
$ \varepsilon_1 $ as a function of space-time rapidity in Fig. 2. The first-order eccentricity vector$ \vec{\mathcal{E}}_{1} $ is defined as [15, 47]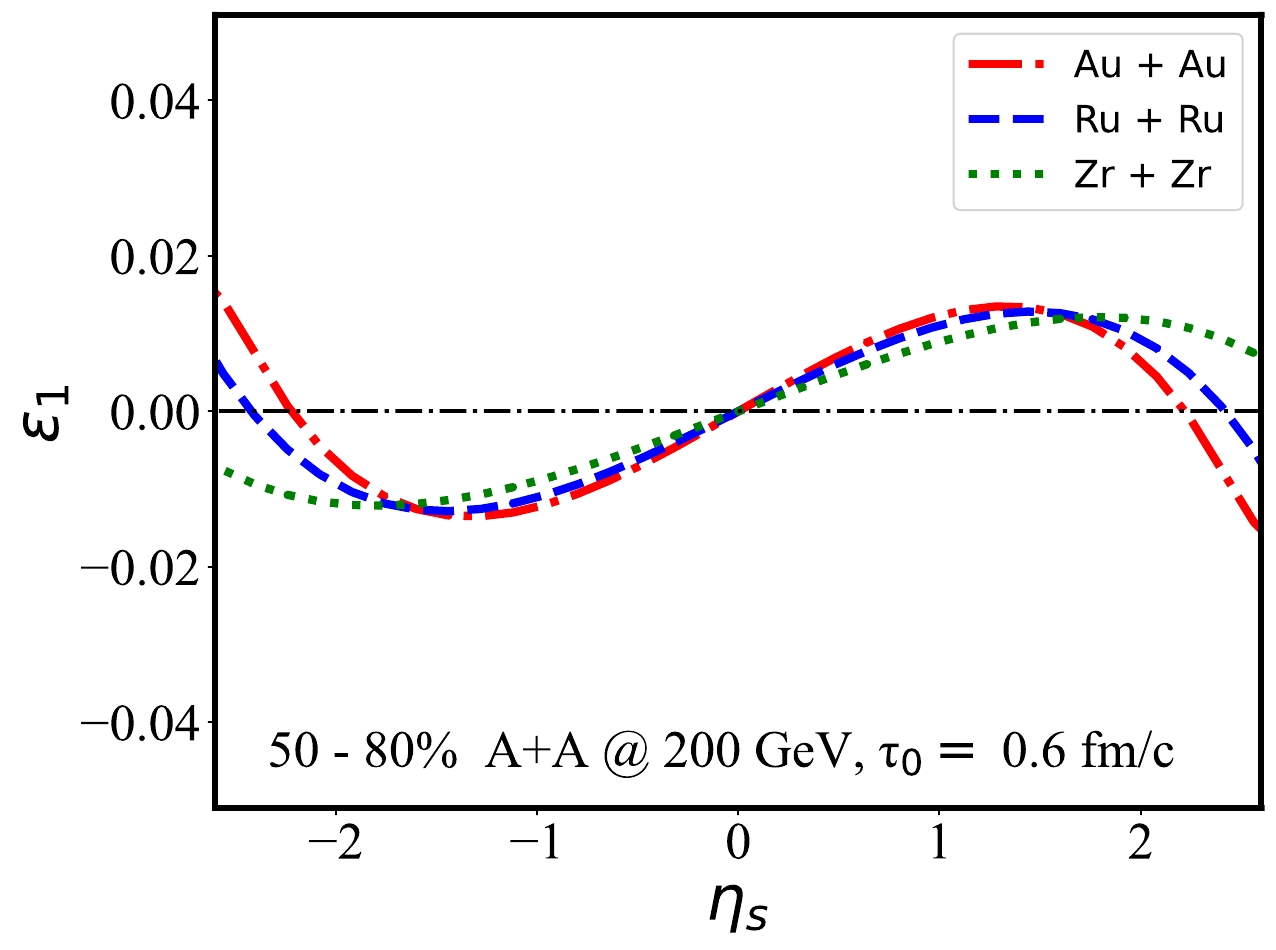
Figure 2. (color online) First-order eccentricity coefficient
$ \varepsilon_{1}(\eta_{s}) $ in 50%–80% nuclei-nuclei collisions at$ \sqrt{s_{NN}}=200 $ GeV.$ \vec{\mathcal{E}}_{1}\equiv\varepsilon_{1}(\eta_{s}) {\rm e}^{{\rm i}\Psi_{1}(\eta_{s})}= - \frac{\displaystyle\int {\rm d}^{2}r \widetilde{r}^{3} {\rm e}^{{\rm i}\widetilde{\phi}}\varepsilon(r,\phi,\eta_{s})}{\displaystyle\int {\rm d}^{2}r \widetilde{r}^{3} \varepsilon(r,\phi,\eta_{s})}, $

(10) where the angular distribution is calculated with respect to the energy density weighted center-of-mass point
$ (x_{0}(\eta_{s}), y_{0}(\eta_{s})) $ in every rapidity slice given by$ x_{0}(\eta_{s}) = \frac{\displaystyle\int {\rm d}^{2} r x \varepsilon(r,\phi,\eta_{s})}{\displaystyle\int {\rm d}^{2}r \varepsilon(r,\phi,\eta_{s})}, $

(11) $ y_{0}(\eta_{s}) = \frac{\displaystyle\int {\rm d}^{2} r y \varepsilon(r,\phi,\eta_{s})}{\displaystyle\int {\rm d}^{2}r \varepsilon(r,\phi,\eta_{s})}, $

(12) where
$ \widetilde{r}(x,y,\eta_{s})=\sqrt{(x-x_{0})^{2}+(y-y_{0})^{2}} $ is the transverse radius, and$ \widetilde{\phi}(x,y,\eta_{s})=\arctan[(y-y_{0})/(x-x_{0})] $ is the azimuthal angle. Note that$ \varepsilon_1 $ in Eq. (10) presents the first-order eccentricity coefficient, and$ \Psi_1 $ gives the corresponding participant plane angle.$ \vec{\mathcal{E}}_{1} $ with respect to$ \eta_s $ quantifies the amount of tilt a fireball requires to produce light hadron$ v_{1} $ .In Fig. 2, we present
$ \varepsilon_1 $ as a function of space-time rapidity in 50%–80% Au+Au and isobar collisions at$\sqrt{s_{NN}}=200$ GeV.$ \varepsilon_1 $ is an odd function of space-time rapidity$ \eta_s $ and is positive/negative in the$ + $ /$ -\eta_s $ region. The slopes of$ \varepsilon_1 $ for three nuclei are positive at mid-rapidity but flip sign within$ |\eta_s| > 1.5 $ . This further affects the evolution of the nuclear medium in the hydrodynamic simulation.In addition to the initial energy density profile along the rapidity direction, we also present the initial pressure gradient
$ -\partial_{x}P $ in the transverse plane, which directly drives the radial flow of nuclear matter. In Fig. 3, the initial$ -\partial_{x}P $ distribution in the x-y plane at a fixed forward rapidity$ \eta_s=1.2 $ is presented for the nuclei Au, Ru, and Zr, where the parameter values of$ H_{t} $ and b are the same as those used for Fig. 1. One may clearly find the positive/negative value of the pressure gradient$ -\partial_{x}P $ in the$ + $ /$ -x $ direction leading to the outward expansion of the nuclear medium. From the top to bottom panels, we see that at$ \eta_s=1.2 $ , the center (zero pressure) regions of these distributions are shifted toward$ +x $ owing to the counter-clockwise tilt of the initial energy density. Whether the average x-component of the final-state hadron momentum will be positive or negative at a given rapidity depends on the average magnitude of$ -\partial_{x}P $ in the corresponding transverse plane and how it evolves with time. This is explored later in this paper. -
We utilize the viscous hydrodynamic model CLVisc [66–68, 81, 82] to simulate the evolution of the QGP medium. The hydrodynamic equation satisfies [22, 83–86]
$ \begin{array}{*{20}{l}} \partial_{\mu}T^{\mu\nu}=0, \end{array} $

(13) where
$ T^{\mu\nu} $ is the energy-momentum tensor and takes the following form:$ \begin{array}{*{20}{l}} T^{\mu\nu}=\varepsilon u^{\mu}u^{\nu}-(P+\Pi)\Delta^{\mu\nu} + \pi^{\mu\nu}. \end{array} $

(14) Here, ε is the energy density,
$ u^{\mu} $ is the fluid four-velocity field, P is the pressure,$ \pi^{\mu\nu} $ is the shear stress tensor, and Π is the bulk pressure. The projection tensor is defined as$ \Delta^{\mu\nu} = g^{\mu\nu}-u^{\mu}u^{\nu} $ , and the metric tensor$ g^{\mu\nu} = \text{diag} (1, -1,-1, -1) $ . In this study, we utilize the lattice QCD equation of state (EoS) from the Wuppertal-Budapest group (2014) [87], and the shear viscosity ratio is set as$ \eta_{v}/s = 0.08 $ ($ \eta_{v} $ for the shear viscosity) for all collision systems. Following recent studies [74, 75], the bulk viscosity and net baryon density are ignored at this moment but will be considered in our future studies [88, 89].When the local temperature of nuclear matter drops below the freeze-out temperature (we set
$ T_\text{frz}=137 $ MeV) [67], the Cooper-Frye mechanism [90] is used to calculate the spectra of hadrons on the freeze-out hypersurface. Contributions from resonance decay are taken into account according to our previous study [74, 75]. -
The hydrodynamic simulation presents how the imbalance of the initial energy density distribution is developed to the anisotropy of the final-state hadron momentum. In this subsection, we present how the fluid velocity
$ \langle v_{x} \rangle $ develops with respect to time at the opposite rapidity$ \eta_s $ . This will help us observe the development of the directed flow$ v_{1} $ and how it depends on the tilted initial geometry of the energy density.As presented in Fig. 3, the tilted initial energy density leads to asymmetry of the pressure gradient along the x direction. In Fig. 4, we present how the average pressure gradient
$ -\langle\partial_{x}P \rangle $ evolves with time at a given$ \eta_{s} $ ($ \pm 0.9 $ here) in 50%–80% Au+Au and isobar collisions at$\sqrt{s_{NN}} = 200$ GeV. We clearly observe that the evolution of$ -\langle\partial_{x}P \rangle $ is significantly affected by the tilted initial energy density distribution. The evolution of the average pressure gradient -$ \langle \partial_{x} P \rangle $ is anti-symmetric. We find that$ -\langle\partial_{x}P \rangle $ remains positive with time at$ \eta_s = -0.9 $ and negative at$ \eta_s = 0.9 $ , leading to a continuous force that accelerates QGP medium outward expansion toward the$ +x $ direction at$ \eta_s = -0.9 $ and toward the$ -x $ direction at$\eta_s = 0.9$ . Little difference in the evolution of$ -\langle\partial_{x}P \rangle $ is observed between the isobar Zr and Ru. Note that unlike the higher-order components of anisotropy, the first order eccentricity coefficient$ \varepsilon_1 $ and pressure gradient$ -\langle\partial_{x}P \rangle $ are not necessarily positively correlated to each other.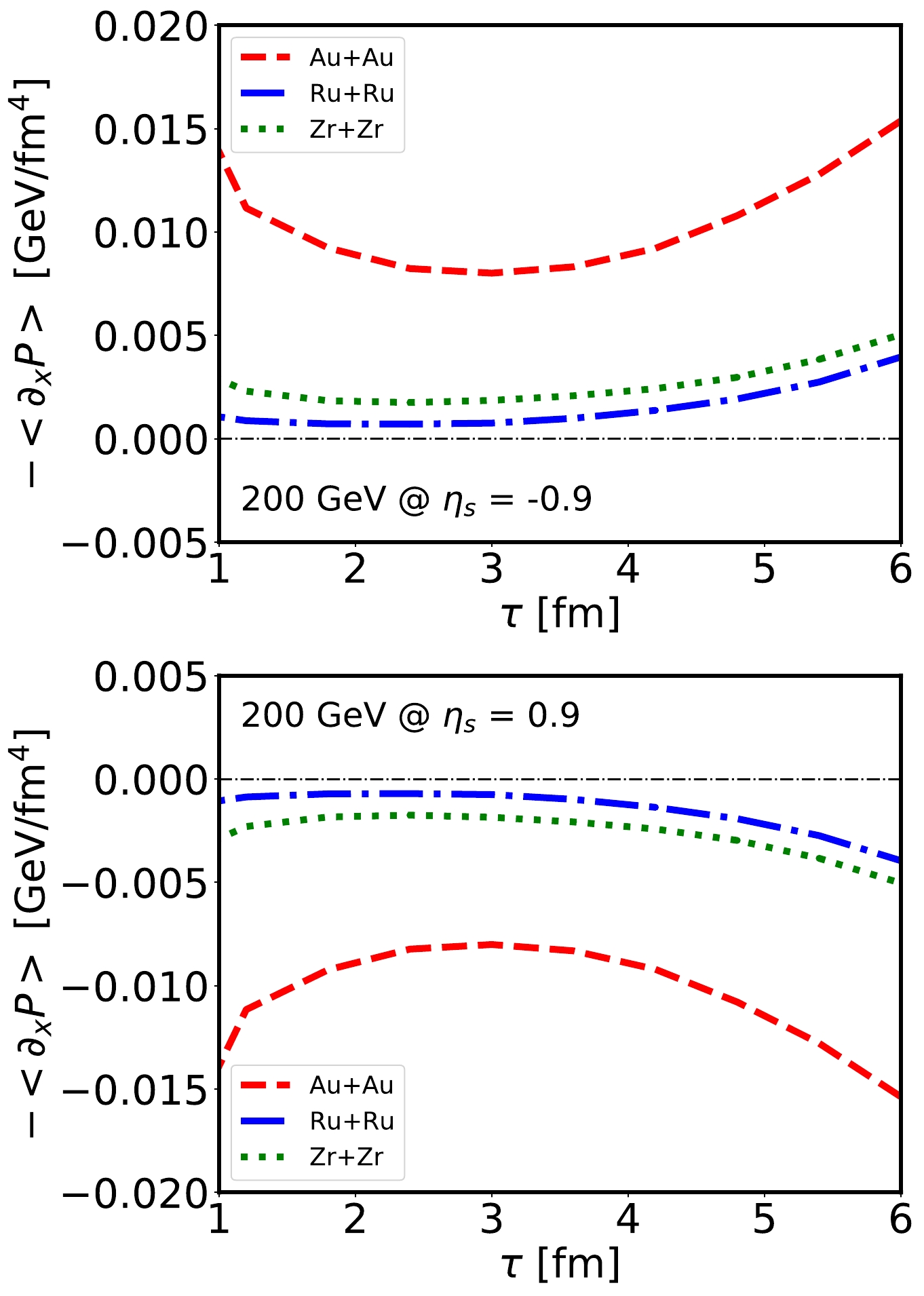
Figure 4. (color online) Time evolution of the average pressure gradient in the x direction at
$ \eta_{s} = -0.9 $ (upper panel) and$ \eta_{s} = 0.9 $ (lower panel) in 50%–80% Au+Au and isobar collisions at$\sqrt{s_{NN}}=200$ GeV.Owing to the tilted deformation of nuclear matter, medium expansion contributes to an overall force toward the
$ + $ /$ -x $ direction at backward/forward rapidity. A direct outcome of such force is the asymmetric flow velocities in the corresponding direction. In Fig. 5, we present how the average flow velocity$ \langle v_{x} \rangle $ develops with time. The average flow velocity at a given proper time and space-time rapidity is defined as [16, 45]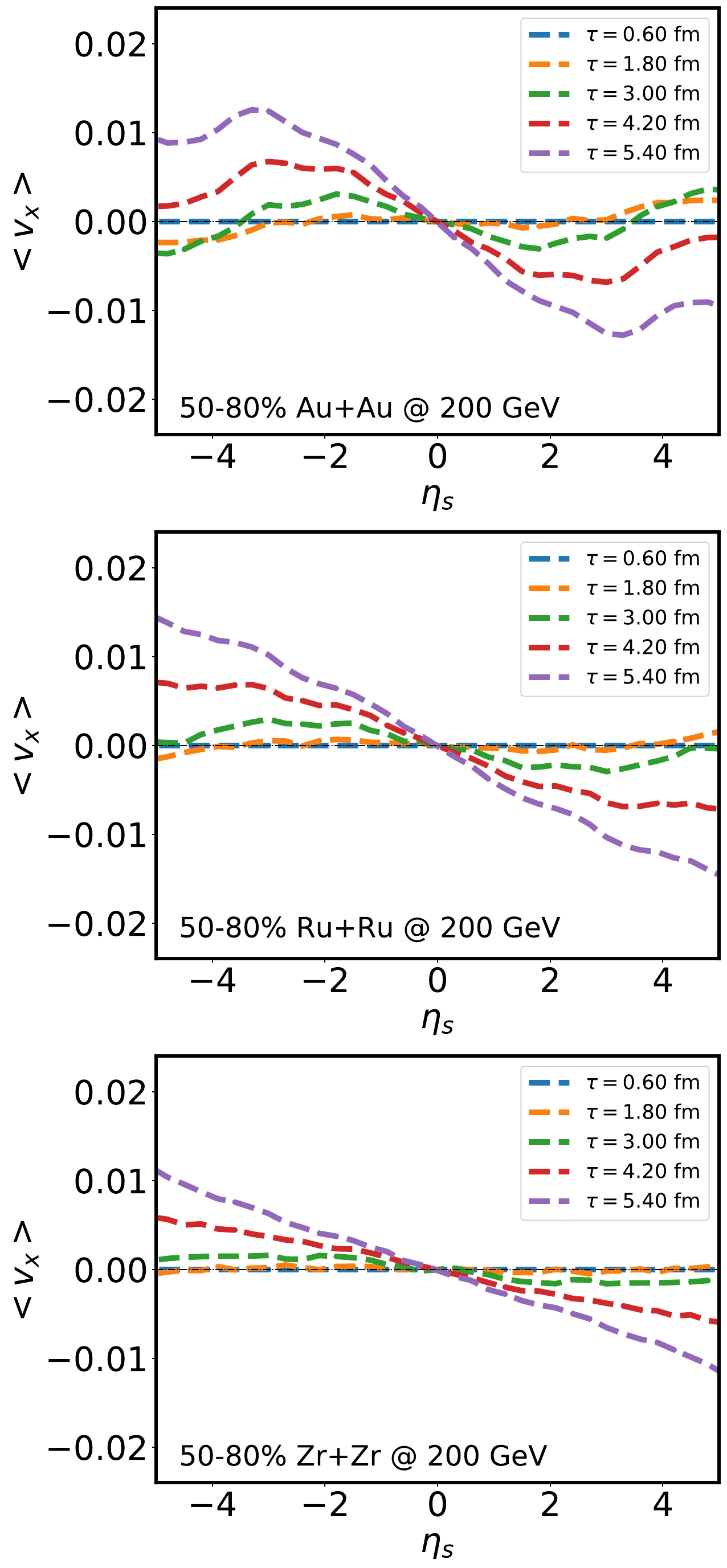
Figure 5. (color online) Space-time rapidity dependence of the average flow velocity in the x direction at different evolution times in 50%–80% Au+Au and isobar collisions at
$\sqrt{s_{NN}}=$ 200 GeV.$ \langle v_{x}(\eta_{s}) \rangle = \frac{\displaystyle\int {\rm d}^{2}r v_{x} \gamma \varepsilon(r,\phi,\eta_{s}) }{\displaystyle\int {\rm d}^{2}r \gamma \varepsilon(r,\phi,\eta_{s})}, $

(15) where
$ \gamma=1/\sqrt{1-v_{x}^{2}-v_{y}^{2}-v_{\eta_{s}}^{2}} $ is the Lorentz boost factor.In Fig. 5, the average flow velocity
$ \langle v_x \rangle $ is positive/ negative at backward/forward rapidity. The magnitude of$ \langle v_x \rangle $ increases with time owing to the non-zero pressure gradient$ -\langle\partial_{x}P \rangle $ . We find that a larger$ |-\langle\partial_{x}P \rangle| $ leads to a larger$ \langle v_x \rangle $ at$ |\eta_s| $ around the$ |\eta_s|\approx 2 $ regime than around the$ |\eta_s|\approx 1 $ regime. Here, the average flow velocity$ \langle v_x \rangle $ will directly produce the directed flow of light hadrons. -
In this section, we present the numerical results for light hadrons yield and directed flow in Au+Au and isobar collisions at
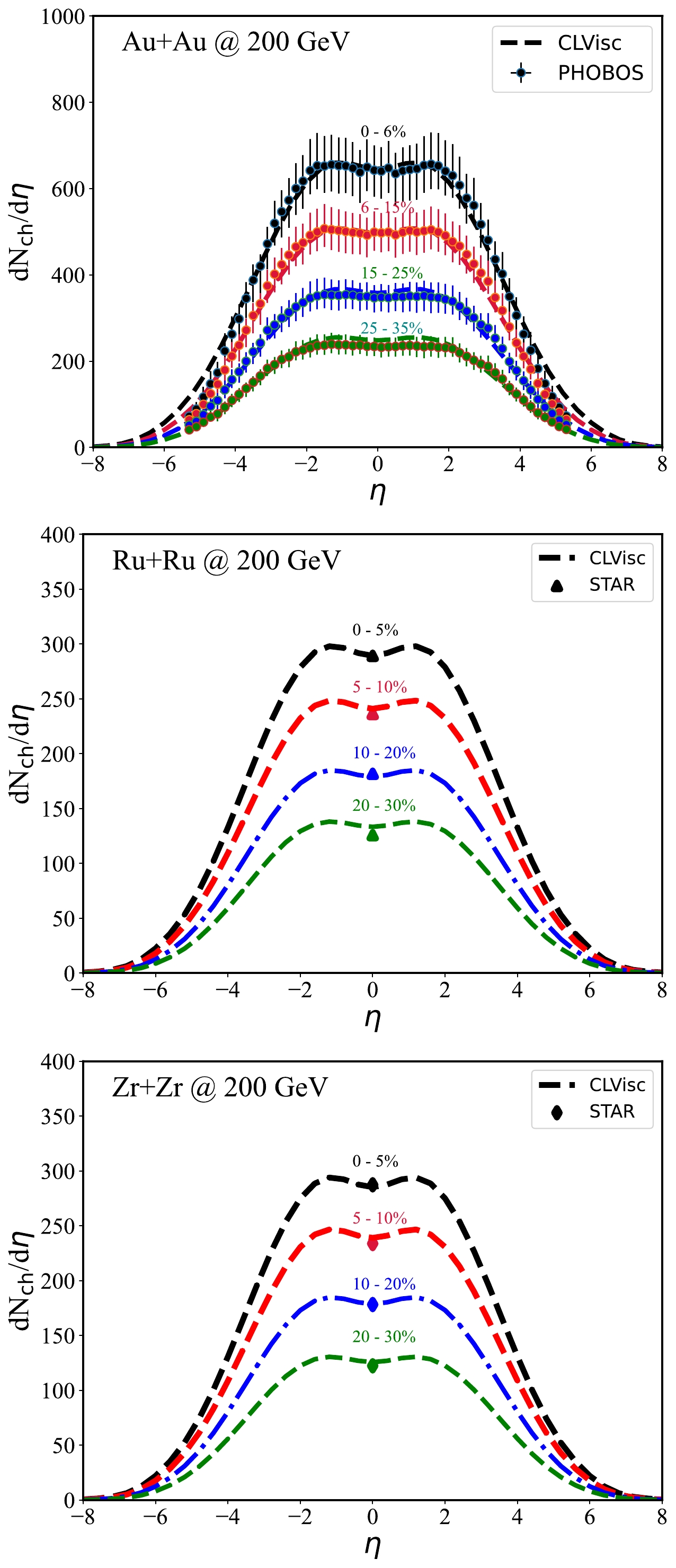
$\sqrt{s_{NN}}=200$ GeV using the above tilted initial condition and the hydrodynamic model CLVisc. In particular, we investigate how the directed flow depends on the effect of the nuclear structure of the isobar Ru and Zr.In Fig 6, we show the pseudorapidity distributions of the charged particles in Au+Au, Ru+Ru, and Zr+Zr collisions at
$\sqrt{s_{NN}}=200$ GeV. As discussed in Sec. IIA, the hydrodynamic model parameters summarized in Table 2 are adjusted to describe the charged light hadron distributions in the most central collisions. As shown in the figures, our calculation presents reasonable descriptions of PHOBOS data on the$ {\rm d} N_\text{ch}/{\rm d}\eta $ distributions for Au+Au collisions in several centralities at$ \sqrt{s_{NN}}=200 $ GeV. In addition, note that the parameter$ H_{t} $ only affects the deformation of the medium geometry and has a weak impact on the${\rm d} N_\text{ch}/{\rm d}\eta$ distributions [75]. This provides a reliable baseline for further investigations on light hadron directed flow. We define centrality bins utilizing the impact parameter, and the contribution from the centrality fluctuation is not included in the current study. In the future, it will be necessary to use the multiplicity distribution with the given experimental data to characterize the centrality bins.We then present the identified particle directed flow
$ v_1 $ as a function of pseudorapidity. Following our previous research [74, 75],$ v_{1}(\eta) $ is calculated via$ v_{1}(\eta)=\langle\cos(\phi-\Psi_{1})\rangle=\frac{\displaystyle\int\cos(\phi-\Psi_{1})\dfrac{{\rm d}N}{{\rm d}\eta {\rm d}\phi}{\rm d}\phi}{\displaystyle\int\dfrac{{\rm d}N}{{\rm d}\eta {\rm d}\phi}{\rm d}\phi}, $

(16) where
$ \Psi_{1} $ is the first-order event plane of the collision [45]. The directed flow$ v_1 $ is analyzed using soft hadrons within$ 0 < p_{T} < 3.0 $ GeV in our current hydrodynamic model. Moreover, because the analysis usually uses$ 0.2 < p_{ {T}} < 2.0 $ GeV for charge particles, we will use this$ p_{ {T}} $ range in future studies. Here, we use the optical Glauber model to construct the initial energy density distribution of nuclear matter, and the initial event-by-event fluctuations are neglected [45, 74]. As a result, the event plane is the same as the spectator plane determined using deflected neutrons in realistic experimental measurements. The Monte Carlo Glauber model contributes the effect of event-by-event fluctuations, which enhances the directed flow at large forward and backward rapidity. A more consistent study will be conducted in future after event-by-event fluctuations are taken into account.Using the above setups, we show light hadron
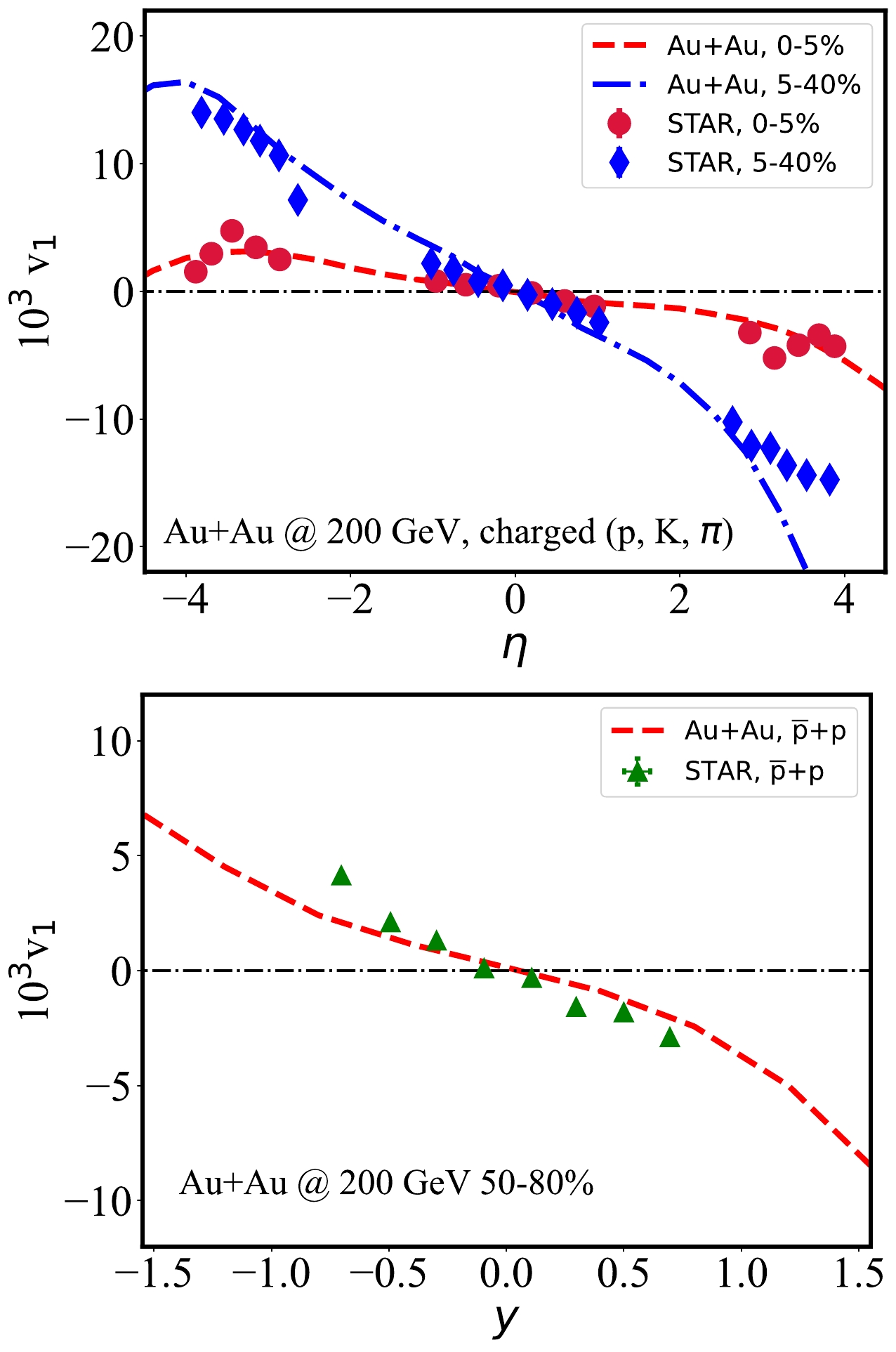
$ v_1 $ in Au+Au collisions for different centrality classes at$\sqrt{s_ {NN}} = 200$ GeV in Fig. 7; the upper panel for charged particles, and the lower for protons (p) and anti-protons ($ \bar{p} $ ). Our calculations for charged particle$ v_1 $ within$ -4.5 < \eta < 4.5 $ are consistent with STAR data. As expected, the distribution of the identified particle$ v_1 $ is consistent with that of the average flow velocity$ v_x $ of nuclear matter.For isobar collisions, as illustrated in Fig. 8, within our hydrodynamic framework, we are able to describe the directed flow
$ v_1 $ of protons ($ p^{\pm} $ ) at either Ru+Ru or Zr+Zr by adjusting the$ H_{t} $ parameter. The difference in the$ v_1 $ value between the two nuclei is less than 0.001 within$ |y|<1.5 $ . If the value of$ H_{t} $ is decreased, the slope of$ v_1 $ vs. y decreases near the mid-rapidity region and further deviates from the experimental data. This implies the importance of the tilted initial energy density distribution in understanding the rapidity dependence of light hadron$ v_1 $ observed in experiments. Based on Figs. 7 and 8, we find that with a different$ H_t $ for isobar and Au+Au collisions at the same centrality bins, a clear system size dependence is observed for directed flow. Smaller nuclei have a smaller$ H_{t} $ , which leads to a smaller directed flow at mid-rapidity.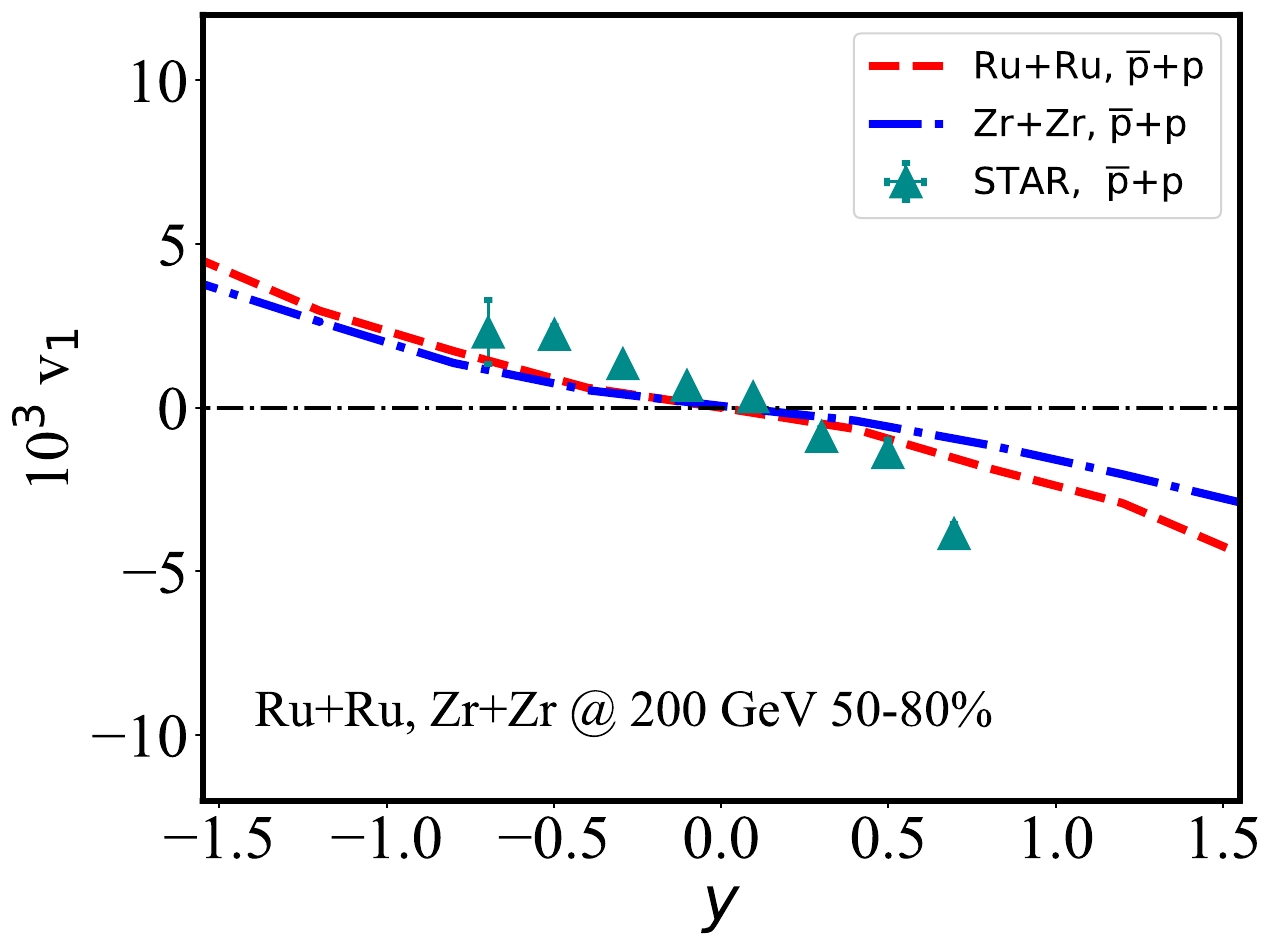
Figure 8. (color online) Rapidity dependence of the directed flow coefficient in 50%–80% Ru+Ru and Zr+Zr collisions at
$ \sqrt{s_{NN}} = 200 $ GeV, compared between the CLVisc hydrodynamic calculation with the Case-1 nuclear structure and STAR data [73].Thus far, we have focused on the discussion of spherical nuclei (from DFT) in which the quadrupole deformity parameter
$ \beta_{2}=0 $ (as listed in Table 1). As noted in Refs. [57, 59–65], elliptic flow in the most central collisions is sensitive to nuclear deformation because deformed nuclei colliding at the impact parameter$ b=0 $ can induce a large eccentricity on the collision orientation. To study the effect of nuclear deformation on light hadron$ v_{1} $ within our hydrodynamic framework, the extended WS parameters of nuclei listed in Table 3 are utilized. The two sets (Case-2 and Case-3) have the same R and a parameters and different deformations, which are constrained by$ e+A $ scattering experiments and calculations based on a finite-range droplet macroscopic model [92, 93] and the folded-Yukawa single-particle microscopic model [94]. Because of the additional protons in Ru, the charge radius of Ru is larger than that of Zr. Other parameters during QGP evolution are the same as those of spherical nuclei (Case-1).Parameter Case-1 Case-2 Case-3 Ru+Ru Zr+Zr Ru+Ru Zr+Zr Ru+Ru Zr+Zr R/fm 5.067 4.965 5.085 5.02 5.085 5.02 d/fm 0.500 0.556 0.46 0.46 0.46 0.46 $ \beta_{2} $ 

0.0 0.0 0.158 0.08 0.053 0.217 Table 3. Nuclear structure parameters for Ru and Zr from Ref. [52].
Figure 9 shows the proton
$ v_{1} $ in Ru+Ru/Zr+Zr collisions at$\sqrt{s_{NN}}=200$ GeV with various combinations of Ru and Zr deformities. The comparison between the three nuclear structures shows that$ \beta_{2} $ deformations may not be essential to change the$ v_{1} $ slope and magnitude at the central pseudorapidity ($ |y|<0.5 $ ). We see that the slope of$ v_{1} $ changes insignificantly due to finite$ \beta_{2} $ between Case-2 and Case-3 for both Ru+Ru and Zr+Zr collisions. The impact of the different parameters R, d, and$ \beta_{2} $ on proton$ v_{1} $ implies that the nuclear structure with quadrupole deformation only slightly affects the directed flow of final state particles. We note here that$ v_{1} $ between Ru and Zr at a large rapidity may be sensitive to the shape of the nuclei. Furthermore, many low energy experiments have shown that Zr has a large octupole deformation corresponding to a large value of$ \beta_{3} $ . Theoretical studies have found that the average of the first-order eccentricity coefficient$ \varepsilon_1 $ is proportional to the average of$ \beta_{3}^{2} $ , and the octupole deformation should affect the$ v_{1} $ of soft hadrons [59, 95]. The effect of octupole deformation will be investigated in an upcoming study.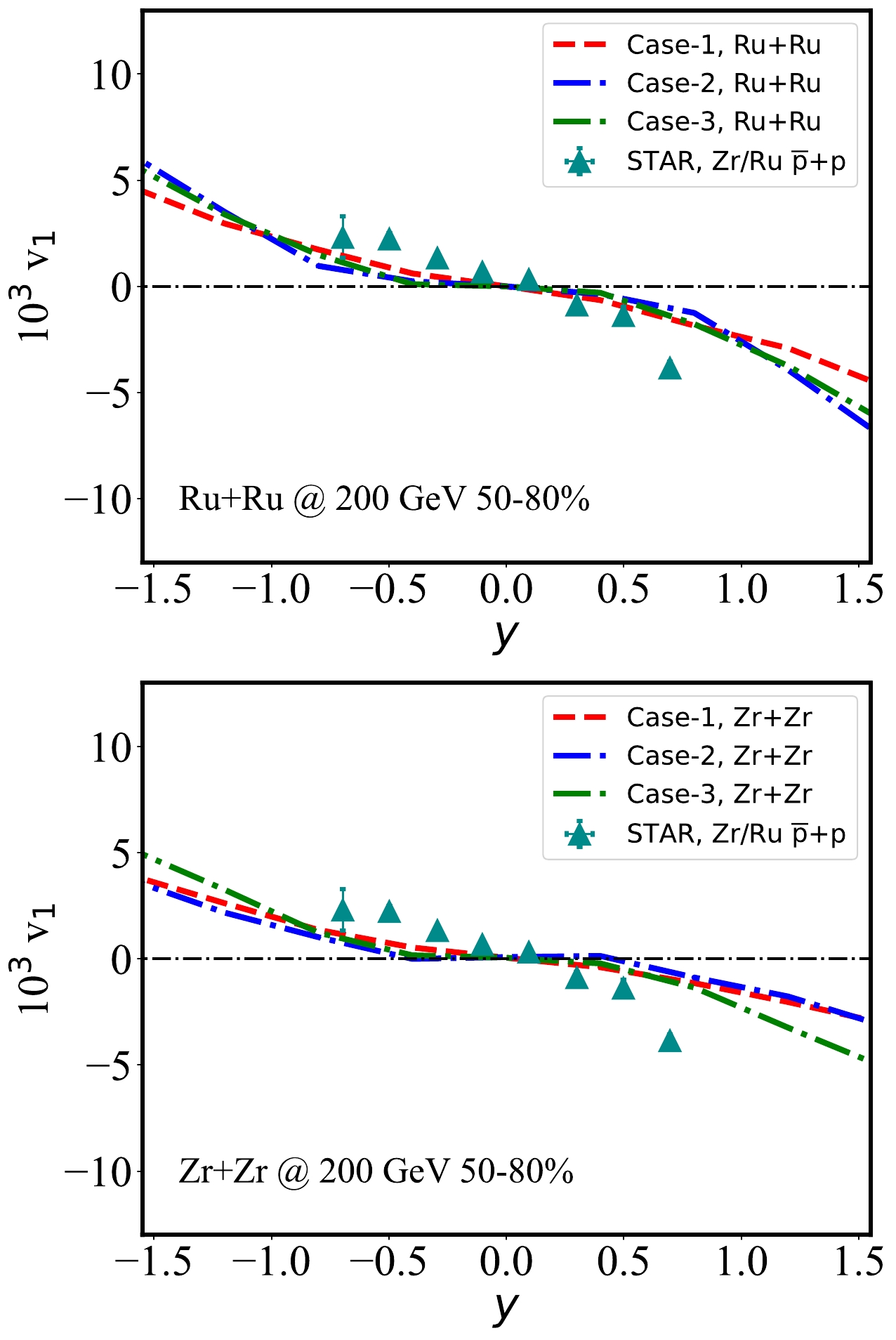
Figure 9. (color online) Rapidity dependence of the directed flow coefficient in 50%–80% Ru+Ru collisions (upper panel) and Zr+Zr collisions (lower panel) at
$ \sqrt{s_{NN}} = 200 $ GeV, compared between the CLVisc hydrodynamic calculation with three nuclear structure setups and STAR data [73].Note that because we use the optical Glauber model (smooth initial condition), our calculation is restricted to the rapidity-odd component of light hadron
$ v_1 $ . The rapidity-even component$ v_1^{ \rm{even}} $ , including its non-trivial$p_{T}$ dependence [96–98], is beyond the scope of this study and will be investigated in the future. -
In this paper, we present a systematic investigation of how the initial medium profile of nuclei evolves to light hadron directed flow in heavy ion collisions. Three different nucleus-nucleus collisions (Au+Au, Ru+Ru, and Zr+Zr) are compared for the tilted initial energy density distribution, and their subsequent space-time evolutions are simulated utilizing the hydrodynamic model CLVisc.
Using our (3+1)-D hydrodynamic model CLVisc, we calculate the directed flow
$ v_{1} $ for light hadrons as a function of (pseudo-)rapidity and centrality for Au+Au and isobar collisions at$\sqrt{s_{NN}}=200$ GeV. Our model can give a good description of light hadron$ v_1 $ in central and peripheral Au+Au and isobar collisions measured by the STAR Collaboration. Our results show that light hadron$ v_{1} $ has a strong system size dependence, that is,$ v_1 $ is larger for small systems, owing to a weaker nuclear stopping effect. The system size dependence is also observed from the centrality dependence:$ v_1 $ becomes large when moving from central to peripheral collisions, which is clearly observed in Au+Au collisions and can be tested by future experiments. We further find that the Au+Au and isobar semi-central collisions generate an imbalance between a forward/backward moving nucleus, induce a counter-clockwise tilt of the initial medium profile in the x-$ \eta_s $ plane, and generate a non-zero average pressure gradient$ -\langle \partial_x P\rangle $ with respect to time at backward/forward rapidity. A comparison to RHIC-STAR data indicates that the tilted initial energy density profile (or fireball geometry) is an essential factor in generating the observed light hadron$ v_1 $ in Au+Au and isobar collisions at$\sqrt{s_{NN}}=200$ GeV. We finally find that the effect of nuclear structure with quadrupole deformation insignificantly affects the light hadron directed flow at mid-rapidity.Our study provides a step toward understanding the origin of light hadron directed flow in Au+Au and isobar collisions. However, in addition to the effect of tilted initial energy density, other sources also contribute to the size and sign of directed flow. See the following examples: (1) The extremely strong electromagnetic field produced in non-central nucleus-nucleus collisions results in directional drift of charged quarks (
$ u,d,s $ ) and influences the charged particle$ v_1 $ [99–101]. Although this effect is suggested to be smaller than the effect of the initial tilted geometry, it is important to understand the splitting of$ v_{1} $ for identified light hadrons in isobar collisions [99]. (2) The fluid velocity field could provide an additional contribution to light hadron directed flow [48]. In particular, it could affect the initial baryon density distribution and thus nuclear matter properties [45]. (3) Light hadron$ v_1 $ can also be affected by the nuclear stopping effect and hadronic cascade after QGP evolution, especially at lower collision energies [47, 48, 51]. (4) The light hadron elliptic flow$ v_{2} $ and triangular flow$ v_{3} $ could set more constraints on the nuclear structure; however, we do not discuss this here because we limit ourselves to a smooth initial condition without the contribution of event-by-event fluctuations. These should be investigated in our future studies for a more exact understanding of directed flow. -
We are grateful for helpful discussions with Xiangyu Wu and Shanshan Cao.
Hydrodynamic simulations of directed flow for light hadrons in Au+Au and isobar collisions at ${ \sqrt{{\boldsymbol s}_{\boldsymbol{NN}}}=}$ 200 GeV
- Received Date: 2022-09-27
- Available Online: 2023-03-15
Abstract: Using a (3+1)-D hydrodynamic model, CLVisc, we study the directed flow (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: