-
In the last few decades, the constituent quark model has successfully explained the composition of most mesons [1]. However, the properties of light scalar mesons are difficult to describe within the constituent quark model. For scalar mesons with masses less than 1 GeV (
$ f_0(500) $ ,$ a_0(980) $ ,$ f_0(980) $ , and$ K(700) $ ), there are different explanations, such as$ q\bar{q} $ states, tetraquark states, or molecular states [2–5]. In addition, the nature of isospin-zero scalar mesons with larger masses, such as$ f_0(1370) $ ,$ f_0(1500) $ , and$ f_0(1710) $ , is also difficult to fully understand [1]. Recently, BESIII and Belle/ Belle II accumulated considerable experimental information about charmed hadrons decays, which provides an important platform to explore the internal structures of these scalar mesons [6–9].For instance, the BESIII Collaboration observed the scalar
$ S(1710) $ ① with a mass of$ 1723\pm 11\pm2 $ MeV and a width of$ 140\pm 14\pm 4 $ MeV in the process$ D_s^+\to K^0_S K^0_S \pi^+ $ [10]. Later, a similar structure was also observed in the process$ D_s^+\to K^+ K^0_S \pi^0 $ by the BESIII Collaboration, associated with a new scalar state$ a_0(1817) $ with a mass of$ 1817 \pm 8\pm 20 $ MeV and a width of$97\pm 22 \pm 15$ MeV [11]. The$ \sim100 $ MeV mass discrepancy between$ S(1710) $ and$ a_0(1817) $ causes doubt as to whether they are isospin partners. However, the line-shapes of$ a_0(1817) $ and$ S(1710) $ in the$ K^+K^0_S $ and$ K^0_SK^0_S $ invariant mass distributions are so similar that the measured mass discrepancy of$ a_0(1817) $ and$ S(1710) $ may be due to the closeness of their peaks to the threshold of the$ K\bar{K} $ mass spectrum. We previously investigated both reactions and found that the BESIII measurements of both reactions could be well reproduced by regarding the intermediate state$ a_0(1817) $ as the$ K^*\bar{K}^* $ molecular state [12, 13], which is also supported by the study in Ref. [14].The BESIII Collaboration recently performed an amplitude analysis of the process
$ D_s^+ \to \pi^{+} \pi^{0} \pi^{0} $ and determined the branching fraction$ \mathcal{B} $ ($ D_s^+ \to \pi^{+} \pi^{0} \pi^{0} $ ) = (2.8$ \pm $ 0.4$ \pm $ 0.4)$ \% $ [15], which improves the precision by a factor of two compared to the results of the CLEO Collaboration [16]. The significant$ f_{0}(980) $ signal and an enhancement structure around 1300 MeV were observed in the$ \pi^{0}\pi^{0} $ invariant mass spectrum, and the latter structure could be associated with the intermediate resonances$ f_0(1370) $ and$ f_2(1270) $ . The scalar$ f_0(980) $ could be explained as the$ K\bar{K} $ molecular state dynamically generated from the S-wave pseudoscalar-pseudoscalar interaction [17, 18], which is supported by many studies [6–9]. In addition, the resonance$ f_0(1370) $ is a broad state, and its mass and width are not well established. There are various explanations for the nature of$ f_0(1370) $ , such as the$ n\bar{n} $ state, molecular state [19–21],$ s\bar{s} $ [22], and glueball [23, 24]. In Refs. [19–21],$ f_2(1270) $ is also explained as a bound system of two vector mesons, which is challenged in Ref. [25]. Therefore, a study of the process$D_s^+ \to \pi^{+} \pi^{0} \pi^{0}$ should help deepen our understanding of the nature of$ f_0(980) $ ,$ f_0(1370) $ , and$ f_2(1270) $ .In this work, we investigate the process
$ D_s^+ \to \pi^{+} \pi^{0}\pi^{0} $ by considering the scalar$ f_0(980) $ generated from the S-wave pseudoscalar-pseudoscalar interaction within the chiral unitary approach and the contributions from the intermediate resonances$ f_0(1370) $ and$ f_2(1270) $ .This paper is organized as follows: In Sec. II, we present the mechanism for the process
$ D_s^+ \to \pi^{+} \pi^{0}\pi^{0} $ . The results and discussions are given in Sec. III, followed by a short summary in the last section. -
In this section, we present the mechanism of the process
$ D_s^+\to \pi^+\pi^0\pi^0 $ . This process occurs in three steps, weak decay, hadronization, and final state interactions [7, 9, 12, 13]. First, the c quark of the initial$ D_s^+ $ weakly decays into an s quark and a$ W^+ $ boson, and the$ W^+ $ boson subsequently decays into a$ \bar d u $ quark pair. Then, all the quarks, along with the quark pair$ q\bar q $ (=$ u\bar u $ +$ d\bar d $ +$ s\bar s $ ) created from the vacuum with the quantum numbers$J^{PC}= 0^{++}$ , hadronize into hadrons, which can be classified as the$ W^+ $ internal emission of Figs. 1(a) and (b) and the$ W^+ $ external emission of Figs. 1(c) and (d).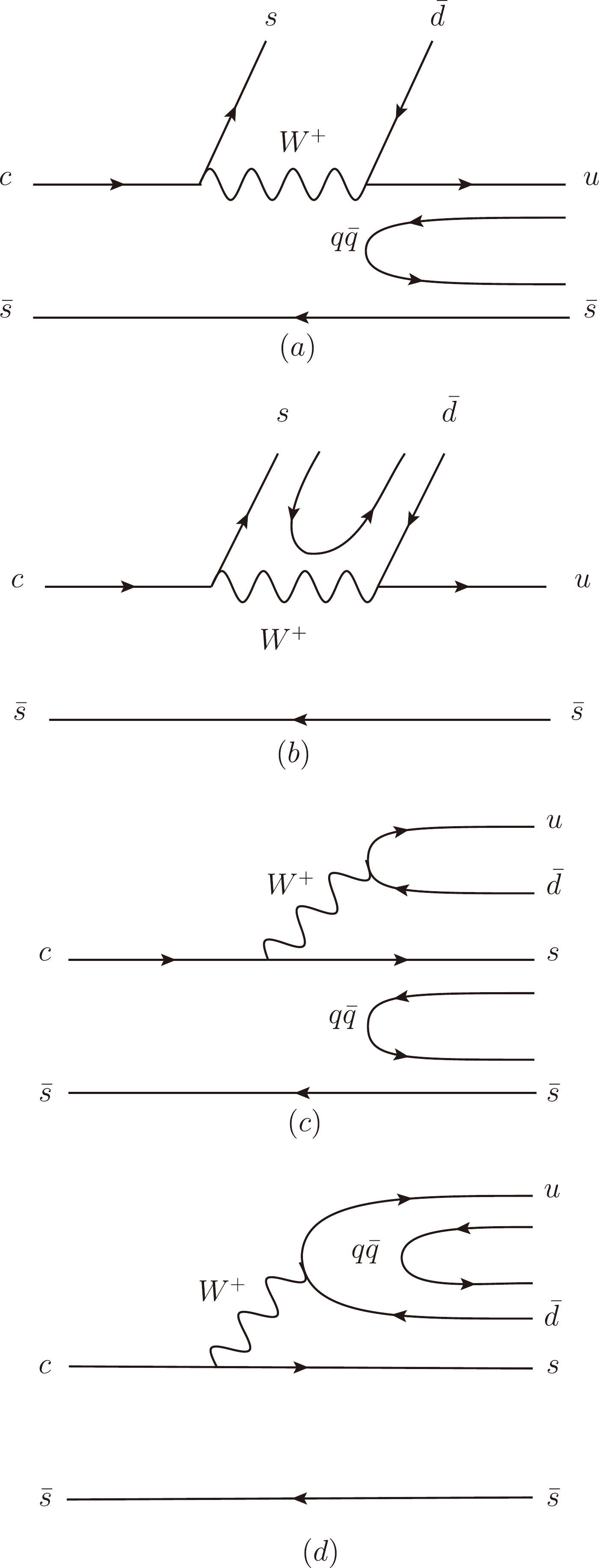
Figure 1. Quark level diagrams for the
$ D_{s}^{+} $ weak decays. (a) Internal emission of$ D_{s}^{+} \to K^{+}u\bar{s} $ , and hadronization of$ u\bar{s} $ through$ q\bar{q} $ with vacuum quantum numbers. (b) Internal emission of$D_{s}^{+} \to $ $ \bar{K}^0s\bar{d}$ , and hadronization of$ s\bar{d} $ through$ q\bar{q} $ with vacuum quantum numbers. (c) External emission of$ D_{s}^{+} \to \pi^{+}s\bar{s} $ , and hadronization of$ s\bar{s} $ through$ q\bar{q} $ with vacuum quantum numbers. (d) External emission of$ D_{s}^{+} \to u\bar{d}\eta $ , and hadronization of$ u\bar{d} $ through$ q\bar{q} $ with vacuum quantum numbers.For the
$ W^+ $ internal emissions of Figs. 1(a) and (b),$ s\bar{d} $ or$ u\bar{s} $ hadronize into$ \bar{K}^0 $ or$K^+$ , and the hadronization of the other quarks may be expressed as$ \sum\limits_{i}u(\bar q_{i} q_i)\bar s=\sum\limits_{i}M_{1i}M_{i3}=(M^2)_{13}, $

(1) $ \sum\limits_{i}s(\bar q_{i} q_{i})\bar d=\sum\limits_{i}M_{3i}M_{i2}=(M^2)_{32}, $

(2) where
$ i=1,\; 2,\; 3 $ correspond to the u, d, and s quarks, respectively, and M is the$ q\bar{q} $ matrix$ \begin{array}{*{20}{l}} M=\left(\begin{array}{ccc} u\bar{u} & u\bar{d} & u\bar{s}\\ d\bar{u} & d\bar{d} & d\bar{s} \\ s\bar{u} & s\bar{d} & s\bar{s} \end{array} \right)\,. \end{array} $

(3) Within
$S U(3)$ flavor symmetry, the matrix M can be written in terms of pseudoscalar mesons as [7]$ \begin{array}{*{20}{l}} M= \left(\begin{array}{ccc} \frac{\pi^0}{\sqrt{2}} +\frac{\eta}{\sqrt{3}}+\frac{\eta^\prime}{\sqrt{6}}& \pi^+ & K^+\\ \pi^-& -\frac{\pi^0}{\sqrt{2}} +\frac{\eta}{\sqrt{3}}+\frac{\eta^\prime}{\sqrt{6}} & K^0\\ K^-& \bar{K}^0 & - \frac{\eta}{\sqrt{3}}+\frac{2\eta^\prime}{\sqrt{6}} \end{array} \right)\,. \end{array} $

(4) Because
$ \eta^\prime $ has a large mass and does not play a role in the generation of$ f_0(980) $ , we ignore the$ \eta^\prime $ component in this study. Then, Eqs. (1) and (2) can be rewritten as$ (M^{2})_{13}=\frac{1}{\sqrt{2}}K^+\pi^0 + \pi^+K^0, $

(5) $ (M^{2})_{32}=K^-\pi^+ - \frac{1}{\sqrt{2}}\bar{K^0}\pi^0. $

(6) For the
$ W^+ $ external emission of Fig. 1(c), the quarks$ u\bar{d} $ of the$ W^+ $ decay hadronize into$ \pi^+ $ , and the$ s\bar{s} $ pair, along with the created$ q\bar{q} $ pair, hadronize into the states$ \begin{aligned}[b] \sum\limits_{i}s(\bar q_{i} q_i)\bar s =&\sum\limits_{i}M_{3i}M_{i3}=(M^2)_{33} \\ =& K^+K^-+K^0\bar{K}^0+\frac{1}{3}\eta \eta. \end{aligned} $

(7) For the
$ W^+ $ external emission of Fig. 1(d), the$ s\bar{s} $ pair may hadronize into the η meson, and the quarks$ u\bar{d} $ of the$ W^+ $ decay, along with the created$ q\bar{q} $ pair, hadronize into$ \pi^+\eta $ , which contributes to the process$ D_s^+\to \pi^+\eta\eta $ . Thus, we have$ \begin{aligned}[b] \sum\limits_{i}u(\bar q_{i} q_i)\bar d (s\bar{s}) =&\sum\limits_{i}M_{1i}M_{i2} M_{33} \\ =&(M^2)_{21} \left(-\frac{1}{\sqrt3}\eta\right)= - \frac{2}{3}\pi^+\eta \eta. \end{aligned} $

(8) Then, the processes involved in the decay of
$ D^+_s $ into all possible states can be expressed as$ H^{(a)} =V_{cs}V_{ud}\left(\frac{1}{\sqrt{2}}\pi^0K^++\pi^+K^{0} \right)\bar{K}^0, $

(9) $ H^{(b)} =V_{cs}V_{ud}\left(\pi^+K^--\frac{1}{\sqrt{2}}\pi^0\bar {K}^0 \right) K^+, $

(10) $ H^{(c)}= CV_{cs}V_{ud}\left(K^+K^-+K^0\bar{K^0}+\frac{1}{3}\eta \eta \right)\pi^+, $

(11) $ H^{(d)}= CV_{cs}V_{ud}\left(-\frac{2}{3}\eta \eta \pi^+\right), $

(12) where
$ V_{ud} $ and$ V_{cs} $ are the CKM matrix elements. Because the external emission of$ W^+ $ bosons is color-favored relative to the$ W^+ $ internal emission, an extra color factor C can be introduced to account for the relative weight of the$ W^+ $ external emission with respect to the$ W^+ $ internal emission. For the$ W^+ $ external emission, the$ u\bar d $ quark pair from the$ W^+ $ decay can form the color singlet$ \pi^+ $ , and u and$ \bar{d} $ have three choices of colors, whereas for the$ W^+ $ internal emission, u,$ \bar{d} $ , s, and$ \bar s $ quarks from the$ W^+ $ decay have fixed colors. Thus, the factor C is taken to be three in this study [26–29]. Now, we have all the possible components after hadronization,②$ \begin{aligned}[b] H=& H^{(a)}+H^{(b)}+ H^{(c)}+ + H^{(d)}\\ =&V_{p}V_{cs}V_{ud}\left\{C( K^+K^-+K^0\bar{K}^0+\frac{1}{3}\eta\eta )\pi^+ \right. \\ &\left. + \bar{K^0}K^0\pi^+ + K^+ K^-\pi^+\right\} \\ =&V_{p}V_{cs}V_{ud}\left\{ (C+1)\left( K^+K^-\pi^++K^0\bar{K}^0\pi^+ \right) \right. \\ &\left. -\frac{C}{3}\eta\eta \pi^+ \right\}, \end{aligned} $

(13) where
$ V_p $ denotes the factors of the production vertices containing all the dynamics. After the preliminary weak decay, the meson pairs of$ K^{+}K^{-} $ ,$ K^{0}\bar{K}^0 $ , and$ \eta\eta $ may undergo the S-wave final state interaction to give rise to the$ \pi^{0}\pi^{0} $ final state, where the scalar meson$ f_0(980) $ can be dynamically generated, as shown in Fig. 2.The amplitude of the S-wave pseudoscalar-pseudoscalar interaction, generating the scalar
$ f_0(980) $ , can now be written as$ \begin{aligned}[b] {\mathcal{M}}_{f_{0}(980)}=&V_p\Bigg[(C+1) G_{K^+K^-}t_{K^+K^-\to \pi^0\pi^0} \\ & +(C+1) G_{K^0\bar{K}^0} t_{K^0\bar{K}^0 \to \pi^0\pi^0 } \\ &\left. -\frac{C}{3} G_{\eta\eta} t_{\eta\eta \to \pi^0\pi^0 } \right] , \end{aligned} $

(14) where
$ G_i $ is the loop function of the two-meson propagator, and$ t_{i\to j} $ is the transition amplitude of the i-channel to j-channel, both of which are functions of the$ \pi^0 \pi^0 $ invariant mass$ M_{\pi^0\pi^0} $ . The loop function is given by$ \begin{equation} G_{i}= {\rm i} \int \frac{{\rm d}^4 q}{(2 \pi)^4} \, \frac{1}{(P-q)^2 - m_1^2 + {\rm i} \epsilon} \, \frac{1}{q^2 - m^2_2 + {\rm i} \epsilon}, \end{equation} $

(15) where
$ m_1 $ and$ m_{2} $ are the masses of the two mesons in the loop of the i-channel, and P and q are the four-momenta of the two-meson system and second meson, respectively. The Mandelstam invariant$ s=P^2=M_{\pi^0\pi^0}^2 $ . The loop function of Eq. (15) is logarithmically divergent, and there are two methods of solving this singular integral, either using the three-momentum cut-off method, or the dimensional regularization method. The choice of a particular regularization scheme does not, of course, affect our argumentation. In this study, we perform the integral for q in Eq. (15) with a cut-off$ |\vec{q}_{\rm max}|= 600 $ MeV [30, 31]. The transition amplitude$ t_{i\to j} $ can be obtained by solving the Bethe-Salpeter equation in coupled channels,$ \begin{equation} T=[1-VG]^{-1}V, \end{equation} $

(16) where V is a
$ 5\times5 $ matrix of the interaction kernel. We take five channels,$ \pi^+\pi^- $ ,$ \pi^0\pi^0 $ ,$ K^+K^- $ ,$ K^0\bar{K}^0 $ , and$ \eta\eta $ . The explicit expressions of the$ 5\times5 $ matrix elements in the S-wave are given by [32–33]$ \begin{aligned}[b]& V_{11}=-\frac{1}{2f^2}s,\; \; \; V_{12}=-\frac{1}{\sqrt{2}f^2}(s-m^2_\pi), \\ & V_{13}=-\frac{1}{4f^2}s,\; \; V_{14}=-\frac{1}{4f^2}s, \\ &V_{15}=-\frac{1}{3\sqrt{2}f^2}m^2_\pi,\; \; \; V_{22}=-\frac{1}{2f^2}m^2_\pi, \\ & V_{23}=-\frac{1}{4\sqrt{2} f^2}s,\; \; \; V_{24}=-\frac{1}{4\sqrt{2} f^2}s, \\ & V_{25}=-\frac{1}{6f^2}m^2_\pi,\; \; V_{33}=-\frac{1}{2f^2}s,\; \; \; V_{34}=-\frac{1}{4f^2}s, \\ &V_{35}=-\frac{1}{12\sqrt{2}f^2}(9s-6m^2_\eta-2m^2_\pi), \\& V_{44}=-\frac{1}{2f^2}s,\; \; V_{45}=-\frac{1}{12\sqrt{2}f^2}(9s-6m^2_\eta-2m^2_\pi), \\&V_{55}=-\frac{1}{18f^2}(16m^2_K-7m^2_\pi), \end{aligned} $

(17) where
$ f=93 $ MeV is the pion decay constant, s is invariant mass square of the meson-meson system, and$ m_\pi $ ,$ m_K $ , and$ m_\eta $ are the masses of the pion, kaon, and η mesons, respectively [1]. The unitary normalization$ |\eta\eta> \to \dfrac{1}{\sqrt{2}}|\eta\eta> $ and$ |\pi^0\pi^0>\to \dfrac{1}{\sqrt{2}}|\pi^0\pi^0> $ is easily considered to identify the particle when using the loop function G without an extra factor [30].In addition to the scalar
$ f_0(980) $ , BESIII has observed the enhancement structure around 1300 MeV in the$ \pi^0\pi^0 $ invariant mass distribution, which could be associated with the resonances$ f_0(1370) $ and$ f_2(1270) $ . Hence, we also take into account contributions from the intermediate resonances$ f_0(1370) $ and$ f_2(1270) $ .For the contribution of
$ f_0(1370) $ in the decay$ D_s^+ \to \pi^+\pi^0\pi^0 $ , we describe it using the Breit-Winger form,$ \mathcal{M}_{f_0(1370)}=\frac{\alpha \times m^2_{f_0(1370)}}{m^{2}_{\pi^{0}\pi^{0}}-M^{2}_{f_{0}(1370)}+ {\rm i} \Gamma_{f_{0}(1370)}M_{f_{0}(1370)}} , $

(18) where α is the strength of
$ f_0(1370) $ . Considering that the mass and width of$ f_0(1370) $ have large uncertainties [1], we fix its mass to be 1300 MeV, the center position of the enhancement structure in the$ \pi^0\pi^0 $ invariant mass distribution of BESIII measurements [15], and take the width as a free parameter.Considering that
$ f_2(1270) $ couples to$ \pi^0\pi^0 $ in the D-wave, we can write the contribution of this resonance as [34]$ \mathcal{M}_{f_2(1270)}=\frac{\beta \times(3{\rm cos}^2\theta-1)\times{\tilde{p}_{\pi^0}^2}}{M^2_{\pi^0\pi^0}-M^2_{f_2(1270)}+ {\rm i} {M_{f_2(1270)}}\Gamma_{f_{2}(1270)}}, $

(19) where β represents the strength of the D-wave amplitudes. The mass and width of
$ f_2(1270) $ are$ M_{f_2(1270)}= $ 1275.5 MeV and$ \Gamma_{f_2(1270)}=186.7 $ GeV, taken from the Review of Particle Physics [1].$ \tilde{p}_{\pi^0} $ is the momentum of$ \pi^0 $ in the$ \pi^0\pi^0 $ rest frame,$ \tilde{p}_{\pi^0}=\frac{\lambda ^{1/2}\left(M^2_{\pi^0\pi^0},m^2_{\pi^0},M^2_{\pi^0}\right)}{2M_{\pi^0\pi^0}}. $

(20) The parameter θ is the angle between the momentum of
$ \pi^0 $ and$ \pi^+ $ in the rest frame of the$ \pi^0\pi^0 $ system [34],$ {\rm cos}\theta=\frac{M^2_{\pi^+\pi^0}-M^2_{D^+_s}-M^2_{\pi^0}+2\tilde p^0_{D^+_s}\tilde p^0_{\pi^0}}{2\tilde p_{\pi^+}\tilde p_{\pi^0}}, $

(21) where
$ \tilde{p}^0_{D_s^+} $ ($ \tilde{p}^0_{\pi^0} $ ) is the energy of$ D_s^+ $ ($ \pi^0 $ ) in the$ \pi^0\pi^0 $ rest frame, and$ \tilde{p}_{\pi^+}=\tilde{p}_{D_s^+} $ is the$ \pi^+ $ ($ D_s^+ $ ) momentum in the same frame. We give the explicit forms of these variables below.$ \begin{aligned}[b] \tilde{p}_{\pi^+}=& \tilde{p}_{D^+_s} = \frac{\lambda^{1/2}\left(M^2_{D^+_s}, M^2_{\pi^0\pi^0}, m^2_{\pi^+} \right)}{2M_{\pi^0\pi^0}} , \\ \tilde{p}^0_{D^+_s} =& \sqrt{M^2_{D^+_s} + \tilde{p}^2_{D^+_s}}, \\ \tilde{p}^0_{\pi^0} =& \frac{M_{\pi^0\pi^0}}{2}, \end{aligned} $

(22) where
$ \lambda(x,y,z)=x^2+y^2+z^2-2xy-2yz-2xz $ .Consequently, the total amplitude of
$ D_s^+ \to \pi^+\pi^0\pi^0 $ can be described by$ {\mathcal{M}}=a_{\rm bg}+{\mathcal{M}}_{f_0(980)}+{\mathcal{M}}_{f_0(1370)}+{\mathcal{M}}_{f_2(1270)}, $

(23) where the constant
$ a_{\rm bg} $ is the background contribution③. As a result, the amplitude of Eq. (23) depends on the two independent invariant masses$ M_{\pi^0\pi^0} $ and$ M_{\pi^+\pi^0} $ , and the double differential width for the process$ D_s^+ \to \pi^+\pi^0\pi^0 $ is given by$ \begin{equation} \frac{{\rm d}^2\Gamma}{{\rm d}M_{\pi^0\pi^0}{\rm d} M_{\pi^+\pi^0}}= \frac{M_{\pi^0\pi^0}M_{\pi^+\pi^0}}{(2\pi)^{3}8m^3_{D^+_{s}}}|\mathcal{M}|^2. \end{equation} $

(24) We can obtain
${{\rm d}\Gamma}/{{\rm d}M_{\pi^0\pi^0}}$ and${{\rm d}\Gamma}/{{\rm d}M_{\pi^+\pi^0}}$ by integrating Eq. (24) over the other invariant mass variable with relations as follows:$ \begin{equation} \frac{{\rm d}\Gamma}{{\rm d}M_{\pi^0\pi^0}}=\int\frac{M_{\pi^0\pi^0}M_{\pi^+\pi^0}}{(2\pi)^{3}8m^3_{D^+_{s}}}|\mathcal{M}|^2 {\rm d} M_{\pi^+\pi^0}. \end{equation} $

(25) With a given
$ M_{\pi^0\pi^0} $ , the upper and lower bounds of$ M_{\pi^+\pi^0} $ are$ \begin{aligned}[b] (M^2_{\pi^+\pi^0})_{\rm max}=&\left(E^*_{\pi^+}+E^*_{\pi^0}\right)^2 \\ & -\left(\sqrt{E^{*2}_{\pi^+}-m^{*2}_{\pi^+}}-\sqrt{E^{*2}_{\pi^0}-m^{*2}_{\pi^0}}\right)^2, \end{aligned} $

(26) $ \begin{aligned}[b] (M^2_{\pi^+\pi^0})_{\rm min}=&\left(E^*_{\pi^+}+E^*_{\pi^0}\right)^2 \\ & -\left(\sqrt{E^{*2}_{\pi^+}-m^{*2}_{\pi^+}}+\sqrt{E^{*2}_{\pi^0}-m^{*2}_{\pi^0}}\right)^2, \end{aligned} $

(27) where
$ E_{\pi^{+}}^{*} $ and$ E^{*}_{\pi^{0}} $ are the energies of$ \pi^{+} $ and$ \pi^{0} $ in the$ \pi^{0}\pi^{0} $ rest frame, respectively,$ \begin{aligned}[b] E^{*}_{\pi^+}=&\frac{m^{2}_{D^+_{s}}-M^{2}_{\pi^0\pi^0}-m^2_{\pi^+}}{2M_{\pi^0\pi^0}}, \\ E^{*}_{\pi^{0}}=&\frac{M^{2}_{\pi^{0}\pi^0}-m^{2}_{\pi^0}+m^2_{\pi^0}}{2M_{\pi^0\pi^0}}. \end{aligned} $

(28) We can similarly obtain the
$ \pi^{+}\pi^{0} $ invariant mass distribution. -
In our model, there are five free parameters, (1)
$ V_p $ , the global normalization of$ f_0(980) $ in Eq. (14), (2) the constant$ a_{\rm bg} $ as the background contribution, (3) α corresponding to the strength of the$ f_0(1370) $ amplitude in Eqs. (18), (4) the width$ \Gamma_{f_{0}(1370)} $ , and (5) β as the strength of the$ f_2(1270) $ amplitude in Eq. (19). To present our numerical results, we fit the free parameters to the BESIII measurements of the$ \pi^0\pi^0 $ and$ \pi^+\pi^0 $ invariant mass distributions. Here, we have$ V_p=200 $ ,$ a_{\rm bg}=300 $ ,$ \Gamma_{f_0(1370)}=236 $ MeV,$ \alpha=85 $ , and$ \beta=250 $ ④.Then, we calculate the
$ \pi^0\pi^0 $ and$ \pi^+\pi^0 $ invariant mass distributions as shown in Fig. 3. The black points with error bars labeled as "BESIII data" are the BESIII data taken from Ref. [15], and the solid black curves labeled as "Total" are our theoretical results for the total contributions of Eq. (23). In addition, we present the contributions from$ f_0(980) $ ,$ f_0(1370) $ ,$ f_2(1270) $ , and the background, which are labeled as "$ f_0(980) $ ," "$ f_0(1370) $ ," "$ f_2(1270) $ ," and "Background," respectively. We can find a significant cusp signal at approximately 980 MeV in the$ \pi^0\pi^0 $ invariant mass distribution, which can be associated with the scalar$ f_0(980) $ dynamically generated from the S-wave pseudoscalar-pseudoscalar interaction. The enhancement structure around 1300 MeV can be well described and mainly originates from the contributions of$ f_0(1370) $ and$ f_2(1270) $ . Indeed, the mass and width of$ f_0(1370) $ have large uncertainties, and it is difficult to extract the exact properties of$ f_0(1370) $ owing to the overlap with the signal of$ f_2(1270) $ . Thus, a more precise$ \pi^0\pi^0 $ mass distribution of$ D^+_s\to \pi^+\pi^0\pi^0 $ should be helpful to shed light on the nature of the resonance$ f_0(1370) $ and$ f_2(1270) $ .
Figure 3. (color online)
$ \pi^0\pi^0 $ (a) and$ \pi^+\pi^0 $ (b) mass distributions for the process$ D_s^+ \to \pi^+\pi^0\pi^0 $ . The experimental data of BESIII are represented by points with error bars, and the fitting results of the theoretical calculations are shown by solid black lines. The colored dashed lines indicate the components of the theoretical model.For the
$ \pi^+\pi^0 $ invariant mass distribution, our results are in agreement with the BESIII results, considering the large experimental uncertainties. Indeed, we find a structure around 1.6 GeV, which may be due to the resonance$\rho(1700)$ . Because the BESIII measurements have large uncertainties, we do not consider the possible contribution from the resonance$\rho$ (1700) in this study. One could perform complicated calculations when more precise data are available.We also present the Dalitz plots of "
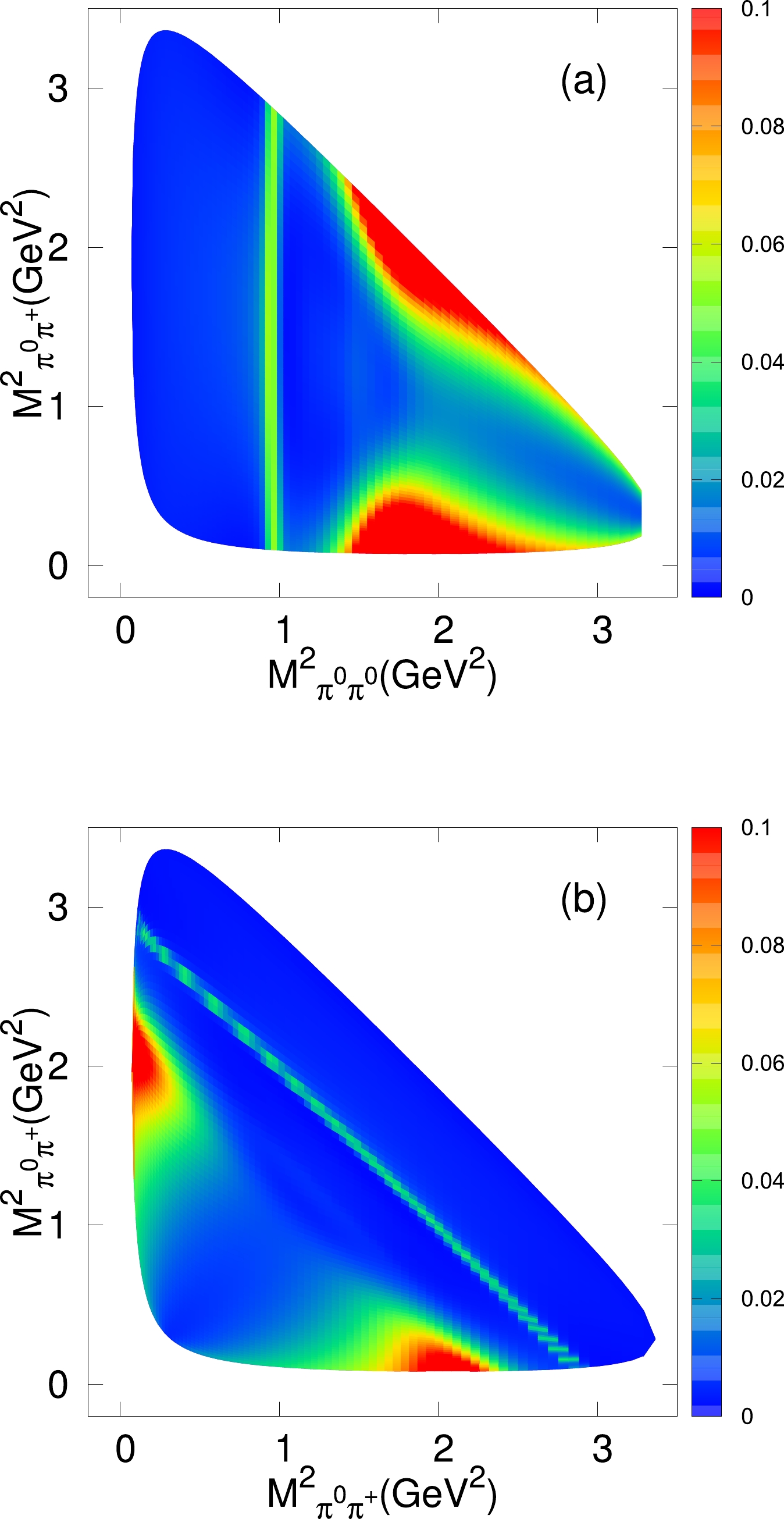
$ M^2_{\pi^+\pi^0} $ " vs. "$ M^2_{\pi^0\pi^0} $ " and "$ M^2_{\pi^+\pi^0} $ " vs. "$ M^2_{\pi^+\pi^0} $ " for the process$ D^+_s\to \pi^+\pi^0\pi^0 $ in Figs. 4(a) and 4(b), from which we can easily find the contributions of$ f_0(980) $ ,$ f_0(1370) $ , and$ f_2(1270) $ . BESIII reported the Dalitz plot of "$ M^2_{\pi^+\pi^0} $ " vs. "$ M^2_{\pi^+\pi^0} $ ," and our results are consistent with the BESIII measurements. -
Motivated by recent BESIII measurements on the decay
$ D_s^+ \to \pi^{+}\pi^{0}\pi^{0} $ [15], we investigate this Cabibbo-favored process by considering S-wave pseudoscalar-pseudoscalar interactions within the chiral unitary approach, which dynamically generates the scalar$ f_0(980) $ . In addition, contributions from the intermediate resonances$ f_0(1370) $ and$ f_2(1270) $ are taken into account.We calculate the
$ \pi^0\pi^0 $ and$ \pi^+\pi^0 $ mass distributions and find a peak around 980 MeV, which may be associated with the scalar$ f_0(980) $ , and an enhancement structure around 1300 MeV, mainly due to the intermediate resonances$ f_0(1370) $ and$ f_2(1270) $ . Our results for both the$ \pi^0\pi^0 $ and$ \pi^+\pi^0 $ invariant mass distributions are in agreement with the BESIII measurements. In addition, we predict the Dalitz plots of "$ M^2_{\pi^+\pi^0} $ " vs. "$ M^2_{\pi^0\pi^0} $ " and "$ M^2_{\pi^+\pi^0} $ " vs. "$ M^2_{\pi^+\pi^0} $ ." -
We thank Prof. Ju-Jun Xie and Prof. Li-Sheng Geng for useful discussions.
Role of the scalar ${{\boldsymbol f}_{\bf 0}\boldsymbol{(980)} }$ in the process ${ {\boldsymbol D}_{\boldsymbol s}^{\bf +}\bf \to \boldsymbol\pi^{\bf +} \boldsymbol\pi^{\bf 0} \boldsymbol\pi^{\bf 0}} $
- Received Date: 2022-12-22
- Available Online: 2023-04-15
Abstract: Based on BESIII measurements of the reaction








 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: