-
Axion-like particles (ALPs) are widely predicted in new physics beyond the standard model (BSM). A well known example is the Pseudo-Nambu-Goldstone boson (PNGB) from new global symmetry breaking, which was designed to solve the strong CP problem [1, 2]. The ALP has received considerable attention in the particle physics and cosmology communities because it can solve the naturalness problems [3, 4] and may be a compelling dark matter candidate for the universe [5–7]. The landscape of ALPs is rich, and the phenomenology is determined by their mass and couplings with SM particles. In general, ALPs may couple to gauge bosons, fermions, and Higgs bosons (see Refs. [8–13] for a general discussion). Many dedicated experiments have been proposed to search for ALPs based on their mass region and couplings. For example, the interactions between ALPs and fermions can be probed in rare decays [10, 14–21]. The bound of couplings to gauge bosons could be constrained by astrophysics and cosmology observations, for example, stellar evolution, big bang nucleosynthesis, and anisotropies in the cosmic microwave background for a light ALP [22–25], and by collider searches for heavy ALPs with light-by-light or vector-boson fusion type scattering [26–49].
In this study, we consider the case in which the ALP a predominantly couples to photons, so that the branching ratio
$ {\rm BR}(a\to \gamma\gamma)=1 $ and the effective Lagrangian can be parameterized as$ \mathcal{L}_{\rm eff}=\frac{1}{2}\left(\partial_\mu a\right)^2-\frac{1}{2}m_a^2a^2-g_{a\gamma\gamma}aF_{\mu\nu}\widetilde{F}^{\mu\nu}, $

(1) where a is the ALP with mass
$ m_a $ , and$ (\widetilde{F}_{\mu\nu}) \; F_{\mu\nu} $ is the (dual) field strength tensor of the photon. The coupling strength$ g_{a\gamma\gamma} $ has been seriously constrained by electron/ proton beam-dump experiments [50, 51],$ e^+e^-\to \gamma $ +invisible [30], inclusive$ e^+e^-\to \gamma\gamma $ [26], a photon-beam experiment [52], and$ e^+e^-\to \gamma a (\to \gamma\gamma) $ at Belle II [33] with a mass range from MeV to 10 GeV. Above 10 GeV, the parameter space can be probed by light-by-light scattering in heavy-ion collisions at the Large Hadron Collider (LHC) energy [31, 49],$ e^+e^-\to \gamma a (\to \gamma\gamma) $ at the LEP [27], and measurements at the LHC [39–43, 48] and future lepton colliders [44–47]. However, the bound from GeV to tens of GeV is less limited by current experiments compared to the MeV (or smaller) mass range. Such light ALPs are desirable for the community because it could be a natural product of new global symmetry breaking if it is a PNGB. In this paper, we propose to search for ALPs via photon fusion production at the upcoming Electron-Ion Collider (EIC) (see Fig. 1)①, which could be complementary to measurements at the LHC, and heavy-ion collisions at the LHC energy and lepton colliders when probing the ALP in this mass range. -
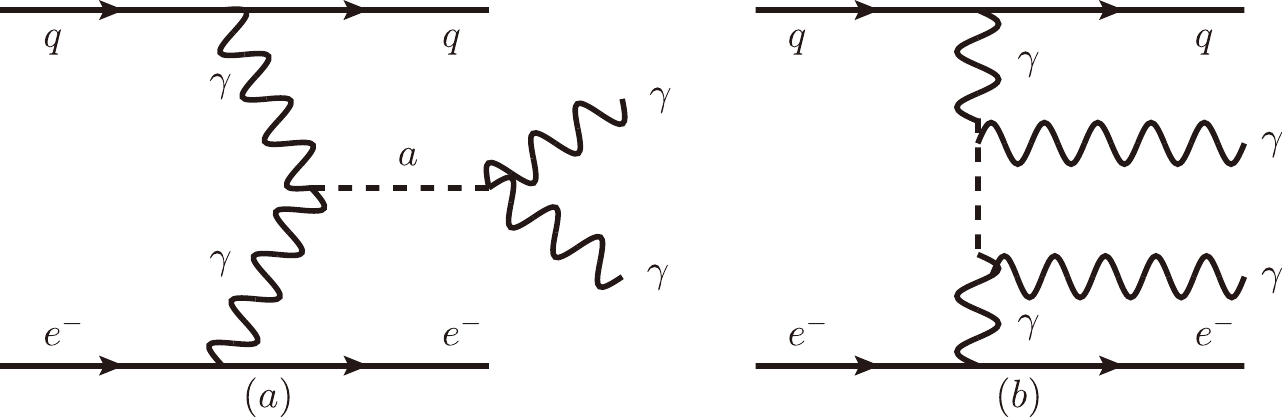
The ALP may be produced through s-channel and t-channel photon fusion scattering at the EIC② (see Fig. 1). The production rate of the signal depends on the coupling strength
$ g_{a\gamma\gamma} $ , ALP mass$ m_a $ , and branching ratio$ {\rm BR}(a\to\gamma\gamma) $ , that is,$ \begin{aligned}[b] \sigma(e^-p\to e^-\gamma\gamma j)=g_{a\gamma\gamma}^2\sigma_s(m_a)\times {\rm BR}(a\to\gamma\gamma)+g_{a\gamma\gamma}^4\sigma_t(m_a), \end{aligned} $

(2) where
$ \sigma_{s,t} $ denotes the cross section from the s-channel and t-channel, respectively. The narrow width approximation is applied for s-channel scattering because the decay width$ \Gamma_a\ll m_a $ [54]. We check that the interference effects between the signal and background is negligible and can be ignored in our analysis. For simplicity, we take the branching ratio$ {\rm BR}(a\to\gamma\gamma)=1 $ in this study.Below, we utilize MadGraph5 [55] to calculate the signal cross section with electron and proton energies of
$ E_e=20\; {\rm GeV} $ and$ E_p=250\; {\rm GeV} $ , respectively, at the leading order with NNPDF sets [56]. The factorization and renormalization scales in our calculation are chosen as the default scale in MadGraph5, that is, the transverse mass. To avoid the soft and collinear divergence, the following kinematic cuts for the final states are applied:$ \begin{aligned}[b] &p_T^{j,e,\gamma} > 5\; \mathrm{GeV},\; |\eta^{j,e,\gamma}|<5, \\ &\Delta R(e,j)>0.4,\; \Delta R(\gamma,\gamma)>0.4, \\ &\Delta R(e,\gamma)>0.4, \; \Delta R(j,\gamma)>0.4, \end{aligned} $

(3) where
$ p_T^m $ and$ \eta^m $ with$ m=j,e,\gamma $ denote the transverse momentum and pseudorapidity of particle m, respectively. The cone distance$\Delta R(m,n)= $ $ \sqrt{(\eta^m-\eta^n)^2+(\phi^m-\phi^n)^2}$ , where$ \phi^m $ denotes the azimuthal angle of particle m. Figure 2 shows the production rates for the processes$ e^-p\to e^- \gamma\gamma j $ (red dashed line),$ e^-p\to e^-a(\to\gamma\gamma)j $ (blue dashed line), and$ e^-p\to e^-aj $ (green dashed line) without any kinematic cuts for the photons in the final state. It clearly shows that the cross section of the signal is dominantly determined by s-channel scattering and the contribution from the t-channel is negligible because of the suppression of the phase space. In addition, the narrow width approximation for s-channel production works well in this process. In the same figure, the solid cyan and black lines represent the cross sections from$ e^-p\to e^- \gamma\gamma j $ and$e^-p\to e^-a(\to\gamma\gamma)j$ , respectively, after we impose the kinematic cuts in Eq. (3) for the photons. Note that the kinematic cuts of the photons decrease the cross section significantly when the ALP mass$ m_a<40\; {\rm GeV} $ . This arises because the invariant mass of a photon pair from an on-shell ALP decay is given by$m_a^2=m_{\gamma\gamma}^2\simeq p_T^{\gamma 1}p_T^{\gamma 2}\Delta R(\gamma 1,\gamma 2)$ , where$ p_T^{\gamma 1,\gamma 2} $ denotes the transverse momentum of the photons. For a heavy ALP, the kinematic cuts could be satisfied automatically, whereas there is a phase space suppression effect for light ALPs, which is induced by the kinematic cuts of the photons (see Eq. (3)). Such an effect also generates a peak at approximatelt$ m_a\sim 16 \; {\rm GeV} $ for the production rate distributions of the processes with the cuts on the photons (see the cyan and black lines).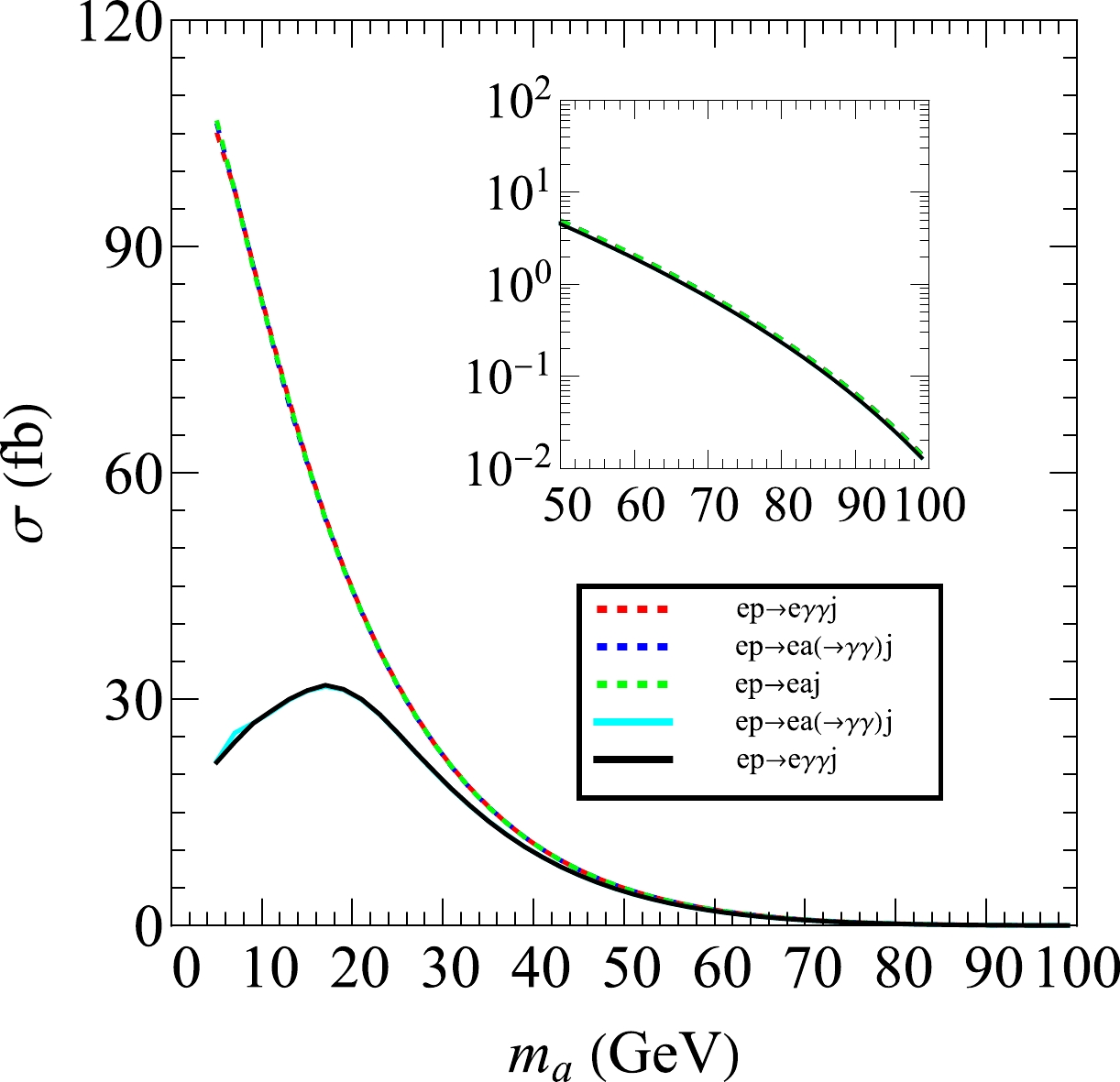
Figure 2. (color online) Cross section of the signal process
$ e^-p\rightarrow e^- \gamma \gamma j $ as a function of the ALP mass with the coupling strength$ g_{a\gamma\gamma}=1\; {\rm TeV}^{-1} $ . The solid and dashed lines correspond to the production rate with and without the kinematic cuts (see Eq. (3)) for the photons in the final states, respectively. We consider both the s-channel and t-channel for the red line, whereas only the contribution from the s-channel is considered for the green and blue lines. -
Next, we perform a detailed Monte Carlo simulation to explore the potential of probing the ALP at the EIC. The main irreducible backgrounds arise from the processes
$ e^-p\to e^- \gamma \gamma j $ and$ e^-p\to e^- \gamma \gamma jj $ . The cross sections after including the kinematic cuts in Eq. (3) are$ \sigma(e^-p\to e^- \gamma \gamma j)=46.9\; {\rm fb} $ and$ \sigma(e^-p\to e^- \gamma \gamma jj)=6.4\; {\rm fb} $ . We also take into account the possibility that an electron or jet is misidentified as a photon in this study. The reducible backgrounds may originate from the processes$ e^-p\to e^-\gamma j \; (18.66\; {\rm pb}) $ and$ e^-p\to e^-\gamma jj \; (2.22\; {\rm pb}) $ . The numbers shown inside the brackets denote the production cross section after imposing the cuts in Eq. (3). The other backgrounds involving multi-electrons and jets, for example,$ e^-p\to e^- e^- e^+ j $ and$ e^-p\to e^-jj(j) $ , are negligible when we consider the basic cuts in Eq. (3) and mistag efficiencies. We generate both the signal and backgrounds using MadGraph5 [55] with the kinematic cuts in Eq. (3). Parton level events are passed to PYTHIA8 [57] for parton showering and hadronization, and the detector effects are simulated by Delphes [58]. In the detector simulation, we use the EIC delphes card, which was generated by Arratia and Sekula [59], based on the parameters in Ref. [60] and utilized in Ref. [61–63]. The detector parameters in Ref. [60] dictate the tracking momentum resolution, secondary-vertex resolutions, calorimeter energy resolutions, and particle identification performance at the EIC. Among them, the photon energy resolution plays a key role in our simulation, which is$ \delta E/E=\mathcal{A}/E/{\rm{GeV}}\oplus \mathcal{B}/\sqrt{E/{\rm{GeV}}}\oplus{\mathcal{C}} $ , with$ \mathcal{A}=1\% $ ,$\mathcal{B}=2.5\%$ , and$ \mathcal{C}=1\% $ . Now, we require the following set of preselection cuts on the reconstruction objects:$ \begin{aligned}[b]& n^\gamma \ge 2,\quad\quad |\eta^m|<3.0, \\& p_T^{m}>7 {\; \rm{GeV}},\quad \quad \Delta R(m,n)>0.4, \end{aligned} $

(4) where
$ m,n=\gamma,e,j $ denote the photon, electron, and jet from the detector reconstruction, respectively. Note that the kinematic threshold for the reconstruction objects at the EIC may be looser compared to that at the LHC owing to the significantly lower collider energy (see the cuts of HERA as a Ref. [64]).In the signal events, photons arise from the decay of the ALP and thus exhibit a peak at approximately
$ m_a $ in the invariant mass distribution. However, the photons of the backgrounds originate from the radiation of the electron and quark; thus, the peak position of the invariant mass distribution from the photon pair is determined by the transverse momentum of the photons; see Fig. 3 for the normalized invariant mass distributions of the photon pair from the signal and backgrounds. Because the typical decay width of the ALP is considerably smaller than the resolution of the di-photon invariant mass at the EIC [60], we further require the invariant mass of the first two leading photons within the mass window,
Figure 3. (color online) Normalized invariant mass distribution of the photon pair from the signal process
$ e^-p\rightarrow e^- \gamma \gamma j $ and the SM backgrounds$ e^-p\rightarrow e^- \gamma \gamma j $ ,$ e^-p\rightarrow e^- \gamma \gamma j j $ , and$ e^-p\rightarrow e^-\gamma j (j) $ after the preselection in Eq. (4).$ \begin{align} |m_{\gamma\gamma} -m_a |<5 \; \mathrm{GeV}. \end{align} $

(5) We also check that other kinematic observables (for example,
$ p_T^{e,j,\gamma} $ ) cannot significantly improve the cut efficiency in this process. This arises from the fact that both the signal and backgrounds share a similar topology to the Feynman diagram, and as a result, both should exhibit a similar$ p_T^{e,j} $ distribution. However, the photons share the energy from the ALP in the signal process; thus, the$ p_T^\gamma $ distribution should peak at$ \sim m_a/2 $ , whereas$ p_T^\gamma $ for the backgrounds tend to produce a soft spectrum because the cross sections are enhanced by the soft and/or collinear singularity in that phase space region. However,$ p_T^\gamma $ information may be correlated to$ m_{\gamma\gamma} $ ; therefore, the additional cut on$ p_T^\gamma $ cannot improve the sensitivity to probe the ALP. We show the cut efficiencies with several benchmark ALP masses after the kinematic cuts from Eqs. (4) and (5) in Table 1. The cut efficiencies of the reducible backgrounds ($ e\gamma j $ and$ e\gamma jj $ ) are smaller than those of the irreducible backgrounds ($ e\gamma\gamma j $ and$ e\gamma\gamma jj $ ). However, the reducible backgrounds would still be dominated after considering the production rates of these processes. Because the kinematic cuts in Eq. (4) may be satisfied automatically for a heavy ALP, the cut efficiency for the signal tends to be constant when$ m_a>40\; {\rm GeV} $ .$m_a /\mathrm{GeV}$ 

11 21 31 41 51 61 $ \epsilon(\text{signal}) $ 

0.394 0.542 0.712 0.746 0.703 0.742 $ \epsilon(e^-\gamma\gamma j) $ 

0.066 0.100 0.046 0.011 $1.1\times 10^{-3}$ 

$1.7\times10^{-4}$ 

$ \epsilon(e^-\gamma\gamma jj) $ 

0.070 0.098 0.033 0.005 $1.9\times10^{-4}$ 

$3.9\times10^{-5}$ 

$ \epsilon(e^-\gamma j) $ 

0.0004 0.0007 0.0005 0.0003 $ 0.0002 $ 

$ 0.0001 $ 

$ \epsilon(e^-\gamma j j) $ 

0.0003 0.0004 0.0003 0.0001 $6.6\times 10^{-5}$ 

$5.7\times 10^{-5}$ 

Table 1. Cut efficiencies for the signal process with the benchmark ALP mass
$ m_a $ and the corresponding SM backgrounds at the EIC.Equipped with the signal and background production cross sections and collider simulation efficiencies, the upper limit on the effective coupling
$ g_{a\gamma\gamma} $ at the$ 2\sigma $ confidence level can be obtained in terms of [65]$ \begin{align} \sqrt{-2\left[n_b \ln\left(\frac{n_s+n_b}{n_b}\right)-n_s\right]} =2, \end{align} $

(6) where
$ n_s $ and$ n_b $ are the numbers of signal and background events, respectively. Given the integrated luminosity of 300 fb$ ^{-1} $ , the upper limit on the effective coupling$ g_{a\gamma\gamma} $ is presented in Fig. 4 (orange region). It shows that$ g_{a\gamma\gamma} $ can be constrained to be$ \sim 0.2 $ TeV$ ^{-1} $ at the$ 2\sigma $ confidence level by assuming null results when directly searching for ALPs with$ m_a<40\; {\rm GeV} $ at the EIC. This result may be further improved if we consider the nucleus beam at the EIC because the cross section would be enhanced by the atomic weight$ A=Z+N $ , where Z and N are the number of protons and neutrons in nucleus, respectively [53]. To roughly estimate the upper limit on$ g_{a\gamma\gamma} $ from the nucleus beam, we use lead (Pb) as an example. The cross sections of the signal and backgrounds from the Pb beam could be obtained by properly rescaling the cross sections at electron-proton collisions, that is,$ \sigma_{e^-{\rm Pb}}\simeq A\sigma_{e^-{\rm P}} $ , with$ A=208 $ for the Pb beam③. Although the mixing of protons and neutrons in the nucleus will change the total density for up and down quarks in the nuclear PDFs relative to those of the proton, the total effects will mildly modify the total cross sections and kinematic distributions [66], which do not significantly alter the conclusions of this study. Under this approximation, we find that the effective coupling$ g_{a\gamma\gamma} $ from the Pb beam may be improved by several times compared to that of the proton beam; see the gray region of Fig. 4.
Figure 4. (color online) Upper limit on the effective coupling
$ g_{a\gamma\gamma} $ from the EIC with a proton beam (orange region) and Pb beam (gray region), light-by-light scattering with p-p collisions with a center-of-mass energy$ \sqrt{s}=13\; {\rm TeV} $ (pink region, projected sensitivity) and Pb-Pb collisions with$ \sqrt{s}=5.02\; {\rm TeV} $ (blue region), off Z-pole at the LEP (green region) and$ Z\to \gamma a $ (yellow region). The excluded regions from other colliders are extracted from Ref. [35]. -
As discussed in Sec. I, ALPs with masses of tens of GeV have been widely searched for by colliders. These searches include the measurements of tri-photons on and off the Z-pole
$ (e^+e^-\to 3\gamma) $ at the LEP [67, 68], searches for the same final states at the LHC [27], and light-by-light scattering in heavy-ion collisions at the LHC energy and pp collisions at the LHC [31, 41, 49]. However, the bounds of$ g_{a\gamma\gamma} $ from several of the above measurements depend on the assumption of the$ aZ\gamma $ interaction. This arises from the fact that both couplings may be generated from the dimension-5 operators$ g^{\prime 2}C_{BB}/\Lambda aB_{\mu\nu}\widetilde{B}^{\mu\nu} $ and$g^2C_{WW}/ \Lambda aW_{\mu\nu}^A\widetilde{W}^{A,\mu\nu}$ , where$ B_{\mu\nu} $ and$ W_{\mu\nu}^A $ are the field strength tensors of$ U(1)_Y $ and$ S U(2)_L $ , and$ g^\prime $ and g are the corresponding gauge couplings. The effective coupling strengths of$ a\gamma\gamma $ and$ aZ\gamma $ are$ g_{a\gamma\gamma}\sim C_{WW}+C_{BB} $ and$g_{aZ\gamma}\sim c_W^2C_{WW}- s_W^2C_{BB}$ , respectively. Therefore, the couplings$ g_{a\gamma\gamma} $ and$ g_{aZ\gamma} $ can be related to each other when considering one operator at a time.We compare the investigation of
$ g_{a\gamma\gamma} $ at the EIC with other measurements in Fig. 4. It is evident that the Z-pole measurement$ Z\to \gamma a $ (yellow region), compared with the other processes, yields the strongest constraint on the value of$ g_{a\gamma\gamma} $ . However, this conclusion is only available when we consider one operator in the analysis. We also notice that the expected limit from the EIC with a proton beam (orange region) may be stronger than the off Z-pole measurement (green region) at the LEP and light-by-light scattering at the LHC (pink region), whereas the expected limit from the Pb beam at the EIC (gray region) may be comparable to the measurement in Pb-Pb collisions (blue region). Finally, we emphasize that photon fusion production at the EIC is complementary to other processes in the measurement of ALP-photon coupling. -
The authors thank Xiaohui Liu and Hao Zhang for helpful discussions.
Searching for the axion-like particle at the EIC
- Received Date: 2022-11-11
- Available Online: 2023-04-15
Abstract: The axion-like particle (ALP) is a well motivated new particle candidate for beyond the standard model. In this study, we propose to probe the ALP via photon fusion scattering at the upcoming Electron-Ion Collider (EIC) with electron and proton energies of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: