Gravastar in the framework of symmetric teleparallel gravity

The Schwarzschild solution is the most intriguing universal spherically symmetric static vacuum solution to the Einstein field equations under the background of general relativity (GR). The line element for the Schwarzschild metric can be expressed as

where M represents the gravitational mass of the object. A black hole (BH) of isolated mass M, with the static spherically symmetric line element (1), is known as a Schwarzschild BH, and $ R_S=2GM $ is known as the Schwarzschild radius. BHs are generated when the core of a massive star collapses toward the termination of its lifespan and are the most fascinating objects in modern astrophysics. Despite being a successful theory, the Schwarzschild metric has two significant flaws:

1. The dynamical singularity at $ r=0,\, 2\,GM $.

2. The presence of event horizon.

To resolve the aforementioned issues with BHs, Mazur and Mottola [1, 2] proposed a new solution that has no singularity and no event horizon, i.e., an ingenious idea of an extremely compact object referred to as the Gravitationally Vacuum Condense Star or simply Gravastar. By applying the concept of Bose-Einstein condensation (BEC) to gravitational systems (i.e., a limited portion of the total number of particles starts to condense into the lowest-energy state below a certain temperature), they proposed a novel theory to explain the endpoint of gravitational collapse of a dying star's core. They create a cold, compact entity with an interior de Sitter condensate phase and an external Schwarzschild geometry of any total mass M, which is removed from all the restrictions of the known classical black hole (CBH). As a result, this theory may be considered as a replacement concept for the CBH and has become a hot topic among researchers.

According to Mazur and Mottola's model, the gravastar contains three distinct regions with different equations of states (EoSs).

1. An inner area with an isotropic de Sitter vacuum situation.

2. A thin shell of an ultra-relativistic rigid fluid substance between the interior and exterior regions.

3. The exterior region is entirely vacuum, and Schwarzschild geometry describes this situation correctly.

Consequently, the following EoSs for different matters in these three regions can be used to define the complete gravastar system:

There are two interfaces (junctions) at distances $ r_1 $ and $ r_2 $ from the center. Here, $ r_1 $ and $ r_2 $ denote the interior and exterior radii, respectively, of the thin shell. To achieve the necessary stability of the system, which is assumed to be expanding by applying an inward force to balance the repulsion from within, the stiff matter must exist on the shell of thickness $ r_1-r_2= \epsilon \ll 1 $.

Although there are a few indirect pieces of evidence in the literature that indicate the existence of gravastars and can be used for future confirmation, there is presently no observable evidence in favor of gravastars. Through the investigation of gravastar shadows, Sakai et al. [3] established a method to identify gravastars. As suggested by Kubo and Sakai [4], who asserted that black holes do not exhibit microlensing effects of maximal brightness, gravitational lensing is another method that might be used to find gravastars. The observation of GW150914 by interferometric LIGO detectors [5, 6] suggested the existence of ringdown signals produced by sources without an event horizon. A gravastar-like shadow was observed in a recent examination of a picture taken by the First M87 Event Horizon Telescope (EHT) [7].

There are several literary works on gravastars that are based on various mathematical and scientific problems. However, the majority of these works are within the context of general relativity. There has been considerable work done on gravastars since Mazur and Mottola's idea. They demonstrated thermodynamic stability in their five-layer gravastar structure. The five-layer Mazur-Mottola model was simplified to three layers by Visser and Wiltshire [8], who also demonstrated its dynamical stability in the face of perturbations due to spherically symmetric matter distributions or gravity fields. By examining relevant constraints for the stability of precise non-singular solutions of gravastars, Carter [9] expanded on this work.

To investigate the gravastar's interior, Bilic et al. [10] replaced the de Sitter interior with a Chaplygin gas equation of state and regarded the system as a Born-Infeld phantom gravastar, whereas Lobo [11] substituted the interior vacuum with dark energy. To overcome the singularity issue, Lobo and Arellano [12] linked the Schwarzschild outside with the internal nonlinear electrodynamic geometries. Anisotropic pressure in the "crust," which is essential for the development of structures like gravastars, was hypothesized by Cattoen et al. [13]. According to Ghosh et al. ([14]), it is impossible to extend a 4-dimensional gravastar to higher dimensions. Additionally, they used the non-singular Kuchowicz metric potential to study several aspects of a gravastar [15]. Rahaman et al. [16] built a gravastar model within the GR framework in (2+1) dimensions. Usmani et al. [17] suggested a gravastar model with a charged interior that allowed conformal motion and whose outer spacetime was defined by the Reissner-Nordström line element. Although Einstein's general relativity is one of the pillars of contemporary theoretical physics and has consistently been successful in revealing a large number of nature's hidden secrets, it has drawbacks from both theoretical and observational standpoints. Theoretically, this idea has been challenged by observational evidence of the universe's accelerated expansion and the existence of dark matter. As a result, numerous different theories of gravity, including $ f(R) $ gravity, $ f(T) $ gravity, $ f(R,T) $, and $ f(Q) $ gravity, have been proposed. All of these hypotheses can be regarded as essential for explaining the structure development and star system evolution in the universe.

Apart from the work on Einstein's GR, there are several works on gravastars that involve modified theories of gravity. Within the context of energy-momentum squared gravity, Sharif et al. [18] explored the impact of the charge on the physical characteristics of gravastars and concluded that the non-singular solutions of the charged gravastar are physically feasible in $ f(R, T^2) $ gravity. Das et al. [19] have identified a collection of precise and singularity-free solutions to the gravastar that exhibits a number of physically significant as well as acceptable characteristics in $ f(T) $ gravity. Sahoo and his group [20] investigated isotropic static spherically symmetric gravastars without charge in the Mazur-Motolla junction under the assumption of braneworld gravity. In particular, the length of the shell, entropy, and energy were studied as more realistic aspects of the gravastar model by Bhatti and his group [21] in $ f(R,G) $ gravity. $ f(R) $ gravity was first introduced in [22], and it is specifically represented by the arbitrary function of the Ricci scalar curvature R. However, there is another approach to explain gravitational interactions, which involve torsion (T) and non-metricity (Q) and are known as the $ f(T) $ and $ f(Q) $ theories of gravity, respectively. Weitzenböck and metric incompatible connections that are different from the GR Levi-Cevita connection are two examples of non-standard metric-affine connections that may be used to acquire both gravities. In this study, we focus on the modified symmetric teleparallel gravitational scenario (also known as $ f (Q) $ gravity) to study the non-charged gravastar. There have been numerous works on compact objects in the background of $ f(Q) $ gravity. Mandal et al. [23] studied the anisotropic compact stars in $ f(Q) $ gravity with the quintessence field. In [24], researchers examined the physical behavior of strange stars using the MIT Bag EoS, accepting the Buchdahl metric for both linear and non-linear models.

Our research may be viewed as a singular study because we examined a more generic isotropic model of uncharged gravastars and investigated the effects of non-metricity on both the interior and exterior solutions of the gravitating system in $ f(Q) $ gravity. We developed a set of advanced solutions for the three distinct areas with their respective EoSs in the present study, which was inspired by the aforementioned publications. We analyzed the surface redshift and the junction requirement for the creation of a thin shell to demonstrate the stability of our concept. We investigated the physical features of gravastars while taking into consideration the three-layer model under the Kuchowicz metric potential, in contrast to Visser and Wiltshire [8], who simply reduced Mazur and Mottola's five-layer construction to three layers to investigate the dynamical stability of gravastars.

In this study, we examined a few physical aspects of gravastars according to the $ f(Q) $ theory of gravity and discovered analytical results for various phases of the structure. The paper is organized as follows:

In Sec. I, we introduce the gravastar model and present the relevant work. In Sec. II, we discuss the mathematical formalism of$ f(Q) $ gravity and calculate the field equation in $ f(Q) $ gravity for the spherically symmetric metric. Three areas of the gravastar structure, i.e., the internal region, the thin shell, and the external region, are examined separately in Sec. III. In Sec. IV, we study the physical features of the thin shell to examine the stability of the model. The junction condition is investigated (along with the EoS) in Sec. V. Finally, we present conclusions regarding the stability of our model in Sec. VI.

For the purposes of STEGR, we assume that the gravastar under consideration exists on the differentiable Lorentzian manifold $ \mathcal{M} $, which may be adequately characterized by the metric tensor $ g_{\mu\nu} $, its determinant g, and its affine connection Γ:

where $ \Gamma^\alpha_{\,\,\,\,\beta} $ is the connection one form, which may be represented in terms of the one forms of the contortion tensor, disformation, and connection of Levi-Civita [25]:

The aforementioned expression can be represented as follows:

where the variables γ, K, and L in Eq. (4) are the affine connection that is consistent with the Levi-Cevita metric, contortion, and disformation tensors, respectively. Assuming $ f(Q) $ gravity formalism, the symmetric teleparallelism that results from the non-metricity one form and associated tensor completely describes the gravitational sector:

where the symmetric portion of the tensor has the following definition:

If contortion disappears, the only terms remaining will be disformation tensor terms:

The following formula defines the disformation tensor:

The non-metricity scalar, which is made up of non-metricity and the so-called superpotential, is the primary gravitational quantity in the STEGR formalism:

where the following complicated form describes the superpotential:

Here, $ Q^{\alpha}=Q^\nu_{\,\,\,\,\alpha\nu} $ and $ \overline{Q}_\alpha=Q^\mu_{\,\,\,\,\alpha\mu} $ are two independent traces of the non-metricity tensor $ Q_{\alpha\mu\nu}=\nabla_\alpha g_{\mu\nu} $. As we have covered all the terms required by the STEGR formalism, we proceed to provide the modified action integral for $ f(Q) $ gravity [26]:

In this case, $ \mathcal{S}_{\mathrm{M}}[g,\Gamma,\Psi_i] $ represents the action integral, which signifies the contribution of an extra matter field $ \Psi_i $ that is both minimally and maximally linked to gravity to the overall Einstein-Hilbert action integral. The abstract field equations for the theory may be obtained by varying Eq. (11) with regard to the metric tensor inverse $ g^{\mu\nu} $:

where $f_Q\equiv\dfrac{{\rm d}f}{{\rm d}Q}$ and the widely used energy momentum tensor $ T_{\mu\nu} $, whose generic form might be represented as:

Here, the Lagrangian density of matter fields is represented by the symbol $ \mathcal{L}_{\mathrm{M}} $ satisfying the relationship $\int {\rm d}^4x \sqrt{-g} \mathcal{L}_{\mathrm{M}}=\mathcal{S}_{\mathrm{M}}[g,\Gamma,\Psi_i]$. Additionally, by changing the action in relation to the affine connection $ \Gamma^\alpha_{\,\,\,\,\mu\nu} $, we obtain

In the next subsection, for spherically symmetric objects, we derive the precise form of field Eqs. (12) and (14) written above.

Within $ f(Q) $ gravity, the field equation or motion equation for a spherically symmetric object takes the following form:

where the line element for the spherically symmetric metric is defined as

As a result, the usual energy-momentum tensor for a perfect fluid matter distribution can be written as follows:

Applying the values of the energy-momentum tensor components to the aforesaid field equations yields the following result:

Therefore, the mathematical form of the non-metricity scalar is

By carefully determining the metric potential ${\rm e}^{\lambda}$ with the use of the field Eqs. (20)–(22), we have explored three distinct regions of the gravastar. In order to determine the metric potential ${\rm e}^{\lambda}$, we have taken the physically feasible, singularity-free metric potential, specifically the Kuchowicz metric potential of the form [27]

to evaluate a compact spherically symmetric astronomical object such as a gravastar accurately. Here, B and C are arbitrary constants. C is a dimensionless parameter, and B is of dimension [$ L^{-2} $]. Using the aforementioned condition (24), we simplified the field Eqs. (20)–(22) for the linear model $ f(Q)=a Q + b $, where a and b are the model parameters. The simplified forms are as follows:

Finally, in $ f(Q) $ gravity, the energy conservation equation for a line element in the (3+1) dimension can be written as

It is clear from the aforementioned equation that the gravitational force must balance out the hydrostatic force or pressure gradient for a gravitating system to be in equilibrium.

We presumed the EoS for the interior area as stated in Mazur and Mottola's work [1, 2]:

This EoS is referred to as the dark energy EoS [28–30] with the parametric value $ \omega=-1 $. The inward gravitational attraction of the shell is balanced by this negative (repulsive) pressure acting radially outward from the center of the spherically symmetric gravitating system. From Eqs. (28) and (29), we obtain

where $ \rho_c $ represents the critical density of the gravastar. With the help of (30), we obtain the metric potential ${\rm e}^{-\lambda}$ from Eq. (25) as

To obtain the regular solution at the center, we can take $ c_1=0 $. Thus,

For making our solution free from central singularity, we have taken $ \dfrac{r^2}{6a }(b-16 \pi \rho_c)\neq -1 $. Thus we get two non-singular space-time metrics for describing the internal structure of the gravastar system. Also, the following equation can be used to determine the active gravitational mass of the internal area,

where $ R_1 $ represents the boundary of the interior region, which is set as R, and r is the radial coordinate.

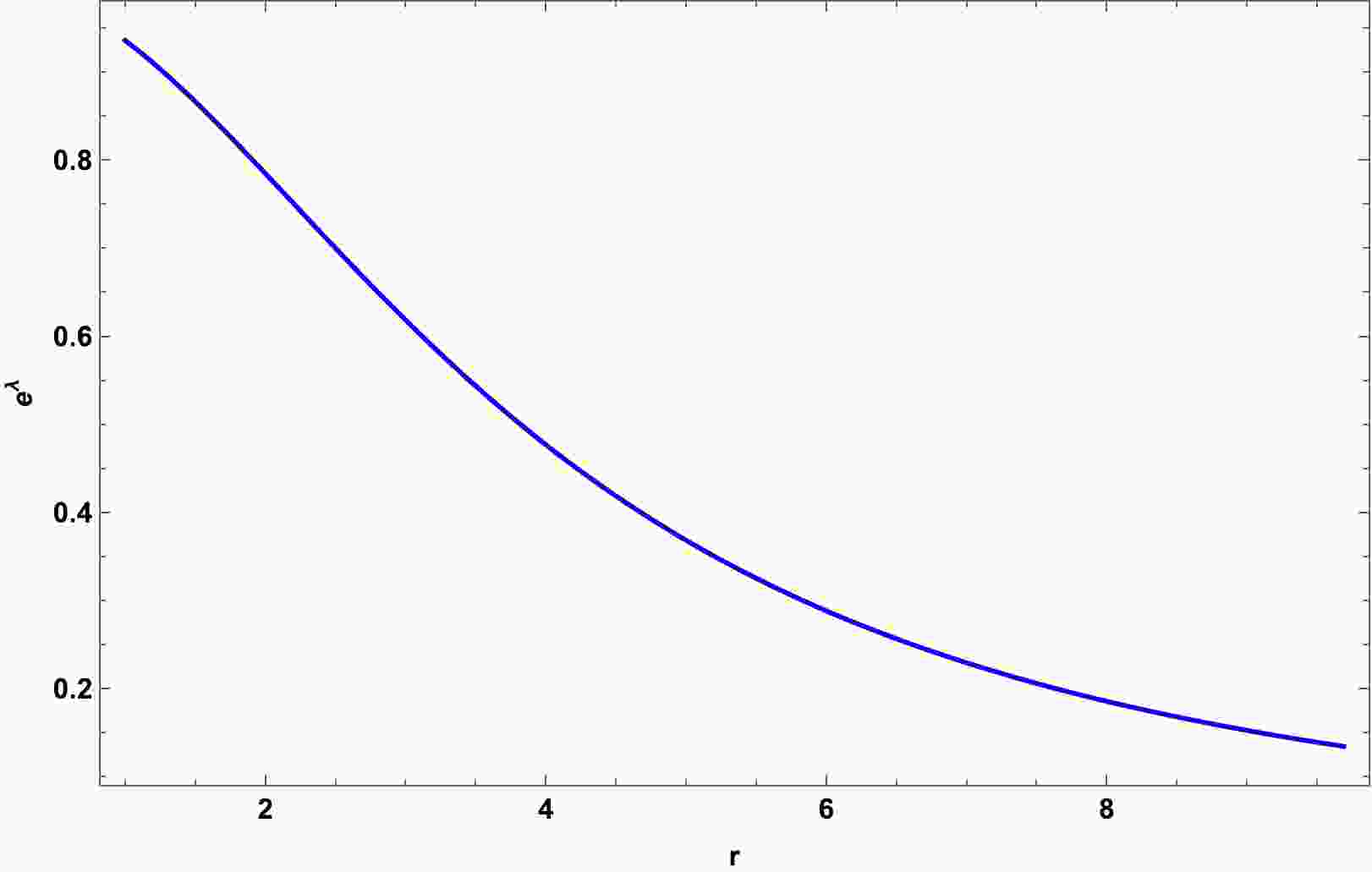
The evolution of the space-time metric ${\rm e}^{\lambda}$ with respect to the radial parameter r is shown in Fig. 1. From the figure, we can physically interpret that the metric potential remains positive throughout the region, and it is regular at $ r=0 $; additionally, it is finite and has no central singularity.

Figure 1.  (color online) Graphical analysis of the metric potential within the interior region with the radial coordinate r(km) for $ a=1.7 $and $ b=0.7 $.

The shell is made of ultrarelativistic fluid, and it abides by the EoS

Zel'dovich [31] originally came up with the concept of this form of fluid in relation to the cold baryonic cosmos, which is also known as the stiff fluid. By equating the isotropic pressure and matter density of the gravastar, we obtain the space-time metric ${\rm e}^{\lambda}$ for the shell region:

The boundary condition can be used to determine the value of integrating constants $ C_1 $.

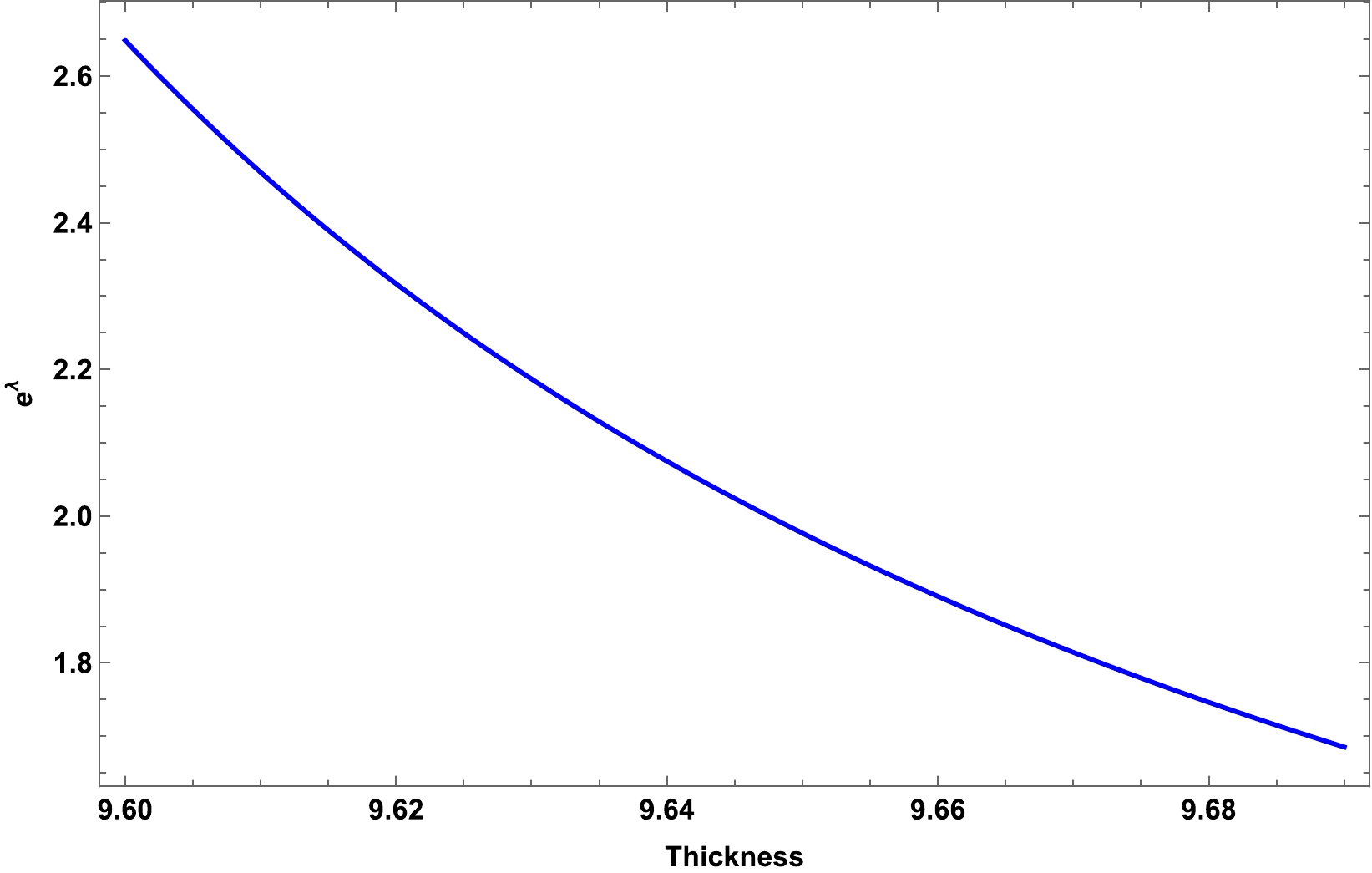
The variation of the metric potential ${\rm e}^{\lambda}$ for the shell region is shown in Fig. 2. From the figure, we can say that the space-time metric within the shell region exhibits the same behavior as the interior region, which establishes a positive behavior in our solution.

Figure 2.  (color online) Graphical analysis of the metric potential within the shell with respect to its thickness ($ \epsilon $ in km) for $ a=1.7 $ and $ b=0.7 $.

It is believed that the gravastar's exterior is fully vacuum outside of the shell and follows the EoS $ p=\rho=0 $ rule. Therefore, the Schwarzschild metric

describes the outside geometry of the gravastar correctly. For the vacuum EoS, we have determined the metric potential ${\rm e}^{\lambda}$ as

Finally, we have three space-time metrics (32), (35), (37) for three different regions.

In order to determine the values of the three constants $ B,\, C,\, C_1 $, we equate our determined metric potential ${\rm e}^{\lambda}$ at the boundaries. There are two limits in the gravastar configuration: one is between the interior and intermediate thin shell at a distance $ R_1 $from the center, and the other is between the shell and outer space at a distance $ R_2 $ from the center. The metric functions at these interfaces must be continuous for any stable system. Therefore, we matched these metric potentials with outer space-time. Finally, we obtain the following form for these constants:

Here, we have taken the PSR J1416-2230 compact star with total mass $ M=1.97 M_{\odot} $and outer radius $ R_2=9.69 $ km. Thus, the ratio $ \dfrac{2M}{R}<1 $ holds for the gravastar configuration. Additionally, we have taken the value of the critical density as $ \rho_c=0.0001 $ and $ \rho_0=1 $. Putting the values of the above quantity along with the model parameter $ a=1.7 $ and $ b=0.7 $, we obtained the numerical values of the constants as follows: $B=0.17301 \;\text{km}^{-2}$, $C_1= 7.3465\times10^9$, $C^2= 1.80065\times 10^{-8}$. The reason why we choose these model parameters is the nature of the constants B and $ C^2 $. Here, the constant B is of dimension $ l^{-2} $; thus, it should take a positive value. Furthermore, the term $ C^2 $ is positive. Thus, for making the positive numerical values of these constants, we have taken such specific values of the model parameters. We have verified that for the aforementioned condition, the model shows similar behavior for different values of a and b. In order to determine the feasibility of our gravastar model, we will verify it through some physical features of the shell region in the next section.

One of the leading indicators of a spherically symmetric object's physical qualities is the variation of the density with respect to radial coordinates. For the shell region using the EoS $ p=\rho $ from Eq. (28), one can easily obtain

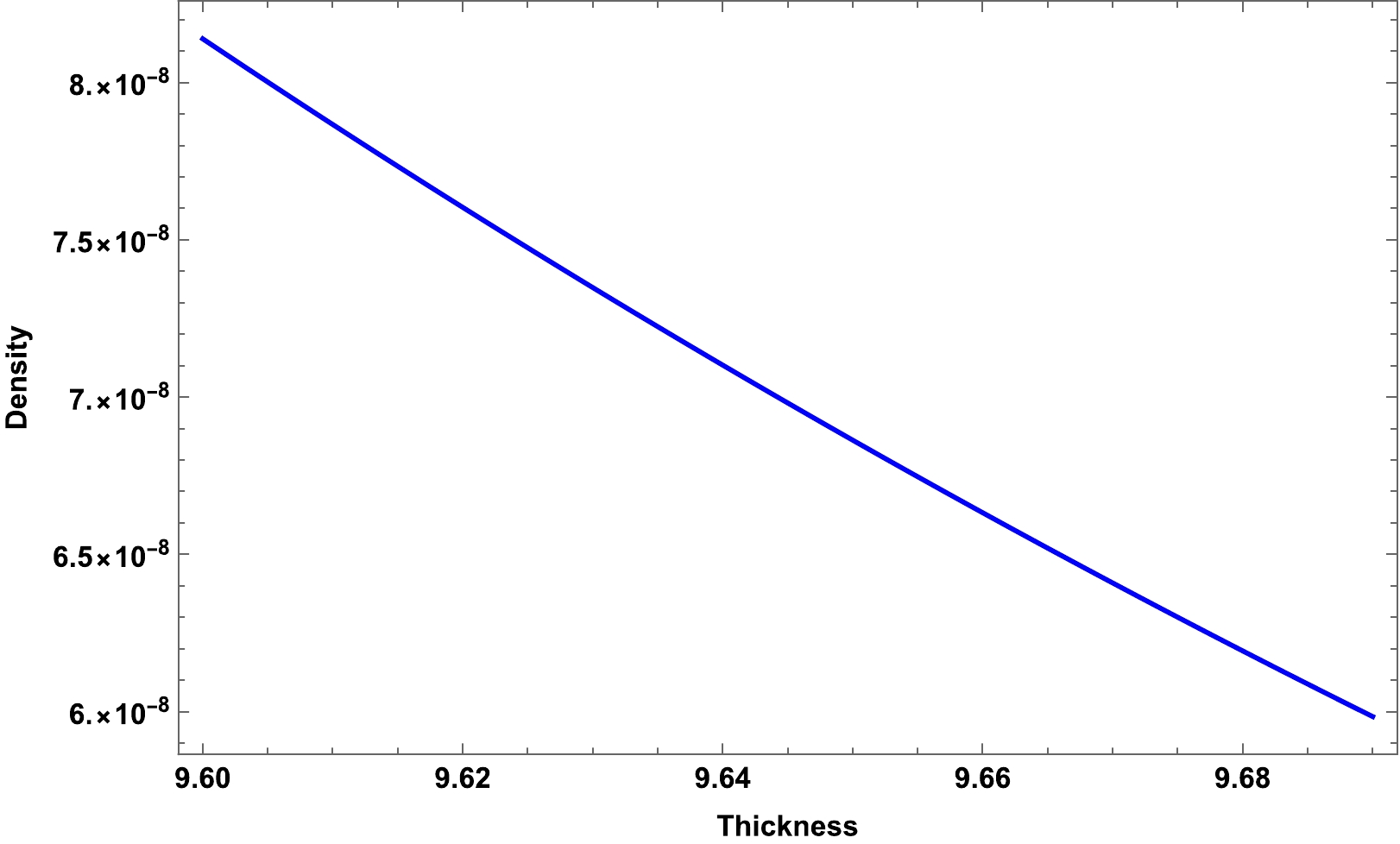
The evolution of the density with respect to the thickness of the shell is shown in Fig. 3. One can see from Fig. 3 that both the pressure and matter density remain positive throughout the shell's range and rapidly decrease with an increase in the thickness.

Figure 3.  (color online) Graphical analysis of the pressure or matter density of the shell with respect to its thickness ($ \epsilon $ in km) for $ a=1.7 $ and $ b=0.7 $.

In accordance with the hypothesis proposed by Mazur and Mottola [1, 2], the phase boundary of the interior area is defined by the stiff fluid shell at $ r=R $, and its proper thickness $ \epsilon $ is considered to be extremely small, i.e., $ \epsilon \ll 1 $. Consequently, the lower limit of the outer region has been taken as $ r=R+\epsilon $. The proper thickness / proper length between two interfaces or that of the shell can be written as

The above expression is very difficult to integrate analytically. Let us assume $ f(r) $ as the primitive of $\sqrt{{\rm e}^{\lambda}}$. Then, by the fundamental theorem of calculus, we have

We used Taylor series expansion to calculate the thickness of the thin shell and confined our calculations to the first-order term of the thickness parameter $ \epsilon $. Finally, we determined the precise thickness of the thin shell as

We numerically plotted the proper length variations with respect to the thickness parameter $ \epsilon $, as shown in Fig. 4. It is observed that as the thickness increases, the proper length of the shell steadily decreases.

Figure 4.  (color online) Graphical analysis of the proper length of the shell with respect to its thickness ($ \epsilon $ in km) for $ a=1.7 $ and $ b=0.7 $.

One may argue that this implies a negative energy area in the inner region when we consider the EoS, i.e., $ p=-\rho $, proving the core's repulsive character. However, it can be determined that the energy contained in the shell is

From Fig. 5, it is discovered that the energy variation for the shell is positive and monotonically increases toward the outer surface. This implies that the shell's outer boundary is denser than its internal limit, which satisfies the condition that the shell's energy increases as the radial distance increases.

Figure 5.  (color online) Graphical analysis of the surface energy of the shell with respect to its thickness ($ \epsilon $ in km) for $ a=1.7 $ and $ b=0.7 $.

The interior of the gravastar must have zero entropy density, which is stable for the single condensate area, according to Mazur and Mottola [1, 2]. The entropy on the shell, however, is typically not zero. The following formula can be used to easily compute the entropy of the relativistic star system (static) gravastar:

where $ s(r)=\alpha \sqrt{p/{2\pi}} $ represents the entropy density, and α is a dimensionless parameter. By applying the same technique once again using the Taylor series approximation up to the first order term of$ \epsilon $, such as determining the proper length, we determined the entropy of the shell as

The variation of the shell entropy is shown in Fig. 6. It is noted that the entropy of the shell decreases as its thickness increases in $ f(Q) $ gravity. This behavior, however, does not suggest that our solution is unstable.

Figure 6.  (color online) Graphical analysis of the entropy of the shell with respect to its thickness ($ \epsilon $ in km) for $ a=1.7 $ and $ b=0.7 $.

One of the most crucial sources of understanding about a gravastar's stability and discovery is the study of its surface redshift. The surface redshift must not exceed 2 for the isotropic compact star fluid (it must not exceed 5 for spacetimes with the current cosmic constant). We employed the following equation to determine the surface redshift:

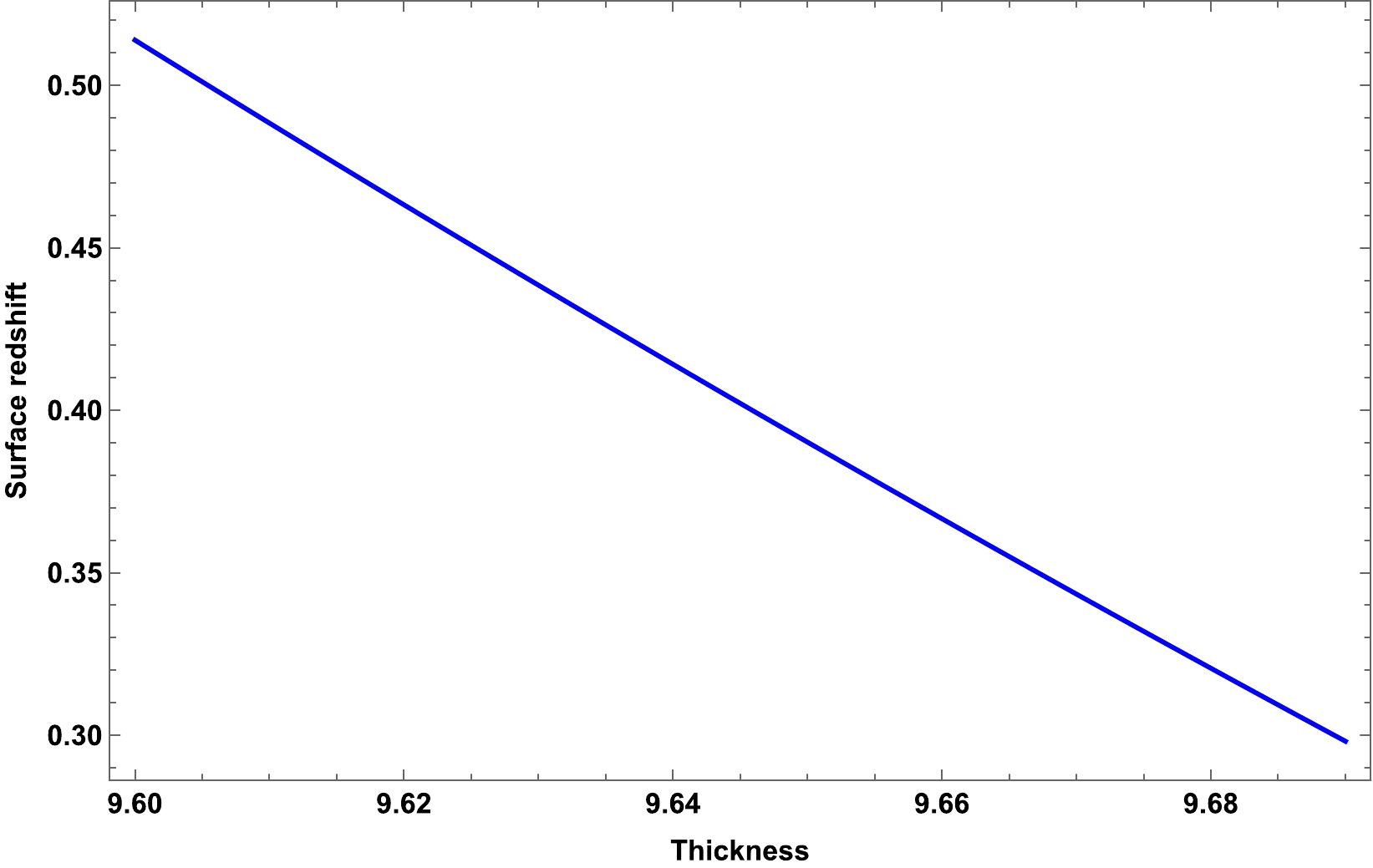
Consequently, we solve Eq. (52) numerically as usual and display the result in Fig. 7 for PSR J1416-2230. As shown, the surface redshift is positive for positive values of a and b and $Z_s < 1$. Therefore, it can be said that our current research on gravastars is both steady and physically acceptable.

Figure 7.  (color online) Graphical analysis of the surface redshift of the shell with respect to its thickness ($ \epsilon $ in km) for $ a=1.7 $ and $ b=0.7 $.

The three regions that gravastars are known to possess are the interior region, exterior area, and shell. This shell serves as a junction between the inside and exterior space. Consequently, it is highly important to the gravastar arrangement. According to the basic junction condition, there must be seamless matching between regions I and III at the junction. According to the work of Darmois-Israel [32, 33], metric coefficients are continuous at the junction surface, but it is possible that the derivatives of these metric coefficients are not. Thus, the following definition can be used to express the stress-energy surface tensor at the junction:

where $ k_{\alpha \beta}=K^{+}_{\alpha \beta}-K^{-}_{\alpha \beta} $. The second elemental form is provided by a thin shell with two sides given by

where $ \phi^{\alpha} $ denotes the intrinsic co-ordinate on the shell. For two-sided unit normals to surface, $ n^{\pm} $ is expressed as

with $ n^{\gamma} n_{\gamma} =1 $. By applying the Lanczos method [34] the surface energy tensor can be found as $ S_{\alpha \beta}=diag(-\sum, P) $, where the surface energy density and surface pressure are denoted as $ \sum $ and P, respectively, and are defined as follows:

Here, f is the metric potential term ${\rm e}^{\lambda}$. Equations (56) and (57) take the following form in our calculations:

Additionally, the EoS parameter ω takes the form

This implies

It is noted that, for the real value of the EoS parameter ω, $ \dfrac{2M}{R}<1 $ and $ \dfrac{R^2(b -16 \pi \rho_c)}{6a} \neq -1 $, similar to our previous condition regarding the solution in Eq. (32) for the interior region. A graphical analysis of the surface energy density is presented in Fig. 8. It shows positive behavior and increases monotonically with an increase in the thickness $ \epsilon $.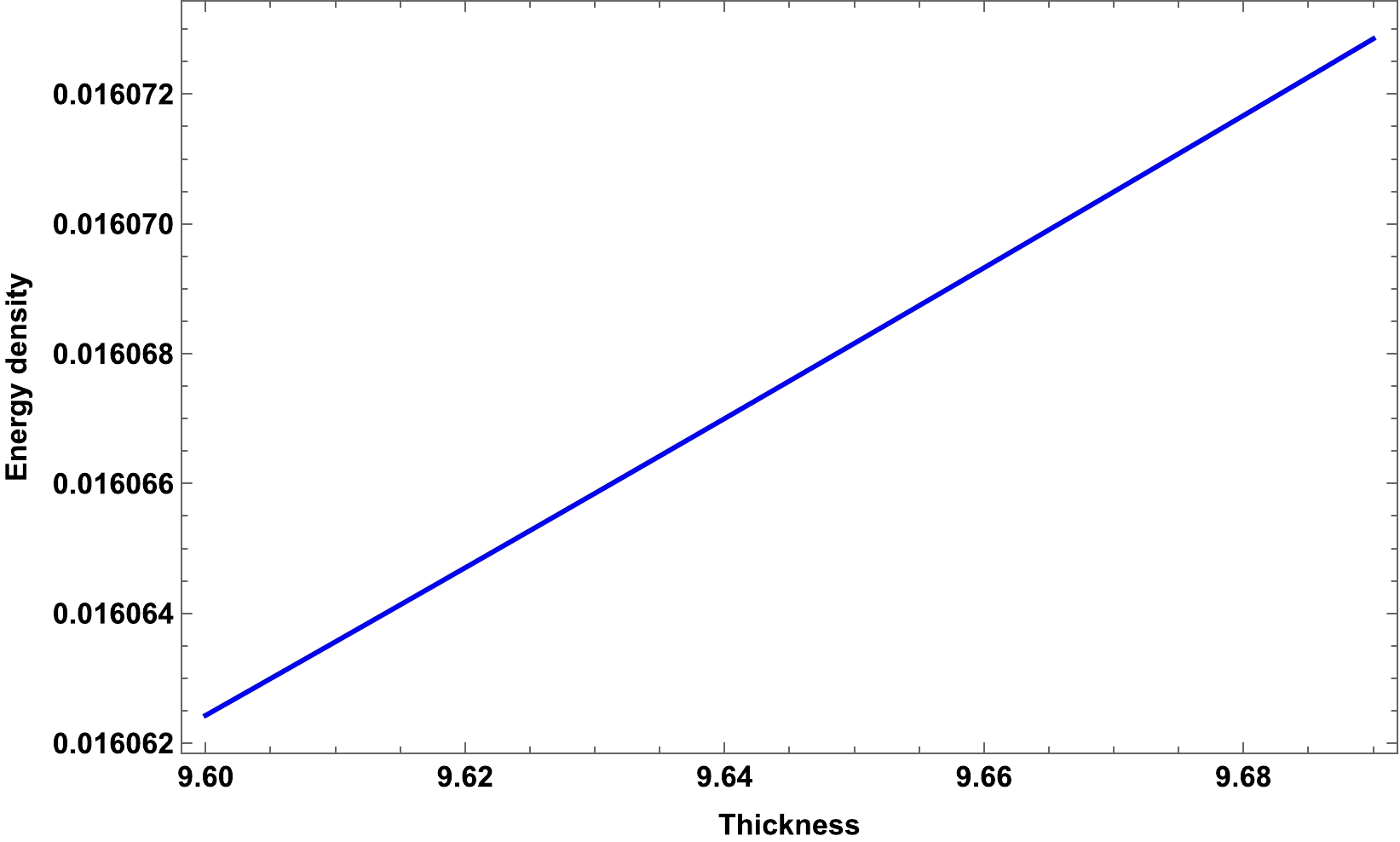

Figure 8.  (color online) Graphical analysis of the surface energy density of the shell with respect to its thickness ($ \epsilon $ in km) for $ a=1.7 $ and $ b=0.7 $.

At last, we calculated the mass of the thin shell ($ m_s $) by applying the formula

Thus, the total gravitational mass (M) of the gravastar can be determined in terms of the shell mass ($ m_s $) as

There are several theories of gravity in which the gravastar has been studied. However, in this work, we attempted to study the gravastar in a novel gravitational framework called symmetric teleparallel gravity. The motivation for working in this gravitational framework is that it is very successful in describing the current accelerated expansion of the universe. Additionally, it is tested by the solar system test to be a self-consistent theory. To proceed further, we presumed the static and spherically symmetric metric with the Kuchowicz metric potential to present physically feasible, singularity-free (to avoid the black hole singularity-like nature of compact spherically symmetric astronomical objects) gravastars. Using this metric with an ideal fluid distribution, we examined different features of the interior, shell, and exterior regions. Furthermore, we analyzed various physical properties of these regions precisely in the framework of $ f(Q) $ gravity as follows:

● Interior region: Using the EoS for the interior region, motion equations, and conservation equation, we found that the solution is free from the singularity, and the energy density and pressure remain constant with dark energy nature.

● Intermediate thin shell: We used the intermediate shell condition for the matter profile and found the metric potential for it. The profile of the obtained metric potential is presented graphically in Fig. 2. The gravastar shell plays a major role in describing the structure of gravastars and differentiating them from black holes. Therefore, we studied various physical properties. Details are presented below.

1. Pressure and matter density: For the shell region, we found the solution for matter density and pressure. The matter density profile with respect to the thickness of the shell is presented in Fig. 3, and it is shown that the matter density decreases with an increase in the thickness.

2. Proper length: The numerical profile of the proper length with respect to the thickness parameter $ \epsilon $ is depicted in Fig. 4. It is observed that when thickness values increase, the proper length of the shell steadily decreases.

3. Energy: From Fig. 5, it is discovered that the energy variation for the shell is positive and monotonically increases toward the outer surface. This implies that the shell's outer boundary is denser than its internal limit, which satisfies the condition that the shell's energy increases as the radial distance increases.

4. Entropy: The evolution of the shell entropy is shown in Fig. 6. It is noted that the entropy of the shell decreases as the shell thickness increases in $ f(Q) $ gravity. This behavior, however, does not suggest that our solution is unstable.

5. Surface redshift: For PSR J1416-2230, we computed the numerical results for the surface redshift and displayed the results in Fig. 7. As shown, the surface redshift is positive for positive values of a and b and $ Z_s<1 $. Therefore, it can be said that our current research on gravastars is both steady and physically acceptable.

6. Exterior region: There are two limits in the gravastar configuration: one is between the interior and intermediate thin shell at a distance $ R_1 $from the center, and the other is between the shell and outer space at a distance $ R_2 $ from the center. The metric functions at these interfaces must be continuous for any stable system. Therefore, we matched these metric potentials with outer space-time.

7. Junction condition and EoS: According to the basic junction condition, there must be seamless matching between regions I and III at the junction. According to the work of Darmois-Israel [32, 33], metric coefficients are continuous at the junction surface. We derived the formulas for the energy density (58) and pressure (59) at the surface. Additionally, we show the physical behavior of energy density in Fig. 8, which describes the increasing behavior of the surface energy density with an increase in the thickness of the shell. We restricted some conditions for having real values of the EoS parameter ω, e.g., $ \dfrac{2M}{R}<1 $ and $ \dfrac{R^2(b -16 \pi\rho_c)}{6a } \neq -1 $, similar to our previous condition regarding the solution in Eq. (32) for the interior region. Finally, we derived the expressions for the mass of the thin shell ($ m_s $) and the total mass (M), as given by Eqs. (62) and (63), respectively.

A gravastar is a theoretically motivated spherically symmetric compact astrophysical object to solve the singularity issue in the black hole geometry. Now, the question arises about the physical existence and discovery of the gravastar in our universe. Despite the fact that grvastars have not yet been observed or found scientifically, there are numerous reasons for and against the theory that gravitational waves (GW) detected by LIGO are the result of merging gravastars or black holes. The theoretical existence of gravastars and their physical feasibility are reported in this article.

Finally, we can conclude that a successful study was performed on gravastars in the context of the symmetric teleparallel theory of gravity with the help of the Kuchowickz metric potential. We obtained a set of physically acceptable and non-singular solutions of the gravastar, which immediately overcame the problem of the central singularity and the existence of the event horizon of the black hole. According to the results that we obtained, we claim the possible existence of gravastars in symmetric teleparallel theory, as obtained in Einstein's GR.

Data availability: There are no new data associated with this article.