-
The origin of high-energy γ-rays has been studied for a long time. There are two mainstream explanations. The first is the leptonic explanation: these γ-rays are produced by electrons through inverse Compton scattering (ICS). The second is the hadronic explanation: the protons produce photons via π-decay. Both of these explanations can give an acceptable γ-ray spectrum under the assumption of a certain initial leptonic/hadronic spectrum. However, why the leptonic/hadronic spectrum for injection should be chosen in such a way still has no satisfactory explanations. In addition, the acceleration mechanism of the leptonic/hadronic is still not clear. The shock wave produced by supernova explosion is the most popular acceleration mechanism [1–3]. The pulsar is another possible source for high-energy γ-rays. It is widely believed that there is a magnetosphere formed by plasmas around pulsars [4–8]. The magnetosphere structure has been studied through numerical simulations for many years [9–13]. In Ref. [14], we studied the acceleration of charged particles around pulsars in terms of the Hertzian magnetic dipole model of pulsars, which can be used to study leptonic/hadronic γ-ray spectra.
The observation of high-energy photons is very difficult because the survival rate of photons decreases exponentially. The main obstacle is caused by the
$ \gamma\gamma\to e^{-}e^{+} $ process, which has been fully studied for many years [15–20]. With the development of technology, PeV photons have been found. Photons around 0.1 PeV have been detected by the Tibet ASγ [21] and the High-Altitude Water Cherenkov GammaRay Observatory (HAWC) [22, 23]. Recently, the Large High Altitude Air Shower Observatory (LHAASO) observed ultrahigh-energy photons even up to 1.4 PeV from 12 γ-ray Galactic sources [24]. In Ref. [25], we showed that the Hertzian magnetic dipole model of pulsars can give the hadronic γ-ray spectra, which can fit with the observations of LHAASO. In this paper, we use the same acceleration mechanism to obtain the energy distributions of leptons and calculate the corresponding leptonic γ-ray spectra. We find that most of the leptonic γ-ray spectra of the suggested origin pulsars can better conform to the LHAASO observed γ-ray spectra of the sources J2226+6057, J1908+0621, and J1825-1326 than the hadronic situation.Focusing on the leptonic origin, the diffusion process is very important, while this process can be ignored in the case of hadrons [24]. Numerous models have been used to describe the diffusion process, such as the slow-diffusion model, two-zone diffusion model [26, 27] and superdiffusion model [28, 29]. In this paper, we choose the simplest model (slow-diffusion model), which is described in detail in Sec. III.
The remainder of this paper is organized as follows. In Sec. II, we introduce the model of pulsars and the acceleration process of electrons, where we show that our injected electronic spectra can be described by the function used in previous works. In Sec. III, we describe our model of the diffusion process and compare our result with the data of LHAASO. We summarize our main conclusions and present discussions in Sec. IV.
-
The first step is to obtain the energy distributions of the electrons. In Ref. [14], we used the Hertzian magnetic dipole model to study the acceleration of charged particles around pulsars. The exact solutions of electromagnetic fields around the pulsars are given as follows:
$ \begin{aligned}[b] \boldsymbol{B}(t, \boldsymbol{x})=&\frac{\mu_{0}}{4\pi}\left(-\frac{\boldsymbol{M}}{r^{3}}-\frac{1}{r^{2} c} \dot{\boldsymbol{M}}-\frac{1}{r c^{2}} \ddot{\boldsymbol{M}}+\frac{3 \boldsymbol{r}}{r^{5}}(\boldsymbol{r} \cdot \boldsymbol{M})\right. \\ &\left.+\frac{3 \boldsymbol{r}}{r^{4}}\left(\boldsymbol{r} \cdot \frac{1}{c} \dot{\boldsymbol{M}}\right)+\frac{\boldsymbol{r}}{r^{3}}\left(\boldsymbol{r} \cdot \frac{1}{c^{2}} \ddot{\boldsymbol{M}}\right)\right)_{\mathrm{ret}}\ , \end{aligned} $

(1) $ \boldsymbol{E}(t, \boldsymbol{x})=-\frac{\mu_{0}}{4\pi}\left(\dot{\boldsymbol{M}}+\frac{r}{c} \ddot{\boldsymbol{M}}\right)_{\mathrm{ret}} \times \frac{\boldsymbol{r}}{r^{3}}\ , $

(2) where r represents the distance from the pulsar,
$\boldsymbol{M}$ represents the magnetic dipole moment, and the subscript "ret" indicates that the time should be taken as$ t-r/c $ . The charged particle in the electromagnetic field obeys the Landau-Lifshit (LL) equation [30]$ m a^{\mu}=e F^{\mu \nu} u_{\nu}+\tau_{0}\left(q \frac{\mathrm{d} F^{\mu \nu}}{\mathrm{\; d} \tau} u_{\nu}+\frac{q^{2}}{m} P_{\nu}^{\mu} F^{\nu \alpha} F_{\alpha \beta} u^{\beta}\right),$

(3) where
$ P_{\nu}^{\mu}=\delta_{\nu}^{\mu}-\frac{u^{\mu} u_{\nu}}{c^{2}}\, , ~~\tau_{0}=\frac{2}{3} \frac{q^{2}}{4 \pi \epsilon_{0} m c^{3}}\ . $

(4) Here,
$ u_{\nu} $ , m, and q represent the 4-velocity, mass, and charge of the particle, respectively. In the first term of Eq. (3),$ F^{\mu \nu} $ is the electromagnetic tensor. The second term of Eq. (3) describes the influence of the particle’s own electromagnetic field. Assuming that the electrons are uniformly distributed from$ 10^{7} $ to$ 10^{9} $ m around the center of the pulsar, we can drive the final energy distribution of electrons, which will be used in the diffusion process.In Fig. 1, we describe the acceleration of electrons at different initial positions. We find that in the Hertzian magnetic dipole model, electrons can be accelerated to PeV within seconds. This result indicates that the initial velocity has little influence on the final energy of electrons as their energy becomes almost constant after a few seconds.
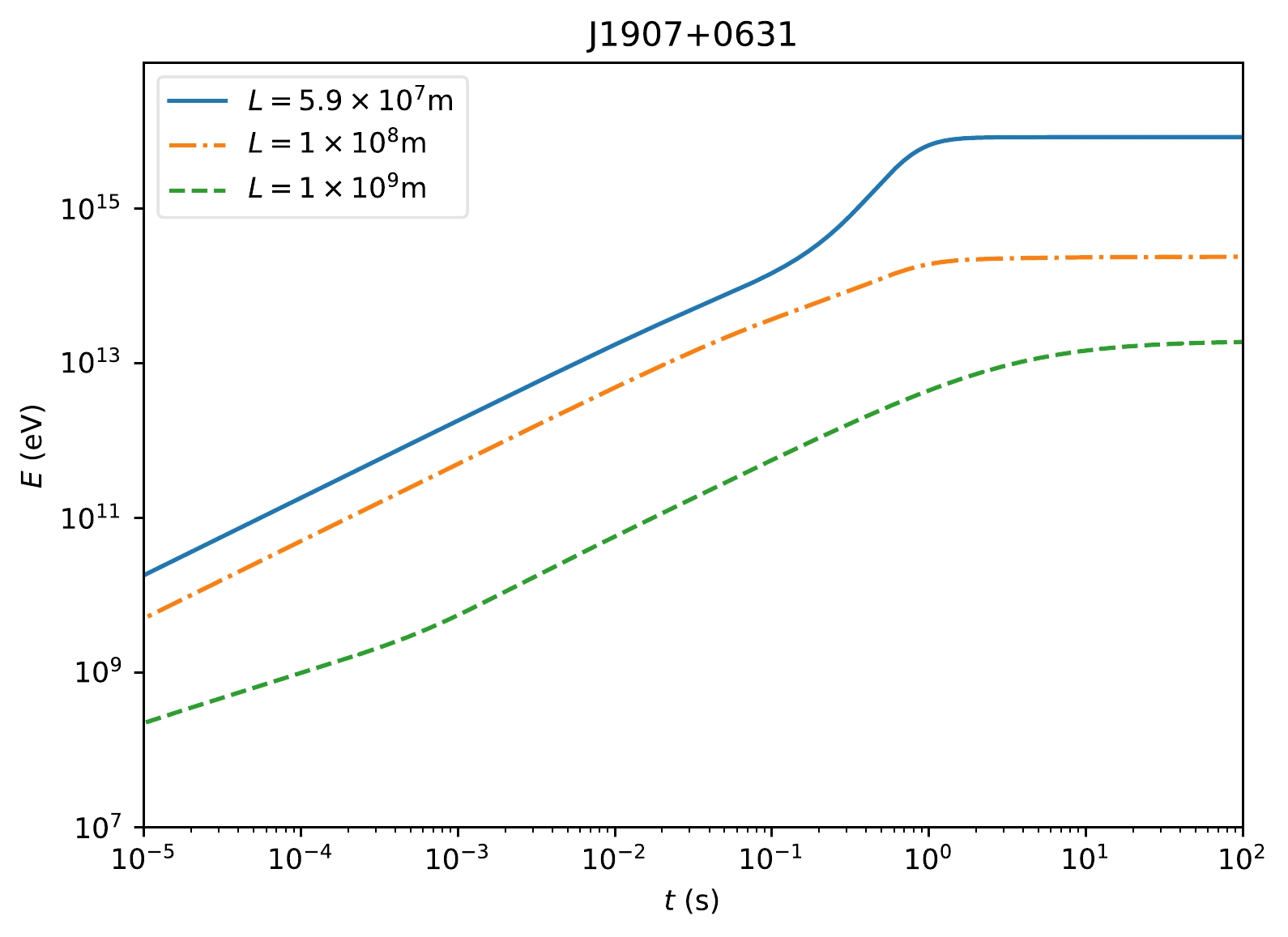
Figure 1. (color online) The acceleration of electrons around a pulsar. We have set the inclination angle of pulsar to
$ \pi/6 $ , the angular speed to$ 6.25\pi\ \mathrm{s}^{-1} $ , and the magnetic moment$ {\boldsymbol M} $ to$2.42\times 10^{28}\,\mathrm{Am}^{2}$ , as in the case of pulsar J1907+0631. The distance from each electron to the pulsar is shown in the upper left corner.In Fig. 2, we show the energy distributions of electrons. We find that the high-energy parts of the electronic spectra can be described by the analytical expressions
$a_{0}E^{-p}{\rm e}^{-(E/E_{c})^{2}}$ or$a_{0}E^{-p}{\rm e}^{-(E/E_{c})}$ with an adjusted$ R^{2} $ greater than 0.999, where$ E_{c} $ represents the cutoff energy. Both of these expressions have been widely used to describe the injected electronic spectrum [24, 31, 32]. Additionally, we find that the low-energy parts of energy distributions of electrons hardly affect the high-energy leptonic γ-ray spectra over 10 TeV.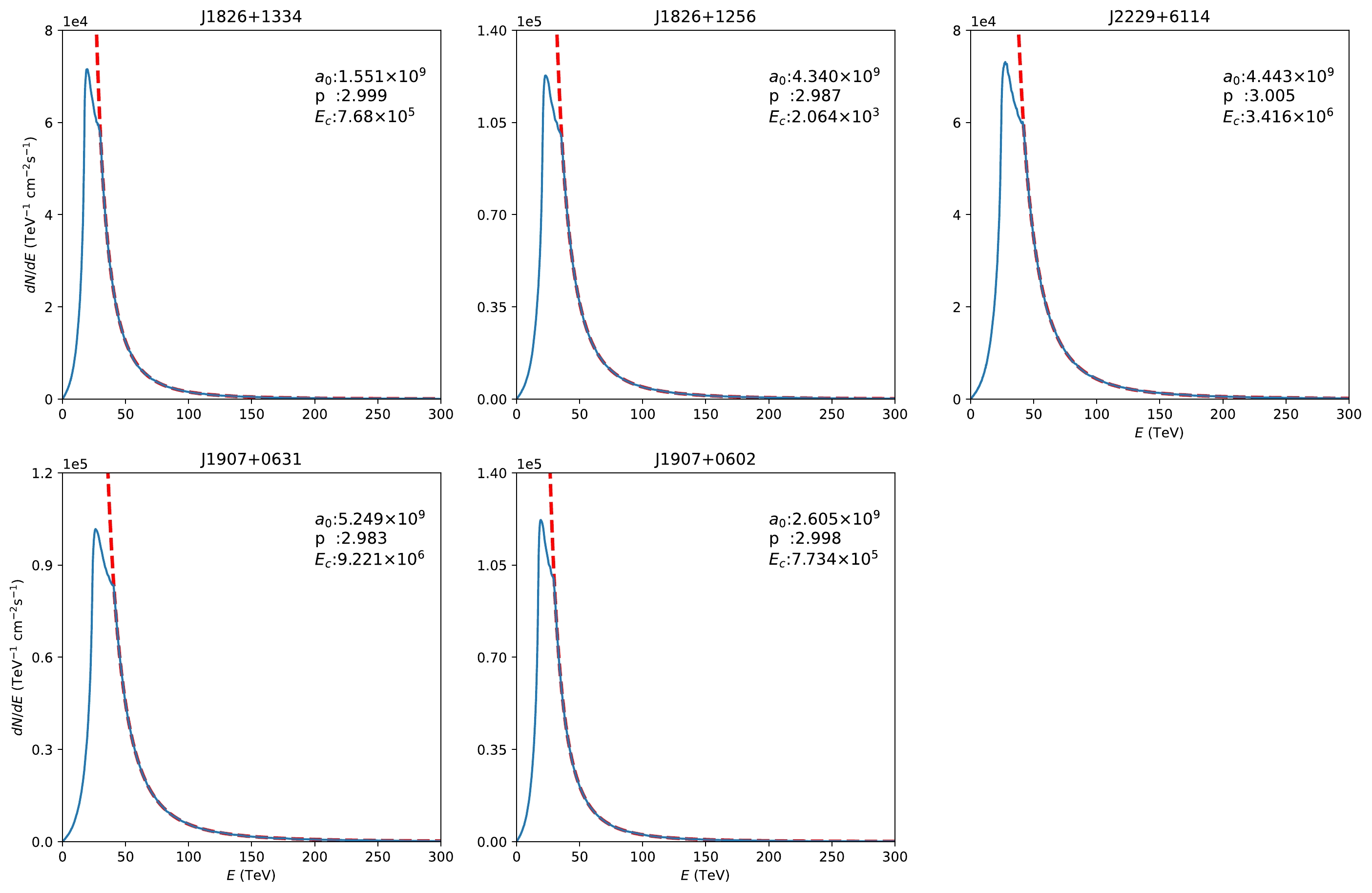
Figure 2. (color online) The solid curves are the electronic spectra from our simulation, while the dashed curves are described by
$a_{0}E^{-p}{\rm e}^{-(E/E_{c})^{2}}$ . We present the parameters used in our simulation in the upper right corner. The$ E_{c} $ we used is far greater than the previous hypothesis. In the high-energy part, this analyzing function can fit our results with an adjusted$ R^{2} $ larger than 0.999. -
For the diffusion process, the propagation equation of leptons is given by
$ \begin{aligned}[b] \frac{\partial N(E_{e}, \boldsymbol{r}, t)}{\partial t}=&\nabla \cdot\left[D(E_{e}) \nabla N(E_{e}, \boldsymbol{r}, t)\right]\\ &+\frac{\partial[b(E_{e}) N(E_{e}, \boldsymbol{r}, t)]}{\partial E_{e}}+Q\left(E_{e}, \boldsymbol{r}, t\right)\ , \end{aligned} $

(5) where
$ N_{e} $ represents the number of electrons per unit energy, and$ D(E_{e}) $ is the diffusion coefficient, which takes the form of$D(E_{e})=D_{0}(E_{e}/100\ {\rm TeV})^{\delta}$ , where δ is the energy index of the diffusion coefficient, which we set to 1/3 in accordance with Kolmogorov’s theory [33, 34]. In this paper, we use the slow-diffusion model. In this model, we assume a space-independent$D_{0} = 3.2\times10^{27} \mathrm{cm}^{2}/\mathrm{s}^{-1}$ . We choose the value of$ D_0 $ used in Ref. [35]. The value of$ D_0 $ around the pulsars can be far smaller than its value in the interstellar medium (ISM) according to the observed spatial morphologies of the γ-ray emission [36, 37]. This phenomenon may be caused by the effects of turbulent scattering [38].$ b(E_{e}) $ represents the energy losing rate, and it is dominated by the synchrotron and ICS. Relevant parameters can be found in Ref. [32]. We take the magnetic field strength as 3$\mu {\rm G}$ to calculate the synchrotron component [39]. The final term$ Q(E_{e}, \boldsymbol{r}, t) $ is the source term.We choose the source term with the form
$ \begin{array}{lr} Q\left(E_{e}, \boldsymbol{r}, t\right)=\left\{\begin{array}{ll} q\left(E_{e},t_{0}\right) \left[\left(t_{\rm age}+t_{\mathrm{sd}}\right) /\left(t+t_{\mathrm{sd}}\right)\right]^{2} \delta\left(\boldsymbol{r}-\boldsymbol{r}_{p}\right), & \\ & \hspace{-1cm} t \geq 0 \\ \\ 0, & \hspace{-1cm} t<0 \\ \end{array}\right.\ , \end{array} $

(6) where
$ q(E_{e},t_{0}) $ represents the energy distribution of electrons we derived in Sec. II. As the electrons are distributed at a distance of$ 10^{7}\sim 10^{9} $ m from the pulsars, which is far smaller than the distance from those pulsars to Earth, we assume that all the electrons are in the same position. Thus, we use the δ function here. The$ t_{\rm age} $ and$ \boldsymbol{r}_{p} $ represent the age and position of the pulsar, respectively. We assume that the injected electrons are proportional to$ [(t_{\rm age}+t_{\rm sd})/(t+t_{\rm sd})]^{2} $ , which is proportional to the spin-down luminosity of the pulsar, and$t_{\rm sd}$ represents the pulsar spin-down timescale. In our research, the pulsars are quite young, and their exact age is unknown; thus, we take$t_{\rm age} = t_{\rm sd}$ .Using the Green function method, we can find the solution to Eq. (5):
$ \begin{aligned}[b] N\left(E_{e}, \boldsymbol{r}, t\right)=&\int_{R^{3}} {\rm d}^{3} \boldsymbol{r}_{0} \int_{t_{\mathrm{ini}}}^{t} {\rm d} t_{0} \frac{b\left(E_{e}^{\star}\right)}{b\left(E_{e}\right)} \frac{1}{\left(\pi \lambda^{2}\right)^{3 / 2}} \\ &\times\exp \left[-\frac{\left(\boldsymbol{r}-\boldsymbol{r}_{0}\right)^{2}}{\lambda^{2}}\right] Q\left(E_{e}^{\star}, \boldsymbol{r}_{0}, t_{0}\right)\ , \end{aligned} $

(7) where
$ \begin{eqnarray} &E_{e}^{\star} \approx \frac{E_{e}}{\left[1-b_{0} E_{e}\left(t-t_{0}\right)\right]}, \end{eqnarray} $

(8) $ \begin{eqnarray} &\lambda^{2}=4 \int_{E_{e}}^{E_{e}^{\star}} \frac{D\left(E_{e}^{\prime}\right)}{b\left(E_{e}^{\prime}\right)} {\rm d} E_{e}^{\prime}, \end{eqnarray} $

(9) $ \begin{eqnarray} &b_{0}=\frac{b(E_{e})}{E_{e}^2}\ . \end{eqnarray} $

(10) Here, t represents the age of the pulsar, and
$t_{\rm ini} = {\rm max}\{t-1/(b_{0}E_{e}),0\}$ . We need the electron surface density$S_{e}(\theta)=\int_{0}^{\infty} N(l_{\theta}){\rm d}l_{\theta}$ to calculate the photon spectra, which is an integral over the direction of vision. We assume that the photon field is isotropic and obeys the graybody distribution; then, the ICS process of electrons can be described as follows:$ \frac{{\rm d} N_{\gamma}}{{\rm d} \omega {\rm d} t}=\frac{T^{3} m_{\mathrm{e}}^{3} c^{3} \kappa}{\pi^{2} \hbar^{3}} \int_{\epsilon_{\gamma} / T}^{\infty} \frac{{\rm d} v_{\gamma}}{{\rm d} \omega {\rm d} N_{\mathrm{ph}} {\rm d} t} \frac{x^{2} {\rm d} x}{\mathrm{e}^{x}-1}\ ,$

(11) where ω represents the energy of upscattered photons, and
$r_{0} = {\rm e}^{2}/(m_{e}c^{2})$ represents the electron classical radius. T represents the temperature of the seed photon field, and κ is the dilution factor.${\rm d} v_{\gamma}/({\rm d} \omega {\rm d} N_{\rm ph}{\rm d} t)$ represents the scattering rate of IC. Details are presented in Ref. [40].We use the
$ \mathrm{Naima} $ code [41] to calculate the ICS process of γ-ray surface brightness$ S_{\gamma}(\theta, E_{\gamma}) $ in the direction of θ from$ S_{e}(\theta) $ . We choose the CMB as the seed photon field. We assume CMB here only because in the energy areas that are of interest to us, the cross-section for scattering higher-energy infrared and optical photons is strongly suppressed [36]. After integrating the γ-ray surface brightness over θ:$\int_{0}^{\theta_{0}}S_{\gamma}(\theta, E_{\gamma}){\rm d}\theta$ , we can obtain the final leptonic γ-ray spectra, where$ \theta_{0} $ is the intrinsic extent of the sources measured by LHAASO [24].We simulate the acceleration of 5 million electrons and obtain the energy distributions of electrons. We derive the leptonic γ-ray spectra of J2226+6057, J1908+ 0621, and J1825-1326. For J1908+0621 and J1825-1326, there are two possible pulsars around each source, and we perform separate calculations for those pulsars. We list some parameters of each pulsar in Table 1. The leptonic γ-ray spectra are shown in Fig. 3. As shown, the leptonic γ-ray spectra of the suggested origin pulsars can be qualitatively consistent with the LHAASO observed γ-ray spectra of the sources J2226+6057, J1908+0621, and J1825-1326.
PSR $P /{\rm ms}$ 

$\dot{P}/{\rm ss^{-1}}$ 

$B_s\sin\theta/{\rm G}$ 

J2229+6114 51.3 $ 7.83\times 10^{-14} $ 

$ 2.1\times 10^{12} $ 

J1907+0602 107 $ 8.68\times10^{-14} $ 

$ 3.0\times10^{12} $ 

J1907+0631 324 $ 4.52\times10^{-13} $ 

$ 1.2\times10^{13} $ 

J1826-1334 101 $ 7.52\times10^{-14} $ 

$ 2.8\times10^{12} $ 

J1826-1256 110 $ 1.21\times10^{-13} $ 

$ 3.7\times10^{12} $ 

Table 1. Some parameters of the five pulsars that are possible candidates of PeV γ-rays. Here, P represents the period of the pulsar, and
$ \dot{P} $ represents its first derivative. The surface magnetic field is denoted as$ B_s $ , and the inclination angle is denoted as θ. These data can be found in Refs. [42–46]. -
In our model, we assumed that the electrons are distributed uniformly in a spherical shell between
$ 10^{7} \sim 10^{9} $ m around the pulsar to avoid the impacts of the possible magnetosphere structure. We studied the leptonic γ-ray spectra of the sources J2226+6057, J1908+0621, and J1825-1326 in terms of the Hertzian magnetic dipole model of pulsars. Using the energy distributions of electrons we obtained, we considered the diffusion process in the slow-diffusion model and calculated the corresponding γ-ray spectra by using the$ \mathrm{Naima} $ code. We concluded that the leptonic γ-ray spectra of the suggested origin pulsars could roughly describe the LHAASO observed γ-ray spectra of the sources J2226+6057, J1908+0621, and J1825-1326. We also showed that our injection of electronic spectra in the high-energy part was consistent with the hypothesis of previous studies.In order to compare our results for the leptonic spectra with the counterparts of hadronic spectra, we calculated the
$ \chi^2 $ of each curve for both cases, as listed in Table 2. We found that the leptonic explanation is better than the hadronic explanation for J1836-1334, J2229+ 6114, and J1907+ 0602. For J1826-1256, the leptonic spectra and hadronic spectra have the same level of fitting. In contrast, for J1907+0631, the hadronic explanation has a better fit. It is possible that only the hadronic explanation is applicable to this situation. This can be a meaningful topic for future research. -
We thank Dr. Q.H. Zhu, Dr. K. Fang, and Prof. X.J. Bi for useful discussions.
Pulsars as candidates of LHAASO sources J2226+6057, J1908+0621, and J1825-1326: The leptonic origin
- Received Date: 2022-11-17
- Available Online: 2023-06-15
Abstract: Recently, from 12 γ-ray Galactic sources, the LHAASO has detected ultrahigh-energy photons up to 1.4 PeV. The γ-ray spectra of the sources J2226+6057, J1908+0621, and J1825-1326 and the suggested origin pulsars near the sources have been published. In our previous work, we studied the hadronic γ-ray spectra of the sources J2226+6057, J1908+0621, and J1825-1326 in terms of the Hertzian dipole model of pulsars. In this paper, we investigate the possibility of the leptonic origin of the γ-ray. We use the Hertzian dipole model to describe the pulsars around the sources. The electrons around the pulsars can be accelerated to PeV by the electromagnetic fields of pulsars. Under the assumption that the initial electrons are uniformly distributed in a spherical shell between





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: