-
Exploring the properties of magnetized hot/dense quark matter is a subject of great interest in high energy nuclear physics relevant to neutron stars and quark-gluon plasma created in non-central relativistic heavy ion collisions. In such a thermomagnetic system, striking phenomena emerge, which are expected to introduce a new aspect of the nonperturbative feature of QCD. In particular, the influence of an external magnetic field on the QCD phase transition is an important phenomenon in understanding quark matter under extreme conditions.
The nonperturbative phenomenon of dynamical chiral symmetry breaking is crucially affected by external magnetic fields in hot/dense QCD matter. At low temperatures, when chiral symmetry is broken, the magnetic field enhances the chiral condensate, which acts as a catalyzer for spontaneous chiral symmetry breaking. This magnetic catalysis (MC) behavior has been observed in the Nambu-Jona-Lasinio (NJL) model [1–3], effective model approaches such as chiral perturbation theory [4], and lattice QCD simulations [5–7].
Effective model analyses provide a clear interpretation of MC: magnetic dimensional reduction induces the enhancement of chiral symmetry breaking, and then MC is realized in the vacuum. In contrast to the case at low temperatures, inverse MC (IMC) arises at approximately the chiral phase transition temperature, which has been observed by lattice QCD simulations [5–7]: the magnetic field promotes chiral symmetry restoration and reduces the critical temperature of the chiral phase transition. As expected, all effective chiral models, including the conventional NJL model, display MC at low temperatures as well as at high temperatures [1–3]. To explain the IMC behavior, additional mechanisms must be considered, such as neutral pion fluctuation [8], chirality imbalance [9], and running coupling with the magnetic field [10].
Recently, the anomalous magnetic moment (AMM) of quarks has attracted considerable interest for offering new insight into QCD matter under a magnetic field. In the perturbative framework of massless QCD, the AMM contribution for quarks is prohibited owing to the presence of chiral symmetry. However, when chiral symmetry is dynamically broken in the low energy regime of QCD, the quarks possess AMM terms. It has been shown in [11] that spontaneous chiral symmetry breaking dynamically generates the AMM, even for massless quarks in the absence of an external magnetic field. The magnetic field effect has also been studied based on the NJL model with tensor interactions [12–15], in which the strong magnetic field induces the dynamical generation of the AMM associated with the emergence of the spin condensate. Furthermore, the magnetized quark-loop contribution to the quark AMM has been calculated in the NJL model, which asymptotically vanishes in the symmetry restored phase [16]. It has been observed in [10] that the existence of the dynamical AMM leads to IMC behavior in the strong magnetic field region even when only the lowest Landau level is considered in quarks, and it was observed in [15] that with the AMM, the behaviors of neutral pion mass and charged pion mass under a magnetic field are qualitatively in agreement with lattice result [17]. Recently, it was shown in [18] that the AMM of quarks contributes 40
$ \% $ to$ \bar{\Lambda}-\Lambda $ polarization splitting.Although the AMM of quarks is expected to be a key factor in investigating thermomagnetic QCD matter, its expression remains obscure in the low energy regime of QCD. In vacuum, the AMM of quarks is conventionally treated as a constant value, and the influence of the constant AMM on the chiral phase transition has been investigated [19–22]. In studies using the NJL [19, 20] and PNJL models [22], the constant AMM contribution has been found to drastically affect the chiral phase transition and trigger an unexpected phase transition contradicting the lattice observation (this AMM effect on the phase transition will be discussed in a later section). Hence, a constant AMM is an improper form for QCD matter under a magnetic field. An alternative expression of the AMM, which involves a behavior proportional to the chiral condensate or the square of the chiral condensate, has also been suggested in the NJL model to evaluate the magnetic effect on meson masses and magnetic susceptibility [14, 15]. However, details on how the form of the quark AMM affects the chiral phase transition were not addressed in [14, 15]. Therefore, there is still room to constrain the effective form of the quark AMM in low-energy QCD while considering the chiral phase transition under magnetic fields.
In this study, we explore the effective form of the quark AMM, which can properly describe thermomagnetic QCD matter. Considering the uncertainty of the explicit expression of the quark AMM, we make assumptions about its effective form. First, we regard the AMM as a constant value for the sake of simplicity. Next, we suppose that the AMM depends on the scalar meson field serving as the chiral order parameter. We deduce the effective form of the AMM from the findings in [11, 19, 20] and a recent study on the magnetic effect on the electron AMM within the QED framework [23]. With the effective AMM forms, we evaluate the influence of the quark AMM on the chiral phase transition based on the two-flavor NJL model and consider the practicable expression of the effective AMM form by comparing the NJL results with the lattice QCD results. Through the comparison, we also show the intrinsic temperature dependence of the quark AMM. The phenomenological implications of the effective AMM are also discussed.
This paper is organized as follows. In Sec. II, we introduce the NJL model, considering the effective interaction of the quark AMM, and assume several forms of the quark AMM. Then, we evaluate the influence of the quark AMM on the chiral phase transition under a constant magnetic field and compare the NJL results with the lattice QCD observations in Sec. III. Finally, a summary and discussion are given in Sec. IV.
-
The regular NJL model consists of four-quark point interactions, which can describe chiral symmetry breaking in vacuum and symmetry restoration at finite-temperatures. As a minimal extension, we work on the NJL model involving the AMM term to explore the effective form of the quark AMM and its influence on the chiral phase transition. We suppose that the chiral condensate and quark AMM take the isospin symmetric form to simply consider the correlation between spontaneous chiral symmetry breaking and the AMM contribution.
In this section, we first briefly introduce the NJL framework. Then, we show several forms of the quark AMM in the NJL-model description.
-
The two-flavor NJL model involving the AMM term is written as
$ \begin{aligned}[b] {\cal L}_{\rm NJL}=& \bar \psi \left({\rm i}\gamma^\mu D_\mu -{{\mathit{\boldsymbol{ m }}}}+\frac{1}{2}\kappa_f q_f F_{\mu\nu} \sigma^{\mu\nu} \right)\psi \\&+G_S\left\{ (\bar \psi \psi)^2 +(\bar \psi {\rm i}\gamma_5\vec \tau \psi)^2 \right\} , \end{aligned} $

(1) where ψ denotes the two-flavor quark field,
$ {\psi}=(u,d)^T $ ;$ {{\mathit{\boldsymbol{ m }}}} $ represents a matrix of the current quark mass$ {{\mathit{\boldsymbol{ m }}}}= {\rm diag}(m_u,m_d) $ , and we take the isospin symmetric limit$ m_u=m_d=m_0 $ ,$ \sigma_{\mu\nu}=\dfrac{\rm i}{2}[\gamma_\mu, \gamma_\nu] $ ; the field strength of the gauge field$ A_\mu $ is given by$ F_{\mu\nu}=\partial_\mu A_\nu -\partial_\nu A_\mu $ ; and$ G_S $ is the coupling constant in the scalar channel of the four-quark interaction term. The covariant derivative acting on the quark field is represented as$ D_\mu=\partial_\mu -{\rm i}q_fA_\mu $ , with the electric charge for quark flavor$ q_u=+2e/3 $ and$ q_d=-e/3 $ . In this study, we consider a constant magnetic field along the z-direction in four-dimensional spacetime, which is embedded in the gauge field$ A_\mu=(0,-By/2,Bx/2,0) $ . The interaction form of the quark AMM is introduced as$ \bar \psi \kappa_f q_f F_{\mu\nu} \sigma^{\mu\nu}\psi $ , with the quark AMM$ \kappa_f $ ; its expression will be given later.Introducing the auxiliary scalar, pseodoscalar fields
$ \sigma\sim \bar \psi \psi $ and$ \vec{\pi} \sim \bar \psi {\rm i} \gamma_5\vec{\tau}\psi $ , and taking the mean field approximation$ \sigma=-2G_S\bar \psi \psi $ and$ \pi=0 $ , we can derive the bosonized NJL Lagrangian as$ \begin{eqnarray} {\cal L}_{\rm mean}= \bar \psi \left({\rm i}\gamma^\mu D_\mu -M+\frac{1}{2}\kappa_f q_f F_{\mu\nu} \sigma^{\mu\nu} \right)\psi -\frac{1}{4G_S}\sigma^2, \end{eqnarray} $

(2) where
$ M=m_0+\sigma $ . By integrating out the quark field in the generating functional for the mean-field Lagrangian$ {\cal L}_{\rm mean} $ , we obtain the effective potential of the NJL model,$ \begin{aligned}[b] V_{\rm eff} (m_0,\sigma, T, eB)= & \frac{\sigma^2}{4G_S} -N_c\sum_{q_f=q_u,q_d} |q_f B| \sum_{l=0}^\infty \sum_{s=\pm1}\\& \int \frac{{\rm d} p_3}{4\pi^2} \left\{ E_{q_f}^{(l,s)}f_{\Lambda,B}^{(l,s)} +2T\ln\left( 1+{\rm e}^{- E_{q_f}^{(l,s)}/T } \right) \right\} \end{aligned} $

(3) where
$ N_c $ denotes the number of colors, l represents the Landau level,$ s=\pm 1 $ represents the spin-up/down of the quarks, and$ E_{q_f}^{(l,s)} $ is the energy dispersion relation of up- and down-quarks in the external magnetic field and with the quark AMM,$ \begin{eqnarray} E_{q_f}^{(l,s)}= \sqrt{ p_3^2+ \left[ \left\{ |q_f B|( 2l+1 -s \xi_f )+M^2 \right\}^{1/2} -s \kappa_fq_f B \right]^2 } . \end{eqnarray} $

(4) Here,
$ p_3 $ denotes the third component in the momentum space, and$ \xi_f={\rm sgn}(q_fB) $ . The vacuum part of the effective potential involves ultraviolet divergence. To regularize the divergence, we use a smooth regularization scheme by inserting the regulator function$ f_{\Lambda,B}^{(l,s)} $ into the effective potential in Eq. (3). In this study, we choose the Lorentzian form factor as follows1 :$ \begin{eqnarray} f_{\Lambda,B}^{(l,s)} = \frac{\Lambda^{10}}{\Lambda^{10}+(\sqrt{p_3^2 +|q_f B|(2l+1-s\xi_f )})^{10} }, \end{eqnarray} $

(5) where Λ is the ultraviolet momentum cutoff.
The expectation value of the auxiliary scalar field
$ \bar \sigma=\langle \sigma \rangle $ can be determined from the stationary condition for the effective potential,$ \begin{eqnarray} \frac{\partial V_{\rm eff}(\sigma) }{\partial \sigma}\Biggl|_{\sigma=\bar \sigma}=0. \end{eqnarray} $

(6) Indeed,
$ \bar \sigma $ plays the role of the order parameter for spontaneous chiral symmetry breaking, which is known as the chiral condensate, and it gives the dynamical quark mass generated by spontaneous chiral symmetry breaking,$ \langle M\rangle=m_0+\bar{\sigma} $ . Using the chiral condensate, we can obtain the quark condensate,$ \begin{eqnarray} \langle \bar \psi \psi \rangle = \frac{\partial V_{\rm eff}}{\partial m_0}\Biggl|_{\sigma=\bar \sigma}. \end{eqnarray} $

(7) -
As shown in the NJL Lagrangian in Eq. (1), the AMM interaction term for quarks can be expressed as
$ \begin{eqnarray} {\cal L}_{\rm int}^{\rm (AMM)}= \frac{1}{2}\kappa_f q_f \bar \psi F_{\mu\nu} \sigma^{\mu\nu} \psi. \end{eqnarray} $

(8) In the Bethe-Salpeter approach for the quark-photon vertex without external magnetic field correction, it has been argued in [11] that the AMM is dynamically generated from spontaneous chiral symmetry breaking. As a consequence, the AMM term vanishes at the chiral limit when chiral symmetry is completely restored. In addition, the dynamical generation of the quark AMM associated with spontaneous chiral symmetry breaking has also been studied based on the two-flavor gauged NJL model in the mean field approximation [16], which was evaluated at the quark one-loop level for the photon-quark-antiquark vertex function. It was shown that the quark AMM is non-linearly correlated with the chiral condensate through the coupled gap equations among
$ \kappa_{u,d} $ and the dynamical quark mass, and thus,$ \kappa_{u,d} $ become vanishingly small after chiral restoration at finite temperatures with an external magnetic field.Though the explicit form of
$ \kappa_{f} $ still remains unclear in low energy dynamics owing to the nonperturbative nature of QCD, several previous studies have implied that quarks dynamically acquire an AMM term. Thus, when expressing the effective interaction term of the quark AMM in Eq. (8), one can expect that the quark AMM$ \kappa_{u,d} $ will depend on the chiral condensate.Furthermore, when we consider quark matter under substantial magnetic fields, the dynamical generation of the quark AMM becomes more intricate owing to the magnetic field correlation to chiral symmetry breaking. Indeed, the external magnetic field induces the dynamical generation of the AMM, which can be called the magnetic-dependent AMM. In the NJL model with tensor interactions [12–15], the spin polarization condensate
$ \langle \bar \psi \sigma^{\mu\nu} \psi\rangle $ is generated and is proportional to the chiral condensate in the strong magnetic field region, which is similar to the case of the quark AMM. This indicates that the chiral condensate enters the AMM form by considering the external magnetic field dependence on the vacuum. We can assume the magnetic-dependent AMM proportional to the chiral condensate$ \kappa_{u,d}\sim \sigma $ as one possible form of the quark AMM.In addition, we also raise an alternative possibility for the expression of the magnetic-dependent AMM. In the QED framework, it was found in [23] that the external magnetic field actually contributes to the AMM for the electron, which is proportional to the electron mass squared with magnetic corrections. From this, we extend the QED framework to the QCD case and promote the electron mass to the dynamical quark mass. Then, we can assume that the magnetic-dependent AMM takes the form
$ \kappa_{u,d}\sim M^2\sim \sigma^2 $ .Given the above facts, we consider the following three cases separately to find the effective form of the quark AMM in the low energy regime of QCD
2 :(a)
$ \kappa_{u,d}={\rm const.} $ ,(b)
$ \kappa_{u,d}=v \sigma $ ,(c)
$ \kappa_{u,d}=\bar v \sigma^2 $ ,where v and
$ \bar v $ are free parameters in the low energy effective model.In the case of (a), we assume that the AMM
$ \kappa_{f} $ takes a constant value for the sake of simplicity. The constant quark AMM is evaluated from the proton and neutron magnetic moment using the constituent quark model [19]:$ \kappa_u= 0.29016~{\rm GeV}^{-1} $ and$ \kappa_d= 0.35986~{\rm GeV}^{-1} $ . In the case of (b) and (c), we assume that$ \kappa_f $ takes the magnetic-dependent forms in the magnetized vacuum. These forms actually vanish after chiral restoration. This implies that the magnetic-dependent AMM may be dynamically generated via spontaneous chiral symmetry breaking.Note that the NJL model including the magnetic-dependent AMM has previously been discussed to study the AMM contribution in meson masses and magnetic susceptibility [14, 15].
In this study, we investigate the influence of the quark AMM on the chiral phase transition to find the effective form of
$ \kappa_f $ through a comparison of the NJL estimates and recent lattice QCD observations. -
In this section, we numerically evaluate the AMM dependence on the chiral condensate (quark condensate) based on the NJL model. Comparing the (subtracted) quark condensate with recent lattice QCD data [25, 26]
3 , we restrict the effective form of the quark AMM in the low energy dynamics of QCD under the magnetic field and discuss the nontrivial correlation between the quark AMM interaction and chiral phase transition.The model parameters are fixed as
$ \Lambda = 681.38\,{\rm GeV} $ ,$ G_S\Lambda^2= 1.860 $ , and$ m_0=4.552~{\rm MeV} $ [24]. With this parameter set, the following physical observables are provided at$ T=0 $ : the dynamical mass$ M=286.19 $ MeV, pion mass$ m_\pi=138 $ MeV, and pion decay constant$ f_\pi= $ 92.4 MeV.This NJL model experiences a chiral crossover at
$ eB=0 $ . The pseudo-critical temperature of the chiral crossover is defined by${\rm d}^2\bar \sigma(T,eB=0)/{\rm d} T^2\bigl|_{T=T_{\rm pc}}=0$ . We find$ T_{\rm pc}^{\rm (NJL)}(eB=0) \simeq167 $ MeV, which is close to the lattice QCD simulation result$ T_{\rm pc}^{\rm (lat.)}(eB=0)\simeq 170 $ MeV in [26].Below, we investigate the influence of the AMM on the chiral condensate by taking the following three forms of the quark AMM separately: (a)
$ \kappa_{u,d}={\rm const.} $ , (b)$ \kappa_{u,d}=v \sigma $ , and (c)$ \kappa_{u,d}=\bar v \sigma^2 $ . -
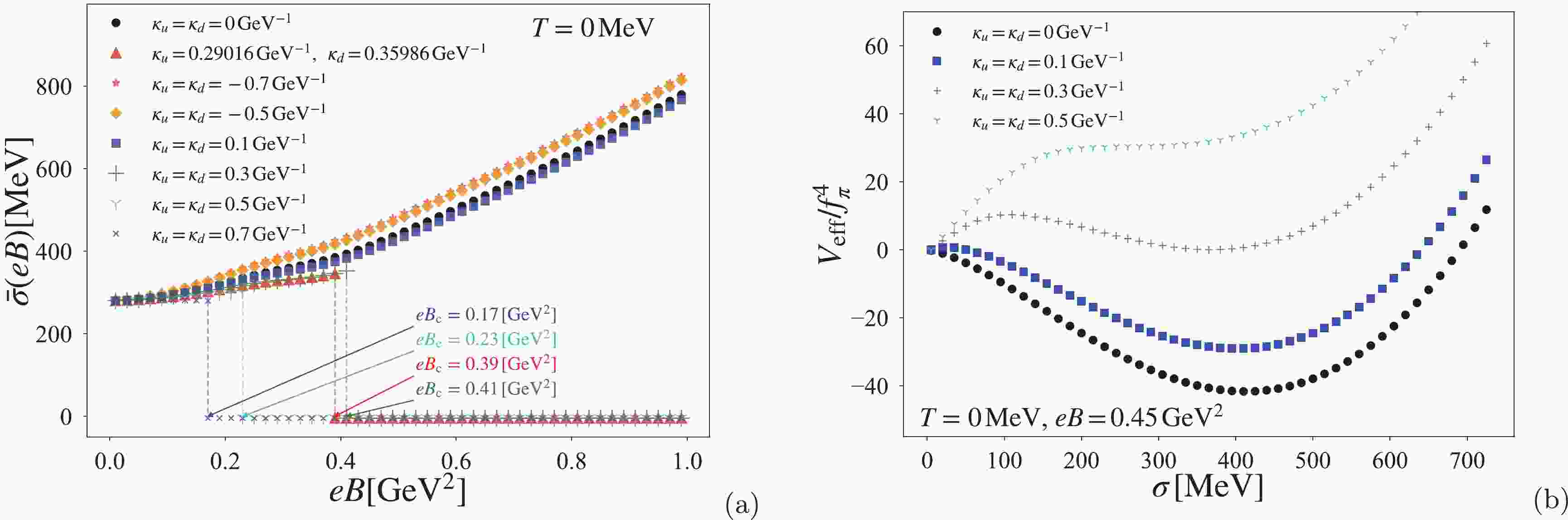
In Fig. 1, we show the constant AMM effect on the chiral condensate at zero-temperature. Note that the magnetic effect on the chiral condensate depends on the regularization procedures for ultraviolet divergence. Indeed, by using an unsuitable ultraviolet-regulator, the chiral condensate (or the quark condensate) oscillates with the increase in the magnetic field [24]. However, the oscillation in the (subtracted) quark condensate is not observed in lattice QCD simulations under a constant magnetic field (at
$ T=0 $ ) [6, 7, 25]. To avoid accidental oscillation in this study, we choose the Lorentzian form factor in Eq. (5)4 .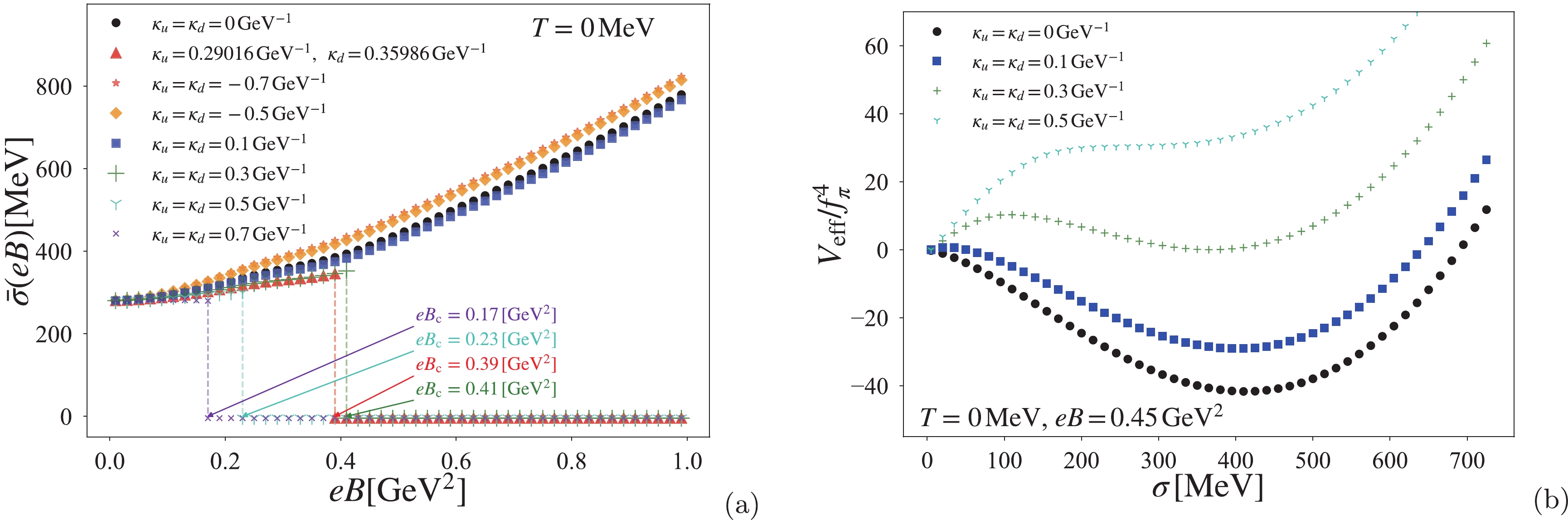
Figure 1. (color online) Constant quark AMM effect on the chiral condensate at
$ T=0 $ . Panel (a) shows the magnetic dependence of the chiral condensate with different values of$ \kappa_u=\kappa_d $ . Panel (b) displays the effective potential$ V_{\rm eff} $ normalized by the fourth power of the pion decay constant$ f_{\pi} $ in vacuum with$ T=0,B=0 $ . The potentials are also normalized by subtracting$ V_{\rm eff}(\sigma=0) $ at$ T=0 $ MeV. This definition of normalized effective potential is applied in subsequent figures.In the absence of the AMM, the chiral condensate
$ \bar \sigma $ monotonically increases as the magnetic scale increases. By switching on the constant AMM with the typical values$ \kappa_u\simeq 0.29~{\rm GeV}^{-1} $ and$ \kappa_d\simeq 0.36~{\rm GeV}^{-1} $ , a jump arises in the chiral condensate at the critical magnetic field$ eB_{\rm c}= 0.39~{\rm GeV}^2 $ . This jump indicates that the NJL model undergoes a first order chiral phase transition induced by the constant AMM. A similar behavior of the induced-first order phase transition has been observed in another analysis of the NJL model [19], in which the unphysical oscillation appeared in the chiral condensate owing to the use of the Woods-Saxon type form factor.The constant AMM unexpectedly triggers the first order phase transition even in the zero temperature system (
$ T=0 $ ). To clearly understand the induced-first order phase transition, we conduct a detailed investigation of the constant AMM effect in the NJL model. For simplicity, we suppose that the constant AMM takes the isospin symmetric form$ \kappa_u=\kappa_d $ , which is varied from$-0.7 ~{\rm GeV}^{-1}$ to$0.7 ~{\rm GeV}^{-1}$ in this study.Panel (a) of Fig. 1 shows that, for a negative constant quark AMM,
$ \kappa_{u,d}<0 $ , the monotonic increase in$ \bar \sigma $ tends to be enhanced by the constant AMM contribution, and the jump does not emerge in the chiral condensate. A negative constant quark AMM,$ \kappa_{u,d}<0 $ , acts as a catalyzer for chiral symmetry breaking under a magnetic field, which is similar to the case of tensor-type spin polarization induced by a magnetic field, as shown in [15]. However, to reconcile the NJL result with the lattice QCD observation, the catalysis behavior induced by the negative constant quark AMM is not a valuable result. For this reason, we discard the negative constant quark AMM contribution for$ \kappa_{u,d}<0 $ in the present NJL analysis.Subsequently, we consider the case of a positive constant quark AMM,
$ \kappa_{u,d}>0 $ . For a small value,$\kappa_u=\kappa_d= 0.1 \,{\rm GeV}^{-1}$ , the jump does not appear in the chiral condensate, as shown in panel (a) of Fig. 1. However, as the constant AMM$ \kappa_{u,d} $ becomes larger, the jump suddenly arises. In addition, the critical magnetic field corresponding to the jump is shifted to smaller values with the increase in the constant AMM.Incidentally, the behavior of the phase transition can be directly observed from the effective potential in Eq. (3). Panel (b) of Fig. 1 shows a sketch of the constant AMM effect on the effective potential at
$ T=0 $ and$eB=0.45~{\rm GeV}^2$ . As clearly presented, the potential structure is significantly deformed by the presence of the constant AMM. The constant AMM creates a potential barrier between the chiral symmetric vacuum ($ \sigma=0 $ ) and the chiral broken vacuum ($ \sigma\neq0 $ ) and pushes up the minimum point at the chiral broken vacuum. Owing to the significant deformation of the effective potential, the chiral first order phase transition is accidentally induced even at zero temperature.5 Next, we move onto the thermal system. Figure 2 shows the thermal effect on the chiral phase transition along the magnetic field, which is induced by the constant AMM. Here, we take the form
$\kappa_u=\kappa_d=0.3~{\rm GeV}^{-1}$ as one of the cases for the induced-first order phase transition at zero-temperature. At temperatures below the critical temperature,$T < T_{\rm pc}^{(\rm NJL)}(eB=0)\, (\simeq 167~{\rm MeV})$ , the chiral phase transition is still of the first order owing to the presence of the potential barrier, as depicted in panel (b) of Fig. 2. However, the potential barrier is washed out by the thermal effect at temperatures above the critical temperature,$ T>T_{\rm pc}^{\rm (NJL)}(eB=0) $ . As a result, the chiral phase transition changes to a second order phase transition.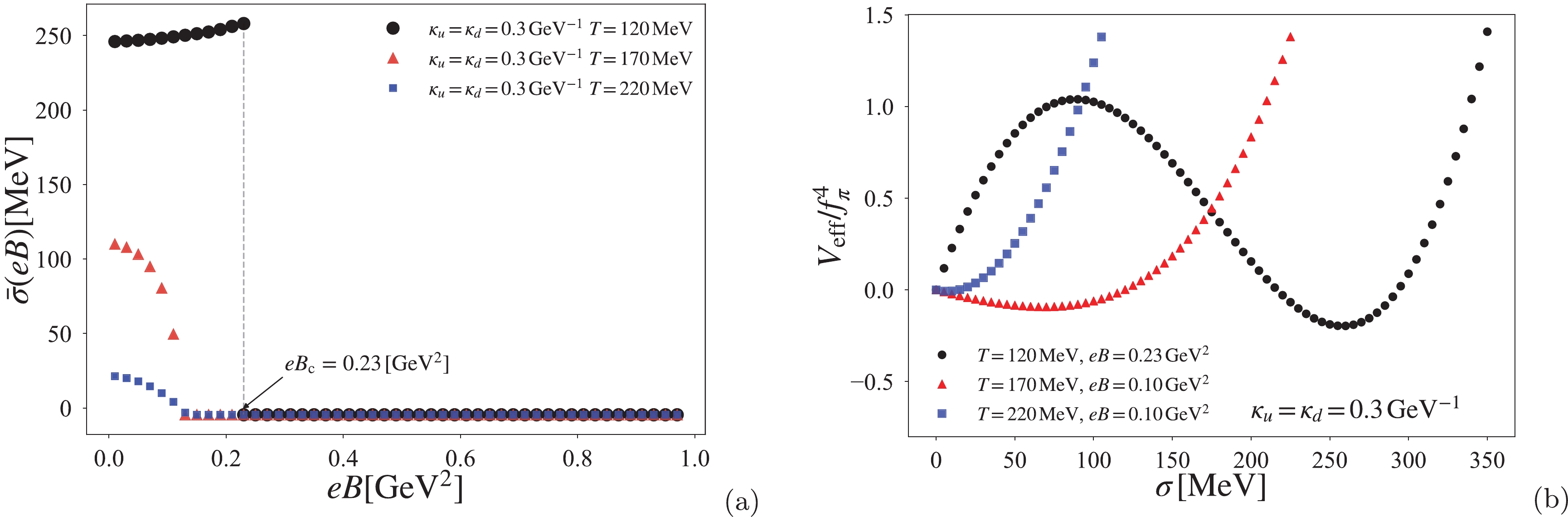
Figure 2. (color online) Chiral phase transition under external magnetic fields with a constant quark AMM in the case of
$\kappa_u=\kappa_d=0.3~{\rm GeV}^{-1}$ for different temperatures. Panel (a) shows the chiral phase transition along the magnetic field with different temperatures. Panel (b) shows the deformation of the normalized effective potential by the pion decay constant$ f_{\pi} $ in vacuum.As mentioned above, in the case of zero-temperature, the small-constant AMM corresponding to
$\kappa_u=\kappa_d= 0.1~{\rm GeV}^{-1}$ hardly contributes to the chiral condensate. However, around the critical temperature$T=T_{\rm pc}^{\rm (NJL)} (eB=0)\, (\simeq 167~{\rm MeV})$ , the small-constant AMM becomes eminent, and the order of the chiral phase transition drastically changes. Figure 3 shows that even with a small-constant AMM, a jump appears and a first order phase transition is realized at approximately$T=T_{\rm pc}^{(\rm NJL)} (eB=0)$ . It is particularly interesting to note that there are two jumps at approximately$eB_{\rm c}= 0.23~{\rm GeV}^{2}$ and$eB_{\rm c}= 0.43~{\rm GeV}^{2}$ for$T=170~{\rm MeV}$ , which might be due to the competition between MC and magnetic inhibition. In fact, the potential barrier is formed around the critical magnetic fields, as shown in panels (b) and (c) of Fig. 3. As the temperature increases, the potential barrier corresponding to$eB_{\rm c}= 0.23~{\rm GeV}^{2}$ vanishes, and hence, the phase transition changes to a second order phase transition. In contrast, the potential barrier corresponding to$eB_{\rm c}= 0.43~{\rm GeV}^{2}$ remains even at a higher temperature ($ T=220 $ MeV), but the critical magnetic field is shifted to the stronger magnetic field region$eB_{\rm c}= 0.75~{\rm GeV}^{2}$ , as shown in panel (a) of Fig. 3.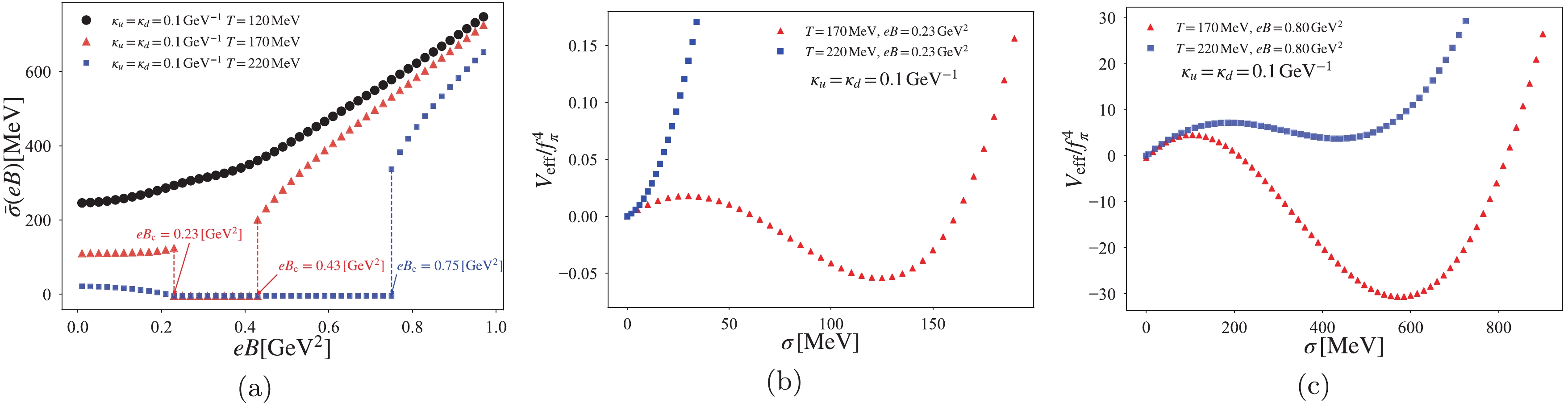
Figure 3. (color online) Similar to Fig. 2, but in the case of
$ \kappa_u=\kappa_d=0.1~{\rm GeV}^{-1} $ . The normalized effective potential at$ eB=0.23~{\rm GeV}^{2} $ in (b) and$ eB=0.8~{\rm GeV}^{2} $ in (c).Note that the chiral phase transitions including the constant AMM effect at finite temperature have already been discussed in the NJL [19, 20] and PNJL models [22]. However, an analysis of the potential deformation has not yet been explicitly reported.
Owing to the presence of the constant AMM, the phase structure becomes rich. However, the result from lattice QCD simulations in a thermomagnetic system yields chiral crossover [5–7, 25, 26], which is inconsistent with the estimate in the NJL model with the constant AMM. This implies that the constant AMM would not be a suitable form for low-energy effective theory based on the underlying QCD. In the next subsection, we deal with another description of the quark AMM.
-
In this subsection, we consider the magnetic-dependent quark AMM proportional to the chiral condensate:
$ \kappa_{u}=\kappa_{d}= v \sigma $ . Figure 4 shows the magnetic-dependent AMM$ \kappa_{u}=\kappa_{d}= v \sigma $ effect on the chiral condensate at zero temperature. First, we set the AMM parameter v to negative values. Panel (a) of Fig. 4 shows that for$ v<0 $ , the magnetic-dependent AMM plays the role of catalyzer for chiral symmetry breaking under the magnetic field. Thus, we also discard the magnetic-dependent AMM contribution for$ v<0 $ in this study, as in the case of the negative value of the constant AMM parameter ($ \kappa_{u,d}={\rm const.} $ ). Below, we only focus on positive values of the AMM parameter v.
Figure 4. (color online) Similar to Fig. 1, but in the case of the magnetic-dependent AMM proportional to the chiral condensate:
$ \kappa_{u}=\kappa_{d}= v \sigma $ . Panel (a) shows that the magnetic-dependent AMM flips the sign on the chiral condensate. In panel (b), the normalized effective potential is evaluated at$ T=0 $ and$ eB=0.8\; {\rm GeV}^{2} $ . The global minimum point of the normalized effective potential jumps from the positive vacuum to the negative vacuum.For
$v=0.01~{\rm GeV}^{-2}$ , the magnetic scaling of the chiral condensate is almost on the same trajectory as that without the quark AMM, as shown in panel (a) of Fig. 4. As the AMM parameter v increases, for$v=0.02~{\rm GeV}^{-2}$ , the striking phenomena emerge in the chiral condensate, i.e., a jump of$ \bar \sigma $ appears at the critical magnetic field, and the sign of the chiral condensate flips from positive to negative. In addition, the negative tendency of the critical magnetic field of$ \bar \sigma $ shifts to a weaker magnetic field when the AMM parameter v increases. This change in the sign of$ \bar \sigma $ can be explicitly viewed from the deformation of the effective potential, as shown in panel (b) of Fig. 4, where the magnetic field is fixed as$eB= 0.8~ {\rm GeV}^{2}$ . The global minimum point of the effective potential jumps from the positive vacuum ($ \bar \sigma>0 $ ) to the negative vacuum ($ \bar \sigma<0 $ ) as the AMM parameter v increases.Note that the magnetic-dependent AMM for
$\kappa_u=\kappa_d= v\sigma$ has already been addressed in the NJL model analysis in [14, 15]. However, the flipped-$ \bar \sigma $ or negative$ \bar \sigma $ solution was simply dropped in [14, 15] because a negative$ \bar \sigma $ indicates a negative dynamical quark mass, which was believed to be unphysical.We also evaluate the thermal effect on the chiral condensate including the magnetic-dependent AMM effect. As shown in panel (a) of Fig. 5, in the case of the small AMM parameter corresponding to
$v=0.01 {\rm GeV}^{-2}$ , the magnetic-dependent AMM hardly contributes to the chiral condensate even at finite temperatures. The monotonically increasing$ \bar \sigma $ for$v=0.01 ~{\rm GeV}^{-2}$ persists, and the change in the sign of$ \bar \sigma $ does not appear at any temperature.
Figure 5. (color online) (a) Thermal effect on the chiral condensate as a function of the magnetic field for
$\kappa_{u}=\kappa_d=0.01 \sigma~ {\rm GeV}^{-1} $ $ (v=0.01~{\rm GeV}^{-2})$ , which is compared with the case without the quark AMM contribution. (b) Corresponding normalized effective potentials for$v=0.01~{\rm GeV}^{-2}$ are evaluated at$eB=0.6~{\rm GeV}^{2}$ .For
$v=0.05~{\rm GeV}^{-2}$ as a case of the flipped-$ \bar \sigma $ , the finite temperature interferes with the flip of$ \bar \sigma $ . The flip-point is shifted to a stronger magnetic field region with increasing temperature (see panel (a) of Fig. 6). This behavior can also be seen from the deformation of the effective potential. In panel (b) of Fig. 6, where the magnetic field is fixed as$ eB=0.6\,{\rm GeV}^{2} $ , the effective potential structure is deformed by the thermal effect, and hence, the global minimum point of the effective potential appears back in the positive vacuum at high temperatures.
Figure 6. (color online) (a) Thermal effect on the chiral condensate as a function of the magnetic field for
$\kappa_{u}=\kappa_d=0.05 \sigma ~{\rm GeV}^{-1} $ $ (v=0.05~{\rm GeV}^{-2})$ . (b) Corresponding normalized effective potentials are evaluated at$eB=0.6~{\rm GeV}^{-2}$ .Although the flip in the sign of the chiral condensate may possibly induce intriguing phenomena in meson dynamics, the flipped-chiral condensate (quark condensate) has not been observed in lattice QCD simulations [5–7, 25, 26]. Thus, the magnetic dependent AMM proportional to the chiral condensate is also an unsuitable effective form to describe the QCD vacuum under a constant magnetic field.
-
Now, we take the magnetic-dependent AMM for
$ \kappa_u=\kappa_d =\bar v\sigma^2 $ 6 . Figure 7 illustrates a similar plot as Fig. 4. This figure shows that at zero temperature, the development of the AMM parameter$ \bar v $ suppresses the enhancement of the chiral condensate with increasing magnetic field. Therefore, the magnetic-dependent AMM for$ \bar v>0 $ plays the role of destructive interference or magnetic inhibition for chiral symmetry breaking under the magnetic field.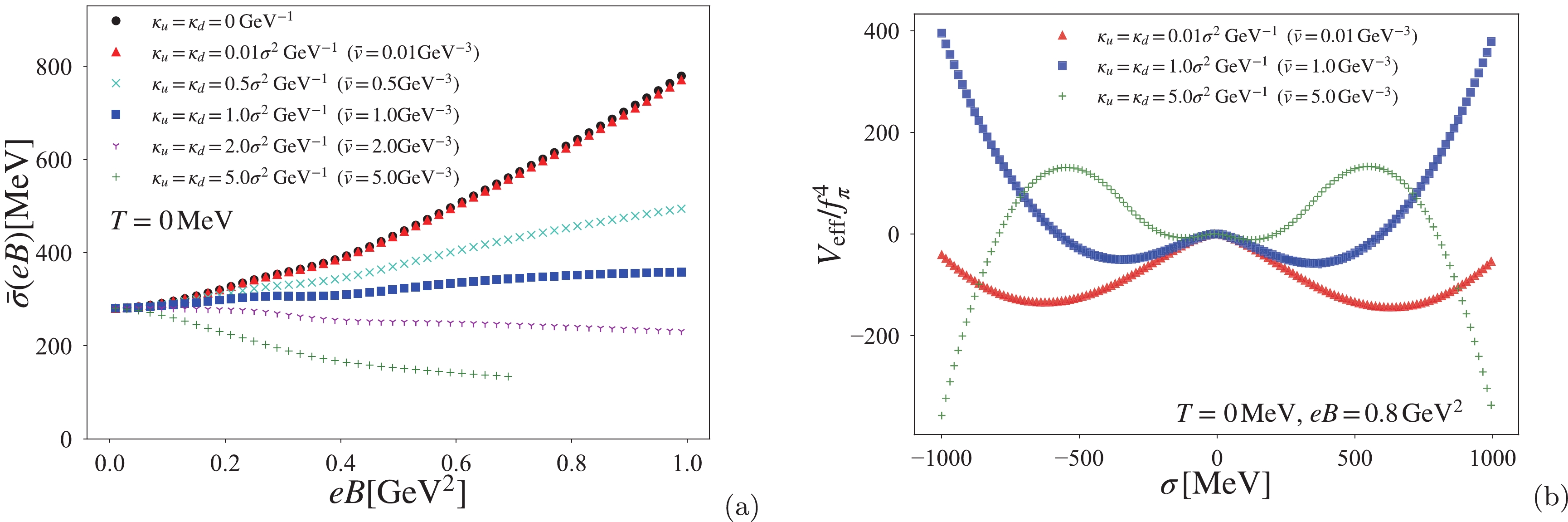
Figure 7. (color online) Similar to Fig. 4, but in the case of the magnetic-dependent AMM proportional to the square of the chiral condensate:
$ \kappa_{u}=\kappa_{d}= \bar v \sigma^2 $ . Panel (a) shows the magnetic effect on the chiral condensate with different values of the AMM parameter$ \bar v $ . Panel (b) shows the normalized effective potential evaluated at$ T=0 $ and$ eB=0.8\; {\rm GeV}^{2} $ .However, when the AMM parameter
$ \bar v $ takes a value larger than$ 2\; {\rm GeV}^{-3} $ , the vacuum structure of the NJL model becomes unstable in the sufficient magnetic field region. As shown in panel (b) of Fig. 7, the magnetic-dependent AMM for$ \bar v=5.0\; {\rm GeV}^{-3} $ catastrophically deforms the effective potential at a strong magnetic field$ eB=0.8~{\rm GeV}^2 $ . Therefore, the vacuum structure collapses owing to the significant contribution of the magnetic-dependent AMM, and then, the global minimum of the effective potential vanishes7 . Consequently, in panel (a) of Fig. (7), the chiral condensate in the case of$ \bar v= 5.0\; {\rm GeV}^{-3} $ vanishes for$ eB\geq0.7~{\rm GeV}^2 $ .We next discuss the vacuum stability at finite temperatures, as well as the chiral condensate. Indeed, for
$0 < \bar v\leq 2.0~{\rm GeV}^{-3}$ , the vacuum maintains a stable structure even at high finite temperatures. Figure 8 shows the thermal effect on the chiral condensate for$\bar v=2.0~{\rm GeV}^{-3}$ and the deformation of the corresponding effective potential. From panel (b) of Fig. 8, we find that the magnetic-dependent AMM barely affects the deformation of the effective potential, and the vacuum structure is still steady in the thermomagnetic system. In this case, observing the magnetic dependence of the chiral condensate at finite temperatures, we also find that the enhancement of chiral symmetry breaking under the magnetic field is inhibited by the presence of the magnetic-dependent AMM, maintaining the stable vacuum structure.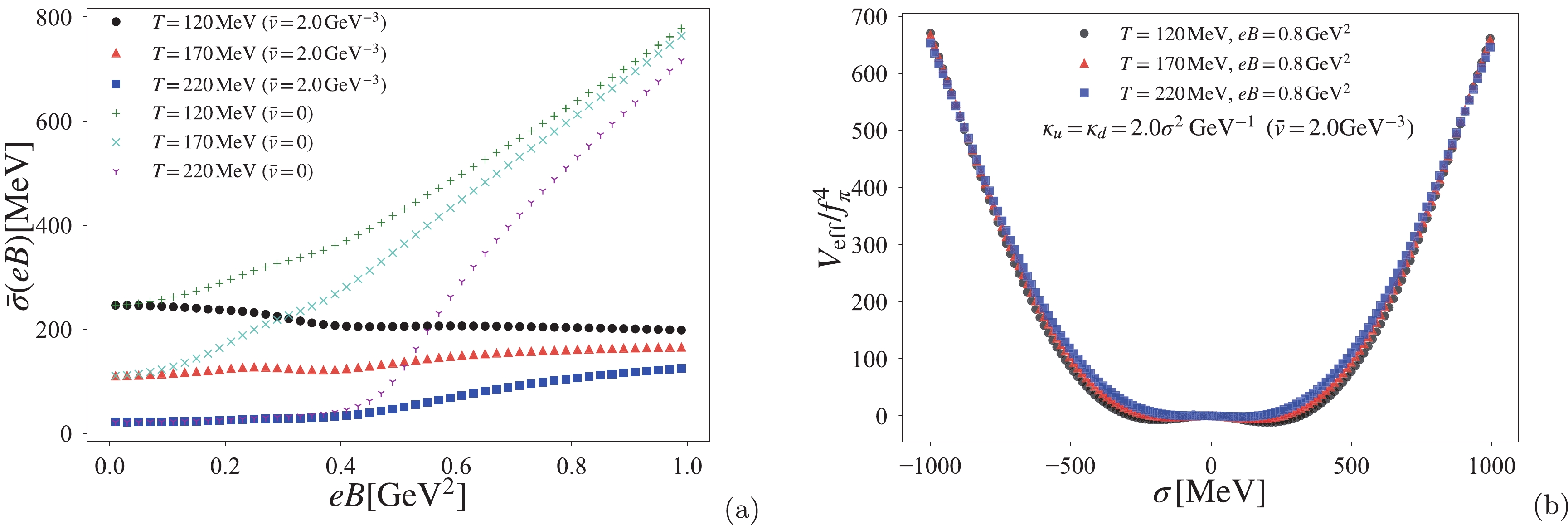
Figure 8. (color online) (a) Thermal effect on the chiral condensate for
$\bar v=2.0~{\rm GeV}^{-3}$ , in comparison with the case without the quark AMM; (b) thermal deformation of the normalized effective potential structure at$ eB=0.8\; {\rm GeV}^2 $ .For
$ \bar v>2~{\rm GeV}^{-3} $ , the thermal effect promotes the destruction of the effective potential structure. In Fig. 9, we take$ \bar v=5.0~{\rm GeV}^{-3} $ as the case of the large AMM parameter. In reality, thermal evolution makes the vacuum structure more unstable, as presented in panel (b) of Fig. 9. As a consequence of the collapse of the vacuum, we find that the chiral condensate vanishes for$ eB>0.65~{\rm GeV}^{2} $ (see panel (a) of Fig. 9).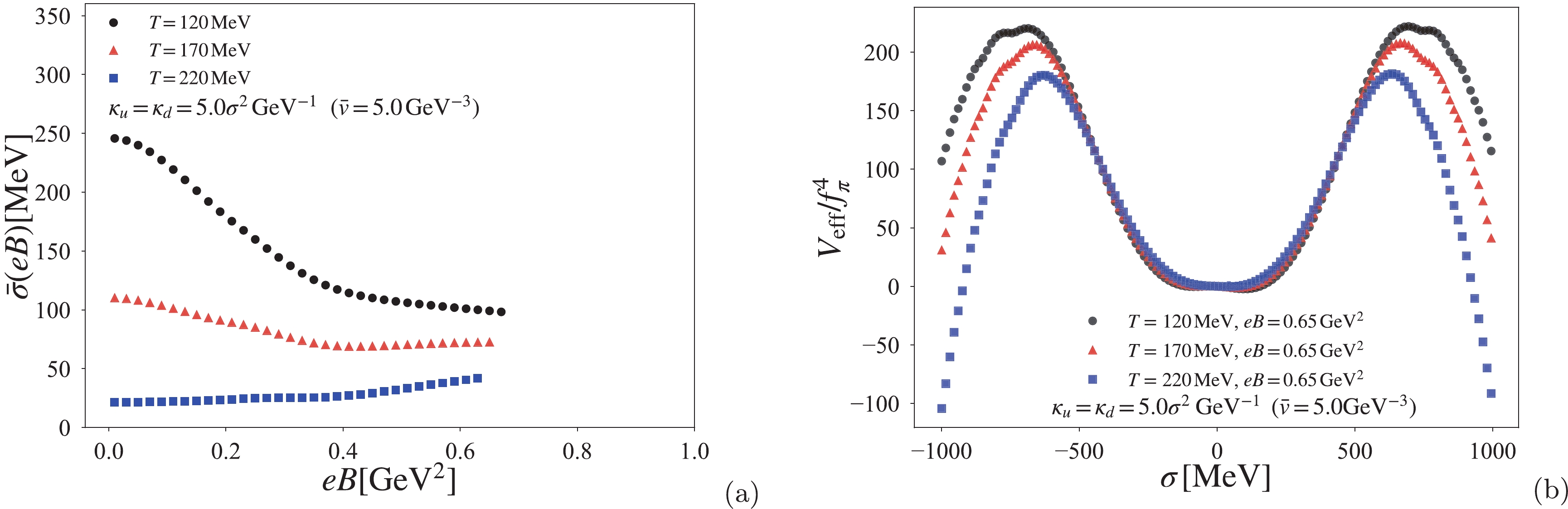
Figure 9. (color online) Thermal effect on vacuum instability for
$\bar v=5.0~{\rm GeV}^{-3}$ . Panel (a) shows the temperature evolution of the chiral condensate. Panel (b) shows the thermal deformation of the normalized effective potential at$ eB=0.65\; {\rm GeV}^2 $ .In the case of the magnetic-dependent AMM proportional (
$ \kappa_{u,d}=\bar v \sigma^2 $ ) to the parameter constraint$ 0<\bar v\leq 2.0~{\rm GeV}^{-3} $ 8 , the effective potential maintains the stable structure while the unexpected behavior does not emerge in the chiral condensate, such as the induced-first order phase transition and the flip in the sign of$ \bar \sigma $ . Instead, the magnetic-dependent AMM sufficiently suppresses chiral symmetry breaking under the magnetic field. Therefore, there is be a possibility that the magnetic-dependent AMM may be a factor contributing to IMC for the chiral condensate. -
Although the proposed extra mechanisms, such as neutral pion fluctuation [8], chirality imbalance [9], and running coupling with the magnetic field [10], lead to IMC behavior for the quark condensate in the effective model analysis, the quark AMM could also possibly reduce the magnetic enhancement of chiral symmetry breaking in the thermomagnetic system, as presented in the previous section. In this subsection, we shall consider how much the magnetic-dependent AMM potentially contributes to the IMC effect. Hence, we compare the results of the quark condensate obtained from the NJL model by considering the magnetic-dependent AMM (
$ \kappa_u=\kappa_d=\bar v \sigma^2 $ ) with those from the lattice QCD calculation [25, 26]. Later, we also show the intrinsic temperature dependence of the AMM parameter$ \bar v $ by fitting the NJL result to lattice QCD data to find a correlation between the magnetic-dependent AMM and chiral phase transition.The quark condensate (chiral condensate) involves ultraviolet divergence at the zero-temperature part and should be renormalized as a finite quantity. To eliminate the divergence arising in the quark condensate under the magnetic field, we use the following dimensionless quantity of the subtracted quark condensate:
$ \begin{aligned}[b] \frac{\Sigma_u+\Sigma_d}{2}=& 1-\frac{m_l}{m_\pi^2 f_\pi^2}\Big[ \bigl( \langle \bar uu\rangle(B,T)-\langle \bar uu\rangle(0,T)\bigl)\\& + \bigl( \langle \bar dd\rangle(B,T) -\langle \bar dd\rangle(0,T) \bigl) \Big]. \end{aligned} $

(9) Figure 10 shows the magnetic dependence of the subtracted quark condensate at zero temperature in comparison with the lattice QCD observation [25]. The subtracted quark condensate, in the case of the NJL model without the AMM term (
$ \kappa_{u,d}=0 $ ), monotonically increases as the magnetic field increases, that is, the MC effect. This predicted magnetic dependence deviates from the lattice QCD data. The NJL result in the absence of the AMM contribution tends to predict larger chiral symmetry breaking under the magnetic field. However, by including the magnetic-dependent AMM ($\kappa_u=\kappa_d= \bar v \sigma^2$ ), the magnetic enhancement in the subtracted quark condensate is suppressed, and the NJL result for$\bar v=0.9~{\rm GeV}^{-3}$ is in good agreement with the lattice QCD results.
Figure 10. (color online) Comparison of the subtracted quark condensate between the NJL result and lattice QCD data at
$ T=0 $ [25].Figure 11 shows a comparison of the subtracted quark condensate of the NJL model prediction and lattice QCD data at finite temperatures [26]. To reconcile the gap between the NJL and lattice results, we tune the value of the AMM parameter
$ \bar v $ . For the low temperature regions where$ T\sim0- 140\; {\rm MeV} $ , panel (a) of Fig. 11 shows that the NJL results fit well with lattice QCD data. However, for the high temperature regions where$ T\sim 170- 280\; {\rm MeV} $ , the AMM term also reduces the magnetic enhancement of the quark condensate, but the NJL results start to deviate from the lattice observation at approximately$ eB=0.4\,{\rm GeV}^2 $ for$ T=170 $ MeV and$ T=210 $ MeV, and at approximately$ eB=0.6\,{\rm GeV}^2 $ for$ T=280 $ MeV, as shown in panel (b) of Fig. 11. Owing to the restriction of the AMM parameter ($ 0\leq \bar v\leq 2~{\rm GeV}^{-3} $ ), the NJL results cannot perfectly fit the lattice observation in entire magnetic field regions. Although the deviation remains in the high temperature regions ($T\sim 170- 280\; {\rm MeV}$ ), the magnetic dependence of the subtracted quark condensate is sufficiently suppressed by the magnetic-dependent AMM and qualitatively agrees with the lattice data.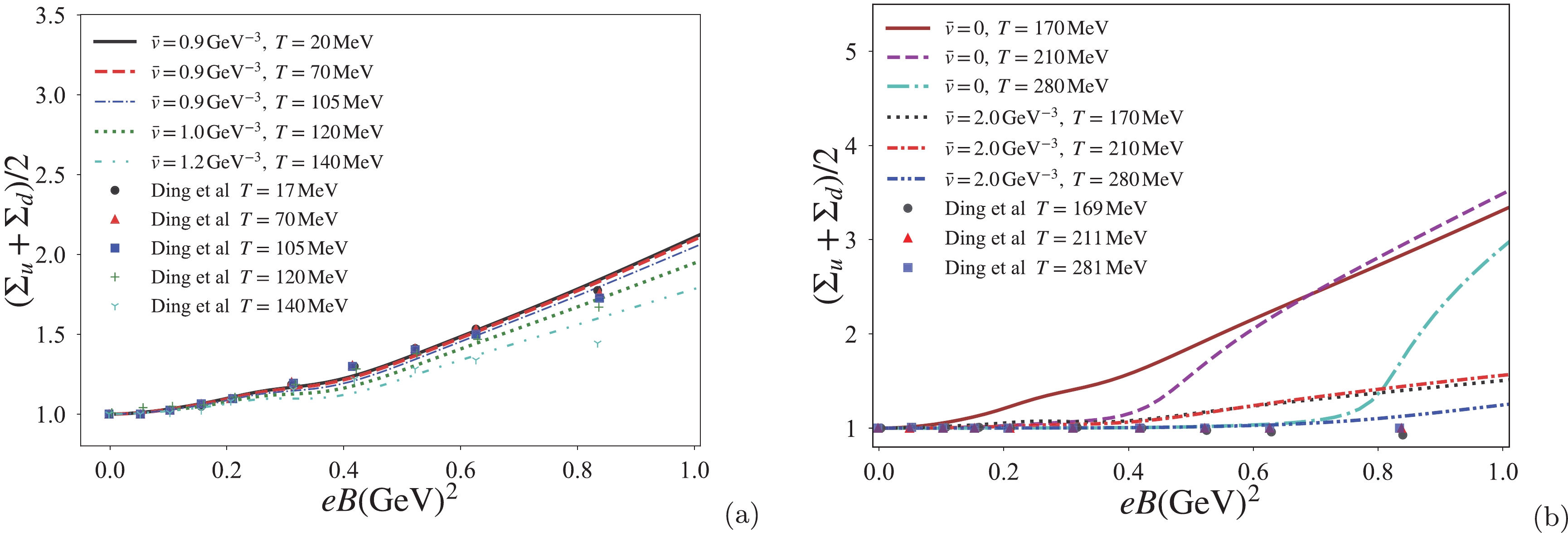
Figure 11. (color online) Comparison of the subtracted quark condensate of the NJL result and lattice QCD data [26] for (a) low temperature regions (
$ T\sim0- 140\; {\rm MeV} $ ), and (b) high temperature regions ($ T\sim 170-280\; {\rm MeV} $ ).In the previous subsections, we attempt to reveal the effective form of the quark AMM through a comparison of the order of the chiral phase transition observed in the lattice QCD simulation. We find that the quark AMM depending on the square of the chiral condensate is an applicable effective form to describe the phase transition order of thermomagnetic QCD. Although its form potentially suppresses the magnetic enhancement in the chiral condensate as shown in Figs. 10 and 11, the AMM form would be still ambiguous owing to the uncertain model parameter
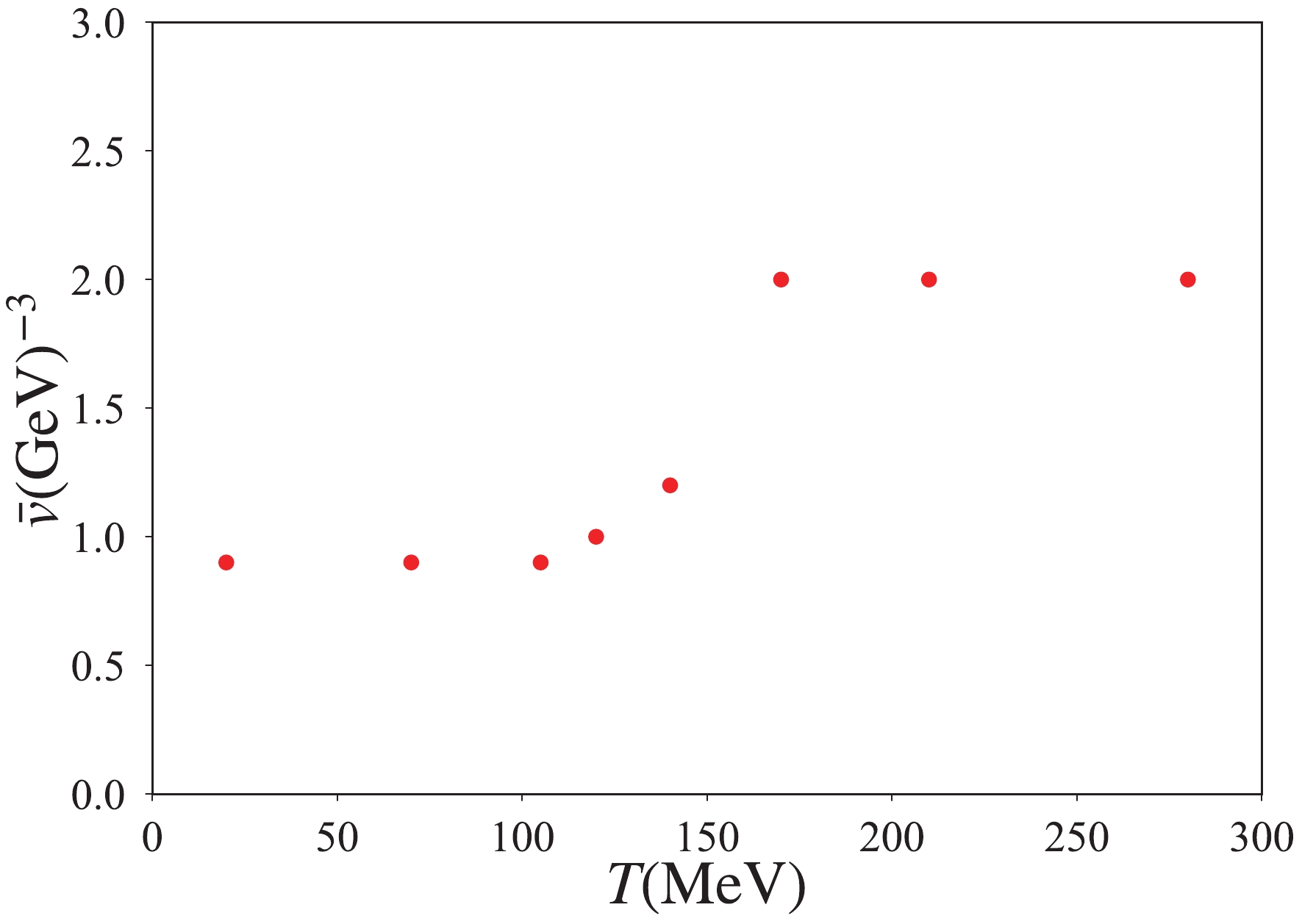
$ \bar v $ ; nonperturbative features associated with spontaneous chiral symmetry breaking may be intrinsically contained in the AMM parameter$ \bar v $ . By considering the temperature dependence of the effective interaction of the quark AMM, one would expect that the AMM parameter$ \bar v $ also depends on temperature and may be related to the thermomagnetic phase transition. To reveal further details on the effective form, we discuss the temperature dependence of the quark AMM using the NJL results tuned by the lattice results. The intrinsic temperature dependence of the AMM parameter$ \bar v $ can be expressed from the tuned results in Figs. 10 and 11 and is plotted in Fig. 12. Around the low temperature regions where$ T\sim0-100 $ MeV, the AMM parameter$ \bar v $ behaves as a constant. As the temperature further increases,$ \bar v $ rapidly increases at approximately the pseudocritical temperature$ T_{\rm pc}\simeq 160 $ MeV ($ T_{\rm pc} $ will be seen later) and then reaches the upper limit of$ \bar v $ ,$ \bar v= 2\,{\rm GeV}^{-3} $ . This thermal behavior implies that the intrinsic temperature dependence of$ \bar v $ may correlate with the chiral phase transition.Using the temperature-dependent AMM parameter
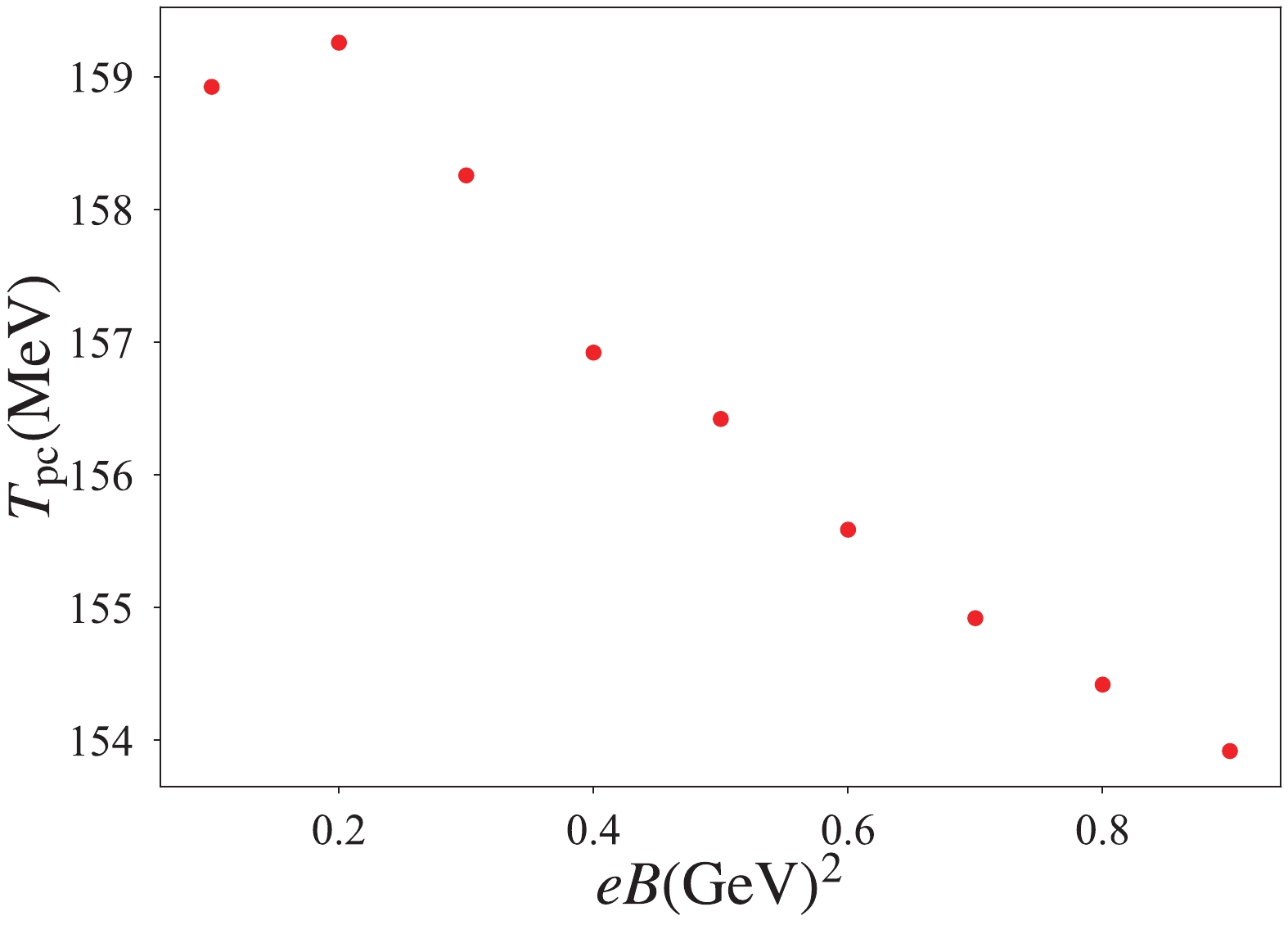
$ \bar v(T) $ estimated in Fig. 12, we finally show the chiral phase diagram for the$ eB-T $ plane in Fig. 139 . This figure shows that the pseudocritical temperature decreases with the development of the magnetic field, and IMC is surely provided by the NJL analysis with the parameter$ \bar v(T) $ (fitted using the lattice observation [26])10 This indicates that the magnetic-dependent AMM with the intrinsic temperature dependence ($ \kappa_{u,d}=\bar v(T)\sigma^2 $ ) somewhat inhibits MC. -
In this study, we explore the effective form of the AMM in thermomagnetic QCD vacuum. Employing the NJL model with the effective interaction of the quark AMM, we discuss the influence of the AMM on the chiral condensate in the following three forms: (a)
$ \kappa_{u,d}={\rm const.} $ , (b)$ \kappa_{u,d}=v \sigma $ , and (c)$ \kappa_{u,d}=\bar v \sigma^2 $ . Although effective AMM forms associated with chiral symmetry breaking have already been suggested in previous studies [12, 13], in our study, we address in detail which effective form suitably describes the chiral phase transition of the thermomagnetic QCD vacuum. Paying attention to the significant AMM effect on the chiral phase transition, we restrict the effective forms of the quark AMM. The restriction on the effective AMM form is an important step to developing our understanding of the quark AMM associated with chiral symmetry breaking, which is first attempted in our extension research from previous studies [12, 13].Our findings in the three forms can be summarized as follows:
(a) For
$ \kappa_{u,d}={\rm const.} $ , the constant AMM significantly deforms the effective potential structure. The potential wall is driven by the constant AMM, so that the chiral first order phase transition is induced at zero and finite temperatures. However, this induced-first phase transition is inconsistent with the lattice QCD result, which shows a crossover for chiral phase transition. Hence, the constant AMM is an unsuitable form.(b) For
$ \kappa_{u,d}=v \sigma $ , the effective potential structure is also deformed by the magnetic-dependent AMM. As a result, the global minimum point of the effective potential jumps from the positive vacuum to the negative vacuum at the critical magnetic field. Thus, the sign of the chiral condensate changes from positive to negative with the increase in the magnetic field at$ T=0 $ and$ T\neq 0 $ . However the flip in the sign of the chiral condensate (subtracted quark condensate) has not been observed in lattice QCD simulations. Thus, the effective AMM form proportional to the chiral condensate is discarded.(c) For
$ \kappa_{u,d}=\bar v \sigma^2 $ , accidental jumps do not emerge in the chiral condensate across the chiral phase transition, such as the induced-first order phase transition and the sign flip of the chiral condensate. Instead, the magnetic-dependent AMM ($ \kappa_{u,d}=\bar v \sigma^2 $ ) inhibits chiral symmetry breaking under the magnetic field while retaining the chiral crossover phase transition. However, instability occurs in the effective potential for large values of the AMM parameter$ \bar v $ . Hence, the AMM parameter$ \bar v $ should be restricted to provide the inhibition for MC, maintaining the stable vacuum. Using the restricted AMM parameter$ \bar v $ , the subtracted quark condensate in the NJL model can quantitatively fit the lattice results at zero and finite temperatures across the chiral crossover. Therefore,$ \kappa_{u,d}=\bar v \sigma^2 $ remains a candidate of the effective form of the quark AMM.Our findings indicate that the magnetic-dependent AMM form
$ \kappa_{u,d}=\bar v \sigma^2 $ would be the practicable effective form to qualitatively describe the property of the thermomagnetic vacuum of QCD. In addition, we also provide the intrinsic temperature dependence of the AMM parameter$ \bar v $ through a comparison of the NJL and lattice QCD results. The fitting-parameter$ \bar v $ implies that the temperature dependence of the magnetic-dependent AMM may be correlated with the chiral phase transition.As mentioned above, the subtracted quark condensate involving the AMM contribution can qualitatively fit the lattice observation but does not perfectly agree with the lattice data, especially at high temperatures. The IMC behavior observed in the lattice QCD simulations cannot be completely explained by only the effective quark AMM (
$ \kappa_{u,d}=\bar v \sigma^2 $ ). The connection between the quark AMM and the IMC effect is still an open question. However, the quark AMM would be dynamically generated associated with chiral symmetry breaking, which may reduce magnetic enhancement in the chiral condensate. Therefore, the contribution of the quark AMM should be considered in the chiral effective model analysis. To provide the a sufficient IMC effect in the chiral effective model with the AMM, the effective form of the AMM may be improved, or an extra mechanism, such as the magnetic dependent coupling constant, would be required, which will be pursued elsewhere.Before concluding this study, we comment on the implications of the magnetic-dependent AMM. A recent lattice QCD simulation also exhibited the magnetic effect on the meson masses at zero-temperature [17]. This shows that pion mass starts to deviate from the point-like particle behavior with increasing magnetic field. To address this deviation, the AMM contribution to meson properties is worth studying. The influence of the magnetic-dependent AMM on meson masses has already been discussed based on the NJL model [12, 13]. However, the vacuum structure and its stability were not considered. Hence, it would be valuable to reevaluate the meson properties with the vacuum structure in mind.
Furthermore, magnetic susceptibility in the thermomagnetic QCD vacuum has recently been revealed via lattice QCD simulation [27, 28]: the magnetized QCD vacuum behaves as diamagnetism at low temperatures but turns out to be paramagnetism with increasing temperature. It is important to investigate the influence of the quark AMM on magnetic susceptibility. Indeed, the NJL model tends to produce paramagnetism at finite temperatures, which is enhanced by the presence of the magnetic-dependent AMM (without the intrinsic temperature dependence of the AMM parameter) [12, 13]. It would also be worth considering the intrinsic temperature dependence of magnetic susceptibility.
Moreover, magnetic susceptibility is closely linked with the spin polarization condensate [27, 28]. In general, a tensor quark bilinearly acquires a nonzero expectation value in the external magnetic field, which is related to the interaction form of the quark AMM. Further investigation of the spin polarization condensate (tensor condensate) may be interesting to find a nontrivial correlation among magnetic susceptibility, the tensor condensate, and the magnetic-dependent AMM.
Though an extra mechanism, such as the use of a coupling
$ G_S(B,T) $ , is one possibility to explain the IMC effect in the NJL model, we still require a selfconsistent understanding of recent lattice results including the IMC effect, neutral and charged pion mass behavior under a magnetic field, and diamagnetism. The AMM of quarks is one of the possible candidates to provide a selfconsistent understanding of recent lattice observations.The predicted magnetic-dependent AMM interaction could be applied to high-dense matter physics with magnetic fields. In particular, a strong magnetic field is generated in neutron stars or magnetars. The mechanism of the the generation of a strong magnetic field has not yet been clarified. In Refs. [29, 30], it was noted that the spin polarization of baryons induces ferromagnetism in magnetars. The quark-spin is crucially related to spontaneous magnetization. In addition, it has been discussed that spontaneous magnetization is driven by the quark AMM in the NJL model with a constant AMM term [31]. Therefore, we anticipate that spontaneous magnetization can be directly linked with dynamical chiral symmetry breaking using the magnetic-dependent AMM instead of a constant one. The magnetic-dependent AMM would be a significant factor in understanding a new aspect of magnetized quark matter as well as magnetars.
In this study, we suppose that the chiral condensate and AMM take the isospin symmetric form:
$ \bar \sigma_u=\bar \sigma_d $ and$ \kappa_u=\kappa_d $ . In fact, chiral symmetry is explicitly broken by the external magnetic field; hence, flavor symmetry breaking should be considered in the chiral condensate and AMM term. We leave the flavor symmetry breaking effect for further studies. -
We are grateful for discussions with Fan Lin, Kun Xu, and Aminul Chowdhury.
-
Here, we discuss the regularization scheme dependence of the first order phase transition induced by a constant AMM at zero temperature. As stated in Sec. III.A, the induced-first order phase transition is actually observed in the NJL model based on both the Lorentzian and Woods-Saxon type form factors [19]. To address how much the choice of the regularization scheme is relevant to the phase transition, we focus on another regularization scheme here.
The Pauli-Villars regularization scheme has previously been applied to avoid the unphysical oscillation of the chiral condensate in two-flavor NJL analysis including a constant AMM [32], where the value of the magnetic field was fixed at
$ eB=10m_\pi^2 $ and the constant AMM$ \kappa_{u,d} $ were taken as$\kappa_u=0.101~{\rm GeV^{-1}}$ and$\kappa_d= 0.175~{\rm GeV^{-1}}$ . However, the magnetic effect on the chiral condensate at zero temperature was not fully studied in [32]. To clarify whether the induced-first order phase transition arises within the framework of the Pauli-Villars regularization scheme, we take the same regularization scheme and model parameter set as in [32] ($m_0=10.3~{\rm MeV}$ ,$\Lambda=744.2~{\rm MeV}$ and$ G_S\Lambda^2=6.21 $ ); however, the constant AMM is varied as a free parameter in the same manner as in our study.In Fig. A1, we show the constant AMM effect on the chiral condensate at zero-temperature based on the Pauli-Villars regularization scheme. As clearly shown in panel (a) of Fig. A1, the chiral condensate undergoes a jump as the constant AMM gets larger. Furthermore, as shown in panel (b) of Fig. A1, the effective potential is deformed by the constant AMM, and the potential barrier is built with the increase in the constant AMM, where the magnetic field is fixed as
$ eB=0.5\,{\rm GeV}^2 $ . Therefore, the induced-first order phase transition occurs even in the case of the Pauli-Villars regularization scheme. Given our investigation of the Lorenztian form factor, Woods-Saxon type form factor, and Pauli-Villars regularization scheme, the choice of regularization scheme is irrelevant to the first order phase transition induced by the constant AMM.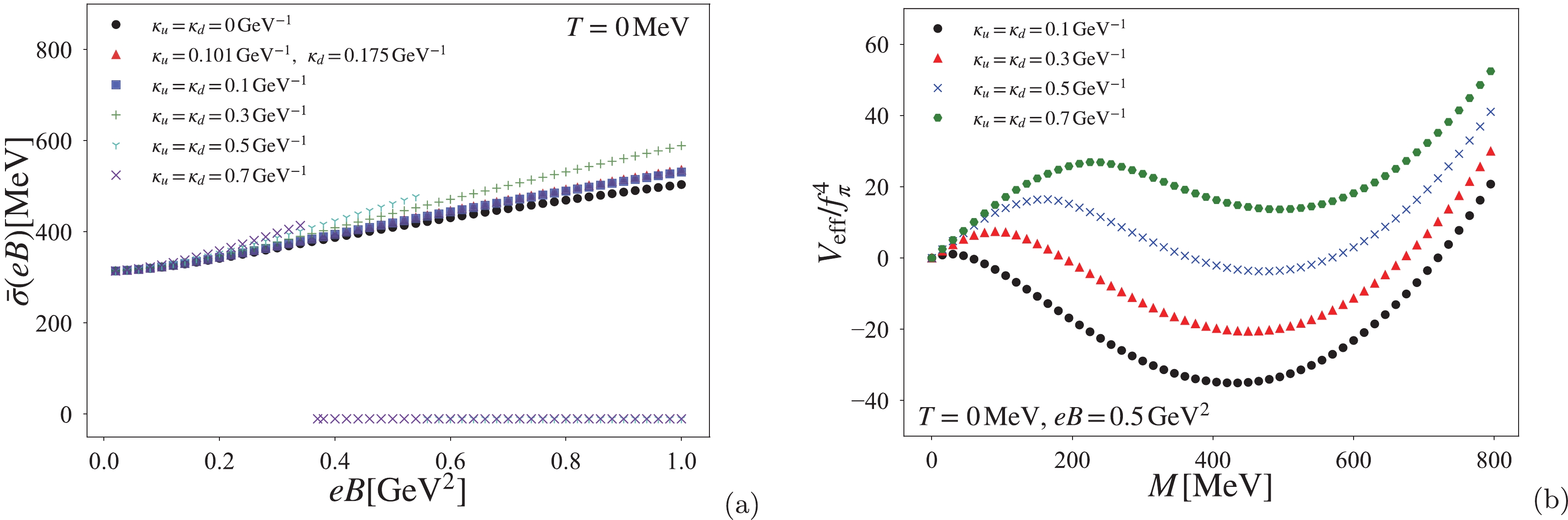
Figure A1. (color online) Similar to Fig. 1 but based on the Pauli-Villars regularization scheme. The panel (a): the magnetic effect on the chiral condensate with the different values of the constant AMM. The panel (b): the normalized effective potential at
$ T=0 $ and$ eB=0.5\,{\rm GeV}^2 $ .
Restriction on the form of the quark anomalous magnetic moment from lattice QCD results
- Received Date: 2023-01-11
- Available Online: 2023-06-15
Abstract: The quark anomalous magnetic moment (AMM) is dynamically generated through spontaneous chiral symmetry breaking. It has been revealed that, even though its exact form is still unknown, the quark AMM is essential to exploring quark matter properties and QCD phase structure under external magnetic fields. In this study, we take three different forms of the quark AMM and investigate its influence on the chiral phase transition under a magnetic field. In general, a negative (positive) quark AMM acts as a magnetic-catalyzer (magnetic-inhibitor) for chiral symmetry breaking. It is found that a constant quark AMM drives an unexpected 1st order chiral phase transition, a quark AMM proportional to the chiral condensate flips the sign on the chiral condensate, and a quark AMM proportional to the square of the chiral condensate suppresses the magnetic enhancement in the chiral condensate at finite temperatures while retaining the chiral crossover phase transition. We also evaluate the intrinsic temperature dependence of the effective AMM form by fitting the effective model result of the chiral condensate to lattice QCD data, which may have a nontrivial correlation with the chiral phase transition.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: