-
The standard model, as a theory of elementary particle interactions, has achieved great success in describing experimental data with various energies. Nevertheless, the
$ \sim 2 $ GeV masses of charmed mesons place them in the region where perturbative QCD is not applicable, which raises the challenges faced by both theory and experiments. In recent years, standard model testing with high precision measurements has become one of the hottest topics in the charm sector.The semi-leptonic decays of charmed mesons, in which hadronic and weak currents can be well separated, provide a clean platform for studying the mechanism of the c quark to
$ d(s) $ quark transition and play an important role in understanding strong and weak interactions. Their partial decay width accesses the product of the hadronic form factor, which describes the strong-interaction in the hadronic current connecting initial and final hadrons, and the Cabibbo-Kobayashi-Maskawa matrix element$ |V_{cs}| $ or$ |V_{cd}| $ , which parameterizes the weak interaction between different quark flavors. Partial wave analyses of the four-body semi-leptonic decays of charmed mesons allow us to extract the form factors in the$ D\to V \ell^+\nu_\ell $ and$ D\to S \ell^+\nu_\ell $ transitions (where$ \ell=e,\mu $ , V and S denote vector and scalar mesons, respectively).$ K^{*}(892)^{-(0)} $ resonance has been studied in the$ D^{0(+)}\to K^{0(-)}\pi^+e^+\nu_e $ decay by the CLEO, BABAR, and BESIII collaborations [1–4]. BESIII has also studied$ \rho^- $ resonance in$ D^{0}\to \pi^-\pi^0e^+\nu_e $ [5], and$ \rho^0 $ , ω, and$ f_0(500) $ resonances in$ D^{+}\to \pi^+\pi^-e^+\nu_e $ [5]. In the near future, more partial wave analyses are expected to be performed with high-statistics datasets, including$ D_{(s)} $ semi-muonic decays1 .However, lepton mass is neglected in the parameterization formula used for the amplitude analyses of charmed meson semi-leptonic decays. This should be manageable in the case of semi-electronic decays, but will cause bias in semi-muonic decays, which downgrades the advantage of high-statistics from the new data and conflicts with the purpose of precision measurement. In this study, we derive the formula while considering the mass of leptons based on Refs. [6, 7]. The results are presented in the format used in experimental analyses; therefore, researchers can easily adopt our results to their experimental analyses. Charge-conjugated decay modes are implied throughout this paper.
-
First, we define the kinematic variables and discuss their relations. The four-body semi-leptonic decay
$ D\to M_{1}M_{2}\ell^+\nu_\ell $ is considered, where D is the parent meson,$ M_{1(2)} $ is the product meson, and$ \ell=e,\,\mu $ . The momentum four-vectors and invariant masses are denoted by p and m, respectively. For convenience, the independent four-vector combinations are defined as$ \begin{aligned}[b]& P^\mu=p^\mu_{M_1}+p^\mu_{M_2},\quad Q^\mu=p^\mu_{M_1}-p^\mu_{M_2},\\ & L^\mu=p^\mu_{\ell}+p^\mu_{\nu},\quad N^\mu=p^\mu_{\ell}-p^\mu_{\nu}. \end{aligned} $

(1) A four-body decay can be uniquely described via kinematic parameterization with five variables (besides spin). The squared masses of the hadronic system
$ M_1M_2 $ and leptonic system$ \ell^+\nu_\ell $ are chosen as two of the five variables,$ \begin{eqnarray} s_M&=&P^2, \,\,\,\ s_L=L^2, \end{eqnarray} $

(2) and the following relations can be easily derived:
$ \begin{eqnarray} Q^2 =2 m_{M_1}^2+2m_{M_2}^2-s_M,~~~ N^2 =2m_{\ell}^2+2m_{\nu}^2-s_L, \end{eqnarray} $

(3) $ \begin{eqnarray} L\cdot P =\frac{ m_D^2-s_M-s_L}{2},\,\,\,\, L\cdot N = m_{\ell}^2-m_{\nu}^2,\,\,\,\, P\cdot Q = m_{M_1}^2-m_{M_2}^2. \end{eqnarray} $

(4) The other three variables are chosen as the angle between the
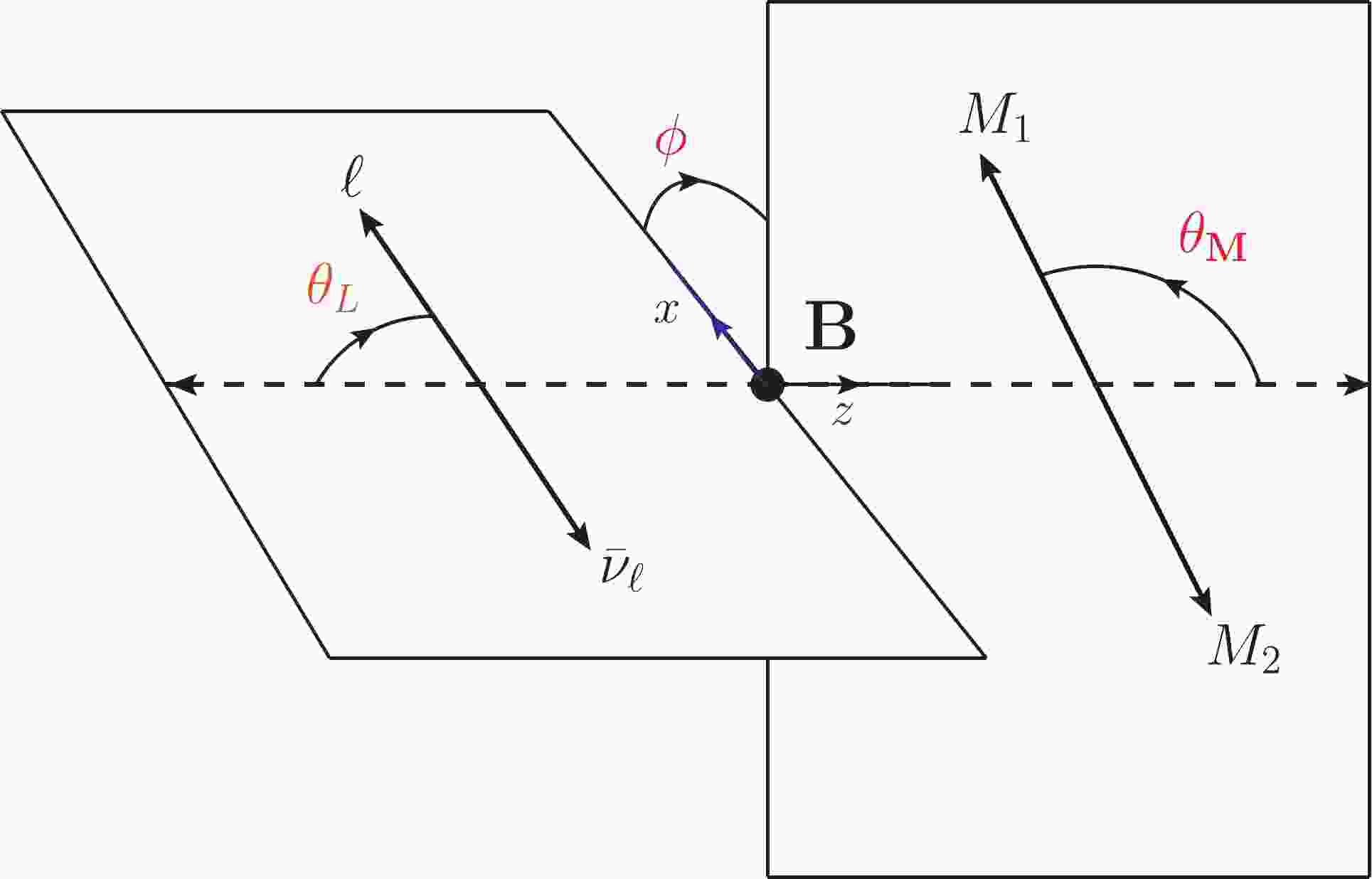
$ M_2 $ three-momentum and the D direction in the$ M_1M_2 $ rest frame ($ \theta_M $ ), the angle between$ \nu_\ell $ and the D direction in the$ \ell^+\nu_\ell $ rest frame ($ \theta_L $ ), and the angle between the two decay planes (ϕ)2 . The angles$ \theta_M $ ,$ \theta_L $ , and ϕ are illustrated in Fig. 1. The various relationships between scalar-product invariants can be written as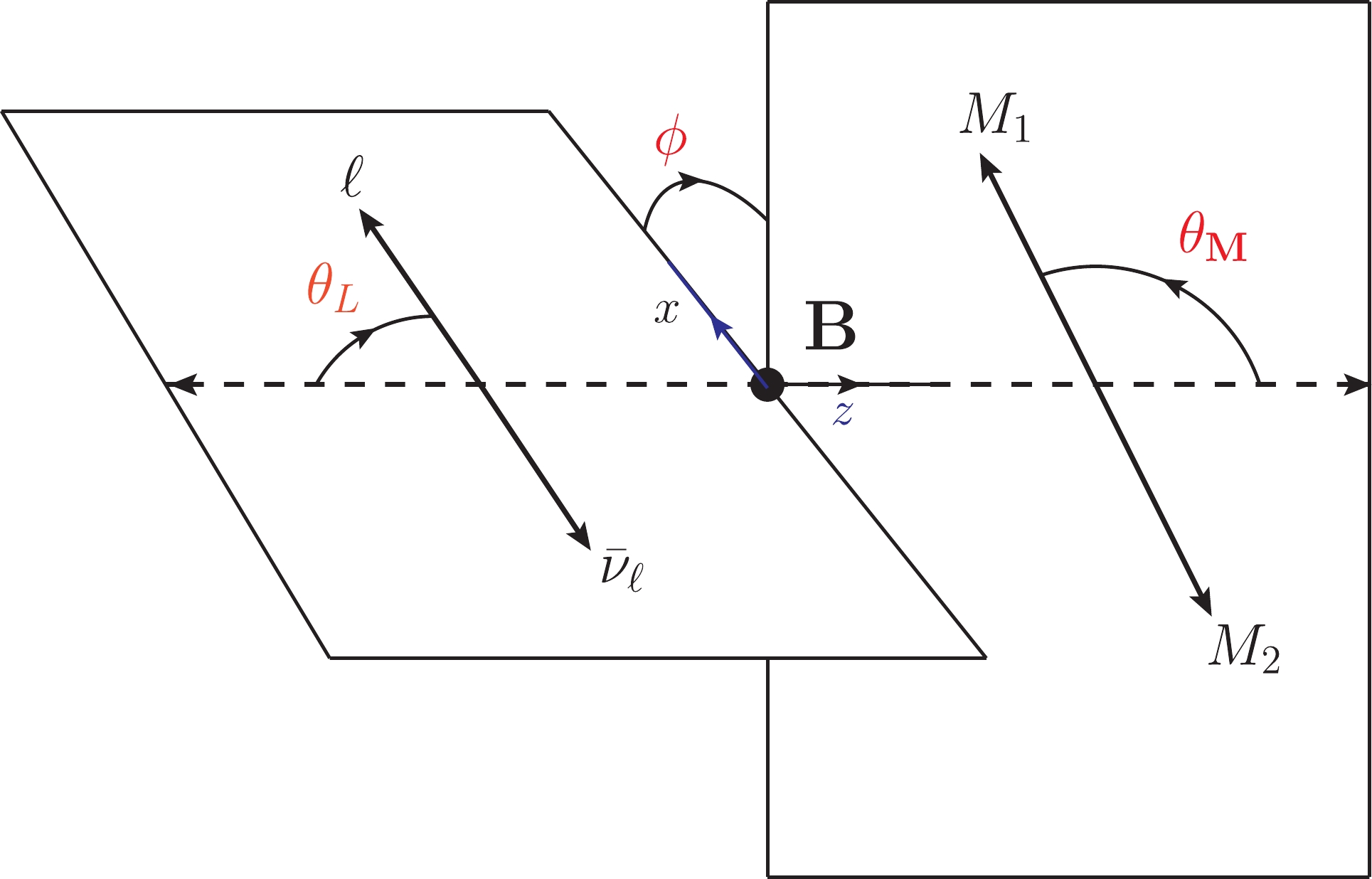
Figure 1. (color online) Definition of angles
$ \theta_L $ ,$ \theta_M $ , and ϕ in the cascade decay$ D\to M_1M_2 \ell^+\nu_\ell $ .$ \begin{aligned}[b] L\cdot Q =& L\cdot P\frac{m_{M_1}^2-m_{M_2}^2}{s_M} +X\beta_M \cos\theta_M\,,\\ N\cdot P =& L\cdot P\frac{m_{\ell}^2-m_{\nu}^2}{s_L} +X\beta_L \cos\theta_L\,,\\ N\cdot Q =&L\cdot P\beta_M \beta_L \cos\theta_M \cos\theta_L +\frac{m_{\ell}^2-m_{\nu}^2}{s_L}X\beta_M \cos\theta_M\\&+\frac{ m_{M_1}^2-m_{M_2}^2}{s_M}X\beta_L \cos\theta_L+L\cdot P\frac{ m_{M_1}^2-m_{M_2}^2}{s_M}\frac{m_{\ell}^2-m_{\nu}^2}{s_L}\\ & -\sqrt{s_M}\sqrt{s_L}\beta_M \beta_L \sin\theta_M \sin\theta_L \cos\phi\,,\\ \epsilon_{\mu\nu\rho\sigma}L^{\mu}&N^{\nu}P^{\rho}Q^{\sigma}= X\sqrt{s_M}\sqrt{s_L}\beta_M \beta_L \sin\theta_M \sin\theta_L \sin\phi\,, \end{aligned} $

(5) where
$ \beta_M $ is the three-momentum modulus of the meson in the center-of-mass frame of the meson-meson system,$ \beta_L $ the three-momentum modulus of the lepton in the center-of-mass frame of the lepton-neutrino system, and X an element of phase space,$ \begin{aligned}[b] \beta_M=&\sqrt{(s_M-m^2_+)(s_M-m^2_-)}/s_M \,,\\ \beta_L=&\sqrt{(s_L-m^2_{L^+})(s_L-m^2_{L^-})}/s_L \,,\\ X=&\sqrt{m_D^4+s_L^2+s_M^2-2s_Dm_L^2-2s_Mm_D^2-2s_Ms_L}/2 \,, \end{aligned} $

(6) with
$ \begin{aligned}[b] m_{L^+}= & m_{\ell}+m_{\nu};~~ m_{L^-}=m_{\ell}-m_{\nu}; \\m_+ =&m_{M_1}+m_{M_2};~~ m_-=m_{M_1}-m_{M_2}. \end{aligned} $

(7) Compared to Refs. [6, 7], we do not neglect the lepton mass.
Next, from the effective Hamiltonian at the quark level for
$ D\to M_{1}M_{2}\ell^+\nu_{\ell} $ , the decay amplitude is given by$ \begin{aligned}[b] & {\cal A}(D\to M_{1}M_{2}\ell^+\nu_{\ell}) \\=& \frac{G_{\rm F}}{\sqrt{2}}V_{q_1q_2}\langle M_{2}M_{1}|\bar{q}_1\gamma_{\mu}(1-\gamma_{5})q_2|D\rangle \bar{u}(p_\ell)\gamma^{\mu}(1-\gamma_{5})v(p_\nu)\,, \end{aligned} $

(8) where
$G_{\rm F}$ is the Fermi constant, and$ V_{q_1q_2} $ is the element of the Cabibbo-Kobayashi-Maskawa matrix. The hadronic matrix element can be written in terms of four form factors,$ w_\pm $ , r, and h, which are defined by$ \begin{aligned}[b]& \langle M_{2}M_{1}|\bar{q}_1\gamma_{\mu}(1-\gamma_{5})q_2|D\rangle\\=& h\epsilon^{\mu\nu\alpha\beta}p_D^\nu P^\alpha Q^\beta+ {\rm i} rL^\mu+{\rm i}w_+ P^\mu+{\rm i} w_-Q^\mu\,, \end{aligned} $

(9) where the form factors
$ w_\pm $ , r, and h are functions of$ s_M $ ,$ s_L $ , and$ \cos\theta_M $ , and$ \epsilon^{\mu\nu\alpha\beta} $ is the Levi-Civita symbol.The differential decay rate takes the form
$\begin{aligned}[b] {\rm d}\Gamma =& \frac{G_{\rm F}^2|V_{q_1q_2}|^2}{(4\pi)^6 m_{D}^3}X\beta_{M}{I}(s_M, s_L, \theta_M, \theta_L, \phi)\\ & \times {\rm d}s_{M} {\rm d} s_{L} {\rm d} {\rm cos} \theta_{M} {\rm d}{\rm cos}\theta_{L} {\rm d}\phi\,.\end{aligned} $

(10) To study the structure of the hadron system, that is, the form factors of the
$ M_1M_2 $ system, the decay intensity I is decomposed with respect to$ \theta_L $ and ϕ, which is written as$ \begin{aligned}[b] I =& I_1+I_2\cos2\theta_L+I_3\sin^2\theta_L\cos2\phi+I_4\sin2\theta_L\cos\phi\\&+I_5\sin\theta_L\cos\phi+I_6\cos\theta_L +I_7\sin\theta_L\sin\phi \\& +I_8\sin2\theta_L\sin\phi+I_9\sin^2\theta_L\sin2\phi, \end{aligned} $

(11) where
$I_{1,2,...,9}$ depend only on$ s_M $ ,$ s_L $ , and ϕ. We can further express$I_{1,2,...,9}$ in terms of form factors,$ \begin{aligned}[b] I_1 =& \frac{1}{4}(2-\beta_L)\beta_L|F_1|^2 +\left(\frac{\beta_L}{2}-\frac{\beta_L^2}{8}\right)\sin^2\theta_M(|F_2|^2+|F_3|^2)\\&+\frac{1}{2}(1-\beta_L)\beta_L|F_4|^2\,,\\ I_2 =& -\frac{\beta_L^2}{4}\left[|F_1|^2-\frac{1}{2}\sin^2\theta_M(|F_2|^2+|F_3|^2)\right]\,,\\ I_3 =& -\frac{\beta_L^2}{4}\left[\sin^2\theta_M(|F_2|^2-|F_3|^2)\right]\,,\\ I_4 =& \frac{\beta_L^2}{2}\sin\theta_M {\rm Re}(F_1F_2^\star)\,,\\ I_5 =& -\beta_L\sin\theta_M\left\{{\rm Re}(F_1F_3^\star)-(1-\beta_L){\rm Re}(F_2F_4^\star)\right\}\,,\\ I_6 =& -\beta_L\sin^2\theta_M {\rm Re}(F_2F_3^\star)-\beta_L(1-\beta_L) {\rm Re}(F_1F_4^\star)\,,\\ I_7=& \beta_L\sin\theta_M \left\{{\rm Im}(F_1F_2^\star)+(1-\beta_L) {\rm Im}(F_3F_4^\star)\right\}\,,\\ I_8 =&-\frac{\beta_L^2}{2}\sin\theta_M {\rm Im}(F_1F_3^\star)\,,\\ I_9 =&\frac{\beta_L^2}{2}\sin^2\theta_M {\rm Im}(F_2F_3^\star)\,,\\[-10pt] \end{aligned} $

(12) where
$F_{1,2,3,4}$ are the form factors$ \begin{aligned}[b] F_1 =&X w_++(\beta_M P\cdot L\cos\theta_M+\frac{m_+m_-}{s_M}X)w_-\,,\\ F_2 =&\beta_M\sqrt{s_M}\sqrt{s_L}w_-\,,\\ F_3 =&X\beta_M\sqrt{s_M}\sqrt{s_L} h\,,\\ F_4 =&s_L r+P\cdot Lw_++(X\beta_M\cos\theta_M+\frac{m_+m_-}{s_M}P\cdot L)w_-\,. \end{aligned} $

(13) For the purpose of discussing the angular momentum of
$ M_1M_2 $ , for example, S- and P-waves, the partial wave expansions in spherical harmonics for the form factors$F_{1,2,3,4}$ are written as$ \begin{aligned}[b] F_1(s_M,s_L,\cos\theta_M) =& \sum_{l=0}^{\infty} F_{1l}(s_M,s_L)P_l(\cos\theta_M)\,,\\ F_2(s_M,s_L,\cos\theta_M) =& \sum_{l=1}^{\infty}\frac{1}{\sqrt{l(l+1)}} F_{2l}(s_M,s_L)\frac{{\rm d} P_l(\cos\theta_M)}{{\rm d}\cos\theta_M}\,,\\ F_3(s_M,s_L,\cos\theta_M) =& \sum_{l=1}^{\infty}\frac{1}{\sqrt{l(l+1)}} F_{3l}(s_M,s_L)\frac{{\rm d}P_l(\cos\theta_M)}{{\rm d}\cos\theta_M}\,,\\ F_4(s_M,s_L,\cos\theta_M) =&\sum_{l=0}^{\infty} F_{4l}(s_M,s_L)P_l(\cos\theta_M)\,. \end{aligned} $

(14) Moreover, the decay
$ D\to M_{1}M_{2}\ell^+\nu_\ell $ may occur via intermediate states, such as vector or scalar mesons, which provides information about the intermediate resonances [8, 9]. The amplitudes of$ D\to(S\to M_{1}M_{2})\ell^+\nu_{\ell} $ and$ D\to(V\to M_{1}M_{2})\ell^+\nu_{\ell} $ can be given by$ \begin{aligned}[b]& {\cal A}(D\to(V\to M_{1}M_{2})\ell^+\nu_{\ell}) \\=& \langle V|\bar{q}_1\gamma_{\mu}(1-\gamma_{5})q_2|D\rangle\epsilon\cdot Q g_{VM_{1}M_{2}} D_{FV} \bar{u}(p_\ell)\gamma^{\mu}(1-\gamma_{5})v(p_\nu)\,,\\ &{\cal A}(D\to(S\to M_{1}M_{2})\ell^+\nu_{\ell}) \\=& \langle S|\bar{q}_1\gamma_{\mu}(1-\gamma_{5})q_2|D\rangle g_{SM_{1}M_{2}}D_{FS} \bar{u}(p_\ell)\gamma^{\mu}(1-\gamma_{5})v(p_\nu)\,, \end{aligned} $

(15) where
$ \begin{aligned}[b] &\langle V|\bar{q}_1\gamma_{\mu}(1-\gamma_{5})q_2|D\rangle= \\& -\epsilon_{\mu\nu\alpha\beta}\epsilon^{\nu\ast}P_{D}^{\alpha}P^\beta\frac{2V_0(s_L)}{m_V+m_D}-{\rm i}\left(\epsilon^{\ast}_\mu-\frac{\epsilon^{\ast}\cdot L}{L^2}L_\mu\right)(m_V+m_D)A_1(s_L)\,,\\ &+{\rm i} \left({P_{D}}_\mu+P_{\mu}-\frac{m^2_D-m^2_V}{L^2}L_\mu\right)\epsilon^{\ast}\cdot L \frac{A_2(s_L)}{m_V+m_D}\\&-{\rm i}\frac{2m_V\epsilon^{\ast}\cdot L}{L^2}L_\mu A_0(s_L)\,,\\ & \langle S|\bar{q}_1\gamma_{\mu}(1-\gamma_{5})q_2|D\rangle = {\rm i}(f^+(s_L)P_\mu+f^-(s_L)L_\mu)\,, \end{aligned} $

(16) with
$ \begin{aligned}[b] \sum\epsilon^{\mu\ast}\epsilon^{\nu} =& -g^{\mu\nu}+\frac{P^\mu P^\nu}{P^2}\,,\\ {\cal A}(D\to M_{1}M_{2}\ell^+\nu_{\ell}) =& {\cal A}(D\to(V\to M_{1}M_{2})\ell^+\nu_{\ell})\\&+{\cal A}(D\to(S\to M_{1}M_{2})\ell^+\nu_{\ell})\,. \end{aligned} $

(17) Here,
$ f^\pm(s_L) $ is the$ D\to S $ form factor,$ A_{0,1,2} $ are the$ D\to V $ axial-vector form factors, and$ V_0 $ is the$ D\to V $ vector form factor [10, 11]. Finally, we can obtain$ F_{1-4} $ in the helicity basis (for S- and P-waves only),$ \begin{aligned}[b] F_1(s_M,s_L,\cos\theta_M) = & Xf^+(s_L)g_{SM_{1}M_{2}}D_{FS}\\ &+\cos\theta_M\beta_Mg_{VM_{1}M_{2}} D_{FV}\sqrt{s_Ls_M} H_0(s_L)\,,\\ F_2(s_M,s_L,\cos\theta_M) =& \frac{1}{2}\beta_Mg_{VM_{1}M_{2}} D_{FV}\sqrt{s_Ls_M} \\ &\times (H_+(s_L)+H_-(s_L))\,,\\ F_3(s_M,s_L,\cos\theta_M) =& \frac{1}{2}\beta_Mg_{VM_{1}M_{2}} D_{FV}\sqrt{s_Ls_M}\\ &\times (H_+(s_L)-H_-(s_L))\,,\\ F_4(s_M,s_L,\cos\theta_M) =&s_Lf^-(s_L)g_{SM_{1}M_{2}}D_{FS}\\ &+2\cos\theta_M\beta_Mg_{VM_{1}M_{2}} D_{FV} \sqrt{s_Ls_M} H_t(s_L)\,, \end{aligned} $

(18) with
$ \begin{aligned}[b] H_0(s_L) =& \frac{1}{\sqrt{s_Ls_M}}\left[P\cdot L(m_V+m_D)A_1(s_L)-2\frac{X^2}{m_V+m_D}A_2(s_L)\right]\,,\\ H_\pm(s_L) =& (m_V+m_D)A_1(s_L)\mp\frac{2X}{m_V+m_D}V_0(s_L)\,,\\ H_t(s_L) =& \frac{X}{\sqrt{s_L}}[A_0(s_L)+A_1(s_L)+A_2(s_L)]\,, \end{aligned} $

(19) where
$ g_{SM_{1}M_{2}}(g_{VM_{1}M_{2}}) $ is the coupling constant,$ D_{FS}(D_{FV}) $ is derived from the propagator for$ S(V) $ . In the case of Breit-Wigner lineshapes,$D_{FS}= 1/(s_M-m^2_S+{\rm i}m_S\Gamma_S)$ and$D_{FV}= 1/(s_M-m^2_V+{\rm i}m_V\Gamma_V)$ , or$D_{FS}=1/(s_M-m^2_S+ {\rm i}\dfrac{s_M}{m_S}\Gamma_S)$ and$D_{FV}=1/(s_M-m^2_V+{\rm i}\dfrac{s_M}{m_V}\Gamma_V)$ if decay width$ \Gamma_{S}(\Gamma_{V}) $ is not negligible [12]. For the scalar meson f0(980), it couples to the channels$K\bar{K} $ and$ \pi\pi $ strongly. Likewise,$ a_0(980) $ couples to$K\bar{K} $ and$ \pi\eta $ strongly. One needs to replace the usual Breit-Wigner lineshape by the Flatté formula [13] to take into account the coupled channel effect. For the broad$ \rho(770) $ resonance, it is customary to adapt the Gounaris-Sakurai model [14] to account for the$\pi\pi$ rescattering. -
In this study, we derive the parameterization formula of a four-body semi-leptonic decay while considering the effects of lepton mass and express the differential decay width in the format used in partial wave analyses. We can obtain the parameterization formula used in Refs. [3–5], which neglects lepton mass (or set
$ \beta_L=1 $ ); however, while this does not significantly influence semi-electronic decays, neglecting the lepton mass can result in a bias of up to$ \sim1\ $ % in partial wave analyses for charmed meson semi-muonic decays.BESIII is accumulating data samples with an integrated luminosity of 20 fb
$ ^{-1} $ at a center-of-mass energy of 3.773 GeV (for$ D^0 $ and$ D^\pm $ mesons) and has collected 7.33 fb$ ^{-1} $ data samples at$ 4.128-4.226 $ GeV (for$ D_s^+ $ mesons) [15]. In addition, the proposed super-tau-charm factory will be able to reach significantly enhanced luminosities. These aim at testing the standard model with high precision in the charm sector; however, precise theoretical parameterization is also needed. With the correction for lepton mass presented in this paper, partial wave analyses can be performed to study the form factors in the$ D_{(s)}\to V\mu^+\nu_\mu $ and$ D_{(s)}\to S\mu^+\nu_\mu $ decays more precisely.
Lepton mass correction in partial wave analyses of charmed meson semi-leptonic decays
- Received Date: 2023-02-22
- Available Online: 2023-06-15
Abstract: We derive a parameterization formula for the partial wave analyses of charmed meson semi-leptonic decays while considering the effects of lepton mass. Because the proposed super-tau-charm factory will reach a significantly enhanced luminosity and BESIII is collecting new






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: