-
The form factor provides critical information about many fundamental aspects of hadron structure. While the weak and electromagnetic form factors of the proton are well-established, our understanding on gravitational form factors (GFFs) is incomplete. The GFFs are defined from matrix elements of the quantum chromodynamics (QCD) energy-momentum tensor (EMT) and provide direct access to the internal structure of the proton, including its mass, spin, and mechanical properties [1, 2]. The sum contributions of the quark and gluon GFFs are measurable quantities defined purely from the internal system, which describes the internal dynamics of the proton system [3].
The GFFs, including the D-form factor, have also been studied in numerous frameworks. Recently, the quark D-form factor
$ D_q(t) $ has been extracted from the deeply virtual Compton scattering (DVCS) experiments at the Thomas Jefferson National Accelerator Facility (JLab), and the pressure distribution inside the proton has been reported [4]. However, because the DVCS is almost insensitive to gluons, the gluon D-form factor is controversial and seldom extracted. On the theoretical side, one study obtained the proton GFFs and investigated the mechanical properties using a light-front quark-diquark model constructed by the soft-wall AdS/QCD [5]. The nucleon form factors of the EMT are studied in the framework of the Skyrme model and in-medium modified Skyrme model [6, 7]. Reference [8] demonstrated the pressure, energy density, and mechanical radius of the nucleon in light-cone QCD sum rule formalism. Conversely, the distributions of pressure and shear forces inside the proton are investigated with lattice QCD calculations [3, 9, 10], enhancing our understanding of the proton GFFs.Unfortunately, there are no experimental constraints on the gluon GFFs directly, and little information about the gluon GFFs is explicit at present. However, at finite momentum transfer, the near-threshold heavy quarkonium photoproduction, such as
$ J/\psi $ and$\Upsilon $ meson, offers a superior path to access the gluon GFFs [11–19]. These processes have gained quite an interest in recent years because they promise to measure the naturalness of proton mass decomposition [17–21]. One reason is that the scalar gluon operator is dominant in the production amplitude of heavy quarkonium. Moreover, heavy vector mesons photoproduction was employed because the high mass of$ J/\psi $ limits the interaction to a short distance interaction. In electroproduction, the short distance is given when$ Q^2 >> 1\text{ GeV}^2 $ , i.e. high photon virtuality. These facts allow us to discuss the gluon GFFs by studying the near-threshold photoproduction data of heavy quarkonium. Conversely, the connection between heavy quarkonium photoproduction and gluon GFFs also faces challenges. One study revealed that this process is light-cone dominated and has no direct connection with gluon GFFs [22]. Thereby, more theoretical research on the related physical mechanisms is still needed.Therefore, experimental information on vector meson photoproduction is essential to gain insight into the gluon GFFs of the proton. Recently, the GlueX Collaboration reported the near-threshold cross section of the reaction
$ \gamma p\to J/\psi p $ [23]. The JLab experiment measured the differential cross section of$ J/\psi $ on proton targets at a photon energy$ E_{\gamma} $ from 9.1 to 10.6 GeV [11], which is the near-threshold energy region. Those experimental data offer a good window for studying the internal characteristics of the proton. Currently, there are plans for future experiments at JLab and Electron Ion Colliders (EICs) to probe the deepest structure inside the proton and collect$ J/\psi $ data [24–26]. High-precision experimental measurements are suggested to be performed at these facilities.This paper is organized as follows. In Sec. II, we provide a formulas for connecting the photoproduction and gluon GFFs, and the process of calculating the proton internal properties. In Sec. III, we determine the gluon GFFs by global fitting the differential and total cross section of
$ J/\psi $ photoproduction. Subsequently, the computation result of the mechanical properties and energy property inside the proton is presented. A summary is given in Sec. IV. -
The
$ (00) $ component of the EMT defines the isotropic form factor in the Breit frame, which can be expressed as follows. [1, 20, 27, 28]$ \begin{array}{*{20}{l}} \left< P^{\prime}|T_{00}|P \right>=\bar{u} (P^{\prime}) u(P)G(t), \end{array} $

(1) where the spinor normalization
$ \bar{u} (P^{\prime}) u(P)=2M $ and M is the proton mass.$ G(t) $ is the proton GFFs, which are parametrized as follows. [1, 20]$ \begin{equation} G(t)= M A_{q+g}(t) + \frac{t}{4M} B_{q+g}(t) - \frac{ t}{4 M } D_{q+g}(t), \end{equation} $

(2) where
$ t=-Q^2 $ is the squared momentum transfer, the form factor$ B_{q+g}(t) =2J_{q+g}(t)-A_{q+g}(t) $ is consistent with zero basically [9, 16, 29]. The form factors$ A_{q+g}(t) $ ,$ J_{q+g}(t) $ , and$ D_{q+g}(t) $ provide the information about the mass, spin, and the mechanical properties of the proton, respectively.The proton GFFs are the sum contributions of the quark and gluon GFFs. Additionally, the component of the gluon GFFs part can be written as follows. [1]
$ \begin{aligned}[b] G_g(t) = & M A_{ g}(t)- \frac{ t}{4 M }\left( -B_{ g}(t)+D_g(t) \right) +M\bar{C}_g(t) \\ =& \frac{3}{4}M A_{ g}(t) - \frac{ t}{4 M } D_{ g}(t) + \frac{3t}{16M} \left( B_g(t)+D_g(t)\right), \end{aligned}$

(3) because the
$ \bar{C}_g(t) $ form factor can be written as [30]$ \bar{C}_g(t)=-\frac{A_g(t)}{4} + \frac{- t}{16 M^2 }\left( B_{ g}(t)-3 D_{ g}(t) \right), $

where the constraint
$ \bar{C}_g(t) +\bar{C}_q(t) =0 $ is due to EMT conservation [1].Many estimatations or models, including QCD sum rule [31, 32], Braun-Lenz-Wittman model, [32] and the asymptotic model [30], show that the
$ B_g(t)+D_g(t) $ are order of magnitudes smaller compared to the$ B_g(t) $ or$ D_g(t) $ results [30]. In this paper, we primarily attribute the gluon GFFs to the first two terms in Eq. (3), as the contribution of the$ B_g(t)+D_g(t) $ is negligible. Therefore, the gluon GFFs are obtained as follows:$ \begin{equation} G_g(t) \approx \frac{3}{4} M A_{ g}(t) - \frac{ t}{4 M } D_{ g}(t). \end{equation} $

(4) Next, we demonstrate the complete analysis of the proton gluon GFFs connecting the gluon part of the EMT and the near-threshold
$ J/\psi $ cross section. Typically, the differential cross section of the$ J/\psi $ photoproduction is given by [33]$ \frac{{\rm d}\sigma_{\gamma p\to J/\psi p}}{{\rm d}t}=\frac{1}{64 \pi W^2} \frac{1}{|{\bf p}_{\gamma }|^2} \left| \mathcal{M}_{\gamma p\to J/\psi p} \right|^2 , $

(5) where W is the center of mass (c.m.) energy and
$ {\bf p}_{\gamma } $ is the c.m. photon momentum in the$ \gamma p\to J/\psi p $ process. As an assumption, the amplitude primarily attributes to the gluon part of the EMT of QCD in this paper, which can be written as follows. [13]$ \begin{array}{*{20}{l}} \mathcal{M}_{\gamma p\to J/\psi p} =- 2 c_2 Q _c M \left< P^{\prime}|g^2 T^g_{00}|P \right> , \end{array} $

(6) where
$ Q_e=2e/3 $ represents the coupling of the photon to the electric charge of the quarks in$ J/\psi $ meson;$ c_2 $ , the short-distance coefficient, is on the order of$ \pi r_{c\bar{c}}^2 $ ; and$ g^2=4 $ is the QCD coupling with$ \alpha_s \approx 0.32 $ [18, 34].By integrating the differential cross section (Eq. (5)) over the allowed kinematical range from
$t_{\rm min}$ to$t_{\rm max}$ , the total cross section are computed and can be written as follows.$ \sigma=\int_{t_{\rm min}}^{t_{\rm max}} {\rm d}t \left(\frac{{\rm d} \sigma}{{\rm d} t} \right) , $

(7) where the limiting values
$t_{\rm min}$ and$t_{\rm max}$ are$ \begin{array}{*{20}{l}} t_{\rm max}( t_{\rm min})= m_{J/\psi}^2-2E_{\gamma} E_{J/\psi} \pm 2 |{\bf p}_{\gamma }||{\bf p}_{J/\psi}| . \end{array} $

(8) The energies and momenta of the photon and vector meson in the c.m. frame are
$ \ \begin{aligned}[b] |{\bf p}_{J/\psi}|=& \frac{1}{2W} \sqrt{(W^2-M^2)^2+ m_{J/\psi}^2(m_{J/\psi}^2-2W^2-2M^2) }, \\ E_{J/\psi}=&\sqrt{{\bf| p}_{J/\psi}| ^2+m_{J/\psi}^2},\; \; |{\bf p}_{\gamma }|= \frac{1}{2W} (W^2-M^2), \; \; E_{\gamma }= {\bf |p_\gamma |}. \end{aligned} $

(9) Thus far, we have established the relationship between the proton GFFs and
$ J/\psi $ photoproduction, including the differential and total cross section in Eqs. (5) and (7).For
$ A_{q+g}(t) $ , the mass distribution of the proton is encoded in the A-form factor, which can be expressed under the dipole form parametrization as follows.$ A_{q+g}(t)= \frac{A_{q}(0)}{(1- t/m_q^{ 2} )^2}+\frac{A_{g }(0)}{(1- t/m_g^2 )^2}, $

(10) where the constraint
$ A_{q}(0)+A_{g}(0)=1 $ is the consequence of momentum conservation [1, 35]. Moreover, the gluon contribution$ A_g(0)=0.414 $ was obtained from CT18 global QCD analysis [36] and agrees with other LQCD results [10, 37, 38]. Therefore, the parameter$ A_g(0) $ in$ A_g(t) $ is fixed in this study, and$ m_g $ is a free parameter determined by fitting experimental data.The D-form factor
$ D_{q+g}(t) $ is an area of significant interest, which has attracted considerable attention recently [1, 11]. The gluon D-form factor$ D_g(t) $ is typically parameterized in the tripole form and provided as follows. [4, 39]$ D_g(t)=\frac{D_g(0)}{(1-t/d_g^2)^{3}}, $

(11) where
$ D_g(0) $ and$ d_g $ are free parameters adjusted to the experimental data. Note that$ D_g(0) $ is negative as the pressure distribution is found to be repulsive near the proton center.It has been determined that the form factor
$ G(t) $ in Eq. (2) and (4) at the momentum transfer t=0 satisfies$ \begin{array}{*{20}{l}} G(0)=M \; \; \; \text{and }\; \; \; G_g(0)=\dfrac{3}{4}MA_g(0). \end{array} $

(12) Therefore, the coefficient
$ c_2 $ can be determined by extracting the near-threshold differential cross section at t=0, which can be written as follows.$ \left.\frac{{\rm d}\sigma_{\gamma p\to J/\psi p}}{{\rm d}t}\right|_{t=0}=\frac{1}{64 \pi W^2} \frac{1}{|{\bf p}_{\gamma }|^2} \left|3 c_2 Q _c g^2 M^3 A_g(0) \right|^2 . $

(13) As the differential cross section at squared momentum transfer t=0 is nonphysical with no experimental measurement, we will identify the left side of Eq. (13) at different c.m. energy based on the model prediction as discussed in Ref. [40], which is described in detail in Sec. III. As a result, reliable gluon GFFs can be obtained while avoiding c.m. energy dependence caused by the differential cross sections at varying photon energies. This approach provides significant information on the gluon GFFs.
Finally, we construct the relationship between the gluon GFFs of the proton and the near-threshold heavy quarkonium photoproduction. Thus one can derive the gluon GFFs, which is the joint effect of
$ J/\psi $ differential and total cross section. -
The pressure
$ p(r) $ and shear forces$ s(r) $ are “good observables” to report the pressure and shear forces distributions, indicating that the average value of the directional static pressure and shear forces along the three Cartesian axes can be expressed as follows. [1, 2]$ s_{q+g}(r) = - \frac{1}{2} r\frac{{\rm d}}{{\rm d}r} \frac{1 }{ r} \frac{ {\rm d} }{{\rm d}r} \widetilde{D} (r), $

(14) $ p_{q+g}(r) = \frac{1}{3} \frac{1 }{ r^2} \frac{{\rm d} }{{\rm d}r} r^2 \frac{{\rm d} }{{\rm d}r} \widetilde{D} (r). $

(15) Here,
$ \widetilde{D} (r) $ is the Fourier transform of$ D_{q+g}(t) $ and can be expressed as follows. [1, 2]$ \begin{aligned}[b] \widetilde{D} (r)&=\int \frac{{\rm d}^3 {\bf \Delta} }{2 M(2\pi)^3 } {\rm e}^{-{\rm i} {\bf \Delta} r} D_{q+g}(- {\bf \Delta}^2) \\ &=\int \frac{{\rm d}^3 {\bf \Delta} }{2 M (2\pi)^3 } {\rm e}^{-{\rm i} {\bf\Delta} r}\left( D_{g}(- {\bf\Delta}^2) +D_{q}(- {\bf\Delta}^2) \right). \\ \end{aligned} $

(16) Note that the pressure distribution
$ r^2 p_{q+g}(r) $ satisfies the internal forces balance inside a composed particle based on [1]$ \int_0^{\infty} {\rm d}r \; r^2 p_{q+g}(r) =0 . $

(17) The normal forces in the composed particle system can be written as [1]
$ F_n(r)=\frac{2}{3} s_{q+g}(r)+p_{q+g}(r), $

(18) where the positive and negative eigenvalues correspond to “stretching" or “squeezing" along the corresponding principal axes, respectively. The normal forces satisfy
$ F_n(r)>0 $ [1]. One can define the proton mechanical radius in terms of the normal forces in the proton, which can be written as [1]$ \begin{equation} \left<R^2_{\rm mech}\right> = \frac{\int {\rm d}^3r \; r^2 F_n^{ q+ g }(r) }{\int {\rm d}^3r \; F_n^{q+ g }(r) } = \frac{ 12 \left( \frac{ D_q(0) }{ d_q}+ \frac{D_g(0)}{ d_g} \right) }{ D_q(0) d_q + D_g(0) d_g } . \end{equation} $

(19) After calculating the form factor
$ D_{q+g}(t) $ , the pressure in the proton center can be computed directly as [1]$ \begin{equation} p(0)=\frac{1}{24 \pi^{2} M} \int_{-\infty}^{0} - (-t)^{3/2} D_{q+g}(t) {\rm d} t, \end{equation} $

(20) which is consistent with the illustration in Eq. (15).
The total energy density
$ T_{00} (r) $ satisfied$ T_{00}(r)>0 $ in a mechanical system is defined for the total system in Eqs. (1) and (2), which can be written as [1]$ \begin{aligned}[b] T_{00}(r)= & \int \frac{d^{3} {\bf\Delta} }{(2 \pi)^{3}} e^{-i r {\bf\Delta} } \left( MA_{q+g}(t)-\frac{t}{4M}D_{q+g}(t) \right) \\ =&\sum_{a=q,g}\frac{ 16 M^2 A_a(0) m_a^3 e^{-m_a r} - (-3 + d_a r) D_a(0 ) d_a^5 e^{-d_a r} }{ 128 \pi M} \end{aligned} $

(21) where
$ -{\bf\Delta}^2= t $ . The total energy density$ T_{00}(r) $ satisfies the following condition:$ \begin{aligned}[b] \int {\rm d}^{3} r T_{00}(r)&=\int {\rm d}^{3} r \left(T^g_{00}(r)+ T^q_{00}(r)\right)\\ &= M \left(A_{q }(0)+A_{g }(0)\right)=M . \end{aligned} $

(22) The energy density satisfies
$ T_{00}(r)>0 $ in a mechanical system, allowing us to introduce the mean square radius of the energy density as follows. [1]$ \begin{equation} \langle R_{E}^{2}\rangle =\frac{\int {\rm d}^{3} r r^{2} T_{00}(r)}{\int {\rm d}^{3} r T_{00}(r)} =6A_{q+g}^{\prime}(0)-\frac{3\left(D_0+d(0)\right)}{2M^2}. \end{equation} $

(23) -
In our previous work [40], the analysis revealed that certain light quarks are strongly suppressed in heavy quarkonium photoproduction and are likely to dominate the two-gluon exchange mechanisms. The obtained numerical results showed that the two-gluon exchange model can explain the near-threshold
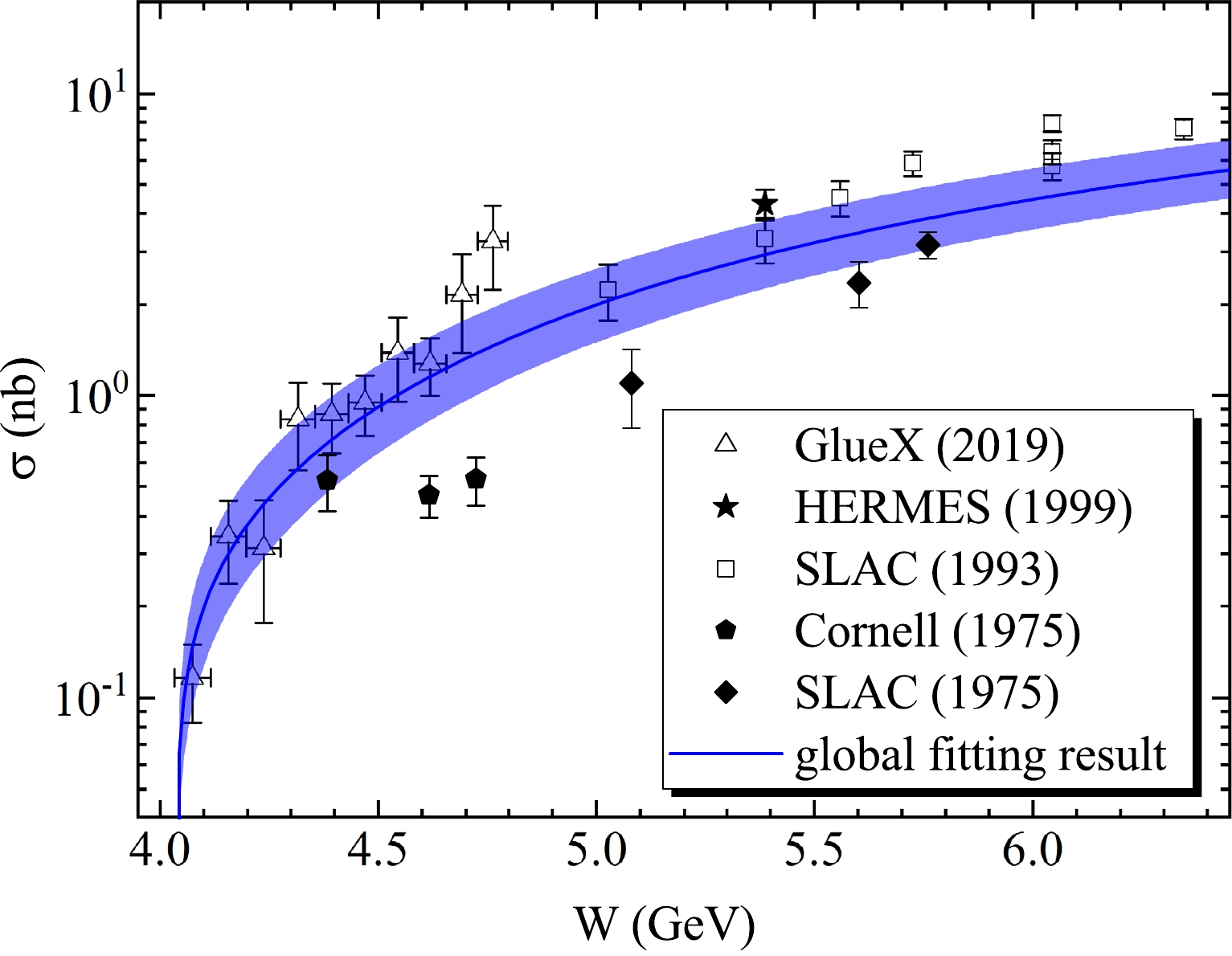
$ J/\psi $ photoproduction experimental data well [40]. Consequently, the differential cross section${\rm d}\sigma/{\rm d}t|_{t=0}$ in Eq. (13) at various c.m. energies is predicted by the two-gluon exchange model, allowing the identification of the corresponding short-distance coefficient$ c_2 $ . Additionally, the introduction of the model is helpful for obtaining a continuous total cross section. Subsequently, the gluon GFFs in Eq. (4) are achieved through fitting Eqs. (5) and (7) simultaneously. By global fitting the near-threshold t-dependence$ J/\psi $ differential cross section and W-dependence total cross section experimental data [11, 23, 41–44], the free parameters$ m_g $ ,$ d_g $ and$ D_g(0) $ in Eq. (4) are computed. The differential and total experimental data used in this study are derived from the experiment results that are currently closest to the threshold. The comparison between the$ J/\psi $ photoproduction (blue solid curves) and experimental measurements (black points) are presented in Figs. 1 and 2, showing a good agreement. The blue bands reflect a statistical error of parameters$ m_g $ ,$ d_g $ , and$ D_g(0) $ . The results of holographic QCD and the GPD+VMD approach were recalculated in Ref. [11] using the latest differential cross section data. The obtained gluon GFFs are compared to that of the holographic QCD, GPD+VMD approach, and LQCD [9–12, 19], as presented in Table 1. Notably, our results are comparable to that of holographic QCD determination and LQCD calculation.
Figure 1. (color online) Global fitting result of
$ \gamma p \to J/\psi p $ differential cross section as a function of$ -t $ at c.m. energy W = 4.25, 4.28, 4.31, 4.35, 4.38, 4.41, 4.45, 4.48, 4.51, 4.54 and 4.58 GeV. The blue bands reflect statistical errors of$ m_g $ ,$ d_g $ and$ D_g(0) $ . References of data can be found in [11, 23].Approach $ m_g $ /GeV

$ D_0 $ 

$ d_g $ /GeV

Holographic QCD [11, 12] 1.575 $ -1.80\pm 0.528 $ 

$ 1.21\pm 0.21 $ 

tripole-tripole GPD + VMD [11, 19] 2.71 $ -0.80\pm 0.44 $ 

$ 1.28\pm 0.50 $ 

tripole-tripole LQCD [9] 1.641 $ -1.932\pm 0.532 $ 

$ 1.07\pm 0.12 $ 

tripole-tripole LQCD [10] 1.13 $ -10.0 $ 

$ 0.48 $ 

dipole-dipole this work $ 1.51\pm 0.10 $ 

$ -1.97 \pm 0.25 $ 

$ 0.86 \pm 0.07 $ 

dipole-tripole As shown in Fig. 3, the values of gluon A-form factor
$ A_g(t) $ (red dashed curve) and gluon D-form factor$ D_g(t) $ (blue solid curve) are compared with the LQCD determinations [10]. Here, the errors of parameters$ m_g $ ,$ D_g(0) $ , and$ d_g $ include all uncertainties of$ A_g(t) $ and$ D_g(t) $ . One finds that the results obtained for gluon D-form factor in this work is comparable with that obtained from the LQCD computations, while the values of$ A_g(t) $ are slightly bigger than the LQCD results slightly. We have also compared the gluon D-form factor with the quark counterparts extracted from the DVCS experiment, and as a result, the gluon and quark D-form factor are approximately comparable, which is in agreement with numerous previous studies [4, 9, 10].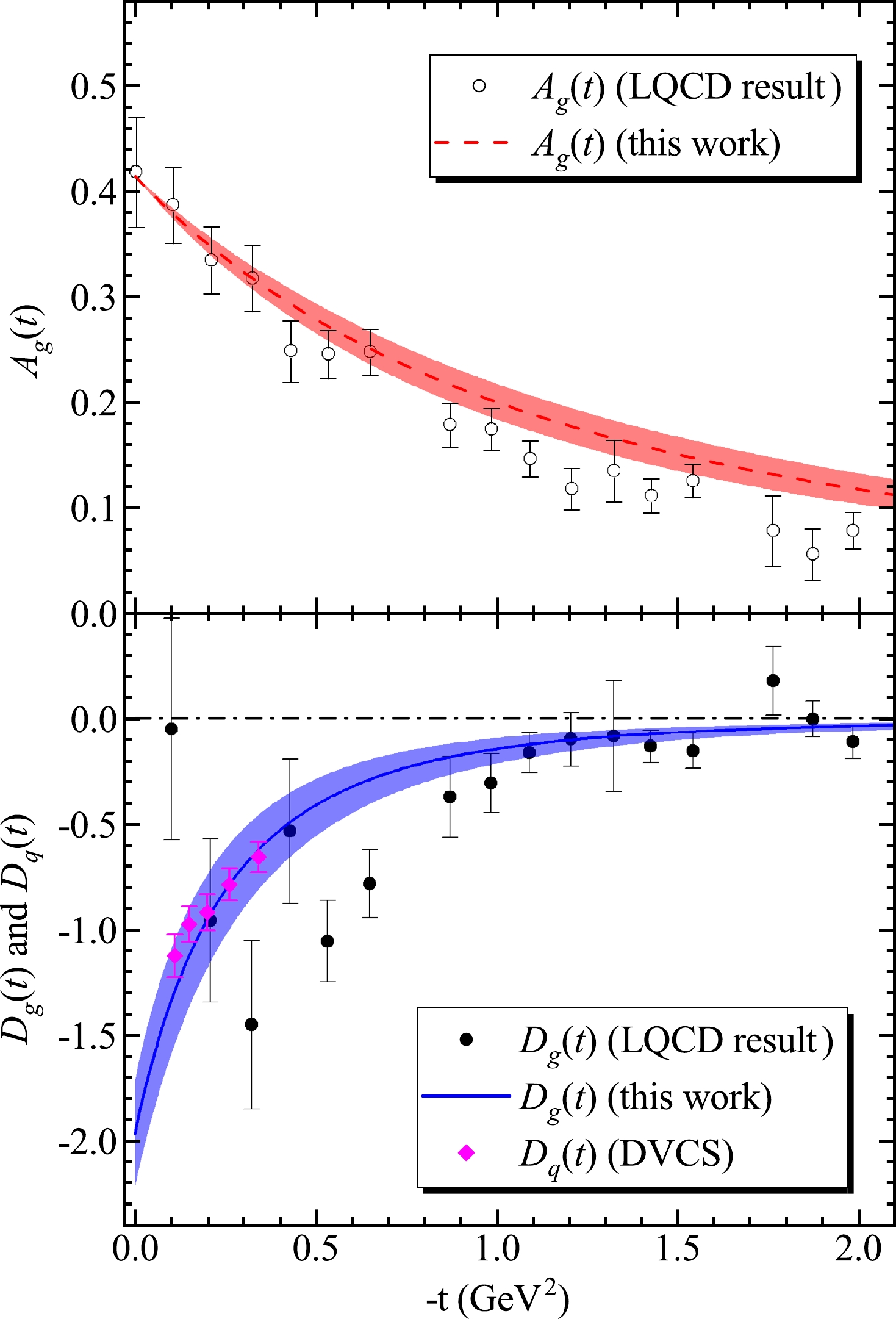
Figure 3. (color online) Top panel: The gluon A-form factor
$ A_{g}(t) $ (red-dashed curve) compared with the LQCD determinations [10]. Bottom panel: The gluon D-form factor$ D_g(t) $ (blue-solid curve) compared with the LQCD determinations [10] and quark D-form factor from DVCS enperiment [4]. The blue band reflects statistical errors of parameters$ m_g $ ,$ D_g(0) $ and$ d_g $ .The sum of the quark and gluon D-form factors
$D_{q+g}(t)$ is a measurable quantity defined solely by the D-term inside the proton. Particularly, one can obtain the quark D-form factor by fitting the DVCS data [4] using the tripole form assumption [39]. Combined with the gluon D-term achieved in this work, one can obtain the proton mechanical properties from$D_{q+g}(t)$ , including the quark and gluon contributions.The pressure and shear force distributions inside the proton are achieved and displayed in Fig. 4. The red-dashed and blue-solid curves indicate the gluon and quark contributions of the pressure and shear force distributions, respectively. The blue and green bands represent the uncertainties that result from the error of parameters
$ d_g $ and$ D_g(0) $ . Here, the positive sign indicates repulsion toward the outside, and the negative sign indicates attraction directed towards the inside. The total pressure and shear force contributions of the sum of the quark and gluon contributions are illustrated as the green-dot-dashed curve in Fig. 4. It was found that the pressure is positive in the inner region and negative in the outer region, with a zero crossing near$ r = 0.67 \text{ fm} $ , which shows that the repulsive and binding pressures dominate in the proton and are separated in radial space. Moreover, the shear force distribution reaches its peak near$ r = 0.63 $ fm in our observation.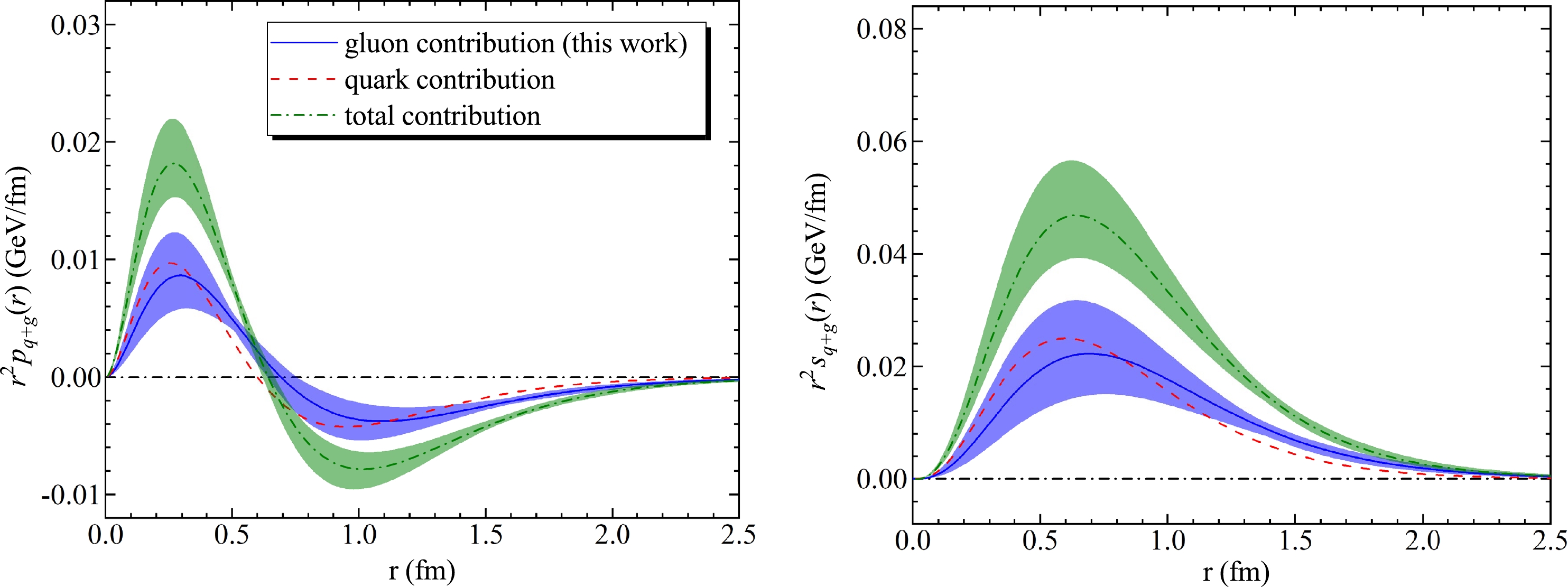
Figure 4. (color online) Left panel: The pressure distribution
$ r^2p(r) $ inside the proton. Right panel: The shear force distribution$ r^2s(r) $ inside the proton. The red-dashed and blue-solid curve shows the quark and gluon contributions, respectively. The green-dot-dashed curve represents the total pressure and shear force distributions. The blue and green bands include all statistical uncertainties of$ D_g(0) $ and$ d_g $ .After discussing the gluon form factors
$ A_{g}(t) $ and$ D_{g}(t) $ , the gluonic contribution to the nucleon mechanical properties can be achieved. An important mechanical quantity, known as$p_{g}(0) $ , denotes the pressure of the gluon contribution at the center of the nucleon and has a value of$0.62_{-0.27}^{+0.42} \text{ GeV} / \text{fm}^{3} $ . One can add the quark contribution$p_{q}(0) = 0.93 \text{ GeV} / \text{fm}^{3} $ and compute the system pressure$ p(0) = 1.55_{-0.27}^{+0.42} \text{ GeV} / \text{fm}^{3} $ at the center of the proton. Moreover, the proton mechanical radius is computed to be$0.75_{-0.03}^{+0.04} \text{ fm} $ . As listed in Table 2, those proton mechanical quantities are compared with other existing theoretical results. As shown in Table 2, our statements on the pressure density differ from the findings in previous studies considerably [7, 8, 45–47]. In fact, the quark contribution to the pressure is bigger than most of those reported previously, regardless of the gluon contribution. The calculation of the mechanical radius is consistent with the results reporetd in Refs. [3, 8, 45–47], subjected to the error margin.Approaches and Models $ p(0) $ /(GeV/fm

$ ^3 $ )

$\sqrt{\left < R^2_{\rm mech}\right > } \;{\rm{ /fm} }$ 

light-front quark-diquark model [46] 4.76 0.50 Skyrme model [7] 0.26 − light-cone QCD [8] 0.67 0.73 light-cone sum rules at leading order [45] 0.84 0.72 lattice QCD (modified z-expansion) [3] − 0.71 lattice QCD (tripole ansatz) [3] − 0.75 $ \pi-\rho-\omega $ soliton model [47]

0.58 − this work $ 1.55_{-0.27}^{+0.42} $ 

$ 0.75_{-0.03}^{+0.04} $ 

Table 2. Numerical values of mechanical quantities of proton, including mechanical radius and pressure at the center of the proton, compared with other predictions from different approaches.
-
This study constructs a connection between the gluon part of EMT and the near-threshold charmonium photoproduction. The gluon GFFs, as functions of the squared momentum transfer t , are determined by a global fitting of the
$ J/\psi $ differential and total cross section experimental data. All gluon form factors$ A_g(t),B_g(t) $ ,$ D_g(t) $ and$ \bar{C}_g(t) $ , which are related to different components of the gluon GFFs, are resolved. One finds that$ D_g(t) $ is comparable with the lattice QCD results, while the value of$ A_g(t) $ is slightly bigger than that of the holographic QCD and LQCD results. Subsequently, the gluon contribution of the energy density at the center of the proton, which are determined by both$ A_g(t) $ and$ D_g(t) $ , is calculated. Combined with the quark D-form factor extracted from the DVCS experiment, the total D-term$ D_{q+g}(t) $ can be used to investigate its potential applications in describing the mechanical properties. Consequently, the pressure and shear force distributions inside the proton, including the gluon and quark contributions, are obtained.It has been suggested that the value of the proton charge radius is [33]
$ \begin{equation*} R_C=0.8409 ~\text{ fm}. \end{equation*} $

The proton mechanical radius we obtained is estimated to be
$ 0.75_{-0.03}^{+0.04} $ fm, which is slightly smaller than the charge radius. Generally, the measurements of the charge distribution and the mechanical properties of the proton can contribute to our understanding of the origin of the proton structure. This study provides useful theoretical insights for the QCD constraints on the gluon GFFs of the proton.In fact, the dipole and tripole forms are typically considered in the
$ A_{q+g}(t) $ and$ D_{q+g}(t) $ form factors, allowing for feasible fitting results in this study. Moreover, this ansatz of the gluon GFFs is convenient to compare with the quark GFFs and other theoretical studies. Nevertheless, it may be feasible to achieve global fitting using artificial neural networks or Schlessinger Point Method [48–50]. Additionally, these new approaches can investigate the model outcomes for${\rm d}\sigma/{\rm d}t|_{t=0}$ . Therefore, this work is only the first step, and we will optimize the computational methods in future studies.The high-precision photo/electroproduction data of vector mesons serve as a crucial foundation for the accurate study of the internal structural properties of the proton. As a result, we recommend relevant experimental measurements based on our findings to be conducted at JLab [23] or EICs [24, 25] facilities.
Gluon gravitational form factors of protons from charmonium photoproduction
- Received Date: 2023-03-18
- Available Online: 2023-07-15
Abstract: Inspired by the recent near-threshold






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: