-
One of the unresolved issues in modern physics is the origin of the neutrino mass. In the standard model (SM) neutrinos are massless, but observation of neutrino oscillation indicates that neutrinos have tiny masses, which requires extension of the SM. The most popular ideas for generating neutrino masses are so-called seesaw mechanisms, which can be classified into three types. The type I/III seesaw introduces three (or at least two) additional singlet/triplet fermions [1−5], whereas the type II seesaw only includes an additional triplet scalar, which provides a minimal framework to explain the origin of neutrino masses [6−11]. In the model of the type II seesaw, the triplet Higgs can directly couple to the lepton sectors, and if the neutral component of the triplet Higgs gets a vev, the Majorana mass of the neutrinos can be generated.
Interestingly, the type II seesaw could also provide feasible leptogenesis if it also plays the role of inflaton, as pointed out by a recent study [12, 13]. Therefore, this simple model could explain three important problems at the same time: the origin of neutrino masses, the baryon asymmetry of our universe, and inflation. Compared with leptogenesis from the type I seesaw, which generally requires a high scale right-handed neutrino [14], type II seesaw leptogenesis allows the triplet Higgs to be as light as the TeV scale, which means it could be directly probed by the Large Hadron Collider (LHC). Indeed, the LHC already performs some surveys and currently sets a limit of around a few hundred GeV for the doubly charged Higgs contained in the triplet Higgs depending on its decay products [15−19]. The decay of the doubly charged Higgs is sensitive to the vacuum expectation value of the triplet Higgs. For a large vev
$ v_\Delta \gtrsim 0.1 $ MeV, it mainly decays into two gauge bosons; otherwise, it decays into dileptons [20]. However, if baryon asymmetry is generated by the type II seesaw, to avoid the lepton number being washed out, a vev of the triplet Higgs$ v_\Delta < 1 $ keV is preferred. Therefore, looking for the triplet Higgs through the leptonic channel would provide a visible way to test type II seesaw leptogenesis. In this paper, we investigate the detection capability of the triplet Higgs in future large hadron colliders. Previous studies on this aspect have been investigated in numerous works including, for example, Refs. [21−32]. A test of type II seesaw leptogenesis from lepton flavor violation can be also found in [33].In the model of the SM with additional triplet Higgs, after electroweak symmetry breaking, besides the SM-like Higgs there are six additional scalars present in the spectrum, which can be denoted as
$ A^0 $ ,$ H^0 $ ,$ H^\pm $ ,$ H^{\pm\pm} $ where$ A^0 $ ,$ H^0 $ are the extra CP-odd/even neutral scalars, and$ H^\pm, H^{\pm\pm} $ are the charged Higgs and doubly-charged Higgs, respectively. The charged Higgs or the doubly-charged Higgs can be pair-produced through the Drell-Yan process, providing good channels to probe the triplet Higgs at the colliders. The ATLAS group already performs a search for the doubly-charged Higgs assuming it mostly decaying into dileptons, and the mass of the doubly-charged Higgs$ H^{\pm \pm} $ up to around 800 GeV is excluded [15, 17]1 . Depending on the number of observed leptons, the detection strategy is classified mainly into three categories: the four-lepton channel, three-lepton channel, and two-lepton channel. Each channel has different sensitivity and the final result is derived from the combination of these three channels. On the other hand, as the triplet Higgs is a triplet under the SM$ S U(2)_L $ group, the charged Higgs can be produced together with the doubly-charged Higgs. This production rate can be even higher than the$ H^{\pm \pm} $ pair production [35]. Noticing that the charged Higgs decays into a lepton and a neutrino, the$ H^{\pm \pm} H^{\mp} $ production can also contribute to the ATLAS search channels and a better sensitivity can be derived. We will demonstrate this point later.In addition, as the charged Higgs decays into a charged lepton and a neutrino, a large missing energy is present for the
$ H^{\pm \pm} H^{\mp} $ pair production. It would be intriguing to search for the$ H^{\pm \pm} H^{\mp} $ pair production via the signal of$ 3e+ {E}^{\rm miss}_{T} $ , which may provide good sensitivity to the triplet Higgs. This paper is organized as follows: in Sec. II we give a brief introduction of the type II seesaw model and the mechanism of type II seesaw leptogenesis. In Sec. III we calculate the production of$ H^{\pm} $ and$ H^{\pm \pm} $ at the LHC. We analysis the sensitivity of the triplet Higgs at the LHC, including the contribution of$ H^{\pm \pm} H^{\mp} $ pair production, and then we show the prospect for$ H^{\pm \pm} H^{\mp} $ searches requiring a large missing energy for the final states in Sec. V. We draw our conclusion in Sec. VI. -
The scalar sector of type II seesaw model contains the SM Higgs doublet Φ and a
$ S U(2)_{L} $ triplet scalar field Δ with hypercharge$ Y= $ 1, which can be written as$ \begin{equation} \Delta= \begin{pmatrix} \dfrac{\delta ^+}{\sqrt{2}}& \delta ^{++} \\ \delta ^{0}&-\dfrac{\delta ^+}{\sqrt{2}} \\ \end{pmatrix}, \quad\quad\quad \Phi= \begin{pmatrix} \phi ^+\\\phi ^{0}\end{pmatrix}. \end{equation} $

(1) The most general renormalizable and gauge invariant Lagrangian for the scalar sector is
$ \begin{equation} \mathcal{L} \supset \left ( D_{\mu } \Phi \right )^{\dagger }D^{\mu }\Phi + {\rm Tr} \left ( D_{\mu }\Delta \right )^{\dagger }D^{\mu }\Delta -V\left ( \Phi ,\Delta \right ). \end{equation} $

(2) Besides SM Yukawa interaction, one can include an additional Yukawa interaction term between the triplet Higgs and leptons,
$ \begin{equation} \mathcal{L}_{\nu}=-y_{\nu }L^{\rm{T}}C \,{\rm i}\,\sigma _{2}\Delta L+{\rm h.c.} , \end{equation} $

(3) where the
$ y_{\nu } $ is the Yukawa coupling, L is the left-handed lepton doublet, and C is the charge conjugation operator. After spontaneous electroweak symmetry breaking (EWSB), the neutral part of Δ and Φ acquire a non-vanishing vacuum,$ \begin{equation} \left< \Delta \right >= \begin{pmatrix} 0 & 0 \\ \dfrac{v_{\Delta}}{\sqrt{2}} & 0 \\ \end{pmatrix}, \quad\quad\quad \left< \Phi \right >= \begin{pmatrix} 0 \\ \dfrac{v_{\Phi}}{\sqrt{2}} \\ \end{pmatrix}, \end{equation} $

(4) where
$ v_{\Delta} $ is the vacuum expectation value of the neutral part of the triplet Higgs. The neutrino mass can then be generated by$ \begin{equation} m_{\nu }= \sqrt{2}y_{\nu }v_{\Delta}. \end{equation} $

(5) Here,
$ m_{\nu } $ is a complex symmetric$ 3 \times 3 $ matrix and the physical neutrino masses can be derived by diagonalizing$ m_{\nu } $ with PMNS matrix U. The gauge invariant potential for the scalar sector can be written as follows:$ \begin{aligned}[b] V(\Phi,\Delta)=&-m_{\Phi}^2\Phi^\dagger\Phi + m_{\Delta}^2\rm{Tr}(\Delta^\dagger\Delta)\\&+\left(\mu \Phi^T\,{\rm i}\,\sigma_2\Delta^\dagger \Phi+\rm{h.c.}\right)+\frac{\lambda}{4}(\Phi^\dagger\Phi)^2 \\ & +\lambda_1(\Phi^\dagger\Phi)\rm{Tr}(\Delta^\dagger\Delta)+\lambda_2\left[\rm{Tr}(\Delta^\dagger\Delta)\right]^2\\&+\lambda_3\rm{Tr}[(\Delta^\dagger\Delta)^2]+\lambda_4\Phi^\dagger\Delta\Delta^\dagger\Phi, \end{aligned} $

(6) where
$ m_{\Phi}^2 $ and$ m_{\Delta}^2 $ are the mass parameters and the μ term provides a source of lepton number violation. The μ term violates lepton number two units for the lepton number assignments of$ l_{\Delta }=-2,l_{\Phi }=0 $ .After electroweak symmetry breaking we have a state of doubly-charged Higgs
$ H^{\pm \pm }\left (\equiv \delta ^{\pm \pm } \right) $ , two states of charged scalars$ H^{\pm} $ and$ G^{\pm} $ , which are combinations of$ \delta ^{\pm} $ and$ \phi ^{\pm} $ , and the CP-even neutral states$ H^{0} $ ,$ h^{0} $ as well as the CP-odd states$ A^{0} $ ,$ G^{0} $ , where$ G^{\pm} $ and$ G^{0} $ are the Goldstone bosons, which will ultimately give the longitudinal degrees of freedom of the$ W^{\pm} $ and Z bosons. The mass-squared of the doubly-charged Higgs is given as$ \begin{equation} m_{H^{\pm \pm }}^{2}= \frac{\sqrt{2}\mu v_{\Phi}^{2}-2\lambda _{3} v_{\Delta}^{3}-\lambda _{4} v_{\Phi}^{2} v_{\Delta}}{2 v_{\Delta}}. \end{equation} $

(7) The mass-squared of the charged Higgs is
$ \begin{equation} m_{H^{\pm }}^{2}=\frac{2\sqrt{2}\mu v_{\Phi}^{2}+4\sqrt{2}\mu v_{\Delta}^{2}-\lambda _{4} v_{\Delta} v_{\Phi}^{2}-2\lambda _{4} v_{\Delta}^{3}}{4 v_{\Delta}}. \end{equation} $

(8) For the mass of the CP-even/odd scalars, one can obtain:
$ \begin{equation} m_{H^{0}}^{2}=\frac{1}{2}[A+C+\sqrt{\left ( A-C \right )^{2}+4B^{2}}], \end{equation} $

(9) $ \begin{equation} m_{h^{0}}^{2}=\frac{1}{2}[A+C-\sqrt{\left ( A-C \right )^{2}+4B^{2}}], \end{equation} $

(10) $ \begin{equation} m_{A^{0}}^{2}=\frac{\mu \left ( v_{\Phi}^{2} +4v_{\Delta}^{2}\right )}{\sqrt{2}v_{\Delta}}, \end{equation} $

(11) where
$ \begin{aligned}[b] & A=\frac{\lambda }{2} v_{\Phi}^{2},\quad B=-\sqrt{2}\mu v_{\Phi}+\left ( \lambda _{1}+\lambda _{4} \right )v_{\Phi} v_{\Delta},\quad \\& C=\frac{\sqrt{2}\mu v_{\Phi}^{2}+4\left ( \lambda _{1}+\lambda _{4} \right )v_{\Delta}^{3}}{2v_{\Delta}}. \end{aligned} $

(12) In the limit of
$ v_{\Delta} \ll v_{\Phi} $ , we have the following mass relation of the physical eigenstates:$ \begin{equation} m_{H^{\pm \pm }}^{2}-m_{H^{\pm }}^{2}\approx m_{H^{\pm }}^{2}-m_{H^{0}/A^{0}}^{2}\approx -\frac{\lambda _{4}v_{\Phi}^{2}}{4}. \end{equation} $

(13) One can define the mass-splitting parameter
$ \Delta m = m_{H^{\pm \pm }}-m_{H^{\pm}} $ which describes the typical mass difference of the spectra for the triplet Higgs sector. The decay behavior of the triplet Higgs is different from different parameter spaces [20, 30, 31, 36]. For$ \Delta m < O(10) $ GeV and$ v_{\Delta}< 10^{-4} $ GeV, the$ H^{\pm \pm }/H^{\pm } $ decays into$ l^{\pm \pm }/l^{\pm }\nu $ . For$ \Delta m< O(10) $ GeV and$ v_{\Delta} > 10^{-4} $ GeV,$ H^{\pm \pm }/H^{\pm } $ decays into$ W^{\pm \pm }/W^{\pm }Z $ or$ W^{\pm }h^{0} $ . If$ \Delta m > O(10) $ GeV, the cascade decay channels become significant. In the case of triplet Higgs leptogenesis, we have$ \Delta m < O(5) $ GeV and$ v_{\Delta}< 10 $ keV [37], and thus the$ H^{\pm \pm }/H^{\pm } $ would mainly decay into dileptons, giving a typical multi-lepton signature at the LHC. In the following we briefly discuss how to achieve leptogenesis. -
It is known that the minimal type II seesaw model cannot successfully lead to thermal leptogenesis, and thus the Affleck-Dine mechanism is considered. In the Affleck-Dine mechanism, the scalar field acquires a large vev along the flat direction during the inflationary epoch. In the subsequent evolution, if the scalar field carries a nonzero baryon or lepton number, the baryon or lepton number violating interactions induce a rotating trajectory for the vev, which can generate baryon or lepton asymmetry and transfer to ordinary particles at the end of inflation. Fortunately, the Affleck-Dine mechanism can be achieved in the minimal type II seesaw model.
Considering the non-minimal couplings of Δ and Φ to gravity, the relevant Lagrangian in the Jordan frame can be written as
$ \begin{aligned}[b] \frac{\mathcal{L}}{\sqrt{-g}}&\supset -\frac{1}{2}M^2_P R - f(\Phi,\Delta) R + g^{\mu\nu}(D_\mu \Phi)^\dagger(D_\nu \Phi) \\&+ g^{\mu\nu}\text{Tr}(D_\mu \Delta)^\dagger(D_\nu \Delta) - V(\Phi,\Delta), \end{aligned} $

(14) where R is the Ricci scalar. To simplify the analysis, we focus on the neutral components
$ \phi^0 $ and$ \delta^0 $ and consider the non-minimal coupling to be$ \begin{equation} f(\Phi,\Delta)=\xi_\Phi |\phi^0|^2 + \xi_\Delta |\delta^0|^2. \end{equation} $

(15) Through a Weyl transformation, the Lagrangian can be written in the Einstein frame, in which the gravitational portion is of Einstein-Hilbert form. It can be shown that the scalar potential in the Einstein frame is
$ \begin{equation} V_E(\Phi,\Delta)=\frac{M_P^4}{\left(M_P^2+2f(\Phi,\Delta)\right)^2}V(\Phi,\Delta), \end{equation} $

(16) which exhibits a flat direction at the large field limit of
$ \phi^0 $ and$ \delta^0 $ . This flat direction can be recognized as a Starobinsky-like inflationary trajectory, and the inflaton is the mixing of$ \delta^0 $ and$ \phi^0 $ .As the triplet Δ carry lepton number
$ l_\Delta=-2 $ and the μ term induces lepton number violating interaction, all the ingredients of Affleck-Dine mechanism are included. During the inflationary evolution, the non-trivial motion of the angular direction of$ \delta^0 $ can generate lepton number asymmetry, which transfers to ordinary particles during reheating. After reheating, a part of the net lepton number is converted to baryon number through the sphaleron process.However, if any lepton number violating processes are in thermal equilibrium after reheating, the generated lepton asymmetry will be washed out. We require that the processes
$ L L \leftrightarrow H H $ and$ H H \leftrightarrow \Delta $ are never in thermal equilibrium:$ \begin{equation} \left.\Gamma\right|_{T=m_{\Delta}}=n\langle\sigma v\rangle \approx y^{2} \mu^{2} / m_{\Delta}<\left.H\right|_{T=m_{\Delta}} ,\end{equation} $

(17) $ \begin{equation} \left.\Gamma_{I D}(H H \leftrightarrow \Delta)\right|_{T=m_{\Delta}} \simeq \frac{\mu^{2}}{32 \pi m_{\Delta}}<\left.H\right|_{T=m_{\Delta}}, \end{equation} $

(18) where
$ \left.H\right|_{T=m_{\Delta}}=\sqrt{\dfrac{\pi^{2} g_{*}}{90}} \dfrac{m_{\Delta}^{2}}{M_{p}} $ . Using$ v_{\Delta} \simeq-\dfrac{\mu v_{\mathrm{EW}}^{2}}{2 m_{\Delta}^{2}} $ and Eq. (18), the necessary condition to avoid the washout effect is found to be$ \begin{equation} v_{\Delta} \lesssim 10^{-5} ~\mathrm{GeV}\left(\frac{m_{\Delta}}{1 ~\mathrm{TeV}}\right)^{-1 / 2}. \end{equation} $

(19) For
$m_{\Delta} \gtrsim 1~ \mathrm{TeV}$ , we require that$v_{\Delta} \lesssim 10 ~\mathrm{keV}$ to prevent the washout effect and achieve successful leptogenesis. -
The triplet Higgs can be produced at the LHC by the neutral current and charged current Drell-Yan process,
$\begin{aligned}[b] & q\bar{q} \overset{{\gamma ^{*}/Z^{*}}} {\longrightarrow}H^{\pm \pm }H^{\mp \mp }/H^{\pm }H^{\mp }/H^{0}A^{0}, \\& q\bar{q}^\prime\overset{W^{*}}{\longrightarrow}H^{\pm \pm }H^{\mp }/H^{\pm }H^{0}/H^{\pm }A^{0}\end{aligned}$

and the Feynman diagrams for
$ H^{\pm \pm }H^{\mp \mp } $ ,$ H^{\pm \pm }H^{\mp } $ production are presented in Fig. 1.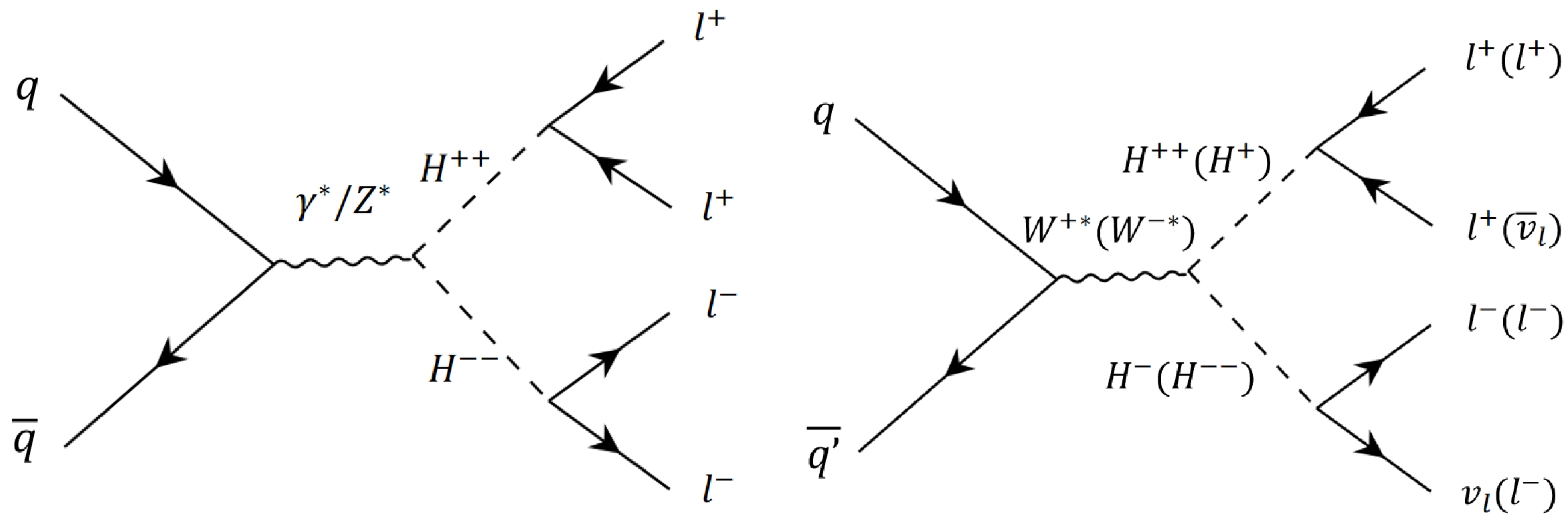
Figure 1. Feynman diagrams of the pair production process
$ pp \to H^{\pm \pm }H^{\mp \mp } $ and$ pp \to H^{\pm \pm }H^{\mp } $ .$ \begin{eqnarray} q(p_1) \, + \, \bar{q}(p_2) \, &\rightarrow H^{++}(k_1)\, + \, H^{--}(k_2),\\ q(p_1) \, + \, \bar{q}'(p_2) \, &\rightarrow H^{++}(k_1)\, + \, H^-(k_2). \end{eqnarray} $

The parton level cross section at leading order (LO) for these processes are:
$ \begin{aligned}[b] & {{\rm d}\sigma\over {\rm d}y}(q \bar{q}\rightarrow H^{++}H^{--}) \\ =& \frac{3\pi \alpha^2 \beta_1^3 (1-y^2)}{N_c {s}} \Big\{ e_q^2 + \frac{ {s}}{({s}-M_Z^2)^2} \, \frac{\cos 2\theta_W}{\sin^2 2\theta_W} \\ &\times\Big[4 e_q g_V^q ({s}-M_Z^2) + 4 (g_V^{q2}+g_A^{q2}) {s}\ \frac{\cos 2\theta_W}{\sin^2 2\theta_W} \Big] \Big\} , \end{aligned} $

(20) $ \begin{eqnarray} {{\rm d}\sigma\over {\rm d}y}(q \bar{q}'\rightarrow H^{++}H^-) = \frac{\pi \alpha^2 \beta_2^3(1-y^2)}{16 N_c \sin^4\theta_W}\frac{s}{(s-M^2_W)^2}, \end{eqnarray} $

(21) where
$ y= p_1 \cdot k_1 $ , s is the partonic center-of-mass energy, and α is the QED coupling evaluated at the scale$ \sqrt{s} $ .$ e_q $ is the electric charge of the quark q.$ \beta_1= \sqrt{1-4m_{H^{\pm \pm }}^{2}/s} $ ,$ \beta_2= \sqrt{(1-(m_{\pm}+m_{H^{\pm\pm}})^2/s) (1-(m_{\pm}-m_{H^{\pm\pm}})^2/s)} $ .In Fig. 2 we show the cross section of
$ H^{\pm \pm }H^{\mp \mp }, H^{\pm }H^{\mp }, H^{\pm \pm }H^{\mp } $ pair production with a varying mass of the triplet Higgs. We consider a K-factor of 1.25 [38] for Fig. 2, and we assume$ H^{\pm \pm } $ ,$ H^{\pm} $ share the same mass parameter. The doubly-charged triplet Higgs has a considerable cross section and a distinctive decay signature, the same-charge lepton final state. Note that$ H^{\pm \pm }H^{\mp } $ has an even larger cross section than$ H^{\pm \pm }H^{\mp \mp } $ production, and thus may provide a better sensitivity of triplet Higgs search.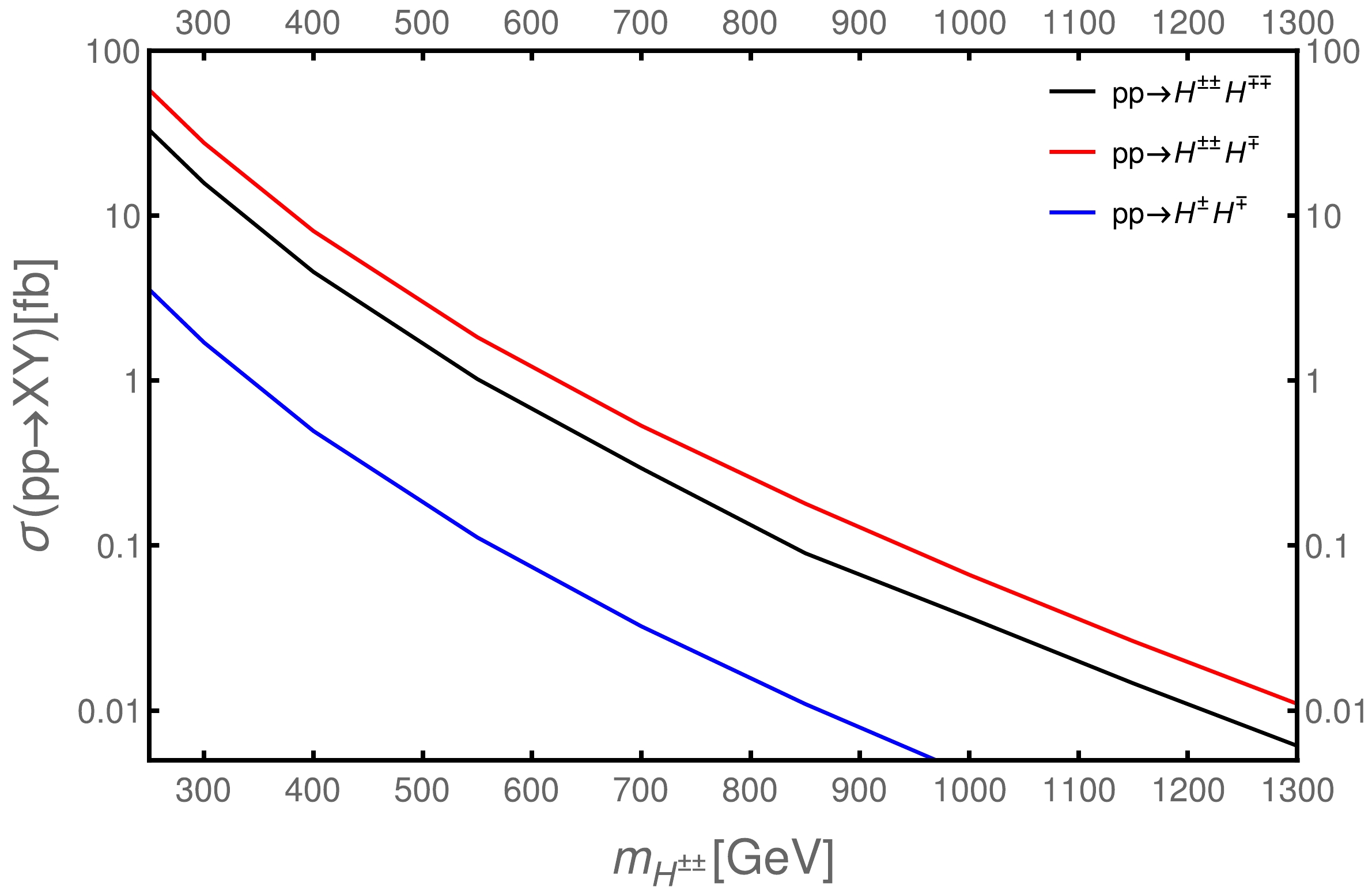
Figure 2. (color online) Pair production cross sections of the triplet scalars at
$ \sqrt{s} = $ 13 TeV for$ \Delta m=0 $ .The decay modes of triplet Higgs with different
$ v_{\Delta}-\Delta{m} $ parameters have been thoroughly discussed in Refs. [20, 30, 31, 36]. We consider$ \Delta m < O(1) $ GeV and$ v_{\Delta}< 10^{-6} $ GeV, and thus the doubly-charged Higgs$ H^{\pm \pm } $ and singly-charged scalars mostly decay to leptonic final states. The decay branching ratios are given by$ \begin{equation} {\rm BR}(H^{\pm \pm }\to l_{i}^{\pm }l_{j}^{\pm })= \frac{2}{1+\delta _{ij}}\frac{\left|y_{ij }^{\nu} \right|^{2}}{\sum_{mn}^{}\left|y_{mn }^{\nu} \right|^{2}}, \end{equation} $

(22) $ \begin{equation} {\rm BR}(H^{\pm}\to l_{i}^{\pm }\nu _{j})= \frac{\left|y_{ij } \right|^{2}}{\sum_{mn}^{}\left|y_{mn } \right|^{2}}, \end{equation} $

(23) with
$y_{\nu }=\dfrac{1}{\sqrt{2}v_{\Delta}}U {\rm diag}({m_{1},}m_{2},m_{3})U^{\rm{T}}$ and$y=\dfrac{\cos\beta }{v_{\Delta}}{\rm diag}(m_{1}, m_{2},m_{3})U^{\rm{T}}$ , where U is the lepton mixing matrix measured in neutrino oscillation experiments. The leptonic branching ratio also depends on the mass order of the neutrino as well as the neutrino mass spectrum. It has been found that for normal hierarchy (NH) and inverted hierarchy (IH) [20],$ {\rm NH:}~ {\rm BR}(H^{++}\to \mu \mu ),{\rm BR}(H^{++}\to \tau \tau )\gg {\rm BR}(H^{++}\to ee),$ $\quad{\rm IH:}~ {\rm BR}(H^{++}\to ee )\gg {\rm BR}(H^{++}\to \mu \mu ),{\rm BR}(H^{++}\to \tau \tau ).$

In this study, we assume
${\rm BR}(H^{++}\to ee)= 100\%$ to present our results. -
The ATLAS collaboration has released a multilepton final state search with an integrated luminosity of 36.1
$ \mathrm{fb^{-1}} $ of pp collisions at$ \sqrt{s} = $ 13 TeV [17]. This analysis focuses on the decays$ H^{\pm \pm }\to e^{\pm }e^{\pm },H^{\pm \pm }\to e^{\pm }\mu ^{\pm } $ , or$ H^{\pm \pm }\to \mu ^{\pm }\mu ^{\pm } $ with a branching ratio around 100%. The events are divided into three signal regions. Their selection criteria are shown in Table 1. The final state events with$2,~3$ electrons are also considered due to the missing electrons in the detector. In this study, we first simulate the experimental process by adding the contribution of$ H^{\pm \pm }H^{\mp } $ to the signal event because it also contributes the$ 2,3 $ electron signal region. In our simulation, we implement the triplet Higgs model in FeynRules [39], and import UFO files [40] into MadGraph [41] to generate signal events. We use the NNPDF23LO1 [42] for parton distribution function and the parton showering and hadronization are simulated with PYTHIA8 [43]. We perform the detector simulations with Delphes [44] and data analysis with ROOT [45].SR2E SR3E SR4E b-jet veto $ \circ $ 

$ \circ $ 

$ \circ $ 

Z veto $ \circ $ 

$ \circ $ 

$ P_{T}\left (e^{\pm } e^{\pm }\right)> 100 $ GeV

$ \circ $ 

$ \circ $ 

$ \sum\left|P_{T}\left (e \right) \right|> 300 $ GeV

$ \circ $ 

$ \circ $ 

$ \Delta R\left (e^{\pm },e^{\pm } \right)< 3.5 $ 

$ \circ $ 

$ \circ $ 

$ \Delta M/\bar{M} $ 

$ \circ $ 

Table 1. Selection criteria in all the signal regions.
For the two-electron and three-electron signal regions (SR2E and SR3E), at least one pair of electrons with the same charge is required. The separation of the same-charge electrons and the scalar sum of the electron transverse momenta are required to be
$ \Delta R\left (e^{\pm }e^{\pm } \right)> 3.5 $ and$ \sum\left|P_{T}\left (e \right) \right| > 300 $ GeV, respectively. The vector sum of the electron transverse momenta is required to be$ P_{T}\left (e^{\pm } e^{\pm }\right)> 100 $ GeV. The selection criteria for electrons are$ \left|\eta \right|< 2.47 $ and$ P_{T}> 30 $ GeV. Besides the pre-selection cut described above, for the signal regions SR3E and SR4E, events are rejected if any opposite-charge same-flavor electron pair is within 10 GeV of the Z boson mass to reduce the background from Z production. In the four-electron signal region (SR4E), there must be two electron pairs with the same charge and the total charge is zero. The$ \Delta M/\bar{M} $ requirement is applied to exclude the background where the two same-charge pairs have incompatible invariant masses$ \left (\Delta M= \left| m^{++}-m^{–}\right|, \bar{M}= \dfrac{m^{++}+m^{–}}{2} \right) $ . In the ATLAS experiment, for different$ \bar{M} $ , the value of$ \Delta M $ is different. We simply take$ \Delta M/\bar{M}<0.1 $ in the four-electron channel. In all signal regions, the invariant masses of same-charge electron pairs are required to be above 200 GeV. In order to restrain background events arising from top-quark decays, events with b-tagged jets are vetoed.To validate our simulation, we first simulate the signal events from
$ pp\to H^{\pm \pm }H^{\mp \mp } $ production and obtain the signal cut efficiency. Using the observed signal event from the article, we apply the$ CLs $ method [46] to obtain the 95% CL upper limits on the$ pp\to H^{\pm \pm }H^{\mp \mp } $ cross section. The result is shown in Fig. 3, denoted as the black dashed curve [17]. As a comparison, the limit from the ATLAS experiment is also shown as the black dotted line. It shows our limit is close to the one derived from the ATLAS experiment.
Figure 3. (color online) Limits for
$B(ee)/B(e\mu)/B(\mu \mu)= 100\%/ $ $ 0\%/0\%$ . The black and red solid lines represent the production cross sections of the$ pp\to H^{\pm \pm }H^{\mp \mp } $ and$ pp\to H^{\pm \pm }H^{\mp } $ processes, respectively. The black dashed line is the 95% CL limit we obtain for the$ pp\to H^{\pm \pm }H^{\mp \mp } $ process, which is comparable to the limit obtained by ATLAS and depicted as a black dotted line. The red dashed line is the 95% CL limit we obtain by adding the contributions of the two processes together.As
$ pp\to H^{\pm \pm }H^{\mp } $ contributes the SR2E and SR3E signal regions, we expect the real limit should be stronger. Therefore, we simulate the process$ pp\to H^{\pm \pm }H^{\mp }\to l^{\pm }l^{\pm }l^{\mp }\nu ^{\pm } $ and obtain the corresponding signal efficiency. To combine our results, we denote$ \sigma _{1,2} $ and$ \varepsilon_{1,2} $ as the cross section and cut efficiency for the$ pp\to H^{\pm \pm }H^{\mp \mp} $ process and$ pp\to H^{\pm \pm }H^{\mp } $ process, respectively, and then the total signal events$ n=\mathcal{L}\sigma _{1}\varepsilon _{1}+\mathcal{L}\sigma _{2}\varepsilon _{2} $ for each signal region. We set the limit on the total signal events. To show our results, we can use an effective cut efficiency of$ \varepsilon_{\rm 2eff}=\varepsilon _{2} + \sigma_1 /\sigma _{2} \varepsilon _{1} $ for the$ pp\to H^{\pm \pm }H^{\mp } $ process and set the limit on the cross section of$ pp\to H^{\pm \pm }H^{\mp } $ production, which is shown as the red dashed curve in Fig. 3. It shows the combined limit is around 100 GeV stronger than the one derived only from the$ pp\to H^{\pm \pm }H^{\mp \mp } $ process. -
Note that
$ pp\to H^{\pm \pm }H^{\mp } $ has a larger cross section and the final states include a missing energy. It is intriguing to examine whether$ 3e+ {E}^{\rm miss}_{ T} $ could provide a better sensitivity to the triplet Higgs.The relevant background for this signal mainly originates from diboson
$ (ZZ,ZW,WW) $ ,$ t\bar{t} $ ,$ t\bar{t}W $ ,$ t\bar{t}Z $ ,$ t\bar{t}h $ , triboson and Drell-Yan processes. However, as shown in the ATLAS paper, for the$ 3l $ process, the diboson background is much more dominant than the other backgrounds. Therefore for the background simulation, we only consider the events from the diboson process. The background and the signal are both simulated by using MadGraph with an MLM matching. For the cross section of the diboson, we also add the K-factor to include the NLO correction. The LO cross-section for the diboson process and the corresponding K-factor at$ \sqrt{s} = $ 13 TeV LHC [47] are shown in Table 2.$ ZZ $ 

$ W^{+}Z $ 

$ W^{-}Z $ 

$ WW $ 

$\sigma_{\rm LO}$ /pb

9.89 15.51 9.53 67.74 K-factor 1.62 1.84 1.91 1.66 Table 2. LO cross sections and K-factors for diboson production at
$ \sqrt{s} = $ 13 TeV.To ensure simulation credibility and validate the charge misidentification effect in the electron channel, the same-charge region (SCR) is also considered, which only exerts b-jet veto. For
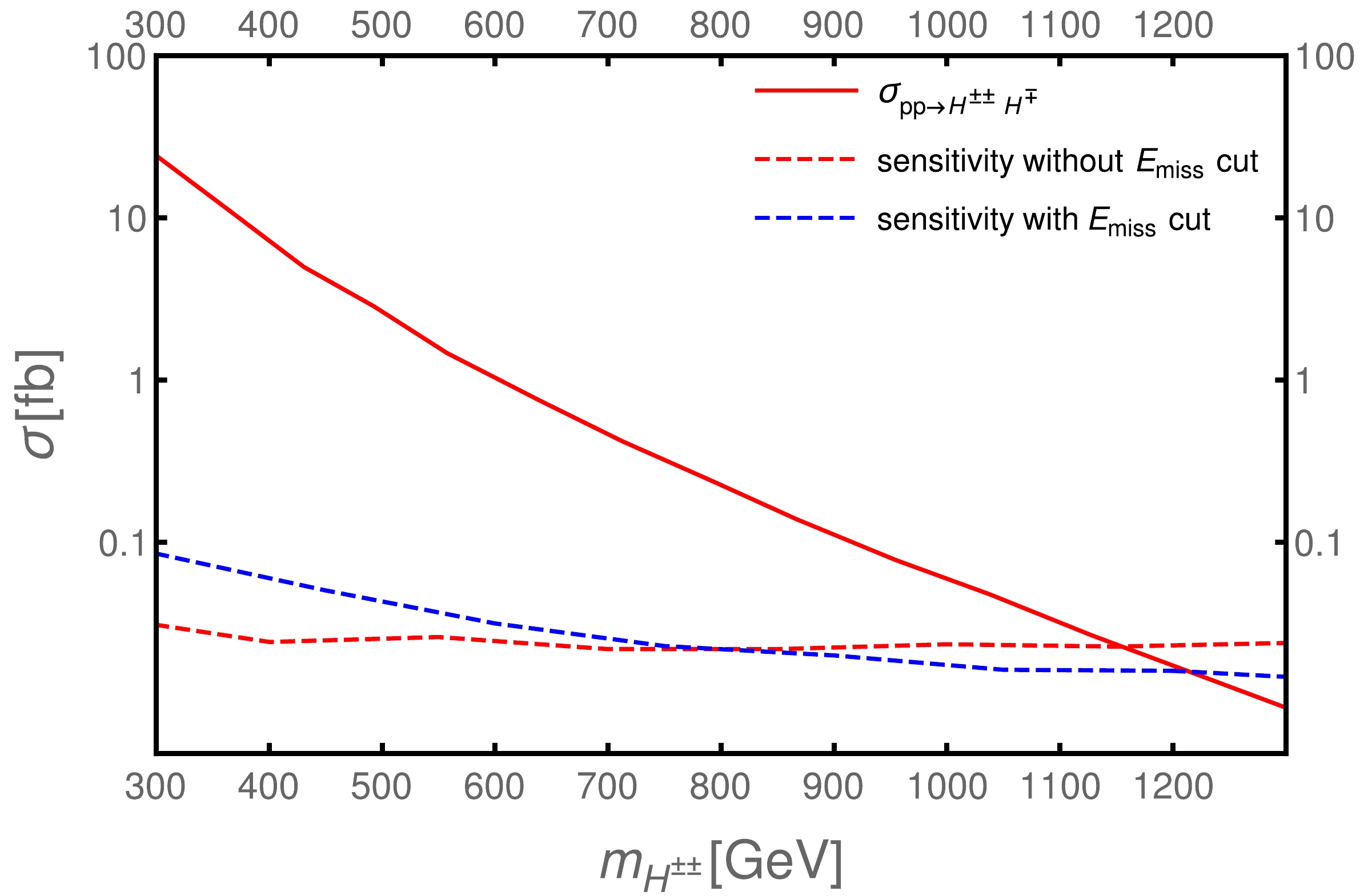
$ pp\to H^{\pm \pm }H^{\mp }\to l^{\pm }l^{\pm }l^{\mp }\nu ^{\pm } $ , large missing transverse energy appears in the final states. We show the missing energy distribution of the diboson process and$ pp\to H^{\pm \pm }H^{\mp }\to l^{\pm }l^{\pm }l^{\mp }\nu ^{\pm } $ process in Fig. 4. It shows that a cut on the missing energy around a few hundred GeV removes much of the background.
Figure 4. (color online) Missing transverse energy distribution of the
$ pp\to H^{\pm \pm }H^{\mp }\to l^{\pm }l^{\pm }l^{\mp }\nu ^{\pm } $ ($B(ee)=100\%$ ) process and diboson background with the pre-selection. The masses of$ H^{\pm \pm } $ ,$ H^{\mp } $ are assumed to be 1 TeV here.The distinction of the missing energy distribution between the signal and diboson background motivates us to add a missing energy cut
$E^{\rm miss}_{T} > 300$ GeV. The cut flow for the background and signal for a luminosity$3000~\rm fb^{-1}$ at 13 TeV LHC are shown in Table 3. It clearly shows that only 10% of the background is left after imposing the cut$E^{\rm miss}_{T} > 300$ GeV, whereas most of the signal events are still kept. Using expected discovery significance$ S/\sqrt{B} $ , the results are shown in Fig. 5 at 13 TeV LHC with luminosity$3000~\rm fb^{-1}$ . We find a triplet mass less than 1.2 TeV can be reached at$ 2\sigma $ for the high luminosity LHC in the future. As a comparison, we also show the$ 2\sigma $ sensitivity for the multi-electron searches channels mentioned in last section where the missing energy cut is not imposed. We find that when the triplet Higgs mass is below 800 GeV, the multi-electron channel still provides better sensitivity for the triplet Higgs. However, the$3e+ {E}^{\rm miss}_{T}$ signal could reach a higher triplet Higgs mass when the triplet Higgs mass is larger than 800 GeV. The main reason for this is that when the mass of the triplet Higgs is low, the missing energy could be lower and the missing energy cut could also hurt the signal. We believe that an even larger missing energy cut could further suppress the background and a better sensitivity for the heavy triplet Higgs can be reached.Diboson BKG 600 GeV 900 GeV 1200 GeV Pre-selection 14518 2249 242 38 $m_{\rm invariant} > 200$ GeV

3037 2199 241 38 $ P_{T}\left (e^{\pm } e^{\pm }\right)> 100 $ GeV

1379 2168 239 37 $ \sum\left|P_{T}\left (e \right) \right|> 300 $ GeV

673 2139 237 37 $ \Delta R\left (e^{\pm },e^{\pm } \right)< 3.5 $ 

490 1596 174 26 $E^{\rm miss}_{T} > 300$ GeV

49.1 790 111 20 Significance − 113 15.8 2.9 Table 3. Cut flow for the diboson background and the signal (
$ m_{H^{\pm \pm } }=600 $ GeV,$ m_{H^{\pm \pm } }=900 $ GeV,$ m_{H^{\pm \pm } }=1200 $ GeV) with an integrated luminosity of$3000~\rm fb^{-1}$ and$ \sqrt{s} = $ 13 TeV. -
Type II seesaw leptogenesis simultaneously explains the origin of neutrino masses, the baryon asymmetry of our universe, and inflation. The LHC provides an opportunity to directly test type II seesaw leptogenesis by looking for the predicted triplet Higgs. In this paper, we perform an analysis of the detection prospect for the triplet Higgs at the LHC through multi-electron channels. We find that due to the contribution of the
$ pp\to H^{\pm \pm }H^{\mp } $ process, the sensitivity of multi-electron channels searching for the doubly-charged Higgs pair production can be improved. We also investigate the$3e+ {E}^{\rm miss}_{ T}$ signals to probe the$ pp\to H^{\pm \pm }H^{\mp } $ production and we find this channel may provide better sensitivity than the multi-electron channels. Our results show that the future LHC could probe a triplet Higgs around 1.2 TeV at the 2σ level with a luminosity of 3000$\rm fb^{-1}$ for the$3e+ {E}^{\rm miss}_{ T}$ search channel. -
Indistinguishable from background hypotheses in the case of few signal events, we use the
$ CL_{s} $ method to improve experimental sensitivity. The usual confidence level for signal and background hypothesis is given by the probability that the test-statistic Q is less than or equal to the value observed in the experiment:$ CL_{s+b}=P_{s+b}(Q\leq Q_{\rm obs})=\int_{-\infty}^{Q_{\rm obs}}\frac{{\rm d}P_{s+b}}{{\rm d}Q}{\rm d}Q, \tag{A1} $

where
$\dfrac{{\rm d}P_{s+b}}{{\rm d}Q}$ is the probability distribution function for signal and background experiments. Likewise, the confidence level in the background-only hypothesis is:$ CL_{b}=P_{b}(Q\leq Q_{\rm obs})=\int_{-\infty}^{Q_{\rm obs}}\frac{{\rm d}P_{b}}{{\rm d}Q}{\rm d}Q, \tag{A2} $

and
$\dfrac{{\rm d}P_{b}}{{\rm d}Q}$ is the probability distribution function for background-only experiments.To obtain the limit, we use the definition of
$ CL_s $ $ CL_{s}=\frac{CL_{s+b}}{CL_{b}}. \tag{A3} $

The signal hypotheses is excluded at the confidence level
$ CL $ when$ 1-CL_{s}\leq CL. \tag{A4} $

To combine the results of the signals from several channels, the test statistic is defined as the likelihood ratio
$ Q= \prod\limits_{i=1}^{n}q_{i} \tag{A5}$

with
$ q_{i}=\frac{\dfrac{{\rm e}^{-(s_{i}+b_{i})}((s_{i}+b_{i})^{N_{i}}}{N!}}{\dfrac{{\rm e}^{-b_{i}}b_{i}^{N_{i}}}{N!}} \tag{A6} $

for counting experiments. The estimated signal and background are
$ s_{i} $ and$ b_{i} $ , respectively, and i labels the channel. N is the number of observed candidates. The final likelihood function should also include the uncertainty of the backgrounds. All of the above calculations can be preformed numerically by the Monte Carlo method.
Testing type II seesaw leptogenesis at the LHC
- Received Date: 2023-05-12
- Available Online: 2023-09-15
Abstract: Type II seesaw leptogenesis simultaneously explains the origin of neutrino masses, the baryon asymmetry of our universe, and inflation. The Large Hadron Collider (LHC) provides an opportunity to directly test type II seesaw leptogenesis by looking for the predicted triplet Higgs. In this paper, we perform an analysis of the detection prospect for the triplet Higgs at the LHC through multi-electron channels. We find that due to the contribution of the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: