Uncertainties of critical temperatures based on higher-order fluctuations of the largest fragment charge

The dynamic response of many body systems in the smooth change of external driving parameters is an interesting topic in statistical mechanics and has been widely investigated [1]. However, the system can be driven far away from equilibrium when physical quantities (such as pressure and temperature) undergo sudden and intense changes. The nonequilibrium relaxation phenomenon thus influences the characteristic changes of order parameters and further brings challenges to the statistical description of phase transitions, which are generally discussed in the framework of the equilibrium hypothesis [2−5]. The heavy ion collisions (HICs) at intermediate energies exhibit a typical nonequilibrium relaxation phenomenon and have been a hot topic in nuclear physics during the last several decades.

In nuclear physics, liquid-gas phase transition (LGPT) is a natural phenomenon in infinite nuclear matter due to the nuclear force of Van-der-Waals type [6−8]. It leads to a spinodal region defined by the negative isothermal compressibility. In the spinodal region, the pure liquid phase is unstable, leading to the breakdown of the system into a mixture of liquid and gas phases at equilibrium [9, 10]. As the counterpart in the finite case, the hot nuclear system produced in the HICs at intermediate energies exhibits the phenomenon of multifragmentation [11−14], which is considered to relate to the LGPT [15, 16]. Some theoretical groups used the statistical model to reproduce the final state of the reaction, and they obtained some LGPT probes [17, 18], such as the bimodality in charge asymmetry [19] and back bending of constant pressures caloric curves [20].

LGPT probes are generally based on the final state population to predict the existence of two-phase transition during the expansion process of the nuclear system. However, the dynamical path from the initial state to final state is important to describe the two-phase transition due to the finite and quantum nature of the nuclear system. This initial-final correlation of the phase space has been recently put forward in HICs both at intermediate and relativistic energies [21−23]. In contrast, the nonequilibrium relaxation of the hot nuclear system in multifragmentation has been deduced in the experiments and theoretical works [23−27]. The critical parameters, such as critical temperature, are significant to describe the LGPT and have been extracted using the HICs [28]. Then, a key question is left unanswered, i.e., will the initial-final correlation and the nonequilibrium relaxation bring the uncertainties of the critical parameters extracted by the HICs?

The signature of the LGPT in HICs has been well described by the higher-order fluctuations of the largest fragment charge [18, 19, 25, 27, 29−31]. The critical temperatures have been extracted based on this signature in $ ^{107,124} $Sn + $ ^{120} $Sn collisions at 600 MeV/nucleon [18]. In our previous work, the higher-order fluctuations of the largest fragment charge have been successfully described with the isospin-dependent quantum molecular dynamics (IQMD) model coupled with the statistical model GEMINI [27, 31]. In this study, the IQMD+GEMINI model is used to simulate the $ ^{124} $Sn + $ ^{120} $Sn collisions at an incident energy from 400 to 1000 MeV/nucleon and the $ ^{124} $Sn + $ ^{A} $Z collisions at 600 MeV/nucleon, where $ ^{A} $Z indicates $ ^{40} $Ca, $ ^{56} $Fe, $ ^{90} $Zr, $ ^{120} $Sn, $ ^{136} $Xe, and $ ^{197} $Au. The higher-order fluctuations of the largest fragment charge and the nuclear temperatures in those reactions are studied. This study focuses on the uncertainties of critical temperatures based on higher-order fluctuations of the largest fragment charge. The uncertainties of critical temperatures are considered from the perspectives of incident energy, mass number of target nuclei, and statistical ensemble selection. During the nuclear collision, the projectile-like system exhibits a significant dynamical effect. The correlation between the dynamical effect and the uncertainties of critical temperatures is also discussed.

The paper is organized as follows. In Sec. II, the theoretical framework is described. In Sec. III, the results and discussions are presented. Finally, Sec. IV presents the conclusions.

In the IQMD model, the wave function of each nucleon is expressed by a Gaussian wave packet

where $ {\bf{r}}_{i} $ and $ {\bf{p}}_{i} $ represent the mean position and momentum of the ith nucleon, respectively, and L is related to the divergence degree of the vector field at each nucleon of the Gaussian wave packet. The N-body wave function of the system is the direct product of these coherent states. By applying the Wigner transformation to the wave function, the classical one phase-space density can be obtained. Otherwise, the N-body phase space density is a product of the phase-space density of each nucleon.

The time evolution of the nucleons in the self-consistently generated mean field is determined by the Hamiltonian equations of motion,

The Hamiltonian can be divided into kinetic energy, Coulomb interaction, and nuclear interaction. The nuclear potential energy density of the asymmetric nuclear matter with density ρ and asymmetry δ is given by

where $ \rho_0 $ is the normal density. The parameters α, β, γ, $ C_{sp} $, and $ \gamma_{i} $ are temperature independent. In Eq. (4), the first and second terms are widely used in the transport models, which are related to the local two-body and three-body interactions. The third term in Eq. (4) is applied to investigate the form of the symmetry potential. The parameters used in this study are α = –356.00 MeV, β = 303.00 MeV, γ = 7/6, $ C_{sp} $ =38.06 MeV, and $ \gamma_i $ = 0.75.

The process of nucleon-nucleon ($ NN $) collisions is also simulated in the IQMD model. It is applied to describe the effect of the short-range repulsive residual interaction and the stochastic change of the phase-space distribution. The differential cross sections of $ NN $ collisions are given by

where $ \sigma^{\rm free} $, $ \mathit{f^{\rm angl}} $, and $ \mathit{f}^{\rm med} $ represent the cross section of $ NN $collisions in the space, angle distribution, and in-medium corrections, respectively. The subscript $ \mathit{i} $ is related to the channels of the $ NN $ collisions, i.e., the elastic proton-proton scatterings ($ \mathit{i} $=$ pp $), elastic neutron-proton scatterings ($ \mathit{i} $ = $ np $), elastic neutron-neutron scatterings ($ \mathit{i} $ = $ nn $), and inelastic nucleon-nucleon collisions ($ \mathit{i} $ = $ in $). The parameterization of $\sigma^{\rm free}$ and $\mathit{f^{\rm angl}}$ are taken from Ref. [32]. The $\mathit{f}^{\rm med}$ of elastic scatterings is written as [33]

The dependence of density can be seen in Eq. (6). $\sigma^{\rm free}$ depends on the energy and isospin; therefore, the in-medium factor is also governed by energy and isospin. In addition, because the effect of using in-medium modified cross sections is weak for the fragment observables in this study, in-medium correction of inelastic $ NN $ collisions are not considered.

To compensate for the fermionic feature in the region where the binary collisions are scarce, the phase-space density constraint (PSDC) method together with the Pauli blocking is applied. The binary NN collisions are allowed with the probability $(1-f_{i}^{\prime})(1-f_{j}^{\prime})$, in which $f_{i}^{\prime}$ and $f_{j}^{\prime}$ are the phase-space densities at the final states before the scattered particle is placed there. In the current study, the PSDC method is used to preserve the fermionic nature better. The phase-space occupation probability $ \overline{\mathit{f}_i} $ is calculated by performing the integration on a hypercube of volume $ \mathit{h}^3 $ in the phase space centered around the $ \mathit{i} $th nucleon at each time step, i.e.,

Here, 0.621 is the contribution itself, and $ \tau _i $ represents the isospin degree of freedom. At each time step, the phase-space occupation $ \overline{\mathit{f}_i} $ for each nucleon is checked. If the phase-space occupation $ \overline{\mathit{f}_i} $ has a value greater than 1, the momentum of the $ \mathit{i} $th nucleon is changed randomly by a procedure similar to that used when treating the elastic scattering of two nucleons. Meanwhile, the Pauli blocking in the binary $ NN $collisions is modified. The many-body elastic scattering is accepted only if $ \overline{\mathit{f}_i} $ and $ \overline{\mathit{f}_j} $ at the final states are both less than 1.

The hot nuclei during the evolution are distinguished by the minimum spanning tree (MST) algorithm. In a hot system, the relative distance of the coordinate and momentum of the nucleon are $ \mid r_i-r_j \mid \le R_0 $ and $ \mid p_i-p_j \mid \le P_0 $, respectively. $ R_0 $ and $ P_0 $ are phenomenological parameters with values $ R_0 $ = 3.5 fm and $ P_0 $ = 250 MeV/c. The excitation energy per nucleon of the hot system can be written as

Here, $ U_i $ and $ p_i $ are the single-particle potential and momentum of the ith nucleon; $ p_f $, $ Z_f $, and $ A_f $ are the average momentum per nucleon, charge number, and mass number of the fragment, respectively; and $B( Z_f$, $ A_f $) is the binding energy of a nucleus with charge number $ Z_f $ and mass number $ A_f $. The summation is for the nucleons belonging to the same hot system. The MST algorithm is applied at each time step; therefore, the projectile spectator can be recognized.

The violent collision of the projectile and target is simulated by the IQMD model. When the excitation energies of the two heaviest prefragments are less than a certain value $ E_{\rm stop} $ ($ E_{\rm stop} $= 2 MeV/nucleon), the simulations of the IQMD model are stopped, and the GEMINI code is switched on. The influence of the $ E_{\rm stop} $ value on the projectile fragmentation has been reported in our previous work [34]. A system ($ \mathit{Z}_0 $,$ \mathit{A}_0 $) with excitation energy $ \mathit{E}^* $ and spin $ \mathit{J}_0 $ emits a light particle ($ \mathit{Z}_1 $,$ \mathit{A}_1 $) with spin $ \mathit{J}_1 $ and leaves the residual system ($ \mathit{Z}_2 $,$ \mathit{A}_2 $) with spin $ \mathit{J}_2 $, which is the Hauser-Feshbach formalism for the light particle evaporation. Therefore, the decay width taken from the Hauser-Feshbach formalism for the light particle evaporation is given by

where $ \mathit{l} $ and ε are the orbital angular momentum and kinetic energy of the emitted particle, respectively; $\mathit{E}_{\rm not}$ is the rotation plus deformation energy of the residual system; $ \rho_0 $ and $ \rho_2 $ are the level densities of the initial and residual systems; and $ \mathit{T_l} $ is the transmission coefficient. $ \mathit{B} $ is the binding energy. The details of GEMINI are given in Ref. [35].

The reliable indication for the phase transition in a finite system can be derived from the fluctuations of central moments [18, 27, 31, 36]. The higher-order fluctuations of the largest fragment charge $K_{i}(Z_{\max})$ are defined as

where $ K_{3} $ is the skewness indicating the distribution of asymmetry, and $ K_{4} $ is the kurtosis excess. All events are classified according to a given observation ($Z_{\rm bound}$, $ E^{*} $, or b); therefore, the events with the same calculated values of this given observation will form an ensemble. The $ \left \langle \right \rangle $ symbol denotes the averaged value of the distributions in the ensemble.

The concept of the isotope thermometer, introduced in Ref. [37], has been widely used to measure the nuclear temperature. It is based on the $ ^{3} $He/$ ^{4} $He and $ ^{6} $Li/$ ^{7} $Li yield ratios, defined as

The momentum fluctuation thermometer for measuring the temperature of hot nuclei was proposed in Ref. [38]. Based on the fluctuation-dissipation theorem, it is proposed that the momentum fluctuation of emitted light fragments is related to the nuclear temperature [39]. Assuming a Maxwell-Boltzmann distribution of the momentum yields, the temperature is deduced from the quadrupole momentum fluctuations defined in a direction transverse to the beam axis,

where $ Q_{xy} $ is equal to $ p_{x}^{2} $ - $ p_{y}^{2} $, and m and p are the mass and linear momentum of emitted particles, respectively. Taking into account the quantum nature of particles, a correction method related to the Fermi-Dirac distribution was also proposed [40],

The Fermi energy $ E_F $ depends on the freeze-out density; therefore, it can be written as $ E_F(\rho) $ = 38$ (\rho/\rho_0)^{2/3} $ MeV. After calculating the ratio between the temperature and Fermi energy $ \dfrac{T_{flu}^{'}}{E_F}=\dfrac{2}{3}\dfrac{\left \langle (\Delta n)^2 \right \rangle }{\bar{n}} $ by the fluctuations of the neutron multiplicity distributions, the temperature $ T_{flu}^{'} $ can be obtained from Eq. (13). The momentum fluctuations of tritium particles are calculated in this study.

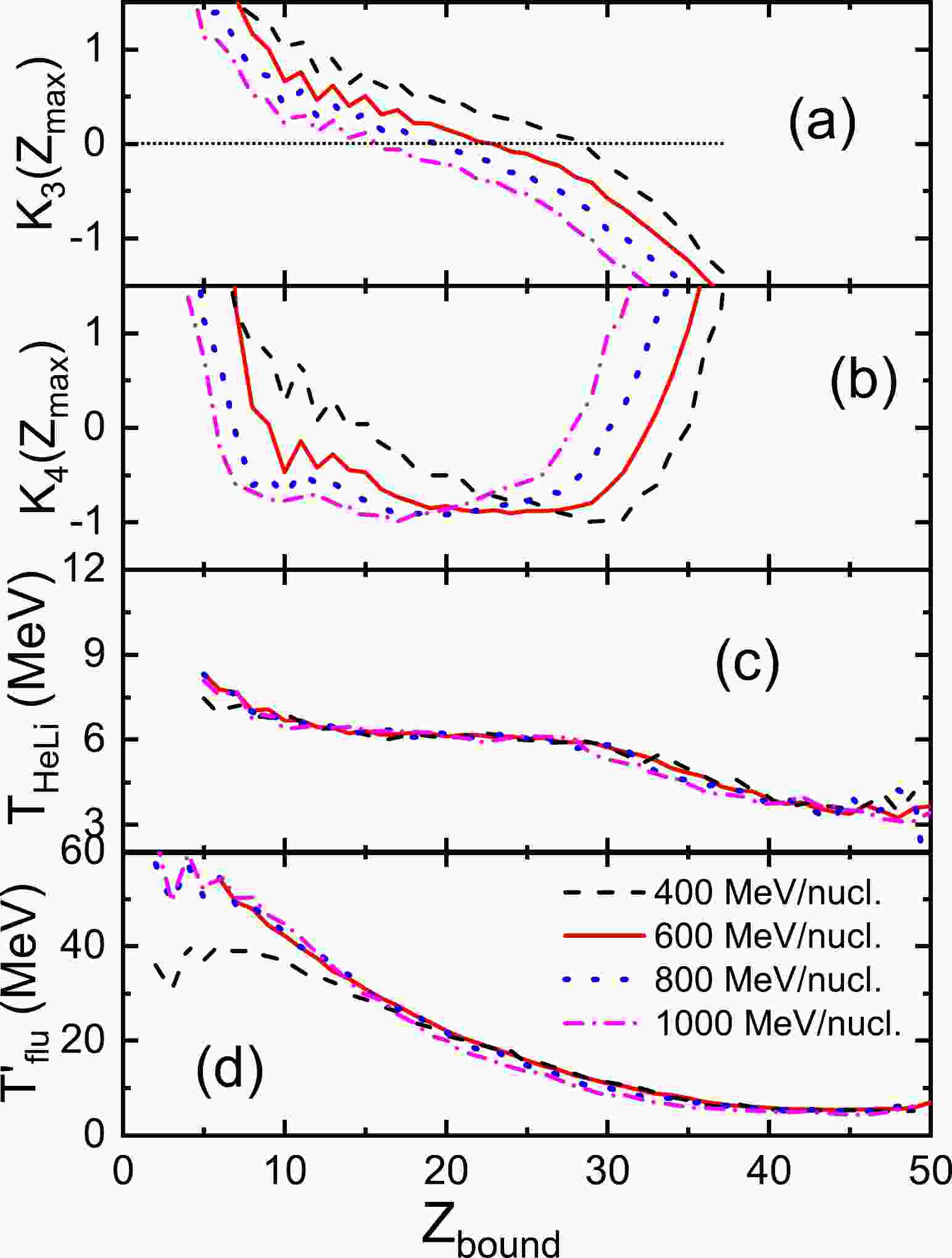
Before presenting the calculations, the impact parameter used in the simulations should be clearly pointed out. In this subsection, the impact parameters of the nuclear reaction are randomly chosen from 0 to $b_{\max}$ fm. The maximum impact parameter is defined by $b_{\max} = 1.2(A_{p}^{1/3} + A_{t}^{1/3})$. $ A_p $ and $ A_t $ are the mass numbers of the projectile and target, respectively.

Figure 1 shows the higher-order fluctuations of the largest fragment charge as well as the temperatures $T_{\rm HeLi}$ and $ T_{flu}^{'} $ as functions of the bound charge $Z_{\rm bound}$ for the $ ^{124} $Sn + $ ^{120} $Sn collisions from 400 to 1000 MeV/nucleon. The quantity $Z_{\rm bound}$ is defined as the sum of the atomic numbers $ Z_{i} $ of all detected fragments, with $Z_{\max} \ge$ 2. $Z_{\rm bound}$ increases monotonically but non-linearly with the impact parameter of the reaction. $ K_{3} $ decreases with increasing $Z_{\rm bound}$. $ K_{4} $ first decreases and then increases with increasing $Z_{\rm bound}$, showing a U-shaped distribution. The pseudo-critical point is indicated by the zero transitions of $ K_3 $ coinciding with the minimum of $ K_4 $, which reveals the balance of reaction mechanisms between the nucleon evaporation mode and multifragmentation mode [27]. The phenomenon of the pseudo-critical point has been exhibited in the experiment reported in Ref. [18]. Similar results can be obtained by taking the impact parameter b for event sorting [31].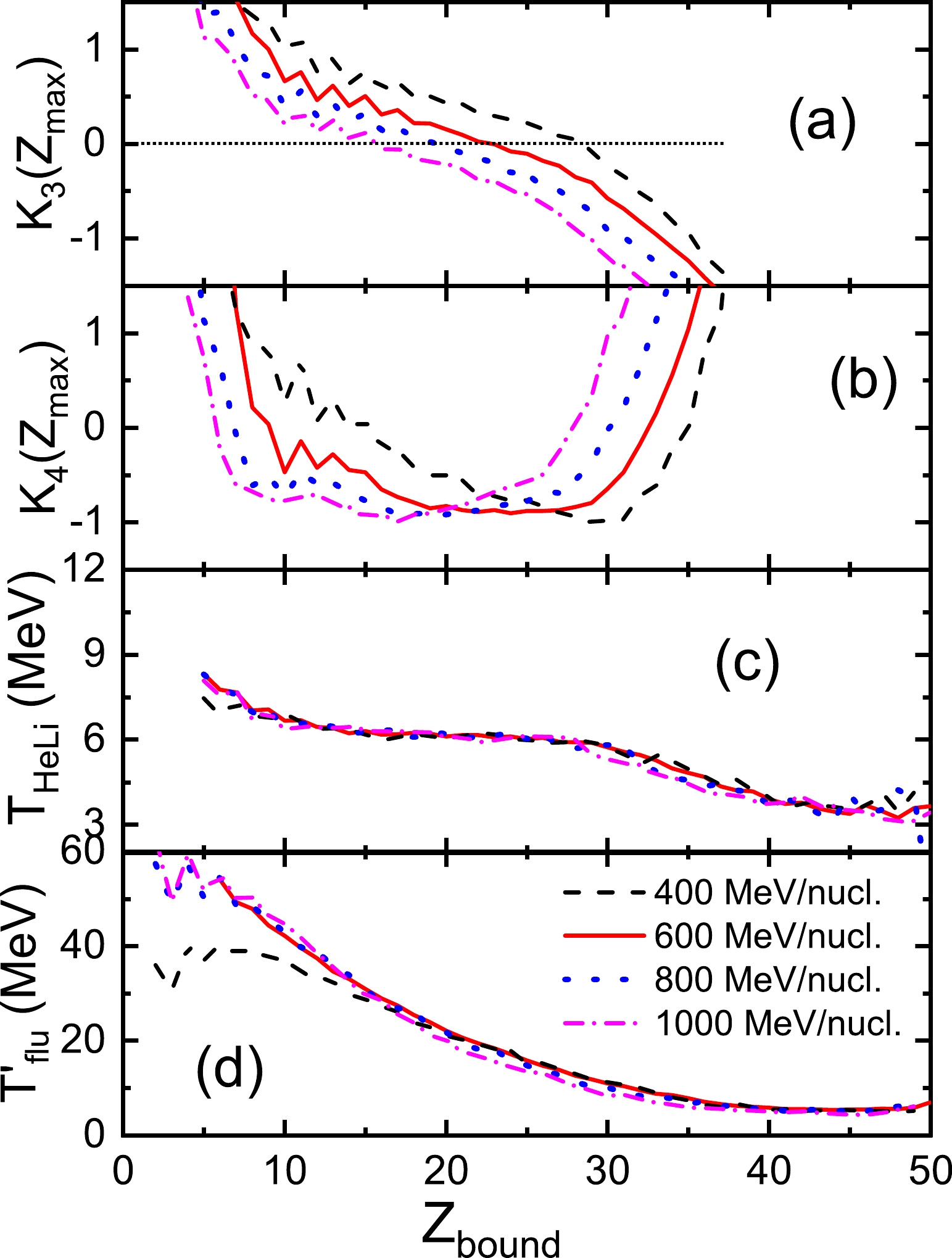

Figure 1.  (color online) (a) Skewness $ K_3 $, (b) kurtosis excess $ K_4 $, (c) temperature $T_{\rm HeLi}$ from the isotope thermometer, and (d) temperature $ T_{flu}^{'} $ from the quantum fluctuation thermometer as a function of the bound charge $Z_{\rm bound}$ for the ¹²⁴Sn + ¹²⁰Sn collisions at energies from 400 to 1000 MeV/nucleon obtained by the IQMD+GEMINI model.

The values of temperatures $T_{\rm HeLi}$ and $ T_{flu}^{'} $ both decrease with increasing $Z_{\rm bound}$, as shown in Figs. 1(c) and 1(d). The $T_{\rm HeLi}$ curves present a plateau, but the $ T_{flu}^{'} $ curves do not. If the system meets the thermodynamic limit and local equilibrium, the temperature determined by the quantum fluctuation thermometer should be the same as that obtained by the isotope thermometer. However, in the projectile fragmentation from 400 to 1000 MeV/nucleon, the value of $ T_{flu}^{'} $ is overall higher than that of $T_{\rm HeLi}$, which implies that the system is finite and does not achieve the local equilibrium. Especially in the small $Z_{\rm bound}$ region ($Z_{\rm bound} <$ 10), $ T_{flu}^{'} $ is seven times larger than $T_{\rm HeLi}$. According to the report of Kelic et al. [41], the isotope thermometer is basically sensitive to the internal excitation energy of fragments produced in the reactions, while the momentum fluctuations deal with the kinetic degrees of freedom of the fragments. The former is limited; otherwise, no fragments would survive in severe collisions, whereas the kinetic energy of highly hot fragments can increase without limit.

With the increase in incident energy, the pseudo-critical points shift to the left, as seen in Figs. 1(a) and 1(b). It means that the violence degree of the reaction will affect the signal of phase transition. The energy dependence of the temperature is small but can be observed. In the $Z_{\rm bound}$ region from 20 to 40, both temperatures decrease with increasing incident energy.

The excitation energy $ E^{*} $ of the hot projectile-like system is calculated by Eq. (8) at the moment when the projectile-like and target-like systems begin to separate. It is applied for event-sorting, leading to an $ E^{*} $ ensemble. In fact, the $Z_{\rm bound}$ ensemble (see Fig. 1) is often applied in experiments because the observable $Z_{\rm bound}$ is easily measured by the final fragment charge. In contrast, the excitation energy $ E^{*} $ is calculated by the properties of the hot source and includes the information of the initial state. The values of $ K_3 $, $ K_4 $, $T_{\rm HeLi}$, and $ T_{flu}^{'} $ as functions of the excitation energy $ E^{*} $ for the $ ^{124} $Sn + $ ^{120} $Sn collisions at energies from 400 to 1000 MeV/nucleon are presented in Fig. 2. Because the excitation energy $ E^{*} $ of the hot projectile-like system monotonically increases with the violence of the reaction, the $ K_3 $ value and temperatures increase with increasing $ E^{*} $. For the $ E^{*} $ ensemble, there are also the pseudo-critical points, which are indicated by the coincidence between the zero transitions of $ K_3 $ and the minima of $ K_4 $. Similar to that in the $Z_{\rm bound}$ ensemble, the $T_{\rm HeLi}$ curves present a plateau, but $ T_{flu}^{'} $ curves do not. The nuclear temperature measured via $ T_{flu}^{'} $ is also higher than that obtained using $T_{\rm HeLi}$. With the increase in incident energy, the pseudo-critical points in the $ E^{*} $ ensemble naturally shift to the right, as shown in Figs. 2(a) and 2(b). However, the incident energy dependence of the temperatures in the $ E^{*} $ ensemble is more obvious than that of the temperatures in the $ Z_{\rm bound} $ ensemble. Especially in Fig. 2(d), at a given $ E^{*} $ value, the calculations of $ T_{flu}^{'} $ decrease with increasing incident energy.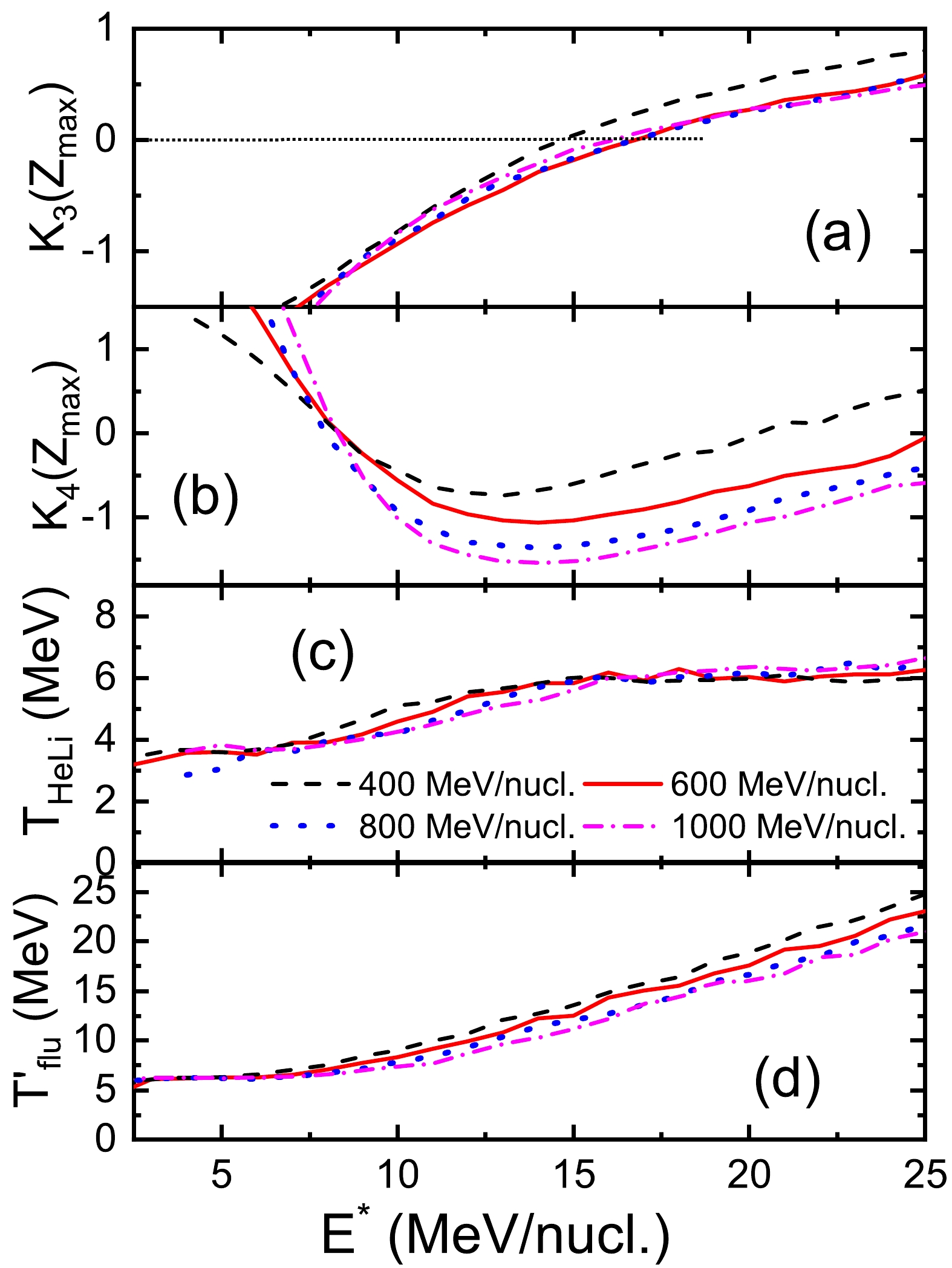

Figure 2.  (color online) Same as Fig. 1 but as functions of the excitation energy of the hot projectile-like system.

The influence of the mass number of the target nuclei on the pseudo-critical point and nuclear temperature is investigated, as displayed in Fig. 3. The calculations are obtained from the $ ^{124} $Sn + $ ^{40} $Ca, $ ^{124} $Sn + $ ^{56} $Fe, $ ^{124} $Sn + $ ^{90} $Zr, $ ^{124} $Sn + $ ^{120} $Sn, $ ^{124} $Sn + $ ^{136} $Xe, and $ ^{124} $Sn + $ ^{197} $Au collisions at 600 MeV/nucleon. The pseudo-critical points can be clearly observed in the projectile fragmentation of $ ^{124} $Sn colliding with different target nuclei. It is interesting to note that the pseudo-critical points in the $ Z_{\rm bound} $ ensemble decrease with increasing mass number of the target nuclei. The violence degree of the reaction increases with the mass number of target nuclei. Therefore, a more violent reaction leads to a small pseudo-critical point, as measured by the $Z_{\rm bound}$ ensemble. The mass number of the target nuclei will affect the signal of phase transition. The temperatures $T_{\rm HeLi}$ and $ T_{flu}^{\prime} $ are weakly dependent on the size of the target nuclei, as shown in Figs. 3(c) and 3(d).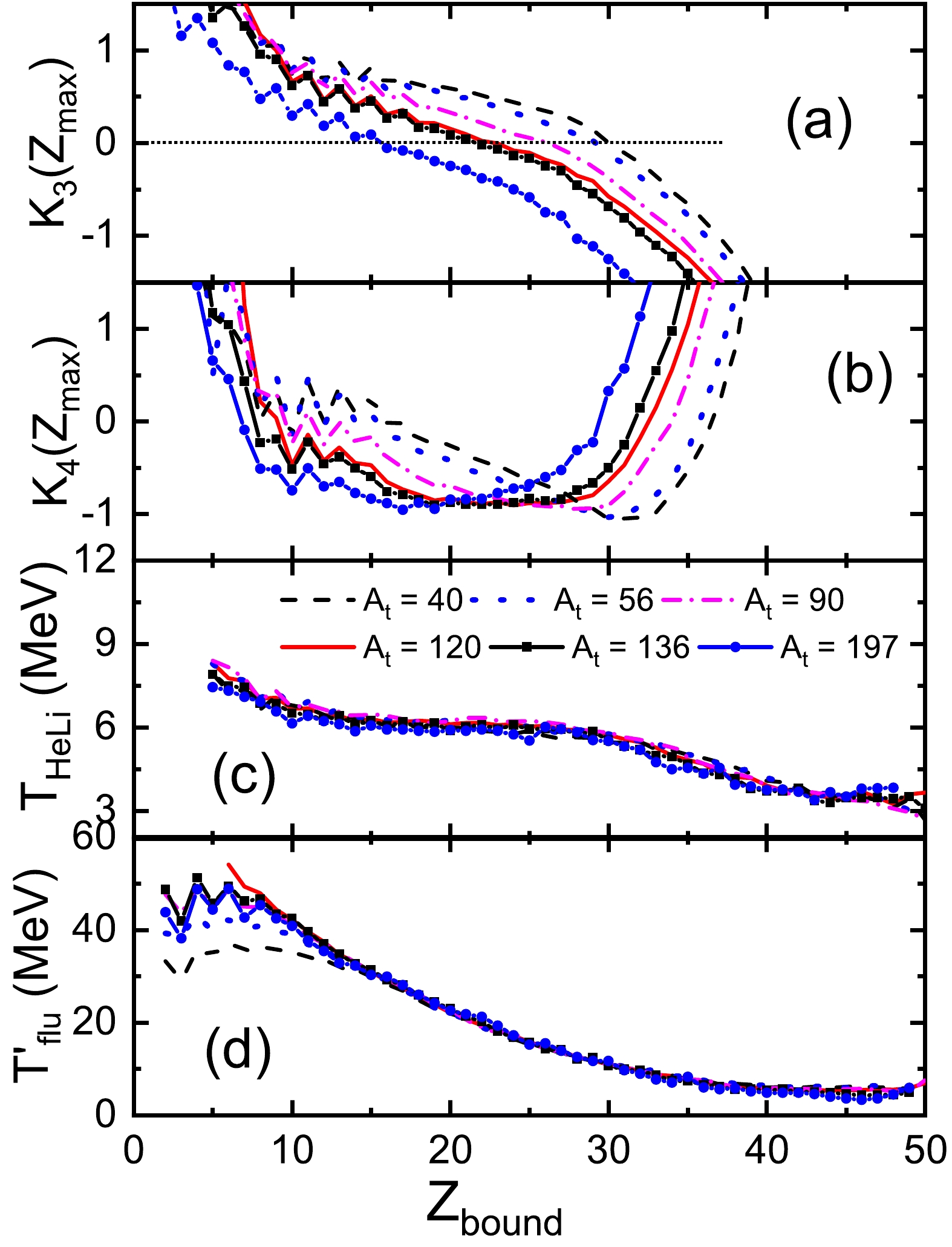

Figure 3.  (color online) Same as Fig. 1 but for the ¹²⁴Sn + ⁴⁰Ca, ¹²⁴Sn + ⁵⁶Fe, ¹²⁴Sn + ⁹⁰Zr, ¹²⁴Sn + ¹²⁰Sn, ¹²⁴Sn + ¹³⁶Xe, and ¹²⁴Sn + ¹⁹⁷Au collisions at 600 MeV/nucleon.

The effect of the target nuclei on the pseudo-critical point and temperature are further discussed in the $ E^{*} $ ensemble, as seen in Fig. 4. At a given projectile, a larger size of target nuclei will lead to a larger violence degree of the reaction. The correlation between the violence degree of the reaction and the signal of phase transition in a finite system can also be reflected in the $ E^{*} $ ensemble. Figures 4(a) and 4(b) show that the pseudo-critical points calculated in the $ E^{*} $ ensemble become larger with increasing mass number of target nuclei. The dependence of the size of the target nuclei on the temperatures $T_{\rm HeLi}$ and $ T_{flu}^{'} $ can be observed in Figs. 4(c) and 4(d). In the region from $ E^{*} $ = 7.5 to $ E^{*} $= 17.5 MeV/nucleon, both temperatures decrease with the increase in mass number of target nuclei for a fixed excitation energy.

Figure 4.  (color online) Same as Fig. 3 but as functions of the excitation energy of the hot projectile-like system.

The dependences of the incident energy and the size of the target nuclei on the higher-order fluctuations of the largest fragment charge are strong, but those on the nuclear temperature is relatively weak. The violence degree of the reaction is positively related to external conditions, such as the incident energy or size of the target nuclei. It is shown that the pseudo-critical points will obviously be affected by the violence degree of the reaction. The pseudo-critical points in the $Z_{\rm bound}$ ensemble decrease (increase in the $ E^{*} $ ensemble) as the violence degree of the reaction rises. In our previous study [27], we found that the pseudo-critical point indicates the balance between nucleon evaporation and multifragmentation. In this study, the signal of the phase transition does not have a fixed indicative value in a finite system. Therefore, when the incident energy or the mass number of target nuclei is larger, the two-phase balance will occur in the system with greater excitation. The statistical results obtained in the $Z_{\rm bound}$ and $ E^{*} $ ensembles provide a consistent description of the liquid-gas phase transition and the nuclear temperature.

The impact parameter was also applied for event-sorting, which is called the b ensemble in our previous work [31]. The pseudo-critical point is measured as the impact parameter $ b_{c} $ at which the collision leads to the zero transitions of K$ _{3} $ coinciding with the minima of K$ _{4} $. Similarly, the values of bounding charge and excitation energy at the pseudo-critical points are $ Zb_{c} $ and $ E^{*}_{c} $. Figure 5 shows the values of $ Zb_{c} $, $ E^{*}_{c} $, and $ b_{c} $ as functions of the incident energy for the $ ^{124} $Sn + $ ^{120} $Sn collision (left column) and as functions of the mass number of target nuclei for the $ ^{124} $Sn + $ ^{A} $Z collisions at 600 MeV/nucleon (right column). The target nucleus $ ^{A} $Z denotes $ ^{40} $Ca, $ ^{56} $Fe, $ ^{90} $Zr, $ ^{120} $Sn, $ ^{136} $Xe, and $ ^{197} $Au. The pseudo-critical points of $ K_{3} $ = 0 do not completely coincide with those of the minimum value of $ K_{4} $. They are displayed as error bars in the figure.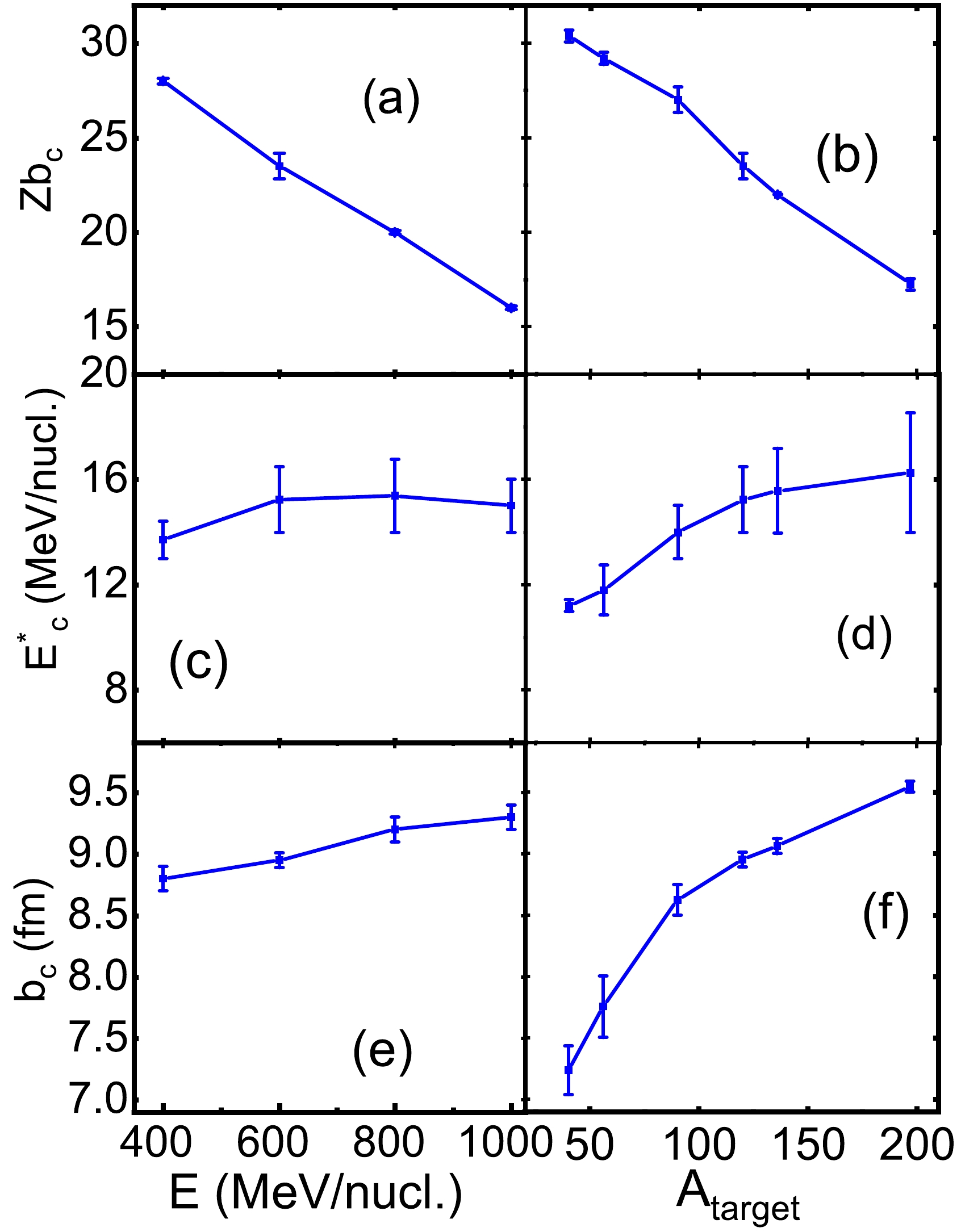

Figure 5.  (color online) Pseudo-critical points obtained in the $Z_{\rm bound}$, $ E^{*} $, and impact parameter b ensembles as functions of the incident energy in the ¹²⁴Sn + ¹²⁰Sn collision (left column) and as functions of the mass number of the target nuclei in the ¹²⁴Sn + ^AZ collisions at 600 MeV/nucleon (right column).

The $ Zb_{c} $ value decreases quickly with the increase in incident energy, as shown in Fig. 5(a). It can be explained that the pre-equilibrium emission becomes stronger when the violence degree of the reaction is higher. The $ E^{*}_{c} $ value slowly increases with increasing incident energy, as seen in Fig. 5(c). In terms of the incident channel effect, the $ b_{c} $ value increases with increasing incident energy, as displayed in Fig. 5(e). If the incident energy of the projectile is larger, the impact parameter should increase moderately to meet the transition of reaction mechanisms. In contrast, the pre-equilibrium emission becomes gradually stronger with increasing mass number of the target nuclei. The $ Zb_{c} $ value thus drops with increasing mass number of the target nuclei; see Fig. 5(b). Figure 5(d) exhibits that the $ E^{*}_{c} $ curves rise slowly with increasing size of target nuclei.

In fact, the pseudo-critical point indicates the balance between the multifragmentation and nucleon evaporation [27]. The nucleon evaporation of the hot projectile-like system leads to a large residue, while the largest fragment in the multifragmentation is quite small. Therefore, the bimodal distribution of the largest fragment charge (or mass) is expected at the pseudo-critical point. However, our previous study has proven that the wide distribution rather than the bimodal distribution is observed in the impact parameter b ensemble [27]. The distributions of the largest fragment mass $A_{\max}$ at the pseudo-critical points in the $Z_{\rm bound}$ ensemble are calculated and shown in Fig. 6(a) for the $ ^{124} $Sn + $ ^{120} $Sn collisions at energies from 400 to 1000 MeV/nucleon. Within the margin of error, the bimodal distributions are not observed. The distributions of the largest fragment mass $A_{\max}$ at the pseudo-critical points in the $ E^{*} $ ensemble are calculated and shown in Fig. 6(b). Two peaks in the distributions are observed in the $ E^{*} $ ensemble. One near $A_{\max}$ = 5 corresponds to the multi-fragmentation events, and the other in the region from $A_{\max}$= 20 to 70 is derived from the nucleon-evaporation events. The bimodality indicates the concomitance of two reaction mechanisms. With the increase in incident energy, the position of the multi-fragmentation peak keeps constant, but the nucleon-evaporation peak moves right and becomes narrower.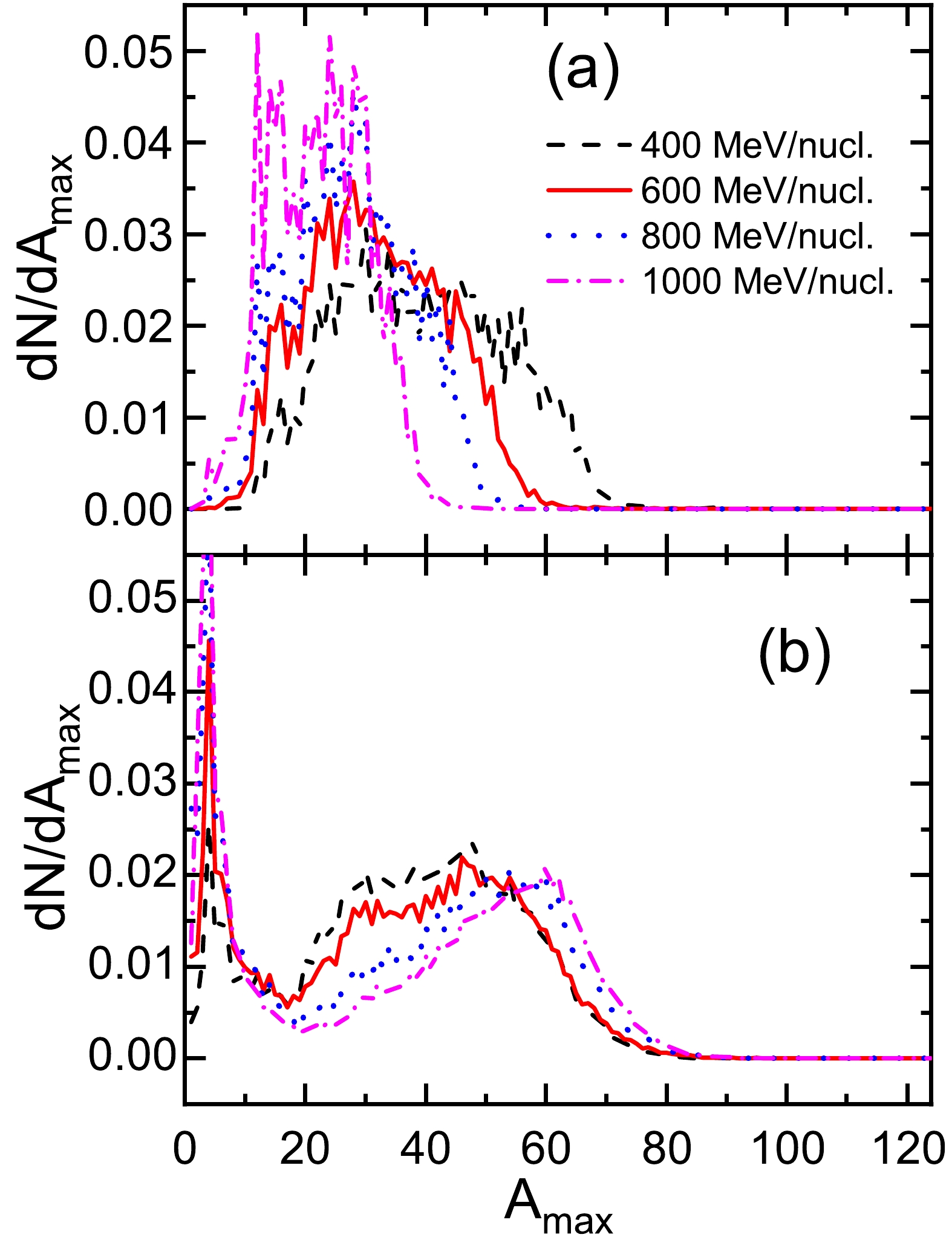

Figure 6.  (color online) Distributions of the largest fragment mass $A_{\max}$ at the pseudo-critical points in (a) the $Z_{\rm bound}$ ensemble and (b) the $ E^{*} $ ensemble for the ¹²⁴Sn + ¹²⁰Sn collisions at energies from 400 to 1000 MeV/nucleon.

Figure 7 is same as Fig. 6 but for the $ ^{124} $Sn + $ ^{A} $Z collisions at 600 MeV/nucleon. The target nucleus $ ^{A} $Z denotes $ ^{40} $Ca, $ ^{56} $Fe, $ ^{90} $Zr, $ ^{120} $Sn, $ ^{136} $Xe, and $ ^{197} $Au. It is observed that the $A_{\max}$ distribution in $Z_{\rm bound}$ ensemble gets narrower and shifts to the left with increasing size of target nuclei; see Fig. 7(a). Still, the wide distributions rather than the bimodal distributions are displayed. The $A_{\max}$ distributions in the $ E^{*} $ensemble show bimodality; see Fig. 7(b). With the increasing mass number of the target, the bimodal distribution gradually shifts to the right.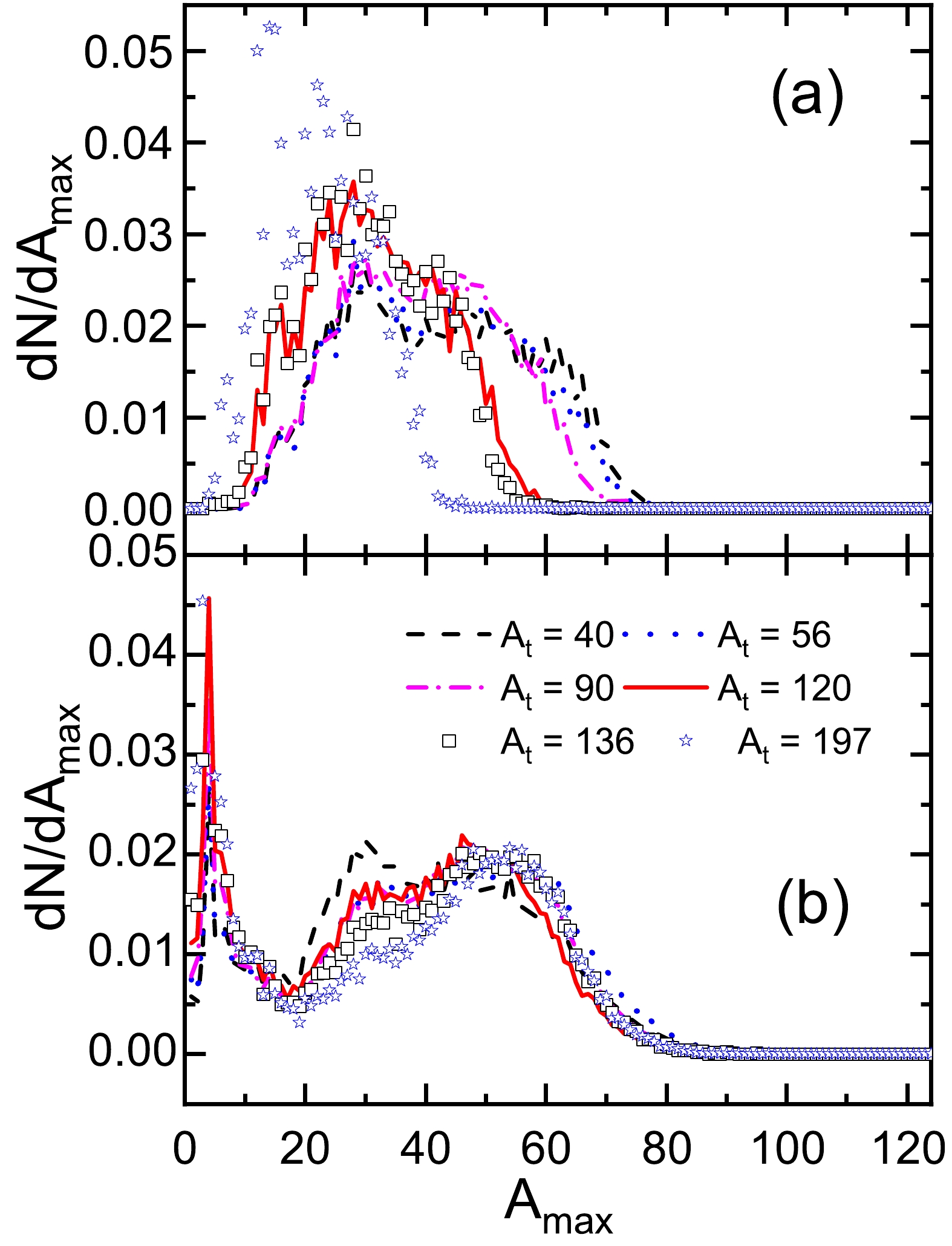

Figure 7.  (color online) Same as Fig. 6 but for the ¹²⁴Sn + ⁴⁰Ca, ¹²⁴Sn + ⁵⁶Fe, ¹²⁴Sn + ⁹⁰Zr, ¹²⁴Sn + ¹²⁰Sn, ¹²⁴Sn + ¹³⁶Xe, and ¹²⁴Sn + ¹⁹⁷Au collisions at 600 MeV/nucleon.

The coordinates and momenta space of nucleons in a hot projectile-like system partly determine the properties of the final fragments, which are referred to as dynamic initial-final correlations [23]. The initial-final correlation also exists in the ultrarelativistic HICs and was reported in [42]. The IQMD+GEMINI model enables us to not only calculate the probability of the final fragments but also describe the dynamical path from the initial to the final state; therefore, the $ E^{*} $ ensemble can be defined. The $Z_{\rm bound}$ is calculated from the final fragments (final state); therefore, the event-sorting by the $Z_{\rm bound}$ ensemble enables one to study the statistical population of the available final states of nuclear reactions. It is the reason why the $Z_{\rm bound}$ ensemble is often applied in experiments. However, the $ E^{*} $ value is calculated from the hot projectile-like system (initial state) and partly determines the properties of the final fragments. Therefore, the initial-final correlation of the statistical properties is applied to explain the difference of the $A_{\max}$ distribution at the pseudo-critical points in the $Z_{\rm bound}$ and $ E^{*} $ ensembles. The mass distribution of the largest fragment in the $ E^{*} $ ensemble is bimodal, but that in the $Z_{\rm bound}$ ensemble is wide. Bimodality is a typical characteristic in the liquid-gas coexistence of a finite system [19]. It indicates that the influence of the initial state of the hot nuclei on the population of the final state cannot be ignored, and this influence cannot be solely reflected in the statistical properties of the final state. Furthermore, it is more reliable to indicate the properties of the nuclear LGPT based on the $ E^{*} $ ensemble.

Figure 8 displays the temperatures at the pseudo-critical points as functions of the incident energy for the $ ^{124} $Sn + $ ^{120} $Sn collisions from 400 to 1000 MeV/nucleon. The temperature at the pseudo-critical point is expected to act as a critical parameter to indicate the transition from nucleon evaporation at low temperature to multifragmentation at high temperature. These temperatures calculated by the isotope thermometer and quantum fluctuation thermometer are shown in Figs. 8(a) and 8(b), respectively. The calculations obtained with $ Zb_{c} $ and $ E^{*} $ ensembles are shown as solid and dash lines, respectively. The temperatures at the point of $ K_{3} $ = 0 are not completely equal to those for the minimum value of $ K_{4} $. This deviation is shown as the error bar in the figure.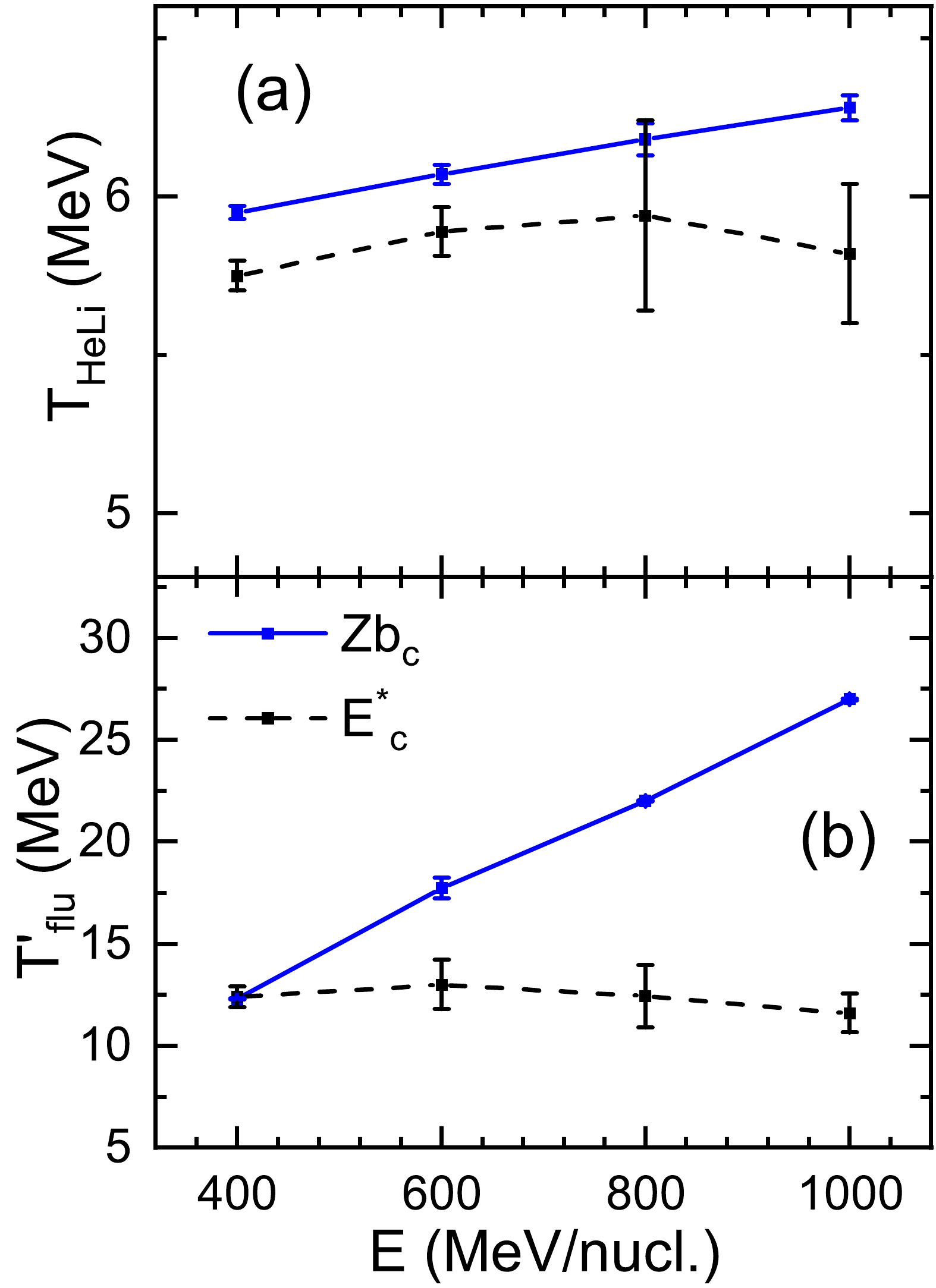

Figure 8.  (color online) Temperatures at the pseudo-critical points as functions of the incident energy for the ¹²⁴Sn + ¹²⁰Sn collisions from 400 to 1000 MeV/nucleon. The calculations based on the $Z_{\rm bound}$ and $ E^{*} $ ensembles are shown as solid and dash lines, respectively.

Figure 8(a) shows that the temperature $T_{\rm HeLi}$ at the pseudo-critical points generally increases with increasing incident energy. These calculations are within the range of 5.6 to 6.2 MeV. The predictions are in close agreement with the data in Ref. [43]. In contrast, the predictions based on the $Z_{\rm bound}$ ensemble are approximately 0.2 MeV larger than those based on the $ E^{*} $ ensemble. It is indicated that the method of event-sorting affects the measurement of the temperature $T_{\rm HeLi}$ at the pseudo-critical point. This difference has a strong influence on the temperature $ T_{flu}^{'} $ at the pseudo-critical points, as shown in Fig. 8(b). The temperature $ T_{flu}^{'} $ based on the $Z_{\rm bound}$ ensemble increases quickly with the increase in incident energy. The calculation even reaches 27 MeV when the incident energy is 1000 MeV/nucleon. In addition, the temperature $ T_{flu}^{'} $ based on the $ E^{*} $ ensemble decreases slowly with increasing incident energy. The temperature $ T_{flu}^{'} $ based on the $ E^{*} $ ensemble is within the range of 11 to 12.5 MeV.

Figure 9 shows the temperatures at the pseudo-critical points as functions of $A_{\rm target}$ for the $ ^{124} $Sn + $ ^{A} $Z collisions at 600 MeV/nucleon. The calculations extracted by the isotope thermometer and quantum fluctuation thermometer are presented as Figs. 9(a) and 9(b), respectively. Figure 9(a) exhibits that the temperature $T_{\rm HeLi}$ at the pseudo-critical points first rises and then falls with increasing mass number of target nuclei. It is shown that the temperature $T_{\rm HeLi}$ at the pseudo-critical points depends not only on the violence degree of the reaction but also on the configuration of the collision. These predictions are for the range from 5.4 to 6.1 MeV. The predictions based on the $Z_{\rm bound}$ ensemble are larger than those based on the $ E^{*} $ ensemble. This again emphasizes that the different method of event-sorting can lead to uncertainty in the temperature $ T_{\rm HeLi} $ at the pseudo-critical point. The selection of the statistical ensembles also has a strong influence on the temperature $ T_{flu}^{'} $ at the pseudo-critical points, as seen in Fig. 9(b). The temperature $ T_{flu}^{'} $ based on the $Z_{\rm bound}$ ensembles ranges between 10 and 27 MeV. In contrast, the temperature $ T_{flu}^{'} $ based on the $ E^{*} $ ensembles rises slowly with the increase in the mass number of target nuclei. Those predictions are within the range from 10 to 13 MeV. It is noted that the predictions between the $Z_{\rm bound}$ and $ E^{*} $ ensembles are slightly different at $A_{\rm target} < 90$ while those are very different at $A_{\rm target} > 90$, as shown in Fig. 9(b). When the projectile is fixed, the violence of the collision increases as the mass number of the target increases. The pseudo-critical points quantified by the $Z_{\rm bound}$ ensemble seem to be sensitive to the violence of nuclear collisions (Fig. 5(b)), which causes the critical temperatures extracted by the quantum fluctuation thermometer to sharply increase with increasing mass number of the target. In contrast, the slope of the curve in Fig. 5(b) is relatively flat at $A_{\rm target} < 90$, which could be explained by the slow growth of the violence of the collision at $A_{\rm target} < 90$. Therefore, when using the $Z_{\rm bound}$ ensemble, the critical temperatures extracted by the quantum fluctuation thermometer increase slowly at $A_{\rm target} < 90$. The temperatures at pseudo-critical points calculated by the $ E^{*} $ ensemble are relatively uniform compared with those calculated by the $Z_{\rm bound}$ ensemble. The discrepancy between the critical temperatures obtained by $Z_{\rm bound}$ and $ E^{*} $ ensembles is thus relatively small at $A_{\rm target} < 90$. Similarly, there is a large discrepancy between the critical temperatures obtained by $Z_{\rm bound}$ and $ E^{*} $ ensembles at $A_{\rm target} > 90$ owing to the sharp descent of the curve in Fig. 5(b).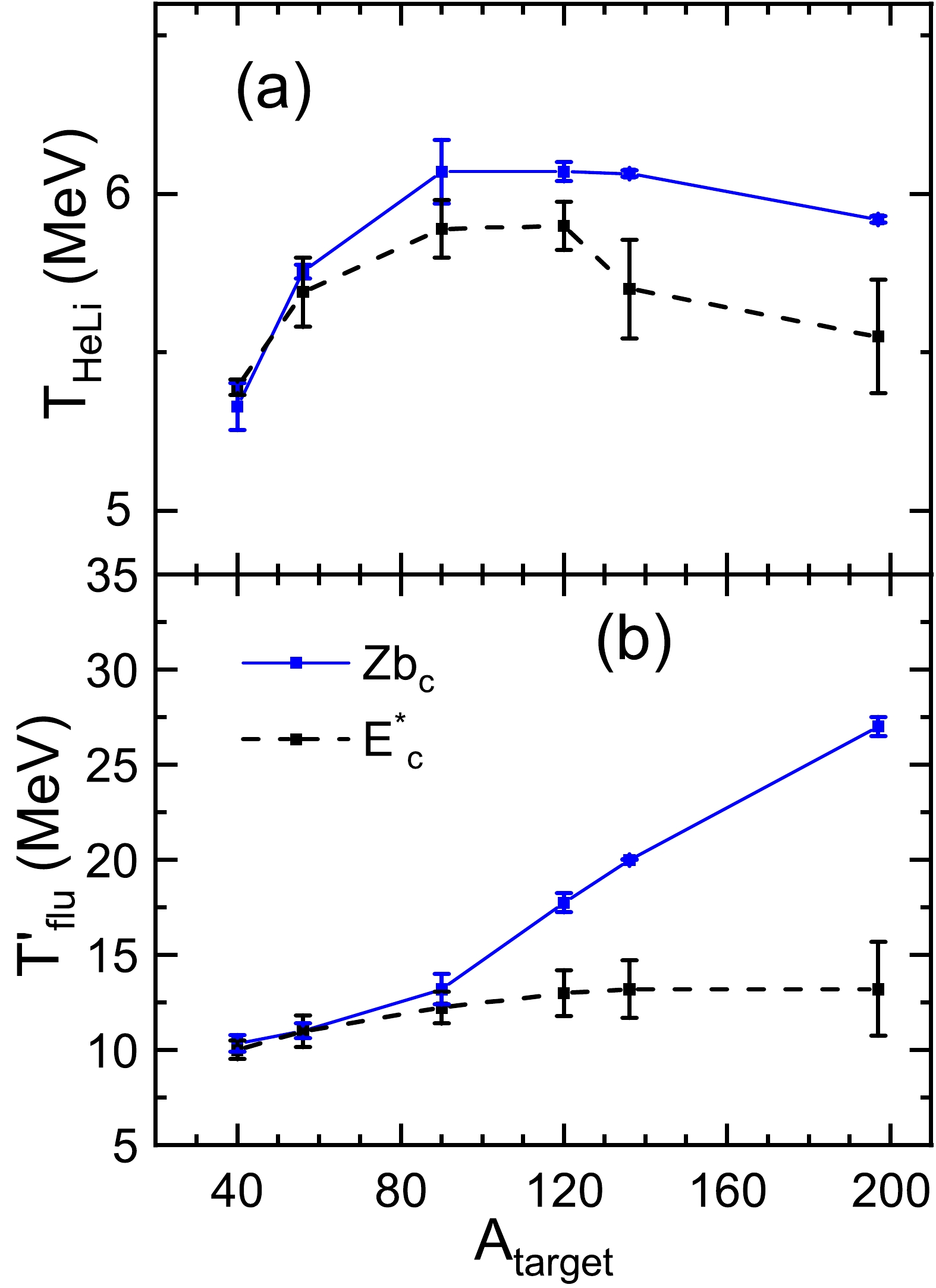

Figure 9.  (color online) Same as Fig. 8 but as functions of the mass number of the target nuclei.

In the above reactions, the temperature $T_{\rm HeLi}$ at the pseudo-critical points is within 5.4 to 6.2 MeV, i.e., remarkably close to the critical temperatures measured in experiments [43]. Therefore, the temperature $T_{\rm HeLi}$ at the pseudo-critical points can reflect the critical temperature of LGPT. The minimum and maximum values of $T_{\rm HeLi}$ at the pseudo-critical points are 5.4 and 6.2 MeV, respectively. The uncertainty can be simply estimated as (max-min)/min. It is shown that the critical temperatures extracted by the isotope thermometer are relatively uniform, and the uncertainty is within 15%. In addition, the temperature $ T_{flu}^{'} $ for the $ E^{*} $ ensembles varies from 10 to 13 MeV, which exhibits 30% deviation. The Coulomb correction for a system of Z = 45/A = 100 is evaluated to be 3 MeV according Ref. [44]. For $ ^{124} $Sn (Z = 50/A = 124), the Coulomb effect should be stronger. Our predictions are in the range of 7 to 10 MeV when considering the Coulomb correction and are generally close to the data [45]. Therefore, the temperature $ T_{flu}^{'} $ based on the $ E^{*} $ ensemble can act as a critical parameter to indicate the LGPT. However, those for the $Z_{\rm bound}$ ensemble even reach 27 MeV, which is much larger than the critical temperature of infinite nuclear matter (T $ \simeq $ 16.6 MeV) [28]. The temperature $ T_{flu}^{'} $ for the $Z_{\rm bound}$ ensemble cannot reflect the critical state of the LGPT. When using the $Z_{\rm bound}$ ensemble to describe the observations of the final state, not only does the mass distribution of the largest fragments lose the bimodality, but the nuclear temperatures at pseudo-critical points cannot reflect the critical state of the LGPT.

It is well known thatt, when the LGPT manifests in a finite system, the typical phase trajectory of the hot nuclei will pass through the spinodal region in the phase diagram [9, 46]. The intersection point between the trajectory and the spinodal region represents the two-phase transition point. The phase trajectory will change with the violence of the nuclear reaction. The transition point naturally covers a range of temperatures and densities. It may reasonably explain why the temperatures at pseudo-critical points do not have a universal value for different reactions. The phase diagram shows the uncertainty of critical temperature caused by the violence of nuclear reaction. However, the initial-final correlation of the statistical properties leading to the uncertainty of critical temperature cannot be observed in the phase diagram. The fragment information required for calculating temperature comes from the final state of the reaction, but there is a significant difference in temperature revealed by the statistical ensembles with the initial state ($ E^{*} $) and the final state ($Z_{\rm bound}$). The critical temperatures based on the $Z_{\rm bound}$ ensemble are obviously higher than those based on the $ E^{*} $ ensemble.

Much effort has been made to reveal the underlying physics of critical points in HICs from the perspectives of isotopin [18, 43, 47], nonequilibrium [23, 25–27], difference of nuclear thermometer [20, 40, 41], and finite-size effects [28, 48, 49]. However, the investigations of uncertainty caused by the initial-final correlation of the statistical properties are scarce. Our study reveals that the critical temperature of a nuclear system is influenced by the incident energy of the reaction and the mass of target nuclei, which can be represented by the phase diagram. In addition, the selection of a statistical ensemble and nuclear thermometer can also lead to the uncertainty of critical temperature. Our results indicate that the uncertainty of the measured critical temperatures can be reduced by using the $ E^{*} $ ensemble and the isotope thermometer.

The properties of the largest cluster represent a significant window to reveal the evolution of the projectile fragmentation and the properties of the LGPT [18, 25]. The multifragmentation of hot nuclei is a fast and nonequilibrium process, which has been deduced in experiments and some theoretical studies. The strong dynamical effect has been indicated in our previous work [27]. The influence of the dynamical effect on the critical temperature of the nuclear system is described in this section. Moreover, the dynamical trajectories can influence the position of transition points. Therefore, the correlation between the dynamical trajectories of the largest cluster and the critical temperature is described in this section. Fig. 10 shows in detail the dynamical evolution during the heating and cooling of the largest cluster for $ ^{124} $Sn + $ ^{120} $Sn collisions with b = 8.9 fm at 600 MeV/nucleon. Here, the pseudo-critical point is at b = 8.9 fm (see Fig. 5). In other words, the nuclear system will reflect the characteristics of phase transition when the $ ^{124} $Sn + $ ^{120} $Sn collision is performed at b = 8.9 fm. The projectile-like system is heated on one side, and then, the heat conduction and the fragmenting occur simultaneously, which is illustrated in panel (a). This can be proven by the $ E^{*} $ v.s. $A_{\max}$ correlations, temperature asymmetry, and density asymmetry during the evolution of the projectile-like system, as shown in panels (b)-(d). Here, $ E^{*} $ and $A_{\max}$ are the excitation energy and mass number of the projectile-like system, respectively. The projectile collides with the target from 60 to 80 fm/c. The excitation energy of a projectile-like system reaches the maximum at 80 fm/c. From 80 to 500 fm/c, the excitation energy of the projectile-like system gradually decreases to a value that is smaller than the threshold of the multifragmentation.

Figure 10.  (color online) (a) Illustration of the heating and cooling of the projectile-like system. (b) Correlations between the excitation energy $ E^{*} $ and mass number of largest cluster $A_{\max}$ for ¹²⁴Sn + ¹²⁰Sn collisions with b = 8.9 fm at 600 MeV/nucleon. (c) Temperature asymmetry and (d) density asymmetry in z and x axes during the evolution of the largest cluster.

Two observables have been defined to describe the asymmetry of the temperature and density in the projectile-like system [27]. The asymmetry of the temperature in the x axis is defined by linear fitting for the kinetic energy as a function of the coordinate

Here, for ith nucleon, its coordinate in the x axis and kinetic energy in the center-of-mass frame are written as $ x_i $ and $ E_i $, respectively. $ \bar{x} $ and $ \bar{E} $ are the mean coordinate in the x axis and kinetic energy of projectile-like system, respectively. N is the nucleon number of the projectile-like system. The temperature is not uniform in the x axis if $ L_x $(E) has a nonzero value. Similarly, the symmetry of the temperature in the z axis can be obtained by replacing x with z. The density symmetry $ L(\rho) $ in the x axis is given by

where $ r_i $ is the position of the ith nucleon, and ρ($ r_i $) is the nucleon density at position $ r_i $. Replacing x by z, one can also obtain the symmetry of the density in the z axis.

In Figs. 10(c) and (d), the large negative values of $ L_x $(E) and $ L_x $(ρ) at 70 fm/c indicate the higher temperature and larger density near the participant side. The rotation of the projectile-like system caused by the collision makes the projectile-like system have a large negative $ L_z $(E) and $ L_z $(ρ) at 80 fm/c, which drives the light fragment emission along the negative direction of the z axis. After 80 fm/c, the heat conduction along the x and z directions results in a decrease in $ L_x $(E) and $ L_z $(E). The temperature asymmetry of the projectile-like system disappears after t = 110 fm/c. In addition, the density asymmetry of the system expressed by $ L_x $(ρ) and $ L_z $(ρ) tends to zero due to the emission of fragments. At the stage from 80 to 110 fm/c, both the heat conduction and emission of fragments occur.

Figure 11 shows the temperature asymmetry and density asymmetry in z and x axes during the evolution of the projectile-like system for $ ^{124} $Sn + $ ^{120} $Sn collisions from 400 to 1000 MeV/nucleon. In order to study the influence of the dynamic effect on the properties of LGPT, these simulations are performed at the pseudo-critical points. The pseudo-critical points are taken in Fig. 5(e). In the region from 400 to 800 MeV/nucleon, the temperature asymmetry of the system with phase transition generally becomes stronger with increasing incident energy, as seen in Fig. 11(a). The temperature asymmetry of the system at 1000 MeV/nucleon is slightly weaker than that at 800 MeV/nucleon. However, the density asymmetry of the system with phase transition has no significant change as the incident energy increases, as shown in Fig. 11(b).

Figure 11.  (color online) (a) Temperature asymmetry and (b) density asymmetry in z and x axes during the evolution of the projectile-like system. The simulations are performed for ¹²⁴Sn + ¹²⁰Sn collisions at pseudo-critical points from 400 to 1000 MeV/nucleon.

Figure 12 shows the temperature asymmetry and density asymmetry in z and x axes during the evolution of the projectile-like system for $ ^{124} $Sn + $ ^{A} $Z collisions at 600 MeV/nucleon. $ ^{A} $Z denotes $ ^{40} $Ca, $ ^{56} $Fe, $ ^{90} $Zr, $ ^{120} $Sn, $ ^{136} $Xe, and $ ^{197} $Au. These simulations are also performed at the pseudo-critical points. The pseudo-critical points are taken in Fig. 5(f). The interesting phenomenon is that the temperature asymmetry of the system with phase transition becomes weaker with increasing mass number of target nuclei, as displayed in Fig. 12(a). However, it is noted that the density asymmetry of the system with phase transition has a strengthening trend with the mass number of target nuclei, as exhibited in Fig. 12(b).

Figure 12.  (color online) (a) Temperature asymmetry and (b) density asymmetry in z and x axes during the evolution of the projectile-like system. The simulations are performed for ¹²⁴Sn + ^AZ collisions of pseudo-critical points at 600 MeV/nucleon. The pseudo-critical points are taken in Fig. 5(f).

The beam energy and projectile-target combinations are two external controllable conditions that affect the dynamic trajectory passing through the phase diagram. In this study, the dynamic effect is reflected by the temperature asymmetry and density asymmetry during the evolution of the projectile-like system. However, these two asymmetries of the system vary independently with the change in beam energy or mass number of target nuclei. The critical temperature extracted by the isotope thermometer is closely related to the combined effect of these two asymmetries. This explains that the critical temperature $T_{\rm HeLi}$increases with increasing incident energy, and it also reasonably describes the phenomenon that this critical temperature first rises and then falls with increasing size of target nuclei. When the excitation energy is used to divide events, the critical temperature extracted by the quantum fluctuation thermometer is significantly related to only the density asymmetry. Therefore, the critical temperature does not change obviously with increasing incident energy but increases slowly with increasing mass number of target nuclei.

It should be noted that the fragment formation is closely related to the LGPT. The dynamics of fragments formation are of great significance for understanding the LGPT. In Ref. [50], it is indicated that the hot nuclei system will undergo a chaotic stage during the process of fragment formation. The chaotic mechanism is thus allowed to describe the fragmentation in finite nuclear systems, and it seems to be crucial for the phase transition. For projectile fragmentation, the system undergoes a strong density and temperature asymmetry stage, and this stage has an influence on LGPT. The density and temperature asymmetry stage seems to have a correlation with chaos. Therefore, the quantification of chaotic mechanisms is worth further investigation.

The projectile fragmentation shows the strong asymmetries of temperature and density of the projectile-like system, as shown in Fig. 10. According to Figs. 11 and 12, the asymmetries of temperature and density are related to the fluctuation of critical temperature. To evaluate the influence of the asymmetries on the critical temperature, the symmetrical system with temperature and density asymmetries close to 0 is initialized by the IQMD model. This symmetrical system is an idealized hot source, but it is helpful to evaluate the dynamic effect on real systems in HICs. Figure 12 shows the higher-order fluctuations of the largest fragment charge, $T_{\rm HeLi}$, and $ T_{flu}^{'} $ as functions of $Z_{\rm bound}$. The solid line indicates the calculations of the $ ^{124} $Sn + $ ^{120} $Sn collisions at 600 MeV/nucleon, while the dashed line shows those of the symmetrical system. For a symmetrical system, the monotonic change of skewness $ K_3 $ and the U-shaped distribution of kurtosis $ K_4 $ are observed; see Figs. 13(a) and 13(b). A noteworthy phenomenon is that the zero transition of $ K_3 $ is coincident with the minimum of $ K_4 $ for the symmetrical system. This signature is thus universal to reveal the LGPT of a finite system. The pseudo-critical point is located at $Z_{\rm bound}$ = 36.5 for the symmetrical system, which is larger than that of the asymmetrical system.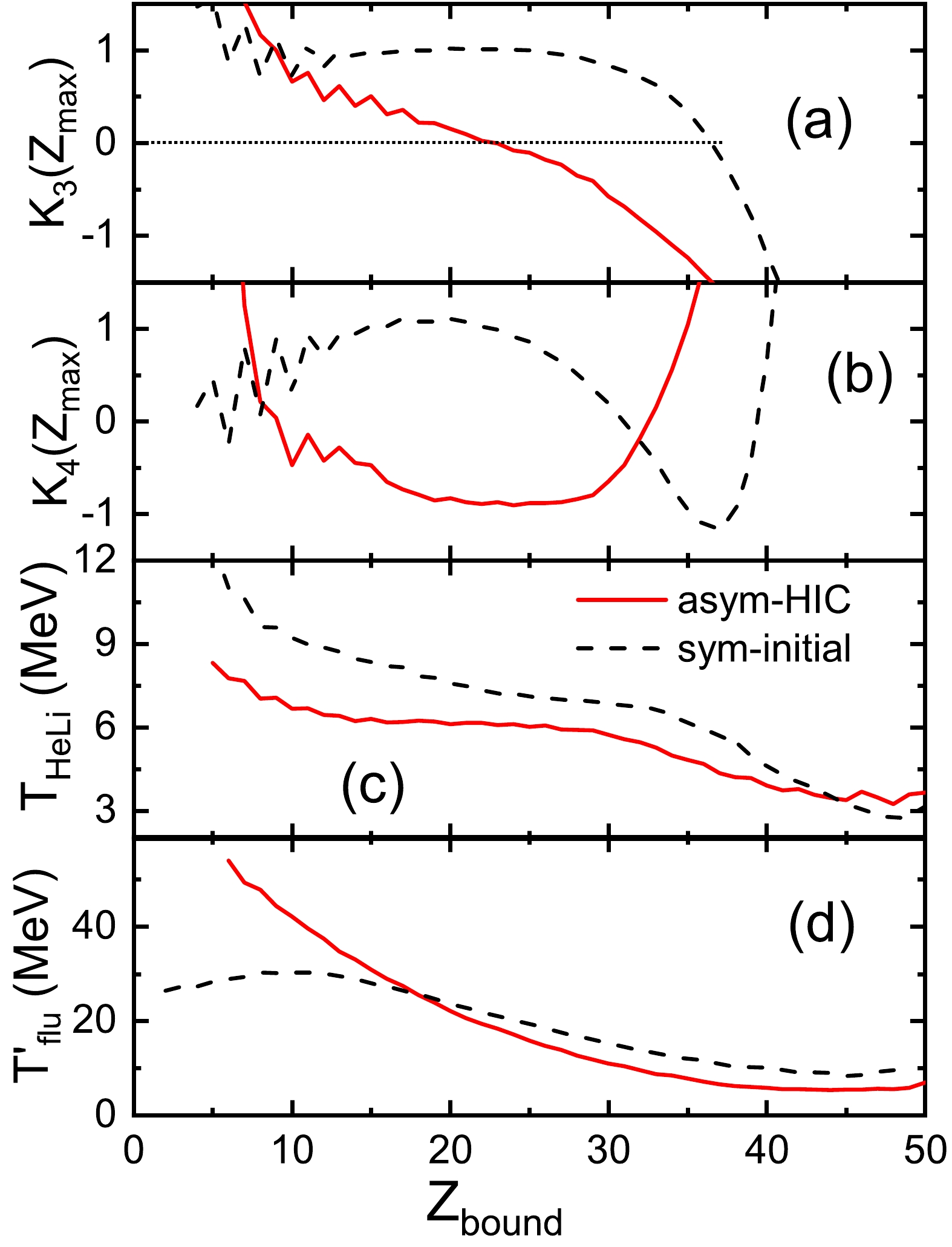

Figure 13.  (color online) (a) Skewness $ K_3 $, (b) kurtosis excess $ K_4 $, (c) temperature $T_{\rm HeLi}$ obtained by the isotope thermometer, and (d) temperature $ T_{flu}^{'} $ obtained by the quantum fluctuation thermometer as functions of the bound charge $Z_{\rm bound}$ for the symmetrical system and the asymmetrical system in the ¹²⁴Sn + ¹²⁰Sn collisions at 600 MeV/nucleon. The calculations of asymmetrical and symmetrical systems are shown as solid and dashed lines, respectively.

The temperature $T_{\rm HeLi}$ of the symmetrical system is larger than that of the asymmetrical system (Fig. 13(c)). Similarly, the temperature $ T_{flu}^{'} $ of the symmetrical system is larger than that of the asymmetrical system in the $Z_{\rm bound}$ region from 18 to 50, as shown in Fig. 13(d). For the symmetrical system, the $T_{\rm HeLi}$ and $ T_{flu}^{'} $ values at the pseudo-critical point are 5.85 and 11 MeV, respectively. In the projectile fragmentation, the critical temperatures extracted by the isotope thermometer are within the range of 5.4 to 6.2 MeV when using the $Z_{\rm bound}$ ensemble, as shown in Figs. 8(a) and 9(a). When considering dynamical correction, the critical temperature extracted by the isotope thermometer is approximately 5.85$ \pm $ 0.4 MeV.

Figure 14 is the same as Fig. 13 but shows functions of the excitation energy. It is naturally observed that the zero transition of $ K_3 $ is coincident with the minimum of $ K_4 $ for the symmetrical system (Figs. 14(a) and 14(b)). The pseudo-critical point is located at $ E^{*} $ = 7.5 MeV/nucleon for the symmetrical system, which is naturally smaller than that of the asymmetrical system. The temperature $T_{\rm HeLi}$ of the symmetrical system is generally larger than that of the asymmetrical system, as shown in Fig. 13(c). The temperature $ T_{flu}^{'} $ of the symmetrical system is larger than that of the asymmetrical system in the region of $ E^{*} < $ 15 MeV/nucleon, but the opposite phenomenon occurs in the region of $ E^{*} > $ 15 MeV/nucleon; see Fig. 13(d). The critical temperatures extracted by the isotope thermometer and quantum fluctuation thermometer are 5.6 and 9.0 MeV, respectively, for a symmetrical system.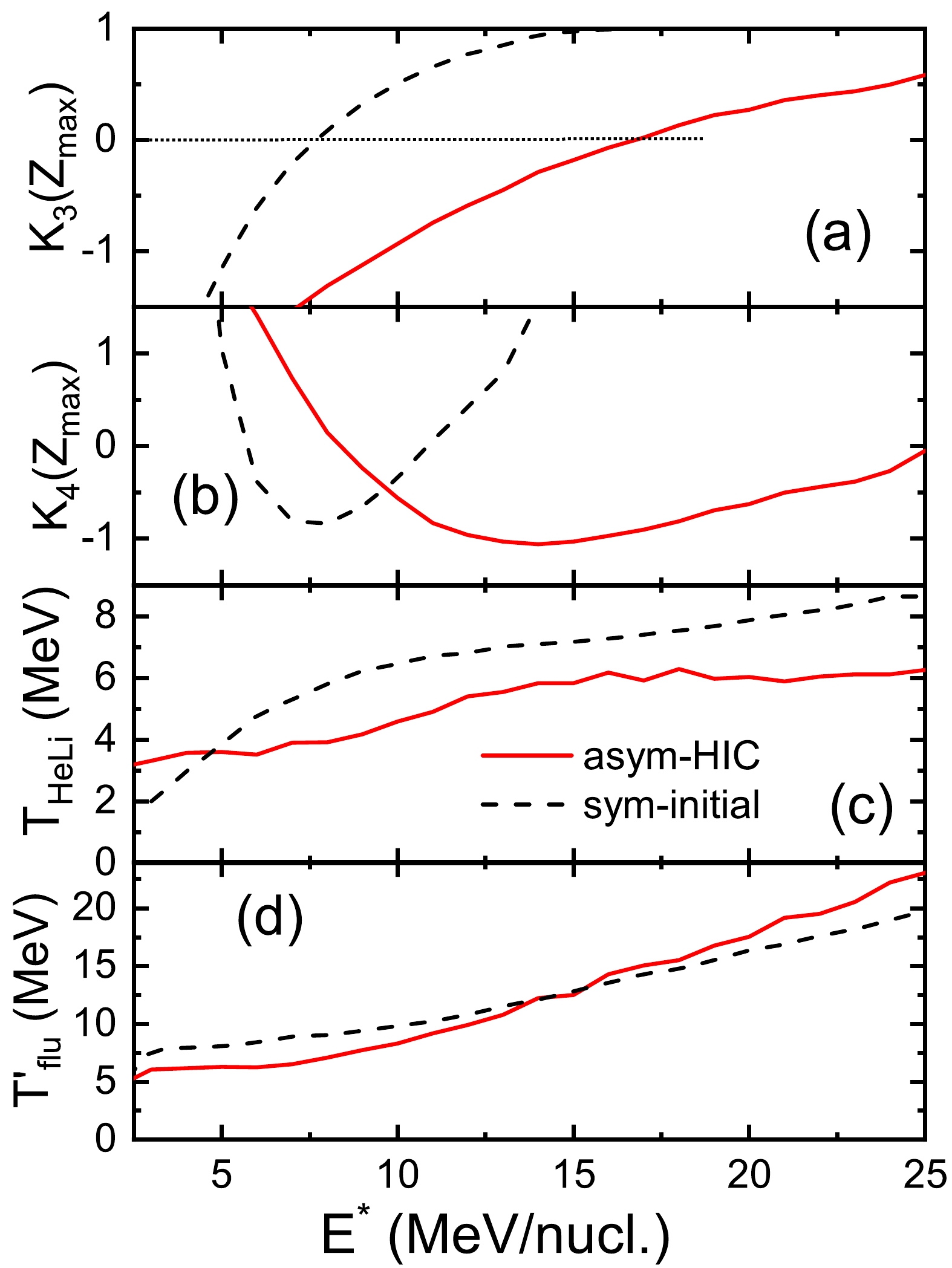

Figure 14.  (color online) Same as Fig. 13 but as functions of the excitation energy.

When using the excitation energy to sort events for the projectile fragmentation, the critical temperatures extracted by the isotope thermometer are within 5.4 to 5.8 MeV, as seen in Figs. 8(a) and 9(a). Therefore, the critical temperature extracted by isotope thermometer (considering dynamic correction) is 5.6 $ \pm $0.2 MeV. In contrast, for the projectile fragmentation, the critical temperatures extracted by the quantum fluctuation thermometer are in the region of 10 to 13 MeV. Therefore, the dynamical effect overestimates the critical temperature extracted by the quantum fluctuation thermometer from 1 to 4 MeV.

It should be noted that the different models, thermometers, and ensembles lead to uncertainties of critical temperatures. First, in Ref. [18], the critical temperatures were extracted by the isotope thermometer based on the SMM model. In our previous works [27, 31], the IQMD model could well describe the experimental data about higher-order fluctuations of the largest fragment charge. The critical temperatures extracted by the isotope thermometer are further investigated in this study. It is found that there is a relatively small difference in the critical temperature extracted by the isotope thermometer between the SMM model and the IQMD model.

Second, due to the different definitions of nuclear temperature, different nuclear thermometers have emerged. These thermometers are expected to measure the real temperature in HICs, but the nuclear temperatures extracted by these thermometers differ from each other even for the same nuclear reaction. Therefore, it is necessary to study the uncertainty of critical temperatures in terms of different thermometers. The isotope temperature describes the population properties of fragments, while the fluctuation temperature describes the kinetic energy properties of fragments. These two properties of the nuclear temperature correspond to two sides of the LGPT "coin'' in a finite system. In this study, it is shown that the critical temperatures extracted by the isotope thermometer are relatively uniform, while those obtained by the quantum fluctuation thermometer strongly depend on the reaction conditions.

Third, in thermodynamics, although the definitions of microcanonical, canonical, and giant canonical ensembles are different, their descriptions are equivalent for the same thermodynamic system. However, the nuclear system is in a nonequilibrium state during HICs, and the fluctuations of the nuclear system between different events are very large. Therefore, the ensemble defined by traditional thermodynamics cannot be used. In this study, some macroscopic quantities ($Z_{\rm bound}$, $ E^{*} $, and b) are used to classify the system and obtain different ensembles. It is found that the critical temperatures based on different ensembles are not equivalent. For fragmented systems, the definition of an ensemble should be further studied.

Recent experimental and theoretical works indicated the signature of LGPT via the higher-order fluctuations of the largest fragment charge [18, 27, 31]. This study investigated the critical properties of LGPT and the influence factors of the critical temperature. The IQMD model coupled with the statistical model GEMINI is used to simulate the $ ^{124} $Sn + $ ^{120} $Sn collisions from 400 to 1000 MeV/nucleon and the $ ^{124} $Sn + $ ^{A} $Z collisions at 600 MeV/nucleon. $ ^{A} $Z denotes $ ^{40} $Ca, $ ^{56} $Fe, $ ^{90} $Zr, $ ^{120} $Sn, $ ^{136} $Xe, and $ ^{197} $Au. Our findings can be summarized as follows.

(I) The pseudo-critical point of the LGPT can be indicated by the skewness and kurtosis excess of the largest fragment charge for the above reactions. The pseudo-critical point reflects the transition of reaction mechanisms from the nucleon-evaporation mode to multifragmentation mode. It is proved that the signature of the LGPT based on the skewness and kurtosis excess of the largest fragment charge is robust.

(II) The isotope thermometer and quantum fluctuation thermometer are applied to extract the critical temperatures based on the pseudo-critical points in a finite nuclear system. In the reactions studied, the critical temperatures extracted by the isotope thermometer are within the range of 5.4 to 6.2 MeV, which is consistent with the data [18, 43]. In the above reactions, the critical temperatures extracted by the isotope thermometer are relatively uniform, and their uncertainty is within 15%. When using the quantum fluctuation thermometer, the critical temperatures measured in the$ E^{*} $ ensemble are between 10 and 13 MeV. If these calculations refer to the Coulomb correction [44], the data will be in this range [45].

(III) It is worth noting that the value $ Z_{\rm bound} $ is the final state observation, while the excitation energy of the system $ E^{*} $ is the initial state observation. The temperatures at pseudo-critical points based on the $Z_{\rm bound}$ ensemble are obviously higher than those based on the $ E^{*} $ ensemble. The extraction of temperature comes from the final state of the reaction; the initial state of the system affects the information of the final state and thus causes the uncertainty of critical temperature. Furthermore, the maximum fragment mass $ A_{\max} $ distribution at the pseudo-critical point shows the initial-final correlation of statistical properties. It is found that the $A_{\max}$ distribution at the pseudo-critical point based on the $Z_{\rm bound}$ ensemble is wide, while that based on the $ E^{*} $ ensemble exhibits bimodality, which is a typical characteristic in the liquid-gas coexistence of a finite system.

(IV) The dynamical evolution from the initial state to the final state is studied. Two observations (L(E) and L(ρ)) are defined to describe the dynamical effect of the projectile-like system at pseudo-critical points. It is found that the phenomenon of heat conduction and fragment emission occur simultaneously in the projectile-like system. With the increase in incident energy, the temperature asymmetry (L(E)) of the system becomes stronger, but the density asymmetry (L(ρ)) does not change significantly. In contrast, with the increase in the size of target nuclei, the temperature asymmetry of the system decreases, but the density asymmetry increases. The critical temperature extracted by the isotope thermometer is closely related to the combined effect of these two asymmetries. This explains that the critical temperature increases with increasing incident energy, and it also reasonably describes the phenomenon that the critical temperature will first rise and then fall with the increasing size of target nuclei. When the excitation energy is used to divide events, the critical temperature extracted by the quantum fluctuation thermometer is significantly related to only the density asymmetry. Therefore, the critical temperature does not change significantly with incident energy but increases slowly with the size of the target nuclei.

The uncertainties of the critical temperatures can be reduced by using the $ E^{*} $ ensemble and the isotope thermometer. This result is helpful in improving the experimental measurement of critical temperature and provides an experimental scheme that can reduce the dynamic effect. To more reasonably describe the uncertainties of critical temperature, the collective effect [38, 40] and coulomb effect [44] should be considered. In the future, we will consider these effects to further reveal the critical properties of LGPT.