HTML
-
In most cases of light nuclei, with
$ A < $ 12, the nucleons may form a group. The group in nuclear physics is often termed as the cluster. The relative motion of such structures determines general characteristics and properties. In this manner, analyzing the cluster structure of light nuclei has emerged as a primary task in nuclear physics, both in terms of theoretical studies and experimental investigations.Nucleus 9Be is an attractive nucleus due to its many internal properties. Specifically, experimental data points, such as the low binding energy of the p-shell neutron
$ - $ 1.66 MeV (e.g., see [1]), large quadrupole moment of +53.3$ \pm 3 $ mb [2, 3], and positive parity in the first excited state$ \dfrac{1}{2}^+ $ at 1.684 MeV (e.g., see [1], indicate its unique structure. Therefore, in the cluster model framework, the nucleus can be supposed to have the configurations, such as$ 2\alpha+n $ , α + 5He, 8Be + n, and others.The cluster structure of 9Be has been extensively studied within the various approaches [4−9]. In recent studies from Refs. [10, 11], the elastic scattering data of α-particles and of d on 9Be have been treated within the cluster models
$ \alpha+ $ 5He and 8Be$ +n $ . The authors demonstrated, using the example of elastic scattering, that the interaction potentials of projectiles can be analyzed using the cluster folding model within various configurations such as$\alpha+$ 5He and 8Be$ +n $ . Furthermore, at backward angles, the spectroscopic amplitudes have been determined through calculations of elastic transfer reactions.It is interesting to note an analysis of the two-neutron transfer in the nuclear reactions induced by 7Be radioactive beam on the target nucleus 9Be [12]. The two-nucleon spectroscopic amplitudes were derived using the shell model framework and applied to the elastic transfer channel. The authors successfully accounted for the experimental data on excess cross sections using Coupled Reaction Channel (CRC) calculations that integrate both elastic scattering and elastic transfer mechanisms. This suggests that the nucleus 9Be may also possess a cluster structure similar to 7Be +
$ 2n $ .In the study [13], the nuclear reactions resulting from
$ ^3 $ He + 9Be at an energy of 63 MeV have been analyzed. The elastic channel as well as the exit channels 7Be + 5He, 6Li + 6Li were calculated within the CRC method. For these channels, all the possible transfer mechanisms were supposed. In particular, the two-step transfer mechanisms beginning with n pick-up effectively enhances the underestimated cross sections for the channels 7Be + 5He and 6Li + 6Li. It shows that the p-shell neutron is loosely bound, and, in turn, the nucleus 9Be has the cluster structure 8Be$ + n $ .The same experimental study with nuclear reaction 3He + 9Be was performed, but at the laboratory energy of 30 MeV [14]. Pure optical model and DWBA calculations performed in this study require more sophisticated theoretical models. Therefore, our aim is to analyze the experimental data [14] within the cluster model of 9Be and to probe all possible transfer mechanisms. We focus on the internal structure of 9Be, presenting fresh data missing in Refs. [14, 15], and on the data in more accurate processed form.
This paper is organized as follows. The first section offers detailed information about the experimental methodology. The second section focuses on both elastic and inelastic scattering. A discussion of the cluster transfer channels is presented in the subsequent section. Finally, the main findings and conclusions are summarized.
-
The experiment on the nuclear reaction 3He and 9Be at a laboratory energy of 30 MeV was conducted at the Nuclear Physics Institute (NPI), Řež, Czech Republic. During the course of the experiment, an average beam current was maintained at 10 enA. The self-supporting 9Be target with a thickness of 11
$ \mu\rm{m} $ was developed with a foil, which was highly purified up to 99%. The resonances of the contamination by the carbon and oxygen isotopes were not detected in the energy spectra.Particle identification was based on the
$ \Delta E $ -E method, i.e. measurements of the energy-loss$ \Delta E $ and residual energy$ E_r $ . Four Si-Si(Li) telescopes consisting of detectors$ \Delta E_0 $ ,$ \Delta E $ , and$ E_r $ were mounted to register scattered ions with the thicknesses of 10 μm, 100 μm, and 3 mm, respectively. The acceptance angle of each telescope was$ \sim 0.6^\circ $ in the scattering plane, and their solid angle was$ \sim 0.2 $ msr. The good energy resolutions of both$ \Delta E $ and$ E_r $ detectors provided unambiguous identification of A and Z of each product. The over-all energy resolution was 150 – 200 keV.The excitation energy spectra for 9Be, 6Be, 6Li, and 5He are shown in Fig. 1. The ground and excited states of the nuclei 9Be, 6Be, 6Li, and 5He were identified in the following reaction channels: 9Be (3He, 3He) 9Be (see panel a), 9Be (3He, 6He) 6Be (b), 9Be (3He, 6Li) 6Li (c), and 9Be (3He, 7Be) 5He (d). The energy calibration of
$ \Delta Es $ and$ E_r $ detectors was performed considering well-known states, which are strongly excited in the spectra. The calibration appeared to be practically linear. This allows us to determine the positions of all excited states in the spectra. The total energies were calculated as the sum over the calibrated energy losses$ \Delta E_s $ and the residual energy$ E_r $ . The excitation energy spectra were constructed as$ E_{g.s} $ (position) -$E_{\rm total}$ .
Figure 1. (color online) Excitation energy spectra of
$ ^9 $ Be (a),$ ^6 $ Be (b),$ ^6 $ Li (c), and$ ^5 $ He (d) for the nuclear reaction$ ^3 $ He$ + ^9 $ Be at$E_{\rm lab}=30$ MeV measured at$\theta_{\rm lab}$ =$ 12^\circ $ . The total fit for each spectrum and subtracted peaks are shown. The background was fitted considering the three-body and four-body breakup processes (For more information, please refer to the text).The peaks were identified using a fitting procedure that employs standard Gaussian decomposition. Utilizing the established energy calibration, the positions and widths of the peaks were fixed in line with widely recognized experimental data. It is important to note that the width of each state in the spectrum may encompass several factors: the natural width, apparatus width of the set-up, and energy spread. The latter is caused by the emitting particles, which may originate either at the beginning or at the end of the target foil. Additionally, the background areas are delineated in Fig. 1. They are mainly due to the phase volumes which depend on the threshold energy in the following break-up processes:
● 9Be
$ \rightarrow $ 8Be + n (see Fig. 1, panel a, red dashed curve) or$ ^4\rm{He} $ + 5He (a, blue dot-dashed);● 6Be
$ \rightarrow $ 4He + 2p (b, red dashed) or$ ^5\rm{Li} $ + p (b, blue dot-dashed);● 6Li
$ \rightarrow $ 4He+ d (c, red dot-dashed) or$ ^4\rm{He} $ + p + n (c, blue dashed);● 5He
$ \rightarrow $ 4He+ n (d, red dashed).The absolute error in measuring the cross section is confined to no more than 15%. This error predominantly arises from several factors: inaccuracies in peak decomposition, statistical errors in the count of events in the subtracted peak, errors in determining the target's thickness, inaccuracies in solid angle values, event losses, and errors in current measurement.
-
Elastic scattering
The differential cross section of the elastic scattering of 3He from the nucleus 9Be was treated within the optical model framework. Numerical calculations were conducted by means of the
$\mathrm{FRESCO}$ code [16]. The optical potential used in the OM calculations was considered in the form:$ \begin{array}{*{20}{l}} \begin{array}{l} U(R)=-V(R)-{\rm i}W(R)+V^{SO}(R)( {l} \cdot \sigma)+V^C(R), \end{array} \end{array} $

(1) where R denotes the distance between 3He and 9Be, and
$ V^{V}, W^{V} $ denote the real and imaginary volume potential terms, and$ V^{SO} $ and$ V^C $ denote the spin-orbit and Coulomb potentials. The volume potentials may represent the Woods-Saxon (WS) potential [17]:$ V\left( R \right) = V_0^V f_{R_V, a_V} \left( R \right),\; \; \; \; f_{R_0, a_0} \left( R \right) = \left[ 1+ \exp \left( \frac{R-R_0}{a_0} \right) \right]^{-1}, $

(2) where
$ V_0 $ denotes the depth of the potential,$ r_0 $ denotes the average distance, and$ a_0 $ denotes the diffusion parameter. The spin-orbit term can be expressed in the following form:$ V^{SO}(R) = V_0^{SO}\left(\frac{\hbar}{m_\pi c}\right)^2 \frac{1}{R} \frac{\rm d}{{\rm d}R} f_{R_{SO} a_{SO}}(R), $

(3) while the Coulomb term was considered as the interaction of a point-charge with a uniformly charged sphere as follows:
$ V^C(R)= \left\{ \begin{array}{*{20}{l}} \dfrac{Z_1 Z_2 {\rm e}^2}{2 R_C} \left( 3- \dfrac{R^2}{R_C^2} \right), & {\rm{for}}\;\; R \leq R_C , \\ \dfrac{Z_1 Z_2 {\rm e}^2}{R}, & {\rm{for}}\;\; R > R_C . \end{array} \right. $

(4) As a staring point for the seeking optical potential, we considered global optical parameters from Ref. [18]. The elastic scattering cross section was fitted on the measured experimental data. It was performed via
$\mathrm{SFRESCO}$ [16]. The obtained potential parameters are listed in Table 1.$ V_0 $ /MeV

$ r_V^{a)} $ /fm

$ a_V $ /fm

$ W_0 $ /MeV

$ r_W^{a)} $ /fm

$ a_W $ /fm

$ V_{i} $ /MeV

$ r_{i}^{a)} $ /fm

$ a_{i} $ /fm

$ r_C^{a)} $ /fm

3He + 9Be 101.9 0.700 0.777 30.81 0.854 0.817 2.5 $ ^{c)} $ 

0.708 0.720 0.767 103.9 $ ^{b)} $ 

23.81 $ ^{b)} $ 

7Be + 5He 258.516 0.588 0.726 18.0 0.773 0.6 45.4 $ ^{d)} $ 

0.566 0.843 0.734 6Li + 6Li 114.0 0.64 0.859 45.6 0.831 0.807 0.649 7Li + 5Li 114.0 0.606 0.853 38.448 0.82 0.809 0.588 α + 8Be 121.0 0.252 1.01 17.0 1.38 0.34 0.724 Table 1. Potential parameters used in the optical model and CRC calculations.
Given that the spin reorientation is not forbidden, e.g.
$ 3/2 \rightarrow 3/2 $ or$ 5/2 \rightarrow 5/2 $ , it was also considered in the CC calculations. The calculated CC results are presented in Fig. 2. Specifically, OM and CC calculations are almost identical. Explicit consideration of the coupling between the inelastic channel and the spin reorientation leads to modifications in the optical potential. Hence, the real part of the optical potential becomes deeper, whereas the depth of the imaginary part decreases (see mOP, Table 1).
Figure 2. (color online) Theoretical cross sections for the elastic scattering
$ ^9{\rm Be}(^3{\rm He}, ^3{\rm He})^9{\rm Be} $ in comparison with measured cross section data at${E}_{\rm lab}=$ 30 MeV. Left panel: Calculated cross sections are provided in ratio to the Rutherford scattering and conducted within the coupled channels (CC,$ {\chi}^2 $ = 28.3) and optical model (OM,$ {\chi}^2 $ = 14.85) methods. Right panel: the same CC cross section in absolute unit, but presented in terms of the optical model cross section with modified potential parameters (mOM), the contribution of inelastic channel ($ 5/2 \rightarrow 3/2 $ ) and the spin re-orientation effect (SR).The role of the inelastic channel,
$ 5/2 \rightarrow 3/2 $ , in the elastic channel turned out to be non-negligible. The effect of spin reorientation is one magnitude lower than the OM estimation. The extrema point of SR coincides with the extrema of mOP. This feature is a typical characteristic of spin reorientation effects. A similar pattern was also reported in Ref. [13].Inelastic scattering
The differential cross sections for the inelastic scattering of 3He on 9Be with the excitation 2.43 MeV is calculated in the framework of coupled channels (CC) method [16]. For the CC calculations, the mOP potential was used.
To explicitly track the couplings, we opted not to use a rotational model but instead employed a more general approach. In this scenario, the strength of the coupling factor is determined by:
$ \begin{array}{*{20}{l}} RDEF(\lambda, J \rightarrow J') = (-1)^{J+J'+|J-J'|} \sqrt{2J+1} \langle JK \lambda 0 \vert J' K \rangle \delta^{J\rightarrow J'}_\lambda \end{array} $

(5) where J and
$ J' $ denote the spins of initial and final states, and K denotes the projection. The deformation length may have the following form:$ \begin{array}{*{20}{l}} \delta^{J\rightarrow J'}_\lambda = \beta^{J\rightarrow J'}_\lambda R_i. \end{array} $

(6) Here,
$ \beta^{J\rightarrow J'}_\lambda $ denotes the deformation parameters, and$ R_i $ denotes the interaction radius.The calculated differential cross sections for the inelastic scattering channel with 9Be excitation at 2.43 MeV are shown in Fig. 3. The spin re-orientation, i.e., the transition
$ \dfrac{5}{2} \rightarrow \dfrac{5}{2} $ , has also been implemented in the coupling scheme.
Figure 3. (color online) Inelastic scattering data in comparison with the CC calculation results in terms of different coupling contributions: the transition from
$ \dfrac{3}{2}^- $ to$ \dfrac{5}{2}^- $ states (dashed) and spin re-orientation for state$ \dfrac{5}{2}^- $ (doted).The calculated cross section for the excitation process initially falls short of matching the experimental data. Nevertheless, when the spin re-orientation effect is factored in, it boosts the cross section, aligning the combined results closely with the experimental observations. However, an exception occurs in the cross section data starting from 65 degrees, likely attributable to the influences of other excitation modes not explicitly incorporated in the CC calculation.
In this study, the best agreement of theoretical analyses with data is obtained if one uses the deformation length
$ \delta^{3/2\rightarrow 5/2}_2= $ 1.97 fm. In the study dedicated to the scattering of α-particles on 9Be in Ref. [19], the length is 1.61 fm. On the contrary, deformation length of 2.63 fm is obtained in Ref. [20] in reactions p + 9Be. Our results on the deformation length occupy an intermediate position when compared to values presented in other sources. Generally, the structure of 9Be should not be influenced by the dynamics of nuclear reactions. However, this variance can be attributed to the distinct nature of the interactions between the projectiles and the protons and neutrons in the target nucleus [21]. Consequently, the deformation lengths derived directly from inelastic scattering caused by various projectiles may also differ.In terms of the Eq. (6), the values of the deformation parameters vary due to the ambiguity in the interaction radius. If the radius parameter of the optical potential mOP is considered as
$ r=0.7 $ fm, the deformation parameter corresponds to 0.8. This reproduces the results of the previous study in Ref. [22] with the same experimental data and applied theoretical method. -
In this study, reaction 9Be (3He, 7Be) 5He is supposed to have both one-step and two-step transfer mechanisms, which are demonstrated schematically in Fig. 4. The one-step mechanism occurs by transferring α-particles, while the two-step mechanisms may have n- 3He, 3He -n, d-d. Moreover, we find that the transfer of
$ 2n $ cluster is also possible at the backward angles of scattering. Therefore, the CRC calculation covers all mentioned transfer mechanisms, and the resulting differential cross section for the reaction 9Be (3He, 7Be) 5He is represented as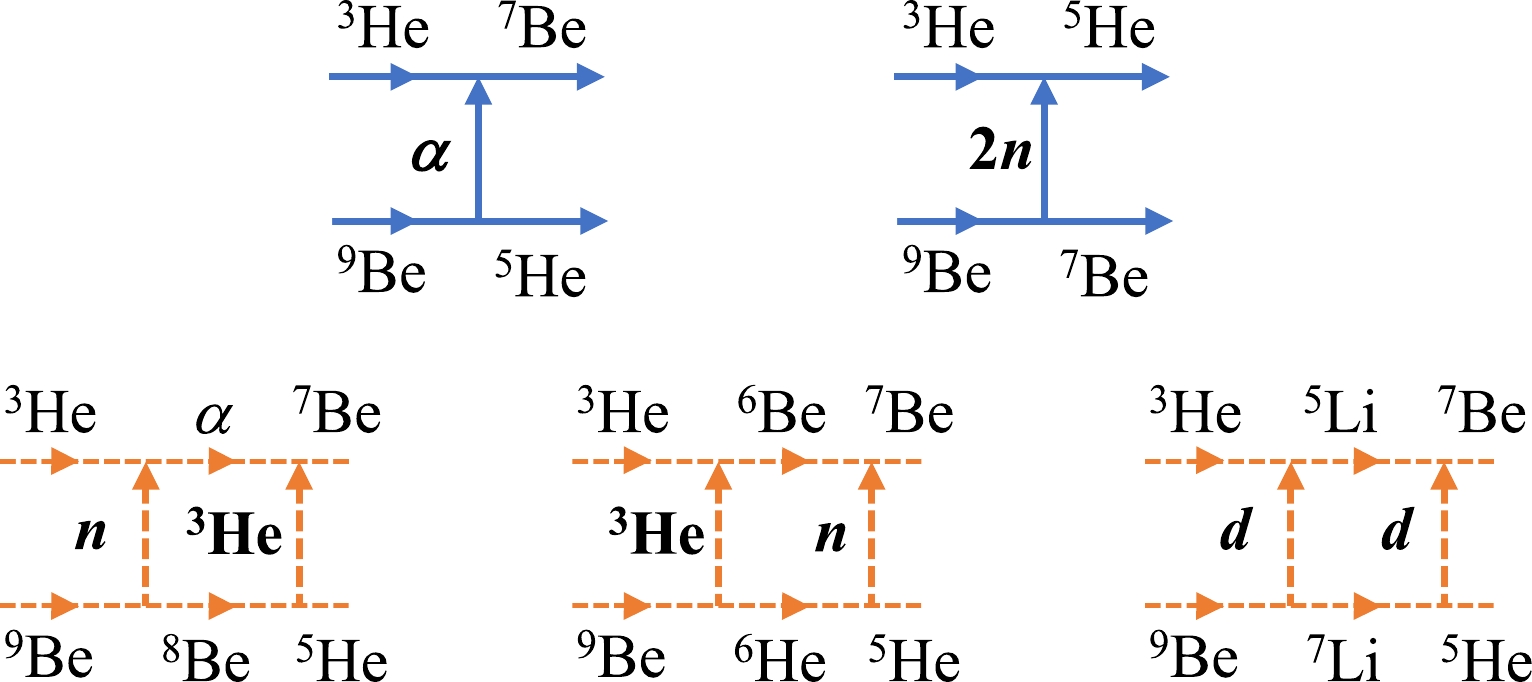
Figure 4. (color online) Reaction schemes for transfer mechanisms in 9Be (3He, 7Be) 5He : one-step (solid) and two-step (dashed) mechanisms.
$ \frac{{\rm{d}} \sigma\left( \theta \right)}{{\rm{d}} \Omega} = \frac{1}{(2J_a+1)(2J_A+1)} \; \vert f_{\rm I}\left( \theta \right)+ f_{\rm II}\left( \theta \right) \vert^2, $

(7) where the amplitudes of the one-step
$ f_{\rm I}\left(\theta \right) $ and two-step$ f_{\rm II}\left(\theta \right) $ transfer mechanisms are as follows:$ \begin{aligned}[b] f_{\rm I}\left( \theta \right)=& f_{\alpha}\left( \theta \right)+f_{2n}\left( \theta - \pi \right), \\ f_{\rm II}\left( \theta \right)=& f_{n{\rm-^3He}}\left( \theta \right)+ f_{{\rm^3He-}n}\left( \theta \right)+ f_{d{\rm-}d}\left( \theta \right). \end{aligned} $

(8) The optical potential mOP is selected as the potential for the entrance channel. For the exit channels, we utilized an optical potential with the global optical parameters from Ref. [23].
The optical potential of the intermediate channel α + 8Be has been preferred to a potential, which reproduces the experimental cross sections of 9Be (3He, α) 8Be in the exit channel. The bound state wave functions have been built on the Woods-Saxon shaped potential, with the depths fitted on the binding energies. However, the resonance states were considerd as the quasi-bound states, i.e. taken by means of the same procedure, but with the binding energy of 0.01 MeV. Spectroscopic amplitudes were considered from Refs. [12, 13, 24] and presented in Table 2.
A C ν $ nlj $ 

SA A C ν $ nlj $ 

SA $ ^6 $ Li

1 $ ^3 $ He

0.5 t 0.5 2 $ S_{0.5} $ 

$ -0.943 $ 

$ ^9 $ Be

1.5 $ ^5 $ He

1.5 α 0 2 $ D_{2 } $ 

$ -0.530 $ 

$ ^6 $ Li

3 $ ^3 $ He

0.5 t 0.5 1 $ D_{2.5} $ 

$ -0.943 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

$ 1_1 $ 

p 0.5 1 $ P_{0.5} $ 

$ -0.657 $ 

$ ^6 $ Li

1 $ ^3 $ He

0.5 t 0.5 1 $ D_{1.5} $ 

$ 0.943 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

3 p 0.5 1 $ P_{1.5} $ 

$ 0.738 $ 

$ ^9 $ Be

1.5 $ ^6 $ Li

$ 1_1 $ 

t 0.5 2 $ P_{0.5} $ 

$ -0.192 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

$ 1_2 $ 

p 0.5 1 $ P_{0.5} $ 

$ 0.147 $ 

$ ^9 $ Be

1.5 $ ^6 $ Li

$ 1_1 $ 

t 0.5 2 $ P_{1.5} $ 

$ -0.215 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

$ 1_2 $ 

p 0.5 1 $ P_{1.5} $ 

$ -0.132 $ 

$ ^9 $ Be

1.5 $ ^6 $ Li

3 t 0.5 2 $ P_{1.5} $ 

$ -0.594 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

$ 1_1 $ 

p 0.5 1 $ P_{1.5} $ 

$ -0.735 $ 

$ ^9 $ Be

1.5 $ ^6 $ Li

3 t 0.5 1 $ F_{3.5} $ 

$ -0.316 $ 

$ ^6 $ Li

$ 1_1 $ 

$ ^5 $ He

1.5 p 0.5 1 $ P_{0.5} $ 

$ -0.596 $ 

$ ^9 $ Be

1.5 $ ^6 $ Li

$ 1_2 $ 

t 0.5 2 $ P_{0.5} $ 

$ -0.118 $ 

$ ^6 $ Li

$ 1_1 $ 

$ ^5 $ He

1.5 p 0.5 1 $ P_{1.5} $ 

$ 0.667 $ 

$ ^9 $ Be

1.5 $ ^6 $ Li

$ 1_2 $ 

t 0.5 1 $ F_{2.5} $ 

$ -0.324 $ 

$ ^6 $ Li

3 $ ^5 $ He

1.5 p 0.5 1 $ P_{1.5} $ 

$ 0.500 $ 

$ ^4 $ He

0 $ ^3 $ He

0.5 n 0.5 1 $ S_{0.5} $ 

$ -0.741 $ 

$ ^6 $ Li

$ 1_2 $ 

$ ^5 $ He

1.5 p 0.5 1 $ P_{0.5} $ 

$ 0.333 $ 

$ ^9 $ Be

1.5 $ ^8 $ Be

0 n 0.5 1 $ P_{1.5} $ 

$ 0.791 $ 

$ ^6 $ Li

$ 1_2 $ 

$ ^5 $ He

1.5 p 0.5 1 $ P_{1.5} $ 

$ 0.298 $ 

$ ^9 $ Be

2.5 $ ^8 $ Be

0 n 0.5 1 $ P_{1.5} $ 

$ -0.816 $ 

$ ^5 $ Li

1.5 $ ^3 $ He

0.5 d 1 1 $ P_{1 } $ 

$ 0.456 $ 

$ ^9 $ Be

2.5 $ ^8 $ Be

2 n 0.5 1 $ P_{1.5} $ 

$ -0.986 $ 

$ ^5 $ Li

1.5 $ ^3 $ He

0.5 d 1 1 $ P_{2 } $ 

$ 1.021 $ 

$ ^9 $ Be

2.5 $ ^8 $ Be

0 n 0.5 1 $ P_{0.5} $ 

$ 0.242 $ 

$ ^9 $ Be

1.5 $ ^7 $ Li

1.5 d 1 2 $ S_{1 } $ 

$ -0.226 $ 

$ ^9 $ Be

2.5 $ ^8 $ Be

2 n 0.5 1 $ P_{0.5} $ 

$ 0.417 $ 

$ ^9 $ Be

1.5 $ ^7 $ Li

1.5 d 1 1 $ D_{1 } $ 

$ 0.111 $ 

$ ^6 $ Li

1.0 $ ^4 $ He

0 d 1.0 2 $ S_{1 } $ 

$ 1.061 $ 

$ ^9 $ Be

1.5 $ ^7 $ Li

1.5 d 1 1 $ D_{3 } $ 

$ -0.624 $ 

$ ^6 $ Li

3.0 $ ^4 $ He

0 d 1.0 1 $ D_{3 } $ 

$ 1.061 $ 

$ ^6 $ Li

$ 1_1 $ 

$ ^5 $ Li

1.5 n 0.5 1 $ P_{0.5} $ 

$ 0.597 $ 

$ ^8 $ Be

0 $ ^6 $ Li

$ 1_1 $ 

d 1.0 2 $ S_{1 } $ 

$ 1.146 $ 

$ ^6 $ Li

$ 1_1 $ 

$ ^5 $ Li

1.5 n 0.5 1 $ P_{1.5} $ 

$ -0.667 $ 

$ ^8 $ Be

0 $ ^6 $ Li

$ 1_1 $ 

d 1.0 1 $ D_{1 } $ 

$ 0.112 $ 

$ ^6 $ Li

3 $ ^5 $ Li

1.5 n 0.5 1 $ P_{1.5} $ 

$ 1.095 $ 

$ ^8 $ Be

0 $ ^6 $ Li

3 d 1.0 2 $ S_{1 } $ 

$ 0.089 $ 

$ ^6 $ Li

$ 1_2 $ 

$ ^5 $ Li

1.5 n 0.5 1 $ P_{0.5} $ 

$ -0.333 $ 

$ ^8 $ Be

0 $ ^6 $ Li

3 d 1.0 1 $ D_{1 } $ 

$ 0.414 $ 

$ ^6 $ Li

$ 1_2 $ 

$ ^5 $ Li

1.5 n 0.5 1 $ P_{1.5} $ 

$ -0.298 $ 

$ ^8 $ Be

0 $ ^6 $ Li

3 d 1.0 1 $ D_{2 } $ 

$ -0.477 $ 

$ ^7 $ Li

1.5 $ ^6 $ Li

$ 1_1 $ 

n 0.5 1 $ P_{0.5} $ 

$ -0.657 $ 

$ ^8 $ Be

0 $ ^6 $ Li

3 d 1.0 1 $ D_{3 } $ 

$ 0.744 $ 

$ ^7 $ Li

1.5 $ ^6 $ Li

$ 1_1 $ 

n 0.5 1 $ P_{1.5} $ 

$ -0.735 $ 

$ ^8 $ Be

0 $ ^6 $ Li

3 d 1.0 2 $ S_{1 } $ 

$ 0.850 $ 

$ ^7 $ Li

1.5 $ ^6 $ Li

3 n 0.5 1 $ P_{1.5} $ 

$ 0.738 $ 

$ ^8 $ Be

2 $ ^6 $ Li

3 d 1.0 2 $ S_{1 } $ 

$ 0.747 $ 

$ ^7 $ Li

1.5 $ ^6 $ Li

$ 1_2 $ 

n 0.5 1 $ P_{0.5} $ 

$ 0.147 $ 

$ ^8 $ Be

2 $ ^6 $ Li

3 d 1.0 1 $ D_{1 } $ 

$ 0.079 $ 

$ ^7 $ Li

1.5 $ ^6 $ Li

$ 1_2 $ 

n 0.5 1 $ P_{1.5} $ 

$ -0.132 $ 

$ ^8 $ Be

2 $ ^6 $ Li

3 d 1.0 1 $ D_{2 } $ 

$ 0.259 $ 

$ ^6 $ He

0 $ ^5 $ He

1.5 n 0.5 1 $ P_{1.5} $ 

$ -0.867 $ 

$ ^8 $ Be

2 $ ^6 $ Li

3 d 1.0 1 $ D_{3 } $ 

$ 0.538 $ 

$ ^7 $ Be

1.5 $ ^6 $ Be

0 n 0.5 1 $ P_{1.5} $ 

$ -0.935 $ 

$ ^8 $ Be

0 $ ^6 $ Li

$ 1_2 $ 

d 1.0 2 $ S_{1 } $ 

$ -0.237 $ 

$ ^6 $ He

0 $ ^4 $ He

0 2n 1.0 1 $ S_{0 } $ 

$ 0.909 $ 

$ ^8 $ Be

0 $ ^6 $ Li

$ 1_2 $ 

d 1.0 1 $ D_{1 } $ 

$ 0.372 $ 

$ ^8 $ Be

0 $ ^6 $ Be

0 d 1.0 1 $ S_{0 } $ 

$ -1.200 $ 

$ ^8 $ Be

2 $ ^6 $ Li

$ 1_2 $ 

d 1.0 2 $ S_{1 } $ 

$ 0.371 $ 

$ ^7 $ Be

1.5 $ ^4 $ He

0 $ ^3 $ He

0.5 2 $ P_{1.5} $ 

$ -1.091 $ 

$ ^8 $ Be

2 $ ^6 $ Li

$ 1_2 $ 

d 1.0 1 $ D_{1 } $ 

$ 0.053 $ 

$ ^8 $ Be

0 $ ^5 $ He

1.5 $ ^3 $ He

0.5 2 $ P_{1.5} $ 

$ -1.102 $ 

$ ^8 $ Be

2 $ ^6 $ Li

$ 1_2 $ 

d 1.0 1 $ D_{2 } $ 

$ -0.356 $ 

$ ^6 $ Be

0 $ ^3 $ He

0.5 $ ^3 $ He

0.5 2 $ S_{0.5} $ 

$ 0.943 $ 

$ ^8 $ Be

2 $ ^6 $ Li

$ 1_2 $ 

d 1.0 1 $ D_{3 } $ 

$ -0.130 $ 

$ ^9 $ Be

1.5 $ ^6 $ He

0 $ ^3 $ He

0.5 2 $ P_{1.5} $ 

$ -0.215 $ 

$ ^5 $ He

1.5 $ ^3 $ He

0.5 2n 0 1 $ P_{1 } $ 

$ -0.913 $ 

$ ^7 $ Be

1.5 $ ^6 $ Be

0 n 0.5 1 $ P_{0.5} $ 

$ -1.091 $ 

$ ^9 $ Be

1.5 $ ^7 $ Be

1.5 2n 0 2 $ S_{0 } $ 

$ 0.247 $ 

$ ^6 $ He

0 $ ^5 $ He

1.5 n 0.5 1 $ P_{1.5} $ 

$ -1.102 $ 

$ ^9 $ Be

1.5 $ ^7 $ Be

1.5 2n 0 2 $ D_{2 } $ 

$ 0.430 $ 

$ ^7 $ Be

1.5 $ ^5 $ Li

1.5 d 1 2 $ S_{1 } $ 

$ -0.647 $ 

$ ^6 $ Li

$ 1_1 $ 

$ ^5 $ He

1.5 p 0.5 1 $ P_{0.5} $ 

$ -0.597 $ 

$ ^7 $ Be

1.5 $ ^5 $ Li

1.5 d 1 1 $ D_{1 } $ 

$ -0.121 $ 

$ ^6 $ Li

$ 1_1 $ 

$ ^5 $ He

1.5 p 0.5 1 $ P_{1.5} $ 

$ 0.667 $ 

$ ^7 $ Be

1.5 $ ^5 $ Li

1.5 d 1 1 $ D_{3 } $ 

$ 0.647 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

$ 1_1 $ 

p 0.5 1 $ P_{0.5} $ 

$ -0.657 $ 

$ ^7 $ Li

1.5 $ ^5 $ He

1.5 d 1 1 $ D_{3 } $ 

$ 0.647 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

$ 1_1 $ 

p 0.5 1 $ P_{1.5} $ 

$ -0.735 $ 

$ ^7 $ Li

1.5 $ ^5 $ He

1.5 d 1 2 $ S_{1 } $ 

$ -0.647 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

2 p 0.5 1 $ P_{1.5} $ 

$ -1.095 $ 

$ ^7 $ Li

1.5 $ ^5 $ He

1.5 d 1 1 $ D_{1 } $ 

$ -0.121 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

$ 1_2 $ 

p 0.5 1 $ P_{1.5} $ 

$ -0.632 $ 

$ ^7 $ Li

1.5 $ ^5 $ He

1.5 d 1 1 $ D_{3 } $ 

$ 0.647 $ 

$ ^7 $ Be

1.5 $ ^6 $ Li

$ 1_2 $ 

p 0.5 1 $ P_{0.5} $ 

$ -0.632 $ 

$ ^7 $ Be

1.5 $ ^3 $ He

0.5 α 0 2 $ P_{1 } $ 

$ -0.950 $ 

$ ^7 $ Be

1.5 $ ^3 $ He

0.5 α 0 2 $ P_{1 } $ 

$ 1.091 $ 

$ ^9 $ Be

1.5 $ ^5 $ He

1.5 α 0 3 $ S_{0 } $ 

$ -0.810 $ 

$ ^9 $ Be

1.5 $ ^5 $ He

1.5 α 0 3 $ S_{0 } $ 

$ -0.810 $ 

$ ^9 $ Be

1.5 $ ^5 $ He

1.5 α 0 2 $ D_{2 } $ 

$ -0.536 $ 

All CRC calculations have been performed using the
$\mathrm{FRESCO}$ code [16]. The two-step transfer reactions have been calculated using the N-step DWBA iteration neglecting the back couplings. The prior and post modes were used for the first and second couplings, respectively, aimed at avoiding the non-orthogonality term. The results of the CRC calculations are shown in Fig. 5. The optical potentials used in these calculations are given in Table 1.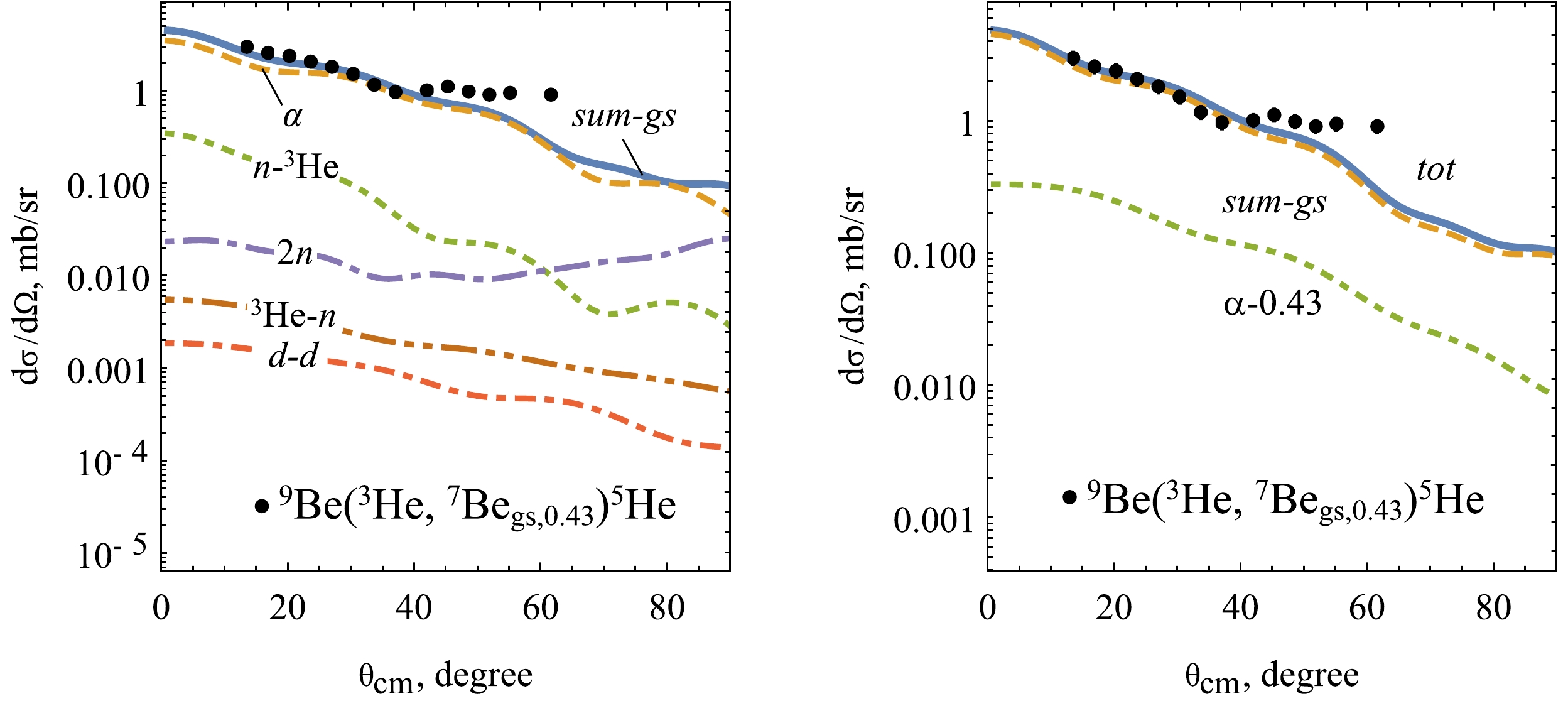
Figure 5. (color online) Calculated CRC cross sections with the experimental data for the nuclear reaction 9Be (3He, 7Begs, 0.43) 5He. Cross sections are shown in terms of each considered transfer mechanism to the ground state of 7Be (left panel). The incoherent sum of cross sections over the ground and first excited 0.43 states of 7Be are also shown (right panel).
The direct transfer of the α-particle obviously prevails on other transfer mechanisms (see Fig. 5, left panel). It is interesting to note the different contribution of the transfer of system n + 3He. It turns out that system n + 3He easily transfers in the way of n- 3He rather that 3He -n. The reason for this may lie in the p-shell valence neutron, which is loosely bound to 9Be. Next contributor to the cross section is 2n transfer at the backward scattering angles. Starting from 60
$ ^\circ $ , it provides only α-transfer. However, starting from 90$ ^\circ $ , the transfer mechanism 2n may stand as a main contributor. To validate this hypothesis, experiments need to be conducted at energies significantly higher than those used in the current study, namely above 30 MeV. Such higher energies would facilitate the identification of particles registered in the rear hemisphere. In similar experimental studies [12, 13] the 2n cluster transfer from 9Be was also explored. In particular, the transfer of 2n cluster was observed by Umbelino et al. [12] in the elastic transfer reactions 7Be + 9Be. The transfer mechanism d-d has the lowest contribution among all of the proposed transfer mechanisms.As a consequence of low detector resolution, we could not differentiate the registered 7Be at the ground and first excited states. Nevertheless, we estimated its weight to the cross section via CRC calculations. It turns out that the cross section to the first excited state impacts less notably than the transfer mechanism n- 3He (see Fig. 5, right panel). The calculated CRC cross sections effectively reproduce experimental data, with the exception of the last few points that have not been described with the proposed model.
-
The transfer mechanisms of cluster t is suggested to exhibit two-step processes as well, as it was suggested in Ref. [13]. The direct transfer t, and two-step transfer mechanisms of cluster t (see Fig. 6): n-d, α-p, 2n-p, and d-n were included in the CRC calculations. Differential cross sections for these transfer mechanisms are obtained analogously as in Eq. (8).
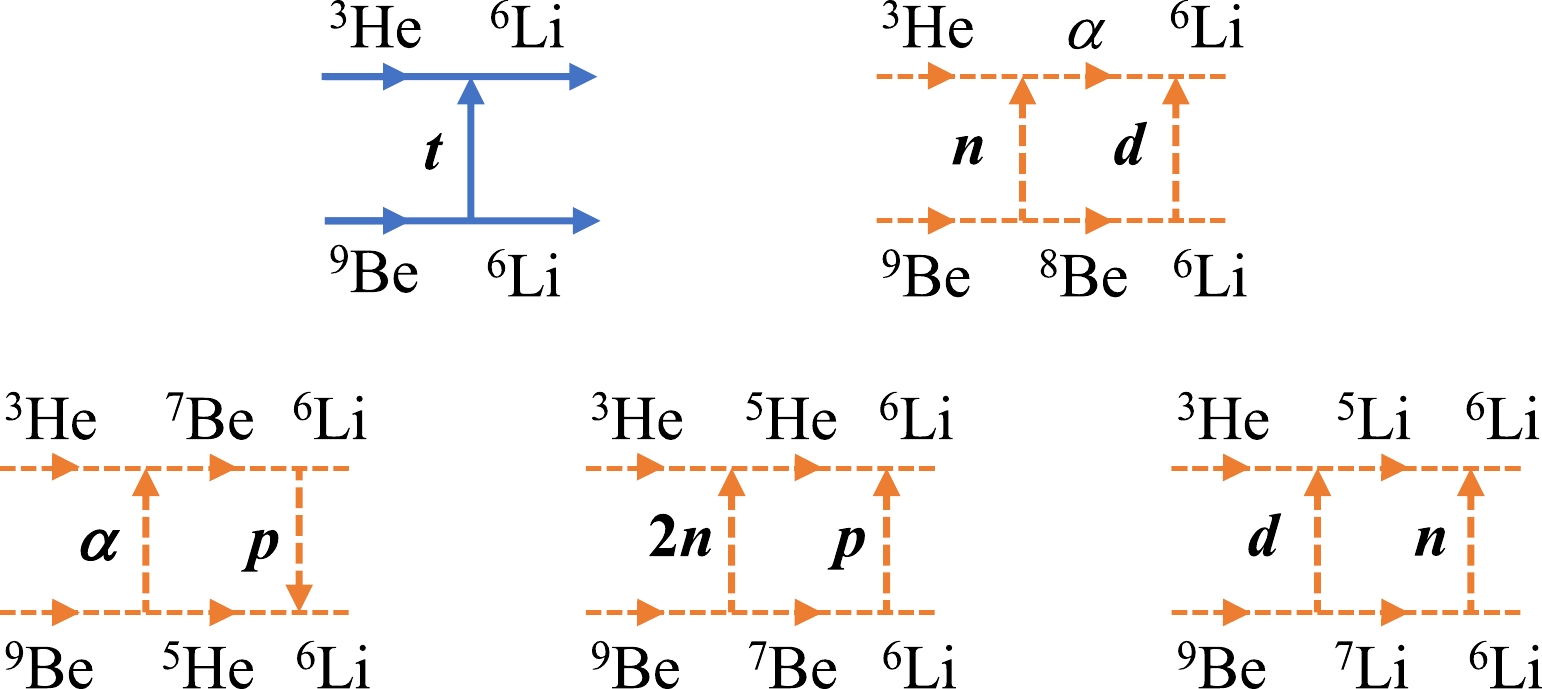
Figure 6. (color online) Same as the caption of Fig. 4but for the reaction 9Be (3He, 6Li) 6Li.
CRC calculations for the transfer of the cluster t utilized the WS optical potential for the entrance channel, and a WS shaped potential for the exit channel 6Li + 6Li. The potential parameters of the exit channel were determined by fitting to the experimental data on the elastic scattering of 6Li + 6Li at an energy of 40 MeV [25]. The obtained optical potential is shown in Table 1.
Apart from the fact that 6Li was detected at the ground state, there were also two registered resonances. In the CRC calculations, they were considered through the coupling with the ground state of 6Li.
The calculated differential cross sections for the channel 6Li + 6Li at the ground state are presented in Fig. 7 (left panel) with the contributions of each transfer mechanisms. The direct transfer of the cluster t dominates at the whole range of angles. The two-step transfer mechanism n-d is turns out to be less contributor than the transfer mechanism t in contrary to the studies by Rudchik et al. [13] within the same reaction, however, at the laboratory energy of 63 MeV. In the work the role of the transfer mechanism, n-d prevails over other processes including the direct transfer t. The cross section of the mechanism n-d has an oscillatory character, and it competes with the mechanism α-p. The latter transfer mechanisms, i.e. 2n-p and d-n, are insignificantly involved to the reaction.
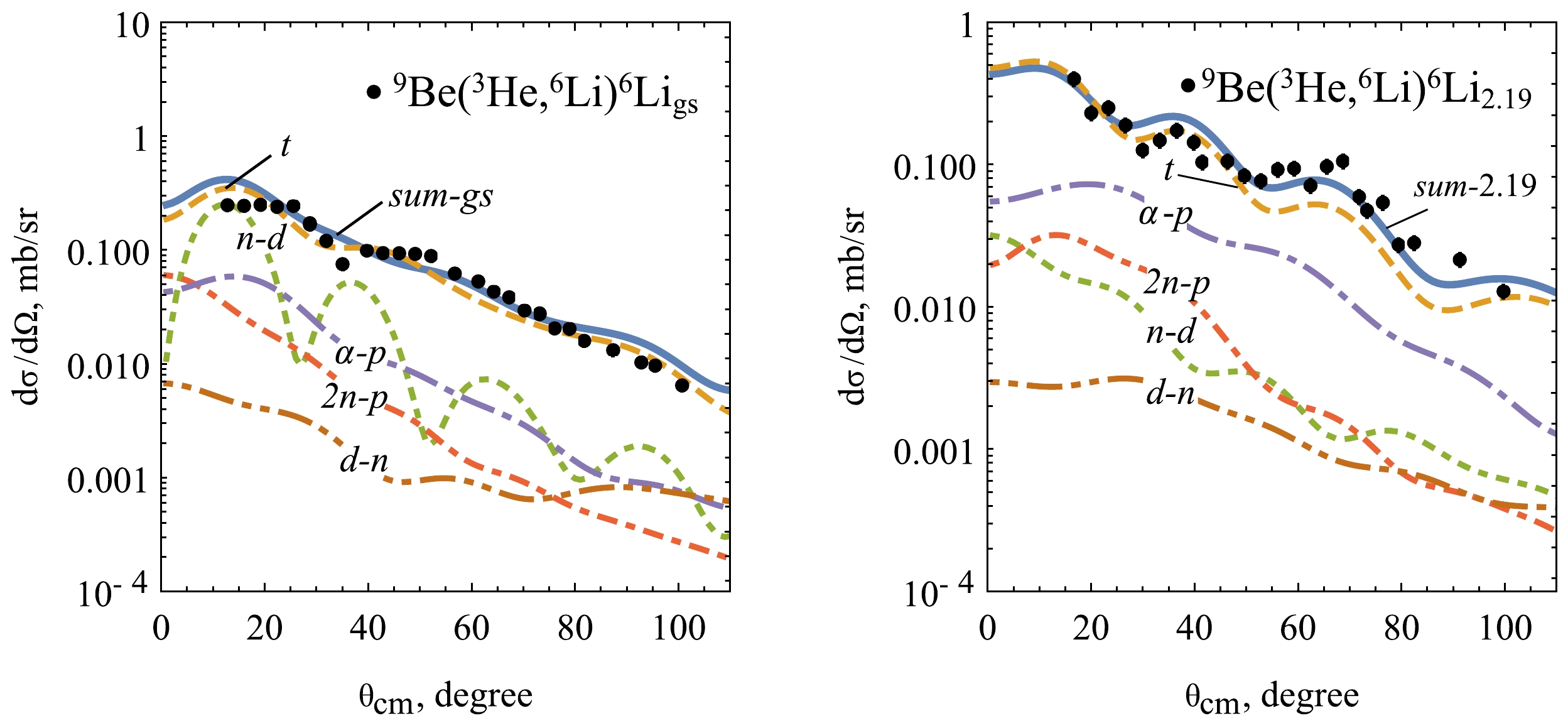
Figure 7. (color online) Experimental data for nuclear reaction
$ ^9 $ Be($ ^3 $ He,$ ^6 $ Li)$ ^6 $ Li$ _{gs} $ (left panel) and$ ^9 $ Be($ ^3 $ He,$ ^6 $ Li)$ ^6 $ Li$ _{2.19} $ (right panel) when compared to the calculated CRC cross sections in terms of channel contributions (please refer to the text for more details).Contribution order changes when 6Li is excited (see Fig. 7, right panel). The transfer mechanism t remains unchanged, while α-p corresponds to the next contributor. Weakening of the mechanism n-d can be interpreted as the switching value in the spectroscopic amplitudes. In particular, the amplitude for the overlap
$ \langle ^6 $ Li$ _{2.19}|^8 $ Be$ \rangle $ with the configuration$ 2S_1 $ is changed to 0.089. This type of a small spectroscopic amplitude would likely result in the n-d transfer mechanism being significantly less prevalent than the d-n mechanism. However, the spectroscopic amplitudes with$ 1D_{1,2,3} $ have non-negligible values, 0.414,$ - $ 0.477, and 0.744, that do not allow n-d to disappear in the reaction.Two resonances at 5.37 MeV and 5.65 MeV are mixed in the differential cross sections due to the experimental limitations. Therefore, we have included two channels into the CRC calculations. Calculation results for 9Be (3He, 6Li) 6Li
$ ^* $ with an excitation of 5.65 MeV are demonstrated in Fig. 8 (left panel) in comparing with experimental data. The reaction mainly occurs through the direct transfer of cluster t. Two transfer mechanisms, 2n-p and α-p, affect nuclear reaction only up to 30$ ^\circ $ . Other transfer mechanisms, i.e., n-d and d-n, almost do not influence the reaction.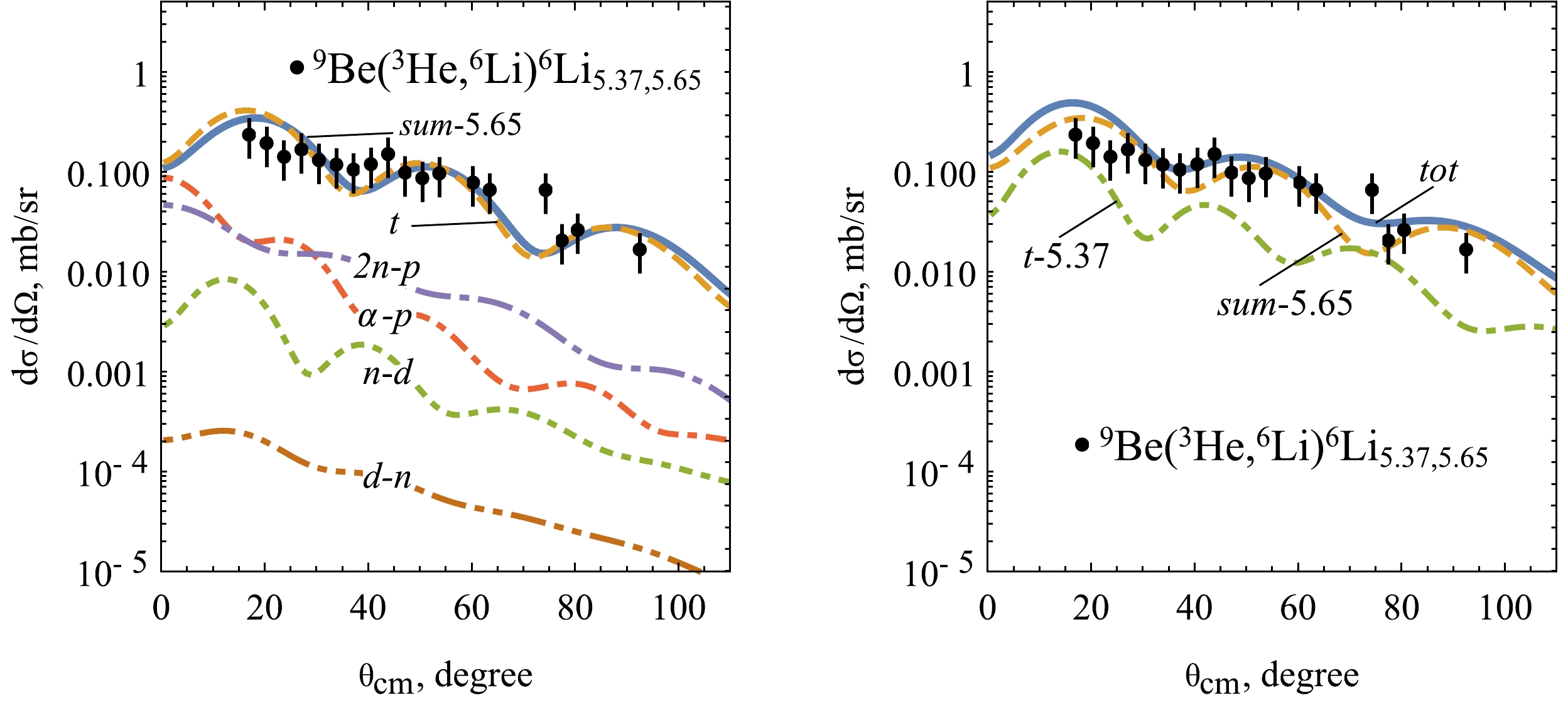
Figure 8. (color online) Experimental data for nuclear reaction 9Be (3He, 6Li) 6Li
$ _{5.37, 5.65} $ when compared to the CRC calculation results. The CRC cross section for the target-like nucleus 6Li$^* $ at 5.65 MeV with the channel contributions (left panel). Total cross section summed incoherently over 5.65 MeV and 5.37 MeV channels (right panel).Given that the transfer of cluster t has been the leading contributor in the 6Li + 6Li channel, the channel with an excitation of 5.37 MeV is calculated only with the transfer of t. The differential cross section of the channel with the 5.37 MeV excited state added incoherently with the channel at 5.65 MeV. Total cross section resulting from the CRC calculations are shown in Fig. 8 (right panel). The channel 6Li+6Li
$^* $ , with the excitation of 5.37 MeV, contributes less than the channel at 5.65 MeV. The calculated differential cross sections effectively reproduce experimental data. -
The channel 6He + 6Be is a unique channel, as the transfer of system 3n is observed at the forward angles of scattering. In his case, we suggest three mechanisms of transfer (see Fig. 9, left panel): the two-step n-2n and 2n-n, and the one-step transfer of the cluster 3He at the back hemisphere. Differential cross sections are obtained as well as they are expressed in Eq. (8). The results of the CRC calculations, detailing cross sections in terms of contributions from each of the three followed mechanisms, are illustrated in Fig. 9 (right panel).
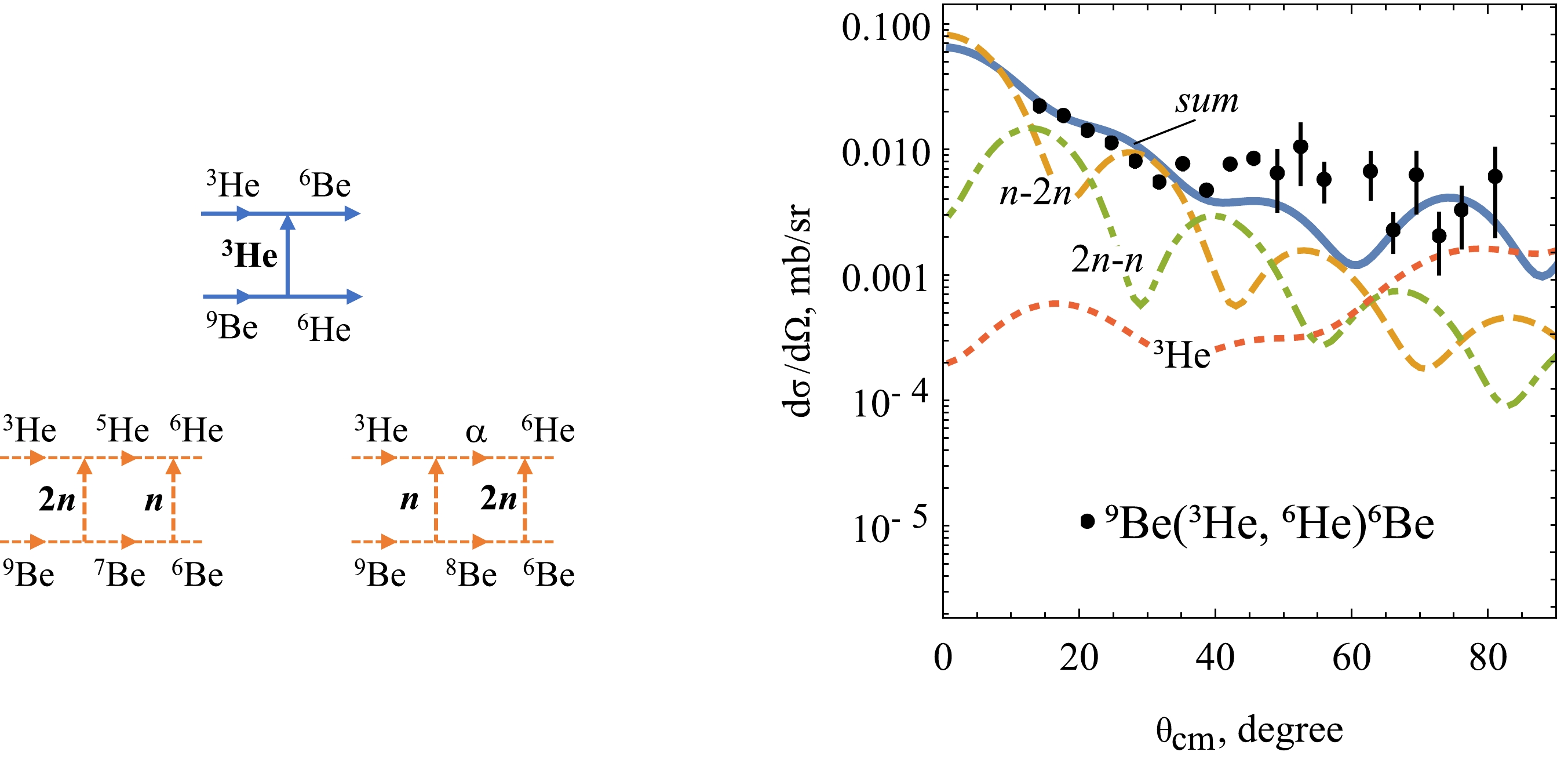
Figure 9. (color online) Left panel: reaction schemes for one-(solid) and two-step (dashed) transfer mechanisms for 9Be (3He, 6He) 6Be. Right panel: comparison of the CRC differential cross sections with the experimental data for the same reaction.
The two-step transfer mechanisms, i.e. n-2n and 2n-n, compete with each other to provide almost smooth cross section. Starting from 60
$ ^\circ $ , the most contribution is due to the transfer of 3He. The CRC calculations are in good agreement with the experimental data.However, CRC calculations for the channel 6He + 6Be were performed using large valued spectroscopic amplitudes. For example, the overlaps
$ \langle $ 6He$ | \alpha \rangle,\; \langle $ 6Be$ | $ 8Be$ \rangle $ exhibit the amplitudes$ \sim 1.2 $ . On the contrary, previous studies [26, 27] reported the amplitude for$ \langle $ 6He$ | \alpha \rangle $ equals$ \sim 1.0 $ . This type of difference between spectroscopic amplitudes indicates that there may be other processes not included in the reaction model. It is plausible that a one-step transfer of the 3n system may occur in the 6He + 6Be channel. However, this issue is a distinct subject for investigation and cannot be precisely resolved using the model presented in this study. To obtain more accurate results, employing the four body problem approach might be beneficial. -
Nuclear reactions involving 9Be induced by 3He at 30 MeV were investigated. The elastic channel was analyzed using the optical model, while the inelastic channel was examined through the CC approach. New parameters for the optical potential of the 3He + 9Be system at 30 MeV were derived. Employing this optical potential, the deformation parameter
$ \delta^{3/2\rightarrow 5/2}_2=0.8 $ was extracted within the CC method, which could reproduce the results from another source [22].In the cluster transfer channels, namely 7Be + 5He, 6Li + 6Li, and 6He + 6Be, all conceivable transfer mechanisms were considered. The differential cross sections for these mechanisms were calculated within the CRC framework, employing spectroscopic amplitudes and optical potentials without modifications. The primary pick-up of the valence neutron was found to be prominent in the cluster transfer channels, except in those involving 6Li excitations. This observation highlights the cluster structure of n + 8Be in 9Be.
Special interest is drawn to the channel 6He + 6Be. Within the CRC framework, we achieved good congruence between the calculated cross sections and experimental data by proposing two-step transfer mechanisms, n-2n and 2n-n. Nonetheless, the high values of spectroscopic amplitudes used in the CRC calculations suggest the potential involvement of other processes, such as the direct transfer of three neutrons.
The investigation of one-nucleon transfer channels, along with charge exchange reaction channels, is planned as a continuation of the series of studies focusing on the reaction 3He + 9Be at an energy of 30 MeV.
-
We would like to thank the Nuclear Physics Institute (NPI) in Řež for providing us with the opportunity to perform this study, as well as the cyclotron staff of the institute for their excellent beam quality.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: