-
The study of the isomeric states of atomic nuclei provides information on the nature of the excited states of atomic nuclei [1−6]. The phenomenon of atomic nucleus isomerism is associated with a significant difference in the spin or deformation of the isomeric state relative to the ground state of an atomic nucleus. The probability of isomer population resulting from photonuclear reactions depends on the reaction energy, orbital momentum of emitted particles, momentum and parity of the final state, and probabilities of cascade transitions from higher-lying states [7]. In this study, in addition to the isomeric ratios, the yields and cross sections of photonuclear reactions in silver and indium samples were investigated.
Natural silver consists of two stable isotopes, with isotope abundances of 51.84% (107Ag) and 48.16% (109Ag). The 107Ag and 109Ag nuclei have Z = 47 protons. From the perspective of the shell model, this is a three-proton-hole state with respect to the magic number Z = 50. The number of neutrons in these is N = 60 and 62, respectively. The ground states of 107Ag (Jπ = 1/2-) and 109Ag (Jπ = 1/2-) are formed as a result of an interaction between two fairly complex proton and neutron configurations [8]. Natural indium also consists of two isotopes, the stable 113In (4.29%) and beta radioactive 115In (95.71%; half-life 4.41×1014 years). The number of protons in the odd-even nuclei of 113In and 115In is close to the magic number Z = 50, and the number of neutrons is N = 64 and 66, respectively. The spin-parity of the ground state of 113In and 115In is determined by the 1g9/2 subshell, which contains nine protons [9].
-
The experiments were performed at the LINAC-200 electron accelerator [10]. A tungsten converter with a size of 4.5 × 4.5 × 0.5 cm was irradiated with 20-MeV electron beams. Samples of silver and indium with dimensions of 0.7 × 0.6 × 0.1 cm and 1.0 × 0.7 × 0.1 cm, respectively, were placed behind the tungsten converter. The natAg and natIn samples were irradiated with a bremsstrahlung flux generated in the tungsten converter during electron beam irradiation with an irradiation time of 40 min, pulse current of 20 mA, pulse frequency of 10 Hz, and pulse duration of 2 μs. The pulse current was measured with an inductive current sensor based on a Rogowski coil. After irradiation, the silver and indium samples were transferred to the test room, and their gamma spectra were measured using a HPGe detector. Eight gamma spectra were measured for each sample with different measurement times. The times from the end of irradiation to the beginning of the measurement of the first spectrum of the natAg and natIn samples were 27 and 36 min, respectively. The gamma spectra obtained were processed using the Deimos32 program [11]. The areas of the identified peaks were determined with the background from the Compton scattering of photons subtracted. The absolute efficiency of the HPGe detector was measured using standard gamma-ray sources at the same distances from the detector at which the silver and indium samples were examined. The set of gamma-ray sources consisted of 54Mn, 57Co, 60Co, 88Y, 109Cd, 113Sn, 133Ba, 139Ce, 152Eu, 228Th, and 241Am. The yields of photonuclear reactions in the samples were determined using the following formula [12]:
$ {Y}_{\rm exp}=\frac{{S}_{p}\cdot {C}_{\rm abs}}{{\varepsilon }_{p}\cdot {I}_{\gamma }}\frac{{t}_{\rm real}}{{t}_{\rm live}}\frac{1}{N}\frac{1}{{N}_{{\rm e}^-}}\frac{{\rm e}^{\lambda \cdot {t}_{\rm cool}}}{1-{\rm e}^{-\lambda \cdot {t}_{\rm real}}}\frac{\lambda \cdot {t}_{\rm irr}}{1-{\rm e}^{-\lambda \cdot {t}_{\rm irr}}}, $

(1) where
$ {S}_{p} $ is the full-energy peak area,$ {\varepsilon }_{p} $ is the full-energy peak detector efficiency,${C}_{\rm abs}$ is the self-absorption correction coefficient,$ {I}_{\gamma } $ is the gamma emission probability,${t}_{\rm real}$ and${t}_{\rm live}$ are the real and live times of the measurement, respectively,$ N $ is the number of atoms in a sample,$ {N}_{{e}^{-}} $ is the integral number of electrons incident on the tungsten converter,$ \lambda $ is the decay constant,${t}_{\rm cool}$ is the cooling time, and${t}_{\rm irr}$ is the irradiation time.The parameter values of the nuclear reactions investigated in this study according to data from [13] and the yields of the measured nuclear reactions are given in Table 1, where Eth represents the reaction thresholds, J, π, and T1/2 are the spin, parity, and half-life of the nuclear reaction products, respectively, Eγ represents the energies of gamma rays emitted by the reaction products, and Yexp denotes the yields of the reactions. The values of the reaction thresholds Eth were obtained from the TALYS-1.96 program [14]. The reaction yields for all the identified gamma rays of radionuclides given in Table 1 were calculated using formula (1). Subsequently, when a radionuclide was identified with more than one gamma line, their reaction yield values were averaged, as given in Table 2.
Nuclear reaction Eth /MeV Jπ of nucleus-product T1/2 Eγ /keV Iγ /% Yexp (atom−1 · electron−1)
107Ag(γ,n)106mAg
9.55
6+
8.28 (2) d511.842 (28) 88 (3) 5.04(31)E-29 1045.83 (8) 29.6 (10) 4.79(26)E-29 717.24 (6) 28.9 (8) 5.00(26)E-29 450.97 (3) 28.2 (7) 4.95(26)E-29 616.174 (24) 21.6 (6) 4.77(25)E-29 748.44 (7) 20.6 (6) 4.63(25)E-29 1527.65 (19) 16.3 (13) 5.15(34)E-29 824.79 (15) 15.3 (4) 4.89(26)E-29 406.17 (3) 13.4 (4) 5.15(28)E-29 429.64 (5) 13.2 (4) 4.93(26)E-29 804.34 (13) 12.4 (5) 4.82(27)E-29 1128.00 (6) 11.8 (5) 5.25(30)E-29 1199.39 (10) 11.2 (5) 5.20(30)E-29
107Ag(γ,n)106gAg
9.55
1+
23.96 (4) min621.94 (3) 0.316 (8) 4.99(28)E-27 873.48 (4) 0.199 (5) 4.76(29)E-27 1050.39 (5) 0.167 (5) 4.61(32)E-27 616.174 (24) 0.142 (5) 4.79(32)E-27 1128.00 (6) 0.0721 (25) 5.18(40)E-27 1194.53 (4) 0.0398 (25) 4.39(52)E-27 1562.24 (5) 0.0172 (5) 4.12(70)E-27
107Ag(γ,2n)105Ag
17.56
1/2-
41.29 (7) d344.520 (21) 41 (1) 2.28(13)E-29 280.41 (6) 30.2 (17) 2.28(14)E-29 63.98 (3) 10.5 (10) 2.50(20)E-29 443.37 (7) 10.5 (5) 1.95(13)E-29 319.14 (6) 4.35 (21) 2.10(23)E-29 113In(γ,γ’)113mIn 1.45 1/2− 1.658 (1) h 391.690 (15) 64.2 (1) 2.56(11)E-28 113In(γ,n)112mIn 9.55 4+ 20.56 (6) min 156.56 (10) 13.2 (3) 1.30(7)E-27 113In(γ,n)112gIn 9.55 1+ 14.97 (10) min 617.516 (11) 4.6 (1) 4.40(47)E-28 606.88 (15) 1.111 (19) 4.10(45)E-28 113In(γ,2n)111In 17.23 9/2+ 2.8047 (5) d 245.395 (20) 94 (1) 3.19(15)E-29 171.28 (3) 90 (1) 3.07(15)E-29
115In(n,γ)116mIn
-
5+
54.29 (17) min1293.558 (15) 84.4 (17) 1.93(8)E-29 1097.326 (22) 56.2 (11) 2.01(9)E-29 416.86 (3) 27.7 (12) 2.01(9)E-29 2112.312 (22) 15.5 (4) 1.97(10)E-29 818.718 (21) 11.5 (4) 2.04(10)E-29 1507.67 (4) 10.0 (3) 1.97(10)E-29 115In(γ,γ’)115mIn 1.27 1/2− 4.486 (4) h 336.240 (12) 45.83 (10) 6.98(25)E-29
115In(γ,n)114mIn
9.28
5+
49.51 (1) d190.29 (3) 15.56 (15) 1.72(6)E-27 558.456 (2) 3.24 (23) 2.02(10)E-27 725.298 (9) 3.24 (23) 1.95(10)E-27 Table 1. Spectroscopic data [13] on the nuclei products and experimental yields of measured nuclear reactions.
Reaction Yield(Exp.) Calc./Exp. Reaction Yield(Exp.) Calc./Exp. 107Ag(γ,n)106mAg 4.94(50)E-29 1.05(11) 113In(γ,n)112gIn 4.24(53)E-28 1.97(25) 107Ag(γ,n)106gAg 4.79(50)E-27 0.40(4) 113In(γ,2n)111In 3.13(34)E-29 1.69(18) 107Ag(γ,2n)105Ag 2.20(24)E-29 1.68(18) 115In(n,γ)116mIn 1.99(20)E-29 0.83(8) 113In(γ,γ’)113mIn 2.56(28)E-28 0.50(5) 115In(γ,γ’)115mIn 6.98(73)E-29 2.51(27) 113In(γ,n)112mIn 1.30(15)E-27 1.91(22) 115In(γ,n)114mIn 1.84(21)E-27 1.60(18) Table 2. Experimental yields of measured reactions [atom−1 · electron−1].
-
Currently, Geant4 [15], FLUKA [16], and MCNP6 [17] are the most common Monte Carlo radiation transport codes for photonuclear reaction studies. In this study, we performed simulations with the Geant4 code. To simulate photonuclear interactions in Geant4, the G4PhotoNuclearProcess class [18] was used. Owing to the difficulty in using a sufficient number of electrons to determine the number of photonuclear reactions with a small uncertainty, we only obtained the fluences of electrons, bremsstrahlung, and neutrons in Geant4 calculations. Furthermore, the yields of the photonuclear reaction and the reaction of neutron capture by the nucleus were determined using formula (2). The reaction cross sections were calculated using the TALYS-1.96 program.
$ {Y}_{\rm calc}=\underset{{E}_{\rm thr}}{\overset{{E}_{\rm max}}{\int }}f\left(E\right)\sigma \left(E\right){\rm d}E, $

(2) where
$ f\left(E\right) $ is the bremsstrahlung fluence (in the case of the neutron capture reaction, the neutron fluence), and$ \sigma \left(E\right) $ is the reaction cross section. -
Using the results of processing the measured gamma spectra, we identified photoneutron reactions with the release of up to two neutrons from nuclei, the inelastic scattering of photons in nuclei, and the capture reaction of secondary neutrons by the nucleus. Table 2 shows the yields of the above reactions in the 107Ag, 113In, and 115In nuclei per electron incident on the tungsten converter with an energy of 20 MeV and their comparison with the simulation results.
According to the Nilsson model, the ground state in 106Ag (1+) can be described as the result of the addition of the proton state 1/2– to the deformed neutron state 1/2– arising from the splitting of the 1h11/2 shell level. The Jπ=6+ state can be obtained by adding the proton level 7/2+ to the neutron level 5/2+ formed upon the splitting of the 1g7/2 level in the deformed potential [8]. For the isomeric pair of odd-odd 112In nuclei, the spin-parity of the metastable state is Jπ=4+, and for the ground state, it is Jπ=1+. One unpaired proton located on the 1g9/2 subshell and a neutron, for example, on the 3s1/2 subshell, form the Jπ=4+ isomeric state. To form the ground state, the neutron must be on a subshell with a large spin (7/2) to form the Jπ=1+ state together with the proton shell 9/2+ [9].
-
According to the experimental data obtained, we determined the isomeric ratios of 112mIn/112gIn and 106mAg/106gAg. To determine the isomeric ratios of the yield in the photoneutron reaction 113In(γ,n)112m,gIn, the following formula (3) was used:
$\begin{aligned}[b] \frac{{Y}_{m}}{{Y}_{g}}=&\Bigg[\frac{{\lambda }_{g}(1-{\rm e}^{-{\lambda }_{m}{t}_{\rm irr}}){\rm e}^{-{\lambda }_{m}{t}_{\rm cool}}(1-{\rm e}^{-{\lambda }_{m}{t}_{\rm real}})}{{\lambda }_{m}(1-{\rm e}^{-{\lambda }_{g}{t}_{\rm irr}}){\rm e}^{-{\lambda }_{g}{t}_{cool}}(1-{\rm e}^{-{\lambda }_{g}{t}_{\rm real}})}\\&\times\left(\frac{{S}_{p,g}}{{S}_{p,m}}\frac{{I}_{\gamma ,m}}{{I}_{\gamma ,g}}\frac{{\epsilon }_{p,m}}{{\epsilon }_{p,g}}\frac{{C}_{{\rm abs},m}}{{C}_{{\rm abs},g}}-p\frac{{\lambda }_{g}}{{\lambda }_{g}-{\lambda }_{m}}\right)+p\frac{{\lambda }_{m}}{{\lambda }_{g}-{\lambda }_{m}}\Bigg]^{-1},\end{aligned} $

(3) where
$ p $ is the branching ratio.The half-life of the 112mIn (4+) isomeric state was 20.56 min. Emitting a gamma quantum with an energy of 156 keV, it decayed to the ground state of 112gIn (1+ ) via an internal transition with a branching intensity of 100%. The gamma quantum yield in the isomeric transition was 13.2%. The ground state of 112gIn (1+) had a half-life of 14.97 min and decayed via EC to 112Cd with a probability of 62% and via β- to 112Sn with a probability of 38%. During the decay of 112gIn (1+), the highest gamma quantum yield was 4.6%, and the corresponding energy was 617.5 keV. The isomeric ratio Ym/Yg for the yield of the 113In(γ,n)112m,gIn reaction was determined from the area of the gamma ray peaks with energies of 156.6 and 617.5 keV. The yield ratio Ym/Yg was 3.15(36), which coincides with the literature data [19−21], as shown in Fig. 1 (a). Using the isomeric ratios Ym/Yg of 112In nuclei, the yield of the reaction 113In(g,n)112gIn was determined. The yield value of the reaction 113In(g,n)112mIn given in Table 1 was determined using formula (1).
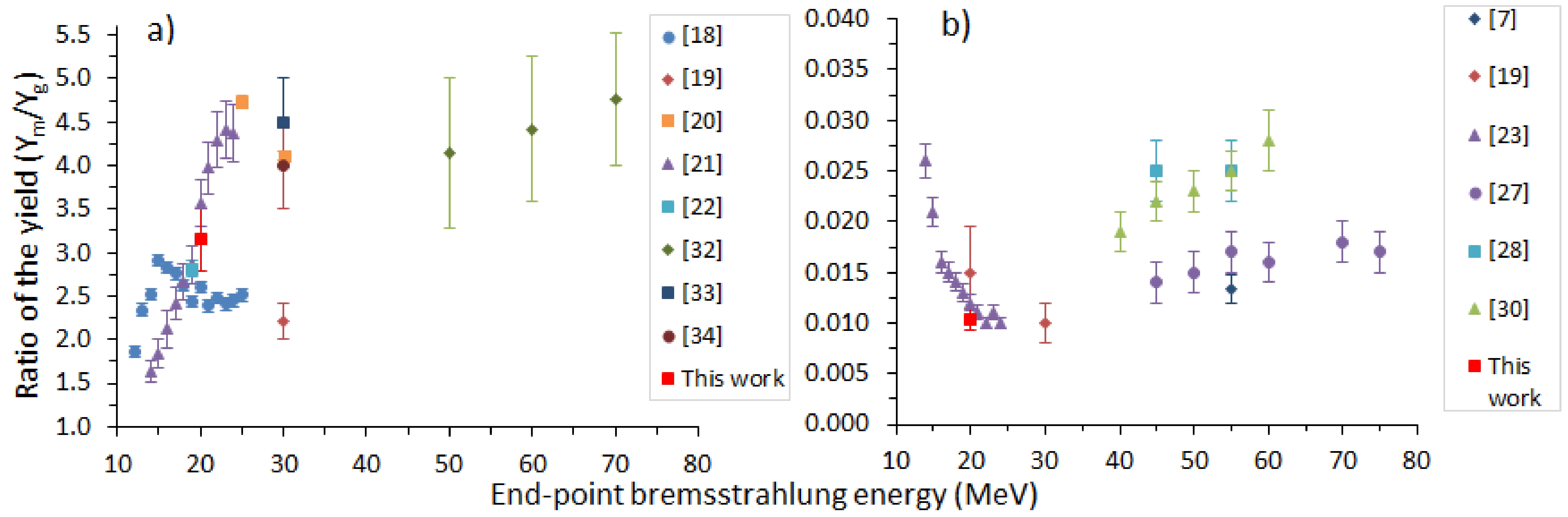
Figure 1. (color online) Dependence of the isomeric yield ratio in the photoneutron reactions 113In(γ,n)112m,gIn (a) and 107Ag(γ,n)106m,gAg (b) on the end-point bremsstrahlung energy.
Determining the isomeric ratios for the 106Ag nucleus was simple. Because the half-lives of the isomeric Jπ=6+ (T1/2 = 8.28 d) and ground Jπ=1+ (T1/2 = 23.96 min) states of the 106Ag nucleus differed, the independent yields Ym and Yg were measured. The isomeric ratio for the 106Ag nucleus was 1.03(11)E-2, which also coincides with literature data [22, 23], as shown in Fig. 1 (b). As shown from the available literature data [7, 13, 19−24, 25−27, 28−30], the average value of the isomeric ratios of 112m,gIn in the reaction 113In(γ,n) increases with an increase in the end-point bremsstrahlung energies (see Fig. 1 (a)). The average value of the isomeric ratios of 106m,gAg in the reaction 107Ag(γ,n) in the region of end-point bremsstrahlung energies of 14 to 75 MeV also increases (see Fig. 1 (b)).
-
In this study, although investigations on photonuclear reactions were performed with bremsstrahlung, it was still possible to determine the cross sections of photonuclear reactions for a specific photon energy by calculating the monochromatic photon spectrum. The reaction cross section can be determined from the reaction yield data by solving formula (2). A method for calculating the quasi-monoenergetic spectrum from the bremsstrahlung spectrum was shown and used in Ref. [31]. This method was also successfully used in Ref. [32]. In this method, to determine reaction cross sections, the effective photon spectrum must be calculated, the shape of which is close to the spectrum of monoenergetic photons. To calculate the monoenergetic spectrum of photons, we used the calculated bremsstrahlung spectra for electrons with energies of 19, 20, and 21 MeV. When calculating the bremsstrahlung spectra with the Geant4 code, we used the statistics of two billion electrons. The bremsstrahlung spectra of the tungsten converter for electrons with energies of 19, 20 and 21 MeV and the calculated quasi-monoenergetic spectrum of photons with an energy of 20 MeV are shown in Figs. 2 (a) and 2(b), respectively.
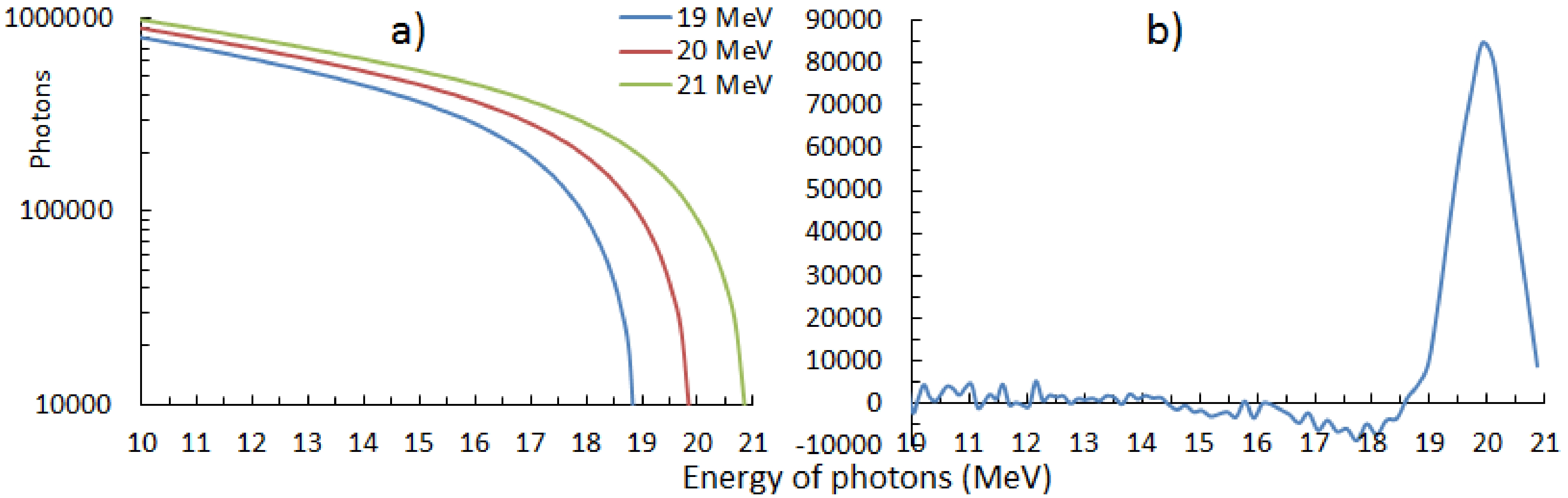
Figure 2. (color online) Bremsstrahlung spectra of the tungsten converter for electrons with energies of 19, 20, and 21 MeV (a). Quasi-monoenergetic spectrum of 20 MeV photons (b).
To determine the cross section of the reaction, we must determine the value of the yield of the reaction caused by photons with energies of 19 to 21 MeV using the experimental data. To do this, the experimental and calculated values of the yield of the reaction with bremsstrahlung produced by electrons with energies of 19, 20, and 21 MeV were required. We only possessed the experimental value of the reaction yield for electrons with an energy of 20 MeV. Those of the 19 MeV and 21 MeV electrons were corrected from the calculated data by consideringthe ratios
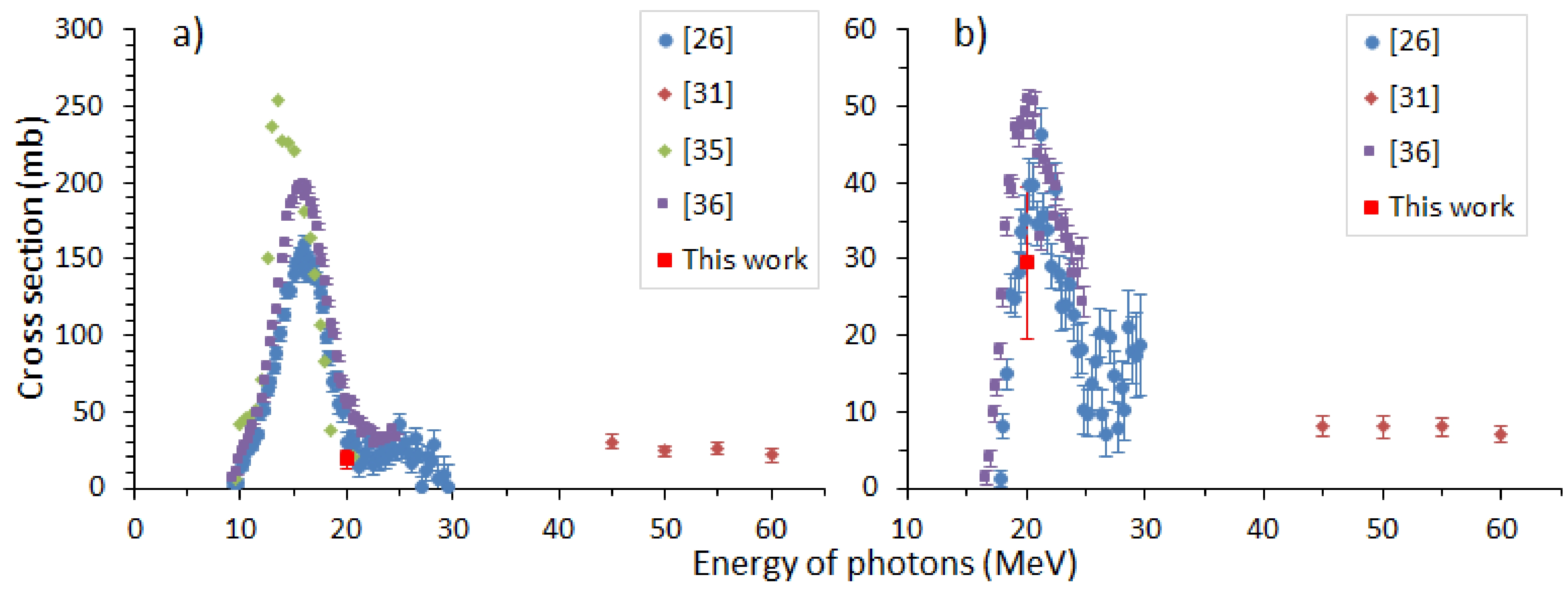
$\dfrac{{Y}_{\rm calc}\left(19{\rm MeV}\right)}{{Y}_{\rm calc}\left(20{\rm MeV}\right)}=\dfrac{{Y}_{\rm exp}\left(19{\rm MeV}\right)}{{Y}_{\rm exp}\left(20{\rm MeV}\right)}$ and$\dfrac{{Y}_{\rm calc}\left(21{\rm MeV}\right)}{{Y}_{\rm calc}\left(20{\rm MeV}\right)}=\dfrac{{Y}_{\rm exp}\left(21{\rm MeV}\right)}{{Y}_{\rm exp}\left(20{\rm MeV}\right)}$ to be correct. The cross sections for the photoneutron reactions 107Ag(γ,n)106gAg and 107Ag(γ,2n)105Ag at an energy of 20 MeV determined using the above method were 19.0 ± 5.7 mb and 29.4 ± 10.0 mb, respectively, which coincide with literature data [33−35] measured with mono-energetic photons, as shown in Figs. 3 (a) and 3 (b). The values of the flux-weighted average cross-sections at bremsstrahlung end-point energies from literature data [36] are also shown in Figs. 3 (a) and 3 (b). A region of giant dipole resonance (9−21 MeV), in which only one nucleon is excited when a γ-quantum is absorbed by the nucleus, can be observed in Fig. 3 (a). Above this region, the quasideuteron mechanism of photoabsorption began to dominate, in which photons were predominantly absorbed by quasideuterons. -
The interaction of bremsstrahlung with silver and indium nuclei at an accelerated electron energy of 20 MeV was studied experimentally and theoretically. The yields of photonuclear reactions in 107Ag, 113In, and 115In nuclei were measured, and the yield of the capture reaction of secondary neutrons with the 115In (9/2+) nucleus with the formation of the 116mIn (5+) isomeric state was measured. Monte Carlo simulations were performed using the Geant4 code, and the results were compared with the experimental values. According to the comparison results, the ratio Calc./Exp. was in the range 0.40−2.51. The isomeric ratios of the yields in the reactions 107Ag(γ,n)106m,gAg and 113In(γ,n)112m,gIn were determined, which coincide with literature data. Using the experimental data, the cross sections for the reactions 107Ag(γ,n)106gAg and 107Ag(γ,2n)105Ag at an energy of 20 MeV were determined, which also coincide with literature data.
Interaction of photons with silver and indium nuclei at energies up to 20 MeV
- Received Date: 2023-08-22
- Available Online: 2024-02-15
Abstract: The yields of photonuclear reactions in the 107Ag, 113In, and 115In nuclei were measured. Monte Carlo simulations were performed using the Geant4 code, and the results were compared with the experimental values. The isomeric ratios of the yields in the reactions 107Ag(γ, n)106m,gAg and 113In(γ, n)112m,gIn were determined, and the cross sections for the reactions 107Ag(γ, n)106gAg and 107Ag(γ, 2n)105Ag at an energy of 20 MeV were calculated based on the experimental data.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: