-
$ Y(4230) $ a.k.a.$ \psi(4230) $ is the first observed Y state, which was detected through the initial-state-radiation (ISR) technique in the process$ e^+e^-\to J/\psi \pi^+\pi^- $ by the BABAR experiment in 2005 [1] and then confirmed by CLEO [2] and Belle [3] in the same process. An accumulation of events with similar characteristics was reported in two other processes$ e^+e^-\to J/\psi\pi^0\pi^0 $ (and$ J/\psi K^+K^- $ ) by CLEO [4] and also in the decay of$ B^-\to \psi $ (4230)$ K^-\to J/\psi \pi^+\pi^- K^- $ by the BABAR [5] collaboration.In 2017, the BESIII collaboration announced a new precise measurement of the
$ e^+e^-\to J/\psi \pi^+\pi^- $ cross section [6], reporting updated values for the mass and width of the$ Y(4230) $ . Particularly, a second resonance is also presented in the$ J/\psi\pi^+\pi^- $ mass spectrum. The values of the two observed resonances are$ (4222.0\pm3.1\pm1.4) $ and$ (44.1\pm4.3\pm2.0) $ MeV for$ Y(4230) $ and$ (4320.0\pm10.4\pm7) $ and$ (101.4^{+25.3}_{-19.7}\pm10.2) $ MeV for, namely,$ Y(4360) $ . Although Ref. [6] proposes that the structure around 4260 MeV could be read as a superposition of these two resonances, and Ref. [7] further suggests them as$ Y(4230) $ and$ Y(4360) $ respectively, this discussion has not yet been settled. Here, our study still concentrates on the$ Y(4230) $ resonant state instead of discussing the combined structure.Experimentally, the
$ Y(4230) $ is directly produced in$ e^+e^- $ annihilation; its spin-parity quantum number should be$ J^{PC}=1^{--} $ , which is consistent with that of a vector charmonium state. Theorists have tried to categorize it into the vector charmonium group. However, because its mass does not fit into any mass of the charmonium states in the same mass region, and$ c\bar{c} $ mainly decays to$ D^{(*)}\bar{D}^{(*)} $ , but the observed Y in such decay does not match the peaks in the$ e^+e^-\to D^{(*)\pm}D^{(*)\mp} $ cross sections measured by the BABAR [7, 8] and Belle [9] collaborations, the Y(4230) does not look like a normal$ c\bar{c} $ state. Furthermore, for the$ 1^{–} $ radially excited charmoniums, four of the S-wave states,$ \psi(1S) $ ,$ \psi(2S) $ ,$ \psi(3S) $ , and$ \psi(4S) $ , have already been assigned to$ J/\psi $ ,$ \psi(3686) $ ,$ \psi(4040) $ and$ \psi(4415) $ mesons, respectively, and two of the D-wave states$ \psi(1D) $ and$ \psi(2D) $ have been assigned to$ \psi(3770) $ and$ \psi(4160) $ mesons, respectively. In addition, the masses of the$ \psi(5S) $ and$ \psi(3D) $ states in the quark model are 4.76 and 4.52 GeV, and are thus higher than that of the$ Y(4230) $ . According to the above analysis, one can conclude that$ Y(4230) $ may not be consistent with any of the$ 1^{--} ~c\bar{c} $ states [10−12].To further explain the structure of
$ Y(4230) $ , many theoretical interpretations have emerged, including that it is a tetraquark state [13−16], a compact tetraquark state [17], a hadrocharmonium state [18, 19], hadronic molecule of$ D_0\bar{D}^* $ ,$ D_1 D $ ,$ D_0 D^* $ or$ \bar{D} D_1(2420) $ [15, 20−22],$ \chi_{c1}\omega $ [23],$ \chi_{c1}\rho $ [24],$ J/\psi K\bar{K} $ [25],$ \psi^\prime f_0(980) $ [26], a$ c\bar{c} $ -gluon hybrid [14, 27, 28], a charm baryonium [29], and a coupled-channel model [30, 31]. However, within the available experimental data, none of these theoretical interpretations can be completely accepted or excluded from the nature of$ Y(4230) $ .For example, in the compact tetraquark model [32], an isospin-violating process
$ Y(4230)\to \eta\pi^0J/\psi $ exists with a sizeable decay width, where both$ \pi^0J/\psi $ and$ \eta J/\psi $ can be produced from$ Z_c^0 $ decay. Therefore, the interpretation of$ Y(4230) $ in the compact tetraquark model can lead to a peak in the$ e^+e^-\to\eta\pi^0J/\psi $ cross section and a very prominent peak should appear in$ \eta J/\psi $ mass spectrum between the$ D\bar{D}^* $ threshold [33]. However, using the data from the BESIII experiment and searching for isospin-violating [34], no$ Y(4230) $ signal is observed. Whatever the case, the compact tetraquark model should have isospin and SU(3)-multiplet partner states. However, none of those partners for ψ(4230) has been observed in experiments so far. If ψ(4230) is a hadrocharmonium, it's structure would be formed by mixing with another hadrocharmonium. These two hadrocharmonia states contain spin 1 and spin 0 compact$ c\bar{c} $ cores, respectively [18]. However, based on BESIII data [6], the decay rate of$ Y(4230) $ to non-$ J/\psi(h_c) $ charmonium states should be suppressed [18], indicating that the above suggestion may not be consistent. If we assign the$ \bar{D}D_1(2420) $ molecule to ψ(4230), the binding energy being approximately 66 MeV is rather large, though this possibility is not excluded [35]. There are other candidates for ψ(4230), e.g.,$ \bar{D}D_1(2430) $ ,$ \bar{D}^*D_0 $ ,$ \bar{D}_{s0}D_s^* $ , and$ \bar{D}_{s}D_{s1} $ , whose open charm thresholds are around 4.26 GeV with$ J^{PC}=1^{–} $ . Unfortunately, besides$ \bar{D}_{s0}D_s^* $ , these candidates have widths that are too broad to make a bound state, which could not be consistent with the total decay width of$ Y(4230) $ [21, 36]. For the$ \bar{D}_{s0}D_s^* $ molecule, its mass is$ 4.42\pm0.10 $ GeV, which should also be excluded [15]. In any case, Y(4230) does not seem to be a hadronic molecule.The
$ Y(4230) $ may also be assumed to be a charmonium hybrid meson. However, in Ref. [37], the authors found that the masses of the$ 1^{--} $ hybrid states lie at$ 4.47 $ GeV, heavier than the mass of the$ Y(4230) $ . In non-relativistic EFTs, the mass of$ Y(4230) $ may be consistent with one state of$ H_1 $ hybrid multiplet, but$ Y(4230) $ disfavors the hybrid interpretation since it decays to spin triplet charmonium while$ H_1 $ is only a spin singlet [38]. In Ref. [39], the color halo picture was found to be compatible with$ Y(4260) $ decay properties, and LHCb and BelleII were suggested to search for$ (0,1,2)^{+-} $ charmonium-like hybrids in$ \xi_{c0,1,2}\eta $ and$ J/\psi\omega(\psi) $ final states. We should not hastily conclude that$ Y(4230) $ can not be the hybrid state.In summary, the structure of
$ Y(4230) $ at this point is not yet fully settled.In this study, we investigate the strong decay of
$ Y(4230)\to J/\psi f_0(980) $ observed in the process$ e^+e^-\to J/\psi \pi^+\pi^- $ . Notice$ Y(4230) $ will decay into a$ f_0(980) $ , which fits the S-wave$ [sq][\bar{s}\bar{q}] $ hypothesis [40]. Furthermore, being a member of the vector charmonium family suggests ψ(4230) a$ [cs][\bar{c}\bar{s}] $ composition. We, therefore, consider$ Y(4230) $ to be a tetraquark state, as in Ref. [41]. This differs from other ideas, i.e., in Ref. [42], the$ Y(4230) $ was suggested to be a$ J/\psi f_0(980) $ bound system. We calculate the strong coupling$ g_{Y J/\psi f_0} $ using the light cone sum rules method, with the interpolating current taken from Ref. [15]. We evaluate the mass of$ Y(4230) $ through a different calculation technique developed in Ref. [43], not the usual way in two-point sum rules [44]. Comparing the mass prediction of$ Y(4230) $ with the result in PDG [45], we confirm our technique generalization is credible. We then extend it to evaluate the decay constant of$ Y(4230) $ , which will be used in the numerical calculation of the strong coupling$ g_{YJ/\psi f_0} $ . Finally, the decay width of$ Y(4230)\to J/\psi f_0(980) $ is obtained, and further results are compared with the experimental measurement and discussed.Our work is organized as follows:
In Section II, we calculate the mass and decay constant of the
$ Y(4230) $ state within the two-point sum rule approach developed by Shifman, Vainshtein, and Zakharov (SVZ sum rules) [46]. We also calculate the strong coupling$ g_{YJ/\psi f_0} $ , which is derived with the light cone sum rules approach. The numerical results and discussions are shown in Section III. We present our summary in Section IV. -
We begin by calculating the mass and the decay constant using the two-point correlation function:
$ \begin{array}{*{20}{l}} \Pi_{\mu\nu}(p)= {\rm i} \displaystyle\int {\rm d}^4x {\rm e}^{{\rm i}px} \left\langle {0|T\{J_{\mu}^{Y}(x)J_{\nu}^{Y\dagger}(0)\}|0} \right\rangle , \end{array} $

(1) where the interpolating currents are given by the following expression:
$ \begin{aligned}[b] J_{\mu}^{Y}(x)=&\frac{\varepsilon_{abc}\varepsilon_{dec}}{\sqrt{2}}\{[s^T_a(x)C\gamma_5c_b(x)][\bar{s}_d(x)\gamma_\mu\gamma_5C\bar{c}_e^T(x)]\\ &-[s_a^T(x)C\gamma_\mu\gamma_5c_b(x)][\bar{s}_d(x)\gamma_5C\bar{c}_e^T(x)]\},\\ J^{Y\dagger}_\nu(0)=&\frac{\varepsilon_{abc}\varepsilon_{dec}}{\sqrt{2}}\{-[\bar{c}_b(0)\gamma_5C\bar{s}_a^T(0)][c_e^T(0)C\gamma_\nu\gamma_5 s_d(0)]\\ &+[\bar{c}_b(0)\gamma_\nu\gamma_5 C\bar{s}_a^T(0)][c_e^T(0)C\gamma_5 s_d(0)]\}. \end{aligned} $

(2) As a first step, we calculate the correlation function by inserting a complete set of hadronic states into Eq. (1):
$ \Pi^{\text{h}}_{\mu\nu}(p)= \frac{\left\langle{0|J_\mu^{Y}|Y(p)}\right\rangle \left\langle{Y(p)|J_\mu^{Y\dagger}|0}\right\rangle }{m_Y^2-p^2} +\int_{s^\prime}^\infty {\rm d} \hat{s}\frac{\rho_{\mu\nu}^{\text{h}}(\hat{s})}{\hat{s}-p^2}, $

(3) where the higher resonances and continuous states are represented by
$ \rho_{\mu\nu}^{\text{h}}(\hat{s}) $ . The subtraction terms are not displayed because they would disappear following the Borel transformation. We define the decay constant$ f_Y $ according to$ \begin{array}{*{20}{l}} \left\langle {0|J_\mu^{Y}|Y(p)}\right\rangle =m_Yf_Y\epsilon_\mu \end{array} $

(4) with
$ \epsilon_\mu $ being the polarization vector of$ Y(4230) $ . After performing the polarization sum equation, we can obtain$ \Pi_{\mu\nu}^{\text{h}}(p)=\frac{m_Y^2f_Y^2}{m_Y^2-p^2}\left(-g_{\mu\nu} +\frac{p_\mu p_\nu}{m_Y^2}\right) +\int_{s^\prime}^\infty {\rm d} \hat{s}\frac{\rho_{\mu\nu}^{\text{h}}(\hat{s})}{\hat{s}-p^2}. $

(5) On the right side of Eq. (5), we begin to observe a pole. The Borel transformation can be performed on Eq. (5) to remove the pole, which yields
$ \begin{aligned}[b] \Pi_{\mu\nu}^{\text{h}}(M^2)= &m_Y^2f_Y^2 {\rm e}^{-m_Y^2/M^2}\left(-g_{\mu\nu}+\frac{p_\mu p_\nu}{m_Y^2}\right)\\&+\int_{s^\prime}^\infty {\rm d} \hat{s}\rho_{\mu\nu}^{\text{h}}(\hat{s}){\rm e}^{-\hat{s}/M^2}. \end{aligned} $

(6) Next, let us consider the correlation function in the OPE side. Following the Wick Theorem for contraction of the heavy and light quarks, we obtain
$ \begin{aligned}[b] &\Pi_{\mu\nu}^{\text{OPE}}(p)\\=&\frac{1}{2}\int \rm{d}^4xe^{ipx}\epsilon_{abc}\epsilon_{dec}\epsilon_{a^\prime b^\prime c^\prime}\epsilon_{d^\prime e^\prime c^\prime}\\ &-\text{Tr}[\tilde{S}^{aa^\prime}_s(x)\gamma_5S_c^{bb^\prime}(x)\gamma_5]\text{Tr}[S^{dd^\prime}_s(-x)\gamma_\mu\gamma_5\tilde{S}_c^{ee^\prime}(-x)\gamma_\nu\gamma_5]\\ &+\text{Tr}[\tilde{S}^{aa^\prime}_s(x)\gamma_5S_c^{bb^\prime}(x)\gamma_\nu\gamma_5]\text{Tr}[S^{dd^\prime}_s(-x)\gamma_\mu\gamma_5\tilde{S}_c^{ee^\prime}(-x)\gamma_5]\\ &+\text{Tr}[\tilde{S}^{aa^\prime}_s(x)\gamma_\mu\gamma_5S_c^{bb^\prime}(x)\gamma_5]\text{Tr}[S^{dd^\prime}_s(-x)\gamma_5\tilde{S}_c^{ee^\prime}(-x)\gamma_\nu\gamma_5]\\ &-\text{Tr}[\tilde{S}^{aa^\prime}_s(x)\gamma_\mu\gamma_5S_c^{bb^\prime}(x)\gamma_\nu\gamma_5]\text{Tr}[S^{dd^\prime}_s(-x)\gamma_5\tilde{S}_c^{ee^\prime}(-x)\gamma_5], \end{aligned} $

(7) where
$ \tilde{S}_q^{ab}(x) $ represents$ CS_q^{ab}(x)C $ . We accept the following expression for propagators of the u, d, and s quarks in coordinate-space [47, 48]:$ \begin{aligned}[b] S_{q,ab}(x)=&\frac{{\rm i} \delta_{ab}\not {x}}{2\pi^2x^4}-\frac{\delta_{ab}m_q}{4\pi^2x^2}-\frac{{\langle \bar{q}q\rangle }}{12}\\ &-\frac{\rm i}{32\pi^2}\frac{\lambda^n}{2}g_sG_{\mu\nu}^n\frac{1}{x^2}(\sigma^{\mu\nu}\not {x}+\not {x}\sigma^{\mu\nu})\\ &+\frac{{\rm i}\delta_{ab}\not {x}m_q{\langle \bar{q}q\rangle }}{48} -\frac{\delta_{ab}{\langle \bar{q}g_s\sigma Gq \rangle}x^2}{192}\\ &+\frac{{\rm i}\delta_{ab}x^2\not {x}m_q\langle\bar{q}g_s\sigma Gq\rangle}{1152}\\ &-\frac{{\rm i}\delta_{ab}x^2\not {x}g_s^2\langle\bar{q}q\rangle^2}{7776}-\frac{\delta_{ab}x^4\langle\bar{q}q\rangle\langle g_s^2GG\rangle}{27648}. \end{aligned} $

(8) The heavy quark propagator is given in terms of Bessel functions of the second kind
$ K_v(x) $ as [49]$ \begin{aligned}[b] S^{ab}_{c}(x)=&\frac{m_Q^2}{4\pi^2}\left[\frac{K_1(m_Q\sqrt{-x^2})}{\sqrt{-x^2}}\delta_{ab}+{\rm i} \frac{\not {x}K_2(m_Q\sqrt{-x^2})}{(\sqrt{-x^2})^2}\delta_{ab}\right]\\ &-\frac{g_sm_Q}{16\pi^2}\int_0^1\rm{d}vG^ {\mu\nu}_{ab}(vx)\Bigg[(\sigma_{\mu\nu}\not {x}+\not {x}\sigma_{\mu\nu})\frac{K_1(m_Q\sqrt{-x^2})}{\sqrt{-x^2}}\\ &+2\sigma^{\mu\nu}K_0(m_Q\sqrt{-x^2})\Bigg]. \end{aligned} $

(9) Notice the heavy quark propagator here is different from the expression presented in the usual way, for example, in Ref. [44], where the heavy quark propagator is expressed in the momentum space. If we use the momentum expression of the propagator in Eq. (7), we have to face divergences in the double integrals such as
$ \int\frac{{\rm d}^4k_1 {\rm d}^4k_2}{(k_1^2-m_c^2)(k_2^2-m_c^2)}. $

(10) As shown in Ref. [43], results without any divergences can be obtained by using an appropriate representation of the modified Bessel functions in the heavy quark propagator, like in Eq. (9). Since here, we are using the SVZ sum rules instead of the LCSR, we have to modify the calculation when the particle distribution function does not participate in Eq. (7). We showed the details of the modification in Appendix V.C.
The correlation function
$ \Pi^{\text{OPE}}_{\mu\nu}(p) $ also has the following decomposition over the Lorentz structures:$ \begin{array}{*{20}{l}} \Pi^{\text{OPE}}_{\mu\nu}(p)=\Pi^{\text{OPE}}(p)g_{\mu\nu}+\widetilde{\Pi}^{\text{OPE}}(p)p_\mu p_\nu, \end{array} $

(11) and we choose to work with the term
$ \sim g_{\mu\nu} $ , which can be represented as the dispersion integral:$ \widetilde{\Pi}^{\text{OPE}}(p)=\int_{4m_c^2}^\infty\rm{d}\hat{s}\frac{\rho^{\text{OPE}}(\hat{s})}{\hat{s}-p^2}, $

(12) where
$ \rho^{\text{OPE}}(\hat{s}) $ is the corresponding spectral density.The Borel transformation and the quark-hadron duality can be applied to
$ \widetilde{\Pi}^{\text{OPE}}(p) $ to obtain$ \begin{aligned}[b] &p_\mu p_\nu\int_{4m_c^2}^\infty\rm{d}\hat{s}\rho^{\text{OPE}}(\hat{s}){\rm e}^{-\hat{s}/M^2}=\\ &m_Y^2f_Y^2{\rm e}^{-m_Y^2/M^2}(\frac{p_\mu p_\nu}{m_Y^2})+p_\mu p_\nu\int_{s_0}^\infty\rho^{\text{h}}(\hat{s}){\rm e}^{-\hat{s}/M^2}. \end{aligned} $

(13) Next, take out the contribution from the continuum to get
$ f_Y^2{\rm e}^{-m_Y^2/M^2}=\int_{4m_c^2}^{s_0}\rm{d}\hat{s}\rho^{\text{OPE}}(\hat{s}){\rm e}^{-\hat{s}/M^2}. $

(14) The
$ Y(4230) $ state mass can be determined by the sum rule:$ m_Y^2=\frac{\displaystyle\int_{4m_c^2}^{s_0}\rm{d}\hat{s}\hat{s}\rho^{\text{OPE}}(\hat{s}){\rm e}^{-\hat{s}/M^2}}{\displaystyle\int_{4m_c^2}^{s_0}\rm{d}\hat{s}\rho^{\text{OPE}}(\hat{s}){\rm e}^{-\hat{s}/M^2}}. $

(15) -
It is necessary to calculate the strong coupling
$ g_{YJ/\psi f_0} $ first, based on the light cone sum rules (LCSR), before predicting the width of$ Y(4230)\to J/\psi f_0(980) $ . We begin by using the two-point correlation function:$ \Pi_{\mu\nu}(p^\prime,q)= {\rm i} \int \rm{d}^4x {\rm e}^{{\rm i} px} \left\langle {f_0(q)|T\{J_{\mu}^{J/\psi}(x)J_{\nu}^{Y\dagger}(0)\}|0}\right\rangle , $

(16) where
$ f_0 $ represents the scalar meson$ f_0(980) $ .$ Y(4230) $ has momentum$ p^\prime=p+q $ , and p, q represent the four-momentum for$ J/\psi $ and$ f_0 $ , respectively.$ J_{\mu}^{J/\psi} $ is the interpolating current of$ J/\psi $ given by [15, 50]$ \begin{array}{*{20}{l}} &J_{\mu}^{J/\psi}(x)=\bar{c}_i(x)\gamma_\mu c_i(x). \end{array} $

(17) Here, i denotes the color indexes, and C is the charge conjugation matrix.
-
Next, we must build a relationship between the correlation function
$ \Pi_{\mu\nu}(p^\prime,q) $ and the strong coupling$ g_{YJ/\psi f_0} $ .By adding two complete sets of hadronic states to Eq. (16), we can construct the phenomenological expression of the correlation function:
$ \begin{aligned}[b] \Pi^{\text{h}}_{\mu\nu}(p^\prime,q)= &\frac{\left\langle {0|J_{\mu}^{J/\psi}|J/\psi(p)}\right\rangle \left\langle {f_0(q)J/\psi(p)|Y(p^\prime)}\right\rangle \left\langle {Y(p^\prime)|J_{\nu}^{Y\dagger}|0}\right\rangle } {(p^{\prime2}-m_{Y}^2)(p^2-m_{J/\psi}^2)}\\ &+\int_{s_1^\prime}^\infty\int_{s_2^\prime}^\infty \frac{{\rm d} s_1 {\rm d} s_2\ \rho_{\mu\nu}^{\text{h}}(s_1,s_2)}{(s_1-p^2)(s_2-p^{\prime2})} +\cdots, \end{aligned} $

(18) where
$ \rho_{\mu\nu}^{\text{h}}(s_1,s_2) $ represents the contributions of the continuum states and higher resonances. The lowest continuum state thresholds are indicated by the symbols$ s_1^\prime $ and$ s_2^\prime $ .By parameterizing the hadronic matrix element
$ \begin{aligned}[b] \left\langle {0|J_{\mu}^{J/\psi}|J/\psi(p)}\right\rangle =&m_{J/\psi}f_{J/\psi}\varepsilon_\mu, \\ \left\langle {Y(p^\prime)|J_{\nu}^{Y\dagger}|0}\right\rangle =&m_{Y}f_{Y}\varepsilon_\nu^{\prime*},\\ \left\langle {f_0(q)J/\psi(p)|Y(p^\prime)}\right\rangle =&g_{YJ/\psi f_0} ((p^\prime\cdot p)(\varepsilon^*\cdot \varepsilon^\prime) \\ & -(p^\prime\cdot \varepsilon^*)(p\cdot\varepsilon^\prime)), \end{aligned} $

(19) and performing the polarization sum, we can easily show that
$ \begin{aligned}[b] \Pi^{\text{h}}_{\mu\nu}(p^\prime,q)=&\frac{m_{J/\psi}m_{Y}f_{J/\psi}f_{Y}g_{YJ/\psi f_0}}{(p^2-m_{J/\psi}^2)(p^{\prime2}-m_{Y}^2)}\\ &\times \left[ \frac{(m_{J/\psi}^2+m_Y^2)}{2}g_{\mu\nu}-p^\prime_\mu p_\nu \right] +\cdots\\ =&\Pi^{\text{Phys}}(p^\prime,q)g_{\mu\nu}+\widetilde{\Pi}^{\text{Phys}}(p^\prime,q)p^\prime_\mu p_\nu, \end{aligned} $

(20) where
$ m_{J/\psi} $ and$ m_{Y} $ are the masses of$ J/\psi $ and$ Y(4230) $ respectively. ε and$ \varepsilon^\prime $ denote the polarization vectors of the$ J/\psi $ and$ Y(4230) $ , respectively.$ g_{YJ/\psi f_0} $ is the invariant constant parameterizing the hadronic matrix element.In this study, we choose to proceed with a structure that is proportional to
$ g_{\mu\nu} $ $ \begin{aligned}[b] \Pi^{\text{h}}(p^\prime,q)=&\frac{m_{J/\psi}m_{Y}f_{J/\psi}f_{Y}g_{YJ/\psi f_0}m^2}{(p^2-m_{J/\psi}^2)(p^{\prime2}-m_{Y}^2)}\\ &+\int_{s_1^\prime}^\infty\int_{s_2^\prime}^\infty\frac{\rm{d}s_1\rm{d}s_2\rho^{\text{h}}(s_1,s_2)}{(s_1-p^2)(s_2-p^{\prime2})}+\cdots, \end{aligned} $

(21) where we define
$ m^2 =\dfrac{m_{J/\psi}^2+m_Y^2}{2} $ . The correlation function in Eq. (21) can be transformed into the equation below by applying the Borel transformations to the variables$ p^2 $ and$ p^{\prime2}=(p+q)^2 $ ,$ \begin{aligned}[b] &\mathcal{B}_{p^2}(M_1^2)\mathcal{B}_{p^{\prime 2}}(M_2^2)\Pi^{\text{h}}(p^\prime,q)\\= &m_{J/\psi}m_{Y}f_{J/\psi}f_{Y}g_{YJ/\psi f_0}m^2\exp\left[-\frac{m_{J/\psi}}{M_1^2}-\frac{m_{Y}}{M_2^2}\right]\\ &+\int_{s_1^\prime}^\infty\int_{s_2^\prime}^\infty\rm{d}s_1\rm{d}s_2 \exp\left[-\frac{s_1}{M_1^2}-\frac{s_2}{M_2^2}\right] \rho^{\text{h}}(s_1,s_2). \end{aligned} $

(22) Thus, we have the following formula for a general dispersion relation:
$ \Pi_{\mu\nu}(p^\prime,q)=\frac{1}{\pi^2}\int\int \frac{{\rm d} s_1{\rm d}s_2\text{Im}\Pi_{\mu\nu}(s_1,s_2)}{(s_1-p^2)(s_2-p^{\prime2})}+\cdots, $

(23) where the subtraction terms and single dispersion integrals are not provided because they would all vanish when the double Borel transformation is applied to Eq. (23). By choosing to proceed with a structure that is proportional to
$ g_{\mu\nu} $ , we can represent the OPE result for the correlation function as$ \Pi^{\text{OPE}}(p^\prime,q) =\int\int \frac{{\rm d}s_1{\rm d}s_2\ \rho^{\text{OPE}}(s_1,s_2)}{(s_1-p^2)(s_2-p^{\prime2})}, +\cdots $

(24) where
$ \rho_{\mu\nu}^{\text{OPE}}(s_1,s_2)=\frac{\text{Im}\Pi(s_1,s_2)}{\pi^2}. $

(25) After performing the Borel transformations, we can derive
$ \begin{aligned}[b] & \Pi^{\text{OPE}}(M_1^2,M_2^2)\\= &\int\int\rm{d}s_1\rm{d}s_2 \exp\left[-\frac{s_1}{M_1^2}-\frac{s_2}{M_2^2}\right] \rho^{\text{OPE}}(s_1,s_2). \end{aligned} $

(26) This is accomplished by applying the quark-hadron duality, which allows the integral of the hadronic spectral density to equal that of the OPE spectral density in a certain region:
$ \begin{aligned}[b] &\int_{s_1^\prime}^\infty\int_{s_2^\prime}^\infty\rm{d}s_1\rm{d}s_2 \exp\left[-\frac{s_1}{M_1^2}-\frac{s_2}{M_2^2}\right] \rho^{\text{h}}(s_1,s_2)\\= &\int_{s_1^0}^\infty\int_{s_2^0}^\infty\rm{d}s_1\rm{d}s_2 \exp\left[-\frac{s_1}{M_1^2}-\frac{s_2}{M_2^2}\right] \rho^{\text{OPE}}(s_1,s_2) . \end{aligned} $

(27) After equating Eqs. (22) and (26) and substituting with Eq. (27), we get the following equation for the strong coupling:
$ \begin{aligned}[b] g_{YJ/\psi f_0}=&\frac{1}{m_{J/\psi}m_{Y}f_{J/\psi}f_{Y}m^2}\exp\left[\frac{m_{J/\psi}}{M_1^2} +\frac{m_{Y}}{M_2^2}\right]\\ &\times\int^{s_1^0}_{4m_c^2}\int^{s_2^{4m_c^2}}_0\rm{d}s_1\rm{d}s_2 \exp\left[-\frac{s_1}{M_1^2}-\frac{s_2}{M_2^2}\right] \rho^{\text{OPE}}(s_1,s_2). \end{aligned} $

(28) As we can see from Eq. (16), since the interpolating currents of
$ Y(4230) $ and$ J/\psi $ are located at points x and$ 0 $ , respectively, there will still be a quark element$ \left\langle {f_0(q)|[\bar{s}(0)s(0)]|0}\right\rangle $ after the$ \bar{c} $ and c quark fields are contracted. This is because$ \left\langle {f_0(q)|[\bar{s}(x)s(0)]|0}\right\rangle $ disappears and reduces to normalization factors when$ x\to 0 $ . This situation can be replaced by the kinematical limit$ q\rightarrow 0 $ , which is called soft-meson approximation [51]. Such approximation leads to the following hadronic representation:$ \Pi^{\text{h}}(p^\prime,q)=\frac{m_{J/\psi}m_{Y}f_{J/\psi}f_{Y}m^2}{(p^2-m^2)^2} g_{YJ/\psi f_0}+\cdots, $

(29) and the Borel transformation on the variable
$ p^2 $ applied to this correlation function yields$ \Pi^{\text{h}}(p^\prime,q)=m_{J/\psi}m_{Y}f_{J/\psi}f_{Y}\frac{m^2}{M^2}g_{YJ/\psi f_0} {\rm e}^{-\frac{m^2}{M^2}}+\cdots, $

(30) Following [51, 52], we apply the operator
$ \left(1-\frac{1}{M^2}\right)M^2 {\rm e}^{m^2/M^2} $

(31) on both sides of the sum rules expression to remove unsuppressed contributions to obtain
$ \begin{aligned}[b] g_{YJ/\psi f_0}=&\frac{1}{m_{J/\psi}m_{Y}f_{J/\psi}f_{Y}m^2}\left(1-\frac{1}{M^2}\right)M^2 {\rm e}^{m^2/M^2}\\ &\times\int^{s_0}_{4m_c^2}\rm{d}\hat{s}\exp\left[\frac{m_{J/\psi}}{2M^2}+\frac{m_{Y}}{2M^2}-\frac{\hat{s}}{M^2}\right] \rho^{\text{OPE}}(\hat{s}), \end{aligned} $

(32) which depends only on
$ \hat{s} $ owing to the soft-meson approximation. -
Considering
$ g_{XJ/\psi \phi} $ has a relationship to the OPE part of the correlation function, we will calculate it. Using the Wick Theorem, we can derive$ \begin{aligned}[b] \Pi_{\mu\nu}(p^\prime,q) =& {\rm i}\int {\rm d}^4x {\rm e}^{{\rm i}px}\left\langle {f_0(q)|T\{J_{\mu}^{J/\psi}(x)J_{\nu}^{Y\dagger}(0)\}|0}\right\rangle \\ =&{\rm i}\int {\rm d}^4x {\rm e}^{{\rm i}px}\frac{\varepsilon_{abc}\varepsilon_{dec}}{\sqrt{2}}\left\langle {f_0(q)|[\bar{s}^a_\alpha(0) s^d_\beta(0)]|0}\right\rangle \\ &\times[(\gamma_5)\tilde{S}^{ib}_c(x)\gamma_\mu \tilde{S}^{ie}_c(-x)\gamma_\nu\gamma_5 \\ &-(\gamma_\nu\gamma_5)\tilde{S}^{ib}_c(x)\gamma_\mu \tilde{S}^{ie}_c(-x)\gamma_5]_{\alpha\beta}. \end{aligned} $

(33) For the heavy quark propagator on the light cone, we employ its expression in terms of [53]
$ \begin{aligned}[b] S^{ab}_{c}(x)=& {\rm i}\int\frac{{\rm d}^4k}{(2\pi)^4} {\rm e}^{-{\rm i}kx} \Bigg[\frac{\delta_{ab}(\not {k}+m_c)}{k^2-m^2_c}\\&-\frac{g_sG_{ab}^{\alpha\beta}}{4}\frac{\sigma_{\alpha\beta}(\not {k}+m)+(\not {k}+m)\sigma_{\alpha\beta}}{(k^2-m^2)^2}\Bigg], \end{aligned} $

(34) where we adopt the notation
$ G_{ab}^{\mu\nu}\equiv G_i^{\mu\nu}t^i_{ab},i=1,2,\cdots,8. $

(35) Substituting the summation and the expansion
$ \begin{aligned}[b]& \bar{s}^d_\alpha(0) s^{d^\prime}_\beta(0)=\frac{1}{3}\delta_{dd^\prime}\bar{s}_\alpha(0) s_\beta(0),\\& \bar{s}_\alpha(0) s_\beta(0)\equiv\frac{1}{4}\Gamma^j_{\alpha\beta}\bar{s}(0)\Gamma^j s(0), \end{aligned} $

(36) into Eq. (33), we can obtain
$ \begin{aligned}[b] \Pi_{\mu\nu}(p^\prime,q)=&{\rm i}\int \rm{d}^4x {\rm e}^{{\rm i}px}\frac{\varepsilon_{abc}\varepsilon_{dec}\delta_{ad}}{12\sqrt{2}}\left\langle {f_0(q)|[\bar{u}(0)\Gamma^j u(0)]|0}\right\rangle \\ &\times\text{Tr}[(\gamma_5)\tilde{S}^{ib}_c(x)\gamma_\mu \tilde{S}^{ie}_c(-x)\gamma_\nu\gamma_5\\ &-(\gamma_\nu\gamma_5)\tilde{S}^{ib}_c(x)\gamma_\mu \tilde{S}^{ie}_c(-x)\gamma_5\Gamma^j]. \end{aligned} $

(37) where
$ \Gamma^j=1,\gamma_5,\gamma_\mu, {\rm i} \gamma_5\gamma_\mu,\frac{\sigma_{\mu\nu}\gamma_5}{\sqrt{2}}. $

(38) After substituting the propagator, using the particle distribution amplitudes (DAs) of
$ f_0(980) $ in Appendix V.A and contracting the color index by the SU(N) algebra,$ \varepsilon_{abc}\varepsilon_{dec}\delta_{ad}\delta_{bi}\delta_{ei}=-C_A(1-C_A)=6, $

(39) we will encounter four-dimensional integrals, for example,
$ \int\frac{{\rm d}^4k_1}{(2\pi)^4}\int\frac{{\rm d}^4k_2}{(2\pi)^4}\frac{{\rm e}^{-{\rm i}(k_1-k_2)x}g_{\mu\nu}k_1\cdot k_2}{(k_1^2-m^2_c)(k_2^2-m^2_c)}. $

(40) In Appendix V.B., we provide the main steps to calculate some four-dimensional integrals like in (40). By choosing the term proportional to
$ g_{\mu\nu} $ , we can derive$ \rho^{\text{OPE}}(\hat{s})=\frac{m_{f_0}\bar{f}_{f_0}(\hat{s}+2m_c^2)\sqrt{2\hat{s}(\hat{s}-4m_c^2)}}{24\pi^2\hat{s}}, $

(41) where
$ m_{f_0} $ and$ \bar{f}_{f_0} $ are the mass and decay constant of$ f_0(980) $ , respectively. The strong coupling is then evaluated using Eq. (32). Besides, we can derive the decay width of$ Y(4230)\to J/\psi f_0(980) $ as [54]$ \begin{aligned}[b] &\Gamma(Y(4230)\to J/\psi f_0(980))\\=&\frac{g^2_{YJ/\psi f_0}m^2_{J/\psi}}{24\pi} \lambda(m_Y,m_{J/\psi},m_{f_0})\\ &\times\left(3+\frac{2\lambda(m_Y,m_{J/\psi},m_{f_0})}{m^2_{J/\psi}}\right), \end{aligned} $

(42) where
$ \lambda(a,b,c)=\frac{\sqrt{a^4+b^4+c^4-2*(a^2b^2+b^2c^2+c^2a^2)}}{2a}. $

(43) -
In this section, we present the mass and decay constant of Y(4230), and analyze the numerical results for the decay width of
$ Y(4230) \to J/\psi f_0(980) $ . We use the following parameters for the numerical calculation. The current charm-quark mass,$ m_c=(1.275\pm 0.025) $ GeV, the$ J/\psi $ -meson mass$ m_{J/\psi}=(3096.900\pm 0.006) $ MeV and the$ f_0 $ (980) mass$ m_{f_0}=(990\pm 20) $ MeV from the Particla Data Group (PDG) [45]. The$ J/\psi $ and$ f_0 $ (980) decay constants are taken as$ f_{J/\psi} $ =$ 0.405 $ GeV [55] and$ \bar{f}_{f_0} $ =$ 0.18\pm 0.015 $ GeV [56], respectively. The current-quark-mass for the s-quark is$ m_s=93^{+11}_{-5} $ MeV from the PDG. In addition, we also need to know the values of the non-perturbative vacuum condensates. The related parameters are [15, 57, 58]$ \begin{aligned}[b] &\langle{\bar{q}q}\rangle=-(0.24\pm 0.01)^3\ \text{GeV}^3,\\ &\left\langle {\bar{s}s}\right\rangle =(0.8\pm0.1)\times \left\langle {\bar{q}q} \right\rangle ,\\ &\left\langle {\frac{\alpha_s}{\pi} GG}\right\rangle =(0.012)\ \text{GeV}^4,\\ &\left\langle {g_s\bar{s}\sigma Gs}\right\rangle =m_0^2\times\left\langle {\bar{s}s}\right\rangle ,\\ &m_0^2=0.8\ {\rm GeV}^2,\\ &m_c=1.275\pm0.025\ \text{MeV}.\\ \end{aligned} $

(44) The sum rule predictions depend on two parameters: continuum threshold
$ s_0 $ and borel mass$ M^2 $ .$ s_0 $ is correlated with the first of the excited states of$ Y(4230) $ . However, the experimental results show that there is no resonance activity associated with the states of$ Y(4230) $ . We can naturally choose$ s_0=(m_X+0.5)^2 \rm ~GeV^2 $ , because the mass gap between the ground state and the first excited state is regularly around$ 0.5 $ GeV in charmonia and bottomonia (Table 1).Masses $ c\bar{c} $ 

$ b\bar{b} $ 

M/GeV \ n n=1 n=2 n=3 n=1 n=2 n=3 $ M_{ ^{1} P_{1}}\left(h_{q}\right) $ 

3.53 3.96 4.37 9.88 10.3 10.6 $ M_{ ^{3}P_{0}}\left(\chi_{q 0}\right) $ 

3.37 3.88 4.30 9.81 10.2 10.7 $ M_{ ^{3} P_{1}}\left(\chi_{q 1}\right) $ 

3.54 3.97 4.33 9.89 10.3 10.6 $ M_{ ^{3} P_{2}}\left(\chi_{q 2}\right) $ 

3.54 3.98 4.34 9.89 10.3 10.6 Table 1. Quark model masses calculated for the first three levels of charmonia and bottomonia [59].
Additionally, Table 2 contains experimental data taken from the PDG that supports the majority of the computations in Table 1.
Masses $ c \bar{c} $ 

$ b \bar{b} $ 

$M /{\rm MeV} \backslash n$ 

$ n=1 $ 

$ n=2 $ 

$ n=3 $ 

$ n=1 $ 

$ n=2 $ 

$ n=3 $ 

$ M_{ ^1P_{1}}\left(h_{q}\right) $ 

$ 3525.38 $ 

$ - $ 

$ - $ 

$ 9899.3 $ 

$ 10259.8 $ 

$ - $ 

$ M_{ ^{3} P_{0}}\left(\chi_{q 0}\right) $ 

$ 3414.75 $ 

$ - $ 

$ - $ 

$ 9859.44 $ 

$ 10232.5 $ 

$ - $ 

$ M_{ ^3 P_{1}}\left(\chi_{q 1}\right) $ 

$ 3510.66 $ 

$ - $ 

$ - $ 

$ 9892.78 $ 

$ 10255.46 $ 

$ 10512.1 $ 

$ M_{ ^3 P_{2}}\left(\chi_{q 2}\right) $ 

$ 3556.20 $ 

$ 3922.5 $ 

$ - $ 

$ 9912.21 $ 

$ 10268.65 $ 

$ - $ 

Table 2. Masses of experimentally observed states in the Particle Data Group listings [36].
Moreover, we can refer to the QCD sum rule calculations listed in Table 3. There is a mass difference of
$ 0.4\sim 0.6 $ GeV between the 1S and 2S tetraquark states. Therefore, we adopt this mass gap and employ$ J^{P C} $ 

1 S 2 S $ \text { Mass difference } $ 

$ \text { References } $ 

$ 0^{++} $ 

$ X(3915) $ 

$ X(4500) $ 

$588~ \mathrm{MeV}$ 

[61, 62] $ 1^{++} $ 

$ X(4140) $ 

$ X(4685) $ 

566 MeV [63, 64] $ 1^{+-} $ 

$ Z_{c}(3900) $ 

$ Z_{c}(4430) $ 

$591~ \mathrm{MeV}$ 

[17, 65, 66] $ 1^{+-} $ 

$ Z_{c}(4020) $ 

$ Z_{c}(4600) $ 

$576~ \mathrm{MeV}$ 

[67, 68] Table 3. Mass difference between the 1S and 2S hidden-charm tetraquark states with the possible assignments [60].
$ \begin{array}{*{20}{l}} (4.23+0.40)^2\ \text{GeV}^2\leq s_0\leq (4.23+0.60)^2\ \text{GeV}^2. \end{array} $

(45) The borel mass
$ M^2 $ can be determined based on two principles:1. The high dimension condensates make up not more than
$ 10$ % of the total contribution to the OPE:$ \mathrm{CVG} \equiv\left|\frac{\tilde{\Pi}^{\left\langle {\bar{q}g_sGq}\right\rangle +\cdots}\left( M^{2},\infty\right)}{\tilde{\Pi}^{\rm OPE}\left(M^{2},\infty \right)}\right| \leq 10{\text{%}}, $

(46) where the ellipsis represents higher dimension contributions.
2. The pole contribution (PC) in Eq. (5) should exceed
$ 50$ %$ \text{PC}=\frac{\tilde{\Pi}^{\rm OPE}(M^2,s_0)}{\tilde{\Pi}^{\rm OPE}(M^2,\infty)}\ge 50{\text{%}} . $

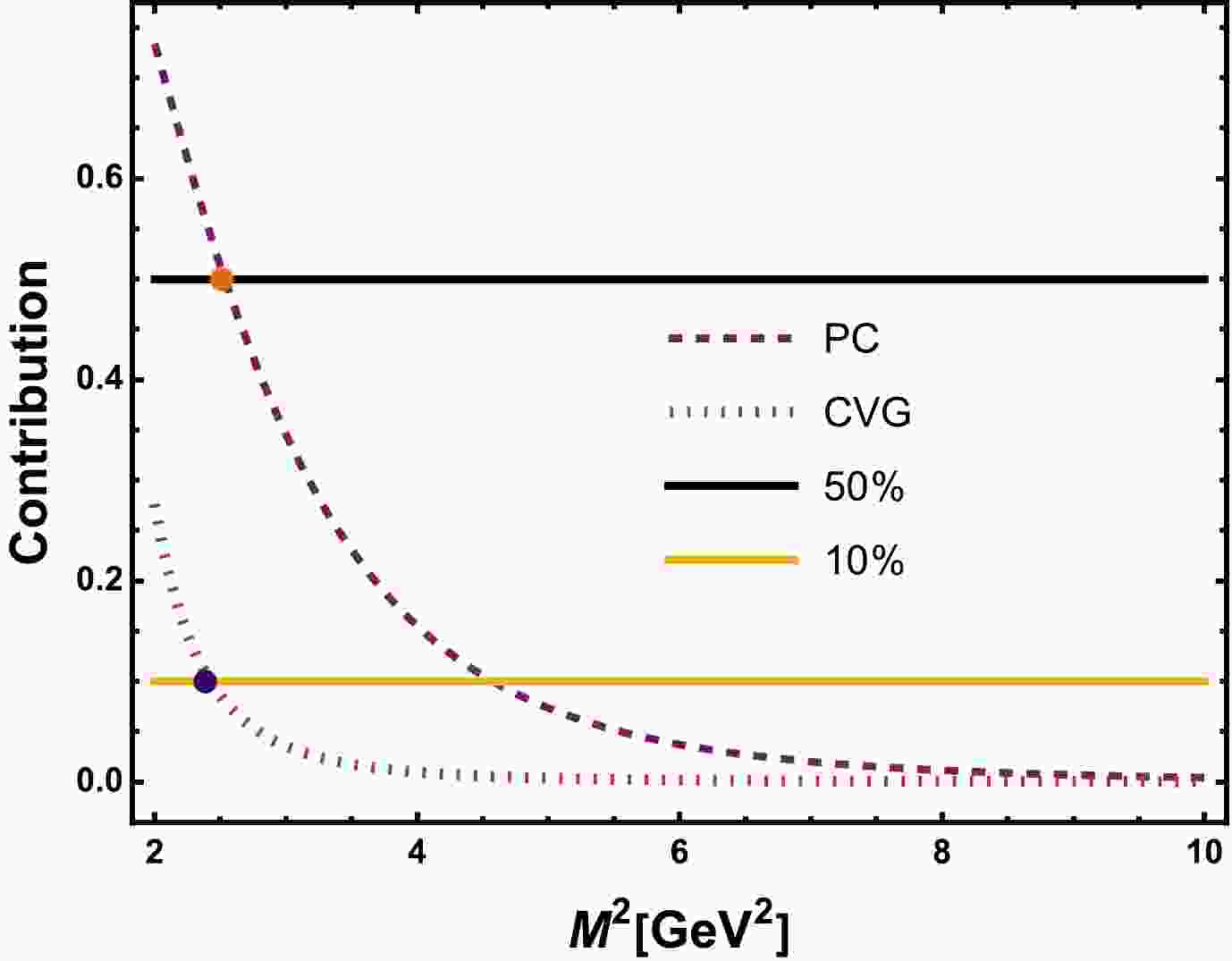
(47) As seen in Fig. 1, the red dot indicates the point at which CVG becomes
$ 50$ %, where the maximum achievable$ M^2 $ can be attained. We can select the minimum$ M^2 $ from the black dot where PC converges with$ 10$ %. Therefore, we require the region of$ M^2 $ to be$ \begin{array}{*{20}{l}} 2.39\ \text{GeV}^2\leq M^2\leq 2.51\ \text{GeV}^2, \end{array} $

(48) -
The outcomes of the mass
$ m_Y $ and the decay constant$ f_Y $ as functions of the parameters$ M2 $ are shown in Fig. 2. The orange shape in the first picture of Fig. 2 corresponds to the measurements taken by the Belle collaboration [6]. The other curves show our prediction at a fixed$s_0\in\{(4.23+0.40)^2,~(4.23+0.50)^2,~(4.23+0.60)^2\}$ . Our prediction is consistent with the measurement. At a fixed point of$M^2=2.45 ~\rm GeV^2$ , our result for the mass reads
Figure 2. (color online) Mass [first] and decay constant of
$ Y(4230) $ [second] as a function of the Borel parameter$ M^2 $ at different fixed values of$ s_0 $ .$ \begin{array}{*{20}{l}} \quad m_Y=4.22^{+0.08}_{-0.07}\ \text{GeV}. \end{array} $

(49) Our mass prediction shows that the generalization of our method is valid. We then extend the method to evaluate the decay constant of
$ Y(4230) $ . The result at the same typical point reads$ \begin{array}{*{20}{l}} f_Y=(0.0568\pm0.003)\ \text{GeV}^4. \end{array} $

(50) The mass and decay constant are input parameters to calculate the decay width of ψ(4230)
$ \to J/\psi f_0(980) $ .The ψ(4230) branching ratios from PDG [45] show that
$ \frac{\Gamma(J/\psi f_0(980),f_0(980)\to \pi^+\pi^-)}{\Gamma(J/\psi\pi^+\pi^-)}=0.17\pm0.13. $

(51) We can estimate the upper limit of
$ \Gamma(J/\psi f_0(980) $ ,$ f_0(980)\to \pi^+\pi^-) $ by assuming that$ \psi\to J/\psi\pi^+\pi^- $ is the only decay process of$ \psi(4230) $ . With the width of$ \Gamma_{\psi}=76.6\pm14.2\pm2.4 $ MeV, we can obtain$ \begin{array}{*{20}{l}} &\Gamma(\psi\to J/\psi f_0(980),f_0(980)\to \pi^+\pi^-)=\\ &\Gamma(\psi\to J/\psi f_0(980))\mathcal{B}(f_0(980)\to \pi^+\pi^-)<13.022\ \text{MeV}. \end{array} $

(52) Also, from the PDG, the
$ f_0 $ (980) branching ratios give$ \frac{\Gamma(\pi\pi)}{(\Gamma(\pi\pi)+\Gamma(K\bar{K}))}=0.75^{+0.11}_{-0.13}, $

(53) and the partial width gives
$ P(f_0(980)\to \gamma\gamma)\equiv\frac{\Gamma(f_0(980)\to \gamma\gamma)}{\Gamma(f_0(980))}=0.31^{+0.05}_{-0.04}. $

(54) $ f_0(980)\to \pi\pi $ ,$ f_0(980)\to K\bar{K} $ , and$f_0(980)\to \gamma\gamma$ are the main decay processes of$ f_0 $ (980). From Eq. (54), we obtain the partial width$P(f_0(980)\to\Gamma(\pi\pi)+\Gamma(K\bar{K}))= 0.69^{+0.04}_{-0.05}$ . So, we estimate$ \begin{aligned}[b] &\mathcal{B}(f_0(980)\to \pi^+\pi^-)\\ \approx&0.75^{+0.11}_{-0.13} \times P(f_0(980)\to\Gamma(\pi\pi)+\Gamma(K\bar{K}))\approx0.52. \end{aligned} $

(55) Then, we can finally conclude that
$ \begin{array}{*{20}{l}} \Gamma(\psi \to J/\psi f_0(980))<25.0\ \text{MeV}. \end{array} $

(56) As shown in Fig. 4, the blue, green, and black curves show a clear dependence of our prediction on
$ s_0 $ and$ M^2 $ . For$ M^2 $ and$ s_0 $ , we use the same values as in the mass analysis. The results are shown in Fig. 3 and Fig. 4. By choosing appropriate parameters, our prediction for$ g_{YJ/\psi f_0} $ is
Figure 4. (color online) Strong coupling
$ g_{YJ/\psi f_0(980)} $ as a function of the Borel parameter$ M^2 $ at different fixed values of$ s_0 $ .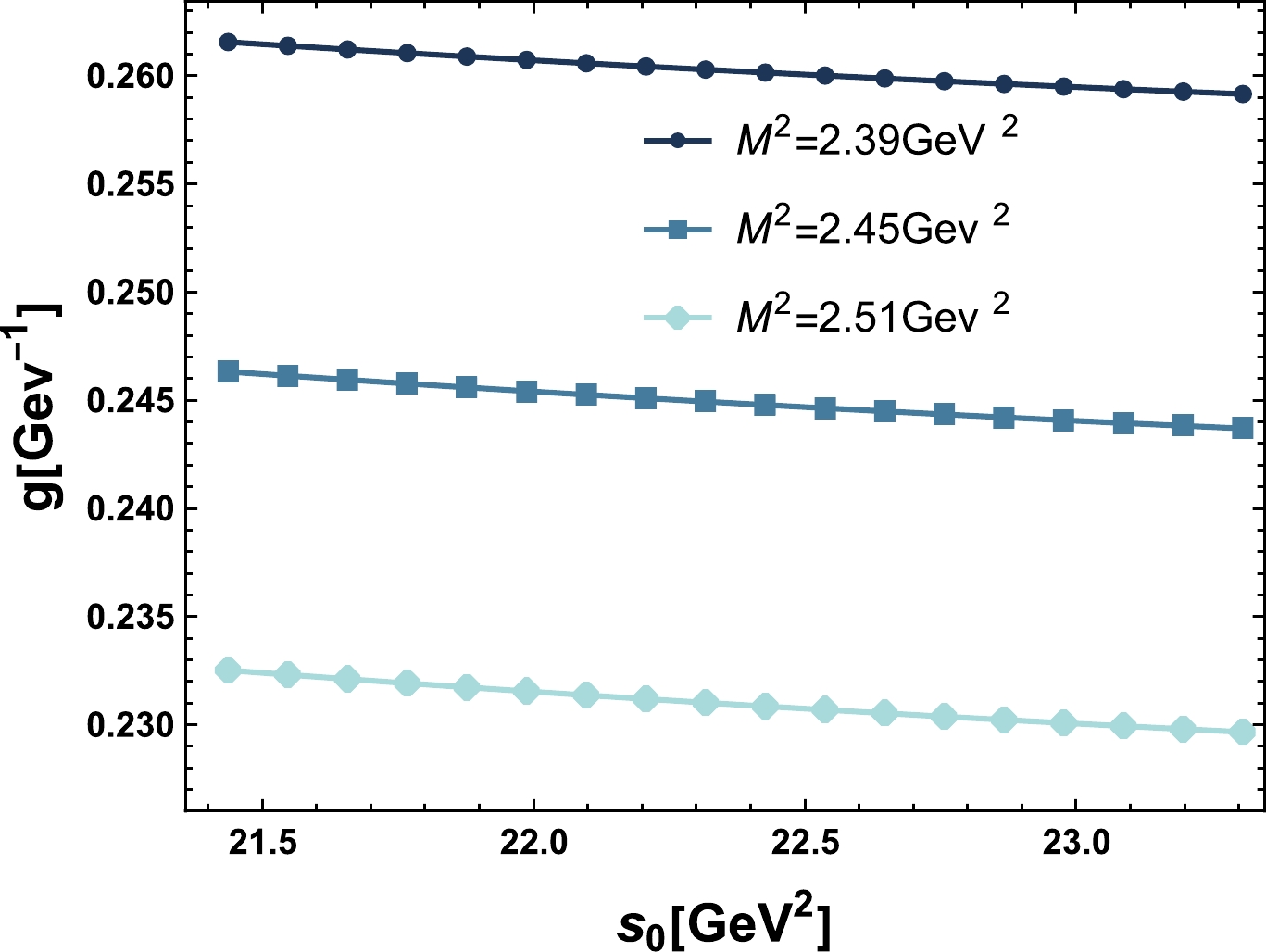
Figure 3. (color online) Strong coupling
$ g_{YJ/\psi f_0(980)} $ as a function of the threshold parameter$ s_0 $ at different fixed values of$ M^2 $ .$ \begin{array}{*{20}{l}} g_{YJ/\psi f_0}=(0.245\pm 0.01)\ \text{GeV}^{-1}. \end{array} $

(57) Taking the average result of
$ g_{YJ/\psi f_0} $ , the width of this decay can be obtained using Eq. (32):$ \begin{array}{*{20}{l}} \Gamma(Y \rightarrow J/\psi f_0(980))=(1.28\pm 0.1)\ \text{MeV}, \end{array} $

(58) which is less than the upper limit of the ψ(4230)
$ \to J/\psi f_0(980) $ decay width. Combining this result with the predicted mass result, we may conclude that Y(4230) could be a tetraquark state. However, owing to the lack of experimental data for the ψ(4230)$ \to J/\psi f_0(980) $ decay width, we still need further experiments to determine whether Y(4230) is a tetraquark state or not. -
In this research, we designate Y(4230) as a vector tetraquark state to concurrently analyze
$ Y(4230) $ 's mass, decay constant, and decay into$ J/\psi f_0(980) $ . The mass of$ Y(4230) $ is evaluated through a different calculation technique developed in two-point sum rules, and the result is in agreement with the mass of$ Y(4230) $ in PDG. Then, we extend the technique to calculate the decay constant of$ Y(4230) $ . Using the light cone sum rules method, we calculate the coupling constant$ g_{YJ/\psi f_0} $ and discover the result for the$ Y\to J/\psi f_0(980) $ decay width. Then, we assume that$ J/\psi\pi\pi $ is the most significant channel, overwhelming all the other channels. Therefore, we can consider the width of$ \psi(4230) $ as the width of$ J/\psi \pi\pi $ . Since we know the branching ratios of$\Gamma(J/\psi f_0(980), f_0(980)\to \pi^+\pi^-)/\Gamma(J/\psi\pi^+\pi^-)$ from PDG, we can estimate the upper limit of the$ J/\psi f_0 $ channel. The decay width of$ Y\to J/\psi f_0(980) $ is less than the upper limit. Our prediction of the mass of$ Y(4230) $ is in agreement with that of$ Y(4230) $ in PDG, and the decay width of$Y(4230)\to J/\psi f_0(980)$ does not exceed its theoretical limits. There is a possibility that Y(4230) could be a tetraquark. In the future, experiments will be more helpful in determining whether or not this structure of$ Y(4230) $ is appropriate. -
The matrix elements of the
$ f_0 $ can be expanded in terms of the corresponding distribution amplitudes. Below, we provide expressions for$ \left\langle {f_0(980)(q)|\bar{d}(x)\Gamma^au(0)|0}\right\rangle $ [56]:$ \begin{aligned}[b] &\left\langle {f_0(q)|\bar{s}(x)\gamma_\mu s(0)|0}\right\rangle =\bar{f}_{f_0}q_\mu\int_0^1 {\rm d} u {\rm e}^{{\rm i}uq\cdot x}\Phi_{f_0}(u),\\ &\left\langle {f_0(q)|\bar{s}(x)s(0)|0}\right\rangle =m_{f_0}\bar{f}_{f_0}\int_0^1{\rm d} u {\rm e}^{{\rm i}uq\cdot x}\Phi_{f_0}^s(u),\\ &\left\langle {f_0(q)|\bar{s}(x)\sigma_{\mu\nu} s(0)|0}\right\rangle \\ =&-\frac{m_{f_0}}{6}\bar{f}_{f_0}(q_\mu x_\nu-q_\nu x_\mu)\int_0^1{\rm d} u{\rm e}^{{\rm i}uq\cdot x}\Phi_{f_0}^\sigma(u), \end{aligned}\tag{A1} $

where the LCDA
$ \Phi_{f_0} $ represents twist-2 light-cone distribution amplitudes of$ f_0(980) $ , and the other two are twist-3 distribution amplitudes. Meanwhile, we use the following normalization$ \int_0^1{\rm d}u\Phi_{f_0}(u)=0,\int_0^1{\rm d}u\Phi_{f_0}^s(u)=1,\int_0^1{\rm d}u\Phi_{f_0}^\sigma(u)=1. \tag{A2} $

-
When calculating the OPE part of the correlation function, we encountered various four-dimensional integrals in the momentum spaces. Before performing the integration, it is common to use the Feynman's parametric integral formula:
$ \begin{aligned}[b] \frac{1}{A_1^{a_1}\cdot\cdot\cdot A^{a_n}_n}=&\frac{\Gamma(a_1\cdot\cdot\cdot a_n)}{\Gamma(a_1)\cdot\cdot\cdot\Gamma(a_n)}\int_0^1{\rm d}x_1\cdot\cdot\cdot\int_0^1{\rm d}x_n\\ & \times \frac{\delta(1-x_1+\cdot\cdot\cdot+x_n)x_1^{a_1-1}\cdot x_2^{a_2-1}\cdot\cdot\cdot x_n^{a_n-1}}{(x_1A_1+\cdot\cdot\cdot+x_nA_n)^{a_1+\cdot\cdot\cdot a_n}}. \end{aligned}\tag{B1} $

In general, Feynman integrals contain
$ I(D;a,q)=\int\frac{{\rm d}^Dp}{(2\pi)^D}\frac{1}{(p^2+2pq+m^2)^a}. \tag{B2} $

This integral can be reduced to
$ \begin{aligned}[b] I(D;a,q)&=\int\frac{{\rm d}^Dp}{(2\pi)^D}\frac{1}{(p^2+2pq+m^2)^a}\\ &=\frac{1}{(4\pi)^{D/2}}\frac{\Gamma(a-D/2)}{\Gamma(a)}(m^2-q^2)^{D/2-a}. \end{aligned}\tag{B3} $

To obtain a formula in proportion to
$ p_\mu $ such as$ \begin{aligned}[b] I(D;a,q)&=\int\frac{{\rm d}^Dp}{(2\pi)^D}\frac{p_\mu}{(p^2+2pq+m^2)^a}\\ &=\frac{1}{(4\pi)^{D/2}}\frac{\Gamma(a-D/2)}{\Gamma(a)}\frac{q_\mu}{(m^2-q^2)^{-D/2+a}}, \end{aligned}\tag{B4} $

we can differentiate equation Eq. (62) with momentum q one time. The higher tensors
$ p_\mu\cdots p_\nu $ in the integrand come form higher differentiations. Now, when the above equation encounters a pole in the Gamma function, where dimension$ D\to 4 $ , i.e.,$ \Gamma(0)\to\infty $ , we can use the equation$ \frac{\Gamma(n-\frac{1}{2}d)}{a^{2n-d}}=\int_0^\infty {\rm d}\lambda\lambda^{n-d/2-1} {\rm e}^{-\lambda a^2} \tag{B5} $

to eliminate the Gamma function and perform the replacement
$ \int_0^\infty \frac{{\rm d}\lambda}{\lambda^n} {\rm e}^{-\lambda K}\to(-1)^n\frac{K^{n-1} ln K}{(n-1)!}. \tag{B6} $

To obtain the final expression of the correlation function, we need the imaginary part of the results and the integration over the Feynman parameters.
-
Here, we present the calculation details of the integral. When dealing with Eq. (7), we need to consider a general integral
$ I(p^2)=\int {\rm d}^4x {\rm e}^{{\rm i}px} \frac{1}{(x^2)^n} \frac{K_i(m_1\sqrt{-x^2})}{(\sqrt{-x^2})^i}\frac{K_j(m_2\sqrt{-x^2})}{(\sqrt{-x^2})^j}. \tag{C1} $

Using the integral representation of the Bessel function
$ \frac{K_i(m_1\sqrt{-x^2})}{(\sqrt{-x^2})^i}=\int_0^\infty\frac{{\rm d}t}{t^{i+1}}\exp{\left[-\frac{m_1}{2}\left(t-\frac{x^2}{t}\right)\right]}, \tag{C2} $

we have
$ \begin{aligned}[b] I=&\frac{1}{4}\int {\rm d}^4x {\rm e}^{{\rm i}px}\frac{1}{(x^2)^n}\int_0^\infty\frac{{\rm d}t_1}{t_1^{i+1}}\exp{\left[-\frac{m_1}{2}\left(t_1-\frac{x^2}{t_1} \right) \right]}\\ &\times\int_0^\infty\frac{{\rm d}t_2}{t_2^{j+1}}\exp{\left[-\frac{m_2}{2}\left(t_2-\frac{x^2}{t_2} \right) \right]}\\ =&\frac{{\rm i}(-1)^n}{4\Gamma(n)}\int {\rm d}^4x {\rm e}^{{\rm i}px}\int_0^\infty {\rm d}\lambda \lambda^{n-1} \exp(-\lambda x^2 )\int_0^\infty\frac{{\rm d}t_1}{t_1^{i+1}}\\ &\times\exp{\left[-\frac{m_1}{2}\left(t_1+\frac{x^2}{t_1} \right) \right]} \int_0^\infty\frac{{\rm d}t_2}{t_2^{j+1}}\exp{\left[-\frac{m_2}{2}\left(t_2+\frac{x^2}{t_2} \right) \right]}. \end{aligned}\tag{C3} $

Introducing new variables
$ \begin{equation} a=\frac{2m_1}{t_1},\ b=\frac{2m_2}{t_2} \to dt_1 =-\frac{2m_1}{a^2}da,\ dt_2 =-\frac{2m_2}{b^2}db, \end{equation}\tag{C4} $

leads to the equation
$ \begin{aligned}[b] I=&\frac{(-1)^n {\rm i}}{4 \Gamma(n)}\frac{1}{(2m_1)^{i}(2m_2)^j} \int_0^\infty {\rm d} a\ a^{i-1} \int_0^\infty {\rm d} b\ b^{j-1} \int_0^\infty {\rm d} \lambda \lambda^{n-1}\\ &\times\exp\left[ -\left(\frac{m_1^2}{a}+\frac{m_2^2}{b} \right) \right] \int {\rm d}^4x \ \exp{\left[-\frac{1}{4}(a+b+4\lambda)x^2-{\rm i} px \right]}\\ =&\frac{(-1)^n {\rm i}}{4 \Gamma(n)}\frac{16\pi^2}{(2m_1)^{i}(2m_2)^j} \int_0^\infty {\rm d} a \int_0^\infty {\rm d} b\ a^{i-1} b^{j-1} \int_0^\infty {\rm d} \lambda \lambda^{n-1}\\ &\times\frac{1}{(a+b+4\lambda)^2} \exp\left[ \frac{-p^2}{(a+b+4\lambda)} \right] \exp\left[ -\left(\frac{m_1^2}{a}+\frac{m_2^2}{b} \right) \right]. \end{aligned}\tag{C5} $

Then, substituting
$ a\to4a $ ,$ b\to4b $ , we obtain$ \begin{aligned}[b] I=&\frac{(-1)^n{\rm i} }{\Gamma(n)}\frac{2^{i+j-2}\pi^2}{(m_1)^{i}(m_2)^j} \int_0^\infty {\rm d} a \int_0^\infty {\rm d}b\ a^{i-1} b^{j-1} \int_0^\infty {\rm d}\lambda \lambda^{n-1}\\ &\times \frac{1}{(a+b+\lambda)^2} \exp\left[ \frac{-p^2}{4(a+b+\lambda)} \right] \exp\left[ -\left(\frac{m_1^2}{4a}+\frac{m_2^2}{4b} \right) \right]. \end{aligned}\tag{C6} $

Now, we introduce the variables ρ, x, and y, defined by
$ \rho=(a+b+\lambda), ~ x=\frac{a}{a+b+\lambda}, ~ y=\frac{b}{a+b+\lambda}. \tag{C7} $

Then, we have
$ \begin{aligned}[b] \rm{d}\lambda\rm{d}a\rm{d}b&= \begin{vmatrix} \dfrac{\partial\lambda}{\partial\rho} & \dfrac{\partial a}{\partial x} &\dfrac{\partial b}{\partial y} \\ \dfrac{\partial\lambda}{\partial\rho} & \dfrac{\partial a}{\partial x} &\dfrac{\partial b}{\partial y}\\ \dfrac{\partial\lambda}{\partial\rho} & \dfrac{\partial a}{\partial x} &\dfrac{\partial b}{\partial y} \end{vmatrix} \rm{d}\rho\rm{d}x\rm{d}y\\ &=\rho^2 \rm{d}\rho\rm{d}x\rm{d}y, \end{aligned}\tag{C8} $

which leads to
$ \begin{aligned}[b] I=&\frac{(-1)^n {\rm i}}{\Gamma(n)}\frac{2^{i+j-2}\pi^2}{(m_1)^{i}(m_2)^j} \int {\rm d} u\varphi(u)\int_0^\infty {\rm d} \rho\int_0^1 {\rm d} x\int_0^1 {\rm d} y(\rho x)^{i-1} \\ &\times (\rho y)^{j-1}(\rho(1-x-y))^{n-1}\exp\left[ \frac{-p^2}{4\rho} \right] \exp\left[ -\left(\frac{m_1^2}{4\rho x}+\frac{m_2^2}{4\rho y} \right) \right]. \end{aligned}\tag{C9} $

Applying the double Borel transformations with respect to
$ -p^2\to M^2 $ , we obtain$ \begin{aligned}[b] \tilde{I}(M^2)=&\frac{(-1)^n {\rm i}}{\Gamma(n)}\frac{2^{i+j-2}\pi^2}{(m_1)^{i}(m_2)^j} \int_0^\infty {\rm d}\rho\int_0^1 {\rm d}x \int_0^1 {\rm d}y (\rho x)^{i-1}\\ &\times (\rho y)^{j-1} (\rho(1-x-y))^{n-1}\delta\left(\frac{1}{M^2}-\frac{1}{4\rho}\right)\\&\times\exp\left[ -\left(\frac{m_1^2}{4\rho x}+\frac{m_2^2}{4\rho y} \right) \right]\\ &=\frac{(-1)^{n}{\rm i}}{\Gamma(n)}\frac{2^{2-2n-i-j}\pi^2}{(m_1)^{i}(m_2)^j}(M^2)^{i+j+n-1}\int_0^1 {\rm d}x \int_0^1 {\rm d}y \\ &\times x^{i-1} y^{j-1} (1-x-y)^{n-1}\exp\left[ -\left(\frac{m_1^2}{M^2x}+\frac{m_2^2}{M^2 y} \right) \right], \end{aligned}\tag{C10} $

where
$ \rho_0=\dfrac{M^2}{4} $ .Introducing new variables,
$ \sigma_i=\dfrac{1}{M_i^2} $ , we have$ \begin{aligned}[b] \tilde{I}(\sigma) =&\frac{(-1)^{n}{\rm i}}{\Gamma(n)}\frac{2^{2-2n-i-j}\pi^2}{(m_1)^{i}(m_2)^j}\frac{1}{\sigma^{i+j+n-1}}\int_0^1 {\rm d}x \int_0^1 {\rm d}y \\ &\times x^{i-1} y^{j-1} (1-x-y)^{n-1} \exp\left[ -\left(\frac{m_1^2}{x}+\frac{m_2^2}{y} \right)\sigma \right]\\ =&\frac{C}{\Gamma(i+j+n-1)}\int_0^1 {\rm d} x \int_0^1 {\rm d} y x^{i-1} y^{j-1} (1-x-y)^{n-1} \end{aligned} $

$ \begin{aligned}[b] &\times \exp\left[ -\left(\frac{m_1^2}{x}+\frac{m_2^2}{y} \right)\sigma\right]\int_0^\infty \rm{d}z\exp[-z\sigma]z^{i+j+n-2}\\ =&\frac{C}{\Gamma(i+j+n-1)}\int_0^1 {\rm d}x \int_0^1 {\rm d}y x^{i-1} y^{j-1} (1-x-y)^{n-1}\\ &\times \int_0^\infty \rm{d}z\exp\left[-\left(z+\frac{m_1^2}{x}+\frac{m_2^2}{y} \right)\sigma\right]z^{i+j+n-2}. \end{aligned}\tag{C11} $

Here,
$C=\dfrac{(-1)^{n}{\rm i}}{\Gamma(n)}\dfrac{2^{2-2n-i-j}\pi^2}{(m_1)^{i}(m_2)^j}$ . Applying the double Borel transformation with respect to$ \sigma\to \dfrac{1}{s} $ , we obtain the spectral density:$ \begin{aligned}[b] \rho(s) =&\frac{C}{\Gamma(i+j+n-1)}\int_0^1 {\rm d}x \int_0^1 {\rm d}y x^{i-1} y^{j-1} (1-x-y)^{n-1}\\ &\times \int_0^\infty \rm{d}z\delta\left[s-\left(z+\frac{m_1^2}{x}+\frac{m_2^2}{y} \right)\right]z^{i+j+n-2}\\= &\frac{C}{\Gamma(i+j+n-1)}\int_0^1 {\rm d}x \int_0^1 {\rm d}y x^{i-1} y^{j-1} (1-x-y)^{n-1}\\ &\times \left(s-\frac{m_1^2}{x}-\frac{m_2^2}{y}\right)^{i+j+n-2}\theta\left(s-\frac{m_1^2}{x}-\frac{m_2^2}{y}\right). \end{aligned}\tag{C12} $

Similarly, we also need to consider the integral
$ \begin{aligned}[b] I=&\int {\rm d}^4x {\rm e}^{{\rm i}px} \frac{x^\mu x^\nu}{(x^2)^n} \frac{K_i(m_1\sqrt{-x^2})}{(\sqrt{-x^2})^i}\frac{K_j(m_2\sqrt{-x^2})}{(\sqrt{-x^2})^j}\\ =&-\partial_\mu^{(p)}\partial_\nu^{(p)}\int {\rm d}^4x {\rm e}^{{\rm i}px} \frac{1}{(x^2)^n} \frac{K_i(m_1\sqrt{-x^2})}{(\sqrt{-x^2})^i}\frac{K_j(m_2\sqrt{-x^2})}{(\sqrt{-x^2})^j}, \end{aligned}\tag{C13} $

and the derived spectral density
$ \begin{aligned}[b] \rho(s) =&\frac{C_1}{\Gamma(i+j+n+1)}\int_0^1 {\rm d} x \int_0^1 {\rm d} y x^{i-1} y^{j-1} (1-x-y)^{n-1}\\ &\times \left(s-\frac{m_1^2}{x}-\frac{m_2^2}{y}\right)^{i+j+n}\theta\left(s-\frac{m_1^2}{x}-\frac{m_2^2}{y}\right)p_\mu p_\nu\\ &+\frac{C_2}{\Gamma(i+j+n)}\int_0^1 {\rm d}x \int_0^1 {\rm d} y x^{i-1} y^{j-1} (1-x-y)^{n-1}\\ &\times \left(s-\frac{m_1^2}{x}+\frac{m_2^2}{y}\right)^{i+j+n-1}\theta\left(s-\frac{m_1^2}{x}-\frac{m_2^2}{y}\right)g_{\mu\nu}, \end{aligned}\tag{C14} $

where
$C_1=\dfrac{(-1)^{n+1}{\rm i}}{\Gamma(n)}\dfrac{2^{4-2n-i-j}\pi^2}{(m_1)^{i}(m_2)^j}$ and$C_2=\dfrac{(-1)^{n+2}{\rm i}}{\Gamma(n)}\dfrac{2^{3-2n-i-j}\pi^2}{(m_1)^{i}(m_2)^j}$ .
Strong decay of $ { \boldsymbol Y({\bf{4230}}){\bf\to}\boldsymbol J/\boldsymbol\psi \boldsymbol f_{\bf 0}({\bf{980}}) }$ in light cone sum rules
- Received Date: 2023-09-17
- Available Online: 2024-02-15
Abstract: In this study, we assign the tetraquark state for the







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: