-
The covariant conservation law of the energy-momentum tensor plays a critical role within Einstein’s framework of general relativity (GR). P. Rastall introduced a theory that posits potential modifications to GR, incorporating a proportionality constant denoted as κ. This constant establishes a linkage between the Einstein and energy-momentum tensors, leading to a transformation of Einstein's field equation to
$ G_{\mu\nu}+\kappa {\lambda} g_{\mu\nu}R =\kappa T_{\mu\nu} $ [1]. Recently, scholarly attention has increasingly focused on exploring Rastall’s theory. Notably, static and spherically symmetric solutions within Rastall gravity have been employed to describe neutron stars, imposing more stringent constraints on deviations from GR as posited by Rastall [2]. Rastall’s theory has revealed a new category of black hole solutions, encompassing both uncharged and charged Kiselev-like black holes [3]. Moreover, Moradpour and colleagues initiated an investigation into traversable wormholes conforming to Rastall’s theory. Their inquiry involved exact solutions with baryonic matter states, revealing the pronounced impact of the theory on wormhole characteristics, intricately tied to Rastall's dimensionless parameter and initial conditions [4]. Additionally, Kumar and co-researchers extended upon the Kerr-Newman black hole solution within the context of Rastall gravity. This extension facilitated the analysis of thermodynamic attributes of rotating Rastall black holes and investigation of the interplay between particle motion and effective potentials [5]. These studies collectively underscore the growing intrigue surrounding the ramifications of Rastall gravity. However, a research gap persists regarding the observable attributes of astrophysical systems as dictated by Rastall's theory. Addressing this gap, we investigated the discernible properties of an accretion disk encircling a black hole enshrouded by a perfect fluid within the ambit of Rastall gravity.The potential displacement of Einstein’s theory by Rastall's theory has sparked an enduring confluence of contention and discourse within the domain of gravitational physics. Investigations led by Visser have proposed a perspective wherein, in a majority of instances, Rastall gravity can be interpreted as a meticulous rearrangement of the matter facet within the confines of the Einstein gravity framework, thereby implying a certain interchangeability of these two gravitational constructs [6]. Therefore, Visser’s analysis sheds light on the potential analogies and correlations that underlie these two theories. By orchestrating this reconfiguration of the matter domain, Rastall gravity introduces an alternate lens through which to perceive the intrinsic nature of gravitational interplays. This divergence of viewpoints poses a challenge to the conventional comprehension of Einstein’s theory and its foundational presumptions. By contrast, Darabi and collaborators posit an alternative narrative, asserting that Rastall gravity represents an “open” paradigm distinct from the tenets of Einstein gravity [7]. This perspective emphasizes a clear demarcation between these two theoretical frameworks. Their perspective accentuates the distinctive attributes inherent to Rastall gravity in contrast to Einstein gravity. According to their portrayal, Rastall gravity introduces novel constituents and characteristics that sets it apart from the well-established edifice of Einstein’s theory. Owing to the “open” character of Rastall gravity, a prospect emerges for a novel physical phenomena, thereby calling for further exploration and scrutiny. Consequently, considerable scholarly endeavor has been channeled into determining the potential equivalence of these two theories [8–12].
The existence of accretion disks surrounding black holes is a well-substantiated phenomenon supported by a wealth of empirical evidence. A significant milestone was reached with the accomplishments of the Event Horizon Telescope (EHT), which provided unparalleled insights into black hole structures. Notably, the iconic depiction of a supermassive black hole within the Messier 87* (M87*) galaxy captured a photon ring of luminosity surrounding the black hole, enveloped by an accretion disk [13]. This phenomenon is mirrored by the supermassive black hole Sagittarius A* (Sgr A*) situated at the core of the Milky Way Galaxy, where the existence of an accretion disk in the vicinity of a black hole has been observed [14]. The inception of accretion disk models traces back to the 1970s, notably exemplified by the Shakura-Sunyaev model, which portrays a geometrically thin, optically thick disk characterized by its optical attributes and thickness [15]. Expanding on this foundation, Luminet employed a semi-analytical approach to explore the primary and secondary images of an accretion disk around a Schwarzschild black hole [16]. Laor proposed a formulation for calculating line profiles emitted from accretion disks around rotating black holes, highlighting the preponderance of a flux emanating from the disk’s inner realm and manifesting as a blue shift in the line peak [17]. The depiction of accretion disks in various modified gravity contexts of black holes has prompted extensive scholarly inquiries [18–22]. Delving into Rastall's theoretical framework to understand black holes enriches the comprehension of this alternative gravitational paradigm. Guo and colleagues, in particular, have undertaken a systematic exploration of the photon ring and slim accretion disk properties in charged black holes within Rastall gravity [23, 24]. Their findings underscore the intricate relationship between accretion morphology, accretion disk positioning, and optical manifestations of black holes.
Galaxies are widely acknowledged to comprise two distinct constituents: stellar and dark matter components. The stellar segment is effectively described through a perfect fluid model, a characterization driven by minimal stickiness, negligible shear stresses, and perceptible visibility [25]. Correspondingly, a model describing dark matter as a perfect fluid has emerged in recent years, introduced by Rahaman and colleagues. This model portrays dark matter as a non-sticky, non-shear stressed, and inherently non-visible perfect fluid [26]. Consequently, in the investigation of galaxies within the context of Rastall gravity, the comprehensive adoption of a perfect fluid representation for the entire galactic matter emerges as a suitable methodology. This approach not only aligns with the inherent attributes of the constituent components but also serves as a pivotal strategy in determining and constricting the gravitational parameters pertinent to Rastall’s theory through astronomical observations.
The exploration of accretion disk properties around black holes is crucial for deepening our comprehension of the fundamental physical mechanisms governing these intricate systems. The present study aims to advance our comprehension by investigating the observable attributes of thin accretion disks within the paradigm of Rastall gravity. Our objective is to elucidate the distinctive impact on the observable properties of accretion structures that arises from modifications to the geometric characteristics of spacetime within the Rastall gravity paradigm. This paper is organized as follows. Section II is focused on the accretion disk of a black hole enveloped by a perfect fluid within Rastall's theoretical framework. The trajectory of the black hole accretion disk enveloped by a radiation fluid was successfully simulated using a numerical integration method. This allowed us to obtain both the primary and secondary images of the observed radiant flux. Furthermore, we conducted a fitting analysis to establish the relationship between the parameters of the black hole and the characteristics of the most stable circular orbit and photon ring. In Section III, we constrained the parameters in Rastall’s gravitational theory by utilizing observational data from 118 strong gravitational lens systems in galaxies, thereby determining the range of values for
$ \kappa \lambda $ . Conclusions and discussions are presented in Section IV. -
The metric of perfect fluid envelopment in Rastall's theory is given by [3]
$ {\rm{d}}s^{2}=-f(r){\rm{d}}t^{2}+\frac{1}{f(r)}{\rm{d}}r^{2}+r^{2}{\rm{d}}\theta^{2}+r^{2}\sin^{2}\theta {\rm{d}}\phi^{2}, $

(1) where
$ f(r) $ represents the metric of a black hole, and its specific form is$ f(r)=1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}-\frac{N_{\rm{r}}}{r^{\xi}}, $

(2) where M is the black hole mass, Q is the black hole charge, and
$N_{\rm r}$ is the radiation field parameter. Moreover,$ \xi \equiv \dfrac{1+3\omega-6\kappa\lambda(1+\omega)}{1-3\kappa\lambda(1+\omega)} $ , where λ is the Rastall parameter, κ is the Rastall gravitational coupling constant, and ω is the equation of state parameter.In our examination, we utilize the Novikov-Thorne model for thin accretion disks to analyze the presence of such a disk encircling the black hole. A comprehensive explanation of this model is available in [16]. For an observer situated at a certain distance, the cumulative alteration of the ray bending angle, leading to subsequent outcomes, is
$ \psi (u) = \int_{u_{\rm{source}}}^{u_{\rm{obs}}}\frac{{\rm{d}}u}{\Omega(u)}=\int_{u_{\rm{source}}}^{u_{\rm{obs}}}\frac{{\rm{d}}u}{\sqrt{\dfrac{1}{b^{2}}-u^{2}f(u)}}, $

(3) where u is a parameter defined as
$ u \equiv \dfrac{1}{r} $ . The integration limits are associated with the photon’s emission point denoted as$ u_{\rm{source}} $ and observer’s position denoted as$ u_{\rm{obs}} $ . In cases where specific ray impact parameters surpass a critical threshold, a radial inflection point denoted as$ u_{0} $ could be evident. Under such circumstances, photon movement can be segregated into two distinct segments: from$ u_{0} $ to$ u_{\rm{source}} $ and from$ u_{\rm{obs}} $ to$ u_{0} $ . The value of the radial inflection point is determined as$ u_{0}=\dfrac{1}{b^{2}f(r)} $ within these segments. To replicate the primary and secondary images of the black hole, numerical integration techniques are employed. The trajectories of photons are calculated using the following integration formula:$ \int_{u_{\rm{source}}}^{u_{\rm{obs}}}\frac{{\rm{d}}u}{\sqrt{\dfrac{1}{b^{2}}-u^{2}f(u)}}=n \pi-\arccos{\frac{\sin{\eta}\tan{\theta_{0}}}{\sqrt{\sin^{2}\eta\tan^{2}\theta_{0}+1}}}. $

(4) Here, we denote the impact parameter as b, the celestial angle as η, and the observer tilt angle as
$ \theta_{0} $ . The parameter n corresponds to the image order, with$ n=0 $ and$ n=1 $ representing the direct and secondary images, respectively. In this equation, the observer’s inclination can be directly determined, allowing the photon trajectory to depend on the impact parameter b, distance r of the orbit from the black hole, and azimuthal angle η. When examining a specific orbit, r can be directly set, thus converting the equation into a relationship between b and η that also includes parameters from the metric (considered as constants). This equation enables a clear observation of how changes in parameters can lead to alterations in the spacetime geometry, ultimately affecting the appearance of the accretion disk. Direct integration to solve for u poses certain challenges; however, by setting η within the range of 0 to$ 2 \pi $ , a root-finding approach can be employed to determine the corresponding value of b, thereby yielding the observed orbital imagery.This study was focused on the optical characteristics of an accretion disk around a black hole, using a specific perfect fluid radiation field mentioned in [3, 27, 28] as an illustrative example. The radiation field under consideration in this investigation is characterized by a specific equation of state parameter denoted as
$ \omega=\dfrac{1}{3} $ . The transformation of Eq. (2) yields$ f_{r}(r)=1-\frac{2M}{r}+\frac{Q^{2}-N_{\rm{r}}}{r^{2}}. $

(5) When
$ N_{\rm{r}}=0 $ , it returns to an RN black hole. Hence, our study encompasses the scenario of RN black holes, which aids in distinguishing between Einstein gravity and Rastall gravity. Typically, when$ f(r)=0 $ , two roots are present, namely the outer event horizon radius ($ r_{+} $ ) and inner event horizon radius ($ r_{-} $ ). By non-dimensionalizing Q and$ N_{\rm{r}} $ and obtaining the relationship between$ q=\dfrac{Q}{M} $ and$ n=\dfrac{N_{r}}{M^{2}} $ , the admissible ranges for Q and$ N_{\rm{r}} $ can be determined to ascertain the presence of a black hole [24].Figure 1 illustrates the direct and secondary images of the accretion disk at radii
$ r=9M $ ,$ 17M $ , and$ 25M $ , while taking into account a variety of parameter configurations. For$ Q=0.5 $ , and varying$ N_{\rm{r}} $ as$ N_{\rm{r}}=0 $ (RN black hole) and$ N_{\rm{r}}=2 $ , a discernible outward expansion in the orbital path of the accretion disk is evident relative to its reference position. Conversely, when keeping$ N_{\rm{r}}=1 $ fixed and incrementing Q to$ Q=0.1 $ and$ Q=0.9 $ , an observable inward contraction of the accretion disk’s orbit is observed. Variations in parameters lead to changes in spacetime geometry that affect the appearance and structure of the accretion disk. Thus, we conducted a highly intuitive comparative analysis of the direct orbital images at$ r=9M $ to visually demonstrate this phenomenon. It was observed that an increase in Q results in a stronger gravitational pull from the black hole, inducing a contraction of the accretion disk towards its center. Conversely, an increase in the value of$ N_{\rm{r}} $ causes the disk to expand outward, which is attributed to the influence of the perfect fluid radiation field on the spacetime structure. This behavior highlights the crucial interplay between gravitational and radiation forces, determining the changes in spacetime geometry within Rastall's theoretical framework that lead to alterations in the appearance of the accretion disk. Furthermore, in the context of Rastall's theory, a detailed comparison between a charged black hole characterized by a perfect fluid radiation field and the established RN black hole reveals minimal observable distinctions. This observation suggests that, in this scenario, the impact of Rastall's theory on the visual features of the accretion disk, such as direct and secondary orbital images, remains relatively consistent with predictions made by the established RN black hole model.
Figure 1. (color online) Direct (red line) and secondary (blue line) images of the accretion disk of a black hole at the observation angle (
$\theta_{0}=75^{\circ}$ ). These lines represent distinct radial distances:$r=9M$ ,$r=17M$ , and$r=25M$ , with the innermost line corresponding to$r=9M$ . In the top panel, the charge is fixed at$Q=0.5$ while the radiation field parameter$N_{\rm{r}}$ is varied concurrently with values of 0 and 2 from left to right. The far right segment illustrates a comparative view of partial direct images for different$N_{\rm{r}}$ values at$r=9M$ . In the bottom panel,$N_{\rm{r}}$ is fixed at 1, and the charge Q is varied from left to right, taking values of 0.1 and 0.9. The rightmost segment shows a comparative view of partial direct images for different Q values at$r=9M$ . The black hole mass is set to$M=1$ . -
The radiant flux of a thin accretion disk is examined in this subsection. The expression for the radiant flux is derived from previous studies [29, 30]:
$ F = - \frac{\dot{M}}{4\pi \sqrt{-g}} \frac{\Omega_{,\rm r}}{(E-\Omega L)^{2}} \int_{r_{\rm{in}}}^{r} (E- \Omega L)L_{,\rm r} {\rm{d}} r. $

(6) In this equation,
$ \dot{M} $ denotes the mass accretion rate, g represents the determinant of the metric, and$ r_{\rm{in}} $ denotes the inner edge of the accretion disk. The variables Ω, E, and L correspond to the angular momentum, energy, and angular velocity, respectively, and are expressed as$ E=-\frac{g_{\rm{tt}}}{\sqrt{-g_{\rm{tt}}-g_{\rm{\phi\phi}}\Omega^{2}}},$

(7) $L=\frac{g_{\rm{\phi\phi}}\Omega}{\sqrt{-g_{\rm{tt}}-g_{\rm{\phi\phi}}\Omega^{2}}}, $

(8) $\Omega=\frac{{\rm{d}}\phi}{{\rm{d}}t}=\sqrt{-\frac{g_{\rm{tt,r}}}{g_{\phi\phi,r}}}. $

(9) Combining equations (2)−(9), we obtain the radiation energy flux on the black hole:
$ F = \frac{\dot{M}(-8Q^{2}r^{\xi}+I)}{4\sqrt{2}\pi r^{4}X}\int_{r_{in}}^{r}\frac{r^{-3-\xi}(Y-N_{r}^{2}r^{4}\xi(2+\xi)-Z)}{\sqrt{2}X} {\rm{d}} r, $

(10) where X, Y, I, and Z are defined as X =
$ \sqrt{\dfrac{-2Q^{2}+2Mr+N_{\rm{r}}r^{\xi-2}\xi}{r^{4}}}(2r^{\xi}(2Q^{2}+r^{2}-3Mr)-N_{\rm{r}}r^{2}(2+\xi)),$ $ Y=-2r^{2\xi}(4Q^{4}-9MQ^{2}r+M(6M-r)r^{2}) $ ,$I=r(6Mr^{\rm{\xi}}+ N_{\rm{r}}r \xi (2+ \xi))$ , and$Z=N_{\rm{r}}r^{2+\xi}(2Mr+Q^{2}(\xi-10)\xi- 2Mr(\xi-6)\xi + r^{2}(\xi-2)\xi)$ , respectively. In the context of a distant observer measuring the radiant flux, it becomes imperative to account for the redshift influence. The observed flux can be accurately described by the following relationship [16]:$ F_{\rm{obs}} = \frac{F}{(1+z)^{4}}. $

(11) Among these parameters, the quantity
$ 1+z $ corresponds to the redshift factor, an essential component that can be determined through a comparison between the energy of the photon emitted, denoted as$ E_{\rm{em}} $ , and the energy of the photon observed, denoted as$ E_{\rm{obs}} $ . The emitted energy$ E_{\rm{em}} $ arises from an integral across the surface of the accretion disk, where both gravitational and Doppler shift effects emerge. In contrast, the observed energy$ E_{\rm{obs}} $ emerges from consideration of the redshift attributed to the motion of the emitting source in relation to the observer. The connection between the energies of emission and observation is properly modeled by$ E_{\rm{obs}}=(1+z)E_{\rm{em}} $ , where the redshift factor z is intimately related to the gravitational potential and the velocity of the emitting source. This factor is critical because it substantially informs the accurate assessment of the observed flux and serves as a conduit to comprehend the characteristics of radiation discharged by the black hole system.$ E_{\rm{em}} $ is expressed as$ E_{\rm{em}}=p_{\rm{t}} \mu^{\rm{t}} + p_{\rm{\phi}} \mu^{\rm{\phi}} = p_{\rm{t}} \mu^{\rm{t}} \Bigg(1 + \Omega \frac{p_{\rm{\phi}}}{p_{\rm{t}}}\Bigg), $

(12) where
$ p_{\rm{t}} $ and$ p_{\rm{\phi}} $ represent the photon 4-momentum. For observers located at a significant distance, the expression$ p_{\rm{t}}=p_{\rm{\phi}} $ represents the impact parameter of the photons in relation to the z-axis. This relationship can be expressed in terms of trigonometric functions as$ \sin \theta_{0} \cos \alpha = \cos \gamma \sin \beta, $

(13) and one can obtain
$ \frac{p_{\rm{t}}}{p_{\rm{\phi}}} = b \sin \theta_{0} \sin \alpha. $

(14) Therefore, we can derive the expression for the redshift factor:
$ 1 + z = \frac{E_{\rm{em}}}{E_{\rm{obs}}} = \frac{1 + b \Omega \cos \beta}{\sqrt{-g_{\rm{tt}} - 2 g_{{\rm{t}} \phi} - g_{\phi\phi}}}. $

(15) By employing equations (8) and (9), images of a thin accretion disk surrounding a black hole, characterized by diverse parameters within Rastall's gravitational framework, can be generated. The primary focus of this inquiry was to attain a profound comprehension of black holes immersed in perfect fluid radiation fields, a paradigm offered as a demonstrative instance. As depicted in Fig. 2, the observational representation is attainable in scenarios where a black hole is immersed in a perfect fluid radiation field modeled by the equation of state parameter
$ \omega=\dfrac{1}{3} $ . Evidently discernible from the figure is the trend that, with a constant parameter Q, an elevation in the value of$ N_{\rm{r}} $ corresponds to a marked reduction in the luminosity of the accretion disk. When$ N_{\rm{r}}=0 $ , corresponding to the RN black hole, the observer witnesses how the radiation flux reaches its maximum, and the innermost stable circular orbit is closest to the event horizon of the black hole. Simultaneously, the innermost stable circular orbit progressively extends as$ N_{\rm{r}} $ increases. Conversely, when$ N_{\rm{r}} $ is maintained at a constant value, an inverse pattern emerges, manifesting varied outcomes for the luminance of the accretion disk and the dimensions of the innermost stable circular orbit. These observations distinctly underscore the profound impact of the perfect fluid radiation field parameter$ N_{\rm{r}} $ on the luminosity and structural stability attributes of the accretion disk that encircles the black hole.
Figure 2. (color online) Observed flux F presented at an inclination angle of
$\theta_{0}=75^{\circ}$ . The inner edge of the disk is located at$r_{\rm{in}} = r_{\rm{isco}}$ , whereas the outer edge of the disk is located at$r=25M$ . In the top panel, we show the results for a charge$Q=0.5$ with varying radiation field parameters$N_{\rm{r}}$ from left to right: 0, 1.5, and 2.9. In the bottom panel, we present the results for$N_{\rm{r}}=1$ with varying charge Q from left to right: 0.1, 0.5, and 0.9. The black hole mass is$M=1$ .Figure 3 illustrates the predicted observational images obtained by adjusting the observer’s tilt angle while maintaining constants
$ Q=1 $ and$ N_{\rm{r}}=2.9 $ . As the observation angle progressively increases ($ \theta_{0}=15^{\circ} $ ,$ 45^{\circ} $ , and$ 75^{\circ} $ ), discernible alterations of the morphology of the accretion disk emerge. In particular, a gradual metamorphosis occurs: the disk-like structure gradually transitions into a configuration reminiscent of a hat. Moreover, the radiant flux intensity exhibits a progressively growing asymmetry between the left and right facets of the accretion disk. This emphasized asymmetry is rooted in the heightened influence of the Doppler effect as the observation angle increases. The origin of this effect can be traced to the relative motion between the observer and the matter emitted within the confines of the accretion disk. Consequently, this Doppler effect results in a more pronounced red or blue shift in the observed radiation, contingent upon the direction of motion. Consequently, the disparity in radiant flux intensity between the left and right boundaries of the accretion disk notably increases with the observation angle. These predicted outcomes align with other research findings and may offer valuable guidance for achieving the scientific objectives of the EHT in future studies.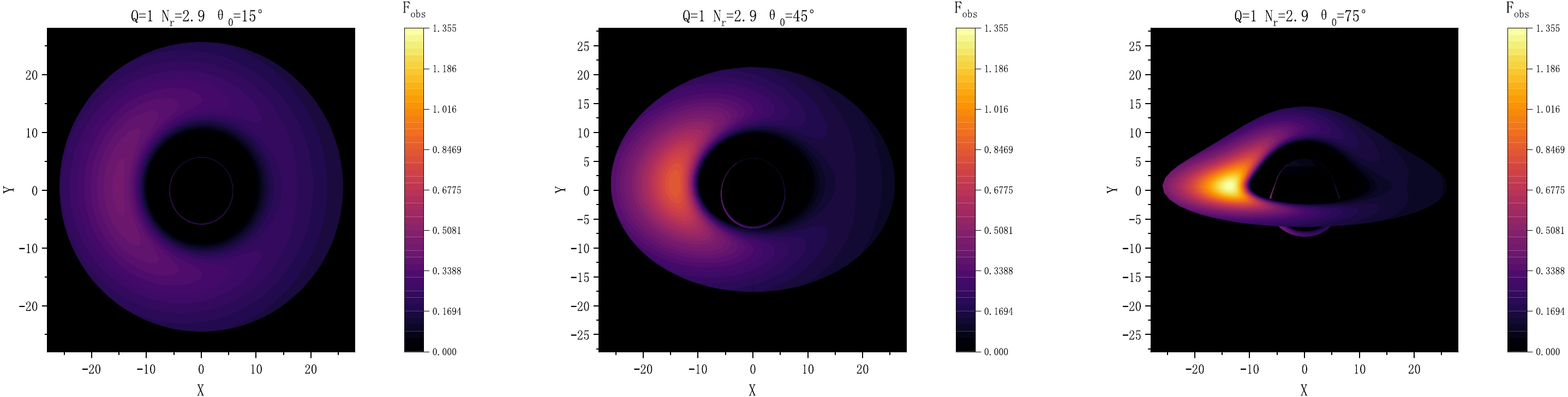
Figure 3. (color online) Observed flux F of the accretion disk presented for three different observer tilt angles:
$\theta_{0}=15^{\circ}$ ,$45^{\circ}$ , and$75^{\circ}$ . The black hole mass is$M = 1$ , the charge is$Q=1$ , and the radiation field parameter is$N_{\rm{r}}=2.9$ . The inner edge of the disk is located at$r_{\rm{in}} = r_{\rm{isco}}$ , and the outer edge of the disk is located at$r=25M$ . -
In this subsection, we further analyze the behavior of a black hole enveloped by a perfect fluid radiation field, with a specific focus on two pivotal features: the photon ring (
$ r_{\rm{ph}} $ ) and the innermost stable circular orbit ($ r_{\rm{isco}} $ ) of the black hole within the environment set by the perfect fluid radiation field. Figure 2 shows the discernible fluctuations in$ r_{\rm{isco}} $ and$ r_{\rm{ph}} $ of the accretion disk as we manipulate the parameters Q and$ N_{\rm{r}} $ . To provide an intuitive description of our findings, we set one parameter constant, either Q ($ Q=1 $ ) or$ N_{\rm{r}} $ ($ N_{\rm{r}}=1 $ ), while systematically varying the other parameter to acquire precise values for$ r_{\rm{isco}} $ ($ Ar_{\rm{isco}} $ ) and$ r_{\rm{ph}} $ ($ Ar_{\rm{isco}} $ ). This method isolates the impact of each parameter and facilitates a detailed examination of how they alter the intrinsic properties of the black hole, leading to changes in the spacetime structure. This, in turn, affects the geodesic paths of photon motion, ultimately resulting in differences in the positions of the photon ring and innermost stable circular orbit.To accurately describe the inherent behavior and facilitate a comprehensive analysis, we employed a numerical fitting technique based on an exponential function to model the acquired data. This fitting methodology demonstrates a robust relationship between parameters and circular geodesics of spacetime metrics. By ascertaining precise fitting parameters, we can elucidate the functional dependencies between Q,
$ N_{\rm{r}} $ ,$ r_{\rm{isco}} $ , and$ r_{\rm{ph}} $ . This enables us to obtain valuable information regarding the interconnections among the black hole, perfect fluid radiation field, and position of the accretion disk.The utilization of numerical fitting and application of an exponential function in our analysis ensure a precise and dependable representation of the data. The fitting curves facilitate interpolation and extrapolation of the behavior of
$ r_{\rm{isco}} $ and$ r_{\rm{ph}} $ for various values of Q and$ N_{\rm{r}} $ , thereby offering a comprehensive understanding of the system’s behavior. This methodology enhances the comprehensibility of our research outcomes and aids in identifying trends and patterns in the variations of the accretion disk’s position.Figure 4 shows the behavior of
$ r_{\rm{isco}} $ and$ r_{\rm{ph}} $ while varying the parameters Q and$ N_{\rm{r}} $ . When Q is held constant, both$ r_{\rm{isco}} $ and$ r_{\rm{ph}} $ exhibit a continuous increase as$ N_{\rm{r}} $ increases. Conversely, when$ N_{\rm{r}} $ is fixed, an increase in Q results in a continuous decrease in$ r_{\rm{isco}} $ and$ r_{\rm{ph}} $ . Notably, changes in$ N_{\rm{r}} $ have a more pronounced impact on$ r_{\rm{isco}} $ and$ r_{\rm{ph}} $ . The figure presents two distinct curves, depicted in black and blue, along with their respective exponential fitting functions, described as follows: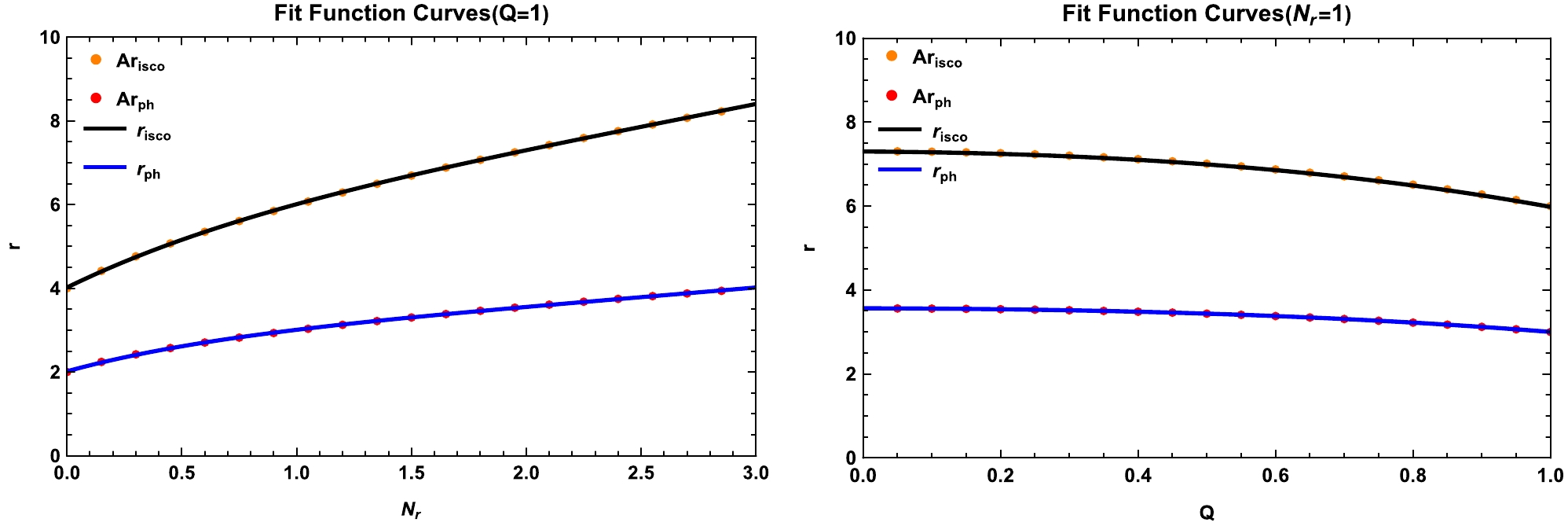
Figure 4. (color online) Exponential function fitting applied to the black hole innermost stable orbit (
$r_{\rm{isco}}$ ) and photon ring ($r_{\rm{ph}}$ ). In the Left Panel, the charge Q is set to 1, and the radiation field parameters$N_{\rm{r}}$ vary from 0 to 2.99. In the Right Panel, the radiation field parameters$N_{\rm{r}}$ is fixed at 1, and the charge Q varies from 0 to 1.$ F(x)= A E^{B x}+C E^{D x}. $

(16) where
$ F(x) $ denotes either$r_{\rm isco}$ or$ r_{\rm ph} $ , and x represents the varying parameter,$N_{\rm r}$ or Q. The values of each parameter in the fitting function are shown in Table 1.$\rm Function$ 

A B C D $ r_{\rm{isco}}(Q=1) $ 

$ 5.977 $ 

$ 0.1173 $ 

$ -1.957 $ 

$ -1.013 $ 

$ r_{\rm{ph}}(Q=1) $ 

$ 2.898 $ 

$ 0.1103 $ 

$ -0.8815 $ 

$ -1.356 $ 

$ r_{\rm{isco}}(N_{r}=1) $ 

$ -379.5 $ 

$ 0.4853 $ 

$ 386.8 $ 

$ 0.4759 $ 

$ r_{\rm{ph}}(N_{r}=1) $ 

$ -1.502 $ 

$ 0.8227 $ 

$ 5.066 $ 

$ 0.237 $ 

Table 1. Exponential fitting function coefficients under various conditions.
-
To rigorously constrain the gravitational parameters inherent to Rastall’s theory within the framework of a perfect fluid, Li et al. adopted a power-law mass density profile for Early Type Galaxies (ETGs) while incorporating Rastall gravity [31]. This inquiry assumes spherical symmetry in mass distribution and characterizes the matter composition as a perfect fluid. In the context of galaxies, the mass density can be reasonably approximated as that of a perfect fluid, given that their dispersion velocity is markedly lower than the speed of light. In this scenario, the following equation may be utilized:
$ M(r_{\rm{g}})= 4 \pi \int r_{\rm{g}}^{2} \rho {\rm{d}}r, $

(17) where
$ r_{\rm{g}} $ is the radius of the galaxy. By assuming a power law total mass density profile for a lens galaxy, the total mass enclosed within a sphere of radius$ r_{\rm{g}} $ can be determined as$ M(r_{\rm{g}})= \frac{2 \Gamma(\dfrac{1}{2}\gamma)}{\Gamma\left(\dfrac{1}{2}\gamma-\dfrac{1}{2}\right) \Gamma\left(\dfrac{1}{2}\right)} D_{l}\theta_{\rm{E}}^{2}\frac{c^{2}}{4 G} \frac{D_{\rm{s}}}{D_{\rm{ls}}}R_{\rm{ein}}^{\gamma-3}r_{\rm{g}}^{3-\gamma}, $

(18) where
$ \theta_{\rm{E}} $ is the Einstein radius,$ D_{\rm{l}} $ and$ D_{\rm{s}} $ represent the angular-diameter distances of the lens and source, respectively,$ D_{\rm{ls}} $ denotes the angular-diameter distance between the lens and source, and γ is the effective slope given by Treu and Koopmans [32]. Owing to the very similar power-law forms of Eqs. (17) and (18), combining both equations yields$ 3-\gamma=\frac{3\kappa \lambda(1+\omega)-3\omega}{1-3\kappa \lambda(1+\omega)}, $

(19) By adjusting the parameter ω, different formulations for
$ \kappa \lambda $ can be derived in various scenarios. Within the framework of Rastall gravity, the Weak Energy Conditions (WEC) ensure that the total energy density of any material field, as measured by an observer following a timelike trajectory, remains non-negative. Additionally, the convergence of geodesics imposes constraints consistent with the Strong Energy Conditions (SEC). Li et al. constrained the$ \kappa \lambda $ Gaussian distribution function by employing 118 gravitational lensing samples while setting ω to 0 [31]. Observational constraints were applied to$ \kappa \lambda $ through both SEC and WEC, as summarized in Table 2, where α serves as an integration constant representing the local field structures.$\rm Integration\; constant$ 

$\rm Coupling\; constant$ 

$\rm Observation\; limitations$ 

$ \alpha> 0 $ 

$ \kappa> 0 $ 

$0 \leq \kappa \lambda \leq \dfrac{1}{6}$ 

$ \alpha< 0 $ 

$ \kappa< 0 $ 

$\dfrac{1}{6} \leq \kappa \lambda \leq \dfrac{1}{4}$ 

Table 2. Rastall gravity parameter limitations under early galaxies.
In the specific scenario under investigation, which involves a perfect fluid radiation field, interesting characteristics emerge. When
$ \omega=\dfrac{1}{3} $ ,$ \kappa \lambda $ remains invariant. At the scale of black holes, Rastall’s gravitational theory could conceivably exert an influence on the mass and morphology of these cosmic entities. This influence may also yield novel predictions pertaining to black hole event horizons and gravitational lensing phenomena associated with them. The observation of a black hole’s gravitational lensing effect provides an approach for constraining the Rastall parameter on the scale of black holes. It is essential to emphasize that a black hole enshrouded within a perfect fluid radiation field retains its exceptional nature within this framework. -
In summary, we thoroughly analyzed the observable characteristics manifested by accretion disks surrounding black holes within the framework of Rastall gravity. In this study, set against the backdrop of Rastall gravity for comparison with Einstein’s theory of gravity, we examined a black hole encompassed by a perfect fluid radiation field. We identified the influence of the observable properties of accretion disks stemming from the changes in the spacetime structure due to the variation of parameters within the Rastall gravity framework. This study has unveiled profound connections between the parameters Q and
$ N_{\rm{r}} $ and the behavior of the accretion disk.First and foremost, we have established that the expansion or contraction of the accretion disk’s orbit is intricately tied to the values of Q and
$ N_{\rm{r}} $ . Increasing the charge parameter Q leads to an intensified gravitational pull from the black hole, thereby inducing a contraction of the accretion disk toward the black hole. Conversely, an increase in the parameter$ N_{\rm{r}} $ triggers an outward expansion of the accretion disk due to the influence of the perfect fluid radiation field. Importantly, the visual appearance of a charged black hole within a perfect fluid radiation field in Rastall's theory exhibits no significant disparities when compared to the RN black hole. This observation suggests that, in terms of appearance, the effects of Rastall gravity and Einstein gravity are akin in this specific scenario.In addition, the brightness and stability characteristics of the accretion disk are intricately linked to the values of the parameters Q and
$ N_{\rm{r}} $ . An increase in the value of$ N_{\rm{r}} $ is associated with a significant reduction in the brightness of the accretion disk. Furthermore, with the increase in$ N_{\rm{r}} $ , the position of the innermost stable circular orbit gradually expands outward. Conversely, keeping$ N_{\rm{r}} $ constant while varying the parameter Q results in an opposing trend in the position of the innermost stable circular orbit and brightness of the accretion disk. These findings underscore the pivotal role of the perfect fluid radiation field parameter$ N_{\rm{r}} $ and charge Q in shaping the luminosity and stability properties of the accretion disk. Moreover, our analysis of the observer’s perspective unveils morphological transformations in the accretion disk as the observation angle increases. The disk undergoes a transformation from a disk-like configuration to a hat-like structure, accompanied by a growing degree of asymmetry in the radiant flux intensity on the left and right sides of the disk. This asymmetry can be attributed to the heightened influence of the Doppler effect, leading to a more pronounced red or blue shift in the observed radiation as the observation angle rises.Astronomical observations wield a critical role in the rigorous constraint of the gravitational parameters intrinsic to Rastall’s theory. By scrutinizing various astrophysical phenomena, such as gravitational lensing effects, black hole properties, and other observational data, we gain valuable insights and constraints on the specific gravitational parameters associated with Rastall’s theory. These observations serve as a cornerstone for refining our comprehension of gravity and its behavior on astronomical scales.
In conclusion, our investigation provides valuable insights into the observable attributes characterizing accretion disks encircling black holes within the framework of Rastall gravity. This underscores the close correlation between the parameters Q and
$ N_{\rm{r}} $ and the behavior of the accretion disk, revealing unique signatures and implications of Rastall gravity in observational properties of these celestial systems. These findings substantially contribute to a deeper understanding of the intricate interplay among black holes, perfect fluid radiation fields, and the resulting properties of accretion disks.
Rastall gravity: accretion disk image in the context of radiation fields and visual transformations compared to Reissner-Nordström black hole
- Received Date: 2023-10-05
- Available Online: 2024-04-15
Abstract: In this study, we investigated the astronomical implications of Rastall gravity, particularly its behavior amidst a radiation field compared to Reissner-Nordström (RN) black holes. We found a crucial correlation between the dynamics of the accretion disk and the parameters Q and





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: