Isoscaling properties for neutron-rich fragments in highly asymmetric heavy ion collision systems

For over a decade, the density dependence of symmetry energy has been a focal point in nuclear physics. Its significance lies in understanding the properties of radioactive isotopes, the dynamics of evolution in low and intermediate energy heavy ion collisions, and various astrophysical phenomena. [1−6]. Although the asymmetry energy term is well constrained at saturation density, its evolution away from the saturation density is still unclear. Isoscaling parameters, which are denoted by α and β, are one of the important probes to examine the symmetry energy at sub-saturation [7−9]. A generalized formula for isoscaling can be obtained via thermodynamic models of nuclear reactions, i.e., for a specific fragment with neutron number N and proton number Z in two systems that share the same environment of reactions (mainly in similar temperatures),

or

where $ Y_2 $ and $ Y_1 $denote the yield of a specific fragment $ (N,Z) $ in reactions with sub-indices 2 and 1 denoting $ n/p $ asymmetric and symmetric indices, respectively. Parameters C, α, and β are fitting parameters to yield ratio $ R_{21}(N,Z) $. It is generally known that α and β are sensitive to the $ n/p $composition of emitting sources. Furthermore, α and β are in forms of

where $ \mu_n $ ($ \mu_p $) is the chemical potential of free neutrons (protons) in the reaction system, and thus, α (β) denotes the difference in the neutron (proton) chemical potential between two reaction systems. Numerous experiments and theoretical models demonstrated that isoscaling applies to a variety of reaction mechanisms dominated by phase spaces, including evaporation, multi-fragmentation, and deeply inelastic scattering and fission [7−10]. In statistical and dynamical models [9, 11, 12], the isoscaling parameter α is related to the symmetry energy coefficient $ C_{\rm sym} $ and isotopic composition of the compound system ($ N_{s} $,$ Z_{s} $),

In a similar fashion,

The value of $C_{\rm sym}$ is determined by the average nuclear density and the temperature T of the emitting source [12, 13]. Hence, measuring $ R_{21}(N,Z) $ can probe the density dependence of symmetry energy [9, 14].

A quantity η is defined to label the ratio $ \beta(N)/\alpha(Z) $ related to a specific fragment,

where $ \beta(N) $ and $ \alpha(Z) $ are determined from its isotonic and isotopic chains, respectively. By definition, η reflects the degree of difference between the proton density and neutron density of the colliding source where the fragment is formed. According to Refs. [12, 15], in the absence of isospin symmetry breaking,

Various experimental and theoretical studies have shown that isoscaling can work very well when $ N/N_{s} $ and $ Z/Z_{s} $ are small ($ \leq $0.35) [7−9]. If one extends observations to a smaller system ($ N_{s} $,$ Z_{s} $) or larger fragment ($ N,Z $), more precisely, to larger $ N/N_{s} $ and $ Z/Z_{s} $, deviations are expected. Historically, isoscaling has been primarily interpreted and implemented within the context of the grand canonical ensemble, based on the assumption that fragment production occurs after a statistical equilibrium state is attained. However, the influence of the asymmetry energy may lead to differences in the neutron and density distribution in neutron-rich nuclei, potentially impacting α and β, especially for small systems subject to volume effects. In Ref. [16], the phenomenon of deviation from isoscaling was discussed. The authors successfully explained the deviations in the experimental data based on small systems via canonical model as opposed to the grand canonical model. Some experimental observations suggested a strong decrease in isoscaling parameters with increasing centrality to values smaller than 50% of those obtained for the peripheral groups [17]. Additionally, it was shown that the isoscaling parameters were different for emitted and projectile-like fragments [18]. Various molecular dynamics simulation studies have shown that isoscaling parameters vary wildly with the evolution of the reaction system [19]. These experimental and theoretical results underscore the significance of comprehending how isoscaling parameters vary with fragments originating from distinct collision zones, which may exhibit diverse production mechanisms or nuclear density distributions.

In this study, the isoscaling properties for neutron-rich fragments produced in highly asymmetric systems were examined. The analysis was conducted based on the inclusive experimental results by Mocko et al. [20]. The fragments were grouped based on their neutron-excess ($I \equiv N-Z$). Specifically, the fragments within the same group were assumed to share the same environment, i.e., the same colliding region, temperature, and nuclear density. We employed experimental data (if available), the Heavy Ion Phase Space Exploration model (HIPSE) plus SIMON simulations, and the Antisymmetrized Molecular Dynamic (AMD) model plus GEMINI simulations to investigate the variations in the isoscaling parameters derived from fragments belonging to different groups. Furthermore, the $ |\beta(N)| \sim \alpha(Z) $ correlation for a specific fragment was adopted to explore the degree of difference between proton density and neutron density of two collision sources where the fragment is formed.

This paper is structured as follows. First, the HIPSE and AMD models, as well as the decay codes, SIMON and GEMINI, are briefly introduced in Sec. II. The isotopic distributions are compared in Sec. III.A. The isoscaling behaviors of fragments in the measured 140 MeV/u $ ^{58,64} $Ni + $ ^9 $Be projectile fragmentation reactions are discussed in Sec. III.B. The $ |\beta(N)| \sim \alpha(Z) $ correlations for $^{40, 48}$Ca, $^{58, 64}$Ni, and $^{78, 86}$Kr induced projectile fragmentation reactions are discussed in Sec. III.C. The results are summarized in Sec. IV.

The HIPSE model was proposed to examine the reaction process with few important parameters in a fully microscopic manner based on a macroscopic-microscopic "phenomenology" and accounts for both the dynamical and statistical properties of nuclear collisions [21]. It has been employed to narrow the divide between statistical models and molecular dynamics models, simplifying the reaction's description to a handful of key parameters and reducing CPU computation time. Leveraging the sudden approximation and geometric hypothesis, it efficiently models heavy-ion interactions across the intermediate energy spectrum for any impact parameter. The HIPSE model breaks down a nuclear reaction into three distinct stages: the collision's approach phase, formation of partitions, and exit channel along with the after-burner phase leading to the detectors.

The interaction between the projectile ($ A_{P},Z_{P} $) and target ($ A_{T},Z_{T} $) is simplified as two classical particles, following the evolution associated with the Hamiltonian,

where $ E_{0} $ denotes the available energy in the center of mass, p denotes the relative momentum, and μ denotes the reduced mass. Furthermore, $ V_{A_{T}A_{P}}(r) $ denotes the interaction potential between the target and projectile with $ r=|r_{T}-r_{P}| $, indicating the relative distance. When $ r > (R_{T}+R_{P}) $ ($ R_{T} $ and $ R_{P} $ denote radii of the target and the projectile respectively), use the proximity potential. When $ r \leq (R_{T}+R_{P}) $, use a simple approximation for the construction of the potential. It is assumed that $ V_{A_{T}A_{P}} $ depends uniquely on r even for a small relative distance. The potential between $ r=0 $ and $ r=R_{T}-R_{P} $ is interpolated using a third-order polynomial and assuming continuity of the derivative of the potential at each point. The value retained at r = 0 is conveniently expressed as

where $ \alpha_{a} $ denotes an adjustable parameter. $V_{A_{T}A_{P}}^{\rm Froz}(r=0)$ denotes the energy of the system given that the two densities of the system overlap completely in the froze density approximation.

The coalescence algorithm is used to create fragments from nucleons. First, one of the nucleons is randonly selected, and it constitutes a coalescence point from which a fragment is built; the other nucleon i in the overlap region is then selected at random. The nucleon i can be captured by the cluster labeled 1 based on the existence condition and position and momentum conditions. First, we check whether the nuclear exists in the experimental mass table, and then the fragment is formed based on the position $ r_{i} $ and momentum $ p_{i} $ of the nucleon as follows

where m denotes the nucleon mass, and $ d_{f} $, $V_{\rm cut}$, a denote adjustable parameters.

During the final state interaction and reaggregation phase, the motion of each cluster is determined by the Hamiltonian,

After this first propagation at high density and the reaggregation phase, the clusters recombine and only the Coulomb interaction between fragments is considered. Subsequently, the model can be coupled with SIMON decay code, an event generator code based on Weisskopf emission rates first proposed by D. Durand [22]. The physics used to describe the decay of the various fragments is based on the statistical model considering the narrowest discrete states for $ Z \leq $ 9 as well as in-flight evaporation. The HIPSE model directly incorporates the SIMON code to account for the de-excitation process of fragments, completing the entire nuclear reaction process.

The HIPSE model is based on providing a generator of events where it is expected that parameters do not change with the entrance channel. It only includes three adjustable parameters $ \alpha_{a} $, $ x_{ex} $ , and $x_{\rm coll}$, which denote the hardness of the potential, percentage of exchange between projectile and target, and percentage of nuclear-nuclear collisions, respectively. These parameters only depend on beam energy. The values of the parameters are adjusted for beam energies of 10, 25, 50, and 80 MeV/u. In the study, values of $ \alpha_{a}= $ 0.55, $ x_{ex}= $ 0.09, and $x_{\rm coll}=$ 0.18 were chosen for the beam energy of 140 MeV/u [23]. Approximately 1,000,000 events were simulated for collisions involving Ca isotopes ($ ^{40} $Ca, $ ^{48} $Ca) and Ni isotopes ($ ^{58} $Ni, $ ^{64} $Ni) with a $ ^{9} $Be target. The impact parameter ranges from 0 to 6 fm for $ ^{40,48} $Ca + $ ^{9} $Be collisions and from 0 to 8 fm for $ ^{58,64} $Ni and $ ^{78,86} $Kr + $ ^{9} $Be collisions. The SIMON code was coupled with the HIPSE model at 300 fm/c for $ ^{40,48} $Ca + $ ^{9} $Be collisions and at 500 fm/c for $ ^{58,64} $Ni and $ ^{78,86} $Kr + $ ^{9} $Be collisions.

The Antisymmetrized molecular dynamics (AMD) model [24] is a microscopic model for nuclear collision that describes the nuclear reaction at the microscopic level of interactions of individual nucleons. In AMD, the nuclear many body system can be expressed by a Slater determinant of Gaussian wave packets as follows:

where the spatial wave functions of nucleons can be expressed:

Furthermore, $ \chi_{\alpha} = p\uparrow, p\downarrow, n\uparrow, $ or $ n\downarrow $ denotes the spin-isospin wave function. Additionally, $ \varphi_{Z} $ denotes the wave function in phase space. The width parameter $\nu=2.5~\rm fm^{-2}$ is treated as constant parameter common to all the wave packets. The complex variables ${{\bf{Z}}\equiv \{{\bf{Z}}_{i};\;i=1,\,2,...,A\}}$, where A denotes the number of nucleons in the system, are the centroids of the wave packets. The equation of motion for Z derived from the time-dependent variational principle can be expressed as follows:

where $ C_{i\sigma,j\tau} $ denotes a Hermitian matrix, and H denotes the expectation value of the effective Hamiltonian after the subtraction of the spurious kinetic energy of the zero-point oscillation of the center of masses of fragments [25],

where $ N_{F}(Z) $ denotes the fragment number and $ T_{0} $ is treated as a free parameter to adjust the binding energies of nuclei. The quantum Hamiltonian,

includes an effective nucleon-nucleon interaction such as the Gogny force and the Skyrme force. All AMD simulations discussed in this paper are based on the Gogny interaction force [26].

The original AMD model has been extended to enhance the prediction of fragment production in heavy-ion collision. The AMD-V [27, 28] or AMD/D elsewhere [29] utilized in this study represents the first extended version of AMD with quantum branching process. This introduces the diffusion process, triple-loop approximation, and wave packet shrinking process by the mean field field propagation to improve the reproduction of the fragmentation data and significantly reduce computation time for heavier collision systems [30]. The comparable production cross sections of α particles to nucleons in heavy-ion collisions indicate a strong cluster correlation effect in reality. To more explicitly account for cluster correlations in AMD, Ono developed the AMD-Cluster and introduced inter-cluster correlation as a stochastic process of inter-cluster binding in the AMD-Cluster [31, 32], which was not considered in this study.

To compare the results with the experimental data, it is usually necessary to perform some simulations with various impact parameters to obtain the production cross sections of the fragments, the particle energy spectra, and so on. The statistical decay code is based on the GEMINI code [33], which is a widely used code to treat the sequential decay of hot fragments. A Monte Carlo technique is employed to follow the decay chains of individual compound nuclei via sequential binary decays until the products cannot undergo further decay. The Hauser-Feshbach formalism [34] is adopted to calculate the decay width for the evaporation of fragments with $ Z \leq $2. In this study, we performed the AMD-V simulations of $ ^{40} $Ca, $ ^{48} $Ca, $ ^{58} $Ni and $ ^{64} $Ni projectile on the $ ^{9} $Be target at 140 MeV/u, adopting the same impact parameters and coupled time as the HIPSE plus SIMON simulation. $ ^{78,86} $Kr+$ ^{9} $Be collisions were not simulated due to the time-consuming nature of AMD simulation.

Figure 1 shows the isotopic distributions for fragments in 140 MeV/u $ ^{40,48} $Ca + $ ^{9} $Be and $ ^{58,64} $Ni + $ ^{9} $Be reactions. The distributions are calculated by the HIPSE + SIMON and AMD + GEMINI models and are compared with the experimental results. As shown in the figure, the HIPSE model, primarily designed to describe collisions at Fermi energies for relatively symmetric systems, is also capable of reproducing experimental measurements of symmetric and asymmetric heavy-ion collisions at energy of 140 MeV/u. However, despite simulating 1,000,000 collision events, HIPSE plus SIMON struggles to obtain extremely neutron-rich fragments. The AMD plus GEMINI simulation accurately reproduces existing experimental data in the $^{40}$Ca and $ ^{48} $Ca-induced reaction. However, it tends to slightly overestimate cross sections for neutron-rich isotopes in $ ^{58} $Ni and $ ^{64} $Ni-induced reactions. The discrepancy can be attributed to the limitations of the AMD-V simulation used, which does not account for cluster correlations. Nevertheless, isoscaling, which explores the ratio of isotope or isotonic yield from two different reactions, can aid in mitigating the effect of overestimation.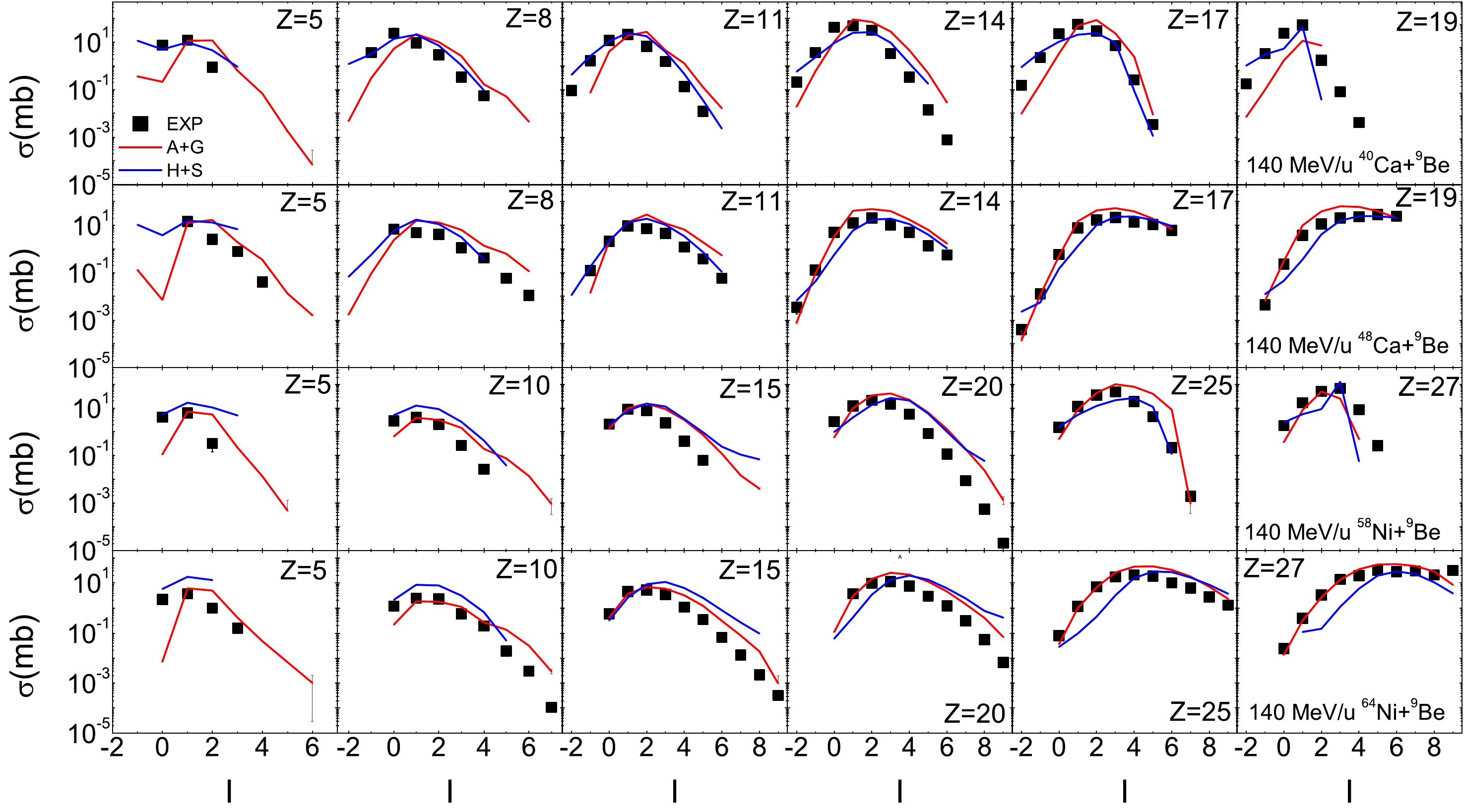

Figure 1.  (color online) The isotopic distributions for fragments with $ 5\leq Z \leq19 $ in $ ^{40,48} $Ca + $ ^{9} $Be at 140 MeV/u and for fragments with $ 5\leq Z \leq27 $ in $ ^{58,64} $Ni + $ ^{9} $Be at 140 MeV/u. The experimental data are taken from Ref. [20]. On the x axis, $ I=N-Z $ denotes the fragment neutron excess. The measured data, AMD plus GEMINI (denoted as A+G) calculations, and HIPSE plus SIMON (denoted as H+S) calculations are plotted as black squares, red lines, and blue lines, respectively.

The isoscaling behavior of hot and cold fragments, isoscaling parameters from light to heavy fragments by the HIPSE model, and effect of the HIPSE model parameters were investigated [35−37]. More information about comparisons of the statistical multi-fragmentation and evaporation models for heavy-ion collisions can be found in Refs. [23, 38].

In the standard isoscaling phenomenon, the isotopic ratio and isotonic ratio obey the linear correlation of Eq. (2). Distortions to isoscaling phenomenon are easily found in isotopic or isotonic ratio distributions in relatively small systems as in the 140 MeV/u $ ^{58,64} $Ni + $ ^{9} $Be reactions measured by Mocko et al. [20], as shown inFig. 2. Based on the isotopic (isotonic) chain from $ Z= $ 5 ($ N= $ 7) to $ Z= $ 27 ($ N= $ 32), the linear correlation is distorted to different degrees within the different mass ranges of fragments. The main reason for this variation could be the influence of the volume effect. When the mass of the nucleus is concentrated in a relatively small volume, the density of the systems is higher, and the interactions between the nucleons are stronger. Additionally, the isoscaling law is easily influenced by changes in the environment, such as nuclear density and temperature. In the following, the fragments are divided into different groups based on their neutron excess ($ I \equiv N-Z $) of $ I= $[–2, 0] (only shown when experimental data are available), [0, 3], [3, 6], and [6, 9], and it is assumed that fragments within the same group share the same environment, i.e., the same collision region, temperature, and nuclear density. This allows us to examine the variations in isoscaling parameters in different environments and thereby obtain information about the nuclear density distributions in these collision regions. Figure 3 shows the isotopic ratio distributions for fragments of different groups, revealing strong linear correlations.

Figure 2.  (color online) Ratios of isotopic and isotonic yields for measured fragments according to Eq. (2) in the measured 140 MeV/u $ ^{58,64} $Ni + $ ^{9} $Be reactions. The lines are for guiding eyes.

Figure 3.  (color online) Ratios of isotopic yield [according to Eq. (2)] for fragments within ranges of $ I= $ [0, 3], [3, 6], and [6, 9] in the measured 140 MeV/u $ ^{58,64} $Ni + $ ^{9} $Be reactions. The lines denote the linear fitting results for each case.

The cross sections of fragments produced in 140 MeV/u $ ^{58,64} $Ni + $ ^{9} $Be reactions are simulated both by the HIPSE + SIMON (denoted by H+S) and AMD + GEMINI (denoted by A+M) models. The isoscaling parameters (α and $ |\beta| $) obtained from fragments within the ranges of $ I= $ [0, 3], [3, 6], and [6, 9] are compared to those from experimental results in Fig. 4. The experimental results indicate that isotopes with larger neutron excess correspond to a larger α value, with the exception of Z = 17 and 18 isotopes within I = [3, 6] and [6, 9], while $ |\beta| $ hardly varies for $ N\leq $ 26 and slightly decreases for $ N > $26. Additionally, with the increasing Z and N, the isoscaling parameters from $ I= $ [0, 3] fragments initially decrease, then stabilize, and finally increase, whereas those from $ I= $ [3, 6] and [6, 9] fragments increase quickly. Compared with the experimental data within the range of $ I= $ [0, 3], the results of the H+S model tend to underestimate those of $ Z < $ 11 and $ N < $12 fragments, and the α ($ |\beta| $) values increase with the Z (N) of the fragments, showing no plateau structures [see Fig. 4(a)]. Furthermore, they also underestimat the results of $ Z< $16 fragments within the range of $ I= $[3, 6], and are significantly different from those of all the fragments within the range of $ I= $[6, 9]. Conversely, the results of the A+G simulations generally underestimate the measured results although they exhibit trends similar to the experimental results, with the exception of $ Z < $ 5 and $ N < $ 10 fragments [see Fig. 4(b)].

Figure 4.  (color online) α and $ |\beta| $ values from fragments within $ I= $ [0, 3], [3, 6], and [6, 9] in 140 MeV/u $ ^{58,64} $Ni + $ ^{9} $Be reactions. Results simulated by the HIPSE + SIMON (denoted as H+S) model (panels (a) and (c)) and those by the AMD + GEMINI (denoted as A+G) model (panels (b) and (d)) are compared with those obtained from measured fragments. The dotted lines denote $ \alpha(Z) $ (or $ |\beta(N)| $) = 0.5.

In neutron-rich nuclei, the symmetry energy within the nucleus leads to an increased difference in density distribution between neutrons and protons, resulting in the formation of a neutron skin or neutron halo [39]. Recently, new methods have been developed for studying the neutron or proton skin and density distribution of the nuclei [40−42]. The parameter α (β) is correlated to the relative neutron- (proton-) density difference between reactions, i.e., $\dfrac{\rho_{n}^{(2)}}{\rho_{n}^{(1)}}=e^{\alpha}$ $\left(\dfrac{\rho_{p}^{(2)}}{\rho_{p}^{(1)}}=e^{\beta} \right)$ [7]. For relatively small fragments primarily originating from center or semi-center collision, the differences in both neutron density and proton density between the $ ^{58} $Ni and $ ^{64} $Ni-induced systems are small, resulting in minimal changes in α and $ |\beta| $ values. This finding is in line with traditional isoscaling research. The upturning behavior of the smaller fragments for $ Z< $8 and $ N< $12 may be caused by secondary decay [18, 43]. As the collision moves towards the periphery, the neutron density difference between the $ ^{58} $Ni and $ ^{64} $Ni-induced systems increases significantly, while the proton density difference decreases, resulting in a significant increase in α and a slight decrease in $ |\beta| $ with the increase in I.

According to Eq. (6), the $ |\beta(N)| / \alpha(Z) $ value for a specific fragment ($ N,Z $) reflects the degree of difference between the proton and neutron densities of the two colliding sources where the fragment is formed. The $ |\beta|\sim \alpha $ correlations for specified fragments produced in $ ^{40,48} $Ca, $ ^{58,64} $Ni, and $ ^{78,86} $Kr-induced reactions are plotted in Figs. 5, 6, and 7, respectively. For any specified fragment ($ N, Z $), the $ |\beta| $ and α values are selected from the linear regression slopes of the fragments in the respective groups within $ I= $ [–2, 0], [0, 3], [3, 6], and [6, 9].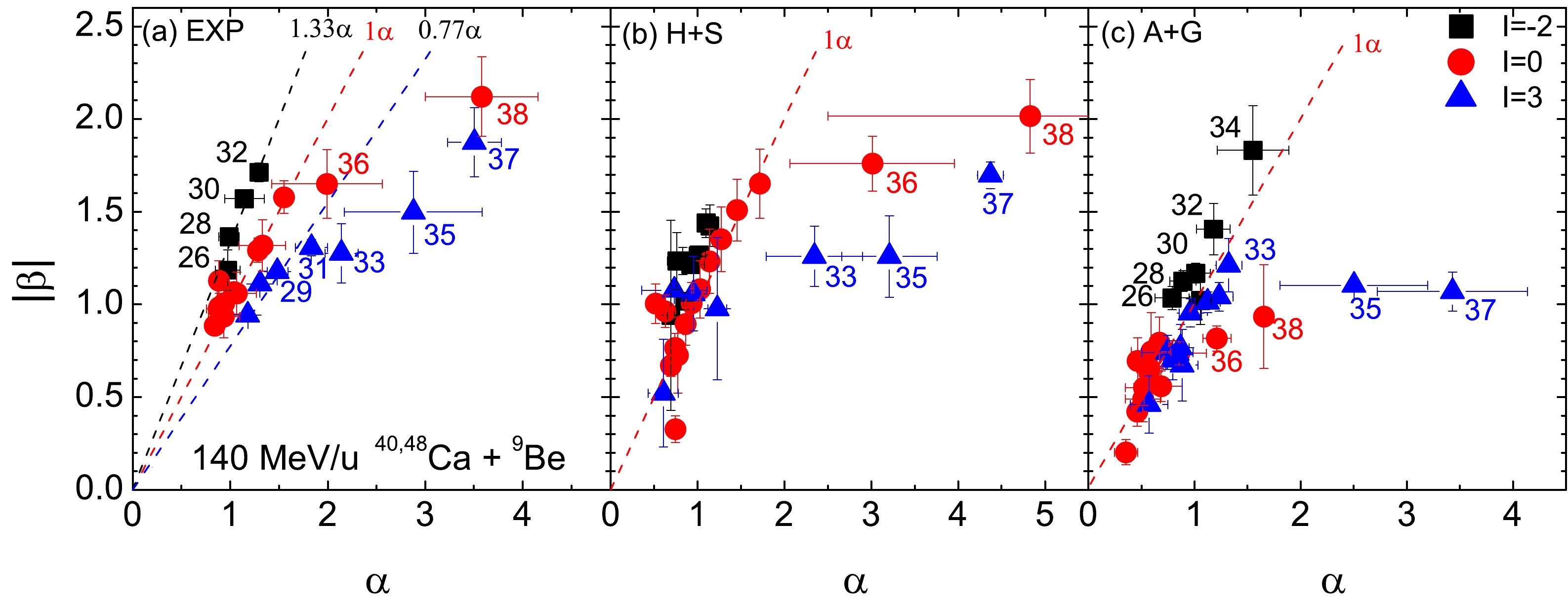

Figure 5.  (color online) Correlations between $ |\beta(N)| $ and $ \alpha(Z) $ for fragments with $ I= $ –2, 0, and 3 in 140 MeV/u $ ^{40,48} $Ca + $ ^{9} $Be reactions. The results in panels (a), (b), and (c) are those extracted from the experimental data, H+S simulation, and A+G simulation, respectively. The numbers refer to the charge number (Z) of the fragment. The number next to each line denotes $ |\beta|=b_1 \cdot \alpha $ , and $ b_1 $ is the slope.

Figure 6.  (color online) Similar results to those shown in Fig. 5 but for fragments with $ I= $ 0, 3, and 6 in 140 MeV/u $ ^{58,64} $Ni + $ ^{9} $Be reactions.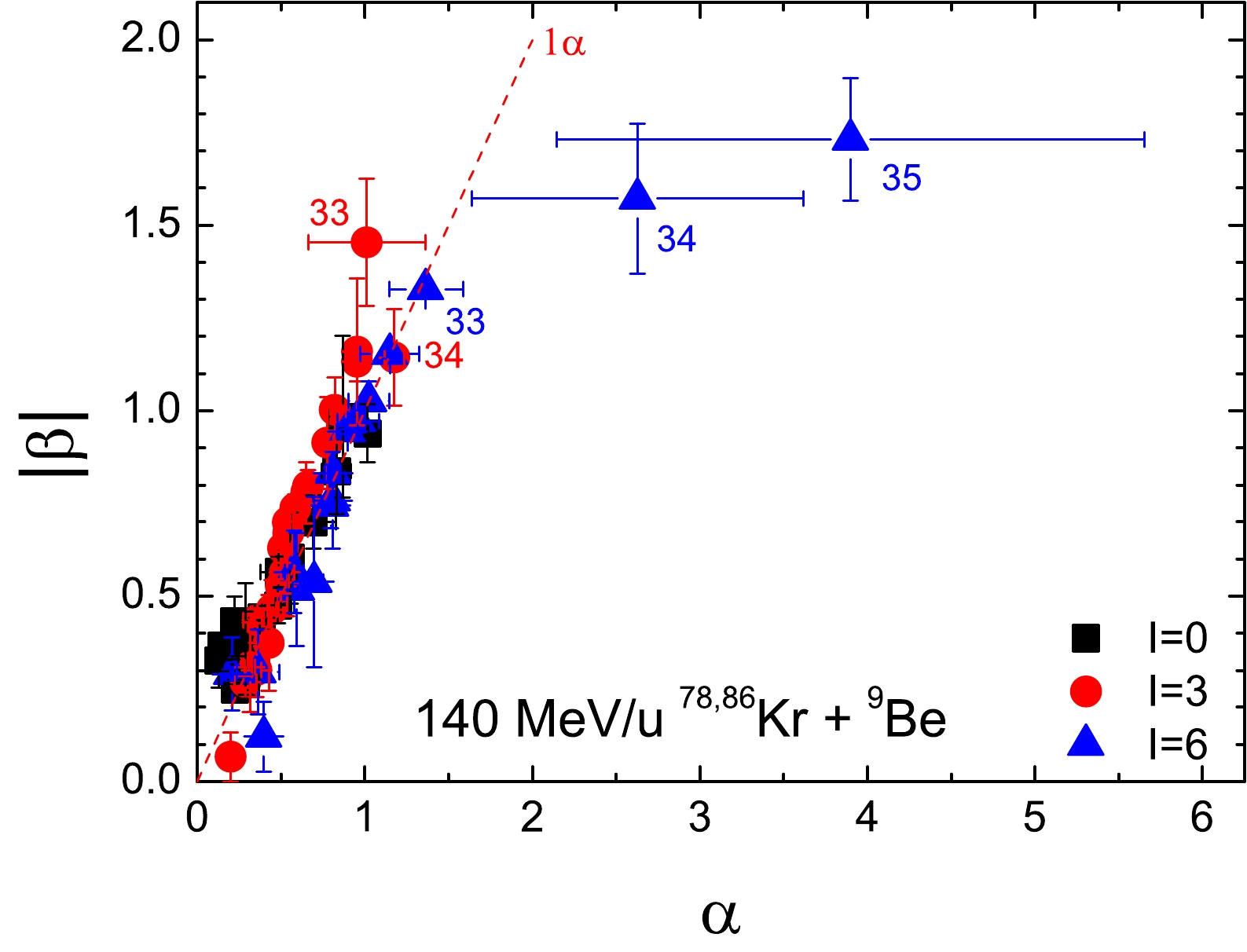

Figure 7.  (color online) Similar results to those shown in Fig. 5 but for fragments with $ I= $ 0, 3, and 6 in 140 MeV/u $ ^{78,86} $Kr + $ ^{9} $Be reactions simulated by H + S models.

Figure 5 illustrates $ |\beta|\sim \alpha $ correlations for fragments with specified I produced in the $ ^{40,48} $Ca + $ ^{9} $Be reactions. The results determined from experimental data for relatively small fragments with $ I= $ –2, 0, and 3 follow $|\beta| = 1.33\alpha$, $ |\beta| = \alpha $, and $ |\beta| = 0.77\alpha $, respectively. However, for the larger-mass fragments of $ A \geq $ 18 with $ I= $ 0 and $ A \geq $ 33 with $ I= $3, the correlations significantly deviate from $ |\beta| = \alpha $ and $ |\beta| = 0.77\alpha $ lines, respectively. This indicates that a significant difference exists between the neutron densities in the surface regions of $ ^{48} $Ca and $ ^{40} $Ca when compared to the proton densities. Experimental studies have shown that the isoscaling parameters extracted from emitted fragments and projectile-like fragments are distinct [18]. This suggests that achieving more accurate isoscaling parameters may necessitate experimental differentiation between projectile-like fragments and emitted fragments. The findings of this study further indicate that, besides differentiating between massive fragments and small fragments, it is important to differentiate fragments with varying neutron excess when analyzing α and β parameters, especially for relatively small colliding systems. This, in turn, imposes more stringent requirements on the modeling software. Unfortunately, the H+S and A+G simulations can only illustrate the differences between massive fragments and small fragments, and they fail to capture the differences for fragments with different values of I.

Similar to Fig. 5, except for massive fragments, the experimental results for fragments with $ I= $ 0, 3, and 6 in 140 MeV/u $ ^{58,64} $Ni+$ ^{9} $Be reactions follow $ |\beta| = 1.29\alpha $, $ |\beta| = \alpha $, and $ |\beta| = 0.72\alpha $, respectively. Furthermore, H+S and A+G simulations fail to capture the differences for fragments with different values of I. Moreover, the underestimation of certain smaller fragments and larger neutron excess values by the H+S model leads to significant discrepancies from experimental results for $ A \leq $ 39 fragments with $ I= $ 3 and with $ I=6 $. Additionally, the results based on the A+G simulation show slight deviations from experimental results. In the H+S simulated $ ^{78, 86} $Kr-induced reactions shown in Fig. 7, the $ |\beta|=\alpha $ relationship is well satisfied by fragments with $ I= $ 0, 3, and 6 fragments with the exception of the massive fragments of $ Z= $ 34 and 35.

According to $ |\beta(N)| \sim \alpha(Z) $ correlations observed in fragments from $ ^{40,48} $Ca to $ ^{78, 86} $Kr-induced reactions, it is observed that, as the volume of the projectile nucleus increases, the fragments tend to exhibit gradually similar α and $ |\beta| $ apart from the massive fragments. Generally, when the neutron and proton densities of the initial excited source differ, the system generally tends to shift toward symmetric matter to maintain equilibrium via evaporation and de-excitation processes, such that $ |\beta(N)| $ is closer to $ \alpha(Z) $ [44]. When the mass of nuclei is concentrated in a smaller volume, the nuclear density increases, leading to a stronger nucleon-nucleon interaction and resulting in variations in $ |\beta(N)| / \alpha(Z) $ from different neutron-excess fragments in $ ^{40,48} $Ca and $ ^{58, 64} $Ni induced systems. $ |\beta| / \alpha $ ratio reflects the degree of difference between the proton and neutron densities of two colliding sources where the fragments are formed, and thus, $ |\beta| / \alpha $ values of fragments in small size and highly isospin asymmetry systems can serve as a probe to investigate variations in neutron and proton densities within different regions of the nucleus.

We investigated the isoscaling properties for neutron-rich fragments produced in highly asymmetric systems on inverse kinematics, specifically $ ^{40,48} $Ca and $ ^{58, 64} $Ni+$ ^{9} $Be at 140 MeV per nucleon, based on the experimental results obtained by Mocko et al. The significant differences in the isoscaling parameters extracted from fragments within different ranges of $ I \equiv N-Z $ emphasize the importance of understanding isoscaling dependencies of fragments produced in different collision regions, which reflect different production mechanisms and density distributions inside the projectile nuclei. Furthermore, the $ |\beta(N)| / \alpha(Z) $ ratio of the specified fragment is adopted to explore the degree of difference in neutron and proton densities between the two colliding sources where the fragments are formed. For the $ ^{40,48} $Ca and $ ^{58,64} $Ni + $ ^{9} $Be at 140 MeV/u reactions, fragments with different I values exhibit varying linear correlations between $ |\beta(N)| $ and $ \alpha(Z) $. The results indicate that the $ |\beta(N)| / \alpha(Z) $ values of fragments in small size and highly isospin asymmetric systems can serve as a probe to investigate variations in neutron and proton densities in different regions of the nucleus. Hence, this imposes more stringent requirements on the modeling software. These findings were compared with those obtained by two different theoretical models, namely HIPSE, a phenomenological hybrid model combining dynamical and statistical hypotheses, and AMD, a microscopic quantum transport model. Unfortunately, both models failed to capture the differences. It is expected that the results of this study can provide support for experimental and theoretical studies on the isoscaling behavior and density dependence of symmetry energy.