-
New vectorlike quarks (VLQs) appear in a variety of extensions of the Standard Model (SM), and they offer a potential solution to the hierarchy problem, such as little Higgs models [1–3], composite Higgs models [4, 5], and other new physics scenarios [6–9]. VLQs are fermions with spin-1/2, and their left-handed and right-handed chiral components have the same transformation characteristic under the electroweak (EW) symmetry group
$S U(2)_{L}\times U(1)_{Y}$ of the SM [10]. Three types of VLQs exist in the renormalizable extensions of the SM: singlets [T, B], doublets [$ \left(X,T\right),\left(T,B\right) $ ,$ \left(B,Y\right) $ ], and triplets [$ \left(X,T,B\right) $ ,$ \left(T,B,Y\right) $ ]. In this study, we focus on the vector-like X-quark (VLQ-X) with an exotic electric charge$ 5e/3 $ , which often occurs in models including an$S U(2)_L \times S U(2)_R$ bi-doublet [11, 12] and multiplets [13–15]. The VLQ-X is generally expected to decay into a top quark and W boson with a 100% branching ratio and have been widely studied (see, for example, [16–29]).At the Large Hadron Collider (LHC), VLQs can be produced in pair via their quantum chromodynamics (QCD) interactions, or singly produced depending on their EW interaction. The limits on their masses and the EW coupling strengths have been obtained by the ATLAS and CMS Collaborations [30–36]. Using an integrated luminosity of 35.9 fb–1 for data at 13 TeV, the CMS Collaboration recently presented a search for the pair-production of VLQ-X in a combination of same-sign dileptons (SSDL) and single-lepton final states [37]. The presence of the VLQ-X with mass of approximately 1.33 (1.30) TeV is excluded at 95% confidence level (CL) for the case of right (left)-handed couplings to W bosons. Such mass bounds could be relaxed if some new decay modes are possible in some NP models [38–40], that is,
$ X_{5/3}\to \bar{b}\pi_{6}\to \bar{b}tt $ ,$ X_{5/3}\to t\phi^{+} $ , and$ X_{5/3}\to b\phi^{++} $ in some realistic composite Higgs models (see, for example [41–44]).As we know, the future linear
$ e^{+}e^{-} $ colliders have the benefits of clear environment with operation at high center-of-mass energies. Especially, the future Compact Linear Collider (CLIC) will operate at energy of 3 TeV at the final stage [45–47]. Some new particles could be produced with a mass up to 1.5 TeV via pair production mechanisms duo to the kinematic limit, and up to 3 TeV via single production processes [48]. As shown in Refs. [49–56], the cross sections of single production processes for various types of VLQs are very sensitive to the EW coupling parameter. However, the cross sections for pair production processes only depend on the mass of VLQs for a given center-of-mass energy [57, 58]. A unique signature of VLQ-X is the inclusion of SSDL, which arises from the decay channel$ X\to t(\to bW^{+})W^{+} $ with the leptonic decay of the W boson. Previous studies [28, 29] have focused on the hadron colliders, such as the High-Luminosity LHC (HL-LHC) with$ \sqrt{s}=14 $ TeV, the High Energy LHC (HE-LHC) with$ \sqrt{s}=27 $ TeV, and the Future Circular Collider operating in hadron-hadron mode (FCC-hh) with$ \sqrt{s}=100 $ TeV. In this work, we focus on the observability of the VLQ-X via the pair production and associated single production processes at the future CLIC with$ \sqrt{s}=3 $ TeV.This paper is structured as follows. In Sec. II, we briefly introduce the simplified VLQ model and present the relevant experiment bounds on the VLQ-X. In Sec. III, we study the effect of initial-state radiation (ISR) on the cross section for pair production and associated single production processes at the 3 TeV CLIC. In Sec. IV, we analyze the properties of the signal and SM background; we also conduct simulations and calculate the exclusion and discovery capabilities at the 3 TeV CLIC. Finally, we provide a summary in Sec. V.
-
In our simplified
$ \left(X,T\right) $ doublet model, the VLQ-X is allowed to mix sizably only with the SM top quark, and the T-quark with electric charge of$ 2/3 $ is a top partner owing to its mixing with the SM up-type quarks. Note that in the$ \left(X,T\right) $ doublet, the mixing terms for left-handed and right-handed components are, respectively, proportional to the light quark masses and Yukawa masses, and thus, the left-handed mixing angle is typically smaller that the right-handed one (for details, see Refs. [10, 16–18]). An effective Lagrangian framework for the interactions of the heavy VLQ-X ($ m_{X}\gg m_{t} $ ) with the SM top quark through W gauge boson exchange is given by1 $\begin{aligned}[b] {\cal L}_{\rm X} =\;& \frac{gg^{\ast}}{\sqrt{2}}[\bar{X}_{R}W_{\mu}^+ \gamma^{\mu} t_{R}]+ \frac{7e}{6\cos\theta_{W}}[\bar{X}B_{\mu}\gamma^{\mu}X]\\&+ \frac{e}{2\sin\theta_{W}}[\bar{X}W^{3}_{\mu}\gamma^{\mu}X]+ {\rm h.c.},\end{aligned} $

(1) where g represents the
$ S U(2) $ gauge coupling constant,$ \theta_{W} $ is the Weinberg angle, and$ g^{\ast} $ indicates the coupling strength to SM quarks in units of standard couplings. Note that for a large mass of the VLQ-X (i.e.,$ m_{X}\gtrsim 1 $ TeV), the contributions of the left-handed components of the VLQ-X are suppressed by a factor$ (m_{t}/m_{X}) $ and can be safely neglected. Thus, the VLQ Lagrangian can be simplified as Eq. (1) at first order in the small light-heavy mixing [16]. From the above equation, we can select the coupling strength$ g^{\ast} $ and mass of the VLQ-X as free parameters. -
Recently, the CMS collaboration has searched for single production of the VLQ-X in the
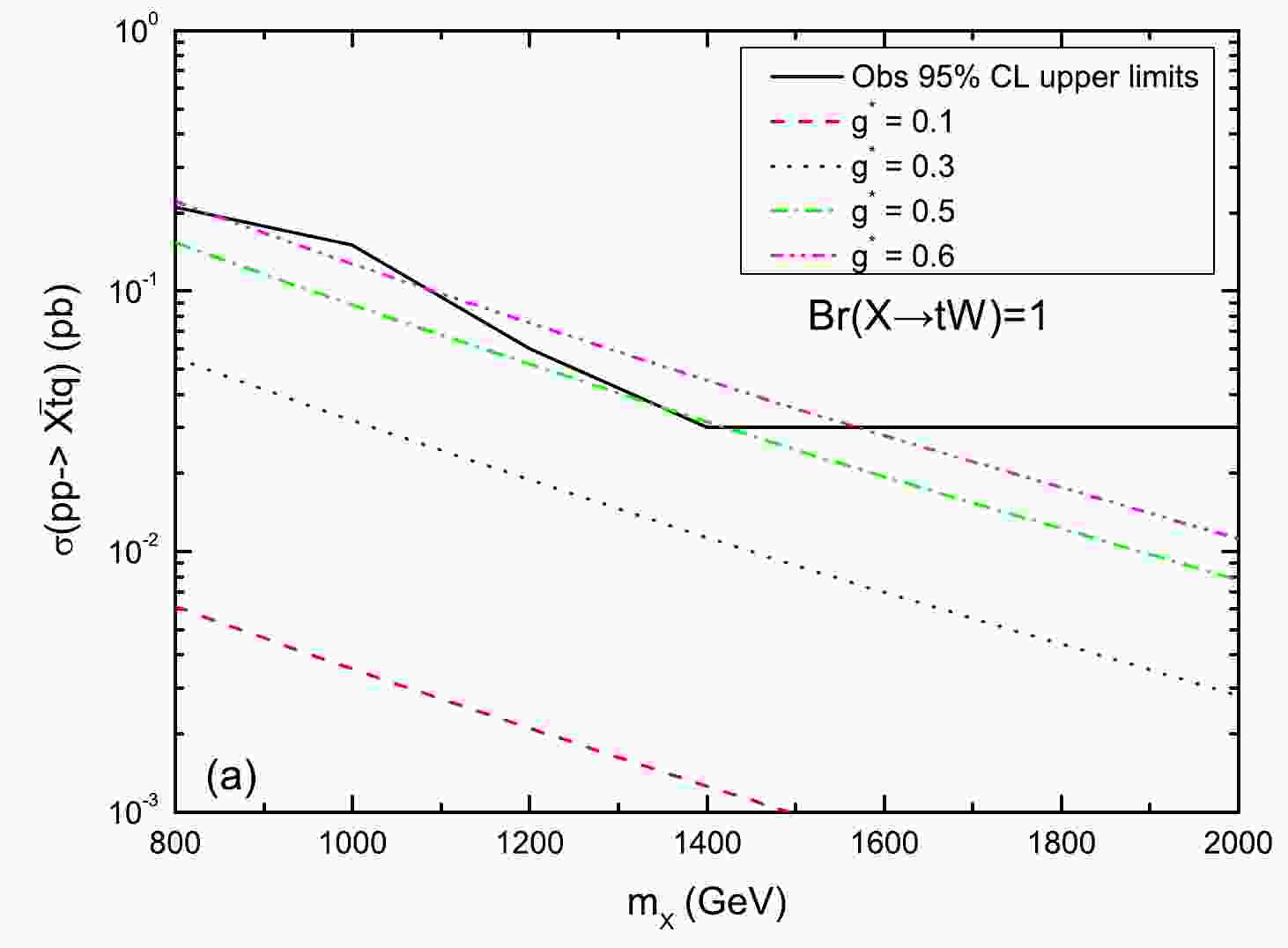
$ Wt $ decay channel by using data with an integrated luminosity of 35.9 fb–1. They focused on the final state including one muon or electron [35]. This search set the exclusion limits at a 95% CL on the product of the production cross section and branching ratio,$ \sigma\times Br(X\to tW) $ , as a function of the mass of the VLQ-X. In Fig. 1, we plot the cross section of the single production process as a function of$ m_X $ for$ Br(X\to tW)=1 $ and different values of$ g^{*} $ . As can be observed, the upper limit on the EW coupling parameter is approximately 0.5 for$ m_X=1400 $ GeV in the$ \left(X,T\right) $ doublet model. The indirect bound arises mainly from the oblique parameters S and T: the precise bound is mass dependent, that is,$ g^{\ast} =\sin\theta_{R}< 0.36\; (0.3) $ for$ m_{X}=1.5\; (2) $ TeV in the$ \left(X,T\right) $ doublet model [59]. The authors of Ref. [60] recently investigated the models with VLQs and performed a global fit in light of the Cabibbo angle anomaly. Here, we adopt a slightly looser value,$ g^{\ast}\leq 0.4 $ , as a phenomenologically guided limit.
Figure 1. (color online) Upper limits at 95% CL on the value of
$ \sigma(pp\to X\bar{t}q) $ as a function of$ m_X $ for${\rm Br} (X\to tW)=1$ and different values of$ g^{*} $ , where the solid line is the observed 95% CL exclusion limit from Ref. [35].Owing to its charge, the VLQ-X is assumed to only decay into a top quark and W boson, and therefore,
$ {\rm Br}(X\to tW) = $ 100%. However, such case could be changed when new decay channels exist for the VLQ-X. Particularly, the SM Higgs sector is extended by introducing new scalars, which are theoretically inspired by some realistic composite Higgs models (see for example [44] and references therein). Thus, for the pair production process, the branching ratio of$ X\to tW $ could be seen as a free parameter. The exclusion mass limits on the VLQ-X are shown in Fig. 2 as a function of its mass for three values of${\rm Br}(X\to tW)$ according to the recent results from CMS [37]. We can obtain that, for a smaller value of${\rm Br}(X\to tW)$ , the mass of the VLQ-X could be less than 1.0 TeV, and thus, the VLQ-X could be pair produced at the future CLIC with$ \sqrt{s}=3 $ TeV.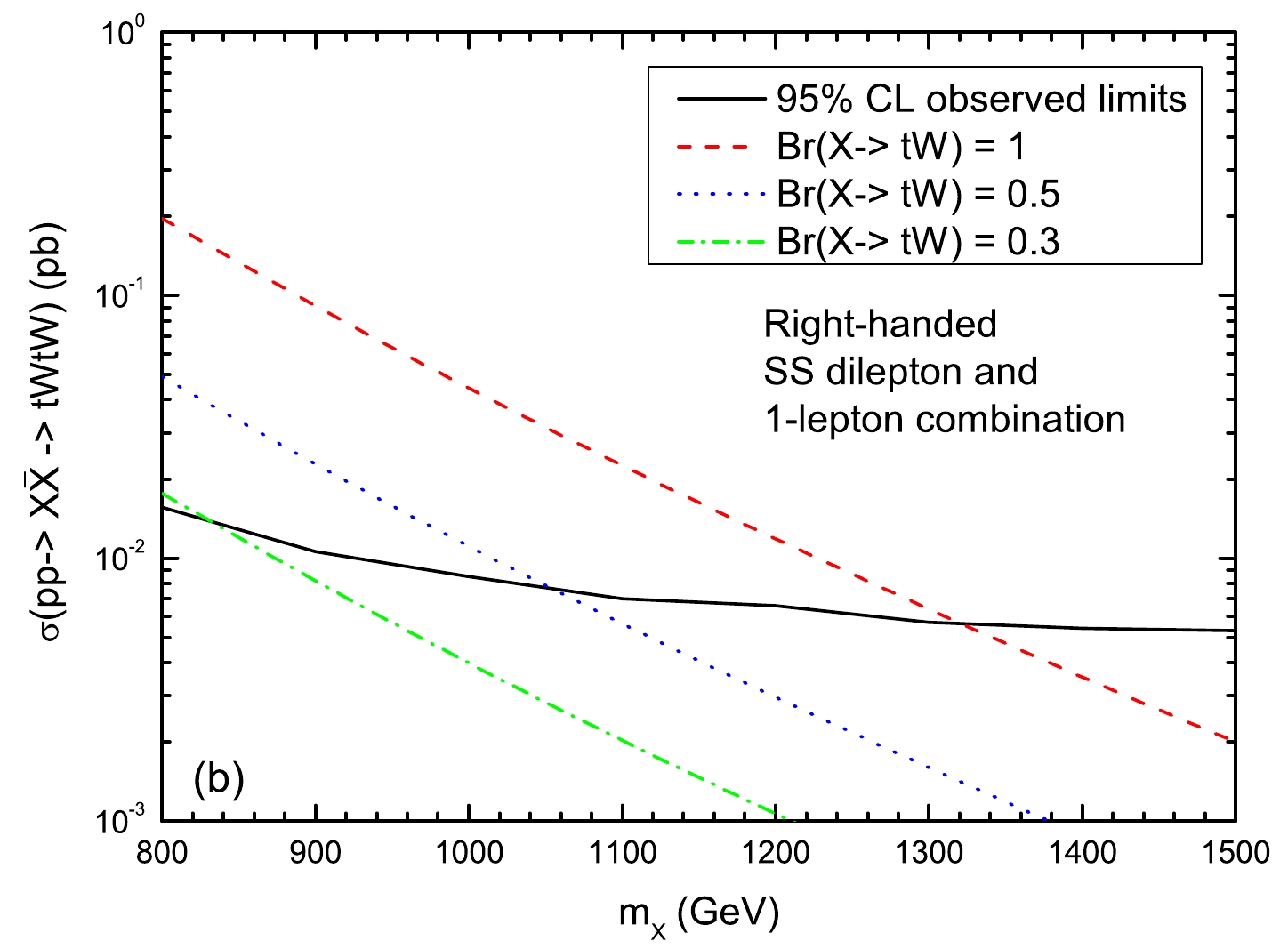
Figure 2. (color online) LHC exclusion limits on the value of
$ \sigma(pp\to X\bar{X}\to tW^{+}\bar{t}W^{-}) $ as a function of$ m_X $ for three different values of${\rm Br} (X\to tW)$ , where the solid line represents the observed 95% CL exclusion limits from the current CMS results [37]. -
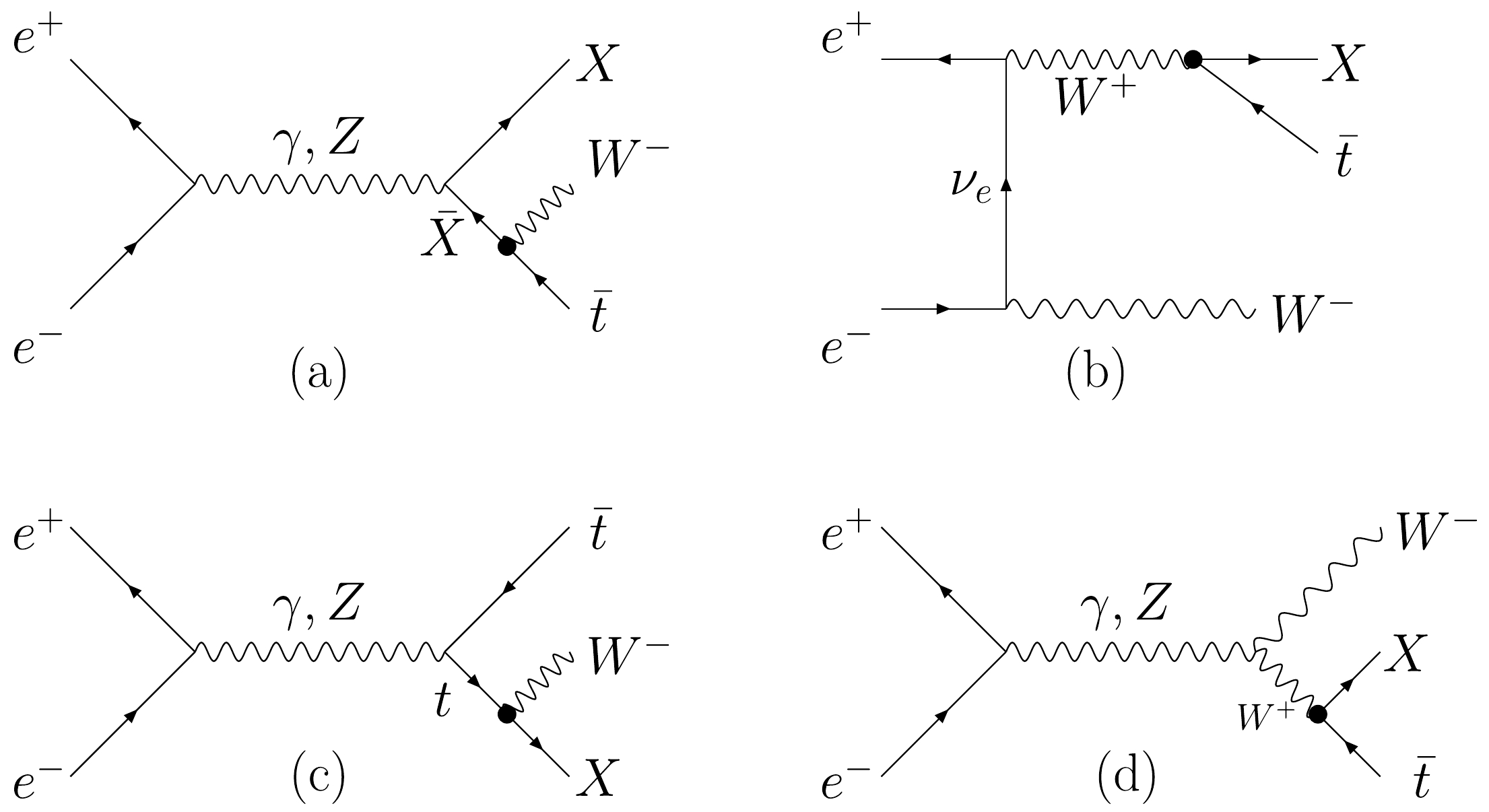
At the future 3 TeV CLIC, the VLQ-X can be pair-produced via the s-channel exchange of
$ \gamma/Z $ or singly-produced associated with a top quark and W boson. The cross section of the pair production process is only dependent on the VLQ-X mass. However, the cross section of the single production process is very sensitive to the coupling strength$ g^{*} $ . In Fig. 3, we show the representative Feynman diagrams at leading order for the single production process$ e^{+}e^{-}\to X\bar{t}W^{-} $ . Note that Fig. 3(a) plays a major role for the production cross section when the VLQ-X mass is smaller than$ \sqrt{s}/2 $ .In Fig. 4, we show the variation in the production cross section σ with the mass of the VLQ-X, with and without ISR and beamstrahlung effects, for the pair and single production processes at the 3 TeV CLIC, respectively. When the mass of the VLQ-X is smaller than half of the center-of-mass, that is, 1500 GeV, the cross section is insensitive to the coupling parameter
$ g^{*} $ . This occurs because the contribution arises mainly from the pair production process, as shown in Fig. 4(a). The cross section sharply changes when$ m_X \geq 1500 $ GeV and the values of σ are proportional to$ (g^{*})^{2} $ for a fixed$ m_X $ , as shown in Fig. 4(b). Meanwhile, the ISR and beamstrahlung effects can reduce the production cross section in the region of$ m_X\in $ [1000, 2500] GeV. For$ m_X=1.45 $ TeV, the cross section can reach approximaely 20.3 (35.5) fb with (without) the ISR and beamstrahlung effects. For$ m_X= $ 1.8 TeV and$ g^{*}=0.2 $ , the cross section is approximately 0.033 (0.047) fb with (without) the ISR and beamstrahlung effects. When the mass of the VLQ-X ranges from 1000 to 2500 GeV, the ratio of the cross-section considering the ISR and beamstrahlung effects to that without these effects changes from 0.96 to 0.57. Thus, it is necessary to account for these effects at the future 3 TeV CLIC. -
We perform a Monte Carlo simulation and explore the discovery potentiality of VLQ-X at the 3 TeV CLIC through the following decay channel:
$ X\to tW^+ \to bW^+W^+\to b\ell^+\ell^++\not E_{T}, $

(2) where
$ \ell=e,\mu $ . A representative Feynman diagram of the pair production and decay chain is presented in Fig. 5. Note that we do not consider the reconstruction or selection for other final particles, such as$ \bar{X}_{-5/3} $ in the pair production process and the associated produced anti-top quark and$ W^{-} $ boson in the single production process.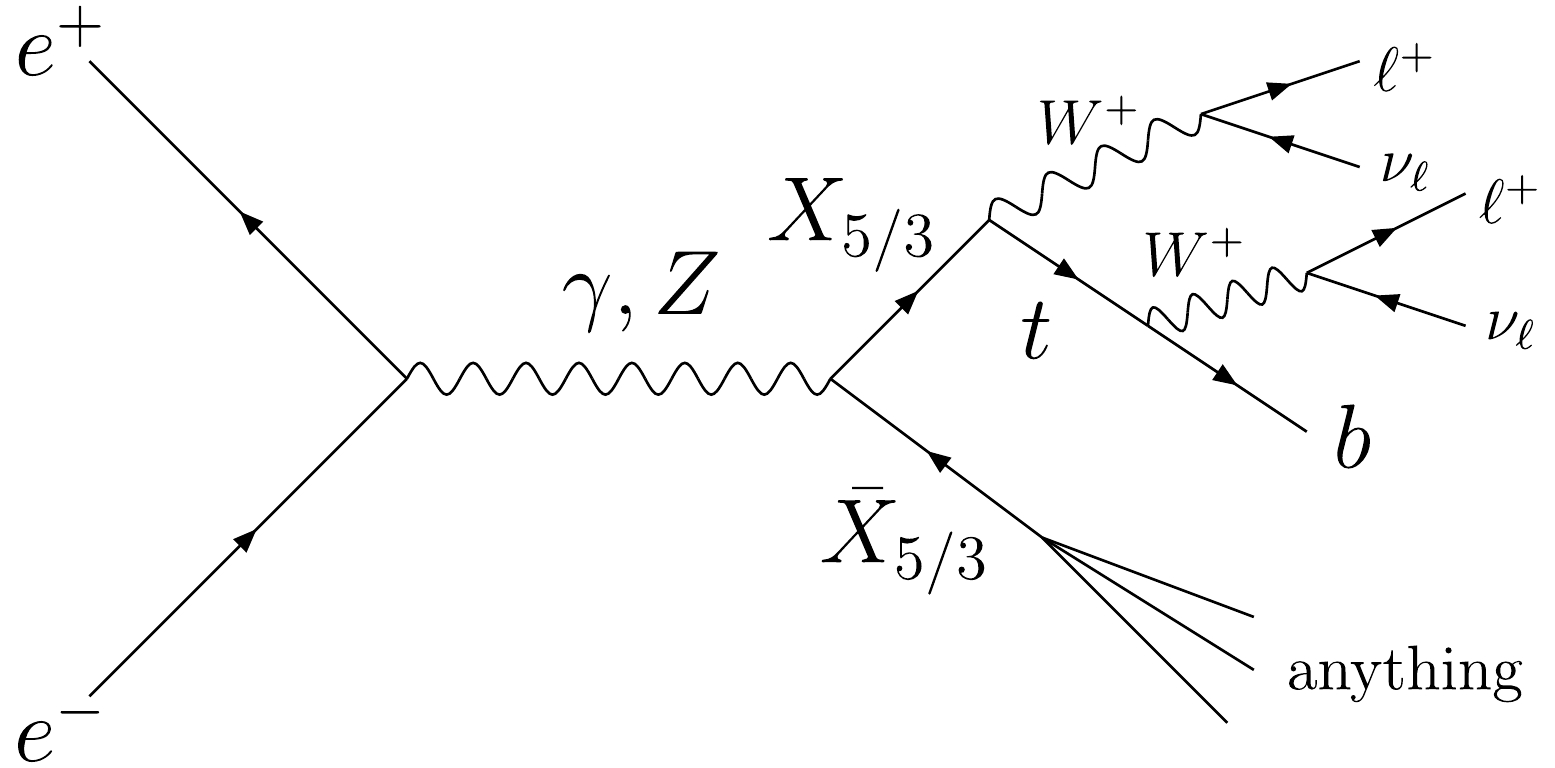
Figure 5. Representative Feynman diagram for the pair production of VLQ-X, including the decay chain
$X\to t(\to bW^{+})W^{+} $ $ \to b\ell^{+}\nu_{\ell}\ell^{+}\nu_{\ell}$ .For the signals, there are at least a pair of same-sign leptons (muons or electrons), one b-tagged jet, and missing transverse energy
$\not E_T$ . The dominant SM backgrounds come from the SM processes$ e^{+}e^{-}\to ZW^{+}W^{-} $ ,$ e^{+}e^{-}\to t\bar{t}Z $ ,$ e^{+}e^{-}\to t\bar{t}W^{+}W^{-} $ , and$ e^{+}e^{-}\to W^{+}W^{-}W^{+}W^{-} $ . We list their production cross sections and relevant decay modes in Table 1.Process Cross section (with ISR)/fb Cross section (no-ISR)/fb Decay modes $ e^{+}e^{-}\to ZW^{+}W^{-} $ 

35.7 33 $ Z\to \ell^{+}\ell^{-} $ ,

$ W^{+}\to \ell^{+} \nu $ ,

$ W^{-}\to jj $ 

$ e^{+}e^{-}\to t\bar{t}Z $ 

1.89 1.66 $ t\to W^{+}b (\bar{t}\to W^{-}\bar{b}) $ ,

$ W^{+}\to \ell^{+} \nu $ ,

$ Z\to \ell^{+}\ell^{-} $ 

$ e^{+}e^{-}\to t\bar{t}W^{+}W^{-} $ 

0.327 0.335 $ t\to W^{+}b (\bar{t}\to W^{-}\bar{b}) $ ,

$ W^{+}\to \ell^{+} \nu $ 

$ e^{+}e^{-}\to W^{+}W^{-}W^{+}W^{-} $ 

1.44 1.47 $ W^{+}\to \ell^{+} \nu $ ,

$ W^{-}\to jj $ 

Table 1. Cross sections of SM backgrounds with and without the ISR and beamstrahlung effects and decay mode at the 3 TeV CLIC.
The Monte Carlo event simulations for signal and SM background are generated using MadGraph5_aMC_ v3.3.2 [61] at the leading order. The parton showering, fragmentation, and hadronization are implemented by Pythia 8.20 [62]. Subsequently, fast detector simulations are performed using Delphes 3 [63]. The CLIC_card designed for 3 TeV is used for detector simulation [64], where the jets are clustered employing the Valencia Linear Collider (VLC) algorithm [65, 66] in exclusive mode, and the b-tagging efficiency is set to be 90%. Finally, data analysis is performed using MadAnalysis 5 [67].
To identify objects, we adopted basic cuts at the parton level for the signals and SM backgrounds as follows:
$\begin{aligned}[b]& p_{T}^{\ell/j/b}>\; 25\; {\rm{GeV}}, \quad |\eta_{\ell/b/j}|<\; 2.5, \\& \Delta R(x,y) > 0.4, \quad \not E_{T}> 50\; {\rm{GeV}}, \end{aligned}$

(3) where
$ p_{T}^{\ell/ j/b} $ denotes the transverse momentum of leptons, light jet, and b-tagged jet, respectively.$ \Delta R=\sqrt{\Delta\eta^{2}+\Delta\phi^{2}} $ is the particle separation in the rapidity (η)-azimuth (ϕ) plane, and x, y indicate different final particles ($ \ell $ , j, b).In Fig. 6, we plot some kinetic distributions for signals and SM backgrounds, such as the transverse momentum distributions of the leading and subleading leptons (
$ p_{T}^{\ell_{1,2}} $ ), the leading b-tagged jet ($ p_{T}^{b_{1}} $ ), and the invariant mass of the b-jet and leading lepton ($ M_{b\ell_{+}} $ ). Based on these distributions, we employ the following selection criteria to distinguish the signal from SM backgrounds: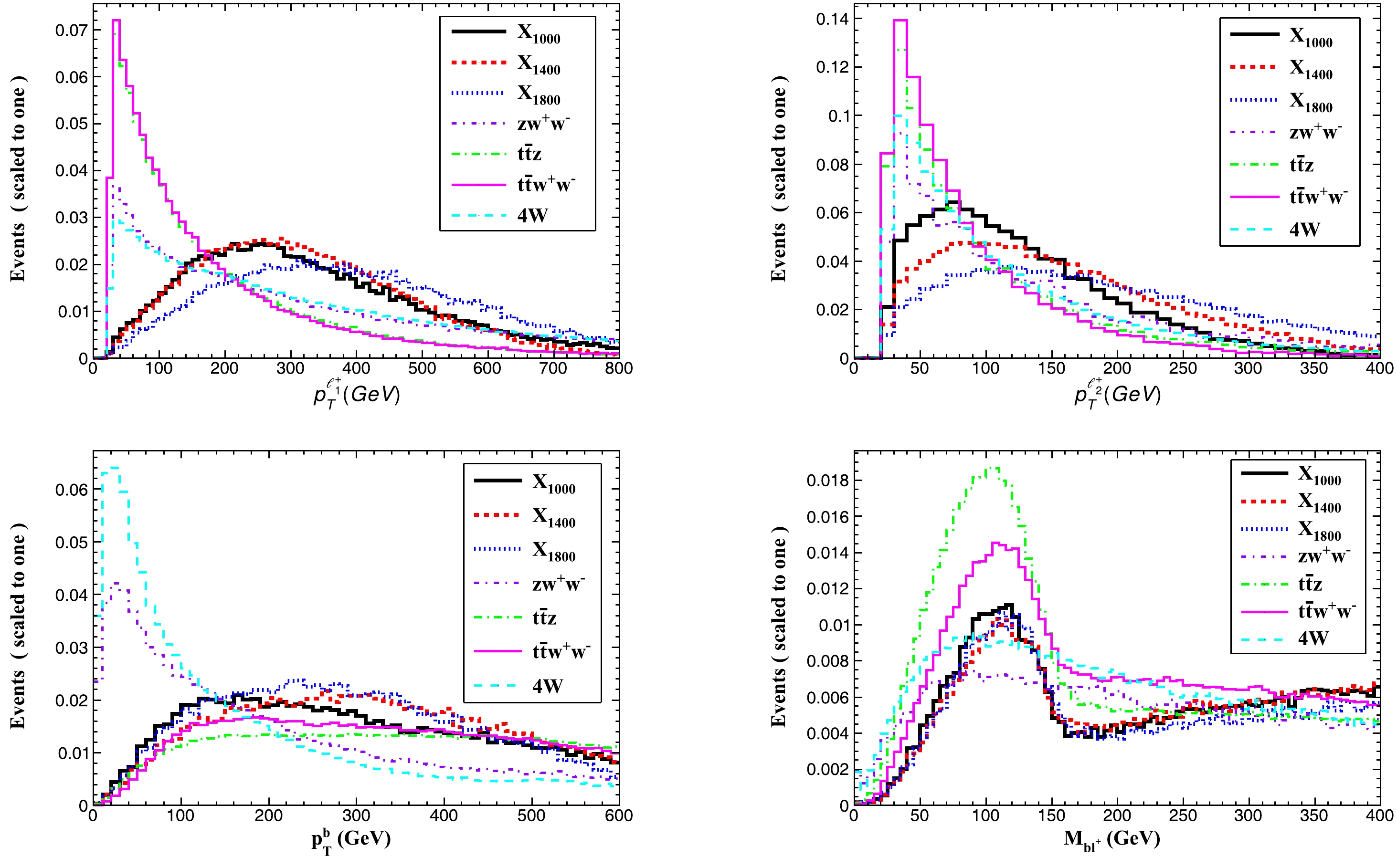
Figure 6. (color online) Normalized distributions for the signals (with
$m_{X}$ =1000, 1400, 1800 GeV) and SM backgrounds.● Cut-1: The events selected in the analysis are required to have exactly two same-sign isolated leptons (
$ N(\ell^{+})=2 $ ) with$ p_{T}^{\ell^{+}_{1}}> 150 \rm \; GeV $ and$ p_{T}^{\ell^{+}_{2}}> 70 \rm \; GeV $ .● Cut-2: For the purpose of suppressing the
$ Z\to \ell^{+}\ell^{-} $ background, events containing a pair of opposite-sign and same-flavour leptons whose invariant mass is within 10 GeV of the Z boson mass are rejected.● Cut-3: At least one b-tagged jet with
$ p_{T}^{b_{1}}> 120 \rm \; GeV $ is included. Besides, the invariant mass of the b-jet and the leading lepton should be$ M_{b\ell^{+}_{1}}< 160 $ GeV.The cross sections of two typical signals (
$ m_X=1000 $ and 1400 GeV) and the relevant backgrounds after imposing the cuts are presented in Table 2. Meanwhile, the cut flow of the efficiency for the signals with different VLQ-X masses is also presented in Table 3. By applying these cuts, it can be observed that the signals still have a relatively good efficiency, whereas the background processes are significantly suppressed.Cuts Signals Backgrounds 1000 GeV 1400 GeV $ ZW^{+}W^{-} $ 

$ t\bar{t}Z $ 

$ t\bar{t}W^{+}W^{-} $ 

$ 4W $ 

Basic 3.53 1.35 8.32 0.66 0.17 0.04 Cut-1 1.82 0.81 0.071 0.0084 0.0033 0.009 Cut-2 1.77 0.76 0.019 0.0021 0.0032 0.0084 Cut-3 1.17 0.53 0.001 0.0016 0.0025 0.00063 Table 2. Cut flows of the cross section (in fb) for the signals and backgrounds at the 3 TeV CLIC.
$ m_X $ (GeV)

1000 1200 1400 1600 1800 2000 Cut-1 0.50 0.55 0.57 0.60 0.62 0.63 Cut-2 0.49 0.52 0.54 0.57 0.59 0.60 Cut-3 0.32 0.35 0.38 0.41 0.43 0.43 Table 3. Signal efficiencies for the selection cuts with different VLQ-X masses.
To analyze the sensitivity, we use the statistical significance for the expected discovery (
$ {\cal{Z}}_{\rm{disc}} $ ) and exclusion ($ {\cal{Z}}_{\rm{excl}} $ ) limits [68]:$ \begin{aligned}[b]\\[-10pt] {\cal{Z}}_{\rm{disc}} &= \sqrt{2\left[(s+b)\ln\left(\frac{(s+b)(1+\delta^2 b)}{b+\delta^2 b(s+b)}\right) - \frac{1}{\delta^2 }\ln\left(1+\delta^2\frac{s}{1+\delta^2 b}\right)\right]} \\ {\cal{Z}}_{\rm{excl}} &=\sqrt{2\left[s-b\ln\left(\frac{b+s+x}{2b}\right) - \frac{1}{\delta^2 }\ln\left(\frac{b-s+x}{2b}\right)\right] - \left(b+s-x\right)\left(1+\frac{1}{\delta^2 b}\right)}, \end{aligned} $ 
(4) with
$ x=\sqrt{(s+b)^2- 4 \delta^2 s b^2/(1+\delta^2 b)}, $

(5) where s and b denote the expected number of events for the signal and background, respectively. These values could be obtained by multiplying the production cross sections after the above cuts and the integrated luminosity, respectively. δ denotes the percentage systematic uncertainty on the estimated SM background. In the remainder of this article, we take a mild systematic uncertainty of δ = 10%.
As discussed before, the pair production process is dominant for
$ m_X<1500 $ GeV, and we can take${\rm Br}(X\to tW)$ as a free parameter. In Fig. 7, we present the exclusion limit ($ 2\sigma $ ) and$ 5\sigma $ discovery potential at the 3 TeV CLIC with four typical integrated luminosities: 100, 300, 3000, and 5000 fb–1. As can be observed, for the 3 TeV CLIC with an integrated luminosity of 5000 (1000) fb–1, the VLQ-X can be excluded in the regions of${\rm Br}(X \to tW)\in [0.002, 0.021]\; ([0.006, 0.041])$ and$ m_X\in $ [1000, 1490] GeV, whereas the discovery regions can reach$ {\rm Br}(X\to tW)\in [0.0064, 0.065]\; ([0.014,0.145]) $ and$ m_X\in $ [1000, 1490] GeV. Even for the integrated luminosity of 100 fb–1, the VLQ-X can be excluded in the regions of$ {\rm Br}(X\to tW)\in [0.026, 0.27] $ and$ m_X\in $ [1000, 1490] GeV, whereas the discovery regions can reach${\rm Br}(X\to tW) \in [0.06, 0.62]$ .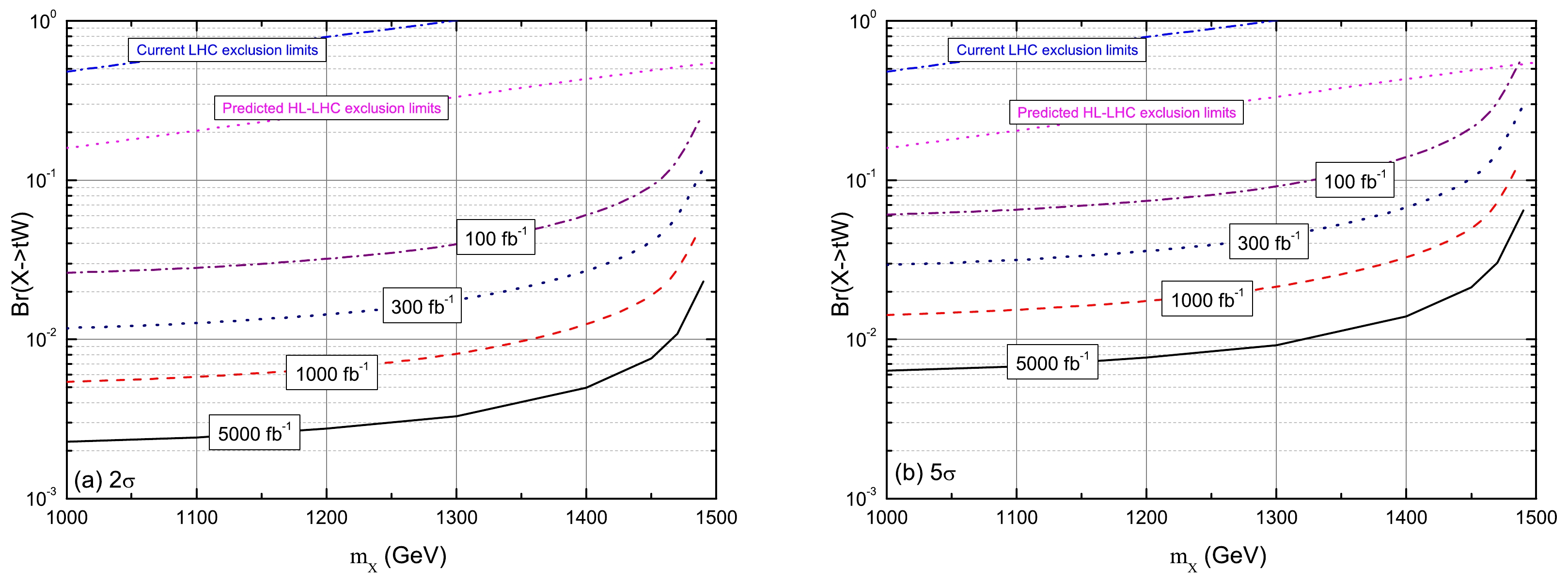
Figure 7. (color online) Exclusion limit (at
$ 2\sigma $ ) and discovery prospects (at$ 5\sigma $ ) contour plots for the signal in${\rm Br}(X\to tW)-m_{X}$ planes at the 3 TeV CLIC with four typical integral luminosities: 100, 300, 3000, and 5000 fb-1.For comparison, we also present the observed 95% CL exclusion limits according to the recent CMS result [37], and the predicted exclusion limits at the HL-LHC reach with a luminosity of 3 ab–1 at 13 TeV. Note that the predicted exclusion limits at the HL-LHC are obtained by rescaling the event numbers of signal and background with the increased luminosity, where the cross sections for the signals induced by the pair production process are proportional to the squared values of
${\rm Br}(X\to tW)$ . We can observe that for$ m_X< 1500 $ GeV, the future CLIC with$ \sqrt{s}=3 \rm \; TeV $ could provide much better sensitivity than those reported in current experimental searches and predicted at the future HL-LHC. Certainly, for a heavier$ m_X $ , we need a more energetic lepton collider, such as the future high-energy muon colliders [69].For a larger VLQ-X mass, that is,
$ m_{X}\geq 1500 $ GeV, the associated single production process is dominant and the cross section is sensitive to the EW coupling parameter. In this case, we take${\rm Br}(X\to tW)=1$ and show the contour plots of exclusion and discovery capability on the$ g^{*} - m_{X} $ plane at the 3 TeV CLIC in Fig. 8. It can be observed that$ 5\sigma $ discovered regions are$g^{*}\in [0.04, 0.4] ([0.06,0.4])$ and$m_{X}\in [1500, 1850 ] ([1500,1800])$ GeV at the 3 TeV CLIC with an integrated luminosity of 5 (3) ab–1. Out of a discovery, the VLQ-X can be excluded in the correlated parameter space of$g^{*}\in [0.023, 0.35] ([0.026,0.4])$ and$ m_{X}\in [1500, 2000 ] $ GeV for the same integrated luminosity. Note that the region in this study is almost located in$ \Gamma_{X}/m_{X} $ < 10%, and thus, the narrow-width approximation is reasonable in our study.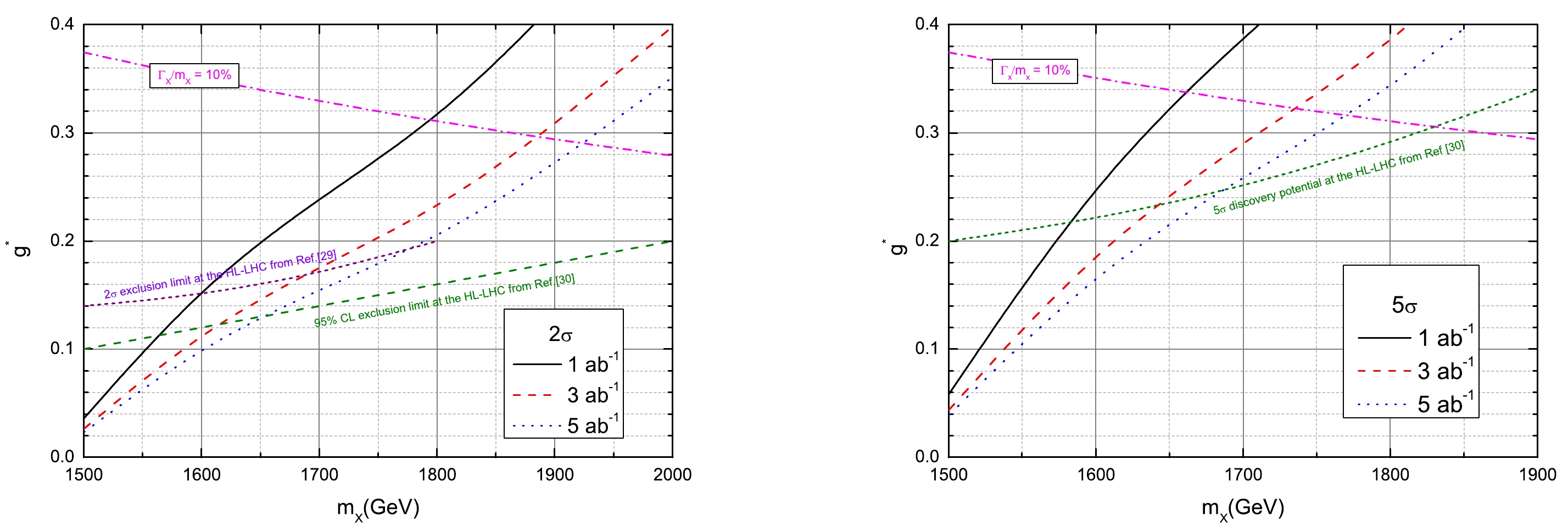
Figure 8. (color online) Exclusion limit (left) and discovery prospects (right) contour plots in the
$ g^{*}-m_{X} $ planes at the future 3-TeV CLIC with three typical integrated luminosities: 1, 3, and 5 ab–1. The short-dashed lines denote the contours of$ \Gamma_{X}/m_{X} $ = 10%. Note that the recent exclusion and discovery capabilities at the HL-LHC are also presented with an integrated luminosity of 3 ab–1 [28, 29].Very recently, the authors in Refs. [28, 29] investigated the expected limits for the right-handed VLQ-X in the (X, T) doublet via the single production of the X followed decay channel
$ X\to tW $ at the HL-LHC and future high-energy$ pp $ colliders. Assuming an integrated luminosity of 3 ab–1 at the HL-LHC with the systematic uncertainty$ \delta=0\; $ (30%), the VLQ-X can be excluded up to approximately 1800 (1680) GeV for the typical coupling parameter$ \sin\theta_{R}=g^{*}=0.2 $ [28]. In Fig. 8, we also display the exclusion and discovery capabilities at the HL-LHC with an integrated luminosity of 3 ab–1 without considering the systematic error. Considering the SSDL final state, the future 14 TeV HL-LHC can exclude the correlated regions of the mixing constant$ g^{*}\in [0.1, 0.2] $ and$ m_{X}\in $ [1500, 2000] GeV for$ R_{L}=0 $ [29], whereas the discovered correlated regions are approximately$ g^{*}\in $ [0.2, 0.34] and$ m_{X}\in [1500, 1900] $ GeV. Thus, we expect that our study can drive complementary searches of a possible doublet VLQ-X at the future 3 TeV CLIC. -
In a simplified model, we investigated the production of the VLQ-X at the future 3 TeV CLIC via the pair and associated single production processes. We performed a detector level simulation for the signals and the relevant SM backgrounds by focusing on the final states including two same-sign leptons (electrons and muons), one b-tagged jet, and missing energy. From our numerical calculations and the phenomenological analysis we drew the following conclusions:
1. For
$ m_{X}< 1500\; $ GeV, the pair production process is dominant, and we take the branching ratio of$ X\to tW $ as a free parameter. Assuming a 10% systematic uncertainty on the background event rate, in the region of$ m_X\in $ [1000, 1490] GeV, the VLQ-X quark can be excluded in the region of${\rm Br} (X\to tW)\in [0.002, 0.021]\; ([0.026,0.27])$ at the 3 TeV CLIC with the integrated luminosity of 5000 (100) fb-1, whereas the discovery region can reach${\rm Br}(X\to tW)\in [0.0064, 0.065]\; ([0.06, 0.62])$ . These sensitivities are much better than those reported in current experimental searches as well as those predicted at the future HL-LHC.2. For
$ m_{X}\geq 1500 $ GeV, the associated single production process is major, and the cross section is proportional to the squared value of the EW coupling strength$ g^{*} $ . At the future 3 TeV CLIC with an integrated luminosity of 5 ab–1, the VLQ-X can be excluded in the regions of$ g^{\ast}\in [0.023, 0.35] $ and$ m_X\in $ [1500, 2000] GeV, whereas the discovery regions can reach$ g^{\ast}\in [0.04, 0.4] $ and$ m_X\in $ [1500, 1850] GeV. We expect that the signatures studied here will provide complementary information for detecting the VLQ-X at the future 3 TeV CLIC. -
The authors are grateful to Y.-B Liu for motivating discussions during the course of this project.
Search for an exotic vectorlike X-quark in same-sign dilepton final states at the future 3 TeV CLIC
- Received Date: 2024-02-29
- Available Online: 2024-07-15
Abstract: Vectorlike quarks (VLQs) with masses at the TeV-scale have been predicted in many new physics scenarios beyond the Standard Model (SM). Based on a simplified





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: