Particle-number conserving analysis of the πd_5/2 band in ^{117,119,121,123,125}Cs

The nuclei in the $ A \approx 120 $ mass region are generally classified as transitional, exhibiting structural characteristics between spherical and well-deformed shapes ($ 2.0 < R_{4/2} < 3.33 $). Due to their complex and diverse nuclear configurations, these nuclei are at the forefront of nuclear structure research, offering valuable insights into the evolution of nuclear shapes and shell structure. Recent studies on the cesium isotopic chain have revealed a variety of exotic nuclear phenomena, including shape coexistence [1], signature inversion [2], octupole correlation [3−5], band termination[6]. These phenomena have been explored through detailed experiments, including the extension of rotational bands to high spin, the measurement of isomer lifetimes, and the assignment of spin and parity for various states based on directional correlation (DCO) ratios[1, 5, 7−19]. These detailed studies reveal unique structural properties throughout the isotopic chain.

Various theoretical models have been applied to investigate these phenomena [2, 13, 15, 16, 18, 20−26]. The characteristics of the $ \pi g_{9/2} $ band in odd-A ^119−125Cs nuclei are reasonably well reproduced within the framework of the particle-plus-rotor and particle-plus-vibrator models [18]. Cranked Shell Model (CSM) has been used to analyze the crossing frequencies for the $ \pi h_{11/2} $ band and the $ \pi g_{9/2} $ band in the odd-mass Cs isotopes[15]. Meanwhile, boson-fermion and core-quasiparticle coupling models have been used to describe the level structure in ¹²³Cs [13]. Although these theories explain various experimental phenomena, the upbending and backbending observed in the $ \pi d_{5/2} $ band of odd-even ^117−125Cs still requires further discussion.

Comprehensive investigations of the rotational bands in the odd-mass ^117−125Cs isotopes have produced an extensive set of experimental data. These analyses consistently reveal the occurrence of upbending and backbending phenomena in both the $ \pi h_{11/2} $ and $ \pi d_{5/2} $ bands across this isotopic chain. It is well known that the backbending and upbending phenomena are caused by the alignment of the high-j low-Ω orbitals [27]. Based on present analysis[7, 9, 12, 15, 16, 21, 28], the upbending observed in the $ \pi h_{11/2} $ band at rotational frequencies around $ \hbar\omega\sim0.40 $ MeV and 0.425 MeV has been attributed to the alignment of a pair of [$ \nu h_{11/2} $]². In contrast, the $ \pi d_{5/2} $ band exhibits distinct upbending and backbending at different frequencies, approximately $ \hbar\omega\sim0.20 $ MeV in ^117,119,121Cs, and at $ \hbar\omega\sim0.40 $ MeV in ^117,119Cs, and and $ \hbar\omega\sim0.70 $ MeV in ¹²¹Cs, in ^123,125Cs the backbending exists at $ \hbar\omega\sim0.30 $ MeV.The variation in the frequency for the $ \pi d_{5/2} $ band across odd-mass ^117−125Cs isotopes suggests that the underlying mechanism may involve contributions from different orbitals, emphasizing the importance of further detailed investigation to elucidate the nature of these alignments.

To investigate the underlying mechanism of the upbending and backbending behavior, the cranked shell model (CSM) with the pairing correlations treated by a particle-number-conserving (PNC) method is employed to study the $ \pi d_{5/2} $ band in odd-mass ^117−125Cs isotopes. Unlike the conventional Bardeen-Cooper-Schrieffer (BCS) or Hartree-Fock-Bogoliubov (HFB) approach, in PNC-CSM method, the Hamiltonian of ground state and excited state are diagonalized in a large CMPC (Cranked many-particle configuration) space directly. Therefore the particle number is conserved exactly and the Pauli blocking effects are taken into account simultaneously [29−31]. The PNC-CSM method has been successfully applied to describle the high-K isomers in the rare-earth [32−36] as well as in superheavy nuclei region[37−42]. In this work, a detailed theoretical investigation of the rotational properties and pairing correlations in odd-A ^117−125Cs isotopes is presented. The results provide valuable insights into the underlying nuclear structure and the evolution of configurations in these nuclei.

The paper is organized as follows. A brief introduction of the PNC treatment of pairing correlations within the CSM is presented in Sec. II. The numerical details, including Nilsson parameters (κ, μ), the deformation parameters, and pairing parameters are given in Sec. III. The PNC-CSM calculation and analysis for the $ \pi d_{5/2} $ band of odd-even ^117−125Cs are presented in Sec. IV. A brief summary is given in Sec. V.

The cranked shell model Hamiltonian of an axially symmetric nucleus in the rotating frame can be written as

where $ H_{\rm 0}=H_{\rm Nil}-\omega J_{x} $ is one-body part of $ H_{\rm CSM} $, $ H_{\rm Nil} $ is the Nilsson Hamiltonian, $ -\omega J_{x} $ is the Coriolis interaction with cranking frequency ω about the x axis, perpendicular to the nuclear symmetrical z axis. $ H_{\rm P}=H_{\rm P}(0)+H_{\rm P}(2) $ is the pairing interaction:

where $ \bar{\xi}(\bar{\eta}) $ labels the time-reversed state of a Nilsson state $ \xi(\eta) $, $ q_2(\xi)=\sqrt{16\pi/5}\langle\xi|r^2 Y_{20}|\xi \rangle $ is the diagonal element of the stretched quadrupole operator. And, $ G_0 $ and $ G_2 $ are the effective strengths of monopole and quadrupole pairing interactions, respectively.

Instead of the usual single-particle level truncation in conventional shell model calculations, a cranked many-particle configuration truncation (Fock space truncation) is adopted which is crucial to make the particle-number conserving calculations for low-lying excited states workable and sufficiently accurate. An eigenstate of $ H_{\rm CSM} $ is written as

where $ |i\rangle $ is a CMPC (an eigenstate of the one-body operator $ H_{\rm 0} $). By diagonalizing $ H_{\rm CSM} $ in a sufficiently large CMPC space to obtain the yrast and low-lying eigenstates.

The angular momentum alignment for the state $ |\psi\rangle $ is

Because $ J_x $ is a one-body operator, $ \langle i|J_x|j\rangle (i\neq j) $ may not vanish when two cranked many-particle configurations $ |i\rangle $ and $ |j\rangle $ differ by only one particle occupation [30]. After a certain permutation of creation operators, $ |i\rangle $ and $ |j\rangle $ can be recast into $ |i\rangle=(-)^{M_{i\mu}}|\mu...\rangle $ and $ |j\rangle=(-)^{M_{j\nu}}|\nu...\rangle $, where the ellipsis “...” stands for the same particle occupation and $ (-1)^{M_{i\mu}} =\pm 1,\quad(-1)^{M_{j\nu}}=\pm 1 $ according to whether the permutation is even or odd, respectively. Therefore, the angular momentum alignment of $ |\psi\rangle $ can be expressed as

where the diagonal contribution $ j_x (\mu) $ and the off-diagonal (interference) contribution $ j_x(\mu\nu) $ can be written as

where $ n_{\mu}=\sum_i|C_i |^2P_{i\mu} $, is the occupation probability of the cranked orbital $ |\mu \rangle $, $ P_{i\mu} $ = 1 if $ |\mu \rangle $ is occupied in $ |i \rangle $, and $ P_{i\mu} $ = 0 otherwise.

In the present work, the Nilsson parameters κ and μ for the odd-mass ^117−125Cs are adopted from Ref. [44]. The effective pairing strengths can be determined based on the odd-even mass differences in binding energies, and are closely related to the size of the truncated cranked many-particle configuration (CMPC) space. For the odd-even ^117−125Cs isotopes, the CMPC space is constructed for both protons and neutrons using the major shells from $ N=3 $ to $ N=5 $, with the configuration space dimension taken to be approximately 1000 for both protons and neutrons. The corresponding effective pairing strengths used in the calculations for ^117,119,121Cs are $ G_{\rm 0p} $ = 0.52 MeV, $ G_{\rm 2p} $ = 0.003 MeV, $ G_{\rm 0n} $ = 0.70 MeV and $ G_{\rm 2n} $ = 0 MeV. For ^123,125Cs, the effective pairing strengths are $ G_{\rm 0p} $ = 0.48 MeV, $ G_{\rm 2p} $ = 0.01 MeV, $ G_{\rm 0n} $ = 0.70 MeV and $ G_{\rm 2n} $ = 0.03 MeV.

The deformation parameters ($ \varepsilon_2, \varepsilon_4 $) adopted in the present study for the odd-mass ^117−125Cs isotopes are listed in Table 1. Among these nuclei, an experimental value of the quadrupole deformation parameter $ \varepsilon_{2}=0.32 $, has been reported only for the $ \pi g_{9/2} $ band in ¹¹⁹Cs [45]. The rotational band structures of ¹¹⁷Cs and ¹²¹Cs exhibit similar characteristics to those observed in ¹¹⁹Cs, hence, their deformation parameters are adopted based on the analysis of ¹¹⁹Cs. Meanwhile, the rotational behaviors of ¹²³Cs and ¹²⁵Cs resemble those of ¹¹³Cs[46] and their deformation parameters are taken from Ref.[47]. It can be seen that the $ \varepsilon_2 $ adopted in the present work decreases with the number of neutron increasing, which is consistent with Ref.[18, 47].

	117Cs	119Cs	121Cs	123Cs	125Cs
$ \varepsilon_2 $	0.330	0.320	0.315	0.228	0.223
$ \varepsilon_4 $	0.020	0.010	0.018	0.032	0.030

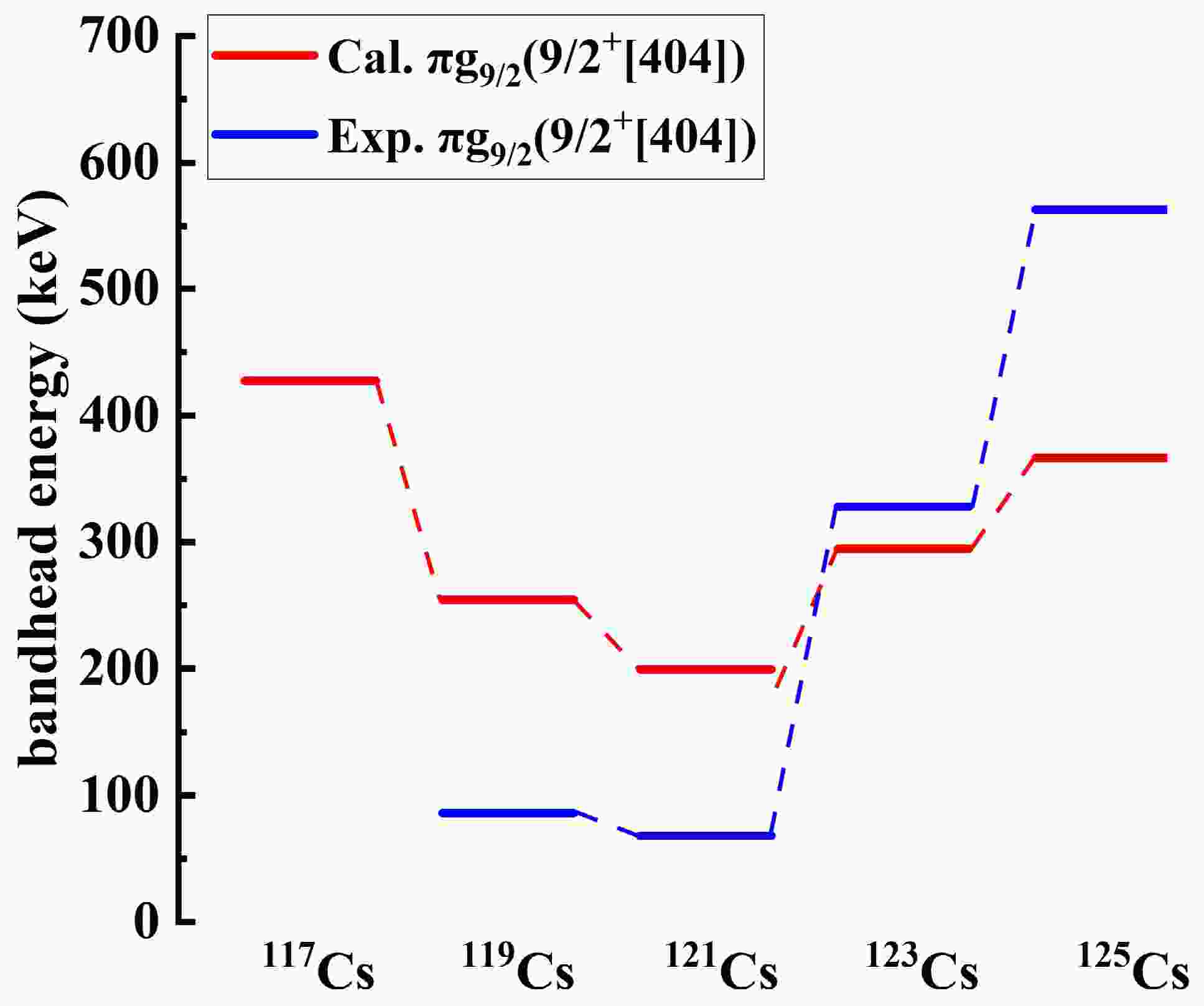
Table 1.  Deformation parameters ($ \varepsilon_2 $,$ \varepsilon_4 $) used in the PNC-CSM calculations for odd-even ^117−125Cs

Fig.1 presents the calculated band-head energies of the $ \pi g_{9/2} $ band obtained using the PNC-CSM approach. The theoretical results are in good agreement with the experimental data, thereby supporting the reliability of the deformation parameters adopted for the odd-even ^117−125Cs isotopes.

Figure 1.  (Color online) The experimental and calculated band-head energies of πg_9/2 band built on the $ \pi[404] $9/2⁺ orbital in odd-even ^117−125Cs. The experimental band-head energies are denoted by blue lines. The calculated band-head energies are denoted by red lines.The experimental data are taken from Refs. [9, 10, 12, 43].

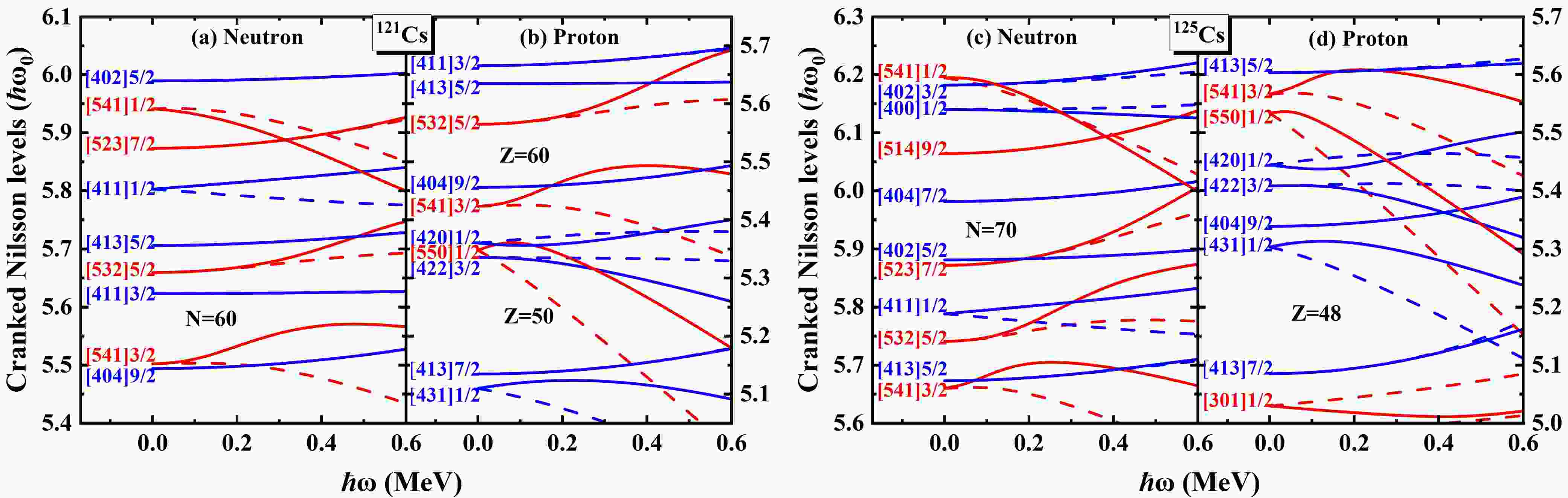
Figure 2 shows the calculated cranked Nilsson levels near the Fermi surface of ¹²¹Cs and ¹²⁵Cs. The positive (negative) parity levels are denoted by blue (red) lines. The signature $ \alpha=+1/2 $ ($ \alpha=-1/2 $) levels are denoted by solid (dotted) lines. The cranked Nilsson level structures near the Fermi surface of ¹¹⁷Cs and ¹¹⁹Cs are similar to those of ¹²¹Cs, while the levels near the Fermi surface of ¹²³Cs exhibit similarities to those of ¹²⁵Cs. These diagrams were employed to determine the quasiparticle orbitals in closest proximity to the proton and neutron Fermi surfaces [9]. Note that for ¹²¹Cs, the $ \pi [420]1/2 $, $ \pi [422]3/2 $, $ \pi [550]1/2 $ and $ \pi [541]3/2 $ ortitals are close to each other, thus the components of the bands built on those orbitals may mix. In the present calculation, it is evident that there is a neutron gap at $ N=60 $ and proton gaps at $ Z=50 $ and 60 in ¹²¹Cs. With decreasing $ \varepsilon_2 $, the $ \pi [431]1/2 $ orbital approaches the Fermi surface, resulting in a shift of the proton shell gap from $ Z=50 $ to $ Z=48 $. In the case of neutrons, a subshell gap is observed at $ N=70 $ for ¹²⁵Cs.

Figure 2.  (Color online) Single-particle Routhians located in the vicinity of the Fermi level of ¹²¹Cs and ¹²⁵Cs as a function of rotational frequency for: (a) and (b) cranked Nilsson levels of ¹²¹Cs; (c) and (d) cranked Nilsson levels of ¹²⁵Cs. Positive (negative) parity Routhians are shown by blue (red) lines. Solid (dotted) lines are used for signature $ \alpha=+1/2 $ ($ \alpha=-1/2 $).

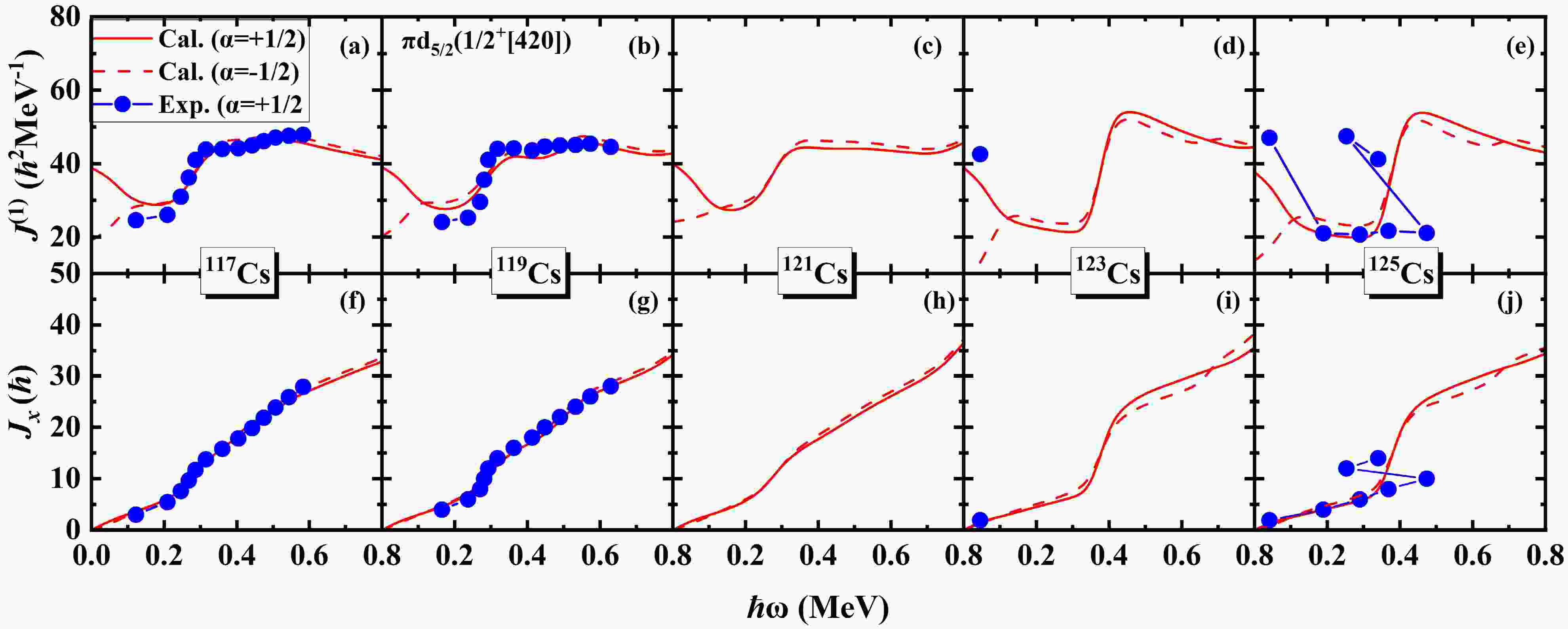
Figure 3 shows the experimental and calculated MOIs and alignments of the $ \pi d_{5/2} $ band in odd-even ^117−125Cs. The experimental MOIs and alignments are denoted by solid dots (α=+1/2). The calculated MOIs and alignments are denoted by solid lines (α=+1/2) and dashed lines (α=-1/2). The PNC-CSM calculations identify this band as the $ \pi1/2^+[420] $ configuration, an orbital which originates from the $ \pi d_{5/2} $ spherical shell. Since no experimental data are available for $ \alpha=-1/2 $, only the theoretical results are displayed. The PNC-CSM calculations agree well with the experimental data for ¹¹⁷Cs and ¹¹⁹Cs. For ¹²¹Cs, where experimental data are unavailable, only calculated results are presented. For ¹²³Cs and ¹²⁵Cs, the calculated results show satisfactory agreement with the experimental data, exhibiting only small discrepancies. As shown in Fig.3, the first upbending in ^117,119Cs occurs at a rotational frequency of approximately $ \hbar \omega\sim0.20 $ MeV, followed by a second upbending around $ \hbar \omega\sim0.40 $ MeV. In the case of ¹²¹Cs, the first upbending is similar to ^117,119Cs which is observed near $ \hbar \omega\sim0.20 $ MeV. The cranked Nilsson levels for ¹²¹Cs are similar to ¹¹⁷Cs and ¹¹⁹Cs, but the neutron Fermi surface changes with the increase of neutron number. Therefore the second upbending for ¹²¹Cs shifts to a higher frequency which is around $ \hbar \omega\sim0.70 $ MeV. For the heavier isotopes ¹²³Cs and ¹²⁵Cs, the backbending occurs around $ \hbar \omega\sim0.30 $ MeV. These systematic variations indicate that the rotational behavior of the $ \pi d_{5/2} (1/2^+[420]) $ band evolves with an increasing mass number in the odd-mass Cs isotopes. It is well known that backbending phenomena is associated with the alignment of high-j intruder orbitals [27], which, in this mass region, correspond to the proton and neutron $ h_{11/2} $ orbitals [46]. The different upbending and backbending mechanisms in odd-even ^117−125 Cs will be discussed separately in the following.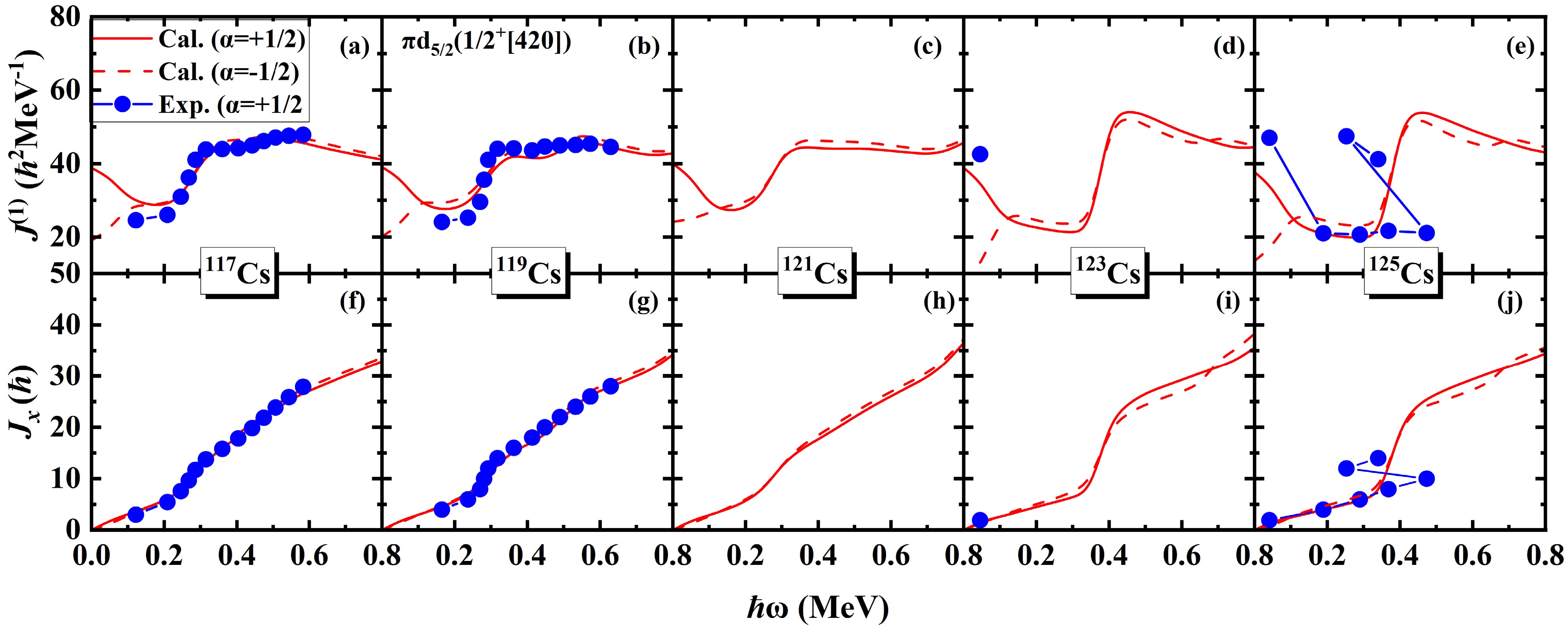

Figure 3.  (Color online) The experimental and calculated MOIs $ J^{(1)} $ (upper panels) and alignments $ J_{x} $ (lower panels) of the $ \pi d_{5/2} (1/2^+[420]) $ band in odd-even ^117−125Cs. The experimental MOIs and alignments are denoted by solid dots (α=+1/2). The calculated MOIs and alignments are denoted by solid lines (α=+1/2) and dashed lines (α=-1/2). The experimental data are taken from Refs. [7, 9, 10, 12].

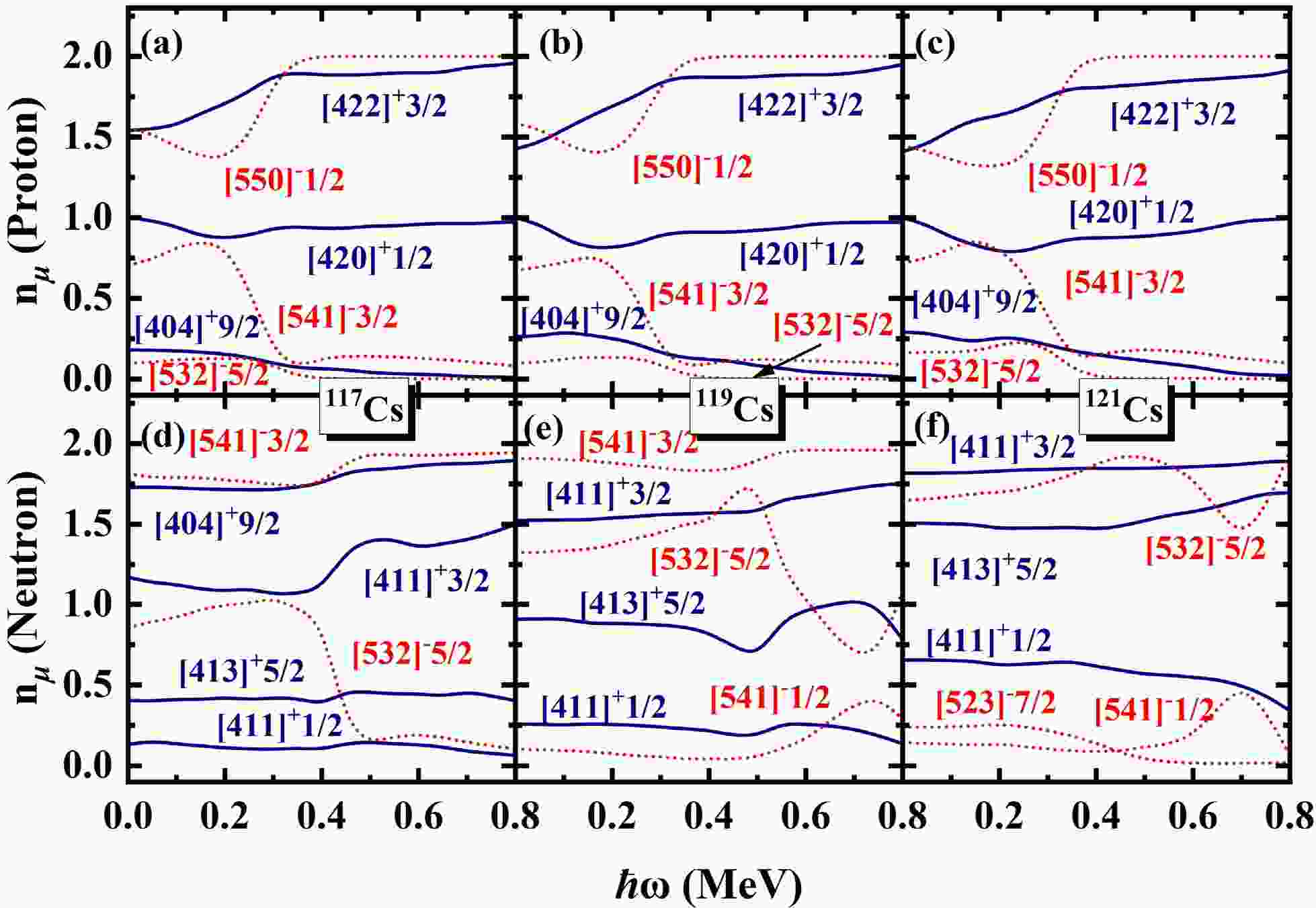
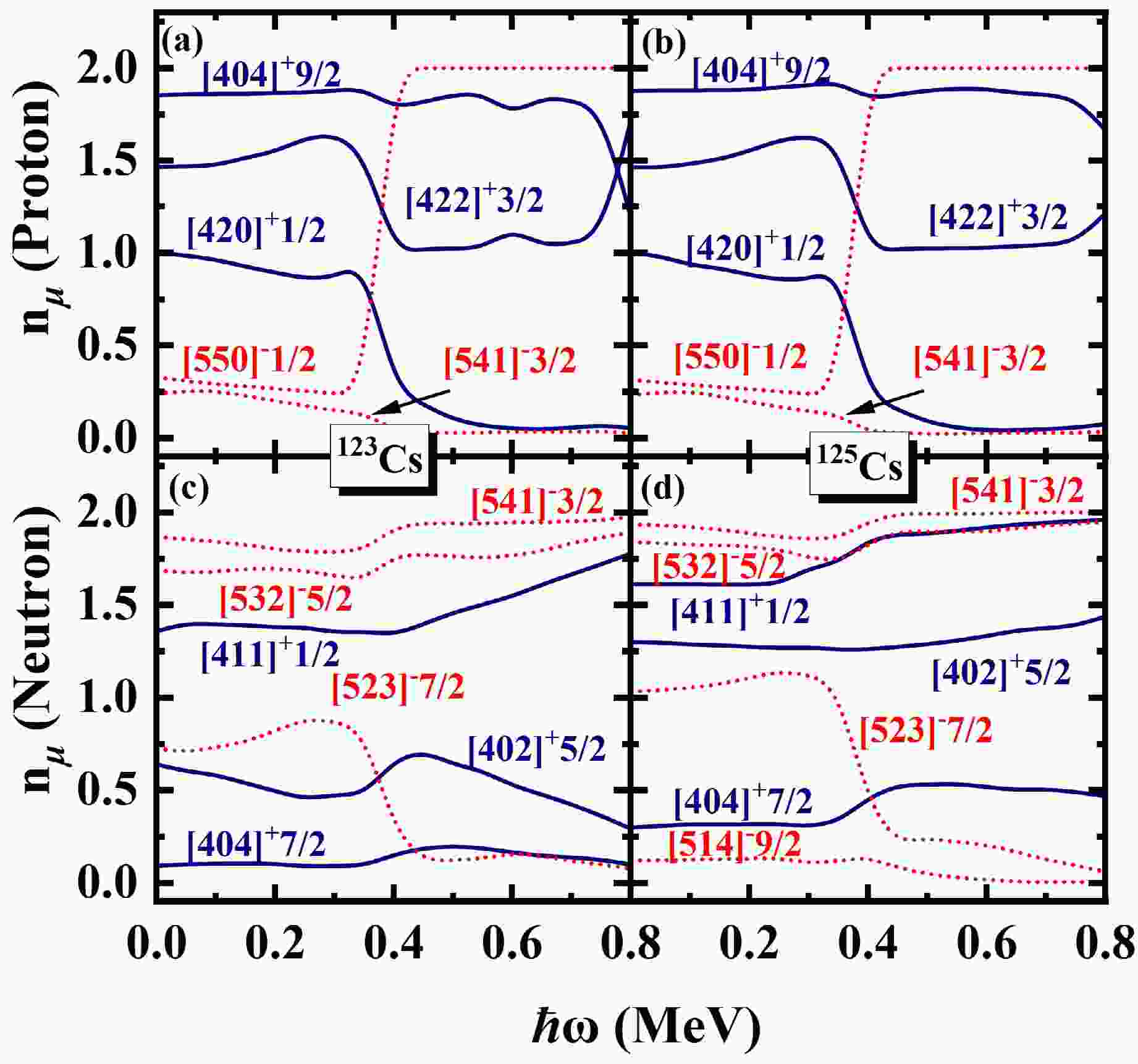
In PNC method, the total particle number $ N=\sum_{\mu}n_{\mu} $ is exactly conserved, whereas the occupation probability $ n_{\mu} $ for each orbital varies with rotational frequency $ \hbar \omega $. This is a key advantage of the PNC approach, as it allows for a more detailed investigation of the evolution of Nilsson levels with rotation. By analyzing the ω dependence of orbitals near to the Fermi surface, valuable insights into the upbending and backbending mechanism can be obtained. The occupation probability $ n_{\mu} $ of each orbital μ near the Fermi surface of the $ \pi d_{5/2} (1/2^+[420]) $ band in ^117,119,121Cs are shown in Fig. 4. The top and bottom rows are for protons and neutrons, respectively. The positive (negative) parity is denoted by blue solid lines (red dotted lines). It is evident from Fig. 4, around the rotational frequency $ \hbar \omega\sim0.20 $ MeV for ^117,119,121Cs, the occupation probability of π[550]1/2 ($ \pi h_{11/2} $) increases sharply from 1.5 to nearly 2.0, while the occupation probabilities of π[541]3/2 and π[532]5/2 decrease. This behavior can be understood from Fig. 2. With increasing $\hbar\omega $, the $ \pi[541]3/2 $ and $ \pi[532]5/2 $ orbitals gradually move away from the Fermi surface, while the $ \pi[550]1/2 $ orbital approaches it. As a result, the occupation probabilities of the $ \pi[541]3/2 $ and $ \pi[532]5/2 $ orbitals decrease with increasing cranking frequency, whereas the occupation probability of the $ \pi[550]1/2 $ orbital increases. For the second upbending of ^117,119,121Cs, it shows in Fig.4(d) the occupation probabilities of $ \nu[541]3/2 $ and $ \nu[411]3/2 $ increase around $ \hbar \omega\sim0.40 $, while the occupation probability $ \nu[532]5/2 $ sharply decreases. In Fig.4(e), around the upbending frequency, the occupation probability of $ \nu[541]3/2 $ and $ \nu[532]5/2 $ increase, corresponding while other the occupation probabilities orbitals become smaller. For ¹²¹Cs, around $ \hbar \omega\sim0.70 $ MeV the occupation probability $ \nu[532]5/2 $ sharply increases, while the occupation probability $ \nu[541]1/2 $ decreases. Similarly, the occupation probability $ n_{\mu} $ of each orbital μ near the Fermi surface of the $ \pi d_{5/2} (1/2^+[420]) $ band in ^123,125Cs are shown in Fig. 5. In Fig. 5, the occupation probability of $ \pi[550]1/2 $ increases gradually from nearly 0 to 2 around $ \hbar \omega\sim0.30 $MeV, while the occpution of $ \pi[422]3/2 $,$ \pi[404]9/2 $ and $ \pi[420]1/2 $ decrease. For neutron, the occupation probability of ν[523]7/2 approaches 0 at $ \hbar \omega\sim0.30 $MeV, meanwhile the occupation probabilities of other orbitals become larger. It can be seen that the first upbending of ^117,119,121Cs mainly comes from the contributions of the $ \pi h_{11/2} $ orbitals and the second upbending of ^117,119,121Cs mainly comes from the contributions of the $ \nu h_{11/2} $ orbitals. For ^123,125Cs, the observed backbending arises predominantly from the combined contributions of both the $ \pi h_{11/2} $ and $ \nu h_{11/2} $ orbitals.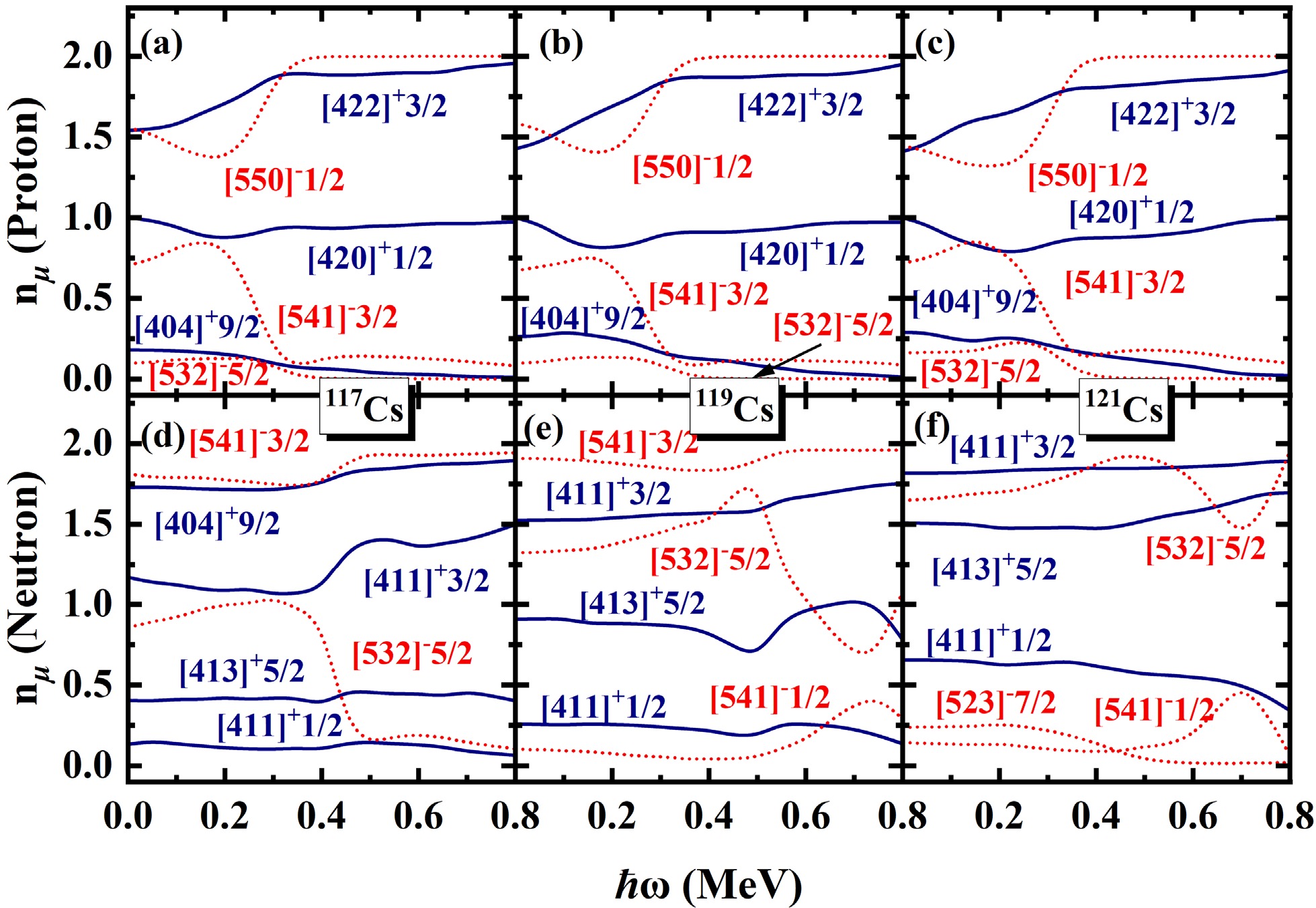

Figure 4.  (Color online) Occupation probability $ n_{\mu} $ of each orbital μ near the Fermi surface for the $ \pi d_{5/2} (1/2^+[420]) $ band in ^117,119,121Cs. The top and bottom rows are for protons ($ \alpha=+1/2 $) and neutrons, respectively. The positive (negative) parity is denoted by blue solid lines (red dotted lines). The Nilsson levels far above the Fermi surface ($ n_{\mu}\sim0 $) and far below ($ n_{\mu}\sim2 $) are not shown.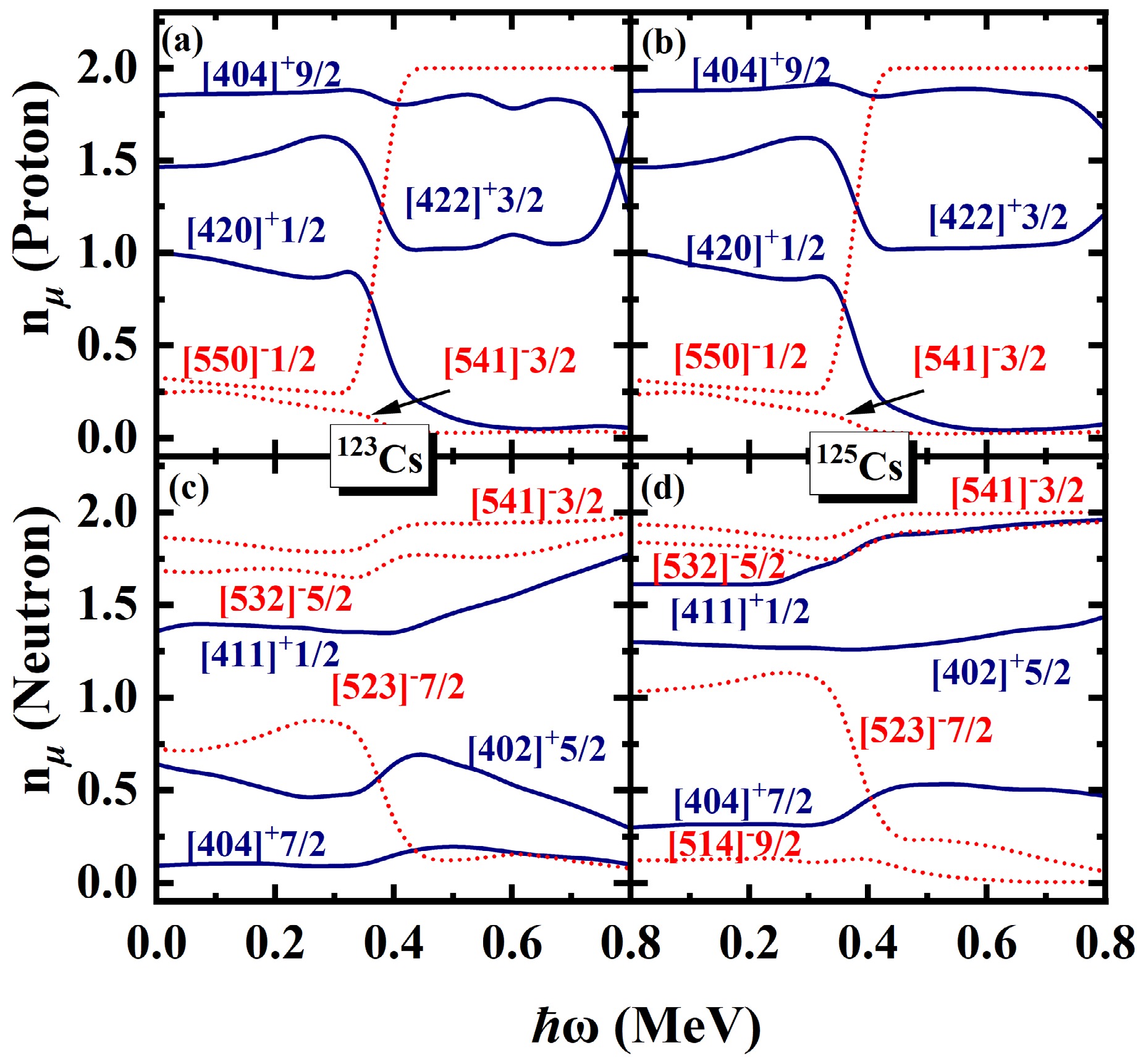

Figure 5.  (color online) The same as in Fig. 4, but for ^123,125Cs

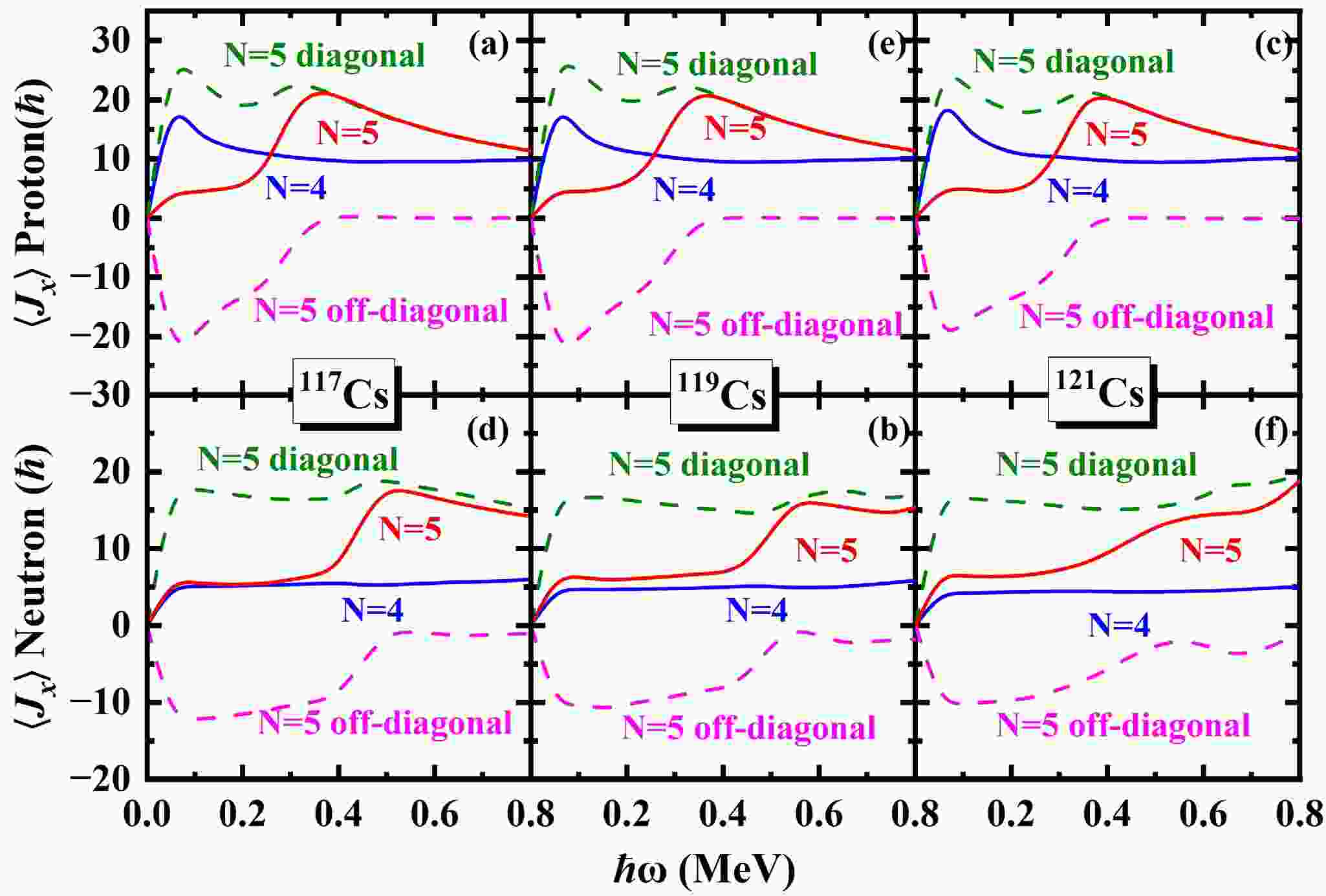
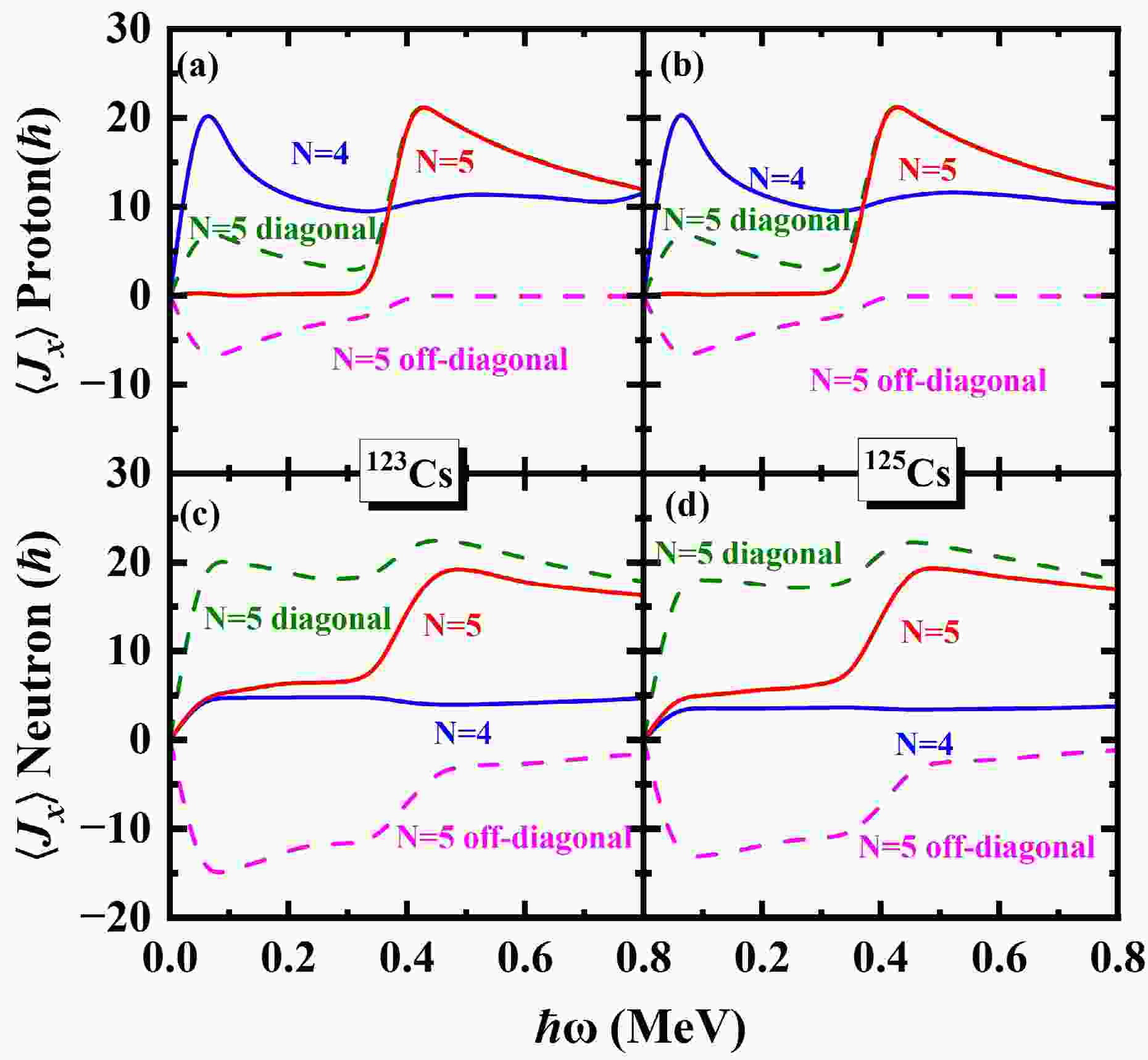
In order to understand clearly the upbending and backbending mechanism, the contributions of each proton and neutron major shell to the angular momentum alignment $ \langle J_x \rangle $ for the $ \pi d_{5/2} (1/2^+[420]) $ band in odd-even ^117−125Cs are shown in Fig. 6 and Fig. 7. The contributions of diagonal $ \sum_{\mu}j_{x}(\mu) $ and off-diagonal $ \sum_{\mu<\nu}j_{x}(\mu\nu) $ from the neutron $ N=5 $ and proton $ N=5 $ major shells are shown as dashed lines. The first upbending observed in the $ \pi d_{5/2} (1/2^+[420]) $ band of ^117,119,121Cs around $ \hbar \omega\sim0.20 $MeV is primarily attributed to the contribution of the proton $ N=5 $ shell. Furthermore, it mainly originates from the off-diagonal part of the proton $ N=5 $ shell, whereas the diagonal part provides a relatively smaller contribution to upbending. For the second upbending observed in ^117,119,121Cs, there is no significant contribution from the proton $ N=4,5 $ shells, the upbending is predominantly driven by the contribution of neutron $ N=5 $ shell. For ¹¹⁷Cs, the dominant contribution arises from the off-diagonal part of the neutron $ N=5 $ shell, while the diagonal part contributes only marginally. Similarly, in ^119,121Cs, the second upbending is mainly driven by the off-diagonal part of the neutron $ N=5 $ shell. In fig. 7, it shows that the angular momentum alignments increase with 12.5$ \hbar $ and 20$ \hbar $ at $ \hbar \omega\sim0.30 $MeV for neutron and proton $ N=5 $ shells, respectively. This simultaneous alignment leads to the backbending observed in the $ \pi d_{5/2} (1/2^+[420]) $ band of ^123,125Cs. The backbending is primarily driven by both the diagonal and off-diagonal components of the neutron $ N=5 $ shell, along with the diagonal part of the proton $ N=5 $ shell. In contrast, the off-diagonal part of the proton $ N=5 $ shell gives little contribution to the backbending.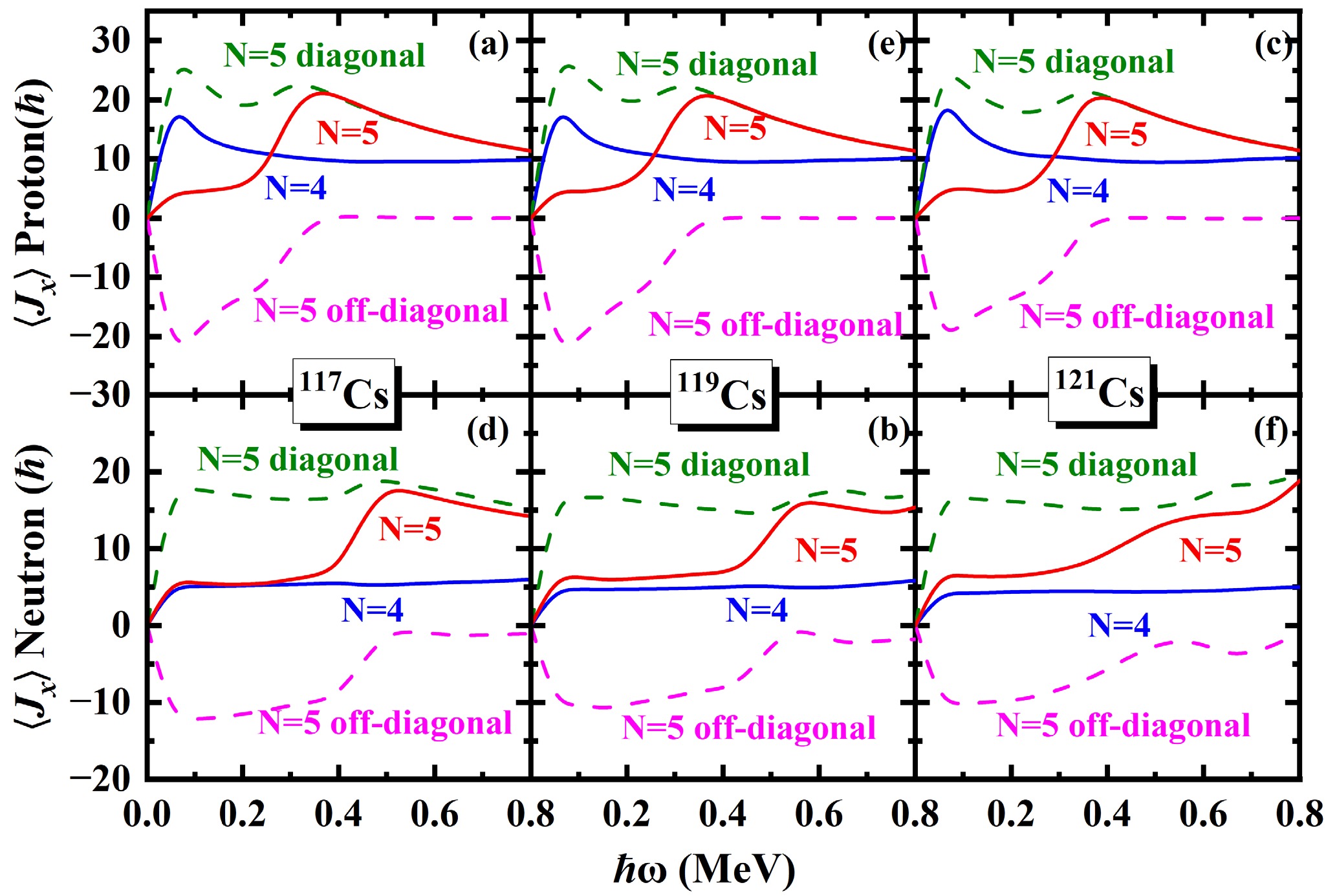

Figure 6.  (Color online) Contribution of each proton and neutron major shell to the angular momentum alignment $ \left \langle J_x \right \rangle $ for the $ \pi d_{5/2} (1/2^+[420]) $ band in ^117,119,121Cs. The contributions of diagonal $ \sum_{\mu}j_{x}(\mu) $ and off-diagonal $ \sum_{\mu<\nu}j_{x}(\mu\nu) $ from the neutron $ N=5 $ and proton $ N=5 $ major shells ($ \alpha=+1/2 $) are shown as dashed lines.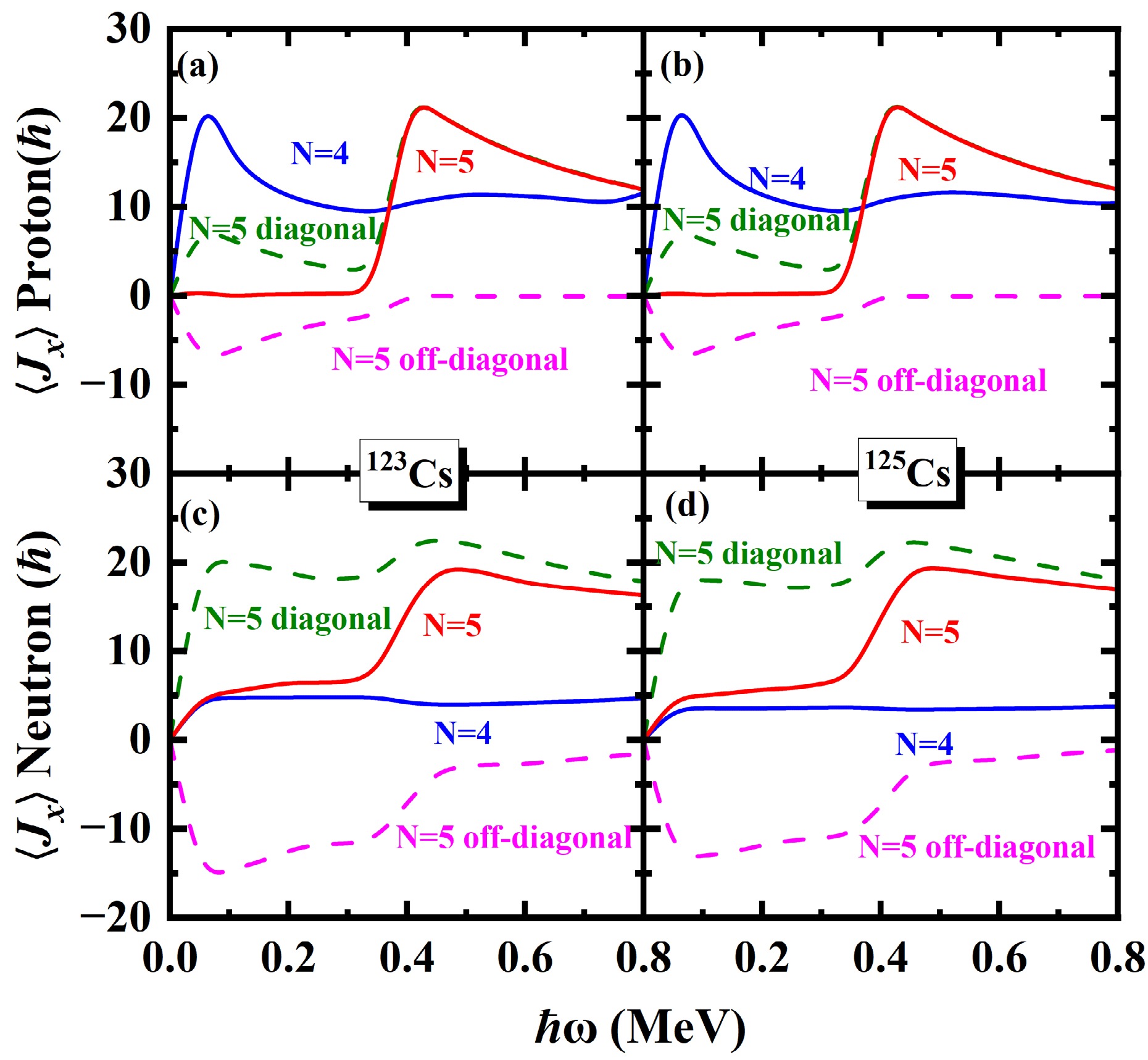

Figure 7.  (color online) The same as in Fig. 6, but for ^123,125Cs

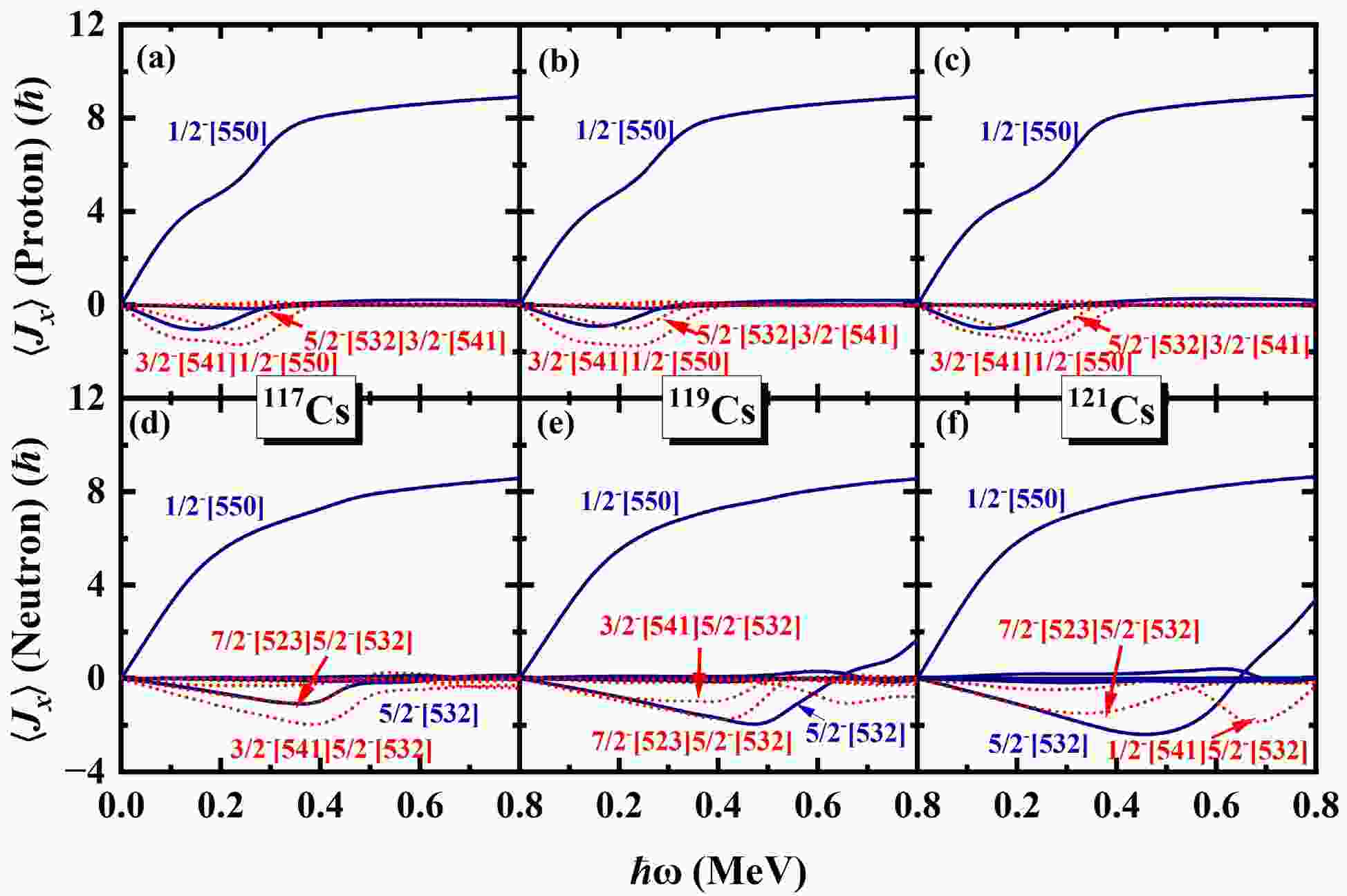
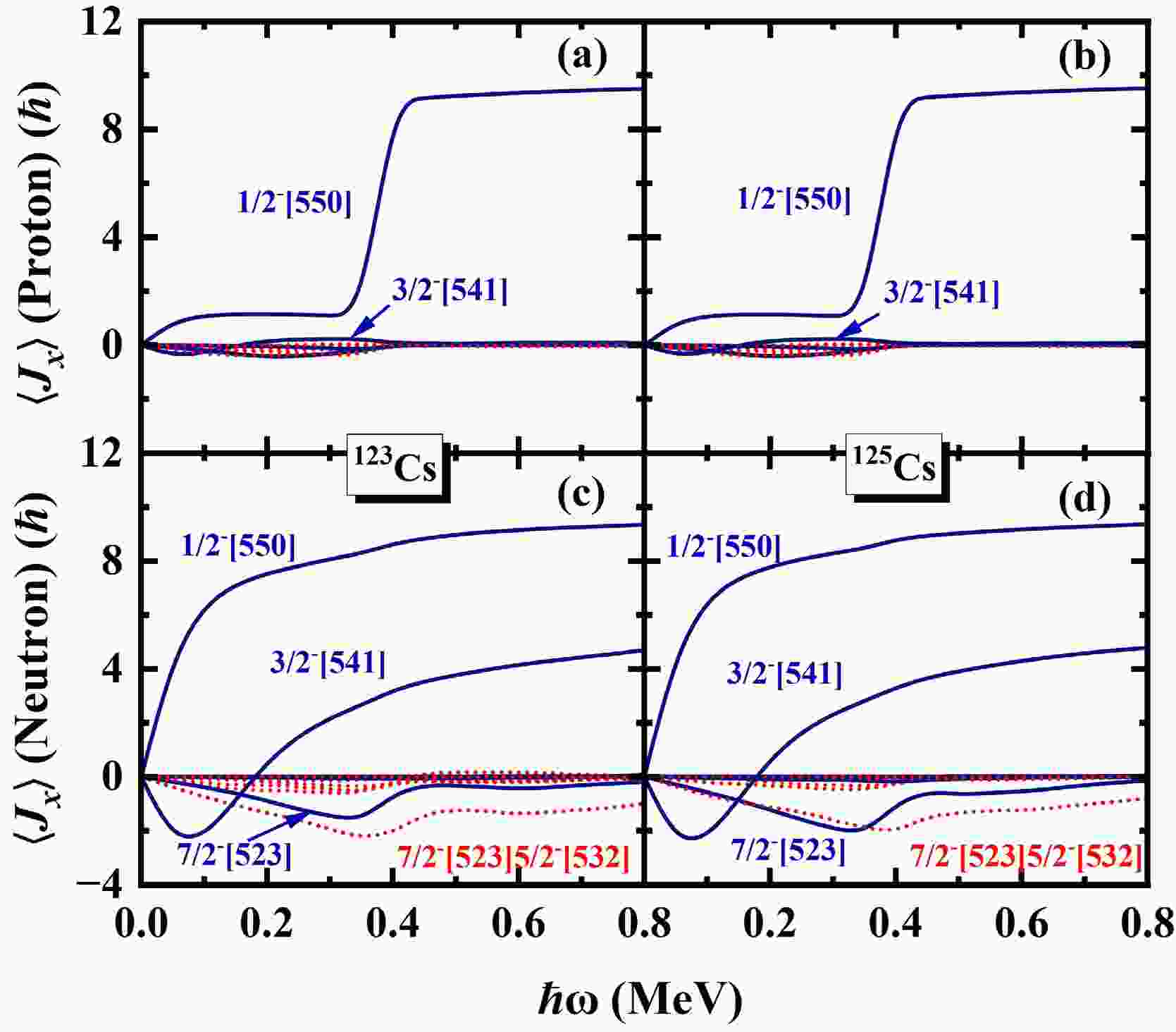
For a deep insight into the upbending and backbending mechanism, the contribution of each proton orbital and neutron orbital in the $ N=5 $ major shell to the angular momentum alignments $ \langle J_x\rangle $ for the $ \pi d_{5/2} (1/2^+[420]) $ band in odd-even ^117−125Cs are presented in Fig.8 and Fig.9. The diagonal (off-diagonal) part $ j_{x}(\mu) $ $ (j_x(\mu\nu)) $ is denoted by blue solid lines (red dotted). In Fig.8 (a-c), around $ \hbar\omega \sim 0.20 $ MeV, it is evident that the off-diagonal contributions $ j_{x}(\pi5/2^{-}[532]\pi3/2^{-}[541]) $ and $ j_{x}(\pi1/2^{-}[550]\pi3/2^{-}[541]) $ increase significantly with increasing rotational frequency in ^117,119,121Cs. These off-diagonal matrix elements are responsible for the first upbending observed in these nuclei. In Fig.8(d), it can be seen that the diagonal part $ j_{x}(\nu5/2^{-}[532]) $ and the off-diagonal parts $ j_{x}(\nu7/2^{-}[523]\nu5/2^{-}[532]) $ and $ j_{x}(\nu3/2^{-}[541]\nu5/2^{-}[532]) $ give contributions to the second upbending of ¹¹⁷Cs. In Fig.8(e), the second upbending of ¹¹⁹Cs is attributed to the off-diagonal parts $ j_{x}(\nu7/2^{-}[523]\nu5/2^{-}[532]) $ and $ j_{x}(\nu3/2^{-}[541]\nu5/2^{-}[532]) $. In ¹²¹Cs, the second upbending is mainly driven by the off-diagonal part $ j_{x}(\nu1/2^{-}[541]\nu5/2^{-}[532]) $. For ^123,125Cs, the diagonal part $ j_{x}(\pi1/2^{-}[550]) $ increases from 2$ \hbar $ at $ \hbar \omega \sim0.30 $ MeV to 9$ \hbar $ at $ \hbar \omega \sim0.40 $ MeV. It gives the main contributions to the backbending of $ \pi d_{5/2} (1/2^+[420]) $ band in ^123,125Cs. Moreover, the backbending is effected by neutron with the off-diagonal part $ j_{x}(\nu5/2^{-}[532]\nu7/2^{-}[523]) $ and diagonal part $ j_{x}(\nu7/2^{-}[523]) $ increasing little at $ \hbar \omega\sim0.30 $ MeV.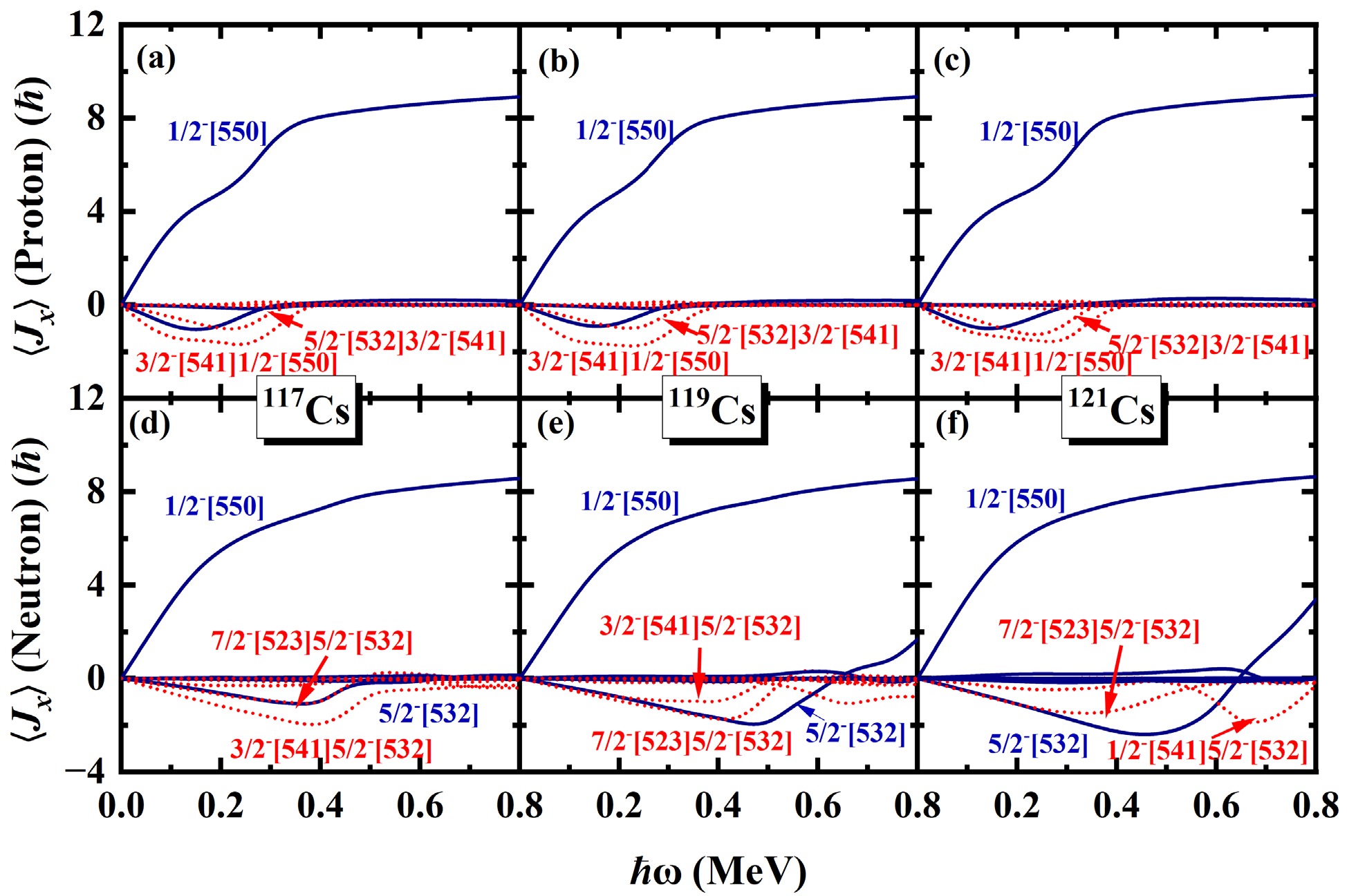

Figure 8.  (Color online) Contribution of each proton orbital for $ \alpha=+1/2 $ (top) and neutron orbital (bottom) in the $ N=5 $ major shell to the angular momentum alignments $ \langle J_x \rangle $ for the $ \pi d_{5/2} (1/2^+[420]) $ band in odd-even ^117,119,121Cs. The diagonal (off-diagonal) part $ j_{x}(\mu) [(j_x(\mu\nu)] $ is denoted by blue solid (red dotted) lines.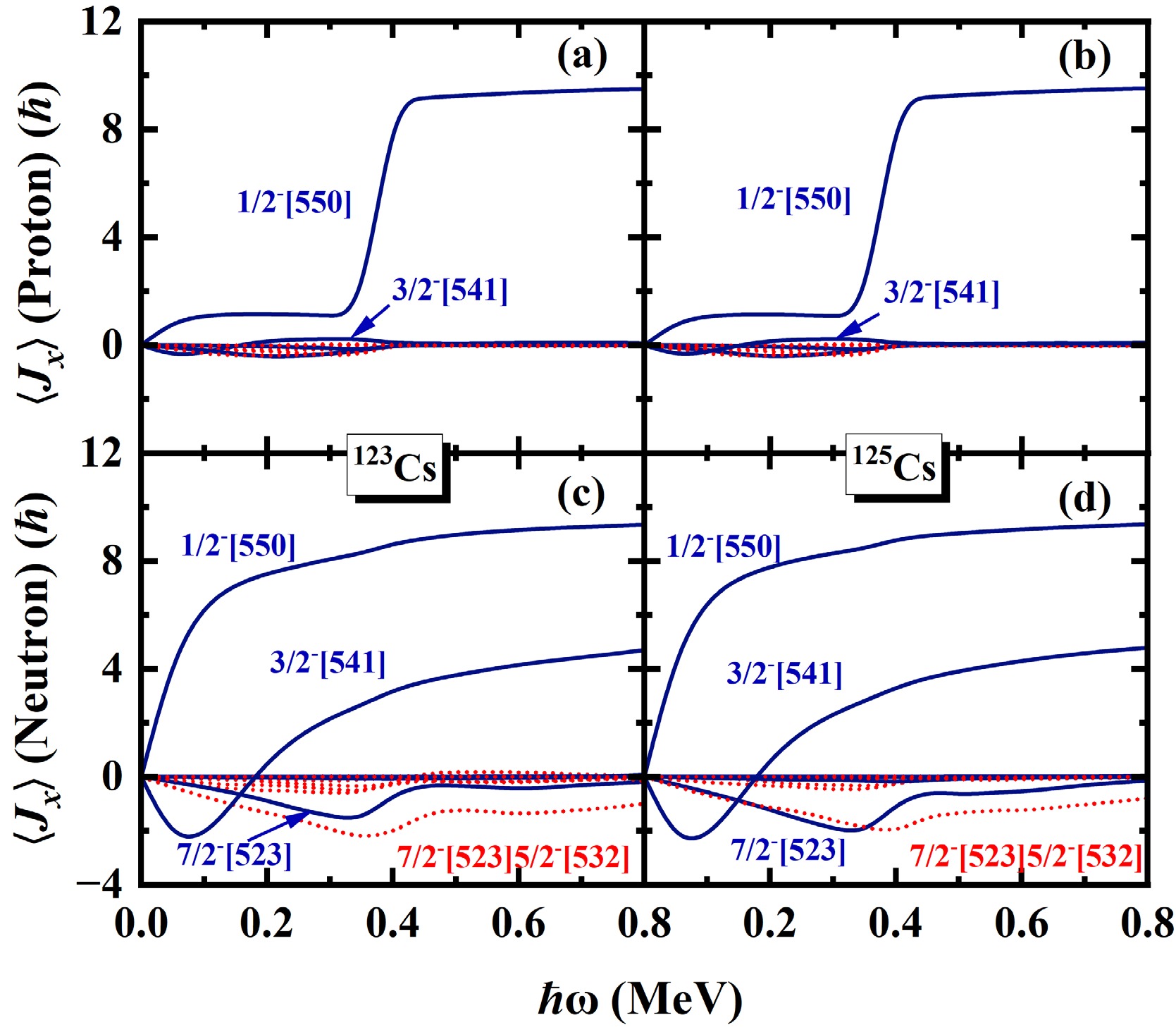

Figure 9.  (color online) The same as in Fig. 8, but for ^123,125Cs

In summary, the $ \pi d_{5/2} $ band for odd-even ^117−125Cs are investigated by using the PNC-CSM. In this work, the calculated band-head energies of the $ \pi g_{9/2} $ band show good agreement with experimental data. The experimental moments of inertia and alignments are reproduced well by the PNC calculations. A comprehensive understanding of the upbending and backbending phenomena in each nucleus is achieved by analyzing the ω dependence of the occupation probability of each cranked Nilsson orbital near the Fermi surface, as well as the contributions of valence orbitals to the angular momentum alignment within each major shell. The first upbending in the $ \pi d_{5/2} $ band of ^117,119,121Cs is primarily caused by the off-diagonal contribution of $ j_{x}(\pi5/2^{-}[532]\pi3/2^{-}[541]) $ and $ j_{x}(\pi1/2^{-}[550]\pi3/2^{-}[541]) $, while the second upbending is driven by the off-diagonal parts of the $ j_{x}(\nu7/2^{-}[523] \nu5/2^{-}[532]) $ and $ j_{x}(\nu3/2^{-}[541] \nu5/2^{-}[532]) $ for ^117,119Cs and the $ j_{x}(\nu1/2^{-}[541] \nu5/2^{-}[532]) $ for ¹²¹Cs. In contrast, for ^123,125Cs the backbending of the $ \pi d_{5/2} $ band arises from the combined contributions of the diagonal $ j_{x}(\pi1/2^{-}[550]) $ and $ j_{x}(\nu7/2^{-}[523]) $ and the off-diagonal $ j_{x}(\nu7/2^{-}[523] \nu5/2^{-}[532]) $. These differences in rotational behavior between ^117,119,121Cs and ^123,125Cs can be attributed to the evolution of single-particle orbitals near the Fermi surface. With increasing neutron number, the $ \pi [550]1/2 $ orbital moves away from the Fermi surface, leading a shift in the crossing frequencies. Consequently, the single-particle evolution drives the proton shell gap from $ Z=50 $ to $ Z=48 $.