Hyperons in neutron-star cores: confronting maximum mass observational constraint of 2M_⊙

Neutron stars, among the most compact objects in the universe, provide a natural laboratory to explore the behavior of strongly interacting matter under extreme conditions. Their interiors reach densities that is several times higher than the nuclear saturation density, extending up to five to ten times that of ordinary nuclear matter. At such extreme conditions, new and exotic degrees of freedom, such as hyperons (baryons with strange quarks), are expected to emerge. This occurs because the nucleon Fermi energy rises with density and eventually becomes comparable to the rest mass energy of hyperons, making their formation energetically favorable. The onset of hyperons typically takes place at densities of about 2–3 times the saturation density of nuclear matter. Strangeness adds a new dimension to the evolving picture of nuclear physics, allowing us to investigate fundamental interactions from a broader perspective. Its presence in finite nuclear systems such as hypernuclei is well established experimentally, and serves as a powerful probe of the deep nuclear interior. This enables the exploration of nuclear phenomena that would otherwise remain inaccessible, thereby providing stringent tests for nuclear models. At supranuclear densities, the onset of exotic degrees of freedom further broadens this picture and can have profound implications for astrophysics. In particular, the appearance of strangeness, whether in a confined forms (hyperons, kaons) or deconfined state (strange quark matter), within the dense inner core of a neutron star is expected to have significant effect on the Equation of state (EoS), internal composition, structural properties, and evolution of these compact objects.

Under the extreme conditions present in the core of neutron stars, the formation of hyperonic matter becomes energetically favourable [1, 2]. Their inclusion in the EoS leads to a noticeable softening of the pressure-density relation, which in turn affects the maximum mass and radius predictions for neutron stars. Their appearance introduces additional degrees of freedom, allowing the system to redistribute energy by populating hyperonic Fermi seas. This redistribution reduces the Fermi pressure exerted by nucleons, effectively softening the EoS. Consequently, for a given energy density, the pressure is lowered, which diminishes the star's ability to counteract gravitational collapse. As a result the maximum mass that a neutron star can sustain is typically reduced by approximately $ 0.5\, M_\odot $ compared to purely nucleonic models [3, 4].

In 1960, Ambartsumyan and Saakyan first explored the appearance of various hyperons in dense matter under chemical equilibrium conditions [1]. This foundational work set the stage for what later became known as the "hyperon puzzle." The puzzle itself stems from an apparent inconsistency: while the inclusion of hyperons in the EoS is energetically favourable at high densities, their presence tends to soften the EoS, consequently reducing the maximum mass of neutron stars. Indeed, many theoretical models incorporating hyperons, without specific repulsive hyperon-hyperon interactions, often predict maximum neutron star masses well below the $ \sim 2 M_\odot $ astrophysical constraint, typically in the range of $ 1.6 M_\odot - 1.8 M_\odot $ [5−9]. This theoretical prediction stands in stark contrast to observed massive pulsars such as PSR J1614-2230 [10], PSR J0348+0432 [11], and PSR J0740+6620 [12, 13], which possess masses surpassing these theoretical limits. This discrepancy forms the crux of the hyperon puzzle. [5]. In response, numerous recent studies have explored the incorporation of hyperonic matter in neutron star matter and their compatibility with astrophysical constraints [14−18]. A primary approach to control the strong softening of the EoS and the subsequent reduction in maximum neutron star mass, a key aspect of the hyperon puzzle, is the introduction of repulsive hyperon-hyperon interaction, frequently achieved by the exchange of vector mesons [5, 7, 9, 19, 20].

The investigation of hyperons in neutron stars within the framework of the RMF model was initiated in the 1980s by Glendenning [3, 21]. In these early models, the coupling strengths between mesons and baryons were often determined based on theoretical considerations and fitting to nuclear properties. The actual appearance of hyperons in neutron star matter is highly sensitive to the underlying hyperon–nucleon and hyperon–hyperon interactions. Crucially, these interactions can be constrained through experimental data on hypernuclei, which provide essential information about the potential depths and couplings relevant to hyperonic matter. Over the past three decades, relativistic mean-field (RMF) parametrizations for nucleon-nucleon and nucleon-hyperon interactions have been significantly refined by fitting ground-state properties of finite nuclei and available hypernuclear experimental data. These improved interactions have been extensively employed to explore the structure and composition of hyperonic neutron stars [22−29].

Hypernuclei are nuclei that include an additional degree of freedom, strangeness arising from the presence of hyperons (e.g., Λ, Σ, Ξ), in contrast to ordinary nuclei, which contain only protons and neutrons. The primary aim of studying hypernuclei is to gain insight into baryon-baryon interactions, which are essential for understanding both hypernuclear structure and the properties of neutron stars. Consequently, hypernuclei have attracted considerable interest in both experimental and theoretical research worldwide. However, due to the challenges associated with hyperon-nucleon and hyperon-hyperon scattering experiments, scattering data are scarce for hyperon-nucleon interactions and entirely lacking for hyperon-hyperon interactions. For instance, observations of $ \Lambda\Lambda $ bond energy for a few double-Λ hypernuclei in light nuclear systems such as $ ^6_{\Lambda\Lambda} $He [30], $ ^{10}_{\Lambda\Lambda} $Be [31], $ ^{13}_{\Lambda\Lambda} $Be [32] with positive values suggest slightly attractive $ \Lambda\Lambda $ interaction. Meanwhile, there are several observed data on the Ξ hypernuclei in the $ ^{12}_{\Xi}Be $ $ (^{11}B + \Xi^{-}) $ [33], $ ^{13}_{\Xi}B $ $ (^{12}C + \Xi^{-}) $ [34] and $ ^{15}_{\Xi}C $ $ (^{14}N + \Xi^{-}) $ [35] systems. In particular the KISO event ($ \Xi^{-} + ^{14}N \rightarrow {^{10}_{\Lambda}Be} + {^{5}_{\Lambda}He} $) gave the first clear confirmation of a deeply bound state of the ($ \Xi^{-} - ^{14}N $) system by an attractive Ξ-nucleon interaction [35].

The theoretical study on hypernuclei ($ ^{40} Ca + Y $ where Y $ = \Lambda, \Sigma^{0,\pm}, \Xi^{0,-} $) in the RMF framework [36] suggests that adding hyperons makes the nuclear system much more bound because of attractive nucleon-hyperons interactions, especially in the hypernuclei $ ^{41}_{\Lambda} Ca $, $ ^{41}_{\Sigma^{0}} Ca $ and $ ^{41}_{\Sigma^{-}} K $. However, this trend does not hold universally for all hyperons. In particular, while Λ and Ξ hyperons typically experience attractive interactions, experimental evidence points to a very different behaviour for the Σ hyperons. These experimental evidence indicates that the Σ–nucleon interaction is predominantly repulsive at saturation density. Analysis of $ (\pi^-, K^+) $ reactions and the notable lack of bound Σ hypernuclei except for $ {^4_{\Sigma}}He $ which was produced in the $ (\pi^-, K^-) $ reaction at KEK [37], suggest that a strongly repulsive Σ-nucleus potential with non-zero size of the imaginary part is required to reproduce the shape of the measured spectra. In RMF models, this is commonly implemented by adopting a repulsive potential depth of $ U_\Sigma^{(N)} \approx +30\,{\rm{MeV}} $, which leads to the delayed appearance or even suppression of Σ hyperons in dense matter [26, 38]. Furthermore, isospin plays a crucial role in the threshold behaviour of the $ \Sigma^- $, $ \Sigma^0 $, and $ Sigma^+ $ hyperons. As part of an isospin triplet ($ I=1 $), these particles couple more strongly to the ρ meson field than nucleons, experiencing enhanced isovector repulsion [39]. This significant isovector repulsion, combined with their repulsive scalar potentials, results in their typically late or absent appearance in many RMF-based neutron star models, particularly in symmetric or slightly neutron-rich regions. Another striking feature of hypernuclei is very small spin-orbit splitting of single Λ states [40]. In ordinary nuclei, the strong spin-orbit force between nucleons produces splittings of several MeV between orbitals such as $ p_{3/2} $ and $ p_{1/2} $. In contrast, spectroscopy of Λ-hypernuclei shows that the corresponding splittings are only a few hundred keV. This suppression can be understood within the relativistic mean-field picture: the spin-orbit potential depends on the radial derivative of the difference between vector and scalar mean fields, which nearly cancel for the Λ or have very small values. Moreover, since the Λ couples more weakly to the mean fields (scaled coupling constants) and has a larger mass than nucleons, the spin-orbit term is further reduced by the $ 1/M_{eff}^{2} $ [36, 41] dependence. The observed small splitting therefore provides an important constraint on hyperon-meson couplings in theoretical models of hypernuclear structure.

Besides hyperons, theoretical studies suggest that another strange degree of freedom may emerge in dense hadronic matter through antikaon ($ K^{-} $) condensation [42]. This phenomenon can coexist with or compete against negatively charged hyperons such as $ \Sigma^{-} $ and $ \Xi^{-} $, since both play a role in maintaining charge neutrality. Within frameworks based on chiral symmetry for kaon–baryon interactions and effective baryon–baryon couplings, it has been shown that the onset density of s-wave kaon condensation in hyperonic matter is shifted to higher values compared with ordinary neutron-star matter [43]. This shift arises because negatively charged hyperons partially replace electrons, thereby lowering the electron chemical potential so that the lowest $ K^{-} $ energy crosses it only at higher densities [43, 44]. The interplay between kaons and hyperons crucially affects the composition of dense matter. As kaon condensation develops, the $ \Sigma^{-} $ fraction is suppressed, while at higher densities the growth of $ \Sigma^{-} $ in turn suppresses kaons. The electron fraction is strongly reduced or even eliminated, as its negative charge is taken over by kaons and hyperons. At extreme densities, protons, Λ, and $ \Sigma^{-} $ hyperons can each contribute significantly to the baryon fraction, while neutrons nearly vanish. Consequently, the total strangeness fraction approaches unity, pointing to a close connection between kaon-condensed hyperonic matter and strange quark matter, where u, d, and s quarks are nearly equally populated. The nature of the phase transition itself depends on the relative appearance of kaons and hyperons: it may proceed continuously or discontinuously, with multiple competing energy minima in the system. Furthermore, the development of kaon condensation softens the equation of state through attractive kaon–baryon interactions and hyperon mixing, though repulsive baryon interactions can restore stiffness at higher densities. Such an intricate interplay among $ K^{-} $ condensates and $ \Sigma^{-} $ hyperons not only influences the maximum mass and internal composition of neutron stars, but also provides a possible pathway to strange quark matter, bridging the hadronic and deconfined phases in the high-density QCD phase diagram [45−47].

Some studies also suggest that hyperons—particularly the Λ and $ \Sigma^{-} $ species may appear within the nuclear pasta phase [48], but only under conditions of finite temperature, and even then their abundances are predicted to be very small. The nuclear pasta phase itself refers to a series of complex, non-spherical configurations of nuclear matter (such as rod, slab or bubble like structures) that are expected to form in the inner crust of neutron stars, near the crust-core transition, due to the competition between nuclear attraction and Coulomb repulsion. In contrast, for cold neutron stars, hyperons are expected to emerge only at much higher densities, typically above about twice the nuclear saturation density [48]. Since the present work focuses exclusively on cold neutron star matter, the possibility of hyperons appearing in the nuclear pasta phase does not arise in our calculations.

In the present study, we employ parametrizations within the framework of the non-linear RMF models to describe β-equilibrated matter composed initially of nucleons only and subsequently extend the model to include hyperonic degrees of freedom. This extension enables us to investigate the influence of hyperons on EoS of dense matter and assess their impact on neutron star structure, with particular emphasis on their role in determining the maximum mass observational constraint of M$ _{max} $ $ \ge $ 2 M$ _{\odot} $ that a star can support. We explore the role of strange baryons in hyperonic stars and their influence on key properties of neutron star such as mass, radius, tidal deformability, and related characteristics. Furthermore, we examine the coupling strengths between mesons and hyperons, particularly focusing on the vector meson-hyperon interactions, which are essential for generating hyperonic star configurations within the current RMF framework.

The study takes a methodical approach, with a brief outline of the RMF model and theoretical formalism in Section 2. Section 3 provides a detailed explanation of our results and findings. We summarized the findings in Section 4.

In the present work, we employ the non-linear RMF models formulated in Refs. [49−51]. The effective Lagrangian incorporates the isoscalar scalar σ, isoscalar vector $ \omega_{\mu} $, and isovector vector $ \rho_{\mu} $ mesons. The corresponding total Lagrangian density of the RMF model is expressed as,

where the baryonic and mesonic Lagrangian $ {\cal L_{BM}} $ can be described as,

In this formalism, the inclusion of hyperons is achieved by extending the summation in the Lagrangian to encompass the entire baryon octet (B) that includes a nucleon doublet N (protons and neutrons) as well as six of the lowest mass hyperons Y: Λ- singlet, Σ- triplet, and Ξ- doublet [49].

The Lagrangian describing self interactions for σ, ω, and ρ mesons can be written as,

The $ {\cal L}_{em} $ is the Lagrangian for electromagnetic interactions and can be expressed as,

Additional “hidden-strangeness” mesons, namely scalar $ \sigma^{*} $ and vector $ \phi_{\mu} $, are introduced. They couple only to hyperons, such that g$ _{N\sigma^{*}} $ = g$ _{N\phi} $ = 0. The hyperon-hyperon interaction is taken into account by introducing two additional mesonic fields, namely the scalar $ \sigma^* $ and the vector ϕ mesons. The corresponding Lagrangian density describing the the hyperon-hyperon (Y–Y) interaction, where $ Y = \Lambda, \Sigma $, and Ξ, can be written as:

The charge-neutral neutron star matter also comprises leptons such as $ e^- $ and $ \mu^- $, in addition to neutrons, protons, and hyperons, at high densities.

The leptonic contributions to the total Lagrangian density can be written as,

The equation of motion for baryons, mesons (σ, $ \omega_{\mu} $, $ \rho_{\mu} $), and photons can be derived from the Lagrangian density defined in Eq. (2) by using conventional Euler-Lagrange approach [52]. From the total Lagrangian density, the corresponding energy–momentum tensor $ T^{\mu\nu} $ can be derived. This tensor is then employed to calculate the Equation of State (EoS), i.e., the pressure (P) and the energy density ($ \cal{E} $), which are given by

The hyperons-meson coupling constants $ g_{iY} $ ($ i = \sigma, \omega, \rho, \sigma^{*}, \phi $) in the respected Lagrangian can be represented in terms of nucleons-mesons couplings stemming from the SU(6) model (additive quark model) of hadrons [49] as,

The properties of neutron stars are found to be quite sensitive to the values of the coupling constants $ g_{\sigma Y} $ and $ g_{\omega Y} $, where Y = $ \Lambda, \Sigma, \Xi $. In contrast, variations in $ g_{\sigma^* Y} $ over a reasonable range do not significantly affect the neutron star properties, provided that $ g_{\phi Y} $ is held fixed [53]. In the present work, we use the hyperon-meson couplings from the SU(6) model as given in Eq. (13). In addition, we also see the effect of vector meson-hyperons couplings $ g_{\omega Y} $ on the threshold density of appearance of hyperons and the mass-radius relationship of neutron stars. For this, we use the values of $ g_{\rho Y} $, $ g_{\sigma^* Y} $ and $ g_{\Phi Y} $ as given by Eq (13) and adjust $ g_{\sigma Y} $ and $ g_{\omega Y} $ to fit experimental estimates of hyperon - nucleon potential U$ _{\Lambda}^{(N)} $.

The coupling constants $ g_{\sigma Y} $ and $ g_{\omega Y} $ are determined through the hyperon-nucleon potential. The experimental studies of hypernuclei and of $ \Sigma^{-} $ atoms provide constraints on the potential energy of a single zero-momentum hyperon in symmetric nuclear matter, denoted as $ U_{Y}^{(N)} $. Within the framework of the non-linear RMF model, the potential depth of a hyperon species Y in nuclear matter at saturation density $ \rho_{\text{sat}} $ is given by

which should be calculated at saturation density $ \rho_{sat} $ and asymmetry parameter δ = $ \dfrac{\rho_{n} - \rho_{p}} {\rho_{n} - \rho_{p}} $ = 0.

The values of $ U_Y^{(N)} $ chosen are as follows [54−56],

Eq. (14) is used to determine g$ _{\Lambda\sigma} $, g$ _{\Sigma\sigma} $ and g$ _{\Xi\sigma} $ for given values of X$ _{\omega Y} $ = 0.6, 0.8, 0.9. Normally, $ g_{\sigma Y} $ is determined for a given value of $ U_{Y}^{(N)}(\rho_{sat}) $ with $ g_{\omega Y} $ taken from SU(6) model.

For the sake of convenience we define,

where, j stands for σ and ω mesons. The rest masses of hyperons are obtained from the work of [57]. In the present work we vary $ X_{\omega Y} $ from $ 0.6, 0.8, 0.9 $ [58].

While the symmetry-constrained SU(6) provides fixed values for hyperon–vector meson couplings based on quark content, its applicability at supranuclear densities like that of in neutron stars is uncertain [26]. To explore this uncertainty and test the robustness of the EoS predictions, we treat $ X_{\omega Y} $ as a free parameter in the range of 0.6–0.9. This phenomenological approach allows us to investigate how deviations from ideal symmetry assumptions influence the threshold densities for hyperon formation and the key properties of neutron stars.

A hyperon species Y emerges when its chemical potential equals the total single-particle energy it experiences in the dense medium [59−61]:

where $ \mu_Y $ is the chemical potential, and $ g_{\omega Y} $, $ g_{\rho Y} $, and $ g_{\phi Y} $ represent couplings to the isoscalar ω, isovector ρ, and hidden-strangeness ϕ mesons, respectively. These mesons mediate repulsive interactions, delaying hyperon formation to higher densities.

The in-medium effective mass $ M_Y^* $ incorporates scalar attraction and is defined as:

where $ (\sigma) $ and $ ( \sigma^* $) denote the non-strange and strange scalar meson fields, respectively. These terms reduce the effective mass, thus favouring hyperon onset [2, 23] Among the vector mesons, ω and ρ couple to both nucleons and hyperons, whereas the ϕ meson, composed of $ s\bar{s} $, couples only to hyperons. At high densities, the inclusion of ϕ mesons becomes particularly relevant, as hyperon-hyperon repulsion contributes to EoS stiffening, counteracting the softening typically induced by hyperons and enabling the support of more massive stars. Therefore, the threshold density for hyperon formation is governed by the competition between scalar attraction, vector repulsion, and the stiffness of the underlying EoS. Lower vector couplings or a softer EoS reduce the energy cost for hyperon appearance, allowing them to emerge at lower baryon densities. This threshold condition forms the theoretical foundation for many modern hyperonic RMF studies, such as those by Schaffner and Mishustin [23], Weissenborn et al. [26], Tsubakihara and Ohnishi [62], and Fortin et al. [63], where scalar and vector meson couplings are systematically tuned to examine hyperon onset and its effect on the neutron star EoS and mass-radius constraints.

In the present work, our analysis of RMF models reveals critical trends in hyperon onset thresholds, with particular emphasis on the influence of hyperon-vector meson coupling strengths $ X_{\omega Y} $. For the nucleon sector, we use various RMF models that are used to reproduce the ground state properties (binding energies, charge rms radii) of finite nuclei and symmetric nuclear matter very well. In addition, these models are also used in confronting the neutron star properties in good agreement with the various astrophysical constraints as imposed by gravitational wave events and NICER missions. The various RMF models used in the present work includes NL3 [64], BIGApple [65], BSR1-BSR7 [49], DOPS1,DOPS2, DOPS3 [66], FSU2H [61], HPU1, HPU2, HPU3 [52], LP and MP [51], HPUA, HPUB, HPUC [50], FSUGold [67], FSUGold2 [68], HPNL [69], IOPB-1 [70],FSUGarnet [71],DBHP [72], SRV00 [73], TM1 [74]. In this study, we examine the effects of hyperon-vector meson coupling strengths $ X_{\omega Y} $ = 0.6, 0.8, 0.9, and the SU(6) symmetry case on the threshold density for the appearance of hyperons, the EoS of a neutron star with a hyperon core, and the resulting neutron star characteristics. Here, we use the values of couplings $ g_{\rho Y} $, $ g_{\sigma^* Y} $ and $ g_{\Phi Y} $ as given by Eq (13) and $ X_{\sigma Y} $ is adjusted for given values of $ X_{\omega Y} $ = 0.6, 0.8, 0.9 by fitting experimental estimates of hyperon-nucleon potential U$ _{\Lambda}^{(N)} $ as given by Eq. (14) and Eq. (15). For the sake of comparison, we also display our results for the meson-hyperon couplings as given by SU(6) models (additive quark model) of hadrons.

In Table 1 we display the threshold densities (in fm$ ^{-3} $) for the onset of various hyperons namely Λ, $ \Sigma^{\pm,0} $, $ \Xi^{-,0} $, computed using various RMF parameter sets which supports a star with observational constraint of M$ _{max} $ $ \geq $ 2 M$ _{\odot} $ after hyperonization. For each parameter set, results are shown for specific fixed vector meson-hyperon coupling strengths (X$ _{\omega Y} $ = 0.6, 0.8, and 0.9), and with couplings based on SU(6) symmetry. It is evident from the table that the Λ hyperon appears for all RMF models considered with couplings X$ _{\omega Y} $ = 0.6, 0.8, 0.9, and with SU(6) symmetry. It is observed that the appearance of the Λ hyperon exhibits a notable dependence on the meson–hyperon coupling scheme. This behavior may primarily be attributed to its attractive scalar interaction with the σ-meson, which lowers its effective mass M$ ^*_{\Lambda}=M_\Lambda - g_{\sigma\Lambda}\sigma $ and thus reduces its chemical potential. Also lack of electric charge eliminates Coulomb repulsion, making it energetically more favorable to appear before charged hyperons in β-equilibrated neutron star matter [60]. Further, at X$ _{\omega Y} $ = 0.6, hyperons such as Λ appear at relatively low densities due to reduced vector repulsion. Increasing to $ X_{\omega Y} = 0.9 $ raises the energy barrier for hyperon formation, thereby pushing their thresholds to higher baryon densities [2, 26, 75−77]. The early onset of $ \Xi^{-} $ can also be noticed from the table, whereas $ \Xi^{0} $ hyperon appearance at relatively high densities (delayed onset)is observed for the various models with couplings X$ _{\omega Y} $ = 0.6, 0.8, 0.9. Also there is no appearance of $ \Xi^{-,0} $ with SU(6) symmetry.

Model	Coupling	Threshold Density (fm$ ^{-3} $)
		Λ	$ \Sigma^+ $	$ \Sigma^0 $	$ \Sigma^- $	$ \Xi^0 $	$ \Xi^- $
NL3	SU(6)	0.260	0.521	0.441	0.238	—	—
	$ X_{\omega Y}=0.6 $	0.274	—	—	—	0.757	0.302
	$ X_{\omega Y}=0.8 $	0.290	—	—	—	0.632	0.294
	$ X_{\omega Y}=0.9 $	0.302	—	—	—	0.613	0.296
BIG Apple	SU(6)	0.332	0.614	0.512	0.252	—	—
	$ X_{\omega Y}=0.6 $	0.320	—	—	—	0.859	0.349
	$ X_{\omega Y}=0.8 $	0.339	—	—	—	0.716	0.343
	$ X_{\omega Y}=0.9 $	0.358	—	—	—	0.695	0.345
DOPS1	SU(6)	0.313	0.620	0.509	0.246	—	—
	$ X_{\omega Y}=0.6 $	0.308	—	—	—	0.871	0.339
	$ X_{\omega Y}=0.8 $	0.324	—	—	—	0.719	0.332
	$ X_{\omega Y}=0.9 $	0.337	—	—	—	0.695	0.334
FSU2H	SU(6)	0.334	0.711	0.555	0.246	—	—
	$ X_{\omega Y}=0.6 $	0.322	—	—	0.450	—	0.354
	$ X_{\omega Y}=0.8 $	0.341	—	—	—	0.895	0.347
	$ X_{\omega Y}=0.9 $	0.358	—	—	—	0.862	0.351
HPU1	SU(6)	0.343	0.654	0.542	0.268	—	—
	$ X_{\omega Y}=0.6 $	0.338	—	—	—	0.891	0.367
	$ X_{\omega Y}=0.8 $	0.357	—	—	—	0.755	0.361
	$ X_{\omega Y}=0.9 $	0.376	—	—	—	0.733	0.363
HPU2	SU(6)	0.331	0.707	0.558	0.256	—	—
	$ X_{\omega Y}=0.6 $	0.326	—	—	0.715	—	0.359
	$ X_{\omega Y}=0.8 $	0.343	—	—	—	0.877	0.353
	$ X_{\omega Y}=0.9 $	0.356	—	—	—	0.846	0.355
HPU3	SU(6)	0.325	0.711	0.563	0.262	—	—
	$ X_{\omega Y}=0.6 $	0.324	—	—	—	—	0.360
	$ X_{\omega Y}=0.8 $	0.343	—	—	—	0.871	0.353
	$ X_{\omega Y}=0.9 $	0.353	—	—	—	0.839	0.353
LP	SU(6)	0.321	0.664	0.532	0.250	—	—
	$ X_{\omega Y}=0.6 $	0.316	—	—	0.662	0.972	0.349
	$ X_{\omega Y}=0.8 $	0.334	—	—	—	0.808	0.341
	$ X_{\omega Y}=0.9 $	0.347	—	—	—	0.783	0.343
MP	SU(6)	0.316	0.699	0.549	0.252	—	—
	$ X_{\omega Y}=0.6 $	0.318	—	—	0.731	—	0.353
	$ X_{\omega Y}=0.8 $	0.334	—	—	—	0.905	0.345
	$ X_{\omega Y}=0.9 $	0.343	—	—	—	0.868	0.346
BSR1	SU(6)	0.313	0.695	0.550	0.252	—	—
	$ X_{\omega Y}=0.6 $	0.312	—	—	0.677	1.007	0.350
	$ X_{\omega Y}=0.8 $	0.328	—	—	—	0.822	0.342
	$ X_{\omega Y}=0.9 $	0.340	—	—	—	0.789	0.342
BSR2	SU(6)	0.334	0.754	0.586	0.254	—	—
	$ X_{\omega Y}=0.6 $	0.324	—	—	0.589	—	0.362
	$ X_{\omega Y}=0.8 $	0.344	—	—	—	0.904	0.353
	$ X_{\omega Y}=0.9 $	0.356	—	—	—	0.864	0.356
BSR3	SU(6)	0.324	0.738	0.575	0.254	—	—
	$ X_{\omega Y}=0.6 $	0.322	—	—	0.657	—	0.360
	$ X_{\omega Y}=0.8 $	0.338	—	—	—	0.914	0.352
	$ X_{\omega Y}=0.9 $	0.348	—	—	—	0.871	0.352
BSR4	SU(6)	0.321	0.714	0.562	0.254	—	—
	$ X_{\omega Y}=0.6 $	0.318	—	—	0.686	1.044	0.354
	$ X_{\omega Y}=0.8 $	0.336	—	—	—	0.850	0.346
	$ X_{\omega Y}=0.9 $	0.348	—	—	—	0.816	0.346
BSR5	SU(6)	0.308	0.675	0.538	0.254	—	—
	$ X_{\omega Y}=0.6 $	0.312	—	—	0.839	0.991	0.346
	$ X_{\omega Y}=0.8 $	0.328	—	—	—	0.810	0.338
	$ X_{\omega Y}=0.9 $	0.338	—	—	—	0.780	0.338
BSR6	SU(6)	0.308	0.704	0.552	0.252	—	—
	$ X_{\omega Y}=0.6 $	0.312	—	—	0.698	—	0.348
	$ X_{\omega Y}=0.8 $	0.328	—	—	—	0.856	0.340
	$ X_{\omega Y}=0.9 $	0.338	—	—	—	0.820	0.340
BSR7	SU(6)	0.290	0.643	0.516	0.250	—	—
	$ X_{\omega Y}=0.6 $	0.300	—	—	0.874	—	0.336
	$ X_{\omega Y}=0.8 $	0.316	—	—	—	0.796	0.328
	$ X_{\omega Y}=0.9 $	0.324	—	—	—	0.763	0.328

Table 1.  Threshold densities computed using various RMF parameter sets. For each parameter set, results are shown for specific fixed vector coupling strengths ($ X_{\omega Y} $ = 0.6, 0.8, and 0.9), and with couplings based on SU(6) symmetry. The threshold densities (in fm$ ^{-3} $) at which various hyperons namely neutral Λ, the negatively charged $ \Xi^{-} $ and $ \Sigma^{-} $, the neutral $ \Xi^0 $ and $ \Sigma^0 $, and the positively charged $ \Sigma^{+} $ first appear.

With increased vector coupling strength at $ X_{\omega Y} = 0.9 $, we observe that the $ \Xi^- $ hyperon consistently appears at lower densities across all parameter sets, followed by the Λ and $ \Xi^0 $ hyperons. This behavior can be attributed to the contribution of the electron chemical potential in the chemical equilibrium condition of the negatively charged $ \Xi^- $, which lowers its onset density [78, 79]. Additionally, the adopted attractive Ξ–nucleon potential $ U_\Xi^{(N)} $ = - 22.5 MeV [54, 56], combined with its relatively smaller vector repulsion compared to other hyperons, facilitates its early appearance even at stronger vector couplings ($ X_{\omega Y} = 0.9 $).

The isospin configuration plays a critical role in the onset sequence of $ (\Sigma $) hyperons. Despite their relatively low bare masses, the appearance of $ \Sigma^0 $ and $ \Sigma^+ $ is delayed compared to $ \Sigma^- $, primarily due to differences in the vector meson interactions, especially the isovector ρ-meson coupling. In the RMF framework, the ρ meson mediates repulsion that depends on the third component of isospin ($ I_3 $), with $ \Sigma^+ $ ($ I_3 = +1 $) and $ \Sigma^0 $ ($ I_3 = 0 $) experiencing stronger or comparable repulsive contributions than $ \Sigma^- $ ($ I_3 = -1 $). Consequently, the repulsive energy shift is greater for $ \Sigma^+ $, delaying its onset under β-equilibrated and charge-neutral conditions. While SU(6)-motivated couplings reduce the overall vector repulsion by prescribing lower coupling constants based on symmetry arguments, the relative isospin-dependent hierarchy of onset is preserved. In the SU(6) model, the vector coupling between the $ \Sigma^- $ hyperon and the ω-meson is given by quark model relations, which results in $ g_{\omega\Sigma} = \frac{2}{3}g_{\omega N} $. This reduced repulsive interaction lowers the energy cost for $ \Sigma^- $ formation in dense matter. As a result, $ \Sigma^- $ appears at comparitively low densities in the models considered around $ \rho_{\rm{th}} \approx 0.24\text{–}0.27\; {\rm{fm}}^{-3} $ while they do not appear in more repulsive couplings. Its early onset is further supported by its negative electric charge, which aids charge neutrality and makes it energetically competitive with leptons. These findings align with the studies demonstrating the sensitivity of hyperon thresholds to vector coupling strengths [26, 59, 61].

This explains why only the full Σ triplet appears in the SU(6) case, and not in the $ X_{\omega Y} = 0.6 $ or $ X_{\omega Y} = 0.8 $,and $ X_{\omega Y} = 0.9 $ schemes, where stronger vector couplings more effectively suppress the neutral and positively charged Σ species. These trends are consistent with earlier studies, such as those by Banik et al. [38] and Fortin et al. [63], who emphasized the isospin-dependent vector repulsion in governing the appearance of charged hyperons. Moreover, recent RMF-based analyses by Kumar et al. [80] reaffirm that the structure and sequence of hyperon appearance are strongly influenced by meson-hyperon couplings, particularly in the presence of isospin asymmetry characteristic of dense neutron star matter.

The weaker coupling case, $ X_{\omega Y} = 0.6 $, allows hyperons to appear at lower densities due to reduced vector repulsion. This leads to the appearance of negatively charged species like $ (\Sigma^- $) and $ \Xi^- $, which softens the EoS more substantially. The SU(6) symmetry-based coupling, which uses fixed ratios among vector couplings derived from quark model symmetries, results in intermediate to weak repulsion for different hyperons. Notably, SU(6) couplings often yield the softest EoS amongst the different schemes, due to relatively small ω–hyperon coupling constants. This results in significantly lowering the maximum masses of neutron star. The absence of appearance of $ \Sigma^- $ hyperons in all EoS models at higher vector coupling strengths ($ X_{\omega Y} = 0.8 $ and $ X_{\omega Y} = 0.9 $) might be due to strong repulsive Σ-nucleon vector interactions that significantly raise their chemical potential thresholds, hence suppressing their appearance [81]. Contrary, the appearance of $ \Sigma^0 $ and $ \Sigma^+ $ hyperons exclusively in the SU(6) coupling scheme reduces the vector repulsion arising from weaker ω-meson couplings that can enable the appearance of otherwise energetically disfavored species. In spite of their higher rest masses, the reduced vector potential in SU(6) lowers their total chemical potentials, allowing these neutral and positively charged hyperons to populate dense matter at relatively higher densities. Charge asymmetry and Coulomb effects in neutron-rich matter tend to favor the inclusion of negatively charged hyperons such as $ \Sigma^- $ and $ \Xi^- $, which can help to maintain charge neutrality with fewer leptons [26, 59, 61]. The onset of these hyperons is highly sensitive to the strength of repulsive vector interactions. If the vector coupling is strong enough, then repulsion can overcome the Coulomb and charge chemical potential advantages, thereby delaying or even preventing their appearance.

The $ \Xi^- $ hyperon consistently appears for all parameter sets in our study for vector coupling strengths X$ _{\omega Y} $ = 0.6, 0.8, and 0.9. It can be noticed from Table 1 that its onset occurs at slightly lower densities for the highest coupling X$ _{\omega Y} $ = 0.9. The onset of $ \Xi^- $ can be explained within the RMF framework by the interplay between scalar attraction, vector repulsion, and the density dependence of chemical potentials. In RMF models, hyperon formation is governed by threshold conditions such as: $ \mu_n - \mu_e \geq \mu_{\Xi^-}^{\ast} $, where $ \mu_{\Xi^-}^{\ast} $ is the in-medium effective chemical potential of the $ \Xi^- $. While stronger vector coupling increases repulsion, it also stiffens the EoS, causing the neutron chemical potential $ \mu_n $ to rise more rapidly with density. This accelerates the satisfaction of the threshold condition despite the enhanced repulsion. Moreover, the attractive Ξ - nucleon potential used in this study, U$ _{\Xi}^{(N)} $ = -22.5 MeV, lowers the in-medium energy of the $ \Xi^- $, promoting its early appearance. Similar findings in earlier RMF studies [60, 76, 81] emphasize that scalar attraction can effectively counterbalance vector repulsion, facilitating the emergence of $ \Xi^- $ even at higher coupling strengths.

In contrast, the $ \Xi^- $ hyperon does not appear in the SU(6)-motivated coupling for all parameter sets. This might be due to the significantly reduced vector coupling for Ξ under SU(6) symmetry, g$ _{\omega \Xi} = \frac{1}{3} g_{\omega N} \quad \Rightarrow \quad X_{\omega \Xi} \approx 0.333 $, which leads to a softer EoS and a slower rise in the neutron chemical potential $ \mu_n $ with density. As a result, the threshold condition for $ \Xi^- $ is not met within the central densities reached in stable neutron stars. This suppression is consistent with earlier findings [76, 82], which show that SU(6)-based couplings can underestimate the repulsion needed for early hyperon onset—particularly for the $ \Xi^- $, whose appearance depends sensitively on the density evolution of $ \mu_n $. Thus, the appearance of the $ \Xi^- $ hyperon reflects an interplay between meson-mediated interactions and EoS stiffness, rather than being governed by vector coupling strength alone. The $ \Xi^0 $ hyperon is absent in the SU(6) motivated couplings scheme for all parameter sets considered in the present study. Furthermore, its threshold density increases with decreasing vector coupling strength X$ _{\omega Y} $, and for some EoS models, it is entirely suppressed at X$ _{\omega Y} $ = 0.6. This behavior arises because the $ \Xi^0 $ requires significantly higher neutron chemical potentials, which can be reached only in the dense cores of stars described by stiff EoS. Unlike its negatively charged counterpart $ \Xi^- $, the $ \Xi^0 $ does not benefit from Coulomb attraction, placing it at an energetic disadvantage. This effect is amplified under weaker vector repulsion, as in the cases of X$ _{\omega Y} $ = 0.6 and SU(6), further delaying or preventing its onset. These findings highlight the complex and highly model-dependent nature of hyperon formation in dense matter. For the $ \Xi^0 $, its appearance is governed not only by its mass and potential depth, but also by its electric neutrality, which removes the Coulomb channel that facilitates earlier onset for charged hyperons like $ \Xi^- $. Additionally, the interplay between isospin asymmetry and meson-mediated interactions, especially the repulsive vector couplings, plays a critical role in determining its threshold. Our results emphasize that even neutral hyperons are strongly influenced by the detailed meson-hyperon coupling structure and the global stiffness of the EoS. These trends are in agreement with previous RMF-based investigations reported in Refs. [60, 81, 83], which similarly found that neutral hyperon populations are highly sensitive to the models' microphysical assumptions.

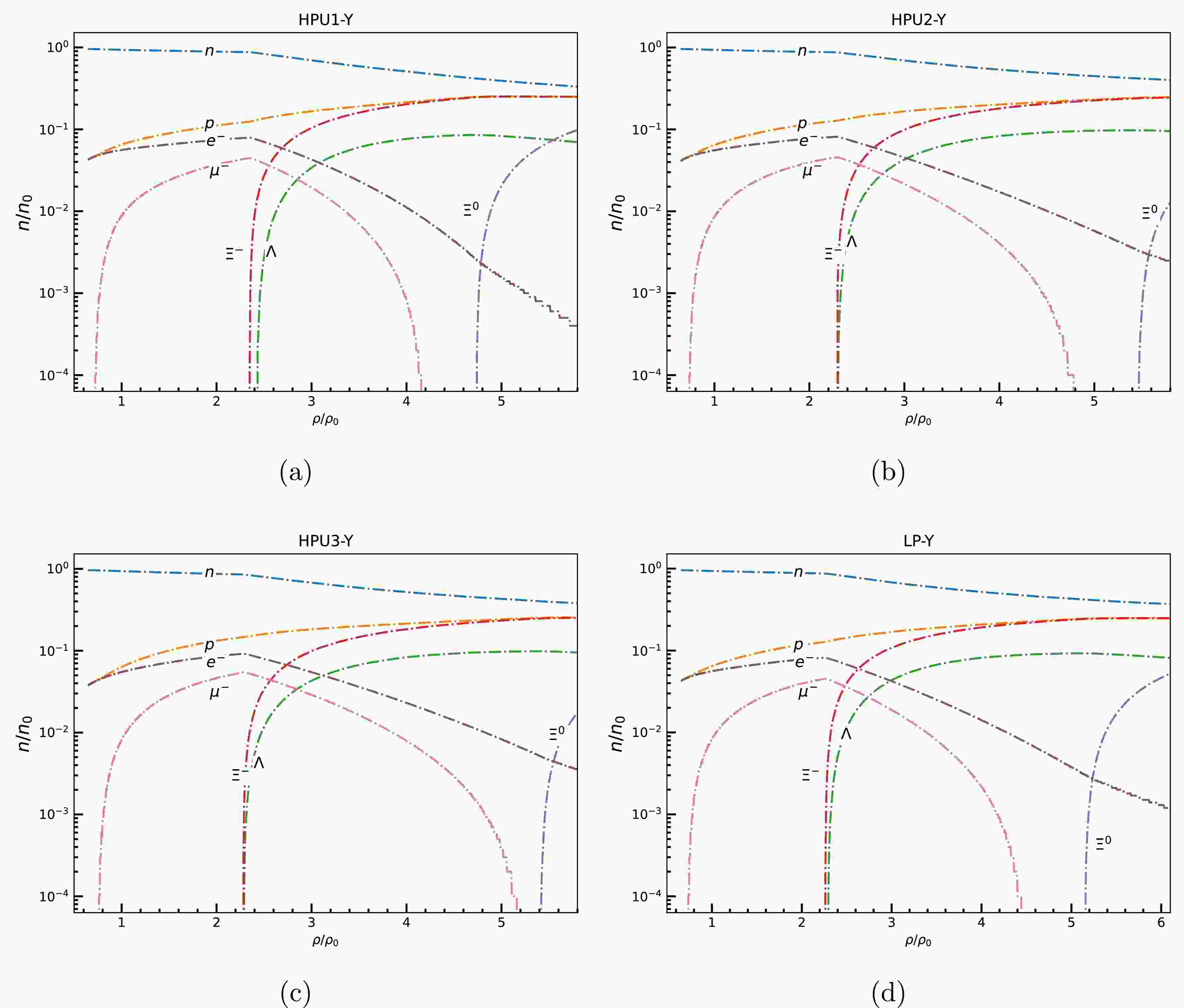
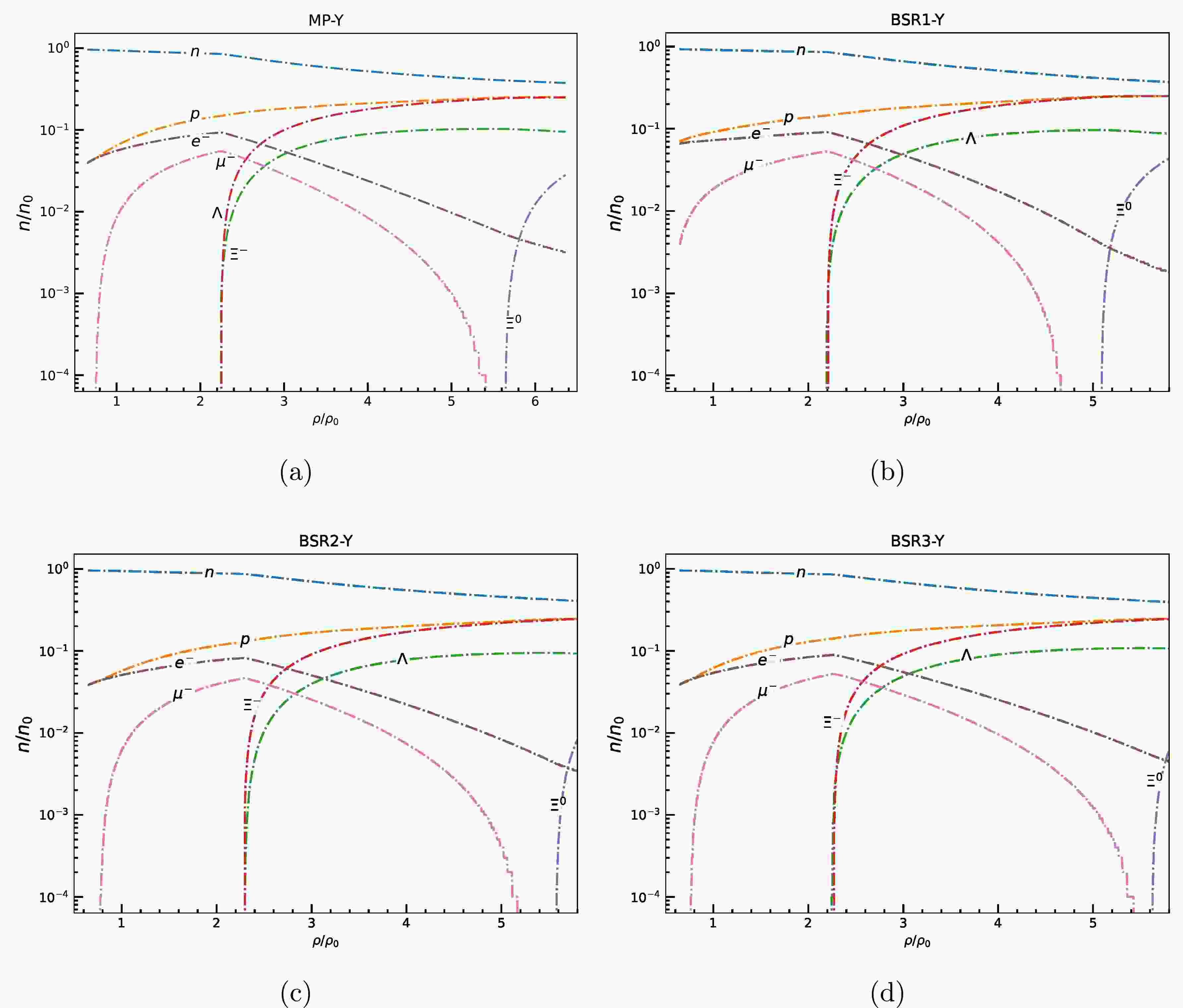
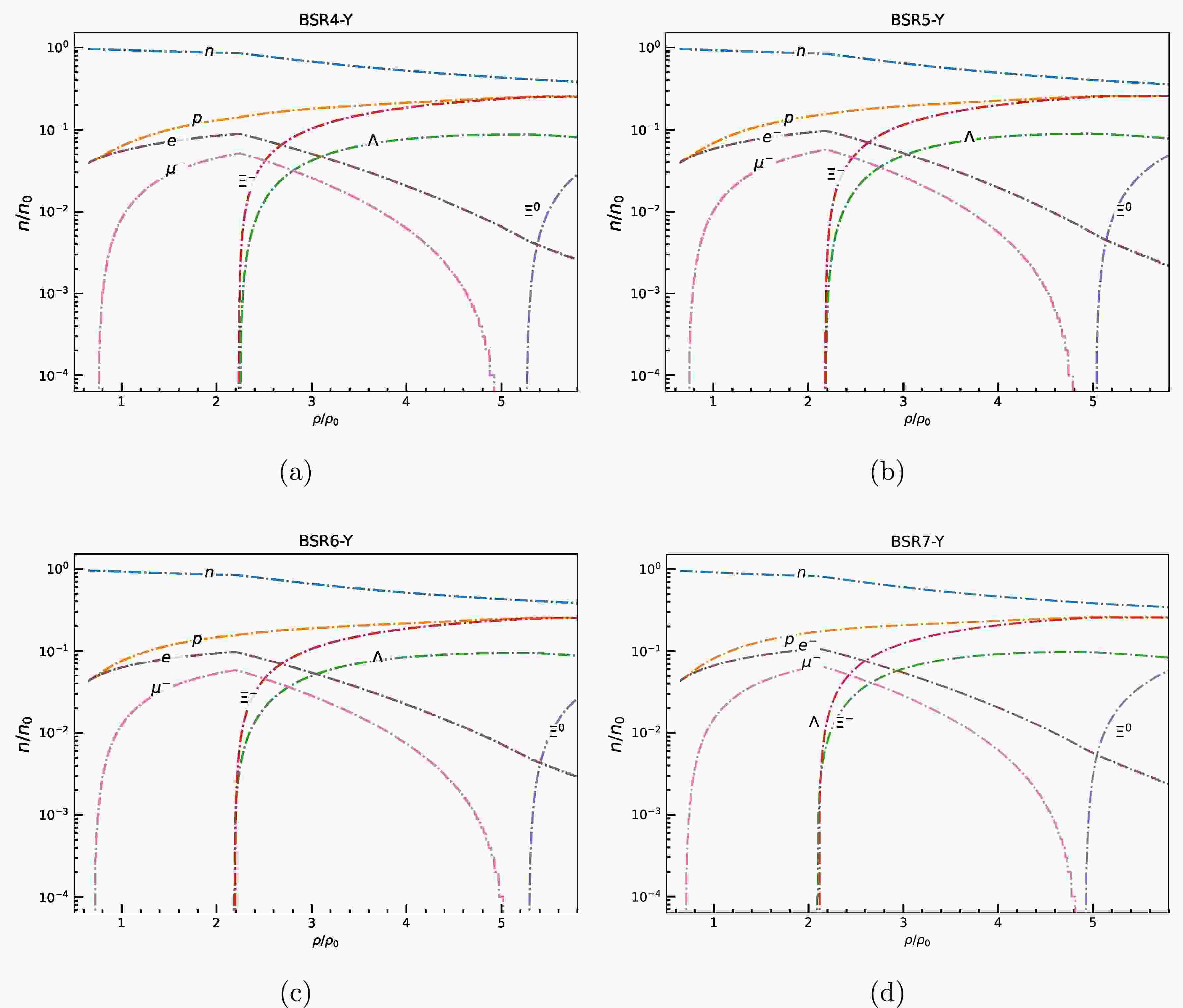
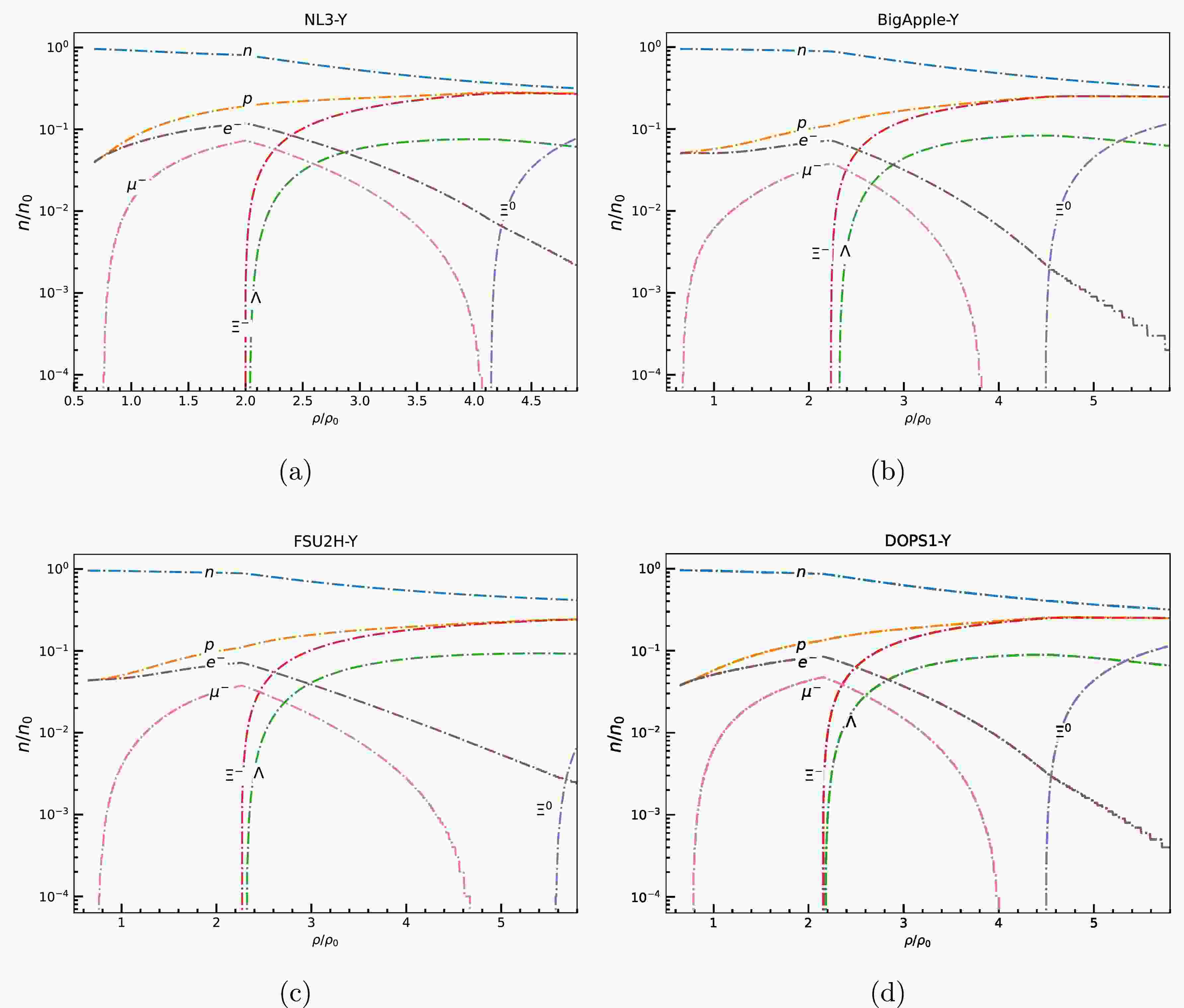
In the present study, it can be observed from the Table 1 that stronger vector couplings ($ X_{\omega Y} = 0.9 $) delay hyperon onset and preserve a stiffer equation of state (EoS)—thus yielding higher maximum masses that are in agreement with the systematic studies by Weissenborn et al. [76],

For the sake of simplicity, in Figs. 1-4 we show the fraction of baryonic species (n/n$ _{0} $) as a function of baryon density scaled to saturation density for the hyperonic star with $ X_{\omega Y} $ $ = $ $ 0.9 $ for those non linear RMF models (Table 1) which supports a star with observational constraint of M$ _{max} $ $ \geq $ 2 M$ _{\odot} $ after hyperonization.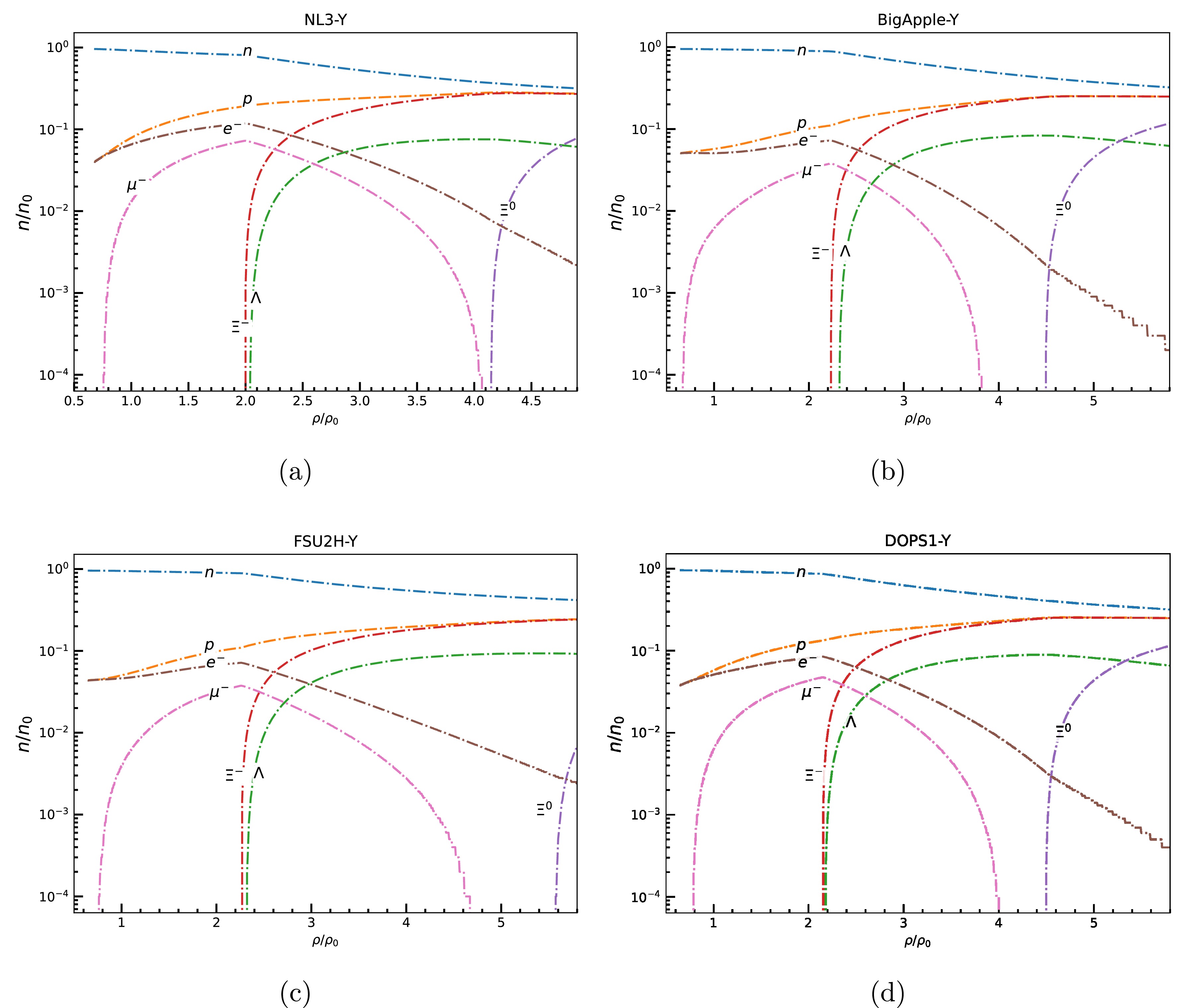

Figure 1.  (color online) Particle fraction evolution as a function of baryon density scaled to saturation density for (a) NL3, (b) BigApple, (c)FSU2H, and (4) DOPS1 models with coupling $ X_{\omega Y} $=0.9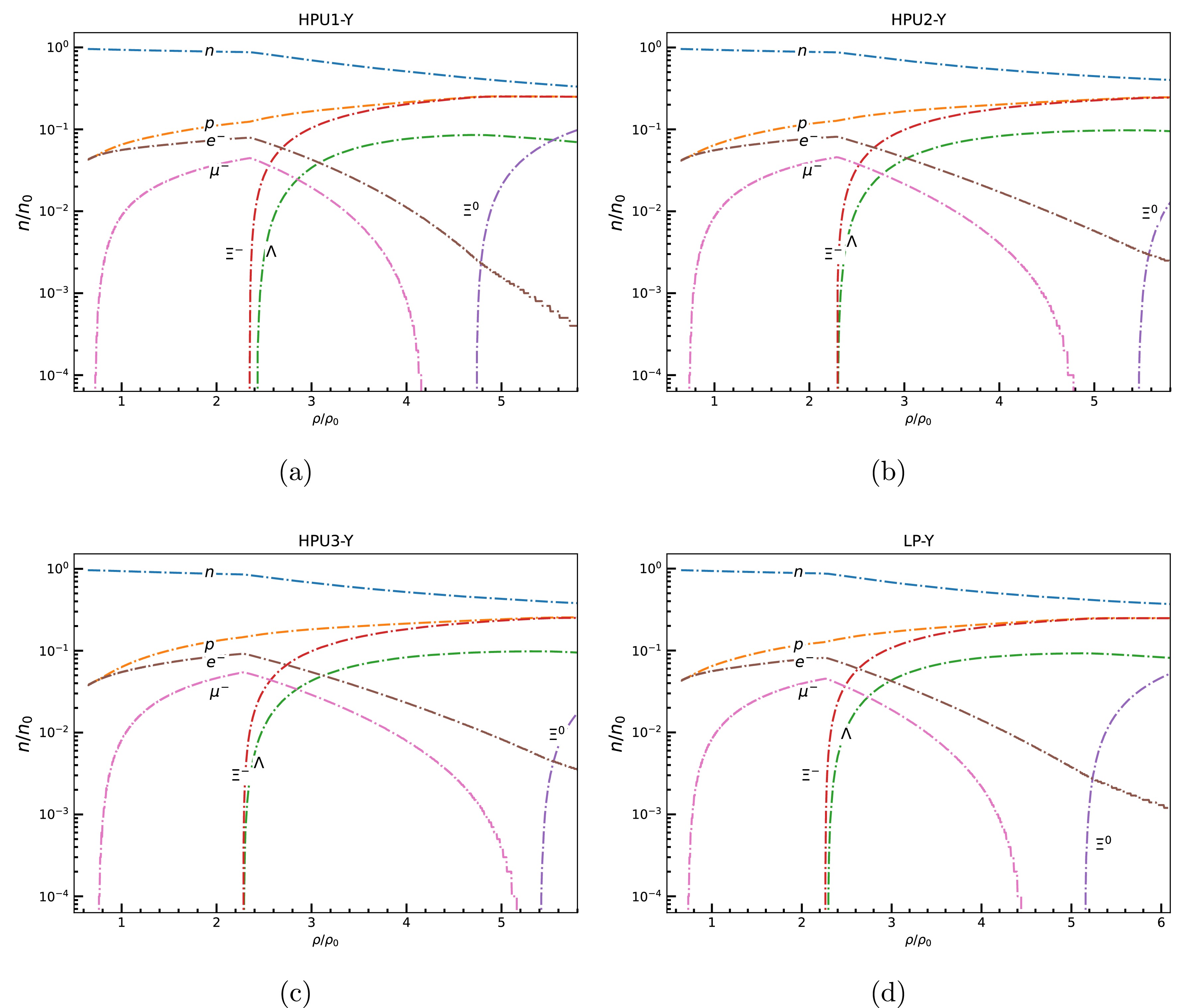

Figure 2.  (color online) Particle fraction evolution as a function of baryon density scaled to saturation density for (a) HPU1, (b) HPU2, (c) HPU3 and (4) LP models with coupling $ X_{\omega Y} $=0.9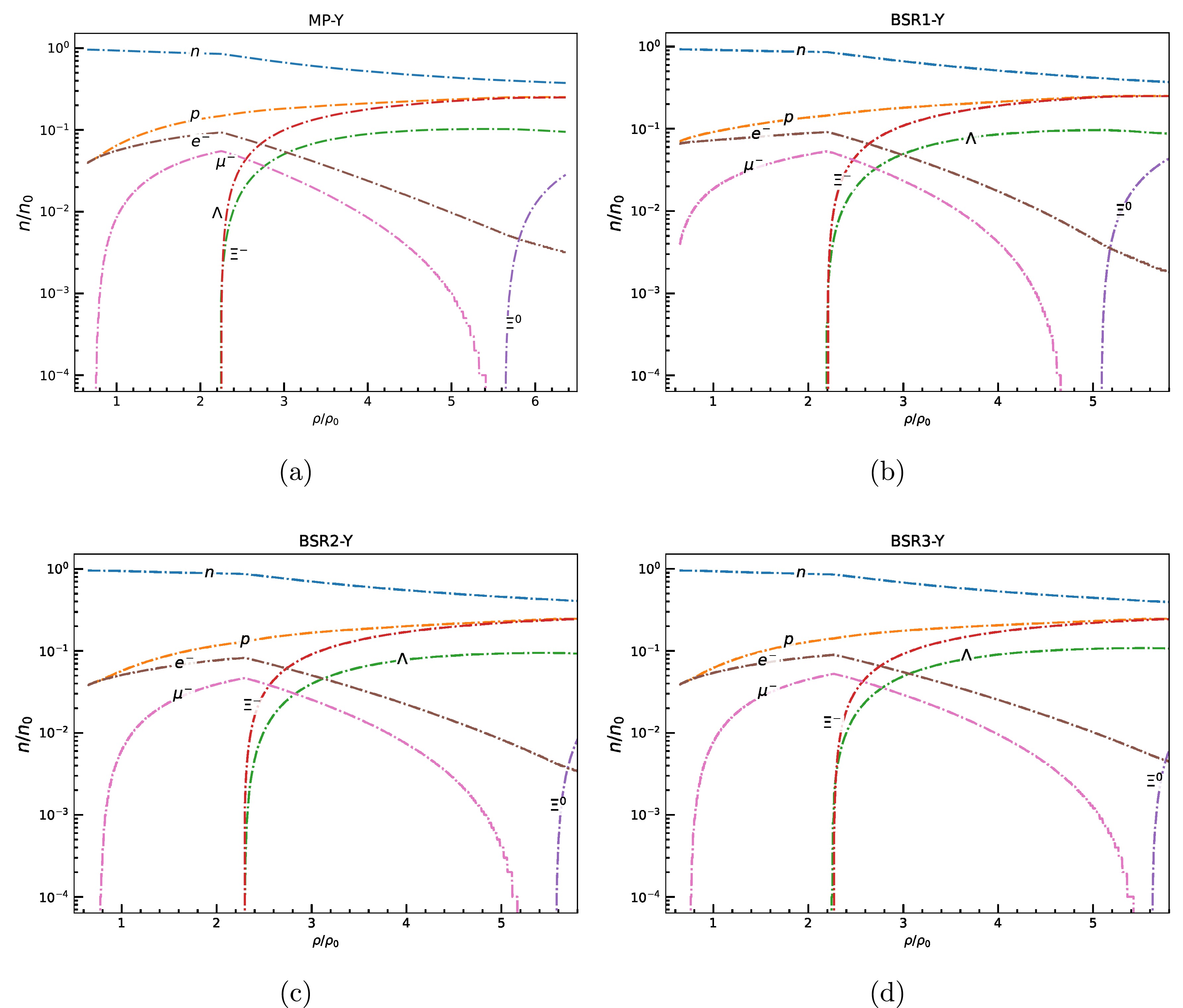

Figure 3.  (color online) Particle fraction evolution as a function of baryon density scaled to saturation density for (a) MP, (b) BSR1 (c) BSR2, (d)BSR3 models with coupling $ X_{\omega Y} $=0.9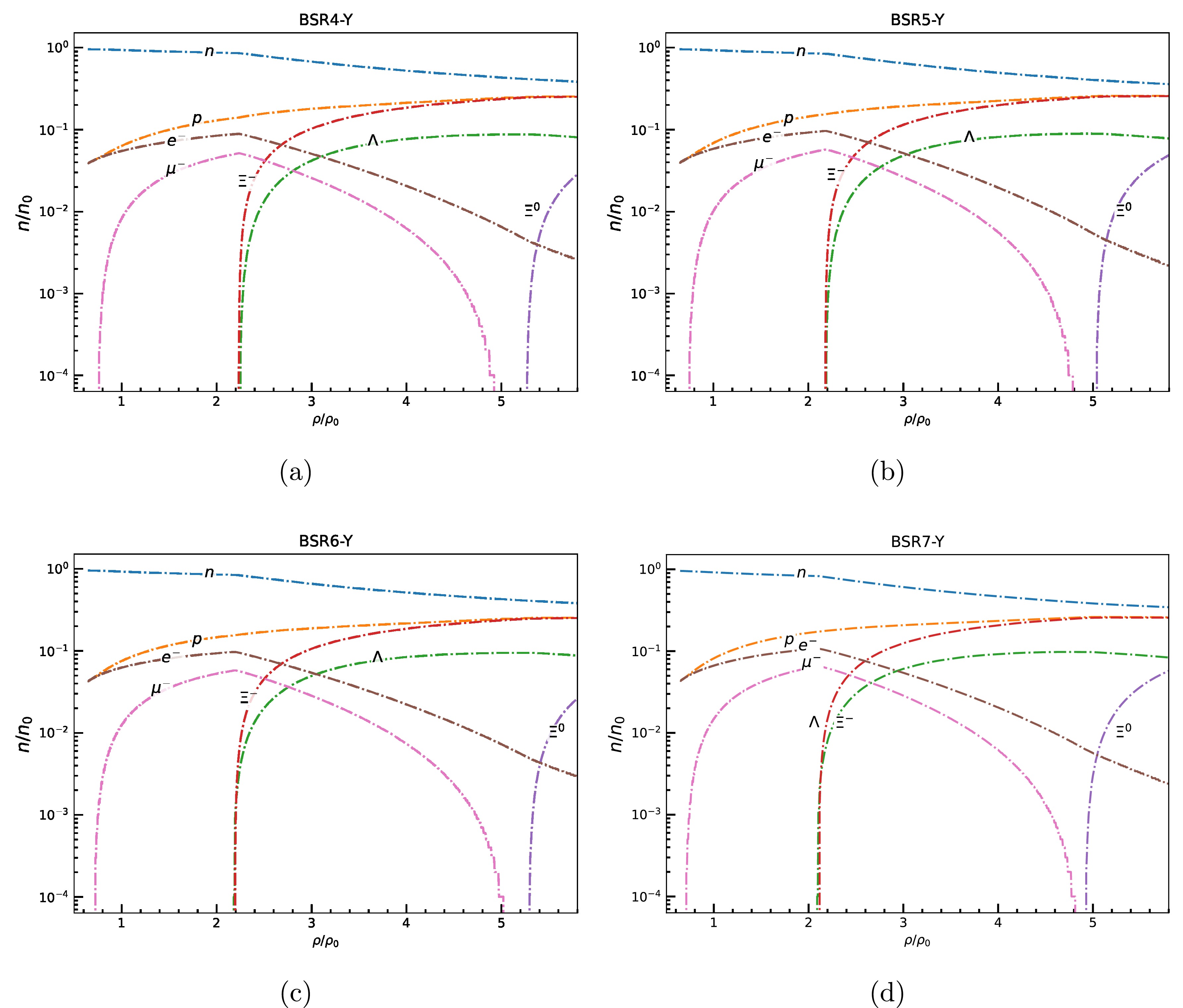

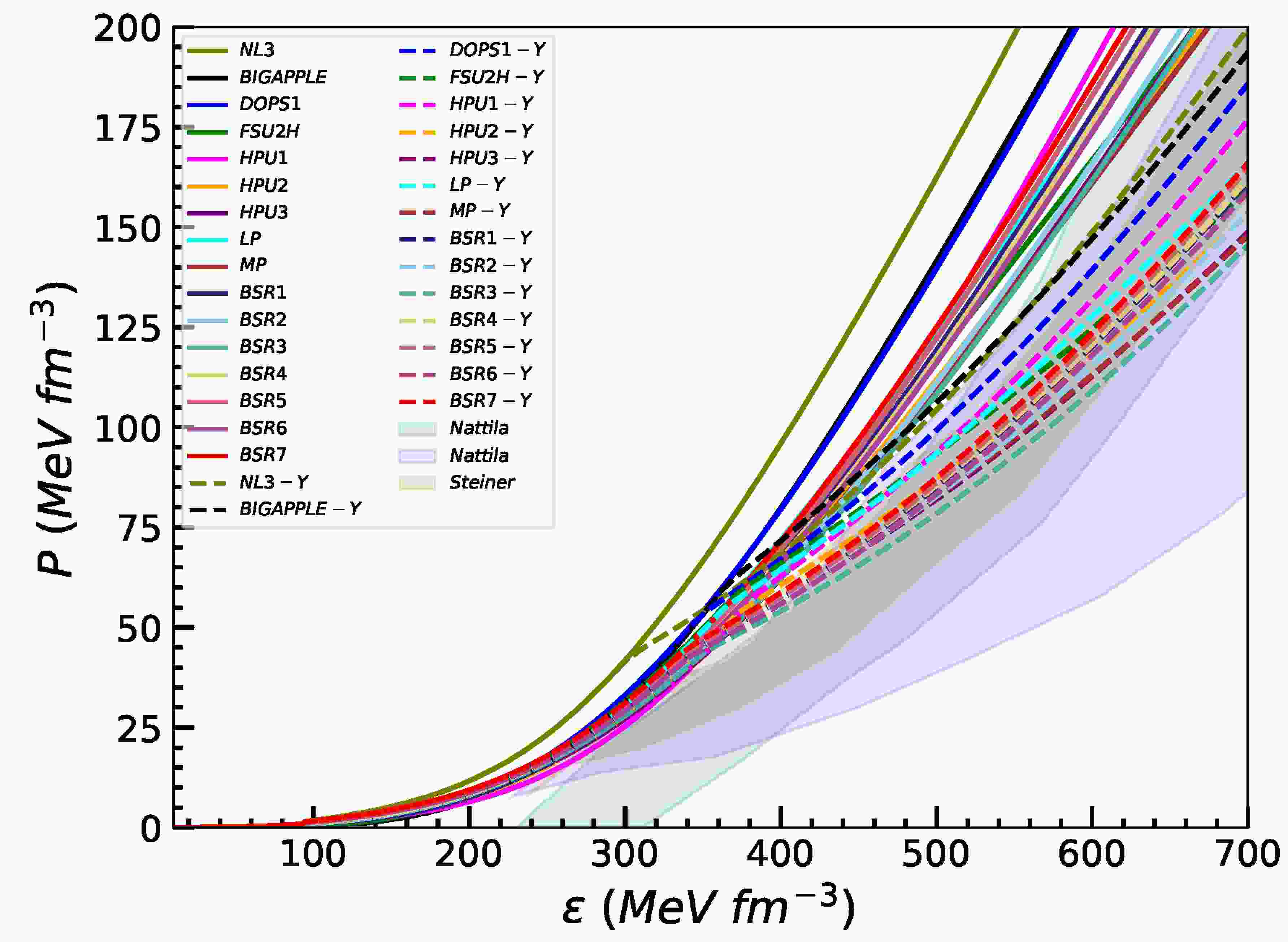
Figure 4.  (color online) Particle fraction evolution as a function of baryon density scaled to saturation density for (a) BSR4 (b) BSR5 (c) BSR6, (d) BSR7 models with coupling $ X_{\omega Y} $=0.9

In the present work, we have computed EoSs i.e., pressure as a function of energy density for nucleonic matter only and nucleonic matter with hyperons in β - equilibrated condition for various models with vector meson - hyperon coupling X$ _{\omega Y} $ = 0.6, 0.8, 0.9 and with SU(6) model. But for the sake of simplicity, we have only displayed the EoSs obtained by RMF models (considered in Table 1) with vector meson hyperon coupling, X$ _{\omega Y} $ = 0.9 in Fig. 5. For each model, the solid lines denote the purely nucleonic EoS, while the corresponding dashed lines depict the EoS modified by the inclusion of hyperons. It can be noticed from the Fig. 5 that EoSs become softer with the inclusion of hyperons as compared to nucleonic matter only. From the present study, it is observed that the softness or stiffness of EoSs are sensitive to the choice of vector meson hyperon couplings, which in turn affect the macroscopic neutron star properties. It is clearly observed that the inclusion of hyperons leads to a universal softening of the EoS, characterized by a reduction in pressure at fixed energy density. This softening becomes pronounced at higher densities $ \varepsilon \gtrsim $ 300 MeV fm$ ^{-3} $, coinciding with the typical onset of hyperons in the dense core. This effect is due to the replacement of high-momentum nucleons by heavier hyperons, which reduce the Fermi pressure, and the relatively weaker vector repulsion in hyperon-meson couplings [2, 87]. The effect of hyperonization is more pronounced in initially stiff EoS, as their larger chemical potentials favor earlier hyperons onset and more significant composition changes. In contrast, softer EoSs already exhibit lower pressures in the nucleonic phase and experience comparatively moderate softening upon inclusion of hyperons. All the hyperonic EOSs computed for RMF models are softer and fall within or near the shaded regions corresponding to the astrophysical constraints from GW170817, NICER mission taken from Ref. [84] and EoS of cold dense matter with a 95% confidence limit [85].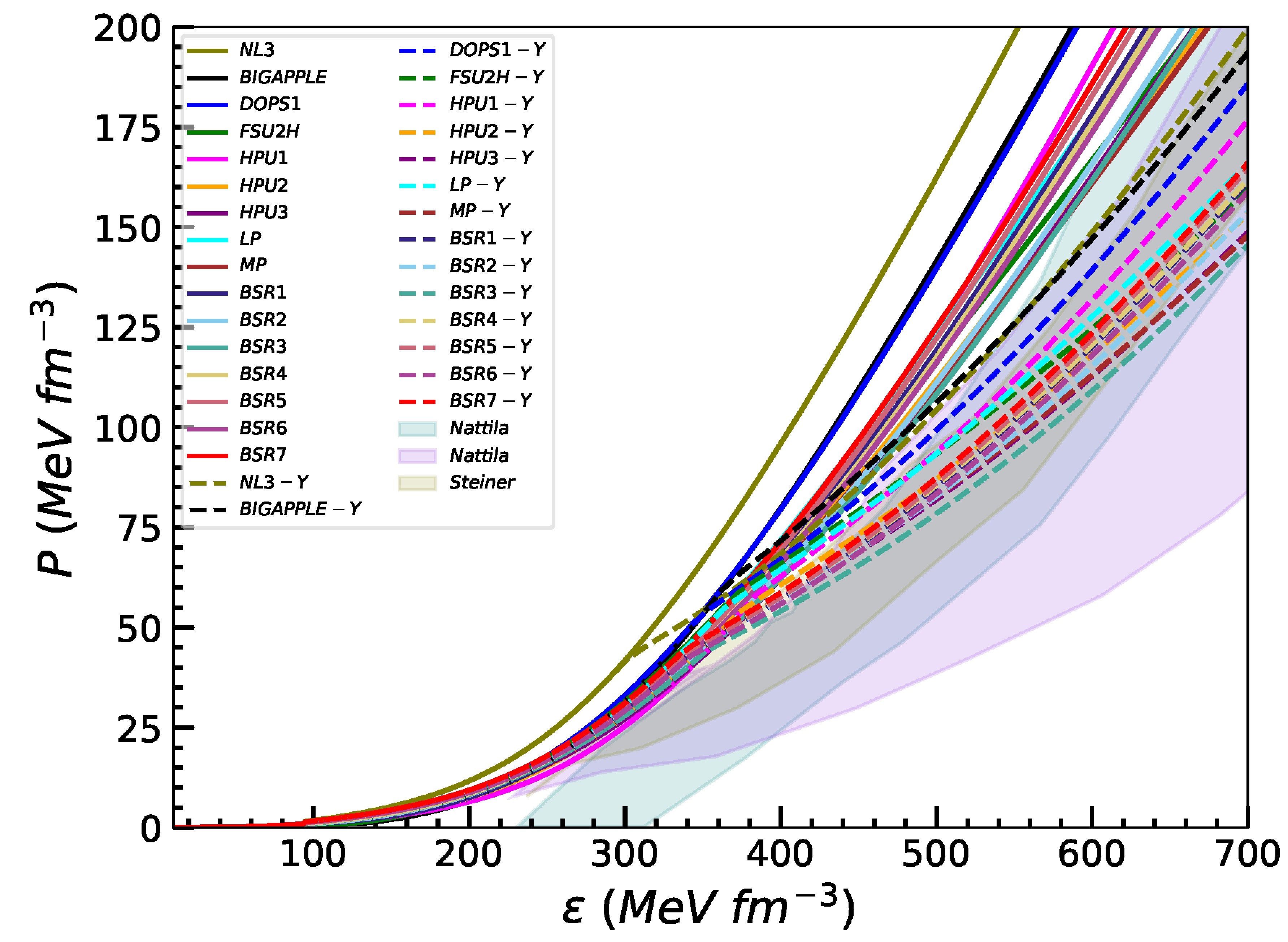

Figure 5.  (Color online) EoS, i.e., pressure as function of energy density computed for various RMF models considered in the present work for nucleonic matter in β-equilibrium condition. The EoSs for nucleonic matter plus hyperons computed with vector meson hyperons coupling, $ X_{\omega Y} $ = 0.9, are shown for comparison (denoted by RMF model-Y). The shaded regions indicate the observational constraints as discussed in Refs. [84, 85].

For the stronger coupling case ($ X_{\omega Y} = 0.9 $), hyperons experience enhanced vector repulsion, which delays their onset and reduces their abundance at intermediate densities. As a result, the conversion of neutrons into hyperons is suppressed, retaining a high neutron fraction ($ Y_n $) over a broader range of baryon densities. This preservation of neutron dominance contributes to maintaining a stiffer equation of state [26, 29, 61]. We also observe early onset of hyperons in models with weaker repulsion X$ _{\omega Y} $ = 0.6, that results in a substantial EoS softening which resembles the study reported in Ref. [38], reducing both mass and radii of the star. This behaviour is also observed in the density-dependent RMF models, such as those used in the work by Kumar et al. [88], where variations in vector meson couplings led to substantial differences in neutron star structure and tidal deformability. In Table 2 we have shown the results for neutron star properties like maximum mass (M$ _{max} $), radius (R$ _{max} $) and dimensionless tidal deformability ($ \Lambda_{max} $) corresponding to M$ _{max} $, the central density ($ \rho_{1.4} $), radius R$ _{1.4} $ and $ \Lambda_{1.4} $ corresponding to a canonical mass (1.4M$ _{\odot} $) star for various RMF models as considered in Table 1. For each parameter set, results are shown without hyperons ("No hyperons"), with hyperons included under specific fixed vector coupling strengths ($ X_{\omega Y} $ = 0.6, 0.8, and 0.9), and with couplings based on SU(6) symmetry. The results obtained with SU(6)- based couplings, predict significantly softer EoSs and lower maximum masses, which corroborate with the findings of Tolos et al. [61] and Fortin et al. [63]. The neutron star properties calculated with couplings based on SU(6) models significantly affects the star properties like M$ _{max} $, R$ _{max} $, R$ _{1.4} $, and $ \Lambda_{1.4} $. This might be due to significant softening of EoSs caused by the early onset of hyperons (Λ, $ \Sigma^{\pm, 0} $) at a density well below the $ \rho_{1.4} $ and which results in lowering the star properties. This indicates that SU(6)- motivated vector couplings, while theoretically appealing, often lead to maximum masses below observed values ($ \ge $ 2 M$ _{\odot} $). It can be noticed from the Table 2 that canonical mass star properties such as R$ _{1.4} $ and $ \Lambda_{1.4} $ calculated for EoSs consisting of nucleonic matter with hyperons under specific fixed vector coupling strength X$ _{\omega Y} $ = 0.6, 0.8, 0.9 remain unaffected and closely resememble with their values calculated for EoSs consisting of nucleonic matter only. This might be attributed to the fact that, even if hyperons appear in the very centre of a 1.4 M$ _{\odot} $ star, their population fraction is extremely small and therefore has a negligible effect on global stellar properties like R$ _{1.4} $ and $ \Lambda_{1.4} $.

Model	Type	$ M_{\text{max}} $ ($ M_\odot $)	$ R_{\text{max}} $ (km)	$ \Lambda_{\text{max}} $	$ \rho_{1.4} $ ($ fm^{-3} $)	$ R_{1.4} $ (km)	$ \Lambda_{1.4} $
NL3	No Hyperons	2.77	13.28	4.44	0.274	14.64	1239.67
	SU(6)	1.83	13.29	99.96	0.341	14.48	1129.63
	$ X_{\omega Y}=0.6 $	2.02	12.83	35.84	0.274	14.64	1243.16
	$ X_{\omega Y}=0.8 $	2.25	12.79	15.95	0.274	14.64	1239.69
	$ X_{\omega Y}=0.9 $	2.32	12.83	13.12	0.274	14.64	1239.68
BIG Apple	No Hyperons	2.60	12.40	4.69	0.330	13.12	713.96
	SU(6)	1.71	12.04	94.17	0.479	12.47	446.81
	$ X_{\omega Y}=0.6 $	1.97	11.85	27.16	0.330	13.16	718.42
	$ X_{\omega Y}=0.8 $	2.18	11.97	13.80	0.330	13.16	715.51
	$ X_{\omega Y}=0.9 $	2.28	12.10	12.83	0.330	13.16	715.51
DOPS1	No Hyperons	2.60	12.51	4.76	0.318	13.57	828.83
	SU(6)	1.74	12.21	81.98	0.463	12.99	546.09
	$ X_{\omega Y}=0.6 $	1.95	11.91	27.33	0.319	13.62	834.08
	$ X_{\omega Y}=0.8 $	2.15	12.01	14.21	0.318	13.62	828.12
	$ X_{\omega Y}=0.9 $	2.24	12.14	12.68	0.318	13.62	828.12
FS2UH	No Hyperons	2.37	12.38	9.63	0.330	13.34	766.87
	SU(6)	1.72	11.71	65.52	0.495	12.63	477.29
	$ X_{\omega Y}=0.6 $	1.86	11.85	38.81	0.330	13.34	768.13
	$ X_{\omega Y}=0.8 $	2.02	12.03	24.87	0.330	13.34	766.87
	$ X_{\omega Y}=0.9 $	2.07	12.11	22.02	0.330	13.34	766.87
HPU1	No Hyperons	2.49	11.94	4.46	0.364	13.00	610.36
	SU(6)	1.59	11.67	108.84	0.564	12.07	323.94
	$ X_{\omega Y}=0.6 $	1.86	11.34	27.13	0.370	12.99	606.29
	$ X_{\omega Y}=0.8 $	2.06	11.47	14.01	0.364	12.99	612.15
	$ X_{\omega Y}=0.9 $	2.16	11.57	12.01	0.364	12.99	611.40
HPU2	No Hyperons	2.33	12.12	8.79	0.351	13.31	699.35
	SU(6)	1.63	11.60	82.21	0.560	12.38	374.69
	$ X_{\omega Y}=0.6 $	1.79	11.60	41.04	0.359	13.30	694.65
	$ X_{\omega Y}=0.8 $	1.96	11.66	22.88	0.351	13.30	701.17
	$ X_{\omega Y}=0.9 $	2.03	11.77	20.55	0.351	13.30	699.36
HPU3	No Hyperons	2.34	11.98	7.26	0.355	13.44	718.82
	SU(6)	1.62	11.56	78.54	0.572	12.53	392.34
	$ X_{\omega Y}=0.6 $	1.76	11.55	42.92	0.369	13.41	711.34
	$ X_{\omega Y}=0.8 $	1.93	11.57	22.86	0.356	13.44	721.27
	$ X_{\omega Y}=0.9 $	1.99	11.61	19.05	0.355	13.44	720.34
LP	No Hyperons	2.43	12.38	7.69	0.334	13.42	748.95
	SU(6)	1.68	11.88	82.33	0.508	12.62	443.77
	$ X_{\omega Y}=0.6 $	1.87	11.66	31.51	0.336	13.41	749.90
	$ X_{\omega Y}=0.8 $	2.04	11.89	19.84	0.334	13.41	749.52
	$ X_{\omega Y}=0.9 $	2.10	12.02	17.82	0.334	13.41	748.94
MP	No Hyperons	2.33	12.15	8.87	0.346	13.49	747.34
	SU(6)	1.61	11.66	89.95	0.567	12.52	393.54
	$ X_{\omega Y}=0.6 $	1.77	11.64	43.55	0.359	13.48	743.37
	$ X_{\omega Y}=0.8 $	1.93	11.66	24.15	0.347	13.49	750.19
	$ X_{\omega Y}=0.9 $	1.99	11.72	20.84	0.346	13.49	748.71
BSR1	No Hyperons	2.45	12.06	5.67	0.342	13.31	721.32
	SU(6)	1.70	11.58	62.59	0.525	12.51	421.94
	$ X_{\omega Y}=0.6 $	1.86	11.36	26.87	0.368	13.28	711.27
	$ X_{\omega Y}=0.8 $	2.03	11.49	15.24	0.345	13.29	720.18
	$ X_{\omega Y}=0.9 $	2.09	11.61	13.70	0.342	13.31	721.48
BSR2	No Hyperons	2.38	11.97	6.42	0.346	13.43	741.56
	SU(6)	1.72	11.43	50.02	0.528	12.68	451.88
	$ X_{\omega Y}=0.6 $	1.84	11.22	24.52	0.361	13.42	741.77
	$ X_{\omega Y}=0.8 $	2.00	11.44	16.04	0.348	13.43	743.41
	$ X_{\omega Y}=0.9 $	2.05	11.55	14.54	0.346	13.43	741.56
BSR3	No Hyperons	2.36	11.93	6.76	0.350	13.47	742.49
	SU(6)	1.63	11.49	72.80	0.571	12.53	396.68
	$ X_{\omega Y}=0.6 $	1.78	11.32	32.67	0.377	13.45	735.66
	$ X_{\omega Y}=0.8 $	1.94	11.39	18.87	0.355	13.47	743.58
	$ X_{\omega Y}=0.9 $	2.00	11.45	16.15	0.351	13.47	742.74
BSR4	No Hyperons	2.44	12.12	5.83	0.338	13.57	778.04
	SU(6)	1.76	11.62	48.57	0.501	12.90	500.75
	$ X_{\omega Y}=0.6 $	1.88	11.26	21.06	0.352	13.56	778.83
	$ X_{\omega Y}=0.8 $	2.05	11.57	14.62	0.339	13.57	779.04
	$ X_{\omega Y}=0.9 $	2.10	11.69	13.27	0.339	13.57	778.04
BSR5	No Hyperons	2.48	12.25	5.58	0.331	13.73	827.53
	SU(6)	1.74	11.86	60.29	0.489	13.07	540.45
	$ X_{\omega Y}=0.6 $	1.88	11.38	22.13	0.345	13.72	824.19
	$ X_{\omega Y}=0.8 $	2.06	11.65	14.48	0.332	13.73	826.35
	$ X_{\omega Y}=0.9 $	2.12	11.77	13.08	0.331	13.73	827.53
BSR6	No Hyperons	2.43	12.11	5.90	0.337	13.71	804.03
	SU(6)	1.71	11.72	59.86	0.513	12.96	495.76
	$ X_{\omega Y}=0.6 $	1.86	11.40	25.08	0.357	13.69	802.09
	$ X_{\omega Y}=0.8 $	2.03	11.52	14.71	0.339	13.71	806.98
	$ X_{\omega Y}=0.9 $	2.08	11.67	13.66	0.337	13.71	804.33
BSR7	No Hyperons	2.50	12.36	5.38	0.322	13.77	900.52
	SU(6)	1.69	12.14	83.97	0.483	13.28	582.64
	$ X_{\omega Y}=0.6 $	1.87	11.69	28.59	0.334	13.95	893.39
	$ X_{\omega Y}=0.8 $	2.05	11.70	14.72	0.323	13.96	900.72
	$ X_{\omega Y}=0.9 $	2.11	11.86	13.60	0.322	13.96	900.72

Table 2.  Neutron star properties computed using various RMF parameter sets. For each parameter set, results are shown without hyperons ("No hyperons"), with hyperons included under specific fixed vector coupling strengths ($ X_{\omega Y} $ = 0.6, 0.8, and 0.9), and with couplings based on SU(6) symmetry.

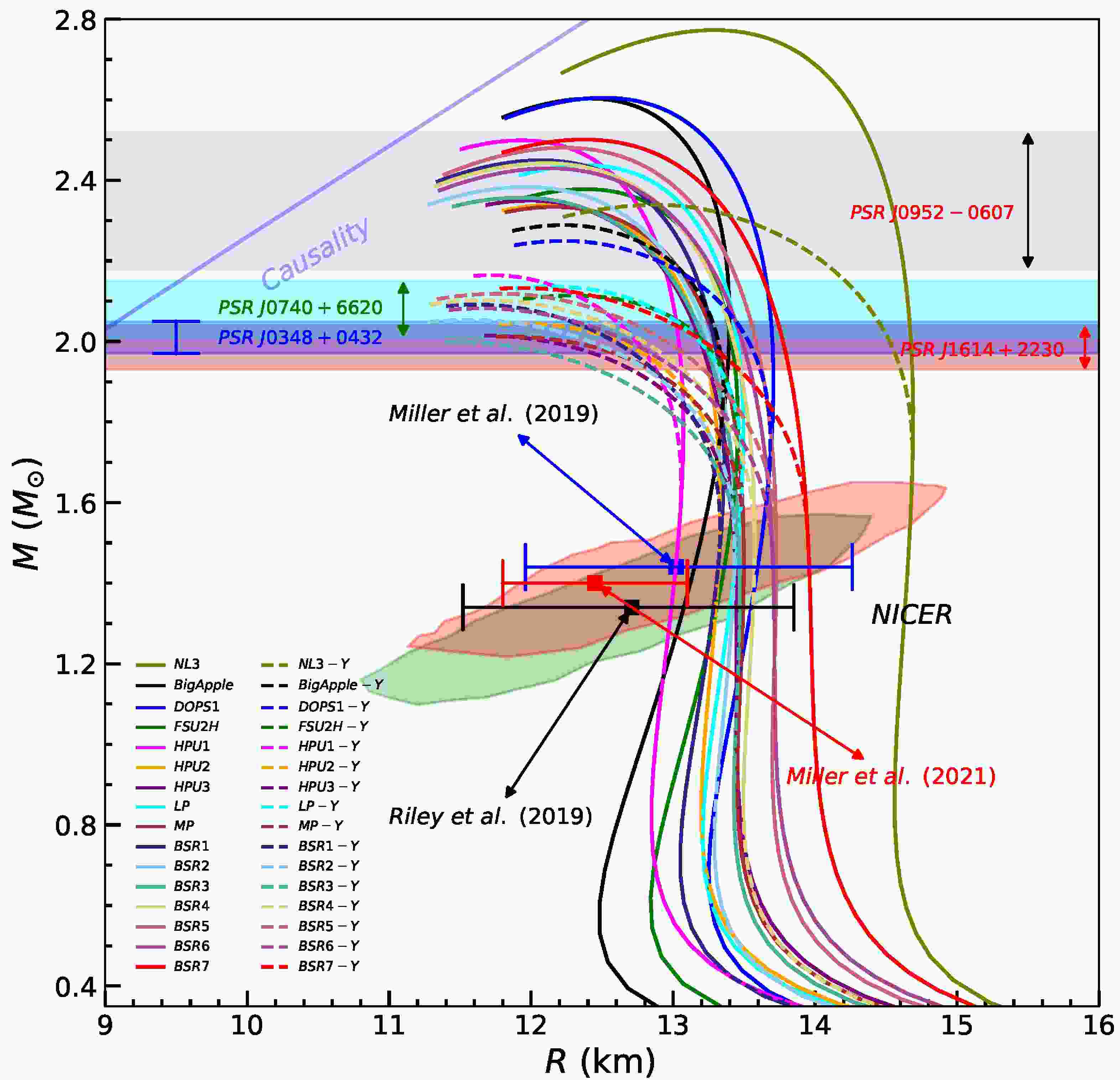
In Fig. 6, we display the results for the gravitational mass of static neutron stars and its radius for EoSs consisting of nucleonic matter computed with RMF models NL3, BigApple, DOPS, FSU2H, HPU1, HPU2, HPU3, LP, MP and BSR1 - BSR7 parametrizations. Similar results calculated for EOSs consisting of nucleonic matter with inclusion of hyperons with vector meson hyperon coupling X$ _{\omega Y} $ = 0.9 are also displayed. It is noteworthy to mention that this coupling X$ _{\omega Y} $ = 0.9 supports a star with a observational constraint of M$ _{max} $ $ \geq $ 2 M$ _{\odot} $ upon inclusion of hyperonic degree of freedom (Table 2). The solid lines denote neutron stars, while dashed lines represent neutron stars with hyperonic matter. The horizontal bands corresponds to the mass $ ( M = 2.35 \pm 0.17 M_\odot $ of PSR J0952–0607 [86], M$ _{max} $ = $ 2.08 \pm 0.07 M_\odot $ of PSR J0740+6620 [89] and PSR J0348+0432 $ 2.01 \pm 0.04 M_\odot $ [11]. The mass radius constraints from astrophysical observations from NICER missions [12, 13, 90, 91] are also shown. It can be observed from the Table 2 that neutron star properties such as M$ _{max} $, R$ _{max} $, and $ \Lambda_{max} $ are strongly affected by the hyperonization for all RMF models. It can also be noticed from the table that as we vary the vector meson-hyperon coupling X$ _{\omega Y} $ from 0.6 to 0.9, the M$ _{max} $ and R$ _{max} $ increase, which might be due to somewhat stiffening in EoS caused due to this vector coupling. Also, it is evident from the table that to support a star with maximum mass M$ _{max} $ constraint ($ \ge $2 M$ _{\odot} $), the vector coupling strength, X$ _{\omega Y} $ should be 0.8 and 0.9. These comparisons reinforce the critical role of vector coupling strength in governing hyperonization and its impact on neutron star observables. Increasing X$ _{\omega Y} $ improves compliance with the 2 M$ _{\odot} $ mass constraint by suppressing early hyperonization.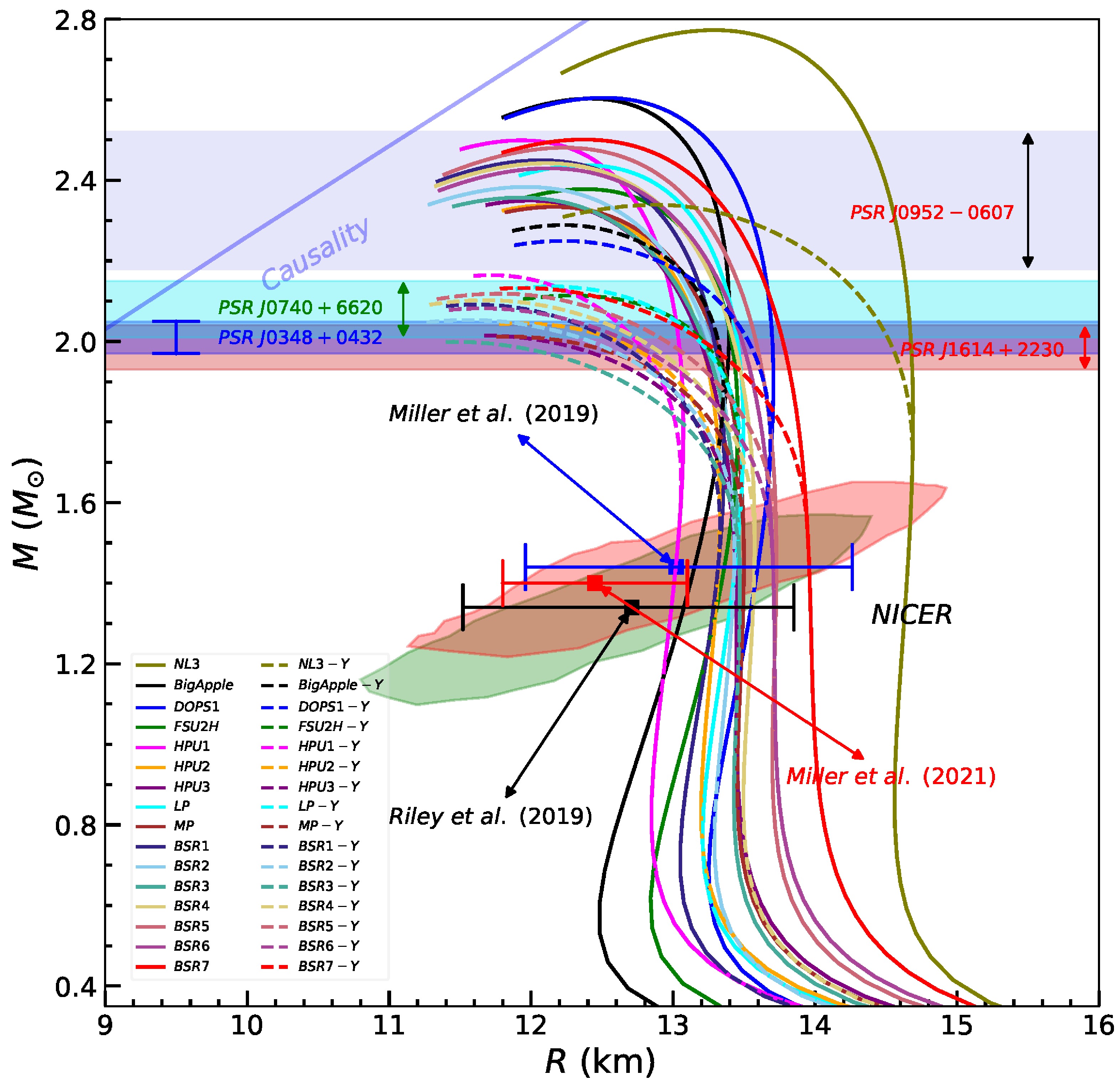

Figure 6.  (Color online) Mass-radius relationship of compact stars for various RMF models. Solid lines denote nucleonic stars, while dashed lines represent neutron star with inclusion of hyperonic matter with $ ( X_{\omega Y} = 0.9 ) $. The horizontal band corresponds to the mass $ ( M = 2.35 \pm 0.17 M_\odot ) $ of PSR J0952–0607 [86]. Observational Constraints from NICER mission [12, 13] are also displayed.

In Table 3 we have shown the results for maximum mass of nucleonic (M$ _{max}^{Nucl} $) and hyperonic (M$ _{max}^{Hyp} $) stars with vector coupling X$ _{\omega Y} $ = 0.9, along with symmetry energy (J), its linear density dependence (L), curvature of symmetry energy (K$ _{sym} $) and its skewness (Q$ _{sym} $) [71] for various RMF models as considered in Table 1 that supports the maximum mass constraint M$ _{max} $ $ \geq $ 2M$ _{\odot} $ along with other RMF models which do not supports this mass constraint upon inclusion of hyperons. It is evident from Table 3 that models NL3, Big Apple, DOPS1, FSU2H, HPU1, HPU2, HPU3, LP, MP, and BSR1 - BSR7 satisfy the $ \approx 2 M_\odot $ mass constraint upon hyperonization [10, 11]. The percentage decrease in M$ _{max} $ of the neutron star upon inclusion of hyperons is indicated by $ \Delta M $ i.e. $ \Delta M $ = [(M$ _{max}^{Nucl} $-M$ _{max}^{Hyp} $)/M$ _{max}^{Nucl} $]$ \times 100 $.

Model	$ M_{\max}^{\text{Nucl}} \ (M_{\odot}) $	$ M_{\max}^{\text{Hyp}} \ (M_{\odot}) $	$ \Delta M $ (【zybfh】)	J (MeV)	L (MeV)	$ K_{\text{sym}} $ (MeV)	$ Q_{\text{sym}} $ (MeV)
NL3	2.77	2.32	16.25	37.40	118.60	100.9	174.27
BIG Apple	2.60	2.28	12.31	31.41	40.30	89.59	1152.13
DOPS1	2.60	2.24	13.85	31.89	65.59	18.01	650.59
FSU2H	2.37	2.07	12.66	29.59	44.37	97.29	536.09
HPU1	2.49	2.16	13.25	34.34	61.21	−96.85	1348.59
HPU2	2.33	2.03	12.88	33.21	63.87	−70.78	1109.63
HPU3	2.34	1.99	14.96	33.22	75.03	−31.42	475.79
LP	2.43	2.10	13.58	33.70	64.01	−54.11	1235.67
MP	2.33	1.99	14.59	34.10	77.55	1.79	453.25
BSR1	2.45	2.09	14.69	39.35	58.49	−52.65	1270.34
BSR2	2.38	2.05	13.86	31.5	62.06	−3.10	408.20
BSR3	2.36	2.00	15.25	32.75	70.49	−7.76	400.95
BSR4	2.44	2.10	13.93	33.16	73.25	−20.74	421.90
BSR5	2.48	2.12	14.52	34.47	83.43	−14.13	346.80
BSR6	2.43	2.08	14.40	35.63	85.73	−49.55	350.62
BSR7	2.50	2.12	15.20	37.26	99.16	−16.97	196.59
HPUA	2.04	1.77	13.24	32.62	56.97	−33.72	835.29
HPUB	2.02	1.73	14.36	35.25	82.22	−72.18	405.32
HPUC	2.04	1.78	12.75	28.37	41.64	81.12	13.20
FSUGold	1.72	1.50	12.79	32.49	60.53	−50.60	424.52
FSUGold2	2.07	1.74	15.94	37.58	112.7	25.39	−164.61
HPNL	2.03	1.74	14.29	35.90	86.71	−66.38	310.12
IOPB-1	2.15	1.86	13.49	33.30	63.85	−37.79	865.14
FSUGarnet	2.06	1.80	12.62	30.97	51.07	58.96	160.67
DBHP	2.03	1.72	15.27	34.68	83.09	−33.09	245.51
SRV00	2.04	1.78	12.75	33.49	65.23	−58.55	820.22
DOPS2	2.12	1.85	12.74	31.77	66.02	−9.31	27.35
DOPS3	2.05	1.78	13.17	31.84	66.74	−0.93	274.73
TM1	2.18	1.82	16.51	36.89	110.8	33.62	−65.95
BSR8	1.96	1.70	13.27	31.07	60.26	−0.75	246.13
BSR9	1.94	1.68	13.40	31.62	63.92	−11.32	209.25
BSR10	1.96	1.69	13.77	32.71	70.83	−16.54	210.50
BSR11	1.94	1.66	14.43	33.69	78.82	−24.73	176.08
BSR12	1.97	1.68	14.72	34.54	79.17	−48.39	343.16
BSR13	1.95	1.67	14.36	35.82	91.10	−41.69	139.98
BSR14	1.96	1.67	14.79	36.32	93.87	−41.96	113.18
BSR15	1.75	1.51	13.71	34.09	71.05	−35.30	169.53
BSR16	1.74	1.52	12.64	31.24	62.35	−24.17	158.29
BSR17	1.75	1.51	13.71	31.99	67.47	−31.59	181.63
BSR18	1.75	1.51	13.71	32.74	72.67	−42.25	203.64
BSR19	1.75	1.51	13.71	33.77	79.47	−50.12	197.54
BSR20	1.76	1.52	13.64	34.54	88.05	−39.91	84.27
BSR21	1.76	1.52	13.64	35.95	92.92	−45.99	68.74

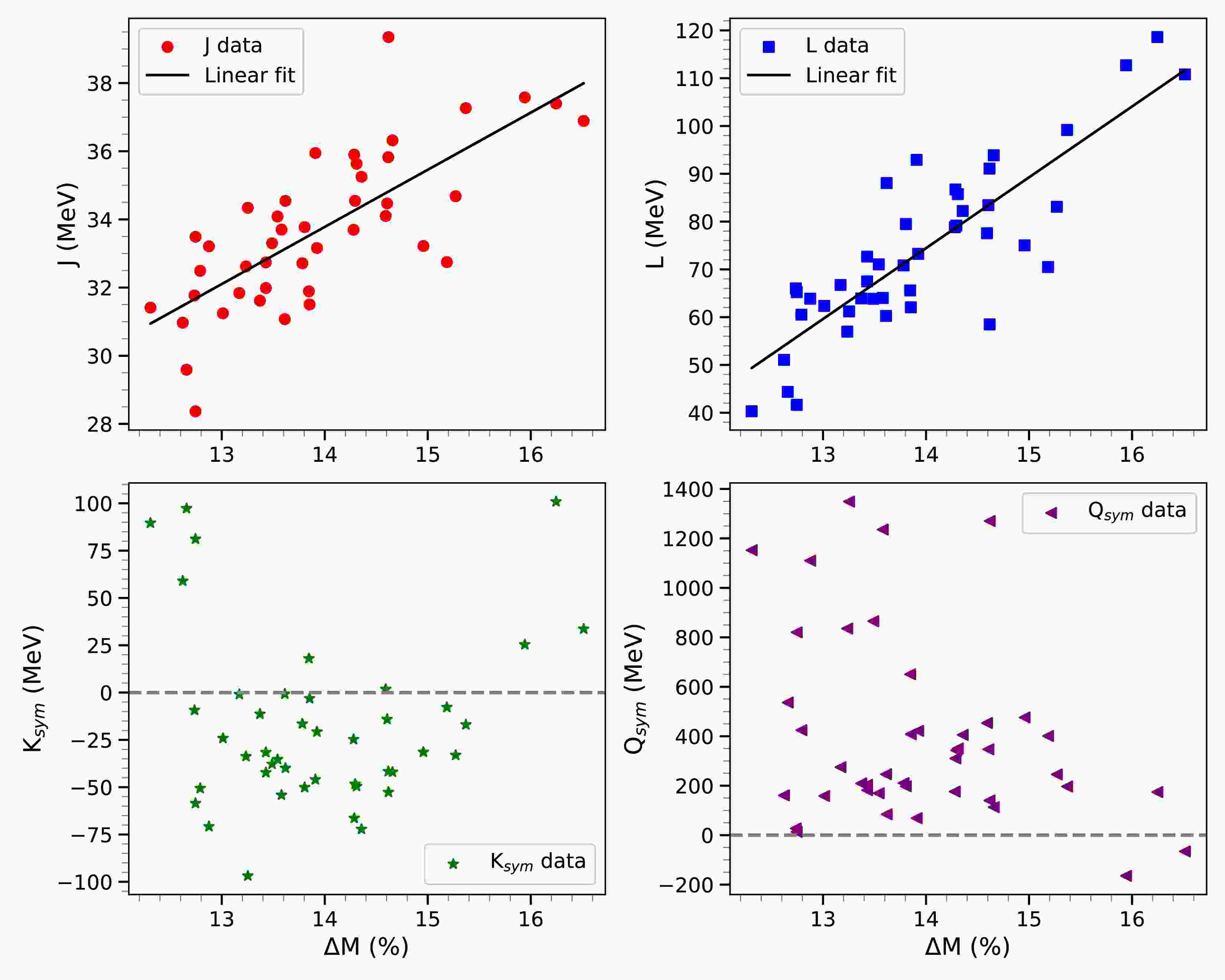
Table 3.  Maximum mass of nucleonic and hyperonic stars with vector coupling $ X_{\omega Y}=0.9 $, along with symmetry energy (J), its linear density dependence (L), and its higher order derivative terms ($ K_{\text{sym}} $, $ Q_{\text{sym}} $) for various RMF models. The $ \Delta M $ is the percentage decrease in $ M_{\max} $ upon inclusion of hyperons. and is expressed as $ \Delta M $ = [(M$ _{max}^{Nucl} $-M$ _{max}^{Hyp}) $/M$ _{max}^{Nucl} $]$ \times 100 $.

The correlation between the slope of the symmetry energy L, and the reduction in the maximum mass of neutron stars ($ \Delta M $) upon inclusion of hyperons becomes even more evident when a broader set of RMF models are examined. As can be seen from Table 3, the values of L span a wide range, from as low as 40.30 MeV (BigApple) to 118.6 MeV (NL3), and the corresponding $ \Delta M $ values vary from 12.31% to 16.25%. Although the symmetry energy (J) contributes to the isospin stiffness of the EoS, its variation across the models is relatively small i.e. 28.37 MeV (HPUC) – 39.35 MeV (BSR1) compared to the wide range in L which varies widely from 40.30 MeV (Big Apple) - 118.60 MeV (NL3). As such, the mass reduction is predominantly governed by the slope L, which controls the linear density dependence of the symmetry energy and, in turn, the chemical potential evolution that is crucial for triggering hyperon formation. This systematic behavior confirms that the degree of hyperons induced softening of the EoS is primarily controlled by L rather than its absolute magnitude (J).

The scatter plots shown in Fig. 7 (isovector correlation plot) provide a direct visualization of this trend: models with high L values cluster toward the upper end of $ \Delta M $, while low L models are consistently associated with smaller mass reductions. For instance, NL3 (L = 118.60 MeV) and TM1 (L = 110.8 MeV) show the steepest declines in maximum mass ($ \Delta M \approx 16-17 $%), while Big Apple (L = 40.3 MeV), HPUC (L = 41.64 MeV) FSU2H (L = 44.37 MeV), FSUGarnet (L = 51.07 MeV) and FSUGold (L = 60.53 MeV) exhibit modest decrease in ($ \Delta M \approx $12.31% - 12.79%). This correlation extends smoothly across the intermediate values of L, such as HPU3 (L = 75.03 MeV, $ \Delta M = 14.96 $%) and MP (L = 77.55 MeV, $ \Delta M = 14.59 $%), suggesting that the slope parameter L plays a continuous and predictable role in regulating hyperonization.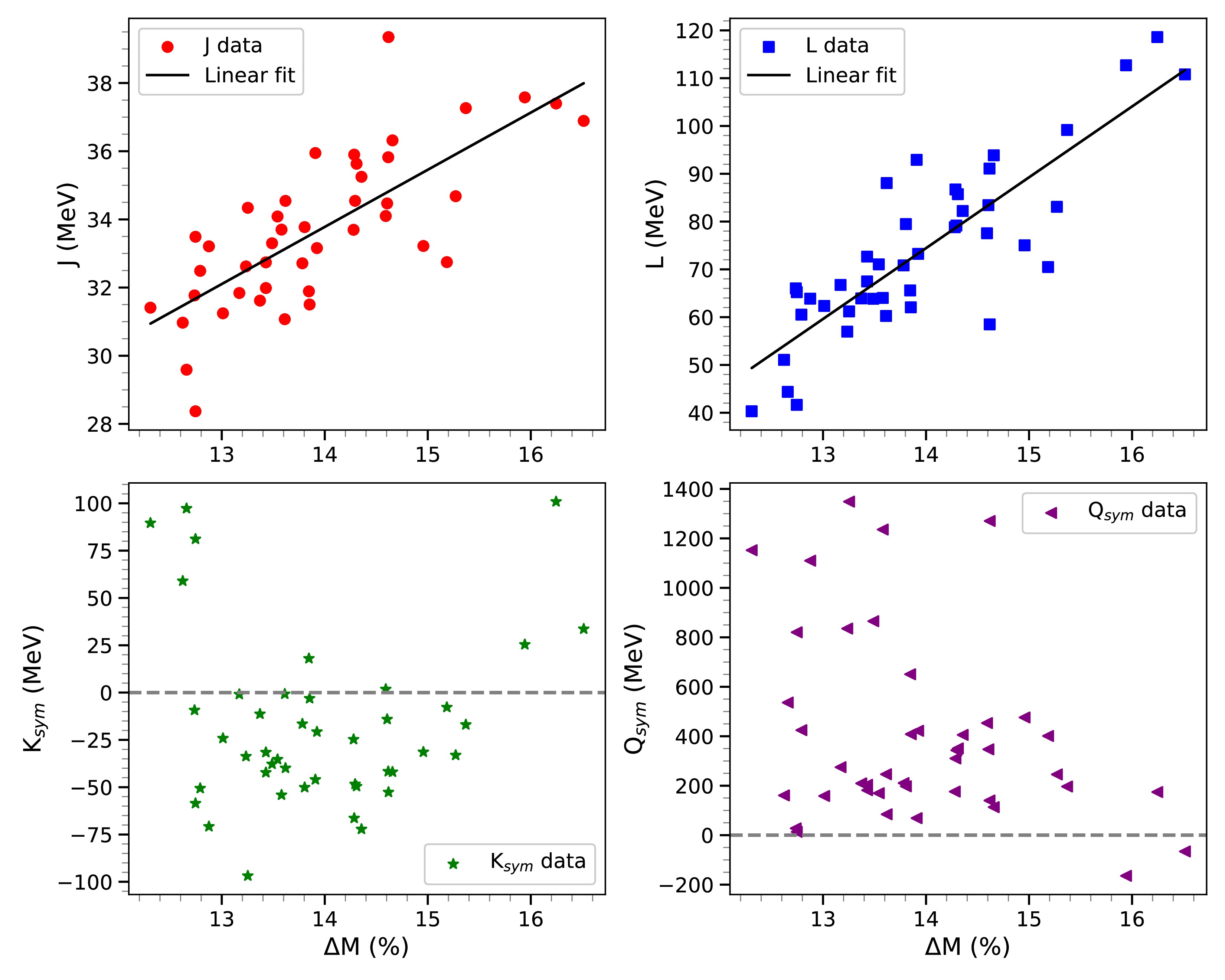

Figure 7.  (Color online) Scatter plots of isovector bulk nuclear matter properties at saturation density such as symmetry energy (J), its linear density dependence (L), curvature of symmetry energy (K$ _{sym} $) and its skewness (Q$ _{sym} $) [71] versus the percentage decrease ($ \Delta M $) in $ M_{max} $ of neutron stars upon hyperonization, for all models listed in Table 3. The black solid lines represent linear fits for the correlations between $ (J, L) $ and $ \Delta M $.

The statistical robustness of this correlation is quantified in Fig. 8 (Pearson correlation plot), which confirms a strong positive correlation between $ \Delta M $ and L. This result establishes that while the variation in J is relatively small across the models (28.37 – 39.35 MeV), the wide spread in L values (40.30 – 118.60 MeV) is the dominant factor. The Pearson analysis also shows weaker or more scattered correlations of $ \Delta M $ with higher-order isovector derivatives ($ K_{sym} $ and $ Q_{sym} $), implying that although these terms can modulate the EoS stiffness at supranuclear densities, their impact on hyperon onset is secondary compared to L. One can also observe a moderate correlation between $ Q_{sym} $ and L, indicating that while L is the dominant parameter governing $ \Delta M $, $ Q_{sym} $ exerts an indirect influence on $ \Delta M $ through its correlation with L.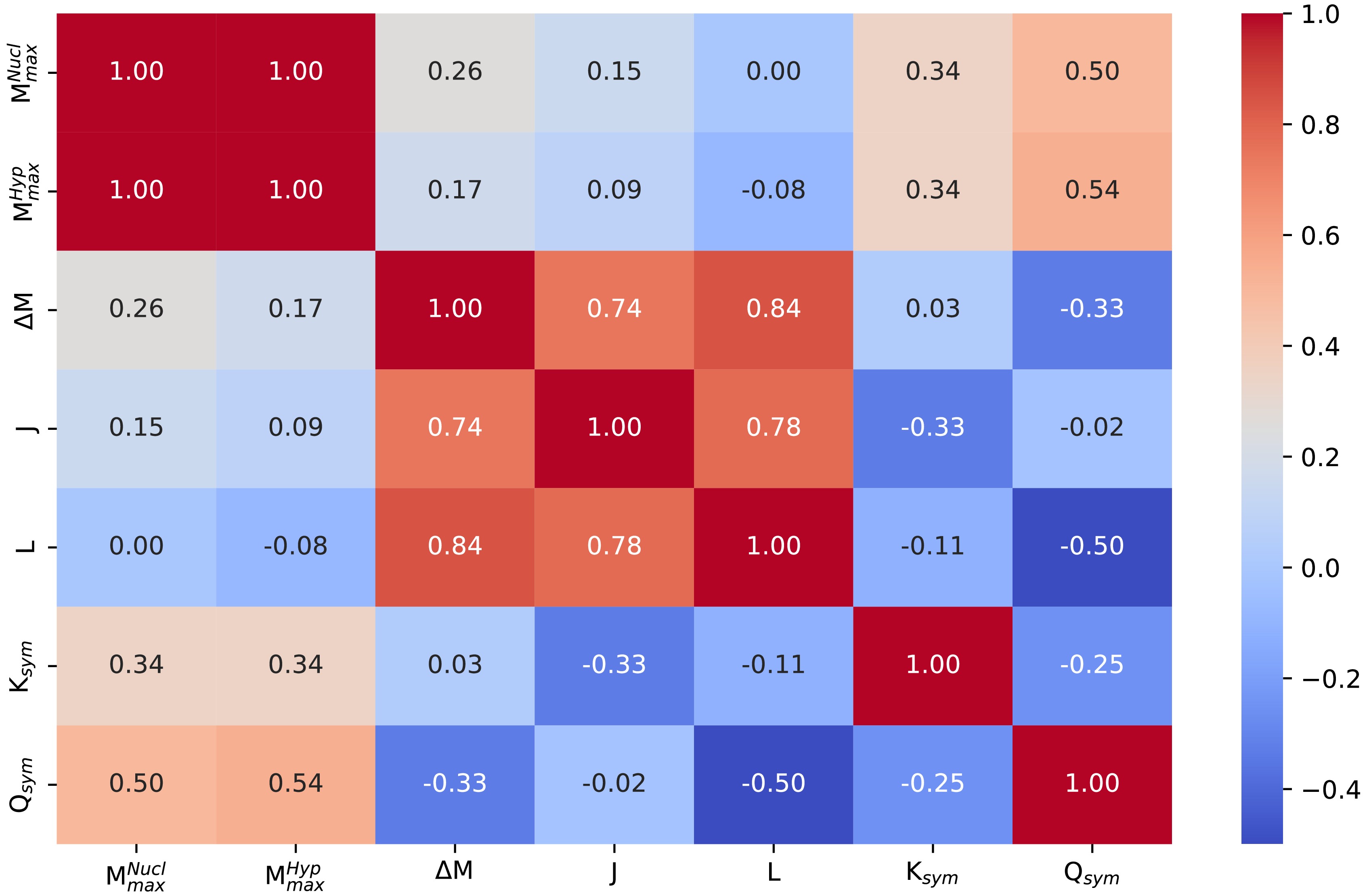

Figure 8.  (Color online) Heat map of Pearson correlation coefficients between the maximum mass of nucleonic stars $ M_{max}^{\text{Nucl}} $ ($ M_{\odot} $), hyperonic stars $ M_{max}^{\text{Hyp}} $ ($ M_{\odot} $), the percentage decrease in maximum mass upon hyperon inclusion ($ \Delta M $), and the isovector bulk nuclear matter properties at saturation density, for all models listed in Table 3.

Physically, this behavior can be understood in terms of the neutron chemical potential. Models with a stiffer isovector channel (large L) predict a more rapid rise in the neutron chemical potential with density, which drives the early appearance of hyperons ($ \Lambda, \Xi^{-} $), which can be seen from Fig. 1, 2, 3 and 4. Their onset softens the pressure support in the stellar core, thereby reducing the maximum mass. By contrast, models with a softer symmetry energy slope (low L) delays hyperonization, leading to a more gradual mass reduction. This also explains why extremely stiff EoS models despite reaching high nucleonic maximum masses are disproportionately sensitive to hyperonization effects.

Interestingly, even within models of similar J, the spread in $ \Delta M $ can be explained by differences in L. For example, HPU3, LP, and HPU2 all exhibit comparable symmetry energies at saturation, yet HPU3 with its higher slope parameter (L = 75.03 MeV) shows a distinctly larger $ \Delta M $. Similarly, models such as FSUGold2 (L = 112.70 MeV, $ \Delta M = 15.94 $%) emphasize how moderately high L values can already trigger substantial mass reductions, even when the nucleonic maximum mass is not exceptionally large. Overall, the combined evidence from the extended dataset (Table 3), the direct correlations (Fig. 7), and the Pearson statistical analysis (Fig. 8) strongly supports the conclusion that the slope of the symmetry energy, L, is the primary regulator of hyperonization effects in neutron stars. Under strong vector repulsion ($ X_{\omega Y} = 0.9 $), where hyperon species such as Λ, $ \Xi^- $, and $ \Xi^0 $ are energetically favoured, the extent of EoS softening and consequently the reduction in maximum mass shows a clear positive correlation with L. A higher L drives a steeper rise in the neutron chemical potential, thereby accelerating hyperon onset and enhancing the associated softening of the EoS.

In this study, we employ a comprehensive set of RMF models to investigate the role of hyperons in dense nuclear matter and their impact on neutron star structure. By exploring models with differing high-density behaviors, symmetry energy parameters, and hyperon–meson coupling schemes, we assess how hyperons affect key stellar properties including the maximum mass ($ M_{\text{max}} $), radius (R$ _{max} $), and tidal deformability ($ \Lambda_{max} $). It is observed that stellar properties such as M$ _{max} $, R$ _{max} $, and $ \Lambda_{max} $ are strongly influenced by hyperonization across all RMF models considered in this work. Varying the hyperon–vector meson coupling strength ($ X_{\omega Y} $) between 0.6 and 0.9 within the SU(6) framework, we find that smaller values of $ X_{\omega Y} $ enhance the hyperon population, leading to significant softening of the EoS and a reduction in $ M_{\text{max}} $. In contrast, stronger vector repulsion ($ X_{\omega Y} = 0.9 $) favors the appearance of $ \Lambda^0 $ and $ \Xi^- $ hyperons, with $ \Xi^0 $ emerging only at higher densities, while at lower couplings additional species such as Σ hyperons appear earlier, modifying the stellar core composition. Across the models examined, hyperonization reduces $ M_{\text{max}} $ by 0.22 M $ _{\odot} $ (for BSR16) – 0.45 M $ _{\odot} $ (for NL3), with some of the parameter sets predicting hyperonic maximum masses following the $ 2\; M_\odot $ constraint, while some of them have been observed to have hyperonic masses below $ 2\; M_\odot $. The magnitude of this reduction is strongly correlated with the slope parameter L of the symmetry energy, rather than its coefficient J. Larger L values promote earlier hyperon onset by steepening the density dependence of the neutron chemical potential, thereby accelerating softening of the EoS. While the variation in J remains small across models, the wide spread in L (40.30 – 118.60 MeV) drives the systematic differences in $ \Delta M $. Pearson correlation analysis confirms this trend and further indicates that higher-order isovector terms ($ K_{\text{sym}} $, $ Q_{\text{sym}} $) play only a secondary, indirect role, with $ Q_{\text{sym}} $ showing a moderate correlation with L. It is observed that canonical star properties like R$ _{1.4} $ and $ \Lambda_{1.4} $ remain largely unaffected to the presence of hyperons in nucleonic EoSs under fixed vector coupling strengths, except when couplings are based on SU(6) symmetry. This behavior can be attributed to the fact that, although hyperons appear in the very centre of a 1.4 M$ _{\odot} $ star, their population fraction is extremely small and therefore produces negligible effect on global stellar properties like R$ _{1.4} $ and $ \Lambda_{1.4} $. However, in the case of hyperon–meson couplings based upon SU(6) symmetry, both R$ _{1.4} $ and $ \Lambda_{1.4} $ are significantly affected, which might be attributed to the relatively stronger softening of the corresponding EoSs. Overall, our results emphasize the critical role of the symmetry energy slope L in regulating the onset of hyperons and their impact on neutron star properties. The correlations found between ($ \Delta M $, L) and (L, $ Q_{sym} $) suggest a robust mechanism linking isovector dynamics to strangeness content and stellar structure. Future multimessenger observations, precise radius and tidal deformability measurements, and experimental constraints on L and hyperon-nucleon interactions will be essential for refining theoretical models and achieving a unified description of dense matter in neutron stars.

The author(s) are thankful to Department of Physics Himachal Pradesh University for providing computational facilities.