-
The study of heavy quarkonium has yielded valuable insights into the nature of the strong interaction, where
$ Q\bar{Q} $ bound states act as a good platform for probing perturbative and nonperturbative QCD. In recent times, the study of the heavy vector meson produced by photon-induced interactions at hadronic colliders has been strongly motivated by the possibility of constraining the dynamics of the strong interactions at high energies [1−5]. It also sheds light on the low-x physics and helps constrain nuclear parton distributions [6−9]. It is well known that this type of mechanism can be theoretically studied using the Weizsäcker-Williams approximation (WWA) [10−12]. The central idea of the WWA is that the moving electromagnetic field of charged particles can be treated as a flux of photons. In an ultrarelativistic ion collider, these photons can interact with the target nucleus in the opposite beam (photoproduction) or with the photons of the opposite beam (two-photon reactions). At CERN Large Hadron Collider (LHC) energies, the intense heavy-ion beams represent a prolific source of quasireal photons, thus enabling extensive studies of photon-induced physics. In the calculations, an important function is the photon flux function, which has different forms for different charged sources.Although considerable progress has been achieved, the features of the WWA in inelastic heavy quarkonium photoproduction in heavy-ion collisions are rarely noticed. The WWA is usually employed beyond its applicable scopes, and imprecise statements pertaining to the advantages of the WWA are provided [13−28]. For instance, the WWA is usually adopted in electroproduction reactions or exclusive processes, where the virtuality
$ Q^2 $ of the photon is very small and depends on$ m_e $ or the coherence condition. However, when the WWA is used in hadronic collisions,$ Q^{2} $ depends on the nucleus mass$ m_N $ , and the validity of the WWA is not evident in this case. Particularly in the ultrarelativistic heavy-ion collisions at LHC energies, the influence of the WWA becomes significant to the accuracy of describing photoproduction processes, since photon flux function scales as$ f_{\gamma}\propto Z^{2}\ln\sqrt{s}/m $ , in which the collision energy$ \sqrt{s} $ and the squared nuclear charge$ Z^{2} $ turn into very large enhancement factors to the cross sections. Thus, heavy-ion collisions have a considerable flux advantage over the proton. For these reasons, it is necessary to present a comprehensive analysis of the WWA in inelastic heavy quarkonium photoproduction in heavy-ion collisions and to estimate the important inaccuracies appearing in its application.Different channels contribute to heavy quarkonium production. From the beam side, multiple photon sources must be considered [29]: coherent-photon emission (coh.), ordinary-incoherent photonemission (OIC), and ultra-incoherent photon emission (UIC). For coh., virtual photons are emitted coherently by the whole nucleus, and it remains intact after photon radiation. During OIC and UIC photon emission, virtual photons are emitted incoherently by the protons and quarks inside nucleus, respectively, and the nucleus dissociates after photon radiation. Hence, in this study, elastic" and "inelastic" refer to cases where the target nucleus remains intact or dissociates after scattering with photons, respectively. When these different photon sources are considered simultaneously, their relative contributions must be calculated in order to avoid double counting. Meanwhile, the final state has two types of inelastic productions: direct and fragmentation contributions [30−32]. The fragmentation process is described by fragmentation functions that specify the probability of the final partons (gluons or quarks) hadronizing into quarkonia bound states. The fragmentation contribution originates from the large
$ p_{T} $ region, where one encounters large logarithms of$ p_{T}^{2}/m_{Q}^{2} $ , such large logs are resummed into the fragmentation functions. Thus, the fragmentation mechanism can be only used in the large$ p_{T} $ region, and one cannot naively add the direct and fragmentation contributions, as this would lead to double counting [32−34]. This double counting is present in most literature, and the fragmentation formalism is employed beyond its validity range [14−22].Although numerous studies have addressesd these processes, the application of UIC, to the best of our knowledge, has received limited attention in the study of inelastic heavy quarkonium photoproduction. For instance, Gonçalves et al. systematically studied the exclusive production of vector mesons in hadronic collisions considering different phenomenological models [35, 36]. Machado et al. studied the inelastic and exclusive heavy quarkonium photoproductions within the color dipole formalism [37, 38]. In Refs. [39−41], Klein and Nystrand studied exclusive vector meson production via photon-Pomeron or photon-meson interactions, and discussed the interlay between photoproduction and two-photon interaction [42]. Ducati et al. investigated exclusive
$ J/\psi $ photoproduction and the radially excited$ \psi(2S) $ state of nucleons in p-p collisions according to the light-cone dipole formalism [43]. Although numerous related studies have been published, they all consider coherent photon emission and neglect incoherent-photon emission. Furthermore, the UIC photoproduction, which is best treated as an inclusive process, can provide additional corrections to central collisions. For instance, the authors of Refs. [18−20] investigated inelastic dilepton, photon, and light vector meson productions at LHC energies. They demonstrated that UIC photoproduction enhances the contribution of massless and light final-state particles in central collisions. However, this correction remains unclear for heavy quarkonium due to its large mass.To address the gaps discussed above, we investigate the inelastic photoproduction of charmonium (
$ J/\psi $ ,$ \psi(2S) $ ) and bottomonium ($ \Upsilon(nS) $ ) in p-p and$\rm Pb $ -$\rm Pb $ collisions at LHC energies. An exact treatment that recovers the WWA near the$ Q^{2}\sim0 $ domain is performed. This treatment can be considered as the generalization of leptoproduction [44]. Full kinematical relations that match the exact treatment are also obtained. We present a consistent analysis of the features of the WWA in heavy-ion collisions by comparing the results of the approximation with the exact results. We also investigate the issue of double counting. Finally, we estimate the contribution of the ultra-incoherent channel to inelastic heavy quarkonia photoproduction.We should mention that Wangmei Zha et al. have addressed similar challenges in determining the validity range of the WWA [45]. Using the QED approach, Wangmei Zha et al. developed a spatially-dependent photon flux distribution and established a more precise relationship between the photon transverse momentum distribution and impact parameters of collisions. They justified the inadequacy of the WWA model in describing the photon flux of electron-ion collisions and noted that the QED approach provides a more realistic basis for calculating the impact parameter dependence of photoproduction processes in electron-ion collisions. Within this refined method, they explored the potential of utilizing nuetron tagging from Coulomb excitation of nuclei to effectively determine the centrality of exclusive photoproduction in electron-ion collisions. Their study offers a new methodology for exploring the spatial and momentum structure of gluons in nuclei and provides novel insights for experimental design and data analysis.
This paper is organized as follows. Sec. II presents the formalism of the exact treatment of inelastic heavy quarkonium photoproduction in heavy-ion collisions. Based on the Martin-Ryskin method, we consider the coh., OIC, and UIC processes simultaneously. Following the BCCKL method, we match the fixed order and fragmentation contributions. In Sec. III, we convert the accurate formula into a WWA one near the region
$ Q^{2}\sim0 $ and study several widely utilized photon fluxes. In Sec. IV, we numerically calculate the$ Q^{2} $ , y, z,$ \sqrt{s} $ , and$ p_{T} $ dependent differential cross sections, along with the total cross sections at LHC energies. Finally, in Sec. V, we summarize the paper. -
For heavy quarkonium production and decay, an effective field theory known as nonrelativistic QCD (NRQCD), has been proposed to explain the huge discrepancy between the theoretical predictions and experimental measurements of the transverse momentum distribution of
$ J/\psi $ production at the Tevatron. This scheme has proven to be highly successful in numerous applications [46]. In this section, we employ this scheme to describe the inelastic heavy quarkonium photoproduction. The NRQCD scheme is based on a double expansion in$ \alpha_{s} $ and ν (the heavy-quark relative velocity in quarkonium rest frame), and its inelastic quarkonium H production form is$ \begin{align} {\rm d}\sigma_{A+B\rightarrow H+X}=\sum_{n}{\rm d}\sigma_{A+B\rightarrow Q\bar{Q}_{[1,8]}[n]+X}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle. \end{align} $

(1) Here,
${\rm d} \sigma_{A+B\rightarrow Q\bar{Q}_{[1,8]}[n]X}$ are the process-dependent short-distance coefficients (SDCs), which can be computed in perturbative QCD by expansion in$ \alpha_{s} $ and correspond to the production of a heavy quark-antiquark pair$ Q\bar{Q}_{[1,8]}[n] $ in a specific color and angular momentum state$ n=^{2S+1}L_{J}^{(c)} $ .$ \langle{\cal{O}}^{H}_{[1,8]}[n]\rangle $ denotes the NRQCD long-distance matrix elements (LDMEs), which describe the probability of hadronization and have a well-defined scaling with v ($ v\simeq0.08 $ and$ 0.25 $ for bottomonia and charmonia, respectively). Since the color-singlet LDME for quarkonium production$ \langle{\cal{O}}^{\psi}[^{3}S_{1}^{(1)}]\rangle $ is related to the color-singlet LDME for quarkonium decay, it can be determined from potential models or the ψ decay rates into lepton pairs in lattice QCD [33]. In contrast, an algorithm for computing the color-octet production LDMEs from first principles remains unknown, and they are usually determined by fitting experimental data. Notably, if NRQCD factorization holds, the LDMEs should be universal.For
$ 1^{--} $ quarkonia production,$ J/\psi $ ,$ \psi\left(2S\right) $ , and$ \Upsilon\left(nS\right) $ , the sum over n truncated at order$ v^{4} $ , involves four LDMEs [46]:$ \langle{\cal{O}}^{H}[^{3}S_{1}^{(1)}]\rangle $ ,$ \langle{\cal{O}}^{H}[^{3}S_{1}^{(8)}]\rangle $ ,$ \langle{\cal{O}}^{H}[^{1}S_{0}^{(8)}]\rangle $ , and$ \langle{\cal{O}}^{H}[^{3}P_{J}^{(8)}]\rangle $ . Due to their lengthy expressions, we summarize them in Appendix A. -
The exact treatment of inelastic heavy quarkonium photoproduction in heavy-ion collisions can be considered as proceeding in two steps. In the first step, the density matrix of virtual photons should be expanded in terms of polarization operators, since photons radiated from a projectile are off mass shell and no longer transversely polarized. In the second step, the square of the electric form factor
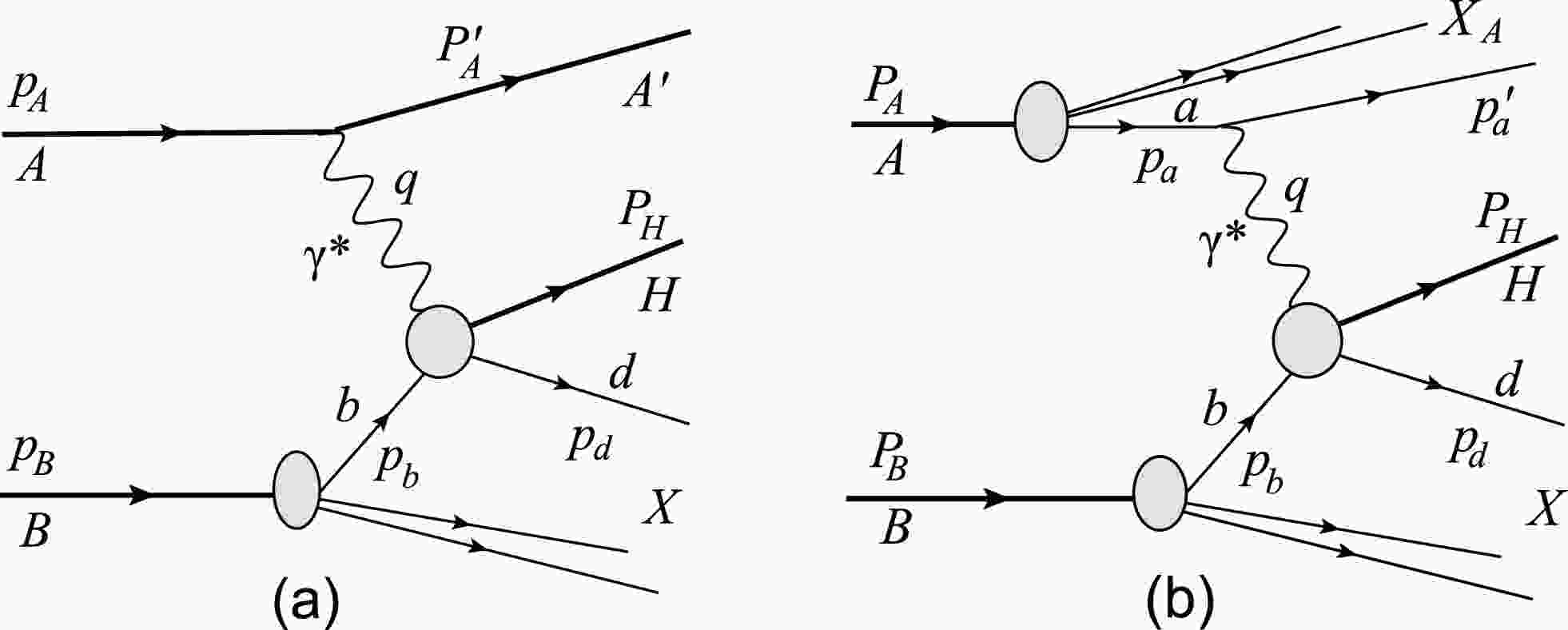
$ D\left(Q^{2}\right) $ must be adopted as the weighting factor (WF) for different charged sources to avoid double counting.By comprehensively analyzing the terms neglected in transiting from the exact formula of Fig. 1(a) to the WWA one, we can naturally estimate the WWA features in heavy-ion collisions. In our case, the details of the result mainly depend on the characteristic behavior exhibited by the photoprocess amplitudes as the photon moves off mass shell. In the first step of the exact treatment, we should derive the general form of the cross section of inelastic heavy quarkonium photoproduction shown in Fig. 1(a):
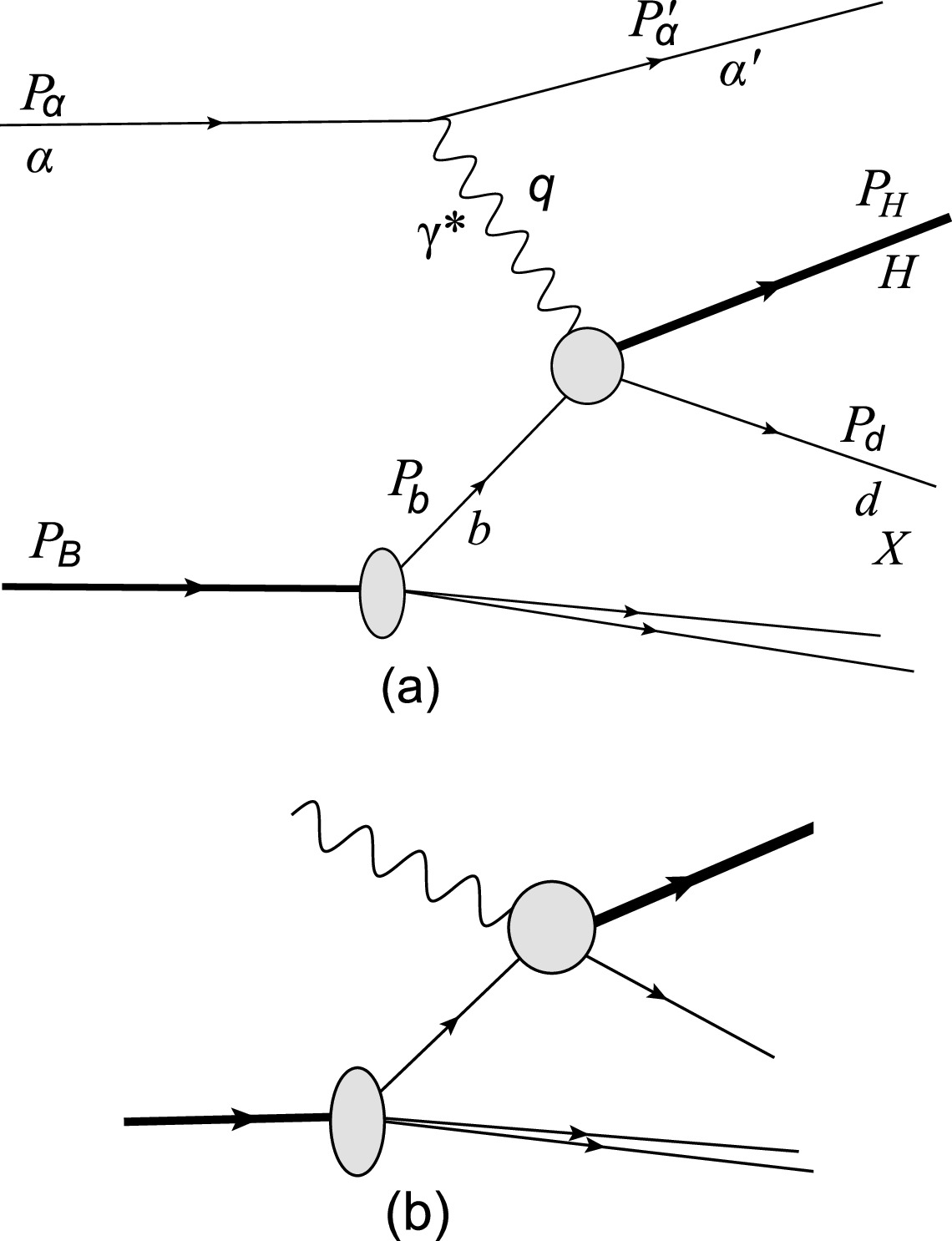
Figure 1. (a): General inelastic heavy quarkonium photoproduction. The virtual photon emitted from α interacts with parton b of nucleus B; α can be the nucleus or its charged parton (protons or quarks). (b): real photoabsorption.
$ \begin{aligned}[b] &{\rm d} \sigma\left(\alpha+B\rightarrow \alpha+H+X\right)\\ =\;&\sum_{b}\int {\rm d} x_{b}f_{b/B}\left(x_{b},\mu^{2}\right){\rm d} \sigma\left(\alpha+b\rightarrow \alpha+H+d\right), \end{aligned} $

(2) where
$ x_{b}=p_{b}/p_{B} $ is the momentum fraction of the massless parton b struck by the virtual photon, and the distribution function of parton b in nucleus B is$ \begin{align} f_{B}\left(x,\mu^{2}\right)=R_{B}\left(x,\mu^{2}\right)\left[Zp\left(x,\mu^{2}\right)+Nn\left(x,\mu^{2}\right)\right], \end{align} $

(3) where
$ R_{B}\left(x,\mu^{2}\right) $ is the nuclear modification factor [47], Z is the proton number, and N is the neutron number.$ p\left(x,\mu^{2}\right) $ and$ n\left(x,\mu^{2}\right) $ are the parton distributions of the proton and neutron, respectively. According to the NRQCD scheme, the partonic cross section in Eq. (2) can be written as$ \begin{aligned}[b] &{\rm d}\sigma\left(\alpha+b\rightarrow \alpha+H+d\right)\\ =\;&\sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle {\rm d}\sigma\left(\alpha+b\rightarrow \alpha+Q\bar{Q}_{[1,8]}[n]+d\right). \end{aligned} $

(4) Denoting the virtual photo-absorption amplitude by
$ M^{\mu} $ , we obtain the SDCs in the parton level$ \begin{aligned}[b] &{\rm d}\sigma\left(\alpha+b\rightarrow \alpha+Q\bar{Q}_{[1,8]}[n]+d\right)\\ =\;&\frac{4\pi e_{\alpha}^{2}\alpha_{\text{em}}}{Q^2}M^{\mu}M^{*\nu}\rho_{\mu\nu}\frac{{\rm d}^{3}p'_{\alpha}}{(2\pi)^{3}2E'_{\alpha}}\\ &\times\frac{(2\pi)^{4}\delta^{4}\left(p_{\alpha}+p_{b}-p'_{\alpha}-k\right){\rm d}\Pi}{4\sqrt{\left(p_{\alpha}\cdot p_{b}\right)^{2}-m_{\alpha}^{2}m_{b}^{2}}}, \end{aligned} $

(5) where
$ e_{\alpha} $ is the charge of α,$ \alpha_{\text{em}} $ is the electromagnetic coupling constant,$ E_{\alpha'} $ is the energy of$ \alpha' $ , and Π is the phase space volume of the produced particle system (with total momentum k). Considering that photons may be emitted by various particles, we derive a generalized density matrix of the virtual photon:$ \begin{aligned}[b] \rho^{\mu\nu}=\;&\frac{1}{2Q^{2}}\text{Tr}\left[\left({\not p}_{\alpha}+m_{\alpha}\right)\Gamma^{\mu}\left({\not p}'_{\alpha}+m_{\alpha}\right)\Gamma^{\nu}\right]\\ =\;&\left(-g^{\mu\nu}+\frac{q^{\mu}q^{\nu}}{q^{2}}\right)C\left(Q^{2}\right)\\ &-\frac{\left(2P_{\alpha}-q\right)^{\mu}\left(2P_{\alpha}-q\right)^{\nu}}{q^{2}}D\left(Q^{2}\right), \end{aligned} $

(6) where
$ C\left(Q^{2}\right) $ and$ D\left(Q^{2}\right) $ are the general form factor notations for α. Note that$ \rho^{\mu\nu} $ is non-diagonal, indicating that the virtual photons are polarized. Eq. (5) is formulated to naturally introduce terminology that is suitable for the WWA. Namely, instead of discussing nucleus-nucleus collisions [Fig. 1(a)], one can refer to the collisions of a virtual photon with the nucleus [Fig. 1(b)].Next, we use Eq. (5) to determine the
$ Q^{2} $ - and y-dependent differential cross sections of inelastic heavy quarkonium photoproduction. It is more convenient to perform the calculations in the rest frame of α, where$ |{\bf{q}}|= |{\bf{p}}_{\alpha'}|=r $ ,$ Q^{2}=-q^{2}=\left(p_{\alpha}-p_{\alpha'}\right)^{2}= 2m_{\alpha}\left(\sqrt{r^{2}+m_{\alpha}^{2}}-m_{\alpha}\right) $ ,${\rm d}^{3}p_{\alpha}'=r^{2}{\rm d}r{\rm d}\cos\theta {\rm d}\varphi$ , and$ y= \left(q\cdot p_{b}\right)/ \left(p_{\alpha}\cdot p_{b}\right)= \left(q_{0}-|{p}_{b}|r\cos\theta/E_{b}\right)/m_{\alpha} $ (which measures the relative energy loss of α in the lab-system). By performing the transformation$ \begin{align} {\rm d}\cos\theta {\rm d}r={\cal{J}}{\rm d}Q^{2}{\rm d}y=\left|\frac{D\left(r,\cos\theta\right)}{D\left(Q^{2},y\right)}\right|{\rm d}Q^{2}{\rm d}y, \end{align} $

(7) the differential cross section of Eq. (5) can be written as (the details of
$ {\cal{J}} $ are given in Appendix B)$ \begin{aligned}[b] &\frac{{\rm d}\sigma\left(\alpha+b\rightarrow \alpha+Q\bar{Q}_{[1,8]}[n]+ d \right)}{{\rm d}Q^{2}{\rm d}y}\\ =\;&\frac{e_{\alpha}^{2}\alpha_{\text{em}}}{4\pi Q^2}\rho_{\mu\nu}M^{\mu}M^{*\nu}f\left(s_{\alpha b},p_{\text{CM}},\hat{s},\hat{p}_{\text{CM}}\right)\\ &\times\frac{\left(2\pi\right)^{4}\delta^{4}\left(p_{\alpha}+p_{b}-p'_{\alpha}-k\right){\rm d}\Pi}{4\hat{p}_{\text{CM}}\sqrt{\hat{s}}}, \end{aligned} $

(8) and
$ \begin{aligned}[b] &f\left(s_{\alpha b},p_{\text{CM}},\hat{s},\hat{p}_{\text{CM}}\right)\\ =\;&\frac{\hat{p}_{\text{CM}}\sqrt{\hat{s}}}{p_{\text{CM}}\sqrt{s_{\alpha b}}} \frac{s_{\alpha b}-m_{\alpha}^{2}-m_{b}^{2}}{\sqrt{\left(s_{\alpha b}-m_{\alpha}^{2}-m_{b}^{2}\right)^{2}-4m_{\alpha}^{2}m_{b}^{2}}}, \end{aligned} $

(9) where
$ s_{\alpha b}=(p_{\alpha}+p_{b})^{2} $ and$ \hat{s}=(q+p_{b})^{2} $ are the squared energies in the α-b and$ \gamma^{*} $ -b partonic processes, respectively.$ p_{\text{CM}} $ and$ \hat{p}_{\text{CM}} $ are the corresponding momenta. Details of these terms are presented in Appendix B.By integrating over the phase space volume Π, Eq. (8) includes the term
$ \begin{align} W^{\mu\nu}=\frac{1}{2}\int M^{\mu}M^{*\nu}\left(2\pi\right)^{4}\delta^{4}\left(q+p_{b}-k\right){\rm d}\Pi, \end{align} $

(10) where
$ W^{\mu\nu} $ is the absorptive part of the$ \gamma b $ amplitude [Fig. 1(b)] and is connected to the cross section in the usual way. The tensors according to which$ W^{\mu\nu} $ is expanded can be constructed only from q,$ p_{b} $ , and$ g^{\mu\nu} $ . Considering the gauge invariance$ q^{\mu}W^{\mu\nu}=q^{\nu}W^{\mu\nu}=0 $ , the following transverse and longitudinal polarization operators become convenient for use [48]:$ \begin{aligned}[b] \epsilon_{T}^{\mu\nu}=&-g^{\mu\nu}+\frac{\left(q^{\mu}p_{b}^{\nu}+p_{b}^{\mu}q^{\nu}\right)}{q\cdot p_{b}}-\frac{p_{b}^{\mu}p_{b}^{\nu}q^{2}}{\left(q\cdot p_{b}\right)^{2}},\\ \epsilon_{L}^{\mu\nu}=&\frac{1}{q^{2}}\left(q^{\mu}-p^{\mu}\frac{q^{2}}{q\cdot p_{b}}\right)\left(q^{\nu}-p^{\nu}\frac{q^{2}}{q\cdot p_{b}}\right), \end{aligned} $

(11) which satisfy the relations
$ q_{\mu}\epsilon_{T}^{\mu\nu}=q_{\mu}\epsilon_{L}^{\mu\nu}=0 $ ,$ \epsilon_{T \mu}^{\mu}=-2 $ , and$ \epsilon_{L \mu}^{\mu}=-1 $ . Furthermore,$ \begin{align} \epsilon^{\mu\nu}=\epsilon_{T}^{\mu\nu}+\epsilon_{L}^{\mu\nu}=-g^{\mu\nu}+\frac{q^{\mu}q^{\nu}}{q^{2}}, \end{align} $

(12) is the polarization tensor of an unpolarized spin-one boson with mass
$ q^{2} $ . Having expanded$ W^{\mu\nu} $ in these tensors, we obtain$ \begin{align} W^{\mu\nu}=\epsilon_{T}^{\mu\nu}W_{\text{T}}\left(Q^{2},q\cdot p_{b}\right)+\epsilon_{L}^{\mu\nu}W_{\text{L}}\left(Q^{2},q\cdot p_{b}\right). \end{align} $

(13) The Lorentz scalar functions
$ W_{\text{T}} $ and$ W_{\text{L}} $ are connected with the transverse and longitudinal photon absorption cross sections$ \sigma_{\text{T}} $ and$ \sigma_{\text{L}} $ , respectively:$ \begin{aligned}[b] W_{\text{T}}=&2\hat{p}_{\text{CM}}\sqrt{\hat{s}}\sigma_{\text{T}}\left(\gamma^{*}+b\rightarrow H+d\right),\\ W_{\text{L}}=&2\hat{p}_{\text{CM}}\sqrt{\hat{s}}\sigma_{\text{L}}\left(\gamma^{*}+b\rightarrow H+d\right). \end{aligned} $

(14) Substituting Eqs. (13) and (14) into Eq. (8), we obtain
$ \begin{aligned}[b] &\frac{{\rm d}\sigma\left(\alpha+b\rightarrow \alpha+Q\bar{Q}_{[1,8]}[n]+d\right)}{{\rm d}Q^{2}{\rm d}y}\\ =\;&\frac{e_{\alpha}^{2}\alpha_{\text{em}}}{4\pi Q^{2}}\left[2\rho^{++}\sigma_{T}\left(\gamma^{*}+b\rightarrow Q\bar{Q}_{[1,8]}[n]+d \right)+\rho^{00}\right.\\ &\left.\times\sigma_{L}\left(\gamma^{*}+b\rightarrow Q\bar{Q}_{[1,8]}[n]+{\rm d}\right)\right]f\left(s_{\alpha b},p_{\text{CM}},\hat{s},\hat{p}_{\text{CM}}\right)\\ =\;&\frac{e_{\alpha}^{2}\alpha_{\text{em}}}{2\pi} d\hat{t}F_{b}[n]\left[\frac{\rho^{++}}{Q^{2}}T_{b}[n]-\rho^{00} L_{b}[n]\right]f\left(s_{\alpha b},p_{\text{CM}},\hat{s},\hat{p}_{\text{CM}}\right),\\ \end{aligned} $

(15) where the relations
${\rm d}\sigma_{T}/{\rm d}\hat{t}=F_{b}[n]T_{b}[n]$ and${\rm d}\sigma_{L}/{\rm d}\hat{t}= -2Q^{2}F_{b}[n]L_{b}[n]$ are employed.$ F_{b}[n] $ ,$ T_{b}[n] $ , and$ L_{b}[n] $ are functions of the Mandelstam variables$ \hat{s} $ ,$ \hat{t} $ ,$ \hat{u} $ , and$ Q^{2} $ , which are detailed in Ref. [26]. The coefficients$ \rho^{ab} $ are the elements of the density matrix in Eq. (6) in the$ \gamma b $ -helicity basis:$ \begin{aligned}[b] 2\rho^{++}&=\epsilon_{T}^{\mu\nu}\rho_{\mu\nu}=\left[\frac{4\left(1-y\right)}{y^{2}}-\frac{4m_{\alpha}^{2}}{Q^{2}}\right]D(Q^{2})+2C\left(Q^{2}\right),\\ \rho^{00}&=\epsilon_{L}^{\mu\nu}\rho_{\mu\nu}=\frac{\left(2-y\right)^{2}}{y^{2}}D\left(Q^{2}\right)-C\left(Q^{2}\right). \end{aligned} $

(16) We can now derive the second step of the exact treatment. The details of the form factors in Eq. (16) must be distinguished in each photon emission channel. In the Martin-Ryskin method [49], the probability or WF of the coherent-photon emission is given by the square of the electric form factor in p-p collisions:
$ w_{\text{coh}}=G_{\text{E}}^{2}\left(Q^{2}\right)= 1/ \left(1+Q^{2}/0.71\; \text{GeV}\right)^{4} $ , where the effect of the magnetic form factor is neglected. We adopt this central idea to deal with the scenario of heavy-ion collisions, where the magnetic form factor is also included. For coherent-photon emission, the photon emitter α is the nucleus, and thus, the general notations$ C(Q^{2}) $ and$ D(Q^{2}) $ in Eq. (16) are the elastic nucleus form factors. In p-p collisions, α presents the proton. Hence,$ C(Q^{2}) $ and$ D\left(Q^{2}\right) $ become Sachs combinations [22]:$ \begin{aligned}[b] &D^{\text{coh}}_{pp}\left(Q^{2}\right)=G_{\text{E}}^{2}\left(Q^{2}\right)\frac{4m_{p}^{2}+7.78 Q^{2}}{4m_{p}^{2}+Q^{2}},\\ &C^{\text{coh}}_{pp}\left(Q^{2}\right)=\mu^{2}_{p}G_{\text{E}}^{2}\left(Q^{2}\right), \end{aligned} $

(17) where
$ \mu_{p}=2.79 $ is the magnetic dipole moment. In$\rm Pb $ -$\rm Pb $ collisions, α is the lead ion; thus,$ C(Q^{2}) $ and$ D(Q^{2}) $ are$ \begin{aligned}[b] &D^{\text{coh}}_{\rm PbPb}\left(Q^{2}\right)=Z^{2}F_{\text{em}}^{2}\left(Q^{2}\right),\\ &C^{\text{coh}}_{\rm PbPb}\left(Q^{2}\right)=\mu^{2}_{\rm Pb}F_{\text{em}}^{2}\left(Q^{2}\right), \end{aligned} $

(18) where
$ \begin{aligned}[b] F_{\text{em}}\left(Q^{2}\right)=\;&\frac{3}{(QR_{A})^{3}}\left[\sin\left(QR_{A}\right)\right.\\ &\left.-QR_{A}\cos\left(QR_{A}\right)\right]\frac{1}{1+a^{2}Q^{2}}, \end{aligned} $

(19) is the electromagnetic form factor parameterization from the STARlight MC generator [50], where
$ R_{A}=1.1A^{1/3} \text{fm} $ ,$ a=0.7\; \text{fm} $ and$ Q=\sqrt{Q^{2}} $ .For ordinary- and ultra-incoherent photon emissions, the contributions must be multiplied by the 'remaining' probability,
$ 1-w_{\text{coh}} $ , to avoid double counting [49]. For ordinary-incoherent photon emission in$\rm Pb $ -$\rm Pb $ collisions, α represents the protons within the lead ion, and the corresponding$ D(Q^{2}) $ and$ C(Q^{2}) $ are$ \begin{aligned}[b] &D^{\text{OIC}}_{\rm PbPb}\left(Q^{2}\right)=\left[1-F_{\text{em}}^{2}\left(Q^{2}\right)\right]D^{\text{coh}}_{pp}\left(Q^{2}\right),\\ &C^{\text{OIC}}_{\rm PbPb}\left(Q^{2}\right)=\left[1-F_{\text{em}}^{2}\left(Q^{2}\right)\right]C^{\text{coh}}_{pp}\left(Q^{2}\right). \end{aligned} $

(20) For ultra-incoherent photon emission, α represents the individual quarks within the nucleus. The corresponding
$ C(Q^{2}) $ and$ D(Q^{2}) $ in p-p collisions have the following form$ \begin{align} D^{\text{UIC}}_{pp}\left(Q^{2}\right)=C^{\text{UIC}}_{pp}(Q^{2})=1-G_{\text{E}}^{2}(Q^{2}). \end{align} $

(21) In
$\rm Pb $ -$\rm Pb $ collisions, since the neutron cannot emit coherent photons, the WFs for the protons and neutrons inside the lead ion are different$ \begin{align} D^{\text{UIC}}_{\rm PbPb}|_{p}(Q^{2})&=C^{\text{UIC}}_{\rm PbPb}|_{p}(Q^{2})=[1-F_{\text{em}}^{2}(Q^{2})][1-G_{\text{E}}^{2}(Q^{2})],\\ D^{\text{UIC}}_{\rm PbPb}|_{n}(Q^{2})&=C^{\text{UIC}}_{\rm PbPb}|_{n}(Q^{2})=[1-F_{\text{em}}^{2}(Q^{2})]. \end{align} $

(22) -
We now apply the general expression [Eq. (15)] to each specific channel involved in inelastic photoproduction processes in heavy-ion collisions. In the initial state, the processes may be direct or resolved, and both are sensitive to the gluon distribution in the nucleus [4]. The photons emitted from the projectile can interact either directly with the quarks participating in the hard-scattering process (direct photoproduction) or via their quark and gluon content (resolved photoproduction). Thus, both the direct and resolved channels contribute to the
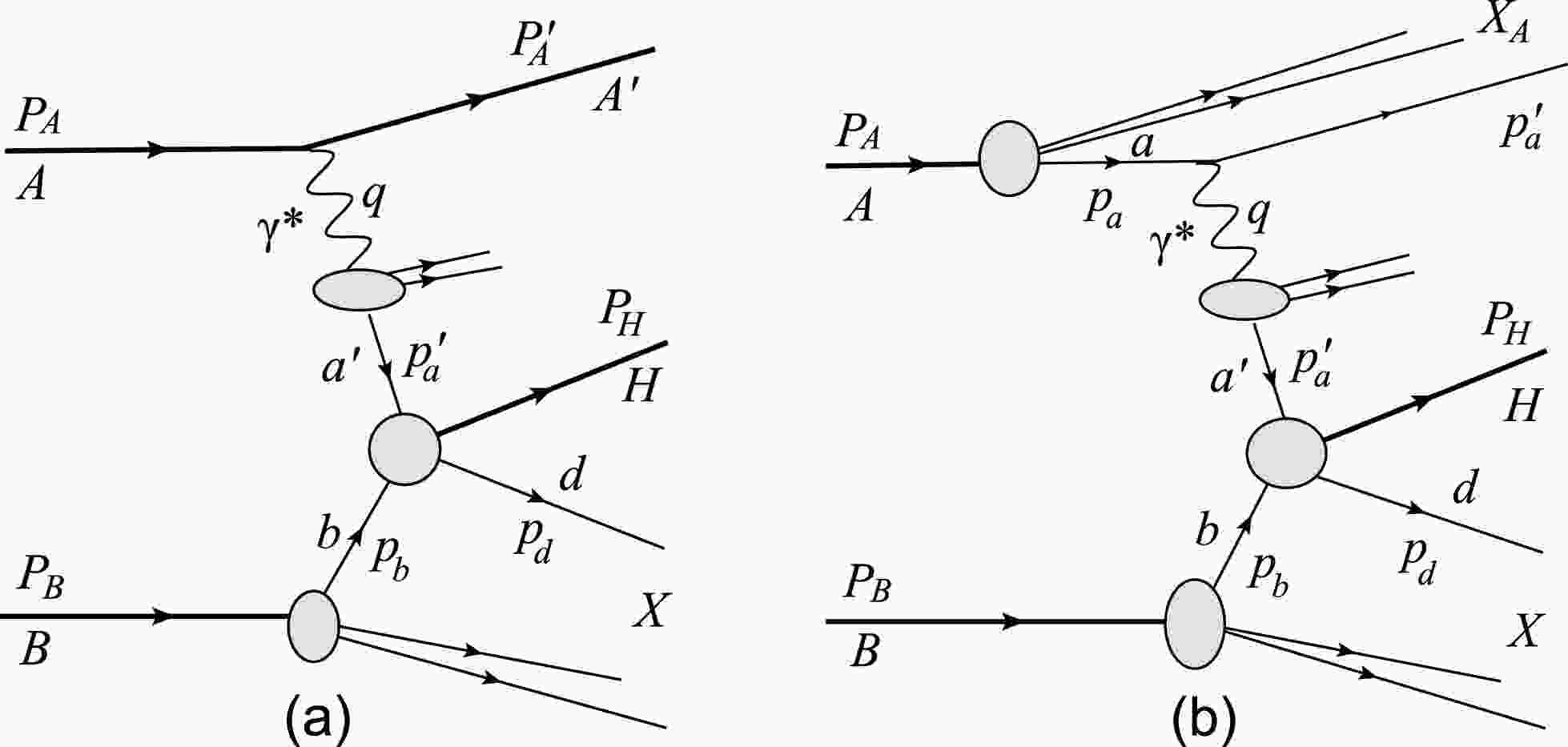
$ \gamma^{*}b\rightarrow H+X $ process. Both contributions are formally on the same order in the perturbative expansion and must be included [51]. However, as is always the case with photons, the situation is highly complex. Along with the types of photon emissions mentioned in Sec. I, the complete description of heavy quarkonium production requires the calculation of six classes of processes [Figs. 2−3]: coherent-direct (coh.dir.), coherent-resolved (coh.res.), ordinary-incoherent direct (OIC dir.), ordinary-incoherent resolved (OIC res.), ultra-incoherent direct (UIC dir.), and ultra-incoherent resolved (UIC res.) processes (these abbreviations will be used in the rest of the paper).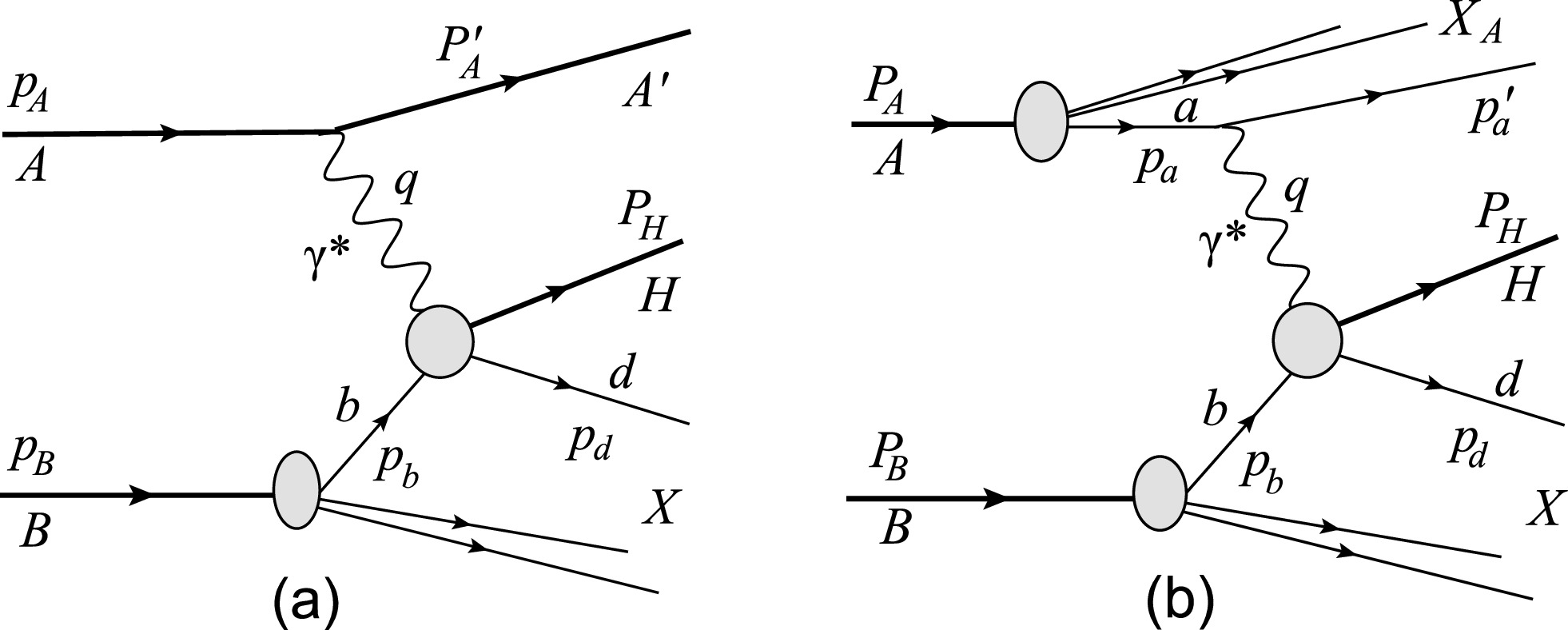
Figure 2. (a): Coherent-direct process in which the virtual photon emitted by the whole incident nucleus A interacts with parton b of the target nucleus B via
$ \gamma^{*} $ -q Compton scattering and$ \gamma^{*} $ -g fusion, and A remains intact after a photon is emitted. (b): Incoherent-direct process in which the virtual photon emitted from the quark a within nucleus A interacts with parton b, and nucleus A is allowed to break up after a photon is emitted. Here, photon emitter a represents a proton and quark for ordinary-incoherent photon emission (OIC) and ultra-incoherent photon emission (UIC), respectively.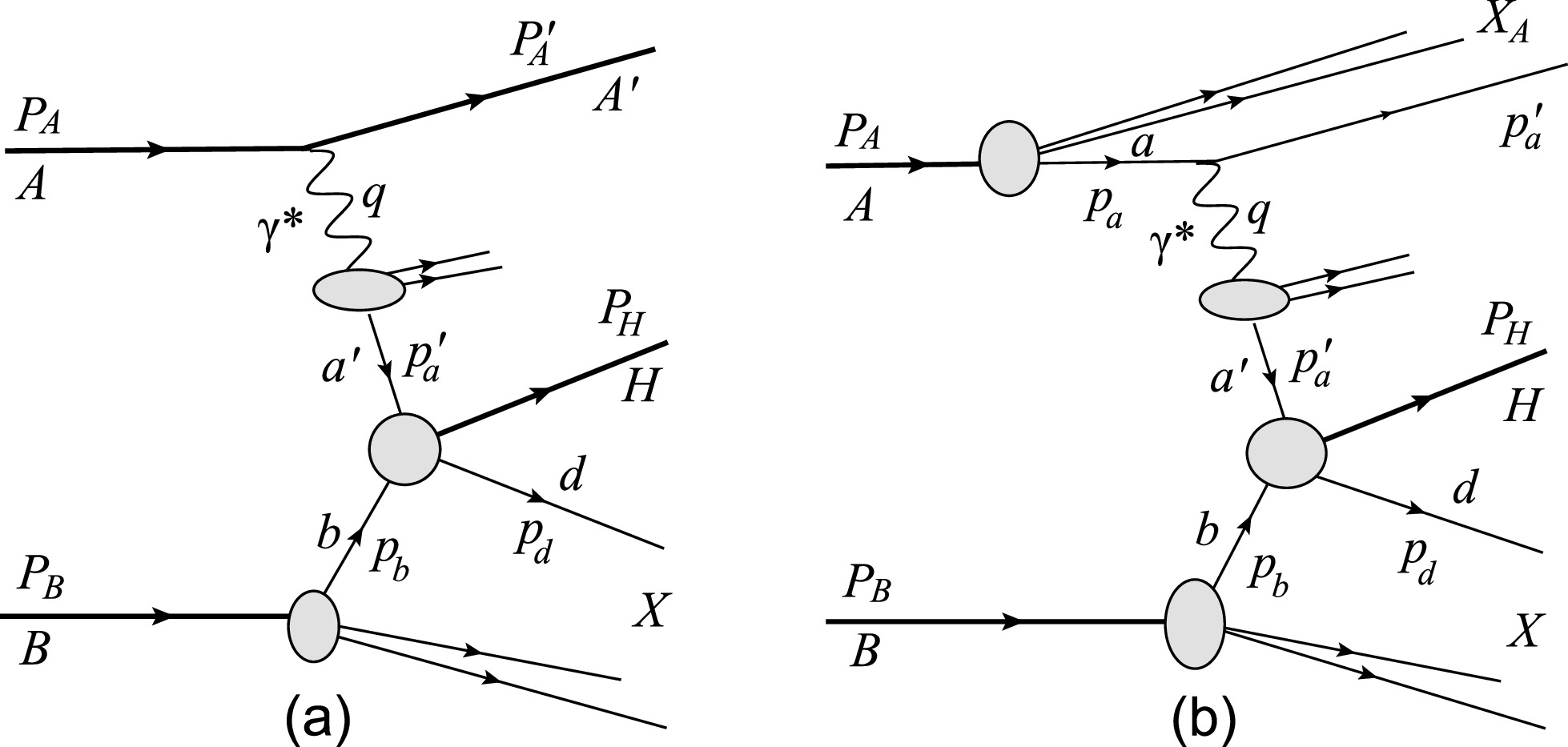
Figure 3. (a): Coherent-resolved process in which the parton
$ a' $ of a hadron-like photon emitted from nucleus A interacts with parton b of the target B via q-g Compton scattering, q-$ \bar{q} $ annihilation, and g-g fusion. (b): Incoherent-resolved process in which the parton a inside nucleus A emits a resolved virtual photon and parton$ a^\prime $ of the resolved photon interacts with parton b inside target B in manner analogous to a hadron. After emmiting the photon, nucleus A breaks up. In the process, photon emitter a represents a proton and quark for ordinary-incoherent photon emission (OIC) and ultra-incoherent photon emission (UIC), respectively.For direct photoproduction [Fig. 2], the corresponding differential cross sections are
$ \begin{aligned}[b] &\frac{{\rm d} \sigma_{\text{coh.dir.}}}{{\rm d}Q^{2}{\rm d}y}\left(A+B\rightarrow A+H+X\right)\\ =\;&2\sum_{b}\int {\rm d} x_{b}{\rm d}\hat{t}f_{b/B}\left(x_{b},\mu^{2}\right)\sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\\ &\times\frac{{\rm d}\sigma}{{\rm d}y{\rm d}Q^{2}{\rm d}\hat{t}}\left(A+b\rightarrow A+Q\bar{Q}_{[1,8]}[n]+d\right), \end{aligned} $

(23) $ \begin{aligned}[b] &\frac{{\rm d}\sigma_{\text{OIC dir.}}}{{\rm d}Q^{2}{\rm d}y}\left(A+B\rightarrow X_{A}+H+X\right)\\ =\;&2Z_{Pb}\sum_{b}\int {\rm d}x_{b}{\rm d}\hat{t}f_{b/B}\left(x_{b},\mu^{2}\right)\sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\\ &\times\frac{{\rm d}\sigma}{{\rm d}y{\rm d}Q^{2}{\rm d}\hat{t}}\left(p+b\rightarrow p+Q\bar{Q}_{[1,8]}[n]+d\right). \end{aligned} $

(24) $ \begin{aligned}[b] &\frac{{\rm d}\sigma_{\text{UIC dir.}}}{{\rm d}Q^{2}{\rm d}y}\left(A+B\rightarrow X_{A}+H+X\right)\\ =\;&2\sum_{a,b} \int {\rm d}x_{a}{\rm d}x_{b}{\rm d}\hat{t}f_{a/A}\left(x_{a},\mu^{2}\right)f_{b/B}\left(x_{b},\mu^{2}\right)\sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\\ &\times\frac{{\rm d}\sigma}{{\rm d}y{\rm d}Q^{2}{\rm d}\hat{t}}\left(a+b\rightarrow a+Q\bar{Q}_{[1,8]}[n]+d\right), \end{aligned} $

(25) where the factor of two arises because both nuclei emit photons and thus serve as targets. The partonic cross section can be derived from Eq. (15) with
$ m_{\alpha}=m_{q}=0 $ and$ e_{\alpha}=e_{a} $ , where$ e_{a} $ is the charge of massless quark a.In the resolved photoproduction [Fig. 3], the corresponding differential cross sections are
$ \begin{aligned}[b] &\frac{{\rm d}\sigma_{\text{coh.res.}}}{{\rm d}Q^{2}{\rm d}y}\left(A+B\rightarrow A+H+X\right)\\ =\;&2\sum_{b}\sum_{a'}\int {\rm d}x_{b}{\rm d}z_{a'}{\rm d}\hat{t}f_{b/B}\left(x_{b},\mu^{2}\right)f_{a'/\gamma}\left(z_{a'},\mu^{2}\right)\\ &\times\frac{Z_{Pb}^{2}\alpha_{\text{em}}}{2\pi}\frac{y\rho^{++}_{\text{coh}}}{Q^{2}}\sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\frac{{\rm d}\sigma_{a'b\rightarrow Q\bar{Q}_{[1,8]}[n]d}}{{\rm d}\hat{t}}, \end{aligned} $

(26) $ \begin{aligned}[b] &\frac{{\rm d}\sigma_{\text{OIC res.}}}{{\rm d}Q^{2}{\rm d}y}\left(A+B\rightarrow X_{A}+H+X\right)\\ =\;&2Z_{Pb}\sum_{b}\sum_{a'}\int {\rm d}x_{b}{\rm d}z_{a'}{\rm d}\hat{t}f_{b/B}\left(x_{b},\mu^{2}\right)f_{a'/\gamma}\left(z_{a'},\mu^{2}\right)\\ &\times \frac{\alpha_{\text{em}}}{2\pi}\frac{y\rho^{++}_{\text{OIC}}}{Q^{2}} \sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\frac{{\rm d}\sigma_{a'b\rightarrow Q\bar{Q}_{[1,8]}[n]d}}{{\rm d}\hat{t}}. \end{aligned} $

(27) $ \begin{aligned}[b] &\frac{{\rm d}\sigma_{\text{UIC res.}}}{{\rm d}Q^{2}{\rm d}y}\left(A+B\rightarrow X_{A}+H+X\right)\\ =\;&2\sum_{a,b}\sum_{a'}\int {\rm d}x_{a}{\rm d}x_{b}{\rm d}z_{a'}{\rm d}\hat{t}f_{a/A}\left(x_{a},\mu^{2}\right)\\ &\times f_{b/B}\left(x_{b},\mu^{2}\right)f_{a'/\gamma}\left(z_{a'},\mu^{2}\right)\frac{e_{a}^{2}\alpha_{\text{em}}}{2\pi}\frac{y\rho^{++}_{\text{UIC}}}{Q^{2}}\\ &\times \sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\frac{{\rm d}\sigma_{a'b\rightarrow Q\bar{Q}_{[1,8]}[n]d}}{{\rm d}\hat{t}}. \end{aligned} $

(28) where
$ z_{a}'=p_{a'}/q $ and$ f_{\gamma}\left(z_{a'},\mu^{2}\right) $ denote the parton's momentum fraction and the parton distribution function of the resolved photon [52], respectively. The involved partonic cross sections can be found in Ref. [51]. -
The distributions of
$ p_{T} $ and inelastic variable$ z=(p_{H}\cdot p_{b})/(q\cdot p_{b}) $ can be obtained using the Jacobian transformation. In the final state, we must classify the two types of inelastic photoproductions. In the first type, heavy quarkonium is directly produced via the γ-g fusion, annihilation, and Compton scattering of partons. In the second type, heavy quarkonium is produced by the final fragmentation of a parton. These aspects are considered in the subsequent discussion. -
Before performing the transformation, the Mandelstam variables in the
$ \gamma^{*} $ -b parton level should be expressed as$ \begin{aligned}[b] \hat{s}=&\left(M_{T}\cosh y_{r}+\sqrt{\cosh^{2}y_{r}M_{T}^{2}+m_{b}^{2}-M_{H}^{2}}\right)^{2},\\ \hat{t}=&M_{H}^{2}-Q^{2}-2M_{T}\left(\hat{E}_{\gamma}\cosh y_{r}-\hat{p}_{\text{CM}}\sinh y_{r}\right),\\ \hat{u}=&M_{H}^{2}-2M_{T}\left(\hat{E}_{b}\cosh y_{r}+\hat{p}_{\text{CM}}\sinh y_{r}\right), \end{aligned} $

(29) where
$ y_{r} $ is the rapidity,$ M_{T}=\sqrt{M_{H}^{2}+p_{T}^{2}} $ is the transverse mass of heavy quarkonium,$ \hat{E}_{\gamma} $ ,$ \hat{E}_{b} $ , and$ \hat{p}_{\text{CM}} $ are the corresponding energies and momentum. Details of these parameters are summarized in Appendix B.For direct-photon processes,
$ x_{b} $ and$ \hat{t} $ should be transformed as$ \begin{align} {\rm d}\hat{t}{\rm d}x_{b}={\cal{J}}{\rm d}y_{r}{\rm d}p_{T}=\left|\frac{D\left(x_{b},\hat{t}\right)}{D\left(y_{r},p_{T}\right)}\right|{\rm d}y_{r}{\rm d}p_{T}, \end{align} $

(30) and the corresponding differential cross sections are
$\frac{{\rm d}\sigma_{\text{coh.dir.}}}{{\rm d}p_{T}{\rm d}y_{r}}\left(A+B\rightarrow A+H+X\right) $

$ \begin{aligned}[b] =\;&2\sum_{b}\int {\rm d}Q^{2}{\rm d}yf_{b/B}\left(x_{b},\mu^{2}\right){\cal{J}}\sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\\ &\times\frac{{\rm d}\sigma}{{\rm d}Q^{2}{\rm d}y{\rm d}\hat{t}}\left(A+b\rightarrow A+Q\bar{Q}_{[1,8]}[n]+{d}\right), \end{aligned} $

(31) $ \begin{aligned}[b] &\frac{{\rm d}\sigma_{\text{OIC dir.}}}{{\rm d}p_{T}{\rm d}y_{r}}\left(A+B\rightarrow X_{A}+H+X\right)\\ =\;&2Z_{Pb}\sum_{b}\int {\rm d}Q^{2}{\rm d}yf_{b/B}\left(x_{b},\mu^{2}\right){\cal{J}}\sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\\ &\times\frac{{\rm d}\sigma}{{\rm d}Q^{2}{\rm d}y{\rm d}\hat{t}}\left(p+b\rightarrow p+Q\bar{Q}_{[1,8]}[n]+d\right), \end{aligned} $

(32) $ \begin{aligned}[b] &\frac{{\rm d}\sigma_{\text{UIC dir.}}}{{\rm d}p_{T}{\rm d}y_{r}}\left(A+B\rightarrow X_{A}+H+X\right)\\ =\;&2\sum_{a,b}\int {\rm d}Q^{2}{\rm d}y{\rm d}x_{a}f_{a/A}\left(x_{a},\mu^{2}\right)f_{b/B}\left(x_{b},\mu^{2}\right){\cal{J}}\\ &\times\sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\frac{{\rm d}\sigma}{{\rm d}Q^{2}{\rm d}y{\rm d}\hat{t}}\left(a+b\rightarrow a+Q\bar{Q}_{[1,8]}[n]+d\right). \end{aligned} $

(33) For resolved processes,
$ \hat{t}^{*} $ and$ z_{a'} $ are chosen for the similar transformation$ \begin{align} {\rm d}\hat{t}^{*}{\rm d}z_{a'}={\cal{J}}{\rm d}y_{r}{\rm d}p_{T}= \left|\frac{D\left(z_{a'},\hat{t}^{*}\right)}{D\left(y_{r},p_{T}\right)}\right|{\rm d}y_{r}{\rm d}p_{T}, \end{align} $

(34) and the corresponding differential cross sections are
$ \begin{aligned}[b] &\frac{{\rm d}\sigma_{\text{coh.res.}}}{{\rm d}p_{T}{\rm d}y_{r}}\left(A+B\rightarrow A+H+X\right)\\ =\;&2\sum_{b}\sum_{a'}\int {\rm d}Q^{2}{\rm d}y{\rm d}x_{b}f_{b/B}\left(x_{b},\mu^{2}\right)f_{\gamma}\left(z_{a'},\mu^{2}\right){\cal{J}}\\ &\times \frac{Z_{\rm Pb}^{2}\alpha_{\text{em}}}{2\pi}\frac{y\rho^{++}_{\text{coh}}}{Q^{2}} \sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\frac{{\rm d}\sigma_{a'b\rightarrow Q\bar{Q}_{[1,8]}[n]d}}{{\rm d}\hat{t}}, \end{aligned} $

(35) $ \begin{aligned}[b] &\frac{{\rm d}\sigma_{\text{OIC res.}}}{{\rm d}p_{T}{\rm d}y_{r}}\left(A+B\rightarrow X_{A}+H+X\right)\\ =\;&2Z_{Pb}\sum_{b}\sum_{a'}\int {\rm d}Q^{2}{\rm d} y{\rm d}x_{b}f_{b/B}\left(x_{b},\mu^{2}\right)f_{\gamma}\left(z_{a'},\mu^{2}\right)\\ &\times {\cal{J}}\frac{\alpha_{\text{em}}}{2\pi}\frac{y\rho^{++}_{\text{OIC}}}{Q^{2}} \sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\frac{{\rm d}\sigma_{a'b\rightarrow Q\bar{Q}_{[1,8]}[n]d}}{{\rm d}\hat{t}}, \end{aligned} $

(36) $ \begin{aligned} &\frac{{\rm d}\sigma_{\text{UIC res.}}}{{\rm d}p_{T}{\rm d}y_{r}}\left(A+B\rightarrow X_{A}+H+X\right)\\ =&2\sum_{a,b}\sum_{a'}\int {\rm d}Q^{2}{\rm d}y{\rm d}x_{a}{\rm d}x_{b}f_{a/A}\left(x_{a},\mu^{2}\right)\end{aligned} $

$ \begin{aligned}[b] &\times f_{b/B}\left(x_{b},\mu^{2}\right)f_{\gamma}\left(z_{a'},\mu^{2}\right){\cal{J}}e_{a}^{2}\frac{\alpha_{\text{em}}}{2\pi}\frac{y\rho^{++}_{\text{UIC}}}{Q^{2}}\\ &\times\sum_{n}\langle{\cal{O}}^{H}_{[1,8]}[n]\rangle\frac{{\rm d}\sigma_{a'b\rightarrow Q\bar{Q}_{[1,8]}[n]d}}{{\rm d}\hat{t}}, \end{aligned} $

(37) where the Mandelstam variables of resolved photoproductions are the same as those in Eq. (29) with
$ Q^{2}=0 $ .For the z distribution, we should rewrite the Mandelstam variables in Eq. (29) as follows:
$ \begin{aligned}[b] &\hat{s}=\frac{M_{H}^{2}}{z}+\frac{p_{T}^{2}}{z\left(1-z\right)},\\ &\hat{t}=-\left(1-z\right)\left(\hat{s}+Q^{2}\right),\\ &\hat{u}=M_{H}^{2}-z\left(\hat{s}+Q^{2}\right), \end{aligned} $

(38) Thus, we perform a similar Jacobian transformation. The relevant cross sections in z distribution can be obtained as follows:
$ \begin{align} \frac{{\rm d}\sigma}{{\rm d}z}=\int^{p^{2}_{T\text{max}}}_{p^{2}_{T\text{min}}}\frac{{\rm d}^{2}\sigma}{{\rm d}z{\rm d}p^{2}_{T}}{\rm d}p^{2}_{T}. \end{align} $

(39) The Jacobian factors
$ {\cal{J}} $ and corresponding kinematical boundaries are summarized in Appendix B. -
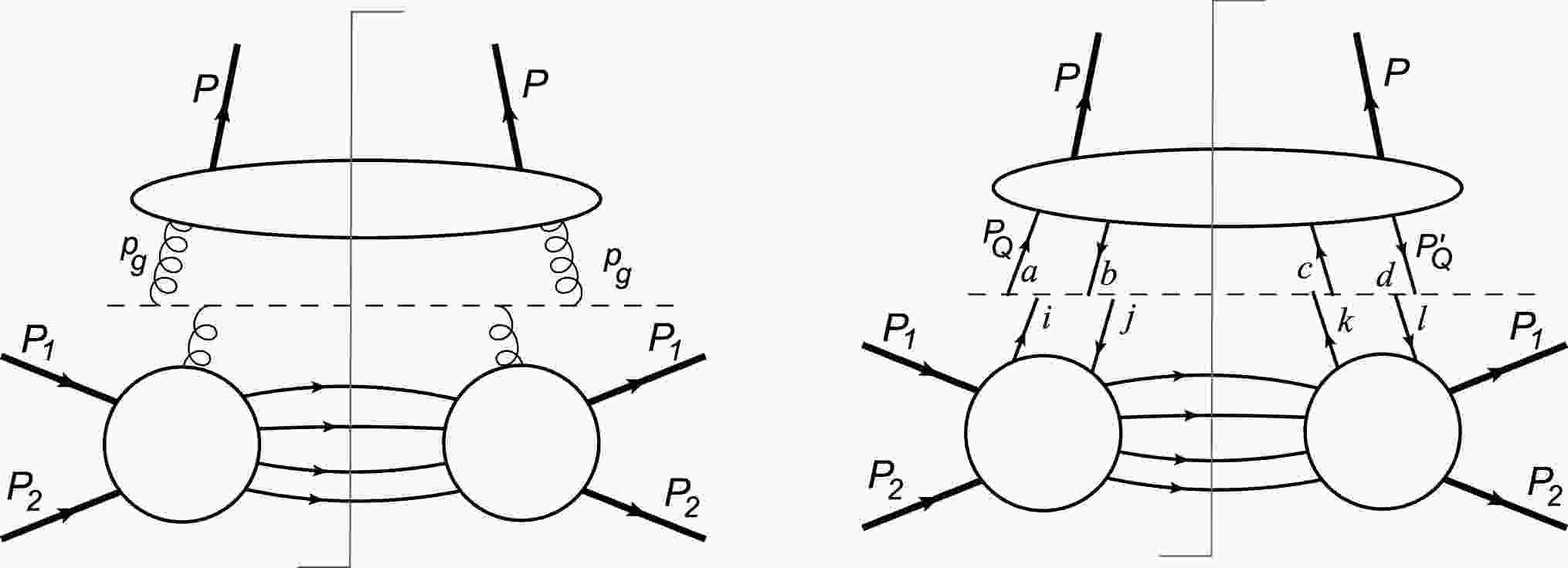
Heavy quarkonium production by fragmentation is an important channel that is described by fragmentation functions (FFs). This factorization theory of quarkonium production that has been proven presents the collinear factorization method [53]. It can be used to compute rates at leading power (LP) or next to leading power (NLP) in
$ m_{Q}^{2}/p_{T}^{2} $ . LP contributions can be factorized into partonic cross sections to produce a specific single parton convolved with single particle FFs [30]. NLP contributions can be factorized to produce two specific partons convolved with two-parton FFs [53]. The Feynman diagrams in the cut diagram notation for these two contributions are shown in Fig. 4. This fragmentation picture dominates all other creation mechanisms for large$ p_{T} $ . In particular, gluon fragmentation represents the dominant source of high energy prompt quarkonia at hadron colliders. Because the LP and NLP contributions represent the leading and first subleading terms in an expansion in powers of$ m_{Q}^{2}/p_{T}^{2} $ , one would not expect them to be valid unless$ p_{T} $ is significantly greater than$ m_{Q} $ . Fragmentation predictions for charmonium differential cross sections are therefore unreliable for small$ p_{T} $ . To suppress NLP contributions and ensure the validity of the fragmentation mechanism, Ref. [54] suggested using the criterion$ p_{T}>3M_{J/\psi} $ for comparing data with theory. In Refs. [32−34], the criterion$ p_{T}>10\; \text{GeV} $ was used for predictions. Similarly, fragmentation results for bottomonium production are untrustworthy for$ p_{T}<15\; \text{GeV} $ [31].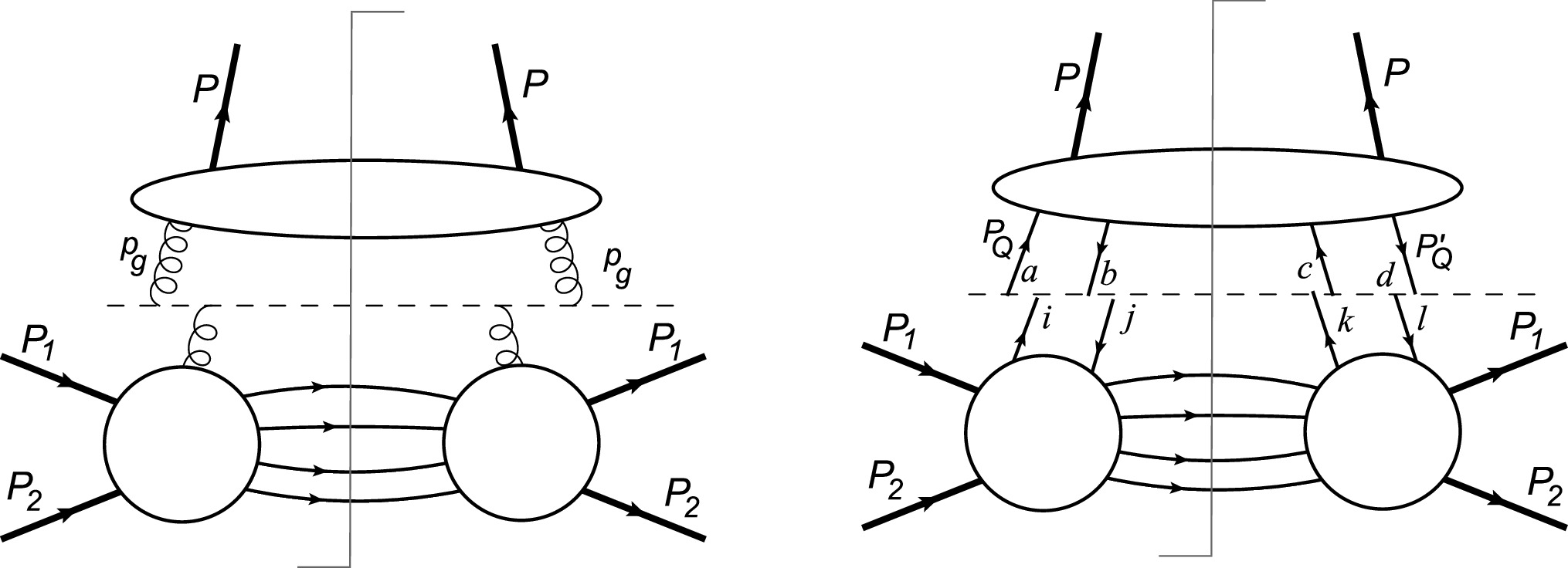
Figure 4. pQCD factorization diagrams of heavy quarkonium production. Left: sing-parton (here taking gluon as an example) fragmentation. Right: heavy quark-pair fragmentation.
In this study, we adopt the LP-factorization formalism to calculate the contributions of fragmentation to heavy quarkonium production. The calculations of these fragmentation contributions, at any given order in
$ \alpha_{s} $ , are much simpler than those of full fixed-order calculations. According to the NRQCD scheme, the inelastic quarkonium H production in two-body collisions can be described using Eq. (1), where the SDCs,$ {\rm d}\sigma_{A+B\rightarrow Q\bar{Q}_{[1,8]}[n]X} $ , describe the production of a$ Q\bar{Q} $ pair in color and angular momentum state n. At large transverse momentum$ p_{T} $ , one can apply LP factorization to the SDCs in Eq. (1). The general expression is [30, 55]$ \begin{align} {\rm d}\sigma^{ \text{LP-frag}}_{A+B\rightarrow Q\bar{Q}[n]+X} =\sum_{c}{\rm d}\hat{\sigma}_{A+B\rightarrow c+X}\otimes D_{c\rightarrow Q\bar{Q}[n]}. \end{align} $

(40) where
${\rm d}\hat{\sigma}_{A+B\rightarrow c+X}$ are the parton production cross sections (PPCSs) for producing a parton c, and$ D_{c\rightarrow Q\bar{Q}[n]} $ are the FFs of parton c that fragments into a$ Q\bar{Q} $ pair in the quantum state n. In LP factorization, the SDCs of Eq. (40) for photoproduction and initial parton hard scattering (had.scat.) can be summarized by the following master formula:$ \begin{aligned}[b] &{\rm d}\sigma^{ \text{LP-frag}}_{A+B\rightarrow Q\bar{Q}_{[1,8]}[n]X}\\ =\;&\sum_{a,b,c}\sum_{a'}f_{a/A}\left(x_{a},\mu^{2}\right)\otimes f_{k/a}\left(z_{a'},\mu^{2}\right)\otimes f_{b/B}\left(x_{b},\mu^{2}\right)\\ & \otimes {\rm d}\sigma_{kb\rightarrow cX}(p_{c}=p'_{c}/z_{c},\mu^{2})\otimes D_{c\rightarrow Q\bar{Q}_{[1,8]}[n]}\left(z_{c},\mu^{2}\right), \end{aligned} $

(41) where
$ z_{c} $ is the longitudinal momentum fraction of the hadron relative to the fragmenting parton,$ f_{a/A}\left(x_{a},\mu^{2}\right) $ is the PDF of parton$ a=g,q,\bar{q} $ in nucleus A or the flux function of photon$ a=\gamma $ , and$ f_{k/a}\left(z_{a'},\mu^{2}\right) $ is$ \delta_{ak}\delta\left(1-z_{a'}\right) $ in the "direct" case (since the parton a is the photon itself) or the PDF of parton k in the resolved photon a. The parton distributions in the photon behave like$ \alpha/\alpha_{s}(Q^2) $ for large$ Q^2 $ . Therefore, the additional power of$ \alpha_{s} $ from the "resolved" component is compensated for as compared to the "direct" one. The hard PPCSs,${\rm d}\sigma_{kb\rightarrow cX}$ , and FFs are calculated to NLO accuracy; their expansions are in powers of$ \alpha_{s} $ $ \begin{aligned}[b] {\rm d}\hat{\sigma}_{\gamma b\rightarrow cX}&=\alpha_{s}{\rm d}\hat{\sigma}^{(1)}_{\gamma b\rightarrow cX}+\alpha_{s}^{2}{\rm d}\hat{\sigma}^{(2)}_{\gamma b\rightarrow cX}+{\cal{O}}(\alpha_{s}^{3}),\\ {\rm d}\hat{\sigma}_{ab\rightarrow cX}&=\alpha_{s}^{2}{\rm d}\hat{\sigma}^{(2)}_{\gamma b\rightarrow cX}+\alpha_{s}^{3}{\rm d}\hat{\sigma}^{(3)}_{\gamma b\rightarrow cX}+{\cal{O}}(\alpha_{s}^{4}),\\ D_{c\rightarrow Q\bar{Q}[n]}&=\alpha_{s}D^{(1)}_{c\rightarrow Q\bar{Q}[n]}+\alpha_{s}^{2}D^{(2)}_{c\rightarrow Q\bar{Q}[n]}+{\cal{O}}(\alpha_{s}^{3}). \end{aligned} $

(42) In this study, we use the LP factorization approximation for the SDCs to compute fragmentation contributions that augment the LO fixed order calculations of the SDCs. Since direct and fragmentation contributions cannot be added without introducing double counting, we applied a matching rule between the fixed-order and fragmentation contributions. This approach was developed by Bodwin, Chao, Chung, Kim, and Lee (BCCKL) [32−34]. Therefore, we combine the LO fixed-order calculations with LP fragmentation corrections [Eq. (40)] according to the formula
$ \begin{align} {\rm d}\sigma={\rm d}\sigma_{ \text{LO}}(\alpha_{s}^{3})+{\rm d}\sigma^{ \text{LP-frag.}}(\alpha_{s}^{4}), \end{align} $

(43) where we denote the LO (
$ \alpha_{s}^{3} $ ) contributions to SDCs by${\rm d}\sigma_{ \text{LO}}$ , as discussed for Eq. (5). We denote the LP fragmentation corrections by${\rm d}\sigma^{ \text{LP-frag.}}$ , and only consider the contributions at order$ \alpha_{s}^{4} $ , because Ref. [33] demonstrated that LP fragmentation contributions of order$ \alpha_{s}^{5} $ are small and have a negligible effect on the predicted photoproduction cross section.For
${\rm d}\sigma^{ \text{LP-frag.}}$ , we combine the PPCSs and FFs of order$ \alpha_{s}^{2} $ . The LP fragmentation process also includes the six classes of sub-processes described in Figs. 2and 3. According to Eq. (40), the LO SDCs [Eqs. (31)−(37)] can be replaced with the convolution of PPCSs and FFs. The PPCSs of the direct and resolved processes have been described in Refs. [56, 57]. We consider gluon and light-quark fragmentations. The gluon FFs$ D_{g\rightarrow Q\bar{Q}[n]} $ are for$ ^{1}S_{0}^{(8)} $ at order$ \alpha_{s}^{2}\; ( \text{LO}) $ , as in Refs. [58, 59]; for$ ^{3}S_{1}^{(8)} $ at orders$ \alpha_{s}\; ( \text{LO}) $ and$ \alpha_{s}^{2}\; ( \text{NLO}) $ , as in Refs. [60, 61]; and for$ ^{3}P_{J}^{(8)} $ at order$ \alpha_{s}^{2}\; ( \text{LO}) $ , as in Refs. [59, 60]. Because the gluon FF for$ ^{3}S_{1}^{(1)} $ begins at order$ \alpha_{s}^{3}\; ( \text{LO}) $ , it is not considered. The light quark FF$ D_{q\rightarrow Q\bar{Q}}[n] $ is given for$ ^{3}S_{1}^{(8)} $ at order$ \alpha_{s}^{2}\; ( \text{LO}) $ , as in Refs. [61, 62], where the other light quark FFs vanishes at order$ \alpha_{s}^{2} $ .To determine
$ p_{T} $ distribution, we rewrite the Mandelstam variables as$ \begin{aligned}[b] &\hat{s}=y\left(s_{\alpha b}-m_{\alpha}^{2}-m_{b}^{2}\right)-Q^{2}+m_{b}^{2},\\ &\hat{t}=\frac{1}{2\cosh y_{r}}\left[Q^{2}\left({\rm e}^{y_{r}}-2\cosh y_{r}\right)-{\rm e}^{-y_{r}}\hat{s}\right],\\ &\hat{u}=-\left(\hat{s}+Q^{2}\right)\frac{{\rm e}^{y_{r}}}{2\cosh y_{r}}, \end{aligned} $

(44) and since parton c is taken to be lightlike because its mass is neglected,
$ z_{c}=p'_{c}/p_{c}=2p_{T}\cosh y_{r}/\sqrt{\hat{s}} $ . Hence,$ z_{c} $ and$ \hat{t} $ can be transformed as$ \begin{align} {\rm d}\hat{t}{\rm d}z_{c}={\cal{J}}{\rm d}y_{r}{\rm d}p_{T}=\left|\frac{D\left(z_{c},\hat{t}\right)}{D\left(y_{r},p_{T}\right)}\right|{\rm d}y_{r}{\rm d}p_{T}. \end{align} $

(45) -
The connection between the processes in Fig. 1(a) and (b) is evident. By Fourier-transforming the electric and magnetic fields of an ultrarelativistic charged point-like particle, the photoproduction process can be expressed in terms of the real photo-absorption cross section with the photon spectrum. This idea was originally proposed by Fermi [10], and Weizsäcker and Williams independently developed the idea for processes involving relativistic collisions of charged particles, thus establishing the WWA [11]. The advantage of the WWA is that it only requires the on-shell photo-absorption cross section for calculations. Details of its off-shell behavior are not essential. This section transforms the accurate expression given in Eq. (15) into its WWA form by taking
$ Q^{2}\rightarrow0 $ and discusses a number of widely employed photon spectra. This transformation results in two simplifications: the scalar photon contribution$ \sigma_{L} $ is neglected and$ \sigma_{T} $ is replaced with its on-shell value. This provides us a powerful approach to study the features of the WWA in inelastic heavy quarkonium photoproduction in heavy-ion collisions.Taking
$ Q^{2}\rightarrow0 $ , Eq. (15) becomes$ \begin{aligned}[b] &\lim_{Q^{2}\rightarrow0}{\rm d}\sigma\left(\alpha+b\rightarrow \alpha+Q\bar{Q}_{[1,8]}+d\right)\\ =\;&\left[\frac{e_{\alpha}^{2}\alpha_{\text{em}}}{2\pi}(y\rho^{++})\frac{{\rm d}y{\rm d}Q^{2}}{Q^{2}}\right] \sigma_{T}\frac{\hat{p}_{\text{CM}}\sqrt{\hat{s}}}{yp_{\text{CM}}\sqrt{s_{0}}}\bigg|_{Q^{2}=0}\\ =&\sigma_{T}{\rm d}n^{\gamma}\bigg|_{Q^{2}=0}, \end{aligned} $

(46) where the contribution of
$ \sigma_{L} $ and the terms proportional to$ Q^{2} $ are neglected in the limit$ Q^{2}\rightarrow 0 $ . In addition, the general form of the photon spectrum$ f_{\gamma}(y) $ , which is associated with various particles, reads$ \begin{align} &f^{\gamma}(y)=\frac{{\rm d}n^{\gamma}}{{\rm d}y}=y\int\frac{{\rm d}Q^{2}}{Q^{2}}\frac{e_{\alpha}^{2}\alpha_{\text{em}}}{2\pi}\rho^{++}\\ =&\frac{e_{\alpha}^{2}\alpha_{\text{em}}}{2\pi}\int\frac{{\rm d}Q^{2}}{Q^{2}}\left\{yC\left(Q^{2}\right)+\left[\frac{2(1-y)}{y} -\frac{2ym_{\alpha}^{2}}{Q^{2}}\right]D\left(Q^{2}\right)\right\}.\\ \end{align} $

(47) For coherent-photon emission, Ref. [5] presented a modified version of Eq. (47) for the photon flux function of the proton. Neglecting the magnetic form factor and adopting the dipole form of the electric form factor of the proton
$ C(Q^{2})=D(Q^{2})=G_{\text{E}}^{2}(Q^{2}) $ and employing the coherent condition$ Q^{2}\leq 1/R^{2}_{A} $ ($ Q^{2}_{\text{max}}=0.027, y_{\text{max}}=0.16 $ ), one obtains$ a=2m_{p}^{2}/Q^{2}_{\text{max}} $ and$ b=2m_{p}^{2}/0.71=2.48 $ ,$ \begin{aligned}[b] f_{\text{MD}}^{\gamma}(y)=\;& \frac{\alpha_{\text{em}}}{2\pi}y\left[a-2x+\left(2x+c_{1}\right)d_{1}+\left(2x+c_{2}\right)d_{2}\right.\\ &+\left.\left(3x+c_{3}\right)d_{3}+\left(2x+c_{4}\right)d_{4}\right], \end{aligned} $

(48) where x depends on y,
$ \begin{eqnarray} x=-\frac{1}{y}+\frac{1}{y^{2}}. \end{eqnarray} $

(49) In general, various widely used photon spectra originate from the plane wave form presented in Ref. [48], given by
$ \begin{aligned}[b] {\rm d}n^{\gamma}(y)=\;&\frac{e_{\alpha}^{2}\alpha_{\text{em}}}{\pi}\frac{{\rm d}y}{y}\frac{{\rm d}Q^{2}}{Q^{2}}\left[\frac{y^{2}}{2}D\left(Q^{2}\right)\right.\\ &\left.+\left(1-y\right)\frac{Q^{2}-Q^{2}_{\text{min}}}{Q^{2}}C\left(Q^{2}\right)\right]. \end{aligned} $

(50) This form is obtained from the complete form given in Eq. (47) by setting
$ Q^{2}_{\text{min}}=y^{2}m_{\alpha}^{2}/(1-y) $ , the LO term of the expression$ \begin{aligned}[b] Q^{2}_{\text{min}}=\;&-2m_{\alpha}^{2}+\frac{1}{2s_{\alpha b}}\left[\left(s_{\alpha b}+m_{\alpha}^{2}\right)\left(s_{\alpha b}-\hat{s}+m_{\alpha}^{2}\right)\right.\\ &\left.-(s_{\alpha b}-m_{\alpha}^{2})\sqrt{(s_{\alpha b}-\hat{s}+m_{\alpha}^{2})^{2}-4s_{\alpha b}m_{\alpha}^{2}}\right]. \end{aligned} $

(51) This approximation holds for
$ m_{\alpha}^{2}\ll1\; \text{GeV}^2 $ . However,$ m_{p}^{2} $ and$ m_{Pb}^{2} $ do not satisfy this condition, which produces errors in the approximations of various spectra. This is partuclarly the case for the lead ion spectra.Drees and Zeppenfeld (DZ) proposed another widely used photon distribution function for the proton [15−21]. This function is the approximate analytic form of Eq. (50). Assuming
$ Q^{2}_{\text{max}}\rightarrow \infty $ ,$ C\left(Q^{2}\right)=D\left(Q^{2}\right)=G_{\text{E}}^{2}(Q^{2}) $ , and$ Q^{2}-Q^{2}_{\text{min}}\approx Q^{2} $ , they obtained$ \begin{aligned}[b] f_{\text{DZ}}^{\gamma}(y)=\;&\frac{\alpha_{\text{em}}}{2\pi}\frac{1+\left(1-y\right)^{2}}{y}\\ &\times\left(\ln A-\frac{11}{6}+\frac{3}{A}-\frac{3}{2A^{2}}+\frac{1}{3A^{3}}\right), \end{aligned} $

(52) where
$ A=\left(1+0.71\; \text{GeV}^{2}/Q^{2}_{\text{min}}\right) $ .$ f^{\gamma}_{\text{DZ}} $ has the appropriate proton electric form factor for describing the proton as a photon emitter. Because the WWA is often used in electroproduction processes, obtaining the proton spectrum from the electron spectrum by replacing$ m_{e} $ with$ m_{p} $ would overestimate the cross section. In Ref. [23], Drees, Ellis, and Zeppenfeld (DEZ) calculated the lead ion spectrum. Assuming$ y\ll1 $ ,$ Q^{2}_{\text{max}}\sim\infty $ ,$ C_{Pb}\left(Q^{2}\right)=0 $ , and$ D_{Pb}\left(Q^{2}\right)\approx \exp\left(-\dfrac{Q^{2}}{Q^{2}_{0}}\right) $ , they obtained$ \begin{aligned}[b] f_{\text{DEZ}}^{\gamma}(y)=\;&\frac{\alpha_{\text{em}}}{\pi}\left[-\frac{\exp(-Q^{2}_{\text{min}}/Q^{2}_{0})}{y}\right.\\ &+\left.\left(\frac{1}{y}+\frac{M^{2}}{Q^{2}_{0}}y\right)\Gamma\left(0,\frac{Q^{2}_{\text{min}}}{Q^{2}_{0}}\right)\right], \end{aligned} $

(53) where
$ Q^{2}_{\text{min}}=m^{2}_{Pb}y^{2} $ , and$ \Gamma(a,Q^{2}_{\text{min}}/Q^{2}_{0})=\int_{y}^{\infty}t^{a-1}{\rm e}^{-t}{\rm d}t $ is the incomplete Gamma Function. It should be noted that$ y\ll1 $ means$ Q^{2}_{\text{max}}\sim0 $ , which contradicts the assumption$ Q^{2}_{\text{max}}\sim\infty $ .Based on Eq. (52), Nystrand derived a modified photon spectrum for the proton that includes the
$ Q^{2}_{\text{min}} $ term in Eq. (50) [25]:$ \begin{aligned}[b] f_{\text{Ny}}^{\gamma}(y)=\;&\frac{\alpha_{\text{em}}}{2\pi}\frac{1+(1-y)^{2}}{y}\\ &\times\left[\frac{A+3}{A-1}\ln A-\frac{17}{6}-\frac{4}{3A}+\frac{1}{6A^{2}}\right]. \end{aligned} $

(54) Kniehl estimated the effect of including the magnetic form factor of the proton; the final expression
$ f^{\text{Kn}}(y) $ (Eq. (3.11) in Ref. [22]) is too long to include here but is discussed later in this paper.Another important approach for modeling the coherent photon spectrum is the semiclassical impact parameter description, which excludes hadronic interactions easily. The calculation of the semiclassical photon spectrum for electric dipole excitation (E1) is discussed in Ref. [63], yielding
$ \begin{aligned}[b] f_{\text{SC}}^{\gamma}(y)=\;&\frac{2Z^{2}\alpha_{\text{em}}}{\pi}\left(\frac{c}{\upsilon}\right)^{2}\frac{1}{y}\bigg\{\xi K_{0}(\xi)K_{1}(\xi)\\ &+\frac{\xi^{2}}{2}\left(\frac{\upsilon}{c}\right)^{2}\left[K^{2}_{0}(\xi)-K^{2}_{1}(\xi)\right]\bigg\}, \end{aligned} $

(55) where υ is the velocity of the point charge
$ Ze $ ,$ K_{0}(x) $ and$ K_{1}(x) $ are the modified Bessel functions, and$ \xi=\omega b_{\text{min}}/ \gamma_{L}v= b_{\text{min}}m_{A}y/v $ . Although the semi-classical photon spectrum is$ Q^{2} $ -independent, the boundary of y should be constrained by the coherence condition [3].Ref. [64] presented the photon spectrum inside a quark using Eq. (50) for ultra-incoherent photon emission. Neglecting the weighting factor in Eqs. (21) and (22) and setting
$ Q_{\text{min}}^{2}=1\; \text{GeV}^{2} $ and$ Q^{2}_{\text{max}}=\hat{s}/4 $ , one obtains$ \begin{align} f_{q}^{\gamma}(y)=e_{\alpha}^{2}\frac{\alpha_{\text{em}}}{2\pi}\frac{1+\left(1-y\right)^{2}}{y}\ln\frac{Q_{\text{max}}^{2}}{Q_{\text{min}}^{2}}. \end{align} $

(56) Finally, Brodsky, Kinoshita, and Terazawa calculated another important incoherent photon spectrum in Ref. [65], originally derived for e-p scattering:
$ \begin{aligned}[b] f_{\text{BKT}}^{\gamma}(y)=\; &\frac{e_{\alpha}^{2}\alpha_{\text{em}}}{\pi}\bigg\{\frac{1+\left(1-y\right)^{2}}{y}\left(\ln\frac{E}{m}-\frac{1}{2}\right)\\ &+\frac{y}{2}\left[\ln\left(\frac{2}{y}-2\right)+1\right]+\frac{\left(2-y\right)^{2}}{2y}\ln\left(\frac{2-2y}{2-y}\right)\bigg\}. \end{aligned} $

(57) In high-energy physics, the WWA is often used in studying hadronic interactions and heavy-ion collisions: Wangmei Zha et al. generalized the WWA to calculate the cross section and
$ p_{T} $ distribution of the Breit-Wheeler process in relativistic heavy-ion collisions and their dependence on the collision impact parameter$ (b) $ [66]. Based on the WWA, these author also analyzed gluon shadowing in heavy nuclei via the Bayesian Reweighting of coherent$ J/\psi $ photoproduction in UPCs [67]. The ATLAS collaboration studied exclusive muon pair production in the two-photon process [68]. d'Enterria and Silveira [69] proposed using equivalent photons from colliding lead ions to observe light-by-light scattering experimentally, and direct observations were made by the ATLAS [70] and CMS [71] collaborations using lead-lead collisions. Monte-Carlo event generators, such as Pythia [72] and STARlight [40], also utilize the WWA. Generally, particle production in hadronic collisions is modeled using the WWA [40, 42]. Although significant development has been achieved, the properties of the WWA in inelastic heavy quarkonium photoproduction in heavy-ion collisions has not been extensively studied, resulting in imprecise descriptions [13−28]. In particular, for ultrarelativistic heavy-ion collisions at LHC energies, the WWA becomes deterministic to the accuracy of describing photoproductions, since$ f_{\gamma}\propto Z^{2}\ln\sqrt{s}/m $ ,$ \sqrt{s} $ , and$ Z^{2} $ are significant factors at these energies. Therefore, we analyze the WWA for heavy-ion collisions at LHC energies and estimate the inaccuracies in the above spectra. -
We can now present the numerical results. For the calculations, we adopted the approximation
$ m_{q}=M_{H}/2 $ for the quark mass, where$ M_{H} $ is the mass of heavy quarkonium. All the masses were obtained from PDG [73]. We used$ m_{p}=0.938\; \text{GeV} $ ,$ \alpha_{\text{em}}=1/137.036 $ , and$ p_{T\text{min}}=M_{H} $ and the two-loop QCD coupling constant$ \alpha_{s} $ with$ n_{f}=3 $ and$ \Lambda=0.2\; \text{GeV} $ [74]. We used the MSHT20 LO (NLO) set for PDFs with$ n_{f}=3 $ [75], and the factorization scale was$ \mu=\sqrt{M_{H}^{2}+Q^{2}} $ . The LDMEs and completed kinematical relations are summarized in the Appendices.As an example, we used
$ J/\psi $ to evaluate the properties of the WWA in inelastic heavy quarkonium photoproduction in heavy-ion collisions. Hence, distributions in$ Q^2 $ , y, z, and$ \sqrt{s} $ are plotted in Figs. 5−8, where all the results are the sum of direct and resolved contributions and do not include fragmentation contributions. The left panels of Figs. 5−8 show the relative errors with respect to the exact results and the central and right panels show the exact cross sections in p-p and$\rm Pb $ -$\rm Pb $ collisions, respectively.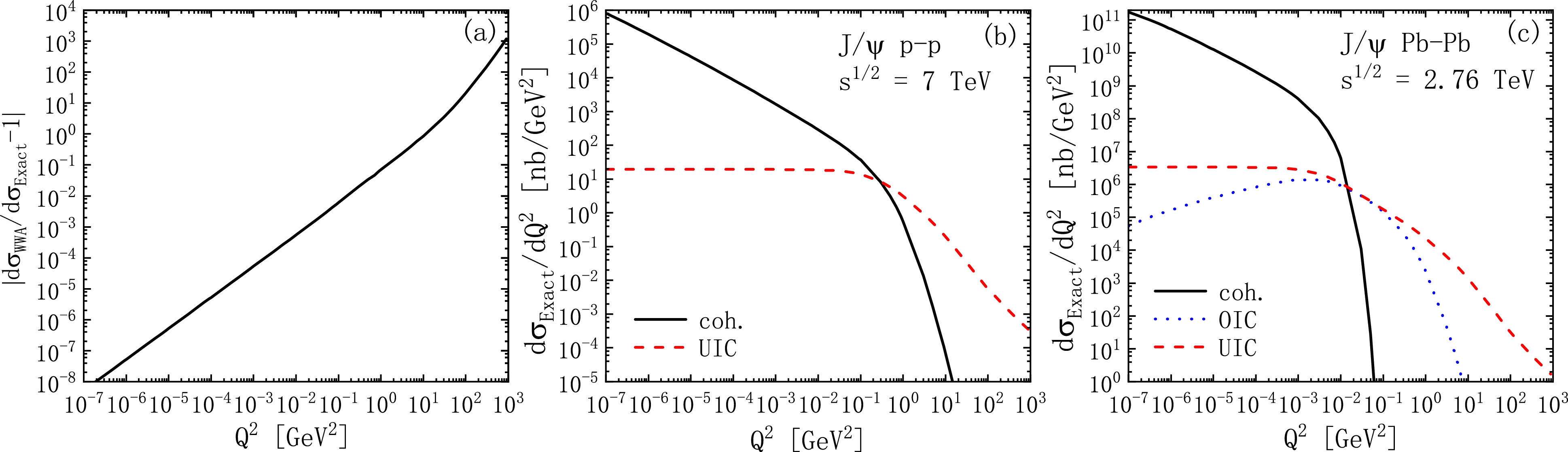
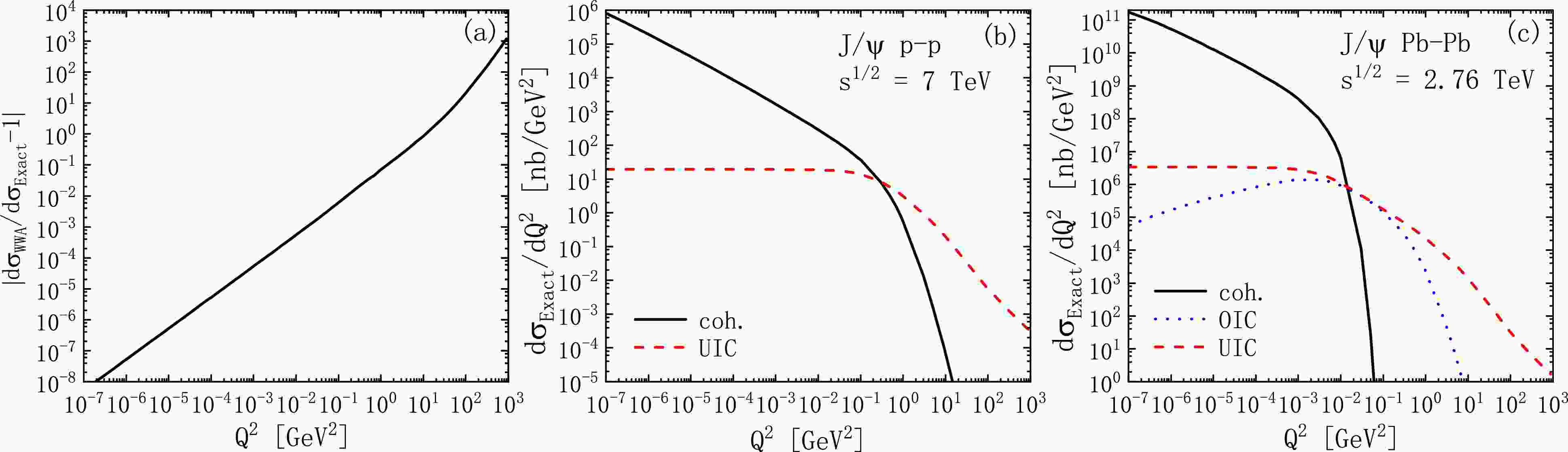
Figure 5. (color online)
$ Q^{2} $ distribution of the$ J/\psi $ photoproduction at LHC energies. (a): Relative error of the WWA with respect to the exact calculations. (b), (c): Exact results of the$ Q^{2} $ -dependent differential cross sections in p-p and$\rm Pb $ -$\rm Pb $ collisions, respectively. Black solid line − coherent-photon emission [coh.(dir.+res.)]. Red dashed line − ultra-incoherent photon emission [UIC (dir.+res.)]. Blue dotted line − ordinary-incoherent photon emission [OIC (dir.+res.)].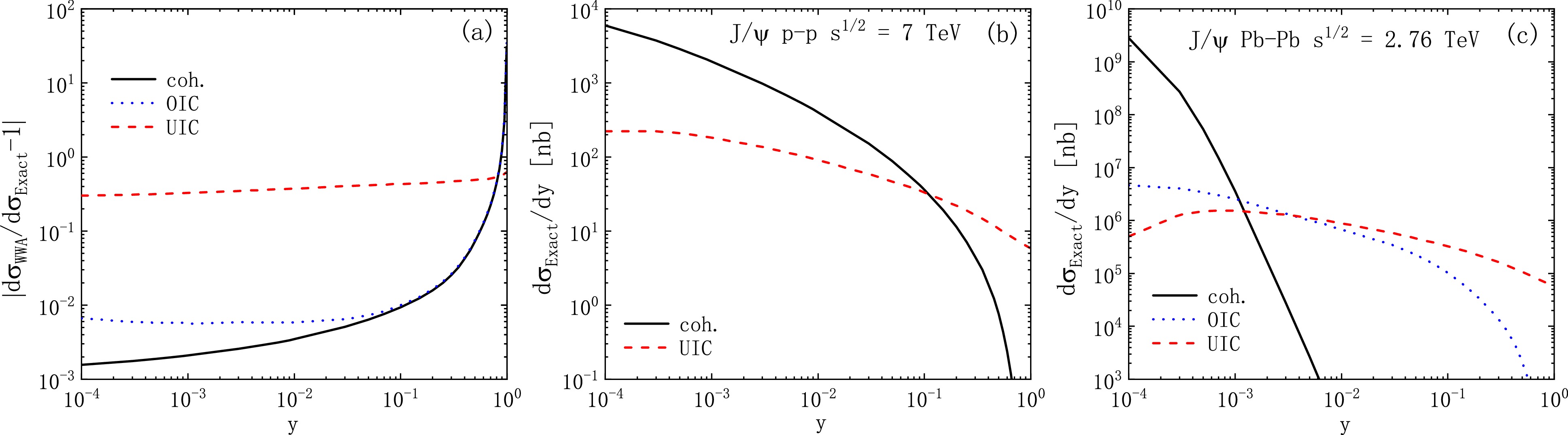
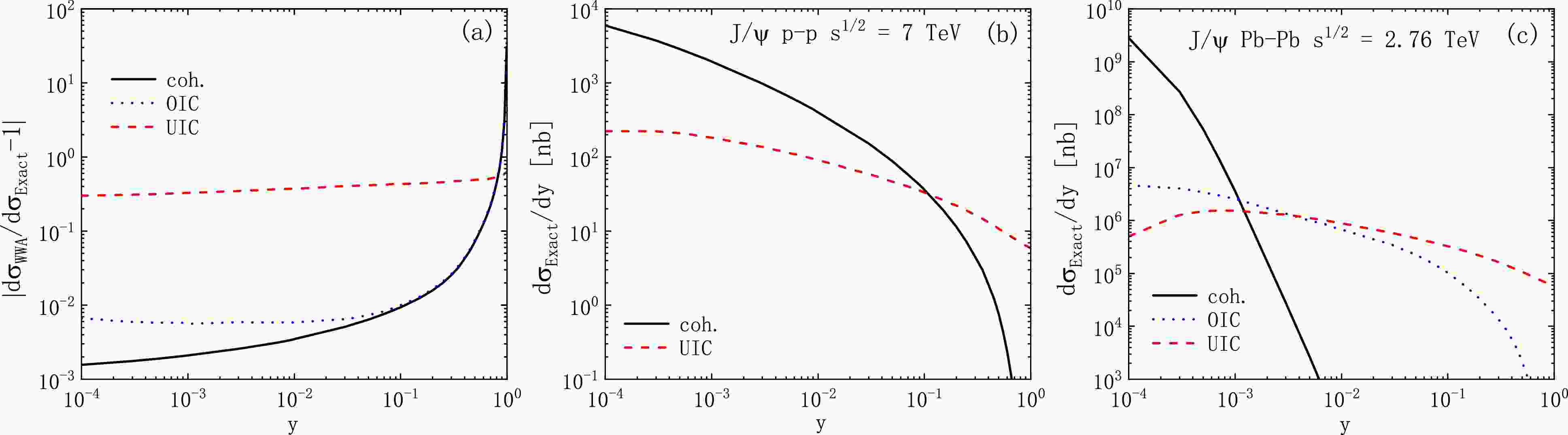
Figure 6. (color online) Same as Fig. 5 but for y distribution.
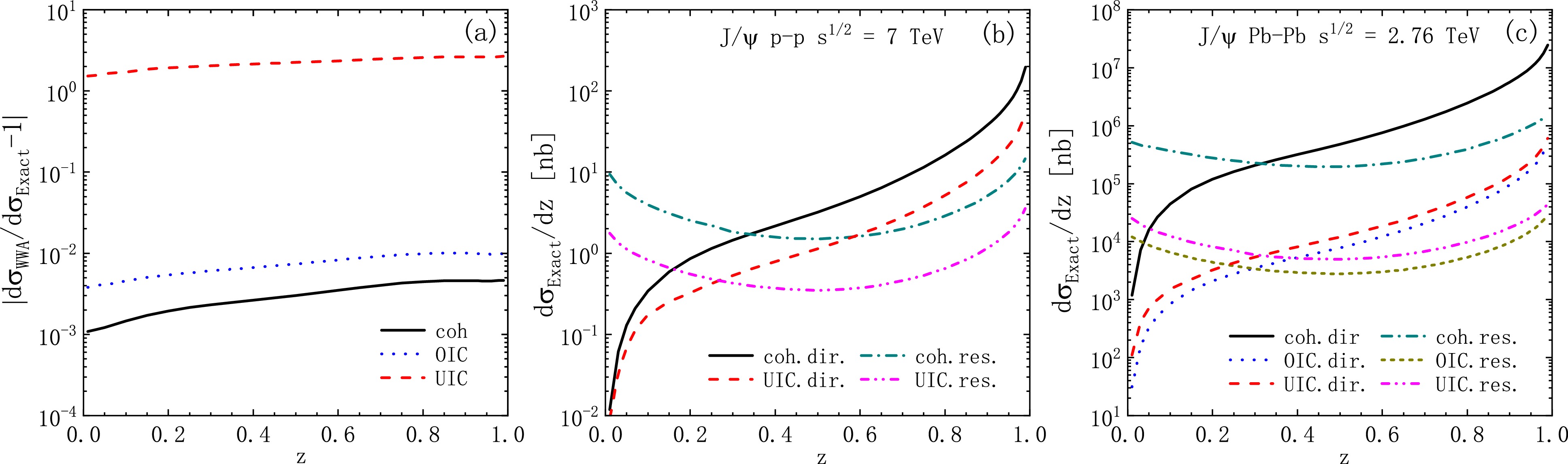
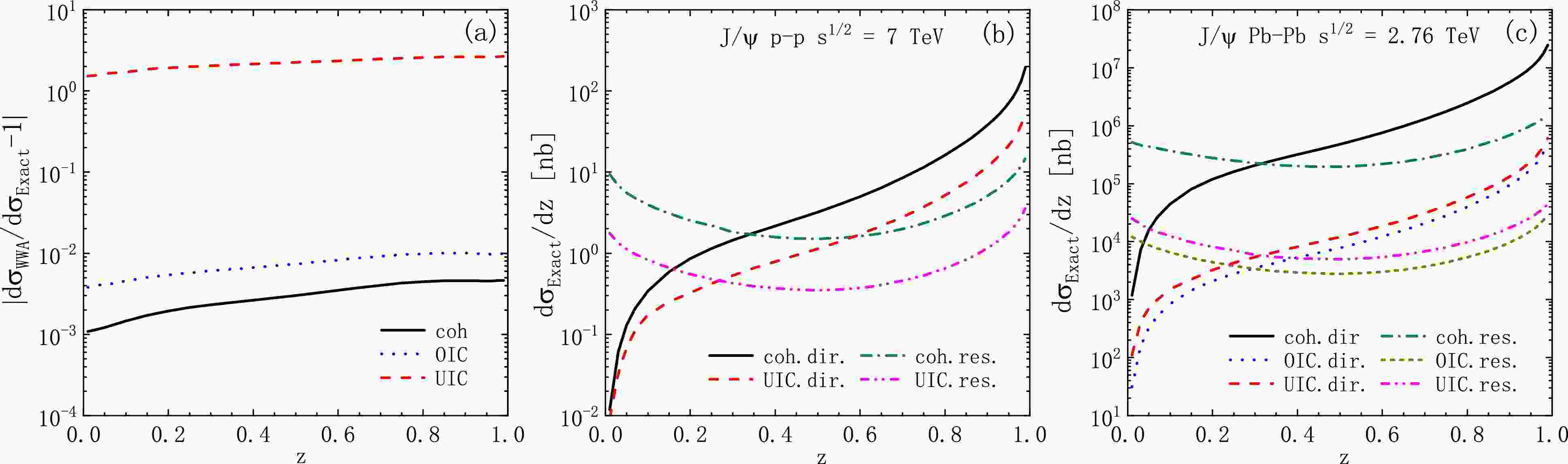
Figure 7. (color online) (a): Relative error of the WWA result with respect to the exact calculations. (b), (c): Exact results of
$ {\rm d}\sigma/{\rm d}z $ in p-p and$\rm Pb $ -$\rm Pb $ collisions. Black solid and dark cyan dot-dashed lines denote the coherent-direct and resolved photon emissions, respectively. Red dashed and magenta dot-dot dashed lines denote the ultra-incoherent direct and resolved photon emissions, respectively. Blue dotted and dark yellow short dashed lines denote the ordinary-incoherent direct and resolved photon emissions, respectively.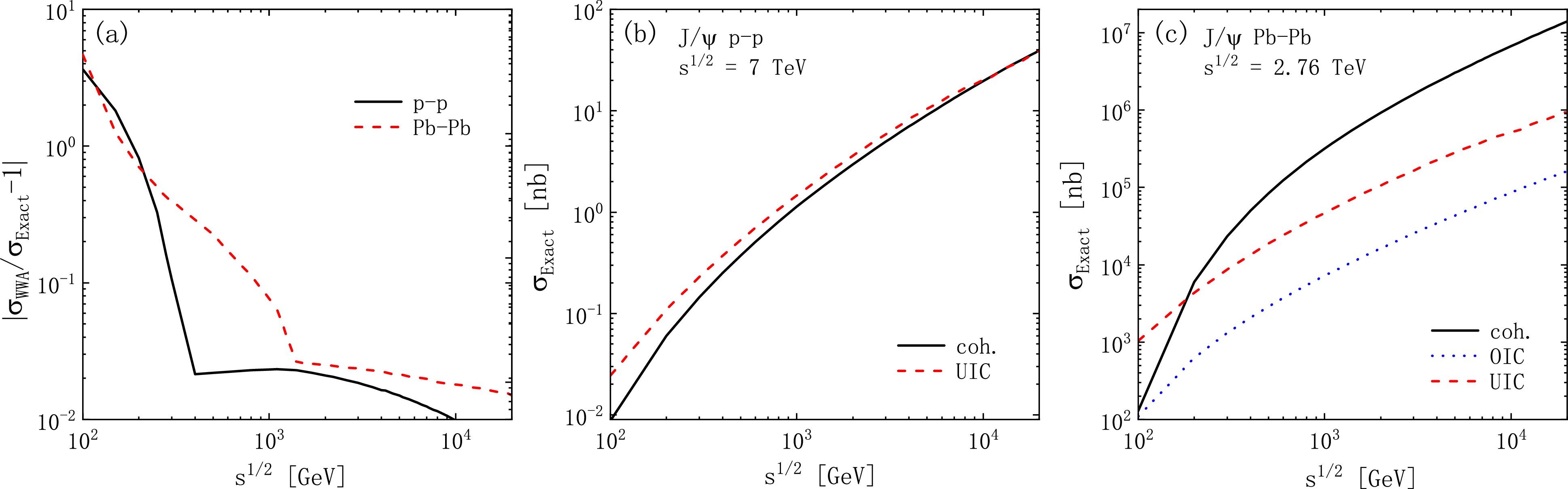
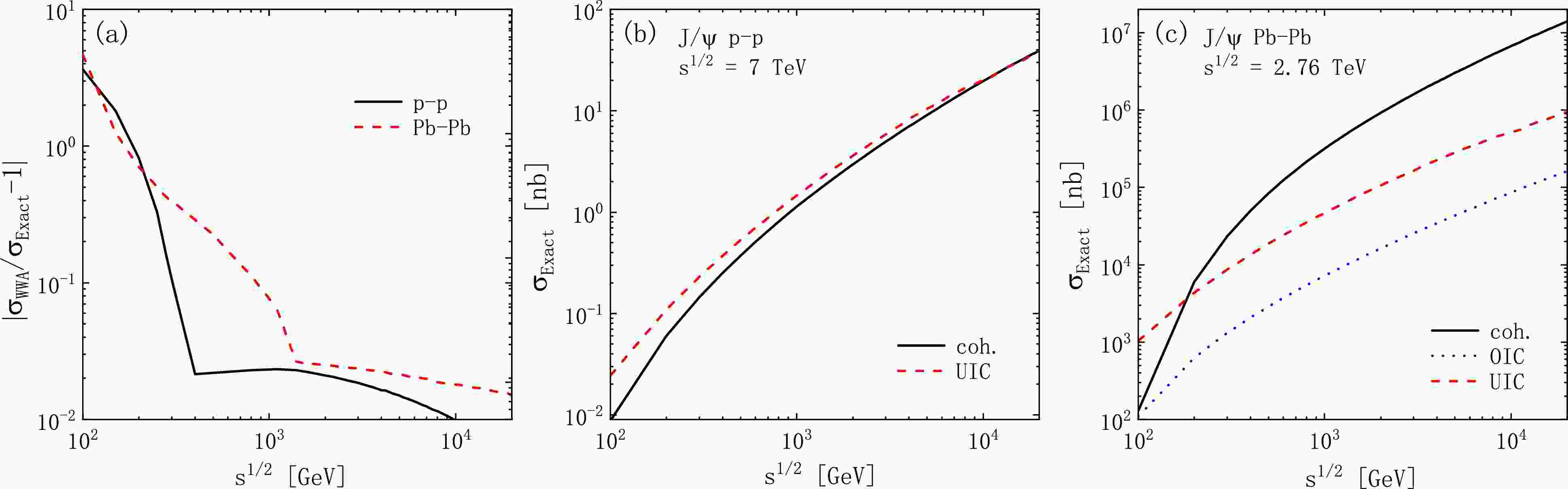
Figure 8. (color online) Same as Fig. 5 but for the total cross sections as a function of
$ \sqrt{s} $ .In Fig. 5, panel
$ (a) $ has a single curve since coh., OIC, and UIC produce coinciding curves. We observe that the relative error is negligible for small$ Q^{2} $ , non-negligible for$ Q^{2}\gtrsim1\; \text{GeV}^{2} $ , and grows rapidly for large$ Q^{2} $ . At$ Q^{2}=1\; \text{GeV}^{2} $ , the relative error is about 7%; at$ Q^{2}=10\; \text{GeV}^{2} $ , the error reaches 86%. Therefore, the WWA has good accuracy for very small$ Q^{2} $ , where the exact treatment recovers the WWA. For large$ Q^{2} $ , the WWA becomes inapplicable, with prominent deviation for$ Q^{2}>1\; \text{GeV}^{2} $ .In panels
$ (b) $ and$ (c) $ , the coherent and ultra-incoherent photon emissions dominate the small and large$ Q^{2} $ regions, respectively. They become comparable at$ Q^{2}=10^{-1} $ and$ 10^{-2}\; \text{GeV}^{2} $ in p-p and$\rm Pb $ -$\rm Pb $ collisions, respectively. We notice that, except for the region$ 10^{-2}<Q^{2}<10^{-1}\; \text{GeV}^{2} $ , the contribution of ordinary-incoherent photon emission is negligible compared with the contributions of the other two channels. According to panel$ (a) $ , the WWA is useful for coherent and ordinary incoherent-photon emissions. Notably, in$\rm Pb $ -$\rm Pb $ collisions, the WWA has a much higher accuracy for the coherent process, which approaches zero before$ Q^{2}=10^{-2}\; \text{GeV}^{2} $ , effectively avoiding errors due to the WWA. However, the WWA is not valid for ultra-incoherent photon emission, which is in the large$ Q^{2} $ domain, where the WWA has prominent errors.In Fig. 6, the results are expressed as a function of y. In panel (a), the curves of coh. and OIC share the same trend, and are consistent with each other in the large y domain. We find that
$ y=0.1 $ is a key point: when$ y<0.1 $ , the WWA results agree with the exact calculations for both channels, and the WWA has a better accuracy in the coherent process than in the OIC process (at$ y=10^{-4} $ , with deviations of about 1.6‰ and 6.7‰ in each case, respectively). However, when$ y>0.1 $ , the relative errors become prominent, with a pronounced peak near$ y=1 $ . Therefore, the WWA is only effective when$ y<0.1 $ and has evident errors for large y. Additionally, the relative error is large for the UIC process (about$ 0.3 $ −$ 0.6 $ ) for all y regions.In panels (b) and (c), the coherent processes dominate the very small y regions, this behaviour guarantees the accuracy of WWA. Conversely, the UIC contributions are predominantly from the regions
$ y>10^{-1} $ and$ y>10^{-3} $ in p-p and$\rm Pb $ -$\rm Pb $ collisions, respectively. Panel (a) demonstrates that the validity range of the WWA is compatible with the coh. and OIC processes. Notably, in$\rm Pb $ -$\rm Pb $ collisions, the WWA has a better accuracy for the coherent process since its contribution diminishes more rapidly. However, for the UIC process, the WWA is inapplicable for all y.In Fig. 7, we provide the cross section
$ {\rm d}\sigma/{\rm d}z $ vs z. Panel (a) shows us that the WWA is applicable for the coh. and OIC processes in the entire z range and has the highest accuracy for the coh. process (with deviations of about 1.1‰−4.7‰). In contrast, the deviations for the UIC process reach up to 153%−268% in the entire z range. Panels (b) and (c) show that the channels have different z behaviours. First, the resolved contributions dominate the lower z region and become smaller than those of the direct contributions when$ z>0.3 $ ; this feature agrees with the traditional perspective that the resolved process has significant contributions only for$ z\leq0.3 $ [76]. Second, the results are divergent near the endpoint$ z=1 $ , mainly owing to the color-octet$ ^{1}S_{0} $ and$ ^{3}P_{J} $ processes. This is because, in the region$ z\lesssim1 $ , where diffractive production occurs, the NRQCD prediction breaks down, and the color-octet channels exhibit collinear singularities. To screen the collinear singularities and suppress elastic production, traditional methods impose the following constraints:$ z<0.9 $ ,$ M_{X'}>10 $ GeV and$ p_{T}>1\; \text{GeV} $ or$ M_{J/\psi} $ (actually, if$ p_{T\; \text{min}}\neq0 $ ,$ z_{\text{max}} $ will naturally less than one). Elastic production at$ z\lesssim1 $ can also be suppressed by choosing a sufficiently large$ Q^{2} $ [26]. However, the bulk of the inelastic contribution would be sacrificed. Finally, the coherent contributions are larger than those of the UIC processes in the entire z range. In particular, for$\rm Pb $ -$\rm Pb $ collisions, the coherent contribution dominates the entire z region, exceeding the contributions of the other channels by approximately an order of magnitude. This dominance is becuase the equivalent photon flux scales as$ Z^{2} $ , which significantly enhances the cross section.Figure 8 shows the total cross section distributions in terms of
$ \sqrt{s} $ . In panel (a), the curves of coh. and OIC are consistent with each other. We do not show the curve of the UIC process, where the deviation is$ 0.38 $ −$ 0.49 $ in the whole$ \sqrt{s} $ range. The curves increase significantly for$ \sqrt{s}<400 $ and$ 1400\; \text{GeV} $ in p-p and$\rm Pb $ -$\rm Pb $ collisions, respectively, and decrease slowly with$ \sqrt{s} $ . The curves exhibit a trend similar to that reported by Kniehl [22]. Therefore, the WWA has significant errors for small$ \sqrt{s} $ (RHIC energies) and has good accuracy at high energies (LHC energies). In panels (b) and (c), the coherent process is slightly smaller than the UIC one in p-p collisions. The opposite is observed for$\rm Pb $ -$\rm Pb $ collisions, where the coherent process becomes critical (it is about one and two orders of magnitude larger than the OIC and UIC processes, respectively). This is because the coherent process scales with$ Z^{2} $ , whereas the OIC and UIC processes scale approximately with Z and$ N_{A} $ , respectively. For$ Z\gg1 $ , the coherent part dominates the production processes. Based on observations from the left panel and previous discussions, we can deduce that the WWA can have high accuracy in the high energy range and in$\rm Pb $ -$\rm Pb $ collisions, where the UIC contribution is significantly suppressed; however, it is not a good approximation in p-p collisions, where the UIC contribution is comparable the coherent contribution.In the discussions of [Figs. 5−8], we obtained the validity range of the WWA. These discussions suggest that kinematical boundaries are crucial for accuracy when deriving equivalent photon spectra based on the WWA.Tables 1−3 list the total cross sections and allow us to discuss the accuracies of the WWA and sources of errors for the widely employed photon spectra mentioned in Section III. In p-p collisions [Table 1], the relative error of
$ f^{\gamma}_{\text{DZ}} $ is the largest because integration is performed in the entire kinematical range that is allowed:$ Q^{2}_{\text{max}}=\infty $ and$ y_{\text{max}}=1 $ . From Figs. 5 and 6, the$ Q^{2}>1\; \text{GeV}^{2} $ and$ y>0.1 $ domains can produce large fictitious contributions. The$ f^{\gamma}_{\text{Ny}} $ spectrum has visibly less deviations than the$ f^{\gamma}_{\text{DZ}} $ spectrum because it includes the$ Q^{2}_{\text{min}} $ term in Eq. (50) and$ f^{\gamma}_{\text{DZ}} $ does not. This term is inversely proportional to$ Q^{4} $ and has a noticeable effect in the small$ Q^{2} $ region that cannot be neglected when calculating the photon spectra; this perspective agrees with the findings of Kniehl [22]. The relative error of$ f^{\gamma}_{\text{Kn}} $ is higher than that of$ f^{\gamma}_{\text{Ny}} $ but lower than that of$ f^{\gamma}_{\text{DZ}} $ because the proton magnetic form factor is included, and its effects are noticeable in the large$ Q^{2} $ range and should be essentially excluded [56]. Finally, the modified proton spectra$ f^{\gamma}_{\text{MD}} $ agrees well with the exact results ($ \delta\sim1 $ %). This is becuase of two reasons:$ f^{\gamma}_{\text{MD}} $ is derived from the complete form Eq. (47) that includes the$ Q^{2}_{\text{min}} $ term and properly excludes the effects of the magnetic form factor. It adopts the coherence condition, where the wavelength of the photon is larger than the size of the nucleus, and the charged constituents inside the nucleus are coherent. This condition effectively reduces errors in the WWA. There are also other limitations that can achieve such high accuracy. However, the key point is that, in most physically interesting cases, a dynamical cutoff exists, causing the photo-absorption cross sections to differ slightly from their values on the mass shell. Further details can be found in Ref. [48].coh.(dir.+res.) Exact $ f_{\text{DZ}}^{\gamma} $ 

$ f_{\text{Ny}}^{\gamma} $ 

$ f_{\text{Kn}}^{\gamma} $ 

$ f_{\text{SC}}^{\gamma} $ 

$ f_{\text{MD}}^{\gamma} $ 

$\sigma /\text{nb}$ 

22.4241 43.3561 35.1059 39.9058 20.3327 22.6512 δ (%) 0.00 93.35 56.55 77.96 9.33 1.01 Relative error with respect to the exact result: $ \delta=|\sigma/\sigma_{\text{Exact}}-1| $ .

Table 1.
$ J/\psi $ photoproduction in the coherent-photon emission channel in p-p collisions [$ 7\; \text{TeV} $ ].coh.(dir.+res.) Exact $ f_{\text{DEZ}}^{\gamma} $ 

$ f_{\text{SC}}^{\gamma} $ 

$\sigma /\text{mb}$ 

2.4854 18.9783 1.9274 $ \delta ( $ %

$) $ 

0.00 663.59 22.45 Table 2. Same as Table 1 but in
$\rm Pb $ -$\rm Pb $ collisions [$ 2.76\; \text{TeV} $ ].$ \sigma_{\text{UIC (dir.+res.)}.} $ 

Exact $ f_{q}^{\gamma} $ 

$ f_{\text{BKT}}^{\gamma} $ 

$ \sigma_{pp}/\text{nb} $ 

24.2773 39.2290 101.3291 $ \delta_{pp} ( $ %

$) $ 

0.00 61.59 317.38 $ \sigma_{\rm PbPb}/\text{mb} $ 

0.2494 0.6023 0.7254 $ \delta_{\rm PbPb}( $ %

$ ) $ 

0.00 141.51 190.87 Table 3. Same as Table 1 but for ultra-incoherent photon emission in p-p [
$ 7\; \text{TeV} $ ] and$\rm Pb $ -$\rm Pb $ [$ 2.76\; \text{TeV} $ ] collisions.In
$\rm Pb $ -$\rm Pb $ collisions [Table 2], the deviation of$ f^{\gamma}_{\text{DEZ}} $ reaches up to 680.19%, since$ f^{\gamma}_{\text{DEZ}} $ is constructed on a contradictory assumption:$ Q^{2}_{\text{max}}\sim\infty $ and$ y\ll1 $ (actually,$ Q^{2}_{\text{max}}\sim\infty $ is equivalent to$ y_{\text{max}}\sim1 $ ). The$ f^{\gamma}_{\text{SC}} $ spectrum roughly agrees with the exact results obtained in both the p-p and$\rm Pb $ -$\rm Pb $ collisions. However, it has deviations that are non-negligible. This is because$ f^{\gamma}_{\text{SC}} $ is calculated from the semiclassical impact parameter description, where the coherence condition is assumed. For$ f^{\gamma}_{\text{SC}} $ , setting$ y_{\text{max}}=1 $ causes errors in the results.For ultra-incoherent photon emission [Table 3], the deviations are prominent and become serious in
$\rm Pb $ -$\rm Pb $ collisions. This quantitatively verifies the inapplicability of the WWA for the UIC process. In particular,$ f^{\gamma}_{\text{BKT}} $ has the largest errors because it was originally derived from e-p scattering but is expanded to describe the probability of finding a photon in any relativistic fermion [20−22], which causes the overestimation of the cross sections. Therefore, the UIC process should be treated with the exact approach, and the results in Refs. [13−28] are not sufficiently accurate, where the mentioned spectra are adopted and serious double counting is present.Next, in Table 4, we estimate the contributions of the UIC channel to heavy quarkonium photoproduction, and discuss the double counting encountered in most studies when different photon emissions are considered simultaneously. In p-p collisions, the outcomes of the UIC process are comparable to those of coh. process for
$ J/\psi $ and become about twice those of the coh. process for$ \Upsilon(1S) $ . In$\rm Pb $ -$\rm Pb $ collisions, the ratio of UIC to coh. is about 10% for$ J/\psi $ and about 29% for$ \Upsilon(1S) $ . Therefore, the UIC channel plays an important role in p-p collisions and meaningfully contributes to$\rm Pb $ -$\rm Pb $ collisions. In addition, the relative contribution of the UIC channel to inelastic heavy quarkonium photoproduction becomes much more obvious for increasing quarkonium mass.Exact Quarkonium coh. UIC Total Total (NWF) $\sigma_{pp}/\text{nb}$ 

$ J/\psi $ 

22.4241 24.2773 46.7014 103.9845 $\sigma_{\rm PbPb}/\text{mb}$ 

$ J/\psi $ 

2.4854 0.2494 2.7348 3.1055 $\sigma_{pp}/\text{pb}$ 

$ \Upsilon(1S) $ 

13.6794 26.9652 40.6446 82.6189 $\sigma_{\rm PbPb}/\mu\text{b}$ 

$ \Upsilon(1S) $ 

0.7345 0.2113 0.9458 1.1262 Table 4. Exact results of the
$ J/\psi $ and$ \Upsilon(1S) $ photoproductions in p-p [$ 7\; \text{TeV} $ ] and$\rm Pb $ -$\rm Pb $ [$ 2.76\; \text{TeV} $ ] collisions. All the results are the sum of the direct and resolved contributions and do not include fragmentation contributions.In contrast,Table 4 shows that double counting is a serious issue. The total results with no weighting factor (NWF) are much larger than those of the exact treatment. These large fictitious contributions are mainly from the region with low
$ Q^{2} $ . Traditionally, these unphysical results are excluded using the cutoff$ Q^{2}>1\; \rm{GeV^{2}} $ when calculating the equivalent photon spectra. As in calculating$ f_{q}^{\gamma} $ [Eq. (56)], the cutoff is adopted to replace the remaining probability factor "$ 1-w_{\text{coh}} $ ." However, the corresponding errors in Table 3 remain significant. Therefore, when different photon emissions are considered simultaneously, each channel should be multiplied by the probability or weighting factor to avoid double counting.Now, we study the contribution of photoproduction processes to the heavy quarkonium production in p-p and
$\rm Pb $ -$\rm Pb $ collisions at LHC energies. Before the discussion, one critical issue must be addressed: heavy quarkonium production in hadronic collisions (especially$\rm Pb $ -$\rm Pb $ ) are spatially limited, with a collision parameter range within$ 2R_{A} $ (where$ R_{A}=A^{1/3}1.2\; \text{fm} $ is the size of the nucleus). When considering the contribution of photonproduction to the hadronic process, the equivalent photon flux should be integrated to$ b_{ \text{max}}=2R_{A} $ . Integrating to infinity artificially enhances the cross section by including unphysical contributions from non-overlapping nuclei at large, violating the spatial constraints of the collision geometry. However, in this study, we performed the calculations and developed our formalism based on the parameterized form factor method, which do not explicitly include impact parameter b (where the form factor is derived from the Fourier transform of the charge density ρ of the nucleus, and approximate plane waves are used). For the consistency of our formalism, we adopted the empirical approximation to include these truncation effects, similar to the approach in literature [3, 4, 63]. The effect of setting$ b_{ \text{max}}=2R_{A} $ is evident in the$ Q^{2}_{ \text{min}} $ cut; details are given in Appendix B. The strict method to incorporate b is the semiclassical impact parameter description, which is better applicable for calculations with heavy ion collisions and is often used in the study of UPCs (recently, Wangmei Zhang et al. developed a spatially-dependent photon flux distribution and established a more precise relationship between the photon transverse momentum distribution and collision impact parameter [45]).In Figs. 9 and 10, we adopt the exact treatment to plot the
$ p_{T} $ distributions of charmonium ($ J/\psi $ ,$ \psi(2S) $ ) and bottomonium ($ \Upsilon(nS) $ ) photoproduction, respectively. The results are the sum of the direct and resolved photon contributions. To visualize the photoproduction contribution and study the$ p_{T} $ behaviour of each photon source, we plot Figs. 9 and 10 in different$ p_{T} $ ranges that complement each other. In Fig. 9, we plot the$ p_{T} $ distribution of charmonium in the range of$ 2\; \text{GeV}<p_{T}<20\; \text{GeV} $ . Fragmentation mechanism is unreliable for this$ p_{T} $ range because the LP and NLP contributions are significant for$ p_{T}\gg m_{H} $ (authors in Ref. [32, 34] have shown that the NLO LP SDCs are different from the accurate NLO fixed-order SDCs for small$ p_{T} $ ; they have suggested the criterion$ p_{T}>3M_{J/\psi}\simeq 10\; \text{GeV} $ to ensure the validity of the fragmentation mechanism and suppress NLP contributions). To consider the NLO effects, the LO results are multiplied by the K factor from Ref. [77]. We choose$ K=1.8 $ and$ 1.3 $ for direct and resolved contributions, respectively. The spectra of photoproductions are compared to the hard scattering of initial partons. In panels (a) and (c), we compare the results with data from the CMS Collaboration [78]. At very small$ p_{T} $ , the color-singlet and color-octet distributions are corrupted by collinear divergences and soft gluon effects [31]. Since the intrinsic motion of incident partons renders the differential cross section uncertain for$ p_{T}\leq2\; \text{GeV} $ , our predictions only concern the range$ p_{T}\geq2\; \text{GeV} $ .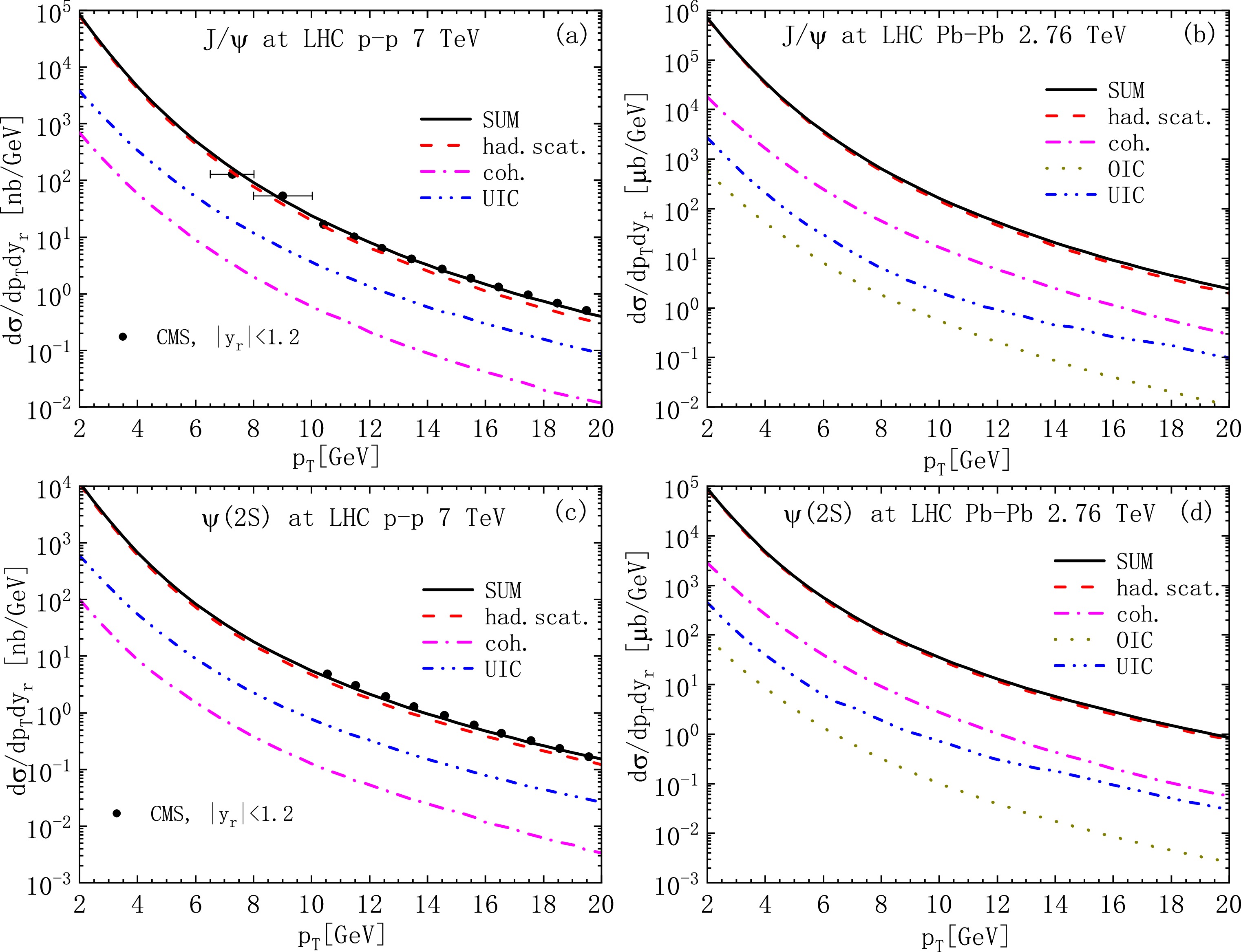
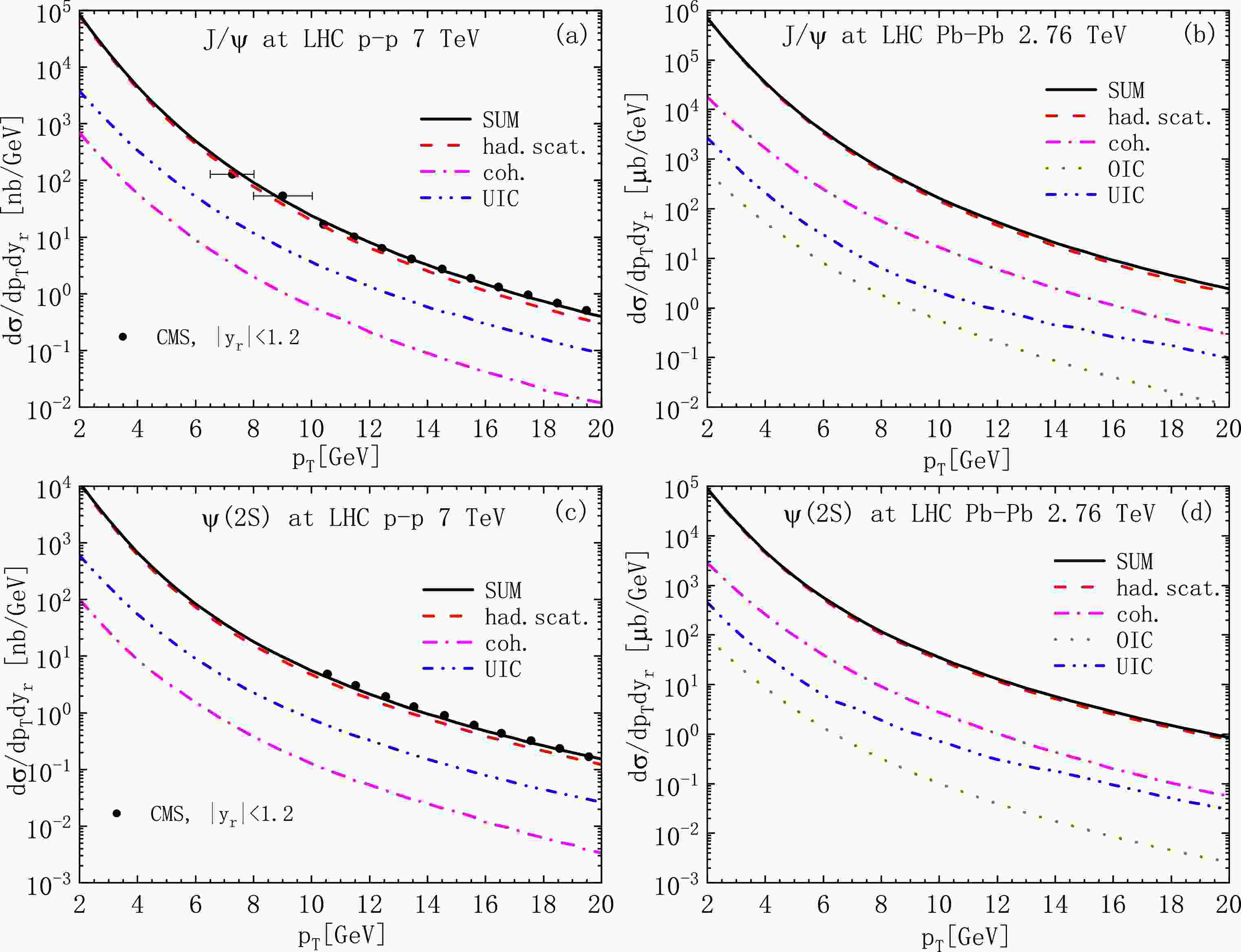
Figure 9. (color online)
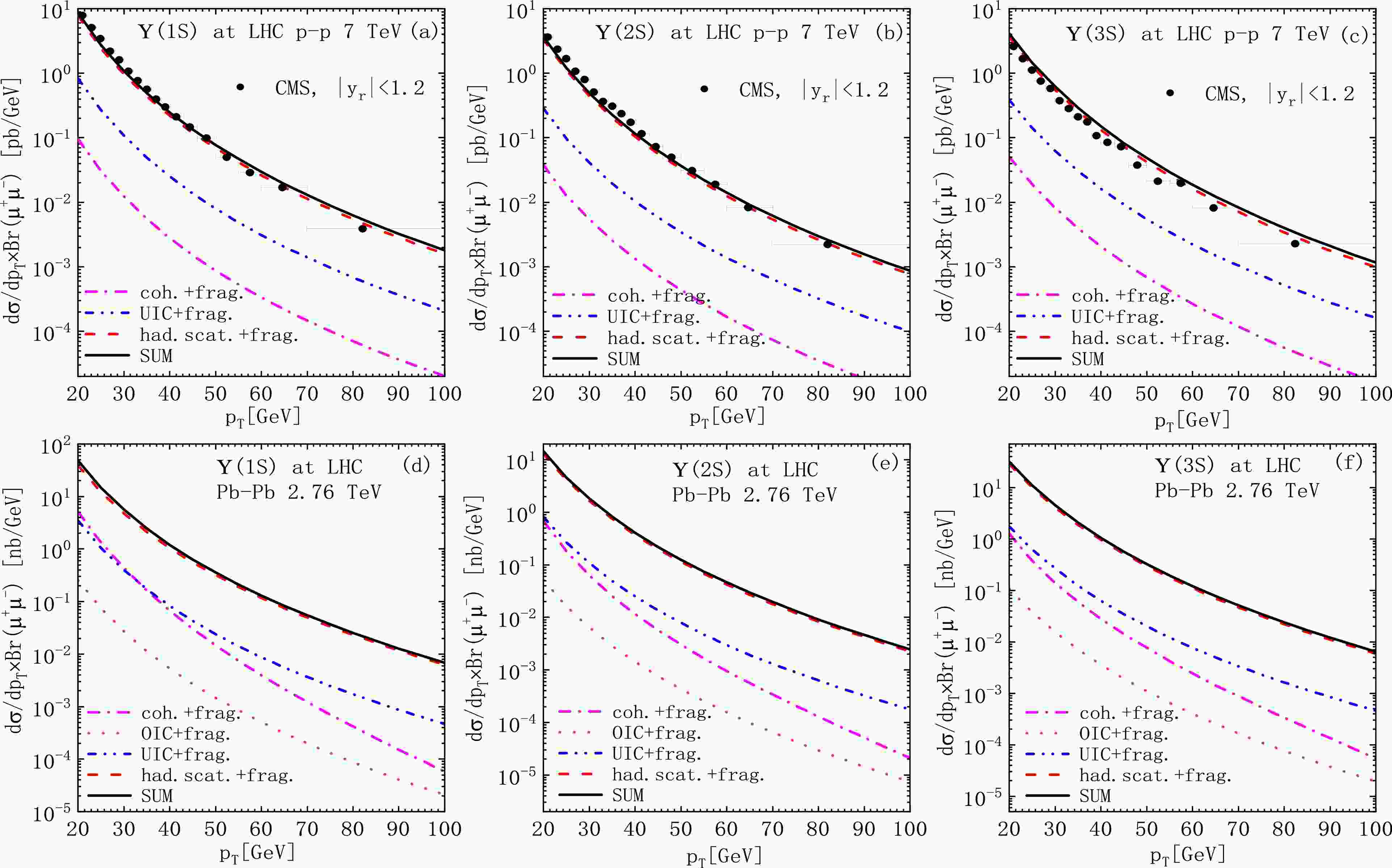
$ p_{T} $ distribution of$ J/\psi $ and$ \psi(2S) $ photoproductions in p-p and$\rm Pb $ -$\rm Pb $ collisions. The red dashed line represents the initial parton hard scattering (had.scat.). The magenta dot-dashed line is for coherent-photon emissions [coh.(dir.+res.)]. The blue dot-dashed line represents ultra-incoherent photon emissions [UIC (dir.+res.)]. The dark yellow dotted line represents the ordinary-incoherent photon emissions [OIC (dir.+res.)]. The black solid line is for the sum of had.scat. and photoproduction processes. The$ J/\psi $ and$ \psi(2S) $ data are from the CMS collaboration [78]. The rapidity$ y_{r} $ is integrated over the experimental range$ |y_{r}|<1.2 $ .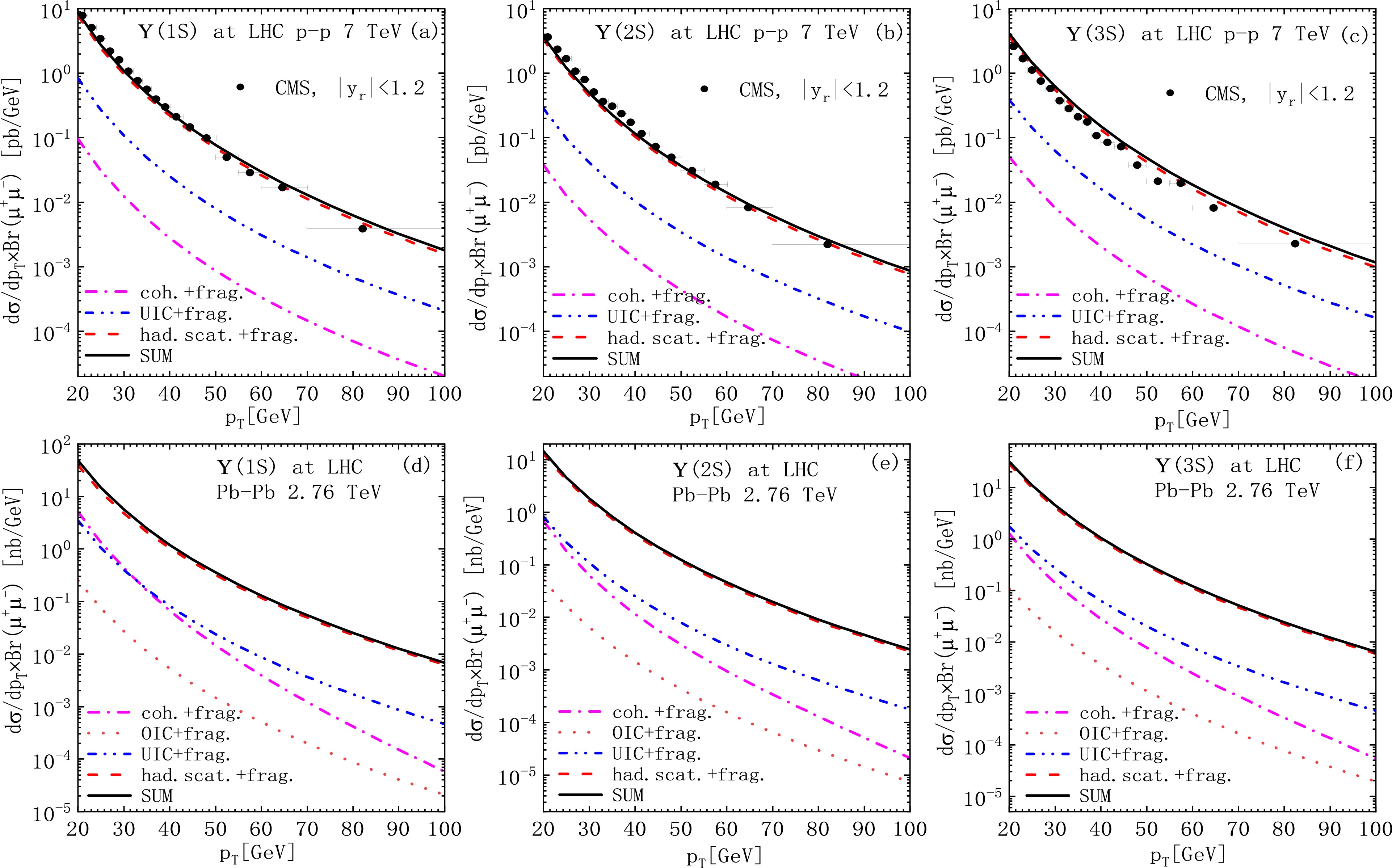
Figure 10. (color online) Same as Fig 9 but for
$ \Upsilon(nS) $ production. All the results are the sum of direct and fragmentation$ \Upsilon(nS) $ productions. The branching fractions are$ B_{r}(\Upsilon(1S)\rightarrow \mu^{+}\mu^{-})=2.48 $ %,$ B_{r}(\Upsilon(2S)\rightarrow \mu^{+}\mu^{-})=1.93 $ %, and$ B_{r}(\Upsilon(3S)\rightarrow \mu^{+}\mu^{-})=2.18 $ %. The$ \Upsilon(nS) $ data are from the CMS collaboration [79]. The rapidity$ y_{r} $ is integrated over the experimental range$ |y_{r}|<1.2 $ .In p-p collisions [panels (a), (c)], the UIC processes have greater contributions than the coh. processes, which confirms the significance of the UIC channel in p-p collisions. However, the coh. contributions are still comparable with the UIC contributions (
${\rm d}\sigma_{\text{coh.}}/{\rm d}\sigma_{\text{UIC}}\sim0.18- 0.13$ in the$ p_{T} $ ranges considered). This differs from the results in Ref. [18], where the coh. contributions are neglected. In$\rm Pb $ -$\rm Pb $ collisions [panels (b), (d)], the coh. contributions are larger than the UIC contributions because the former contributions scale with$ Z^{2} $ , whereas the latter contributions scale with$ N_{A} $ . We disagree with the results in Refs. [20, 21], where the observation is opposite to that of ours: the UIC contributions are approximately an order of magnitude larger than the coh. contributions. Finally, we notice that the charmonium photoproduction processes provide valuable corrections to had.scat. when$ p_{T}>4\; \text{GeV} $ . These corrections become more evident with increasing$ p_{T} $ . The corrections are more pronounced in$\rm Pb $ -$\rm Pb $ collisions than in p-p collisions. This is also different to the the results in Refs. [20, 21], where the contribution of photoproduction is even larger than that of the hadronic process. This is because they did not use the cut$ b_{ \text{max}}=2R_{A} $ , which artificially enhances the cross section by including unphysical contributions from non-overlapping nuclei at large. This cut excludes the large contribution from the small$ Q^{2} $ region [see Fig. 5], making the coherent contribution much smaller (for the incoherent channel, this cut has only small effects).Figure 10 shows the plots of the exact results of bottomonium (
$ \Upsilon(nS) $ ) photoproduction and fragmentation. To avoid double counting, we adopt the BCCKL method, where a matching rule is applied between the fixed-order and fragmentation [32−34]. Since fragmentation bottomonium production is unreliable in the$ p_{T}<15\; \text{GeV} $ range [31], to suppress the next to leading power (NLP) contributions, our theoretical predictions were for$ p_{T}>20\; \text{GeV} $ . In the top panels, the exact results are compared to the CMS data [79]. For p-p collisions [panels (a)-(c)], the differences between the UIC and coh. processes become much larger than those of$ J/\psi $ productions in Fig. 9. For$\rm Pb $ -$\rm Pb $ collisions [panels (d)-(f)], the UIC channel becomes larger than the coh. channel at sufficiently large$ p_{T} $ values. This observation is opposite to that in panels (b) and (d) in Fig. 9. We disagree with the results in Ref. [21], where the UIC contributions are much larger than the coh. contributions in the entire$ p_{T} $ range; moreover, the fragmentation formalism is used beyond its validity scope, and double counting is present. Thus, the relative contribution of the UIC channel to heavy quarkonium photoproduction increases with the quarkonium mass. The UIC process begins to dominate the photoproduction processes at large$ p_{T} $ values. Finally, we find that the contributions of the photoproduction and fragmentation processes are still non-negligible in bottomonium production. -
Using the NRQCD framework, we studied the production of heavy quarkonium originating from inelastic photoproduction and fragmentation processes in p-p and
$\rm Pb $ -$\rm Pb $ collisions at LHC energies. We derived an exact treatment by performing a consistent analysis of the terms neglected in transiting from the exact formula to the WWA one, where the Martin-Ryskin method is adopted to weight the different photon sources, and the BCCKL method is adopted to match the fixed-order and fragmentation contributions. The full partonic kinematics matched with the exact treatment were also given. Through a comprehensive discussion of the$ Q^{2} $ -, y-, z-, and$ \sqrt{s} $ -dependence behaviours of cross sections, we obtained the features of the WWA in inelastic heavy quarkonium photoproductions in heavy-ion collisions. To estimate errors in the widely employed photon spectra, we calculated their total cross sections. Meanwhile, double counting problems and the relative contributions of the ultra-incoherent channel were also discussed. Finally, we calculated$ p_{T} $ -dependent cross sections to discuss the contributions of photoproduction and fragmentation processes to inelastic heavy quarkonium production.The inelastic photoproduction and fragmentation processes provide valuable contributions to heavy quarkonium production, especially in the large
$ p_{T} $ range. While ultra-incoherent photon emission plays an essential role in p-p collisions and can provide meaningful contributions in$\rm Pb $ -$\rm Pb $ collisions, its relative contribution to inelastic heavy quarkonium photoproduction rapidly increases with the quarkonium mass and begins to dominate the photoproduction process at large$ p_{T} $ ranges.The validity scopes of the WWA in the processes discussed in this study are highly restricted and are compatible with the characteristics of the coh. and OIC processes. They are accurate only in the ranges of
$ Q^{2}< 1\; \text{GeV}^{2} $ ,$ y<0.1 $ ,$ Z\gg1 $ , and$ \sqrt{s}>400 $ and$ 1400\; \text{GeV} $ in p-p and$\rm Pb $ -$\rm Pb $ collisions, respectively. In particular, the WWA has a much higher accuracy in$\rm Pb $ -$\rm Pb $ collisions, where the coh. process is enhanced by$ Z_{Pb}^{2} $ and the UIC process is greatly suppressed. Conversely, the kinematic behavior of the UIC process contradicts that of the WWA, as it is concentrated in regions where the WWA exhibits significant errors. Therefore, the WWA is not a suitable approximation in p-p collisions, where UIC contributions become dominant. Furthermore, we found that the aforementioned equivalent photon spectra are generally derived beyond the applicable scope of the WWA, and considering different channels simultaneously causes serious double counting. Indeed, the exact treatment is necessary to accurately address inelastic heavy quarkonium photoproduction in p-p and$\rm Pb $ -$\rm Pb $ collisions at LHC energies.It should be noted that, when considering the contribution of photonproduction to the hadronic process, the equivalent photon flux should be integrated to
$ b_{ \text{max}}=2R_{A} $ . Integrating to infinity artificially enhances the cross section by including unphysical contributions from non-overlapping nuclei at large. In this study, we adopt an empirical approximation to account for the truncation effect. The proper method to incorporate b is the semiclassical impact parameter description (Glauber model), which is more appropriate for calculating heavy ion collisions (recent study, see Ref. [45]). In future studies, we shall conduct investigations within a b-dependent framework. -
For the reader's convenience and for completeness, this section lists the involved LDMEs. The masses of heavy quarkonia are
$ M_{J/\psi}=3.097\; \text{GeV} $ ,$ M_{\psi(2S)}= 3.686\; \text{GeV} $ ,$ M_{\Upsilon(1S)}=9.460\; \text{GeV} $ ,$ M_{\Upsilon(2S)}=10.023\; \text{GeV} $ , and$ M_{\Upsilon(3S)}= 10.355 \; \text{GeV} $ [73]. The LDMEs of the charmonium are given by [77−81]$ \begin{aligned}[b] & \langle{\cal{O}}^{J/\psi}[^{3}S_{1}^{(1)}]\rangle=1.32\; \text{GeV}^{3},\\ & \langle{\cal{O}}^{J/\psi}[^{1}S_{0}^{(8)}]\rangle=(4.50\pm0.72)\times10^{-2}\; \text{GeV}^{3},\\ & \langle{\cal{O}}^{J/\psi}[^{3}S_{1}^{(8)}]\rangle=(3.12\pm0.93)\times10^{-3}\; \text{GeV}^{3},\\ & \langle{\cal{O}}^{J/\psi}[^{3}P_{0}^{(8)}]\rangle=(-1.21\pm0.35)\times10^{-2}\; \text{GeV}^{5}, \end{aligned} $

(A1) $ \begin{aligned}[b] & \langle{\cal{O}}^{\psi(2S)}[^{3}S_{1}^{(1)}]\rangle=0.76\; \text{GeV}^{3},\\ & \langle{\cal{O}}^{\psi(2S)}[^{1}S_{0}^{(8)}]\rangle=(0.0080\pm0.0067)\; \text{GeV}^{3},\\ & \langle{\cal{O}}^{\psi(2S)}[^{3}S_{1}^{(8)}]\rangle=(0.00330\pm0.00021)\; \text{GeV}^{3},\\ & \langle{\cal{O}}^{\psi(2S)}[^{3}P_{0}^{(8)}]\rangle=(0.0080\pm0.0067)m_{c}^{2}\; \text{GeV}^{3}. \end{aligned} $

(A2) The LDMEs of the bottomonium [81] are
$ \begin{aligned}[b] &\langle{\cal{O}}^{\Upsilon(1S)}[^{3}S_{1}^{(1)}]\rangle=9.28\; \text{GeV}^{3},\\ &\langle{\cal{O}}^{\Upsilon(1S)}[^{1}S_{0}^{(8)}]\rangle=(13.60\pm2.43)\times10^{-2}\; \text{GeV}^{3},\\ &\langle{\cal{O}}^{\Upsilon(1S)}[^{3}S_{1}^{(8)}]\rangle=(0.61\pm0.24)\times10^{-2}\; \text{GeV}^{3},\\ &\langle{\cal{O}}^{\Upsilon(1S)}[^{3}P_{0}^{(8)}]\rangle=(-0.93\pm0.5)m_{b}^{2}\times10^{-2}\; \text{GeV}^{3}, \end{aligned} $

(A3) $ \begin{aligned}[b] &\langle{\cal{O}}^{\Upsilon(2S)}[^{3}S_{1}^{(1)}]\rangle=4.63\; \text{GeV}^{3},\\ &\langle{\cal{O}}^{\Upsilon(2S)}[^{1}S_{0}^{(8)}]\rangle=(0.62\pm1.98)\times10^{-2}\; \text{GeV}^{3},\\ &\langle{\cal{O}}^{\Upsilon(2S)}[^{3}S_{1}^{(8)}]\rangle=(2.22\pm0.24)\times10^{-2}\; \text{GeV}^{3},\\ &\langle{\cal{O}}^{\Upsilon(2S)}[^{3}P_{0}^{(8)}]\rangle=(-0.13\pm0.43)m_{b}^{2}\times10^{-2}\; \text{GeV}^{3}, \end{aligned} $

(A4) $ \begin{aligned}[b] &\langle{\cal{O}}^{\Upsilon(3S)}[^{3}S_{1}^{(1)}]\rangle=3.54\; \text{GeV}^{3},\\ &\langle{\cal{O}}^{\Upsilon(3S)}[^{1}S_{0}^{(8)}]\rangle=(1.45\pm1.16)\times10^{-2}\; \text{GeV}^{3},\\ &\langle{\cal{O}}^{\Upsilon(3S)}[^{3}S_{1}^{(8)}]\rangle=(1.32\pm0.20)\times10^{-2}\; \text{GeV}^{3},\\ &\langle{\cal{O}}^{\Upsilon(3S)}[^{3}P_{0}^{(8)}]\rangle=(-0.27\pm0.25)m_{b}^{2}\times10^{-2}\; \text{GeV}^{3}. \end{aligned} $

(A5) The multiplicity relations
$ \langle{\cal{O}}^{H}[^{3}P_{J}^{(8)}]\rangle=(2J+1)\langle{\cal{O}}^{H}[^{3}P_{0}^{(8)}]\rangle, $

(A6) are used, where
$ m_{c} $ and$ m_{b} $ are the charm quark and bottom quark masses, respectively. -
We provide a detailed treatment of the partonic kinematics, which is consistent with the exact formulation.
The energy and momentum in the α-b parton level are
$ \begin{aligned}[b] E_{\alpha}&=\frac{\left(s_{\alpha b}+m_{\alpha}^{2}\right)}{2\sqrt{s_{\alpha b}}},\\ E_{b}&=\frac{\left(s_{\alpha b}-m_{\alpha}^{2}\right)}{2\sqrt{s_{\alpha b}}},\\ p_{\text{CM}}&=\frac{\left(s_{\alpha b}-m_{\alpha}^{2}\right)}{2\sqrt{s_{\alpha b}}}, \end{aligned} $

(B1) where the
$ s_{\alpha b} $ expressions for each photon emission are$ \begin{aligned}[b] &s_{\alpha b}|_{\text{coh}.}=m_{A}^{2}+\frac{x_{b}}{N_{B}}\left(s-m_{A}^{2}-m_{B}^{2}\right),\\ &s_{\alpha b}|_{\text{OIC}}=m_{p}^{2}+\frac{x_{b}}{N_{A}N_{B}}\left(s-m_{A}^{2}-m_{B}^{2}\right),\\ &s_{\alpha b}|_{\text{UIC}}=m_{a}^{2}+\frac{x_{a}x_{b}}{N_{A}N_{B}}\left(s-m_{A}^{2}-m_{B}^{2}\right), \end{aligned} $

(B2) where
$ s=\left(p_{A}+p_{B}\right)^2=\left(N_{A}+N_{B}\right)^{2}s_{NN}/4 $ is the squared energy in the A-B process, while the energy and momentum at the$ \gamma^{*} $ -b parton level are$ \begin{aligned}[b] \hat{E}_{\gamma}&=\frac{\left(\hat{s}-Q^{2}\right)}{2\sqrt{\hat{s}}},\; \; \; \; \hat{E}_{H}=\frac{\left(\hat{s}+M_{H}^{2}\right)}{2\sqrt{\hat{s}}},\\ \hat{p}_{\text{CM}}&=\frac{\left(\hat{s}+Q^{2}\right)}{2\sqrt{\hat{s}}},\; \; \; \hat{p}_{\text{CM}}'=\frac{\left(\hat{s}-M_{H}^{2}\right)}{2\sqrt{\hat{s}}}. \end{aligned} $

(B3) The Mandelstam variables involved in direct photoproduction are
$ \begin{aligned}[b] \hat{s}&=\left(q+p_{b}\right)^{2}=y\left(s_{\alpha b}-m_{\alpha}^{2}\right)-Q^{2},\\ \hat{t}&=\left(q-p_{H}\right)^{2}=-\left(1-z\right)\left(\hat{s}+Q^{2}\right),\\ \hat{u}&=\left(p_{b}-p_{H}\right)^{2}=M_{H}^{2}-z\left(\hat{s}+Q^{2}\right), \end{aligned} $

(B4) while those for resolved photoproduction are
$ \begin{aligned}[b] \hat{s}^{*}&=\left(p_{a'}+p_{b}\right)^{2}=yz_{a'}\left(s_{\alpha b}-m_{\alpha}^{2}\right),\\ \hat{t}^{*}&=\left(p_{a'}-p_{H}\right)^{2}=-\left(1-z\right)\hat{s}^{*},\\ \hat{u}^{*}&=\left(p_{b}-p_{H}\right)^{2}=M_{H}^{2}-z\hat{s}^{*}. \end{aligned} $

(B5) The kinematical boundaries of the mentioned distributions are given in Table B1 and Table B2. When we calculate the contribution of photoproduction to the hadronic process in Figs. 9 and 10, the cut
$ b_{ \text{max}}=2R_{A} $ must be used to avoid unphysical contributions from non-overlapping nuclei at large. Using the central ideas of Refs. [3, 63], the squared transverse momentum of the photon can be written asVariables Coherent direct UIC direct Coherent resolved UIC resolved $ z_{\text{min}} $ 

$ \left[(M_{H}^{2}+\hat{s})-\sqrt{(\hat{s}-M_{H}^{2})^{2}-4p_{T \text{min}}^{2}\hat{s}}\right]/(2\hat{s} $ )

$ z_{\text{max}} $ 

$ \left[(M_{H}^{2}+\hat{s})+\sqrt{(\hat{s}-M_{H}^{2})^{2}-4p_{T \text{min}}^{2}\hat{s}}\right]/(2\hat{s} $ )

$ \hat{t}_{\text{min}} $ 

$ -(1-z_{\text{min}})(\hat{s}+Q^{2}) $ 

$ -(1-z_{\text{min}})\hat{s}^{*} $ 

$ \hat{t}_{\text{max}} $ 

$ -(1-z_{\text{max}})(\hat{s}+Q^{2}) $ 

$ -(1-z_{\text{max}})\hat{s}^{*} $ 

$ z_{a' \text{min}} $ 

$ \backslash $ 

$ \backslash $ 

$ \hat{s}^{*}_{\text{min}}/[y(s_{\alpha b}-m_{\alpha}^{2})] $ 

$ \hat{s}^{*}_{\text{min}}/(yx_{a}x_{b}s_{NN}) $ 

$ z_{a' \text{max}} $ 

$ \backslash $ 

$ \backslash $ 

1 1 $ x_{b \text{min}} $ 

$ (\hat{s}_{\text{min}}+Q^{2})/[y(s_{\alpha b}|_{x_{b\text{max}}}-m_{\alpha}^{2})] $ 

$ (\hat{s}_{\text{min}}+Q^{2})/(yx_{a}s_{NN}) $ 

$ \hat{s}^{*}_{\text{min}}/[y(s_{\alpha b}|_{x_{b\text{max}}}-m_{\alpha}^{2})] $ 

$ \hat{s}^{*}_{\text{min}}/(yx_{a}s_{NN}) $ 

$ x_{b \text{max}} $ 

1 $ x_{a \text{min}} $ 

$ \backslash $ 

$ (\hat{s}_{\text{min}}+Q^{2})/(ys_{NN}) $ 

$ \backslash $ 

$ \hat{s}^{*}_{\text{min}}/(ys_{NN}) $ 

$ x_{a \text{max}} $ 

$ \backslash $ 

1 $ \backslash $ 

1 $ y_{\text{min}} $ 

$ (\hat{s}_{\text{min}}+Q^{2})/(s_{\alpha b}|_{x_{b\text{max}}}-m_{\alpha}^{2}) $ 

$ \hat{s}^{*}_{\text{min}}/(s_{\alpha b}|_{x_{b\text{max}}}-m_{\alpha}^{2}) $ 

$ y_{\text{max}} $ 

$ \left[\sqrt{Q^{2}(4m_{\alpha}^{2}+Q^{2})}-Q^{2}\right]/(2m_{\alpha}^{2}) $ 

$ Q^{2}_{\text{min}} $ 

$ -2m_{\alpha}^{2}+\left[(s_{\alpha b}+m_{\alpha}^{2})(s_{\alpha b}-\hat{s}+m_{\alpha}^{2})-(s_{\alpha b}-m_{\alpha}^{2})\sqrt{(s_{\alpha b}-\hat{s}+m_{\alpha}^{2})^{2}-4s_{\alpha b}m_{\alpha}^{2}}\right]/(2s_{\alpha b}) $ 

$ Q^{2}_{\text{max}} $ 

$ y(s_{\alpha b}|_{x_{b\text{max}}}-m_{\alpha}^{2})-\hat{s}_{\text{min}} $ 

Table B1. Kinematical boundaries of the
$ Q^{2} $ and y distributions.$ \hat{s}_{\text{min}}=\hat{s}^{*}_{\text{min}}=(m_{T}+p_{T\text{min}})^{2} $ ,$ p_{T}^{2}=\hat{t}(\hat{s}\hat{u}+Q^{2}M_{H}^{2})/(\hat{s}+Q^{2})^{2} $ .Variables Coherent direct UIC direct Coherent resolved UIC resolved $ Q^{2}_{\text{min}} $ 

$ x^{2}_{1}m^{2}_{\alpha}/(1-x_{1}) $ 

$ Q^{2}_{\text{max}} $ 

$ 1/R_{\alpha}^{2} $ 

$ (1-x_{1})s_{NN} $ 

$ 1/R_{\alpha}^{2} $ 

$ (1-x_{1})s_{NN} $ 

$ |y_{r \text{max}}| $ 

$ \ln[(\hat{s}_{\text{max}}+M_{H}^{2}+\sqrt{(\hat{s}_{\text{max}}-M_{H}^{2})^{2} -4p^{2}_{T}\hat{s}_{\text{max}}})/(\hat{s}_{\text{max}}+M_{H}^{2}-\sqrt{(\hat{s}_{\text{max}}-M_{H}^{2})^{2} -4p^{2}_{T}\hat{s}_{\text{max}}})]^{1/2} $ 

$ p^{2}_{T\text{min}} $ 

$ M^{2}_{H} $ 

$ p^{2}_{T\text{max}} $ 

$ (1-z)\left[z(s_{\alpha b}|_{x_{b\text{max}}}-m_{\alpha}^{2})-M_{H}^{2}\right] $ 

Table B2. Kinematical boundaries of the
$ p_{T} $ and z distributions, where$ x_{1}=\hat{s}/s_{\alpha b} $ . Other boundaries are the same as those of Table B1.$ \begin{aligned}[b] Q^{2}_{ \text{T}}&=(1-x)\left(Q^{2}-\frac{x^{2}}{1-x}m_{p}^{2}\right)\sim\frac{1}{b^{2}},\\ Q^{2}_{ \text{min}}&=\frac{b^{-2}_{ \text{max}}+x^{2}m_{p}^{2}}{1-x}. \end{aligned} $

(B6) where
$ b_{ \text{max}}=2R_{A} $ ($ R_{A}=A^{1/3}1.2\; \text{fm}) $ .Finally, we determine the Jacobian determinant
$ {\cal{J}} $ for each distribution. For the$ Q^{2} $ and y distributions, we have$ \begin{align} {\cal{J}}=\frac{2r^{2}\left|{p}_{b}\right|}{E_{\alpha'}E_{b}}=\frac{2r^{2}}{\sqrt{\left(r^{2}+m_{\alpha}^{2}\right)}}, \end{align} $

(B7) while those for the z distribution are
$ \begin{align} {\cal{J}}_{\text{dir.}}=&\frac{x_{b}}{z\left(1-z\right)},\; \; {\cal{J}}_{\text{res.}}=\frac{z_{a}}{z\left(1-z\right)}, \end{align} $

(B8) and that of the
$ p_{T} $ distribution is$ \begin{align} {\cal{J}}=&\frac{\left(\hat{s}^{3/2}+Q^{2}\sqrt{\hat{s}}\right)}{y\left(s_{\alpha b}|_{x_{b\text{max}}}-m_{\alpha}^{2}\right)\left(\sqrt{\hat{s}}-\cosh y_{r}m_{T}\right)} \end{align} $

(B9) for the coherent-direct process. The relations between Eq. (B9) and the rest of the cases are
$ {\cal{J}}_{\text{incoh.dir.}}={\cal{J}}/x_{a} $ ,$ {\cal{J}}_{\text{coh.res.}}={\cal{J}}/x_{b} $ , and$ {\cal{J}}_{\text{incoh.res.}}={\cal{J}}/x_{a}x_{b} $ . For the fragmentation processes,$ {\cal{J}}=\left(\hat{s}+Q^{2}\right)/\left(\cosh y_{r}\sqrt{\hat{s}}\right) $ .
Inelastic heavy quarkonium photoproduction in p-p and Pb-Pb collisions at LHC energies
- Received Date: 2025-03-14
- Available Online: 2025-10-15
Abstract: We study the inelastic charmonium (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF










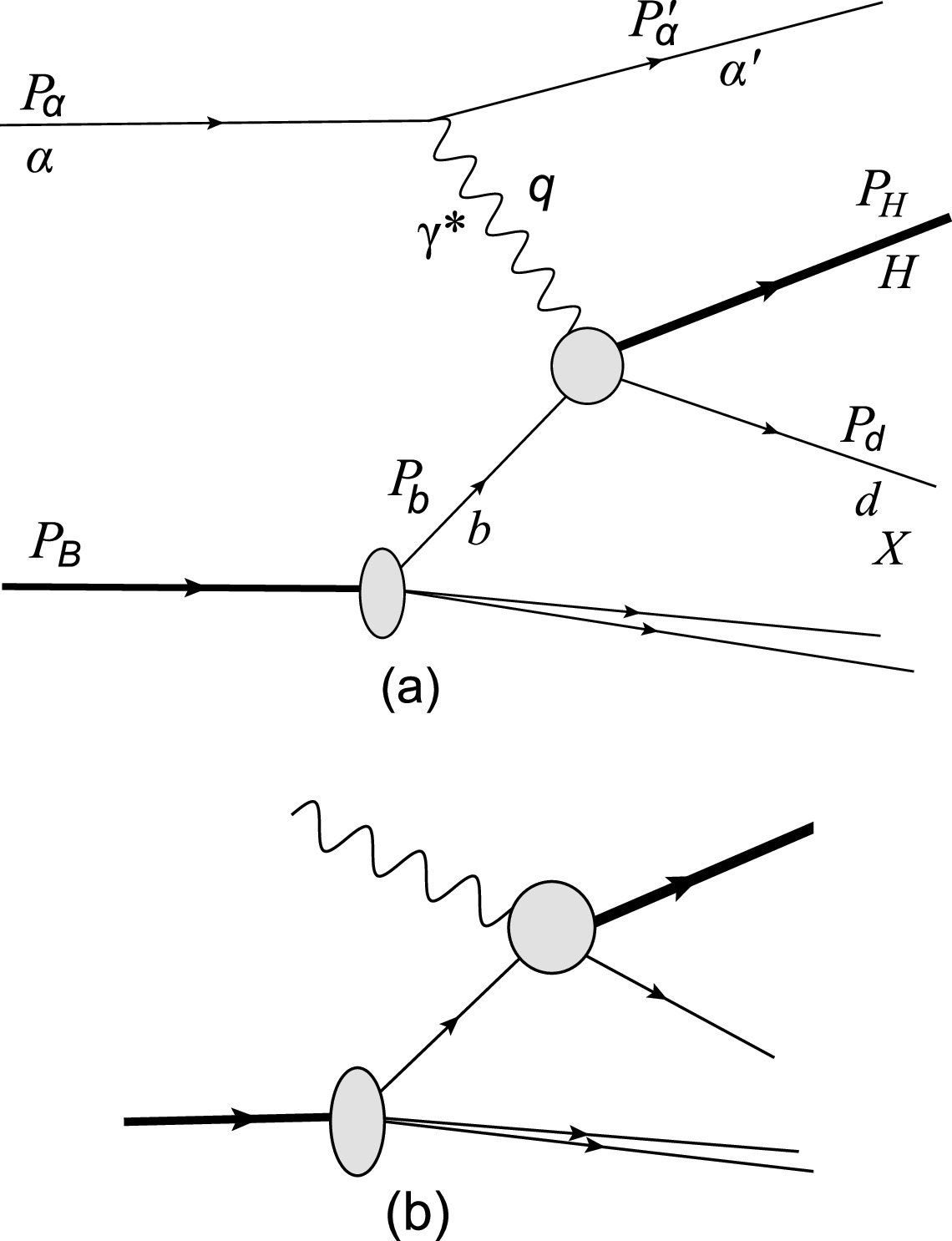













 DownLoad:
DownLoad: