HTML
-
Ever since the description of the mechanism of superconducting-type pair correlations in atomic nuclei [1], a huge amount of experimental data has been collected and a significant number of effective theoretical models has been proposed to describe the importance of neutron and proton pairs for various properties of atomic nuclei [2-4]. However, due to the constant development of experimental techniques, it became possible to expand the range of the nuclei studied in the region far from stability and to refine significantly the experimental data for known isotopes, which led to a new wave of theoretical studies of the structure and dynamics of atomic nuclei. One of the important questions discussed at present concerns the neutron-proton correlations in atomic nuclei [5-9]. The analysis of np pairing is of particular interest since it is possible in this case to study the relationship between the isoscalar (T = 0) and isovector (T = 1) pairing of nucleons, and to map the change of this relation as function of the mass number A. Traditionally, the main object of the np-paring studies is the chain of nuclei with N = Z. These nuclei are a clear example of the isospin symmetry of the nucleon-nucleon interaction, which is a consequence of the charge independence of nuclear forces.
One of the ways to study the structure of atomic nuclei, including the effects of two-nucleon correlations, is to systematically analyse the mass surface of atomic nuclei, its global behaviour and local fluctuations. This is an important source of information as the experimental values of nuclear masses are known with high accuracy, and the number of isotopes for which this information is available is constantly increasing [10]. Mass relations allow to extract the information concerning the magnitude of the interaction between nucleons as function of the mass number A and of the occupation probabilities of the subshells near the Fermi energy. For example, it is well known that pairing of identical nucleons leads to stratification of the mass surface and can be quantified from the odd-even staggering (OES) value [11-13]. Several approximate relations for the pairing energy of identical nucleons in even-even isotopes based on the masses of neighbouring nuclei have been studied in detail, but despite the long history of the problem, the question of which relation corresponds best to the pair interaction is still under discussion [14-19].
The mass relations for neutron-proton pairing are more diverse [6, 20-23]. In this case, however, they are mainly studied for nuclei with N = Z, and primarily for odd-odd nuclei. These nuclei allow to address both the isovector spin-zero and isoscalar deuteron-like (or maximum spin neutron-proton) coupling. Due to the assumption that isoscalar pairing of nucleons in heavy nuclei contributes significantly to collective effects, the analysis of calculations based on mass relations should allow to draw conclusions regarding the effect of np pairing, and of the possibility of treating np pairs as deuteron-like states in nuclei. The analysis of mass relations for the chain N = Z is made more complicated by the presence of the Wigner energy, which is closely connected with np-pairing [5, 24-26].
In this paper, the ideas underlying various mass relations associated with neutron-proton correlations in different types of atomic nuclei are considered. Examples of N − Z = Const chains are studied in order to compare the behaviour of the mass relations under consideration. Binding energy parametrization based on the Shell Model makes it possible to clarify the structure of the mass relations obtained, and to reveal their relationship with the np interaction.
-
There is a large number of indicators for np correlations based on the masses of neighbouring nuclei available in literature. Below we consider the basic relations.
-
In our previous work [19], relationship between different mass formulas and their connection with the pairing energy of identical nucleons was shown. Various indicators of like-nucleon pairing based on the odd-even splitting of the mass surface with different degrees of averaging were considered, as was the correspondence of these relations with the explicit definition of the nucleon pairing energy, given as the difference between two-nucleon separation energy in nucleus (A) and the doubled one-nucleon separation energy in nucleus (A−1):
$ \begin{eqnarray}{\Delta }_{nn}(N, Z)\, ={S}_{2n}(N, Z)-2{S}_{n}(N-1, Z), \end{eqnarray} $
(1) where S2n and Sn are two- and one-neutron separation energies, respectively. This relation gives the magnitude of neutron pairing. A similar relation for the proton pairing energy Δpp(N, Z), using the proton separation energies S2p and Sp, can be obtained by interchanging N and Z.
To determine the neutron-proton pairing energy in an odd-odd nucleus having an np-pair above the double-closed core, one should consider the difference between the np separation energy in (N, Z) nucleus and the separation energies of a neutron and of a proton in nuclei (N, Z−1) and (N−1, Z), respectively [27]:
$ \begin{eqnarray}\begin{array}{lll}{\Delta }_{np}(N, Z)&=&{S}_{np}(N, Z)-[{S}_{n}(N, Z-1)+{S}_{p}(N-1, Z)]\\ &=&B(N, Z)+B(N-1, Z-1)\\ &&-B(N-1, Z)-B(N, Z-1), \end{array}\end{eqnarray} $
(2) where Snp(N, Z) is the np-pair separation energy, and B(N, Z) is the binding energy. This relation, suggested in [28] for both even and odd N and Z, was widely applied [29-36].
Averaging Δnp over nuclei (N, Z) and (N+1, Z+1) belonging to the chain N-Z = Const
$ \begin{eqnarray}{\Delta }_{np}^{(7)}(N, Z)=\frac{1}{2}({\Delta }_{np}(N, Z)+{\Delta }_{np}(N+1, Z+1)).\end{eqnarray} $
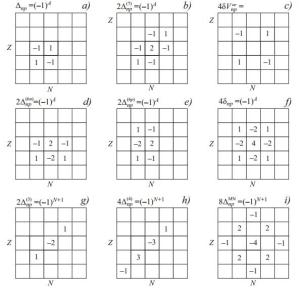
(3) can give a more accurate estimate of np-correlations. Illustrative diagrams with multipliers of binding energies of neighbouring nuclei in formulas (2) and (3) are shown in Fig. 1(a) and (b).

Figure 1. Diagrams of various indicators of np-correlations in nuclei. The coefficients are multipliers of the binding energies in the relations for (a) Δnp - indicator (2), (b)
$2{\Delta }_{np}^{(7)}$ — (3), (c)$4\delta {V}_{np}^{ee}$ — (6), (d)$2{\Delta }_{np}^{(6n)}$ — (12), (e)$2{\Delta }_{np}^{(6p)}$ — (13), (f) 4δnp — (19), (g)$2{\Delta }_{np}^{(3)}$ — (14), (h)$4{\Delta }_{np}^{(4)}$ — (16), (i)$8{\Delta }_{np}^{MN}$ — indicator (18), for nuclei with even A.Fig. 2 shows the dependence of indicators Δnp and
${\Delta }_{np}^{(7)}$ on the mass number A in self-adjoint nuclei N = Z. The monotonous dependence and agreement between the values of Δnp and${\Delta }_{np}^{(7)}$ for A>10 are worth pointing out. Indeed, the results of formula (2) for neighbouring even-even and odd-odd nuclei are not only very close for the chain N = Z, but also in other isotope regions. This can be seen from the diagrams in Fig. 1: the difference in the indicators Δnp for nuclei (N, Z) and (N+1, Z+1) leads to the well-known Garvey-Kelson mass relations [37, 38]: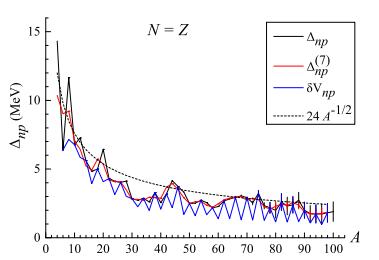
Figure 2. (color online) Indicators Δnp(A),
${\Delta }_{np}^{(7)}(A)$ and δVnp for even-even and odd-odd nuclei as function of the mass number A in nuclei N = Z. The dashed line corresponds to 24/A1/2. Nuclear mass data are from [10].$ \begin{eqnarray}\begin{array}{ll}&M(N+2, Z-2)-M(N, Z)+M(N, Z-1)\\ -&M(N+1, Z-2)+M(N+1, Z)-M(N+2, Z-1)=0;\\ &M(N+2, Z)-M(N, Z-2)+M(N+1, Z-2)\\ -&M(N+2, Z-1)+M(N, Z-1)-M(N+1, Z)=0.\end{array}\end{eqnarray} $
(4) The accuracy of the Garvey-Kelson mass relations was verified on a large set of experimental data, and these relations, as well as the generalized formulas derived from them, are widely used for estimating the mass of nuclei far from stability [39, 40].
The fact that the Δnp values for odd-odd and even-even nuclei are very close does not necessarily mean that this indicator describes precisely the np-correlation, especially for nuclei with N = Z, where the presence of the Wigner cusp significantly changes the picture. For even-even nuclei, the applicability of formula (2) is not so obvious. Indeed, in the case of an even number of external nucleons of the same type above the closed core, in addition to the np-interaction, the like-nucleon correlations should also be taken into account. Thus, for an even-even nucleus with two np pairs, np-pairing should be defined as the difference between the separation energy of all four nucleons from the core and the separation energies of neutron and proton pairs in nuclei (N, Z-2) and (N-2, Z) [7]:
$ \begin{eqnarray}\begin{array}{ll}{\Delta }_{np}^{ee}(N, Z)=&\frac{1}{4}(B(N-2, Z-2)+B(N, Z)\\ &-B(N-2, Z)-B(N, Z-2)).\end{array}\end{eqnarray} $
(5) The coefficient 1/4 arises as a result of taking into account the interaction of each proton with each neutron. The corresponding diagram is shown in Fig. 1(c). From the diagrams, it can be seen that for even-even nuclei this indicator may be obtained from four Δnp terms:
$ \begin{eqnarray*}\begin{array}{ll}\delta {V}_{np}=&{\Delta }_{np}(N, Z)+{\Delta }_{np}(N-1, Z-1)\\ &-{\Delta }_{np}(N, Z-1)-{\Delta }_{np}(N-1, Z).\end{array}\end{eqnarray*} $
The difference between the binding energies of four even-even nuclei as an estimator of np-interaction energy was proposed in [21], and analysed in [24, 25, 41] in connection with the structure of the Wigner term. However, the indicator δVnp in [21], was calculated using (5) in accordance with the np interaction in odd-odd nuclei (N+1, Z+1) only.
The indicator δVnp in both interpretations is still subject to extensive consideration [20, 42-47]. In [24], a variant of the generalised formula (5) for different types of nuclei was proposed:
$ \begin{eqnarray}\delta {V}_{np}(N, Z)=\left\{\begin{array}{ll}\frac{1}{4}[B(N, Z)-B(N, Z-2)-B(N-2, Z)+B(N-2, Z-2)],&\, ({\rm{even}}, \, {\rm{even}}), \\ \frac{1}{2}[B(N, Z)-B(N, Z-1)-B(N-2, Z)+B(N-2, Z-1)],&\, ({\rm{even}}, \, {\rm{odd}}), \\ \frac{1}{2}[B(N, Z)-B(N, Z-2)-B(N-1, Z)+B(N-1, Z-2)],&\, ({\rm{odd}}, \, {\rm{even}}), \\ B(N, Z)-B(N, Z-1)-B(N-1, Z)+B(N-1, Z-1),&\, ({\rm{odd}}, \, {\rm{odd}}).\end{array}\right.\end{eqnarray} $
(6) In Fig. 2, the indicator δVnp(A) given by formula (6) is compared to Δnp. In this case, the indicators Δnp and δVnp coincide for odd-odd nuclei, while for even-even nuclei formula (6) consistently produces lower estimates of the np pairing energy. The indicator δVnp shows a pronounced zigzag shape due to the relation
$\delta {V}_{np}^{oo}\gt \delta {V}_{np}^{ee}$ . Since δVnp(A) is obtained empirically, it may contain components of different nature. The chain N = Z is an anomalous case due to the Wigner energy; the structure of the Wigner term and the empirical nature of δVnp could help to clarify it [24]. -
When considering np-correlations, the so-called Wigner term is of special importance. This contribution was first considered on the basis of analysis of the SU(4) spin-isospin symmetry of nuclear forces by Wigner [48], who showed that the symmetry energy, in addition to a term proportional to (N-Z)2/A, must also have a term proportional to the isospin asymmetry |I| (I=(N-Z)/A), which leads to an enhancement of the binding energy near N = Z. In the mass formula for the droplet model, the Wigner term was adopted in the form [49]
$ \begin{eqnarray*}\begin{array}{l}{E}_{W}=W(|I|+d), \, {\rm{where}}\, W=30\, {\rm{MeV}}, \\ d=\left\{\begin{array}{l}\frac{1}{A}\, ({\rm{odd-odd}}), \, N=Z\\ 0\, {\rm{otherwise}}.\end{array}\right.\end{array}\end{eqnarray*} $
The correction for (N = Z) odd-odd nuclei (term d) was added “because it is clearly called for by the experimental masses” (see [38], Table I). The generalization of the Wigner term, performed in [14], results in three terms:
$ \begin{eqnarray*}{{E}}_{{W}}{=-{b}}_{1}{|{I}|+{b}}_{2}{/{a}+{b}}_{3}/{A}, \end{eqnarray*} $
where the term b3 corresponds to (N = Z) odd-odd nuclei, and the term b2 is related to the possible α-correlation effect. Currently, the standard expression for the Wigner term is
$ \begin{eqnarray}{E}_{W}=W(A)|N-Z|+d(A){\pi }_{np}{\delta }_{NZ}, \end{eqnarray} $
(7) where
${\pi }_{np}=\frac{1}{4}(1-{\pi }_{n})(1-{\pi }_{p})$ , and πn = (−1)N and πp = (−1)Z are the nucleon-number parities. The question of d/W is still open: as mentioned above, some estimates suggest that d/W = 1 [49], while the analysis of experimental masses leads to d/W = 0.56±0.27 [14]. It seems appropriate to use the empirical mass relations to define the parameters of the Wigner term. Indicator δVnp (5) was used for investigating the np-correlation energy, and it was shown that it is sensitive to the Wigner energy and can be used as term d in the expression (7) [24, 41]. The mass relations for δVnp, obtained in [24] from supermultiplet theory, are given above (eq. (6)). In [25], certain combinations of δVnp(N, Z) were suggested to obtain W(A) and d(A). The difference between even-even and odd-odd nuclei is not limited to the presence of a special term d; the mass relation for W(A) is also different in these two cases:$ \begin{eqnarray}\begin{array}{l}{\rm{for}}\, N=Z, \, {\rm{even-even}}\\ W(A)=\delta {V}_{np}(N, Z)-\frac{1}{2}[\delta {V}_{np}(N, Z-2)+\delta {V}_{np}(N+2, Z)]\end{array}\end{eqnarray} $
(8) $ \begin{array}{l}{\rm{for}}\, N&=&Z, \, {\rm{odd-odd}}\\ W(A)&=&-\delta {V}_{np}(N+1, Z-1)\\ &+&\frac{1}{2}[\delta {V}_{np}(N-1, Z-1)+\delta {V}_{np}(N+1, Z+1)]\end{array} $
(9) $ \begin{eqnarray}\begin{array}{ll}d(A)=&-4\delta {V}_{np}(N+2, Z)\\ &+2[\delta {V}_{np}(N+1, Z-1)+\delta {V}_{np}(N+3, Z+1)].\end{array}\end{eqnarray} $
(10) Experimental values are consistent with the simple relation dT=0/W ≈ 1. Analysis of the Wigner energy in terms of np pairs of a given angular momentum and isospin shows that the Wigner term cannot be explained only in terms of correlations of deutron-like np pairs.
Significant effort is still needed to determine the precise structure of the symmetry energy and to extract the Wigner term [5, 26, 50-52]. The interpretation of the term d using mass relations is still open to discussions in literature. It may be useful to consider different mass relations for np-correlations not only for odd-odd (N = Z) nuclei, but also for nuclei with different N, Z parity with N-Z ≥ 1.
-
Estimates of np-correlations can be obtained by considering either neutron or proton separation energies along the chains of isotones or isotopes, respectively. Indeed, it follows from (2) that for odd-odd nuclei
$ \begin{eqnarray*}\begin{array}{ll}{\Delta }_{np}(N, Z)&=[{S}_{n}(N, Z)-{S}_{n}(N, Z-1)]\\ &=[{S}_{p}(N, Z)-{S}_{p}(N-1, Z)].\end{array}\end{eqnarray*} $
The neutron Sn and proton Sp separation energies in isotopes Sn (Z = 50) and Sb (Z = 51) are shown in Fig. 3 as functions of the number of neutrons.
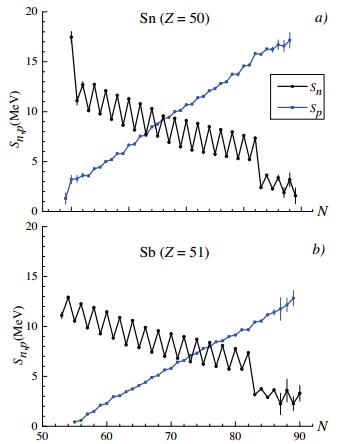
Figure 3. (color online) Neutron and proton separation energies Sn and Sp in Sn (a) and Sb (b) isotopes. Nuclear mass data are from [10].
The dependence of Sn(N) has a zigzag shape, which is related to neutron pairing. The dependence of Sp(N) shows even-odd jumps as well despite the fact that Z is constant, due to the additional interaction of a proton with an odd neutron. The distance between parallel lines drawn through isotopes with even and odd Z corresponds to the np-interaction [53, 54].
The dependence Sn(Z) in a chain of isotones is shown schematically in Fig. 4. The different behaviour of Sn(Z) for even and odd number of neutrons is of importance. In the case of even N, the largest values of Sn also correspond to even values of Z; for isotones with odd N, the maxima correspond to odd values of Z. These features of Sn(Z) and Sp(Z) were explained in [54] in the framework of the Shell Model. According to the diagram in Fig. 4, the expression for Δnp should include a term depending on the parity of A:
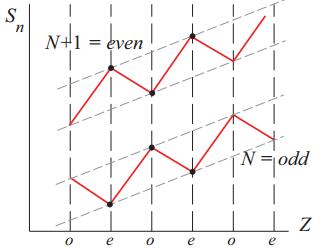
Figure 4. (color online) Schemes used to determine the properties of the pairing interaction using nucleon separation energies. a) like-nucleon correlation (Sn(N) for Z = Const), b) neutron-proton correlation (Sn(N) for N = Const)
$ \begin{eqnarray}\begin{array}{ll}{\Delta }_{np}(N, Z)&={(-1)}^{A}[{S}_{n}(N, Z)-{S}_{n}(N, Z-1)]\\ &={(-1)}^{A}[{S}_{p}(N, Z)-{S}_{p}(N-1, Z)].\end{array}\end{eqnarray} $
(11) However, the experimental data for Sp(Z), given in Fig. 3, show that introducing a dependence on parity of A is not so obvious, since the relations
${S}_{p}^{oo}(N, Z)\gt {S}_{p}^{eo}(N+1, Z)$ and${S}_{p}^{ee}(N+1, Z)\gt {S}_{p}^{oe}(N+1, Z+1)$ are not always satisfied. In fact, these inequalities appear not to be valid in most cases. Therefore, when constructing the empirical dependence of Δnp, a term depending on the parity of A is not included in [55, 56]. Since the study of empirical values of np-pairing is based on the chains of nuclei with even A, the question of the dependence on A-parity is not so important. Furthermore, the value of Δnp in odd-A nuclei is close to zero. Nevertheless, we choose to keep the (−1)A ‘phase' for constructing the mass relation.As in the case of relations for identical nucleon pairing [19], it seems reasonable to average the values of Δnp for two or more neighbouring nuclei, which leads to formulas [14]:
$ \begin{eqnarray}\begin{array}{lll}{\Delta }_{np}^{(6, n)}(N, Z)&=&\frac{1}{2}[{\Delta }_{np}(N+1, Z)+{\Delta }_{np}(N, Z)]\\ &=&\frac{{(-1)}^{A}}{2}[-{S}_{n}(N+1, Z)-{S}_{n}(N, Z-1)\\ &&+{S}_{n}(N, Z)+{S}_{n}(N+1, Z-1)].\end{array}\end{eqnarray} $
(12) Similar considerations for the proton separation energy Sp in isotones Z = Const leads to the formula:
$ \begin{eqnarray}\begin{array}{lll}{\Delta }_{np}^{(6, p)}(N, Z)&=&\frac{1}{2}[{\Delta }_{np}(N, Z+1)+{\Delta }_{np}(N, Z)]\\ &=&\frac{{(-1)}^{A}}{2}[-{S}_{p}(N, Z+1)-{S}_{p}(N-1, Z)\\ &&+{S}_{p}(N, Z)+{S}_{p}(N-1, Z+1)].\end{array}\end{eqnarray} $
(13) Diagrams for the indicators (12) and (13) are shown in Fig. 1(d) and (e). As can be seen, formula (12) averages the differences of neutron separation energies for even and odd A by using two chains of isotones: N and N+1. The formula that is most symmetric is the one that averages the neutron separation energy differences both in the neighbouring isotonic chains and in the neighbouring nuclei in each chain Z and Z+1 (see Fig. 1(f)). This diagram shows that averaging in accordance with formulas (12) and (13) leads to the same result. Indeed, it is evident from Fig. 1(d) and (e) that the difference in these values leads to the well-known Garvey-Kelson mass relations (4).
The indicator Δnp(A) for a chain of nuclei with N=Z consisting of even-even and odd-odd isotopes, and for a neighbouring chain of odd nuclei with N = Z + 1, are shown in Fig. 5. While the values of Δnp for N = Z are large and are, in general, in accordance with the analytical relation 24A−1/2, the corresponding values for odd nuclei (N=Z+1 chain) are smaller and tail to zero, having even negative values for large A. Accordingly, for the chain with N=Z, the indicator
${\Delta }_{np}^{(6, n)}(A)$ (12), which is the average between these two chains, is substantially below Δnp. This example illustrates best the contribution of the symmetry energy for N = Z nuclei, although this trend also holds for nuclei with neutron excess.
Figure 5. (color online) Indicators Δnp (black line) and
${\Delta }_{np}^{(6, n)}$ (blue line) in nuclei with N=Z. Dotted line shows Δnp(A) in nuclei N=Z+1; dashed line corresponds to 24A−1/2.Indicator
${\Delta }_{np}^{(6, n)}(A)$ (12) was used for estimating the np-pairing term in several papers [14, 18, 20]. This indicator includes a difference between nuclei having different A-parity, and it therefore reflects the complexity of np-correlations, and not only the np-pairing in odd-odd nuclei. Thus, this relation can be interpreted differently, for example as an indication of α-clustering in even-even nuclei [57]. -
The indicators for np-pairing Δnp (2) and
${\Delta }_{np}^{(7)}$ (3) are obtained using the masses of neighbouring nuclei for both even and odd A, as well as N and Z. As the corresponding estimates of like-nucleon pairing are based on isotone and isotope chains, a significant difference is seen between these estimates and indicators (2) and (3).Variants of np-pairing indicators constructed by analogy with the formulas for neutron OES and proton OES use the binding energies of even or odd A nuclei for the chain with N-Z = Const. Indeed, for a chain of even-A nuclei, one notes the splitting of binding energies into two groups, for even-even and odd-odd nuclei. Since the mass number A increases quickly for this sequence, the splitting is small compared to the general increase of the binding energy. As in the case of like-nucleons, this effect is more pronounced for the difference in binding energies of neighbouring isotopes [19]. In the case of the N = Z chain, this corresponds to the deuteron separation energy, corrected for its binding energy:
$ \begin{eqnarray*}{S}_{d}(N, Z)=B(N, Z)-B(N-1, Z-1)-2.22\, {\rm{MeV}}.\end{eqnarray*} $
The A-dependence of the deuteron separation energy Sd in nuclei with N = Z is shown in Fig. 6. Similar to Sn(Z) and Sp(N), it shows a zigzag shape with an overall tendency of gradual decrease and stabilization of the even-even - odd-odd splitting for heavier isotopes. The energy of np-pairing in odd-odd nucleus (N, Z) based on this dependence corresponds to half of the difference of deuteron separation energies for even-even and odd-odd nuclei:

Figure 6. Deuteron separation energy Sd(A) in nuclei with N=Z. Nuclear mass data are from [10].
$ \begin{eqnarray}\begin{array}{lll}{\Delta }_{np}^{(3)}(N, Z)&=&\frac{1}{2}({S}_{d}(N+1, Z+1)-{S}_{d}(N, Z))\\ &=&\frac{1}{2}(B(N+1, Z+1)-2B(N, Z)\\ &&+B(N-1, Z-1)).\end{array}\end{eqnarray} $
(14) This relation was used in [26, 58] for estimating the isovector np-interaction. Indeed, one can see that in the case of even A, the deuteron separation energy is not larger than the distance between the even-even and odd-odd mass surfaces, corrected for the deuteron binding energy Bd. The averaging indicator
${\Delta }_{np}^{(3)}$ cancels Bd and corresponds to$ \begin{eqnarray*}B{E}_{ee}-B{E}_{oo}\approx {\Delta }_{p}+{\Delta }_{n}\approx 2\Delta .\end{eqnarray*} $
Charge independence of nuclear forces implies that isovector np-pairing in odd-odd (N = Z) nuclei must be the same as neutron pairing in the neighbouring (N+1, Z−1) isotope and proton pairing in the (N−1, Z+1) isotope. Therefore, the indicator
${\Delta }_{np}^{(3)}$ in the chain of N = Z isotopes can be used to study np-correlations. It must be different for isotopes with N−Z≥2; nevertheless, it makes sense to examine the behaviour of indicators constructed by analogy with mass relations for like-nucleon pairing in isotopes chains with N−Z = Const ≥ 2.Relation (14) is analogous to the formula for OES for neutron pairing [12]:
$ \begin{eqnarray}\begin{array}{lll}{\Delta }_{n}^{(3)}(N, Z)&=&\frac{{(-1)}^{N+1}}{2}({S}_{n}(N+1, Z)-{S}_{n}(N, Z))\\ &=&\frac{{(-1)}^{N+1}}{2}(B(N+1, Z)-2B(N, Z)\\ &&+B(N-1, Z)).\end{array}\end{eqnarray} $
(15) By analogy with the averaged estimates of the OES effect, one can introduce an indicator based on binding energies of four nuclei [59]:
$ \begin{eqnarray}\begin{array}{lll}{\Delta }_{np}^{(4)}(N, Z)&=&\frac{1}{2}({\Delta }_{np}^{(3)}(N, Z)+{\Delta }_{np}^{(3)}(N-1, Z-1))\\ &=&\frac{{(-1)}^{N+1}}{4}({S}_{d}(N+1, Z+1)-2{S}_{d}(N, Z)\\ &&+{S}_{d}(N-1, Z-1)).\end{array}\end{eqnarray} $
(16) The diagrams of the coefficients for
${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ are given in Fig. 1(g) and (h), respectively. The (−1)N+1 multiplier is used only for chains of even-A nuclei. For these chains, the OES effect appears to be prominent, as the deuteron separation energy in even-even nuclei is consistently greater than in odd-odd nuclei. No such relation exists for odd-A nuclei, and the (−1)N+1 factor is omitted for the corresponding chains.The indicators
${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ for nuclei with N = Z are shown in Fig. 7(a). Since the deuteron separation energy Sd(A) does not have a common slope,${\Delta }_{np}^{(3)}(N, Z)$ and${\Delta }_{np}^{(4)}(N, Z)$ practically coincide. The dependence is smooth, with jumps in the regions of double magic numbers 16, 40, 56. The general shape of the dependence is in accordance with the approximation 2Δ = 24/A1/2 given in [12]. In the region of light nuclei, the majority of${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ values are above, and for A>40 - below this approximation. Further down in Fig. 7,${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ are shown for chains of odd-A nuclei with N=Z+1 (b), and even-A nuclei with N=Z+2 (c). From Fig. 7(b), it is clear that for most nuclei with odd A both indicators have practically zero values. All plots show similar behaviour, except that in the case of N=Z+2,${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ are smaller due to the absence of the Wigner term.
Figure 7. (color online) Indicators of np-correlations in the chains a) N=Z, b) N=Z+1, c) N=Z+2:
${\Delta }_{np}^{(3)}(A)$ (red line),${\Delta }_{np}^{(4)}(A)$ (green line),${\Delta }_{np}^{(13)}(A)$ (blue line), δnp(A) (dashed black line). The thin dotted line corresponds to 24/A1/2. Nuclear mass data are from [10].As we will see later,
${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ have a complex structure and are indirectly related to np-correlations. That is why there are different interpretations in literature. For example, in [14] the indicator${\Delta }_{np}^{(4)}$ was proposed as an estimator of four-nucleon correlations. -
The mass surface splitting is primarily due to the pairing of identical nucleons, but the estimate of the fluctuation between experimental masses of even-even and odd-odd nuclei is somewhat less than the sum of OES effects for protons Δp and neutrons Δn. This discrepancy is generally attributed to the presence of residual neutron and proton interactions [12], and in order to calculate the splitting between the mass surfaces for even-even and odd-odd nuclei one uses the relation [60-62]:
$ \begin{eqnarray}{E}_{ee}-{E}_{oo}={\Delta }_{n}+{\Delta }_{p}-\delta .\end{eqnarray} $
(17) The correction δ, arising from the residual attractive interaction of the unpaired proton and unpaired neutron, is interpreted as an np interaction and approximated by δ=20/A MeV [12].
Madland and Nix [61] obtained formulas for Δn, Δp and δ as finite differences on the basis of Taylor expansion to fourth-order. Thus, if five neighbouring isotopes or isotones are used to calculate the OES effect for neutrons Δn and protons Δp, then data for a substantially larger number of neighbouring nuclei are required to calculate the np-interaction indicators:
$ \begin{eqnarray}{\Delta }_{np}^{MN}(N, Z)={\Delta }_{n}+{\Delta }_{p}-{\delta }_{np}, \end{eqnarray} $
(18) where δnp(N, Z) is the correction for np-interactions:
$ \begin{eqnarray}\begin{array}{ll}{\delta }_{np}(N, Z)&=\frac{{(-1)}^{A}}{4}(2[B(N+1, Z)+B(N-1, Z)+B(N, Z+1)+B(N, Z-1)]-4B(N, Z)\\ &-[B(N+1, Z+1)+B(N-1, Z+1)+B(N-1, Z-1)+B(N+1, Z-1)]).\end{array}\end{eqnarray} $
(19) Proton and neutron OES in this case depend on the parity of the corresponding nucleons:
$ \begin{eqnarray}{\Delta }_{n}=\left\{\begin{array}{ll}{\Delta }_{n}^{(5)}(N, Z),&\, {\rm{even}}\, N\\ {\Delta }_{n}^{(5)}(N, Z)+{\delta }_{np},&\, {\rm{odd}}\, N\end{array}\right.\end{eqnarray} $
(20) $ \begin{eqnarray}{\Delta }_{p}=\left\{\begin{array}{ll}{\Delta }_{p}^{(5)}(N, Z),&\, {\rm{even}}\, Z\\ {\Delta }_{p}^{(5)}(N, Z)+{\delta }_{np},&\, {\rm{odd}}\, Z\end{array}\right.\end{eqnarray} $
(21) $ \begin{eqnarray}\begin{array}{ll}{\Delta }_{n}^{(5)}(N, Z)=&\frac{{(-1)}^{N}}{8}[{S}_{n}(N+2, Z)-3{S}_{n}(N+1, Z)\\ &+3{S}_{n}(N, Z)-{S}_{n}(N-1, Z)], \end{array}\end{eqnarray} $
(22a) $\begin{array}{c}{\Delta }_{p}^{(5)}(N, Z)=\frac{{(-1)}^{Z}}{8}[{S}_{p}(N, Z+2)-3{S}_{p}(N, Z+1)\\ \quad \quad +3{S}_{p}(N, Z)-{S}_{p}(N, Z-1)].\end{array}$
(22b) Diagrams for the indicators
${\Delta }_{np}^{MN}$ (18) and δnp (19) are shown in Fig. 1(i) and (f), from where the relationship between δnp and previously introduced indicators Δnp,${\Delta }_{np}^{(6, n)}$ and${\Delta }_{np}^{(6, p)}$ is clear. In fact, as in the case of identical nucleons, the relations from [61] are an additional averaging of the np-interaction energy Δnp over the mass surface.As mentioned above, the OES indicator
${\Delta }_{np}^{MN}$ (18) is indirectly related to the np-correlation, but we include it as a well-studied reference point. According to the diagram in Fig. 1(i), one can see that${\Delta }_{np}^{MN}$ for even-A nuclei is also an average, but of the indicator${\Delta }_{np}^{(3)}$ (14):$ \begin{eqnarray}\begin{array}{ll}{\Delta }_{np}^{MN}(N, Z)=&\frac{1}{4}(2{\Delta }_{np}^{(3)}(N, Z)-{\Delta }_{np}^{(3)}(N+1, Z-1)\\ &-{\Delta }_{np}^{(3)}(N-1, Z+1)), \end{array}\end{eqnarray} $
(23) It is interesting to note the similarity between
${\Delta }_{np}^{MN}$ (18) and the term d(A) in the Wigner energy (eq. 7). The latter can also be expressed as a combination of${\Delta }_{np}^{(3)}$ terms:$ \begin{eqnarray}\begin{array}{ll}d(A)=&\frac{1}{2}({\Delta }_{np}^{(3)}(N, Z)+{\Delta }_{np}^{(3)}(N+2, Z-2)\\ &-{\Delta }_{np}^{(3)}(N, Z-2)-{\Delta }_{np}^{(3)}(N+2, Z)).\end{array}\end{eqnarray} $
(24) The values
${\Delta }_{np}^{MN}(A)$ obtained from eq. (18) for nuclei with N = Z are shown in Fig. 7(a) and compared with Δnp(A). The dependence${\Delta }_{np}^{MN}(A)$ is smoother; in the region A>40 the indicators coincide to a high degree.Table 1 shows the results of fitting the various Δnp(A) indicators presented above with the power function C·A−b, for the chain of nuclei N = Z. In general, the results can be divided into two large groups. Indicators
${\Delta }_{np}^{MN}$ ,${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ , appropriate for assessment of mass splitting, and indicators Δnp and${\Delta }_{np}^{(7)}$ , based on the definition of np-pairing in odd-odd nuclei, all correspond to the approximation 2Δ = 24/A1/2 in [12], and they can be approximated with sufficient accuracy by the power functions A1/2 or A2/3 used to describe the pairing energy of nucleons in modern macroscopic models. The neutron OES effect, when fitted as${\Delta }_{n}^{(4)}={C}_{n}\cdot {A}^{-1/2}$ using the current data set results in a coefficient Cn slightly less than 12 MeV, Cn = 10.77±0.06 MeV [63]. This result is in good agreement with the fitting parameters for${\Delta }_{np}^{MN}(A)$ . Such an outcome can be explained by the fact that smooth formulas were used for approximating both Δn(A) and Δnp(A).N=Z N−Z=2 C/MeV b C/MeV b Δnp(A) 29.4±1.8 0.60±0.02 5.8±0.8 0.37±0.04 ${\Delta }_{np}^{(7)}(A)$ 23.3±1.6 0.53±0.03 6.0±0.6 0.39±0.03 ${\Delta }_{np}^{(6n)}(A)$ 10.3±1.4 0.56±0.05 1.0±0.3 0.14±0.08 ${\Delta }_{np}^{(6p)}(A)$ 9.3±1.3 0.52±0.04 0.0±0.1 -0.7±0.3 ${\delta }_{np}^{}(A)$ 6.9±1.1 0.45±0.05 0.2±0.1 0.2±0.1 ${\Delta }_{np}^{(3)}(A)$ 25.9±1.3 0.53±0.02 10.8±0.8 0.33±0.02 ${\Delta }_{np}^{(4)}(A)$ 32.7±2.1 0.59±0.02 12.2±0.8 0.36±0.02 ${\Delta }_{np}^{MN}(A)$ 19.9±1.6 0.48±0.02 15.2±0.6 0.41±0.01 Table 1. Parameters of the fits Δnp(A)=C·A−b in nuclei with N=Z and N−Z=2.
Significantly smaller values of the fitting parameter C are obtained for
${\Delta }_{np}^{(6n)}, {\Delta }_{np}^{(6p)}$ and δnp. The small values and their significant fluctuations indicate that the approximations are unreliable. It should be noted, however, that the parameters of the approximations for these indicators are in good agreement with each other.
2.1. Mass relations “by definition” and the δVnp indicator
2.2. Wigner term
2.3. np-correlation from Sn and Sp
2.4. Mass relations based for deuteron separation energy
2.5. Mass surface OES
-
The first step in interpreting the mass relations obtained can be made within the framework of the Shell Model [55]. Consider a nucleus with n neutrons in the state j1 and p protons in the state j2 above the closed core (N0, Z0). The binding energy of such a configuration can be represented as a sum:
$ \begin{eqnarray}\begin{array}{ll}B({N}_{0}+n, {Z}_{0}+p)=&B({N}_{0}, {Z}_{0})+n{\varepsilon }_{n}+p{\varepsilon }_{p}\\ &+W({j}_{1}^{n})+W({j}_{2}^{p})+I({j}_{1}^{n}, {j}_{2}^{p}), \end{array}\end{eqnarray} $
(25) where εn and εp denote single-particle central-field energies of the j1 neutrons and j2 protons, respectively. Terms W(j) correspond to the interaction energy of nucleons in a given shell, while I(j1, j2) denotes the interaction energy between nucleons located on different shells. The contribution of the interaction of n identical nucleons in the state j can be written as the sum of two terms:
$ \begin{eqnarray}W({j}^{n})=\frac{1}{2}\left(n-\frac{1-{(-1)}^{n}}{2}\right)\pi +\frac{n(n-1)}{2}d, \end{eqnarray} $
(26) the first of which is due to the coupling of identical nucleons with “pairing energy” π. The second term describes the additional interaction of two nucleons with strength d, which is independent of the relative orientation of their spins, and is of repulsive nature. The relationship of these quantities is clearly seen in the dependence of Sn(N) for Z = Const (Fig. 3). The pairing energy π is responsible for the zigzag behaviour of the curve and is determined by the difference between Sn(N) in neighbouring nuclei with even and odd N. The value of d defines the slope of the curve and can be estimated from the difference Sn(N+1)−Sn(N−1). Fig. 4 shows the scheme that allows to estimate the values of π and d using Sn(N) in isotones. The mass difference relations for identical nucleons were considered in detail in our previous paper [19].
The interaction of n neutrons in state j1 and p protons in state j2 can be written as the sum of two terms [64]:
$ \begin{eqnarray}I({j}_{1}^{n}, {j}_{2}^{p})=np{I}^{0}+\frac{(1-{(-1)}^{n})(1-{(-1)}^{p})}{4}{I}^{^{\prime} }, \end{eqnarray} $
(27) where the contribution I0 does not depend on the nucleon spin orientation and is determined by the scalar interaction. The contribution I′ depends on the value of the total spin J, represents the “pairing properties” of the interaction and, accordingly, is present in odd-odd nuclei only.
Therefore, relation (25) can be rewritten in the form [55]:
$ \begin{eqnarray}\begin{array}{ll}B({N}_{0}+n, {Z}_{0}+p)=&B({N}_{0}, {Z}_{0})+n{\varepsilon }_{n}+p{\varepsilon }_{p}+\frac{n}{2}{\pi }_{n}+\frac{p}{2}{\pi }_{p}\\ &+\frac{n(n-1)}{2}{d}_{n}+\frac{p(p-1)}{2}{d}_{p}+np{I}^{0}-\delta, \end{array}\end{eqnarray} $
(28) where the parity term δ is given by
$ \begin{eqnarray}\delta =\left\{\begin{array}{ll}0,&ee, \\ \frac{1}{2}{\pi }_{p},&eo, \\ \frac{1}{2}{\pi }_{n},&oe, \\ \frac{1}{2}{\pi }_{n}+\frac{1}{2}{\pi }_{p}-{I}^{^{\prime} },&oo.\end{array}\right.\end{eqnarray} $
(29) This relation is simplistic but allows to identify some regularities in the behaviour of the indicators based on mass differences.
The neutron separation energy in this representation depends on the parity of N and Z:
$ \begin{eqnarray}{S}_{n}(N, Z)=\left\{\begin{array}{ll}{\varepsilon }_{n}+(n-1){d}_{n}+p{I}^{0}+{\pi }_{n},&ee\\ {\varepsilon }_{n}+(n-1){d}_{n}+p{I}^{0},&oe\\ {\varepsilon }_{n}+(n-1){d}_{n}+p{I}^{0}+{\pi }_{n}-{I}^{^{\prime} },&eo\\ {\varepsilon }_{n}+(n-1){d}_{n}+p{I}^{0}+{I}^{^{\prime} },&oo\end{array}\right.\end{eqnarray} $
(30) Hence, the following relations hold for pairing of neutrons in an even-even nucleus:
$ \begin{eqnarray}{\Delta }_{nn}={\pi }_{n}+{d}_{n}, \end{eqnarray} $
(31) $ \begin{eqnarray}{\Delta }_{nn}^{(3)}={\pi }_{n}-{d}_{n}, \end{eqnarray} $
(32) $ \begin{eqnarray}{\Delta }_{nn}^{(5)}=2{\Delta }_{n}^{(5)}={\pi }_{n}.\end{eqnarray} $
(33) In this model, as d < 0, Δnn for even N is always smaller than for odd N. Furthermore,
${\Delta }_{nn}^{(3)}$ has an inverse relation, and the averaging indicator${\Delta }_{nn}^{(5)}$ depends only on the neutron pairing energy πn. The value of d can also be extracted from the mass relations as the difference$({\Delta }_{nn}-{\Delta }_{nn}^{(3)})/2$ . -
Let us consider the structure of the previously introduced mass relations for np-correlations. The values of the indicators Δnp (2) and
${\Delta }_{np}^{(7)}$ (3) significantly differ for even and odd A:$ \begin{eqnarray}{\Delta }_{np}={\Delta }_{np}^{(7)}={I}^{^{\prime} }+{I}^{0}\, (ee, oo), \end{eqnarray} $
(34) $ \begin{eqnarray}{\Delta }_{np}={\Delta }_{np}^{(7)}={I}^{^{\prime} }-{I}^{0}(oe, eo).\end{eqnarray} $
(35) Good agreement of these relations was shown above on the example of even A nuclei (see Fig. 2). It should be noted that the averaging in the relation
${\Delta }_{np}^{(7)}$ does not allow to separate contributions of I0 and I′.The contribution of I′ can be determined, by analogy with like-nucleon pairing, from the indicators
${\Delta }_{np}^{(6, n)}$ (12) and${\Delta }_{np}^{(6, p)}$ (13):$ \begin{eqnarray*}{\Delta }_{np}^{(6, n)}={\Delta }_{np}^{(6, p)}={I}^{^{\prime} }\end{eqnarray*} $
and consequently by the indicator
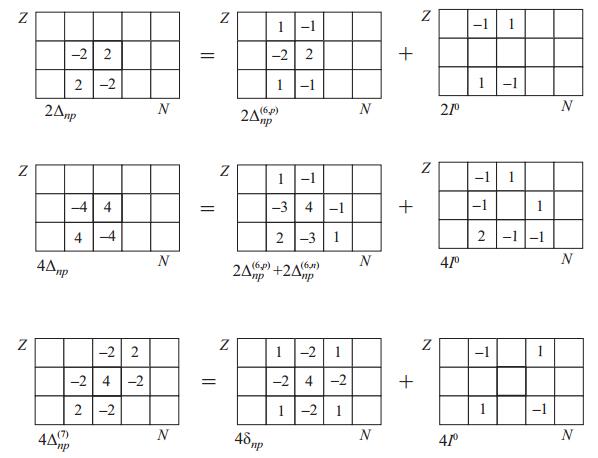
${\delta }_{np}(N, Z)=({\Delta }_{np}^{(6, p)}(N, Z)+{\Delta }_{np}^{(6, p)}(N+1, Z))/2={I}^{^{\prime} }$ (see eq. (19)). Comparison of the diagrams for the indicators Δnp and${\Delta }_{np}^{(6, p)}$ (see Fig. 8, first row) leads to the expression for the parameter I0 in even-A nuclei:$ \begin{eqnarray}\begin{array}{ll}{I}^{0}(N, Z)=&\frac{1}{2}[B(N, Z+1)-B(N-1, Z+1)\\ &+B(N-1, Z-1)-B(N, Z-1)].\end{array}\end{eqnarray} $
(36) One can obtain a similar formula for
${\Delta }_{np}^{(6, n)}$ . As shown earlier, the results for${\Delta }_{np}^{(6, n)}$ (12) and${\Delta }_{np}^{(6, p)}$ (13) differ slightly and it is useful to average them.Diagrams for this case are shown in the second row of Fig. 8, and the results of calculations are presented in Fig. 9 by solid lines. The values of I0 lie above I′, and for nuclei with N = Z agree well with the dependence 12/A1/2, which was proposed to describe the pairing effect. The values of I′ fluctuate much more. With increasing A, the values of I0 and I′ converge, but the ratio between them can vary. Dashed lines show I0 and I′ calculated using the averaged formula for I′=δnp. The diagrams in this case are symmetrical (see the third row of Fig. 8). The sum I0+I′ is related to the indicator
${\Delta }_{np}^{(7)}$ , and the expression for I0 is of the form: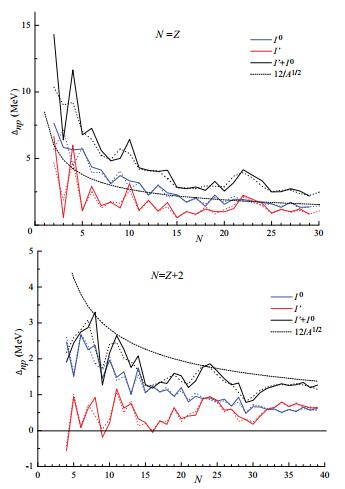
Figure 9. (color online) Comparison of Δnp, I0, I′ in chains of nuclei with N = Z (a) and N−Z = 2 (b). Solid lines show the results for averaged parameters from the second row in Fig. 8 (
${I}^{^{\prime} }=({\Delta }_{np}^{6, p}+{\Delta }_{np}^{6, n})/2$ ); dashed lines correspond to the third row (I′=δnp).$ \begin{eqnarray}\begin{array}{ll}{I}^{0}(N, Z)=&\frac{1}{4}[B(N+1, Z+1)-B(N-1, Z+1)\\ &+B(N-1, Z-1)-B(N+1, Z-1)].\end{array}\end{eqnarray} $
(37) This formula coincides with the expression for the empirical np-interaction of the last neutron with the last proton in even-even nuclei δVnp from [21, 23, 41]. The important point here is that in this case the binding energies of odd-odd nuclei are used in the calculations, in contrast to relation (5), where
$\delta {V}_{np}^{ee}$ is based on B(N, Z) in even-even isotopes. This difference does not significantly change the numerical results in general, but should be taken into account in more accurate models.Table 2 gives the coefficients C when the parameters π and d for identical nucleon interaction are approximated by the function C·A−b. The parameters were fitted without taking into account the magic and self-adjoint nuclei, in accordance with the selection rules from [13]. The fixed exponents b were chosen to be close to the fits with two free parameters C and b. For the parameters πn and πp, the fitted values of b are 0.30±0.01 and 0.32±0.01, respectively, which is close to 1/3. For the parameters dn and dp, the chosen value of b is unity, which agrees well with the fit coefficient b for neutrons (0.93±0.03); for protons, the deviation of the fit coefficient b from unity is more significant due to the effect of Coulomb interaction (0.56±0.01).
neutrons protons π(A)=C/A1/3 10.22±0.06 11.48±0.06 d(A)=C/A −23.0±0.3 −56.7±0.6 Table 2. Coefficients C (MeV) for fitting π and d for like-nucleons with the power function C·A−b
The values of the coefficient C when the parameters I0 and I′ are approximated by the power function C·A−b are given in Table 3 for various values of b. The fixed values of b allow to compare I0 and I′ to each other, and to π and d. The fit of I0 and I′ by a power function with a free exponent gives the values of b equal to 0.83±0.01 and 0.67±0.02, respectively. Thus, the best approximation for I0 is C/A, whereas C/A2/3 describes I′ well. For all b, the coefficients C for I0 and I′ are similar, but C for I0 is always larger.
I0 I′ C/A 41.9±0.3 30.7±0.4 C/A2/3 9.43±0.06 7.04±0.08 C/A1/3 1.93±0.02 1.46±0.02 Table 3. Coefficients C (MeV) for fitting I0 and I′ with the power function C·A−b for various fixed b
-
The splitting of the mass surface
${\Delta }_{np}^{MN}(N, Z)$ , given by formula (18), does not depend on the parity of N and Z in the Shell Model with parametrization (25), and has the form:$ \begin{eqnarray}{\Delta }_{np}^{MN}(N, Z)=\frac{{\pi }_{n}}{2}+\frac{{\pi }_{p}}{2}-{I}^{^{\prime} }, \end{eqnarray} $
(38) which corresponds to the definition of the indicator. However, it is important to note that this relation is valid only for nuclei with even A; for odd-A nuclei the meaning of this indicator is not obvious. More significant are the indicators
${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ . Indicator${\Delta }_{np}^{(3)}(N, Z)$ depends on the parity of N and Z:$ \begin{eqnarray}{\Delta }_{np}^{(3)}(N, Z)=\frac{1}{2}\left\{\begin{array}{ll}(({\pi }_{n}-{d}_{n})+({\pi }_{p}-{d}_{p}))-2({I}^{^{\prime} }+{I}^{0}),&ee\\ (-({\pi }_{n}-{d}_{n})+({\pi }_{p}+{d}_{p}))+2{I}^{0},&oe\\ (({\pi }_{n}+{d}_{n})-({\pi }_{p}-{d}_{p}))+2{I}^{0},&eo\\ (({\pi }_{n}+{d}_{n})+({\pi }_{p}+{d}_{p}))-2({I}^{^{\prime} }-{I}^{0}),&oo\end{array}\right.\end{eqnarray} $
(39) The expression for even-even nuclei corresponds to the splitting of the mass surface between even-even and odd-odd nuclei
$ \begin{eqnarray*}{\Delta }_{np}^{(3)}(ee)=\frac{1}{2}({\Delta }_{nn}^{(3)}(ee)+{\Delta }_{pp}^{(3)}(ee))-{\Delta }_{np}(ee), \end{eqnarray*} $
The relation for nuclei with odd A contains the energy difference of identical nucleon pairing, and includes a small splitting of the mass surface between even-odd and odd-even nuclei.
The relations for the indicator
${\Delta }_{np}^{(4)}$ depend on the parity of A:$ \begin{eqnarray}{\Delta }_{np}^{(4)}(N, Z)=\frac{1}{2}\left\{\begin{array}{ll}({\pi }_{n}+{\pi }_{p})-2{I}^{^{\prime} },&ee, oo\\ ({d}_{n}+{d}_{p})+2{I}^{0},&oe, eo\end{array}\right.\end{eqnarray} $
(40) This expression for even A agrees with the expression for
${\Delta }_{np}^{MN}$ . The degree of accordance can be seen in Fig. 7 on the example of the chain of N=Z nuclei. The figure shows the dependence of indicators${\Delta }_{np}^{MN}, {\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ on the mass number, and it is clear that while${\Delta }_{np}^{MN}$ and${\Delta }_{np}^{(4)}$ agree well only in the region A>40, indicators${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ agree to good accuracy for all N and Z, except for the magic numbers. From the approximate equality${\Delta }_{np}^{(3)}\approx {\Delta }_{np}^{(4)}$ for odd-odd nuclei, it follows:$ \begin{eqnarray}\begin{array}{ll}\frac{1}{2}(({\pi }_{n}+{d}_{n})+({\pi }_{p}+{d}_{p}))&-({I}^{^{\prime} }-{I}^{0})\approx \frac{1}{2}({\pi }_{n}+{\pi }_{p})-{I}^{^{\prime} }, \\ &\frac{1}{2}({d}_{n}+{d}_{p})+{I}^{0}\approx 0.\end{array}\end{eqnarray} $
(41) The last relation links the values of the parameters d and I0, and also shows that for odd A,
${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ are close to zero. Indeed, the estimates of π, d and I made in [55] on the array of stable nuclei, show that dn is about −0.1 MeV, dp is about −0.5 MeV, and I0 has a value of about 0.3 MeV. The fact that the values of${\Delta }_{np}^{(3)}$ and${\Delta }_{np}^{(4)}$ are close to zero for odd A points to the equality of the pairing forces of identical nucleons:$ \begin{eqnarray}\begin{array}{ll}\frac{1}{2}(-({\pi }_{n}-{d}_{n})+({\pi }_{p}+{d}_{p}))+&{I}^{0}\approx \frac{1}{2}({d}_{n}+{d}_{p})+{I}^{0}\approx 0, \\ &{\pi }_{p}\approx {\pi }_{n}, \end{array}\end{eqnarray} $
(42) which follows from the charge independence of nuclear forces. The degree of agreement of these relations is clearly seen in the values of the coefficients C for π, d and I in Tables 2 and 3.
3.1. Neutron - proton interaction
3.2. “Deuteron-type” relations and mass staggering
-
Mass relations based on even-odd staggering of the mass surface are widely used to estimate the identical nucleon pairing in atomic nuclei. By analogy, a significant number of mass indicators are constructed for np-correlations in order to estimate the value of np-pairing. However, the difficulty of extracting experimental information for odd-odd nuclei significantly limits the possibilities of analysing the values obtained.
In this paper, various indicators Δnp are considered for both odd-odd and even-even nuclei. The estimates of the np-pair separation and the relations constructed by analogy with the estimates for like-nucleon pairing, can both serve as basis for construction of different mass relations. It turns out that almost all formulas are related to each other. They are based on the standard expression for the neutron-proton correlation in an odd-odd nucleus:
$ \begin{eqnarray*}\begin{array}{ll}{\Delta }_{np}=&B(N, Z)+B(N-1, Z-1)\\ &-B(N-1, Z)-B(N, Z-1), \end{array}\end{eqnarray*} $
and are either an average or a difference of their respective values for the neighbouring nuclei. Thus, the widely discussed quantity δVnp, which coincides with the definition of Δnp for odd-odd nuclei, is an average of Δnp over four isotopes when applied to even-even nuclei. The correction for the np interaction, δnp, commonly mentioned in discussions of the mass surface splitting, is also an average of Δnp over four neighbouring nuclei, performed, however, by taking into account the zigzag features of the neutron separation energy in isotopes (or proton separation energy in isotones).
This approach is similar to the method used to obtain an estimate of like-nucleon pairing energy, but it can lead to different results. In general, the zigzag relation depends on two parameters, π and d, which determine the amplitude of the oscillations and the general slope of the dependence. While for identical nucleons π and d differ considerably, the parameters Sn(Z) in isotones and Sp(N) in isotopes used to construct the mass relations are close in magnitude. Furthermore, the relationship between various nuclear parameters can change within an isotope chain. Such changes inevitably affect the results of calculations using formulas analogous to those for like-nucleon pairing, and lead to appearance of alternating quantities.
To clarify the structure of various indicators Δnp, parametrization of the binding energy of the atomic nucleus based on the Shell Model was used. This approach effectively takes into account both the residual interaction of identical nucleons in a single state, and the interaction of nucleons on different subshells, such as between external neutrons and protons. Such a parametrization makes it possible to show more clearly the relationship of different mass formulas, and to elucidate their physical meaning. In the context of this parametrization, the pair interaction of identical nucleons is described by the sum of two terms
$ \begin{eqnarray*}{\Delta }_{nn(pp)}={\pi }_{n(p)}+{d}_{n(p)}.\end{eqnarray*} $
The first term is responsible for pairing of identical nucleons with the “pairing energy” π, while the second describes the additional repulsive interaction of a nucleon pair with strength d, independent of the relative orientation of the nucleon spins. However, taking into account the typical values of π and d, using only parameter π to describe the pairing forces does not greatly affect the result. In this approach, the np interaction in odd-odd nuclei should include both contributions
$ \begin{eqnarray*}{\Delta }_{np}={I}^{0}+{I}^{^{\prime} }.\end{eqnarray*} $
As the values of I0 and I′ are similar, taking into account only one of these parameters changes the result by a factor of two. This is best seen from the comparison of the indicator Δnp with the averaged quantities
${\Delta }_{np}^{(6, n)}$ ,${\Delta }_{np}^{(6, p)}$ and δnp, which are all about Δnp/2.Approximation of I0 and I′ by a power function C/Ab, with various constant values of b, demonstrates a clear relationship of various parameters in the whole modern range of atomic nuclei. The coefficients C, when dn, dp and I0 are approximated by C/A, are of the same order of magnitude, and are related as dn+dp≈−2I0. In turn, the pairing parameters of identical nucleons πn and πp are well described by C/A1/3, with the coefficients C having similar values slightly above 10 MeV. The coefficient C in the approximation of I′ by C/A1/3 is almost an order of magnitude smaller, 1.38±0.02 MeV, which clearly illustrates the relationship of the pairing effects of identical nucleons and the np-interaction.
The authors would like to thank Dr. D. Lanskoy and L. Imasheva for fruitful discussions and technical support.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: