-
Over the past few years, much effort in both theory and experiment has been directed to the study of reactions induced by weakly-bound nuclei, especially the elastic scattering, breakup and fusion [1-5]. The occurrence of breakup of weakly-bound nuclei may lead to further reactions, which makes the whole reaction process more complicated [4]. 92,93Nb are the residues of the 6Li+89Y experiment performed at LNL-INFN in Italy, with the goal of studying the reaction mechanisms of a weakly-bound nuclear system [6, 7]. In the following, the processes that produce 92,93Nb nuclei and that involve fusion-evaporation and can be identified with γ-particle coincidence measurements are discussed. Since gamma-gamma coincidence measurements were performed in the present experiment, it was an opportunity to further explore the level schemes of 92,93Nb.
It is well known that the level structure of nuclei N=50,51 is dominated by single-particle excitations, even for states with high spin. On the other hand, nuclei with N≥55 exhibit collective behavior [8, 9].
As it si a nearly spherical nucleus with N=51 in the A~90 mass region, the studies of the excited states of 92Nb are of importance for establishing and testing the residual interactions in shell model calculations. Previously, the level structure of 92Nb was mainly investigated by proton and 3He induced reactions [10-13], and the energies of excited states were extended up to 3797 keV by the 88Sr (7Li, 3n)92Nb experiment [14]. Recently, high-spin states of 92Nb were studied in the heavy ion fusion-evaporation reaction 82Se (14N,4n)92Nb [15]. For the middle-low excited states of 92Nb, the information is relatively scarce, and thus it is important to further explore this nucleus experimentally. From the theoretical point of view, 92Nb was studied within the framework of the shell model, and its low-lying levels below Elevel=2287 keV [12] were described by taking the even-even nucleus 88Sr as the inert core, while the valance nucleons occupy the πp1/2, g9/2 and νd5/2 orbitals. Nevertheless, from the theoretical point of view, further study of 92Nb is still necessary.
As a “transitional” nucleus with N=52, the excitation of 93Nb is relative intricate [8]. In an earlier work, 93Nb was studied in the (n, nγ) and (p,2nγ) reactions [16]. The Iπ=3/2- at 1840 keV and Iπ=5/2- at 2013 keV were identified as mixed-symmetry states, which can be viewed as low-energy collective modes where protons and neutrons move uncoupled. High-spin states were studied in the 82Se(16O, p4n)93Nb reaction, with the level schemes up to excitation energy of 11 MeV [17]. An M1 rotational band was reported and showed the characteristics of oblate collective rotational band. The investigation of the level structure of 93Nb can provide additional information for a systematic study of nuclei with N=52.
In this work, the low-lying structure of 92Nb was further studied, and its proposed level scheme was calculated using the shell model code NushellX with SNE valence space, and compared with the experimental results. In addition, two new transitions were observed in 93Nb, as discussed in the following section.
-
The study of the 6Li+89Y reaction was performed at LNL-INFN in Italy. A 550 μg/cm2 89Y target, which was supported by a 340 μg/cm2 12C foil, was bombarded by the Elab=34 MeV 6Li3+ beam with an average intensity of 1.0 enA, provided by the Tandem-XTU accelerator. The γ-rays were detected by the GALILEO array, which is composed of 25 Compton-suppressed high-purity germanium (BGO-HPGe) detectors arranged in 4 rings: 10 at 90° and 15 at 119°, 129°, 152° with respect to the beam direction [18]. The EUCLIDES 4π Si-telescope array, which consists of 5 segmented and 35 single plates of ΔE/E Si telescopes (the thicknesses of the ΔE and E detectors are 130 μm and 1000 μm, respectively) was used to collect the emitted light charged particles [19]. The distance between the center of the Si telescopes and the center of the target was around 6.2 cm. An Al cylinder was inserted inside EUCLIDES, so that backward angles larger than 150° were unshielded. The thickness of the Al cylinder was 200 μm, so as to stop the intense scattered beam particles from destroying the Si detectors. The energy and efficiency calibrations of each Ge detector in the real geometrical conditions were performed with the following standard sources: 60Co, 241Am, 133Ba, 152Eu, 88Y, covering the energy region from 39.522 keV (152Eu) to 2734 keV (88Y). After further delicate energy calibrations and gain matching with characteristic γ-rays of the residual nuclei, the recorded γ-γ coincidence events were sorted into a two-dimensional Eγ-Eγ symmetric matrix, and two asymmetric ADO matrices. In this experiment, about 14×106 γ-γ coincidence events (without any particle selection) were collected.
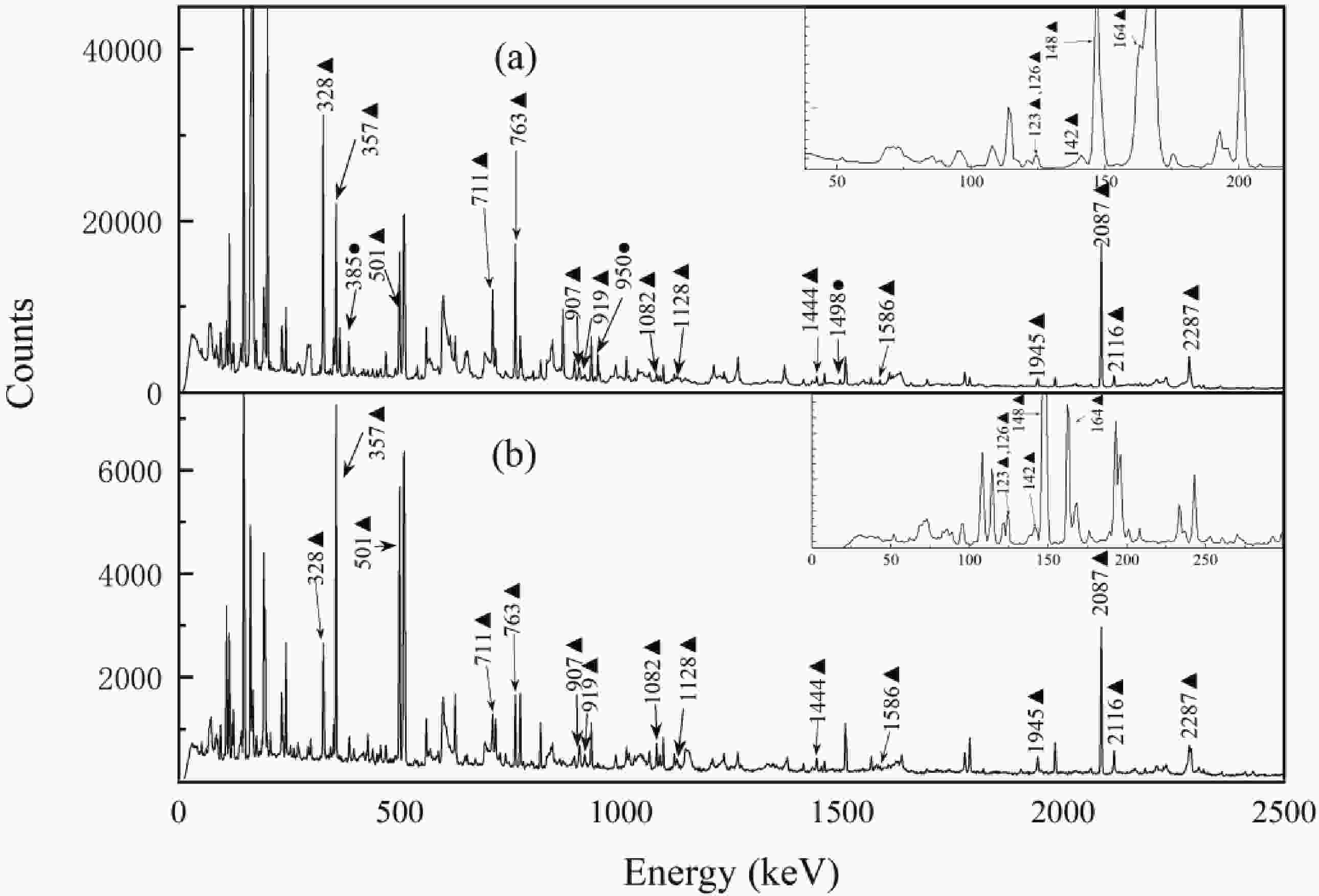
The fusion reaction induced by a weakly-bound projectile at near-barrier energies is complicated due to low breakup threshold [6, 20]. When the projectile completely fuses with the target nucleus without breakup (BU), the process is a direct complete fusion (DCF). When the projectiles breakup, then: 1) if all the fragments fuse with the target nucleus, the process is a sequential complete fusion (SCF); or 2) if only part of the fragments fuse with the target nucleus, the process is an incomplete fusion (ICF) [6]. In addition, when a medium-mass target nucleus is involved, the fusion process can evaporate not only neutrons but also light charged particles including protons and alpha particles. In the present experiment, 92Nb can be produced in a complete fusion of 6Li with the 89Y target nuclei, followed by the 1p2n evaporation channel. As a result, the characteristic γ-rays from 92Nb are in coincidence with protons emitted from the compound nucleus, as shown in Fig. 1(a). In addition, the 92Mo residue from the reaction can only be produced by the CF process. The yield ratio of 92Nb to 92Mo (92Nb/92Mo) in the present experiment is around 0.38, which is larger than given by the statistical evaporation model (around 0.26). Such an increment of the 92Nb/92Mo ratio indicates that the ICF process may contribute to the production of 92Nb. Fig. 1(b) shows the γ-ray spectrum measured in coincidence with deuterons, in which the characteristic gamma rays of 92Nb are clearly visible. It is concluded that 92Nb can also be populated in the ICF process of 6Li, where alpha particles from the breakup of 6Li fuse with the 89Y target nucleus, and simultaneously, the other fragment (deuteron) escapes and is detected. In summary, the 92Nb residue observed in this experiment was populated in the 89Y(6Li, p2n)92Nb and 89Y(α,n)92Nb reactions.
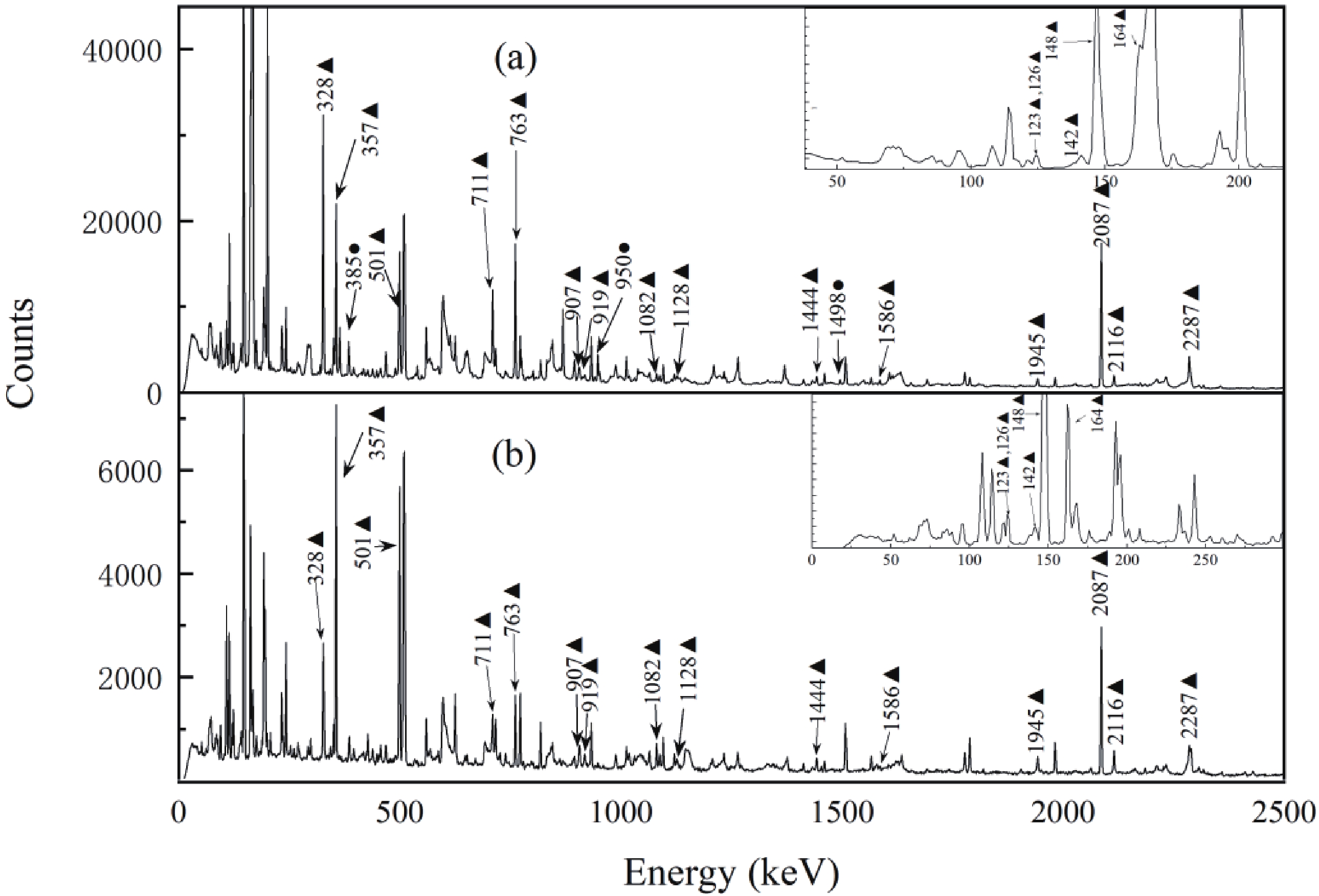
Figure 1. γ-energy spectra in coincidence with protons (a) and deuterons (b). Representative γ-rays from 92Nb and 93Nb are marked with black triangles and black circles, respectively.
The 93Nb residue in the present experiment can be produced by the complete fusion of 6Li with 89Y , followed by the 1p1n evaporation channel, as can be seen in the proton gated spectrum shown in Fig. 1(a). The cross-section for alpha particle stripping from 6Li on a 89Y target producing 93Nb is small, and this process can be neglected.
-
The level structure of 92Nb was studied by several researchers [10-14]. The high-spin states of 92Nb were recently studied in the 82Se(14N,4n)92Nb reaction by Wu et al [15]. The projectile used in the present experiment brings lower excitation energy to the compound nucleus, so that the relatively lower excited states of 92Nb can be populated and the middle-low level structure of 92Nb studied. The proposed level scheme of 92Nb is shown in Fig. 2, which is extended up to ~5.4 MeV excitation energy, and 20 new transitions and 8 new levels are added to 92Nb. Sample coincidence spectra, gated on 2287, 387, 328 and 115 keV, are shown in Fig. 3(a)-(d). The relative intensities (Iγ) and the initial and final states (
$ E_{\rm i}^\pi $ and$ E_{\rm f}^\pi $ ) of the observed transitions in 92Nb are summarized in Table 1.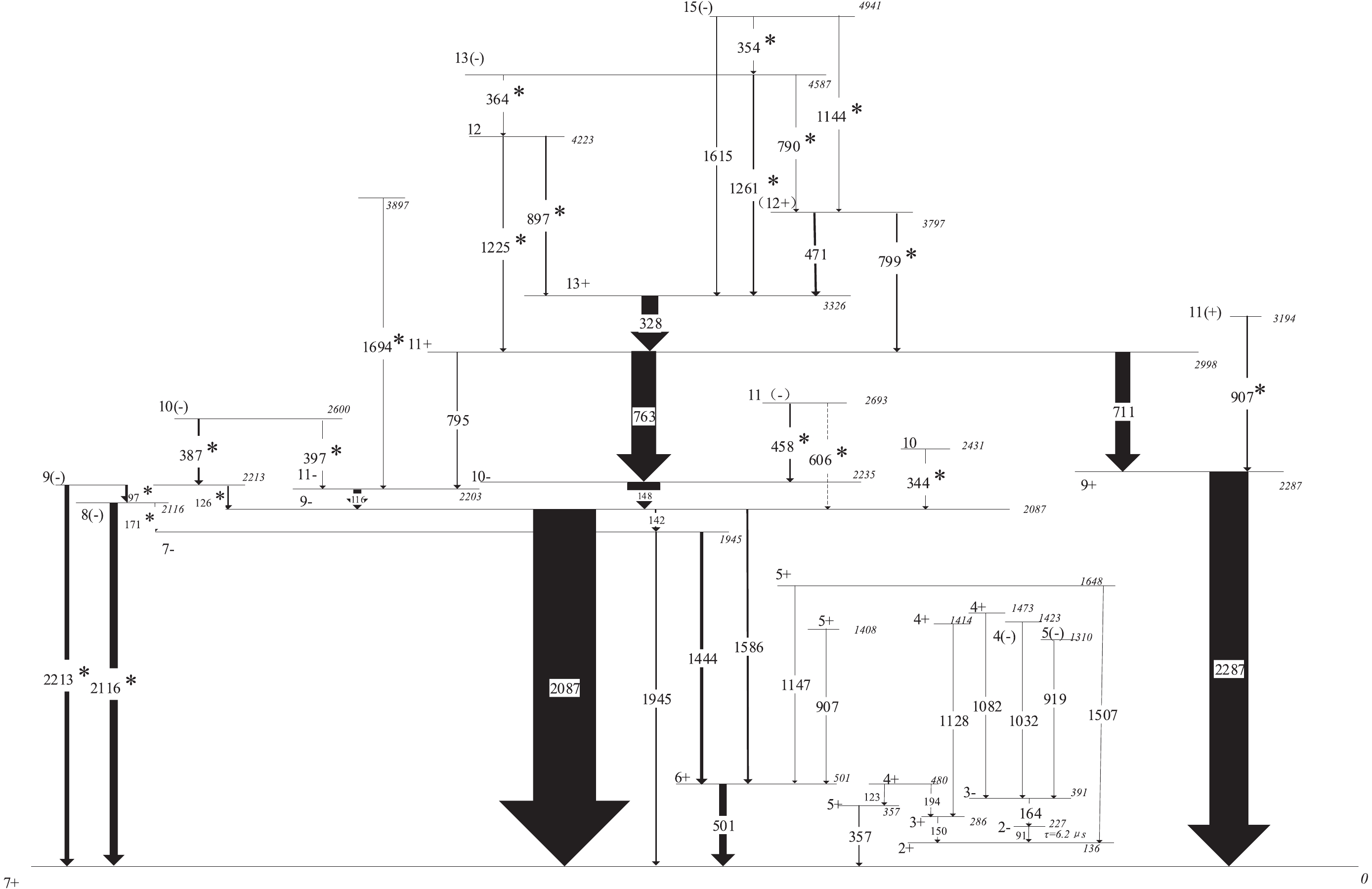
Figure 2. Level scheme of 92Nb proposed by the present work. New transitions are denoted with asterisks. The width of arrows indicates relative intensity of γ-rays.
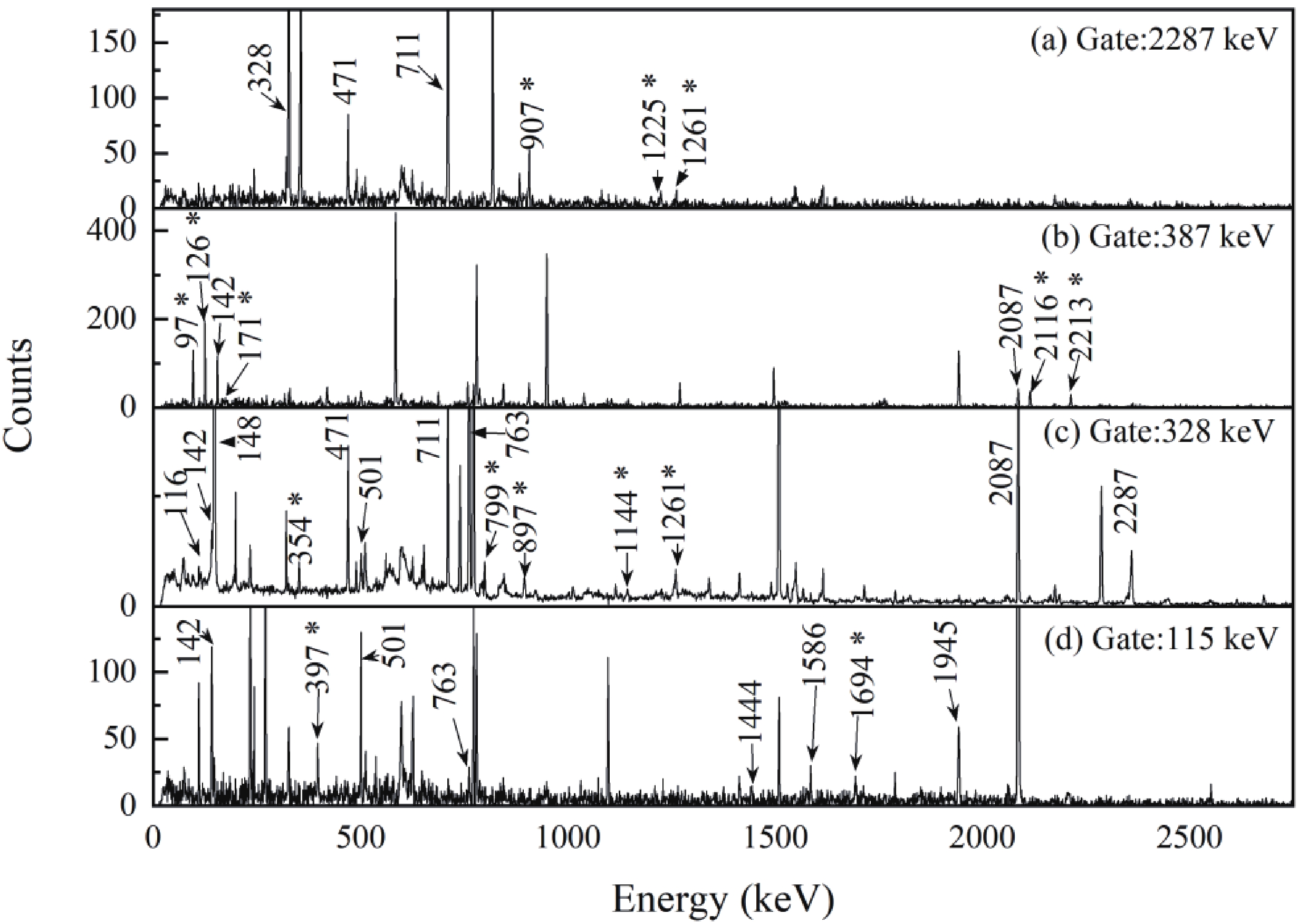
Figure 3. Typical prompt γ-γ coincidence spectra for 92Nb, gated on 2287, 387, 325, and 115 keV, respectively.
Eγ /keV Iγa Eiπ→Efπ RADOc Jiπ→Jfπ 97* 8.79(159) 2213→2116 0.71(13) 9(−)→8(−) 116 15.08(80) 2203→2087 1.40(10) 11−→9− 126* 2.68(23) 2213→2087 1.58(25) 9(−)→9− 142 3.07(27) 2087→1945 1.63(33) 9−→7− 148 53.81(280) 2235→2087 0.94(5) 10−→9− 171* 0.49(18) 2116→1945 — 8(−)→7− 328 27.18(151) 3326→2998 1.52(9) 13+→11+ 344* 0.82(12) 2431→2087 0.96(23) 10→9− 354 * 0.66(8) 4941→4587 1.46(37) 15(−)→(13−) 364* 0.43(7) 4587→4223 0.96(30) (13−)→12(−) 387* 3.03(41) 2600→2213 0.96(13) 10(−)→9(−) 397* 0.92(25) 2600→2203 0.94(36) 10(−)→11− 458* 1.92(18) 2693→2235 0.71(15) 11(−)→10− 471 3.53(25) 3797→3326 0.88(8) (12+)→13+ 501 12.77(180) 501→0 0.80(11) 6+→7+ 606* Wb 2693→2087 — 11(−)→9(−) 711 23.85(126) 2998→2287 1.80(11) 11+→9+ 763 39.35(168) 2998→2235 0.95(6) 11+→10− 790* 0.66(11) 4587→3797 1.00(25) (13−)→(12+) 795 1.78(26) 2998→2235 — 11+→11− 799* 2.07(26) 3797→2998 — (12+)→13+ 897* 1.67(76) 4223→3326 0.91(16) 12−→11+ 907* 2.29(34) 3194→2287 1.78(49) 11(+)→9+ 1144* 0.19(6) 4941→3797 — 15−→(12+) 1225* 1.67(18) 4223→2998 0.95(46) 12(−)→11+ 1261* 4.09(52) 4587→3326 1.51(20) (13−)→13+ 1444 5.05(62) 1945→501 0.94(12) 7−→6+ 1586 3.09(45) 2087→501 — 9−→6+ 1694* Wb 3897→2203 — →11− 1945 2.74(56) 1945→0 1.37(27) 7−→7+ 2087 100 2087→0 1.40(8) 9−→7+ 2116* 12.83(358) 2116→0 0.83(19) 8(−)→7+ 2213* 7.67(170) 2213→0 1.66(67) 9(−)→7+ 2287 61.98(367) 2287→0 1.66(14) 9+→7+ a The errors of the relative intensity include the fitting and efficiency corrections. Wb The intensities of transitions are too weak. c The errors of the ADO ratios include the fitting and efficiency corrections. Table 1. Transition energies (Eγ) of 92Nb, relative intensities of γ-rays (Iγ), initial and final states for γ-rays, ADO ratios, initial and final spins of the transitions.
In order to obtain the multipolarity of the newly observed γ-rays, the angular distributions of each γ-ray from the oriented residues (ADO) were analyzed. Assuming that γ1 and γ2 are the cascading transitions in the same nucleus, the ADO ratio of γ1 is deduced by Iγ1(152°)/Iγ1(90°), where Iγ1(152° or 90°) represents the intensity of γ1-rays collected by the detectors at 152° or 90° , and in coincidence with γ2-rays measured by all detectors. By calculating the ADO ratio of γ-rays with known multipolarity in 92Mo, 91Mo, 92Nb, 93Nb, 90Zr, 89Zr produced in the present experiment, typical ADO ratios Iγ(152°)/Iγ(90°) for quadrupole and dipole transitions are around 1.6 and 0.8, respectively, as shown in Fig. 4(a). The spins of the states of 92Nb are assigned tentatively. For the two lower transitions, 97 and 126 keV, the intensity balance rule is used, which supports to some extent the spin assignment of the levels .

Figure 4. (color online) (a) Representative ADO ratios in 92Mo, 92Nb, 91Mo, 93Nb, 89Zr, 90Zr. Typical RADO is given as around 1.6 indicating stretched quadrupole (or ΔI=0) transition, and around 0.8 indicating stretched dipole transition; (b) RADO of transitions plotted against energies of γ-rays in 92Nb.
Two new transitions, 504 and 572 keV, are added to the level scheme of 93Nb feeding into the 2180 keV state, as shown in Fig. 5. From the summed spectrum of 689 and 541 keV, shown in Fig. 6, the peaks of the new transitions 504 and 572 keV can be clearly seen. The ADO ratios for the two transitions are 1.45 and 0.94, indicating quadrupole and dipole properties, respectively. Therefore, the spins of the 2752 keV and 2684 keV states are assigned as 21/2, and 19/2, respectively. The relative intensities of partial γ-rays from 93Nb are given in Table 2.
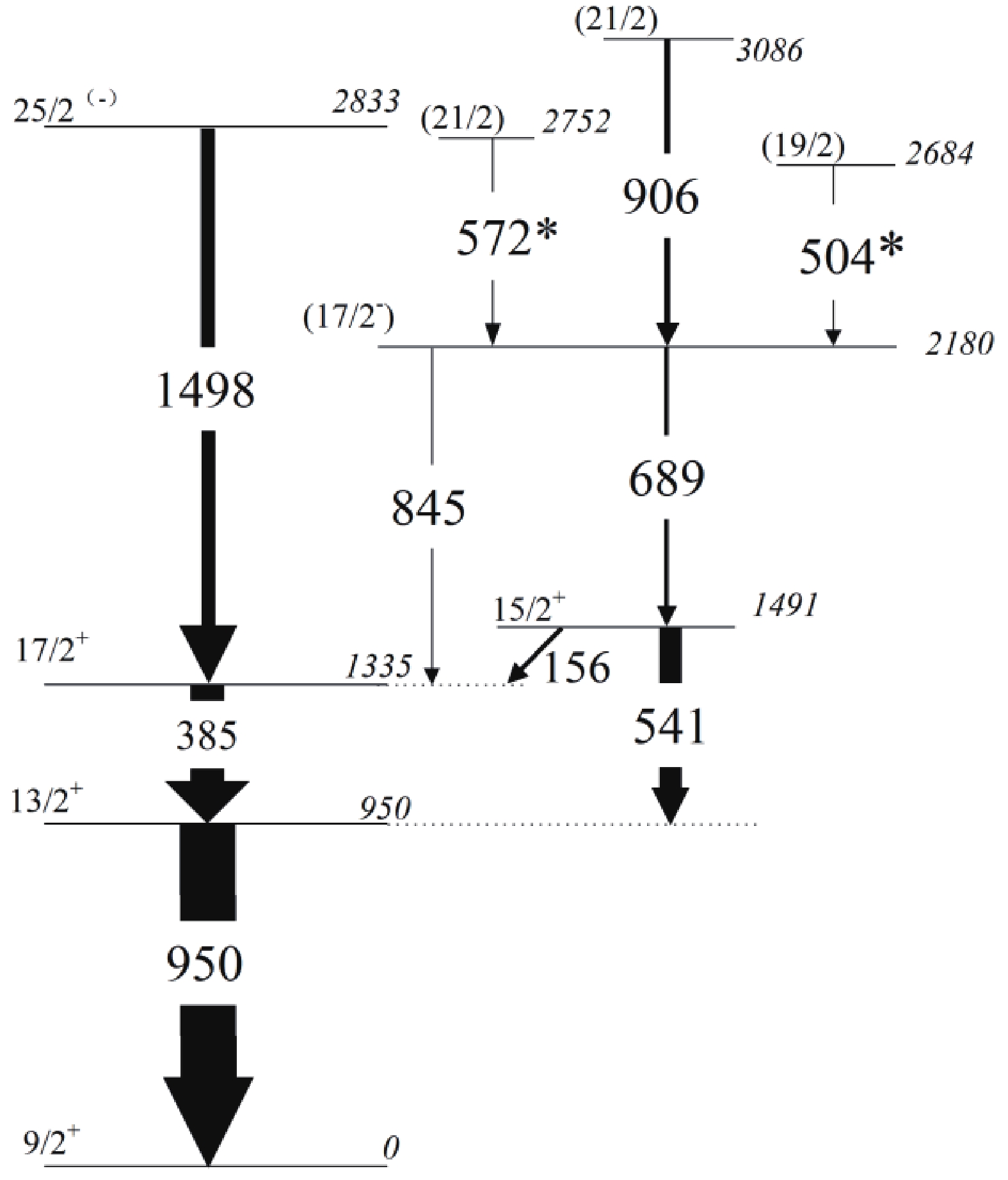
Figure 5. Level scheme of 93Nb proposed in the present work. New transitions are marked with asterisks. The width of the arrows indicates the relative intensity of γ-rays.

Figure 6. Typical prompt γ-γ coincidence spectrum for 93Nb with two new transitions marked with asterisks.
Eγ/keV Iγa E iπ→Efπ Jiπ→Jfπ 156 8.1(19) 1491→1335 15/2+→17/2+ 385 58.8(69) 1335→950 17/2+→13/2+ 504 * 2.8(6) 2684→2180 (19/2)→(17/2−) 541 39.9(69) 1491→950 15/2+→13/2+ 572* 1.5(5) 2752→2180 (21/2)→(17/2−) 689 7.1(21) 2180→1491 (17/2−)→15/2+ 845 2.2(3) 2180→1335 (17/2−)→17/2+ 906 10.8(24) 3086→2180 (21/2)→(17/2−) 950 100 950→0 13/2+→9/2+ 1498 25.7(36) 2833→1335 25/2(−)→17/2+ a The errors on the relative intensity include the fitting and efficiency corrections. Table 2. Transition energies (Eγ) of 93Nb, relative intensities of γ-rays (Iγ), initial and final spins of the transitions.
-
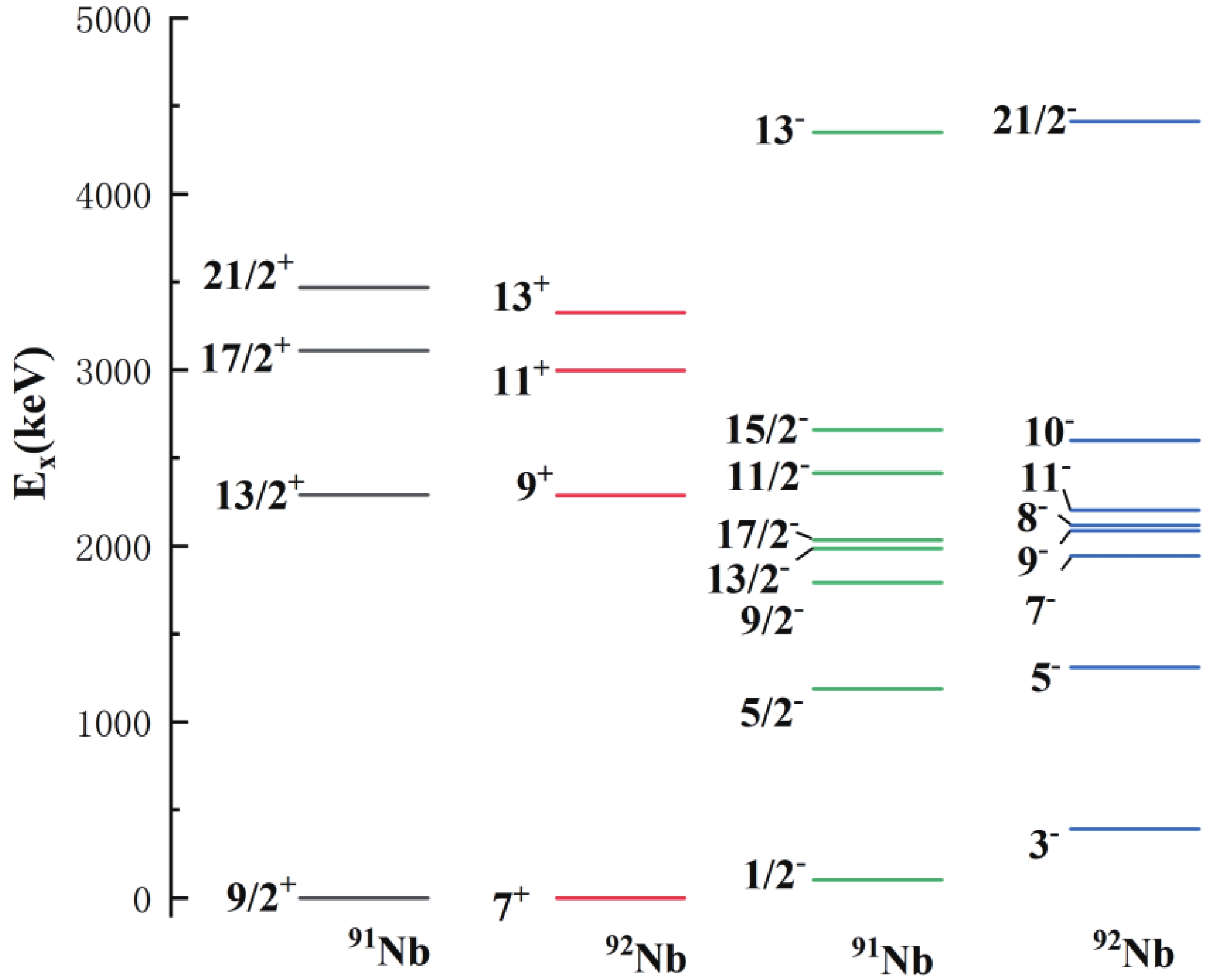
The excitation of a nearly spherical nucleus is usually considered to be of two types: single particle excitations inside a major shell, and excitations that cross the shell gap(s) [21]. The core excitation has been previously reported in A~90 neighboring nuclei, e.g., 89Y [22], 91-94Mo [8, 23-25], and 94-96Ru [26], which exhibit the characteristics of several parallel transitions with energy around 2 MeV feeding into the same level. The low-lying states may be dominated by single particle excitations inside one major shell. As it is a nearly spherical nucleus, the states of 92Nb should be amenable to shell model calculations.
In order to study the levels in 92Nb, we performed shell model calculations with the code NushellX. The SNE model space and SNET interaction were adopted, which were previously used for level structures of nearly spherical nuclei 85Br [27], 96Ru [26], 94Mo [8]. The model space includes 8 proton orbitals (1f5/2, 2p3/2, 2p1/2, 1g9/2, 1g7/2, 2d5/2, 2d3/2, 3s1/2) and 9 neutron orbitals (1f5/2, 2p3/2, 2p1/2, 1g9/2, 1g7/2, 2d5/2, 2d3/2, 3s1/2, 1h11/2) relative to the inert 56Ni (Z = 28, N = 28) core.
The low-excited states of 92Nb behave like single particle excitation, and thus we describe the low-excited states of 92Nb as pure configurations, which means that each state corresponds to one proton orbital and one neutron orbital. The pure configuration calculations were also carried out for the low-excited states of 91Zr, 93Mo, 95Ru [28]. Since the Fermi levels of 92Nb lie at the πg9/2 and νd5/2 orbitals, the quasi-magic nucleus 90Zr is taken as the inert core to describe the low-lying states of 92Nb, so that the 1f5/2, 2p3/2, 2p1/2 proton orbitals and the 1f5/2, 2p3/2, 2p1/2, 1g9/2 neutron orbitals are fully occupied. The first six positive parity states of 92Nb (Iπ=2+~7+) have been previously interpreted as the π(1g9/2)
$\otimes $ ν(2d5/2) configuration, and the first two negative parity states of 2- and 3- are dominated by the π(2p1/2)$\otimes $ ν(2d5/2) configuration [11, 13]. As 92Nb has one neutron more than 91Nb, it should have similar level structure for low-excited states, as shown in Fig. 7. Hence, the low-lying levels of 92Nb are described as 91Nb$\otimes $ νd5/2 as shown in Table 3, where the negative parity states Iπ=7-, 8-, 9-(1), 9-(2), 10-(1), 10-(2) are described as a proton excited from the p1/2 orbital to the g9/2 orbital, and the positive parity states 9+, 11+, 12+, 13+ are described as a pair of protons excited from the p1/2 orbital to the g9/2 orbital. The calculation results for the one proton-neutron coupled configuration, πg9/2$ \otimes$ νd5/2, and for the two proton-hole neutron-particle coupled configuration, πp1/2-1(g9/2)2$\otimes $ νd5/2 and π(p1/2)-2 (g9/2)3$\otimes $ νd5/2 , are listed in Table 3. As can be seen from this table, the shell model predictions for the low-excited states agree well with the experimental data, which confirms the assignments of Ref. [13] , where the first six positive parity states Iπ=2+~7+ and the first two negative parity states 2- and 3- are πg9/2$\otimes$ νd5/2 and πp1/2-1(g9/2)2$\otimes $ νd5/2, respectively.I π configuration Eexp/MeV Ecal1/MeV 2+ πg9/2 $ \otimes$ νd5/2

0.136 0.326 3+ 0.286 0.402 4+ 0.480 0.495 5+ 0.357 0.372 6+ 0.501 0.515 7+ 0 0 2− π(p1/2)-1(g9/2)2 $ \otimes$ νd5/2

0.227 0.275 3− 0.391 0.314 7− 1.945 1.83 8− 2.116 2.028 9−(1) 2.088 1.900 9−(2) 2.213 2.54 10−(1) 2.235 2.203 10−(2) 2.6 2.643 9+ π(p1/2)-2(g9/2)3 $ \otimes$ νd5/2

2.287 2.552 11+ 2.998 3.295 12+ 3.797 3.859 13+ 3.326 3.528 1 the result of shell model calculation with pure configurations. Table 3. Dominant configurations of the low-lying excited states of 92Nb proposed by the shell model calculations with a pure configuration and SNET interaction, calculated results and experimental level energies.
For the higher excited states of 92Nb, 90Zr is not an ideal core anymore, which makes the configuration of the high-excited states more complicated, as the pure configurations cannot describe the high-excited states properly. In order to study the high-excited states of 92Nb, a large-basis shell model calculation is necessary.
To obtain a more appropriate description of the observed high-excited states of 92Nb, large-basis shell model calculations are used. 92Nb has 13 valence protons and 23 valence neutrons outside the 56Ni core. Due to the large number of active orbitals, truncation of the model space is necessary. In the calculations of 92Nb, the valance space is restricted to π(1f5/24-6, 2p3/22-4, 2p1/20-2, 1g9/21-6, 1g7/20-0, 2d5/20-0, 2d3/20-0, 3s1/20-0)
$ \otimes$ (1f5/26-6, 2p3/24-4, 2p1/22-2, 1g9/29-10, 1g7/20-1, 2d5/20-2, 2d3/20-0, 3s1/20-0, 1h11/20-1). A comparison between the experimentally determined excitations and the large-basis shell model results is shown in Table 4.I π Eexp /MeV Ecal2/MeV configuration partition(%) 9+ 2.287 2.111 6 4 0 3 $ \otimes$ 6 4 2 10 0 1 0 0 0

50.24 4 4 2 3 $ \otimes$ 6 4 2 10 0 1 0 0 0

13.84 11+ 2.998 3.146 6 4 0 3 $ \otimes$ 6 4 2 10 0 1 0 0 0

58.88 12+ 3.797 3.746 6 4 0 3 $ \otimes$ 6 4 2 10 0 1 0 0 0

64.89 13+ 3.326 3.325 6 4 0 3 $ \otimes$ 6 4 2 10 0 1 0 0 0

61.88 8− 2.116 2.320 6 4 0 3 $ \otimes$ 6 4 2 10 0 0 0 0 1

38.79 6 4 2 1 $ \otimes$ 6 4 2 10 0 0 0 0 1

21.59 9− 2.088 2.232 6 4 0 3 $ \otimes$ 6 4 2 10 0 0 0 0 1

30.85 6 4 2 1 $ \otimes$ 6 4 2 10 0 0 0 0 1

12.36 9−(2) 2.213 2.777 6 4 1 2 $ \otimes$ 6 4 2 10 0 1 0 0 0

52.03 10− 2.235 1.863 6 4 0 3 $ \otimes$ 6 4 2 10 0 0 0 0 1

41.57 10−(2) 2.6 2.841 6 4 1 2 $ \otimes$ 6 4 2 10 0 1 0 0 0

49.4 13− 4.587 4.797 6 4 0 3 $ \otimes$ 6 4 2 10 0 0 0 0 1

31.97 15− 4.941 5.207 6 4 0 3 $ \otimes$ 6 4 2 10 0 0 0 0 1

65.92 2 the result of shell model calculation with mixed configurations. Table 4. Main partition of the wave function for high-spin states of 92Nb. Each angular momentum is composed of several different partitions. Each partition is of the form p=π[p(1), p(2), p(3), p(4)]
$ \otimes$ ν[n(1), n(2), n(3), n(4), n(5), n(6), n(7), n(8), n(9), n(10)], where p(i) represents the number of valence protons in the 1 f5/2, 2p3/2, 2p1/2 and 1g9/2 orbitals, and n(j) represents the number of valence neutrons in the 1 f5/2, 2p3/2, 2p1/2, 1g9/2, 1g7/2, 2d5/2 2d3/2 3s1/2 1h11/2 orbitals, respectively. One neutron is excited to the g7/2 and h11/2 orbitals in these calculations. -
Excited states of 92,93Nb were studied in the reactions induced by the weakly-bound nucleus 6Li. The states of 92Nb were populated in the 89Y(6Li, p2n)92Nb and 89Y(α, n)92Nb reactions, and of 93Nb in the 89Y(6Li, pn)93Nb reaction. A total of 20 new transitions, 8 new states of 92Nb and two transitions in 93Nb were observed and added to the level schemes of the two nuclei. The multipolarity of the states of 92,93Nb was analyzed following the ADO ratio. Shell model calculations were performed with the code NushellX to reconstruct the level structure of 92Nb, where SNE valence space and SNET interaction were used. For the low-excited states, a pure configuration with 90Zr as an inert core was employed. Large-basis shell model calculations were performed to study the higher excited states of 92Nb. The results agree well with the experimental data.
We are grateful to the INFN-LNL staff for providing stable 6Li beam throughout the experiment. This research was also supported by the HIRFL User Project, CAS.
Low-lying states of 92,93Nb excited in the reactions induced by the weakly-bound nucleus 6Li near the Coulomb barrier
- Received Date: 2019-05-26
- Available Online: 2019-10-01
Abstract: Excited states of odd-odd nucleus 92Nb and odd-A nucleus 93Nb were populated in the 6Li+ 89Y reaction with an incident energy of 34 MeV. The processes that produce 92,93Nb and can be measured by a combination of light charged particle and gamma ray measurements are discussed. Twenty new transitions are observed and eight new levels are constructed in 92Nb, and in addition two new transitions are added to the level scheme of 93Nb. Using shell model calculations, the low-lying structure of 92Nb is investigated and compared with the experimental results.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: