-
Understanding the structural properties of super-heavy nuclei (SHN) has become an attractive and interesting problem of nuclear physics. Heavy nuclei can be formed above the uranium nuclei
$ (Z > 92) $ by the nuclear reaction method. The half-life time is very small for the higher elements, which are yet to be observed for super-heavy isotopes. The first heavy element that is neptunium$ (Z = 93) $ have been evaluated at Lawrence Berkeley Laboratory in Berkeley (USA) [1]. These elements are mostly super-heavy elements (SHEs) that are far from the uranium nuclei. The main objective of this study is to investigate structural properties of super-heavy nuclei. Although the theoretical model identifies island stability of super-heavy elements [2, 3], their half-life extends from minutes to years. One of the exciting challenges in this region is to find the stable nuclei beyond$ ^{208}{\rm{Pb}}$ . Currently, the search for the magic island is an interesting topic in the super-heavy region. Generally, super-heavy nuclei are experimentally formed through hot and cold fusion reaction processes. Some of them have been synthesized by cold fusion reactions with$ Z = 107-112 $ at GSI, Darmstadt, and RIKEN, Japan [4, 5] and the hot fusion reaction with$ Z = 113-118 $ at JINR, Dubna [6-8]. The element Z = 113 was synthesized by a cold-fusion reaction at RIKEN, Japan [9]. In 2009 Oganessian et al. have attempted to synthesize the SHN with$ Z = 120 $ by the hot fusion reaction process [10]. However, SHN generally decay to known stable nuclei via α, β, and other decay modes. The prediction of the theoretical model has a remarkable contribution in the search for shell/sub-shell structure in the super-heavy region.The theoretical model plays a crucial role in the formation and prediction of island of stability beyond
$ Z = 82 $ and$ N = 126 $ . During the last twenty years, theoretical formalism has drawn attention to the formation and distinct properties of super-heavy nuclei. All these calculations are made to realize magic numbers beyond$ Z = 82 $ ,$ N = 126 $ . Many theoretical calculations have been proposed to expose possible shell closure, however different models give different results like FRDM, which provides the magic number at$ Z = 114 $ and$ N = 184 $ [11], whereas the Skyrme Hartree-Fock (SHF) model concludes shell closure at$ Z = 120 $ or$ Z = 126 $ and$ N = 184 $ [12, 13]. This is also calculated in the study of Ref. [14] using the same RMF model, obtaining the magic nuclei at$ N = 172 $ with$ Z = 120 $ . However, this discrepancy is related to the location of nuclei with the strongest shell effects and thus the longest α-decay half-lives. This is the reason that regions of SHEs are dominated by α-decay. The shell effects are sensitive to various terms of the mean-field, such as spin-orbit coupling, scalar, and effective masses. This is one of the causes for small variations in predictions of shell closures on the effective Lagrangian used in RMF. The calculated proton magic numbers of SHN are quite different, whereas the neutron magic number is almost the same in every phenomenological calculation. Thus, the search for the magic island is highly dependent on the formalism deciding which model is to be applied.To find possible shell or sub-shell closure in the super-heavy region, the study of structural properties along with the study of decay modes have equal importance to confirm regarding the shell stability. In this regard, spontaneous fission and the alpha decay process need to be revised thoroughly. Therefore, in this study, we simultaneously investigate both the structure and decay modes of this super-heavy nuclei presented in Figs. 1–7 and Table 1. Theoretical calculations and predictions on structures and decay modes in SHN have been obtained in Refs. [15-20]. As the shell closure is one of the important outcomes of the study of decay probability in SHN, we performed a detailed study of the isotopes of SHE
$ Z = 130 $ . Since the shell closure exhibits some exotic behavior, such as binding energy (B.E.), it may affect the fission barrier and hence the half-life [18, 21, 22]. To find the compatibility between the half-lives and the Q-value and hence the possible shell closure, Wang et al. [23] studied the decay modes of SHN using 20 mass models. Among all these models, the WS4 mass method [24] provides fine experimental results for$ Q_{\alpha} $ values, and the SemFIS2 formulae [25] gives the most accurate results for the alpha decay half-life of super-heavy nuclei. Models such as UNIV2 formula [25], VSS [26], SP [27] and NRDX [28] formulae are in good agreement with these experimental results. Microscopic investigations were performed this study, addressing various possible decay modes for the neutron-rich SHN using the Q-value obtained from the RMF model [29, 30] with the NL3 force parameter set [31]. Since the RMF model has been well-accepted and applied in the study of nuclear structures regarding beta-stability as well as areas in the total nuclear landscape including super-heavy nuclei [32–36], we choose this model here as a tool to obtain structural properties of the SHE$ Z = 130 $ . Refs. [37, 38] estimated the half-life of$ ^{298}{\rm{Fl}}$ to the order of 107 to 108 years. The half-life of the longest-lived isotope of the 126th element with a mass number of 342 is 106 to 107s (or 0.03...0.33 years). Between$ ^{298}{\rm{Fl}}$ and 342126, there is an island (or shallow) for long-lived highly deformed nuclides close to the optimal N/Z ratio, which determines the equilibrium of the forces of nuclear (manifestation of strong), electromagnetic. and weak interactions. This is also characteristic of the longest-lived heavy and super-heavy nuclei. The probability of a shallow formation around the nucleus 342126 [37, 38] stretched towards the larger N may contain relatively long-lived nuclei of the 128,130 as well as 127th elements necessarily close to the optimal ratio N/Z. This is due to the zero electric charge of the neutron and the absence of additional Coulomb forces destabilizing the nucleus. Further, the increasing survival probabilities of the measured SHE from Z = 114 to Z = 118 seem to indicate enhanced shell effects with increasing Z and therefore a possible proton and/or neutron magic shell in the super-heavy region. This corresponds to the position of the super-heavy island, in the region Z$ \geq $ 120. This is why we choose Z = 130 a case study in this manuscript. This effort intends is to investigate the structural properties of the isotopes of super-heavy nuclei with$ Z = 130 $ and the favorable decay modes between alpha decay and fission processes to understand the stability of the nuclei taking into account the spin-orbit coupling. That is why we choose the RMF model for our calculation. The present paper consists of four sections, Section 1 provides the introduction, Section 2 provides the formalism that tells about a squat depiction of the RMF theory. In Section 3 and Section 4, unique results and the conclusion are presented.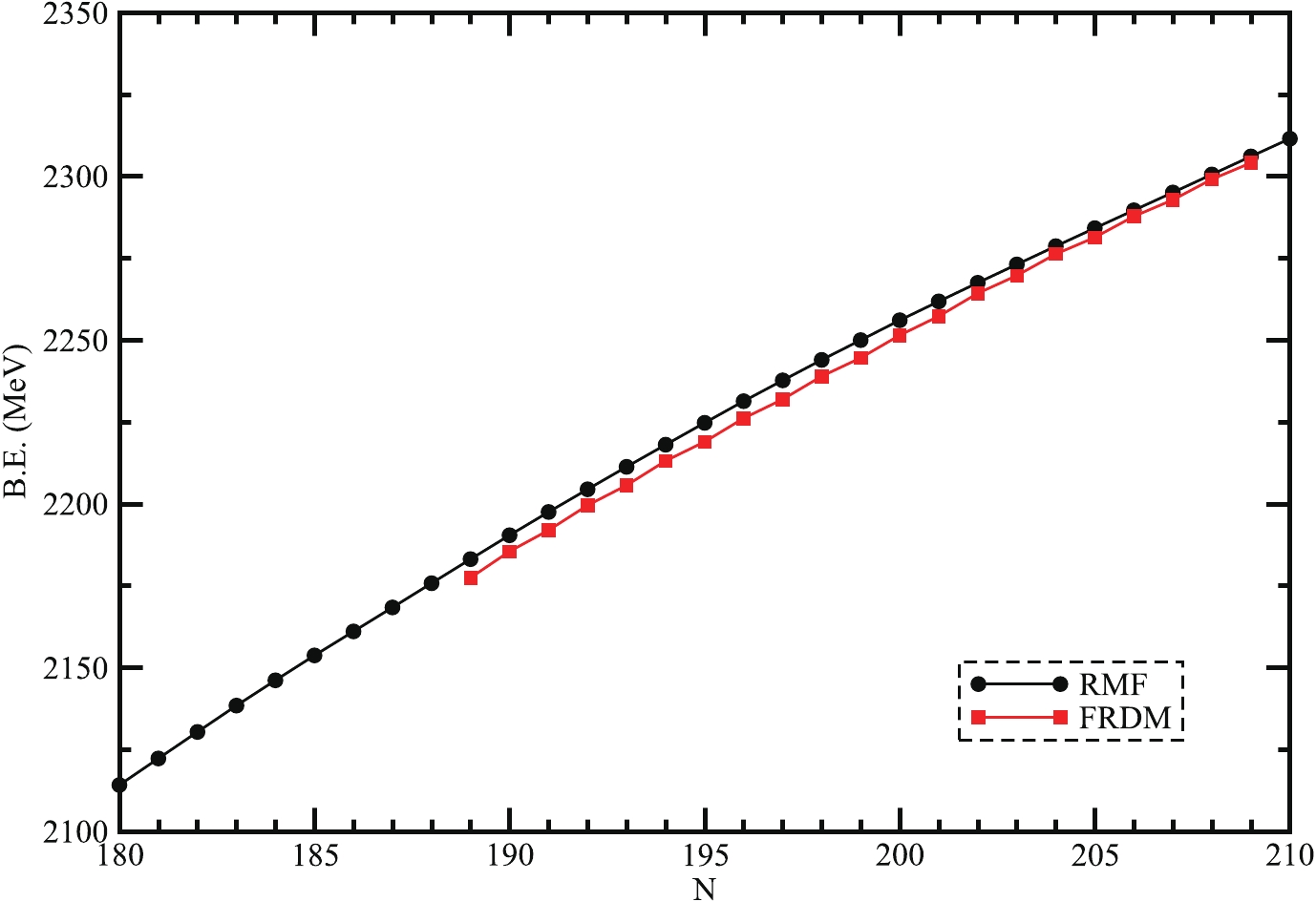
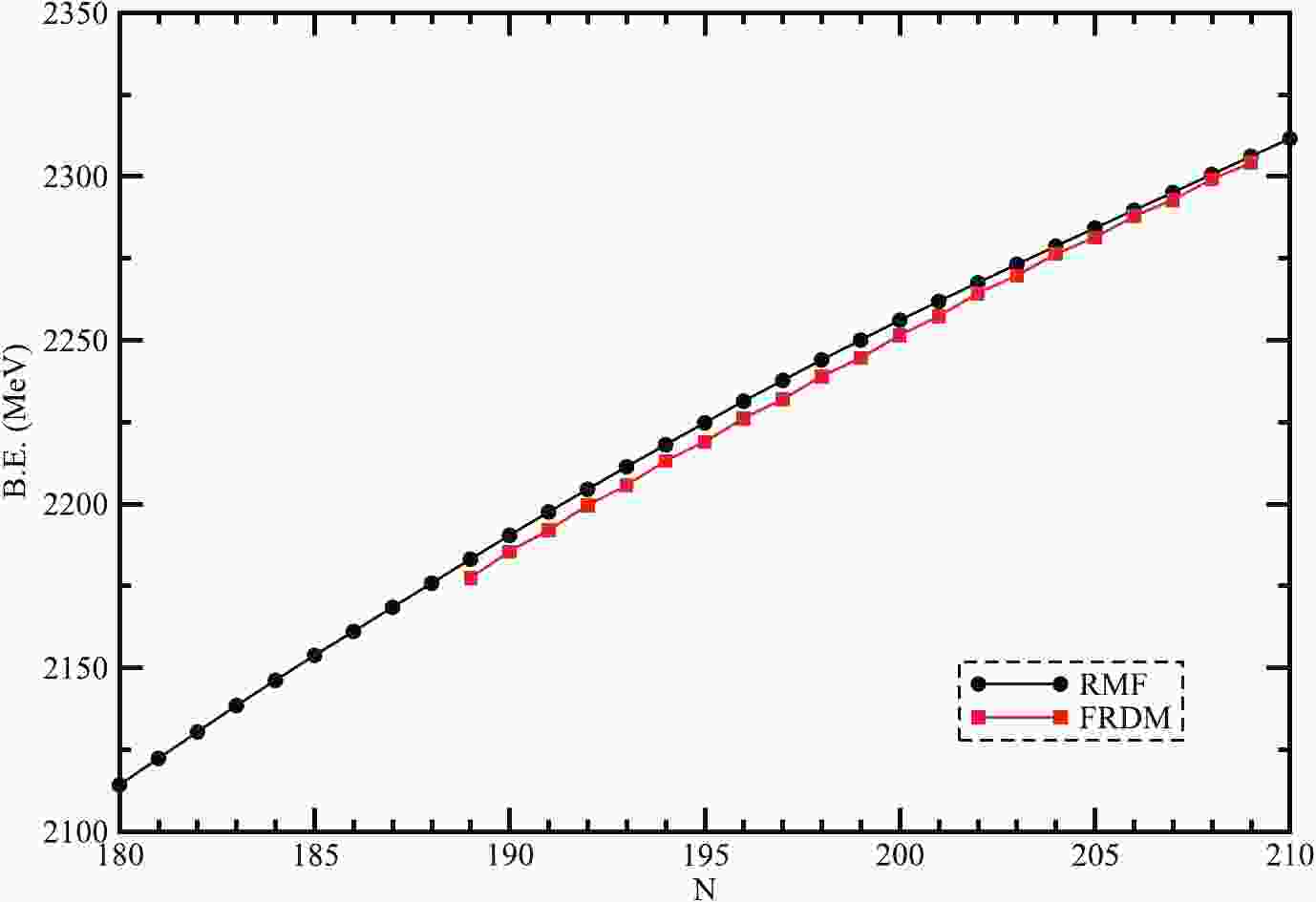
Figure 1. (color online) Binding energies (B.E.) plot as a function of neutron number(N) of super-heavy nuclei with Z = 130 nuclei.
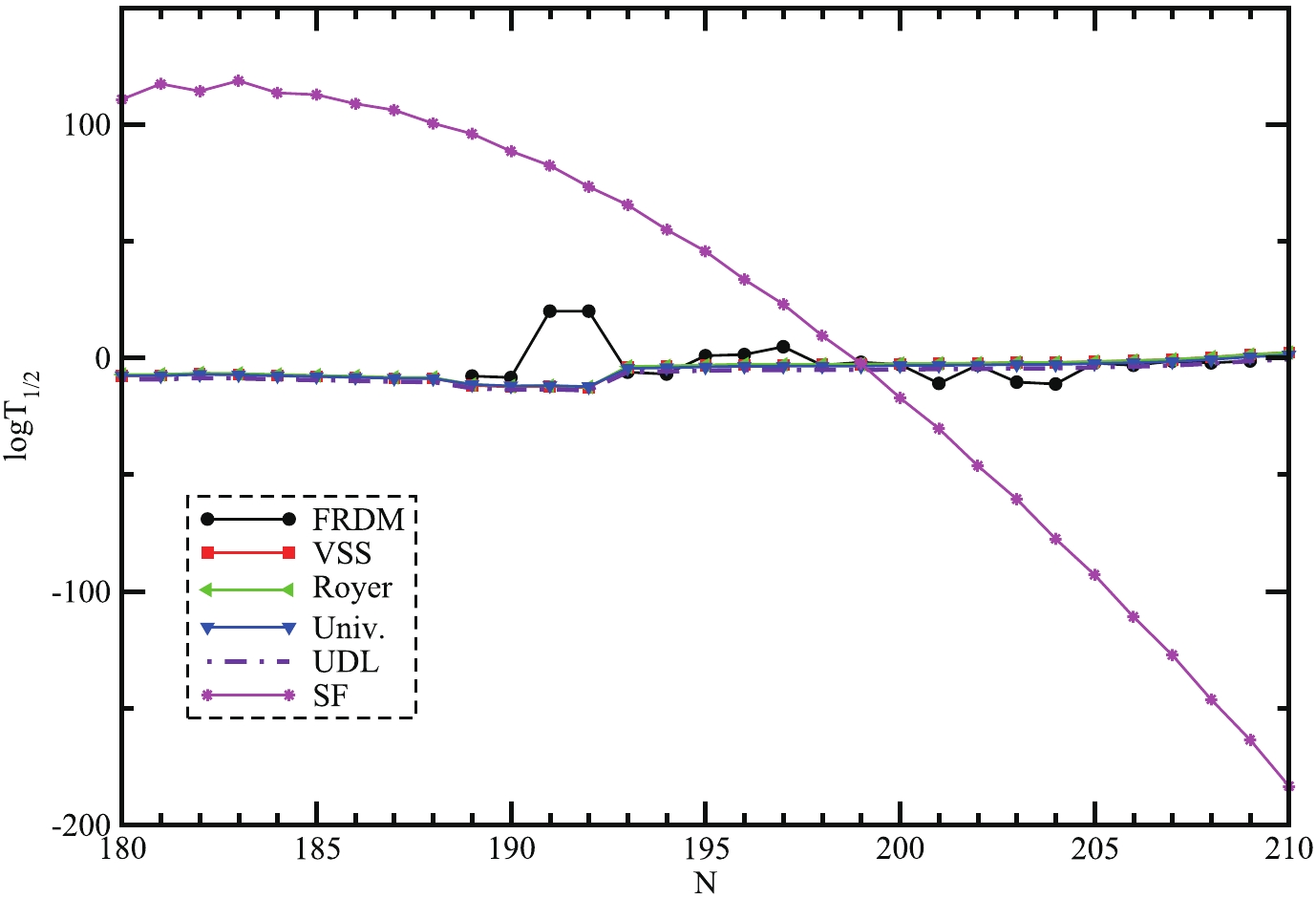
Figure 7. (color online) Half-life time
$({\rm log}_{10}T_{1/2})$ of super-heavy nuclei with Z = 130 as a function of parent neutron number (N).A N Q-value(MeV) VSS Royer Univ. UDL SF Decay Modes 310 180 15.585 −7.639 −7.138 −7.671 −9.202 110.713 α 311 181 15.566 −7.60 −7.124 −7.65 −9.186 117.28 α 312 182 15.211 −6.99 −6.534 −7.116 −8.650 114.182 α 313 183 15.302 −7.155 −6.710 −7.276 −8.806 118.636 α 314 184 15.561 −7.598 −7.170 −7.694 −9.217 113.469 α 315 185 15.76 −7.93 −7.520 −8.011 −9.530 112.682 α 316 186 15.982 −8.296 −7.902 −8.355 −9.871 108.803 α 317 187 16.248 −8.723 −8.345 −8.752 −10.268 106.122 α 318 188 16.3 −8.805 −8.445 −8.841 −10.354 100.403 α 319 189 18.352 −11.763 −11.413 −11.449 −13.030 95.936 α 320 190 18.871 −12.434 −12.100 −12.034 −13.647 88.482 α 321 191 18.748 −12.278 −11.962 −11.915 −13.518 82.330 α 322 192 19.133 −12.762 −12.463 −12.338 −13.967 73.240 α 323 193 13.64 −4.016 −3.757 −4.526 −6.107 65.502 α 324 194 13.484 −3.692 −3.452 −4.237 −5.828 54.875 α 325 195 13.309 −3.322 −3.100 −3.905 −5.507 45.645 α 326 196 13.144 −2.966 −2.763 −3.585 −5.199 33.572 α 327 197 13.153 −2.985 −2.800 −3.619 −5.229 22.943 α 328 198 13.115 −2.903 −2.734 −3.556 −5.167 9.513 α 329 199 13.119 −2.911 −2.760 −3.579 −5.187 −2.428 SF 330 200 12.988 −2.623 −2.490 −3.323 −4.940 −17.128 SF 331 201 12.938 −2.512 −2.397 −3.233 −4.852 −30.299 SF 332 202 12.876 −2.373 −2.276 −3.117 −4.740 −46.186 SF 333 203 12.741 −2.068 −1.988 −2.843 −4.477 −60.505 SF 334 204 12.74 −2.065 −2.003 −2.856 −4.487 −77.500 SF 335 205 12.557 −1.643 −1.599 −2.470 −4.119 −92.888 SF 336 206 12.387 −1.243 −1.217 −2.105 −3.770 −110.914 SF 337 207 12.17 −0.719 −0.712 −1.621 −3.311 −127.297 SF 338 208 11.784 0.246 0.234 −0.710 −2.453 −146.280 SF 339 209 11.343 1.410 1.378 0.394 −1.417 −163.584 SF 340 210 11.03 2.278 2.227 1.219 −0.648 −183.454 SF Table 1. Alpha decay of Z = 130 nuclei

Figure 2. (color online) Binding energy per particle (B.E./A) for super-heavy nuclei with Z = 130 as a function of parent neutron number (N).
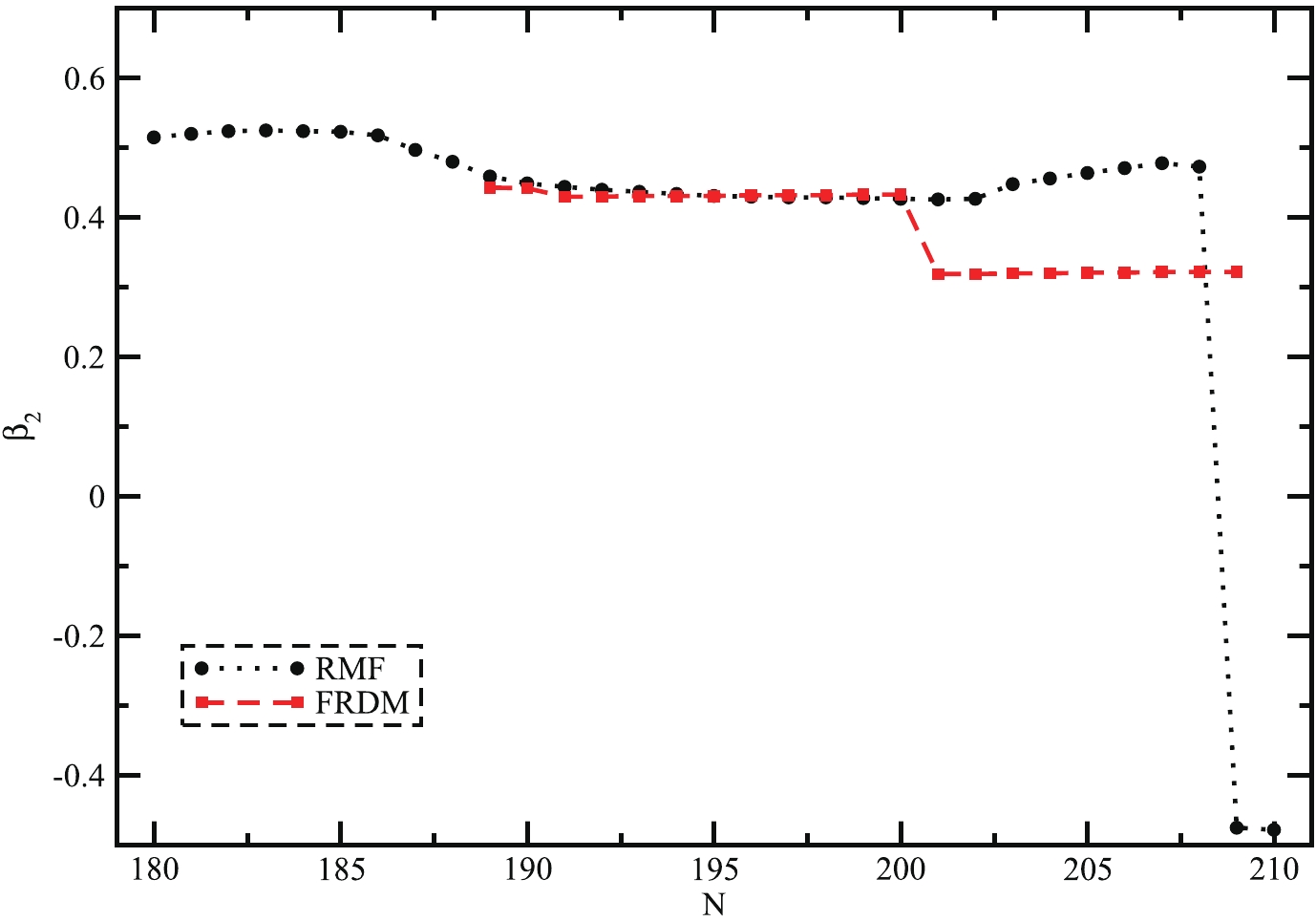
Figure 3. (color online) Quadrupole deformation parameter β2 of super-heavy nuclei with Z = 130 nuclei as a function of neutron number (N).
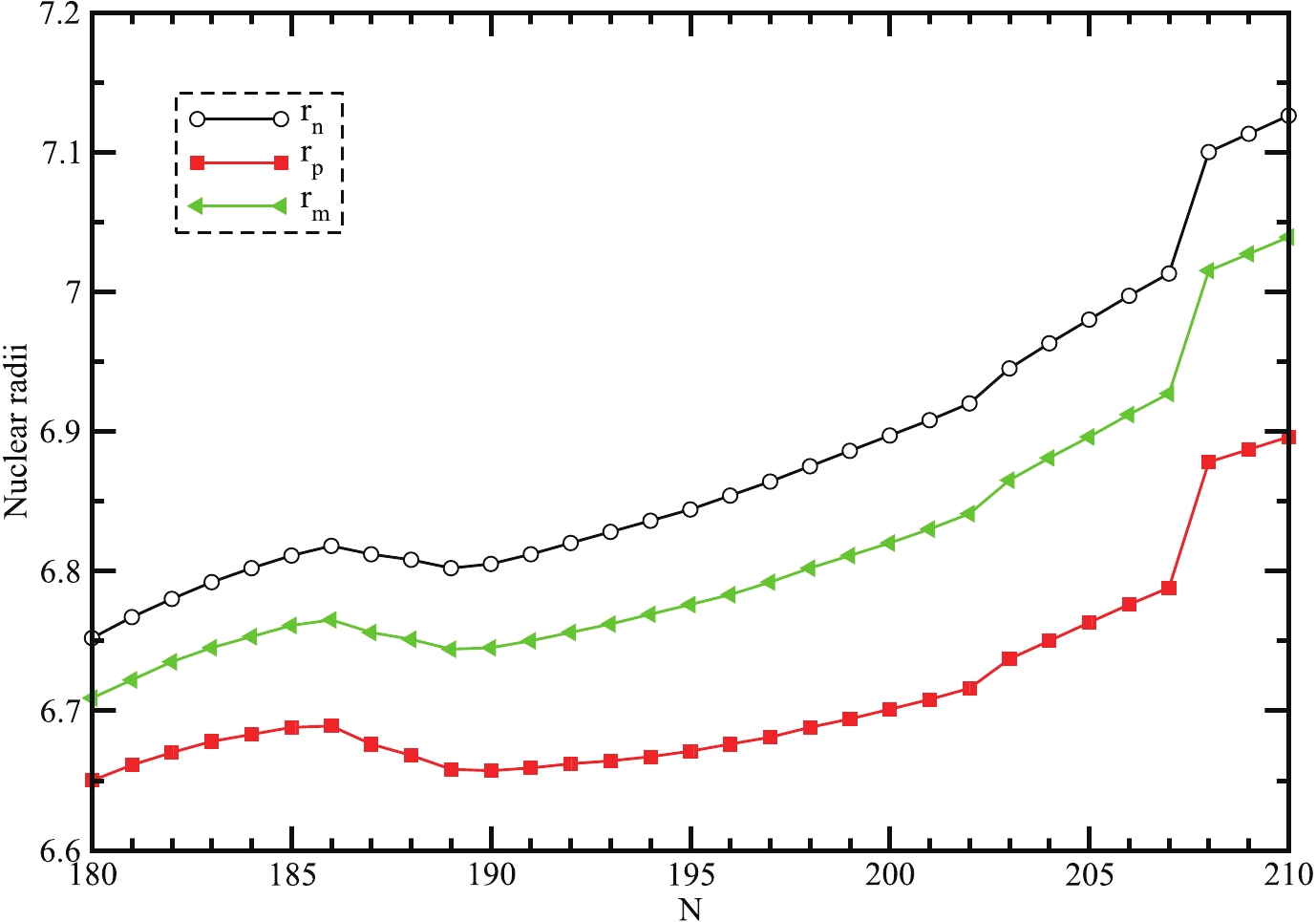
Figure 4. (color online) Radii of neutron and proton and total radius of super-heavy nuclei with Z = 130 nuclei as a function of neutron number (N).
-
The relativistic mean-field Lagrangian density for many-body systems can be written as [29, 30, 34, 39, 40],
$ \begin{split} L =& \bar{\psi_{i}}(i\gamma^{\mu}\partial_{\mu}-M)\psi_{i} +\frac{1}{2}\partial^{\mu}\sigma\partial_{\mu}\sigma -\frac{1}{2}m_{\sigma}^{2}\sigma^{2}-\frac{1}{3}g_{2}\sigma^{3} \\& -\frac{1}{4}g_{3}\sigma^{4}-g_{s}\bar{\psi_{i}}\psi_{i}\sigma -\frac{1}{4}\Omega^{\mu\nu}\Omega_{\mu\nu} +\frac{1}{2}m_{\omega}^{2}\; V^{\mu}\; V_{\mu} \\& +\frac{1}{4}c_{3}(V_{\mu}V^{\mu})^{2} -g_{\omega}\bar{\psi_{i}}\gamma^{\mu}\; \psi_{i}\; V_{\mu} -\frac{1}{4}\overrightarrow{B}^{\mu\nu}\overrightarrow{B}_{\mu\nu} +\frac{1}{2}m_{\rho}^{2}\overrightarrow{R}^{\mu}.\overrightarrow{R_{\mu}} \\& -g_{\rho}\bar{\psi_{i}}\gamma^{\mu}\overrightarrow{\tau}\psi_{i}.\overrightarrow{R^{\mu}} -\frac{1}{4}F^{\mu\nu}F_{\mu\nu}-e\bar{\psi_{i}}\gamma^{\mu}\frac{(1-\tau_{3i})}{2}\psi_{i}A_{\mu}. \end{split} $

(1) Here, all the terms have their usual meanings. By solving the above Lagrangian equation, we can obtain the field equations for both nucleons as well as mesons. Within an axially deformed harmonic oscillator basis, the field equations are solved with an initial deformation value
$ \beta_{0} $ [29, 30, 41]. To find the ground state solution, calculations are performed starting with a spherical to both prolate and oblate$ \beta_{0} $ value. The center of mass-energy$ (E_{c.m.}) $ is calculated from the formula$ E_{c.m.} = $ $ \displaystyle\frac{3}{4}\; (41A^{-1/3}) $ , here A indicates nucleus mass number,$ \beta_{2} $ is the total quadrupole deformation factor, which can be determined from the neutron quadrupole moment along with the proton quadrupole moments i.e.,$ Q = Q_{n}+ $ $Q_{p} = \sqrt{\displaystyle\frac{16\pi}{5}}\; \left(\displaystyle\frac{3}{4\pi}AR^{2}\beta_{2}\right) $ . Here, R indicates the nuclear radius. The nuclear matter radius is expressed as$\langle{r}_{m}^{2}\rangle = $ $ \displaystyle\frac{1}{A}\; \int\rho\; (r_{\bot},z)r^{2}\; {\rm d}\tau $ . Here, A represents the nucleus mass number and$ \rho\; (r_{\bot},z) $ provides the axially deformed density. The total energy of a given system can be written as$ E_{\rm total} = E_{\rm part} + E_{\sigma} + E_{\omega} + E_{\rho} + E_{c} +$ $ E_{\rm pair} + E_{c.m.} $ , where$ E_{\rm part} $ is the addition of all the nucleon energies, and the other terms such as$ E_{\sigma} $ ,$ E_{\omega} $ ,$ E_{\rho} $ ,$ E_{c.m.} $ ,$ E_{\rm pair} $ these are the meson field contributions,$ E_{c} $ is Coulomb energy and$ E_{\rm pair} $ is the pairing energy. The RMF-BCS pairing effect has been taken care in our calculation as in Refs. [40, 42-47] with the constant gap for proton$ \bigtriangleup_{p} = RB_{s}e^{sI-tI^{2}}/Z^{1/3} $ and constant gap for neutron$ \bigtriangleup_{n} = RB_{s}e^{-sI-tI^{2}}/A^{1/3} $ and$ R = 5.72 $ ,$ s = 0.118 $ ,$ t = 8.12 $ ,$ B_{s} = 1 $ , and$ I = (N-Z)/(N + Z) $ . -
Geiger and Nuttall were the first to provide an the analytical expression between the decay energy
$ Q_{\alpha} $ and decay half-life$ T_{\alpha} $ in 1911. After that, Viola and Seaborg put on a new formula from the Geiger and Nuttall law in 1966 and referred to it as the Viola-Seaborg relationship [26] i.e.$ \begin{array}{l} {\rm log}_{10}\; T_{\alpha} = (aZ+b)\; Q_{\alpha}^{-1/2}+(cZ+d)+h_{\rm log}. \end{array} $

(2) Here, the Q-value is measured in MeV, and Z is the proton number of the parent nucleus. The parameters a, b, c, and d are the experimental fitting parameters whose values are
$ a = 1.66175 $ ,$ b = -8.5166 $ ,$ c = -0.20228 $ ,$ d = -33.9069 $ . The term$ h_{\rm log} $ indicates the hindrances factor, which is associated with the odd/even proton number as well as odd/even neutron numbers, as given by Viola and Seaberg [26]. Here, we have taken the hindrances factor as,$ h_{\rm log} $ = 0, for N = even, Z = even;$ h_{\rm log} $ = 0.772, for N = even, Z = odd;$ h_{\rm log} $ = 1.066, for N = odd, Z = even;$ h_{\rm log} $ = 1.114, for N = odd, Z = odd. -
The simple analytical formula for the logarithmic alpha decay half-lives has been given by G. Royer and obtained by data analysis procedure of 373 alpha emission nucleus. The formula is obtained with a rms deviation of 0.42 [48], which is revealed as,
$ \begin{aligned} {\rm log}_{10}[T_{1/2}(s)] = a_{1} + b_{1}A^{1/6}\sqrt{Z} + \frac{c_{1}Z}{\sqrt{Q_{\alpha}}}. \end{aligned} $

(3) Where
$ a_{1} = -25.68 $ ,$ b_{1} = -1.1423 $ , and$ c_{1} = 1.5920 $ are the experimental fitting parameters. Here, A indicates the mass number of the parent nucleus, and Z indicates the atomic number of the parent nucleus. The$ Q_{\alpha} $ indicates the energy released at the time of the reaction. -
The universal (Univ) curve formula is one of the important formulae with which one can calculate both the alpha decay as well as cluster decay properties. Poenaru et al. were derived the universal (Univ) curve by fission theory, established on the quantum tunneling process [49-51] as;
$ \begin{array}{l} \lambda = \ln2/T = \nu\; SP_{s}. \end{array} $

(4) Here
$ \lambda $ indicates the disintegration constant for fission-like as well as α-like theories, which is relevant with the partial decay half-life T of the parent nucleus. Here ν is the frequency, S represents the preformation probability, and the quantum penetrability is given by$ P_{s} $ . The above equation can be drafted in decimal form as follows,$ \begin{array}{l} {\rm log}_{10}\; T_{1/2}(s) = -{\rm log}_{10}\; P-{\rm log}_{10}\; S+[{\rm log}_{10}({\rm ln}2)-{\rm log}_{10}\; \nu]. \end{array} $

(5) Here, S is preformation probability of the cluster, and ν is a constant frequency, which depends on the emitted cluster mass number. The decimal logarithm of the preformation factor is given as i.e.,
$ {\rm log}_{10}\; S = -0.598(A_{e}-1) $ . For the even-even nucleus, the additive constant is written as,$ C_{ee} = [-{\rm log}_{10}\; \nu + {\rm log}_{10}({\rm ln}2)] = -22.16917 $ . Here, we calculate the Q-value using the estimated binding energies analytically.$ -{\rm log}_{10}\; P = 0.22873(\mu_{A}Z_{d}Z_{e}R_{b})^{1/2}\times[{\rm arccos}\sqrt{r} - \sqrt{r(1-r)}] $ Where$ \mu $ is defined as the reduced mass,$ r = R_{t}/R_{b} $ ,$ R_{t} = 1.2249(A_{d}^{1/3} + A_{e}^{1/3}) $ ,$ R_{b} = 1.43998\; Z_{d}\; Z_{e}/Q $ . -
The half-life can be written in the form as [52, 53],
$ \begin{array}{l} {\rm log}_{10}T_{1/2} = aZ_{e}Z_{d}\sqrt{\frac{A}{Q_{e}}}+b\sqrt{AZ_{e}Z_{d}(A_{d}^{1/3}+A_{e}^{1/3})}+c, \end{array} $

(6) $ \begin{array}{l} {\rm log}_{10}T_{1/2} = a\chi'+b\rho'+c. \end{array} $

(7) The universal decay law describes the decay half-life with the Q-value of the emitting particle along with the mass of the nuclei and charge of the nuclei involved in the decay process. Here, the cluster Q-value is derived by
$ Q_{e} = \mu\nu^{2}/2 $ , and the standard value of$ R = R_{0}(A_{d}^{1/3}+A_{e}^{1/3}) $ with$ R_{0}\sim 1.2 $ Fermi [54]. The factors$ \chi' $ and$ \rho' $ defined as,$\begin{split} \chi' = &\frac{\hbar}{e^{2}\sqrt{2m}}\chi = Z_{e}Z_{d}\sqrt{\frac{A}{Q_{e}}}\;{\rm{and}} \;\;\\ \rho' =& \frac{\hbar}{\sqrt{2mR_{0}e^{2}}}(\rho\chi)^{1/2} = \sqrt{AZ_{e}Z_{d}(A_{d}^{1/3}+A_{e}^{1/3})}. \end{split}$

where
$ A = A_{d}A_{e}/(A_{d} + A_{e}) = \mu/m $ and the mass of the nucleon is given by 'm' here. The coefficient constant parameters are$ a = 0.3671 $ ,$ b = -0.3296 $ , and$ c = -26.2681 $ . -
The successive equations to evaluate the spontaneous fission half-lives for both e-e nuclei and odd-A nuclei [55, 56] can be expressed as;
$ \begin{split} {\rm log}_{10}T_{1/2}/yr =& c_{1}+c_{2}(\frac{Z^{2}}{A}+k)+c_{3}(\frac{Z^{2}}{A}+k)^{2} \\&+c_{4}(\frac{Z^{2}}{A}+k)^{3} +(c_{5}+(\frac{Z^{2}}{A}+k))(c_{6}(Z-82)^{2} \\&+c_{7}(N-126)^{2}+c_{8}(N-Z))+h. \\ \end{split} $

(8) where
$ c_{1} = 31.196159 $ ,$ c_{2} = -5.086737 $ ,$ c_{3} = -0.0742314 $ ,$ c_{4} = -0.161829 $ ,$ c_{5} = 0.0398652 $ ,$ c_{6} = 0.0585024 $ ,$ c_{7} = -0.0124953 $ ,$ c_{8} = 0.108390 $ and$ k = -30.444904 $ [56] and h is the blocking factor, where$ h = 0 $ for even-even nuclei and$ h = 4.302383 $ for odd-A nuclei. -
In the present study, we studied the structural properties and α-decay half-lives of Z = 130 super-heavy element within the mass range
$ 310 \leq A \leq 340 $ by employing the RMF theory with the NL3 force parameter set [31]. We evaluate the ground state properties such as binding energies, quadrupole deformation, nuclear radii, neutron separation energies, and other bulk properties. To analyze the structures in the super-heavy region, the α-decay process is a very common method followed by spontaneous fission (SF). Therefore, we describe all the α-decay half-life values to make out the favored decay mode. We correlate our calculated half life formulas using the Viola-Seaberg semi-empirical (VSS) relationship, analytical formulas of Royer, the universal (Univ) curve of Poenaru, and universal decay law (UDL). Hence, we can compare our estimated alpha decay half-life to the spontaneous fission half-life. To this end, we have taken the oscillator basis$ N_{F} = N_{B} = 20 $ , which is the best fit for the convergence limits of the current RMF models. We have compared our calculated results with the available FRDM results [57], and it can be seen that the evaluated results are well matched with FRDM predictions. As the RMF formalism is one of the most successful and acceptable tools [31], we choose it for our study. The RMF calculations give the basic idea about the nuclear field as well as the relation between the nucleon-nucleon interaction. They also provide other bulk properties, which help to know more about the nuclear structure. The binding energy observable plays a vital role in the stabilization of nuclei. Fig. 1 shows the total binding energy obtained in RMF formalism (black solid line with the circle), and the comparison with FRDM results (red solid line with square). The figure clearly shows that the B.E. obtained in both the RMF models and FRDM show a similar nature. In Fig. 2, the binding energy per particle (B.E./A) is shown concerning the neutron number$ (N) $ . The results by FRDM seem to represent the even-odd effects. However, the results by RMF do not observe this effect. Here, the B.E./A increases with an increase in the neutron number N and attains a peak value at A = 321 (N = 191, Z = 130). Thus, one may say that the$ ^{321}130 $ isotope is the most stable one in the isotopic chain of Z = 130.Fig. 3 shows the plot between the quadrupole deformation parameter (
$ \beta_{2} $ ) of super-heavy nuclei with Z = 130 nuclei as a function of the neutron number (N). The figure shows both the ground state as well as intrinsic excited-state properties, which are obtained from the RMF formalism throughout the isotopic chain (the black dotted line with the circle) [31]. The obtained results are compared with the FRDM results (red dashed line with square) [57]. The quadrupole moment derived from RMF formalism is well reproduced with the experimental data, as given in Ref. [33]. From the Fig. 3, it is clearly showing that the quadrupole deformations by RMF located at$ \beta_{2} = -0.47 $ for neutron number N = 209, 210 while the FRDM shows the prolate deformation value. Fig. 3 shows that$ \beta_2 $ values drastically change between N = 208 and N = 209, which is possibly the reason that shapes the transition from prolate to highly oblate shape. Hence, one can conclude that the ground-state average energy together with the deformations is model dependent. From this comparative study, all the isotopes of Z = 130 super-heavy nuclei are a highly deformed shape and matching well with the FRDM results.The nuclear radii for neutron
$ r_{n} $ (black solid line with the circle), proton$ r_{p} $ (red solid line with square), and matter distribution$ r_{m} $ (green solid line with the triangle), in RMF formalism is shown in Fig. 4 [31]. As expected, the radius of neutrons, protons, and also total radius enhances with the increase in neutron number of parent nuclei. The figure shows the nuclear radii are monotonically increasing till A = 310 and after that, it attains a high peak value at$ A = 338 $ $ (N = 208,Z = 130) $ . All the nuclear radii exhibit a similar behavior. There is no other information available for comparison.Separation energy is also an important discernible, where the magic number of nuclei can be identified. Thus, the separation energy can be evident to know about the magic number nuclei. In single-particle energy levels, the magic number of nuclei is identified by the large shell gap. A sudden fall in the neutron separation energy provides the exotic behavior, as it takes heed of even-odd effects. For that reason only, the study of two-neutron separation energy is more imperative. The two-neutron separation energy (
$ S_{2n} $ ) can be calculated from the variation in binding energies with the two isotopes by use of the relations,$ \begin{array}{l} S_{2n}(N,Z) = BE(N,Z)-BE(N-2,Z). \end{array} $

(9) The two-neutron separation energy (
$ S_{2n} $ ) for Z = 130 super-heavy nuclei within the range$ 310 \leqslant A \leqslant 340 $ are shown in Fig. 5 (black solid line with a circle shows the RMF value [31] and red solid line with the square shows FRDM values) [57] as a function of parent neutron number. From the Fig. 5, it is clearly shown that the neutron separation energy decreases with increase the neutron number except for the neutron number at$ N = 189, 209 $ $ (A = 319, 339) $ in the RMF model, whereas the FRDM model shows the peak at N = 202, 207. Here, we found a sudden sharp peak, possibly the reason for the shell closure. From the figure, it is clearly shown that at$ N = 209 $ the possible shell closure is there. Interestingly, from the figure, we may say that these neutron numbers are close to either N = 188 or 196 magic numbers. The microscopic RMF calculations for the two-neutron separation energy$ S_{2n} $ values are in good agreement with FRDM results. The differential variation of the$ S_{2n} $ has been observed in Fig. 6.The differential variation of the two-neutron separation energy
$ {\rm d}S_{2n} $ has been done concerning the parent neutron number (N) i.e.$ {\rm d}S_{2n}(Z,N) $ that can be written as,$ \begin{aligned} {\rm d}S_{2n}(Z,N) = \frac{S_{2n}(Z,N+2)-S_{2n}(Z,N)}{2}. \end{aligned} $

(10) The
$ {\rm d}S_{2n}(Z,N) $ is a meaningful aspect shown in Fig. 6 (black solid line with a circle shows the RMF value and red solid line with the square shows FRDM values) [31, 57] to obtain the nearby rate of change of separation energy as a function of neutron number of parent nuclei in an isotopic chain series. From the figure, we found that the calculated values for$ S_{2n} $ as well as$ {\rm d}S_{2n}(Z,N) $ by RMF theory coincide well with the FRDM data, and we find sharp peaks at$ N = 189 $ and 209 with local maxima. This clearly shows the possible shell closure at$ N = 209 $ in the neutron drip-line region of$ Z = 130 $ .With regard to the decay modes in SHN, the decay energy
$ Q_{\alpha} $ value is obtained from the same binding energy, calculated from RMF formalism. As α-decay is the major decay in SHN that provides useful information for the stability of nuclei, here we show the half-lives$ ({\rm log}_{10} T_{1/2}) $ as a function of the parent neutron number in Fig. 7. The α-decay half-lives are compared with the results obtained from Ref. [58] i.e., FRDM (black solid line with the circle) results with our calculated values by taking Q-values, obtained from RMF model using different formulae such as the Viola-Seaberg-Sobiczewski approach (red solid line with square), analytical formulas of Royer (green solid line with the left triangle), universal curve formula of Poenaru (blue solid line with the down triangle), universal decay law (violet dash line with a single dot), and spontaneous fission half live calculation (magenta solid line with the star) of odd-even nuclei. In Fig. 7, a systematic study of α-decay half-lives of super-heavy nuclei has been revealed. From the figure, it is clearly observed that the empirical formula according to experimental values is near to our calculated half-life values using our estimated Q-values. These investigations have been made to identify the mode of decay of these isotopes. The study reveals that the isotopes that fall within the mass range$ 310 \leqslant A \leqslant 328 $ undergo α-decay, while those at mass$ A\geqslant 329 $ do not survive fission and hence completely undergo SF. Moreover, as the density of a nucleus has gross information about the size, shape, and distribution of nucleons, one should perform the study of bubble structure [59]. However, the thorough investigation of bubble structures for the nuclei starting from Z = 105 – 118 along with the predicted proton magic Z = 120 in our earlier work [60] reveals that most of the nuclei achieve the prolate shape as their ground state solution in RMF calculations. In conclusion, we do not find a significant bubble structure, i.e., no good amount of depletion fraction is observed for that shape, except a few cases. Thus, from the above analysis, this reveals that α-decay and SF is the principal modes of decay in a majority of the isotopes of this super-heavy element Z = 130. Hence, the calculations for the α-decay and SF half-lives of Z = 130 may be of enormous use for further experimental analysis for the synthesis of new super-heavy isotopes. -
We analyzed the ground state properties like binding energy quadrupole deformation, nuclear radii, and other bulk properties of super-heavy nuclei with Z = 130 by using axially deformed RMF formalism with NL3 parametrization. From the B.E./A plot, we found that the A = 321 (N = 191, Z = 130) isotope is the most stable isotope in the isotopic chain series. From the obtained binding energy, we also calculated the two-neutron separation energy (
$ S_{2n} $ ) and differential form of two-neutron separation energy ($ {\rm d}S_{2n} $ ), which shows the possible major shell closure at N = 189, 209 for this isotopic chain series. From the deformation figure, we found that most of the configurations are suggested prolate in the ground state. The results produced by RMF are in good agreement with FRDM data. This states that the average energy of ground-state deformation is model dependent. Further, we have analytically evaluated the half-lives and presented absolute plausive decay modes of parametrization Z = 130 super-heavy nuclei in Table 1. Our deliberate decay energy$ Q_{\alpha} $ and half-life time$ T_{\alpha} $ are in good agreement with FRDM calculations. The alpha-decay and SF half-life study of Z = 130 super-heavy nuclei may be of great use for the prior experimental analysis in the super-heavy region.One of the authors, B.B. Sahu, highly acknowledges the support of Dr. S.K. Patra Associate Professor in Institute of Physics, Bhubaneswar, Odisha, India.
Structure and reaction dynamics of SHE Z = 130
- Received Date: 2019-05-17
- Available Online: 2019-10-01
Abstract: This study investigates the structural properties of super-heavy nuclei with Z = 130 by adopting the relativistic mean-field (RMF) theory within an axially deformed oscillator basis with the NL3 force parameter set. We study the binding energies, quadrupole deformation, nuclear radii, neutron separation energies, and other bulk properties. Moreover, we analyze the favorable decay modes for clear cognitive content of nuclei, such as alpha decay, using different formulae including the Viola-Seaberg, analytical formula of Royer, universal curve formula, and universal decay law. We compare these with the corresponding fission process. The spontaneous fission of super-heavy nuclei is studied with





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: